Open Access Article
Open Access ArticlePerformance optimization of perovskite solar cells with an automated spin coating system and artificial intelligence technologies†
Naoto
Eguchi
 *,
Taro
Fukazawa
*,
Taro
Fukazawa
 *,
Hiroyuki
Kanda
*,
Hiroyuki
Kanda
 ,
Kohei
Yamamoto
,
Kohei
Yamamoto
 ,
Takashi
Miyake
,
Takashi
Miyake
 and
Takurou N.
Murakami
*
and
Takurou N.
Murakami
*
National Institute of Advanced Industrial Science and Technology (AIST), Central 5, 1-1-1 Higashi, Tsukuba, Ibaraki 305-8565, Japan. E-mail: n-eguchi@aist.go.jp; taro.fukazawa@aist.go.jp; takurou-murakami@aist.go.jp
First published on 14th April 2025
Abstract
Organic–inorganic hybrid perovskite solar cells are promising candidates for application in next-generation solar technologies owing to their high power conversion efficiencies, suitability for deposition on flexible substrates, and low fabrication costs. Despite their potential, optimizing the relative proportions of organic and inorganic compounds in perovskite precursor solutions with appropriate process parameters, such as the coating speed and heating temperature, to achieve stable materials and high conversion efficiencies, remains challenging. Another issue is the performance reproducibility of perovskite solar cells, which often varies even when the same researcher prepares them. In this paper, we present a method for rapidly optimizing the composition of perovskites and the process conditions by integrating an automated spin-coating system with Bayesian optimization. Using only our own data in combination with Bayesian optimization, we adjusted four key parameters: the amounts of methylammonium chloride and lead iodide(II), rotation speed during spin-coating, and heating temperature to form the perovskite layer. After exploring only 0.36% of all the possible combinations, this method afforded a power conversion efficiency of 21.4%, which is higher than the efficiency of 20.5% that was previously achieved manually using the same materials. Time-resolved fluorescence spectra of multiple samples obtained during the Bayesian optimization cycle showed that the carrier lifetime increased as the optimization progressed. The integration of an automated spin-coating system with Bayesian optimization has been shown to be useful for optimizing the composition of perovskite precursor solutions and processing conditions.
Broader contextTo advance the development of high-efficiency perovskite solar cells, it is crucial to identify optimal conditions from the vast array of possible perovskite compositions and film formation process combinations. This study leverages Bayesian optimization to systematically and efficiently explore these complex parameter spaces. Using an automated spin-coating system previously developed in our team, which enabled precise addition of an anti-solvent during spin-coating, we minimized performance variation and collected high-quality experimental data. Through this approach, we identified a set of processing conditions that achieved a maximum power conversion efficiency of 21.4% after testing just 51 combinations. This work highlights the effectiveness of Bayesian optimization as a transformative tool for accelerating the discovery and optimization of materials in solar energy research. By streamlining the development of perovskite solar cells, this study contributes to advancing scalable, high-efficiency photovoltaic technologies, with significant potential for impacting future renewable energy systems. |
Introduction
Perovskite solar cells (PSCs), also known as organic–inorganic hybrid solar cells, have recently achieved power conversion efficiencies (PCEs) exceeding 25%, which represents a significant increase from the 3.8% they originally delivered.1–3 Along with their excellent optical and electrical properties, such as their high absorption coefficient in the ultraviolet-visible spectral region, high carrier mobility, and long electron–hole diffusion length, their suitability for deposition on flexible substrates and cost-effectiveness makes them promising candidates for application in next-generation solar cells. These cells feature light-absorbing layers composed of a blend of organic and inorganic materials. Selected physical properties, such as their band gaps and energy bands, are adjustable, leading to a diverse range of compositions that enhance their solar cell performance.4–6 However, the possible combinations of materials are vast,7,8 and optimized manufacturing conditions are necessary for each composition to maximize its potential. Optimizing such a high-dimensional parameter space remains a major challenge that would require considerable time and effort, even for skilled researchers.As a solution to these issues, machine learning has attracted considerable attention for the design of new materials, prediction of material properties, and optimization of conversion efficiency.9–11 In particular, Bayesian optimization has proven effective for optimization in high-dimensional spaces and has found successful application in various fields, including perovskite solar cell development.12–15 For example, Sun et al. performed Bayesian optimization using a combination of first-principles and high-throughput calculations to optimize the composition of CsxMAyFA1–x–yPbI3 and enabled them to discover stable halide perovskites.16 Liu et al. also developed a sequential learning framework using stochastic constraints to efficiently optimize the open-air process and this enabled them to develop perovskite solar cells with a PCE of 18.5%.17
Another approach involved conducting high-throughput and automated experiments using robots to accelerate the development of materials.18–21 Recently, studies in which these methods were used to develop perovskite solar cells were reported.22–28 For example, Meftahi and co-workers optimized the material composition and process conditions of quasi-two-dimensional (2D) Ruddlesden–Popper PSCs using high-throughput experiments and a machine-learning technique, and identified conditions that resulted in a PCE of 16.9%.29 Zhang and co-workers optimized the manufacturing parameters of perovskite thin films using an automated spin-coating platform to achieve an efficiency of 21.6%.30
In addition to the complex optimization problem, the reproducibility of PSC performance is also problematic. The antisolvent method, a PSC fabrication technique, is an effective approach for producing PSCs with high PCE in a single step during the spin-coating process.31–33 Despite its simplicity and widespread adoption in many laboratories, the PCE can vary owing to slight differences in the antisolvent drop timing and rate of antisolvent dropping.34–36 This variation is one of the factors that adversely affect the reproducibility in the production of PSCs using the antisolvent method. Many studies have been conducted to improve the reproducibility of the antisolvent method.37–39 However, performance discrepancies may arise not only between different researchers, but also within batches produced by the same researcher. To address this issue, our group developed an automated spin-coating system that enhanced the consistency of PSC production by automating critical steps like antisolvent drops, substrate transport, and heating while the perovskite layer is being deposited via spin-coating.40 This automated system is expected to effectively eliminate human factors from the production of PSCs, thereby reducing performance variations within batches.
In this study, we simultaneously optimized the composition of the perovskite precursor solution and the process conditions by integrating our automated spin-coating system with Bayesian optimization. Specifically, we focused on optimizing four parameters: the concentrations of lead(II) iodide (PbI2) and methylammonium chloride (MACl) in the precursor solution, maximum spin-coating speed, and temperature at which the perovskite layer was annealed. Using this approach, the champion cell achieved a PCE of 21.4% by sampling only 0.36% of all the possible experimental conditions. Time-resolved fluorescence spectra of multiple samples during the Bayesian optimization cycle showed that the carrier lifetime increased as the optimization was progressively refined. This high PCE exceeds that of solar cells previously optimized using the same perovskite materials without automation and optimization. The integration of an automated spin-coating system with Bayesian optimization was demonstrated to be useful for optimizing the composition of perovskite precursor solutions and process conditions.
Experimental
Materials
FTO glass (thickness = 1.6 mm; sheet resistance ≤10 ohm per square) was acquired from Nippon Sheet Glass. The SnO2 colloidal solution (8% in H2O colloidal dispersion) was purchased from Taki Chemical Co., Ltd. Formamidine hydroiodide (FAI; >98.0%), lead(II) iodide (PbI2, >99.99%), methylamine hydrochloride (MACl, >99.0%), 4-tert-butylpyridine (tBP, >96.0%), and n-octylammonium iodide (OAI, >98.0%) were purchased from Tokyo Chemical Industry Co. Ltd. N,N-Dimethylformamide (anhydrous, 99.8%), dimethyl sulfoxide (anhydrous, >99.9%), bis(trifluoromethane) sulfonamide lithium salt (LiTFSI), FK 209 Co(III) TFSI salt (CoTFSI, 98%), and chlorobenzene (anhydrous, 99.8%) were purchased from Sigma-Aldrich. Diethyl ether (super dehydrated, 99.5%) was purchased from FUJIFILM Wako Pure Chemical Corporation. 2,2′,7,7′-Tetrakis(N,N-di-p-methoxyphenylamino)-9,9′-spirobifluorene (spiro-OMeTAD, 99.9%) was purchased from Nippon Fine Chemical Co., Ltd. All materials were used as received without further purification.Device fabrication
The device structure was FTO/SnO2/CsAPbI3/OAI/spiro-OMeTAD/Au. Before use, the bare FTO glass substrates were subjected to ultraviolet (UV) ozone treatment for 30 min. A layer of SnO2 (4%, diluted with DI water) was then deposited on the FTO via spin-coating at 3000 revolutions per minute (rpm) for 20 s and annealed in ambient air at 150 °C for 30 min. The perovskite precursor solution was prepared according to the conditions obtained via Bayesian optimization and the work was conducted in a glove box. The perovskite precursor solution was spin-coated using the following sequence: static time 20 s, slope 2 s, and spinning at 1000 rpm for 10 s; slope 2 s, 6000 rpm for 30 s, and slope 3 s. During the spin-coating step, 0.5 mL of diethyl ether was dropped onto the precursor using an automatic solution-dropping device after applying the maximum rotational speed for 14 s. After spin-coating, the substrates were annealed on a hot plate at 70−150 °C for 5 min. After annealing, the substrate was allowed to cool to room temperature (approximately 25 °C) and spin-coated with a 39 mM OAI/IPA solution at 4000 rpm for 20 s. The OAI layer was annealed at 100 °C for 5 min. The solution for the hole transport layer was prepared by dissolving 100.0 mg of spiro-OMeTAD, 8.7 mg of LiTFSI, 9.3 mg of CoTFSI, and 39.0 mL of tBP in 1.279 mL of chlorobenzene. The solution was spin-coated at 4000 rpm for 20 s. The hole transport layer was annealed at 65 °C for 10 min. Finally, Au was thermally deposited as the top layer of the cell to form the back electrode. All layers were deposited in a dry-air atmosphere.Characterization
AM1.5 pseudo-solar light (100 mW cm−2) was generated using a solar simulator equipped with a xenon lamp (Bunkou Keiki Co., Ltd). Standard silicon solar cells were used to calibrate the incident light intensity. The cells fitted with KG-5 filters were produced by the Japan Quality Assurance Organization. The current–voltage (J–V) curves were generated using a direct-current voltage/current source monitor (Keithley, 2401) at a scan rate of 100 mV s−1. All devices were characterized using a 0.157 cm2 metal aperture to precisely define the effective measurement area. White light interference microscopy was performed using a VKX-3000 microscope (Keyence). Steady-state and time-resolved PL spectral measurements were performed using a Fluorolog-QM spectrofluorometer (HORIBA Scientific). The excitation wavelength for steady-state PL spectra was 500 nm. The PL lifetimes were measured using a time-correlated single-photon counting system, and fitting was performed to calculate the carrier lifetime using the software supplied with the Fluorolog-QM. Incident photon-to-current efficiency (IPCE) spectra were acquired using an HQE-25D (Bunkoukeiki Co., Ltd). UV-vis measurements were recorded using a UV3600 spectrometer (Shimadzu). Scanning electron microscopy (SEM) images were captured using an SU9000 instrument (Hitachi High-Tech Corporation). XRD measurements were performed by using a SmartLab with Cu Kα radiation (λ = 1.5406 Å) (Rigaku). The scan rate is 8° min−1 at a step of 0.01°. Photoelectron yield spectroscopy measurement was performed by using a BIP-KV100 (Bunkoukeiki Co., Ltd). Measurements were carried out under vacuum conditions.Bayesian optimization
To maximize PCE, we employed Bayesian optimization to systematically refine the material composition and process conditions by optimizing each parameter. This scheme involves constructing a stochastic model using a Gaussian process with a radial basis function kernel and suggests candidates that can maximize the PCE with a small number of experiments. Here, we used the PHYSBO package,41 and adopted a strategy known as Thompson sampling, which balances prediction-based and exploration-oriented recommendations.Results and discussion
Selection of optimization parameters
The machine-learning-assisted experiment was initiated by identifying the critical process parameters for optimization, along with their respective constraints. The selected process parameters included the spin-coating speed and annealing temperature that were used to prepare the perovskite layer. The spin-coating speed, which influences the film thickness, was increased from 2000 to 6000 rotation per minute (rpm) in increments of 500 rpm. The annealing temperature, which affects the crystallization of the perovskite layer, was adjusted between 70 °C and 150 °C in 10 °C increments. These parameters were chosen because of their known significant ability to enhance the efficiency of PSCs. In addition, the material composition parameters, specifically the molar percentages (mol%) of MACl and PbI2 relative to that of FAI, were optimized. The amount of MACl, which improved the crystallinity and grain orientation of the perovskite films, was varied from 0 to 80 mol% in 5% increments. The amount of PbI2 was adjusted from 80 to 140 mol% in increments of 5 mol%, as many researchers have reported its effect on the performance of PSCs.42–44 Based on this setup, a parameter space comprising 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 901 possible combinations (9 × 9 × 17 × 13) was defined, as shown in Fig. 1a. To minimize the bias of the initial dataset, the chemist randomly selected 20 combinations of conditions for device fabrication (Fig. 1b).
901 possible combinations (9 × 9 × 17 × 13) was defined, as shown in Fig. 1a. To minimize the bias of the initial dataset, the chemist randomly selected 20 combinations of conditions for device fabrication (Fig. 1b).
 | ||
| Fig. 1 (a) The parameter types to be optimized and the upper and lower limits for each parameter; (b) list of experimental conditions for the initial data. | ||
Spin-coating automation system
We employed the automated spin-coating system that was previously developed by our team for the fabrication of perovskite solar cells (Fig. 2a). This system automates substrate transport, spin-coating, antisolvent dropping, and substrate heating, thereby minimising variations in the device performance attributable to human factors. It precisely controls the timing of the antisolvent drop during spin-coating, as well as the interval between the end of the spin-coating step and the start of the annealing step on the hot plate. This automation ensures that reproducible data are generated with low noise, an essential requirement for machine-learning analyses. The architecture of the perovskite solar cells used in this study is illustrated in Fig. 2b. Tin oxide (SnO2), which has a deeper conduction band and higher electrical mobility than TiO2, was employed as the electron transport layer. CsFAPbI3, a perovskite layer comprising a combination of FAPbI3 with cesium, was used because it has better thermal stability compared to MAPbI3. As the passivation layer, we selected the widely used n-octylammonium iodide (OAI).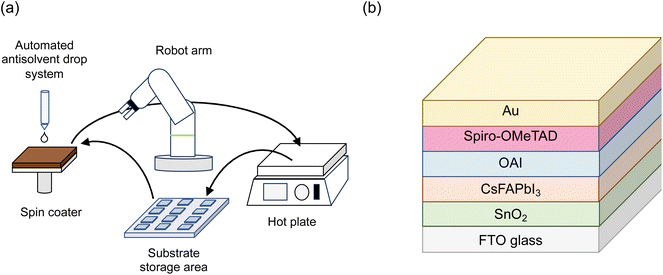 | ||
| Fig. 2 (a) Schematic of the automated spin-coating system; (b) architecture of the solar cell fabricated in this experiment. | ||
Solar cell performances with the automated spin coating system and Bayesian optimization
The solar cells that were fabricated in the initial phase under 20 different conditions using the automated spin-coating system achieved a maximum PCE of 12.6%. Aiming to improve the PCE beyond this level, we employed the Bayesian optimization scheme by starting with the dataset generated with the initial 20 conditions. In each step, five new conditions were proposed by the Bayesian optimization process. These conditions were then used to fabricate new solar cells of which the performance parameters were measured. The measurement results obtained in this way were fed back into the model and used to recommend new conditions for the next step. This iterative feedback process was designed to improve the efficiency of solar cells by refining the experimental conditions.Fig. 3 illustrates the progression of the PCE in the reverse scans up to the 9th cycle of the Bayesian optimization process. By the end of the 9th cycle, 65 different sets of experimental conditions had been tested. The PCE of the champion cell in each cycle and the corresponding fabrication conditions are listed in Table 1. In the last row of Table 1, we show the conditions we previously optimized with the same combination of materials (reference condition), as well as the highest PCE of the solar cells produced under these conditions. Table S1† provides a comprehensive list of these conditions and the corresponding photovoltaic performances. The results of this cycle showed that the highest conversion efficiency for the data collected in the initial experimental phase was 12.6%, whereas the highest efficiency of 21.4% was achieved in the 7th cycle by repeating the Bayesian optimization loop. The gradual increase in the efficiency across successive cycles highlighted the ability of optimization to continuously refine the experimental conditions. Fig. S1–S3† show the progression of the short-circuit current density, open-circuit voltage, and fill factor. Interestingly, some conditions, specifically #44 and #62, resulted in a significantly lower efficiency. These results can be attributed to the use of exploratory conditions within the Bayesian optimization framework. After achieving 21.4% under the #51 condition of the 7th cycle, the Bayesian optimization cycle was repeated through the 8th and 9th cycles. However, as the maximum PCE did not improve, the optimization cycle was stopped after the 9th cycle.
 | ||
| Fig. 3 Progression of power conversion efficiency in the reverse scan from the initial data to the 9th cycle. Five new experimental conditions were added per cycle. | ||
| Condition | Cycle | Condition | Champion cell PCE (%) | |||
|---|---|---|---|---|---|---|
| Process conditions | Material conditions | |||||
| Spin-coating speed (rpm) | Annealing temperature (°C) | MACl (mol%) | PbI2 (mol%) | |||
| #20 | Initial | 6000 | 150 | 80 | 140 | 12.6 (12.5 ± 0.1) |
| #25 | 1st cycle | 6000 | 150 | 80 | 130 | 14.3 (13.4 ± 0.9) |
| #26 | 2nd cycle | 5000 | 150 | 50 | 130 | 19.0 (18.6 ± 0.6) |
| #35 | 3rd cycle | 5000 | 150 | 50 | 135 | 19.2 (18.8 ± 0.4) |
| #36 | 4th cycle | 5000 | 150 | 35 | 130 | 20.0 (19.7 ± 0.2) |
| #45 | 5th cycle | 5000 | 150 | 35 | 135 | 20.1 (18.9 ± 0.9) |
| #49 | 6th cycle | 5000 | 150 | 30 | 130 | 20.9 (20.3 ± 0.4) |
| #51 | 7th cycle | 6000 | 140 | 25 | 125 | 21.4 (20.7 ± 0.5) |
| #57 | 8th cycle | 6000 | 140 | 20 | 135 | 20.7 (19.6 ± 1.1) |
| #65 | 9th cycle | 6000 | 150 | 25 | 130 | 21.1 (20.9 ± 0.2) |
| Reference | — | 6000 | 150 | 9.4 | 115 | 20.5 (20.0 ± 0.4) |
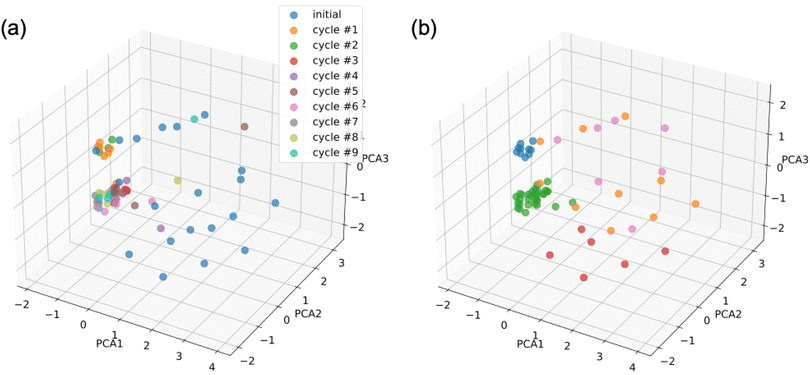
Fig. 4 shows the distribution of conditions in three-dimensional space reduced from the original space using principal component analysis (PCA). PCA is a method for reducing the dimensions of high-dimensional data and finding new axes (principal component) that maximize the variance of the data. This allows data to be visualized efficiently while retaining their characteristics. The figure on the left shows the cycle in which the data were obtained. The initial data are uniformly distributed in the search space. Data resulting from Bayesian optimization tend to combine and form clusters. The figure on the right shows the cluster structure of the data obtained by dividing them into five groups using Ward's method. Ward's method is a clustering approach for combining two clusters that minimizes the change in variation before and after combining, considering the variation in samples within the cluster.45 Two clusters (blue and green) could be distinguished. The remaining uniformly distributed initial data were separated into three regions, owing to the simplicity of the clustering method.
These two figures show the transition from the initial search stage to the stage in which the model was employed. The recommendations in the first two cycles (cycles #1 and #2) were trapped in a local pseudo-maximum region (corresponding to the blue cluster in the figure on the right) and converged to a system with an efficiency of less than 20%. After these two cycles, the Bayesian scheme conducted a global search by exploring the other unexamined conditions in the search space. Ultimately, the scheme examined and converged to the green region in the figure on the right, where the maximum score was obtained.
For several sets of conditions generated during the optimization cycle, charge recombination in the perovskite film was investigated using steady-state and time-resolved fluorescence spectroscopy. The samples for the PL measurements were prepared by spin-coating the perovskite layer on a glass substrate. These results showed that the maximum emission wavelengths of #22, #48, #51, #55, #60, and the reference were 798, 800, 799, 800, 801, and 803 nm, respectively (Fig. 5a). The time-resolved PL (TRPL) spectra were analyzed by fitting a double exponential decay model of the form I(τ) = A1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−τ/τ1) + A2
exp(−τ/τ1) + A2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−τ/τ2) (Fig. 5b). The fitting results for each film were then used to derive the fluorescence lifetime of the perovskite film fabricated under condition #51, which had the highest PCE. The fluorescence lifetime of approximately 5400 ns of the film fabricated under condition #51 indicated a longer carrier lifetime than that of the perovskite films fabricated under the other conditions. The rapid decay component (τ1) is associated with surface recombination, whereas the slow decay component (τ2) is associated with bulk recombination in perovskite structures.46 The extended τ1 and τ2 observed under condition #51 indicate that both surface and bulk recombination are minimized in the optimized perovskite film, effectively reducing non-radiative deactivation processes.
exp(−τ/τ2) (Fig. 5b). The fitting results for each film were then used to derive the fluorescence lifetime of the perovskite film fabricated under condition #51, which had the highest PCE. The fluorescence lifetime of approximately 5400 ns of the film fabricated under condition #51 indicated a longer carrier lifetime than that of the perovskite films fabricated under the other conditions. The rapid decay component (τ1) is associated with surface recombination, whereas the slow decay component (τ2) is associated with bulk recombination in perovskite structures.46 The extended τ1 and τ2 observed under condition #51 indicate that both surface and bulk recombination are minimized in the optimized perovskite film, effectively reducing non-radiative deactivation processes.
 | ||
| Fig. 5 (a) Fluorescence spectrum of the perovskite layer under each condition. (b) Time-resolved fluorescence spectrum of the perovskite layer. | ||
The τ1 of the perovskite layer fabricated under condition #51 annealed at 140 °C is approximately 350 ns longer than that of the perovskite layer fabricated under condition #60 annealed at 150 °C. In addition, samples #22, #48, and #55 were prepared using different MACl concentrations. The film fabricated under condition #48 with 20 mol% MACl, which had the highest PCE, had a longer τ2 lifetime, suggesting that recombination in the bulk was suppressed. These results show that the quality of the perovskite layer improves as the PCE is optimized using Bayesian optimization with the aim of maximising the PCE. In other words, one of the reasons why the PCE increased was that the quality of the perovskite Table 2 layer improved, and the carrier lifetime increased as the annealing temperature, MACl, and PbI2 concentrations were optimized by Bayesian optimization.
| Condition | Spin-coating speed (rpm) | Annealing temperature (°C) | MACl (mol%) | PbI2 (mol%) | J SC (mA cm−2) | V OC (V) | FF | PCE (%) | τ 1 (ns) | τ 2 (ns) |
|---|---|---|---|---|---|---|---|---|---|---|
| #22 | 6000 | 150 | 80 | 135 | 23.08 | 0.906 | 0.676 | 14.1 | 3303 | 4105 |
| #48 | 6000 | 150 | 20 | 135 | 23.49 | 1.123 | 0.791 | 20.9 | 3903 | 9100 |
| #51 | 6000 | 140 | 25 | 125 | 23.55 | 1.119 | 0.811 | 21.4 | 5407 | 8113 |
| #55 | 6000 | 150 | 25 | 135 | 23.54 | 1.117 | 0.766 | 20.2 | 4073 | 6934 |
| #60 | 6000 | 150 | 25 | 125 | 23.12 | 1.112 | 0.793 | 20.4 | 5048 | 8293 |
| reference | 6000 | 150 | 9.4 | 115 | 23.70 | 1.080 | 0.800 | 20.5 | 3548 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 617 617 |
Other reasons for the improvement in the conversion efficiency via Bayesian optimization were examined by analysing the surface roughness of the perovskite film that was prepared under the conditions that yielded the highest PCE through Bayesian optimization and, for reference purposes, under the conditions we had previously optimized. Fig. 6 shows white light interference microscopy images of the perovskite layer. The area of analysis was 64 mm2. The arithmetic mean height Sa, which is one of the two-dimensional surface roughness indicators, is defined by using the following equation.
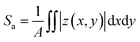 | (1) |
 | (2) |
 | ||
| Fig. 6 White light interference micrographs of the perovskite layer spin-coated under the optimized conditions (a) and reference conditions (b). | ||
Fig. 7a shows the J–V curves of solar cells fabricated under the best conditions (#51) optimized by Bayesian optimization compared with those of the solar cell fabricated under the conditions we previously optimized using the same combination of materials. Table 3 lists the solar cell parameters of the best cell under each condition. The solar cell fabricated under condition #51 had a short-circuit current density of 23.6 mA cm−2, an open-circuit voltage of 1.12 V, a fill factor of 0.81, and a PCE of 21.4%. On the other hand, the solar cell fabricated under the conditions we had previously optimized had a short-circuit current density of 23.7 mA cm−2, an open-circuit voltage of 1.08 V, and a fill factor of 0.80, with a PCE of 20.5%. Although the short-circuit current densities (JSC) of both of these solar cells were similar, the solar cells optimized via Bayesian optimization exhibited improved open-circuit voltages. The improvements in VOC and FF suggest that charge recombination is suppressed at the interfaces, an important factor for improving the efficiency. This finding is consistent with the TRPL results. It is important to note that these comparisons must be interpreted with caution because of the differences in the amount of MACl added under each condition. Despite these differences, the observed improvements in the photovoltaic performance parameters indicate the effectiveness of the Bayesian optimization method in refining the composition and process conditions.
| Condition | Scan direction | J SC (mA cm−2) | V OC (V) | FF | PCE (%) |
|---|---|---|---|---|---|
| #51 | Forward | 23.6 | 1.10 | 0.70 | 18.0 |
| Reverse | 23.6 | 1.12 | 0.81 | 21.4 | |
| Reference | Forward | 23.7 | 1.07 | 0.73 | 18.6 |
| Reverse | 23.7 | 1.08 | 0.80 | 20.5 |
Fig. 7b shows the IPCE spectra of solar cells fabricated under each condition. The current density calculated from the IPCE spectra was 23.3 mA cm−2 for the solar cell fabricated under conditions #51 and 23.5 mA cm−2 for the solar cell fabricated under the reference conditions. This result is consistent with the current density obtained from the J–V measurement.
Fig. S4† compares the UV-vis absorption spectra of the perovskite layers fabricated under condition #51 and the reference condition. These spectra of each perovskite layer indicated that the long wavelength side of the onset wavelengths is the same for both the reference condition and condition #51, indicating that the band gap of each perovskite layer is the same. Fig. S5† shows the photoelectron yield spectroscopy (PYS) measurement of the perovskite film prepared under reference conditions and condition #51. As shown in Fig. S5,† the HOMO energy level of the reference perovskite film is −5.75 eV, and that of the perovskite film fabricated under condition #51 is −5.52 eV. From the PYS measurement of the hole transport layer (spiro-OMeTAD) shown in Fig. S5(c),† the HOMO level of the hole transport layer is −5.45 eV, so it was found that the perovskite film prepared under condition #51 has an energy level closer to that of the hole transport layer. The SEM images (top and cross-sectional views) of the solar cells fabricated under each condition are shown in Fig. S6.† The cross-sectional image shows that the perovskite layer fabricated under condition #51 is slightly thicker than the perovskite layer fabricated under the reference conditions.
XRD spectra of the perovskite film prepared under condition #51 and reference conditions were measured. The perovskite films used for the measurement were spin-coated on an FTO/SnO2 substrate. XRD spectra and peak information are shown in Fig. S7 and Table S2.† The peak at around 12.6° is derived from the (001) plane of PbI2, and the peak at around 13.9° is derived from the (110) plane of CsFAPbI3. The intensity of the two peaks was almost the same, and the full width at half maximum (FWHM) was approximately the same. The peak derived from PbI2 was higher in the #51 film, which is due to the higher concentration of PbI2 used in the precursor solution than in the reference. These results suggest that the crystallinity of the perovskite films prepared under the reference conditions and condition #51 is almost the same.
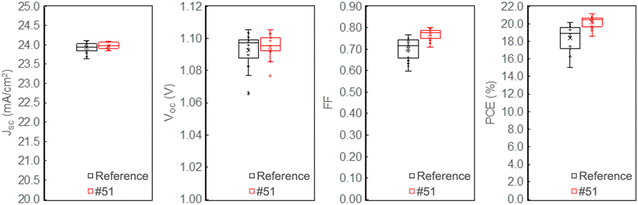
Finally, we evaluated the variations in the solar cell parameters between the reference and optimized devices by increasing the sample size for comparison. Fig. 8 presents a box-plot diagram illustrating the distribution of the various solar cell parameters for devices fabricated under the reference conditions and condition #51. The black boxes correspond to the reference conditions, while the red boxes represent condition #51. Table 4 lists the average values and standard deviations of the 18 cells for each solar cell parameter. These results show that devices fabricated under the optimized conditions have improved short-circuit current density, open-circuit voltage, and fill factor values compared with devices fabricated under the reference conditions. Additionally, all the solar-cell parameters of the optimized devices varied to a lesser extent compared with those of the reference device. This shows that solar cells fabricated under optimized conditions not only have improved PCE but the performance variability between devices is reduced.
| Condition | J SC (mA cm−2) | V OC (V) | FF | PCE (%) |
|---|---|---|---|---|
| #51 | 23.98 ± 0.08 | 1.095 ± 0.007 | 0.77 ± 0.02 | 20.2 ± 0.7 |
| Reference | 23.93 ± 0.13 | 1.092 ± 0.011 | 0.70 ± 0.05 | 18.3 ± 1.4 |
In summary, the process conditions and composition optimized by Bayesian optimization were as follows: the spin-coating rotation speed of the perovskite layer was 6000 rpm, the heating temperature was 140 °C, the concentration of MACl was 20 mol% relative to FAI, and the concentration of PbI2 was 125 mol% relative to FAI. Compared to our previously optimized conditions, the spin-coating rotation speed remained unchanged, while the annealing temperature was reduced by 10 °C. Additionally, the concentrations of MACl and PbI2 were both increased. Regarding the impact of these conditions, the spin-coating rotation speed is primarily associated with the film thickness, which remained optimal at 6000 rpm.
Furthermore, increasing the concentrations of MACl and PbI2 contributed to an improvement in initial device performance. While previous studies have reported that moderate MACl addition enhances perovskite crystallinity and grain orientation, our XRD spectra (Fig. S6†) did not show a notable improvement in crystallinity. However, excess PbI2 has been reported to provide a passivation effect, which aligns with our time-resolved PL spectral results indicating extended carrier lifetimes.
Conclusion
This study was aimed at improving the PCE of perovskite solar cells by optimizing the composition and process conditions, and this was achieved by using an automated spin-coating system and Bayesian optimization. Based on the first 20 different data points collected, a Bayesian optimization approach was used to output new conditions that would maximize PCE. Then, solar cells were fabricated using the proposed conditions, and the results obtained from these measurements were again used as the input for processing with Bayesian optimization to generate newly refined output conditions. Eventually, the 65th set of conditions yielded results with enhanced performance, which exceeded that obtained under the previously optimized conditions, and the highest PCE of 21.4% was obtained with the 51st set of conditions. This was higher than the efficiency of the reference device manufactured using previously optimized conditions and the same combination of materials (20.5%). Time-resolved fluorescence spectroscopy measurements of several samples during Bayesian optimization showed that the carrier lifetime of the perovskite layer increased as the optimization progressed. In addition, the perovskite layer fabricated under the conditions that achieved the highest PCE had a lower surface roughness over a wide area. Thus, the improvement in PCE achieved via Bayesian optimization was due to the improvement in the quality of the perovskite film. Furthermore, when multiple devices were fabricated under the optimized conditions found in this study, the performance variation was suppressed compared to that obtained under the previously optimized conditions. This result emphasizes the effectiveness of using Bayesian optimization to explore optimal compositions and manufacturing processes and offers great potential for the selection of materials and identification of optimal conditions for perovskite solar cells. The automated spin-coating system and machine-learning approach presented herein are expected to facilitate the discovery of highly efficient and stable perovskite materials. This approach is expected to greatly benefit the scientific study of photovoltaic materials and optimization of perovskite solar cells with more complex compositions.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This study was supported by the New Energy and Industrial Technology Development Organization (NEDO, JPNP21016).References
- A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, J. Am. Chem. Soc., 2009, 131, 6050–6051 CrossRef CAS PubMed.
- M. M. Lee, J. Teuscher, T. Miyasaka, N. T. Murakami and J. H. Snaith, Science, 2012, 338, 643–647 CrossRef CAS PubMed.
- Y. Zhao, F. Ma, Z. Qu, S. Yu, T. Shen, H.-X. Deng, X. Chu, X. Peng, Y. Yuan, X. Zhang and J. You, Science, 2022, 377, 531–534 CrossRef CAS PubMed.
- K. L. Ono, J. E. Juarez-Perez and Y. Qi, ACS Appl. Mater. Interfaces, 2017, 9, 30197–30246 CrossRef PubMed.
- J. H. Noh, S. H. Im, J. H. Heo, T. N. Mandal and S. I. Seok, Nano Lett., 2013, 13(4), 1764–1769 CrossRef CAS PubMed.
- B. Suarez, V. Gonzalez-Pedro, S. T. Ripolles, S. R. Sanchez, L. Otero and I. Mora-Sero, J. Phys. Chem. Lett., 2014, 5, 1628–1635 CrossRef CAS PubMed.
- W.-J. Yin, B. Weng, J. Ge, Q. Sun, Z. Li and Y. Yan, Energy Environ. Sci., 2019, 12, 442–462 RSC.
- T. Nakajima and K. Sawada, J. Phys. Chem. Lett., 2017, 8, 4826–4831 CrossRef CAS PubMed.
- T. K. Butler, W. D. Davies, H. Cartwright, O. Isayev and A. Walsh, Nature, 2018, 559, 547–555 CrossRef PubMed.
- R. Gómez-Bombarelli, J. Aguilera-Iparraguirre, D. T. Hirzel, D. Duvenaud, D. Maclaurin, A. M. Blood-Forsythe, S. H. Chae, M. Einzinger, D.-G. Ha, T. Wu, G. Markopoulos, S. Jeon, H. Kang, H. Miyazaki, M. Numata, S. Kim, W. Huang, I. S. Hong, M. Baldo, P. R. Adams and A. Aspuru-Guzik, Nat. Mater., 2016, 15, 1120–1127 CrossRef PubMed.
- Q. Tao, P. Xu, M. Li and W. Lu, npj Comput. Mater., 2021, 7(1), 23 CrossRef.
- A. Seko, A. Togo, H. Hayashi, K. Tsuda, L. Chaput and I. Tanaka, Phys. Rev. Lett., 2015, 115(20), 205901 CrossRef PubMed.
- I. P. Frazier and J. Wang, Information science for materials discovery and design, 2016, vol. 225, pp. 46–75 Search PubMed.
- S. Greenhill, S. Rana, S. Gupta, P. Vellanki and S. Venkatesh, IEEE Access, 2020, 8, 13937–13948 Search PubMed.
- K. Tsoi and S. Yerci, Adv. Theory Simul., 2024, 7(4), 2301013 CrossRef CAS.
- S. Sun, A. Tiihonen, F. Oviedo, Z. Liu, J. Thapa, Y. Zhao, P. T. N. Hartono, A. Goyal, T. Heumueller, C. Batali, A. Encinas, J. J. Yoo, R. Li, Z. Ren, M. I. Peters, J. C. Brabec, G. M. Bawendi, V. Stevanovic, J. Fisher and T. Buonassisi, Matter, 2021, 4, 1305–1322 CrossRef CAS.
- Z. Liu, N. Rolston, C. A. Flick, W. T. Colburn, Z. Ren, H. R. Dauskardt and T. Buonassisi, Joule, 2022, 6, 834–849 CrossRef CAS.
- B. Burger, M. P. Maffettone, V. V. Gusev, M. C. Aitchison, Y. Bai, X. Wang, X. Li, M. B. Alston, B. Li, R. Clowes, N. Rankin, B. Harris, S. R. Sprick and I. A. Cooper, Nature, 2020, 583, 237–241 CrossRef CAS PubMed.
- J. N. Szymanski, B. Rendy, Y. Fei, E. R. Kumar, T. He, D. Milsted, J. M. Mcdermott, M. Gallant, D. E. Cubuk, A. Merchant, H. Kim, A. Jain, J. C. Bartel, K. Persson, Y. Zeng and G. Ceder, Nature, 2023, 624, 86–91 CrossRef PubMed.
- O. E. Pyzer-Knapp, W. J. Pitera, J. W. P. Staar, S. Takeda, T. Laino, P. D. Sanders, J. Sexton, R. J. Smith and A. Curioni, npj Comput. Mater., 2022, 8, 84 CrossRef.
- M. Kodera and K. Sayama, Digital Discovery, 2023, 2, 1683–1687 RSC.
- X. Du, L. Lüer, T. Heumueller, J. Wagner, C. Berger, T. Osterrieder, J. Wortmann, S. Langner, U. Vongsaysy, M. Bertrand, N. Li, T. Stubhan, J. Hauch and J. C. Brabec, Joule, 2021, 5, 495–506 CrossRef CAS.
- E. Gu, X. Tang, S. Langner, P. Duchstein, Y. Zhao, I. Levchuk, V. Kalancha, T. Stubhan, J. Hauch, J. H. Egelhaaf, D. Zahn, A. Osvet and J. C. Brabec, Joule, 2020, 4, 1806–1822 CrossRef CAS.
- K. Higgins, M. Ziatdinov, V. S. Kalinin and M. Ahmadi, J. Am. Chem. Soc., 2021, 143, 19945–19955 CrossRef CAS PubMed.
- S. Chen, L. Zhang, Y. Liu, Z. Zhang, Y. Li, W. Cai, H. Lv, Y. Qin, Q. Liao, B. Zhou, T. Yan, J. Ren, S. Chen, X. Xiang, S. Dai, K. S. So, X. Wang, S. Yang and B. Xu, J. Mater. Chem. A, 2021, 9, 25502–25512 RSC.
- P. B. Macleod, L. G. F. Parlane, D. T. Morrissey, F. Häse, M. L. Roch, E. K. Dettelbach, R. Moreira, E. P. L. Yunker, B. M. Rooney, R. J. Deeth, V. Lai, J. G. Ng, H. Situ, H. R. Zhang, S. M. Elliott, H. T. Haley, J. D. Dvorak, A. Aspuru-Guzik, E. J. Hein and P. C. Berlinguette, Sci. Adv., 2020, 6, eaaz8867 CrossRef PubMed.
- S. Chen, Y. Hou, H. Chen, X. Tang, S. Langner, N. Li, T. Stubhan, I. Levchuk, E. Gu, A. Osvet and J. C. Brabec, Adv. Energy Mater., 2018, 8, 1701543 CrossRef.
- J. Zhang, J. Wu, A. Barabash, T. Du, S. Qiu, L. M. V. Corre, Y. Zhao, K. Zhang, F. Schmitt, Z. Peng, J. Tian, C. Li, C. Liu, T. Heumueller, L. Lüer, A. J. Hauch and J. C. Brabec, Energy Environ. Sci., 2024, 17, 5490–5499 RSC.
- N. Meftahi, A. M. Surmiak, O. S. Fürer, J. K. Rietwyk, J. Lu, R. S. Raga, C. Evans, M. Michalska, H. Deng, P. D. Mcmeekin, T. Alan, D. Vak, S. R. A. Chesman, J. A. Christofferson, A. D. Winkler, U. Bach and P. S. Russo, Adv. Energy Mater., 2023, 13(38), 2203859 CrossRef CAS.
- J. Zhang, B. Liu, Z. Liu, J. Wu, S. Arnold, H. Shi, T. Osterrieder, A. J. Hauch, Z. Wu, J. Luo, J. Wagner, G. C. Berger, T. Stubhan, F. Schmitt, K. Zhang, M. Sytnyk, T. Heumueller, M. C. Sutter-Fella, M. I. Peters, Y. Zhao and J. C. Brabec, Adv. Energy Mater., 2023, 13(48), 2302594 CrossRef CAS.
- J. N. Jeon, H. J. Noh, C. Y. Kim, S. W. Yang, S. Ryu and I. S. Seok, Nat. Mater., 2014, 13, 897–903 CrossRef PubMed.
- M. Xiao, F. Huang, W. Huang, Y. Dkhissi, Y. Zhu, J. Etheridge, A. Gray-Weale, U. Bach, Y. B. Cheng and L. Spiccia, Angew. Chem., Int. Ed., 2014, 53, 9898–9903 CrossRef CAS PubMed.
- S. Ghosh, S. Mishra and T. Singh, Adv. Mater. Interfaces, 2020, 7, 2000950 CrossRef CAS.
- J. Kumar, R. Kumar, K. Frohna, D. Moghe, D. S. Stranks and M. Bag, Phys. Chem. Chem. Phys., 2020, 22, 26592–26604 RSC.
- Q. An, L. Vieler, P. K. Goetz, O. Telschow, J. Y. Hofstetter, R. Buschbeck, D. A. Taylor and Y. Vaynzof, Adv. Energy Sustainability Res., 2021, 2, 2100061 CrossRef CAS.
- D. A. Taylor, Q. Sun, P. K. Goetz, Q. An, T. Schramm, Y. Hofstetter, M. Litterst, F. Paulus and Y. Vaynzof, Nat. Commun., 2021, 12(1), 1878 CrossRef PubMed.
- M. Awais, T. D. Gangadharan, F. Tan and I. M. Saidaminov, Chem. Mater., 2022, 34, 8112–8118 CrossRef CAS.
- K. Wang, M. C. Tang, X. H. Dang, R. Munir, D. Barrit, D. M. Bastiani, E. Aydin, D. M. Smilgies, D. S. Wolf and A. Amassian, Adv. Mater., 2019, 31, 1808357 CrossRef PubMed.
- P. K. Goetz and Y. Vaynzof, ACS Energy Lett., 2022, 7, 1750–1757 CrossRef.
- E. Naoto, Y. Kohei, K. Hiroyuki, M. Santa and N. M. Takurou, ChemRxiv, 2025, preprint, DOI:10.26434/chemrxiv-2025-g86dx.
- Y. Motoyama, R. Tamura, K. Yoshimi, K. Terayama, T. Ueno and K. Tsuda, Comput. Phys. Commun., 2022, 278, 108405 CrossRef CAS.
- Z. Ma, D. Huang, Q. Liu, G. Yan, Z. Xiao, D. Chen, J. Zhao, Y. Xiang, C. Peng, H. Li, M. Zhang, W. Zhang, L. Duan and Y. Huang, J. Energy Chem., 2022, 66, 152–160 CrossRef CAS.
- C. Y. Kim, J. N. Jeon, H. J. Noh, S. W. Yang, J. Seo, S. J. Yun, A. Ho-Baillie, S. Huang, A. M. Green, J. Seidel, K. T. Ahn and I. S. Seok, Adv. Energy Mater., 2016, 6, 1502104 CrossRef.
- L. Wang, C. McCleese, A. Kovalsky, Y. Zhao and C. Burda, J. Am. Chem. Soc., 2014, 136(35), 12205–12208 CrossRef CAS PubMed.
- T. Calinski and J. Harabasz, Commun. Stat. Theor. Methods, 1974, 3, 1–27 CrossRef.
- P. Chen, Y. Bai, S. Wang, M. Lyu, J. H. Yun and L. Wang, Adv. Funct. Mater., 2018, 28, 1706923 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5el00007f |
| This journal is © The Royal Society of Chemistry 2025 |