Immediate remaining capacity estimation of heterogeneous second-life lithium-ion batteries via deep generative transfer learning†
Shengyu
Tao
 ab,
Ruohan
Guo
c,
Jaewoong
Lee
ab,
Ruohan
Guo
c,
Jaewoong
Lee
 b,
Scott
Moura
b,
Lluc Canals
Casals
d,
Shida
Jiang
b,
Junzhe
Shi
b,
Stephen
Harris
b,
Scott
Moura
b,
Lluc Canals
Casals
d,
Shida
Jiang
b,
Junzhe
Shi
b,
Stephen
Harris
 e,
Tongda
Zhang
f,
Chi Yung
Chung
c,
Guangmin
Zhou
e,
Tongda
Zhang
f,
Chi Yung
Chung
c,
Guangmin
Zhou
 *a,
Jinpeng
Tian
*a,
Jinpeng
Tian
 *c and
Xuan
Zhang
*c and
Xuan
Zhang
 *a
*a
aTsinghua Shenzhen International Graduate School, Tsinghua University, Shenzhen, China. E-mail: guangminzhou@sz.tsinghua.edu.cn; xuanzhang@sz.tsinghua.edu.cn
bEnergy, Controls, and Applications Lab (eCAL), Department of Civil and Environmental Engineering, University of California, California, USA
cDepartment of Electrical and Electronic Engineering and Research Centre for Grid Modernisation, The Hong Kong Polytechnic University, Hong Kong, China. E-mail: jinpeng.tian@polyu.edu.hk
dEnvironmental Engineering Research Group (ENMA), Department of Project and Construction Engineering, Universitat Politècnica de Catalunya·BarcelonaTech (UPC), Barcelona, Spain
eEnergy Storage and Distributed Resources Division, Lawrence Berkeley National Laboratory, California, USA
fSystems Optimization Laboratory, Stanford University, California, USA
First published on 20th June 2025
Abstract
The reuse of second-life lithium-ion batteries (LIBs) retired from electric vehicles is critical for energy storage in underdeveloped regions, where power infrastructures are weak or absent. However, estimating the relative remaining capacity (RRC) of second-life batteries using field-accessible data stream remains challenging due to its scarcity and heterogeneity, despite efforts in battery passports and other initiatives to secure data integrity. This study proposes a deep generative transfer learning framework to address these two-fold challenges by generating voltage dynamics across state-of-charge (SOC) and using deep correlation alignment (CORAL) to align heterogeneities resulting from different aging patterns (domains) of second-life LIBs. We generate voltage response dynamics data across various SOC conditions from 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 160 samples under 10 SOC values, demonstrating high statistical similarities and confidence. The model estimates the RRC with minimal field data availability, specifically 2% of the full sample size, achieving a mean absolute percentage error of 7.2% and 3.6% for second-life batteries with different degradation behaviors, respectively. The model preserves established knowledge in the available domain while reducing RRC estimation risks in new domains where data availability is limited. The maximum RRC estimation risk is reduced by 49% at a 95% confidence level. This unified data generation and transfer learning paradigm outperforms the state-of-the-art machine learning and equivalent circuit model-method across all data availability conditions. The “generate and transfer” paradigm enlightens many potential applications in other predictive management tasks by preferentially generalizing in-distribution data and then adapting to out-of-distribution conditions under guidance of limited field data.
160 samples under 10 SOC values, demonstrating high statistical similarities and confidence. The model estimates the RRC with minimal field data availability, specifically 2% of the full sample size, achieving a mean absolute percentage error of 7.2% and 3.6% for second-life batteries with different degradation behaviors, respectively. The model preserves established knowledge in the available domain while reducing RRC estimation risks in new domains where data availability is limited. The maximum RRC estimation risk is reduced by 49% at a 95% confidence level. This unified data generation and transfer learning paradigm outperforms the state-of-the-art machine learning and equivalent circuit model-method across all data availability conditions. The “generate and transfer” paradigm enlightens many potential applications in other predictive management tasks by preferentially generalizing in-distribution data and then adapting to out-of-distribution conditions under guidance of limited field data.
Broader contextAs the global transition to electric mobility accelerates, large volumes of lithium-ion batteries are approaching retirement. Repurposing these batteries for second-life applications offers a critical opportunity to extend their value, reduce environmental waste, and enable cost-effective energy storage, particularly in under-resourced regions lacking stable grid infrastructure. However, assessing the health and usability of retired batteries remains a major barrier due to the absence of usage history and significant variability in design and degradation. This study introduces a deep generative transfer learning framework that enables immediate estimation of remaining capacity using only minimally available field data. By generating synthetic voltage responses across charge conditions and aligning heterogeneous battery types via domain adaptation, the method circumvents the need for extensive historical records or laboratory calibration. Scientifically, it advances the integration of generative modeling and transfer learning in battery diagnostics, offering a principled way to handle out-of-distribution uncertainty. The approach enables a scalable solution to battery reuse by reducing testing time, minimizing deployment risks, and enhancing decision-making under data constraints. More broadly, it demonstrates how data-efficient, adaptive learning models can support sustainable energy systems by unlocking the latent value of discarded resources, providing both technological and environmental benefits in the circular energy economy. |
1 Introduction
Lithium-ion batteries (LIBs) have enabled electric vehicles (EVs) to transform the transport sector with clean and durable energy. The most recent California Code of Regulations (CCR) in the US requires the manufacturers of battery EVs and plug-in hybrid EVs to warrant at least 70% capacity deterioration for eight years or 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 miles, whichever first occurs.1 The CCR demonstrates an ambitious goal that battery life cycle sustainability shall be secured by preventing early retirement from EV usage.2,3 This is particularly compelling for underdeveloped regions, where reliable energy storage is vital to addressing challenges posed by weak or nonexistent power grid infrastructure.
000 miles, whichever first occurs.1 The CCR demonstrates an ambitious goal that battery life cycle sustainability shall be secured by preventing early retirement from EV usage.2,3 This is particularly compelling for underdeveloped regions, where reliable energy storage is vital to addressing challenges posed by weak or nonexistent power grid infrastructure.
EV battery diagnosis and prognosis play critical roles in informing manufacturers and users of current and future degradation expectations, which have been well-studied even before the release of the CCR.4–8 These efforts focus on prior-retired EV batteries, assuming considerable homogeneity, i.e., fixed material types, physical formats, capacity designs, observable state of charge (SOC), and state of health (SOH), even though driving profiles might vary significantly. These different battery states, referred to as domains, can be transferred from the trained model and updated for cross-operation-condition tasks.9–11 However, this typically involves an infeasible assumption that historical information is available. For post-retired EV batteries, historical data are not guaranteed since access to the battery management system (BMS) can be denied due to privacy restrictions due to ownership changes,12 and the information might even be destroyed by poorly managed battery transportation, leading to significant data scarcity.13–15 As a key interest of second-life usage, immediate knowledge of remaining capacity is a bottleneck due to the lack of historical information. Pulse tests have been documented as effective, rapid, and non-destructive SOH estimation methods with a core idea of exciting battery dynamics for voltage signal responses from pulse current that was injected into batteries, where voltage response signals could be mapped to SOH.16–18 However, these “voltage-SOH” pairs are sensitive to second-life heterogeneities, i.e., varied SOC, material types, physical formats, and capacity designs of batteries.17–22
Instead of spanning physical experiments at scale, deliberate data generation is promising to address the twofold challenge of data scarcity and heterogeneity. Broadly, this has been brought to the attention of the researchers in many energy-related tasks, such as thermal runaway prediction,23 energy consumption estimation,24 state of energy estimation,25 SOC estimation,26 SOH estimation,27 remaining useful life prediction,28 and degradation path prediction.29 However, it remains questionable whether generative models can adequately deal with the data heterogeneity, especially for out-of-distribution (OOD) observations in a second-life context. Indeed, it is fundamentally challenging to the battery modeling community that the generative model can hardly estimate OOD batteries unless prior knowledge is secured to guide model generalization and increase transferability. Such priors are never easy to obtain from second-life batteries, which restricts the fidelity of data generation. Thus, a careful evaluation of the accessibility of the priors from the field test site is critical to a successful, more importantly affordable, domain knowledge transfer from established models.30–33 Rasheed et al. proposed a single pulse test set method that enables generalized remaining useful life and battery classification ignoring prior usage, validated through broad datasets.34 While the idea of using immediately available pulse test for another critical task, such as remaining capacity estimation, holds promises, the pulse injection at consecutive SOC is challenging in real-world settings due to the randomly distributed SOC of second-life batteries at the collection site. To date, there has been no unified framework for estimating the immediate remaining capacity of heterogeneous second-life LIBs that can address data scarcity and heterogeneity simultaneously.
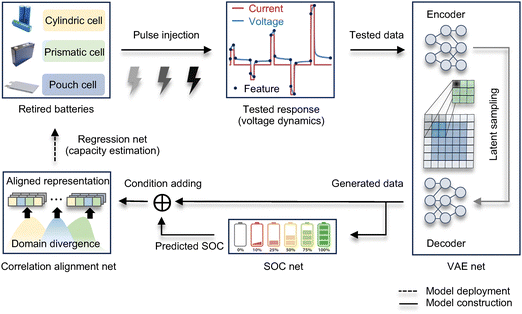
This study demonstrates a deep generative transfer learning approach to address the two-fold data scarcity and heterogeneity challenges in estimating the remaining capacity of second-life batteries, which is sensitive to SOC. To do so, a variational autoencoder (VAE net) is introduced to generate “voltage-SOH” pairs across SOCs to mitigate data scarcity by learning the voltage response dynamics that are subject to the same current inputs, reducing the number of experiments under different SOC levels. The VAE net takes the already-tested voltage dynamics and the measurement condition (SOC) as input for training the encoder. The decoder reconstructs voltage response dynamics from noise signals representing untested SOCs, which are free of test time and cost. The purpose of the variational encoder is to learn a continuous latent representation of the input data and generate new data samples that resemble the training data. Using generated data, the immediate remaining capacity estimation of second-life lithium-ion batteries can be achieved by prioritizing the prediction of SOC states, which are utilized as conditional information for the remaining capacity prediction. Otherwise, the SOC information requires a long-term charge and discharge test to obtain. To align with practical usage and address data heterogeneities, the generated data were split by physical formats and capacity designs into distinct domains. Deep correlation alignment (CORAL), a transfer learning method, was employed to transfer knowledge from any known domain to new domains with minimal field data and reduced uncertainties.
Fig. 1 provides a detailed workflow. The proposed approach is promising in terms of saving intensive data curation time and showing flexibility in updating trained models to new domains without retraining from scratch. The proposed unified data generation and knowledge transfer paradigm is promising for many other energy predictive tasks by preferentially generalizing non-OOD data and then adapting to OOD conditions under the guidance of available field data.
2 Definition of relative remaining capacity (RRC)
There are concepts such as state of health (SOH) for residual value evaluation, but the term health could indicate multiple meanings, e.g., energy, power, and resistance. To avoid distractions, this study focuses on the relative remaining capacity (RRC) of second-life batteries since it is the most direct indicator to evaluate the residual value, which serves as the label of the estimation problem. The RRC is defined as: | (1) |
Q real is determined with a standard constant current constant voltage (CCCV) charging and discharging procedure. First, the second-life batteries are discharged to a lower cut-off voltage (2.7 V) using a 1C constant current. Second, the second-life batteries are charged to the upper cut-off voltage (4.2 V) using a 1C constant current, then charged using constant voltage until the current drops to 0.05C. Third, the second-life batteries are then discharged to the lower cut-off voltage (2.7 V) using a 1C constant current. C stands for charge (discharge) rate when a 1 hour of charge (discharge) is performed, which is a dimensionless scalar number.
3 Data curation
The data used in this study are obtained from accelerated aging tests of several independent fresh batteries to characterize the second-life batteries with different SOH values. Multiple pulse tests are performed at different SOC values to expand the dataset, simultaneously accounting for the varieties of pulse-induced voltage dynamic signals produced from SOC randomness. Three types of NMC (nickel manganese cobalt oxide) fresh cells are investigated to demonstrate capacity design and physical format diversities, as shown in Table 1. Note that there are some RRC values larger than 1, a normal observation for batteries with overloaded materials (discharged capacity is more than rated value). In total, there were 96 second-life batteries simulated from accelerated aging tests using 17 independent batteries. The experiments are performed only once to simulate real-world requirements where one might want to know the RRC with minimal data, even in the presence of measurement uncertainty, which accounts for the proposed model's estimation capability and its ability to handle the constrained uncertainties.| Domain | Q (A h) | Physical format | Battery quantity (simulated quantity) | Data entry | RRC range | RRC mean (deviation) |
|---|---|---|---|---|---|---|
| #1 | 2.1 | Cylinder | 12 (67) | 670 | 0.61–0.92 | 0.81 (0.07) |
| #2 | 3.1 | Pouch | 2 (14) | 140 | 0.68–1.01 | 0.87 (0.08) |
| #3 | 5.2 | Pouch | 3 (15) | 150 | 0.50–1.02 | 0.83 (0.16) |
In each accelerated aging cycle, all batteries were charged with a 2C constant current followed by a constant voltage at 4.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V with C/200 or 30-minute cut-off condition followed by a 5-minute rest. The same constant discharge current was applied with a cut-off voltage of 3 V followed by a 5-minute rest. Note that C stands for rate of charge (discharge) relative to that for a 1 hour of charge (discharge). After every 100 accelerated aging cycles, the batteries were rested for 30 minutes to reach a steady state, preparing for pulse injection. The pulse injection is performed at 10 SOC levels, i.e., from 5% to 50%, with an increment of 0.05, as the second-life batteries are typically stored with relatively low SOC before redeployment. The current used to adjust SOC was 1C. Thus, the time for moving across SOC levels is 3 minutes. We used identical rest time, i.e., 25s, between all injected pulses. The pulse width was 5s and the amplitude was ±0.5C, ±1C, and +2C. The +2C pulse is the final pulse of each experiment, then the SOC adjustment is continued until the 50% SOC level is hit. The ambient temperature was set at 25 °C. Note that positive and negative pulses alternate to cancel the electric charge injection, so that no SOC calibration is required between different pulse injections. Since there are 10 SOC levels tested, the data entry in each domain is ten times that of the simulated battery quantity. The tested SOC are taken as the true SOC label in this paper. Specifically, data entry numbers for domains 1–3 are 670, 140, and 150, respectively, thus a total of 960 data entries were generated. The detailed workflow is explained in Fig. S1 (ESI†). The alternating setting between the accelerated aging test and the pulse test demonstrates that the safety of the pulse test within the wide observed RRC ranges, i.e., from 0.5 to fresh cells, even under 2C harsh cycling conditions.
V with C/200 or 30-minute cut-off condition followed by a 5-minute rest. The same constant discharge current was applied with a cut-off voltage of 3 V followed by a 5-minute rest. Note that C stands for rate of charge (discharge) relative to that for a 1 hour of charge (discharge). After every 100 accelerated aging cycles, the batteries were rested for 30 minutes to reach a steady state, preparing for pulse injection. The pulse injection is performed at 10 SOC levels, i.e., from 5% to 50%, with an increment of 0.05, as the second-life batteries are typically stored with relatively low SOC before redeployment. The current used to adjust SOC was 1C. Thus, the time for moving across SOC levels is 3 minutes. We used identical rest time, i.e., 25s, between all injected pulses. The pulse width was 5s and the amplitude was ±0.5C, ±1C, and +2C. The +2C pulse is the final pulse of each experiment, then the SOC adjustment is continued until the 50% SOC level is hit. The ambient temperature was set at 25 °C. Note that positive and negative pulses alternate to cancel the electric charge injection, so that no SOC calibration is required between different pulse injections. Since there are 10 SOC levels tested, the data entry in each domain is ten times that of the simulated battery quantity. The tested SOC are taken as the true SOC label in this paper. Specifically, data entry numbers for domains 1–3 are 670, 140, and 150, respectively, thus a total of 960 data entries were generated. The detailed workflow is explained in Fig. S1 (ESI†). The alternating setting between the accelerated aging test and the pulse test demonstrates that the safety of the pulse test within the wide observed RRC ranges, i.e., from 0.5 to fresh cells, even under 2C harsh cycling conditions.
4 General algorithm workflow
A more detailed description of the general methodology of the algorithm, which better articulates the main idea of the work, i.e., how to predict the RRC in the target domain (domain of interest) using immediately available voltage data from pulse injection, can be found in Fig. S2 (ESI†). There are eight steps in total. For the first step, second-life batteries with random SOC conditions are subject to the pulse test. For the second step, the voltage curves obtained from the pulse test are manipulated with a feature engineering process, where the voltage points with zero second-order derivative of the voltage curve are extracted as features. For the third step, feature and SOC pairs are fed into the VAE net to learn the latent relationship between them. For the fourth step, SOC signals simulated by the random noise are fed into the trained VAE net, specifically the decoder network part, to generate voltage feature data that is generalized to the continuous SOC values. For the fifth step, the generated voltage feature data, together with SOC values, are used to train a SOC net that learns a mapping from voltage feature to its related SOC condition. For the sixth step, predicted SOC values associated with the extracted voltage features are fed into a regression net to predict RRC within one specific domain. For the seventh step, noting that the regression model cannot be generalized from the source domain to the target domains, the partial data from other domains are used to guide the CORAL transfer learning, which minimizes the joint SOC and RRC estimation error in a unified form. For the eighth step, RRC in the target domain is predicted using established knowledge in the source domain and partial knowledge in the target domain of interest. Assuming that knowledge in the source domain can be obtained, the proposed methodology requires only limited testing samples and minimal test time from the target domain. Thus, the RRC prediction is immediate compared to the state-of-the-art pulse test that ignores prior usage.34 Mathematical formulation and parameter setting can be found in the Methods section.5 Results
5.1 The data heterogeneity
The feature engineering process is easy to implement, where the features are extracted from the turning points of the voltage curve, i.e., the points with zero second-order derivative of the voltage curve.17 Thus, 21 feature points, from U1 to U21, are extracted, as illustrated in Fig. 2a. Mathematically, the feature set Uk can be formulated as: | (2) |
The voltage dynamics have a clear physical meaning: second-life batteries exhibit a higher polarization resistance, resulting in a higher voltage response, when subjected to an identical current input. The pulse injections were performed at ten different SOC levels instead of 5% SOC, resulting in a total pulse injection dataset with 960 observations. Thus, the dataset used in this study encompasses 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 160 voltage dynamics feature points, including different capacity designs, physical formats, and SOC distributions. Fig. 2b illustrates that when physical formats and capacities differ, the batteries can respond significantly differently. Specifically, the same physical formats do not necessarily guarantee a uniform voltage response behavior, as shown in voltage dynamics for Pouch31 and Pouch52, where divergences can even be more pronounced than those of Cylind21 and Pouch52. Noticeably, domain divergences can be more than 0.2 V, which accounts for the polarization increase from fresh cells to around 80% relative remaining capacity within a single domain. Therefore, knowledge transfer between domains is necessary to ensure real-world deployment, where domain divergence exists but cannot be known as prior information at the test site.
160 voltage dynamics feature points, including different capacity designs, physical formats, and SOC distributions. Fig. 2b illustrates that when physical formats and capacities differ, the batteries can respond significantly differently. Specifically, the same physical formats do not necessarily guarantee a uniform voltage response behavior, as shown in voltage dynamics for Pouch31 and Pouch52, where divergences can even be more pronounced than those of Cylind21 and Pouch52. Noticeably, domain divergences can be more than 0.2 V, which accounts for the polarization increase from fresh cells to around 80% relative remaining capacity within a single domain. Therefore, knowledge transfer between domains is necessary to ensure real-world deployment, where domain divergence exists but cannot be known as prior information at the test site.
5.2 The mixed state-of-charge (SOC)
Here, we illustrate the effectiveness of the pulse injection method in assessing the RRC of second-life batteries at fixed SOC, as well as the challenges encountered under mixed SOC conditions (without prior SOC knowledge). In Fig. 3a, a clear correlation is observed between the RRC and the voltage dynamics value in most feature dimensions and SOC regions, although some dimensions demonstrate a decreased representation capability due to over-discharging under low SOC levels using negative pulses. The negative correlation values can be rationalized by the increased voltage polarizations of the degraded batteries, which are accompanied by decreased RRC values. Note that such a strong correlation is observed under the ideal assumption that the explicit SOC (grouped by unique SOC) is known for second-life batteries. However, second-life batteries exhibit different SOC distributions when collected from EV companies or vendors, thus, prior information on SOC can hardly be guaranteed. It can be seen from Fig. 3b that if we do not know the SOC information (mixed SOC) of second-life batteries, the pulse injection method can lead to considerable malfunctions in predicting the RRC from voltage dynamics. Therefore, the mixed SOC directly motivates us to predict the SOC first rather than inferring the RRC from the voltage dynamics signals in the first place.5.3 The data scarcity
Before predicting SOC from the voltage dynamics signal, the data scarcity issue should be resolved so that we have continuous data observations for continuous SOC levels, where physical tests merely cover those discrete SOC measurement levels. The heterogeneity challenge demonstrated in Fig. 2b can also be evidenced by the accelerated aging behavior in Pouch31 given the soaring polarization response with aging, while for Cylind21 and Pouch52, the degradation can be considered uniform until the test stops.In Fig. 4a, the Cylind21, Pouch31, and Pouch52 second-life battery groups exhibit linear, non-linear, and sub-linear aging, respectively, with distinct degradation behaviors noticeable. This implies a phenomenon where even if the data scarcity issue can be resolved within one domain, it is insufficient to generalize the model for OOD RRC estimations. Thus, it is necessary to train separate generative models for different domains to facilitate learning distinct degradation mechanisms and then design transferring mechanisms if the data scarcity challenge can be resolved.
Using the trained VAE net, a uniform data observation enrichment for continuous SOC levels is observed, as depicted in Fig. 4a. Multiple test points at the same SOC refer to the fact that batteries with different RRC are tested. In another way, one physical battery with one specific RRC is tested under multiple SOC, where an arrow was used to indicate the aging direction. Essentially, the VAE net learns polarization behaviors across SOC in one specific domain characterized by distinct degradation behaviors, i.e., linear, sublinear and accelerated aging. In Fig. 4b, the generative capability of the VAE net is quantified, finding that the tested and generated data distributions are similar to each other with low KL-divergence (KLD) values of 0.68, 0.63, and 0.25 for Pouch52, Pouch31, and Cylind21, respectively. Note that KLD is a statistical measure used to quantify the difference between two probability distributions. There is no universal threshold for a “good” KLD value because it depends on the scale and nature of the distributions. Instead of aiming for an absolute KLD, it is preferable to compare KLD values across models. Despite different degradation mechanisms, physical formats, and capacity designs, the data generation performance is consistent across all 21 voltage dynamics dimensions, with minor KLD values, as demonstrated in Fig. 4c. Thus, the data scarcity issue is addressed by generating extensive data observations across different SOCs, which are not easily covered by separate physical measurements.
5.4 Deep generative transfer learning performance
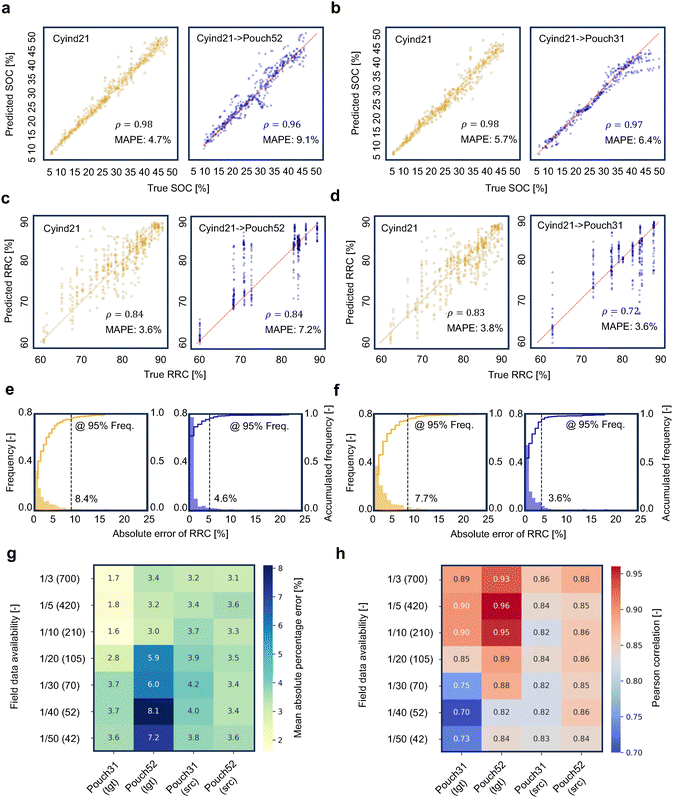
This section presents various domain adaptation scenarios to illustrate the effectiveness of the proposed deep generative transfer learning approach. This approach prioritizes SOC predictions across various domains, and then the predicted SOC values are used as conditional information for voltage response dynamics signals, facilitating immediate RRC prediction.In Fig. 5a, the predictive performance of the SOC net is presented. Data collected from Cylind21 is the source domain, assuming the data are available due to cumulative data collection over time. The SOC net can immediately infer SOC values from voltage dynamics without any capacity test. Again, this SOC information is otherwise obtained by long-term charge and discharge tests. A 9.1% MAPE for SOC prediction of the Pouch52 second-life batteries is observed when using the full size of Cylind21 data and only 2% of the Pouch52 data, equivalent to 42 second-life battery samples collected at the test field. The Pearson correlation of 0.96 indicates a strong linear correlation between the predicted and actual SOC values, indicating that the prediction is highly reliable. More importantly, the SOC net does not compromise the source domain's predictive capability, as evidenced by a 3.6% MAPE and a 0.96 Pearson correlation. In Fig. 5b, for another task with larger domain divergences, as shown in the voltage dynamics differences between Cylind21 and Pouch31 in Fig. 2b, the SOC net still performs robustly. With only 2% of the Pouch31 data, the SOC net can immediately infer SOC levels with a 6.4% MAPE and a 0.97 Pearson correlation. We observe that the SOC prediction in the higher SOC region of the Clind21 → Pouch31 is slightly divergent. This observation can be rationalized by increased domain divergence resulting from accelerated aging patterns in Pouch31 (see the aging direction of Pouch31 in Fig. 4b), which makes transfer between Clind21 and Pouch31 more challenging.
Having access to the SOC information predicted by the SOC net, the voltage dynamics are helpful to predict the RRC of the second-life batteries; otherwise, the representability of voltage dynamics to battery degradation is complicated by the mixed SOC distributions, as shown in Fig. 3b. The predicted SOC condition is appended to the voltage dynamics values immediately obtained from the test field for RRC prediction. Fig. 5c shows an RRC prediction with a 7.2% MAPE and a 0.84 Pearson correlation, which requires only 2% of the data availability. The predicted RRC points exhibit a noticeable concentration along the perfect prediction line (the red diagonal line), regardless of the mixed SOC levels, indicating that CORAL successfully transforms heterogeneities resulting from physical formats and capacity designs into a shared statistical space. In Fig. 5d, we observe a robust result for Pouch52 second-life batteries, with a 3.6% MAPE and a 0.72 Pearson correlation. Since the batteries with the same RRC are tested multiple times across different SOC levels, we note that some prediction points are located far from the diagonal line. However, the number of these outlier samples is relatively small, which does not significantly impact the overall RRC prediction error.
We perform absolute error frequency analysis to examine prediction uncertainties and risks since second-life batteries are more safety-conscious. In Fig. 5e, a concentrated absolute error distribution is observed, where the error frequency is calculated as the ratio of the number of instances within a certain error range to the total number. When considering a 95% accumulated error frequency, the target domain prediction is robust, with a 4.6% MAPE. In Fig. 5f, when transferring to a challenging condition with a larger domain difference, the prediction result remains stable with a 3.6% MAPE.
We summarize error values reported in Fig. 5a–f in Table 2 for a clear presentation and discussion. In Table 2, both the backward transfer and forward transfer are evaluated. The − and + symbol refer to backward transfer and forward transfer, respectively. The backward transfer refers to the scenario where the transferred model is used to make predictions in the domain from which it was initially transferred, i.e., the source domain. While the forward transfer means that the transferred model was used to make predictions in target domain that guided the transfer. The backward transfer and forward transfer evaluate the model's preservation of established knowledge and its transferability to new knowledge, respectively. It can be seen from Table 2 that both SOC predictions and RRC predictions demonstrate good knowledge preservability in the original domain, even if the difficulties vary upon different transfer scenarios. Thus, we conclude that the proposed CORAL transformation finds a domain-invariant representation of both source (Cylind21) and target (Pouch52, Pouch31) domain tasks. It is noted that the maximum prediction risk also decreases when transferring knowledge from the source domain to the target domain, which is preferable to second-life applications since they can be relevant to improved estimation reliability, and robust second-life battery warranty strategy designs. The observed maximum RRC estimation risk given a 95% confidence level is reduced by 49% averagely (45.23% and 53.25% reduction for Cylind21 → Pouch52, and Cylind21 → Pouch31 transfer scenarios, respectively).
| Transfer scenario | SOC prediction | RRC prediction | |||
|---|---|---|---|---|---|
| ρ | MAPE (%) | ρ | MAPE (%) | Max risk (%) | |
| Cylind21 → Pouch52 (−) | 0.98 | 4.7 | 0.84 | 3.6 | 8.4 |
| Cylind21 → Pouch52 (+) | 0.96 | 9.1 | 0.84 | 7.2 | 4.6 |
| Cylind21 → Pouch31 (−) | 0.98 | 5.7 | 0.83 | 3.8 | 7.7 |
| Cylind21 → Pouch31 (+) | 0.97 | 6.4 | 0.72 | 3.6 | 3.6 |
For the practical usage of the proposed deep generative transfer learning approach, one may be concerned about the impact of the field data availability that is critical to guide the model to generalize, which has significant relevance to time and cost feasibility. In Fig. 5g and h, we carefully examine the impact of field data availability on target and source domain tasks. It perfectly aligns with the intuition that predictive performance increases with the availability of field data for all tasks. However, in turn, data scarcity challenges the model performance, especially when faced with changing data distributions resulting from different physical formats and capacity designs. For 33.3% of the field data availability, the model shows 1.7% and 3.4% MAPEs for Cylind21 → Pouch31 and Cylind21 → Pouch52 tasks, respectively. Interestingly, when field data availability decreases to 10%, the model performance is better than that of its counterparts with even more data availability, with 1.6% and 3.0% MAPEs for Cylind21 → Pouch31 and Cylind21 → Pouch52 tasks, respectively. This phenomenon inspires us to carefully examine the trade-off between the scale of the spanning dataset and the improvement in predictive performance. More importantly, seeing that MAPE for source domain tasks fluctuates with 1% even though the field data availability decreases drastically from 33.3% to 2%, as shown in Fig. 5g, the model hardly forgets about the previous domain tasks, which is challenging for transfer learning and continual learning tasks. For the source domain of Pouch52, this stability is as low as 0.2% MAPE, given a considerable change in field data availability from 33.3% to 2%. In Fig. 5h, similar stability is observed for the source domains of Pouch52 and Pouch31 tasks, respectively. However, it has been brought to our attention that the performance in terms of MAPE is higher for Pouch52 than that of Pouch31; counterintuitively, the Pearson correlation is higher for the Pouch52 task. This abnormality can be rationalized by the lower bound of RRC distribution reaching 0.50 while that of Pouch31 is 0.68, as shown in Table 1, where lower RRC values can lead to higher MAPEs given the same absolute prediction error. Among the two domain adaptation scenarios studied, the transfer from Cylind21 to Pouch31 is more challenging than to Pouch52 as illustrated by the domain divergence. This can be attributed to both distributional and degradation behavior differences. As observed in Fig. 2b, Pouch31 exhibits voltage dynamics that deviate more substantially from the source domain (Cylind21), and Fig. 4a further reveals a nonlinear, accelerated degradation trajectory unique to Pouch31. In contrast, Pouch52 shows a relatively consistent aging pattern, resulting in a smaller domain gap. These differences make CORAL alignment more difficult in the Cylind21 → Pouch31 case, as the feature distribution shift includes both covariate and conditional shifts, which is evidenced by the lower Pearson correlation coefficient as compared to the Cylind21 → Pouch52 case.
5.5 Model performance comparisons
The proposed deep generative transfer learning approach is compared to the state-of-the-art machine learning models under varied field data availability scenarios. The setting is the target domain only, which means that all models have access to data in the target domain. The prediction models are trained and tested only with target domain data, except that the proposed deep generative transfer learning approach can use existing data from the source domain, even though the data can be significantly different due to data heterogeneities.Note that the minimal field data availability is set at 2%, as no knowledge of the target domain can result in large errors due to domain divergence, as shown in Fig. 2b. In Fig. 6a and b, the deep generative transfer learning approach consistently shows lower MAPE across various field data availability and knowledge transfer tasks. In the linear regression, the prediction presents two orders of higher errors than our methods due to insufficiency in handling data scarcity and heterogeneity. When the field data availability increases from 2% to 5%, the deep neural network method approaches the deep generative transfer learning approach in an accelerated manner.
 | ||
| Fig. 6 Benchmarking performance of (a) and (b) mean absolute percentage error (MAPE) in log space and (c) and (d) Pearson correlation coefficient under limited field data availability scenarios. The benchmarking settings are practical scenarios in which field data are limited but can be collected over time. All models only use the field data except for the proposed generative transfer learning method using data from other domains to learn a knowledge transfer mapping. See the Methods section for detailed experimental settings. The experimental data can be found in Tables S1–S4 (ESI†). | ||
Fig. 6c shows that the deep neural network lags behind the deep generative transfer learning approach by 0.2 and 0.15 Pearson correlation values for Pouch31 and Pouch52, respectively. This phenomenon indicates that data size is crucial for making accurate predictions, although it is still hindered by data heterogeneity. Fig. 6d illustrates a better linearity of prediction when transferring from Cylind21 to Pouch52, which is understandable because the transferability between Cylind21 and Pouch52 is superior to that between Cylind21 and Pouch31, as seen in Fig. 2b. This demonstrates a delicate trade-off between the necessity of knowledge transfer to correct for domain divergences and the extent to which these divergences can be transferred. Unfortunately, it is a significant challenge that we often face due to insufficient data access for new domains, forcing us to generate high-fidelity data from existing datasets and transfer established model knowledge from old domains into new ones. In short, this paper establishes a pulse test-based method that is fast, non-intrusive, generalizable, and transferable from previously measured voltage features within one domain to target domains. The data volume requirement for such target domains is demonstrated to be as low as 2% compared to that in the established domain. Compared to other state-of-the-art machine learning techniques, our approach stands out as a stable method with low prediction error and minimized field data requirements.
Since the main claim of the proposed method is that one can immediately estimate the residual capacity of the retired batteries with minimal field data, it is particularly relevant to compare the performance with non-learning-based methodologies, i.e., parameter identification from an equivalent circuit model.35,36 These model-based methods require no historical data to train, see Note S1 (ESI†) for detailed problem formulation. To maximize the generalizability of such comparison, typical begin-, middle-, and end-of-life batteries from the Cylind21 dataset are selected, with their RRC values being 0.91, 0.88, and 0.66, respectively. The MAPE values of these estimations are 4.9%, 11.9%, and 51.9% compared to their ground truth, as shown in Table S5 (ESI†). The result can be rationalized by selecting an open-circuit-voltage (OCV)–SOC relationship at the beginning-of-life, which is a fundamental assumption in the equivalent circuit model-based parameter identification paradigm. However, this OCV–SOC relationship cannot be immediately obtained for second-life batteries, which leads to an increased estimation error caused by divergences between begin-, and end-of-life batteries. The proposed deep generative transfer learning method fundamentally reduces the need for considerable data and facilitates immediate residual value estimation of retired batteries.
6 Conclusions
This study addresses the gap in immediate RRC estimation for second-life batteries under data scarcity and heterogeneity, where previous methods rely on historical data that is often unavailable at the test site. This study proposes a deep generative transfer learning approach to generate synthetic data and adapt across formats (and capacity designs), providing accurate RRC predictions without historical information. The model achieves reliable SOC predictions with an MAPE of 9.1% for Pouch52 and 6.4% for Pouch31. Using predicted SOC as conditional information, the RRC estimation obtained an MAPE of 7.2% for Pouch52 and 3.6% for Pouch31. The results were obtained using only 2% of the available field data, and thus, considerable data curation and cost could be saved. Distinct from previous models that struggle with domain divergence or require extensive historical data curation, the proposed approach generalizes effectively with minimal field data requirements. This presents significant advances for battery reuse and recycling decision-making, where data availability is often limited.The limitation of this work lies in its handling of OOD data distribution, as it focuses on studying battery formats and capacity designs. However, heterogeneities can also arise from cathode chemistry types and historical usage patterns. Demonstrating its applicability to cells with different cathode chemistries (e.g., lithium iron phosphate, lithium manganese oxide, lithium nickel cobalt aluminum oxide, lithium cobalt oxide-based cells) would significantly reinforce the perceived utility and robustness of the framework. Although the pulse test has been demonstrated to be a safe technique in the observational data presented in this work, more in-depth degradation patterns should be further investigated to ensure a comprehensive understanding of the safety margin for applying pulse tests. We have focused on the SOC dependence of voltage dynamics, which reflects degradation. However, other degradation patterns, such as loss of active material, loss of lithium inventory, and their mixtures, should be explicitly included. Future studies could integrate pulse current injection with various pulse durations, magnitudes, and combinations to validate its effectiveness. Second-life battery packs with cell-to-cell variabilities, rather than disassembled individual cells, should be studied to engage practical interest.37 Another limitation of this work is that second-life batteries are simulated based on accelerated aging tests, where calendar aging is not included. However, these batteries are typically stored in the warehouse for a few months before they are given a “second life”. Despite the calendar aging itself being challenging to decouple from cycling aging, future studies should consider the joint impact of cycling and calendar aging. Thus, sophisticated internal state monitoring of the second-life battery states is recommended to enable the inclusion of calendar aging effects by establishing the empirical models.38
The observed backward transfer phenomenon is likely attributed to fundamental differences in degradation mechanisms between domains, such as varied polarization behavior or nonlinear degradation dynamics. Interestingly, such backward transfer, i.e., performance decrease with increased target-domain data, can offer practical insights by implicitly revealing domain-specific degradation pathways, thereby providing a valuable signal for sorting and classification strategies in second-life applications. From a deployment perspective, when backward transfer occurs, rapid correction through minimal target domain sampling emerges as a promising direction for future research. This also highlights a key operational insight: more data does not always yield better predictive performance. Instead, it is recommended to develop a data-efficiency-aware approach that seeks a balance between the sampling cost and model utility. On a theoretical basis, future work should aim to define transferability metrics to help practitioners determine whether a task in a new domain can benefit from existing models or requires retraining with extra domain-specific knowledge.
In conclusion, the proposed deep generative transfer learning approach addresses the challenges of data scarcity and heterogeneity in joint SOC and RRC estimation problems for second-life batteries, which often have minimal field data availability. The results demonstrate that the predictions are stable and have low statistical risk. The proposed method suggests that one could preferentially generalize non-OOD data (already measured) and then transfer to OOD conditions (test field site) under the guidance of available field data, as data curation time and cost are significant challenges for many other energy-related control and management tasks. Broadly, the proposed approach is promising in reducing environmental and financial costs associated with large-scale data curation, offering a transformative impact on second-life battery applications, especially in underdeveloped regions, where reliable energy storage is vital to addressing the challenges posed by weak or non-existent power grid infrastructure.
7 Methods
7.1 Variational autoencoder (VAE) net for pulse voltage signal generation across SOC
The VAE net is designed to resolve the data scarcity challenge, which has three components, i.e., an encoder, a sampling layer, and a decoder. The encoder is implemented by a fully connected layer with 128 neurons and ReLU activation. The encoder network receives the voltage response dynamics and SOC pairs, i.e., [Um×21, SOCm×1] as input, where m is the number of observations (data entries) and 21 stands for the dimension of features. The VAE net is trained by each unique RRC value due to considerable complexity resulting from the impact of battery degradation on [Um×21, SOCm×1] pairs.Two separate parameters, i.e., the mean  and log-variance
and log-variance 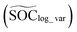 are produced from the encoder. The sampling layer is defined as:
are produced from the encoder. The sampling layer is defined as:
 | (3) |
 ,
, 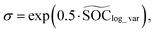 and
and  is a random sample from a standard normal distribution, i.e.,
is a random sample from a standard normal distribution, i.e.,  and it is where the generative capability of the VAE net comes from. The decoder is also implemented by a fully connected layer with 128 neurons and ReLU activation. Thus, the VAE net describes the following relationship:
and it is where the generative capability of the VAE net comes from. The decoder is also implemented by a fully connected layer with 128 neurons and ReLU activation. Thus, the VAE net describes the following relationship: | (4) |
 . The loss function of the VAE net constitutes two parts, i.e., reconstruction loss and the Kullback–Leibler (KL) divergence loss. The reconstruction loss is set as mean square error (MSE), see Evaluation metrics, which calculates the MSE between originally tested voltage response Uk and generated voltage response Ũk, i.e., lxentMSE.
. The loss function of the VAE net constitutes two parts, i.e., reconstruction loss and the Kullback–Leibler (KL) divergence loss. The reconstruction loss is set as mean square error (MSE), see Evaluation metrics, which calculates the MSE between originally tested voltage response Uk and generated voltage response Ũk, i.e., lxentMSE.
KL divergence loss LossKL, i.e., the KL divergence between originally tested and generated data, is given by:
 | (5) |
| LossVAE_net = ωxent·lxentMSE + ωKL·lKL | (6) |
The training epoch is 1000, the batch size is 32, the latent dimension (size of sampling layer) is 2, and the sampling intensity is 10. Sampling intensity refers to the ratio of the number of generated and the originally tested observations, which is implemented by regulating the number of points taken from  . Sampling intensity is set as 10 in this work.
. Sampling intensity is set as 10 in this work.
7.2 SOC net for charge level prediction from immediate available pulse voltage signal
The SOC net is designed to learn a map from Ũ to . The SOC net is a 10-layer deep neural network, with 512, 512, 256, 256, 128, 128, 64, 64, 32, and 32 neurons in each layer. The activation functions are all set as ReLU function. The input of the SOC net is generated, appended with the originally tested voltage dynamics signals [Ũ;U]while the output is the predicted SOC value
. The SOC net is a 10-layer deep neural network, with 512, 512, 256, 256, 128, 128, 64, 64, 32, and 32 neurons in each layer. The activation functions are all set as ReLU function. The input of the SOC net is generated, appended with the originally tested voltage dynamics signals [Ũ;U]while the output is the predicted SOC value 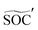 .
.
7.3 Regression net for relative remaining capacity prediction
The regression net is designed to predict the RRC. The regression net is a 5-layer neural network, with 256, 256, 128, 128, and 64 neurons in each layer. The activation functions are all set as ReLU function. The input of the regression net is the originally tested voltage dynamics signals appended with the predicted SOC values, which is while the output is the predicted
while the output is the predicted  value. In this way, immediate remaining capacity can be achieved from pulse tested voltage signals given the
value. In this way, immediate remaining capacity can be achieved from pulse tested voltage signals given the  is generated from learning the latent distribution between the [Um×21, SOCm×1] pairs, thus
is generated from learning the latent distribution between the [Um×21, SOCm×1] pairs, thus 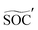 is free of physical testing cost. In a practical sense, this method enables quick knowledge of the SOC value by learning from voltage signals, and thus enabling remaining capacity prediction from voltage signals with the help of the prediction SOC condition.
is free of physical testing cost. In a practical sense, this method enables quick knowledge of the SOC value by learning from voltage signals, and thus enabling remaining capacity prediction from voltage signals with the help of the prediction SOC condition.
7.4 Correlation alignment (CORAL) net for transferable relative remaining capacity prediction
Till now, the model has no transferability, i.e., model cannot be generalized from one domain (in this paper, physical formats and capacity designs) to others. The CORAL net aims to correct these domain differences from physical formats and capacity designs. This idea was directly inspired by the cross-operation-condition lifetime prediction of in-service lithium-ion batteries.9 However, essential difference lands on the integration of CORAL metrics into the loss function of the designed deep neural network, instead of aligning features in the feature engineering stage, where the name of CORAL net comes from. The CORAL loss aligns the distributions of source and target features by minimizing the Frobenius norm of the difference between the covariance matrices: | (7) |
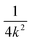 normalizes the loss concerning the dimensionality of the features, ensuring that the loss values remain comparable even for different feature dimensions.
normalizes the loss concerning the dimensionality of the features, ensuring that the loss values remain comparable even for different feature dimensions.
The loss function of the CORAL net is designed as:
 | (8) |
7.5 Benchmark models
Linear regression, ridge regression, Gaussian process regression, support vector machine, k-nearest neighbor, and random forest model are adopted from the sci-kit learn package (version 1.3.2) with default settings instead of finely tuning the hyperparameters of these models. The deep neural network has 256, 256, 128, 128, 64, and 1 neuron in each layer with ReLU activation functions in each layer. The training epoch was 200, and after this epoch, the deep neural network performance did not increase significantly.7.6 Evaluation metrics
The mean square error (MSE) error is defined as: | (9) |
 | (10) |
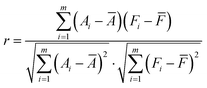 | (11) |
Author contributions
S. T. conceptualized, implemented experiments, performed model construction, and wrote the paper. R. G., J. L., L. C., J. S., and S. J. reviewed and discussed the work from technical perspectives. S. M. proposed the model-based parameter identification method, reviewed, and discussed this work. C. C., S. H., and T. Z. reviewed and discussed the work from industry perspectives. G. Z., J. T. and X. Z. reviewed, discussed, and acquired funding resources for this work.Conflicts of interest
The authors declare no competing interests.Data availability
Code and code of this work are deposited at https://github.com/terencetaothucb/Immediate-remaining-capacity-estiamtion-of-second-life-batteries and https://github.com/terencetaothucb/ECM-ParaID-for-second-life-batteries. Data used in this work are presented in manuscript and available in ESI.†Acknowledgements
The first author acknowledges Professor Scott J. Moura for the useful discussion and algorithm design of equivalent circuit model parameter identification. This research work was supported by Key Scientific Research Support Project of Shanxi Energy Internet Research Institute (Grant No. SXEI2023A002) [X. Z.], Meituan Scholar Program-International Collaboration Project (Grant No. 202209A) [X. Z.], Tsinghua Shenzhen International Graduate School Interdisciplinary Innovative Fund (Grant No. JC2021006) [X. Z. and G. Z.], Tsinghua Shenzhen International Graduate School-Shenzhen Pengrui Young Faculty Program of Shenzhen Pengrui Foundation (Grant No. SZPR2023007) [G. Z.], Guangdong Basic and Applied Basic Research Foundation (Grant No. 2023B1515120099) [G. Z.].References
- CCR, Warranty Requirements for Zero-Emission and Batteries in Plug-in Hybrid Electric 2026 and Subsequent Model Year Passenger Cars and Light-Duty Trucks, 2022.
- R. Ma, S. Tao, X. Sun, Y. Ren, C. Sun and G. Ji, et al., Pathway decisions for reuse and recycling of retired lithium-ion batteries considering economic and environmental functions, Nat. Commun., 2024, 15(1), 7641 CrossRef CAS PubMed.
- G. Crabtree, The coming electric vehicle transformation, Science, 2019, 366(6464), 422–424 CrossRef CAS PubMed.
- X. Hu, L. Xu, X. Lin and M. Pecht, Battery Lifetime Prognostics, Joule, 2020, 4(2), 310–346 CrossRef CAS.
- K. A. Severson, P. M. Attia, N. Jin, N. Perkins, B. Jiang and Z. Yang, et al., Data-driven prediction of battery cycle life before capacity degradation, Nat. Energy, 2019, 4(5), 383–391 CrossRef.
- P. M. Attia, A. Grover, N. Jin, K. A. Severson, T. M. Markov and Y.-H. Liao, et al., Closed-loop optimization of fast-charging protocols for batteries with machine learning, Nature, 2020, 578(7795), 397–402 CrossRef CAS PubMed.
- D. Roman, S. Saxena, V. Robu, M. Pecht and D. Flynn, Machine learning pipeline for battery state-of-health estimation, Nat. Mach. Intell., 2021, 3(5), 447–456 CrossRef.
- M.-F. Ng, J. Zhao, Q. Yan, G. J. Conduit and Z. W. Seh, Predicting the state of charge and health of batteries using data-driven machine learning, Nat. Mach. Intell., 2020, 2(3), 161–170 CrossRef.
- S. Tao, C. Sun, S. Fu, Y. Wang, R. Ma and Z. Han, et al., Battery Cross-Operation-Condition Lifetime Prediction via Interpretable Feature Engineering Assisted Adaptive Machine Learning, ACS Energy Lett., 2023, 8(8), 3269–3279 CrossRef CAS.
- S. Fu, S. Tao, H. Fan, K. He, X. Liu and Y. Tao, et al., Data-driven capacity estimation for lithium-ion batteries with feature matching based transfer learning method, Appl. Energy, 2024, 353, 121991 CrossRef CAS.
- Y. Che, Y. Zheng, S. Onori, X. Hu and R. Teodorescu, Increasing generalization capability of battery health estimation using continual learning, Cell Rep. Phys. Sci., 2023, 4(12), 101743 CrossRef.
- S. Tao, H. Liu, C. Sun, H. Ji, G. Ji and Z. Han, et al., Collaborative and privacy-preserving retired battery sorting for profitable direct recycling via federated machine learning, Nat. Commun., 2023, 14(1), 8032 CrossRef CAS PubMed.
- H. Bai, X. Hu and Z. Song, The primary obstacle to unlocking large-scale battery digital twins, Joule, 2023, 7(5), 855–857 CrossRef.
- A. Weng, E. Dufek and A. Stefanopoulou, Battery passports for promoting electric vehicle resale and repurposing, Joule, 2023, 7(5), 837–842 CrossRef.
- N. Guo, S. Chen, J. Tao, Y. Liu, J. Wan and X. Li, Semi-supervised learning for explainable few-shot battery lifetime prediction, Joule, 2024, 8, 1820–1836 CrossRef.
- B. Nowacki, J. Ramamurthy, A. Thelen, C. Tischer, C. L. Pint and C. Hu, Rapid estimation of lithium-ion battery capacity and resistances from short duration current pulses, J. Power Sources, 2025, 628, 235813 CrossRef CAS.
- S. Tao, R. Ma, Y. Chen, Z. Liang, H. Ji and Z. Han, et al., Rapid and sustainable battery health diagnosis for recycling pretreatment using fast pulse test and random forest machine learning, J. Power Sources, 2024, 597, 234156 CrossRef CAS.
- Z. Zhou, A. Ran, S. Chen, X. Zhang, G. Wei and B. Li, et al., A fast screening framework for second-life batteries based on an improved bisecting K-means algorithm combined with fast pulse test, J. Energy Storage, 2020, 31, 101739 CrossRef.
- A. Ran, M. Cheng, S. Chen, Z. Liang, Z. Zhou and G. Zhou, et al., Fast Remaining Capacity Estimation for Lithium-ion Batteries Based on Short-time Pulse Test and Gaussian Process Regression, Energy Environ. Mater., 2023, 6(3), e12386 CrossRef CAS.
- A. Ran, Z. Liang, S. Chen, M. Cheng, C. Sun and F. Ma, et al., Fast Clustering of Retired Lithium-Ion Batteries for Secondary Life with a Two-Step Learning Method, ACS Energy Lett., 2022, 7(11), 3817–3825 CrossRef CAS.
- A. Ran, Z. Zhou, S. Chen, P. Nie, K. Qian and Z. Li, et al., Data-Driven Fast Clustering of Second-Life Lithium-Ion Battery: Mechanism and Algorithm, Adv. Theory Simul., 2020, 3(8), 2000109 CrossRef CAS.
- S. Tao, R. Ma, Z. Zhao, G. Ma, L. Su and H. Chang, et al., Generative learning assisted state-of-health estimation for sustainable battery recycling with random retirement conditions, Nat. Commun., 2024, 15(1), 10154 CrossRef CAS PubMed.
- Y. Wang, X. Feng, D. Guo, H. Hsu, J. Hou and F. Zhang, et al., Temperature excavation to boost machine learning battery thermochemical predictions, Joule, 2024, 8, 2639–2651 CrossRef CAS.
- Y. Ma, W. Sun, Z. Zhao, L. Gu, H. Zhang and Y. Jin, et al., Physically rational data augmentation for energy consumption estimation of electric vehicles, Appl. Energy, 2024, 373, 123871 CrossRef.
- C. Zhang, Y. Zhang, Z. Li, Z. Zhang, M. S. Nazir and T. Peng, Enhancing state of charge and state of energy estimation in Lithium-ion batteries based on a TimesNet model with Gaussian data augmentation and error correction, Appl. Energy, 2024, 359, 122669 CrossRef.
- C. Hu, F. Cheng, Y. Zhao, S. Guo and L. Ma, State of charge estimation for lithium-ion batteries based on data augmentation with generative adversarial network, J. Energy Storage, 2024, 80, 110004 CrossRef.
- J. Lu, R. Xiong, J. Tian, C. Wang and F. Sun, Deep learning to estimate lithium-ion battery state of health without additional degradation experiments, Nat. Commun., 2023, 14(1), 2760 CrossRef CAS PubMed.
- S. Kim, N. H. Kim and J.-H. Choi, Prediction of remaining useful life by data augmentation technique based on dynamic time warping, Mech. Syst. Signal Process., 2020, 136, 106486 CrossRef.
- H. Gao, K. Lin, Y. Cui and Y. Chen, Quantum assimilation-based data augmentation for state of health prediction of lithium-ion batteries with peculiar degradation paths, Appl. Soft Comput., 2022, 129, 109515 CrossRef.
- V. Sulzer, P. Mohtat, A. Aitio, S. Lee, Y. T. Yeh and F. Steinbacher, et al., The challenge and opportunity of battery lifetime prediction from field data, Joule, 2021, 5(8), 1934–1955 CrossRef.
- A. Aitio and D. A. Howey, Predicting battery end of life from solar off-grid system field data using machine learning, Joule, 2021, 5(12), 3204–3220 CrossRef.
- V. Steininger, K. Rumpf, P. Hüsson, W. Li and D. U. Sauer, Automated feature extraction to integrate field and laboratory data for aging diagnosis of automotive lithium-ion batteries, Cell Rep. Phys. Sci., 2023, 4(10), 101596 CrossRef CAS.
- J. Zhang, Y. Wang, B. Jiang, H. He, S. Huang and C. Wang, et al., Realistic fault detection of li-ion battery via dynamical deep learning, Nat. Commun., 2023, 14(1), 5940 CrossRef CAS PubMed.
- R. Ibraheem, P. Dechent and G. dos Reis, Path signature-based life prognostics of Li-ion battery using pulse test data, Appl. Energy, 2025, 378, 124820 CrossRef CAS.
- S. Jiang, J. Shi and S. Moura, Relax, estimate, and track: a simple battery state-of-charge and state-of-health estimation method, arXiv, 2024, preprint, arXiv:2408.01127 DOI:10.48550/arXiv.2408.01127.
- S. Jiang, J. Shi, M. Borah and S. Moura, Weaknesses and Improvements of the Extended Kalman Filter for Battery State-of-Charge and State-of-Health Estimation, 2024 American Control Conference (ACC), IEEE, 2024.
- P. V. H. Seger, P.-X. Thivel and D. Riu, A second life Li-ion battery ageing model with uncertainties: from cell to pack analysis, J. Power Sources, 2022, 541, 231663 CrossRef CAS.
- I. Mathews, B. Xu, W. He, V. Barreto, T. Buonassisi and I. M. Peters, Technoeconomic model of second-life batteries for utility-scale solar considering calendar and cycle aging, Appl. Energy, 2020, 269, 115127 CrossRef CAS.
- D. P. Kingma and M. Welling, Auto-encoding variational bayes, arXiv, 2013, preprint, arXiv:1312.6114 DOI:10.48550/arXiv.1312.6114.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ee02217g |
| This journal is © The Royal Society of Chemistry 2025 |