Flooding revisited: electrolyte management ensures robust electrochemical CO₂ reduction

Abstract

Flooding, one of the main performance fading mechanisms of CO₂ electrolysers, is vaguely defined, and often used for very different phenomena that cause cell/stack failure. The term itself is also controversial, as a fully wet electrode is often observed after high-performing zero-gap electrolyser cells are disassembled. To resolve this apparent contradiction, we investigated the cation balance in a zero-gap CO₂ electrolyser cell operated under different conditions, and also actively controlled cation concentration in the cathode compartment to study its effect on the electrolyser performance. While a given cation concentration is needed for high-rate CO-formation, its further increase boosts the hydrogen evolution rate and decreases the CO₂ reduction rate (through two different mechanisms). When the cation content in the cathode is too high, hydrogen evolution occurs also on the carbon cathode support and the availability of CO₂ decreases at the cathode catalyst. During continuous operation, the cation flux from the anolyte to the cathode might change, which is also reflected in the cell performance. We demonstrate that such changes in performance can be counteracted by actively controlling the anolyte composition. We also suggest descriptors of the “health” of the cell, to ensure durable operation via the active control of the cation concentration at the cathode.

---

Broader context

The electrochemical reduction of CO₂ is expected to play a role in closing the artificial carbon cycle, using a harmful greenhouse gas as feedstock for valuable chemicals. Building on recent achievements, high reaction rate and selectivity can be routinely achieved. Measurements at high current densities, however, brought several further scientific challenges to daylight, mostly regarding process stability. A key factor is maintaining ideal chemical conditions at the cathode, by ensuring the presence of cations and water at the catalyst surface, while minimizing the diffusion length of CO₂ in liquid phase. Here we demonstrate that the cation buildup at the cathode depends heavily on the applied conditions. There is an optimal cation concentration at the cathode, where CO₂ reduction occurs at the highest rate. Below this concentration, the activity of the catalyst decreases. At higher concentrations, the cathode support carbon paper becomes an active catalyst for the parasitic hydrogen evolution reaction, and at very high concentrations, the vigorously forming hydrogen blocks the path of CO₂ to the catalyst. These effects are reversible, and their extent can be quantified from EIS measurements. Our findings pave the way for long-term operation of CO₂ electrolyzers under continuously adjusted reaction conditions.

Introduction

Electrochemical CO₂ reduction (CO₂R) can be employed to produce raw materials and chemical products,^1,2 while using CO₂ as a feedstock. Despite the rapid developments, CO₂ electrolysers still need to be improved to reach the performance metrics required for industry adoption. These metrics include energy efficiency, reaction rate, selectivity, conversion, and durability.^3,4 Importantly, industrially relevant values of each have already been approached separately, but their combination is still a great challenge. Particularly, there is room for improvement in mitigating performance decay during continuous operation.

When using commercial cell components, performance fading is most often attributed to the flooding within the cathode gas diffusion electrode (GDE).^3,5,6 Nonetheless, flooding is rather vaguely defined. The term originates from the fuel cell community, where the original meaning was the accumulation of water in the GDEs, due to inadequate water removal.⁷ This leads to partial blockage and hence the decrease of the electrochemically active surface area. While the mechanistic investigation of electrochemical flooding has a rich literature on proton exchange membrane fuel cells (PEMFCs),⁸ for CO₂ electrolysers such studies have appeared just recently, most importantly via advanced imaging and spectroscopic means.^9–15 In CO₂ electrolysers, a decrease in CO₂R^15–17 rate and an increase in hydrogen evolution reaction¹⁶ (HER) rate are both typically referred to as flooding, although these might occur because of very different reasons.

Furthermore, the contribution of these mechanisms depends on the electrolyzer cell structure – in a microfluidic electrolyzer cell, a liquid film forms on the backside of the GDE, therefore blocking CO₂ from reaching the catalyst. In zero-gap electrolyzer cells the picture is even murkier, as described in what follows. An important and obvious difference between PEMFCs and CO₂ electrolysers is the presence of alkali metal ions in the cell in the latter case, that can induce electrowetting^15,17,18 and/or carbonate precipitate formation.¹⁹ Both processes directly influence the open pore structure and wetting of the GDE. Beyond the cell design^20–22 and water management,²³ the electrolyte balance of the electrolyser cell²⁴ can therefore be a critical factor in the quest against flooding. Anion-exchange membrane (AEM) separated zero-gap CO₂ electrolysers generally operate employing a dilute alkali metal salt containing solution as anolyte,²⁵ instead of pure water. Although AEMs should completely block the flow of cations from the anode side to the cathode side, there is growing evidence for cation crossover^26–28 (Fig. 1a). As recent studies revealed,^29–31 alkali cations are needed at the cathode catalyst surface to boost the CO₂R rate and ensure high reaction selectivity for CO formation. Rather interestingly, this imperfect cation filtering of AEMs is the reason that allows CO₂R to proceed at a high rate.^26,28 Increasing the anolyte concentration beyond a certain level, however, can undesirably impact the durability of the electrolyser cell.¹⁹ Previously, we have developed a possible solution to this problem, which is based on the periodic enrichment of the cathode with an alkali metal salt solution (activation) while using pure water as the anolyte.²⁶ While the current density and selectivity of the cell can be maintained by this method, its industrial applicability is not straightforward.

Fig. 1 Illustration of the apparent paradox. (a) Simplified depiction of transport phenomena in the membrane electrode assembly (MPL – microporous layer, PTL – porous transport layer). (b) Back side of the GDE (cathode) in the disassembled cell after 6 hours of electrolysis at 300 mA cm⁻² current density using 0.05 M CsHCO₃ anolyte. At the end of the electrolysis the CO faradaic efficiency was over 80%. The two experimental approaches used in this study: (c) anolyte control, (d) active control of the Cs⁺ concentration in the cathode GDE.

In many studies, the degradation of the cell performance was assigned to flooding and/or salt precipitate formation.^19,32–37 According to our experience, however, zero-gap electrolyser cells can show high and stable performance despite notable amounts of water and alkali metal cations present in the GDE during operation (Fig. 1b). To resolve this apparent paradox, the exact alkali metal ion-, and water balance^33,38 of the cell, and their evolution in time must be revealed. Here, we investigated the alkali metal ion transport in the cell and repurposed the activation from our previous work²⁶ as a tool to investigate the effects of cations on the performance of the CO₂ electrolyzer cell. Through this, we uncovered a much broader picture about flooding, and proposed a mitigation approach ensuring long-term durability.

Results and discussion

Experimental approaches

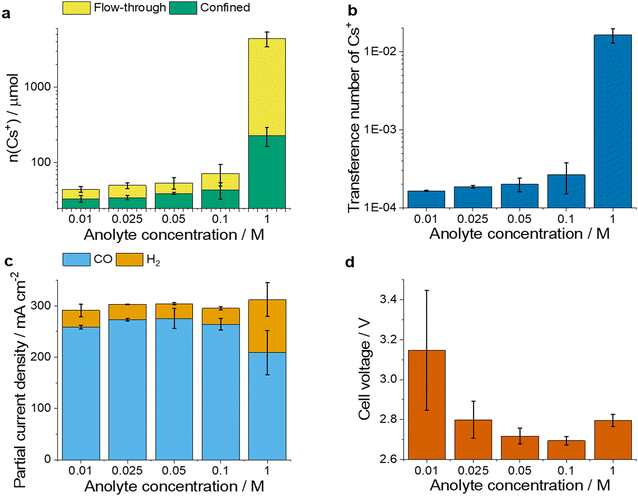
To better understand the effect of the Cs⁺ concentration in the cathode GDE on CO₂R, we designed two experimental methods. The first was tracking the cation transport from the anolyte during CO₂R (cross-over) while operating the electrolyser cell at different conditions (Fig. 1c), including varied current density and anolyte concentration. During these experiments, we collected the liquid phase percolating through the GDE during electrolysis and determined its Cs⁺ ion content – this will be referred to as the flow-through Cs⁺ amount. After electrolysis, the pores of the GDE were thoroughly washed with a water-isopropanol mixture, to collect the second fraction of Cs⁺-containing liquid. The amount of Cs⁺ ions in this liquid aliquot will be referred to as confined Cs⁺ amount (see Methods and Fig. S1, ESI† for details). The second approach was the controlled injection of ions into the catalyst layer (referred to as activation in our previous work²⁶), hence the active control of the cation balance of the cell (Fig. 1d). To determine the Cs⁺ amount in the GDE, the same washing protocol was applied here as in the case of the first method to determine the amount of confined Cs⁺. This way, we aimed to quickly create the conditions in the GDE that develop during longer operations.

Cs⁺ ion transport under varying operating conditions

First, the effect of anolyte concentration on the CO₂R rate and the Cs⁺ crossover was studied at a fixed current density (j = 300 mA cm⁻²), see Fig. 2. Conclusions were drawn from 3-hour-long measurements to exclude any transient effects from the initial period of the electrolysis. We found that the amount of flow-through and confined Cs⁺, as well as the transference number (calculated as the ratio of the charge carried by the transported Cs⁺ ions and the total charge passed over the same period) of Cs⁺ increased when more concentrated anolytes were used (Fig. 2a and b). Particularly large amounts of Cs⁺ ions (over 4400 μmol, 60 times more than normal operation with 0.1 M anolyte) were detected at the cathode when the anolyte concentration was increased to 1.0 M, showing a drastic reduction of the membrane permselectivity in accordance with previous studies.²⁸ The partial current density for CO (j_CO) and H₂ (j_H2) formation did not change with the anolyte concentration between 0.01 M and 0.1 M (Fig. 2c), while at 1.0 M the selectivity changed in favor of hydrogen evolution. The latter can be attributed to the high (more than ten times larger) Cs⁺ amount (also concentration) at the cathode.

Fig. 2 The dependence of Cs⁺ transport and electrolyser performance on anolyte concentration. (a) The amount of flow-through and confined Cs⁺ (b) transference number of Cs⁺ for different anolyte concentrations (0.01–1 M CsHCO₃) after 3 h of galvanostatic electrolysis. (c) j_CO and j_H2 and (d) cell voltages for different anolyte concentrations (0.01–1 M CsHCO₃) at 2.5 ± 0.15 h during galvanostatic CO₂R. The current density was 300 mA cm⁻². The values are means and the error bars represent the standard deviation of at least 2 independent measurements.

We also observed changes in the cell voltage with the varying anolyte concentration (Fig. 2d). As the anolyte concentration increased from 0.01 M to 0.1 M the cell voltage decreased (consistent with the CO₂R promoting role of Cs^+ 30,39). At 1.0 M anolyte concentration, however, the cell voltage increased again, possibly indicating transport losses and/or changes in the accessible catalytic surface area. These results are in line with former scattered results reported in the literature,^28,34 and clearly show that the cation crossover intensifies with the increasing anolyte concentration. They also suggest that too large amounts of cations in the cathode decrease the CO₂R process selectivity.

Next, we investigated the effect of current density on the Cs⁺ transport. The amount of flow-through and confined Cs⁺ (Fig. 3a), as well as the transference number of Cs⁺ (Fig. 3b) increased gradually with the current density up to 600 mA cm⁻². Above this current, however, these values seemed to reach a plateau. The trends in the confined Cs⁺ amounts indicate the saturation of the catalytically active surface (i.e., charging the double layer). Trends in the flow-through Cs⁺ amount and the transference number are more complex. Importantly, a similar trend was observed when a Sustainion AEM was used instead of the PiperION AEM (Fig. S2, ESI†). The transport of Cs⁺ ions might occur via migration and diffusion (convection through the membrane can be neglected in this system), and transport rate will be dictated by the rate of these two processes combined. We attribute the increase in the transference number of Cs⁺ mostly to locally elevated temperatures at high current densities,⁴⁰ and to the possibly caused changes in the structure and hydration of the membrane and the cathode catalyst layer.⁴¹ Furthermore, the migration rate of Cs⁺ ions is also increased by the increasingly negative cathode potentials at higher current densities. The diffusion rate also increases with local heating, but is decreased by the build-up of higher cathodic Cs⁺ concentration, which decreases the concentration gradient across the AEM.

Fig. 3 Current density-dependent cell operation. (a) The amount of flow-through and confined Cs⁺ and (b) transference number of Cs⁺ after 3 h of galvanostatic electrolysis. (c) j_CO and j_H2 (d) cell voltages at different current densities (300–800 mA cm⁻²) at 2.5 ± 0.2 h during galvanostatic CO₂R measurement. The anolyte was 0.1 M CsHCO₃. The values are means and the error bars represent the standard deviation of at least 2 independent measurements.

Importantly, the j_CO mirrored the amount of confined Cs⁺ (Fig. 3c) which can be explained by the well-documented promoting effect of Cs⁺ on CO₂R rate.³⁹ At higher total current densities, the j_H2 and cell voltage increased notably (Fig. 3c and d). Interestingly, the CO formation rate was not decreasing, even at current densities above 600 mA cm⁻². This implies that the active sites for CO₂R are not (largely) blocked, but additional active sites become active for HER in case of large Cs⁺ amounts in the cathode GDE.

Active control of the Cs⁺ content of the cathode while using pure-water anolyte

To better control the local chemical environment at the cathode, its Cs⁺-content was influenced by activation with different concentration solutions (Fig. S3, ESI†), meanwhile running the electrolyser cell with pure water anolyte (see Methods for details). We assume that due to the rapid solution injection, the local concentration of Cs⁺ ions will be identical to that in the activation solution, resulting in a better understanding of the effect of local concentration.

Not surprisingly, the confined amount of Cs⁺ (Fig. 4a) was practically zero for the control experiments performed without activation and activation with 0 M solution (i.e., solvent mixture with no added electrolyte). In line with our aforementioned assumption, the amount of confined Cs⁺ monotonically increased with increasing activation solution concentration. When performing a similar set of experiments with a 0.1 M CsHCO₃ anolyte instead of pure water (Fig. S4, ESI†), a similar trend, but notably higher Cs⁺ contents were measured, highlighting the prominent impact of cation transport from the anolyte on the local chemical environment at the cathode.

Fig. 4 The effects of activation with different concentrations of activation solution using water as anolyte. (a) The amount of confined Cs⁺ (b) j_CO and j_H2 5 minutes after activation with different activation solution concentrations or without activation during chronoamperometric CO₂ reduction reaction measurement. The anolyte was ultrapure water. The cell voltage was 3.0 V without iR compensation. The values are means and the error bars represent the standard deviation of at least 3 independent measurements. The different background colours in (b) are only used to highlight the different regions.

As a specific example, the confined amount of Cs⁺ for a cell operated with 0.1 M anolyte without activation at larger current densities was approximately 150 μmol (Fig. 3). A very similar amount was measured for the pure-water anolyte case with 0.7 M activation solution concentration.

We note that for some measurement points, the standard deviation of the detected Cs⁺ amount is particularly large. This can be mostly attributed to the instability of the electrolyser under unfavourable conditions (high current densities, high activation solution concentrations, and very low or high anolyte concentration). The reproducibility of measurement under favourable conditions (low-to-medium current densities, moderate activation solution concentration, and moderate anolyte concentration) was much better. This highlights, how sensitive the operation of such CO₂ electrolyzer cells to the applied conditions is, which will be a key issue for long-term operation.

The activation manifested in different effects, depending on the concentration of the activation solutions. We defined four different regions based on the reaction selectivity (Fig. 4b). In the first region the j_CO is less than 200 mA cm⁻² because of the insufficient Cs⁺ content^29,39 of the cathode GDE, but gradually increases with the increasing concentration of the activation solution. In this region, j_H2 remains below 100 mA cm⁻² and is constant within experimental error. In the second region, the j_CO is around 500 mA cm⁻², while j_H2 is low (around 20 mA cm⁻²).

This region is the “sweet spot” of Cs⁺ amount, in which the optimal cell performance occurs. In the third region, j_H2 increased, but j_CO did not change notably. In this region, the Cs⁺ content of the GDE enhances HER rates but does not yet affect the CO₂R rate significantly. In the fourth region, the j_CO decreases gradually (to 0 mA cm⁻² at the highest concentration applied here) while a high and gradually increasing HER rate is observed (up to 750 mA cm⁻²). In this region, the excessive Cs⁺ content of the cathode GDE hinders CO₂R and enhances HER proportionally to the Cs⁺ amount. A similar trend was observed when performing the activation measurements with KOH solutions (Fig. S5, ESI†), suggesting that our conclusions are general, and can be qualitatively extended to other systems as well.

We mention that no precipitate formation was observed with the naked eye after electrolysis during cell disassembly. This, however, does not mean that there is no precipitate in the cell during electrolysis. It was found by others that even in acidic electrolytes there can be (bi)carbonate precipitate formation during CO₂ electrolysis,³⁶ suggesting that the local gradients (pH, cation and (bi)carbonate concentration) allow the formation of phases that are not stable in the bulk electrolyte. We assume that the decrease in CO₂R rate is either caused by carbonate precipitate formation^19,32–37 or mass transport inhibition by electrolyte solution saturation of the pores of the cathode GDE,⁴² or by the decrease of available CO₂ as the result of pH increase by HER/CO₂R.^12,43 A combination of these effects can also occur.

From a performance standpoint, the 0.1 M anolyte case without activation is similar to the pure-water anolyte case with 0.5 M activation, despite the two times larger amount of confined Cs⁺ in the former case (Fig. S4, ESI,†vs.Fig. 4). This suggests that the spatial distribution of Cs⁺ might also be different in the activation and the regular cell operation cases. To visualize the spatial distribution of Cs⁺, cross-section elemental composition analysis was performed on GDEs after activation experiments at different concentrations.

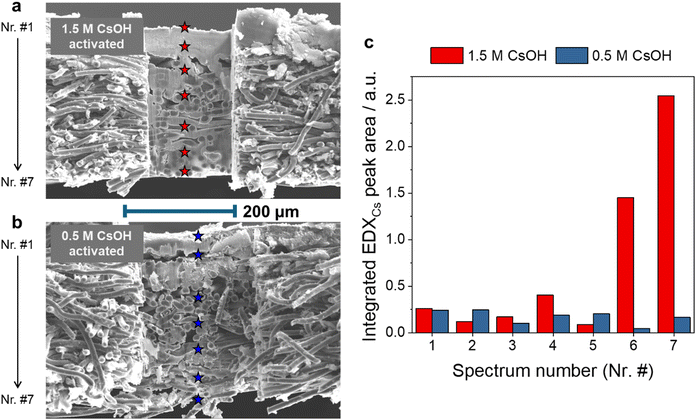
A very similar Cs⁺ accumulation was observed in the microporous layer when activation was performed with either 0.5 M or 1.5 M concentration solutions (Fig. S6, ESI† and Fig. 5a–c). A major difference between these cases is seen for the macroporous layer, and especially its part that is farthest from the catalyst layer. The large amount of Cs⁺ in this region for the 1.5 M activation solution concentration also suggests either local precipitate formation or the presence of a large volume of liquid, which can hinder the transport of CO₂ to the catalyst layer, and therefore the lower CO2R selectivity in this case.

Fig. 5 Spatial distribution of Cs⁺ within the GDE after the activation experiments. SEM images of FIB-treated GDEs after activation experiments with (a) 1.5 M CsOH and (b) 0.5 M CsOH solutions. (c) Integrated peak areas related to the Cs content of the samples, in the function of sampling location. #1 denotes the Ag catalyst layer, while #7 is the back of the GDL.

We performed further activation experiments while using CsHCO₃ electrolyte solution (0.1 M and 0.05 M concentrations, Fig. S4 and S7, ESI,† respectively) as anolyte instead of pure water. In these cases, already without activation we observed high CO₂R rate and low HER rate (second region), as expected because of the above-shown cation crossover from the anode to the cathode. Interestingly, activation with a low concentration of CsOH solution (up to 0.1 M) resulted in a decrease in the amount of Cs⁺, indicating that the local Cs⁺ concentration at the cathode is higher than 0.1 M (in the case of 0.1 M CsHCO₃ anolyte). When we carried out activation with a CsOH solution with a concentration ≥0.5 M, we reached the region of gradual performance decay (gradual increase of HER and decrease of CO₂R rate). The threshold activation solution to get into the third and fourth region, however, was slightly lower when CsHCO₃ anolyte was used instead of pure water (0.5 M vs. 0.7 M and 1.0 M vs. 1.5 M respectively), in accordance with the additional Cs⁺ transport from the anolyte through the membrane.

To better understand the changes in the electrolyser performance we performed electrochemical impedance spectroscopy (EIS) measurements during the activation experiments, in line with recent studies correlating the EIS response of the cell with the flooding.^44,45 Note that we could not differentiate among the contributions of the cell components in the EIS spectra, therefore the capacitance value is derived from fitting the data using an R₁/R₂ + Q₂ circuit, which describes the measured datapoint reasonably well (Fig. S8, ESI†). The such derived “overall capacitance” is related to the whole electrolyser cell, including contributions from all components (anode, membrane, cathode). We assume that the most notable changes occur at the cathode upon activation, and therefore the change in this “overall capacitance” reflects the capacitance change of the cathode catalyst. To correlate the EIS measurements with the electrochemical performance, the results of the activation experiments were plotted as the function of the derived capacitance (Fig. 6a, note the logarithmic scale). When the capacitance exceeded 6 mF cm⁻², j_H2 drastically increased, eventually reaching as high as 750 mA cm⁻². Parallelly, j_CO diminished to 0 mA cm⁻². The capacitance of 6.25 mF cm⁻² corresponds to the highest estimate⁴⁶ for the porous Ag catalyst (considering all Ag amount to contribute to the capacitance, see Methods section for its calculation). The high capacitance (up to 20 mF cm⁻²) (Fig. S9a and b, ESI†) value at high activation concentrations therefore suggests that not only the silver catalyst layer is the electrochemically active material, but other components of the cathode compartment also participate in the electrochemical process. Measurements in which 0.1 M CsHCO₃ solution was used as anolyte show the same phenomenon at approximately the same threshold capacitance around 6 mF cm⁻² (Fig. S10a, ESI†), and a similar trend in HER rates (Fig. S10b, ESI†).

Fig. 6 The role of carbon GDL in increased HER selectivity. (a) Dependence of j_H2 and j_CO on capacitance (b) j_H2 5 minutes after activation using activation solutions with different concentrations during chronoamperometric CO₂ reduction reaction measurement. The cathode was Ag catalyst coated carbon GDL (a) or a catalyst-free carbon GDL (b). The anolyte was ultrapure water. The cell voltage without iR compensation was 3.0 V.

To elucidate the possible role of the carbon gas-diffusion layer (GDL) in the increased j_H2 after activation, we performed measurements with catalyst-free carbon GDLs instead of Ag GDEs. Surprisingly, a notable increase in j_H2 was witnessed in this case as well upon activation with 0.5 M or 1 M activation solution (Fig. 6b)! The measured HER rate at 1 M activation concentration was very close to that observed with Ag GDEs (Fig. 4b) under identical experimental conditions. Very little to no CO was detected when using catalyst-free carbon GDLs. More interestingly, the quantified amounts of confined Cs⁺ during this experiment were almost identical when using a catalyst-free GDL or a silver-coated GDE (Fig. S11, ESI†), and a high concentration activation was performed. The confined amount was higher for the GDE (compared to the bare GDL) at low activation concentrations, which can be explained by a fraction of the ions being trapped in the catalyst layer. The almost identical value at high concentrations indicates that most ions are restrained in the GDL structure, as evidenced from the FIB-SEM analysis (Fig. 5a and c), leading to increased HER rates.

Activation with concentrated solutions (i.e., 0.7 M and 1.5 M) leads to a decrease in CO formation rate compared to optimal activation (0.5 M; j_CO = 500 mA cm⁻²), which is assumed to be caused by the hindered access of Ag catalyst to CO₂, as indicated by the cation (and assumedly liquid) build-up in the back of the GDE (Fig. S6, ESI† and Fig. 5). This was further confirmed by analysing the anode gas composition,⁴⁷ which is dictated by the ion transport processes in the electrolyser cell. In a similarly structured, well-performing CO₂ electrolyser,⁴⁸ the value lies around 66.7% CO₂ (with 33.3% O₂). This large amount of CO₂ in the anode gas is caused by the reaction of excess CO₂ with the cathodically formed hydroxide ions (CO₂ + 2e⁻ + H₂O → CO + 2OH⁻ and CO₂ + 2OH⁻ → CO₃²⁻ + H₂O). The 2 : 1 CO₂ : O₂ ratio implies that CO₃²⁻ ions are the species participating in the ion conduction process.⁴⁸ When activating with 0.7 M or 1.5 M solutions, the CO₂ concentration in the anode gas decreases below 66.7% (Fig. S12, ESI†). This indicates that the ion conduction in the AEM is not purely maintained by CO₃²⁻ ions, but rather a mixed CO₃²⁻/OH⁻ conduction occurs (note, that in case of pure hydroxide conduction the CO₂ concentration in the anode gas would be 0). This implies that the catalyst layer near the AEM lacks sufficient CO₂ for the neutralization of electrogenerated OH⁻ ions. It is reasonable to argue that in this case the catalyst does not have enough CO₂ for optimal CO₂R, and this leads to decreased j_CO.

Flooding in CO₂ electrolysers is therefore not only related to the excess amount of water in the GDE, but rather to the presence of an electrolyte solution with high enough concentration. To operate the cell efficiently, the electrolyte concentration in the cathode GDE must be kept within an optimal range. A good indicator of the local Cs⁺ amount at the cathode can be the capacitance extracted from EIS. If it is too low, more Cs⁺ is needed, if it is too high less Cs⁺ is needed in the cathode GDE.

Observation and control of the Cs⁺ transport during longer electrolysis

While injecting electrolyte solutions into the cathode compartment is an efficient way to maintain high electrolyser performance, the cost associated with using an organic solvent mixture and large amounts of KOH/CsOH electrolyte is rather high. These experiments, however, reveal the optimal concentration of cations at the cathode, which shall be sustained during operation. One of the most effective methods for controlling the Cs⁺ flow into the cathode is to actively control the anolyte concentration, according to the actual state of the electrolyser cell/stack.

We examined the Cs⁺ transport during a 10-day-long continuous operation in a custom-built, almost autonomously operating electrolyser test station⁴⁹ (Fig. 7a, b and Fig. S13, ESI†). In this case, we only collected the flow-through fraction of Cs⁺, to avoid any disturbance in the cell operation (thus Cs⁺ transport), which would have been caused by the periodic washing of the cathode compartment. When looking at this longer timescale, the amount of Cs⁺ ions flowing through the cell hourly (Cs⁺ flux) increased until reaching a maximum after ca. 25 hours of operation time.

Fig. 7 The long-term (in)stability of a CO₂ electrolyser. (a) j_CO, j_H2 and total current density (b) flow-through rate of Cs⁺ during galvanostatic long-term CO₂R measurement at j = 300 mA cm⁻² applying a 0.1 M CsHCO₃ anolyte. The conductivity measurement was sampled at fixed time intervals to avoid showing artefacts caused by the daily temperature fluctuation. (c) and (d) Long-term operation of the CO₂ electrolyzer cell at j = 300 mA cm⁻², with a voltage limit of 3.5 V. The anolyte was varied during the experiments: 0.05 M CsHCO₃ in the regions with a light brown background, pure water with an orange background and 1 M CsHCO₃ with a red background. Adjacent averaging was applied to reduce the noise in the curves for clarity.

Subsequently, it started to decrease, finally stabilizing around zero. In other words, a steady-state was reached (Fig. 7b). We note that as the Cs⁺ flux increased j_CO decreased and j_H2 increased, and when the crossover rate of Cs⁺ started to decrease, the cell started to recover (i.e., the CO/H₂ ratio improved). Finally, when negligible net Cs⁺ transport took place through the membrane, the cell operation stabilized (Fig. 7b). Looking at the cell voltage (Fig. S13, ESI†), a trend almost identical to the change in Cs⁺ flux was observed. The initial 2.75 V cell voltage increased to ca. 2.9 V in the first 30 hours when it reached a peak value. A decrease in cell voltage was observed after this peak, in parallel with the decreasing Cs⁺ flux. This suggests an initial cation build-up in the electrolyzer cell, ensuring a stable further operation.

The above observations clearly show that the CO₂ electrolysis in zero-gap cells is very dynamic (particularly in the initial stage). The parallel change in the cell voltage and selectivity with the changing cation flux also highlights the possibility of affecting cell operation by controlling the anolyte composition. This was demonstrated by performing a continuous electrolysis experiment for 200+ hours, while the anolyte composition was varied as follows: applying a 0.05 M CsHCO₃ solution as anolyte, the cell was run until a stable cell operation was achieved. At this point, the anolyte was changed to pure water (to decrease the cation concentration). After ca. 5 hours the cell voltage increased substantially and reached the set 3.5 V limit, while the CO : H₂ ratio decreased below 1. Therefore, the pure water was exchanged for 0.05 M CsHCO₃ anolyte, which quickly recovered the cell performance. When the cell operation stabilized, a similar back-and-forth switch using 1 M CsHCO₃ anolyte solution was performed (Fig. 7c). The more concentrated anolyte notably decreased the cell voltage, the CO-selectivity, however, dropped massively. Most interestingly, after switching back from the 1 M anolyte to the dilute CsHCO₃ solution, a decreased cell voltage and increased selectivity were observed compared to the base case, when the cell was operated continuously with the 0.05 M anolyte. This again suggests that a cation concentration build-up in the GDE facilitates proper cell operation. In contrast, the cell voltage is higher, and the selectivity is lower (compared to the base case) when the pure water is exchanged to the original dilute anolyte. This was confirmed by repeating the same experiment in reverse order – first switching to higher concentration anolyte, and then to pure water (Fig. 7d).

These results suggest that applying a constant anolyte concentration for the entire duration of the electrolysis, as it is generally aimed for in other industrial electrolysis processes, might not be optimal for CO2R. Instead, the active and adaptive control of the anolyte concentration shall be performed, based on the continuous monitoring of descriptors such as the gas cathode and anode gas composition, and cell voltage/current. Furthermore, flooding caused by the excess amount of cations in the GDE is reversible, the cell selectivity can be restored by applying conditions where this excess is removed. Depriving the cell from cations on the other hand deteriorates the cell performance, which is more difficult to restore. We note that by controlling the anolyte concentration, only the cation content at the cathode can be controlled. Other performance fading causes, such as the formation of polyacrolein on catalysts forming more complex products,⁵⁰ possibly requires a different mitigation strategy.

Conclusions

Here we studied the influence of electrolyte concentration in the GDE on the performance of CO₂R cells. We found that the presence of liquid water or dilute electrolyte solution in the cathode GDE alone is not detrimental to zero-gap CO₂ electrolysers, therefore using the term flooding for this phenomenon might be misleading. On the contrary, performance-decreasing flooding occurs when the concentration of cations in the GDE reaches a threshold value. In this case, the GDL becomes active in the electrochemical process shown by the appearance of the parasitic HER, occurring also on the carbon support. In more severe cases, the transport of CO₂ to the Ag catalyst gets hindered, therefore the CO₂R rate decreases. The hindered CO₂ transport has multiple possible causes: carbonate precipitation due to local gradients, electrolyte saturation of the pores of the cathode GDE, and the decrease of local CO₂ concentration because of local pH increase. On the other hand, a certain amount of cations is required for selective and high-rate CO₂R. Therefore, the electrolyte concentration in the cathode GDE must be kept in an optimal, narrow range. This is not straightforward, as the flow of cations to the cathode GDE under electrochemical CO₂R conditions changes over time. Therefore, the active control of the anolyte concentration is needed, to properly manage the cation supply. We have demonstrated that such active control is indeed possible, which paves the way for industrial implementation.

Experimental

Materials

The CsOH·H₂O and Ag nanopowder (d_avg < 100 nm, 99.5%, 5.0 m² g⁻¹) was purchased from Sigma-Aldrich. The PiperION (40 μm thick PiperION-A40-HCO3) membrane and PiperION ionomer dispersion (PiperION-A5-HCO3-EtOH, 5 wt% in EtOH) was purchased from Versogen. The IrO_x catalyst and the Freudenberg H23C6 gas-diffusion layer were purchased from FuelCellStore. MilliQ grade (ρ = 18.2 MΩ cm) ultrapure deionized water was produced using a Millipore Direct-Q 3 UV instrument and was used to prepare all the solutions.

The CsHCO₃ electrolyte solution was obtained from CsOH solution by bubbling CO₂ gas through it until saturation (for at least 30 minutes).

Electrode preparation

The cathode catalyst dispersion consisted of Ag nanopowder with 5 wt% PiperION ionomer (m(ionomer)/(m(ionomer) + m(Ag)) dispersed in a 1 : 1 isopropanol/water solvent mixture with a concentration of 24 mg cm⁻³ (Ag). The anode catalyst dispersion consisted of IrO_x nanoparticles with 15 wt% PiperION ionomer (m(ionomer)/(m(ionomer) + m(IrO_x)) dispersed in an identical solvent with a concentration of 17 mg cm⁻³ (IrO_x). The IrO_x dispersion was homogenized with a magnetic stirring bar at 600 rpm. The silver nanoparticles were dispersed with a high-power immersion sonotrode (3 min) and a regular ultrasonic bath for 20 min, and the dispersion was kept sonicated in the ultrasonic bath for the duration of spray coating (while keeping the bath temperature below 35 °C by additions of ice cubes).

The GDEs were fabricated using a hand-held airbrush. The Ag dispersion was spray coated onto preheated Freudenberg H23C6 GDLs on a hotplate at 100 °C until reaching a loading of 1.0 ± 0.1 mg cm⁻² (Ag). The anode catalyst dispersion was spray coated similarly, onto a porous Ti frit to reach a loading of 1.0 ± 0.1 mg cm⁻² (IrO_x). The loading was calculated from the substrate weight difference before and after the spray coating. The GDE was soaked in CsOH equivalent concentration to the anolyte 10 minutes before use, and washed with ultrapure water immediately before use. For example, for 0.1 M CsHCO₃ anolyte the GDE was soaked in 0.1 M CsOH.

Membrane pretreatment

The membranes were ion-exchanged before use for at least 24 hours in a 1 M CsOH solution, which was exchanged for a fresh solution after the first 5 hours. Immediately before cell assembly, the membrane was cut to size and placed into ultrapure water for 10 minutes and was thoroughly rinsed with ultrapure water.

Electrochemical measurements and cell assembly

All electrochemical measurements were performed in a custom-designed direct gas feed zero-gap electrolyser cell (Fig. S9, ESI†) with an active area of 8 cm². Commercially available AEM (40 μm thick PiperION-A40-HCO3) was used to separate the anode and the cathode chambers. The cell was assembled starting from the anode flowplate, continuing with the catalyst-coated Ti frit (anode), the anion exchange membrane, the PTFE gasket, the catalyst coated gas-diffusion layer (cathode) and finished with the cathode flowplate. The PTFE gasket was 200 μm thick to achieve the necessary compression for the approximately 250 μm thick catalyst-coated gas-diffusion layer. The cell assembly is secured with 6 bolts and nuts, tightened in three steps to 3 N m.

A Biologic VMP-300 potentiostat/galvanostat was used for chronoamperometry, chronopotentiometry and EIS measurements. The cell voltage refers to the voltage between the anode and cathode endplates without IR compensation. The CO₂ inlet gas flow rate was 12.5 cm³ cm⁻², controlled with a Bronkhorst MASS-STREAM D-6321 type mass flow controller. The CO₂ was humidified by bubbling it through ultrapure water heated to 60 °C. The gas line between the humidifier and the cell was heated to avoid any condensation. An external heating mantle heated the anolyte to achieve a cell temperature of 60 °C.

Capacitance determination

The capacitance was determined from a potentiostatic EIS measured at 3.0 V cell voltage from 200 kHz to 0.1 Hz. The potentiostatic EIS was fitted with an R₁ + R₂/Q₂ equivalent circuit (Fig. S8, ESI†), to calculate the double-layer capacitance.

The highest estimate of the capacitance of the Ag GDE was calculated by multiplying the Ag areal capacitance⁴⁶ (125 μF cm⁻²) by the specific surface area of the silver nanopowder provided by the supplier (5.0 m² g⁻¹) and the areal mass loading of the GDE (1 mg cm⁻²).

Gas product detection (cathode)

The gas products of the CO₂ electrolysis were detected using a Shimadzu Nexis-GC-2010 equipped with a BID detector. A Restek Shincarbon ST column was used to separate the zero-gap cell outlet gas, using grade 6.0 He carrier gas. The outlet flow rate was measured with an Agilent ADM flow meter. For long-term measurements, an online infrared-thermal conductivity gas analyzer (Gasboard-3100, customized for CO₂–CO–H₂ mixtures, Hubei Cubic-Ruiyi) was used, coupled with a McMillan S-110-4 Flo-Meter for continuous outlet flow rate measurement. The partial current densities were calculated from the outlet gas flow rate and the composition of the outlet gas.

Activation, washout protocol and Cs⁺ solution collection

A typical activation measurement starts with 40–45 minutes of electrolysis at 3.0 V to reach a stable state, while the gas products are being periodically analyzed. After this period, activation is performed (without stopping the chronoamperometry) resulting in a current spike (Fig. S2, ESI†). Approximately 5 minutes after activation the gas products were analyzed and the electrolysis was terminated. A washout step (see below) is performed right after finishing the electrolysis, to quantify the confined Cs⁺ amount.

The process of activation was described in detail in our previous work.²⁶ Briefly, 5 cm³ solution containing CsOH in a mixture of 75 vol% H₂O : 25 vol% isopropanol is loaded into a bypass loop. By turning two valves simultaneously, the solution is pushed through the cathode space by the action of the CO₂ flow used during electrolysis.

During the washout protocol to determine the amount of confined Cs⁺, 7 cm³ 75 vol% H₂O:25 vol% isopropanol mixture was loaded into a syringe, pushed into the gas inlet of the cell and then the liquid remaining in the pores of the GDE was removed by the CO₂ flow. This was repeated 4 times, bringing the total solvent used for washout to 28 cm³. The Cs⁺-containing liquid was collected from the gas outlet.

During CO₂ electrolysis, the fluid accumulating in the water trap of the gas outlet was collected and later analysed to determine the amount of flow-through Cs⁺.

Cs⁺ and K⁺ quantification

The collected Cs⁺ ion containing samples, were diluted with ultrapure water to a known volume. The concentration of Cs⁺ in the diluted samples was determined with ion chromatography. The amount of Cs⁺ was calculated from the volume after dilution and the measured concentration. The amount of flow-through Cs⁺ refers to the Cs⁺ determined from the liquid collected during the electrolysis from the fluid trap. The amount of confined Cs⁺ refers to the moles of Cs⁺ determined from liquid collected during the washout after the electrolysis. The same experimental procedure was applied for the quantification of the confined K⁺ amount for the activation experiments with KOH solutions.

The flow-through rate of Cs⁺ for the long-term measurement was determined by conductivity measurement (Fig. S8b, ESI†). The condensate from the water trap was channelled to a beaker covered with a plastic film. A conductometer was placed into the beaker, and its signal was recorded continuously. 100 cm³ ultra-pure water was poured into the beaker to make sure the conductometer probe was submerged. The amount of Cs⁺ in the accumulated fluid was calculated by multiplying its volume (Fig. S8c, ESI†) with the Cs⁺ concentration calculated from electrical conductivity. For calculating Cs⁺ concentration from electrical conductivity a calibration was measured with known concentration of CsHCO₃ solutions. The measured volumes were interpolated to obtain data points for all conductivity data points. The change over time in moles of Cs⁺ of the accumulated fluid with 48 h smooth (Savitzky–Golay, points of window 144 (48 h), polynomial order: 2) was plotted as flow-through rate of Cs⁺.

Morphology and composition characterization

A Thermo Scientific Apreo 2 scanning electron microscope (SEM), equipped with an EDX detector was used to collect information on the morphology and composition of the formed electrodes. To avoid the distortion of the GDE structure (that inevitably happens when a blade is used to prepare a sample for cross-section investigation), a ditch was formed in the GDE by focused ion beam (FIB) technique applying Ga ions, using with a Thermo Scientific Scios 2 SEM-FIB instrument.

Author contributions

Péter Gyenes: conceptualization, data curation, investigation, methodology, visualization, writing – original draft. Angelika A. Samu: investigation, methodology, visualization. Dorottya Hursán: data curation, investigation, methodology, supervision. Viktor Józó: investigation, data curation. Andrea Serfőző: investigation, methodology. Balázs Endrődi: conceptualization, data curation, supervision, writing – review & editing. Csaba Janáky: conceptualization, funding acquisition, supervision, writing – review & editing.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Conflicts of interest

There are patent applications pending, filed by the authors of this paper and their institutions. Application numbers: PCT/HU2019/095001 + PCT/HU2020/050033. Specifically, the first patent application covers the details of the cell architecture, description of the individual components of the cell. The second application covers the electrolysis process, including the regeneration and activation protocols. A third patent application has been submitted before the publication of this paper on the adaptive anolyte control process (SZTNH_EBEJ-20250611-02917).

Acknowledgements

Project no. RRF-2.3.1-21-2022-00009, titled National Laboratory for Renewable Energy, has been implemented with the support provided by the Recovery and Resilience Facility of the European Union within the framework of Programme Széchenyi Plan Plus. This project has received funding from the European Union's Horizon Europe research and innovation programme under grant agreement No. 101099284. The research was supported by the National Research, Development and Innovation Office (NKFIH) through the SNN-146476 project. D. H. thanks the funding provided by the Alexander von Humboldt Foundation. The authors thank Gergely F. Samu for his support with the SEM-FIB sample preparation.

References

1. M.-Y. Lee, K. T. Park, W. Lee, H. Lim, Y. Kwon and S. Kang, Crit. Rev. Environ. Sci. Technol., 2020, 50, 769–815.
2. Q. Lu and F. Jiao, Nano Energy, 2016, 29, 439–456.
3. J. M. Álvarez-Gómez and A. S. Varela, Energy Fuels, 2023, 37, 15283–15308.
4. W. Lai, Y. Qiao, Y. Wang and H. Huang, Adv. Mater., 2023, 35, 2306288.
5. U. O. Nwabara, E. R. Cofell, S. Verma, E. Negro and P. J. A. Kenis, ChemSusChem, 2020, 13, 855–875.
6. B. Huang, R. R. Rao, S. You, K. Hpone Myint, Y. Song, Y. Wang, W. Ding, L. Giordano, Y. Zhang, T. Wang, S. Muy, Y. Katayama, J. C. Grossman, A. P. Willard, K. Xu, Y. Jiang and Y. Shao-Horn, JACS Au, 2021, 1, 1674–1687.
7. H. Li, Y. Tang, Z. Wang, Z. Shi, S. Wu, D. Song, J. Zhang, K. Fatih, J. Zhang, H. Wang, Z. Liu, R. Abouatallah and A. Mazza, J. Power Sources, 2008, 178, 103–117.
8. J. Ihonen, M. Mikkola and G. Lindbergh, J. Electrochem. Soc., 2004, 151, A1152.
9. H. Hu, Y. Kong, M. Liu, V. Kolivoška, A. V. Rudnev, Y. Hou, R. Erni, S. Vesztergom and P. Broekmann, J. Mater. Chem. A, 2022, 11, 5083–5094.
10. K. Yang, R. Kas, W. A. Smith and T. Burdyny, ACS Energy Lett., 2021, 6, 33–40.
11. L. M. Baumgartner, C. I. Koopman, A. Forner-Cuenca and D. A. Vermaas, ACS Appl. Energy Mater., 2022, 5, 15125–15135.
12. A. Inoue, T. Harada, S. Nakanishi and K. Kamiya, EES Catal., 2023, 1, 9–16.
13. Y. Kong, M. Liu, H. Hu, Y. Hou, S. Vesztergom, M. D. J. Gálvez-Vázquez, I. Zelocualtecatl Montiel, V. Kolivoška and P. Broekmann, Small Methods, 2022, 6, 2200369.
14. A. M. Kalde, M. Grosseheide, S. Brosch, S. V. Pape, R. G. Keller, J. Linkhorst and M. Wessling, Small, 2022, 18, 202204012.
15. J. Osiewacz, M. Löffelholz, B. Ellendorff and T. Turek, J. Power Sources, 2024, 603, 234430.
16. E. W. Lees, B. A. W. Mowbray, F. G. L. Parlane and C. P. Berlinguette, Nat. Rev. Mater., 2021, 7, 55–64.
17. L. M. Baumgartner, A. Goryachev, C. I. Koopman, D. Franzen, B. Ellendorff, T. Turek and D. A. Vermaas, Energy Adv., 2023, 2, 1893–1904.
18. S. Brosch, F. Wiesner, A. Decker, J. Linkhorst and M. Wessling, Small, 2024, 20, 2310427.
19. E. R. Cofell, U. O. Nwabara, S. S. Bhargava, D. E. Henckel and P. J. A. Kenis, ACS Appl. Mater. Interfaces, 2021, 13, 15132–15142.
20. U. O. Nwabara, A. D. Hernandez, D. A. Henckel, X. Chen, E. R. Cofell, M. P. De-Heer, S. Verma, A. A. Gewirth and P. J. A. Kenis, ACS Appl. Energy Mater., 2021, 4, 5175–5186.
21. S. Liang, N. Altaf, L. Huang, Y. Gao and Q. Wang, J. CO₂ Util., 2020, 35, 90–105.
22. T. H. M. Pham, J. Zhang, M. Li, T. H. Shen, Y. Ko, V. Tileli, W. Luo and A. Züttel, Adv. Energy Mater., 2022, 12, 202103663.
23. D. G. Wheeler, B. A. W. Mowbray, A. Reyes, F. Habibzadeh, J. He and C. P. Berlinguette, Energy Environ. Sci., 2020, 13, 5126–5134.
24. J. Y. Zhao, Y. Liu, W. Li, C. F. Wen, H. Q. Fu, H. Y. Yuan, P. F. Liu and H. G. Yang, Chem Catal., 2023, 3, 100471.
25. Z. Liu, H. Yang, R. Kutz and R. I. Masel, J. Electrochem. Soc., 2018, 165, J3371–J3377.
26. B. Endrődi, A. Samu, E. Kecsenovity, T. Halmágyi, D. Sebők and C. Janáky, Nat. Energy, 2021, 6, 439–448.
27. B. Ó. Joensen, J. A. Zamora Zeledón, L. Trotochaud, A. Sartori, M. Mirolo, A. B. Moss, S. Garg, I. Chorkendorff, J. Drnec, B. Seger and Q. Xu, Joule, 2024, 8, 1754–1771.
28. G. A. El-Nagar, F. Haun, S. Gupta, S. Stojkovikj and M. T. Mayer, Nat. Commun., 2023, 14, 2062.
29. M. C. O. Monteiro, F. Dattila, B. Hagedoorn, R. García-Muelas, N. López and M. T. M. Koper, Nat. Catal., 2021, 4, 654–662.
30. L. D. Chen, Nat. Catal., 2021, 4, 641–642.
31. S. J. Shin, H. Choi, S. Ringe, D. H. Won, H. S. Oh, D. H. Kim, T. Lee, D. H. Nam, H. Kim and C. H. Choi, Nat. Commun., 2022, 13, 5482.
32. M. Sassenburg, M. Kelly, S. Subramanian, W. A. Smith and T. Burdyny, ACS Energy Lett., 2023, 8, 321–331.
33. M. Li, M. N. Idros, Y. Wu, T. Burdyny, S. Garg, X. S. Zhao, G. Wang and T. E. Rufford, J. Mater. Chem. A, 2021, 9, 19369–19409.
34. S. Garg, Q. Xu, A. B. Moss, M. Mirolo, W. Deng, I. Chorkendorff, J. Drnec and B. Seger, Energy Environ. Sci., 2023, 16, 1631–1643.
35. Y. Xu, J. P. Edwards, S. Liu, R. K. Miao, J. E. Huang, C. M. Gabardo, C. P. O’Brien, J. Li, E. H. Sargent and D. Sinton, ACS Energy Lett., 2021, 6, 809–815.
36. F. Bernasconi, N. Plainpan, M. Mirolo, Q. Wang, P. Zeng, C. Battaglia and A. Senocrate, ACS Catal., 2024, 8232–8237.
37. S. Kato, S. Ito, S. Nakahata, R. Kurihara, T. Harada, S. Nakanishi and K. Kamiya, ChemSusChem, 2024, 17, e202401013.
38. T. H. Shen, L. Spillane, J. Peng, Y. Shao-Horn and V. Tileli, Nat. Catal., 2022, 5, 30–36.
39. S. J. Shin, H. Choi, S. Ringe, D. H. Won, H. S. Oh, D. H. Kim, T. Lee, D. H. Nam, H. Kim and C. H. Choi, Nat. Commun., 2022, 13, 5482.
40. J. Wang, Y. Zhao, B. P. Setzler, S. Rojas-Carbonell, C. Ben Yehuda, A. Amel, M. Page, L. Wang, K. Hu, L. Shi, S. Gottesfeld, B. Xu and Y. Yan, Nat. Energy, 2019, 4, 392–398.
41. J. Disch, L. Bohn, S. Koch, M. Schulz, Y. Han, A. Tengattini, L. Helfen, M. Breitwieser and S. Vierrath, Nat. Commun., 2022, 13, 6099.
42. S. Brosch, F. Wiesner, A. Decker, J. Linkhorst and M. Wessling, Small, 2024, 20, 2310427.
43. A. J. Welch, A. Q. Fenwick, A. Böhme, H. Y. Chen, I. Sullivan, X. Li, J. S. DuChene, C. Xiang and H. A. Atwater, J. Phys. Chem. C, 2021, 125, 20896–20904.
44. M. E. Leonard, L. E. Clarke, A. Forner-Cuenca, S. M. Brown and F. R. Brushett, ChemSusChem, 2020, 13, 400–411.
45. A. B. Moss, S. Garg, M. Mirolo, C. A. Giron Rodriguez, R. Ilvonen, I. Chorkendorff, J. Drnec and B. Seger, Joule, 2023, 7, 350–365.
46. N. A. Hampson, D. Larkin and J. R. Morley, J. Electrochem. Soc., 1967, 114, 817.
47. S. Brückner, Q. Feng, W. Ju, D. Galliani, A. Testolin, M. Klingenhof, S. Ott and P. Strasser, Nat. Chem. Eng., 2024, 1, 229–239.
48. Á. Vass, B. Endrödi, G. F. Samu, Á. Balog, A. Kormányos, S. Cherevko and C. Janáky, ACS Energy Lett., 2021, 6, 3801–3808.
49. A. A. Samu, A. Kormanyos, E. Kecsenovity, N. Szilagyi, B. Endrodi and C. Janaky, ACS Energy Lett., 2022, 7, 1859–1861.
50. M. K. Kovalev, H. Ren, M. Zakir Muhamad, J. W. Ager and A. A. Lapkin, ACS Energy Lett., 2022, 7, 599–601.

---

Footnote

† Electronic supplementary information (ESI) available: Detailed description of our methodology, further electrochemical and materials characterization results. See DOI: https://doi.org/10.1039/d5ee01464f

---