Aging matrix visualizes complexity of battery aging across hundreds of cycling protocols

Abstract

To reliably deploy lithium-ion batteries, a fundamental understanding of cycling aging behavior is critical. Battery aging consists of complex and highly coupled phenomena, making it challenging to develop a holistic interpretation. In this work, we generate a diverse battery cycling dataset with a broad range of degradation trajectories, consisting of 359 high energy density commercial Li(Ni,Co,Al)O₂/graphite + SiO_x cylindrical 21 700 cells cycled across 207 unique cycling protocols. We consolidate aging via 16 mechanistic state-of-health (SOH) metrics, including cell-level performance metrics, electrode-specific capacities/state-of-charges (SOCs), and aging trajectory metrics. We develop a framework using interpretable machine learning and explainable features to generate an aging matrix that visually deconvolutes the complex battery degradation behavior. This generalizable data-driven mechanistic framework simplifies the complex interplay between cycling conditions, degradation modes, and SOH, acting as a hypothesis-generation tool to aid battery users in identifying key degradation regimes for further study and experimentation.

---

Broader context

The growing demand for energy storage solutions in electrifying transportation and decarbonizing the electricity grid underscores the need to accelerate advancements in battery technology to meet various performance and cost requirements. Understanding battery aging is one of the most resource consuming tasks in developing new battery technologies due to complex and intercoupled degradation pathways. To expedite battery technology development, methodologies summarizing degradation across diverse operating conditions are necessary. In this work, we use data-driven methodologies in combination with interpretable metrics to summarize degradation across hundreds of cycling conditions visually with an aging matrix. This aging matrix highlights how 16 state-of-health indicators depend on both operating conditions and other mechanistic state-of-health metrics. This aging matrix and the corresponding methodology allow battery designers to quickly visualize their battery degradation space, and researchers to identify areas of interest for further experimentation or analysis.

1 Introduction

Lithium-ion batteries are a key enabler for electrifying transportation and decarbonizing the electricity grid.^1–8 Optimizing new battery designs is challenging due to the need to simultaneously meet multiple performance targets while satisfying design constraints. Improving battery lifetime is especially difficult due to the slow, nonlinear, and coupled physics of the aging process.^9–18 It is time- and resource-consuming to observe the impact that design choices have on battery life and to understand why one battery degrades more rapidly than another.

While characterization at the materials and cell level can offer a mechanistic understanding of battery aging,^19–22 it is slow and low throughput.²³ Instead, modeling offers a more accessible route to understanding battery aging. Physics-based models, such as the Doyle–Fuller–Newman model,^24–26 utilize fundamental electrode parameters, capture physical principles such as conservation laws, and explicitly model degradation mechanisms leading to more interpretable behavior. Nonetheless, predicting battery lifetime under unseen conditions remains challenging due to the complexity of interconnected aging phenomena¹⁴ and challenges of model parameter identifiability.²⁷ Another approach uses mechanistic models to estimate electrode-specific capacities and lithium inventory.^28–30 These models capture aggregate physical mechanisms with fewer model parameters than physics-based simulations.^31–35 Tracking electrode-specific capacities independently provides a clearer picture of what types of degradation occur under various operating conditions.^23,36

In recent years, machine learning (ML) techniques have been developed to analyze battery aging through a data-driven lens.^37–56 While ML techniques are high throughput and predictive, a pure data-driven approach with complex black-box models (e.g. deep learning) obscures relationships between cycling conditions and battery aging mechanisms, overlooking key scientific and engineering insights.⁵⁷ Data-driven models with interpretable characteristics could build trust by reproducing known trends, and inform engineering decisions from physical insights all while retaining flexibility and ease of use.

Existing battery aging datasets are typically collected with specific applications in mind.^58–66 To give application examples, Attia, Severson, and colleagues^67,68 focused on optimizing electric vehicle fast charging protocols. Diao et al.⁶⁹ examined different temperatures to understand how temperatures accelerate battery aging. Paulson, Ward, and colleagues^48,70 tested various cell chemistries to understand the differences in their aging and build transferable ML models. Wildfeuer et al.⁷¹ examined different state-of-charge (SOC) ranges and temperatures in both cycling and calendar aging tests to investigate different experimental factors, but did not use multi-variate analyses, such as ML techniques, to deconvolute the multiple aging factors at play. To capture degradation across a variety of use cases data must span across use cases, including a wide range of SOC, charging, and discharging protocols (see ESI,† Table S5 for an overview of cycling datasets).⁷² Many of these studies first analyze the data with a traditional methodology relying on holding all cycling parameters constant, and varying one cycling parameter at a time to get the influence of a selected cycling parameter.^{69,71,73–77} However, as the dimensionality of cycling parameters increases and one probes an increasingly broad degradation space, the cycling parameters' complex and intercoupled influence on battery degradation can make conventional analysis intractable. Additionally, if one wants to relate measured inputs that cannot be controlled by an operator to be constant, such as capacity or resistance, to battery degradation, a traditional univariate approach does not generalize well to these use cases. Instead, interpretable data-driven models comprehensively applied to large datasets can be leveraged as a critical tool to bridge the gap between pure data-driven approaches and traditional methodologies, allowing researchers to better understand their battery systems.

In this work, we propose and develop a physically interpretable, data-driven understanding of lithium-ion battery aging. We first generate a large dataset consisting of 359 cells under 207 unique cycling conditions spanning diverse use cases and aging trajectories in-house. We then develop a comprehensive understanding of degradation, within the bounds of the gathered dataset, by calculating 16 mechanistic SOH metrics across the degradation aging trajectory. By combining interpretable ML with explainable features, we extract complex correlations to these SOH metrics to identify factors contributing significantly to degradation. In doing this, we demonstrate that physically meaningful features should be used in combination with methods that robustly extract feature importance to gather insights from large datasets.^78–82 This approach addresses the challenges of analyzing a comprehensive set of SOH metrics across diverse operating conditions using traditional univariate methods, and the limited system-level insight offered by standalone black-box models or early prediction models with features that are not easily interpretable, such as the features employed in Severson et al.⁶⁷ By using an explainable data-driven model in combination with a diverse battery aging dataset, we generate an aging matrix to analyze and visually summarize battery degradation across a comprehensive set of SOH metrics. More generally, constraining ML models to use features that have clear physical meaning dramatically enhances explainability, complementing pure data-driven featurization approaches.

2 Methods

2.1 Comprehensive aging characterization

The dataset collected in this paper includes electrochemical data from 359 Li(Ni,Co,Al)O₂/graphite + SiO_x cylindrical 21 700 cells cycled for over 2 years (Fig. 1a). To induce diverse aging trajectories, we explore a broad range of cycling voltage windows (varying the upper and lower voltage cutoff) and cycling rates (varying the charging C-rates in two-step charging, and the discharge C-rate); however, we do not vary the temperature in this study to allow for equal comparison of the diagnostic cycle (Fig. 1a and b, additionally see Section S.2.3 for all cycling parameters varied and their values, ESI†). We note that degradation modes can change drastically with different ambient temperatures, for example biasing towards lithium plating or solid electrolyte interphase growth, however these effects are not further analyzed in this work and will be the topic of future work.^69,83,84 To compare the effects of different cycling conditions, we apply a standardized, periodic diagnostic cycle to comprehensively probe SOH and resistance over cell lifetime (typically every 100 aging cycles – Fig. 1b). Given the variation of voltage windows values (discharge cutoff voltage spanning 2.7–3.7 V, and charge cutoff voltage spanning 3.7–4.2 V) and cycling rates (spanning 0.2–3C) throughout the dataset, we compare cell lifetime using capacity throughput-based equivalent full cycles (EFCs).⁷³ EFCs are calculated by taking the total capacity throughput of the battery and dividing it by the nominal capacity before cycling (4.84 A h), normalizing for the fact that the batteries are tested between different voltage ranges. This metric is closer to the total miles driven when considered under an electric vehicle application, and is often used in replacement of cycles when the tested voltage ranges vary. In total we examine 359 batteries cycled under 207 unique aging protocols yielding EFCs at end of life (EOL) ranging from 44 to 994 (or 63 to 4641 cycles for their respective protocol). EOL is defined as when the 0.2C rate reference performance test (RPT), Q_RPT,0.2C, reaches 80% of the 4.84 A h nominal capacity. Critically, because a single health metric, such as low-rate capacity, does not capture all facets of degradation (Fig. 1c, d and ESI,† Section S.8), we select, calculate, and track 16 mechanistic SOH metrics (see ESI,† Table S1 for a summary of abbreviations). The term ‘mechanistic SOH metrics’ is used to broadly refer to the collection of features used to quantify degradation in this study.

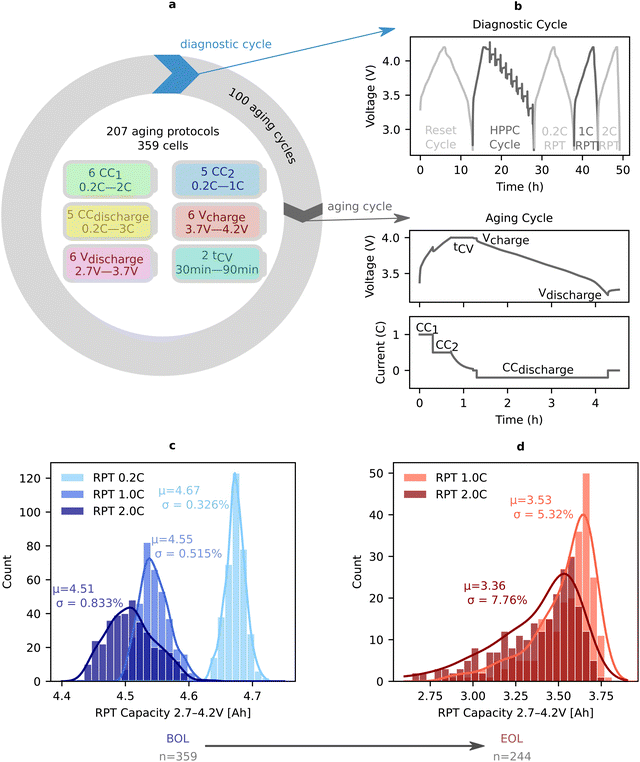Fig. 1 Overview of the dataset. (a) We highlight the diverse cycling parameters varied in our dataset. All batteries in this dataset are cycled in a chamber with a temperature set point of 25 °C. The nominal cycling experiment structure is shown schematically with a loop where cells go through a diagnostic “checkup” cycle, followed by 100 aging cycles repeating until end of life (EOL). (b) The diagnostic cycle consisting of a reset cycle, a hybrid pulse power characterization (HPPC),⁸⁵ and three rate reference performance tests (RPTs) at 0.2C, 1C, and 2C discharge currents (see ESI,† Table S2 for full conditions). Mechanistic SOH metrics are extracted from various parts of this diagnostic cycle data (see ESI,† Section S.4 for further details). Additionally, the aging cycle voltage and current vs. time traces are shown with cycling parameter names overlaid on the areas they would affect. (c) The distribution of rate-dependent capacities at the beginning of life (BOL). Means and coefficients of variation are included in the plot, showcasing the tight distribution at BOL. (d) The distribution of rate-dependent capacities at EOL (defined by 0.2C RPT capacity reaching 80% of the nominal capacity, 4.84 A h). For further information on BOL to EOL variability see ESI,† Section S.8.⁸⁶

We first quantify six cell-level performance metrics: (1) total EFCs at EOL, (2) 1C rate-specific capacity: Q_RPT,1C, (3) 2C rate-specific capacity: Q_RPT,2C, (4) ohmic resistance: R_ohm, (5) charge transfer resistance: R_ct, and (6) polarization resistance: R_p. We calculate resistances through pulse measurements performed during the hybrid pulse power characterization (HPPC) sequence of the diagnostic cycle at various SOCs (see ESI,† Section S.4.2 for definitions and calculation details for resistance metrics). Unless otherwise specified, the resistances reported are at 50% SOC.

Second, to determine electrode-specific capacities/SOCs, we implement differential voltage fitting (DVF), a mechanistic model algorithm. DVF is a non-invasive degradation probe that fits a measured full cell voltage profile with an emulated profile created from the underlying cathode and anode voltage profiles (see more details in Sections S.4.3 and S.6 (ESI†) where we also justify the validity and emphasize limitations of our results obtained with a moderate current (0.2C) data). Similar methodologies have been implemented by other groups.^{23,32,34,87–89} Using DVF we extract electrode capacities (Q_PE and Q_NE) and lithium inventory (Q_Li). Additional information, such as the SOC of either electrode at a full cell specified voltage is further calculated. We specifically select SOC_PE,2.7V, SOC_NE,2.7V, SOC_PE,4.0V, and SOC_NE,4.0V because the electrode-specific SOCs near the fully discharged and fully charged states heavily influence aging.⁹⁰

These cell-level and electrode-specific metrics are calculated at every diagnostic cycle for each cell and tracked from beginning of life (BOL) to EOL. As would be expected for commercial cells, these metrics have low variability at BOL (coefficient of variations <1%, Fig. 1c). At EOL however, there is high variation in the rate capability (approximately 5% and 8% for RPT1.0C and RPT2.0C respectively), resistance, and electrode-specific capacities/SOCs (Fig. 1d and ESI,† Section S.8). This observation underscores the importance of using a comprehensive set of SOH metrics and confirms that the cycling conditions in this work induce a wide range of degradation trajectories.

In addition to probing cell-level and electrode-specific metrics with each diagnostic cycle, we also quantify the aging trajectory over the entire battery lifetime using metrics we refer to as trajectory metrics.^9,91 We define three trajectory metrics: (1) knee indicator: knee, (2) resistance growth factor: R′′, and (3) negative/positive capacity (N/P) ratio: NP Ratio. The knee indicator describes a sudden and accelerated capacity-based degradation (i.e., a knee in the capacity vs. EFC curve) with knee indicator >0 if a knee exists at any point in the cell lifetime. The resistance growth factor captures the curvature of resistance with respect to EFCs, indicating whether resistance grows at an accelerating or decelerating rate during cycling. NP ratio is commonly used in battery manufacturing to determine how much active mass of cathode and anode material to coat onto an electrode sheet. In this case we dynamically calculate an NP ratio with the ratio of the estimated Q_NE and Q_PE at EOL. While the exact ratio depends on the half cell voltage bounds, this metric gives a measure of cell balancing between positive and negative electrode remaining capacities.⁹² Section S.7 (ESI†) details the calculations of these trajectory metrics.

We combine these 16 total cell-level performance metrics, electrode-specific capacities/SOCs, and trajectory metrics, collectively referred to as mechanistic SOH metrics, to comprehensively quantify battery aging. By concurrently assessing these metrics, we reveal their relationships to 207 cycling conditions to develop a comprehensive summary of aging. Fig. 2 visualizes selected metrics calculated on all cells in the dataset. The lifetime of these cells ranges from less than 50 EFCs to nearly 1000 EFCs, forming a broad set of trajectories. Similar trends are seen across the cell-level performance metrics and electrode-specific capacities.

Fig. 2 Mechanistic SOH metric degradation trajectories. (a) The cell-level performance metrics column shows the trajectories of selected performance metrics: the 0.2C RPT discharge capacity (Q_RPT,0.2C) (top) and the combination of R_ohm, R_ct, R_p (R_tot) at 50% SOC (bottom). (b) The electrode-specific capacities/SOCs column depicts the trajectories of electrode-specific capacities, Q_NE, Q_PE, and Q_Li, on the left. A utilization plot showing electrode-specific SOCs at the charged and discharged state is on the right. (c) The trajectory metrics row shows histograms of the values for the NP ratio, resistance growth factor, and knee indicator. The highlighted protocol (in dark blue) represents the CC_discharge = 0.2C, CC₁ = CC₂ = 0.2C, V_charge = 4.2 V, and V_discharge = 2.7 V aging condition. This protocol has four experimental repeats, shown by the scatter markers, with the solid line representing the mean trajectory. The gray lines in the background showcase the mean trajectory of all other unique protocols. This protocol appears as a dark blue vertical bar in the trajectory metric histograms. All batteries in this dataset are cycled in a chamber with a temperature set point of 25 °C.

2.2 Shapley additive explanations reveal feature importance

By varying six cycling parameters across this dataset (ESI,† Table S4), we induce a diverse range of EOL states and trajectory metrics (Fig. 2a–c). However, determining the importance of each of the six individual cycling parameters on mechanistic SOH metrics is challenging in a high-dimensional and convoluted degradation space. A traditional univariate approach involves holding all cycling conditions constant and varying a single experimental cycling condition. However, due to the high-dimensional space of battery degradation, this methodology falls short in several cases. For example, a traditional methodology where a subset of cycling conditions with all parameters constant except for one varied independent variable is shown in Fig. 3a–c. The different color lines have different values of cycling parameters held constant, and depending on what these values are, from Fig. 3a and b it is possible to conclude that increasing V_charge or CC_discharge has a negative, neutral, or positive effect on EFC. In more subtle cases, the magnitude of the effect of a given cycling parameter depends on the other cycling parameters, as illustrated in Fig. 3c. If the other parameters were not varied, this phenomenon would not be seen within the bounds of the dataset. As the number of different testing conditions and SOH metrics to track increases, plotting all of the data to learn from underlying trends quickly becomes intractable. Instead, a methodology to summarize and visualize all the various trends of degradation in a dataset is needed to allow researchers to focus on what the dominating contributors to degradation are (see Section S.3 (ESI†) for an approach built on traditional methodology).

Fig. 3 Understanding feature importance through ML models and SHAP. (a–c) A traditional approach to understanding a feature's importance varying one parameter at a time, such as V_charge, while holding the others constants and analyzing the impact on mechanistic SOH metrics such as EFC. Because of the highly convoluted degradation space, the impact of a parameter can drastically change depending on the values of the other controlled parameters. This is shown with three differently colored curves representing different parameters held constant while (a) V_charge, (b) CC_discharge, and (c) CC₁ is allowed to vary (see ESI,† Section S.3 for the aging conditions and further discussion). (d) ML model structure, with cycling conditions as inputs and mechanistic SOH metrics (here EFC) as output. (e) Leveraging SHAP analysis, feature importance is revealed. Each row represents a feature, and its spread correlates with its impact. (f) Each feature impact in (e) is aggregated for all data points by taking the mean absolute SHAP value and the resulting feature strengths are summarized in one line for each SOH metric model (here the EFC model). The stronger the color, the more impactful the feature. The relative absolute error (RAE) is additionally plotted alongside feature importance as model performance is critical in extracting the sensible feature importance.

To account for the complex interdependence and convoluted degradation space, we utilize machine learning in combination with Shapley additive explanations (SHAP)⁹³ analysis to determine the features that are the most important. A nonlinear machine learning model, in this case a random forest model, is first used to learn the complex correlations of cycling parameters to a SOH metric of interest (Fig. 3d). We then utilize SHAP analysis to attribute model prediction to individual feature importance which calculates the features' average marginal contributions to the model prediction, taking into account all possible combinations.⁹⁴ As we are using these models to capture complex correlations, well-performing models and features are critical to extract sensible feature importances (Parity plots in ESI,† Section S.10.7). The SHAP importance value for the input features for all cells present in the training dataset is reported in Fig. 3e. Finally, we collapse this plot by taking the mean absolute value of the SHAP values for each of the features on each cell in the dataset to generate a heatmap plot (Fig. 3f). This heatmap visualizes what features on average have the greatest importance for a SOH metric of interest. This information directs the battery pack designer, or researcher to the most impactful cycling parameters for further analysis. In the case of EFC prediction, we see that CC₁ is the most important feature and CC₂ is the second most important feature. Additionally, as SHAP values describe the generated model, the error of the model is critical in qualifying whether the model and the corresponding SHAP values have captured meaningful trends. Because of this, the relative absolute error (RAE) is plotted alongside the feature importances in Fig. 3f. To see how this approach compares to a state-of-the-art univariate comparison where one parameter is varied while others are held constant to assess the importance of each feature individually, see ESI,† Section S.3. Another key advantage of this approach is that it works in cases where the model inputs are not control parameters that can be held constant, such as calculated features (resistance, capacity, etc.) that are influenced by control parameters. This use case is explored in Sections 3.2 and 3.3.

3 Results and discussion

3.1 Impact of cycling conditions on mechanistic SOH metrics

We first develop and deploy SHAP analysis on protocol models that use cycling protocol parameters alone as inputs. These protocol models are useful, for example, when a battery pack designer or battery management system engineer wants to understand how usage conditions, such as charging rate, affect a battery system's lifetime. Protocol models that achieve low prediction error allow for a reliable SHAP analysis (more details in ESI,† Section S.10.7 for performance, and ESI,† Section S.10.2 for train/test split). Each model and corresponding feature importances are represented by a single row in Fig. 4b. Together these models create an aging matrix visually summarizing degradation and identifying areas to further explore to uncover the underlying dominant degradation modes.

Fig. 4 Impact of cycling conditions. (a) ML model structure, with cycling conditions as inputs and EOL mechanistic SOH metrics as outputs. This is the full expanded version of what was shown in Fig. 3d–f. (b) SHAP feature importances for each protocol model, one line representing a model for one specific mechanistic SOH metric. A darker hue indicates higher feature importance. This degradation matrix representation visualizes the impact of cycling conditions on degradation in a high-dimensional space and the corresponding model training errors.

No single cycling parameter dominates all mechanistic SOH metrics. For example, the cell-level performance metrics Q_RPT,1C and Q_RPT,2C are dominated by CC₂, while R_ct is dominated by V_charge. Conversely, EFC is more convoluted and is impacted by both charging currents CC₁ and CC₂, but also by V_discharge. On the one hand, higher charging currents cause lithium plating and side reactions. On the other hand, lower V_discharge utilizes more silicon, which degrades faster than graphite.⁹⁵ These hypotheses can be validated by further analysis and experimentation. For example, disassembling cells that have a higher charging currents and low EFC and observing through scanning electron microscopy (SEM) if the anode shows comparatively more lithium plating to see if lithium plating is the dominant degradation mode for this cycling condition. Similarly, for low V_discharge and low EFC one can again observe the anode through SEM to see if there is comparatively more cracking due to cycling the silicon region of the anode. Across metrics, V_discharge and t_CV appear less frequently as the dominant feature (within the bounds of this dataset) for most mechanistic SOH metrics (except V_discharge for EFC), despite previous reports stating their importance.^96,97

Additionally, our visual aging matrix representation makes it easy to identify mechanistic SOH metrics governed by the same features by reading the matrix column by column. For example, one can notice that EFC and R_p, the polarization resistance, are both dominated by CC₁. The correlation between EFC and R_p is verified in ESI,† Fig. S24, with a Spearman coefficient of −0.81. This suggests that long-term battery degradation is governed by the long time-scale effects such as diffusion limitations in the electrodes rather than by the growth of resistive films or sluggish reactions. These latter two phenomena, represented by the ohmic and charge transfer resistances R_ohm and R_ct are both dominated by V_charge. Additionally, Fig. 4 underlines the detrimental role of V_charge on SOC_PE,4.0V, as cathodes are known to suffer from structure instabilities and side reactions at high SOC.^98–100 To test these hypotheses one can disassemble the batteries that have high V_charge and large ohmic and charge transfer resistance, and perform EIS on the cathode electrode sheet. However, this phenomenon does not seem to affect the battery cycle life, likely because of the conservative maximum charge cutoff voltage of 4.2 V. Moreover, Fig. S17 (ESI†) shows that degradation at the anode (Q_NE) is more pronounced than that on the cathode (Q_PE), suggesting that EOL is anode-limited (within the bounds of this dataset). This is also reported in the dynamic NP ratio at EOL. One could experimentally verify these findings by disassembling the batteries and performing a low rate capacity check up in a half cell.

We note that many of the electrode-specific capacities/SOCs have higher RAE error and low SHAP feature importance across all features, so the results should be taken more cautiously. With that being said, Q_Li has a strong CC₁ dependence alongside EFC and R_p potentially indicating similar degradation modes. The electrode-specific SOCs, calculated from electrode-specific capacities, depend most strongly on V_charge and CC_discharge, potentially sharing degradation modes with resistance metrics such as R_ct and R_ohm.

Finally, for the trajectory metrics, the knee indicator depends most strongly on CC₁ and CC_discharge, the resistance growth factor (R′′) on V_charge and CC_discharge, and the convoluted degradation metric NP ratio has a high RAE and low feature importance across parameters. For detailed information on the influence of cycling conditions on mechanistic SOH metrics, as well as model performance, see ESI,† Section S.10.7.

To summarize, this aging matrix representation directly visualizes important trends to design cycling limits, not just to maximize cycle life but also a wide range of other performance metrics. For example, suppose it is important to prevent capacity knees, from this analysis, we see that modifying CC₁ and CC_discharge will have the greatest impact, whereas modifying the V_discharge would be less effective. Generating this aging matrix allows us to visually summarize battery degradation across numerous conditions and mechanistic SOH metrics, and the aging matrix serves as a hypothesis-generating tool by highlighting features and responses that should be further investigated. This aging matrix allows a battery pack designer or researcher to design hypotheses and focus their efforts on the components of degradation that are dominant in their dataset. While this analysis highlights regions of interest, further study and experimentation, such as the cell teardown studies proposed in this work, can be performed to confirm hypotheses. Additionally, we emphasize that while we chose a representative set of 16 mechanistic SOH metrics, this framework can be extended to additional design-specific SOH metrics and operating conditions depending on the use case. If the design space of the operating conditions or the battery chemistry differs significantly, the models used here would need to be fine-tuned or retrained on newly collected data to remain representative.

3.2 Fundamental investigation of performance metric degradation

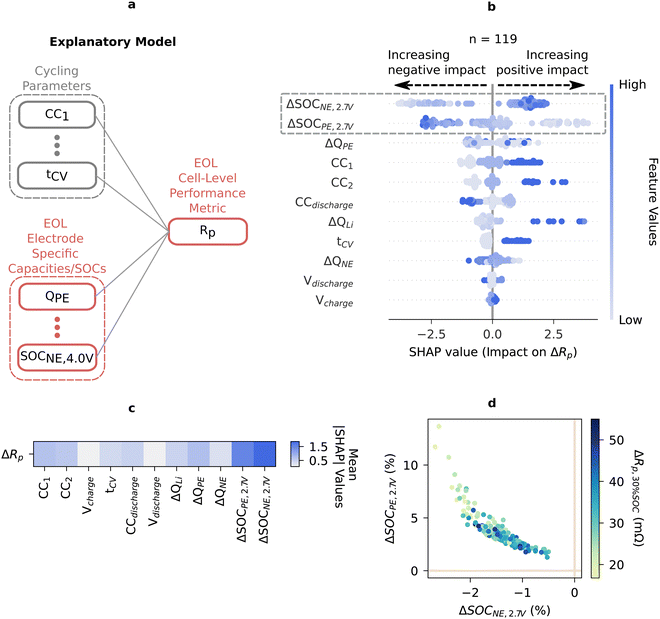
Having examined and simplified the relationship between 16 mechanistic SOH metrics and cycling conditions using an aging matrix, we evidenced the role of R_p on battery lifetime. To further understand what degradation mechanism drives R_p growth, we deploy our explanatory ML framework and address an exemplary yet important question: “how does anode and cathode degradation contribute to the polarization resistance growth in a battery?” It is challenging to understand where resistance growth inside a battery originates using only full cell measurements because of the convolution of multiple effects from both electrodes. The resistances of individual electrodes depend strongly on their respective electrode's lithiation state and degradation. In addition, as cells age under diverse usage conditions, individual electrodes proceed via various degradation pathways such as cathode structural changes¹⁰¹ and anode SEI formation.¹⁰² These changes lead to varying degrees of electrode slippage or SOC shifts, adjusting the relative lithium composition of the cathode and anode at a given full cell SOC (ESI,† Fig. S23).

We built an “explanatory model” by adding electrode-specific capacities/SOCs metrics as input features to understand their impact on the output R_p (Fig. 5). Specifically, these features are the changes in mechanistic SOH metrics from BOL to EOL (represented by Δ). Low SOC resistance is of particular interest here as it is the most influential for determining when a battery reaches a voltage cutoff. Fig. 5 shows the analysis results for R_p at 30% SOC.

Fig. 5 Analyzing EOL cell-level performance metrics through electrode capacities/SOCs. (a) Schematic representation of the explanatory models to understand the degradation of cell-level performance metrics. Gray rectangles indicate cycling parameters, and red rectangles indicate mechanistic SOH metrics that are obtained at EOL. (b) SHAP feature importance based on the random forest model fit on 30% SOC R_p resistance in descending order. The ΔSOCs are the most important features, but show an opposite relationship with resistance increase. (c) A row of matrix plot summarizing the feature importance in the SHAP analysis. (d) ΔSOC_PE,2.7V plotted against ΔSOC_NE,2.7V at EOL for 180 cells. Color bar indicates full cell polarization resistance growth at 30% SOC. The high correlation indicates that feature importance can be convoluted. At low SOC, resistance increase is driven by the cathode lithiation level (lower ΔSOC_PE,2.7V).

Fig. 5b lists the most dominant features contributing to the observed polarization resistance growth R_p. From the SHAP analysis, we observe that two electrode-specific features, ΔSOC_PE,2.7V and ΔSOC_NE,2.7V, are dominant features impacting the total resistance but show opposite relationships with resistance growth (Fig. 5b and c). Surprisingly, negative electrode over-discharging (ΔSOC_NE,2.7V decreasing) leads to lower resistance increase. This is unexpected because electrode kinetics are typically most sluggish at the SOC extremes; therefore, at low SOC, we expect that resistance should increase in the direction of deeper discharge for an electrode.⁹⁷

To understand the origin of this effect, we recall how ΔSOC_PE,2.7V and ΔSOC_NE,2.7V are calculated. These quantities are calculated at a specified full cell voltage (2.7 V for this example) and, as a result, are highly correlated (Fig. 5d and ESI,† Section S.9.1). This correlation arises because when one electrode's SOC shifts, regardless of the aging mechanism, the other electrode's SOC must inversely shift to produce the same measured full cell voltage (ESI,† Fig. S23 explores this in further detail). In general, SHAP is unable to differentiate between highly correlated features, and repeating the SHAP analysis multiple times reveals that either ΔSOC_PE,2.7V or ΔSOC_NE,2.7V can emerge as the most dominant feature (ESI,† Fig. S21). However, if ΔSOC_NE,2.7V is removed from this explanatory model, for example, ΔSOC_PE,2.7V appears as the sole dominant feature (ESI,† Fig. S22).

From Fig. 5d, we show that, at low SOC, while negative electrode over-discharging (decreasing ΔSOC_NE,2.7V) correlates with lower resistance increase, over-discharged positive electrodes (decreasing ΔSOC_PE,2.7V) correlate to higher resistance increase. As resistance increasing with overdischarging of an electrode is in line with the understanding that electrode kinetics are most sluggish at SOC extremes, we rationalize that low SOC resistance rise is dominated by more lithiated positive electrode.

Lastly, charging currents (CC₁, and CC₂) and discharging current (CC_discharge) both impact R_p at 30% SOC, but with opposite correlations (CC₁ and CC₂ have a positive correlation while CC_discharge has a negative correlation, indicated by the color scheme in Fig. 5b). It has previously been reported that fast delithiation current (high CC₁ and CC₂) expedites cathode capacity fade and impedance rise, while fast lithiation current (high CC_discharge) can effectively avoid the kinetically limited region of cathodes and enhance the cyclability of cathodes.¹⁰³ Our results point to these potential hypotheses.

While our framework based on a random forest model and SHAP explainability does not differentiate between the contributions from two highly correlated electrodes, explainable features together with scientific knowledge contribute to hypothesize causation. Although in this section, we highlight and analyze low SOC resistance as one example, we emphasize that this approach generalizes to any mechanistic aging feature of interest (ESI,† Section S.9.3).

3.3 Explainable features in early prediction

Building upon our previous section where random forest regression models are employed to correlate aging features to cycling parameters (protocol models), we now use both cycling parameters and early values of the mechanistic SOH metrics (specifically, the evolution between the 1st and 3rd diagnostic cycle or cycle 0 to cycle 130 respectively) as inputs to our interpretable ML model (Fig. 6a). These models termed “diagnostic-aided models” differentiate cells with the same cycling parameters, allowing cell-to-cell variability to be accounted for in fixed aging conditions. Additionally, as these models are using early values of the explainable SOH metrics used in this work, this early prediction aging matrix conserves interpretability.

Fig. 6 Early prediction of mechanistic SOH metrics. (a) The architecture of the diagnostic-aided model where the blue rectangles indicate values that are extracted early in the cycling and red rectangles are extracted at EOL. (b) SHAP analysis degradation matrix plot showcasing the importance of cycling protocols and early prediction features on predicting mechanistic SOH metrics. All early prediction features are extracted as the difference of mechanistic SOH metrics from 1st to 3rd (0 and 130 cycles respectively for most cases) diagnostic cycle (annotated as d3-d1).

We then apply the framework demonstrated in the previous sections on our diagnostic-aided model and present the results in an aging matrix plot in Fig. 6b (see ESI,† Section S.10.7 for parity plots and full SHAP analysis). For the mechanistic SOH metrics, the diagonal entries of the aging matrix are highlighted and correspond to self-prediction (i.e., predicting the EOL value of a given metric using its early value). Interestingly, while the features on this diagonal might be expected to consistently be the most predictive, this is not always the case. For example, the early prediction of R_ct is dominated by V_charge. Additionally, while Q_RPT0.2C is used to define the EOL cutoff, and thus EFC at EOL, the early prediction of EFC is dominated by R_p and the higher rate capacities, rather than by Q_RPT0.2C. These results highlight the importance of detailed tracking of battery SOH across multiple metrics. While a given degradation mode might dominate the EOL values of certain mechanistic SOH metrics, the best early indicators for the onset of that mode may be a different metric or set of metrics.

Since SHAP analysis cannot differentiate between correlated input features, in order to draw robust conclusions about the importance of early cycle features, it is insightful to also consider a “diagnostic-only” model, excluding cycling parameters as input features (ESI,† Section S.10.6). In principle, this may affect the relative feature importance of the early cycle features which correlate with specific cycling parameters. In addition, this type of model is preferred in cases where a user either does not directly have access to cycling conditions, such as battery second life repurposing or online EV health estimation; the cycling conditions are kept constant, such as probing production quality control; or the relationship to cycling conditions is not the focus, such as in process or battery design optimization.¹⁰⁴

4 Conclusions

In this study, we develop an aging matrix to visually simplify and highlight coupled battery aging pathways by combining interpretable ML, physically derived mechanistic SOH metrics, and a diverse dataset spanning over 200 distinct cycling conditions. By tracking a comprehensive set of 16 mechanistic aging features, we robustly describe the battery SOH through an aging matrix, and provide insight into battery degradation mechanisms. By leveraging SHAP analysis, we identify key relationships between cycling conditions and end-of-life metrics that can be validated in further studies with experimental teardowns. In particular, we evidence that the charging current (CC1) critically impacts both the battery lifetime and the polarization resistance, two metrics found to be highly correlated. Thorough analyses reveal that the low SOC resistance growth is triggered by cathode over-lithiation. Finally, in the case of early prediction, non-self prediction features, are critical in predicting mechanistic SOH metrics such as EFCs to EOL.

Through our interpretable ML framework, we deepen our physical understanding of battery degradation within the high dimensionality of a diverse dataset. While interpretable ML tools can be used to generate hypotheses and summaries of the dataset, the findings must be further validated with physical characterization to gain confidence. This model framework is extensible to include various other use-case specific SOH metrics or cycling conditions. We encourage the field to use this methodology in the analysis of large datasets that span other chemistries and operating conditions such as those spanning wide temperature ranges, dynamic operational usage profiles for grid storage or EVs,¹⁰⁵ battery manufacturing optimization,¹⁰⁶ and other tasks. In these cases where the design space is sufficiently different, the models will need to be retrained or fine-tuned on these new datasets. We urge the field to use the dataset presented here to expand upon this work while keeping interpretability in mind to enrich our understanding of battery degradation.

Author contributions

V. N. L., B. V. V., X. C., W. E. G., W. C. C., conceived and conducted the full-cell cycling experiments. V. N. L. compiled the manuscript, figures and edits from authors. P. A. A. and B. V. V. conceptualized, implemented, and constructed visualizations for the protocol-only, diagnostic-aided, and diagnostic-only machine learning models and their SHAP analysis. P. A. A., B. V. V., V. N. L., and X. C. conceptualized the mechanistic SOH metrics used. X. C. conceptualized and implemented the explanatory model and its SHAP analysis. P. A. A. and J. S. conceptualized and implemented the DVF algorithm in strong collaboration with B. V. V. P. K. H., C. B. G., S. S., and A. T. performed data management and data processing pipeline support. N. G., V. N. L., and H. L. T. designed the methodology for full cell disassembly, pouch cell assembly, and half cell voltage extraction. N. G. and V. N. L. conducted the pouch cell experiments. D. G., V. N. L., B. V. V., X. C., A. G. and P. A. A. contributed to conceptualizing and implementing the visual representations of the work. All authors edited, reviewed, and discussed the work. W. C. C. and R. D. B. supervised the work.

Code availability

Code for figure generation and random forest model building can be found at https://data.matr.io/11/.

Data availability

Raw data and data structured via the BEEP pipeline¹⁰⁷ can be found at https://data.matr.io/11/.

Conflicts of interest

W. C. C., B. V. V., W. E. G., V. N. L., P. K. H., C. B. G., P. A. A., R. D. B., X. C., have filed a patent related to this work: US Application No. 20220137149A1, dated 15 May 2022.

Acknowledgements

This work was supported by the Toyota Research Institute through the Accelerated Materials Design and Discovery program. V. N. L. and D. G. acknowledge support by the National Science Foundation Graduate Research Fellowship. X. C. acknowledges support by the Stanford Data Science Scholars Program. N. R. G. acknowledges support from the U.S. Department of Defense through the National Defense Science & Engineering Graduate Fellowship Program. We also thank D'Arcy Seamon for contributions on experiments related to half-cell voltage extraction. Additionally, we thank Alex Dunn for contributions in developing the BEEP python package.

References

1. A. Jaiswal, Renewable Sustainable Energy Rev., 2017, 72, 922–934.
2. G. Zubi, R. Dufo-López, M. Carvalho and G. Pasaoglu, Renewable Sustainable Energy Rev., 2018, 89, 292–308.
3. C. Lorenzo, R. Tabusse, D. Bouquain, S. Hibon and D. Hissel, IEEE Vehicle Power and Propulsion Conference, 2021.
4. T. Chen, Y. Jin, H. Lv, A. Yang, M. Liu, B. Chen, Y. Xie and Q. Chen, Trans. Tianjin Univ., 2020, 26, 208–217.
5. W. Chen, J. Liang, Z. Yang and G. Li, Energy Proc., 2019, 158, 4363–4368.
6. B. Diouf and R. Pode, Renewable Energy, 2015, 76, 375–380.
7. J. B. Dunn, L. Gaines, J. C. Kelly, C. James and K. G. Gallagher, Energy Environ. Sci., 2015, 8, 158–168.
8. B. Zhou, Y. Wu, B. Zhou, R. Wang, W. Ke, S. Zhang and J. Hao, Energy, 2016, 96, 603–613.
9. P. M. Attia, A. Bills, F. B. Planella, P. Dechent, G. dos Reis, M. Dubarry, P. Gasper, R. Gilchrist, S. Greenbank, D. Howey, O. Liu, E. Khoo, Y. Preger, A. Soni, S. Sripad, A. G. Stefanopoulou and V. Sulzer, J. Electrochem. Soc., 2022, 169, 060517.
10. Y. Li, K. Liu, A. M. Foley, A. Zülke, M. Berecibar, E. Nanini-Maury, J. V. Mierlo and H. E. Hoster, Renewable Sustainable Energy Rev., 2019, 113, 109254.
11. J. Rivera-Barrera, N. Muñoz-Galeano and H. Sarmiento-Maldonado, Electronics, 2017, 6, 102.
12. W. Xie, X. Liu, R. He, Y. Li, X. Gao, X. Li, Z. Peng, S. Feng, X. Feng and S. Yang, J. Energy Storage, 2020, 32, 101837.
13. J. S. Edge, S. O'Kane, R. Prosser, N. D. Kirkaldy, A. N. Patel, A. Hales, A. Ghosh, W. Ai, J. Chen, J. Yang, S. Li, M.-C. Pang, L. B. Diaz, A. Tomaszewska, M. W. Marzook, K. N. Radhakrishnan, H. Wang, Y. Patel, B. Wu and G. J. Offer, Phys. Chem. Chem. Phys., 2021, 23, 8200–8221.
14. K. B. Hatzell, A. Sharma and H. K. Fathy, American Control Conference, 2012, pp. 584–591.
15. J. S. Edge, S. O'Kane, R. Prosser, N. D. Kirkaldy, A. N. Patel, A. Hales, A. Ghosh, W. Ai, J. Chen, J. Yang, S. Li, M.-C. Pang, L. B. Diaz, A. Tomaszewska, M. W. Marzook, K. N. Radhakrishnan, H. Wang, Y. Patel, B. Wu and G. J. Offer, Phys. Chem. Chem. Phys., 2021, 23, 8200–8221.
16. A. Weng, P. Mohtat, P. M. Attia, V. Sulzer, S. Lee, G. Less and A. Stefanopoulou, Joule, 2021, 5, 2971–2992.
17. S. X. Drakopoulos, A. Gholamipour-Shirazi, P. MacDonald, R. C. Parini, C. D. Reynolds, D. L. Burnett, B. Pye, K. B. O'Regan, G. Wang, T. M. Whitehead, G. J. Conduit, A. Cazacu and E. Kendrick, Cell Rep. Phys. Sci., 2021, 2, 100683.
18. A. Eldesoky, M. Bauer, T. Bond, N. Kowalski, J. Corsten, D. Rathore, R. Dressler and J. R. Dahn, J. Electrochem. Soc., 2022, 169, 100531.
19. J. Lu, T. Wu and K. Amine, Nat. Energy, 2017, 2, 17011.
20. P. P. Paul, E. J. McShane, A. M. Colclasure, N. Balsara, D. E. Brown, C. Cao, B.-R. Chen, P. R. Chinnam, Y. Cui, E. J. Dufek, D. P. Finegan, S. Gillard, W. Huang, Z. M. Konz, R. Kostecki, F. Liu, S. Lubner, R. Prasher, M. B. Preefer, J. Qian, M.-T. F. Rodrigues, M. Schnabel, S.-B. Son, V. Srinivasan, H.-G. Steinrück, T. R. Tanim, M. F. Toney, W. Tong, F. Usseglio-Viretta, J. Wan, M. Yusuf, B. D. McCloskey and J. N. Weker, Adv. Energy Mater., 2021, 11, 2100372.
21. D. Juarez-Robles, J. A. Jeevarajan and P. P. Mukherjee, J. Electrochem. Soc., 2020, 167, 160510.
22. D. Juarez-Robles, S. Azam, J. A. Jeevarajan and P. P. Mukherjee, J. Electrochem. Soc., 2021, 168, 110501.
23. C. R. Birkl, M. R. Roberts, E. McTurk, P. G. Bruce and D. A. Howey, J. Power Sources, 2017, 341, 373–386.
24. T. F. Fuller, M. Doyle and J. Newman, J. Electrochem. Soc., 1994, 141, 1–10.
25. S. Atalay, M. Sheikh, A. Mariani, Y. Merla, E. Bower and W. D. Widanage, J. Power Sources, 2020, 478, 229026.
26. M. Doyle, T. F. Fuller and J. Newman, J. Electrochem. Soc., 1993, 140, 1526–1533.
27. M. D. Berliner, H. Zhao, S. Das, M. Forsuelo, B. Jiang, W. H. Chueh, M. Z. Bazant and R. D. Braatz, J. Electrochem. Soc., 2021, 168, 090546.
28. D. Zhang, L. D. Couto and S. J. Moura, IEEE Control Syst. Lett., 2021, 5, 1657–1662.
29. S. E. J. O'Kane, W. Ai, G. Madabattula, D. A. Alvarez, R. Timms, V. Sulzer, J. S. Edge, B. Wu, G. J. Offer and M. Marinescu, Phys. Chem. Chem. Phys., 2022, 24, 7909–7922.
30. B.-R. Chen, C. M. Walker, S. Kim, M. R. Kunz, T. R. Tanim and E. J. Dufek, Joule, 2022, 6, 2776–2793.
31. C. Lv, X. Zhou, L. Zhong, C. Yan, M. Srinivasan, Z. W. Seh, C. Liu, H. Pan, S. Li, Y. Wen and Q. Yan, Adv. Mater., 2021, 34, 2101474.
32. M. Dubarry, C. Truchot and B. Y. Liaw, J. Power Sources, 2012, 219, 204–216.
33. M. Dubarry and D. Beck, Acc. Mater. Res., 2022, 3, 843–853.
34. M. Dubarry and D. Beck, J. Power Sources, 2020, 479, 228806.
35. S. Schindler, G. Baure, M. A. Danzer and M. Dubarry, J. Power Sources, 2019, 440, 227117.
36. M. Dubarry, M. Berecibar, A. Devie, D. Anseán, N. Omar and I. Villarreal, J. Power Sources, 2017, 360, 59–69.
37. J. Mao, J. Miao, Y. Lu and Z. Tong, Chin. J. Chem. Eng., 2021, 37, 1–11.
38. X. Shu, S. Shen, J. Shen, Y. Zhang, G. Li, Z. Chen and Y. Liu, iScience, 2021, 24, 103265.
39. J. Schaeffer, E. Lenz, W. C. Chueh, M. Z. Bazant, R. Findeisen and R. D. Braatz, Comput. Chem. Eng., 2024, 180, 108471.
40. S. Jin, X. Sui, X. Huang, S. Wang, R. Teodorescu and D.-I. Stroe, Electronics, 2021, 10, 3126.
41. M. Berecibar, Nature, 2019, 568, 325–326.
42. X. Sui, S. He, S. B. Vilsen, J. Meng, R. Teodorescu and D.-I. Stroe, Appl. Energy, 2021, 300, 117346.
43. S. Kim, Z. Yi, B.-R. Chen, T. R. Tanim and E. J. Dufek, Energy Storage Mater., 2022, 45, 1002–1011.
44. W. Li, N. Sengupta, P. Dechent, D. Howey, A. Annaswamy and D. U. Sauer, J. Power Sources, 2021, 482, 228863.
45. D. Roman, S. Saxena, V. Robu, M. Pecht and D. Flynn, Nat. Mach. Intell., 2021, 3, 447–456.
46. T. Lombardo, M. Duquesnoy, H. El-Bouysidy, F. Årén, A. Gallo-Bueno, P. B. Jørgensen, A. Bhowmik, A. Demortière, E. Ayerbe, F. Alcaide, M. Reynaud, J. Carrasco, A. Grimaud, C. Zhang, T. Vegge, P. Johansson and A. A. Franco, Chem. Rev., 2021, 122, 10899–10969.
47. P. Gasper, N. Collath, H. C. Hesse, A. Jossen and K. Smith, J. Electrochem. Soc., 2022, 169, 080518.
48. N. H. Paulson, J. Kubal, L. Ward, S. Saxena, W. Lu and S. J. Babinec, J. Power Sources, 2022, 527, 231127.
49. R. R. Richardson, M. A. Osborne and D. A. Howey, J. Power Sources, 2017, 357, 209–219.
50. B. Jiang, W. E. Gent, F. Mohr, S. Das, M. D. Berliner, M. Forsuelo, H. Zhao, P. M. Attia, A. Grover, P. K. Herring, M. Z. Bazant, S. J. Harris, S. Ermon, W. C. Chueh and R. D. Braatz, Joule, 2021, 5, 3187–3203.
51. W. Li, H. Zhang, B. van Vlijmen, P. Dechent and D. U. Sauer, Energy Storage Mater., 2022, 53, 453–466.
52. P. K. Jones, U. Stimming and A. A. Lee, Nat. Commun., 2022, 13, 4806.
53. J. Zhu, Y. Wang, Y. Huang, R. B. Gopaluni, Y. Cao, M. Heere, M. J. Mühlbauer, L. Mereacre, H. Dai, X. Liu, A. Senyshyn, X. Wei, M. Knapp and H. Ehrenberg, Nat. Commun., 2022, 13, 2261.
54. T. Li, Z. Zhou, A. Thelen, D. A. Howey and C. Hu, Cell Rep. Phys. Sci., 2024, 5, 101891.
55. A. Thelen, Y. H. Lui, S. Shen, S. Laflamme, S. Hu, H. Ye and C. Hu, Energy Storage Mater., 2022, 50, 668–695.
56. J. Schaeffer, E. Lenz, D. Gulla, M. Z. Bazant, R. D. Braatz and R. Findeisen, Cell Rep. Phys. Sci., 2024, 5, 102258.
57. J. Schaeffer, G. Galuppini, J. Rhyu, P. A. Asinger, R. Droop, R. Findeisen and R. D. Braatz, Proceedings of the American Control Conference, 2024, pp. 763–768.
58. G. dos Reis, C. Strange, M. Yadav and S. Li, Energy AI, 2021, 5, 100081.
59. W. He, N. Williard, M. Osterman and M. Pecht, J. Power Sources, 2011, 196, 10314–10321.
60. Y. Xing, E. W. Ma, K.-L. Tsui and M. Pecht, Microelectron. Reliab., 2013, 53, 811–820.
61. S. Zhang, X. Guo, X. Dou and X. Zhang, Sustainable Energy Technol. Assessments, 2020, 40, 100752.
62. D. Burzyński and L. Kasprzyk, Knowledge-Based Systems, 2021, 219, 106900.
63. S. J. Harris, D. J. Harris and C. Li, J. Power Sources, 2017, 342, 589–597.
64. B. Saha and K. Goebel, NASA AMES prognostics data repository, 2007.
65. X. Liu, B.-B. Zou, Y.-N. Wang, X. Chen, J.-Q. Huang, X.-Q. Zhang, Q. Zhang and H.-J. Peng, J. Am. Chem. Soc., 2024, 146, 33012–33021.
66. F. Stroebl, R. Petersohn, B. Schricker, F. Schaeufl, O. Bohlen and H. Palm, Sci. Data, 2024, 11, 1020.
67. K. A. Severson, P. M. Attia, N. Jin, N. Perkins, B. Jiang, Z. Yang, M. H. Chen, M. Aykol, P. K. Herring, D. Fraggedakis, M. Z. Bazant, S. J. Harris, W. C. Chueh and R. D. Braatz, Nat. Energy, 2019, 4, 383–391.
68. P. M. Attia, A. Grover, N. Jin, K. A. Severson, T. M. Markov, Y.-H. Liao, M. H. Chen, B. Cheong, N. Perkins, Z. Yang, P. K. Herring, M. Aykol, S. J. Harris, R. D. Braatz, S. Ermon and W. C. Chueh, Nature, 2020, 578, 397–402.
69. W. Diao, S. Saxena and M. Pecht, J. Power Sources, 2019, 435, 226830.
70. L. Ward, J. Kubal, S. J. Babinec, W. Lu, A. Dunlop, S. Trask, B. Polzin, A. Jansen and N. H. Paulson, Dataset of NMC battery Tests from CAMP, 2023 Release, Materials data facility, Argonne National Laboratory Technical Report, 2023.
71. L. Wildfeuer, A. Karger, D. Aygül, N. Wassiliadis, A. Jossen and M. Lienkamp, J. Power Sources, 2023, 560, 232498.
72. L. Ward, S. Babinec, E. J. Dufek, D. A. Howey, V. Viswanathan, M. Aykol, D. A. Beck, B. Blaiszik, B.-R. Chen, G. Crabtree, S. Clark, V. De Angelis, P. Dechent, M. Dubarry, E. E. Eggleton, D. P. Finegan, I. Foster, C. B. Gopal, P. K. Herring, V. W. Hu, N. H. Paulson, Y. Preger, D. Uwe-Sauer, K. Smith, S. W. Snyder, S. Sripad, T. R. Tanim and L. Teo, Joule, 2022, 6, 2253–2271.
73. Y. Preger, H. M. Barkholtz, A. Fresquez, D. L. Campbell, B. W. Juba, J. Romàn-Kustas, S. R. Ferreira and B. Chalamala, J. Electrochem. Soc., 2020, 167, 120532.
74. S. S. Choi and H. S. Lim, J. Power Sources, 2002, 111, 130–136.
75. L. Zhang, C. Zhang, N. Li and W. Tong, J. Electrochem. Soc., 2020, 167, 120509.
76. S. Saxena, Y. Xing, D. Kwon and M. Pecht, Int. J. Electron. Power Energy Syst., 2019, 107, 438–445.
77. Y. Gao, J. Jiang, C. Zhang, W. Zhang, Z. Ma and Y. Jiang, J. Power Sources, 2017, 356, 103–114.
78. M. Aykol, C. B. Gopal, A. Anapolsky, P. K. Herring, B. van Vlijmen, M. D. Berliner, M. Z. Bazant, R. D. Braatz, W. C. Chueh and B. D. Storey, J. Electrochem. Soc., 2021, 168, 030525.
79. A. G. Li, A. C. West and M. Preindl, Appl. Energy, 2022, 316, 119030.
80. D. P. Finegan, J. Zhu, X. Feng, M. Keyser, M. Ulmefors, W. Li, M. Z. Bazant and S. J. Cooper, Joule, 2021, 5, 316–329.
81. X. Hu, L. Xu, X. Lin and M. Pecht, Joule, 2020, 4, 310–346.
82. V. Sulzer, P. Mohtat, A. Aitio, S. Lee, Y. T. Yeh, F. Steinbacher, M. U. Khan, J. W. Lee, J. B. Siegel, A. G. Stefanopoulou and D. A. Howey, Joule, 2021, 5, 1934–1955.
83. M. Schimpe, M. E. von Kuepach, M. Naumann, H. C. Hesse, K. Smith and A. Jossen, J. Electrochem. Soc., 2018, 165, A181–A193.
84. T. Waldmann, M. Wilka, M. Kasper, M. Fleischhammer and M. Wohlfahrt-Mehrens, J. Power Sources, 2014, 262, 129–135.
85. J. P. Christopherson, Battery Test Manual For Electric Vehicles, Idaho National Laboratory, U.S. Department of Energy Technical Report, 2015.
86. T. Baumhöfer, M. Brühl, S. Rothgang and D. U. Sauer, J. Power Sources, 2014, 247, 332–338.
87. C. R. Birkl, E. McTurk, M. R. Roberts, P. G. Bruce and D. A. Howey, J. Electrochem. Soc., 2015, 162, A2271–A2280.
88. J. Schmitt, M. Schindler, A. Oberbauer and A. Jossen, J. Power Sources, 2022, 532, 231296.
89. J. Sieg, M. Storch, J. Fath, A. Nuhic, J. Bandlow, B. Spier and D. U. Sauer, J. Energy Storage, 2020, 30, 101582.
90. K.-J. Park, J.-Y. Hwang, H.-H. Ryu, F. Maglia, S.-J. Kim, P. Lamp, C. S. Yoon and Y.-K. Sun, ACS Energy Lett., 2019, 4, 1394–1400.
91. T. Raj, A. A. Wang, C. W. Monroe and D. A. Howey, Batteries Supercaps, 2020, 3, 1377–1385.
92. G. Mu, S. Agrawal, P. Sittisomwong and P. Bai, Electrochim. Acta, 2022, 406, 139878.
93. S. M. Lundberg and S.-I. Lee, Advances in Neural Information Processing Systems, 2017, pp. 4768–4777.
94. C. Molnar, Interpretable Machine Learning: A Guide for Making Black Box Models Explainable, Leanpub, Victoria, British Columbia, Canada, 2nd edn, 2022.
95. N. Kirkaldy, M. A. Samieian, G. J. Offer, M. Marinescu and Y. Patel, ACS Appl. Energy Mater., 2022, 5, 13367–13376.
96. J. Li, J. Harlow, N. Stakheiko, N. Zhang, J. Paulsen and J. Dahn, J. Electrochem. Soc., 2018, 165, A2682–A2695.
97. K. J. Nelson, G. L. d'Eon, A. T. B. Wright, L. Ma, J. Xia and J. R. Dahn, J. Electrochem. Soc., 2015, 162, A1046–A1054.
98. W. Li, H. Y. Asl, Q. Xie and A. Manthiram, J. Am. Chem. Soc., 2019, 141, 5097–5101.
99. W. E. Gent, G. M. Busse and K. Z. House, Nat. Energy, 2022, 7, 1132–1143.
100. A. Mikheenkova, O. Gustafsson, C. Misiewicz, W. R. Brant, M. Hahlin and M. J. Lacey, J. Energy Storage, 2023, 57, 106211.
101. S.-T. Myung, F. Maglia, K.-J. Park, C. S. Yoon, P. Lamp, S.-J. Kim and Y.-K. Sun, ACS Energy Lett., 2017, 2, 196–223.
102. M. Uitz, M. Sternad, S. Breuer, C. Täubert, T. Traußnig, V. Hennige, I. Hanzu and M. Wilkening, J. Electrochem. Soc., 2017, 164, A3503–A3510.
103. S. Oh, A.-R. Jeon, G. Lim, M. K. Cho, K. H. Chae, S. S. Sohn, M. Lee, S.-K. Jung and J. Hong, Energy Storage Mater., 2024, 65, 103169.
104. A. Geslin, B. van Vlijmen, X. Cui, A. Bhargava, P. A. Asinger, R. D. Braatz and W. C. Chueh, Joule, 2023, 7, 1956–1965.
105. A. Geslin, L. Xu, D. Ganapathi, K. Moy, W. C. Chueh and S. Onori, Nat. Energy, 2025, 10, 172–180.
106. X. Cui, S. D. Kang, S. Wang, J. A. Rose, H. Lian, A. Geslin, S. B. Torrisi, M. Z. Bazant, S. Sun and W. C. Chueh, Joule, 2024, 8, 3072–3087.
107. P. Herring, C. B. Gopal, M. Aykol, J. H. Montoya, A. Anapolsky, P. M. Attia, W. Gent, J. S. Hummelshøj, L. Hung, H.-K. Kwon, P. Moore, D. Schweigert, K. A. Severson, S. Suram, Z. Yang, R. D. Braatz and B. D. Storey, SoftwareX, 2020, 11, 100506.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ee05609d

‡ These authors contributed equally to this work.

---