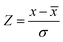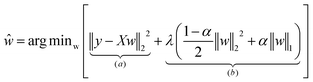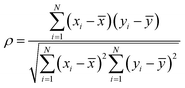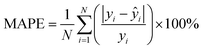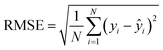Battery lifetime prediction using surface temperature features from early cycle data

Abstract

Lithium-ion batteries (LIBs) are highly sensitive to cycling conditions and show a nonlinear degradation pattern, typically noticeable in later stages. This affects the accuracy of most battery health prognostic models, especially those relying on long-term data collected under varying operational conditions. To tackle these challenges, we propose using statistical features extracted from the battery surface temperature during the first 10 cycles and developing a data-driven machine learning (ML) model for early-cycle lifetime prediction. Models are trained on each of the selected open-source datasets comprising 223 LIBs and tested on their respective datasets with non-stratified data splits using a balanced ratio. These datasets include lithium iron phosphate (LFP), nickel cobalt aluminum oxide (NCA), and nickel manganese cobalt oxide (NMC) cells, tested under different environmental temperatures and cycling protocols. In one comprehensive dataset, our model achieved competitive performance compared to state-of-the-art studies that rely on features extracted from much longer cycling data—up to ten times the duration. This work provides valuable insights into the strong correlation between early-cycle surface temperature and battery lifetime across various battery chemistries, cycling rates, and environmental temperatures.

---

Broader context

Lithium-ion batteries (LIBs) are integral to our daily lives, powering everything from smartphones to electric vehicles. As demand for these batteries grows, ensuring their safety and reliability becomes increasingly critical. One major challenge is detecting potential manufacturing errors early, as these can lead to safety issues and reduced battery lifespan. Traditional methods for predicting battery health often require extensive data and complex equipment, making them less practical for widespread use. This work addresses this challenge by developing a new approach that uses data from the first 10 cycles of a battery's life to predict its overall lifespan. By analyzing the surface temperature of the battery during these early cycles, we can identify patterns that indicate future performance. This method is not only more efficient but also adaptable to different battery chemistries and operating conditions. Our work offers a more accessible and cost-effective way to ensure the safety and longevity of LIBs, which is crucial as we continue to rely more on renewable energy and electric transportation. By improving early detection of potential issues, our approach can help prevent failures, reduce costs, and enhance the overall reliability of battery-powered devices and systems. This advancement represents a meaningful step forward in the quest for safer, more sustainable energy solutions.

Introduction

Extensive research on LIB systems has made them widespread across industries like electric vehicles and common appliances, attributed to their competitive price, long operational lifespan, and high energy density since their commercial debut.^1–3 The rapid growth in LIB production, fueled by increasing demand, has raised concerns about potential declines in product quality due to unnoticed manufacturing errors. Various diagnostic and prognostic techniques have been employed to evaluate the health and predict the end-of-life (EOL) of battery cells.^4,5 This proactive strategy is instrumental in identifying faulty cells, thus ensuring quality and safety. Achieving this goal requires highly accurate battery life predictions based on minimal cycling history. However, most LIBs exhibit a knee-point degradation pattern that emerges in the later stages of aging, primarily due to their complex and non-linear degradation behavior.^6,7 Furthermore, factors such as inhomogeneous cell aging and variations in degradation under differing operational conditions like cycling rate and environmental temperature, limit the robustness and accuracy of battery health diagnostic and prognostic models.^7–10

State of health (SOH) quantifies the ratio of maximum functional battery discharge capacity during a given cycle to its rated nominal capacity. Various parameter estimation techniques have been used to estimate SOH, including conventional direct measurements (e.g., resistance and open-circuit voltage),^11,12 equivalent circuit model (ECM),^13–15 and physics-based model.^16,17 Based on the current battery SOH, its remaining useful life (RUL) until a failure threshold point (i.e. EOL) can be projected, commonly set as 80% SOH or below,¹⁸ at which point the battery performance typically declines disproportionately. Alternative model-based techniques for RUL estimation, such as mechanistic/electrochemical and hybrid models,^5,19 are widely used and often paired with filtering methods including particle or Kalman filters^20,21 to process historical data. Although promising results have been reported, these techniques face challenges in real-world applications, primarily due to the impracticality of in situ electrochemical impedance measurement^15,22,23 and the decreased accuracy of empirical non-linear parameters under broader operating conditions.^7,24 Moreover, while physics-based models excel at capturing aging mechanisms at the micro-scale, their effectiveness may be limited by the computational constraints of onboard systems and the potential for overlooking certain degradation events.^19,25 As a result, many researchers have attempted to enhance semi-empirical aging models, for example, some have coupled these models with impedance-based electrothermal models²⁶ or incorporated onboard measurements under complex operation conditions.²⁷ Despite these efforts, battery lifetime prediction continues to yield unsatisfactory results.

Data-driven methods have become increasingly popular across various fields due to their ability to identify patterns in data and target variables without relying on predefined outcomes. Unlike traditional models, these approaches are also chemistry-agnostic. Consequently, many studies have applied ML in the energy storage sector, including material characterization, design, synthesis, and battery diagnosis/prognosis.^28–31 This surge is fueled by advancements in computing capabilities and the growing availability of published datasets.^32,33 Several studies have explored different ML techniques for battery diagnosis/prognosis. For instance, Roman et al.³⁴ estimated SOH using multiple models based on a set of engineered features derived from segments of charge voltage and current curves, Tian et al.³⁵ employed a deep neural network to predict complete charging curves using less than 10 minutes of accumulated charging data, Zhang et al.³⁶ constructed neural network and random forest models to predict RUL based on health indicators (HIs, used interchangeably with features) extracted from partial charging voltage curves, and Severson et al.³⁷ developed linear early-lifetime prediction models with remarkable performance by using statistical features from discharge voltage curves within the first 100 cycles on their generated dataset, which has since been widely used in other studies.^34,38,39 While battery lifetime prediction models are well-established, further investigation into highly correlated HIs from earlier cycles, especially under diverse conditions, could lead to significant breakthroughs.

Surface temperature is an important yet underexplored battery attribute^40,41 that reflects the intensity of internal chemical reactions. In this study, we aim to minimize the required cycling data as model input by investigating the prognostic potential of surface temperature-related HIs, while attaining equivalent or better performance with reported studies. We extracted a statistical summary of cycling temperature data from the first 10 cycles and validated it by developing a linear early-cycle prediction model on multiple open-sourced datasets: Severson et al.,³⁷ Preger et al.,⁴² Juarez-Robles et al.,⁴³ and Wang et al.⁴⁴ With a total of 223 cells, these datasets were selected to evaluate the trained models based on our proposed temperature HIs across different chemistries, environmental temperatures, and cycling protocols. To provide a comprehensive comparison, we adjusted the input range of the models proposed by Severson et al. to use only the first 10 cycles, and we employed these models as benchmarks across the datasets. Our findings showed that the best-performing benchmark model yielded a mean absolute percentage error (MAPE)/root-mean-square error (RMSE) of 26.8%/380 cycles on the validation set for the Severson et al. dataset. In contrast, our proposed temperature model significantly reduced the validation errors to 15.7%/257 cycles under similar conditions. Moreover, by incorporating additional complementary features,³⁷ our model achieved even lower validation errors of 14.2%/203 cycles, showcasing competitive performance compared to their original model, which required 100 cycling data. Additionally, we examined the impact of varying amounts of cycling data input on the feature extraction process. Our findings indicate that the majority of the trained models maintained their predictive accuracy despite the use of varying cycling data amounts, with observable fluctuations in certain cases. Finally, our proposed temperature model outperformed all benchmark models across the datasets, highlighting its universal applicability to different cathode materials and operating conditions.

Early-cycle temperature model framework

Framework overview. The proposed framework for the early-cycle temperature ML model consists of three main stages: temperature feature engineering, model development, and evaluation of early-cycle lifetime prediction, as shown in Fig. 1. First, temperature data from the first 10 cycles are collected, processed, and transformed to create a set of statistical temperature HI candidates which serve as the model input. To select the optimal subset of feature inputs for accurate lifetime prediction, Elastic net regularization⁴⁵ is applied to eliminate underperforming and redundant HIs and optimize their coefficients during the model training process (see Methods). This framework employs a linear model algorithm because of its low computational cost for matrix operations and retains the capability to interpret the correlation between statistical surface temperature-related HIs and cycle life (i.e., EOL). The developed model is then used to predict the lifetime of a test set of cells that were not part of the training data. Its performance is evaluated using several error metrics, including the mean absolute error (MAE), MAPE, RMSE, and root-mean-square percentage error (RMSPE). Furthermore, we assess the robustness of the proposed temperature HIs by applying our methodology to several published datasets, which include various LIB cathode chemistries and cycling conditions to investigate the universality and practicality of the trained model across different constraints. In one of the datasets, we validated the interoperability of the proposed temperature HIs by building two models–one using only the temperature HIs and another incorporating additional complementary features. These models were then compared against an adapted version of the Severson et al. models,³⁷ which served as benchmarks. Overall, we developed an early-cycle data-driven ML model capable of predicting battery lifetime under unknown conditions, using HIs with universal and chemistry-agnostic traits as inputs. Our objective is to investigate highly correlated HIs and reduce the amount of cycling data required for accurate early-cycle predictions. This approach presents significant benefits for practical applications such as battery development and production lines.

Fig. 1 Overview of the early-cycle temperature ML model. Multiple sources of LIB datasets with different chemistries, environmental temperatures, and cycling protocols were used in this study. Surface temperature data from charge and discharge regions were collected from the first 10 cycles and engineered into statistical features. These early-cycle features serve as input for the ML model to predict battery lifetime. This simplified early prediction application has the potential to minimize the timely data collection costs while maintaining quality in rapid battery production.

Battery datasets. We selected six datasets of LIBs with different cathode chemistries, comprising a total of 223 cells from four online sources. Each dataset has a distinct combination of cycling settings, including cycling rate and environmental temperature as described in Table 1. These datasets provide a multidimensional foundation for evaluating the predictive capability of the developed linear ML across a range of cycling conditions using the proposed temperature HIs.

Table 1 Summary of all datasets

Dataset	SNL–NMC^a	SNL–NCA	SNL–LFP	UL–NCA^b	TRI^c	XJTU^d
a Sandia National Laboratories. b Underwriters Laboratories Inc. – Purdue University. c Toyota Research Institute. d Xi’an Jiaotong University. e Information provided from corresponding author/manufacturer. f Filtered with 100% (and 94%) DOD and removed anomaly. g Fast-charging protocols under CC–CV setting. Cycling protocols for each dataset are combinations of the specified charge and discharge rates. Refer to ESI for more details.
Manufacturer	LG Chem	Panasonic	A123 Systems	Panasonic	A123 Systems	LISHEN
Cell shape	Cylindrical 18 650
Cathode^e	LiNi0.8Mn0.1Co0.1O2	LiNi0.8Co0.15Al0.05O2	LiFePO4	LiNi0.8Co0.15Al0.05O2	LiFePO4	LiNi0.5Mn0.3Co0.2O2
Total cells^f	21	16	19	21	123	23
Charge rate	0.5C (CC–CV)	0.5C (CC–CV)	0.5C (CC–CV)	0.5C (CC–CV)	Multiple^g	2, 3C (CC–CV)
Discharge rate	1, 2, 3C (CC)	1, 2C (CC)	1, 2, 3C (CC)	0.5C (CC)	4C (CC–CV)	1C (CC)
Temperature	15, 25, 35 °C	15, 25, 35 °C	15, 25, 35 °C	23 °C	30 °C	23 °C

---

The first three datasets, generated by Preger et al.⁴² at Sandia National Laboratories (SNL), consist of cells with different cathode materials: NMC, NCA, and LFP, were designed to study the impact of environmental temperature (i.e. 15, 25, 35 °C), depth of discharge (DOD), and discharge current (i.e., 1, 2, 3C) on battery aging, with constant 0.5 CC–CV charging. These datasets enable the examination of cells with varying chemistries cycled under slow-to-fast discharge rates, allowing for an analysis of the relationship between temperature profile fluctuations and battery lifetime. Since DOD is not our primary focus, only cells with 100% (and 94%) DOD are considered. In addition, we selected another dataset of NCA/graphite cells from Underwriters Laboratories Inc. and Purdue University (UL–NCA)⁴³ to evaluate the proposed HIs under monotonic 0.5C slow-rate cycling and 23 °C environment. Each of these four datasets was randomly split into equal-sized training and testing sets.

Next, the Toyota Research Institute (TRI) dataset,³⁷ which contains 124 LFP/graphite cells under multi-step fast-charging conditions (e.g., 5.4C(50% SOC)-3C), was selected to analyze the significance of rapid temperature increases during cycling, caused by significant heat generation from side reactions. High-magnitude temperature variations serve as key indicators that can provide valuable insights into electrochemical degradation.^5,9 All cells were subjected to either a one-step or two-step fast-charging policy with varying duration from 8–13.3 minutes until 80% SOC, followed by 1C CC–CV charging, and discharged at 4C CC–CV in a controlled 30 °C environmental chamber with various resting periods. We adopted a similar data indexing method used by Severson et al.³⁷ partitioning into a training set (41 cells), primary testing set (42 cells), and secondary testing set (40 cells), where training and primary testing sets consist of cells with similar cycling protocols, whereas the secondary testing set includes cells with different cycling protocols, i.e. out-of-distribution (OOD). Thus, the model performance will be evaluated on cells with “unknown” protocols in the secondary test set, providing insight into the generalization ability of the proposed temperature HIs.

Finally, we include two batches of the NMC532 dataset generated by Xi’an Jiaotong University (referred to as XJTU),⁴⁴ which consists of 23 cells cycled at room temperature, approximately 23 °C. These cells are divided into two batches of unique cycling protocol: the first batch (8 cells) was cycled at a fixed charge/discharge rate of 2C/1C, while the second batch (15 cells) was cycled at a higher rate of 3C/1C. For this dataset, batch 2 was selected as the training set, and batch 1 as the secondary test set. This setup resulted in a train-to-test ratio of 2 : 1, allowing us to directly evaluate the model generalizability on a testing set composed of OOD and out-of-protocol (OOP) cells, presenting a unique challenge for our model to make accurate predictions under unseen operating conditions due to different charging C-rates. More details on dataset screening and accessibility, along with battery specifications, are available in the Method and Data availability sections, and Table S1 (ESI†).

Temperature features and model training. Temperature plays a critical role in the cycling performance of LIBs by affecting material properties such as the ionic conductivities of electrodes and electrolytes.^7,9 As a result, the chemical reaction changes exponentially following the classical Arrhenius equation,⁴⁶ as a greater proportion of molecules surpass the activation energy threshold. The heat generated during battery usage provides valuable insights in distinguishing between reversible and irreversible electrochemical processes.^9,47 Reaction heat is a reversible process resulting from entropic changes and working temperature, while irreversible heat – such as ohmic heating, active polarization, heat of mixing, and enthalpy changes^9,48 – is primarily generated by resistive component behaviors. Xiao et al.⁴⁸ suggest that reversible heat contributes minimally to aging effects at high currents, indicating that the observed increase in heat generation over cycling is dominated by irreversible heat. This claim is supported by G. Liu et al.⁴⁹ who concluded that Joule (or ohmic) heat tends to increase as the battery ages. The increase is mainly attributed by degradation processes such as solid electrolyte interface, lithium plating, and active material decomposition under different operating conditions.^4,7,10,45 Consequently, the vast heat generation, reflected in the battery surface temperature, can be used in capturing electrochemical evolution inside the cells, and it can be measured in situ conveniently with inexpensive cost and minimal setup. Several temperature-related parameters – such as the temperature integral,³⁷ temperature profile shape,⁵⁰ and rate of temperature change⁴⁰ – have been utilized to assess battery health and diagnose potential issues.

This work aims to explore insightful temperature-related HIs derived from early cycling data by computing seven statistical HIs: mean, variance, skewness, kurtosis, minimum, maximum, and amplitude (i.e., maximum–minimum). Although statistical feature extraction has been commonly applied to other measurements^37,50 (e.g., capacity), its comprehensive use for surface temperature is rare. These HIs are computed on both the interpolated temperature and rate of temperature change vectors for the first 10 cycles, excluding the initialization cycle(s) (see Method and Supplementary Note S2, ESI†). To illustrate the extraction process of the proposed temperature HIs and analyze their correlation with battery cycle life, we use the TRI dataset due to its extensive data and fast-cycling protocols, as depicted in Fig. 2. The temperature profiles for CC–CV charging during the first 10 cycles of a battery sample are plotted in Fig. 2a, with the end of CC-stage marked by vertical dotted lines. The seven statistical HIs are computed for each cycle, producing nine values from the first 10 cycles for each HI. These nine values are then averaged to yield single-valued HIs, thereby stabilizing any fluctuations. This process is repeated for all cells across each dataset. Selected HIs are plotted against the log₁₀ cycle life for each cycling mode as illustrated in Fig. 2b–g. The Pearson correlation coefficient, ρ, provides information about the strength and direction of the relationship between the HIs and log₁₀ cycle life. For instance, cells with higher values of variance (T[Q]) and maximum (dT/dQ) tend to have shorter cycle lives, as shown in Fig. 2c and e, respectively. This is supported by their coefficients (i.e., ρ = −0.55 and −0.58, respectively), where values close to 1 (or −1) indicate a strong linear relationship. These informative HIs can be exploited from very early cycles, as they are closely associated with the initial internal resistance and reaction kinetics of the battery, enabling accurate estimation of its cycle life. In comparison, other degradation indicators, such as capacity, may not yield high ρ coefficients (refer to Fig. S1, ESI†) when extracted over the first 10 cycles. These indicators typically require an extended cycling period to provide robust information on capacity fade degradation.³⁷ Additionally, the statistical temperature HIs are well-suited to capture degradation information from the varying heat generation profiles due to different cycling rates, particularly across diverse cathode chemistries where they play a critical role in shaping the battery properties. For example, cathode materials like NMC and NCA are less thermally stable than olivine-structured LFP,^8,10 attributed to their higher energy density impacted by their nickel content.^7,51 Furthermore, variations in the empirical active material ratios, taking NMC811 and NMC532 for instance, influence the heat generation profile and intensity, an essential key in reflecting battery degradation and ultimately, battery lifetime.

Fig. 2 Visualization of the feature extraction process on the first 10 cycles and the derived statistical HI examples using temporal temperature and rate of temperature change on TRI dataset. (a) Schematic illustrating the process to compute averaged statistical temperature HIs from the first 10 cycles. Battery with code ‘b2c3’ and 335 cycles lifetime is used as the sample. This process is applied separately for both charge and discharge data. The extracted log₁₀ HI_Avg10 examples for the TRI dataset are shown on (b)–(d) for temporal temperature: b, Minimum and c, Variance of the charge T[Q]_Avg10, and d, Minimum of the discharge T[V]_Avg10; and (e)–(g) shows the rate of temperature change: (e), maximum and (f), mean of the charge dT/dQ_Avg10, and (g), maximum–minimum of the discharge dT/dV_Avg10, with correlation coefficient, ρ of 0.47, −0.55, 0.40, −0.58, −0.56 and −0.35 respectively. HIs are plotted against the cycle life (y-axis) under a logarithmic scale. In all figures, the opacity of both red and blue colors indicates the cycle number and EOL of cells, respectively.

The practice of averaging the extracted features from the first 10 cycles, determined arbitrarily, is intended to ensure the stability of the model inputs. Fluctuations in the ρ-coefficients for each HI across different cycle numbers can be observed through the heatmap color opacity in Fig. 3, which shows the first 50 cycles from both the training and primary testing sets of the TRI dataset. Fig. 3a presents the temperature plotted against capacity during charging for a sample cell, highlighting the variation in starting temperature values and slight gradient differences across four selected cycles. These differences are attributed to residual spontaneous heat⁵² from the previous cycle, which arises due to protocol settings like insufficient resting time after discharge. The inconsistency of ρ-coefficients across cycle numbers may negatively impact the predictive performance of the HIs. As a result, single-cycle HIs are avoided, and instead, the average value from the first 10 cycles (excluding the initialization cycles) is used for each HI in the model development and prediction presented in this work.

Fig. 3 Heatmap comparison of Pearson's correlation coefficient between cycle life and temperature HIs from the charging section as a function of cycle number on TRI dataset. (a) Charging temperature profile plots of several cycle numbers as a function of charge capacity for a cell with a cycle life of 2237. (b)–(c), Heatmap plot of the correlation coefficient, ρ for (b), Training data. (c) Primary test data. The heatmap colors indicate the ρ in a range from −1 (red) to +1 (blue). Slight fluctuations across different cycle numbers are observed due to environmental temperature fluctuation and inadequate resting time between cycles for some cells as seen in (a).

Results and discussion

Seven early-cycle linear models were initially developed using features taken from the first 10 cycles to predict battery cycle life. Each of the six datasets trained a unique linear model with a distinct set of feature inputs, which included only the proposed statistical temperature HIs, referred as to the “temperature” model. Additionally, a “hybrid” model was developed specifically for the TRI dataset, which incorporates the proposed temperature HIs with other reported features that are unavailable in the other five datasets. As each model is evaluated within its respective dataset, it is assumed that factors influencing heat generation, such as the components of the battery (i.e., cathode active materials, anode, electrolyte, and binder), are uniform across all 18 650-cylindrical cells in each dataset. Given this assumption, the statistical temperature HIs derived from the cycling data are anticipated to indirectly reflect combined effects of material variations. As a result, all models demonstrated strong generalization across the datasets, consistently surpassing the accuracy of benchmark models adopted from Severson et al.,³⁷ which were limited to using data from the first 10 cycles, as shown by the Figures and Table in this section. Furthermore, we explored alternative approaches to study the impact of training the temperature model using HIs extracted from single cycles instead of averaged values over the first 50 cycles, as well as employing lesser (and more) cycling data than the mentioned first 10 cycles, for averaging the extracted HIs. A comprehensive evaluation of the model performance is discussed further, and additional information regarding the HIs utilized in all models is available in Tables S2 and S3 (ESI†).

The predicted cycle lives (y-axis) for all models are plotted against the true cycle lives (x-axis) in Fig. 4, with their performance summarized in Table 2. An inset plot of residual errors and the coefficient of determination (R²) are included inside each plot, located on the upper left and bottom right respectively. The SNL datasets, which were subjected to various environmental temperatures and discharge C-rates (as indicated by marker outline colors and shapes on the figure legend, respectively) with different battery chemistries, along with the slow cycling UL–NCA and fast-charging XJTU datasets, were used to develop the first five linear temperature models: Fig. 4a for SNL–NMC, Fig. 4b for SNL–NCA, Fig. 4c for SNL–LFP, Fig. 4d for UL–NCA, and Fig. 4e for XJTU. Most models achieved R² values above 0.8, successfully predicting battery aging trends based on environmental temperature effects, as captured by HIs such as the mean temperature. In colder conditions, NMC and NCA typically showed shorter cycle life due to lithium plating becoming the primary degradation mechanism below 25 °C,^7,42 while LFP exhibited improved performance. Additionally, subjecting LFP to higher C-rates significantly increases heat generation due to the rapid change in internal resistance^6,47 following ohmic law, which can be quantified by the temperature amplitude and maximum rate of temperature change. In contrast to the first four models, XJTU was subjected to higher charging rates which resulted in greater cycling temperature fluctuations (see Fig. S2, ESI†). The temperature model, which was trained using 3C-charging data, demonstrated a remarkable prediction accuracy for the OOP secondary test set containing 2C-charging data, achieving a very low RMSPE of 6.4%. This outcome indicates that the proposed statistical temperature HIs are capable of maintaining consistent predictive accuracy for OOD and OOP cells. To verify this conclusion, the temperature model will be trained and tested with both in-protocol data (primary test) and OOP data (secondary test set), available on the TRI dataset. Overall, the five models accurately predicted cycle life, as shown in Table 2. The worst-performing model in SNL–NMC achieved a MAPE of 17.1% and RMSPE of 21.9% on the test set. One potential factor limiting the model performance is associated with the shape of temperature profile, which is directly linked to the cycling rate. For instance, the small temperature fluctuation at slow charging rates may limit the ability of HIs to capture the degradation of thermally stable cathodes. We also observed that in the SNL–NMC dataset, a possible safety measure was activated under high C-rate and elevated temperature conditions, reducing the current to prevent excessive temperature increases (see Fig. S2, ESI†). This consequently led to irregular temperature fluctuation that might compromise the quality of our temperature-related HIs. Finally, it is essential to emphasize that, within the SNL datasets, the model predictions are validated solely within the temperature and cycle rate limits defined by the training and primary test data, i.e., in-distribution test predictions. While extrapolation beyond these specified conditions is generally anticipated to result in reduced accuracy, the model demonstrated unexpectedly high accuracy on the secondary test set from XJTU. Given this promising outcome, it is advisable to incorporate much larger data points covering a broader range of environmental temperatures and cycling rates to facilitate OOD predictions, thereby enabling extrapolation beyond the training conditions range.

Fig. 4 ElasticNet model estimated vs. true cycle lives for all datasets using the derived temperature HIs. Temperature model predictions are compared to the true observed cycle life using the average value of temperature HIs taken from each of the first 10 cycles, for the dataset: (a) SNL–NMC, (b) SNL–NCA, (c) SNL–LFP, (d) UL–NCA, (e) XJTU, (f)–(g) TRI dataset using (f), temperature HIs only (temperature), and (g), temperature HIs integrated with other Severson's features (hybrid). For (a)–(c), the cells are cycled under various environment temperature and discharge rate settings as indicated by the marker outline color and shape, respectively. An inset plot of the histogram of residual errors and the model coefficient of determination (R²) are included for all figures. HIs used by the models shown above are available in Tables S2 and S3 (ESI†).

Table 2 Dataset prediction error metrics for Fig. 4

	MAE^a (MAPE^b)			RMSE^c (RMSPE^d)
	Train	Test	Secondary test	Train	Test	Secondary test
a Mean absolute error (cycle). b Mean absolute percentage error (%). c Root mean-squared error (cycle). d Root mean-squared percentage error (%). The train set is used to build the model and evaluated on the primary and secondary test (if any) set. Details on the partition of cells used as train, primary test, and secondary test set in each dataset are available in Table S1 (ESI).
SNL–NMC	73 (16.2)	97 (17.1)	—	108 (22.7)	144 (21.9)	—
SNL–NCA	32 (6.9)	30 (6.4)	—	45 (9.6)	37 (7.4)	—
SNL–LFP	112 (5.3)	264 (10.2)	—	161 (8.5)	329 (12.3)	—
UL–NCA	24 (7.2)	39 (13.3)	—	42 (10.3)	61 (18.4)	—
XJTU	18 (8.4)	—	21 (5.1)	26 (12.6)	—	26 (6.4)
TRI (Temp)	107 (14.4)	129 (14.7)	174 (15.7)	180 (19.7)	216 (18.5)	257 (20.9)
TRI (hybrid)	63 (8.4)	94 (12.0)	148 (14.2)	103 (12.3)	146 (16.1)	203 (18.3)

---

The last two models were developed using the fast-charging TRI dataset: temperature (Fig. 4f) and hybrid model (Fig. 4g) which combines supplementary HIs related to charge time, internal resistance, and temperature features proposed by Severson et al.³⁷ The TRI dataset includes a secondary testing set containing unknown charging protocols distinct from both the training and primary testing sets, which is crucial for validating the generalizability of our proposed temperature HIs under unfamiliar protocols. First, the temperature model yielded a MAPE/RMSE of 15.7%/257 cycles for the secondary test set, mainly caused by the significant prediction deviations from the diagonal line in the higher cycle life regions (around 1500 cycles). This can be attributed to insufficient cell data with high cycle life, thereby prompting the development of the hybrid model, which incorporated additional HIs to capture more informative degradation patterns. As a result, the hybrid model reduced the MAPE/RMSE of the secondary testing set to 14.2%/203 cycles respectively, while also decreasing both training and primary testing errors. Based on these results, the proposed statistical temperature HIs provide sufficient information for accurate battery predictions under diverse conditions and can be further improved by working in tandem with other types of degradation HI. We also compared temperature models using averaged HI values versus single-cycle HIs, shown in Fig. 5. Models trained on averaged HIs from the first 10 cycles achieved lower RMSE values (i.e., solid horizontal line) compared to the fluctuating RMSE values of the single-cycle models, up to the first 50 cycles. This suggests that averaging HI values provides a more robust and accurate linear model.

Fig. 5 RMSE performance of single-cycle temperature models on the test sets for the first 50 cycles. Temperature model is trained using the identical set of single-cycle HIs instead of the averaged HI values, and evaluated on the first 50 cycles for each dataset (see Tables S2 and S3, ESI†): (a) SNL–NMC, (b) SNL–NCA, (c) SNL–LFP, (d) UL–NCA, (e) XJTU, (f) TRI. The horizontal solid and dashed lines in each plot represent the RMSE of the temperature model using average HI values of the first 10 cycles and single-cycle values, respectively. The blue lines denote the primary test sets, while the orange lines indicate the secondary test sets, which are only available for datasets (e), XJTU, and (f), TRI.

To evaluate the effectiveness of our trained models, we compared them against naïve constants and prior research models as benchmarks. Naïve constants are univariate models prepared with minimal data manipulation. For this study, we used the discharge capacity at cycle 2 and the average cycle life of the train set. Additionally, we adopted the models presented by Severson et al.³⁷ – variance, discharge, and full models – which were originally trained using features extracted from the first 100 cycles. We recreated their early-cycle lifetime models by modifying their feature pool to use data from the first 10 cycles only. The full model, which utilizes several features related to internal resistance, was only available for the TRI dataset, as the necessary data was unavailable in the other datasets. Therefore, the TRI dataset is the only one that includes all three benchmark models. The RMSPE of both temperature and hybrid models was compared to these benchmark models as shown in Fig. 6. The naïve constants (see Table S4, ESI†) performed significantly worse across all datasets, with error values up to four times higher than those of the proposed models, except in a few cases. For instance, Q_{d_cycle2} in the UL–NCA dataset exhibited a slightly higher RMSPE of 22.9% on the test set compared to the temperature model (18.4%) due to their implementation of two different DOD settings (i.e., 94% and 100%). Discharge capacity-related HIs can lead to data leakage that captures the inverse correlation between DOD and cycle life. Despite this advantage, the temperature model performed better compared to the Q_{d_cycle2} benchmark. Furthermore, variance and discharge models failed to provide comparable results (except for the discharge model in UL–NCA), often performing similar to or worse than the naïve benchmarks. The full model, which uses the most diverse set of features on TRI, fit the training data well and achieved RMSPE values of 15.3%, 18.1%, and 29.7% for training, primary testing, and secondary testing sets, respectively. In comparison, the temperature model, while showing a higher training RMSPE of 19.7%, exhibited a similar RMSPE of 18.5% on the primary test set, but more importantly, it achieved greater accuracy on the secondary test set with an RMSPE of 20.9% on TRI. In addition, the hybrid model demonstrated the lowest error values across all three data splits, with RMSPE of 12.3%, 16.1%, and 18.3%, for the training, primary, and secondary test sets, respectively. These results suggest that the proposed temperature HIs utilized in both models have effectively mitigated overfitting compared to the full model, which showed a significant increase in RMSE on the secondary test set. Although all the proposed and benchmark models were trained using HIs extracted from the first 10 cycles, our hybrid model in the TRI dataset performed comparably to the best result reported by Severson et al.,³⁷ which utilized features extracted from the first 100 cycles.

Fig. 6 RMSPE comparison of the proposed models on the test sets. The temperature (and hybrid) model for each dataset is plotted against an adapted version of Severson et al. models: (i) variance, (ii) discharge, and (iii) full (only applicable in TRI), built using features extracted from only the first 10 cycling data.

Finally, we analyzed the performance of our models by using average HI values derived from varying cycle ranges, up to the first 100 cycles. We expanded on the initial approach of averaging the first 10 cycles for feature extraction by considering the first x cycles ranging from 3 to 100 cycles, to train individual models with the same set of HIs for each dataset (refer to Tables S2 and S3, ESI†) to predict cycle life. Subsequently, we evaluated these models on the test set(s) of each dataset, visualizing the resulting MAE and RMSE values in Fig. S11 (ESI†). As anticipated, the most accurate predictions were obtained when x was around 10 cycles, where these sets of features were optimized during model training presented in Fig. 4. While the model performance generally stabilized beyond this point, we observed fluctuations and elevated error values for x values below 10 cycles across most datasets. This phenomenon can be attributed to the evolution of temperature profiles during charging in the initial cycles. In most of the datasets, we noticed fluctuations in the starting charging temperature with cycle number until it eventually stabilized, as illustrated in a sample cell in Fig. 3. The variability in starting charging temperature could be influenced by factors such as spontaneous heat released from the preceding discharge cycle without sufficient resting period,⁵² leading to disruptions in statistical values like minimum or skewness, thereby affecting the predictive accuracy of the temperature models. This issue was mitigated by incorporating non-temperature HIs, as demonstrated in Fig. S11f (ESI†) by the hybrid model at lower cycle counts, as well as after cycle 55, where temperature fluctuation in the environmental chamber was reported in TRI primary test set data.³⁷ To ensure a consistent temperature profile, adjustments such as modifying resting times may be necessary to enable model training with fewer than 10 cycles. Additionally, we observed sharp or consistent error increases at later cycles as observed in Fig. S11a, b, & d, (ESI†) attributed to disruptions in temperature measurements, such as periodic reference performance test (RPT) cycling, or cycling interruptions. We also explored optimal sets of HIs for the temperature and hybrid models with x values below 10 (refer to Tables S5 & S6, ESI†) and found that the optimal sets were similar to those for x = 10 reported in Table 2. In conclusion, while it is feasible to train models with fewer than 10 cycles, our proposed temperature HIs consistently yielded satisfactory results or even improved outcomes across different cycle average ranges.

The proposed temperature-related HIs have demonstrated significant predictive capabilities in estimating battery lifetime spanning up to thousands of cycles, based on statistical analysis of the first 10 cycles or less. This is evident from extracting statistical summary at critical points, temperature profile shape, and more, including the rate of temperature change over time. Their generalizability and predictive strength have been confirmed through testing on datasets comprising diverse cycling modes and environmental temperature settings, showcasing their superiority over the inflexible benchmark models under OOD operating conditions and limited cycling data, as demonstrated in the XJTU and TRI secondary test sets. While the temperature linear models perform well across various constraints, the SNL and UL–NCA datasets may lack sufficient data points for robust model training to justify this conclusion, and some limitations could have impacted the performance of the proposed temperature HIs. For instance, in the SNL–NMC dataset, elevated temperature and C-rate settings triggered safety measures that reduced the discharge current once the temperature reached its maximum allowable value. This affected the temperature profile, potentially compromising its quality. Similarly, in the TRI dataset, inadequate temperature cooling due to short rest intervals may also have an influence. Additionally, while the proposed temperature HIs leverage complete cycling data, future work should explore partial cycling segments to extract valuable insights with prognostic value. Moreover, there is a need to develop a unified model capable of predicting battery lifetime across datasets containing diverse cathode chemistries, operating conditions, and cell configurations. By incorporating additional battery components information, such as cathode composition, electrolyte characteristics, and detection of volume changes due to initial cycle gassing in NMC cells,⁵¹ the prediction model can enhance its accuracy by adapting to specific cell characteristics through ML and transfer knowledge techniques. This approach may yield more interpretations and further improve the model accuracy in predicting battery degradation under various cycling dimensionality.

Conclusion

In summary, this study investigated the effectiveness of using averaged statistical cell surface temperature HIs taken from the first 10 cycles to predict battery lifetime. The ElasticNet algorithm was applied to build early-cycle prediction models based on these temperature HIs across the SNL, UL–NCA, XJTU, and TRI datasets, which represent different cathode materials, environmental temperatures, and cycling rates. The linear temperature model performed with high accuracy on all datasets, particularly on the TRI dataset, which contains 123 cells with an average lifetime of approximately 800 cycles. Both the temperature and hybrid models outperformed the benchmark models. The hybrid model, which combined the proposed temperature HIs with other previously reported features, notably achieved a MAPE/RMSE of 14.2%/203 cycles on the unknown TRI, as well as XJTU, secondary test set, indicating strong adaptability and predictive generalization.

While more complex ML algorithms may yield lower prediction errors, our simple linear model highlights the predictive power of surface temperature measurements, which are applicable under a wide range of cycling constraints. Although the SNL, UL–NCA, and XJTU datasets had fewer data points, potentially compromising population representativeness, we accommodated this limitation by applying a close to equal train-test data partitioning ratio. Larger datasets will be necessary to fully validate the robustness of the temperature-related HIs, especially for a wider range of battery chemistries and operational conditions. Nevertheless, this study has shown that statistical temperature HIs provide valuable early-cycle prognostic insights. In future work, we will focus on identifying additional early-cycle HIs to develop a flexible and universal model, potentially incorporating more advanced algorithms and transfer learning techniques. The proposed HIs demonstrated commendable performance considering the inherent heat generation characteristics of this intercalation-based system. However, it may be advantageous to explore additional thermal HIs across various systems, including conversion chemistries and emerging battery technologies, to promote all types of practical prognostic applications. We believe that data-driven ML methods will continue to play an increasingly important role in advancing the research and development of future electrochemical energy storage systems.

Methods

In this study, we evaluated the prognostic trait of surface temperature HIs extracted from early cycling data of LIBs. To achieve this, we developed linear models using ElasticNet regularization to predict the battery lifetime based on datasets compiled from multiple sources. Several steps were considered to select eligible cells, engineer features, and build models that are adaptable to the diverse characteristics of the datasets, and will be discussed in the following sections.

Temperature data interpolation

To ensure consistency across datasets, we sampled temperature from voltage recordings, which allowed us to segregate specific regions, i.e., the CC region during charge or discharge stages. Before extracting features, we applied data interpolation to address missing recordings, often resulting from low-frequency logging. The raw cycling data was interpolated between the lower voltage limit (V_lower) and the upper voltage limit (V_upper) using S steps of equal voltage intervals (ΔV), formulated as:

ΔV = (V_upper − V_lower)/S

choosing S = 100 generated a discretized temperature vector, T[V], consisting of 100 temperature elements spaced with an equal ΔV interval. We calculated the rate of temperature change (dT/dV) by subtracting successive elements of T[V] and dividing by ΔV, resulting in a vector of S − 1 elements (i.e., 99). The V_lower and V_upper used were set according to the manufacturer specifications for each dataset, with a small overpotential added to the starting voltage for both charge and discharge data (see Supplementary Note S1, ESI†). Using this voltage-referencing method, the CC-region was selected for all datasets, except for the TRI dataset, where temperature was interpolated with capacity (denoted as T[Q] and dT/dQ) instead of voltage. This adjustment was necessary due to the multi-step charging protocols in the TRI dataset, which resulted in a non-monotonic voltage function that complicated interpolation.

Dataset screening

To maintain the accuracy of our predictions for each dataset, we excluded cells that exhibited inconsistencies. For instance, one outlier from the TRI dataset with a rapid cycle life decay (148 cycles) was removed, leaving 123 out of the original 124 LFP cells. In the battery archive datasets,^42,43 one cell with an unusually high lifetime of 723 cycles under 15 °C was removed from the SNL–NCA dataset, and we focused on cells cycled with 100% DOD, selecting 19 out of 30 cells from SNL–LFP, 16 out of 25 from SNL–NCA, and 21 out of 32 from SNL–NMC. All 21 cells from UL–NCA were included, as their DOD values (e.g. 94%) were close to 100%, and data availability was limited. For XJTU, only 2 dataset batches were cycled with 100% DOD, namely batch 1 and batch 2, selecting 23 of the total 55 cells.

The EOL for TRI, SNL–NCA, and SNL–NMC datasets was set to 80% SOH. However, for the UL–NCA dataset, cycling terminated at multiple capacity fade levels, while the SNL–LFP dataset was incomplete at the start of our study due to ongoing cycling, thus we set the EOL to 85% and 90% SOH for the UL–NCA and SNL–LFP datasets, respectively (see Table S1 and Supplementary Note S1 for more details, ESI†).

Feature engineering

Before conducting statistical feature extraction, the temperature data must be standardized into vectors of equal length. Due to the varying measurement frequencies across and within datasets, we applied linear interpolation to the time-series cycling data, as described previously. Following this process, a T[V] (or T[Q]) vector, as well as the rate of temperature change, dT/dV (or dT/dQ), were obtained from each cycle. From these T[V] and dT/dV vectors, we calculated the 7 statistical summaries on both charge and discharge regions separately, producing a total of 28 statistical temperature HIs for each cycle, where their average of the first 10 cycles were finally computed. To prepare the data for model training, the HIs were normalized using the z-score method, where each feature was scaled by subtracting the mean and dividing by the standard deviation:
where x̄ is the mean, and σ is the standard deviation of feature x.

Data-driven model development and validation

For each dataset, we compiled a pool of 28 HI candidates. These were subjected to feature selection using ElasticNet regularization,⁴⁵ a method that combines the penalties of ridge (L₂) and lasso (L₁) regression to improve feature selection and model generalization. The early-cycle lifetime model was developed using a training set for each dataset, aiming to predict the EOL of battery cells on either regular or log₁₀ cycle life values. The linear model is represented as:

ŷ_i = w^Tx_i

where w is the weight matrix, x_i is the m-dimensional feature vector, and ŷ_i is the estimated cycle life output of the i-th battery. The ElasticNet regression process minimizes the error between the true y and predicted ŷ values using the following objective function:
where y is the n-dimensional true cycle life vector, X is the n × p feature matrix, and the hyperparameters λ ≥ 0, and 0 < α < 1 that control the balance between feature elimination and weight uniformity. This formula returns the optimal weight matrix, where the objective function (a) is known as the ordinary least-squares method. The first term in the penalty function (b) applies L₂ regularization, and the second term applies L₁ regularization which can be tuned using both parameter values of λ and α.

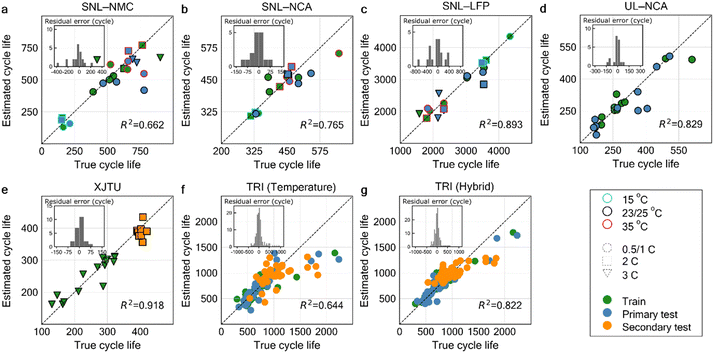
To tune the hyperparameters, we used k-fold cross-validation and random Monte Carlo sampling on the training set. In k-fold cross-validation, the data is split into k subsets, and the model is trained and validated k times, each time using a different subset as the validation set. For the XJTU and TRI datasets, we set k = 4, while for other datasets with fewer samples, we used leave-one-out cross-validation (i.e., k = n_train). In this case, ElasticNet was particularly beneficial in handling datasets with limited samples and high-dimensional feature sets (i.e., m > N) due to its additional hyperparameter, α, which regulates highly correlated features.⁴⁵ The best model(s) for each dataset was selected based on the obtained lowest prediction variance from the true values, as measured by the coefficient of determination, R², defined as

where N is the total number of observed samples, and ȳ is the mean cycle life of the observed sample set. Since, the correlation between a HI and cycle life may vary across datasets, using a fixed set of HIs for all datasets may not yield optimal results. To address this, we employed an exhaustive search to identify the optimal subset of features for each dataset. This process involved training the model with all possible combinations of HIs, from single features up to combinations of j = 15 features out of 28, to find the best subset. By limiting the search to a maximum of 15 features, we were able to significantly reduce computation time. The features were initially screened by comparing the Pearson correlation coefficient, ρ, with cycle life, defined as
where x̄ is the mean of the feature. Finally, to evaluate the generalizability of the trained model, we validated its performance on the test set(s) using several error metrics, including MAE, MAPE, RMSE, and RMSPE, with the formula:

All raw data were processed using both MATLAB and Python, with feature extraction and model development carried out in Python using the NumPy,⁵³ pandas,⁵⁴ scikit-learn,⁵⁵ and SciPy⁵⁶ packages.

Author contributions

L. S. and Y.-C. L. conceived the project, analyzed the experimental data, interpreted the results, and wrote the manuscript. L. S. conducted the feature engineering, visualization, machine learning methodology development, and model validation. Z. H. and Y.-C. L. reviewed and edited the manuscript. Y.-C. L. supervised the project.

Code availability

Code for data visualization and processing is available from the corresponding authors upon request.

Data availability

The datasets used in this study are available online, for (1) TRI, https://data.matr.io/1/projects/5c48dd2bc625d700019f3204, for (2) UL–NCA, SNL datasets, https://www.batteryarchive.org/, and for (3) XJT, https://zenodo.org/records/10963339

Conflicts of interest

The authors declare no competing interests.

Acknowledgements

This work is supported by a grant from the Research Grants Council (RGC) of the Hong Kong Administrative Region, China, under project No. T23-701/20-R. Y.-C. L. acknowledges the support from Xplorer Prize by New Cornerstone Science Foundation.

References

1. M. Li, J. Lu, Z. Chen and K. Amine, Adv. Mater., 2018, 30, 1800561.
2. R. Schmuch, R. Wagner, G. Hörpel, T. Placke and M. Winter, Nat. Energy, 2018, 3, 267–278.
3. J. Xie and Y.-C. Lu, Nat. Commun., 2020, 11, 2499.
4. J. Zhang and J. Lee, J. Power Sources, 2011, 196, 6007–6014.
5. A. Barré, B. Deguilhem, S. Grolleau, M. Gérard, F. Suard and D. Riu, J. Power Sources, 2013, 241, 680–689.
6. J. Wang, P. Liu, J. Hicks-Garner, E. Sherman, S. Soukiazian, M. Verbrugge, H. Tataria, J. Musser and P. Finamore, J. Power Sources, 2011, 196, 3942–3948.
7. S. Schuster, T. Bach, E. Fleder, J. Müller, M. Brand, G. Sextl and A. Jossen, J. Energy Storage, 2015, 1, 44–53.
8. S. Paul, C. Diegelmann, H. Kabza and W. Tillmetz, J. Power Sources, 2013, 239, 642–650.
9. S. Ma, M. Jiang, P. Tao, C. Song, J. Wu, J. Wang, T. Deng and W. Shang, Progress Nat. Sci., 2018, 28, 653–666.
10. X. Han, L. Lu, Y. Zheng, X. Feng, Z. Li, J. Li and M. Ouyang, eTransportation, 2019, 1, 100005.
11. C. Weng, J. Sun and H. Peng, J. Power Sources, 2014, 258, 228–237.
12. D. Stroe and E. Schaltz, IEEE Trans. Ind. Appl., 2019, 56, 678–685.
13. Z. Guo, X. Qiu, G. Hou, B. Liaw and C. Hang, J. Power Sources, 2014, 249, 457–462.
14. S. Tong, M. Klein and J. Park, J. Power Sources, 2015, 293, 416–428.
15. M. Galeotti, L. Cinà, C. Giammanco, S. Cordiner and A. D. Carlo, Energy, 2015, 89, 678–686.
16. A. Jokar, B. Rajabloo, M. Désilets and M. Lacroix, J. Power Sources, 2016, 327, 44–55.
17. J. Li, K. Adewuyi, N. Lotfi, R. Landers and J. Park, Appl. Energy, 2018, 212, 1178–1190.
18. M. Chen, X. Ma, B. Chen, R. Arsenault, P. Karlson, N. Simon and Y. Wang, Joule, 2019, 3, 2622–2646.
19. X. Hu, L. Xu, X. Lin and M. Pecht, Joule, 2020, 4, 310–346.
20. K. Goebel, B. Saha, A. Saxena, J. Celaya and J. Christophersen, IEEE Instrum. Meas. Mag., 2008, 11, 33–40.
21. E. Walker, S. Rayman and R. White, J. Power Sources, 2015, 287, 1–12.
22. D. Andre, M. Meiler, K. Steiner, C. Wimmer, T. Soczka-Guth and D. Sauer, J. Power Sources, 2011, 196, 533.
23. A. Guha and A. Patra, IEEE Trans. Instrum. Meas., 2018, 67, 1836–1849.
24. M. Ahwiadi and W. Wang, IEEE Trans. Instrum. Meas., 2018, 68, 923–935.
25. P. Northrop, B. Suthar, V. Ramadesigan, S. Santhanagopalan, R. Braatz and V. Subramanian, J. Electrochem. Soc., 2014, 161, E3149.
26. M. Ecker, J. Gerschler, J. Vogel, S. Käbitz, F. Hust, P. Dechent and D. Sauer, J. Power Sources, 2012, 215, 248–257.
27. E. Sarasketa-Zabala, E. Martinez-Laserna, M. Berecibar, I. Gandiaga, L. Rodriguez-Martinez and I. Villarreal, Appl. Energy, 2016, 162, 839–852.
28. J. Wei, X. Chu, X. Sun, K. Xu, H. Deng, J. Chen, Z. Wei and M. Lei, InfoMat, 2019, 1, 338–358.
29. M. Ng, J. Zhao, Q. Yan, G. Conduit and Z. Seh, Nat. Mach. Intell., 2020, 2, 161–170.
30. T. Lombardo, M. Duquesnoy, H. El-Bouysidy, F. Årén, A. Gallo-Bueno, P. B. Jørgensen, A. Bhowmik, A. Demortière, E. Ayerbe, F. Alcaide, M. Reynaud, J. Carrasco, A. Grimaud, C. Zhang, T. Vegge, P. Johansson and A. A. Franco, Chem. Rev., 2022, 122, 10899–10969.
31. Z. Huang, L. Sugiarto and Y. Lu, EcoMat, 2023, 5, e12345.
32. A. Jain, S. Ong, G. Hautier, W. Chen, W. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. Persson, APL Mater., 2013, 1, 1.
33. G. Dos Reis, C. Strange, M. Yadav and S. Li, Energy AI, 2021, 5, 100081.
34. D. Roman, S. Saxena, V. Robu, M. Pecht and D. Flynn, Nat. Mach. Intell., 2021, 3, 447–456.
35. J. Tian, R. Xiong, W. Shen, J. Lu and X. Yang, Joule, 2021, 5, 1521–1534.
36. Y. Zhang, R. Xiong, H. He, X. Qu and M. Pecht, eTransportation, 2019, 1, 100004.
37. K. Severson, P. Attia, N. Jin, N. Perkins, B. Jiang, Z. Yang, M. Chen, M. Aykol, P. Herring, D. Fraggedakis and M. Bazant, Nat. Energy, 2019, 4, 383–391.
38. P. Attia, A. Grover, N. Jin, K. Severson, T. Markov, Y. Liao, M. Chen, B. Cheong, N. Perkins, Z. Yang and P. Herring, Nature, 2020, 578, 397–402.
39. B. Jiang, W. Gent, F. Mohr, S. Das, M. Berliner, M. Forsuelo, H. Zhao, P. Attia, A. Grover, P. Herring and M. Bazant, Joule, 2021, 5, 3187–3203.
40. H. Feng and D. Song, J. Energy Storage, 2021, 34, 102118.
41. A. Geslin, B. van Vlijmen, X. Cui, A. Bhargava, P. Asinger, R. Braatz and W. Chueh, Joule, 2023, 7, 1956–1965.
42. Y. Preger, H. Barkholtz, A. Fresquez, D. Campbell, B. Juba, J. Romàn-Kustas, S. Ferreira and B. Chalamala, J. Electrochem. Soc., 2020, 167, 120532.
43. D. Juarez-Robles, J. Jeevarajan and P. Mukherjee, J. Electrochem. Soc., 2020, 167, 160510.
44. F. Wang, Z. Zhai, Z. Zhao, Y. Di and X. Chen, Nat. Commun., 2024, 15, 4332.
45. H. Zou and T. Hastie, J. R. Statist. Soc. B, 2005, 67, 301–320.
46. K. Laidler, J. Chem. Edu., 1984, 61, 494.
47. W. Shen, N. Wang, J. Zhang, F. Wang and G. Zhang, ACS Omega, 2022, 7, 44733–44742.
48. M. Xiao and S. Choe, J. Power Sources, 2013, 241, 46–55.
49. G. Liu, M. Ouyang, L. Lu, J. Li and X. Han, J. Therm. Anal. Calorim., 2014, 116, 1001–1010.
50. Y. Li, P. Huang, L. Gao, C. Zhao and Z. Guo, J. Electrochem. Soc., 2023, 170, 040507.
51. L. Kraft, T. Zünd, D. Schreiner, R. Wilhelm, F. Günter, G. Reinhart, H. Gasteiger and A. Jossen, J. Electrochem. Soc., 2021, 168, 020537.
52. S. Zhu, C. He, N. Zhao and J. Sha, J. Power Sources, 2021, 482, 228983.
53. C. Harris, K. Millman and S. van der Walt, Nature, 2020, 585, 357–362.
54. J. Reback and W. McKinney, Zenodo, 2020 DOI:10.5281/zenodo.3509134.
55. F. Pedregosa, J. Mach. Learn. Res., 2011, 12, 2825–2830.
56. P. Virtanen, R. Gommers and T. E. Oliphant, Nat. Methods, 2020, 17, 261–272.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ee05179c

---