Performance advancements in P-type TaFeSb-based thermoelectric materials through composition and composite optimizations

Abstract

Half-Heusler compounds exhibit significant potential in thermoelectric applications for power generation up to 1000 K, notwithstanding the substantial challenges posed by the cost of constituent elements and the imperative to augment the average thermoelectric figure-of-merit (zT_ave) for more practical applications. Overcoming these obstacles demands advancing high-performance p-type TaFeSb thermoelectric materials with diminished Ta content. This investigation systematically explores the quaternary-phase space encompassing Ta, Nb, V, and Ti to ascertain an optimal composition, namely Ta_0.42Nb_0.3V_0.15Ti_0.13FeSb. This composition is characterized by a remarkable reduction in Ta concentration and an enhancement in zT, peaking at 1.23 at 973 K. Moreover, the integration of a high-mobility secondary phase, InSb, fosters enhancements in both the Seebeck coefficient and electrical conductivity, resulting in a 23% augmentation in the average power factor in the optimized composite, Ta_0.42Nb_0.3V_0.15Ti_0.13FeSb-(InSb)_0.015. This optimized material achieves a peak zT of 1.43 at 973 K, and a record-setting zT_ave of 1 from 300 K to 973 K, marking a significant advancement among p-type half-Heusler materials. Additionally, a single-leg device demonstrates a peak efficiency of approximately 8% under a temperature difference of 823 K vs. 303 K. These findings underscore the substantial potential of the proposed material design and fabrication methodologies in fostering efficient and sustainable thermoelectric applications.

---

Broader context

Over two-thirds of energy from fossil fuels is lost as waste heat, worsening pollution and the energy crisis. Thermoelectric power generation, which directly converts heat to electricity, offers a green solution, especially in high-temperature environments. However, its widespread adoption is limited by high material costs and the need for improved performance, often measured by the figure of merit (zT). This study refines TaFeSb-based p-type half-Heusler compounds, known for their potential but constrained by the high cost of Ta and performance challenges. By exploring a combination of Ta, Nb, V, and Ti, we identified a composition that reduces reliance on expensive Ta without compromising performance. Adding InSb as a high-mobility secondary phase further improved electrical conductivity and power factor. As a result, we achieved an average zT of 1 from 300 K to 973 K, alongside exceptional thermoelectric efficiency in a single-leg device. This work provides an affordable and efficient pathway for advancing thermoelectric technologies, paving the way for sustainable energy solutions.

1. Introduction

In light of the world's expanding demand for sustainable energy sources, a profound focus on the global energy infrastructure becomes increasingly necessary. In this context, the field of thermoelectric (TE) generators (TEGs) has garnered a lot of interest and research over the past few decades due to their ability to convert heat into electricity and vice versa in the solid state, thus providing a clean and sustainable energy source.^1,2 The performance of TE materials is encapsulated by the dimensionless figure-of-merit (zT), expressed as zT = (S²σ)/(κ_L + κ_e)T. Here, S²σ constitutes the thermoelectric power factor (PF), comprising the Seebeck coefficient (S) and electrical conductivity (σ). The summation of lattice thermal conductivity (κ_L) and electronic thermal conductivity (κ_e) is the overall thermal conductivity, denoted as κ. T denotes absolute temperature. Achieving higher zT is a central challenge in the field of thermoelectrics due to the intricate interplay among three parameters (σ, S, and κ).^3–7

Among bulk thermoelectric materials, half-Heusler (HH) compounds stand out, especially for applications requiring mid-high temperatures from 800 K to 1000 K. These materials are highly suited for power-generating applications due to several important characteristics such as high PF values, high thermal stability, and robust mechanical properties.⁸ Due to a filled valence shell, HH materials with a valence electron count of 18 per unit cell display semiconductor characteristics. Besides, the structure of HH materials constitutes three interpenetrating fcc sub-lattices, thus rendering a plethora of doping/alloying possibilities on each sublattice.^9–13 However, a significant drawback of HH compounds is their relatively high thermal conductivity, which can reach as high as 20 W m⁻¹ K⁻¹ at room temperature.¹⁴ To enhance electrical properties and/or suppress lattice thermal conductivity, various strategies have been employed including nano-structuring,^15–17 alloying,^18,19 phase separation,^20–22 energy filtering,^23–26 composite,²⁷ and defect engineering.^28–30 These strategies achieved great success for HH materials, particularly for n-type MNiSn (M: Ti, Zr, and Hf) materials, which have repeatedly and reliably achieved peak zT > 1.2 at 800 K to 1000 K.^31,32 Similarly, p-type HH compounds, particularly the RFeSb (with R being Ta, Nb, and V) compounds have garnered attention due to their high zT, lower cost (free of Hf), huge power factor, and large carrier pocket degeneracy (N_v) of the valence band.^33,34 Through alloying at the R sites among Ta, Nb, and V and doping by titanium (Ti), the peak zT values of 1.4 to 1.6 were reported at 973 K to 1200 K.^35,36 Despite the considerable success, the material development encountered several challenges. For example, the high melting point of Ta makes it practically difficult to synthesize a pure-phase material. This challenge has been addressed by Yu et al.,³⁷ and Zhu et al.,^36,38 by floating-zone melting and high-energy ball milling, respectively. Nevertheless, the price of Ta is higher than the other elements in this system (refer to the ESI,† Fig. S1). Therefore, the amount of Ta should be significantly reduced compared to the previously reported Ta-based compound with Ta_0.74V_0.1Ti_0.16FeSb composition (zT = 1.52 at 973 K).³⁶ Note that by the quaternary alloying among Ta, Nb, V, and Ti, there exists a great opportunity to find a high-performing composition with reduced Ta concentration. However, this huge compositional space has not been sufficiently investigated.

Moreover, advancements in TE properties have explored the effectiveness of a composite strategy through the introduction of secondary phases in HH compounds. Secondary phases, such as Al₂O₃, WO₃, NiO, HfO₂, and grain boundary (GB) phases, etc. have been instrumental in enhancing thermoelectric performance.^27,39,40 Notably, InSb, with its remarkably high carrier mobility stands out as a particularly promising inclusion. Introducing InSb into NbFeSb significantly enhances electrical conductivity through modifying the GB chemistry as shown in our previous system,⁴¹ and hence successfully enhances the electrical conductivity while maintaining the high Seebeck coefficient and low thermal conductivity.^41,42

In this work, we apply both concepts to optimize TaFeSb-based thermoelectrics. Firstly, to lower the Ta content while keeping a high thermoelectric performance, we looked into the quaternary phase space among Ta, Nb, V, and Ti to find an optimized composition. Second, to further enhance the thermoelectric properties, we employed a composite approach by introducing InSb to modify the grain boundaries. This incorporation of InSb within the TaFeSb-based system represents a novel advancement in the field and is reported here for the first time. In the first step, we developed an optimized composition, Ta_0.42Nb_0.3V_0.15Ti_0.13FeSb, which achieved a 33% reduction in the material cost compared to the previously reported Ta_0.74V_0.1Ti_0.16FeSb,³⁶ while still maintaining a competitive peak zT value of 1.23 at 973 K. Furthermore, the inclusion of InSb for sample Ta_0.42Nb_0.3V_0.15Ti_0.13FeSb-(InSb)_0.015 modified the GBs, and enabled further ∼23% enhancement of average power factor in the range of 300–973 K. This has further yielded a peak zT value of 1.43 at 973 K. Moreover, an average zT (zT_ave) of ∼1 between 300–973 K and zT of 0.4 at 300 K are demonstrated, the highest value among p-type half-Heusler compounds to the authors’ knowledge. Besides, based on the optimized composition Ta_0.42Nb_0.3V_0.15Ti_0.13FeSb-(InSb)_0.015, thermoelectric conversion efficiency of ∼8% is demonstrated for a single-leg device between a cold-side temperature (T_c) of ∼303 K and a hot-side temperature (T_h) of 823 K. Overall, these results demonstrate the significant potential of our material design and fabrication techniques for low-cost, sustainable, and high-performance thermoelectric materials and devices.

2. Results and discussion

2.1. Ta-reduction for TaFeSb-based half-Heusler compounds

Our research endeavors to assess the optimal thermoelectric performance of TaFeSb-based half-Heusler compounds by simultaneously alloying Nb, V, and Ti at the Ta sites. Given the vast compositional space resulting from the complexity of the quaternary-alloying nature, it is imperative to apply certain empirical rules to navigate the composition domains and impose specific limitations to reduce the degrees of freedom in such navigation. Initially, we classified these four elements into two distinct groups: Ta and Nb in the first group, and V and Ti in the second group. This classification is based on the observation that Ta and Nb possess comparable atomic radii, despite significant differences in atomic mass arising from the lanthanide contraction of Ta. Consequently, we anticipate that the introduction of Nb at the Ta sites will primarily influence the thermal properties, while having minimal impact on the electrical properties, similar to a previous studies on different systems conducted by Liu et al. and He et al. on the n-type (Zr, Hf)CoSb half-Heusler series.^6,35 On the other hand, V and Ti exhibit closely aligned atomic masses and radii, resulting in considerable lattice distortion when they are alloyed at the Nb/Ta sites. As a consequence, both electrical and thermal conductivities are expected to be effectively reduced. Therefore, careful optimization of the amounts of V and Ti is crucial to strike the most favorable “trade-off” between electrical and thermal conductivity. To initiate the optimization process, we have predetermined the starting composition as Ta_0.75V_0.1Ti_0.15FeSb, which closely aligns with our previously reported high-performance composition.³⁶ Subsequently, a series of systematic investigations will be conducted to progressively optimize the concentrations of (1) Nb, (2) Ti, and (3) V. Besides, any nominal adjustments to Nb, Ti, and V will be counterbalanced by corresponding changes in Ta to maintain the overall quantity of Ta, Nb, Ti, and V at unity.

The detailed optimization procedure is delineated in Fig. 1a and b, and the complete thermoelectric properties from room temperature to 973 K can be found in the ESI† (Fig. S2). Notably, the optimization criterion hinges on attaining the highest achievable zT value at 973 K, which represents the highest applicable temperature range for the majority of half-Heusler materials. The zT values at 973 K for each composition are also illustrated in Fig. 1a and b. The optimization process unfolds as follows: in step 1, we introduce considerable amounts of Nb into the Ta sites, leading to the formulation of a compositional series denoted as Ta_0.75−xNb_xV_0.1Ti_0.15FeSb with x = 0.25, 0.3, 0.35 and 0.4. Within this series, the peak zT value at 973 K is attained as 1.18 when x = 0.3. Proceeding to step 2, we maintain x = 0.3 while subtly optimizing the Ti content in Ta_0.45−yNb_0.3V_0.1Ti_0.15+yFeSb with y = 0.02 and −0.02, resulting in an intermediate compositional optimization denoted as Ta_0.47Nb_0.3V_0.1Ti_0.13FeSb, which exhibits a zT value of 1.20 at 973 K. Finally, in step 3, we optimize the z element in Ta_0.47−zNb_0.3V_0.1+zTi_0.13FeSb with z = −0.05, 0.05, and 0.1, culminating in an optimized composition denoted as Ta_0.42Nb_0.3V_0.15Ti_0.13FeSb, exhibiting a zT value of 1.23 at 973 K. Overall, exploring the compositional phase space yielded an enhancement of maximum zT of ∼9% from 1.13 to 1.23 and the zT_ave value is competitive within the TaFeSb-based system and is in the range of high compared to those reported for many other HHs (Fig. 4f). Furthermore, the concomitant reduction in Ta usage marks an important development considering the higher cost and weight of Ta compared to other constituent elements (Fig. 1c and Fig. S1, ESI†). The 33% cost reduction over earlier effort³⁶ favors developing a lower-cost and lightweight material and technology for real-world applications.

Fig. 1 The step-wise optimization procedure of (Ta,Nb,V,Ti) FeSb-based half-Heusler compound. (a) The whole quaternary phase among Ta (green axis), Nb (blue), V (brown), and Ti (yellow). The purple spheres represent the investigated compositions in this work. (b) The enlarged view of the left. The zT values labelled at each composition are experimental results at 973 K, (c) price comparison between most promising p-type HHs^36,43–45 and this study.

2.2. Improving the thermoelectric performance through a composite strategy

2.2.1. Electronic transport properties. In our previous work, incorporating 2% InSb into Nb_0.95Ti_0.05FeSb modified the grain boundary chemistry, resulting in a notable improvement in electrical conductivity without affecting the Seebeck coefficient. This led to nearly a two-fold increase in the power factor.⁴¹ It is important to note that this enhancement was observed only at a moderate doping level, specifically 5% Ti at the Nb sites. No performance improvement was seen by compositing InSb into a heavily-doped material, such as 20% Ti at the Nb sites. For the optimized composition in step 2 (Section 2.1), Ta_0.47Nb_0.3V_0.1Ti_0.13FeSb, the doping level (Ti = 0.13) falls between these two extremes. It remains uncertain whether compositing would be an effective strategy in this case. To explore this, we prepared nominal compositions Ta_0.42Nb_0.3V_0.15Ti_0.13FeSb-(InSb)_δ, where δ = 0, 0.01, 0.015, 0.02, 0.025, and 0.03. For clarity, we focus our discussion on three representative compositions (δ = 0, 0.015, and 0.03), with the complete set of transport properties available in the ESI.† As shown in Fig. S3 of the ESI,† the XRD patterns of InSb-containing (over δ ≥ 0.02) specimens reveal extra peaks corresponding to the InSb standard, alongside the half-Heusler matrix phase.

In Fig. 2a, it is evident that σ increases with the addition of InSb. The enhancement is particularly prominent at room temperature, with a maximum increase of 20% observed for δ = 0.03. Notably, the InSb-containing sample (δ = 0.015) exhibit very good repeatability (Fig. S4, ESI†) and cyclability with repeated heating and cooling (Fig. S5, ESI†), even though the measurement temperature exceeds the melting point of InSb. Additionally, as Fig. S3c (ESI†) shows, the Ta_0.42Nb_0.3V_0.15Ti_0.13FeSb-(InSb)_0.025 sample's XRD figure revealed InSb peaks after six times cycling and proved InSb phase's stability in the material. These results indicate an excellent thermal stability of our composites. Furthermore, as Fig. S6 (ESI†) and Fig. 2a (black dots) illustrate, the electrical conductivity of all specimens follows a power law with temperature (σ ∝ T^α) with index values, α of ∼−1 across the recorded temperatures. This α value differs from that of typical degenerate semiconductors, which usually takes α ∼ −1.5 because of the deformation-potential-induced lattice vibration scattering,⁴⁶ as has been observed in typical degenerate semiconductors such as n-type Mg₃Sb₂ where the Hall concentration (n_H) was optimized at ∼3 × 10¹⁹ cm⁻³.⁴⁷ To understand the observed α ∼ −1, we performed Hall measurement for our specimens. Table 1 shows much higher n_H values in this work that are located in the range of 2–3 × 10²¹ cm⁻³. As suggested by Ziman, greater screening can diminish the strength of scattering when the carrier concentration is raised, therefore reducing the temperature dependency to α ∼ −1.⁴⁶ Furthermore, Table 1 suggested that adding InSb increases the Hall mobility (μ_H) by increasing δ until 0.015, then the μ_H decreases by further adding InSb. These results suggest a dual-role played by InSb in the mobility. This can be understood as like this: InSb itself is a semiconductor that exhibits high electron mobility of 7–8 m² V⁻¹ s⁻¹ at room temperature. Its addition to a half-Heusler mixture can initially increase overall mobility by facilitating easier movement of carriers (Table 1). However, after 1.5% InSb, μ_H decreases, which likely stem from an enhanced secondary phase scattering and carrier-carrier scattering due to the increased n_H.

Fig. 2 Electrical properties of Ta_0.42Nb_0.3V_0.15Ti_0.13FeSb-(InSb)_δ (δ = 0, 0.015 and 0.03) half-Heuslers. (a) Temperature-dependent electrical conductivity and the power-law curve (black dotted plot). The pink color background shows distinctive “bumps” at temperatures higher than 750 K for specimens containing InSb, (b) temperature-dependent Seebeck coefficient, (c) weighted mobility versus temperature, (d) average power factor versus InSb content and power factor versus temperature.

Table 1 Carrier concentration and Hall mobility of Ta_0.42Nb_0.3V_0.15Ti_0.13FeSb-(InSb)_δ at 300 K

δ	0	0.01	0.015	0.02	0.025	0.03
n H (10^21 cm^−3)	2.16	2.20	2.22	2.34	2.41	2.71
μ H (cm^2 V^−1 s^−1)	7.43	7.57	8.08	7.46	7.33	7.07

---

The Seebeck coefficient (S) of the material, as shown in Fig. 2b, exhibits a peculiar behavior with increasing InSb content. At room temperature, S rises from 118 μV K⁻¹ to 127 μV K⁻¹ as δ increases from 0 to 0.015 and degrades to 105 μV K⁻¹ when δ increases to 0.03. Note that from δ = 0 to δ = 0.015, n_H is nearly unchanged at ∼2.2 × 10²¹ cm⁻³, suggesting that In hardly functions as a dopant. In addition, by repeating the experiments, it is found that the S enhancement at δ = 0.015 is robust against batch variations, instead of due to measurement uncertainties (Fig. S7, ESI†). This non-monotonic trend in S has also been observed in other composite systems.²³ For attaining deeper insights, we employ the Pisarenko relation to interrogate the impact of InSb on the Seebeck coefficient, where . Herein, 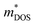, k_B and h signify the density-of-states (DOS) effective mass, Boltzmann constant and Planck constant respectively. Degenerate band extrema allow for an increase in , , where is the band effective mass (Fig. S8, ESI†).⁸ The Seebeck coefficient is increased and does not follow the usual inverse relationship with carrier concentration after addition of a small amount of InSb phase as shown in Fig. S8 (ESI†), which means the variation of S with InSb content is linked to the scattering parameter. The value of for the InSb-absent specimen is fitted as 9.5 m_e, whereas an increase to 10.5 m_e is observed with δ = 0.015. Conversely, upon reaching a δ value of 0.03, the Seebeck coefficient decreases and also decreases to 9 m_e. Variations in the effective mass of the density of states as shown by the Pisarenko plot fitting (Fig. S8, ESI†), point to a selective scattering process, suggesting that preferential scattering may occur for some charge carriers at certain energy levels, leading to changes in 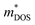when trace amount InSb is added. However, more InSb addition increases n_H, which will potentially shift the Fermi level away from the range where the selective-scattering effect is effective, resulting in a diminished effective mass. These observations align with the theoretical discussion that the nonmonotonic trend of the Seebeck coefficient relates an energy-dependent electronic scattering time when changing the concentration of the second phase.²⁵ Furthermore, we adopted the weighted mobility concept⁴⁸ as shown in Fig. 2c, the weighted mobility (μ_w) exhibited a consistent decrease with increasing temperature. Interestingly, the results highlighted that the introduction of modest amount of InSb (δ = 0.015) led to an increase in the μ_w, e.g., by 25% at 300 K, enabling a 23% enhancement of average PF (PF_ave) from 300 K to 973 K, as shown in Fig. 2d. Also note that analogous enhancements in power factor are also evident in samples featuring δ values of 0.01, 0.02, and 0.025, as shown in Fig. 2d and also in the ESI† (Fig. S9). The pronounced improvement in weighted mobility and power factor proves the efficacy of our composite approach, which has immense potential to enhance the electrical properties of more thermoelectrics.

The role of InSb in tuning electronic transport properties is complex and multifaceted. On one hand, the InSb phase enhances overall mobility by introducing a high-mobility secondary phase. On the other hand, it increases charge carrier scattering due to the presence of the secondary phase. These two mechanisms – high-mobility phase enhancement and selective scattering – are distinct yet interconnected, with diverse implications for thermoelectric optimization. Notably, both mechanisms may coexist synergistically, depending on the orientation of charge carrier transport relative to the grain boundaries. When charge carriers travel parallel to the InSb-modified grain boundaries, the high-mobility phase enhances mobility (Fig. S10a, ESI†). In contrast, perpendicular transport increases scattering due to a Kapitza-like effect (Fig. S10b, ESI†). In real conditions, electrons likely approach the grain boundaries at tilted angles (Fig. S10c, ESI†), striking a balance where parallel transport improves mobility while perpendicular scattering contributes to an enhanced Seebeck coefficient.

However, understanding the impact of InSb inclusion on transport properties remains challenging due to material complexity, including composition and carrier concentration. For example, in our previous study, InSb addition enhanced mobility in Nb_0.95Ti_0.05FeSb but did not improve the Seebeck coefficient.⁴¹ This discrepancy may arise from a chemistry-dependent mismatch in electronic properties, which affects the Kapitza resistance. Variations in chemistry shift relative energy levels in the band structure, altering the degree of mismatch and, consequently, the strength of the Kapitza effect. Comprehensive insights require further studies, such as interface ab initio calculations, high-resolution microscopy, transport property modeling, and atomic probe tomography, to unravel these mechanisms and guide future research.

2.2.2. Microstructural characterization. The discussions above suggest that InSb inclusions have multifaceted effects on the transport properties of charge carriers. To make sense of this phenomenon, it is crucial to keep in mind that InSb has an effectively negative Seebeck coefficient.⁴² Therefore, the Seebeck coefficient of the p-type half-Heusler compounds would decrease when elevating the concentrations of InSb.⁴⁹ On the other hand, InSb melts at approximately 800 K,⁵⁰ which is usually lower than the onset sintering temperature of TaFeSb-based compounds. It is thus expected that a thin liquid layer rich in In and Sb may grow in between the HH powders, which would modify the HH grain boundaries upon cooling. This type of structural feature, if confirmed, would provide the microstructural basis for a preferential scattering of lower-energy carriers to enhance the Seebeck coefficient,⁵¹ to test the microstructural hypothesis of our HH-InSb composite, we conducted an analysis on the specimen with δ = 0.015. Initially, we employed energy-dispersive X-ray spectroscopy (EDX) within a scanning electron microscope (SEM) to examine the overall elemental distribution. Elemental quantification from different spots confirms the sample composition's homogeneity and uniform distribution of elements except for the dispersed presence of TiO_x nanoparticles (Fig. S11 and S12, Table S1, ESI†), similar to other Ti-containing HH compounds.⁵² The influence of oxides on thermoelectric performance remains uncertain due to a lack of systematic studies, as they may exhibit both beneficial and detrimental effects. Oxides like TiO_x may enhance the Seebeck coefficient and reduce lattice thermal conductivity, but their insulating nature will lower electrical conductivity,⁵³ though this effect is minimal in heavily doped materials with high charge carrier concentrations. On the other hand, the enrichment of oxygen in TiO_x nanoparticles indicates that the amount of oxygen has been minimized elsewhere in the lattice, and therefore it has the potential to purify the HH matrix and facilitate the charge carrier transport, contrary to initial assumptions. Overall, the impact of these oxides on thermoelectric performance warrants further investigation as a key research direction.

To gain a deeper insight into the microstructures at the nanometer scale, we show in Fig. 3 EDX analysis conducted in a scanning transmission electron microscope (STEM). Fig. 3a contains a high-angle annular dark field (HAADF)-STEM image containing a GB, and the elemental mapping results are shown in Fig. 3b, which displays a clear enrichment of In and Sb at the GB, confirming our hypothesis. Additionally, we integrated the spectra to plot the composition profiles of different elements along the red arrow across the GB from the highlighted region in Fig. 3a. As shown in Fig. 3c, the line profiles give a quantitative view of the segregation and depletion of different elements across the GB. In addition to the enrichment of In and Sb, the depletion of matrix elements Ta, Nb, and Fe are observed. Moreover, note that the analysis showed an increase in Ti at the GB, whereas V hardly changes in composition across the GB. Indeed, Ti segregation at GBs has been observed in Nb_0.8Ti_0.2FeSb,⁴⁰ participating in the formation of TiSb-like GB phases, which are found to be electrically conductive. Therefore, we can conclude that the GB phase in this material is enriched in (In,Ti)Sb. This result differs from the previous one of Nb_0.95Ti_0.05FeSb-InSb_0.02 where the GB is rich only in In and Sb, suggesting that the changes of the chemical potentials can drive the GB modification in the compositions. Our findings provide insights into the role of GB modification in tailoring the transport properties and validate the microstructural foundation that is necessary for filtering low-energy carriers.

Fig. 3 HAADF-STEM image with EDX mapping of the GB of Ta_0.42Nb_0.3V_0.15Ti_0.13FeSb-(InSb)_0.015. (a) HAADF-STEM image, (b) EDX maps from the area highlighted by the red box in (a) for In, Sb, Ta, Nb, Fe and Ti, (c) concentration line profiles of the elements across the GB.

2.2.3. Thermal transport properties and figure of merit. We further explore the thermal transport characteristics of Ta_0.42Nb_0.3V_0.15Ti_0.13FeSb-(InSb)_δ (δ = 0, 0.015, and 0.03) compounds. The comprehensive datasets are provided in the ESI† (Fig. S13). Fig. 4a shows that, across the entire range of specimens, the total thermal conductivities manifest in the range of 3.5 W m⁻¹ K⁻¹ to 4 W m⁻¹ K⁻¹ at room temperature. This range is notably lower compared to those observed in unalloyed compounds such as VFeSb, NbFeSb, and TaFeSb,¹⁸ highlighting the importance of alloying among Ta, Nb, V, and Ti in impeding heat transport. Furthermore, we calculate the lattice contribution of thermal conductivity by separating the electronic contribution (κ_L = κ − κ_e) via the Wiedmann–Franz law, κ_e = LσT wherein L is the Lorenz number derived from the expression as proposed by Kim et al.⁵⁴ We observed that InSb slightly reduces κ_L as δ increases from 0 to 0.015, which compensates the enhanced κ_e so that the κ value changes insignificantly. The minimum κ_L at 300 K is around 2 W m⁻¹ K⁻¹ in this work, which ranks among the lowest values for RFeSb compounds, as shown in Fig. 4b and c.^{8,34,36,37,41,55} Nevertheless, upon further elevating δ to 0.03, the κ enhances obviously due to the enhanced κ_e. It is also pertinent to observe the “jumps” in the thermal conductivity profiles of InSb-incorporated samples around 773 K. This behavior is closely associated with the melting point of InSb (T_m ∼ 800 K) and is also confirmed by differential scanning calorimetry (DSC) measurement (Fig. S14 in the ESI†). The multi-element composition of our system generates a high density of point defects due to variations in atomic mass and size among Ta, Nb, V, and Ti. The random distribution of components causes significant lattice distortion, and disrupts phonon pathways, resulting in strong phonon scattering and a reduced relaxation time (τ) particularly affecting low- and mid-frequency phonons.⁵⁶ Additionally, the high charge carrier concentration in our system enhances screening, leading to the softening and deceleration of optical phonons. This phenomenon also induces avoided crossing between the acoustic and optical phonon branches, suppressing the group velocity (v_g) of acoustic phonons, thereby reducing lattice thermal conductivity.⁵⁷ The synergistic effects of these mechanisms are critical to our system's performance. High carrier concentrations not only enhance screening but also increase phonon scattering, providing a further explanation for the observed low κ_L.

Fig. 4 Thermal transport properties and dimensionless fig of merit. (a) Temperature-dependent total thermal conductivity and electrical conductivity and, (b) temperature-dependent lattice thermal conductivity. The pink color background shows distinctive “bumps” at temperatures higher than 750 K for specimens containing InSb, (c) comparison of lattice thermal conductivity in RFeSb (R: Ta, Nb, and V) HHs^{8,34,36,37,41,55} (d) temperature dependent zT, and (e) zT_aveversus InSb of Ta_0.42Nb_0.3V_0.15Ti_0.13FeSb-(InSb)_δ, (f) comparison zT average among different p-type HHs^{8,36,38,43–45,55,58–60} and this study.

The integration of InSb inclusions and alloying led to a remarkable synergistic enhancement in the power factor and the suppression of lattice thermal conductivity. Combined effect of these factors led to a significant improvement in the zT throughout the whole measured temperature range with a peak zT reaching 1.43 at 973 K (Fig. 4d). Moreover, for practical applications, the average zT (zT_ave) is more important than the peak value. As shown in Fig. 4e, increasing the parameter δ from 0 to 0.015 resulted in a significant 25% improvement in the zT_ave from 300 K to 973 K. By bringing the zT_ave to 1.0, this improvement represents an enhancement compared to the earlier p-type HHs (Fig. 4f).^{8,36,38,43–45,55,58–60} In addition, our strategy not only increased performance but also reduced production costs due to the efforts in reducing the Ta content, which is beneficial for the technology's applicability (Fig. 1c). This cost savings together with the increases in thermoelectric efficiency are in line with our objective of creating a lightweight, more affordable material and technology that may be used in real-world applications. The transport properties of our best composition, Ta_0.42Nb_0.3V_0.15Ti_0.13FeSb-(InSb)_0.015, were further validated by measuring three individual samples and repeatedly measuring one specimen 6 times, and the thermoelectric properties are comparable (as shown in Fig. S4 and S5, ESI†). This shows that the high thermoelectric performance of the mentioned sample is stable and repeatable. This enhancement presents a promising avenue for the development of thermoelectric materials through selectively scattering lower-energy carriers via GB engineering.

3. Modules’ performance for power generation

We systematically measured both heat-to-electricity conversion efficiency (η) and output power (P_out) using a single-leg thermoelectric device within a custom-made system. The thermoelectric leg, featuring a cross-sectional area of 1.86  ×  1.91 mm² and a length of 11.236 mm, was positioned between a heater and a copper plate using mechanical force. To maintain the cold-side temperature, water circulation was employed, while PID control effectively regulated the hot-side temperature. Notably, these experiments were conducted in a high vacuum environment (below 10⁻⁶ mbar) to minimize heat conduction.

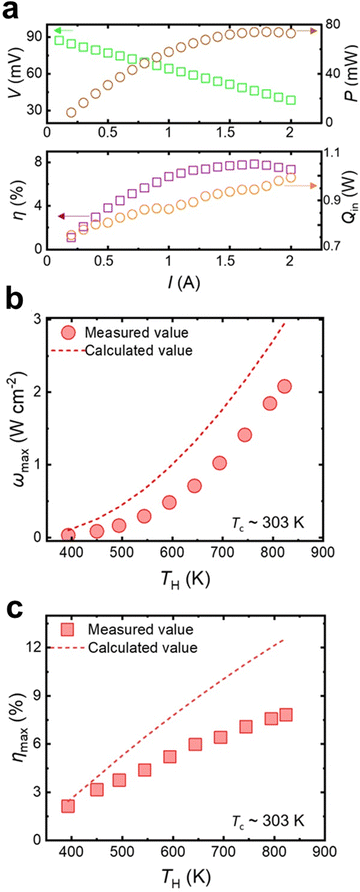
For the determination of conversion efficiency (η), concurrent measurements of output heat flow from the cold side (Q_out) and generated power (P) were undertaken. Based on Fourier's law, a bulk polycrystalline copper, possessing known geometry and thermal conductivity, was positioned beneath the cold side to quantify heat flow (Q_out). K-type thermocouples integrated at the interfaces facilitated the measurement of temperature differences in both the leg and copper bulk. It is pertinent to mention that the hot-side temperature of the copper served as the cold-side temperature of the leg. The calculation of η was performed using the equation. Radiation heat loss was omitted as it is challenging to measure. Nevertheless, this treatment is deemed reasonable given that in practical thermoelectric modules, radiation loss can be minimized through proper engineering of module geometries and also applying advanced packing techniques, as partially investigated in our previous work.⁶¹ Through the adjustment of current in the circuit, we conducted a series of measurements for both Q_out (output heat) and P (output power), enabling the determination of maximum η and P. The parameters for the single-leg Ta_0.42Nb_0.3V_0.15Ti_0.13FeSb-(InSb)_0.015 were simultaneously acquired, including temperature difference, electric current (I), voltage (V), P_out, and Q_in, as illustrated in Fig. 5a. Due to the limited heating power of the system, the hot-side temperature (T_h) could only be elevated to approximately 823 K. The experimentally measured hot-side-temperature-dependent maximum output power density (ω_max) and maximum efficiency (η_max) are presented in Fig. 5b and c. The peak efficiency reached around 8% at a hot-side temperature of approximately 823 K (Fig. 5c). It is essential to highlight that the obtained results exhibit a discrepancy with theoretical calculations, especially at high temperatures. This deviation is primarily attributed to parasitic electrical and heat losses. We anticipate that minimizing these adverse effects will bring the measured maximum efficiency and output power density closer to calculated values (approximately 12% and 3 W cm⁻², respectively, at a hot-side temperature of around 823 K), as determined through simulations using the finite element method (FEM).

Fig. 5 Performance of a single-leg device based on the optimized material Ta_0.42Nb_0.3V_0.15Ti_0.13FeSb-(InSb)_0.015. (a) Measured voltage, output power, input power, and efficiency with varying currents. The cold side and hot side of the device are fixed at ∼303 K and 823 K, respectively. Hot-side-temperature-dependent. (b) Maximum output power density (ω_max) and (c) maximum efficiency (η_max).

4. Conclusion

In summary, we successfully synthesized high-performing p-type TaFeSb-based half-Heusler materials with reduced Ta content while preserving high thermoelectric performance by alloying within the quaternary phase space among Ta, Nb, V, and Ti. Improved thermoelectric performances were obtained in an optimized composition, Ta_0.42Nb_0.3V_0.15Ti_0.13FeSb, where the peak zT reached 1.23 at 973 K and the zT_ave reached 0.8 between 300 K and 973 K. Furthermore, we applied a composite strategy by using InSb, yielding a subsequent gain of performances in composition Ta_0.42Nb_0.3V_0.15Ti_0.13FeSb-(InSb)_0.015. A simultaneous improvement of the Seebeck coefficient and electrical conductivity, along with a further decrease in lattice thermal conductivity, resulted in a peak zT value of 1.43 at 973 K and a zT_ave of ∼1 between 300 K and 973 K. To the best of the authors' knowledge, the resultant zT_ave is the highest value among p-type half-Heusler compounds. Furthermore, we obtained a maximum conversion efficiency of around 8% at cold-side temperatures of 303 K and 823 K based on a single-leg device measurement. These findings highlight the exciting potential of our material design and production methods for not only this system but also shed light on the possibility of other materials systems for effective thermoelectric applications.

5. Experimental

5.1. Materials preparation

Specimens of p-type RFeSb-(InSb)_δ with nominal δ = 0, 0.01, 0.015, 0.02, 0.025, and 0.03 were prepared by mechanical alloying and sintering. In total 6 g of raw elements, including Ta powders (99.8%, Alfa Aesar), Nb powders (99.8%, Alfa Aesar), V powders (99.98%, Alfa Aesar), Fe granules (99.98%, Alfa Aesar), Ti sponges (99.95%, Alfa Aesar), In shot (99.9%, Alfa Aesar) and Sb pieces (99.999%, MaTecK) were weighted according to the stoichiometry in an Ar-filled glovebox with O₂ and H₂O levels lower than 1 ppm. Mechanical alloying was done for 25 hours by using a high-energy ball mill (SPEX 8000D), and the ball-milled powders were compacted to a disk by a field-assisted sintering technique (FAST, FCT Systeme GmbH) under a pressure of 50 MPa in vacuum for 3 min at 1123 K. Fast cold press before sintering process increases the density of the product and reducing the porosities. The densities of the sintered sample are determined by Archimedes's method, reaching 99% of the theorical densities.

5.2. Characterization

The phase structure, morphology, grain size, and chemical composition of the specimens have been analyzed by X-ray diffraction (XRD), scanning electron microscopy (SEM), electron backscatter electron (EBSD) as well as scanning transmission electron scanning microscopy- energy-dispersive X-ray spectroscopy (STEM-EDX), respectively. Room temperature X-ray diffraction patterns of sintered bulk were measured by a Bruker D8 Advance diffractometer (Co K_α radiation) to characterize the phases. Thin samples for STEM experiments have been prepared using a Scios2 ThermoFisher focused ion beam following the procedure described by Schaffer et al.⁶² The specimen has been thinned down to <150 nm by 30 kV Ga⁺ beam and a final thinning has been performed at 5 and 2 kV. STEM experiments have been performed in a probe-corrected ThermoFisher Titan operated at 300 kV with a collection semiangle of 24 mrad and approx. <1 Å probe size. STEM-EDX maps were acquired using a four-quadrant silicon-drift EDX detector (Super-X) in approx. 30 min acquisition time for each map. Multivariate statistical analysis⁶³ has been performed for noise reduction and the Cliff–Lorimer formula has been used for elemental quantification EBSD maps have been acquired according to Wilkinson et al.⁶⁴ using a Sigma 500 SEM (ZEISS) operated at 15 kV and a Hikari EBSD camera. APEX software (EDAX) was used for acquisition and the OIM Analysis 8 software (EDAX) was used for analysis.

5.3. Measurement

The sintered compounds were cut and polished into rectangular bar shapes for electrical conductivity and Seebeck coefficient measurements on a commercial device high-temperature LSR-3 (Linseis) system at the same time under an inert gas (He) atmosphere. The thermal conductivity (κ = DC_pd) was calculated as a multiplication of thermal diffusivity (D) via the LFA-Linseis system, specific heat (C_p) (DSC 404, Netzsch), and mass density (d) (Archimedes’ kit). The measurement errors were 4%, 5%, and 12% for σ, S, and κ, respectively. Explicitly, the uncertainties of κ originated from 2% in mass density, 4% in diffusivity, and 6% in specific heat. Therefore, the nominal uncertainties in power factor and zT were 10% and 20%, respectively. The degree of uncertainty can be reduced upon reproducing the specimens, as implemented in this work. To increase the readability of the graphs, the error bars were not added to the curves. Hall carrier concentrations (n_H) were taken on a quantum design physical properties measurement system (PPMS) with a magnetic field of ±9 T and an electric current of 8 mA at room T. Hall mobility (μ_H) was then calculated from μ = σ/n_He, were e is the elemental charge.

5.4. Simulation and measurement for the single-leg device

COMSOL Multiphysics with heat transfer module is used to perform the three-dimensional finite-element simulations of the power-generation characteristics for the thermoelectric single leg. A geometrical model with the same dimensions as the experimental leg is used to calculate the electric power and heat flow outputs. The temperature-dependent Seebeck coefficient, electrical conductivity, and thermal conductivity for the material are taken from the measured data as material properties in the simulations. The efficiency of the single thermoelectric leg was assessed using a custom-built system. The leg, measuring 1.86 mm by 1.91 mm by 11.24 mm, was directly integrated into the setup for data collection, following the established double four-point probe method as detailed in a prior publication.⁶⁵ The components – including the heater, single leg, heat meter, and heat sink – were aligned in series from top to bottom, with thermal grease applied to minimize thermal resistance. The entire measurement process was carried out under a vacuum of less than 10⁻⁶ bar. The heat meter situated beneath the thermoelectric leg was constructed from oxygen-free copper, featuring a cross-sectional area of 1.85 × 10⁻⁵ m² and a length of 0.15 m. To mitigate potential errors arising from heat resistance and hysteresis at the interface, two thermocouples were strategically positioned at the center of the bar, spaced 0.01 m apart, to monitor thermal flow accurately.

Author contributions

R. H. and Z. H. proposed the research. R. H. N. carried out the experiments and most thermoelectric measurements. R. B. V. D. A. M. and S. Z. performed SEM, EBSD, HAADF-STEM, and EDX experiments and gave their insight in the entire article. S. B. performed Hall measurement. P. Y. performed the simulation of the single-leg module. S. S. prepared and measured the module performance. K. N., C. S., and Z. R. commented on the results. R. H. N. and R. H. drafted the manuscript. R. H. N., R. H., S. Z., Z. H., and R. B. V. revised the manuscripts. All authors read and commented on the manuscript.

Data availability

Data for this article, including the data files are available at Zenodo at [https://doi.org/10.5281/zenodo.13946591].

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

This work is supported by Deutsche Forschungsgemeinschaft (DFG), Project Number 453261231. H. Z. acknowledges the financial support from the National Natural Science Foundation of China, Project Number 52172262, and the National Key Research and Development Program of China, Project Number 2022YFB3803900. C. S. and S. Z. acknowledge funding from the DFG within the Collaborative Research Centre SFB 1394 (Project ID 409476157). The authors acknowledge Birgit Bartusch for Cp measurement. R. H. N acknowledges the support from Prof. Jeff Snyder from Northwestern University and Ms Xin Ai from IFW for fruitful discussions.

References

1. W. Liu, Q. Jie, H. S. Kim and Z. Ren, Acta Mater., 2015, 87, 357–376.
2. B. Poudel, Q. Hao, Y. Ma, Y. Lan, A. Minnich, B. Yu, X. Yan, D. Wang, A. Muto, D. Vashaee, X. Chen, J. Liu, M. S. Dresselhaus, G. Chen and Z. Ren, Science, 2008, 320, 634–638.
3. G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105–114.
4. H. Tang, J. F. Dong, F. H. Sun, Asfandiyar, P. Shang and J. F. Li, Sci. China Mater., 2019, 62, 1005–1012.
5. J. Mao, Z. Liu, J. Zhou, H. Zhu, Q. Zhang, G. Chen and Z. Ren, Adv. Phys., 2018, 67, 69–147.
6. Y. Liu, C. Fu, K. Xia, J. Yu, X. Zhao, H. Pan, C. Felser and T. Zhu, Adv. Mater., 2018, 30, e1800881.
7. M. Zebarjadi, K. Esfarjani, M. S. Dresselhaus, Z. Ren and G. Chen, Energy Environ. Sci., 2012, 5, 5147–5162.
8. R. He, D. Kraemer, J. Mao, L. Zeng, Q. Jie, Y. C. Lan, C. H. Li, J. Shuai, H. S. Kim, Y. Liu, D. Broido, C. W. Chu, G. Chen and Z. Ren, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 13576–13581.
9. T. Graf, C. Felser and S. S. P. Parkin, Prog. Solid State Chem., 2011, 39, 1–50.
10. S. Anand, K. Xia, I. V. Hegde, U. Aydemir, V. Kocevski, T. Zhu, C. Wolverton and G. J. Snyder, Energy Environ. Sci., 2018, 11, 1480–1488.
11. S. Chen and Z. Ren, Mater. Today, 2013, 16, 387–395.
12. T. Zhu, C. Fu, H. Xie, Y. Liu and X. Zhao, Adv. Energy Mater., 2015, 5, 1500588.
13. W. G. Zeier, J. Schmitt, G. Hautier, U. Aydemir, Z. M. Gibbs, C. Felser and G. J. Snyder, Nat. Rev. Mater., 2016, 1, 16032.
14. R. He, T. Zhu, P. Ying, J. Chen, L. Giebeler, U. Kühn, J. Grossman, Y. Wang and K. Nielsch, Small, 2021, 17, 2102045.
15. S. J. Poon, J. Phys. D: Appl. Phys., 2019, 52, 493001.
16. X. A. Yan, G. Joshi, W. S. Liu, Y. C. Lan, H. Wang, S. Lee, J. W. Simonson, S. J. Poon, T. M. Tritt, G. Chen and Z. Ren, Nano Lett., 2011, 11, 556–560.
17. G. Joshi, X. Yan, H. Wang, W. Liu, G. Chen and Z. Ren, Adv. Energy Mater., 2011, 1, 643–647.
18. R. J. Quinn and J. W. G. Bos, Mater. Adv., 2021, 2, 6244–6266.
19. J. W. G. Bos and R. A. Downie, J. Phys.:Condens. Matter, 2014, 26, 433201.
20. M. Schwall and B. Balke, Phys. Chem. Chem. Phys., 2013, 15, 1868–1872.
21. R. A. Downie, D. A. MacLaren and J. W. G. Bos, J. Mater. Chem. A, 2014, 2, 6107.
22. S. Populoh, M. H. Aguirre, O. C. Brunko, K. Galazka, Y. Lu and A. Weidenkaff, Scr. Mater., 2012, 66, 1073–1076.
23. W. J. Xie, Y. G. Yan, S. Zhu, M. Zhou, S. Populoh, K. Galazka, S. J. Poon, A. Weidenkaff, J. He, X. F. Tang and T. M. Tritt, Acta Mater., 2013, 61, 2087–2094.
24. L. I. Bytenskii, T. S. Gudkin, E. K. Iordanishvili, S. A. Kazmin, V. I. Kaidanov, S. A. Nemov and Y. I. Ravich, Sov. Phys. Semicond., 1977, 11, 894–896.
25. S. V. Faleev and F. Léonard, Phys. Rev. B:Condens. Matter Mater. Phys., 2008, 77, 214304.
26. J. P. Heremans, C. M. Thrush and D. T. Morelli, J. Appl. Phys., 2005, 98, 063703.
27. R. He, H. Zhu and S. Chen, in Novel thermoelectric materials and device design concepts, ed. S. Skipidarov and M. Nikitin, Springer, 2019.
28. X. Ai, B. Lei, M. O. Cichocka, L. Giebeler, R. Bueno Villoro, S. Zhang, C. Scheu, N. Pérez, Q. Zhang, A. Sotnikov, D. J. Singh, K. Nielsch and R. He, Adv. Funct. Mater., 2023, 33, 2305582.
29. L. Abdellaoui, Z. Chen, Y. Yu, T. Luo, R. Hanus, T. Schwarz, R. Bueno Villoro, O. Cojocaru-Mirédin, G. J. Snyder, D. Raabe, Y. Pei, C. Scheu and S. Zhang, Adv. Funct. Mater., 2021, 31, 2101214.
30. L. Abdellaoui, S. Zhang, S. Zaefferer, R. Bueno-Villoro, A. Baranovskiy, O. Cojocaru-Mirédin, Y. Yu, Y. Amouyal, D. Raabe, G. J. Snyder and C. Scheu, Acta Mater., 2019, 178, 135–145.
31. A. Page, A. Van der Ven, P. F. P. Poudeu and C. Uher, J. Mater. Chem. A, 2016, 4, 13949–13956.
32. Y. Kimura and Y. W. Chai, JOM, 2015, 67, 233–245.
33. C. G. Fu, T. J. Zhu, Y. Z. Pei, H. H. Xie, H. Wang, G. J. Snyder, Y. Liu, Y. T. Liu and X. B. Zhao, Adv. Energy Mater., 2014, 4, 1400600.
34. C. G. Fu, T. J. Zhu, Y. T. Liu, H. H. Xie and X. B. Zhao, Energy Environ. Sci., 2015, 8, 216–220.
35. R. He, H. Zhu, J. Sun, J. Mao, H. Reith, S. Chen, G. Schierning, K. Nielsch and Z. Ren, Mater. Today Phys., 2017, 1, 24–30.
36. H. Zhu, J. Mao, Y. W. Li, J. F. Sun, Y. M. Wang, Q. Zhu, G. N. Li, Q. C. Song, J. W. Zhou, Y. H. Fu, R. He, T. Tong, Z. H. Liu, W. Y. Ren, L. You, Z. M. Wang, J. Luo, A. Sotnikov, J. M. Bao, K. Nielsch, G. Chen, D. J. Singh and Z. Ren, Nat. Commun., 2019, 10, 270.
37. J. Yu, C. Fu, Y. Liu, K. Xia, U. Aydemir, T. C. Chasapis, G. J. Snyder, X. Zhao and T. Zhu, Adv. Energy Mater., 2018, 8, 1701313.
38. H. Zhu, W. Li, A. Nozariasbmarz, N. Liu, Y. Zhang, S. Priya and B. Poudel, Nat. Commun., 2023, 14, 3300.
39. T. Luo, F. Serrano-Sánchez, H. Bishara, S. Zhang, R. Bueno Villoro, J. J. Kuo, C. Felser, C. Scheu, G. J. Snyder, J. P. Best, G. Dehm, Y. Yu, D. Raabe, C. Fu and B. Gault, Acta Mater., 2021, 217, 117147.
40. R. Bueno Villoro, D. Zavanelli, C. Jung, D. A. Mattlat, R. Hatami Naderloo, N. Pérez, K. Nielsch, G. J. Snyder, C. Scheu, R. He and S. Zhang, Adv. Energy Mater., 2023, 13, 2204321.
41. R. Bueno Villoro, R. Hatami Naderloo, D. A. Mattlat, C. Jung, K. Nielsch, C. Scheu, R. He and S. Zhang, Mater. Today Phys., 2023, 38, 101240.
42. Z. L. Du, J. He, X. L. Chen, M. Y. Yan, J. H. Zhu and Y. M. Liu, Intermetallics, 2019, 112, 106528.
43. N. S. Chauhan, S. Bathula, A. Vishwakarma, R. Bhardwaj, K. K. Johari, B. Gahtori and A. Dhar, J. Mater., 2019, 5, 94–102.
44. P. Luo, C. Lin, Z. Li, J. Zhang and J. Luo, ACS Appl. Energy Mater., 2023, 6, 10070–10077.
45. R. He, H. S. Kim, Y. Lan, D. Wang, S. Chen and Z. Ren, RSC Adv., 2014, 4, 64711–64716.
46. J. M. Ziman and A. H. Kahn, The theory of transport phenomena in solids, Oxford University Press, 1961.
47. K. Imasato, C. Fu, Y. Pan, M. Wood, J. J. Kuo, C. Felser and G. J. Snyder, Adv. Mater., 2020, 32, 1908218.
48. G. J. Snyder, A. H. Snyder, M. Wood, R. Gurunathan, B. H. Snyder and C. Niu, Adv. Mater., 2020, 32, 2001537.
49. S. Zhu, Doctor of Philosophy Physics's thesis, Clemson University, 2013.
50. K. F. Hulme and J. B. Mullin, Solid-State Electron., 1962, 5, 211–IN210.
51. C. Gayner and Y. Amouyal, Adv. Funct. Mater., 2020, 30, 1901789.
52. R. Bueno Villoro, M. Wood, T. Luo, H. Bishara, L. Abdellaoui, D. Zavanelli, B. Gault, G. J. Snyder, C. Scheu and S. Zhang, Acta Mater., 2023, 249, 118816.
53. Z. Ren, Y. Lan and Q. Zhang, Advanced thermoelectrics: materials, contacts, devices, and systems, CRC Press, 2018.
54. H. S. Kim, Z. M. Gibbs, Y. Tang, H. Wang and G. J. Snyder, APL Mater., 2015, 3, 041506.
55. S. Ghosh, A. Nozariasbmarz, H. Lee, L. Raman, S. Sharma, R. B. Smriti, D. Mandal, Y. Zhang, S. K. Karan, N. Liu, J. L. Gray, M. Sanghadasa, Y. Xia, S. Priya, W. Li and B. Poudel, Joule, 2024, 8, 1–10.
56. B. Abeles, Phys. Rev., 1963, 131, 1906–1911.
57. S. Han, S. Dai, J. Ma, Q. Ren, C. Hu, Z. Gao, M. Duc Le, D. Sheptyakov, P. Miao and S. Torii, Nat. Phys., 2023, 19, 1649–1657.
58. H. Zhu, R. He, J. Mao, Q. Zhu, C. Li, J. Sun, W. Ren, Y. Wang, Z. Liu, Z. Tang, A. Sotnikov, Z. Wang, D. Broido, D. J. Singh, G. Chen, K. Nielsch and Z. Ren, Nat. Commun., 2018, 9, 2497.
59. X. Bao, K. Liu, X. Ma, X. Li, H. Yao, S. Ye, F. Cao, J. Mao and Q. Zhang, ACS Appl. Mater. Interfaces, 2024, 16, 3502–3508.
60. C. Fu, S. Bai, Y. Liu, Y. Tang, L. Chen, X. Zhao and T. Zhu, Nat. Commun., 2015, 6, 8144.
61. P. Ying, H. Reith, K. Nielsch and R. He, Small, 2022, 18, 2201183.
62. M. Schaffer, B. Schaffer and Q. Ramasse, Ultramicroscopy, 2012, 114, 62–71.
63. S. Zhang and C. Scheu, Microscopy, 2017, 67, i133–i141.
64. A. J. Wilkinson and T. B. Britton, Mater. Today, 2012, 15, 366–376.
65. Q. Zhu and Z. Ren, Energy, 2020, 191, 116599.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ee04819a

---