Intrinsic point defect tolerance in selenium for indoor and tandem photovoltaics

Abstract

Selenium has reemerged as a promising absorber material for tandem and indoor photovoltaic (PV) devices due to its elemental simplicity, unique structural features, and wide band gap. However, despite rapid recent improvements, record Se solar cells only reach a third of their achievable efficiencies at the radiative limit, primarily due to a low open-circuit voltage relative to the band gap. The origins of this voltage deficit, along with the high doping densities often reported for trigonal selenium (t-Se), remain unclear. Here, we explore the point defect chemistry of t-Se combining first-principles calculations with experimental studies of thin-films from state-of-the-art PV devices. Our findings reveal a remarkable ability of the helical t-Se chains to reconstruct and form low-energy amphoteric defects, particularly in the case of self-vacancies and hydrogen, pnictogen, and halogen impurities. While chalcogen impurities and self-interstitials also form low-energy defects, these are electrically neutral. We also find that both intrinsic and extrinsic point defects do not contribute significantly to doping, either due to electrical inactivity (chalcogens) or self-compensation (hydrogen, halogens, pnictogens). Finally, we show that intrinsic point defects do not form detrimental non-radiative recombination centres and propose that PV performance is instead limited by other factors. These findings highlight the potential of Se as a defect-tolerant absorber, while optimising interfaces and extended structural imperfections is key to unlocking its full performance potential.

---

Broader context

Solar energy is a cornerstone of sustainable power generation, critical for reducing reliance on fossil fuels and combating climate change. To meet the growing global demand for clean energy, there is an urgent need to develop materials that are efficient, scalable, and cost-effective. Traditional photovoltaic (PV) materials, such as silicon, have dominated the market for decades, but emerging materials offer the potential to unlock higher efficiencies and new applications. One such material is selenium, which was historically the first material used in solar cells but has recently undergone a resurgence in research. Selenium's combination of elemental simplicity, ease of processing, and environmental friendliness makes it particularly well-suited for next-generation PV technologies, including tandem and indoor devices. Recent breakthroughs have improved selenium-based cell efficiencies. However, challenges remain, particularly in understanding and mitigating the factors that limit its performance, such as voltage deficits and defect-induced doping. Our study addresses these challenges by investigating the point defect chemistry of selenium, offering insights that could help unlock its full potential as a high-efficiency solar absorber.

Elemental selenium (Se) exhibits a number of low-energy allotropes in the solid state, both crystalline and amorphous, due to its ability to concatenate and form ring- and chain-like structures.^1–4 While amorphous Se has been studied for photo-detection applications, its crystalline form has received attention as a candidate absorber material in photovoltaic (PV) devices, having been used in the first solar cell reported in 1883.⁵ The most stable polymorph at room temperature is the chain-like trigonal phase (t-Se) with space group P3₁21 (shown in Fig. 1), also termed ‘hexagonal’ (h-Se) or ‘crystalline’ Se (c-Se) due to the hexagonal lattice system and chain packing.²

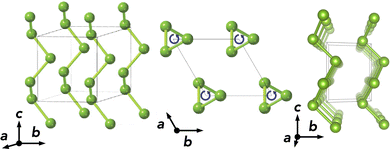Fig. 1 Crystal structure of trigonal selenium (t-Se) along various lattice directions. Adapted with permission from Kumagai et al.³

Trigonal Se presents a number of advantageous properties for solar cells: low-temperature solution processing and vacuum deposition (aided by its low melting point of 220 °C); good long-term stability in ambient, oxygenated and humid atmospheres^2,6; a wide band gap (tunable within 1.2–2.0 eV via Te alloying^7–9) ideally suited for visible-light photodiodes,^10–12 indoor PV^13–15 or top-cells in tandem devices^16,17; a chain-like crystal structure which is likely to yield benign grain boundaries for electron–hole recombination, to name a few.^2,4,17,18 Moreover, the high vapour pressure of Se allows efficient recycling through closed-space evaporation, as demonstrated for indoor Se PV devices.¹⁴ Another benefit is the ‘simple’ chemistry of a single-element system which, in theory, reduces degrees of freedom in processing and characterisation. However, the limited chemical potential space is a double-edged sword, also reducing tunability and the scope of process engineering—particularly for the intrinsic defect chemistry.

The large band gap of t-Se (1.8–2 eV)^4,18–25 makes it an ideal absorber for single-junction indoor PV or a tandem PV top-cell, with theoretical maximum power-conversion efficiencies of ∼50% (Fig. S6, ESI†)²⁶ and ∼40% (if combined with a suitable low band gap material such as Si) respectively.^16,27 While research on Se-based tandem PV is still in its infancy,¹⁷ a number of recent studies^13,15,24 have demonstrated impressive efficiencies up to 18% for single-junction indoor PV devices²⁴—surpassing those of market-dominant amorphous Si cells and lead-free perovskites. The first single-junction outdoor Se solar cell achieved a modest power-conversion efficiency η of less than 1% in 1883.^2,5 Inorganic solar cell research moved on to diamond-like semiconductors, such as Si, CdTe, CuIn_xGa_1−xSe₂ (CIGS), and Cu₂ZnSnS₄ (CZTS), and the efficiency of selenium solar cells stagnated for nearly a century. In the mid-1980s, work from two separate groups in Japan^28,29 bumped record efficiencies to just over 5%, with research interest then stalling once again. In 2017, Todorov et al.²⁵ fabricated t-Se solar cells with η = 6.51% and an open-circuit voltage V_oc = 0.97 V by overhauling the prevailing device architecture to give improved front and back contacts, using a FTO/ZnMgO/Se/MoO_x/Au heterojunction stack and an ultra-thin 100 nm Se film.§ Record efficiencies of 7.2% and 8.1% have since been achieved by Lu et al.²⁴ in 2024 and Liu et al.³⁰ in 2025, through engineering strategies which boosted short-circuit current densities J_sc without changes to V_oc. Respectively, these included using FTO-coated glass with antireflective coating in the device stack, and then a substrate-heating strategy to maximise c-axis orientation of the t-Se film.

While t-Se is sometimes referred to as a ‘direct’ band gap (E_g) absorber in the experimental literature—due to a small energy difference and weak signal of indirect absorption in thin films, it is in fact a ‘pseudo-direct’ gap material with (ΔE_{g,direct/indirect} ≃ 0.1 eV).^{4,18,23,31–33} Taking the experimentally-reported fundamental band gap of ∼1.85 eV and assuming a thin-film architecture with weak indirect absorption contributions, t-Se has a theoretical maximum efficiency of η ≃ 22.6% and V_oc,max = 1.56 V for a single-junction solar cell, under the detailed-balance limit.³⁴ We see that current record efficiencies of single-junction Se photovoltaics (8.1% and 18.0% for solar and indoor PV) stand at around a third of the theoretical limits (22.6% and ∼50% respectively). As with most emerging solar absorbers,^35–37 the primary origin of efficiency loss relative to the radiative limit is a relatively low open-circuit voltage V_oc. The record V_oc for selenium solar cells sits at just under 1 V,¹⁸ corresponding to a voltage deficit (ΔV_oc) of about 0.56 V, or 36%, compared to the ideal value at the radiative limit. The dominant contribution to this V_oc deficit, whether Urbach tailing, limited doping densities, electron–hole recombination or other mechanisms, has been the focus of several studies in recent years, however the exact split of the relative contributions is not yet known.^{6,11,18,24,25,38} Nevertheless, it is thought that defect-mediated non-radiative electron–hole recombination is a primary contributor to the V_oc deficit¹⁸—being the typical limiting factor for emerging solar cell technologies.^35–37

A related open question is the origin of the apparent high doping densities in as-grown t-Se samples. In early research on crystalline selenium, it was reported that single crystals had hole densities on the order of 10¹⁴ cm⁻³, while polycrystalline samples exhibited a wide range of reported hole concentrations between 10¹³–10¹⁷ cm⁻³.^4,8,39–43 Nielsen et al.¹⁸ and others^6,13 have reported doping densities on the order of 10¹⁵–10¹⁶ cm⁻³ in as-grown, nominally-undoped polycrystalline t-Se samples, using capacitance–voltage (CV) techniques. In contrast, Todorov et al.²⁵ reported a much lower hole concentration of 3 × 10¹² cm⁻³ in their polycrystalline t-Se samples using alternating-current (AC) Hall measurements. The variance in reported values, discrepancies between measured doping and carrier densities, and atomistic origins of hole doping in t-Se – whether intrinsic/extrinsic defects, interfaces or otherwise, have not yet been resolved.

Here, we present a combined theoretical and experimental investigation of the intrinsic and extrinsic point defect chemistry of t-Se. We start by characterising the bulk electronic structure and allotropic phase behaviour, finding anisotropy and deformability to be key factors connected to PV performance. This is followed by an analysis of the intrinsic point defect thermodynamics, along with their impact on non-radiative electron–hole recombination, revealing the benign nature of intrinsic point defects. Lastly, we investigate the behaviour of impurity species in t-Se, through experimental measurements of elemental distributions in high-quality selenium films, and first-principles predictions of solubility and doping behaviour. We find that point defects, whether intrinsic or extrinsic, cannot explain the reported carrier concentrations in Se films. Interpreting our results in the context of recent experiments,^10,11 we propose that extended defects and interfaces are the current limiting factors for efficiencies in t-Se devices.

Results

t-Se has a quasi-one-dimensional crystal structure, whereby trigonal helical chains oriented along the c-axis are packed together to give a trigonal lattice with space group P3₁21 (Fig. 1). Our computational setup results in bulk lattice parameters of a = 4.34 Å and c = 4.96 Å, closely matching the room temperature experimental values of a = 4.37 Å and c = 4.95 Å.^4,44–46 Several crystalline and amorphous Se phases exist within room temperature thermal energy (k_BT) of t-Se – see Section S2 (ESI†), indicating a possible difficulty in obtaining phase-pure samples due to potential low-energy metastable chain rearrangements or ring-like formations in the bulk – a point revisited in the discussion. Notably, van der Waals (vdW) dispersion interactions are key to the structural parameters and relative energies of these low-dimensional pure-covalent compounds, compressing unit cell volumes by ∼25% on average (Table S3, ESI†).⁴⁷

Bulk electronic structure

The calculated electronic structure of t-Se is shown in Fig. 2, exhibiting a slightly indirect fundamental band gap due to the splitting of the valence band maximum about the k-point. We calculate an indirect band gap of 1.71 eV and a direct gap of 1.83 eV, neglecting any electron–phonon coupling effects. As noted in the introduction, while some confusion has lingered in the experimental literature, the indirect nature of the t-Se band gap was observed in low-temperature optical measurements from the 1960s and 1970s^4,23,31–33 – with ΔE_{g,direct/indirect} ≃ 0.1 eV as predicted here. While the effect of spin–orbit coupling (SOC) on the fundamental indirect band gap – and indeed for most electronic states across the Brillouin zone – is relatively small (ΔE_g,SOC = −0.02 eV), the effect on the direct band gap is significant, decreasing it by ΔE_g,SOC,direct = −0.14 eV. The primary origin of this difference in direct band gap is a large upshift in the highest energy valence bands near the Hk-point, due to strong SOC splitting of the band crossing at this point (Fig. S2, ESI†). Se solar cells typically employ thin films in the range of a few hundred nm^18,24,25 – to maximise crystallinity and carrier collection – and so indirect phonon-assisted absorption is insignificant, translating into a slight reduction in achievable J_sc and thus efficiency (Δη ∼ 1.5%) for a ∼1.85 eV gap absorber.

Fig. 2 Bulk electronic structure of t-Se, calculated using hybrid density functional theory (DFT) (HSE06) including spin–orbit coupling (SOC) and the D3 van der Waals dispersion correction. (a) Electronic band structure alongside the density of states (DOS) – with 0.5 eV Gaussian broadening, see Fig. S3 (ESI†) – with experimental data from Ultraviolet Photoemission Spectroscopy (UPS) measurements.¹⁷ The real-space charge densities of the conduction band minimum (CBM) and valence band maximum (VBM) are shown on the right-hand side. (b) Electronic band alignment to the vacuum level, calculated using surface slab calculations with HSE06 + D3 + SOC (see Methods) and showing the direct band gap, while those of F-doped SnO₂ (FTO),⁴⁸ Sb₂Se₃,^49–51 and MAPbI3⁵² are taken from the literature for comparison. The experimentally-determined band positions from UPS measurements¹⁷ are overlaid in red. (c) Optical absorption of single-crystal t-Se, as a function of light propagation direction (i.e. perpendicular to polarization direction), with 0.1 eV Gaussian broadening. Experimental data from spectroscopic ellipsometry with integrating sphere is plotted alongside.¹⁷ The calculated and experimentally-measured polarisation-dependent complex dielectric functions are compared in Fig. S5 (ESI†), also showing good agreement.

The calculated and measured natural electronic band alignment of t-Se relative to the vacuum level is shown in Fig. 2b, alongside values of some related materials for comparison. We see that t-Se exhibits similar band edge positions to the halide perovskite methylammonium lead iodide (MAPbI3), indicating that similar choices of carrier transport layers could be made. t-Se has deeper valence band maximum (VBM) than the emerging PV material Sb₂Se₃⁵³ as expected due to the anti-bonding Sb s – Se p lone-pair interaction at the VBM in Sb₂Se₃, contrasted with the non-bonding/weak inter-chain bonding Se p interactions at the t-Se upper valence band.

For the optical band gap, values in the range of 1.8–2 eV have been experimentally reported,^4,20–24 though a value around 1.95 eV is most common,^18,25 which is slightly underestimated by our calculated direct gap of 1.83 eV.¶ Given the close match in calculated structural and dielectric parameters with experiment, it is suggested that this remaining mismatch is likely due to electron–phonon coupling (band gap renormalisation at room temperature) and/or minor inaccuracies in the hybrid DFT functional (further discussion in Section S3.3, ESI†). Notably, along with the low phonon frequencies shown in Fig. S1 (ESI†), we find quite a small bulk modulus of 15.0 GPa and inter-chain surface energy of 0.177 J m⁻² for t-Se (in good agreement with the experimental values of 14.9 GPa⁴⁶ and 0.175 J m⁻² (ref. 54)), indicating the facile compressibility and weak inter-chain binding. Despite a low enthalpic cost, the band gap remains sensitive to volume deformation, varying by ±0.25 eV while the energy varies by only 2 meV per atom within the ±5% volume range, as shown in Fig. S7 (ESI†). Strong temperature effects are common in vdW solids, and this combination of high deformation potentials and low elastic constants^4,31,46,55 is likely to yield significant thermal fluctuations of the band gap in t-Se. Indeed, this is evidenced by the close match of the calculated and measured electronic density of states (DOS) (Fig. 2a) at high levels of thermal broadening (σ = 0.5 eV; Fig. S3, ESI†), as well as the broad onset of absorption – with DFT showing a slightly higher energy onset despite the slight under-estimation of the band gap discussed above. Such strong thermal fluctuations are expected to contribute to the moderate Urbach energies (E_U) measured for t-Se (E_U = 44 meV; Fig. 7c) and reduced carrier mobilities, along with the possibility of locally-strained regions near interfaces with spatially-varying electronic potentials.⁵⁶ We note that the impact of strain and anisotropy on electronic properties has been heavily investigated in the closely-related elemental Te compound, which is iso-structural and lies one row below Se in the chalcogen family, with the main difference being the much smaller band gap (∼0.33 eV).^57,58

The combination of low carrier effective masses along the Se chain direction (||)¹⁸|| and high band degeneracies at both band edges for t-Se results in high-frequency dielectric constants of ε_∞,⊥ = 6.71, ε_∞,|| = 10.28, which are large for a semiconductor with a band gap just under 2 eV, given the typical 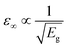relation.⁵⁹ In contrast, the ionic contributions to the static dielectric constant are extremely small due to the covalent bonding, giving an overall dielectric constant of ε_⊥= 7.34, ε_|| = 11.22, matching well with the experimental values of ε_⊥ = 7.43, ε_|| = 12.24.^4,60 As expected given the low-dimensional connectivity (Fig. 1), significant anisotropy is found in the physical properties of t-Se, as exemplified by the ε_∞,||/⊥ values above and the hole conductivity mass ratio m_h,⊥/m_h,|| ≃ 4,^18,61 along with the absorption profiles shown in Fig. 2c where light propagating along the Se chain direction shows greater absorption at energies just above the band gap. In combination with the fact that t-Se films oriented along the c-axis (chain direction) are expected to favour benign grain boundaries^62–64 – similar to the case of Sb₂Se₃ solar cells,^53,65 this indicates that t-Se films primarily oriented along the c-axis should exhibit greater photovoltaic efficiencies due to increases in both J_sc and V_oc.⁶⁶

If we account for the finite absorption of t-Se at energies just above the direct band gap, the short-circuit current density (J_sc) is still thickness-dependent at typical values of 100–300 nm^18,25,66 as shown in Fig. S6 (ESI†), despite the steep absorption onset (due to high band edge degeneracies as discussed above). Using the spectroscopically-limited maximum efficiency (SLME) metric, the maximum terrestrial solar PV efficiency is predicted to drop from 22.3% at the radiative limit, to 21.1% at absorber thicknesses t = 300 nm and 18.2% at t = 100 nm** under indoor light sources (FL10 or WLED), a higher sensitivity to absorber thickness is found, with η_max ≃ 51%, 48%, 38% at thicknesses t = 1 m, 300 nm and 100 nm. Importantly, this metric assumes perfect carrier collection and neglects non-radiative recombination, and so the optimal absorber thickness for real-world devices will be a trade-off between J_sc – which can be boosted using structured surfaces and/or antireflective coatings^67,68 – and carrier collection. Accounting for the orientation dependence of optical absorption (Fig. 2c) shows that the SLME would drop from 21.1% to 18.8% for a 300 nm t-Se film oriented perpendicular to the chain direction, or from 48.0% to 41.9% under FL10 indoor light, which in addition to the greater in-chain carrier mobilities indicates the importance of controlled crystal orientation for t-Se PV. Indeed the latest efficiency record of 8.1% for t-Se solar cells reported by Liu et al.³⁰ at the start of this year was achieved through a substrate-heating strategy which maximised the c-axis orientation of the t-Se film.

Intrinsic defect chemistry

Se has only two possible native point defects: vacancies and interstitials. The calculated charge-dependent formation energies are shown in Fig. 3. Briefly, these diagrams plot the calculated formation energies of defects as a function of the Fermi level (electronic chemical potential).^35,69–71 As defects can adopt various charge states depending on the occupation of their associated electronic states, and the formation energies (E_f) of charged defects depend linearly on the Fermi level position (E_F); E^f_X,q ∝ qE_F – eqn (S1) (ESI†) the formation energy lines are sloped and only the lowest energy charge state at a given Fermi level is shown. The Fermi level positions at which the ground-state defect charge changes are termed thermodynamic charge transition levels, corresponding to the defect levels often represented in energy level diagrams as shown on the right-hand side of Fig. 3.

Fig. 3 Formation energies of intrinsic point defects in t-Se, as a function of Fermi level position within the band gap. The corresponding single-charge transition levels are shown alongside a vertical energy level diagram.

For most Fermi level positions within the band gap, neutral interstitials Se⁰_i are found to be the lowest energy native defect, with a formation energy of 0.82 eV. As shown in Fig. 4, Se⁰_i adopts a split-interstitial type geometry – as is common for chalcogen/oxygen interstitials,^72–76 where the additional Se inserts itself in one of the chains and displaces nearby atoms. The Se chain twists and buckles around this interstitial position, yielding a local four-fold symmetry helix, where two Se atoms are now split across one of the original host lattice sites. This results in minimal disruption to the bonding within the Se chain, with two compressed Se–Se bond lengths of 2.29 Å on either side of the split-interstitial Se–Se bond of 2.35 Å, compared to a bulk Se–Se bond length of 2.36 Å, while the Se bond angles also deviate by <5 from the bulk value of 103.7°. The retention of the ideal bulk-like bond lengths and angles – facilitated by the split-interstitial geometry – and thus minimal strain or bond-breaking energy penalties results in a low formation energy for this species.

Fig. 4 Geometry of the neutral self-interstitial (Se⁰_i) in t-Se, along various lattice directions. The two Se atoms at the split-interstitial position are highlighted in midnight blue.

Moreover, the absence of any dangling bonds or excess charge for this species, with no in-gap single-particle states as shown in the eigenvalue plots in Fig. S12 (ESI†), renders the electrically-inactive neutral state quite stable for Se_i. Consequently, the −2 charge state is only stabilised at Fermi levels close to the conduction band, while Se⁻¹_i is never the ground-state charge state (Fig. 3a).†† As such, there are no defect levels corresponding to a single charge transition (i.e. q ± 1, where q is the defect charge state) for Se_i within the band gap – a requirement for efficient charge-carrier recombination,^77–79 and so it is expected to be recombination-inactive in optoelectronic devices.

Selenium vacancies present significantly different behaviour to the interstitials, being amphoteric and exhibiting three deep charge-state transition levels spread throughout the band gap as shown in Fig. 3a and b.‡‡ The location of these defect levels in the mid-gap region suggests they could be active for electron–hole recombination, potentially harming the efficiency of t-Se PV devices. The formation energy of the vacancy, though still relatively low at ≤1.5 eV, is significantly higher than the self-interstitial for most Fermi levels and so is expected to only present in relatively low concentrations. However, the actual defect concentrations in as-grown samples will depend on synthesis procedures, which may result in non-equilibrium defect populations due to kinetic trapping. Beyond the bulk of the material, a higher prevalence of vacancy-type defects is to be expected at grain boundaries and interfaces.

The calculated geometries for the various charge states adopted by V_Se are shown in Fig. 5a, with further discussion given in Section S5 (ESI†). In the neutral state (expected to be the dominant charge state under the typical weakly p-type Fermi levels reported in t-Se), the two dangling Se chains on either side of the vacancy remain separated and slightly contract the terminal Se–Se bonds to 2.25 Å (c.f. 2.36 Å for bulk t-Se). This results in a bipolaron state, where two hole polarons are localised to the Se p orbitals of the terminal atoms at the vacancy site, akin to the recombination-active p-orbital bipolarons observed for in CdTe⁷⁹ and V⁻¹_P in NaP.³ Using the ShakeNBreak^80,81 defect structure-searching method, an additional metastable geometry is also found for the neutral vacancy in which the two dangling Se chains ends displace toward each other to form a bond across the void, passivating their dangling bonds. As shown in Fig. 5b, the energy of this metastable state is predicted to be only 27 meV higher than the ‘bipolaron’ V⁰_Se ground state, with a small 65 meV barrier for the structural transition, indicating that a non-negligible fraction of neutral Se vacancies will adopt this structure (∼25% at T = 300 K) – particularly during annealing and growth.⁸²

Fig. 5 (a) Geometries of the intrinsic vacancy (V_Se) in t-Se, under various charge states, looking down the⁸³ lattice direction. The two neighbouring Se atoms to the vacancy site are shown in teal as a guide to the eye. refers to the metastable neutral vacancy, and V⁻²_Se is additionally shown along the [110] direction to make the bridging bonds between Se chains visible. (b) Potential energy surface along the lowest energy path between the ground-state (‘split’/‘bipolaron’) V⁰_Se and metastable (‘self-healed’) structures, calculated using hybrid DFT including spin–orbit coupling within the nudged elastic band (NEB) approach.

The higher energy of the neutral Se vacancy, along with unoccupied single-particle states in the band gap, allows the emergence of charged vacancy species for various Fermi level positions in the band gap. For V⁺¹_Se which is stable for Fermi levels close to the VBM, we see that one of the dangling Se chains bonds with a neighbouring chain, while for V⁻¹_Se which is stable in the upper portion of the band gap, we retain a similar structure to V⁰_Se with the single hole polaron now split across the two terminating Se atoms, as shown in Fig. 5. Lastly for V⁻²_Se which becomes stable for n-type Fermi levels near the conduction band minimum (CBM), the ground-state geometry involves the ‘self-healed’ vacancy structure as for , but with displacement of Se in a neighbouring chain toward the vacancy site.

The structures of both intrinsic point defects in the neutral state – expected to be their preferred charge state in most samples – are indicative of low migration barriers along the c-direction, both involving only relatively small perturbations of the chain (an extra twist for Se⁰_i, a longer bond for 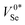)§§ which are expected to easily propagate along the chain with acoustic vibrations of the Se positions. This property, related to the low-dimensional crystal structure, may allow even lower intrinsic defect concentrations – particularly for vacancies – with sufficient mobilities to achieve equilibrium defect distributions at room temperature.⁸ The close relationships between bond distortions and defect energetics discussed here, and facile compressibility despite electronic sensitivity, indicate that strain could significantly affect defect behaviour in this system, potentially allowing its use as a materials engineering strategy for t-Se devices.

Overall, for the intrinsic point defect chemistry of t-Se, self-interstitials are lowest in energy and thus present in relatively high concentrations due to their split-interstitial type geometry. However, they are inactive for doping or electron–hole recombination (the primary mechanisms by which defects impact PV performance) due to the dominance of the neutral state across most of the band gap. On the other hand, Se vacancies adopt a variety of charge states and so can contribute to both doping and recombination, however, their higher formation energies suggest that they will be present in much lower concentrations.

Intrinsic defect recombination activity

To investigate the electron–hole recombination activity of intrinsic point defects in t-Se, we calculate the potential energy surfaces (PES) between equilibrium defect geometries for a given charge transition (i.e. charge states q and q ± 1). From these PES and the underlying electronic structure calculations, we compute the nuclear wave function overlaps via the 1D Schrödinger equation and the electron–phonon coupling coefficients via static coupling perturbation theory, which yields the carrier capture coefficients C_e/h and cross-sections σ_e/h. As discussed above, Se vacancies are the only intrinsic point defect which present single-charge transition levels (i.e. defect levels) ε(q/q − 1) in the band gap – a prerequisite for recombination activity. As such, we calculate the energy surfaces for all possible V_Se charge capture transitions involving deep defect levels, including those involving the metastable neutral vacancy which could accelerate these processes,^72,78,84 as shown in Fig. 6.

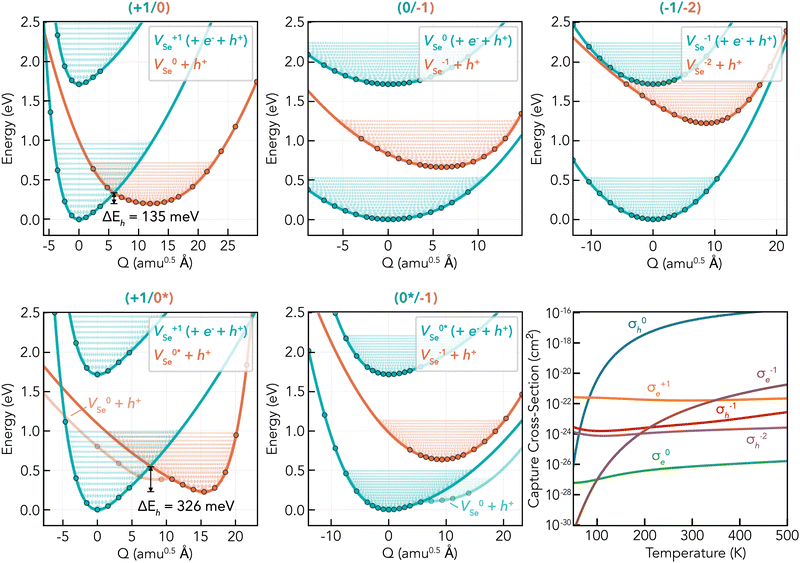Fig. 6 Potential energy surfaces (PES) and corresponding charge capture cross-sections of vacancy defects in t-Se. Each plot shows V_Se PES in two charge states; X^q in blue, X^q−1 + h⁺_VBM in orange, and X^q again with an electron–hole pair of energy equal to the band gap E_g (upper blue PES); along the linear path in structural space between their equilibrium configurations, with the corresponding defect level given as the plot title (q/q −1). The transition from the upper blue (X^q + e⁻ + h⁺) to middle orange (X^q−1 + h⁺) PES corresponds to electron capture by X^q, while that from middle orange to lower blue (X^q) corresponds to hole capture by X^q−1. The x-axis corresponds to the structural/configurational coordinate Q, given in units of mass-weighted displacement (Ångstrom times the square root of the atomic mass unit; amu^0.5 Å). ΔE_h/e denotes the activation energy barrier to hole/electron capture, here for the two cases which show a crossing between PES and thus a classical capture barrier. Filled circles represent calculated energies, and the solid lines are spline fits to the data. A portion of the effective vibrational wave functions are also shown for illustration. “0*” indicates the metastable neutral vacancy. In the bottom-right plot, the corresponding charge capture cross-sections of each vacancy defect level are plotted as a function of temperature. The charge of the defect is given by the superscript, and the charge carrier is denoted by the subscript; e/h for electron/hole; σ^q_e/h. For transitions involving the neutral state, the faster of the rates are shown; which is V⁰_Se in all cases except for σ⁰_e – which is extremely slow in both cases. The charge capture coefficients are plotted in Fig. S11 (ESI†).

While several factors enter the final rate equation for defect charge capture rates, it is predominantly the vibrational overlap between PES and the corresponding thermal population in the initial charge state which determines the overall rate. The connection between these PES and the capture cross-sections σ_e/h can thus be intuitively understood by considering the classical energy barrier to the transition (indicated by ΔE_e/h in Fig. 6), upon which the capture rate is inverse-exponentially dependent, due to the exp(−E/k_BT) Boltzmann population factor for the overlapping states. If no classical barrier exists (i.e. ε(0/−1) & ε(0*/−1)), then charge capture proceeds primarily via quantum tunnelling, which is typically slow with weak temperature dependence as seen in the cross-sections in Fig. 6.

The fastest charge capture rate is given by σ⁰_h (hole capture at the ε(+1/0) transition level) as expected, which exhibits a relatively small classical capture barrier of 135 meV. The large hole capture cross-section σ⁰_h = 3.2 × 10⁻¹⁷ cm⁻² @ T = 300 K is of similar magnitude to the Se atomic cross-section σ_Se = π(a_Se)² ≃ 4.5 × 10⁻¹⁶ cm⁻²,¶¶ classifying it as a ‘giant’ hole trap.^72,85,86 All other capture cross-sections for V_Se, however, are >5 orders of magnitude smaller at room temperature – primarily due to soft and anharmonic PES, with further discussion in Section S5.2 (ESI†) – corresponding to weak traps. Overall, while we find relatively fast hole capture by neutral Se vacancies (σ_h) which may act to impede hole-carrier mobilities, no fast electron capture transitions are witnessed for V_Se. Thus no efficient electron–hole recombination cycles can be established for isolated Se vacancies, meaning they will not contribute significantly to non-radiative recombination in t-Se. Even if we assumed a high non-equilibrium vacancy population of 10¹⁸ cm⁻³ in as-grown t-Se, the limit on carrier lifetime by V_Se would still be as high as ∼100 μs. Thus we conclude that intrinsic point defects in the bulk material do not limit the efficiencies of t-Se solar cells.

Doping and extrinsic defect chemistry

Turning our focus to the impact of intrinsic defects on charge-carrier populations, we can see that there are no charged defects which are low energy for all Fermi levels in the band gap in t-Se (i.e. no low energy acceptors near the VBM or donors near the CBM), as discussed above. Thus, Se_i and V_Se on their own do not contribute significantly to doping in t-Se, as shown in the thermodynamics analyses in Fig. S8 (ESI†), where calculated equilibrium hole concentrations in as-grown Se films do not reach 10¹⁰ cm⁻³ even up to the melting temperature (T = 493 K).⁸⁷ We note that the typical synthesis procedure for t-Se, involving crystallisation from the amorphous phase, may induce higher defect concentrations than equilibrium predictions due to kinetic trapping. However, the approximate orders of magnitude are still expected to be reliable estimations, especially given the proximity to the melting temperature and low expected migration barriers (discussed later) which should favour rapid equilibration.

Intrinsic defects may increase the concentration of charge carriers (doping) or decrease them through charge compensation. This balance can be described in terms of ‘doping windows’,^71,75,88 which are related to the formation energy of the lowest energy charge-compensating species at the corresponding band edge (i.e. the lowest energy intrinsic donor/acceptor at the valence/conduction band). For t-Se, we have no n-type doping window, with the formation of the dominant intrinsic acceptor becoming spontaneous (E_f (V⁻²_Se) < 0) at Fermi levels just below the CBM, while we have an extremely large p-type doping window of 1.29 eV, set by the formation energy of V⁺¹_Se at the VBM. The presence of this large p-type doping window can be ascribed to the limited number of inequivalent intrinsic point defects in this single-element system, the covalent bonding (and resultant low dielectric constant which disfavours charged defects), and relatively high energy cost of breaking the Se chains. Similar behaviour is found in other covalent semiconductors such as Si and Ge.^89–91 Consequently, while intrinsic point defects do not directly contribute to doping in t-Se and n-type doping is mostly prevented by the low energy of V⁻²_Se, extrinsic p-type doping should be accessible.

From the above discussions, we see that low carrier lifetimes in state-of-the-art Se solar cells cannot be explained by electron–hole recombination mediated by intrinsic point defects. Intrinsic defects also fail to explain the reported hole densities of 10¹³–10¹⁷ cm⁻³ in polycrystalline samples.^8,39–42 We therefore revisit the state-of-the-art photovoltaic device from Nielsen et al.¹⁸ – exhibiting a record V_oc of 0.992 V (Fig. 7a), to further investigate photovoltaic losses and impurity concentrations. In Fig. 7b, the experimental current–voltage (JV)-curve and the reconstructed JV-curve from Suns-V_oc measurements (which determine the open-circuit voltage as a function of light intensity) are shown, illustrating the various contributions to photovoltaic losses. This includes a fill factor (FF) loss originating from parasitic series resistance R_S, and a more significant loss in current density due to incomplete photon absorption and carrier collection – in line with our optical results (Fig. 2 and Fig. S6, ESI†) and measured external quantum efficiency (EQE) of ∼65% (Fig. S21, ESI†) for a 300 nm-thick film. While the use of an Au back contact in single-junction devices already boosts absorption by acting as a reflective surface, further light-trapping strategies could avoid this loss, as demonstrated by the visible-light EQEs close to 100% recently reported by Lu et al.,²⁴ using an anti-reflective coating. Fig. 7b also shows the loss from carrier management (i.e. V_oc deficit) which typically results from non-radiative recombination, but is also influenced by band tailing – investigated in Fig. 7c. A moderate Urbach energy of 44 meV is extracted from the fit of the absorption onset in the EQE spectrum (as elaborated in Section S6, ESI†). However, the band tailing deviates from a linear trend in the semilog plot, indicating that standard Urbach behaviour may not fully explain the observed tailing.

Fig. 7 Experimental device characterisation of a state-of-the-art selenium thin-film solar cell, and impurity analysis of the absorber. (a) Illumination-dependent open-circuit voltage (Suns-V_oc) demonstrating a record open-circuit voltage.¹⁸ (b) Current–voltage (JV) curve of the experimental device, the reconstructed JV-curve from Suns-V_oc assuming the short-circuit current density from experiment (green) or the detailed-balance (DB) limit (blue), and the DB-limit JV curve – using the photovoltaic band gap of t-Se, E^PV_g,²⁷ obtained from the inflection point of the external quantum efficiency (EQE) spectrum. The photovoltaic losses which account for the difference between curves have been explicitly highlighted, including parasitic series resistance (R_S), light management (absorption losses), and carrier management (recombination losses, indirect band edges, etc.). (c) The Urbach band tailing derived from EQE measurements (Fig. S21, ESI†). (d) Cross-sectional scanning electron microscopy (SEM) of the thin-film selenium photo-absorber synthesised on a silicon substrate for impurity analysis. (e) Time-of-flight Secondary Ion Mass Spectrometry (ToF-SIMS) results, integrated while sputtering through the bulk of the selenium thin-film. Among the unintentional impurities, we detect F and Cl, whereas O and Te were only observed at the surface and interface with the substrate (see Section S7, ESI†).

Turning our focus to the chemical purity of our t-Se samples, we perform time-of-flight secondary ion mass spectrometry (ToF-SIMS) measurements on photoabsorbers fabricated in parallel with the absorber of the device to ensure a representative sample (Fig. 7d). The sputter depth profile is integrated through the bulk of the crystallised Se absorber layer (Fig. S22, ESI†) to get a representative measurement of the extrinsic elements present in the bulk of the thin film. Quantification of impurity concentrations requires elemental standards, which were not present, and the results presented in Fig. 7e should therefore be treated only as a qualitative demonstration of the presence of F and Cl in the absorber. O and, particularly, Te are also present, but only at the surface and interface. These are expected in higher concentrations than the halogens, given the use of an ultra-thin trigonal Te substrate to favour the trigonal Se allotrope and aid adhesion, and O from thermal annealing in air during crystallisation. The halogen impurities are verified to originate from the Te source material using ToF-SIMS (Fig. S23, ESI†).⁹² Moreover, the rich variety of naturally-occurring isotopes of both Se (⁷⁶Se, ⁷⁷Se, ⁷⁸Se and ⁸²Se all >5% natural abundance) and Te (¹²⁵Te, ¹²⁶Te, ¹²⁸Te, ¹³⁰Te; >5% abundance) makes the identification of Br (⁷⁹Br/⁸¹Br) and I (¹²⁷I) difficult given the strong overlap of masses, and so they may also be present in significant amounts.⁹³

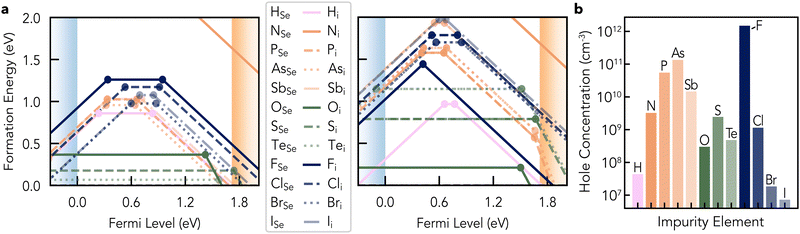
Given these known impurities, we calculated the formation energies of their corresponding point defects (substitutions and interstitials) in t-Se, including H (given its ubiquity and invisibility to ToF-SIMS) and the pnictogen family (given their position to the right of selenium on the periodic table, and thus potential acceptor dopant behaviour)⁹⁴ as well as the first 4 rows of chalcogen and halogen groups. From the formation energy diagrams in Fig. 8, we observe consistent behaviour in energies and charge states within each periodic group. Within the same group, there are mostly rigid shifts of formation energies due to size effects, with larger anions tending to be lower energy as X_Se substitutions, but higher energy as X_i interstitials – as is typically the case. N is an outlier to these trends, being high energy in both cases and only stable in the neutral and singly-negative charge states. Each impurity shows similar electrical behaviour (charge state preferences) as both substitution and interstitial defects (X_Se & X_i), due in part to the neutral oxidation state of the substitutional site (Se). Each heterovalent impurity species investigated (halogens, pnictogens and hydrogen; with preferred valence differing from Se by ±1) shows amphoteric behaviour, having stable +1 and −1 charge states – except for nitrogen. X⁺¹_Se and X⁺¹_i defects exhibit geometries similar to V^+1/+2_Se (Fig. 5 and Fig. S10, ESI†), with bridging bonds between Se chains stabilising the positive charge states – behaviour which has been termed ‘valence alternation’;⁹⁵ Section S5.1 (ESI†). Homovalent impurities (chalcogens) adopt neutral charge states for most Fermi levels in the band gap, consistent with their covalent nature and dominance of neutral Se_i.

Fig. 8 (a) Formation energies of extrinsic point defects (impurities) in t-Se, as a function of Fermi level position within the band gap, under X-rich conditions where X is the impurity species. Substitutions (X_Se) are shown on the left and interstitials (X_i) are shown on the right. Impurities are coloured according to their periodic group, with changing linestyle and decreasing opacity as the group is descended. (b) Hole carrier concentrations due to impurity point defects in t-Se, as output by the doped defect simulation python package using the HSE06 + D3 + SOC defect formation energies and electronic density of states. An annealing temperature of 500 K, quenched temperature of 300 K and X-rich conditions (where X is the impurity element) is assumed, with only a single impurity element present in each case.

The neutral chalcogen interstitials insert in the Se chains similar to the split-interstitial Se⁰_i geometry discussed above, while the neutral substitutions incur minimal bond distortions around the X_Se site, helping to explain the low formation energies. Te substitutions are extremely low energy (E_f (Te_Se)) = 67 meV), explaining the ready uptake of Te in Se films,¹¹ particularly when grown on trigonal Te substrates as discussed above. However, the tight in-chain binding of the chalcogen substitutions and interstitials means their diffusibility is likely low, while that of the negatively-charged halogen interstitials – which are essentially free ions between the Se chains – is likely high. This rationalises the impurity distributions measured by ToF-SIMS (Fig. S22, ESI†), with Te and O present in high concentrations but only at the absorber interfaces, while halogens (which originate from the Te substrate; Fig. S23, ESI†) are present throughout the film – potentially accumulating at grain boundaries or interfaces. While the formation energies of all extrinsic point defects here are still relatively low (<2 eV, except for nitrogen), substitutional defects are found to be lower energy than interstitials in most cases. For both substitutions and interstitials, chalcogens tend to be the lowest energy impurities (though are electrically inactive), while halogen/pnictogen impurities are highest in energy and H-related defects are intermediate. Further analysis of defect geometries and electronic structures of impurities in t-Se is given in Section S5 (ESI†). We note that ref. 38 and 47 also performed initial screenings of some point defects in t-Se using semi-local DFT, however, we obtain qualitatively different results for most defect properties. We attribute these discrepancies to the use of semi-local DFT functionals, strained supercells, and neglect of vdW interactions and structure-searching (Section S5.5, ESI†),^80,96,97 giving shallower defect levels, unphysically low capture coefficients, and negative formation energies.

Once again, no potential impurity species are expected to contribute significantly to carrier doping in t-Se, as each extrinsic defect is either low-energy and electrically-neutral, or higher-energy and amphoteric (i.e. self-compensated). In fact, several of these impurities are low-energy amphoteric species with ε(+1/−1) transition levels near the mid-gap, which will act to compensate both p and n-type doping, including H interstitials, halogen substitutions and pnictogen substitutions. The most p-type conditions are obtained for F doping due to the lower position of the self-compensated F_Seε(+1/−1) level at 0.42 eV above the VBM, giving a maximum hole concentration ∼10¹² cm⁻³ as shown in Fig. 8b. However, this still does not explain the apparent p-type doping/acceptor density of 10¹⁴–10¹⁶ cm⁻³ in as-grown polycrystalline Se samples.^{4,18,39–41,98} Looking at the experimental literature, we note that Nijiland,³⁹ Plessner⁹⁹ and D’Almeida et al.¹⁰⁰ reported that addition of halogens (Br & I) improved the conductivity of polycrystalline t-Se, but that this was not due to changes in carrier concentrations (in agreement with our predictions) but rather increased carrier mobilities by reducing the resistivities of grain boundaries and remnant crystalline-amorphous interfaces in the samples. Notably, Todorov et al.²⁵ reported a much lower hole concentration of 3 × 10¹² cm⁻³ in polycrystalline t-Se using AC Hall measurements. However, Nielsen et al.⁹⁸ recently expanded on these findings through carrier-resolved photo-Hall and temperature-dependent Hall measurements, revealing that the observed carrier densities at room temperature in the dark are significantly affected by carrier freeze-out and depletion through surface and/or interface defects. These findings suggest that the true acceptor density is on the order of N_A ∼ 10¹⁶ cm⁻³.⁹⁸

Our results above show that while halogen impurities are present and may contribute low levels of hole doping, neither intrinsic nor extrinsic point defects can explain the reported doping concentrations in t-Se PV devices. Se is a soft, highly-deformable solid as discussed above and evidenced by the low formation energies of competing allotropes (Table S2, ESI†), low bulk modulus and low defect formation energies. Coupled with its ability to catenate and bond in a variety of chain and ring-like structures, this indicates the potential inclusion of non-crystalline regions in t-Se films, comprised of over- and under-coordinated Se atoms in inter-chain bridging bonds, stacking faults, ring-like formations and/or amorphous clusters. Indeed, Nijiland³⁹ and others^41,99 have reported polycrystalline t-Se samples to consist of 'well-conducting crystals embedded in badly conducting layers of more or less amorphous selenium', while Lu et al.²⁴ reported improved crystallinity (and optoelectronic performance) with their critical-melting annealing treatment. We further note that all charged intrinsic defect species in t-Se involved the formation of bridging bonds between Se chains, which are expected to occur at any grain boundaries or extended defects, indicating the potential doping activity of these regions. Thus it is certainly possible that significant concentrations of extended defects and/or non-crystalline regions may be present in the as-grown t-Se films and contribute to doping, by forming or attracting charged defects. This possibility would also be exacerbated by the typical growth process of t-Se; where amorphous Se is first prepared and then annealed just below the melting temperature (often on a trigonal-Te substrate) to yield the trigonal phase,^18,24 which is likely to give increased defect concentrations and potentially incomplete removal of amorphous phases. Indeed, Plessner⁴¹ found carrier concentrations in selenium films to be highly sensitive to the annealing and crystallisation conditions, with greater crystal quality yielding much lower hole concentrations, in agreement with these conclusions. Other possible origins of unexpected doping measurements include complex defect formation or surface effects due to unpassivated Se chain terminations in thin films.

Finally, turning to the question of the remaining V_oc deficit in Se solar cells, we recall our earlier conclusion that intrinsic point defects do not limit carrier lifetimes in t-Se. Extrinsic point defects or their complexes (with V_Se or each other) could contribute to recombination. Several (non-chalcogen) impurities exhibit deep defect levels in the band gap as shown in Fig. 8 and tabulated in Section S5 (ESI†). Recently, however, both Chen et al.¹¹ and Li et al.¹⁰ independently found the amplitude of deep level transient spectroscopy signals for defect levels in Se and Se_xTe_1−x alloys to be linearly dependent on the filling pulse widths, which suggests they originate from extended rather than point defects. Our predictions support this conclusion, indicating a significant role of extended defective regions in the defect chemistry of as-grown t-Se. Moreover, several recent experiments^6,8,13,98 have reported large differences between acceptor densities (N_A) from capacitance–voltage (CV) and drive-level capacitance profiling (DLCP) measurements. N_A,CV is sensitive to both bulk and interfacial defects, while N_A,DLCP is typically sensitive only to bulk defects, and so the large differences (N_A,CV – N_A,DLCP) ∼10¹⁶ cm⁻³ indicate high interfacial defect concentrations. As such, extended defects, interfaces (whether at the edges of t-Se films or internally at non-crystalline inclusions), and/or grain boundaries are proposed to dominate recombination and V_oc deficits in t-Se (despite the expectation of benign grain boundaries in vdW-bonded solids).^56,63,64

Overall, our results provide strong evidence that extended defects and interfaces are the current limiting factors in champion t-Se PV devices, with point defects being mostly benign for recombination and electrically inactive. This is a promising finding, as extended defects are often easier to avoid than point defects – provided their origins are known – due to the lack of an unavoidable entropic driving force. Consequently, materials engineering strategies which can minimise the prevalence and impact of these deleterious species are key to further improvements in open-circuit voltages and device efficiencies in t-Se. This places a high level of importance on synthesis and crystallisation routes. t-Se crystal quality and electronic properties are highly sensitive to annealing and crystallisation conditions,^24,41,83 with a key challenge being the low melting temperature (220 °C) and high vapour pressure which limit the admissible annealing temperature range. The recently-reported critical-melt annealing (CMA) approach²⁴ achieved an efficiency breakthrough attributed to improved crystallinity and reduced extended structural disorder – a hypothesis supported by our results. In the past few years, several annealing strategies have been trialled, including closed-space annealing,⁸³ rapid thermal annealing,⁶ photo-annealing⁶⁶ and laser crystallisation,⁶² with varying levels of success. To further disfavour disordered chains or amorphous inclusions in as-grown films, promising approaches would include the combination of the successful variants of these annealing strategies (such as closed-space annealing, which allows above-melting temperatures,⁸³ under illumination, which improves film morphology⁶⁶), with long annealing times to favour more complete re-organisation of Se chains, or direct epitaxial growth of crystalline t-Se on Te substrates (rather than the typical thermal crystallisation from the amorphous phase) using molecular beam epitaxy (MBE) for example. Given the demonstrated strain sensitivity, application of strain could also possibly be used to alter concentrations and/or recombination activities of extended defects.

An alternative approach would be to target passivation of extended defects, rather than their complete removal, similar to CdCl₂ treatments commonly applied to reduce recombination at grain boundaries in commercial CdTe solar cells.¹⁰¹ For t-Se, a promising approach could be the intentional incorporation of halogen dopants during growth. As mentioned above, halogen addition has been found to boost conductivity in polycrystalline t-Se^39,99,100 without changing the carrier density (in agreement with our predictions; Fig. 8), indicating a passivating effect at remnant crystalline-amorphous interfaces and/or grain boundaries. As such, electrically-neutral halogen doping could be a promising route to improving V_oc deficits in champion t-Se devices, by reducing carrier resistivities and non-radiative recombination rates at extended defects.

Another consideration is the thickness of the t-Se thin film. A reduced film thickness, along with controlled growth along the c-axis, could give a reduced prevalence and impact of extended defects on carrier lifetimes, in addition to improved carrier separation. However, incomplete absorption will begin to occur for thicknesses below ∼400 nm as discussed above (Fig. S6, ESI†). Current record efficiency devices^24,30 employed a 1 μm-thick Se film. Our results suggest that a film thickness of 200–400 nm is likely ideal for t-Se PV performance, retaining complete absorption (particularly if films are preferentially-oriented along c) while minimising the potential impact of trapping and recombination at extended defects. Measuring PV parameters and performance over a range of film thicknesses will be valuable for identifying the optimal trade-off between these effects.

Our findings call for a shift in focus from point defects to extended defects in t-Se solar cells. Extended defects and interfaces generally present more challenges for characterisation (both theoretically and experimentally), but thorough investigation of their origin and effects on voltage deficits in t-Se will be key to unlocking further efficiency improvements. Experiments combining spectroscopic and microscopic methods will likely be most useful here. High-resolution transmission electron microscope (HRTEM) analysis of controlled-orientation films could allow structural disorder and extended defects such as stacking faults to be directly observed. In particular, multi-modal microscope techniques which combine local structural and electronic probes (such as nano X-ray diffraction with nano X-ray fluorescence)¹⁰² would allow the electronic states introduced by extended defects to be directly imaged and correlated with their structural signatures. In addition, analysing the dependence of deep levels associated with extended defects – measured by recent deep-level transient spectroscopy (DLTS) measurements^10,11 – on growth temperature, synthesis approach and possibly halogen doping would help to understand their origin and how they may be avoided or passivated. On the modelling front, accurate methods for extended defects are typically challenging and computationally-intensive – particularly for electron–hole recombination. This is an active area of research however, with further advances such as the use of machine-learned interatomic potentials facilitating their direct prediction.^103–108

Conclusions

In summary, we characterise the intrinsic and extrinsic point defect chemistry of t-Se by both theoretical and experimental means. We first analyse the intrinsic structural and electronic properties of Se thin films; including their allotropic and highly-deformable nature, likely inducing tolerance to non-crystalline inclusions or ring-like formations; imperfect band-edge absorption, making achievable PV efficiency sensitive to film thickness and light-trapping strategies; strong thermal fluctuations in the band gap, possibly contributing to moderate Urbach energies (Fig. S21, ESI†)¹⁰⁹; and highly-anisotropic optical and electronic properties, highlighting the importance of controlled grain orientation in t-Se films. We find the crystal dimensionality to play a key role in the behaviour of defects in this system, favouring self-interstitials and chalcogen substitutions while disfavouring vacancies and heterovalent defects, due to its structural flexibility, high energy cost of chain rupturing and pure-covalent bonding. Self-interstitials are low-energy and electrically-neutral, while vacancies are electrically-active but higher energy, thus do not significantly contribute to (self-)doping. Analysing the effect of a range of relevant extrinsic impurities in t-Se samples, we show the presence of F, Cl, O and Te using ToF-SIMS measurements (Fig. 8 and Fig. S22, ESI†), while Br and I are also expected to be present. Computing the electronic and energetic properties of these species and other likely impurities, we find that most extrinsic species are inactive for doping, either due to electrical-inactivity (chalcogens) or self-compensation (hydrogen, halogens, pnictogens). F interstitials are the most doping-active species, though only yielding modest hole concentrations of ∼10¹² cm⁻³, and so neither intrinsic nor extrinsic point defects are found to contribute significantly to doping.

We conclude that intrinsic point defects in the bulk absorber layer do not limit performance in t-Se solar cells, through impacts on doping or recombination, bestowing a positive outlook on the achievable photovoltaic efficiencies. In light of these results, we propose that extended defects, grain boundaries and/or interfaces are the likely origins of V_oc deficits and limited efficiencies in Se PV devices, as supported by recent experiments.^10,11 These conclusions call for research on Se PV to focus on characterising, avoiding and passivating extended defects in as-grown films, as the next frontier in achieving breakthrough efficiencies. Encouragingly, extended defects are often more amenable to materials engineering strategies than unavoidable point defects,¹¹⁰ and we propose a number of promising avenues to passivate their effects and understand their origins.

Computational methods

All calculations were performed using Density Functional Theory (DFT) within periodic boundary conditions through the Vienna Ab Initio Simulation Package (VASP).^111–116 Using the projector-augmented wave (PAW) method, scalar-relativistic pseudopotentials were employed to describe the interaction between core and valence electrons.¹¹⁷ Unless otherwise specified, the range-separated screened hybrid DFT functional of Heyd, Scuseria and Ernzerhof (HSE06)¹¹⁸ was used for all calculations, along with the D3 dispersion correction of Grimme et al.¹¹⁹ using the zero-damping function, to account for vdW dispersion forces – found to be crucial for accurate modelling of Se (Table S3, ESI†).⁴⁷ To account for relativistic effects, spin–orbit interactions were included (HSE06 + D3 + SOC) in all total energy, electronic and optical calculations. A plane wave energy cutoff of 300 eV and k-point density of 0.42 Å⁻¹ (4 × 4 × 4 for the 3-atom P3₁21 unit cell) were found to give total energies converged to within 1 meV per atom – using vaspup2.0,¹²⁰ and so were used in all calculations unless otherwise specified.

The doped⁷¹ defect simulation package was used for all steps in the defect modelling workflow, including structure and input file generation, calculation parsing, analysis and plotting. The standard supercell approach for computing defect formation energies was employed,^70,79 and self-consistent defect/carrier concentrations were computed using the total charge neutrality condition (Section S4, ESI†).¹²¹ For defect calculations, an 81-atom supercell was used, produced from a 3 × 3 × 3 expansion of the primitive P3₁21 unit cell, along with a 2 × 2 × 2 k-point mesh (rounding up from the converged k-point density of 0.42 Å⁻¹). Convergence of defect formation energy with respect to supercell size was confirmed by re-generating relaxed defect structures of all intrinsic defects in larger 234 and 648-atom supercells, using the utility functions in doped.utils.stenciling (which can re-generate relaxed defect structures in arbitrary supercell sizes and shapes) to significantly reduce computational cost, before re-relaxing and re-calculating the formation energies, for which the formation energies changed by less than 35 meV in all cases. The ShakeNBreak^80,81,96 defect structure-searching method was employed in all cases, finding many low-energy defect geometries which are missed by standard gradient relaxations of unperturbed or ‘rattled’ defect supercells (with ΔE up to 1 eV), particularly for extrinsic impurities. Further details are provided in Section S5.S (ESI†).

Spin–orbit coupling was not included during defect geometry relaxation (adding unnecessary cost with negligible impact on structures as confirmed here), but included in a final static total-energy calculation in each case. To account for spurious finite-size supercell effects, the Kumagai-Oba¹²² (eFNV) charge correction scheme was used, as automated in doped⁷¹via the pydefect¹²³ API. Charge-carrier capture coefficients were calculated using the one-dimensional configuration coordinate approach of Alkauskas et al.,⁷⁷ with electron–phonon coupling matrix elements computed using nonrad.¹²⁴ CarrierCapture.jl¹²⁵ was used to fit the potential energy surfaces (PES) and solve the 1D vibrational Schrödinger equation, allowing the use of anharmonic PES which are found to significantly impact recombination rates here.^72,79,126 For more details on these calculations, the reader is directed to ref. 53, 77, 79 and 124.

AMSET¹²⁷ was used for deformation potential analysis, and aTLC¹²⁸ was used to analyse the effect of non-radiative recombination on PV parameters. Potential secondary phases in the presence of extrinsic species, which determine the chemical potential limits which enter the defect formation energy equation, were generated and parsed using the algorithms in doped.⁷¹ Here, all compounds which could border t-Se on the phase diagram, taking the Materials Project¹²⁹ energies and assuming an error range of 0.1 eV per atom, were re-computed with the HSE06 + D3 + SOC hybrid DFT functional. Pre-relaxed crystal structures of competing phases, using HSE06(+D3), were taken from calculations performed in ref. 3 and 130–132 to expedite geometry optimisations. The SLME tools from pymatgen^133–135 were combined with reference indoor light spectra¹³⁶ to obtain thickness-dependent efficiency plots (Fig. S6, ESI†), and colour maps from cmcrameri^137,138 were used in Fig. 8.

A dense Γ-centred k-point mesh of 16 × 16 × 16, using tetrahedron smearing and downsampling of the Fock exchange matrix by a factor of 2 (to reduce computational cost with no loss to accuracy confirmed), was employed for bulk electronic structure and optical calculations to ensure a well-converged density of states (DOS). A convergence criterion of 0.01 eV Å⁻¹ was imposed on the forces on each atom during geometry optimisations, and an increased energy cutoff of 550 eV was used to avoid Pulay stress. Charge carrier effective masses were obtained from non-parabolic fitting of the electronic band edges using the effmass,¹³⁹ electronic band structure diagrams were generated using sumo¹⁴⁰ and Galore¹⁴¹ was used for photo-electron cross-sections (Fig. S3, ESI†). Surface slab calculations to obtain vacuum band alignments were performed using surfaxe,¹⁴² for which slab and vacuum thicknesses of 20 Å each were found to give well-converged electrostatic potential plateaus, for a surface cut along the (100) plane (i.e. between Se chains). Phonon calculations were performed using phonopy¹⁴³ and ThermoParser¹⁴⁴ with the HSE06 + D3 functional and a 4 × 4 × 4 supercell of the primitive t-Se unit cell. The ionic dielectric response was calculated using linear response theory under finite electric fields (with the HSE06 + D3 functional).

Experimental methods

The solar cell characterised in this work follows the device architecture FTO/ZnMgO/Te/Se/MoO_x/Au, fabricated using physical vapour deposition techniques. Details of the fabrication process are provided in ref. 18. Suns-V_oc measurements of the photovoltaic device were performed using the accessory stage of a WCT-120 from Sinton Instruments. This setup features an illumination sensor calibrated for intensities ranging from 0.006 to 6 suns, and the temperature of the sample chuck controlled at 25 °C.

The Se thin-film on Si, used for impurity analysis, was synthesized through thermal evaporation of amorphous Se (99.999+%, metals basis) and Te (99.9999%, metals basis) shots, both purchased from Alfa Aesar, followed by a thermal annealing step at 190 °C in air. Scanning electron microscopy (SEM) images were acquired using a Supra 40 VP SEM from Zeiss. Time-of-flight secondary ion mass spectroscopy (ToF-SIMS) was conducted using a Cs-ion source with a sputter beam energy of 3 kV and a liquid Bi-ion gun for analysis at 25 kV. The sputter area was set to 200 × 200 μm, with an analysis area of 100 × 100 μm, and the measurements were performed using a sawtooth raster mode. A total of half a million channels were used, and the signals were integrated between the signals corresponding to the native oxide and the Si substrate to separate contributions from the surface and interface in the bulk impurity analysis.

Author contributions

Seán R. Kavanagh: computational methodology, writing – original draft, project administration. Rasmus S. Nielsen: experimental methodology. Alp E. Samli: computational methodology. Aron Walsh & David Scanlon: conceptualisation, funding acquisition. All authors: discussion, writing – review & editing.

Data availability

All relevant data and code for analysis generated in the course of this work is freely available at doi.org/10.5281/zenodo.13888307.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge Kasper Tolborg, Irea Mosquera-Lois and Adair Nicolson for discussions regarding substrate charge transfer and prevalence of amorphous phases, vibrational free energies, and indoor PV metrics, respectively. SRK acknowledges the Harvard University Center for the Environment (HUCE) for funding a fellowship. RSN acknowledges the Carlsberg Foundation for funding a fellowship, grant CF24-0200. PCKV acknowledges the Independent Research Fund Denmark (DFF) grant 0217-00333B. The computations described in this article were performed using the University of Birminghams BlueBEAR HPC service, the Baskerville Tier 2 HPC service (https://www.baskerville.ac.uk/, funded by the EPSRC and UKRI through the World Class Laboratories scheme (No. EP/T022221/1) and the Digital Research Infrastructure programme (No. EP/W032244/1)), and the Sulis Tier 2 HPC platform hosted by the Scientific Computing Research Technology Platform at the University of Warwick (funded by EPSRC Grant No. EP/T022108/1 and the HPC Midlands+ consortium). Through our membership of the UKs HEC Materials Chemistry Consortium, which is funded by the UK Engineering and Physical Sciences Research Council (EPSRC) (No. EP/L000202, EP/R029431, EP/T022213), this work also used ARCHER2 UK National Supercomputing Services. We are also grateful to the UK Materials and Molecular Modelling Hub for computational resources, which is partially funded by EPSRC (No. EP/T022213/1, EP/W032260/1, and EP/P020194/1). This article is based upon the work from COST Action RenewPV CA21148, supported by COST (European Cooperation in Science and Technology).

Notes and references

1. W. Lu, Z. Li, M. Feng, L. Zheng, S. Liu, B. Yan, J. S. Hu and D. J. Xue, J. Am. Chem. Soc., 2024, 146, 6345–6351.
2. M. Zhu, G. Niu and J. Tang, J. Mater. Chem. C, 2019, 7, 2199–2206.
3. Y. Kumagai, S. R. Kavanagh, I. Suzuki, T. Omata, A. Walsh, D. O. Scanlon and H. Morito, PRX Energy, 2023, 2, 043002.
4. O. Madelung, Semiconductors: Data Handbook, Springer, Berlin, Heidelberg, 2004, pp. 419–433.
5. C. E. Fritts, Am. J. Sci., 1883, 3, 465–472.
6. L. Fu, J. Zheng, X. Yang, Y. He, C. Chen, K. Li and J. Tang, Faraday Discuss., 2022, 239, 317–327.
7. I. Hadar, X. Hu, Z.-Z. Luo, V. P. Dravid and M. G. Kanatzidis, ACS Energy Lett., 2019, 4, 2137–2143.
8. J. Zheng, L. Fu, Y. He, K. Li, Y. Lu, J. Xue, Y. Liu, C. Dong, C. Chen and J. Tang, Front. Optoelectron., 2022, 15, 36.
9. S. D. Deshmukh, C. K. Miskin, A. A. Pradhan, K. Kisslinger and R. Agrawal, ACS Appl. Energy Mater., 2022, 5, 3275–3281.
10. R. Li, X. Chen, S. Bai, W. Xu, C. Xia, B. Zhang, Z. Jia, Y. Liu, H. Liu, X. Tian, Q. Cui and Q. Lin, Chem. Mater., 2024, 36, 5846–5854.
11. X. Chen, S. Bai, R. Li, Y. Yang and Q. Lin, Phys. Rev. Mater., 2024, 8, 033805.
12. Y. Adachi and T. Kobayashi, Phys. Status Solidi A, 2023, 220, 2200636.
13. B. Yan, X. Liu, W. Lu, M. Feng, H.-J. Yan, Z. Li, S. Liu, C. Wang, J.-S. Hu and D.-J. Xue, Sci. Adv., 2022, 8, eadc9923.
14. X. Wang, Z. Li, B. Jin, W. Lu, M. Feng, B. Dong, Q. Liu, H.-J. Yan, S.-M. Wang and D.-J. Xue, Adv. Sci., 2024, 11, 2400615.
15. Z. Wei, W. Lu, Z. Li, M. Feng, B. Yan, J.-S. Hu and D.-J. Xue, J. Mater. Chem. A, 2023, 11, 23837–23843.
16. T. H. Youngman, R. Nielsen, A. Crovetto, B. Seger, O. Hansen, I. Chorkendorff and P. C. K. Vesborg, Sol. RRL, 2021, 5, 2100111.
17. R. Nielsen, A. Crovetto, A. Assar, O. Hansen, I. Chorkendorff and P. C. Vesborg, PRX Energy, 2024, 3, 013013.
18. R. Nielsen, T. H. Youngman, H. Moustafa, S. Levcenco, H. Hempel, A. Crovetto, T. Olsen, O. Hansen, I. Chorkendorff, T. Unold and P. C. K. Vesborg, J. Mater. Chem. A, 2022, 10, 24199–24207.
19. R. Nielsen, T. H. Youngman, A. Crovetto, O. Hansen, I. Chorkendorff and P. C. K. Vesborg, ACS Appl. Energy Mater., 2021, 4, 10697–10702.
20. V. Prosser, Czech. J. Phys., 1960, 10, 306–316.
21. A. K. Bhatnagar, K. V. Reddy and V. Srivastava, J. Phys. D: Appl. Phys., 1985, 18, L149–L153.
22. V. Prosser and H. K. Henisch, Mater. Res. Bull., 1967, 2, 75–83.
23. W. J. Choyke and L. Patrick, Phys. Rev., 1957, 108, 25–28.
24. W. Lu, M. Feng, Z. Li, B. Yan, S. Wang, X. Wen, X. An, S. Liu, J.-S. Hu and D.-J. Xue, Joule, 2024, 8, 1430–1442.
25. T. K. Todorov, S. Singh, D. M. Bishop, O. Gunawan, Y. S. Lee, T. S. Gershon, K. W. Brew, P. D. Antunez and R. Haight, Nat. Commun., 2017, 8, 682.
26. J. K. W. Ho, H. Yin and S. K. So, J. Mater. Chem. A, 2020, 8, 1717–1723.
27. T. Kirchartz and U. Rau, Adv. Energy Mater., 2018, 8, 1703385.
28. H. Ito, M. Oka, T. Ogino, A. Takeda and Y. Mizushima, Jpn. J. Appl. Phys., 1984, 23, 719.
29. T. Nakada and A. Kunioka, Jpn. J. Appl. Phys., 1985, 24, L536.
30. Q. Liu, X. Wang, Z. Li, W. Lu, X. Wen, X. An, M. Feng, H.-J. Yan, J.-S. Hu and D.-J. Xue, Adv. Mater., 2025, 37, 2410835.
31. G. G. Roberts, S. Tutihasi and R. C. Keezer, Phys. Rev., 1968, 166, 637–643.
32. W. Lingelbach, J. Stuke, G. Weiser and J. Treusch, Phys. Rev. B, 1972, 5, 243–253.
33. F. Eckart and W. Henrion, Phys. Status Solidi B, 1962, 2, 841–849.
34. W. Shockley and H. J. Queisser, J. Appl. Phys., 1961, 32, 510–519.
35. Y.-T. Huang, S. R. Kavanagh, D. O. Scanlon, A. Walsh and R. L. Z. Hoye, Nanotechnology, 2021, 32, 132004.
36. U. Rau, B. Blank, T. C. Müller and T. Kirchartz, Phys. Rev. Appl., 2017, 7, 044016.
37. A. Zakutayev, J. D. Major, X. Hao, A. Walsh, J. Tang, T. K. Todorov, L. H. Wong and E. Saucedo, J. Phys.: Energy, 2021, 3, 032003.
38. H. Moustafa, J. Kangsabanik, F. Bertoldo, S. Manti, K. S. Thygesen, K. W. Jacobsen and T. Olsen, Phys. Rev. Mater., 2024, 8, 015402.
39. N. M. Nijland, Philips Res. Rep., 1954, 9, 259–264.
40. J. Stuke and K. Wendt, Phys. Status Solidi B, 1965, 8, 533–542.
41. K. W. Plessner, Proc. Phys. Soc., London, Sect. B, 1951, 64, 671.
42. K. Shen, Y. Zhang, X. Wang, C. Ou, F. Guo, H. Zhu, C. Liu, Y. Gao, R. E. I. Schropp, Z. Li, X. Liu and Y. Mai, Adv. Sci., 2020, 7, 2001013.
43. H. W. Henkels, Phys. Rev., 1950, 77, 734–736.
44. D. R. McCann and L. Cartz, J. Appl. Phys., 1972, 43, 4473–4477.
45. P. Cherin and P. Unger, Inorg. Chem., 1967, 6, 1589–1591.
46. R. Keller, W. B. Holzapfel and H. Schulz, Phys. Rev. B, 1977, 16, 4404–4412.
47. A. Stoliaroff, C. Latouche and S. Jobic, Phys. Rev. B, 2021, 103, 094111.
48. M. G. Helander, M. T. Greiner, Z. B. Wang, W. M. Tang and Z. H. Lu, J. Vac. Sci. Technol., A, 2011, 29, 011019.
49. C. H. Don, H. Shiel, T. D. C. Hobson, C. N. Savory, J. E. N. Swallow, M. J. Smiles, L. A. H. Jones, T. J. Featherstone, P. K. Thakur, T.-L. Lee, K. Durose, J. D. Major, V. R. Dhanak, D. O. Scanlon and T. D. Veal, J. Mater. Chem. C, 2020, 8, 12615–12622.
50. K. Bhorkar, L. Sygellou, M. Cathelinaud, D. Ren, J.-L. Adam and S. N. Yannopoulos, ACS Appl. Electron. Mater., 2022, 4, 4814–4822.
51. H. Shiel, O. S. Hutter, L. J. Phillips, J. E. N. Swallow, L. A. H. Jones, T. J. Featherstone, M. J. Smiles, P. K. Thakur, T.-L. Lee, V. R. Dhanak, J. D. Major and T. D. Veal, ACS Appl. Energy Mater., 2020, 3, 11617–11626.
52. F. Brivio, K. T. Butler, A. Walsh and M. van Schilfgaarde, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 155204.
53. X. Wang, S. R. Kavanagh, D. O. Scanlon and A. Walsh, Joule, 2024, 8, 2105–2122.
54. L.-H. Lee, J. Non-Cryst. Solids, 1971, 6, 213–220.
55. D. Royer and E. Dieulesaint, J. Appl. Phys., 1979, 50, 4042–4045.
56. J. Fujimura, Y. Adachi, T. Takahashi and T. Kobayashi, Nano Energy, 2022, 99, 107385.
57. G. Jnawali, Y. Xiang, S. M. Linser, I. A. Shojaei, R. Wang, G. Qiu, C. Lian, B. M. Wong, W. Wu, P. D. Ye, Y. Leng, H. E. Jackson and L. M. Smith, Nat. Commun., 2020, 11, 3991.
58. H. Ning, O. Mehio, C. Lian, X. Li, E. Zoghlin, P. Zhou, B. Cheng, S. D. Wilson, B. M. Wong and D. Hsieh, Phys. Rev. B, 2022, 106, 205118.
59. Y. Fu, H. Lohan, M. Righetto, Y.-T. Huang, S. R. Kavanagh, C.-W. Cho, S. J. Zelewski, Y. W. Woo, H. Demetriou, M. A. McLachlan, S. Heutz, B. A. Piot, D. O. Scanlon, A. Rao, L. M. Herz, A. Walsh and R. L. Z. Hoye, Nat. Commun., 2025, 16, 65.
60. E. J. Danielewicz and P. D. Coleman, Appl. Opt., 1974, 13, 1164–1170.
61. G. Weiser and J. Stuke, Phys. Status Solidi B, 1971, 45, 691–703.
62. R. Nielsen, T. H. Hemmingsen, T. G. Bonczyk, O. Hansen, I. Chorkendorff and P. C. K. Vesborg, ACS Appl. Energy Mater., 2023, 6, 8849–8856.
63. H. Shi, W. Ming and M.-H. Du, Phys. Rev. B, 2016, 93, 104108.
64. R. Lomas-Zapata, K. McKenna, Q. Ramasse, R. Williams, L. Phillips, K. Durose, J. Major and B. Mendis, PRX Energy, 2024, 3, 013006.
65. Y. Zhou, L. Wang, S. Chen, S. Qin, X. Liu, J. Chen, D. J. Xue, M. Luo, Y. Cao, Y. Cheng, E. H. Sargent and J. Tang, Nat. Photonics, 2015, 9, 409–415.
66. I. Hadar, T.-B. Song, W. Ke and M. G. Kanatzidis, Adv. Energy Mater., 2019, 9, 1802766.
67. B. Blank, T. Kirchartz, S. Lany and U. Rau, Phys. Rev. Appl., 2017, 8, 024032.
68. S. R. Kavanagh, C. N. Savory, D. O. Scanlon and A. Walsh, Mater. Horiz., 2021, 8, 2709–2716.
69. S. Kim, S. N. Hood, J.-S. Park, L. D. Whalley and A. Walsh, J. Phys.: Energy, 2020, 2, 036001.
70. C. Freysoldt, B. Grabowski, T. Hickel, J. Neugebauer, G. Kresse, A. Janotti and C. G. Van de Walle, Rev. Mod. Phys., 2014, 86, 253–305.
71. S. R. Kavanagh, A. G. Squires, A. Nicolson, I. Mosquera-Lois, A. M. Ganose, B. Zhu, K. Brlec, A. Walsh and D. O. Scanlon, J. Open Source Softw., 2024, 9, 6433.
72. S. R. Kavanagh, D. O. Scanlon, A. Walsh and C. Freysoldt, Faraday Discuss., 2022, 239, 339–356.
73. A. Kononov, C.-W. Lee, E. P. Shapera and A. Schleife, J. Phys.: Condens. Matter, 2023, 35, 334002.
74. A. G. Squires, L. Ganeshkumar, C. N. Savory, S. R. Kavanagh and D. O. Scanlon, ACS Energy Lett., 2024, 9, 4180–4187.
75. K. Li, J. Willis, S. R. Kavanagh and D. O. Scanlon, Chem. Mater., 2024, 36, 2907–2916.
76. A. A. Sokol, A. Walsh and C. R. A. Catlow, Chem. Phys. Lett., 2010, 492, 44–48.
77. A. Alkauskas, Q. Yan and C. G. Van de Walle, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 075202.
78. A. Alkauskas, C. E. Dreyer, J. L. Lyons and C. G. Van de Walle, Phys. Rev. B, 2016, 93, 201304.
79. S. R. Kavanagh, A. Walsh and D. O. Scanlon, ACS Energy Lett., 2021, 6, 1392–1398.
80. I. Mosquera-Lois, S. R. Kavanagh, A. Walsh and D. O. Scanlon, npj Comput. Mater., 2023, 9, 1–11.
81. I. Mosquera-Lois, S. R. Kavanagh, A. Walsh and D. O. Scanlon, J. Open Source Softw., 2022, 7, 4817.
82. I. Mosquera-Lois, S. R. Kavanagh, J. Klarbring, K. Tolborg and A. Walsh, Chem. Soc. Rev., 2023, 52, 5812–5826.
83. R. S. Nielsen, M. Schleuning, O. Karalis, T. H. Hemmingsen, O. Hansen, I. Chorkendorff, T. Unold and P. C. K. Vesborg, ACS Appl. Energy Mater., 2024, 7, 5209–5215.
84. B. Dou, S. Falletta, J. Neugebauer, C. Freysoldt, X. Zhang and S.-H. Wei, Phys. Rev. Appl., 2023, 19, 054054.
85. A. M. Stoneham, Rep. Prog. Phys., 1981, 44, 1251–1295.
86. B. Cordero, V. Gómez, A. E. Platero-Prats, M. Revés, J. Echeverría, E. Cremades, F. Barragán and S. Alvarez, Dalton Trans., 2008, 2832–2838.
87. T. H. L. G. W. C. Kaye, Tables of Physical and Chemical Constants, Longmans, Green and Co, 1911.
88. A. Goyal, P. Gorai, S. Anand, E. S. Toberer, G. J. Snyder and V. Stevanović, Chem. Mater., 2020, 32, 4467–4480.
89. P. Śpiewak, J. Vanhellemont and K. J. Kurzydłowski, J. Appl. Phys., 2011, 110, 063534.
90. P. Śpiewak and K. J. Kurzydłowski, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 195204.
91. S. Ma and S. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 193203.
92. T. D. C. Hobson, L. J. Phillips, O. S. Hutter, H. Shiel, J. E. N. Swallow, C. N. Savory, P. K. Nayak, S. Mariotti, B. Das, L. Bowen, L. A. H. Jones, T. J. Featherstone, M. J. Smiles, M. A. Farnworth, G. Zoppi, P. K. Thakur, T.-L. Lee, H. J. Snaith, C. Leighton, D. O. Scanlon, V. R. Dhanak, K. Durose, T. D. Veal and J. D. Major, Chem. Mater., 2020, 32, 2621–2630.
93. M. Berglund and M. E. Wieser, Pure Appl. Chem., 2011, 83, 397–410.
94. N. Ashcroft and N. Mermin, Solid State Physics, Brooks Cole, New York, New edn, 1976.
95. M. Kastner, D. Adler and H. Fritzsche, Phys. Rev. Lett., 1976, 37, 1504–1507.
96. I. Mosquera-Lois and S. R. Kavanagh, Matter, 2021, 4, 2602–2605.
97. M. Arrigoni and G. K. H. Madsen, npj Comput. Mater., 2021, 7, 1–13.
98. R. S. Nielsen, O. Gunawan, T. Todorov, C. B. Møller, O. Hansen and P. C. K. Vesborg, Phys. Rev. B, 2025, 111, 165202.
99. K. W. Plessner, Proc. Phys. Soc., London, Sect. B, 1951, 64, 681.
100. K. D'Almeida, K. Napo, G. Safoula, S. O. Djobo and J. C. Bernede, J. Mater. Sci., 2000, 35, 2985–2991.
101. M. A. Scarpulla, B. McCandless, A. B. Phillips, Y. Yan, M. J. Heben, C. Wolden, G. Xiong, W. K. Metzger, D. Mao, D. Krasikov, I. Sankin, S. Grover, A. Munshi, W. Sampath, J. R. Sites, A. Bothwell, D. Albin, M. O. Reese, A. Romeo, M. Nardone, R. Klie, J. M. Walls, T. Fiducia, A. Abbas and S. M. Hayes, Sol. Energy Mater. Sol. Cells, 2023, 255, 112289.
102. K. Frohna, M. Anaya, S. Macpherson, J. Sung, T. A. S. Doherty, Y.-H. Chiang, A. J. Winchester, K. W. P. Orr, J. E. Parker, P. D. Quinn, K. M. Dani, A. Rao and S. D. Stranks, Nat. Nanotechnol., 2022, 17, 190–196.
103. I. Mosquera-Lois, S. R. Kavanagh, A. M. Ganose and A. Walsh, npj Comput. Mater., 2024, 10, 1–9.
104. J. A. Quirk, B. Miao, B. Feng, G. Kim, H. Ohta, Y. Ikuhara and K. P. McKenna, Nano Lett., 2021, 21, 9217–9223.
105. C.-J. Tong and K. P. McKenna, J. Phys. Chem. C, 2019, 123, 23882–23889.
106. M. J. Watts, P. Hatton, R. Smith, T. Fiducia, A. Ali, R. Greenhalgh, J. M. Walls and P. Goddard, Phys. Rev. Mater., 2021, 5, 035403.
107. S. Lany and A. Sharan, 2021 IEEE 48th Photovoltaic Specialists Conference (PVSC), Fort Lauderdale, FL, USA, 2021, pp. 1464–1465.
108. S. R. Kavanagh, Identifying Split Vacancies with Foundation Models and Electrostatics, arXiv, 2024, preprint, arXiv:2412.19330 DOI:10.48550/arXiv.2412.19330.
109. J. Stuke, J. Non-Cryst. Solids, 1970, 4, 1–26.
110. I. Mosquera-Lois, Y.-T. Huang, H. Lohan, J. Ye, A. Walsh and R. L. Z. Hoye, Multifaceted nature of defect tolerance in halide perovskites and emerging semiconductors, arXiv, 2024, preprint, arXiv:2408.16663 DOI:10.48550/arXiv.2408.16663.
111. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
112. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
113. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
114. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269.
115. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
116. M. Gajdoš, K. Hummer, G. Kresse, J. Furthmüller and F. Bechstedt, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 045112.
117. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
118. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215.
119. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
120. S. R. Kavanagh, vaspup2.0, 2023, https://zenodo.org/record/8408542.
121. J. Buckeridge, Comput. Phys. Commun., 2019, 244, 329–342.
122. Y. Kumagai and F. Oba, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 195205.
123. Y. Kumagai, N. Tsunoda, A. Takahashi and F. Oba, Phys. Rev. Mater., 2021, 5, 123803.
124. M. E. Turiansky, A. Alkauskas, M. Engel, G. Kresse, D. Wickramaratne, J.-X. Shen, C. E. Dreyer and C. G. Van de Walle, Comput. Phys. Commun., 2021, 267, 108056.
125. S. Kim, S. N. Hood, P. V. Gerwen, L. D. Whalley and A. Walsh, J. Open Source Softw., 2020, 5, 2102.
126. S. Kim, S. N. Hood and A. Walsh, Phys. Rev. B, 2019, 100, 041202.
127. A. M. Ganose, J. Park, A. Faghaninia, R. Woods-Robinson, K. A. Persson and A. Jain, Nat. Commun., 2021, 12, 2222.
128. S. Kim and A. Walsh, Appl. Phys. Lett., 2021, 118, 243905.
129. A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002.
130. S. R. Kavanagh, C. N. Savory, S. M. Liga, G. Konstantatos, A. Walsh and D. O. Scanlon, J. Phys. Chem. Lett., 2022, 13, 10965–10975.
131. S. M. Liga, S. R. Kavanagh, A. Walsh, D. O. Scanlon and G. Konstantatos, J. Phys. Chem. C, 2023, 127, 21399–21409.
132. C. J. Krajewska, S. R. Kavanagh, L. Zhang, D. J. Kubicki, K. Dey, K. Gałkowski, C. P. Grey, S. D. Stranks, A. Walsh, D. O. Scanlon and R. G. Palgrave, Chem. Sci., 2021, 12, 14686–14699.
133. K. Choudhary, M. Bercx, J. Jiang, R. Pachter, D. Lamoen and F. Tavazza, Chem. Mater., 2019, 31, 5900–5908.
134. S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2013, 68, 314–319.
135. L. Yu and A. Zunger, Phys. Rev. Lett., 2012, 108, 068701.
136. Y. Peng, T. N. Huq, J. Mei, L. Portilla, R. A. Jagt, L. G. Occhipinti, J. L. MacManus-Driscoll, R. L. Z. Hoye and V. Pecunia, Adv. Energy Mater., 2021, 11, 2002761.
137. C. Rollo, callumrollo/cmcrameri, 2024, https://github.com/callumrollo/cmcrameri, original-date: 2020-05-06T16:04:02Z.
138. F. Crameri, Scientific colour maps, 2023, https://zenodo.org/records/8409685.
139. L. D. Whalley, J. Open Source Softw., 2018, 3, 797.
140. A. M. Ganose, A. J. Jackson and D. O. Scanlon, J. Open Source Softw., 2018, 3, 717.
141. A. J. Jackson, A. M. Ganose, A. Regoutz, R. G. Egdell and D. O. Scanlon, J. Open Source Softw., 2018, 3, 773.
142. K. Brlec, D. W. Davies and D. O. Scanlon, J. Open Source Softw., 2021, 6, 3171.
143. A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5.
144. K. B. Spooner, M. Einhorn, D. W. Davies and D. O. Scanlon, J. Open Source Softw., 2024, 9, 6340.

---

Footnotes

† Electronic supplementary information (ESI) available: Further analysis of crystal structures, allotropes, electronic structure, defect thermodynamics and experimental data (ToF-SIMS & Urbach). See DOI: https://doi.org/10.1039/d4ee04647a

‡ These authors contributed equally to this work

§ FTO = Fluorine-doped tin oxide.

¶ Though notably Lu et al.²⁴ found a direct band gap of 1.85 eV following their critical melting-annealing (CMA) strategy to obtain improved crystallinity for their t-Se samples.

|| Here _⊥ refers to the direction perpendicular to the helical Se chains in t-Se, equivalent to the a, b lattice directions, while || is parallel to the Se chains, equivalent to the c direction.

** The η = 6.5% and η = 7.2%/8.1% devices reported by Todorov et al.²⁵ and Lu et al.²⁴ /Liu et al.³⁰ employed absorber thicknesses of t = 100 nm and t = 1 μm respectively.

†† Further in-depth analyses of the structural and electronic properties of point defects in t-Se are provided in Section S5 (ESI†).

‡‡ The ε(+2/+1) defect level for V_Se is located 5 meV above the VBM and so is not considered deep.

§§ For Se vacancies the ground-state geometry is the split-chain bipolaron arrangement (Fig. 5a), but the ‘self-healed’ type metastable is only slightly higher in energy with a small transition energy barrier (Fig. 5b).

¶¶ Here a_Se is the covalent atomic radius of Se.

---