 Open Access Article
Open Access ArticleChallenges and opportunities in using Kinetic Monte Carlo for battery research and innovation
Mohammed
Bin Jassar
 *a,
Theodorus
De Bruin
*a,
Theodorus
De Bruin
 b,
Carlos
Nieto-Draghi
b,
Carlos
Nieto-Draghi
 b and
Stephan N.
Steinmann
b and
Stephan N.
Steinmann
 *c
*c
aLaboratoire CPCV, Département de Chimie, École normale supérieure, PSL University, Sorbonne Université, CNRS, 75005 Paris, France. E-mail: mohammed.bin-jassar@ens.psl.eu
bIFP Energies nouvelles, 1 & 4 avenue de Bois Préau, 92852 Rueil Malmaison, France
cCNRS, ENS de Lyon, LCH, UMR 5182, 69342, Lyon cedex 07, France. E-mail: stephan.steinmann@ens-lyon.fr
First published on 19th June 2025
Abstract
With the increasing reliance on batteries, particularly in electric vehicles, understanding the kinetics of chemical reactions – especially undesired side reactions causing aging and failures – is crucial for improving safety and lifespan. Conventional macroscopic models used in battery management systems (BMS) often face limitations due to inaccuracies and difficulties in determining parameters, which leads to large uncertainties. In contrast, bottom-up approaches, like Kinetic Monte Carlo (KMC) simulations, offer more precise modeling by bridging molecular-scale phenomena with macroscopic models, balancing computational cost and accuracy. Traditionally utilized in catalysis, KMC is now showing potential in battery applications, although it faces challenges related to the combined presence of evolving solid interfaces (e.g., solid electrolyte interphase), complex electrochemical reactions, ion/electron transport and mechanical degradation during cycling. This perspective explores how KMC can assist computational and experimental chemists in understanding and obtaining critical physical/chemical parameters from microscopic-level insights, e.g., chemical composition and temporal concentration profiles. These insights can enhance BMS at the macroscopic level, optimize battery performance, and inspire innovative mitigation strategies. The perspective also highlights challenges in estimating rate constants, handling timescale disparities, and modeling complex environments, concluding with future research directions for this evolving field.
Broader contextUnderstanding the kinetics of chemical reactions in batteries – especially undesired side reactions causing aging and failures – is crucial for improving safety and lifespan. Macroscopic models used in battery management systems often face large uncertainties due to difficulties in determining parameters. Kinetic Monte Carlo (KMC) simulations offer more precise modeling by bridging molecular-scale phenomena with macroscopic models, balancing computational cost and accuracy. Traditionally utilized in catalysis, KMC is now showing potential in battery applications. This perspective explores how KMC assists computational and experimental chemists via microscopic-level insights and how KMC could enhance battery management systems at the macroscopic level and thus optimize battery performance. Despite the achieved insights and successes of current KMC approaches, models and algorithms need further improvements. The most important limitations identified by our perspective are: (i) the need for non-uniform lattices to account for the heterogeneity of battery assemblies, i.e., evolving solid interfaces (e.g., solid electrolyte interphase) and mechanical degradation; (ii) better algorithms for dealing with timescale disparities to focus the computational effort on slow (rare) events that are key for aging; (iii) more accurate rate constants and lateral interactions from molecular simulations in representative environments. |
1. Introduction
The battery technology market was valued at approximately 112 billion USD in 2021 and is projected to reach 424 billion USD by 2030, reflecting an annual growth rate of around 17%. Lithium-ion batteries (LIBs) are expected to remain the dominant segment.1 With such rapid growth, understanding the complex chemical reactions within these devices – particularly at the electrode/electrolyte interface – is crucial, as these reactions significantly impact both battery performance and lifespan.2–6 Researchers are actively investigating these interfacial processes to uncover fundamental mechanisms and develop more sustainable materials for next-generation energy storage. Experimental studies have advanced our understanding of these interfaces by providing insights into various properties e.g., chemical compositions, and oxidation state. This approach can become frustrating when dealing with slow processes where a single experiment could take years like in battery aging. Furthermore, some interfacial processes (e.g., thermodynamics and kinetics of side reactions at the electrode/electrolyte interface) remain beyond the resolution of currently used experimental instruments.7–10 Theoretical models can be used to complement these experimental studies by providing molecular insights.2 These models range from quantum mechanical methods to kinetic Monte Carlo (KMC) and macroscopic models fitted to experiment. Each model comes with its own set of benefits and drawbacks in terms of accuracy and computational cost. First-principles quantum mechanical methods, while highly accurate, are computationally expensive and limited to small systems, making them inadequate for handling complex interfacial environments. In contrast, fast traditional continuum methods often lack detailed molecular insights and are plagued by parameter uncertainties, which can severely affect their predictive accuracy given that the uncertainty could vary over 4 to 5 orders of magnitude.11,12 These parameters are integral to what is known as the Battery Management System (BMS) in electronic devices. The BMS plays a crucial role in minimizing risks associated with overcharging, overheating, and short circuits, while simultaneously working to optimize battery performance and extend its lifespan.11,12KMC-based methods have become increasingly popular for bridging the gap between quantum and continuum scales as they offer a good balance between accuracy and computational cost. For example, KMC methods have been extensively used in the literature to model various processes mostly in the context of heterogeneous catalysis such as oxidative catalytic dehydrogenation of light alkanes (e.g., ethane/propane over PtNi(111)13,14), the water–gas shift reaction which produces high-purity H2 from H2O and CO over Cu(111)15 and Pd(100),16 the Ostwald process,17 and many others.18,19 Such KMC studies provide insightful details about the possible reaction pathways, selectivity and catalyst longevity aligning with experimental findings. In the last decades, the state of KMC has matured in the field of computational catalysis, as indicated by the rise of several user-friendly software packages, as discussed in recent reviews.18,19 In this perspective, we shed light on the rapidly growing field of KMC applied to energy storage (mainly batteries).20–51 We are convinced that KMC will continue to play a pivotal role in accurately modeling these systems not only to improve our understanding, but also to optimize designs, enhance performance, and ensure safety.52–56
2. The principles of KMC
KMC-based methods perform simulations through repeated random sampling. In general, for a kinetic Monte Carlo method, the description of the evolution of any physical/chemical processes is described by a an equation called the Markovian Master equation:57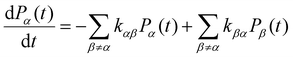 | (1) |
| pαβ(t) = kαβe−kαβ(t) | (2) |
Once the rate constants for all processes in the system of interest are obtained (experimentally or theoretically), KMC can perform the simulation of the system. One of the most used algorithms in KMC is the variable step size method in which the KMC starts with a particular configuration of the system and then predicts subsequent events. To elaborate, let us consider all possible processes w for the system to escape the current state, with associated rate constants kw. The total rate constant for the system is given by:
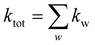 | (3) |
Let us consider process q, occurring after q − 1 previous events. The probability of q to occur is determined via:
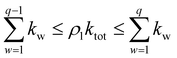 | (4) |
Note that the left-hand side and right-hand side define an interval that corresponds to the combined rates of events up to a certain number of iterations. By generating a random number (ρ1∈[0,1)) and multiplying it by the total rate, we pick a value between zero and the sum of all event rates. The event q is then selected so that this value lies between the sum of the rates of all earlier events and the sum including event q. This method ensures that events with higher rates have a proportionally greater chance of being chosen, accurately reflecting the physical likelihood of each process. Once the process is chosen and executed, the time is updated according to the following equation:
 | (5) |
The algorithm continues the simulation through choosing subsequent events and evolving the time until the maximum simulation time or number of iterations is reached. This stochastic nature and coarse-graining approach of KMC make it uniquely powerful in extending simulation times far beyond those achievable by other atomistic models. At the same time, it surpasses macroscopic models by maintaining atomic or molecular resolution. It is important to note that numerous KMC packages are available, each optimized for different applications. Recent reviews18,19 have provided detailed comparisons between these software tools.
KMC comes in two main forms: lattice KMC and off-lattice KMC. Lattice KMC has gained popularity and is frequently used to model reactions at interfaces and surface growth processes due to its relative speed compared to the off-lattice models. Hence, it will be discussed in this review. The main benefit of the lattice KMC is that it simplifies the molecular representation of the system by representing species (atoms/molecules) as points occupying discrete lattice sites. Fig. 1 shows a representation of the lattice KMC model highlighting diffusion and energetic interactions events. For the rest of the article and for convenience, we will be refereeing to the lattice KMC as just “KMC”, unless stated otherwise.
 | ||
| Fig. 1 A representation of lattice KMC events (represented by the letter e) where SB, 1NN and 2NN denotes single-body interactions, first nearest-neighbor interactions, and second nearest-neighbor interactions respectively. Reprinted (adapted) with permission from ref. 58 Copyright 2020 American Chemical Society. | ||
3. Insights from KMC for battery systems
Stability in battery systems strongly depends on the nature of the electrode interface, where the reactions of various chemical species on the electrode surface lead to the formation of solid/solid or solid/quasi-solid (porous) interfaces, with the most famous one being the solid electrolyte interphase (SEI). These interfaces play a crucial role in determining battery performance and stability. KMC methods have been used to model these layers, providing valuable insights into aspects such as composition, surface growth thickness, and structural properties. An example is the study by Yin et al.59 where a KMC model was developed to simulate the growth process of Li2O2 thin films during the discharge of Li–O2 batteries. The discharge process in Li–O2 battery initiates with the reaction between the dissolved O2 and Li+ and an electron on the electrode surface, resulting in the formation of LiO2 (ion pairs). Subsequently, LiO2 (ion pairs) undergoes further reduction to produce Li2O2. As the Li2O2 layer grows over the electrode surface, it reduces the reaction rate due to its passive nature, i.e., Li+ and electron-transport is limited. When modeling this process using KMC, the reaction's rate constant prefactors were obtained theoretically as k0 = νcP°, where νc represents the normalized frequency of the reactant particles colliding with the pore wall surface, and P° is the probability of electron transfer upon a single collision at open circuit potential.60 The diffusion events were obtained from the Stokes–Einstein equation. To include the effect of the passive layer during the simulation, Yin et al.59 implemented a modification of the Butler–Volmer equation where they introduced a multiplicative factor to modify the rate constant, see eqn (6). | (6) |
 goes to zero, implying that there is no electrochemical event anymore. In the study, two electrodes were investigated: a bare carbon nanofiber air electrode and a catalyst coated carbon nanofiber electrode. In this case the oxygen-reduction catalyst is typically made of a noble metal or metal oxide nanoparticles. Fig. 2A and B illustrate schematic representations of Li2O2 film formation on carbon nanofibers and catalyst-coated carbon nanofibers in Li–O2 batteries. The KMC results revealed that the ordering of the Li2O2 thin film is governed by the interplay between diffusion and reaction kinetics. In the case of the carbon nanofiber air electrode, an ordered crystalline formation of Li2O2 is observed, while the catalyst-coated carbon nanofibers lead to an amorphous structure.
goes to zero, implying that there is no electrochemical event anymore. In the study, two electrodes were investigated: a bare carbon nanofiber air electrode and a catalyst coated carbon nanofiber electrode. In this case the oxygen-reduction catalyst is typically made of a noble metal or metal oxide nanoparticles. Fig. 2A and B illustrate schematic representations of Li2O2 film formation on carbon nanofibers and catalyst-coated carbon nanofibers in Li–O2 batteries. The KMC results revealed that the ordering of the Li2O2 thin film is governed by the interplay between diffusion and reaction kinetics. In the case of the carbon nanofiber air electrode, an ordered crystalline formation of Li2O2 is observed, while the catalyst-coated carbon nanofibers lead to an amorphous structure.
 | ||
| Fig. 2 Panels A and B represent a schematic representation of Li2O formation over carbon nanofiber and catalyst-coated carbon nanofiber in Li–O2 batteries respectively, the radial distribution functions g(r) correspond to the fully discharge state. Planes 1–3 correspond to the points where the nanofiber intersects at 5, 20, and 35 nm, respectively. Panels C and D represent the effects of solvent/Li-ion activation energy and temperature on the SEI thickness and charging time in LIBs, respectively. Panel A and B are reprinted (adapted) with permission from ref. 59 Copyright 2017 American Chemical Society. Panel C and D are reprinted (adapted) with permission from ref. 61 Copyright 2017 American Chemical Society. | ||
We now turn our discussion to another battery technology, i.e., Li–S batteries, where KMC simulations have been employed to model the evolution of the carbon/sulfur mesostructure during the discharge process.62 The adopted model was inspired by previous studies59,60 where the rate constants were obtained from the Butler–Volmer equation and the diffusion rates were calculated using the Stokes–Einstein equation. Their KMC simulation provides insights into key aspects such as the concentration profiles of dissolved species, the population of solid sulfur-based particles, and changes in mesostructure porosity. Specifically, the simulation of discharge curves reveals that the porosity of mesostructured carbon/sulfur (C/S) cathodes evolves dynamically.62 During the sloped phase, the porosity increases as long-chain S8 reduces to medium-chain polysulfides (S42−). As the discharge progresses into the flat phase, the porosity decreases along with the reduction of S42− to S22− and the precipitation of Li2S, aligning with various theoretical and experimental observations.
KMC simulations have also been employed to model the critical process of battery aging, which refers to the gradual decline in battery performance over time.9,63 Battery aging occurs through two primary mechanisms: cyclic aging, which takes place during use, and calendar aging, which occurs even when the battery is idle. One of the most significant challenges in experimental investigations of battery aging is the slow nature of these processes. To overcome this challenge, researchers often accelerate aging by conducting experiments at high temperatures. While effective in reducing time requirements, this approach can distort the actual kinetics that occur under standard operating conditions, trigger side reactions, and compromise the reliability of the kinetic data. Together, these distortions might misrepresent the battery's true long-term behavior. Another challenge lies in the variability of experimental capacity loss patterns, which range from non-linear behaviors (e.g., square root dependence8) to linear trends7 and mixed patterns.64 These patterns stem from various physical phenomena, such as diffusion, charge transfer, mechanical cracking, or a combination of these processes. A lack of understanding of the origins of these patterns hampers progress in interpreting battery behavior and optimizing future designs. Additionally, the variability in time scales – spanning months to years even under similar experimental conditions – highlights the complexity of battery systems and the uncertainties arising from experimental setups and material compositions. In the context of LIBs, aging is predominantly governed by the formation and growth of the solid electrolyte interphase (SEI) layer. The SEI is a heterogeneous, nanometer-thin layer that forms at the interface between the negative electrode and the electrolyte due to the reduction of the electrolyte by electrons from the anode. Initially, the SEI acts as a protective passive layer, preventing further reduction of the electrolyte. However, over time, the SEI undergoes various chemical and physical changes, contributing to capacity loss and, ultimately, battery failure. As such, SEI growth is widely regarded as the primary aging mechanism in LIBs.6,10
In view of the critical role of the SEI layer, the majority of KMC-based studies have concentrated on understanding its formation and growth. Most importantly, KMC models have investigated the effects of parameters such as temperature and charging rate on charging time and SEI thickness.9,10,52,61,65–68 In a key study, Mukherjee and co-workers found that both charging time and SEI thickness decrease with the increase in activation energy of the solvent's molecules diffusing through the SEI layer, see Fig. 2C.61 However, the SEI thickness was found to increase with temperature due to the increase of diffusion. At lower temperatures, a high Li reduction rate was observed, but also a higher resistance of the SEI (due to increased current density), diffusion mostly being the limiting process (see Fig. 2D). On the other hand, at higher temperatures, a low Li reduction rate causes increased total charging time. Recent KMC models have investigated the SEI structure and predicted the formation of a multi-layered SEI in agreement with the experimental findings.56,65,69 For example, in our recent study,65 we have investigated how the inorganic species of the SEI influence both its composition and the kinetics of its growth. Using a combined DFT-KMC approach, we investigated the relationship between SEI growth and capacity loss over time (see Fig. 3a–h). We focused on the decomposition of the solvent ethylene carbonate on two key surfaces – Li2CO3(001) and Li2O(111) – which are representative of the inorganic layer of the SEI. Our KMC simulations revealed the formation and growth of the SEI structure, identifying different capacity loss behaviors – nonlinear, linear, and mixed – reflected by the loss of Li0, which correspond to the kinetics during the initial stage without inorganic species (Fig. 3b) and after the inorganic layer (Li2CO3) forms (Fig. 3f). Additionally, Fig. 3c and g illustrate the spatially heterogeneous distribution of SEI species before and after inorganic layer formation, respectively. KMC captures the accumulation of inorganic species like Li2CO3 near the Li-metal anode and organic species such as alkyl carbonate (dilithium butylene dicarbonate Li2BDC) near the electrolyte. These findings provide a molecular explanation for the diverse capacity loss patterns and the multilayered heterogeneous SEI structure observed experimentally, demonstrating how KMC bridges molecular simulations with experimental observations.
 | ||
| Fig. 3 Panels (a–d) show details of the initial ethylene carbonate (EC) decomposition reactions in the absence of the inorganic layer: (a) initial conditions, (b) variation in species concentration over time, (c) specific mass density profile along the Z-axis of the simulation box, and (d) snapshots of the simulation box after 0.6 μs. Panels (e–h) illustrate the EC decomposition reactions over Li2CO3 (001): (e) initial conditions, (f) variation in species concentration over time, (g) specific mass density profile along the Z-axis of the simulation box, and (h) snapshots of the simulation box after 1.2 ms. Here, ρtotal denotes the total density. Reprinted (adapted) with permission from ref. 65 Copyright 2023 American Chemical Society. | ||
Another critical process related to the SEI layer is lithium dendrite formation, which can lead to short circuits, performance degradation, and safety risks such as thermal runaway and explosions. KMC models have explored dendrite growth by analyzing the effects of various operating conditions.70–72 For instance, Menzel et al.71 showed that voltage significantly affects dendrite size and morphology, providing insights into their growth mechanisms. These findings are crucial for understanding and mitigating dendrite formation, a major challenge in advancing Li-metal battery technology, which offers energy densities far exceeding those of current LIBs.
KMC being a generally useful method, it has been adopted to model the diffusion in various battery technologies.21,55,73,74 For example, Xiao et al.55 have investigated Li atom intercalation in the commercial cathode material LiFePO4 found in LIBs. The parameters for the KMC were obtained using DFT through applying a cluster expansion approach. The model revealed the formation of an ordered phase of Li0.5FePO4, with alternating Li-rich and Li-poor planes as seen in Fig. 4A, explaining the X-ray diffraction experiments that detected peaks linked to an intermediate-Li phase. In the context of Na-ion batteries, a recent study by Wang et al.21 has investigated Na-ion transport in three Na superionic conductor electrode materials: NaxTi2(PO4)3, NaxV2(PO4)3, and NaxCr2(PO4)3. To estimate the rate constant, the activation energy for the diffusion events were calculated using DFT, while the prefactor was estimated to 1013 s−1, which is typical used for diffusion/first order reactions.75Fig. 4B shows the Na-vacancy sublattice and the computed activation barriers with various Na composition and different transition metals. Their study revealed that Na+ transport is primarily governed by the local chemical environment, which is shaped by the arrangement of sodium ions and their vacancies, and the oxidation states of transition metals. Furthermore, they have also found that the ordering and disordering of Na vacancies also impacts the transport. Their study suggests that changing the local charge patterns through modifying the transition metals could potentially increase the capacity of these electrode materials.
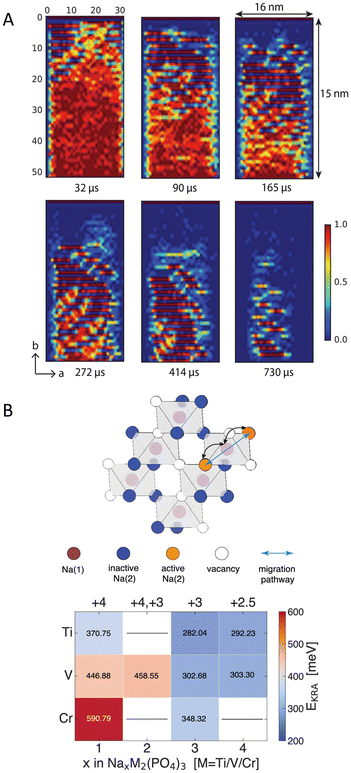 | ||
| Fig. 4 Panel A shows the arrangement of Li during the charging process of LiFePO4. The ordered pattern with alternating layers of Li-rich and Li-deficient atoms is shown along the b axis (Li concentration around 0.5 represents the intermediate phase). Reprinted (adapted) with permission from ref. 55 Copyright 2018 American Chemical Society. Panel B shows an illustration of the Na-vacancy sublattice in NaSICON, and the computed kinetically resolved activation barriers (EKRA) with varied Na compositions (x) and transition metals (M). Top x-axis is the oxidation state of the transition metals while the bottom x-axis is the Na composition. Reprinted (adapted) with permission from ref. 21 Copyright 2023 American Chemical Society. | ||
Overall, one can see that the use of KMC is beneficial for shedding light on the various reaction pathways and mechanisms governing a wide range of battery systems. However, KMC faces challenges that need to be addressed to enhance its robustness and broaden its applicability in providing accurate insights for experimental and theoretical battery research. In the following sections we will discuss the key challenges in KMC, including the consequences of its lattice nature to model the complex battery interfaces, accurate estimation of rate constants, time disparity, and lateral interactions.
4. The lattice nature of KMC and the complexity of battery modeling
Even though the lattice nature of KMC is its strongest feature in reducing the computational effort, it also entails many intrinsic limitations and challenges that need to be addressed when describing physical and chemical processes. For example, density and concentration profiles are usually over/under-estimated because KMC represents both small and large species as points on a lattice, without accounting for their actual physical volumes.59,65 This makes it hard to compare with the concentration profiles obtained from experiments. Vacant sites can increase/decrease concentrations during the simulation or as part of the initial system setup. For instance, consider a decomposition reaction like C → A + B. In a fixed-lattice KMC, this reaction is represented as C + vacant site → A + B. The need for a vacant site is essential for the reaction to take place (two sites for reactants and two sites for products; conservation of the number of sites). As a consequence, if the decomposition reaction is very fast but the number of vacant sites is very low, then, the rate limiting step would be the presence of the vacant site rather than the real probability of the event. Thus, the kinetics would become nonphysically slow, which would induce erroneous conclusions.59,65,76A challenge also arises when dealing with interfaces (e.g., solid/liquid) in fixed-lattice KMC simulations. In a solid atoms are closely packed, but when representing the liquid phase, the lattice will inherently include many vacant sites due to the lower packing density of the liquid compared to the solid. Such challenges becomes even more pronounced when dealing with polymerization reactions. For example, the formation of polymers in the SEI typically slows down the diffusion of species. However, if the simulation setup includes an excessive number of vacant sites, it can create numerous diffusion pathways that may not accurately reflect the physical behavior of the system. In such cases, the large number of vacant sites can lead to an overestimation of diffusion coefficients, distorting the actual impact of polymer formation on diffusion.65,76 As a result, the kinetics predicted by the KMC simulation may not align with experimental observations, leading to inaccurate conclusions about the effects of polymer formation on the kinetics and stability of battery systems.65,76
Overcoming the fixed lattice nature of KMC is quite challenging as it is tightly linked to the basics of lattice-based KMC. However, one can modify the algorithm to make a model as close as possible to the real physical system. One way to address these challenges is to modify the KMC scheme to allow large species to occupy multiple lattice sites, corresponding to their actual volumes. For example, a molecule C could occupy 3 sites, while molecules A and B occupy 1 and 2 sites respectively, reflecting their respective volumes. This approach resolves issues related to the presence of vacant sites in decomposition reactions. Implementing such modifications would lead to a more realistic description of density and concentration profiles, leading to more meaningful comparisons with experimental data. Moreover, such approaches to account for the “actual” size of species would greatly facilitate the (re-)construction of the 3D atomistic model corresponding to the simulated system. These 3D reconstructions are necessary to extract further physical/structural properties such as the radial distribution function and pore size distribution, as well as the evaluation of properties like ionic conductivity. To the best of our knowledge, only the KMOS77 software package allows species to occupy more than one site in 3D. However, we expect that other KMC packages will soon adopt his feature, as each KMC package has unique characteristics that makes it appealing for specific applications.18,19
Modeling the dynamic nature of solids represent another major challenge for KMC. For example, mechanical cracking of solids often occurs in various battery systems due to the stresses and strains associated with ion movement during charging and discharging. Specifically, in LIBs, the amount of Li0 at the negative electrode constantly changes. Li0 concentration increases during charging and decreases during discharging due to the insertion and extraction of Li+. As a result, the structure of the negative electrode and the SEI experiences volume changes, which can lead to the formation of cracks over time, altering the kinetics and accelerating degradation. It should be noted that incorporating the impact of cracking would help distinguishing calendar aging from the capacity loss during cycling (where cracking primarily occurs due to the movement of species between the electrodes). At the atomic level, cracking occurs when mechanical stress and strain exceed the material's tolerance, leading to local strain.78,79 This strain results from a size mismatch between the original lattice and the ions, which, when too large, triggers mechanical cracking. For instance, the cracking of the SEI layer exposes the “fresh” solid surface to the electrolyte. In KMC simulations, accurately modeling this process is complex, as it requires incorporating rules to detect excessive strain and define cracking events. This involves accounting for the stress and strain in the solid, adjusting the energetics of the lattice sites to reflect the mechanical failure, and capturing the material's response to cracking events.71,78,79
5. Lateral interactions
In the context of solid interfaces, lateral interactions refer to the interactions between adsorbed species over the solid surface. These interactions play a crucial role in determining the surface coverage, reaction kinetics and adsorption energy. Additionally, they are essential for understanding scenarios where solvent molecules (e.g., water in aqueous batteries) preferentially adsorb onto the surface over solutes, thereby distinguishing between inner-sphere and outer-sphere interactions.80 Previous studies have primarily explored the impact of lateral interactions in heterogeneous catalysis, with CO oxidation over Pd(111)81 being a prototypical example. However, in the context of batteries, these interactions have yet to be incorporated. Ignoring lateral interactions can lead to significant errors in simulation predictions, resulting in inaccurate adsorption patterns and misinterpretations of surface morphology.18,82 The inclusion of these interactions would significantly enhance our understanding of the various important processes at the electrode interface such as diffusion processes, passive layer formation, and dendrite growth mechanisms.70,71 For example, it has been shown that lateral interactions near metal surfaces lead to a low hydrogen-bond density, which restricts proton transport across the interface, playing a key role in the kinetic pH effect observed in electrocatalysis.83,84 In the context of battery systems, recent studies have highlighted the importance of lateral interactions for ion transport, surface adsorption, and reaction pathways and, thus, our understanding of electrochemical performance, stability, and interfacial kinetics.44,69,85 We here discuss two particularly relevant examples of lateral interaction in the context of batteries. First, we have investigated how varying initial Li content in a graphite model system affects lateral interactions among Li0 atoms.85 We found that as the number of intercalated Li0 atoms increases, the reaction energy per Li0 becomes slightly more exothermic (by 10–20 kJ mol−1) up to about five Li0 atoms, suggesting favorable lateral interactions at low coverage. This behavior is likely due to structural deformation being shared among neighboring intercalated Li0 atoms, which locally stabilize each other by collectively expanding the graphitic layers. However, beyond this point, additional Li0 atoms lead to less exothermic reaction energies. A notable drop (∼40 kJ mol−1) in average intercalation energy is observed when moving from half-lithiated to fully lithiated graphite (LiC12 to LiC6). This is attributed to the partial positive charge on Li0 atoms that enhances repulsive lateral interactions at higher coverages, limiting further stabilization. These results highlight that lateral interactions among intercalated lithium atoms offer valuable insights into the battery's state of charge (SOC). In particular, they help explain the slowdown in charging at high SOC: as more lithium is intercalated, repulsive interactions between neighboring Li atoms increase, reducing the availability of favorable insertion sites and thereby hindering further lithium insertion. Second, strong lateral interactions between SEI salts, such as Li2O and Li2CO3, were found to lead to the formation of patches and/or layered structures. This underscores the critical role of these interactions in passivating the electrode surface and enhancing the stability of the SEI. Furthermore, the relative stability of these inorganic species was found to depend significantly on the size of the nanoparticle they form, with stabilization energies reaching up to −350 kJ mol−1 compared to the isolated molecular units.Given the importance of lateral interactions, various methods have been developed to identify and incorporate them,86–89 with previous studies comparing these approaches.18,19 In this section, we will be focusing on two methods – cluster expansion-based (CE) and machine learning (ML)-based approaches – which have gained widespread attention for their effectiveness in capturing these complex interactions, see Fig. 5.
 | ||
| Fig. 5 How lateral interactions between adsorbates are typically considered: analytic relationships, machine learning (ML)-parameterized cluster expansions (CE), and advanced deep learning models, like graph convolutional neural networks. Reprinted (adapted) with permission from ref. 82 Copyright 2022 Elsevier. | ||
The nature of CE is to represent the electronic energy of the lattice as a sum of interacting clusters that encapsulate the energetics of adsorbate arrangements, including 1-body, 2-body, and n-body interactions,87–89 see eqn (7), where Nads is the number of adsorbed molecules in a geometry gi, and E(n)(gi) is the adsorption energy contribution of the n-body effects only. What makes CE advantageous over simplified models (e.g., analytical/linear models) is that CE considers the spatial arrangement of surface species on lattice sites when predicting the energetics of elementary steps.
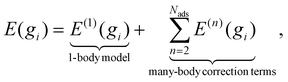 | (7) |
It should be noted that a major challenge for CE-based models is the need to train the Hamiltonian using extensive datasets, which can be difficult and time-consuming to develop. These datasets must be sufficiently diverse to capture both common and rare surface coverage patterns. At the same time the computational cost of optimizing each geometry with DFT necessitates a training set that should not be very big in size, focusing solely on chemically relevant geometries crucial for accuracy. However, the processes of selecting these geometries often relies on personal intuition or random sampling, making it arbitrary and time consuming.
ML techniques can help address these challenges by enhancing model accuracy and managing complex datasets. Approaches like cross-validation, regularization, and pattern recognition, when integrated with CE, have proven effective in predicting adsorption energies and refining model performance.82 ML-based methods like deep learning techniques in the framework of graph convolutional neural networks, have been used to predict adsorption energies via analyzing large datasets of surface configurations.82 However, and similar to all other ML-based methods, they also suffer from the limited availability of accurate training data, the substantial computational cost required to generate it, and the lack of a physical basis in these models, which limits their interpretability.82
The complexity of batteries arises from the intricate electrode/electrolyte interface, where the SEI forms. In this context, lateral interactions are highly complex, involving multiple layers, including the electrode, inorganic species, organic species (e.g., polymers), and the electrolyte. This complexity significantly increases the computational cost, surpassing that of heterogeneous catalysis, which, while simpler, still encounters challenges in accounting for lateral interactions.18,19 Building a training set using DFT becomes particularly challenging for large systems due to the computational cost, making the process increasingly difficult to manage. A promising alternative is to employ more affordable methods, such as semiempirical approaches. Semiempirical methods have a quantum mechanical foundation that explicitly accounts for valence electrons, enabling the modeling of chemical reactions and complex processes such as charge transfer. Still, even in this case many-body effects involved in lateral interactions might be difficult to capture accurately.90 By leveraging these methods, large training datasets can be efficiently generated through molecular dynamics simulations combined with enhanced sampling techniques. This approach provides a cost-effective way to construct training sets for the system of interest. Once these large datasets are available, various ML techniques can be utilized to analyze and model lateral interactions. For instance, the datasets can guide the exploration of the system's configuration space, train graph neural networks to capture complex lateral interactions, or develop machine learning potentials for extended molecular dynamics simulations as they are even faster than semiempirical methods.
6. Estimating the rate constant from transition state theory
The rate constants (k) of the various chemical reactions can be obtained from transition state theory (TST) according to Eyring's equation: | (8) |
In surface reactions (like those in batteries), molecules are adsorbed onto a solid and are constrained to at most two-dimensional movements, which in KMC corresponds to the surface area of the solid. This gives rise to an entropy term known as configurational entropy, Sconfads. This configurational entropy accounts for the multiple possible configurations that the adsorbed molecules can adopt on the surface, see eqn (9).
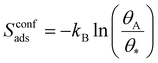 | (9) |
The accuracy of the rate constants used in KMC simulations heavily relies on the theoretical level applied to estimate the contributions of ΔS‡ and ΔH‡, as outlined in eqn (8). Selecting an appropriate energy expression involves a trade-off between accuracy and computational cost. In order to model bond formation or breaking during chemical reactions, quantum mechanical methods (primarily DFT) are commonly employed to calculate activation energies. While DFT is the standard method used in the battery community for reactions, its accuracy can vary significantly: differences of up to 90 kJ mol−1 for the same reaction have been reported when changing the level of theory.56 It is tempting to advocate the use of reliable wave function-based methods such as DLPNO-CCSD(T) instead of DFT. While this is a suitable option for gas-phase reactions,94,95 the associated computational cost is prohibitive in the condensed phase for routine applications.96 In other words it is important to choose the most reliable, accessible level of theory for each reaction in question and not to be overconfident in the activation energies that come directly out of DFT. Still, first-principles should provide reasonable activation energies that lead to useful qualitative results. The situation is worse for large systems where DFT is computationally (too) expensive. In such instances, alternative methods like reactive force fields, machine learning potentials (MLPs), and semiempirical methods can be used as faster alternatives.9,85 For example, in a recent study, a pretrained MLP, SevenNet,97 was applied to simulate liquid electrolytes in LIBs. Although originally trained on inorganic compounds, SevenNet demonstrated strong predictive performance for properties such as solvation structures and diffusivities. However, it showed limitations in predicting liquid densities due to undersampled and ill-described long-range intermolecular interactions. Similar approaches have also been explored in the context of semiempirical methods: a particular study98 examined how the thickness of the passive SEI layer affects tunneling barriers during electrolyte decomposition to estimate rate constants for incorporation into KMC simulations. These findings offer valuable insight into interfacial stability and decomposition kinetics. In the case of reactive force fields,99 studies of the cathode–electrolyte interface revealed that the presence of specific cations can suppress manganese dissolution into the bulk electrolyte. This suppression enhances battery performance, particularly by improving long-term stability. Such studies underscore a broader interest in developing fast computational methods for modeling complex electrochemical environments.85,97–99 However, these methods require careful parameterization with sufficient training data (usually from DFT) to ensure their accuracy. The difficulty in obtaining accurate rate constants means that using KMC to model the timescale of a process is often a qualitative approach.65 While other properties, such as structural properties, can still be valid, they rely on the assumption that the rate constants obtained from DFT are qualitative and that the relative energies are valid.
Obtaining accurate rate constants for battery interfaces can be conceptually categorized into two primary scenarios. The first involves electrolyte species in direct contact with the electrode surface, or scenarios where dendrite formation occurs during battery operation. In these cases, reaction kinetics are strongly influenced by solid–electrolyte interaction environment including the applied voltage, reminiscent of electrocatalytic interfaces. As the battery continues to operate, passive interfaces such as the SEI begin to form, and the reaction environment gradually shifts away from the charged electrode surface, as a new interface is formed: electrode/SEI/electrolyte, the second scenario. Furthermore, in most commercial batteries, a pre-formed SEI is typically present as a passive layer from the outset.100,101 The SEI/electrolyte interface resembles a heterogeneous catalytic interface, where reactions occur across complex, spatially extended, and chemically diverse surfaces. However, what distinguishes battery systems from conventional heterogeneous catalysis is the presence of a wide variety of ionic species, often at high concentrations. For example, in aqueous batteries employing water-in-salt electrolytes, the interfacial structure and reactivity are dramatically influenced by the nature and concentration of the electrolyte components.102 In that case, the rate constant will be highly dependent on the local environment. Moreover, in contrast to catalysis, reversible and irreversible reactions are of prime interest: the former are characteristic for the proper functioning of the battery, while the latter describe degradation.
It should be noted that KMC's reliance on predefined reaction pathways and rate constants is very challenging in battery systems with strongly coupled reactions that are difficult to resolve. One alternative strategy is to identify the rate-determining steps and estimate their rate constants using low-cost computational techniques, such as semiempirical methods, MLPs, or reactive force fields, combined with enhanced sampling methods like umbrella sampling or metadynamics. These estimates can then be incorporated into the KMC framework. However, this approach depends heavily on chemical intuition to correctly identify the rate-limiting steps – a task that is often nontrivial and system-dependent. To overcome these limitations, advanced methods such as the ones implemented in the EON software,103 which enables long-timescale atomic-scale simulations, and Red Moon (RM) approach104 have been developed. EON integrates automated saddle-point searches with adaptive KMC to discover and simulate rare events on-the-fly, efficiently exploring complex reaction networks without prior knowledge of the mechanisms involved. Meanwhile, The RM approach is a hybrid simulation method that employs molecular dynamics to capture short-time-scale molecular motions and uses Monte Carlo to sample rare events (chemical reactions) according to a transition-rate criterion. RM efficiently simulates complex reaction systems – particularly molecular aggregates – where direct sampling of reaction events by MD alone would be prohibitively slow. Given this strength, RM has been successfully applied to battery systems like LIBs and Na-ion batteries, revealing key insights such as the differences in SEI formation between solvents like ethylene carbonate and propylene carbonate. Another approach involves applying KMC by treating certain complex or poorly characterized processes in a coarse-grained or effective manner – i.e., lumping diffusive or reactive events. This enables KMC to extend beyond purely atomistic modeling and function as a mesoscale framework that captures system-level behavior. For instance, SEI formation can be modeled as a layered growth process guided by experimental trends rather than relying on a full molecular lattice representation where detailed mechanistic data are unavailable. This strategy retains the stochastic and kinetic rigor of KMC while broadening its applicability to study the effects of operating conditions (such as temperature) and material design in a computationally efficient and experimentally grounded way.
7. Disparity of timescales in KMC: the slow process of battery aging
One of the major challenges for KMC is handling slow and fast processes at the same time.18,105–107 To elaborate, let us consider a hypothetical system where there are fast diffusive events (e.g., in the range of nanosecond) and some slow reactive events (e.g., in the range of seconds). In such cases the KMC simulation becomes stiff, i.e., the simulation will spend an excessive amount of time sampling the fast diffusive events, while it struggles to accurately capture the much slower, but critical, reactive processes.Traditionally, to overcome the problem of timescale disparity in KMC, researchers used manual scaling of the fastest process (highest rate constant), while monitoring the effect on the accuracy of the model.105 More sophisticated and automated methods and algorithms have been developed over the years.19,106,108–113 For example a method called accelerated superbasin KMC (AS-KMC)108 can automatically handle the scaling without user input. Such methods are based on the assumption that fast processes become quasi-equlibrated with time, limiting the need for further simulation of these processes. Hence, the algorithms force the system to exit the current superbasin through scaling the rate of these fast quasi-equilibrated processes. The process illustrated in Fig. 6 depicts a hypothetical scenario where a superbasin is defined as a collection of lattice configurations between which the system transitions via quasi-equilibrated processes only (meaning the jumps are easy and happen frequently). A typical battery-relevant example would be the electrolyte diffusion. The occurrence of a non-equilibrated process signals the system's transition into a new superbasin, which requires overcoming a higher energy barrier. In LIBs this could, for instance, be the solvent degradation. On one hand, this approach is simple and effective. On the other hand, it faces difficulties for complex system with many configurations, as fully sampling even a single superbasin can be time-consuming. Algorithms have undergone various improvements over time and led to the development of ever more advanced methods to handle the time disparity challenge.19 To illustrate how such algorithms work, we consider an example of a more recent method of rate constant rescaling (RCR) developed by Núñez et al.106 In their study, they compared the speedup factor for theRCR algorithm, against other alternative approaches, including parallel processing and the likelihood ratio sensitivity analysis (LRSA) method, across three different systems, one of which was the water–gas shift reaction. Parallel processing refers to the case when running multiple trajectories at the same time, which maximizes the sampling efficiency within a given simulation period. LRSA is a statistical method used to estimate the sensitivity of rates. It employs parallel processing, and post-processing trajectory derivatives (how sensitive the system's behavior is to parameter changes) with covariance statistics that increase the efficiency by reducing the need for repeated simulations. As shown in Fig. 7A, the RCR algorithm outperforms the others, achieving a speedup factor approaching 104.
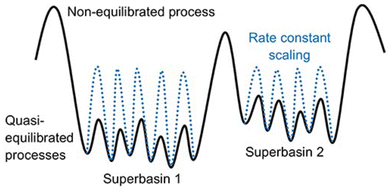 | ||
| Fig. 6 An illustration of the potential energy surface (PES) for a system with processes occurring over large differences in timescales, due to varying barriers. The KMC simulation is accelerated using a constant rate rescaling method, where, prior to rescaling, the system spends most of its time sampling the smaller barriers. After applying the rescaling method (represented by the blue dotted line), the barriers become closer, allowing for faster transitions between states and enhancing the sampling of neighboring regions on the PES. Reprinted (adapted) with permission from ref. 19 Copyright 2019 Frontiers. | ||
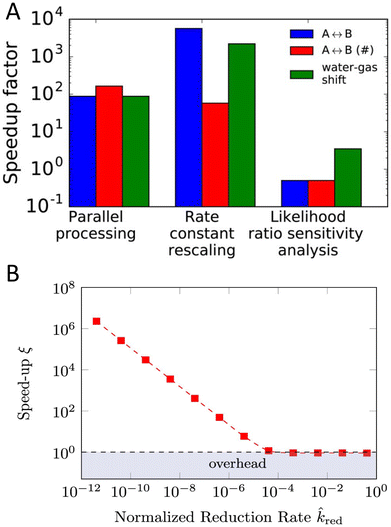 | ||
| Fig. 7 Panel A shows a comparison of the speedup factor for the RCR algorithm, parallel processing, and the likelihood ratio sensitivity analysis method is made across three systems. The first model (A ↔ B) involves the adsorption of reactant A onto a catalyst, its isomerization to B, and subsequent desorption. The symbol # represents the same model with different parameters, while the third model is the water–gas shift reaction (CO + H2O ↔ CO2 + H2). Reprinted (adapted) with permission from ref. 106 Copyright 2017 American Institute of Physics. Panel B represents the speed up factor ξ for modeling the fast electronic processes and the slow reduction reactions at the interface in hybrid organic–aqueous electrolyte. ξ represents the ratio between per reduction event of the reference simulations and of the accelerated simulations. Reprinted (adapted) with permission from ref. 110 Copyright 2022 American Chemical Society. | ||
The main principle in RCR is that the equilibrated elementary step is reduced by a factor of αi ≥ 1 during each step of the algorithm. It should be noted that both of ki (forward rate constant) and 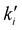 (backward rate constant) need to be divided by the same rescaling factor αi to maintain the thermodynamics (equilibrium constant
(backward rate constant) need to be divided by the same rescaling factor αi to maintain the thermodynamics (equilibrium constant  ), so the rescaling process alters only the transition states, not the overall thermochemistry. The algorithm starts by identifying whether an elementary step is in equilibrium using partial equilibrium criteria, and identifies the fastest irreversible step. Then, it imposes an upper bound on how much the rate constant of any elementary step can be rescaled without affecting the slow dynamics. While effective, it should be noted that the value of this upper bound in theRCR algorithm is system specific which requires intensive and careful testing. This task becomes particularly challenging when dealing with reactions at interfaces, where different media – such as solids, gases, or liquids – introduce varying diffusion scales, densities, and lattice packing arrangements. To overcome the specific case of disparity between diffusion and reactive events, various methods have been developed.110–113 For example, a recent algorithm developed by Gößwein et al.110 combined the superbasin concept with a local, particle-based criterion for identifying quasi-equilibrium processes. They give an example of the disparity between reactive and diffusive events in hybrid organic–aqueous electrolyte where the acceleration of KMC was several orders of magnitude, see Fig. 7B. Kaiser et al.114 have developed an accelerated scheme that samples the diffusion events through identifying the critical superbasins at the beginning of the simulation. Their algorithm was found to be faster than the AS-KMC algorithm for a 1D-chain example. They have also investigated the time-of-flight of charge carriers in organic semiconductors. The scheme was found to achieve up to 65 times faster results while keeping the errors minimal.114
), so the rescaling process alters only the transition states, not the overall thermochemistry. The algorithm starts by identifying whether an elementary step is in equilibrium using partial equilibrium criteria, and identifies the fastest irreversible step. Then, it imposes an upper bound on how much the rate constant of any elementary step can be rescaled without affecting the slow dynamics. While effective, it should be noted that the value of this upper bound in theRCR algorithm is system specific which requires intensive and careful testing. This task becomes particularly challenging when dealing with reactions at interfaces, where different media – such as solids, gases, or liquids – introduce varying diffusion scales, densities, and lattice packing arrangements. To overcome the specific case of disparity between diffusion and reactive events, various methods have been developed.110–113 For example, a recent algorithm developed by Gößwein et al.110 combined the superbasin concept with a local, particle-based criterion for identifying quasi-equilibrium processes. They give an example of the disparity between reactive and diffusive events in hybrid organic–aqueous electrolyte where the acceleration of KMC was several orders of magnitude, see Fig. 7B. Kaiser et al.114 have developed an accelerated scheme that samples the diffusion events through identifying the critical superbasins at the beginning of the simulation. Their algorithm was found to be faster than the AS-KMC algorithm for a 1D-chain example. They have also investigated the time-of-flight of charge carriers in organic semiconductors. The scheme was found to achieve up to 65 times faster results while keeping the errors minimal.114
Even though significant progress has been achieved to overcome the challenge of time scale disparity, each algorithm comes with its own strengths and weaknesses. Indeed, these algorithms are often built for specific processes (e.g., linear radical polymerization111) and cannot easily be transposed to different processes. In other words, a transferable approach for dealing with the presence of fast and slow elementary steps in KMC is still to be developed.
8. Conclusion and outlooks
The use of KMC in battery research represents a highly promising approach to understanding the underlying mechanisms of battery aging and failures and thereby to accelerate the optimization and design of future systems. KMC has been instrumental in providing various insights into the SEI of LIBs, such as the porosity, diffusion coefficients and growth mechanims. These parameters are crucial for BMS found in electronic devices, contributing to improved safety and extended lifespan of existing batteries. Furthermore, KMC aids in understanding patterns of capacity loss, whether nonlinear (e.g., diffusion-limited) or linear (e.g., constrained by slow reactions). Such insights are essential for identifying areas of improvement.Despite the achieved insights and successes of KMC, models and algorithms need further improvements to account for the heterogeneity and complexity of interfaces in batteries. One key step is moving beyond single lattice points to account for the spatial heterogeneity of battery systems, particularly at the electrode interfaces. Additionally, given the wide range of timescales associated with reactions relevant in batteries, addressing the timescale disparity in KMC requires the development of transferable algorithms that can effectively differentiate between fast and slow events and sample them accordingly without extensive testing and user-intervention.
To further enhance KMC performance, the accurate determination of rate constants and the inclusion of lateral interactions are essential. These improvements will enable more realistic simulations through the inclusion of the reaction environment. In this regard, we anticipate an increased reliance on cheaper alternatives to DFT, such as semiempirical methods, reactive force fields, and MLPs.9,85 Overall, it is important to note that while reactive force fields and MLPs typically deliver faster performance than semiempirical methods, the latter, owing to their quantum mechanical nature, performs better in extrapolating to regions outside the training data or when no prior information about the reaction pathways is available. To improve the estimates of kinetic prefactors from activation entropies, the atomic scale simulation methods should be coupled with enhanced sampling techniques such as thermodynamic integration, umbrella sampling, or metadynamics. These combinations hold great promise for improving the sampling of rare events in molecular dynamics simulations while maintaining computational efficiency. Moreover, ML-based methods (when coupled to methods like cluster expansion) can complement these efforts by improving lateral interaction predictions at manageable computational cost through advanced approaches like deep graph neural networks.
Looking forward, KMC could be implemented in real-time to optimize the BMS in devices like electric vehicles, laptops, and cell phones by integrating real-time data such as charging/discharging rates, state of charge and temperature. For example, KMC could simulate ion migration through the SEI and solid electrolytes under operating conditions, detecting uneven ion distribution and identifying areas of lithium accumulation. These accumulations could lead to dendrite formation or interfacial instabilities, increasing internal resistance and/or the risk of short circuits. By modeling the impact of these factors on SEI stability, KMC would enable the BMS to dynamically adjust charging strategies, such as modulating the rate or halting charging to prevent overheating, thereby minimizing SEI degradation and enhancing battery longevity. Achieving this vision will require advancements in KMC algorithm physics and processing speed to support effective real-time applications.
Author contributions
MBJ: data curation, conceptualization, writing – original draft; TDB: writing – review & editing, CND: conceptualization, writing – review & editing, SNS: conceptualization, supervision, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Data availability
No primary research results, software or code have been included and no new data were generated or analysed as part of this review.References
- R. Melissa, Global Battery Market Insights, 2024, https://statzon.com/insights/global-battery-market Search PubMed.
- A. Y. S. Eng, C. B. Soni, Y. Lum, E. Khoo, Z. Yao, S. Vineeth, V. Kumar, J. Lu, C. S. Johnson and C. Wolverton, et al. , Sci. Adv., 2022, 8, eabm2422 CrossRef CAS PubMed.
- R. Li, N. D. Kirkaldy, F. F. Oehler, M. Marinescu, G. J. Offer and S. E. O'Kane, Nat. Commun., 2025, 16, 2776 CrossRef CAS PubMed.
- B. Aktekin, L. M. Riegger, S.-K. Otto, T. Fuchs, A. Henss and J. Janek, Nat. Commun., 2023, 14, 6946 CrossRef CAS PubMed.
- G. Qian, Y. Li, H. Chen, L. Xie, T. Liu, N. Yang, Y. Song, C. Lin, J. Cheng and N. Nakashima, et al. , Nat. Commun., 2023, 14, 6048 CrossRef CAS PubMed.
- M. Armand and J.-M. Tarascon, Nature, 2008, 451, 652–657 CrossRef CAS PubMed.
- A. Krupp, R. Beckmann, T. Diekmann, E. Ferg, F. Schuldt and C. Agert, J. Energy Storage, 2022, 45, 103506 CrossRef.
- M. Naumann, M. Schimpe, P. Keil, H. C. Hesse and A. Jossen, J. Energy Storage, 2018, 17, 153–169 CrossRef.
- M. Bin Jassar, C. Michel, S. Abada, T. De Bruin, S. Tant, C. Nieto-Draghi and S. N. Steinmann, Adv. Funct. Mater., 2024, 2313188 CrossRef CAS.
- A. A. Franco, A. Rucci, D. Brandell, C. Frayret, M. Gaberscek, P. Jankowski and P. Johansson, Chem. Rev., 2019, 119, 4569–4627 CrossRef CAS PubMed.
- Y. Wang, J. Tian, Z. Sun, L. Wang, R. Xu, M. Li and Z. Chen, Renewable Sustainable Energy Rev., 2020, 131, 110015 CrossRef.
- C. Edouard, M. Petit, C. Forgez, J. Bernard and R. Revel, J. Power Sources, 2016, 325, 482–494 CrossRef CAS.
- S. Kattel, J. G. Chen and P. Liu, Catal. Sci. Technol., 2018, 8, 3748–3758 RSC.
- Z. Lian, S. Ali, T. Liu, C. Si, B. Li and D. S. Su, ACS Catal., 2018, 8, 4694–4704 CrossRef CAS.
- H. Prats, L. Álvarez, F. Illas and R. Sayós, J. Catal., 2016, 333, 217–226 CrossRef CAS.
- A. Chutia, A. Thetford, M. Stamatakis and C. R. A. Catlow, Phys. Chem. Chem. Phys., 2020, 22, 3620–3632 RSC.
- D. Borodin, I. Rahinov, O. Galparsoro, J. Fingerhut, M. Schwarzer, K. Golibrzuch, G. Skoulatakis, D. J. Auerbach, A. Kandratsenka and D. Schwarzer, et al. , J. Am. Chem. Soc., 2021, 143, 18305–18316 CrossRef CAS PubMed.
- M. Pineda and M. Stamatakis, J. Chem. Phys., 2022, 156, 120902 CrossRef CAS PubMed.
- M. Andersen, C. Panosetti and K. Reuter, Front. Chem., 2019, 7, 202 CrossRef CAS PubMed.
- J. Wagner-Henke, D. Kuai, M. Gerasimov, F. Röder, P. B. Balbuena and U. Krewer, Nat. Commun., 2023, 14, 6823 CrossRef CAS PubMed.
- Z. Wang, T. P. Mishra, W. Xie, Z. Deng, G. S. Gautam, A. K. Cheetham and P. Canepa, ACS Mater. Lett., 2023, 5, 2499–2507 CrossRef CAS.
- J. Yu, E. Baudrin and A. A. Franco, Batteries Supercaps, 2025, 8, e202400430 CrossRef CAS.
- J. Li, X. Hu and T. Li, Energy Mater. Adv., 2024, 5, 0137 CrossRef CAS.
- W. Cistjakov, J. Hoppe, J. Jung, F. Röder, H.-T. Kim and U. Krewer, Adv. Mater. Interfaces, 2025, 12, 2400632 CrossRef CAS.
- M. Tian, Z. Wang, H. Y. Yang and S. Chen, Adv. Energy Mater., 2025, 15, 2403443 CrossRef CAS.
- L. Katzenmeier, M. Gößwein, A. Gagliardi and A. S. Bandarenka, J. Phys. Chem. C, 2022, 126, 10900–10909 CrossRef CAS.
- K. Zelič, M. Esmaeilpour, S. Jana, I. Mele, W. Wenzel and T. Katrašnik, J. Power Sources, 2025, 627, 235814 CrossRef.
- S. S. Behara and A. Van der Ven, Chem. Mater., 2024, 36, 11236–11245 CrossRef CAS PubMed.
- M. Feng, X. Liu, S. J. Harris, B. W. Sheldon and Y. Qi, J. Mech. Phys. Solids, 2024, 193, 105878 CrossRef CAS.
- S. K. Saha, P. Mondal, D. Mondal, N. Vasudeva, A. Anshu, A. Narayan, G. Reddy and A. Pandey, J. Phys. Chem. Lett., 2024, 15, 9474–9480 CrossRef CAS PubMed.
- S. V. Pershina, Y. A. Morkhova, A. A. Kabanov, K. S. Okhotnikov, E. A. Filippov, V. A. Elterman, T. A. Kuznetsova, V. I. Voronin and G. N. Starostin, J. Phys. Chem. C, 2024, 128, 14871–14879 CrossRef CAS.
- J. Kullgren, J. H. Chang, S. Loftager, S. Dhillon, T. Vegge and D. Brandell, Energy Adv., 2024, 3, 2271–2279 RSC.
- Y. A. Morkhova, A. V. Antonyuk, A. A. Kabanov and V. A. Blatov, ChemPhysChem, 2024, 25, e202400067 CrossRef CAS PubMed.
- F. Fernandez, E. M. Gavilán-Arriazu and M. Otero, J. Solid State Chem., 2024, 1–23 CAS.
- Y. A. Morkhova, A. V. Antonyuk and I. A. Naugolnova, J. Solid State Chem., 2024, 28, 3665–3671 CAS.
- A. I. Romo, L. Bello, S. Pudar, N. Ibrahim, Y. Wang, M. J. Baran, Q. Wu, R. H. Ewoldt, B. A. Helms and C. Sing, et al. , J. Am. Chem. Soc., 2024, 146, 17474–17486 CrossRef CAS PubMed.
- J. Hwang and D. Kim, Energy Storage Mater., 2024, 69, 103412 CrossRef.
- M. Nagaoka, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2024, 14, e1714 CAS.
- M. Soleymanibrojeni, C. R. C. Rego, M. Esmaeilpour and W. Wenzel, J. Mater. Chem. A, 2024, 12, 2249–2266 RSC.
- F. Flatscher, J. Todt, M. Burghammer, H.-S. Søreide, L. Porz, Y. Li, S. Wenner, V. Bobal, S. Ganschow and B. Sartory, et al. , Small, 2024, 20, 2307515 CrossRef CAS PubMed.
- Z. Jadidi, T. Chen, L. Barroso-Luque and G. Ceder, Chem. Mater., 2023, 35, 9225–9234 CrossRef CAS.
- D. Rajagopal, A. Koeppe, M. Esmaeilpour, M. Selzer, W. Wenzel, H. Stein and B. Nestler, Adv. Energy Mater., 2023, 13, 2301985 CrossRef CAS.
- X. Jiao, Y. Wang, O. O. Kapitanova, X. Xu, V. S. Volkov, Y. Liu, Z. Song, A. Matic and S. Xiong, Energy Storage Mater., 2023, 61, 102916 CrossRef.
- P. Hai, C. Wu, X. Ding and Y. Li, Phys. Chem. Chem. Phys., 2023, 25, 21045–21053 RSC.
- L. Katzenmeier, M. Gößwein, L. Carstensen, J. Sterzinger, M. Ederer, P. Müller-Buschbaum, A. Gagliardi and A. S. Bandarenka, Commun. Chem., 2023, 6, 124 CrossRef CAS PubMed.
- T. Hwang, P. Conlin, M. Cho and K. Cho, J. Phys. Chem. C, 2023, 127, 7528–7535 CrossRef CAS.
- K. Pardikar, J. Entwistle, R. Ge, D. Cumming and R. Smith, JPhys Energy, 2023, 5, 022002 CrossRef CAS.
- J. Schuett, A. S. Kuhn and S. Neitzel-Grieshammer, J. Mater. Chem. A, 2023, 11, 9160–9177 RSC.
- T. Chen, Y. Ye, Y. Wang, C. Fang, W. Lin, Y. Jiang, B. Xu, C. Ouyang and J. Zheng, Phys. Chem. Chem. Phys., 2023, 25, 8734–8742 RSC.
- M. Esmaeilpour, S. Jana, H. Li, M. Soleymanibrojeni and W. Wenzel, Adv. Energy Mater., 2023, 13, 2370055 CrossRef.
- S. Anniés, C. Scheurer and C. Panosetti, Electrochim. Acta, 2023, 444, 141966 CrossRef.
- S. Perez-Beltran, D. Kuai and P. B. Balbuena, ACS Energy Lett., 2024, 9, 5268–5278 CrossRef CAS PubMed.
- E. M. Gavilán-Arriazu, M. Mercer, D. Barraco, H. E. Hoster and E. P. M. Leiva, Prog. Energy, 2021, 3, 042001 CrossRef.
- E. M. Gavilán-Arriazu, O. A. Pinto, B. L. De Mishima, D. Barraco, O. A. Oviedo and E. P. M. Leiva, Electrochim. Acta, 2020, 331, 135439 CrossRef.
- P. Xiao and G. Henkelman, ACS Nano, 2018, 12, 844–851 CrossRef CAS PubMed.
- E. W. C. Spotte-Smith, R. L. Kam, D. Barter, X. Xie, T. Hou, S. Dwaraknath, S. M. Blau and K. A. Persson, ACS Energy Lett., 2022, 7, 1446–1453 CrossRef CAS.
- K. A. Fichthorn and W. H. Weinberg, J. Chem. Phys., 1991, 95, 1090–1096 CrossRef CAS.
- S. Ravipati, M. d'Avezac, J. Nielsen, J. Hetherington and M. Stamatakis, Phys. Chem. A, 2020, 124, 7140–7154 CrossRef CAS PubMed.
- Y. Yin, R. Zhao, Y. Deng and A. A. Franco, Phys. Chem. Lett., 2017, 8, 599–604 CrossRef CAS PubMed.
- G. Blanquer, Y. Yin, M. A. Quiroga and A. A. Franco, J. Electrochem. Soc., 2015, 163, A329 CrossRef.
- F. Hao, Z. Liu, P. B. Balbuena and P. P. Mukherjee, Phys. Chem. C, 2017, 121, 26233–26240 CrossRef CAS.
- V. Thangavel, O. X. Guerrero, M. Quiroga, A. M. Mikala, A. Rucci and A. A. Franco, Energy Storage Mater., 2020, 24, 472–485 CrossRef.
- J. Yu, G. Shukla, R. P. Fornari, O. Arcelus, A. Shodiev, P. De Silva and A. A. Franco, Small, 2022, 18, 2107720 CrossRef CAS PubMed.
- M. Ecker, J. B. Gerschler, J. Vogel, S. Käbitz, F. Hust, P. Dechent and D. U. Sauer, J. Power Sources, 2012, 215, 248–257 CrossRef CAS.
- M. Bin Jassar, C. Michel, S. Abada, T. De Bruin, S. Tant, C. Nieto-Draghi and S. N. Steinmann, ACS Appl. Energy Mater., 2023, 6, 6934–6945 CrossRef CAS.
- K. Hankins, M. H. Putra, J. Wagner-Henke, A. Groß and U. Krewer, Adv. Energy Mater., 2024, 2401153 CrossRef.
- M. Gerasimov, F. A. Soto, J. Wagner, F. Baakes, N. Guo, F. Ospina-Acevedo, F. Röder, P. B. Balbuena and U. Krewer, J. Phys. Chem. C, 2023, 127, 4872–4886 CrossRef.
- Q. Ma, C. Mao, H. Shi, Z. Chen, H. Zhang, H. Su and Q. Xu, J. Electrochem. Soc., 2023, 170, 112501 CrossRef CAS.
- J. W. Abbott and F. Hanke, J. Chem. Theory Comput., 2022, 18, 925–934 CrossRef CAS PubMed.
- H. Lee, N. Sitapure, S. Hwang and J. S.-I. Kwon, Comput. Chem. Eng., 2021, 153, 107415 CrossRef CAS.
- S. Menzel, P. Kaupmann and R. Waser, Nanoscale, 2015, 7, 12673–12681 RSC.
- D. Tewari, Z. Liu, P. B. Balbuena and P. P. Mukherjee, J. Phys. Chem. C, 2018, 122, 21097–21107 CrossRef CAS.
- J. Yu, E. Baudrin and A. A. Franco, Batteries Supercaps, 2025, 8, e202400430 CrossRef CAS.
- A. Jaberi, M. L. Trudeau, J. Song and R. Gauvin, ACS Appl. Energy Mater., 2024, 7, 7724–7736 CrossRef CAS.
- A. Ramasubramanian, V. Yurkiv, T. Foroozan, M. Ragone, R. Shahbazian-Yassar and F. Mashayek, Phys. Chem. C, 2019, 123, 10237–10245 CrossRef CAS.
- M. Ciantar, C. Mellot-Draznieks and C. Nieto-Draghi, Phys. Chem. C, 2015, 119, 28871–28884 CrossRef CAS.
- M. J. Hoffmann, S. Matera and K. Reuter, Comput. Phys. Commun., 2014, 185, 2138–2150 CrossRef CAS.
- S. Esmizadeh and H. Haftbaradaran, Mech. Mater., 2022, 172, 104366 CrossRef.
- S. R. Yeratapally, C. Lang and E. H. Glaessgen, AIAA Scitech 2020 Forum, 2020, p. 1386 Search PubMed.
- M. Bin Jassar, Q. Yao, F. Siro Brigiano, W. Chen and S. Pezzotti, Phys. Chem. Lett., 2024, 15, 11961–11968 CrossRef CAS PubMed.
- S. Piccinin and M. Stamatakis, Top. Catal., 2017, 60, 141–151 CrossRef CAS.
- T. Mou, X. Han, H. Zhu and H. Xin, Curr. Opin. Chem. Eng., 2022, 36, 100825 CrossRef.
- P. Li, Y. Jiang, Y. Hu, Y. Men, Y. Liu, W. Cai and S. Chen, Nat. Catal., 2022, 5, 900–911 CrossRef CAS.
- X.-L. Zhang, P.-C. Yu, S.-P. Sun, L. Shi, P.-P. Yang, Z.-Z. Wu, L.-P. Chi, Y.-R. Zheng and M.-R. Gao, Nat. Commun., 2024, 15, 9462 CrossRef CAS PubMed.
- M. Bin Jassar, C. Michel, S. Abada, T. De Bruin, S. Tant, C. Nieto-Draghi and S. N. Steinmann, J. Phys. Chem. C, 2024, 128, 3269–3280 CrossRef CAS.
- J. E. Sutton, J. M. Lorenzi, J. T. Krogel, Q. Xiong, S. Pannala, S. Matera and A. Savara, ACS Catal., 2018, 8, 5002–5016 CrossRef CAS.
- K. G. Papanikolaou and M. Stamatakis, Front. Nanotechnol, Elsevier, 2020, vol. 17, pp. 95–125 Search PubMed.
- L. M. Herder, J. M. Bray and W. F. Schneider, Surf. Sci., 2015, 640, 104–111 CrossRef CAS.
- L. Cao, C. Li and T. Mueller, J. Chem. Inf. Model., 2018, 58, 2401–2413 CrossRef CAS PubMed.
- Q. Wang, M. Gu, C. Michel, N. Goldman, T. Niehaus and S. N. Steinmann, J. Chem. Theory Comput., 2025, 21, 5267–5278 CrossRef CAS PubMed.
- J. Nørskov, F. Studt, F. Abild-Pedersen and T. Bligaard, in Surface Equilibria, John Wiley & Sons, Ltd, 2014, ch. 3, pp. 26–46 Search PubMed.
- C. T. Campbell, L. H. Sprowl and L. Árnadóttir, J. Phys. Chem. C, 2016, 120, 10283–10297 CrossRef CAS.
- A. Savara, J. Phys. Chem. C, 2016, 120, 20478–20480 CrossRef CAS.
- A. Altun, F. Neese and G. Bistoni, J. Chem. Theory Comput., 2020, 16, 6142–6149 CrossRef CAS PubMed.
- H.-J. Werner and A. Hansen, J. Chem. Theory Comput., 2023, 19, 7007–7030 CrossRef CAS PubMed.
- B. X. Shi, A. Zen, V. Kapil, P. R. Nagy, A. Grüneis and A. Michaelides, J. Am. Chem. Soc., 2023, 145, 25372–25381 CrossRef CAS PubMed.
- S. Ju, J. You, G. Kim, Y. Park, H. An and S. Han, Digital Discovery, 2025, 4, 1544–1559 RSC.
- Y. Li and Y. Qi, J. Phys. Chem. C, 2018, 122, 10755–10764 CrossRef CAS.
- M. K. Talkhoncheh, H. Ghods, M. Doosthosseini, J. Silberberg, I. Kyprianou and A. C. van Duin, J. Phys. Chem. C, 2024, 128, 6538–6550 CrossRef CAS.
- P. Niehoff, S. Passerini and M. Winter, Langmuir, 2013, 29, 5806–5816 CrossRef CAS PubMed.
- B. Han, Z. Zhang, Y. Zou, K. Xu, G. Xu, H. Wang, H. Meng, Y. Deng, J. Li and M. Gu, Adv. Mater., 2021, 33, 2100404 CrossRef CAS PubMed.
- C.-Y. Li, M. Chen, S. Liu, X. Lu, J. Meng, J. Yan, H. D. Abruna, G. Feng and T. Lian, Nat. Commun., 2022, 13, 5330 CrossRef CAS PubMed.
- S. T. Chill, M. Welborn, R. Terrell, L. Zhang, J.-C. Berthet, A. Pedersen, H. Jonsson and G. Henkelman, Modell. Simul. Mater. Sci. Eng., 2014, 22, 055002 CrossRef.
- M. Nagaoka, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2024, 14, e1714 CAS.
- M. Novotny, Phys. Rev. Lett., 1995, 74, 1 CrossRef CAS PubMed.
- M. Núñez, T. Robie and D. Vlachos, J. Chem. Phys., 2017, 147, 164103 CrossRef PubMed.
- I. Kouroudis, M. Gößwein and A. Gagliardi, J. Phys. Chem. A, 2023, 127, 5967–5978 CrossRef CAS PubMed.
- A. Chatterjee and A. F. Voter, J. Chem. Phys., 2010, 132, 194101 CrossRef PubMed.
- A. Savara and J. E. Sutton, J. Phys.: Condens. Matter, 2018, 30, 295901 CrossRef PubMed.
- M. Gößwein, W. Kaiser and A. Gagliardi, J. Chem. Theory Comput., 2022, 18, 2749–2763 CrossRef PubMed.
- Y. Fang and H. Gao, Macromolecules, 2023, 56, 8484–8496 CrossRef CAS.
- C. Ding, J. Weng, T. Shen and X. Xu, J. Comput. Chem., 2020, 41, 2115–2123 CrossRef CAS PubMed.
- X.-M. Cao, Z.-J. Shao and P. Hu, Phys. Chem. Chem. Phys., 2020, 22, 7348–7364 RSC.
- W. Kaiser, M. Gößwein and A. Gagliardi, J. Chem. Phys., 2020, 152, 174106 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2025 |
