 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Transport characterization of solid-state Li2FeS2 cathodes from a porous electrode theory perspective†
Tim
Bernges
*a,
Lukas
Ketter
ab,
Bianca
Helm
c,
Marvin A.
Kraft
 d,
Kimberly A.
See
d,
Kimberly A.
See
 e and
Wolfgang G.
Zeier
e and
Wolfgang G.
Zeier
 *abd
*abd
aInstitute of Inorganic and Analytical Chemistry, University of Münster, D-48149 Münster, Germany. E-mail: tbernges@uni-muenster.de; wzeier@uni-muenster.de
bInternational Graduate School for Battery Chemistry, Characterization, Analysis, Recycling and Application (BACCARA), University of Münster, D-48149 Münster, Germany
cBavarian Center for Battery Technology (BayBatt), University of Bayreuth, D-95447 Bayreuth, Germany
dInstitute of Energy Materials and Devices (IMD), IMD-4: Helmholtz-Institut Münster, Forschungszentrum Jülich, 48149 Münster, Germany
eDivision of Chemistry and Chemical Engineering, California Institute of Technology, Pasadena, 91125 California, USA
First published on 14th January 2025
Abstract
The abundance and cost of resources for current state-of-the-art cathode active materials makes the search for alternative cell chemistries inevitable. Nonetheless, especially in solid-state batteries, establishing new cell chemistries comes at the challenge of optimizing the transport of both charge carriers, electrons and ions, through the electrode. Limitations in transport of either species lead to underutilization of the electrode caused by insufficiently contacted particles and/or nonuniform reaction rates and state-of-charge gradients through the electrode. In this work, we investigate the capabilities of Li2FeS2 as alternative active material in all-solid-state cathodes by thorough investigation of the initial utilization and rate capability as a function of the cathode loading. The cathode loading is increased from 1.8 to 7.3 mA h cm−2 by increasing the fraction of active material from 32 to 74 vol%, and the thickness of the composite electrode from 73 to 145 μm. Careful characterization of the effective electronic and ionic transport, and consideration of the δ-parameter from porous electrode theory, guides the understanding of the electrode performances. With that, this work shows that Li2FeS2 solid-state cathodes with high areal loadings and gravimetric energy densities can be realized.
Broader contextSolid-state batteries are explored to replace lithium-ion batteries soon. However, a move from liquid electrolytes to solid state electrolytes requires the fabrication of all-solid electrodes and with-it optimization of the composition, electrode thickness and applied – as well as possible practical high – current densities. This work uses the active material Li2FeS2 as a case study to describe electrode transport by using a descriptor for electrode transport that allows a qualitative characterization of the quality of electrode transport of different active materials, solid electrolyte and additive systems for cathodes and anodes alike in solid-state batteries. Overall, the discussion factors in the thickness of the electrode and the applied current density, therefore setting the results and discussion in context of desired high-energy density electrodes and fast-charging scenarios. This allows a first prediction of the onset of transport limitations when targeting practically desired cell loadings in solid-state batteries. |
Introduction
Li-ion batteries pose an integral part of todays energy economics but are expected to run into limitations of achievable energy density in the future, motivating the investigation of different technologies, e.g., solid-state batteries.1,2 In both, conventional Li-ion and solid-state batteries, the layered oxides LiNi1−xMnyCo1−x−yO2 (NCM) are the most utilized and thoroughly investigated cathode active material.3 Nonetheless, among other things, the relative scarcity of Co and Mn, and resulting material costs make the search for alternatives a promising endeavour.4–6 The cathode active material Li2FeS2 offers a cost-effective alternative given the large abundance of both iron and sulfur,4 comparable to the promised benefits of other alternative chemistries such as LiFePO4 (LFP) and Li–S.7,8 At the same time, moving from NCM to Li2FeS2 means higher mechanical compatibility, and moving from high- to low-potential electrodes promises better alignment with the stability window of the state-of-the-art sulfur-based solid-electrolytes.9In addition to these benefits, Li2FeS2 on paper offers a two electron reaction following full delithiation from Li2FeS2 to FeS2. Considering this range, the theoretical capacity of Li2FeS2 amounts to 400 mA h g−1, exceeding the theoretical capacity of NCM811 that is ≈280 mA h g−1 but coming at the disadvantage of a lower potentials of operation. Nonetheless, Hansen and coworkers10 recently proposed that the reaction is limited to the chemical space between Li2FeS2 and Li0.5FeS2 relating to a theoretical capacity of 300 mA h g−1 in the investigated voltage range, as corroborated by other reports.11 This conclusion is reached by state-of-charge dependent characterizations using in situ X-ray diffraction as well as ex situ Fe and S K-edge XANES experiments.10 The proposed reaction mechanism is as follows:10,12,13 first the delithiation of Li2FeS2 to Li1.5FeS2 is charge balanced by the oxidation of Fe2+ to Fe3+. At the nominal composition Li1.5FeS2, an ordering of the Fe2+/3+ and Li+ substructure occurs. Further delithiation takes place in a two-phase regime between Li1.5FeS2 and Li0.5FeS2, where charge is balanced by sulfur dimer formation, i.e., the formal oxidation of S2− to (S2)2−. In Li0.5FeS2, half of all sulfur ions are dimerized and further delithiation faces a large energetic barrier. This is in agreement with the computational work by Wei et al.14 that suggests that while further delithiation from Li0.5FeS2 to FeS2 is hindered by a significant increase of the formation enthalpies, it may be achieved if the potential barrier is overcome.
While the cathode active material Li2FeS2 has been successfully utilized in Li-ion batteries using organic liquid electrolytes,10,12 its potential for solid-state batteries is scarcely investigated to date.15,16 The transition from porous electrodes infiltrated with liquid electrolyte to solid-state cathodes means the change to solid–solid cathode composites containing cathode active material (CAM) and solid electrolyte (SE). With that the question of the optimal mixing ratio of both components arises. From a transport perspective, the mixing (volumetric) ratio determines the effective ionic and electronic conductivity in and through the cathode composite to a major extent. With electrochemical reactions requiring both charge carriers, sufficiently fast transport of both through the entire thickness of the cathode is necessary for high cathode utilization.17–19 Generally, electronic conductivity is contributed by either the CAM itself or by conductive additives,17,20 such that the effective electronic conductivity increases with the volume fraction of CAM in the composite. Opposed to that, the effective ionic transport mainly provided by the SE increases with its volume fraction and consequently decreases with the CAM fraction in the composite.17 This interdependence of both conductivities on the volumetric ratio of the components makes optimizing cathode composite transport a challenging task.21
The situation is further complicated by the general goal of designing high energy density cathodes that are feasible for application. An increase of the energy density of the cathode, or its areal loading (in units of mA h cm−2), can be achieved by increasing the CAM volume fraction given the simultaneous reduction of formaly electrochemically inactive SE.3 The increase of the CAM fraction leads to an increase in the effective electronic conductivity of the composite but has detrimental influence on the effective ionic conductivity.17 This leads to the system being ion transport limited, i.e., to insufficiently fast ion transport, when going to the desired high volume fractions of CAM. Underutilization of the cathode and saturation or decline of the achievable energy density follow.21 The saturation behavior can be understood considering that increasing the areal loading above a threshold of the CAM volume fraction leads to a significant loss in cathode utilizations and a net-zero win in achievable energy density. This trend is schematically depicted in Fig. 1 (red shading). Various examples of ionic transport limitations leading to cathode underutilziation can be found in literature, e.g., for Li6PS5Cl–Graphite anode composites,20 in Li–S solid-state cells,19 and in Li6PS5Cl–LiNi0.6Co0.2Mn0.2O2 cathodes.17
Nonetheless, the energy density of the cathode can be increased above this threshold by increasing the cathode thickness (schematically depicted in Fig. 1, blue shading).3 But, the increase in cathode thickness can amplify and exacerbate already existing transport limitations at medium to high CAM fraction again limiting the achievable energy densities. This can be intuitively understood by the elongated conduction paths for both charge carriers, that require even faster effective transport through the electrode. In agreement with this viewpoint, Kato and coworkers18 reported on a decrease of the cathode utilization in LiCoO2–Li10GeP2S12 cathodes when increasing the cathode thickness and simulations on a comparable system using Li3PS4 as SE indicate that reaction fronts and state-of-charge gradients are the underlying reasons.22
In this work, we investigate the solid-state cathode system Li5.5PS4.5Cl1.5 (SE)–Li2FeS2 (CAM) with varying volume fractions of CAM to identify potential onsets of kinetic limitations. This is done by evaluating the effective conductivities using chronoamperometry, impedance spectroscopy, and effective medium modelling. Successively, the influence on cathode utilization is investigated and related to the transport characteristics of the system. The porous electrode theory developed by Newman and Tobias23 is revisited and a dimensionless descriptor identified to describe transport limitations of the system. This descriptor is used to qualitatively guide the understanding of our results. From this, it is shown that high volume fraction CAM cathodes can be realized that show good cathode utilization at low applied current densities even when aiming for thicker electrodes. Nonetheless, lower rate capability at higher applied current densities is a consequence of increasing the cathode loading, i.e., the cathode energy density. With that, this work shows the general capabilities of Li2FeS2 as CAM in solid-state batteries and reveals limitations in the field of solid-state batteries in general that have to be targeted by future research.
Experimental section
Sample preparation
Cathode composites of Li2FeS2 and Li5.5PS4.5Cl1.5 were prepared using a shaker mill with a frequency of 15 Hz for five minutes. Synthesis details and quality control of the synthesized materials are given in the ESI (Fig. S1, Tables S1 and S2†). The ZrO2 shaker mill cup (15 mL) was filled with 200 mg of a Li2FeS2 and Li5.5PS4.5Cl1.5 mixture in the targeted volumetric ratio. Composites with Li2FeS2 volume fractions of 0.32, 0.41, 0.51, 0.62 and 0.74 were prepared corresponding to weight fractions of 0.4, 0.5, 0.6, 0.7 and 0.8. Twenty 3 mm ZrO2 milling media were filled in the shaker cup for the processing. Sample handling and preparation was exclusively done under inert atmosphere in an Ar-filled glovebox.Partial transport characterization
Two techniques were employed to evaluate the partial conductivities of the composites. The electronic conductivity was exclusively measured by chronoamperometry in electron conducting/ion blocking conditions, created by placing the sample between stainless steel current collectors. The ionic conductivity is determined in electron-blocking but ion conducting conditions by stacking SE and In/LiIn symmetrically on both sites of the sample. The polarization experiments were performed in a range of −45 mV to 50 mV, and 1 mV to 8 mV, for the electronic and ionic conductivity, respectively. All raw data and details of the data evaluation are given in the ESI.† Potentiostatic impedance spectroscopy was conducted to corroborate the partial ionic conductivity of the composites. The spectra were collected in a half cell configuration of In/LiIn|Li5.5PS4.5Cl1.5|Li2FeS2/Li5.5PS4.5Cl1.5. The investigated frequency range was 7 MHz to 50 mHz, with 25 sampled frequencies per decade using an excitation amplitude of 10 mV. The response was analyzed using a Z-type transmission-line model. Simultaneous determination of the partial electronic conductivities could not be done reliably. This is, because the significantly lower resistance contributions lead to increased uncertainties during fitting. Thus, the electronic resistance where fixed to the expected value from chronoamperometry to stabilize the fitting procedure. Details of the data evaluation are given in the main text and the ESI.†Electrochemical characterization
Half-cells were constructed using 12 mg Li2FeS2/Li5.5PS4.5Cl1.5 cathode composites (≈73–85 μm), 80 mg of Li5.5PS4.5Cl1.5 separator and a In/LiIn anode (In-foil towards separator, Li-foil towards current collector) in a press cell setup (10 mm diameter) with stainless steel current collectors.24 The separator and composite are densified at a pressure of 370 MPa before application of the anode. The relative densities of the composite layer are in the range of 85 ± 3% independent of composition. The anode is prepared by first placing In-foil (ChemPur, 0.1 mm, 99.999%) on the separator, followed by Li foil that has been freshly prepared from a Li rod (abcr GmbH, 99.8%). For the evaluation of thicker electrodes, the cathode mass was increased to 18 and 24 mg. All cells were cycled at a controlled temperature of 298 K with an applied pressure of 40 MPa and with a rate of 0.134C (assuming theoretical capacity 300 mA h g−1). The rate capability was characterized by cycling the cells for five cycles at step-wise increasing current densities starting from 0.134C (≈0.24 to 0.98 mA cm−2) going to a maximum applied current density of 5.1 mA cm−2. An overview of all applied current densities in terms of C-rate and the approximated cathode thicknesses is given in Table S3 of the ESI.†Results and discussion
Porous electrodes in (solid-state) batteries
Extensive work has been done in the past to theoretically describe the electrochemical behavior of electrodes that consist of a porous, electron conducting active material (matrix) infiltrated by ion conducting liquid electrolyte.23,25,26 The theory of porous electrodes aims to describe the spatial distribution of current densities and reaction rates throughout the electrode that depend on the electrode geometry, the effective electronic and ionic conductivity, and the polarization behavior of the active material. These distributions, if nonuniform, can be considered the underlying reason for cathode underutilization, or the creation of state-of-charge gradients over the electrode. Not considered specifically in the porous electrode theory, the approximations commonly made to the solvent-based electrolyte, e.g., no concentration gradients, neglecting electrochemical double-layer formation and dismissing convection, are fulfilled in SE.27 Consequently, the results of the porous electrode theory should persist to the solid-state configuration.Newman and Tobias23 derived a description of reaction current distributions through the electrode in one dimension. In the one-dimensional approximation, the current densities and reaction rates are only a function of the relative position x in the electrode located between the separator (x = 0) and the current collector (x = L) interface (schematically shown in Fig. 2, left). The electronic current density ie in the active material and ionic current density iion in the electrolyte are described by Ohms law:23,28
 | (1) |
 | (2) |
In the model, it is assumed that charge is transferred exclusively between the electrolyte and active material at their interface. Charge transfer is a function of the polarization at the active material–electrolyte interface, given by the general form of:
 | (3) |
Newman and Tobias23 showed that this set of equations can be cast into a differential equation to describe the reaction current density distribution. The differential equation can be solved numerically using appropriate boundary conditions. From this assessment, dimensionless descriptors were identified that scale with and give a measure of the uniformity of the reaction current density distribution. For Tafel polarization and considering symmetric charge transfer coefficients in the polarization equation, the uniformity of the reaction current density distribution is proportional to a dimensionless current density δ:23,27
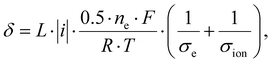 | (4) |
Considering that both, the thickness and the applied current density are desired to be high to improve energy density and enable fast charging, the conductivity term is the free composite design parameter for achieving low values of δ. The δ-parameter as a function of both effective conductivities is shown in Fig. 2b for an exemplary thickness of 200 μm and a current density of 5 mA cm−2. It shows that the δ-parameter is low, and reaction rates are uniform, when both conductivities are high and equal (diagonal in Fig. 2b). When one effective conductivity is significantly lower than its counterpart, δ is high (lower and left boundaries in Fig. 2b). With that, the uniformity of the reaction rate distribution, inversely proportional to δ, is limited by the lower conductivity. Exemplarily, this means that changing σe in the situation σion ≪ σe, while keeping σion constant, does not lead to significant changes in δ until the condition σion ≈ σe is reached (staying on the contour lines in Fig. 2b). Opposed to that, changing σion in the same case has drastic influences (“moving” perpendicular to contour lines in Fig. 2b). By changing the volume fractions of electrolyte and active material or the microstructure of the composite, both conductivities of the porous electrode change simultaneously, complicating this assessment.
In this work, we consider the δ-parameter as stated by Newman and Tobias.23,27 Nonetheless, similar descriptors are derived by Wagner,28 Micka25 and Euler and Nonnenmacher26 treating either specific electrode cases or considering different polarization equations. In the following, we evaluate the potential of the δ-parameter as a qualitative descriptor to guide the design of solid-state battery electrodes by investigating the transport and performance of cathode composites with changing SE to CAM volume ratio, changing thickness and applied current density.
Effective conductivities of the cathode composites
Characterization of transport in cathode composites is important for the understanding and improvement of cathode utilization, both, proposed by the δ-parameter analysis (Fig. 2b and eqn (6)), and shown experimentally for various solid electrolyte–active material composites such as Li6PS5Cl–LiNi0.6Co0.2Mn0.2O2,17 Li3PS4–LiNi0.6Co0.2Mn0.2O2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22 and Li6PS5Cl–Graphite.20 In this work, two experimental approaches are taken: chronoamperometry (CA or direct-current (DC) polarization) and electrochemical impedance spectroscopy (EIS).
22 and Li6PS5Cl–Graphite.20 In this work, two experimental approaches are taken: chronoamperometry (CA or direct-current (DC) polarization) and electrochemical impedance spectroscopy (EIS).
The electronic conductivities σe of composites in the compositional range ΦCAM = 0.32 to 1.00, with ΦCAM denoting the volume fraction of cathode active material (Li2FeS2) in Li5.5PS4.5Cl1.5–Li2FeS2 composites, were determined by chronoamperometry. To do so, the samples were placed between stainless steel current collectors creating ion-blocking conditions to exclusively measure the electronic current response to the applied voltages. The resulting electronic currents follow the applied voltages linearly in agreement with Ohms law as exemplarily shown for ΦCAM = 0.51 (Fig. 3a, blue markers and axis). With that, σe can be determined from the electronic resistance, Re ∝ slope, and the geometrical information of the sample. An analogous experiment under different boundary conditions can be conducted to determine the ionic conductivity σion of the composites. For this, SE and In/LiIn layers are symmetrically applied to both sides of the sample creating ion conducting, electron blocking conditions. With that, the resulting current response can be related exclusively to the transport by ions. The ionic currents again follow Ohm's law (Fig. 3a, red markers and axis) allowing the determination of the ionic resistance Rion and after subtraction of the electrode contributions, the ionic conductivity of the composites. These experiments reveal a significantly lower ionic conductivity compared to the electronic conductivity throughout the entire compositional range. While exemplarily shown for ΦCAM = 0.51, all chronoamperometry results can be found in the ESI (Fig. S2–5†).
To corroborate the results of the chronoamperometry experiments, the effective ionic conductivity was determined from electrochemical impedance spectroscopy of half-cells in the configuration In/LiIn|Li5.5PS4.5Cl1.5|Li2FeS2/Li5.5PS4.5Cl1.5. A Z-type transmission line model31,32 was used to fit the experimental results that describes ionic contact of the composite in direction of the separator and In/LiIn reference anode, and electronic contact in direction of the current collector (exemplarily shown for ΦCAM = 0.51, Fig. 3b). The equivalent circuit shown as inset in Fig. 3b consists of an impedance ZSE+In/LiIn describing separator (RSE) and interface contributions of the electrodes (parallel RIn/LiIn and constant phase element with CIn/LiIn) as well as infinitely expanding branches of ionic and electronic resistances (Rion and Re) describing transport through the composite. During the fitting procedure Re was fixed to the value approximated from chronoamperometry. With that, the applied equivalent circuit leads to a good description of the half-cell impedance response throughout the entire compositional range allowing the determination of the composite ionic conductivities. Again, all spectra and fits are shown in the ESI (Fig. S6†).
All conductivities are shown in Fig. 4a as a function of the CAM volume fraction. In the case of σion, the average and standard deviations from both deployed techniques are depicted. The effective conductivities change exponentially as a function of the volume fraction of the active material. The ionic conductivity increases from σion,CAM = 5.4 ± 0.3 × 10−4 mS cm−1 to σion,SE = 6.1 ± 0.2 mS cm−1 between the pure phases, while the electronic conductivity decreases between σe,CAM = 100 ± 1 mS cm−1 and σe,SE = 10−6 mS cm−1,33 respectively. This is the expected trend for the partial conductivities in composites considering effective medium theory.34,35
Effective medium theory describes the changes to the effective transport parameter in a composite as a function of the volume fraction of its constituents.34,36,37 Multiple variations of effective medium theories exist and the reader is referred to the works by McLachlan and coworkers36,37 for an overview. Here, we use the model derived by Wu and coworkers35 that is closely related to the general Bruggeman34,38 equation to describe the observed trends in the effective conductivities. The model describes the relation between the effective conductivity of the composite and the conductivity of its constituents following:35
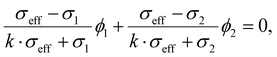 | (5) |
In the next step, to understand potential transport limitations in the cathodes, the model by Newman and Tobias for porous electrodes is taken into consideration.23 Specifically, we evaluate if the dimensionless current density δ (eqn (4)) can guide our understanding of transport related differences in cathode performance as a qualitative descriptor. Again, δ is a function of the effective conductivities, the cathode thickness and the applied current density and introduced as a descriptor for the tendency of the cathode to show nonuniform reaction rate distributions (δ ≫ 1), the buildup of reaction fronts and state-of-charge gradients.19,30 It must be considered that this descriptor, without accounting for important microstructural features like CAM-SE contact area, and kinetic parameters such as exchange current densities, can only be evaluated as qualitative, and not quantitative descriptor to predict potential transport limitations in the cathode. Nonetheless, we expect these transport limitations to scale with transport-related performance properties of the cathode, e.g., the cathode utilization (general contacting of CAM and SE) and rate capability and these trends are reported in literature, where cathode utilization decreases because either σion or σe are insufficiently high or when the cathode thickness and applied current density are increased.17,18,20,22
The δ-parameters characterizing the investigated Li2FeS2–Li5.5PS4.5Cl1.5 cathodes are shown in Fig. 4b. The depicted values are calculated according to eqn (4) using the experimental (markers) and effective medium modelled effective conductivities (dashed line and shaded area) as input parameter. Moreover, the thicknesses L and current densities i of the cathodes later investigated as a function of the CAM volume fraction are utilized for the calculation. These are in the range of 85 μm to 73 μm, and 0.24 mA cm−2 to 0.49 mA cm−2 (0.134C) for ΦCAM between 0.32 and 0.74 at constant cathode mass, respectively. An overview of the parameters is given in Table S3 of the ESI.†
The experimental δ-parameters express a minimum of 0.3 at ΦCAM = 0.41, with a steady increase to 2.8 at ΦCAM = 0.74. These values are close to or below the empirical condition of δ ≲ 1 for which a uniform distribution of reaction rates is expected.23,27 Considering σion and σe from effective medium theory, the minimum of δ occurs at even lower ΦCAM just before the percolation threshold of electronic conduction is reached. For fractions of ΦCAM > 0.74, δ increases significantly as a consequence of reaching the percolation threshold of σion. With that, for pure Li2FeS2, a value of 300 is obtained indicating the onset of strong transport limitations (δ ≫ 1). Following, cathodes relating to these δ-parameters are investigated in terms of electrochemical performance and the potential of δ as a qualitative descriptor is evaluated.
Performance of the cathode composites
The electrochemical performance of the cathodes with varying fraction of CAM have been investigated in half cells using a In/LiIn counter electrode and Li5.5PS4.5Cl1.5 as separator. Initially, cells with constant cathode composite mass loading (15.3 mg cm−2) are characterized to evaluate the influence of ΦCAM on the performance at comparable cathode thicknesses. These are, approximated by the relative density of the cathode and its mass, in the range of 73 μm to 85 μm (Table S3†). All composites were first cycled at a constant C-rate of 0.134C assuming a theoretical specific capacity of 300 mA h g−1 (corresponding to 0.1C assuming a theoretical capacity of 400 mA h g−1 for full delithiation). Afterwards, rate capability was tested at constant current densities instead. An overview of all 0.134C rates in terms of current densities, and all current densities in terms of C-rates, is given in Table S3 of the ESI.† In addition, scanning electron micrographs and energy dispersive X-ray spectroscopy signals are shown in Fig. S8† characterizing the composite microstructures.The voltage profiles of the solid-state cathodes do not significantly change as a function of the cathode composition. A comparison of the profiles at the first cycle is given in Fig. 5a. The charge profile is characterized by a monotonically increase of the voltage with weakly pronounced features below 1.9 V. In this regime, delithiation is charge balanced by oxidation of Fe2+ to Fe3+ corresponding to the nominal compositional range of Li2FeS2 to Li1.5FeS2 and the profiles of the solid-state cathodes agree well with reports using liquid electrolyte (dashed line in Fig. 5a).10 At 1.9 V, a voltage plateau representing the two-phase regime of Li1.5FeS2–Li0.5FeS2 establishes. This region can contribute a theoretical capacity of 200 mA h g−1. This is the case in liquid electrolyte based cells,10 while the plateau is generally lower capacity in the investigated solid-state cathodes (Fig. 5a).
 | ||
| Fig. 5 The legend in the top right defines datasets in all subplots. Additionally, a conversion from the 0.134C rates to the applied current densities for cells with varying CAM volume fraction ΦCAM is given color coded in the top right. (a) Voltage profiles of cells employing Li5.5PS4.5Cl1.5–Li2FeS2 cathodes of varying CAM volume fraction ΦCAM during the first cycle under a rate of 0.134C. The profile of the first cycle is compared to Li2FeS2 cathodes using liquid electrolyte10 (dashed line). (b) Capacity retention at a constant rate of 0.134C and (c) upon increasing the applied current density tested for composites with three compositions (see inset). Standard deviations from triplicates for each dataset are given at an arbitrary representative cycle. | ||
Furthermore, solid-state cells show significantly lower Coulomb efficiencies in the first cycle with values between 77% and 82% in the solid-state, compared to ≈90% in the liquid electrolyte based cells.10 Low first cycle efficiencies are common in other solid-state battery chemistries, e.g., using Li(Ni,Co,Mn)O2 as active material and generally, they are related to contact losses between the active material and the SE due to volumetric expansion as well as the formation of a SE-CAM interphase (CEI).39,40 The capacity retentions reflect the low initial efficiency in the first cycle, with gradual capacity losses afterwards (Fig. 5b). The capacity retentions are comparable in general, but cathodes with the highest ΦCAM show a lower overall capacity retention of 73% (average Coulomb efficiency of 98.3%) compared to 85% (average Coulomb efficiency of 99.5%) for cathodes with the lowest ΦCAM after 40 cycles. Given the special role of the first charge cycle, these relative retentions and average efficiencies are referring to or count from the second charge onward. In addition to the capacity retention with ongoing cycling, the rate capability was tested for exemplary compositions of ΦCAM = 0.32, 0.51 and 0.74 (Fig. 5c). In agreement with the constant C-rate cycling, no strong compositional trends can be observed in the rate retention upon first visual inspection of the data.
Based on this first assessment, we now discuss the performance as a function of the cathode configuration in detail. Thereby, focus lies on performance parameters that are related to the effective transport properties of the cathode discussed beforehand (Fig. 4), the initial cathode utilization and the rate performance.
Initial cathode utilization and areal capacity
The initial cathode utilization is related to the transport given that it is a measure of the contacted and electrochemical active CAM in the composite, i.e., how accessible and at which rate active material particles are for both charge carriers. In the following, the initial cathode utilization is measured by the average capacity per gram CAM QCAM. The average includes both, the average over the first five cycles (excluding first charge) of each individual cell, and the average and standard deviation of all cells investigated with the same composition.The comparison of QCAM as a function of ΦCAM acquired at a rate of 0.134C shows no strong changes of the cathode utilization, with a maximum difference of 15% between the highest capacity of QCAM = 229 ± 28 mA h g−1 at ΦCAM = 0.62 and the lowest of 195 ± 10 mA h g−1 at ΦCAM = 0.74 (Fig. 6a, left). Given the absence of a strong loss of capacity utilization, and to explore limitations of the cell chemistry, the areal loading is further increased by testing the extreme of a pure Li2FeS2 cathode (ΦCAM = 1.0) and by increasing the cathode thickness from 73 μm to 110 μm and 145 μm for a cathode with ΦCAM = 0.74. A drastic decrease of the cathode utilization occurs going to ΦCAM = 1.0, with a decrease by 90% to capacities of 25 ± 3 mA h g−1. At the same time, increasing the thickness of the composite only leads to a QCAM decrease from 195 ± 10 mA h g−1 to 181 ± 14 mA h g−1 (7% decrease).
 | ||
| Fig. 6 (a) Initial charge capacity per mass CAM (QCAM) as a function of (left) the CAM volume fraction and (right) the δ-parameter (eqn (6)). Uncertainties correspond to the standard deviation of at least three cells per composition. (b) The corresponding experimentally achieved areal capacities as a function of the areal loading for the cells depicted in (a). The gray-dashed line gives a reference for full cathode utilization. ΔΦ and ΔL highlight trends with increasing CAM volume fraction and cathode thickness. | ||
Porous electrode theory can guide the understanding of these trends given that it aims to describes the reaction rate distribution throughout the cathode, as quantified by the δ-parameter (eqn (4) and Fig. 2). With that, the δ-parameter (eqn (4) and Fig. 4b) should be capable of capturing qualitative trends in cathode utilization. The capacities of all cells as a function of δ are depicted in the right subplot of Fig. 6a. As a reminder, δ not only considers changes to the effective conductivities by changing ΦCAM, but variations in the applied current density, a consequence of using constant C-rates, and the cathode thickness. Moreover, no strong changes to the cathode utilization should occur for cathodes characterized by values of δ ≲ 1 that describes the condition of uniform reaction rate distributions.
This is the case for all composites in the range of ΦCAM = 0.32 to 0.74 at 0.134C and with thicknesses between 85 μm and 73 μm (Fig. 6a, right). For these cells, the δ-parameter ranges between 0.3 and 2.8 (Fig. 4b). Consequently, the δ-parameter analysis predicts high uniformity of the reaction rate distribution and gives a rational for the marginal changes in cathode utilization. Increasing the cathode thickness and, considering constant C-rates, the applied current density, increases the value of δ from 2.8 to 6.3 and 11.1, moving away from the desired condition of δ ≲ 1 and explaining the decrease of the cathode utilization going to a thick electrode configuration. For the edge case of pure Li2FeS2 as cathode, the δ-parameter significantly increases to ≈300 driven by the orders of magnitude loss in effective ionic conductivity (Fig. 4). This strong increase manifests as a 90% decrease of the cathode utilization. With that, the δ-parameter captures the observed trends in the initially achieved capacities qualitatively. Moreover, a decrease of QCAM with the logarithm of δ can be observed, acknowledging the scattering in the dataset (Fig. 6a). Not considered in this analysis is the residual porosity of the electrodes. Nonetheless, given that the relative density does not change significantly with an average of 85 ± 3% for all investigated electrodes, the effect is assumed to be negligible in first approximation.
This qualitative trend agrees with literature results considering the δ-parameters approximated from reported values of σ, i and L. Systems that indicate first signs of transport limitations and underutilization of the electrode are characterized by values of ≈19 (LiNi0.6Co0.2Mn0.2O2–Li3PS4),22 ≈ 22 (LiCoO2–Li10GeP2S12)18 and ≈31 (Graphite–Li6PS5Cl).20 Moreover, Bradbury and coworkers19 showed that severe reaction fronts occur in Li–S cells that are characterized by a δ-parameter of ≈200 agreeing with the significant utilization loss when going to pure Li2FeS2 (δ ≈ 300).
The relatively small variations in QCAM by 15% between all ΦCAM of comparable thickness, and by 7% when doubling the cathode thickness at constant composition, rationalized by the δ-parameter analysis, are promising outlooks for the Li2FeS2 battery chemistry. While these are significant changes to the cathode utilization, the loss in utilization is marginal compared to the areal loading increase from 1.8 mA h cm−2 to 3.7 mA h cm−2 with increasing ΦCAM, and to 7.3 mA h cm−2 upon increasing the cathode thickness. This increase of the areal loading by a factor of approximately five compensates the at maximum 22% loss in cathode utilization, so that the achieved areal capacities increase from 1.2 mA h cm−2 to 4.4 mA h cm−2 going from the lowest to the highest areal loadings (Fig. 6b). Clearly, the higher δ – for instance in thicker electrodes – the more deviations of the attained capacity to the theoretical capacity can be expected.
Rate capability
The analysis of the initial cathode utilizations and areal capacities shows that Li5.5PS4.5Cl1.5–Li2FeS2 cathodes with high volume fractions of CAM can be realized successfully. Moreover, the achievable areal capacities can be increased further with the thickness of the cathode. Nonetheless, fast charging is desired for application and the rate capability of the electrodes needs to be considered. Therefore, electrodes with ΦCAM = 0.32, 0.51 and 0.74 (L ≈ 80 μm), and with L = 73, 110 and 145 μm (for ΦCAM = 0.74) have been tested for five cycles per current density step, starting with a current density corresponding to the theoretical rate of 0.134C (respective current densities listed in Table S3†). Subsequently, the applied current density was stepwise changed between 0.6 mA cm−2 and 5.1 mA cm−2. This routine was chosen to compare the composites at constant current densities despite changes to the cathode loading and with that the C-rates. The average capacity QCAM of the five charge cycles per current density step, and the average of triplicates as well as their standard deviation, are considered in the following discussion. The rate retention as a function of the applied current density is shown in the ESI (Fig. S12†). Here, we rescale the applied current density to a practical rate of charge denoted r as proposed by Tian and coworkers.41 The practical rate in units of h−1 is defined, following:41| r = I/Qexp(I), | (6) |
The cathode utilizations as a function of the practical rate are shown in Fig. 7a. At the highest applied current density, cathodes with ΦCAM = 0.32 and 0.74 and comparable thickness achieve similar capacities of 55 mA h g−1 and 51 mA h g−1, respectively. Nonetheless, this capacity is achieved at a significantly higher practical rate of 14.9 h−1 (3.1C) for ΦCAM = 0.32 compared to 8.2 h−1 (1.6C) for ΦCAM = 0.74 showing better rate performance of cathodes with lower CAM fractions. Increasing the thickness from 73 μm to 145 μm for the composition ΦCAM = 0.74 leads to further lowering of the rate capability. Again, considering the highest applied current, the capacity per CAM mass is lowered to 44 mA h g−1 and acquired at an even lower rate of 4.8 h−1 (0.8C). This indicates a systematic decrease of rate capability when increasing the areal loading of the cathode, e.g., by increasing ΦCAM or its thickness.
 | ||
| Fig. 7 (a) Capacity retention of cells with varying cathode composition and thickness as a function of the practical rate r as defined in the main text. Dashed lines correspond to fits to the data using the semi-empirical analytical model proposed by Tian et al.41 (b) The parameters τ (blue) and n (red) obtained from fitting the data shown against the areal loading of the cells and (c) the average δ over the investigated current density range. | ||
To test this hypothesis, we use the semi-empirical model proposed by Tian and coworkers41 to quantify the rate behavior. The model relates the capacity, or cathode utilization QCAM(r), to the practical rate r, following:41
| QCAM(r) = QCAM,0[1 − (rτ)n(1 − e−(rτ)−n)], | (7) |
Applying this model, eqn (7) describes the rate performance of the investigated cathodes (dashed lines in Fig. 7a). Moreover, the resulting parameters τ and n confirm the initial hypothesis from visual inspection with both showing a detrimental linear increase with the areal loading of the cathode (Fig. 7b). To understand this observation, we again consider the δ-parameter introduced in the porous electrode theory. While at a rate of 0.134C, the δ-parameter was close to unity for most of the investigated cathodes, indicating uniform reaction rates and explaining the good cathode utilization even at high CAM volume fractions (Fig. 6a), the average δ-parameter over the investigated current density range δavg is significantly increased. At a composition of ΦCAM = 0.32 this translates to δavg = 3, while for the highest CAM volume fraction and thickness this value is increased to δavg = 22. This significant increase of δavg with increase of ΦCAM and the cathode thickness indicates that nonuniformity of the reaction rate distribution, measured by δavg, can occur as consequence of applying higher current densities. In fact, the parameters τ and n quantifying the rate capability increase linearly as a function of δavg (Fig. 7c) corroborating this hypothesis.
With that, it can be assumed that the decrease of rate performance with areal loading (Fig. 7b) can at least be partly explained by the onset of reaction rate nonuniformities at higher rates (Fig. 7c). Nonetheless, it must be noted that QCAM cannot be unambiguously related to δ. An overview of all QCAM(ΦCAM, L, i) as a function of δ(ΦCAM, L, i) is shown in the ESI (Fig. S13†). Other factors such as poor ionic contacting of the CAM at high ΦCAM and the increased likelihood of isolated CAM regions in thick electrode configuration can contribute to the decreased cathode utilization and rate performance additionally and are not captured by the δ-parameter analysis.
Energy density and transport balancing of the cathode
After examination of the initial capacity retention (Fig. 6) and the rate capability (Fig. 7), cathode composites are now evaluated regarding their (rate dependent) gravimetric energy density. In agreement with the discussion of the rate capability, the energy density is calculated from the average capacities of five cycles at a certain current density step, and the average and standard deviation of triplicates (with that relating to the data depicted Fig. 7a). Furthermore, only the mass of the cathode, the In/LiIn and the separator are considered for calculation of the gravimetric energy density. The latter two are constant for all investigated cathodes.Comparing the gravimetric energy densities for cells with ΦCAM = 0.32, 0.51 and 0.74 as a function of the practical rate (eqn (6)), it becomes evident that the gravimetric energy density can be significantly increased from 11.4 to 41.4 W h kg−1 by increasing ΦCAM and the cathode thickness L (Fig. 8a) at low rates. This is, because the areal loading of the cathode is increased from 1.8 to 7.3 mA h cm−2, while the simultaneous cathode utilization decrease is negligible in comparison in agreement with the δ-parameter analysis (Fig. 6b). Nonetheless, this strong energy density increase is relativized going to higher rates, i.e., higher applied current densities (overview in Table S3†). At higher rates, and with that upon increasing δ significantly, the energy densities of all investigated cells start to converge to ≈5 W h kg−1 given the systematic decrease of the rate capability (Fig. 7) when increasing the areal loading of the cathode.
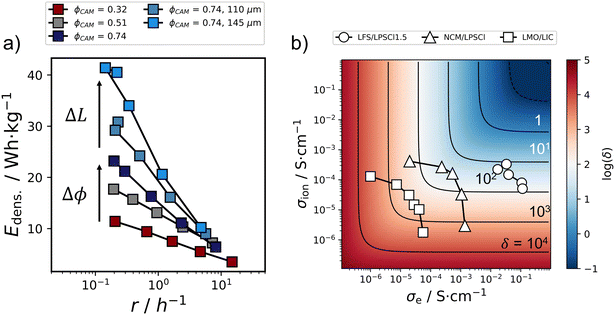 | ||
| Fig. 8 (a) Gravimetric energy density as a function of the practical rate (eqn (6)). ΔΦCAM and ΔL highlight trends with increasing CAM volume fraction and cathode thickness. (b) Partial ionic and electronic conductivity of different electrode composites with varying CAM volume fraction in context of the δ-parameter (eqn (4), L = 200 μm, i = 5 mA cm−2). The depicted data correspond to Li2FeS2 (LFS)/Li5.5PS4.5Cl1.5 (LPSCl1.5, this work), LiNi0.6Co0.2Mn0.2O2 (NCM)/Li6PS5Cl (LPSCl, Minnmann et al.17) and LiMn2O4 (LMO)/Li3InCl6 (LIC, Hendriks et al.44). The δ-parameter scale is calculated for a two-electron reaction (ne = 2 in eqn (4)) with that slightly overestimating the expected values for NCM and LMO. | ||
This highlights that high energy densities can be practically achieved at low rates, but Li2FeS2/Li5.5PS4.5Cl1.5 solid-state cathodes require further improvement regarding their rate capability. This can be achieved, e.g., by improving the processing of the solid composites and by controlling the particle size distribution of its constituents. Both strategies have the ability to improve the transport properties42,43 of cathodes at a constant ΦCAM and with that are suitable attempts to increase the rate performance for cathodes with high areal loading. Nonetheless, Li2FeS2 solid-state electrodes show overall promising performances, especially given the vast design space that has yet to be explored for this novel CAM, e.g., the use of coatings to increase the longevity, or further processing to control crystallinity in addition to the particle sizes.
The comparison of achievable energy densities further highlights the importance of evaluating cell chemistries at realistic, application-relevant areal loadings, i.e., high CAM volume fractions, in thick electrode configuration and at high applied current densities, given the strong influence on electrode utilization. These trends, often intuitive for battery scientists, can be understood qualitatively by considering the δ-parameter introduced by Newman and Tobias.23
With that, a widespread analysis of electrodes considering this descriptor can guide electrode design and detect or predict potential problems heading to application, even in the early stages of research and development. Considering the transport of different active material/electrolyte systems, e.g., Li2FeS2/Li5.5PS4.5Cl1.5 (this work), LiNi0.6Co0.2Mn0.2O2/Li6PS5Cl (Minnmann et al.17) and LiMn2O4/Li3InCl6 (Hendriks et al.44), on this unified δ-parameter scale, allows their direct comparison from a transport perspective (Fig. 8b). At a thickness of 200 μm and an applied current density of 5 mA cm−2, the most transport-optimized LiNi0.6Co0.2Mn0.2O2- (triangles) and Li2FeS2-based (circles) electrodes are characterized by δ ≈ 30 (LiNi0.6Co0.2Mn0.2O2) and ≈11 (Li2FeS2) and with that are expected to still show reasonable performance. This is supported by the results in this work, where cathodes with low CAM volume fraction show the best rate performance (Fig. 7a), and in agreement with the reported rate performances by Minnmann and coworkers.17 In both cases, this optimum in rate performance is achieved in cathode compositions closest to the condition of σe ≈ σion (diagonal in Fig. 8b) that minimizes the conductivity term of the δ-parameter (eqn (4) and Fig. 2b). Moreover, this analysis shows that the investigated system is strongly limited by σion and that increasing the cell performance is intimately tied to the improvement of the ionic conductivity in the composite (to reach the condition of σe ≈ σion). The highest electrode utilization in the system LiMn2O4/Li3InCl6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 44 is also reported at the composition fulfilling the condition σe ≈ σion in agreement with the δ-parameter assessment. Nonetheless, the analysis predicts that the system should suffer from transport limitations in thick electrode configurations and during fast charging (δ ≈ 160) even at the optimized composition given the lower order of magnitude in both conductivities.
44 is also reported at the composition fulfilling the condition σe ≈ σion in agreement with the δ-parameter assessment. Nonetheless, the analysis predicts that the system should suffer from transport limitations in thick electrode configurations and during fast charging (δ ≈ 160) even at the optimized composition given the lower order of magnitude in both conductivities.
In general, this assessment shows that solid-state cathode composites are limited by their ionic conductivity that is <1 mS cm−1, while the electronic conductivity between active materials spreads a wide range and can be optimized more freely by introducing electron conducting additives. Consequently, the search for faster ion conducting solid electrolytes, and the improvement of the solid electrolyte percolation in the electrode, are of highest importance for the development of solid-state batteries in outlook on application. This need for higher conducting solid electrolyte is further emphasized by the exponential loss17,44 in ionic conductivity (Fig. 4a) when increasing the CAM volume fraction in the cathode that is necessary to enable high areal loadings. This additionally shows that good ionically conducting active materials should be explored, as they promise a softening of the loss in effective (ionic) conductivity when going to high volume fractions of active species.
Lastly, it has to be noted that while the δ-parameter gives an intuitive way of comparing chemistries regarding their electrode utilization, and potential challenges in rate retention, it does not include information about other important metrics such as cycle stability. In addition, the transport discussion in this study is based exclusively on as-prepared cathodes, but state-of-charge dependent conductivities should be considered to provide a full understanding of transport-related effects on performance, if available.
Conclusion
In conclusion, this work highlights the importance of balanced transport in composite cathodes and shows that the “transport quality” of the electrode can be qualitatively captured by the δ-parameter derived in porous electrode theory. With that, it is shown that transport is sufficiently balanced in Li2FeS2/Li5.5PS4.5Cl1.5 cathodes, allowing cathode configurations with high areal loadings of 7.3 mA h cm−2 to perform well at low rates with initial capacities of 4.4 mA h cm−2. Nonetheless, increasing the areal loading by deviating from optimal transport balancing subsequently leads to a worsening of the rate performance, as both, the increased cathode thickness (73 to 145 μm) and current densities (0.6 to 5.1 mA cm−2) amplify existing transport limitations. These trends can be understood considering the δ-parameter. Moreover, the δ-parameter has the potential to unify the assessment of electrode quality and potential of different cell chemistries. For example, introducing an arbitrary cut-off in δ, the maximum CAM volume fraction, thickness (areal loading), and applied current densities, achievable before reaching this condition, can be evaluated. Porous electrode theory proposes the absence of transport limitations for δ ≲ 1 and the onset of significant cathode utilization losses are observed in the range 1 ≤ δ ≤ 10 in this work, with higher sensitivity for changes in current density than electrode thickness and CAM volume fraction.The loss in rate capability with increased areal loading motivates studies that focus on processing optimization and particle size matching as strategies to improve transport in cathodes with high areal loading. This is because improving the partial ionic conductivity will lower the δ-parameter independent on electrode thickness and applied current density. Moreover, this work highlights the importance of investigating electrodes with realistic energy densities already on the lab-scale. Thereby, the potential of new cell chemistries in outlook to application can be evaluated from the start and problems can be targeted before upscaling of the technology is attempted.
Author contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript. T. B.: conceptualization, experimental investigation, formal analysis, data curation, writing, visualization. L. K.: data evaluation, experimental investigation, writing-review and editing. B. H.: experimental investigation, writing-review and editing. M. A. K.: conceptualization, methodology, writing-review and editing. K. A. S.: experimental investigation, writing-editing and review. W. G. Z.: conceptualization, resources, writing-review and editing, supervision.Data availability
The data that support the findings of this study have been archived at https://doi.org/10.17879/45968568801.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge financial support by the Bundesministerium für Bildung und Forschung (BMBF; projects KAROFEST 03XP0498B). We further acknowledge funding from the Deutsche Forschungsgemeinschaft under project number 459785385. The authors acknowledge the help of Andrew J. Martinolich in the early stages of this study.References
- J. Janek and W. G. Zeier, Nat. Energy, 2016, 1, 1–4 CrossRef.
- J. Janek and W. G. Zeier, Nat. Energy, 2023, 8, 230–240 CrossRef.
- S. Randau, D. A. Weber, O. Kötz, R. Koerver, P. Braun, A. Weber, E. Ivers-Tiffée, T. Adermann, J. Kulisch, W. G. Zeier, F. H. Richter and J. Janek, Nat. Energy, 2020, 5, 259–270 CrossRef.
- H. C. Urey, Phys. Rev., 1952, 88, 248–252 CrossRef.
- C. H. Jung, H. Shim, D. Eum and S. H. Hong, J. Korean Ceram. Soc., 2021, 58, 1–27 CrossRef.
- G. Whang and W. G. Zeier, ACS Energy Lett., 2023, 8, 5264–5274 CrossRef.
- W. J. Zhang, J. Power Sources, 2011, 196, 2962–2970 CrossRef.
- P. G. Bruce, S. A. Freunberger, L. J. Hardwick and J. M. Tarascon, Nat. Mater., 2012, 11, 19–29 CrossRef PubMed.
- Y. Zhu, X. He and Y. Mo, J. Mater. Chem. A, 2016, 4, 3253–3266 RSC.
- C. J. Hansen, J. J. Zak, A. J. Martinolich, J. S. Ko, N. H. Bashian, F. Kaboudvand, A. Van Der Ven, B. C. Melot, J. Nelson Weker and K. A. See, J. Am. Chem. Soc., 2020, 142, 6737–6749 CrossRef.
- J. Barker and E. Kendrick, J. Power Sources, 2011, 196, 6960–6963 CrossRef CAS.
- A. J. Martinolich, J. J. Zak, D. N. Agyeman-Budu, S. S. Kim, N. H. Bashian, A. Irshad, S. R. Narayan, B. C. Melot, J. Nelson Weker and K. A. See, Chem. Mater., 2021, 33, 378–391 CrossRef CAS.
- L. Blandeau, G. Ouvrard, Y. Calage, R. Brec and J. Rouxel, J. Phys. C: Solid State Phys., 1987, 20, 4271–4281 CrossRef CAS.
- C. D. Wei, H. T. Xue, X. D. Zhao and F. L. Tang, Phys. Chem. Chem. Phys., 2023, 25, 8515–8523 RSC.
- K. Takada, Y. Kitami, T. Inada, A. Kajiyama, M. Kouguchi, S. Kondo, M. Watanabe and M. Tabuchi, J. Electrochem. Soc., 2001, 148, A1085 CrossRef CAS.
- K. Takada, K. Iwamoto and S. Kondo, Solid State Ionics, 1999, 117, 273–276 CrossRef CAS.
- P. Minnmann, L. Quillman, S. Burkhardt, F. H. Richter and J. Janek, J. Electrochem. Soc., 2021, 168, 040537 CrossRef CAS.
- Y. Kato, S. Shiotani, K. Morita, K. Suzuki, M. Hirayama and R. Kanno, J. Phys. Chem. Lett., 2018, 9, 607–613 CrossRef CAS.
- R. Bradbury, G. F. Dewald, M. A. Kraft, T. Arlt, N. Kardjilov, J. Janek, I. Manke, W. G. Zeier and S. Ohno, Adv. Energy Mater., 2023, 13, 2203426 CrossRef CAS.
- A. L. Davis, V. Goel, D. W. Liao, M. N. Main, E. Kazyak, J. Lee, K. Thornton and N. P. Dasgupta, ACS Energy Lett., 2021, 6, 2993–3003 CrossRef CAS.
- A. Bielefeld, D. A. Weber and J. Janek, J. Phys. Chem. C, 2019, 123, 1626–1634 CrossRef.
- K. G. Naik, B. S. Vishnugopi and P. P. Mukherjee, ACS Appl. Mater. Interfaces, 2022, 14, 29754–29765 CrossRef.
- J. S. Newman and C. W. Tobias, J. Electrochem. Soc., 1962, 109, 1183 CrossRef.
- W. Zhang, D. A. Weber, H. Weigand, T. Arlt, I. Manke, D. Schröder, R. Koerver, T. Leichtweiss, P. Hartmann, W. G. Zeier and J. Janek, ACS Appl. Mater. Interfaces, 2017, 9, 17835–17845 CrossRef.
- K. Micka, ACS Advances in Chemistry, 1969, pp. 73–81 Search PubMed.
- J. Euler and W. Nonnenmacher, Electrochim. Acta, 1960, 2, 268–286 CrossRef.
- J. Newman and W. Tiedemann, AIChE J., 1975, 21, 25–41 CrossRef.
- C. Wagner, J. Electrochem. Soc., 1951, 98, 116–128 CrossRef.
- E. J. F. Dickinson and A. J. Wain, J. Electroanal. Chem., 2020, 872, 114145 CrossRef.
- A. M. Stavola, X. Sun, D. P. Guida, A. M. Bruck, D. Cao, J. S. Okasinski, A. C. Chuang, H. Zhu and J. W. Gallaway, ACS Energy Lett., 2023, 8, 1273–1280 CrossRef PubMed.
- Z. Siroma, N. Fujiwara, S. I. Yamazaki, M. Asahi, T. Nagai and T. Ioroi, Electrochim. Acta, 2015, 160, 313–322 CrossRef.
- J. Bisquert, G. Garcia-Belmonte, F. Fabregat-Santiago and A. Compte, Electrochem. Commun., 1999, 1, 429–435 CrossRef.
- P. Gorai, T. Famprikis, B. Singh, V. Stevanović and P. Canepa, Chem. Mater., 2021, 33, 7484–7498 CrossRef.
- B. Tjaden, S. J. Cooper, D. J. Brett, D. Kramer and P. R. Shearing, Curr. Opin. Chem. Eng., 2016, 12, 44–51 CrossRef.
- Z. Wu and M. Liu, Solid State Ionics, 1996, 93, 65–84 CrossRef CAS.
- D. S. McLachlan, Mater. Res. Soc. Symp. Proc., 1996, 411, 309–320 CrossRef CAS.
- D. S. McLachlan, M. Blaszkiewicz and R. E. Newnham, J. Am. Ceram. Soc., 1990, 73, 2187–2203 CrossRef CAS.
- D. A. G. Bruggeman, Ann. Phys., 1935, 24, 636–663 CrossRef CAS.
- R. Koerver, I. Aygün, T. Leichtweiß, C. Dietrich, W. Zhang, J. O. Binder, P. Hartmann, W. G. Zeier and J. Janek, Chem. Mater., 2017, 29, 5574–5582 CrossRef CAS.
- Y. Ma, J. H. Teo, D. Kitsche, T. Diemant, F. Strauss, Y. Ma, D. Goonetilleke, J. Janek, M. Bianchini and T. Brezesinski, ACS Energy Lett., 2021, 6, 3020–3028 CrossRef CAS.
- R. Tian, S. H. Park, P. J. King, G. Cunningham, J. Coelho, V. Nicolosi and J. N. Coleman, Nat. Commun., 2019, 10 DOI:10.1038/s41467-019-09792-9.
- P. Minnmann, F. Strauss, A. Bielefeld, R. Ruess, P. Adelhelm, S. Burkhardt, S. L. Dreyer, E. Trevisanello, H. Ehrenberg, T. Brezesinski, F. H. Richter and J. Janek, Adv. Energy Mater., 2022, 12, 2201425 CrossRef CAS.
- E. Schlautmann, A. Weiß, O. Maus, L. Ketter, M. Rana, S. Puls, V. Nickel, C. Gabbey, C. Hartnig, A. Bielefeld and W. G. Zeier, Adv. Energy Mater., 2023, 13, 1–9 Search PubMed.
- T. A. Hendriks, M. A. Lange, E. M. Kiens, C. Baeumer and W. G. Zeier, Batteries Supercaps, 2023, 6, 202200544 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Synthesis details and structural characterization, chronoamperometry and transmission-line modelling of impedance spectra, details of effective-medium modelling, additional information and depictions regarding the electrochemical characterization. See DOI: https://doi.org/10.1039/d4eb00005f |
| This journal is © The Royal Society of Chemistry 2025 |




