Iron oxide nanospheres: dual functionality as MRI contrast agents and magnetic fluid hyperthermia therapeutics

Abstract

Magnetic nanoparticles offer the possibility of combining diagnostic and therapeutic purposes within a single nano-object. In this work, we explore two distinct sets of iron oxide-based nanospheres for their application as contrast agents in magnetic resonance imaging and as heating mediators in magnetic fluid hyperthermia. The nanoparticles were produced with the green microwave polyol-assisted method. The nanoparticles in the first set have a mean core diameter of 11 nm and are coated with polyacrylic acid (PAA), carboxymethyl-dextran (CM-D), or dimercaptosuccinic acid (DMSA). The second set has nanoparticles of a mean diameter of 14 nm, which are coated with PAA or CM-D. The longitudinal and transverse ¹H-NMR nuclear relaxivities (r_1,2) exhibit a field behavior that depends on the particle core size and on the coating. It is shown that the combination of size and coating is relevant to optimize the relaxometric efficiency, with the PAA coating being able to double the r₂ efficiency for the smallest size. The heating release was evaluated under various combinations of external alternating magnetic fields, with frequency values ranging from 102.2 kHz to 971.2 kHz and amplitude values ranging from 7 mT to 40 mT. The results indicate that the heating efficiency is independent of the coating for both the 11 and 14 nm particles, while it is significantly higher for the samples of largest size. We conclude that the combination of size and coating (i.e., surface modifications) of the magnetic nanoparticles can play a crucial role in the relaxometric and heating properties of magnetic nanoparticles with core size of <15 nm.

---

1 Introduction

One of the key advantages of magnetic nanoparticles (MNPs) is their ability to combine therapeutic and diagnostic functions within a single nano-object.^1–3 Iron oxide-based MNPs, in particular, are widely used due to their high magnetization, superparamagnetic behavior and good biocompatibility.^4–6 These properties make them ideal for use as contrast agents (CAs) in magnetic resonance imaging (MRI) and as heating mediators in magnetic fluid hyperthermia (MFH).^7,8 Magnetite (Fe₃O₄) and maghemite (γ-Fe₂O₃) MNPs are particularly suitable due to their low toxicity and the body's natural metabolic pathways for iron absorption and excretion.^9,10 MRI is a diagnostic tool that offers high spatial resolution, but is often limited by its low sensitivity,^11,12 which makes it challenging to detect small lesions, such as, for example, early-stage tumors. The use of contrast agents can significantly enhance MRI sensitivity. Besides, the contrast in MRI is correlated to differences in signal intensity associated with the concentration of molecules containing hydrogen within the tissue (and their mobility, i.e. diffusion, flow), and also to the values of spin–lattice T₁ and spin–spin T₂ relaxation times of the hydrogen nuclei.^13–15 MNPs decrease the longitudinal (T₁) and transverse (T₂) relaxation times of hydrogen nuclei close to the MNPs according to their biodistribution, thereby enhancing the contrast in MRI scans. The nuclear relaxivity (r_i, i = 1,2), i.e., the inverse of the relaxation time per unit magnetic center with respect to the pure dispersant, quantifies the contrast efficiency and it is influenced by a variety of factors, including the temperature and composition of the solvent, the strength of the external magnetic field, and the kind of contrast agent.^16,17 Furthermore, the contrast efficiency is affected by the size, the magnetic moment, and the aggregation of nanoparticles, as well as the type and thickness of their coating and the number of water ¹H nuclei bound to the magnetic core among other factors.^18,19

In magnetic fluid hyperthermia (MFH), the MNPs are injected into tumors and subjected to an external alternating magnetic field (AMF) with an amplitude of tens of milliTesla and a frequency of the order of hundreds of kHz so that heat is generated by the interaction between the AMF and their magnetization.^20,21 In the therapeutic temperature range of 40–45 °C, MFH has an antitumor effect by disrupting important cancer cell structures such as membranes, organelles, and DNA. As a result, the combination of MFH with chemotherapy, radiotherapy, or surgery can improve the life expectancy of cancer patients.^10,22,23 The specific absorption rate (SAR) measures the heat released per MNP mass unit and it depends on factors such as particle size, static magnetic properties, and spin dynamics, as described by various heuristic or theoretical models.²⁴ It is worth noting that the SAR can also be evaluated from the magnetic and structural properties of MNPs, as shown in ref. 25.

Our research is aimed at developing magnetic nanoparticles that combine both diagnostic and therapeutic functions within a single nano-object. The application of iron oxide nanoparticles as dual-purpose agents for MRI and MFH has been explored and documented by using a wide range of methodologies and approaches.^26–28 The work of Perton et al.²⁷ introduced magnetic and fluorescent nanocomposites with an iron oxide core, a stellate silica shell, and quantum dots, coated with human serum albumin (HSA) for biocompatibility. These nanocomposites are effective for dual imaging (fluorescence and MRI) and magnetic hyperthermia, showing enhanced therapeutic potential, especially when combined with doxorubicin. Wang's study²⁸ developed multifunctional SPIO-M2pep nanoparticles that target M2 macrophages, enhancing MRI-guided magnetic hyperthermia in a breast cancer model. The nanoparticles, with a high r₂ relaxivity of 149 mM⁻¹ s⁻¹, remodeled the tumor immune microenvironment, reduced immunosuppressive factors, increased antitumor immune responses, and showed strong potential for MR imaging-assisted therapy.

In our study, we have investigated two sets of iron oxide-based nanospheres: the first with MNPs of 11 nm core size, coated with polyacrylic acid (PAA), dimercaptosuccinic acid (DMSA), or carboxymethyl-dextran (CM-D), and the second with MNPs of 14 nm core size, coated with either PAA or CM-D. The selected coatings ensure high colloidal and magnetic stability of the MNPs and, additionally, they promote biocompatibility, reducing possible side effects and extending the permanence of MNPs in the human body; they also allow for specific targeting.^29–33

This work aims at producing effective theranostic agents by using the relatively new microwave polyol-assisted technique,³⁴ a green method that exploits polyols as a solvent, reducer and surfactant, and microwaves as a heating source, saving energy costs and time, and preserving a narrow size distribution.³⁵

The focus is on finding the right combination of size and coating, and on the crucial role of the kind of coating. By tailoring the core size and surface coating, we found the microscopic parameters that optimize the dual functionality of these nanoparticles, enhancing their performance as contrast agents in MRI and as heating mediators in MFH. This approach seeks to maximize their clinical effectiveness, paving the way toward more precise and effective cancer diagnosis and treatments.

2 Experimental

2.1 Materials

Iron(II) acetate and diethylene glycol (DEG) were purchased from Sigma-Aldrich (St Louis, MO, USA), while poly(acrylic acid) sodium salt (PAANa, MW: 2100 g mol⁻¹), carboxymethyl-dextran sodium salt (CM-dextran, MW: 10 000–20 000 g mol⁻¹) and meso 2,3 dimercaptosuccinic acid (DMSA, MW: 182.22 g mol⁻¹) were acquired to coat and thus stabilize the MNPs. All reactants were used as received without further purification.

2.2 Synthesis of γ-Fe₂O₃ nanospheres

For the synthesis of MNPs, 300 mg (1.73 mmol) of iron(II) acetate was mixed with 18.3 mL of DEG and 0.4 mL or 0.7 mL of milliQ water, respectively, for 11 nm and 14 nm sized particles. The precursors were combined in a 30 mL vial and stirred magnetically for 20 minutes. The synthesis was conducted in a Monowave300 (Anton Paar GmbH) synthesis reactor by heating the samples to 170 °C over 50 min, maintaining this temperature for 2 h, and then cooling them to 55 °C. Gallo et al.'s work³⁴ was used as a reference for the synthesis procedure. We will refer to the produced particles as NS11 for the 11 nm set and NS14 for the 14 nm set.

2.3 Stabilization of MNPs with CM-D/PAA/DMSA

Colloidal and magnetic stabilization of the MNPs was performed by surface modification with CM-dextran (CM-D), poly(acrylic acid) sodium salt (PAANa), or dimercaptosuccinic acid (DMSA). The MNPs were dispersed in deionized (DI) water (16.6 mg of MNPs in 3.25 mL for CM-D and 20 mg of MNPs in 4 mL for PAA/DMSA) and the pH was adjusted to 2.5–3 using HNO₃. Separately, solutions of the modifying agents (CM-D, PAANa, or DMSA) were prepared in DI water, maintaining specific molar ratios of the modifier to iron: 0.0029 for CM-D, 0.0368 for PAANa, and 0.1 for DMSA. While sonicating, the modifying agent solutions (3.125 mL of CM-D and 3 mL of PAA or DMSA) were added dropwise to the MNP dispersions, followed by at least 2 hours of sonication at room temperature. The pH was then increased to 9–10 using KOH, and the mixtures were dialyzed for at least one day using membranes with a molecular weight cutoff of 12 kDa (pore size < 2.5 nm), with frequent changes of DI water. After dialysis, the pH was readjusted to 9–10 using KOH, and the dispersions were filtered through a 0.22 μm pore-size filter to remove impurities.

The different coatings will be marked in each series with the “@PAA”, “@CM-D”, and “@DMSA” tags.

Hydrodynamic sizes below 100 nm are required to favor colloidal stability under the magnetic fields applied for conducting evaluations (data are included in the ESI†).

2.4 Transmission electron microscopy (TEM)

Transmission electron microscopy (TEM) was conducted on samples prepared by air-drying a few drops of the MNP colloidal dispersion placed on a carbon-coated copper grid. TEM images were captured using a JEOL-JEM 1010 microscope operating at 100 keV equipped with a Gatan Orius 200 SC digital camera. Image analysis was performed using ImageJ software, with measurements taken from at least 150 particles. The particle diameters were then fitted to a log-normal distribution, and the most probable diameter, μ, and its associated error, σ_μ, were determined from this distribution, being μ = R₀e^σ2/2, where R₀ is the mean radius and σ its standard deviation, .

2.5 X-ray diffraction (XRD)

The X-ray diffraction (XRD) technique was utilized to obtain the XRD patterns of the samples using a Bruker D8 Advance powder diffractometer with a Cu Kα radiation source and an energy discriminator. The measurements were carried out on finely powdered samples pressed onto a silicon crystal sample holder, covering a 2θ range from 10° to 70° with an angular step of 0.04°. The resulting diffraction pattern was analyzed to determine the peak positions and widths. The crystal size of the MNPs was calculated using Scherrer and Bragg equations, taking into account instrumental broadening. In addition, the lattice parameters for each sample were derived from the XRD data using Bragg's law.

2.6 Atomic force microscopy (AFM)

AFM imaging was performed using a Nanoscope Multimode IIId system (Bruker, Santa Barbara, CA, USA) operating in tapping mode. AFM images were obtained using the RMS amplitude of the cantilever as the feedback signal for the vertical sample position. The RMS free amplitude of the cantilever was approximately 15 nm and the relative set-point was above 95% of the free amplitude. Rectangular silicon nitride probes with a nominal spring constant of ∼2.5 N m⁻¹ (NT-MDT, Russia) and cantilever length of 20 μm were used. The cantilever resonance frequency was about 130 kHz. The mica support (Ted Pella, CA, USA) was glued to a metal disk that was magnetically fixed to the AFM sample holder. The images were recorded at a line rate of ∼1 Hz, and a resolution of 512 × 512 pixels per image was chosen. All AFM images were subjected to a line-by-line subtraction of the linear background to eliminate sample tilt from the images and correct for stepwise changes between individual scan lines. The size of the MNPs, evaluated from the AFM data, has been reported in the work as the mean value ± standard deviation calculated considering n = 30 single MNPs visualized in several images of AFM topography.

2.7 Fourier transform infrared (FTIR) spectroscopy

Fourier transform infrared (FTIR) spectra were recorded to confirm the presence of the coating layers of CM-dextran, PAA, and DMSA. The measurements were performed using a Bruker Vertex 70 V spectrophotometer on a KBr pellet from dried powdered samples. 100 scans for the samples were acquired, ranging from 250–4000 cm⁻¹, with a resolution of 0.2 cm⁻¹.

2.8 Magnetometry

The magnetization curves as a function of the applied magnetic field were acquired at 300 K, ranging from −2 T to 2 T, using a Quantum Design MPMS-5 SQUID magnetometer. The samples were made of capsules filled with cotton, where the MNP suspensions were dried. The concentration of the samples was used to correct the acquisitions, and this was measured by elemental analysis (inductively coupled plasma optical emission spectroscopy, ICP-OES) after digestion in acid.

2.9 Nuclear magnetic resonance (NMR) and relaxivity

The longitudinal, T₁, and transverse, T₂, nuclear relaxation times were acquired over a wide range of Larmor frequencies (0.01 < ν < 63 MHz), i.e., external static magnetic fields of μ₀H = 0.00023 − 1.5 Tesla (, where ν is the Larmor frequency and γ/2π = 42.58 MHz T⁻¹). The relaxivity, i.e. the efficiency of MNPs as a CA, was evaluated at each frequency. The magnetic field range was chosen to cover the most typical fields used in clinical and research laboratory MRI tomography (μ₀H = 0.2, 0.5, and 1.5 T). Different instrumentation and acquisition sequences were used depending on the frequency range.

2.9.1 0.01 MHz < ν < 7.2 MHz. The fast field cycling technique was performed using a fast-field-cycling NMR SMARTracer relaxometer (Stelar s.r.l., Mede, Italy).³⁶ In the case of measurements using ν < 3.7 MHz, pre-polarized (PP) pulse sequences were applied to overcome the low signal-to-noise ratio: saturation recovery (SR) for T₁ and spin-echo (SE) for T₂. For ν > 3.7 MHz, no pre-polarization procedure was applied, and thus no pre-polarized (NP) pulse sequences were used. For T₁ and T₂ measurements, the standard SR sequence and a classical Carr–Purcell–Meiboom–Gill (CPMG) sequence were applied, respectively.

2.9.2 7.2 MHz < ν < 63 MHz. The acquisitions were performed by using a classic electromagnet, MAGNET B-E 25 from Bruker (Billerica, MA, USA) and a Tecmag Apollo Fourier transform NMR spectrometer with standard SR pulse sequence to acquire T₁, while CPMG was used for T₂ acquisitions.

All measurements were conducted at room temperature. The samples were prepared by diluting the MNPs in DI water to achieve a millimolar concentration.

From the T₁ and T₂ measurements, we extracted the nuclear relaxivities. The longitudinal (i = 1) and transverse (i = 2) nuclear relaxivity, r_i, represent the efficiency of the particles in shortening the T₁ and T₂ values of ¹H nuclei, i.e., in enhancing the image contrast in MRI. The relaxivities are defined as:

where C is the concentration of the paramagnetic centers (millimolar, mM), T_i,m is the relaxation time of hydrogen nuclei in the presence of contrast agents (i.e., MNPs), and T_i,dia is the relaxation time of the hydrogen nuclei in the dispersant medium (diamagnetic, dia). The measurements were performed after diluting the former stock solution; from the relaxivity values, we obtained the NMR-dispersion (NMR-d) profiles for each sample. The error on the relaxivity values was calculated a priori to be ∼10%, due to the electronics and the error on the acquisition parameters.

2.10 Magnetic fluid hyperthermia and specific absorption rate

The hyperthermia measurements were conducted on aqueous dispersions of MNPs. The acquisitions of temperature variations vs. time (of the AMF application) were carried out using a Magnetherm™ NAN201006 instrument (nanoTherics Ltd, Warrington, UK). A high field strength option and an 18-turn water-cooled copper coil were properly used to adjust the frequencies of the external magnetic field from 102.2 kHz to 971.2 kHz, and its amplitude from 7 mT to 40 mT (the maximum magnetic field strength depends on the AMF frequency).

The frequencies and their corresponding maximum magnetic field strengths are summarized in Table 1. The system is equipped with two fiber-optic temperature probes. To ensure consistent and reproducible magnetic field applications, the sample was carefully positioned at the center of the coil. The sample dispersions were tested at magnetic nanoparticle (MNP) concentrations ranging from 0.2 mg mL⁻¹ to 2 mg mL⁻¹.

Table 1 Maximum magnetic field peak strength and AMF frequencies used for the measurements of this work performed with the Magnetherm™ system; ν = frequency and μ₀H = AMF intensity

ν (kHz)	102.20	167.10	250.80	423.70	598.90	971.20
μ0H (mT)	30	40	38	30	28	20
ν·μ0H (kA s^−1 m^−1)	24.4 × 10^5	53.2 × 10^5	75.8 × 10^5	101.1 × 10^5	133.4 × 10^5	1545.6 × 10^5

---

The SAR of the MNPs was determined from the temperature increase rate acquired from calorimetric experiments, utilizing the following expression:

where m_H2O and m_γ-Fe2O3 represent the masses of water and maghemite in the colloidal solutions, respectively; c_H2O = 4.18 JK⁻¹ g⁻¹ and c_γ-Fe2O3 = 0.75 JK⁻¹ g⁻¹ are the specific heat of water and maghemite, respectively.

3 Results and discussion

3.1 Morpho-structural properties

The TEM images are displayed in Fig. 1. The first set of MNPs has a mean core diameter of 11 ± 2 nm and MNPs were coated with PAA, DMSA, or CM-D, while the second set has a mean core diameter of 14 ± 2 nm and MNPs were coated with PAA or CM-D.

Fig. 1 TEM images of the investigated samples. The magnetic cores are coated with a thin layer of DEG, which results from the synthesis process prior to surface modification with PAA, CM-D, or DMSA. (a) NS11 sample. (b) NS14 sample.

Spherical particles with a mean size below a critical diameter display a single domain configuration,³⁷ which for maghemite is estimated to be about 168 nm³⁸ while for magnetite, it is estimated to be about 100 nm.^39–41 By further reducing the size, the coercivity is reduced to zero and superparamagnetic (SPM) behavior is observed (usually below ∼20 nm).⁴²

The AFM technique enabled the assessment of the overall size of the MNPs, which includes both the magnetic core and the surrounding coating (see Fig. 2 and ESI_Fig. 1†). Furthermore, AFM allowed for the differentiation between MNP agglomerates and individual MNPs. As anticipated, the average diameter measured by AFM was larger than that estimated from the TEM data, as expected because of the coating. The thickness of the coating, estimated from the difference in diameters obtained by the two techniques, is approximately of the order of 1 nm for both MNP sets and for the different coatings studied in this work (Table 2). The resulting thickness of the coatings does not take into account the number of layers deposited; as a consequence, it could happen that smaller molecules yield a thicker coating.

Fig. 2 AFM topography images of the studied PAA-coated MNPs. Single particles and MNP small clusters are visualized on a mica support; the images were collected in air in tapping mode. Scan area: 1 × 1 μm². Range of the vertical color scale: 0–15 nm. (a) NS11 sample. (b) NS14 sample.

Table 2 Dimensions of the investigated samples, estimated from the TEM and AFM analyses: core diameter d_TEM and overall MNP diameter d_AFM (core + coating)

Sample	Coating	dTEM (nm)	dAFM (nm)
NS11@PAA	PAA	11 ± 2	13.5 ± 0.8
NS11@CM-D	CM-D	11 ± 2	13.8 ± 1.0
NS11@DMSA	DMSA	11 ± 2	14.1 ± 1.0
NS14@PAA	PAA	14 ± 2	15.8 ± 1.1
NS14@CM-D	CM-D	14 ± 2	16.2 ± 1.1

---

The X-ray diffraction (XRD) patterns, shown in Fig. 3, confirm the presence of a cubic spinel structure. The crystal size and lattice parameters were determined using the Scherrer equation, which was applied to the width of the peak corresponding to the reflection of the (4 0 0) crystallographic plane. The values are shown in Table 3, where we can see that the resulting crystal size is always comparable with the TEM size, within the experimental error. In terms of lattice parameters, the NS11 set displays values that fall between those of maghemite (a = 8.3461 Å, JCPDS 39-13⁴³) and magnetite (a = 8.396 Å, JCPDS 19-062940). In contrast, the lattice parameter of NS14 particles can be associated with just the presence of maghemite.

Fig. 3 XRD patterns of the NS11 and NS14 magnetic cores.

Table 3 Elemental composition, crystal size, lattice constant, and saturation magnetization of the cores of the investigated samples

Sample	Composition	Crystal size (nm)	Lattice constant (A)	Saturation magnetization (Am^2 kg^−1)
NS11	γ-Fe2O3	11.0 (2)	8.36 (0.01)	87.7 (0.2)
NS14	γ-Fe2O3	15.3 (3)	8.34 (0.01)	88.6 (0.1)

---

The FTIR transmittance spectra shown in Fig. 4 confirm the presence of coatings on the surface of the particles. Some common features are found in the peaks observed at 3422 cm⁻¹ and at 2925 cm⁻¹, assigned respectively to O–H and C–H vibrations due to water molecules absorbed at the surface and to the hydroxyl groups present in the molecules coating the particles; as well as in the initial DEG, the peaks between 1400 cm⁻¹ and 1300 cm⁻¹ were assigned to CH₂ bond vibrations while the peaks located at 1154 cm⁻¹, 1107 cm⁻¹ and 1012 cm⁻¹ were assigned to C–O vibrations.^44,45

Fig. 4 FTIR transmittance spectra of the uncoated (magnetic cores) and coated (with PAA, CM-D, and DMSA) MNPs. (a) NS11 samples. (b) NS14 samples.

The peaks observed are indicative of bond formation between the coatings and the iron oxide surface. For the PAA, the peaks at 1560 and 1454 cm⁻¹ correspond to the R–COO⁻ antisymmetric and symmetric stretching vibrations, indicating that PAA was coordinated directly with the surfaces of iron oxides.⁴⁶ The same was observed for the DMSA (peak at 1590 cm⁻¹) and for the CM-D (peak at 1596 cm⁻¹); these peaks can also be related to the vibrations of the carboxylic group (COO⁻) of DMSA and CM-D bound to the particle surface. Unbound carboxylic groups will present an absorption band at 1710 cm⁻¹.

The peaks found for all the samples in the 630 and 400 cm⁻¹ region (light red area in Fig. 4) are representative of the bending and stretching vibrations of Fe–O. Upon oxidation to form maghemite, these peaks become more complex. Samples from both sets of MNPs display this feature, which is more pronounced in the NS14 core, suggesting a higher degree of oxidation than that in the NS11 sample, in agreement with the XRD data.

3.2 Magnetic properties

The magnetic behavior of the particles was studied by recording the hysteresis loops at 300 K (Fig. 5) for particle dispersions dried on cotton. The coercive field that resulted in both cases was lower than 0.0015 T, suggesting the substantially superparamagnetic nature of the systems, which is expected for particles of comparable size.⁴⁷ The saturation magnetization of the NS11 samples is 87.8 Am² kg_[MNP]⁻¹ and that of the NS14 sample is 88.1 Am² kg_[MNP]⁻¹, which are in line with the values reported for particles produced with classic thermal decomposition in organic solvents (82 Am² kg_[MNP]⁻¹ (ref. 48)) and with the proposed synthesis method (78 Am² kg_[MNP]⁻¹ (ref. 49)). Despite the larger size of NS14 particles compared to that of NS11 particles, their magnetization values are similar. XRD and IR analyses revealed that the NS11 core has a lattice parameter and a transmittance peak indicative of the presence of unoxidized magnetite (maghemite); in fact maghemite has a disordered internal structure, and thus a lower magnetic response. This may contribute to the higher saturation magnetization (M_S) observed in the smaller particles. As the magnetization values are corrected by using the TGA results, we can also consider the coercive field H_C variation (more significant): the largest H_C for the NS11 particles agrees well with the presence of magnetite, which has a larger magnetic anisotropy than maghemite.

Fig. 5 Hysteresis loops of the studied MNPs acquired at 300 K. The values are expressed in Am² kg⁻¹ of MNPs.

In Table 3, the morphological and magnetic properties of the investigated particles are summarized.

3.3 Nuclear magnetic resonance

In Fig. 6 and 7, the longitudinal (r₁) and transverse (r₂) relaxivity profiles for the sets of 11 nm and 14 nm MNPs are shown. The commercial contrast agent Endorem (withdrawn from the market), indicated with grey stars, shows lower efficiency compared to all of the samples studied here.

Fig. 6 Longitudinal (r₁) and transverse (r₂) relaxivity ¹H-NMR-d profiles of the NS11@DMSA, NS11@PAA, and NS11@CM-D samples. Acquisitions were performed at RT. Endorem r_1,2 values are marked with grey stars. Endorem is used as a reference for CA efficiency evaluation. (a) Longitudinal relaxivity. (b) Transverse relaxivity.

Fig. 7 Longitudinal (r₁) and transverse (r₂) relaxivity ¹H-NMR-d profiles of the NS14@PAA and NS14@CM-D samples. Acquisitions were performed at RT. Endorem r_1,2 values are marked with grey stars. Endorem is used as a reference for CA efficiency evaluation. (a) Longitudinal relaxivity. (b) Transverse relaxivity.

The longitudinal ¹H-NMR-d profiles of the 11 nm particles display a peak in r₁ relaxivity at ∼2 MHz, where the signal for the sample coated with PAA is marginally more intense. The absence of dispersion features at low frequencies suggests high values of magnetic anisotropy energy. The 14 nm-sized particles with diverse coatings exhibit a frequency behavior essentially superimposed, within the experimental error: the peak is missing and the relaxation rate increases monotonously as it approaches the zero-field limit. The high relaxivity values at the lowest frequencies (r_1,2 > 200 s⁻¹ mM⁻¹) are signatures of high anisotropy. As the external field approaches zero, Néel relaxation becomes the dominant mechanism, which depends on the energy barrier K_effV, where K_eff is the effective anisotropy constant and V is the magnetic core volume.

The transverse r₂ relaxivity profiles reach a plateau at ∼2.5–3 MHz in both sets of samples, even though relaxivity of NS11@PAA is apparently still slightly increasing. For the smallest NS11 set, different coatings give rise to different r₂ plateau intensities at high frequencies, while for the largest NS14 set, r₂ values of samples with different coatings are comparable within the experimental error. The r₂ plateau values observed in the smallest NS11 set are ∼264 s⁻¹ mM⁻¹ (NS11@CM-D), ∼382 s⁻¹ mM⁻¹ (NS11@DMSA), and ∼557 s⁻¹ mM⁻¹ (NS11@PAA), with the PAA-coated particles being more efficient. CM-D molecules may cover the magnetic core non-homogeneously, with a layer that is usually thick when compared with DMSA and PAA molecules, which influences surface spin exposure to the surrounding environment;³² moreover, the smaller PAA molecules are rich in carboxylic groups and coat the magnetic core homogeneously, thus promoting higher surface spin order and reduced spin canting. This could positively influence the magnetic response of the particles, and potentially their transverse r₂ relaxivity, but the dependency of r₂ efficiency on the dynamics has to be considered also; therefore, the coating structure alone might not be enough to explain the resulting data. Since the magnetic core of the NS11 set is the same, the change of r₂ values with coating indicates that the type, the thickness and permeability of the coating can impact the global spin dynamics. The results show that by tailoring the dimensions of the core and the type of coating, it is possible to manage the relaxometric efficiency of MNPs. Interestingly, in the case of the present samples, the coating effect is already evident at unexpected particle dimensions compared to past results.⁵⁰ However, in the case of ref. 50, different types of coatings were considered and, consequently, it can be concluded that for the same (or similar) size, the type of coating is crucial in determining effects on r₁ and r₂.

For all samples, above 1 MHz, the r₂/r₁ value was found to be higher than 2 (Fig. 8), indicating that these samples may be suitable as T₂ contrast agents in this frequency region.^51,52 As shown in ref. 53, the outer-sphere theory implies that the r₂/r₁ ratio increases with increasing particle size. It is deduced that in this case, both sets are very efficient T₂-shortening agents, with NS14 being on average the more efficient. The resulting hydrodynamic sizes (ESI_Fig. 2 and ESI_Table 1†) do not show significant discrepancies among the differently coated particles.

Fig. 8 The r₂/r₁ ratio as a function of the frequency for all the investigated samples.

Regarding the effect of the size, one can conclude that the NS11 set exhibits the characteristic peaked profile at around 2 MHz of r₁ vs. frequency typical of MNPs with dimensions < 20 nm, although the low-frequency “dispersion” point is missing. Conversely, the peak disappears for the largest MNPs of the NS14 set, as expected for higher magnetic anisotropy.

Regarding the effect of the coating, it is found that 11 nm particles show r₁ peak intensity values at ∼2 MHz that seem partially affected by the coating, whereas the peak intensity of NS11@PAA is the most pronounced. The transverse r₂ plateau values (∼3 MHz for NS14 and ∼11 MHz for NS11) show differences when the coating is changed and particularly PAA doubles the CM-D r₂ relaxometric efficiency. For the 14 nm particles, the resulting r_1,2 values are comparable within the experimental error, indicating the equivalence (for spin dynamics) of PAA and CM-D coatings.

3.4 The Roch–Müller–Gillis (RMG) heuristic model

The r₁ profiles were fitted using the Roch–Müller–Gillis (RMG) heuristic model⁵⁴ (more details can be found in the ESI†) to obtain microscopic information about the chemico-physical properties of the MNPs. The obtained fitting curves are shown in Fig. 9. This analysis provided insights into parameters such as the core size r_C, the Néel relaxation time τ_N, and the distance of minimum approach R between the magnetic centers and the water molecules. The values of the parameters extracted from the fit are summarized in Table 4. The fittings were done by fixing the temperature T at 300 K, the diffusion coefficient D at a theoretical value of 2.3 × 10⁻⁹ m² s⁻², and the saturation magnetization M_S at the values obtained from magnetic measurements, namely 87.8 Am² kg⁻¹ for the NS11 and 88.1 Am² kg⁻¹ for the NS14 sets.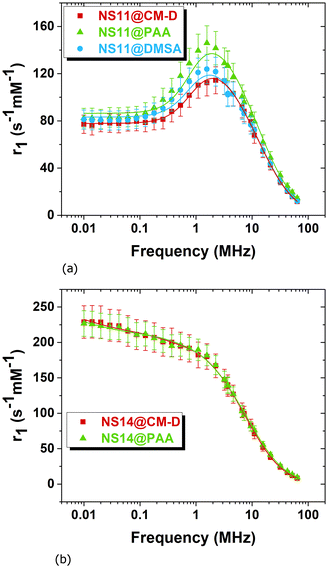

Fig. 9 Longitudinal relaxivity r₁ profiles of the NS11@CM-D, NS11@PAA, and NS11@DMSA samples (a) and the NS14@CM-D and NS14@PAA samples (b) fitted with the Roch–Müller–Gillis heuristic model.

Table 4 Parameters extracted from the fit of the r₁ ¹H-NMR-d profiles with the RMG model. M_S was fixed at values resulting from the magnetic measurements. The core size r_C was a free parameter initialized with the r_TEM for the NS11 set, while it was fixed to the r_TEM for the NS14 one. The Néel relaxation time τ_N and the distance of minimum approach R are also listed

Sample	MS (Am^2 kg^−1)	rTEM (nm)	rC (nm)	τN (s)	R (nm)
NS11@DMSA	87.8	5.5 ± 1	6.5 ± 0.4	(1.53 ± 6.0) × 10^−8	8.1 ± 0.3
NS11@PAA	87.8	5.5 ± 1	6.5 ± 0.4	(1.16 ± 5.0) × 10^−8	8.3 ± 0.3
NS11@CM-D	87.8	5.5 ± 1	6.4 ± 0.2	(2.97 ± 0.65) × 10^−8	8.3 ± 0.1
NS14@PAA	88.1	7 ± 1	7.0	(1.30 ± 0.7) × 10^−6	9.78 ± 0.01
NS14@CM-D	88.1	7 ± 1	7.0	(2.26 ± 1.0) × 10^−6	10.32 ± 0.02

---

Regarding the core radius, it was treated as a free parameter for the smallest MNPs of the NS11 set, initialized with the value estimated from TEM analysis and constrained within the experimental error, while for the largest MNPs of the NS14 set, it was fixed at the resulting r_TEM value to allow for the convergence of the fitting procedure. Regarding the fitting results, it is found that the resulting core radius r_C is compatible with r_TEM. The Néel relaxation times τ_N are of the order of 10⁻⁸ s for NS11, while for the NS14 set Néel relaxation times are of the order of 10⁻⁶ s or less, in agreement with the proportionality of the anisotropy and volume of MNPs.§ However, this τ_N value is longer than that usually observed for 14 nm-sized particles (another sign of the high anisotropy of the NS14 set of particles). The distance of minimum approach R resulted in [1.6 nm ÷ 3.3 nm] > r_C, suggesting the presence of a thick non-permeable additional layer in both NS11 and NS14 sets.

In summary, the main outcomes of the fits by the Roch–Müller–Gillis heuristic model of the experimental longitudinal r₁ ¹H-NMR-d profiles are: (i) the Néel relaxation time τ_N is on the order of 10⁻⁸ s for the NS11 particles and on the order of 10⁻⁶ s for the NS14 ones. Considering the model constraints (non-interacting particles) and the τ_N ≪ τ_D condition, more quantitative information about different coatings are difficult to be estimated. (ii) The distance of minimum approach R exceeds the core radius, indicating a thick, partially non-penetrable layer for both sets of MNPs and their coatings.

3.5 Magnetic fluid hyperthermia

In Fig. 10, the specific absorption rate (SAR) values evaluated using eqn (2) at different AMF frequencies f and amplitudes H are shown. As the coating is changed, no significant variations are observed at each (ν, μ₀H) combination, while if considering the size variations, it is found that the largest NS14 particles are more efficient in releasing heat; under the highest field conditions (971.2 kHz, 20 mT), the NS14 set has a SAR of ∼ 170 W g⁻¹, while the NS11 set has a SAR on average of ∼106 W g⁻¹. In ref. 55, it is found that under the field conditions of 109.8 kHz and 20 mT, 10 nm DMSA-coated MNPs showed SAR values comparable with our results under field conditions of 102.2 kHz and 20 mT for the NS11 set of MNPs (SAR ∼ 8 W g⁻¹), while if we consider 14 nm-sized particles under the same field conditions, the results for our MNPs are ∼50% less efficient than those for MNPs described in the literature; this discrepancy can be traced back to different synthesis techniques: our MNPs were synthesized thorough MW-assisted thermal decomposition in a polyol medium, whereas in ref. 55, the synthesis was carried out thorugh classic thermal decomposition in an organic medium. Additionally, the discrepancy may also arise from the reduced homogeneity of our particle size distribution. By considering the work of Lemine et al.,⁵⁶ it is observed that 14 nm particles synthesized with a sol–gel method, under similar field conditions (110 kHz, 18 mT), display a SAR value of 30 W g⁻¹, meaning a lower efficiency when compared with our results (∼50 W g⁻¹).

Fig. 10 SAR values of the samples dispersed in water vs. the applied H at different f values. The LRT model validity limits are indicated by the grey bar (ξ < 1 with its uncertainty). The continuous lines mark the best-fitting curves obtained using the LRT model (applied within its validity limits). The dotted lines represent the best fit to the free-exponent model. The dark blue rhombi represent 971.2 kHz, the blue stars represent 598.9 kHz, the light blue flipped triangles represent 423.7 kHz, the light yellow circles represent 250.8 kHz, the light brown triangles represent 167.2 kHz, and the brown squares represent 102.2 kHz. (a) NS11@CM-D. (b) NS11@DMSA. (c) NS11@PAA. (d) NS14@CM-D. (e) NS14@PAA.

It is worth being reminded that the LRT model (linear response theory model), in which SAR = αH²,⁵⁷ is valid for ξ = μ₀M_SvVH_max/k_BT < 1, where μ₀ is the vacuum permeability, M_Sv is the volumetric saturation magnetization and k_B is the Boltzmann constant. The ξ < 1 region is limited for the NS11 set in the 3.4 < μ₀H_max < 10.2 mT range, while for the NS14 set, it is limited in the 5.3 < μ₀H_max < 24.7 mT range. Beyond these limits, the free-exponent model SAR(H) = βH^x was used.

3.6 SAR vs. H

The SAR vs. field amplitude was investigated in and out of the LRT regime.

For the smallest NS11 particles, the NS11@DMSA, NS11@PAA, and NS11@CM-D samples are well represented by the LRT model within the ξ < 1 region (continuous lines in Fig. 10a–c); for NS11@CM-D at a frequency of 971.2 kHz, the model reaches its limits. On the other hand, the free-exponent power-law model SAR(H) = βH^x was used out of the LRT regime (ξ > 1) (dotted lines in Fig. 10a–c). The value of the exponent x ranges from 2 to 3 and corresponds to regime behavior intermediate between the LRT model and the Rayleigh model, with the latter being valid for multidomain particles and described by the power-law model SAR = γH³.

Regarding the largest NS14 particles, all data fall outside the area of the LRT model and so they were fitted only with the free-exponent power-law model. The fitting curves are in agreement with the experimental data (dotted lines in Fig. 10d and e). A small constant term was added to the SAR expression to account for the contribution of the sample holder.

The energy absorbed by the MNPs and subsequently dissipated in the environment is described by the imaginary susceptibility χ′′ of the system. The susceptibility can be evaluated by using the LRT model as χ′′(f) = αC/μ₀πf, where C is the concentration of the MNPs and α represents the coefficient of the slope of the quadratic power-law model used to fit the data within the range of the LRT limits. Only the NS11 set satisfies the ξ < 1 condition, giving the possibility of calculating the χ′′(f) values of NS11@PAA, NS11@DMSA, and NS11@CM-D, which resulted in the range of 10⁻²–10⁻¹; τ values were extracted by fitting χ′′(f) as a function of f, using the expression , where V is the volume of a single MNP and Φ is the volumetric fraction occupied by the magnetic material, calculated as V_NP/V_disp (V_NP is the volume occupied by all the MNPs and V_disp is the total volume of the measured sample). The order of magnitude of τ is 10⁻⁸ s, comparable to the results obtained from the ¹H-NMR-d fit.

3.7 SAR vs. f at constant H

Conducting further analysis, we focused on the SAR variation vs. frequency f of the applied AMF at 10 mT, 20 mT, and 30 mT.

For the NS11 set, the SAR increases monotonously with f for all the samples at each frequency.

For the NS14 set, one can observe a minimum at 167 ± 32 kHz for every field amplitude and coating (see Fig. 11) (some points are experimental while others were extracted from the free-exponent fitting curves and marked in the graphs with black arrows). A minimum is representative of a quasi-static response of the system. The effective relaxation time τ_eff = 1/ω = 1/2πf_min was evaluated with this tentative procedure, which includes some approximations, and it was found to be (9.5 ± 2.0) × 10⁻⁷ s. Since the Brownian contribution can be considered negligible for this core dimension, it might be assumed that τ_eff represents the Néel relaxation time, paying attention to the fact that the size distribution of our MNPs includes larger particles, and so this assumption may not be entirely correct. The resulting value is consistent with the values obtained from the ¹H-NMR Roch–Müller–Gillis fitting parameters, roughly confirming the order of magnitude of the Néel correlation time, which is unusually long for spherical particles of this size.

Fig. 11 SAR vs. f of the NS14-coated samples at AMF amplitude H values of 10, 20, and 30 mT. The black arrows indicate the points evaluated from the free exponential best-fit curves.

In summary, the NS11 set follows the linear response theory model up to 24 mT, i.e., the quadratic model accurately describes the SAR increase with H, SAR = αH², except in NS11@CM-D for f ≃ 971.2 kHz. The NS14 set never falls within the LRT model validity conditions; thus the free-power law model was applied (SAR = βH^x), and the exponent value always fell between 2 and 3, i.e., below the Rayleigh model value of x = 3.

For the NS11 particles, we estimated the imaginary component of the susceptibility χ′′ inside the LRT regime, and then we tentatively evaluated the effective correlation time , which resulted of the order of 10⁻⁷ s, in agreement with the NMR Roch–Müller–Gillis model. The Brownian rotation (τ_B) can thus be assumed to be irrelevant in the heating release process, but it should be noted that the size distribution of MNPs includes also larger particles that can partially contribute through Brownian relaxation.

4 Conclusions

Spherical γ-Fe₂O₃ nanoparticles of different sizes and with different coatings were investigated to assess their dual role as contrast agents in magnetic resonance imaging and as heating mediators in magnetic fluid hyperthermia.

It has been observed that (i) the combination of size and coating turned out to be significant for small MNPs that can act as T₂ MRI contrast agents, with the r₂ plateau of the NS11 set being increased about 2 times when PAA is used, a result that is not reproduced in the NS14 set, possibly due to the lower surface/volume ratio that leads to different effects (diverse dynamics of surface spins, core spin contribution, etc.) and (ii) larger size leads to more efficient hyperthermic agents for MFH.

Thus, this study shows how the NMR-detected spin dynamics of nanosystems is subject to modification due to morphological and surface properties. The understanding of the variation of the corresponding physical properties could allow their characteristics to be fine-tuned to optimize their application performances across multiple fields of interest.

Author contributions

Conceptualization, A. L. and M. P. M.; synthesis, M. P. and C. D.-U.; characterization measurements, M. P.; coating process, M. P. and C. D.-U.; NMR setup, M. P., F. B. and M. M.; NMR measurements and analysis, M. P.; AFM measurements and analysis, F. O.; discussions, M. P., F. B., M. P. M. and A. L.; writing – original draft preparation, M. P. and F. B.; writing – review and editing, A. L., P. A., and M. P. M.; supervision, A. L. and M. P. M. All authors have read and agreed to the published version of the manuscript.

Data availability

Supporting data of this study are available from the corresponding author upon reasonable request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The INFN-CSN5 MATHER3D (MAgnetic hyperthermia and hadron THERapy applied to 3D cellular scaffolds) is gratefully acknowledged for its financial support and contribution to this research. The MIUR Dipartimento di Eccellenza 2018–2022 project F11I18000680001 is also gratefully acknowledged. F. Borsa is gratefully acknowledged for discussions and reading the manuscript. The European projects, 101007629-NESTOR (H2020-MSCARISE-2020) and IMAGINE (Implementing Magnetic targeting of nano-Guided ImmuNE cells, funded by the European Science Foundation, Fight Kids Cancer 2020), are also acknowledged.

References

1. B. Rezaei, P. Yari, S. M. Sanders, H. Wang, V. K. Chugh, S. Liang, S. Mostufa, K. Xu, J.-P. Wang and J. Gomez-Pastora, et al., Small, 2024, 20, 2304848.
2. A. K. A. Silva, A. Espinosa, J. Kolosnjaj-Tabi, C. Wilhelm and F. Gazeau, Iron Oxides: From Nature to Applications, 2016, pp. 425–472.
3. F. Brero, Multifunctional modalities of iron oxide magnetic nanoparticles: applications in diagnostics and magnetic fluid hyperthermia, PhD thesis, Università di Pavia, 2021.
4. S. E. Sanni and R. E. Sadiku, in Nanostructured Materials for Biomedical Applications, Elsevier, 2024, pp. 203–228.
5. B. Sabzi Dizajyekan, A. Jafari, M. Vafaie-Sefti, R. Saber and Z. Fakhroueian, Sci. Rep., 2024, 14, 1296.
6. W.-Y. Huang and J. J. Davis, Dalton Trans., 2011, 40, 6087–6103.
7. S. Sanchez-Cabezas, R. Montes-Robles, J. Gallo, F. Sancenon and R. Martinez-Manez, Dalton Trans., 2019, 48, 3883–3892.
8. C. Xu and S. Sun, Dalton Trans., 2009, 5583–5591.
9. Y. Q. Meng, Y. N. Shi, Y. P. Zhu, Y. Q. Liu, L. W. Gu, D. D. Liu, A. Ma, F. Xia, Q. Y. Guo and C. C. Xu, et al., J. Nanobiotechnol., 2024, 22, 24.
10. S. Patri, N. T. K. Thanh and N. Kamaly, Nanoscale, 2024, 16(33), 15446–15464.
11. T. Tegafaw, S. Liu, M. Y. Ahmad, A. K. A. A. Saidi, D. Zhao, Y. Liu, S.-W. Nam, Y. Chang and G. H. Lee, Pharmaceutics, 2023, 15, 1745.
12. Y. X. J. Wáng and J.-M. Idée, Quant. Imaging Med. Surg., 2017, 7, 88.
13. A. Avasthi, C. Caro, E. Pozo-Torres, M. P. Leal and M. L. García-Martín, Surface-modified nanobiomaterials for electrochemical and biomedicine applications, 2020, pp. 49–91.
14. S. Rahmati and A. E. David, Appl. Mater. Today, 2024, 37, 102087.
15. D. Liu, J. Li, C. Wang, L. An, J. Lin, Q. Tian and S. Yang, Nanomedicine, 2021, 32, 102335.
16. F. Ahmadpoor, A. Masood, N. Feliu, W. J. Parak and S. A. Shojaosadati, Front. Nanotechnol., 2021, 3, 644734.
17. P. Hermann, J. Kotek, V. Kubíček and I. Lukeš, Dalton Trans., 2008, 3027–3047.
18. L. Kubíčková, MSc thesis, Univerzita Karlova, Matematickofyzikální fakulta, 2021.
19. P. Arosio, F. Orsini, F. Brero, M. Mariani, C. Innocenti, C. Sangregorio and A. Lascialfari, Dalton Trans., 2023, 52, 3551–3562.
20. H. Etemadi and P. G. Plieger, Adv. Ther., 2020, 3, 2000061.
21. F. Reyes-Ortega, Á.V Delgado and G. R. Iglesias, Nanomaterials, 2021, 11, 627.
22. L. Beola, N. Iturrioz-Rodríguez, C. Pucci, R. Bertorelli and G. Ciofani, ACS Nano, 2023, 17, 18441–18455.
23. F. Brero, P. Calzolari, M. Albino, A. Antoccia, P. Arosio, F. Berardinelli, D. Bettega, M. Ciocca, A. Facoetti and S. Gallo, et al., Nanomaterials, 2023, 13, 791.
24. H. Gavilán, K. Simeonidis, E. Myrovali, E. Mazarío, O. Chubykalo-Fesenko, R. Chantrell, L. Balcells, M. Angelakeris, M. P. Morales and D. Serantes, Nanoscale, 2021, 13, 15631–15646.
25. I. D. Shabalkin, A. S. Komlev, S. A. Tsymbal, O. I. Burmistrov, V. I. Zverev and P. V. Krivoshapkin, J. Mater. Chem. B, 2023, 11, 1068–1078.
26. A. Adam, K. Parkhomenko, P. Duenas-Ramirez, C. Nadal, G. Cotin, P.-E. Zorn, P. Choquet, S. Bégin-Colin and D. Mertz, Molecules, 2021, 26, 971.
27. F. Perton, M. Tasso, G. A. M. Medina, M. Ménard, C. Blanco- Andujar, E. Portiansky, M. B. F. van Raap, D. Bégin, F. Meyer and S. Begin-Colin, et al., Appl. Mater. Today, 2019, 16, 301–314.
28. W. Wang, F. Li, S. Li, Y. Hu, M. Xu, Y. Zhang, M. I. Khan, S. Wang, M. Wu and W. Ding, et al., J. Mater. Sci. Technol., 2021, 81, 77–87.
29. G. Dalei and S. Das, J. Drug Delivery Sci. Technol., 2022, 78, 103988.
30. L. Zhang, X. Wang, J. Zou, Y. Liu and J. Wang, Chem. Res. Toxicol., 2015, 28, 1961–1974.
31. F. Paulini, A. R. Marangon, C. L. Azevedo, J. L. Brito, M. S. Lemos, M. H. Sousa, F. H. Veiga-Souza, P. E. Souza, C. M. Lucci and R. B. Azevedo, Nanomaterials, 2022, 12, 3513.
32. Y. Portilla, S. Mellid, A. Paradela, A. Ramos-Fernandez, N. Daviu, L. Sanz-Ortega, S. Perez-Yague, M. P. Morales and D. F. Barber, ACS Appl. Mater. Interfaces, 2021, 13, 7924–7944.
33. V. Ayala, A. P. Herrera, M. Latorre-Esteves, M. Torres-Lugo and C. Rinaldi, J. Nanopart. Res., 2013, 15, 1874.
34. Á. Gallo-Cordova, A. Espinosa, A. Serrano, L. Gutiérrez, N. Menéndez, M. del Puerto Morales and E. Mazarío, Mater. Chem. Front., 2020, 4, 3063–3073.
35. F. Fiévet, S. Ammar-Merah, R. Brayner, F. Chau, M. Giraud, F. Mammeri, J. Peron, J.-Y. Piquemal, L. Sicard and G. Viau, Chem. Soc. Rev., 2018, 47, 5187–5233.
36. E. Anoardo, G. Galli and G. Ferrante, Appl. Magn. Reson., 2001, 20, 365–404.
37. G. F. Goya, T. Berquo, F. C. Fonseca and M. Morales, J. Appl. Phys., 2003, 94, 3520–3528.
38. D. L. Leslie-Pelecky and R. D. Rieke, Chem. Mater., 1996, 8, 1770–1783.
39. Q. Li, C. W. Kartikowati, S. Horie, T. Ogi, T. Iwaki and K. Okuyama, Sci. Rep., 2017, 7, 9894.
40. J. Baumgartner, L. Bertinetti, M. Widdrat, A. M. Hirt and D. Faivre, PLoS One, 2013, 8, e57070.
41. S. Zhao, Q. Sun, R. Wang and Y. Han, Sci. China:Phys., Mech. Astron., 2011, 54, 1208–1212.
42. K. N. Koo, A. F. Ismail, M. H. D. Othman, N. Bidin and M. A. Rahman, et al., J. Fundam. Appl. Sci., 2019, 15, 23–31.
43. A. Demortiere, P. Panissod, B. Pichon, G. Pourroy, D. Guillon, B. Donnio and S. Bégin-Colin, Nanoscale, 2011, 3, 225–232.
44. G. Liu, R. Hong, L. Guo, Y. Li and H. Li, Appl. Surf. Sci., 2011, 257, 6711–6717.
45. K. Vasić, Ž Knez, E. A. Konstantinova, A. I. Kokorin, S. Gyergyek and M. Leitgeb, React. Funct. Polym., 2020, 148, 104481.
46. H. Hu, J. Saniger, J. Garcia-Alejandre and V. Castaño, Mater. Lett., 1991, 12, 281–285.
47. J. Dulińska-Litewka, A. Łazarczyk, P. Hałubiec, O. Szafrański, K. Karnas and A. Karewicz, Materials, 2019, 12, 617.
48. A. G. Roca, S. Veintemillas-Verdaguer, M. Port, C. Robic, C. J. Serna and M. P. Morales, J. Phys. Chem. B, 2009, 113, 7033–7039.
49. A. Gallo-Cordova, S. Veintemillas-Verdaguer, P. Tartaj, E. Mazarío, M. d. P. Morales and J. G. Ovejero, Nanomaterials, 2021, 11, 1052.
50. F. Brero, P. Arosio, M. Albino, D. Cicolari, M. Porru, M. Basini, M. Mariani, C. Innocenti, C. Sangregorio and F. Orsini, et al., Nanomaterials, 2023, 13, 804.
51. H. Amiri, L. Bordonali, A. Lascialfari, S. Wan, M. P. Monopoli, I. Lynch, S. Laurent and M. Mahmoudi, Nanoscale, 2013, 5, 8656–8665.
52. K. E. Kellar, D. K. Fujii, W. H. Gunther, K. Briley-Sæbø, A. Bjørnerud, M. Spiller and S. H. Koenig, J. Magn. Reson. Imaging, 2000, 11, 488–494.
53. C. F. Geraldes and S. Laurent, Contrast Media Mol. Imaging, 2009, 4, 1–23.
54. A. Roch, R. N. Muller and P. Gillis, J. Chem. Phys., 1999, 110, 5403–5411.
55. M. Avolio, A. Guerrini, F. Brero, C. Innocenti, C. Sangregorio, M. Cobianchi, M. Mariani, F. Orsini, P. Arosio and A. Lascialfari, J. Magn. Magn. Mater., 2019, 471, 504–512.
56. O. Lemine, K. Omri, M. Iglesias, V. Velasco, P. Crespo, P. De La Presa, L. E. Mir, H. Bouzid, A. Yousif and A. Al-Hajry, J. Alloys Compd., 2014, 607, 125–131.
57. M. Cobianchi, A. Guerrini, M. Avolio, C. Innocenti, M. Corti, P. Arosio, F. Orsini, C. Sangregorio and A. Lascialfari, J. Magn. Magn. Mater., 2017, 444, 154–160.

---

Footnotes

† Electronic supplementary information (ESI) available: Fig. 1: AFM images. Fig. 2: hydrodynamic size. Table 1: hydrodynamic size, PDI, and Z-potential. RGM heuristic model equations. See DOI: https://doi.org/10.1039/d5dt00609k

‡ These authors contributed equally to this work.

§ : Arrhenius (or Voghel–Fulcher) law, where τ₀ is the pre-exponential factor.

---