Thermal properties and ultra-low thermal conductivity of Zn₂GeSe₄

Abstract

Material-related discovery continues to drive advancements in technologically significant fields of interest. Moreover, an understanding of the thermal properties of materials is essential for any application of interest. Here we report on the structural, optical and thermal properties of Zn₂GeSe₄, which forms in the sphalerite crystal structure with an indirect 1.85 eV band gap, as obtained from our optical spectroscopy measurements. Analyses and modeling of the temperature-dependent thermal properties reveal a low speed of sound and Debye temperature, with ultra-low thermal conductivity over a large temperature range due to low-frequency soft modes as well as strong lattice anharmonicity. Our findings are presented and discussed in the context of the current intense interest in metal chalcogenides and will facilitate the development of these and similar materials for applications where low thermal conductivity is of interest.

---

Introduction

Material discoveries are integral in advancing technological applications of interest, and investigations that relate structure and stoichiometry with specific physical properties are key to technological advancements in addition to enhancing our fundamental knowledgebase. Multinary chalcogenides encompass one general class of materials that have recently generated strong interest. They have diverse physical properties that arise from varied structural, bonding and chemical features as well as stoichiometry and lattice disorder. Disorder in particular can play a key role in governing the physical properties of materials, and in certain cases can also provide tunability beyond typical property modifications such as doping and stoichiometric variations.^1–5

Multinary chalcogenides with compositions I–II₂–III–VI₄, where I is Cu or Ag, II is Cd, Zn, Co or Fe, III is In, Ga or Al and VI is S, Se or Te, form in the sphalerite-type crystal structure and have only recently been investigated.^6–11 As compared to I₂–II–IV–VI₄ quaternary chalcogenides, which have been studied extensively,^12–15 I–II₂–III–VI₄ are much less investigated. The I–II₂–III–VI₄ class of materials is a family of compounds that can be thought of as being derived as a result of atomic cross substitutions accompanied by lattice mutations, in which the atomic valence states are preserved and charge neutrality of the periodic lattice is maintained.^16,17 This structure type can accommodate extreme off-stoichiometric variations.¹⁸ Zn₂GeSe₄ represents a particularly unique example within this family of compounds, combining a sphalerite-derived structure with compositional features that introduce cation-site vacancies. Such structural features provide an interesting pretext for exploring their effects on the thermal properties. Moreover, only a few ternary compositions with sphalerite-like crystal structures have been reported to date.^19–21 To the best of our knowledge, the thermal properties of Zn₂GeSe₄ with a sphalerite-like crystal structure have not been previously investigated. In this work, we investigated and modeled the thermal properties, including temperature-dependent heat capacity and thermal conductivity over a large temperature range, as well as the optical and structural properties in order to develop an understanding of the effect of the compositional features on the thermal properties of Zn₂GeSe₄.

Experimental

Polycrystalline Zn₂GeSe₄ was synthesized via mechanical alloying and densified by hot pressing. High-purity Zn (99.9%, Alfa Aesar), Ge (99.9999%, Alfa Aesar) and Se (99.999%, Alfa Aesar) powders were weighed in a stoichiometric ratio into a stainless-steel jar together with stainless steel balls in a ball-to-powder ratio of 40 : 1. The jar was evacuated before being sealed under high-purity argon and subsequently ball milled at 425 rpm for 2 hours. Employing a TA Instruments Q600, differential thermal analyses were conducted under a nitrogen gas flow revealing thermal stability until 573 K. This information was important for densification via hot-pressing (Thermal Technology model HP20-4560-20) into a dense polycrystalline material for physical property measurements. The powder was loaded into a custom graphite die and molybdenum punch assembly and densified at 573 K and 160 MPa for 2 hours under a nitrogen atmosphere. The resulting pellet had a density of 4.66 g cm⁻³ (97% of theoretical density) as determined from its mass and dimensions. The Atomic Force Microscopy (AFM) microstructure analyses of a cross section of the densified pellet revealed grain sizes in the range of a few micrometers.

X-ray diffraction (XRD) data were collected employing a Bruker AXS D8 FOCUS X-ray diffractometer with Cu Kα radiation. The Rietveld refinement was performed using GSAS II software.²² Optical spectra were acquired using UV–vis–NIR spectrophotometry in the wavelength range of 400 nm to 1200 nm using a Shimadzu, Inc. 3600i Plus spectrophotometer equipped with a 60 mm integrating sphere and PMT/InGaAs detectors. The optical band gap was determined from the Tauc plot of the Kubelka–Munk function.

The thick densified 12.8 mm diameter pellet was cut into a parallelepiped of dimensions 2 × 2 × 5 mm³ for low-temperature thermal conductivity, κ, measurements, and a 1 mm thick disk for high temperature thermal diffusivity measurements. Thermal diffusivity, α_th, was measured in a temperature range of 300 K to 573 K using a NETZSCH LFA457 system employing the laser flash method in a flowing argon environment, with an estimated uncertainty of ±5%. Temperature-dependent κ was determined using the formula κ = Dα_thC_v. Here D denotes the measured density of the specimen and C_v, the isochoric specific heat capacity, was estimated from the Dulong–Petit limit, C_v = 3n_aR, where n_a is the number of atoms per formula unit and R is the gas constant.²³ For the low-temperature κ measurements, the thermal transport option (TTO) module of a Quantum Design Physical Property Measurement System (PPMS) was used. The specimen was mounted onto the TTO module using Au coated manganin leads for κ measurements where Ag epoxy (H20E) was used to establish electrical and thermal contact between the specimen and the leads. A maximum experimental uncertainty of ±3% was calculated for the κ measurements. Low-temperature κ measurements of standards employing a custom designed instrument^24,25 are used to calibrate PPMS data. Isobaric heat capacity, C_p, measurements were performed using the heat capacity (HC) module of PPMS in a temperature range from 1.8 K to 303 K accompanied by an appropriate addendum measurement. The specimen was attached to the mounting stage using thermal N-grease. The measurements were conducted employing a two-tau model with a maximum 2% sample temperature rise. A maximum experimental uncertainty of ±1% was calculated for the C_p measurements.

Results and discussion

Fig. 1(a) shows the experimental powder XRD data, the profile fit and the profile difference from Rietveld refinement. The results from the Rietveld refinement are given in Tables 1 and 2. The crystal structure can be described as a derivative of the zinc blende structure, where the cation site partially occupied by Zn and Ge atoms forms tetrahedral coordinated environments with the Se atoms (see Fig. 1(b)). The UV–vis–NIR reflectance spectra are shown in Fig. 2. Zn₂GeSe₄ exhibits a broad absorption onset, and an indirect optical band gap of 1.85 eV was obtained from a linear fit to the steepest gradient of a Tauc plot of the Kubelka–Munk function^26,27 constructed by plotting (αhν)^1/2 as a function of photon energy hν.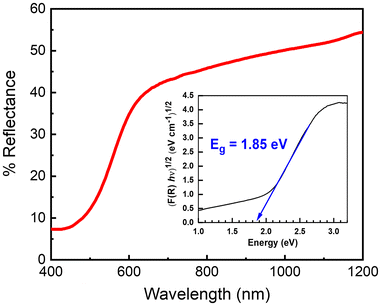

Fig. 1 (a) Experimental powder XRD pattern for Zn₂GeSe₄ including profile fit and profile difference from Rietveld refinement. The inset shows the AFM image of the densified pellet. The scale bar corresponds to 5 μm. (b) The crystal structure of Zn₂GeSe₄ where Zn (grey) and Ge (purple) partially occupy the 4a cation site with the solid lines representing the unit cell.

Fig. 2 UV–vis–NIR reflectance spectrum, with the corresponding Tauc plot of the Kubelka–Munk function indicating an indirect optical band gap of 1.85 eV.

Table 1 Summary of Rietveld refinement results

Compound	Zn2GeSe4
Space group	F4̄3m (#216)
a (Å)	5.6710(21)
V (Å^3)	182.38(20)
d calc. (g cm^−3)	4.7271
Zn/Ge–Se (Å)	2.4556(3)
Se–Zn/Ge–S (°)	109.47(1)
Radiation	Graphite monochromated
	Cu Kα (1.5406 Å)
2θ range (°)	20–100
wRp, Rp	0.06535, 0.04998

---

Table 2 Atomic coordinates and fractional occupancies

Atom	Site	x	y	z	Occ.
Zn	4a	0	0	0	0.5
Ge	4a	0	0	0	0.25
Se	4c	1/4	1/4	1/4	1

---

Fig. 3 shows temperature-dependent κ data revealing very low values across the entire measured temperature range. The excellent agreement between the high and low κ data is an indication of the quality and homogeneity of the polycrystalline specimens used in this study. Above 100 K, the relatively flat temperature dependence of the data implies deviation from the standard phonon gas model. Such behavior has been reported in other materials, and can stem from a large atomic mass difference, such as partial vacancies, and lattice anharmonicity,^28–38 prompting low-T temperature dependences that are atypical of crystalline materials. Moreover, as compared to structurally similar chalcogenides such as Cu₃SbSe₄,³⁹ CuInSe₂,⁴⁰ CuInSnSe₄ ⁴¹ and Cu₂ZnSnSe₄,⁴² as well as sphalerite CuZn₂InS₄ ⁷ (see Table 3), the κ values for Zn₂GeSe₄ are significantly lower. In order to evaluate the measured values for κ, we calculated the minimum thermal conductivity, κ_min, for Zn₂GeSe₄ employing the modified Cahill relation⁴³

where k_B denotes the Boltzmann constant and n = 3.78 × 10²² cm⁻³ is the number density of atoms. The average speed of sound, υ_s, and the Debye temperature, θ_D, were obtained from analyses of heat capacity data, as described below. From this analysis κ_min was estimated to be 0.4 W m⁻¹ K⁻¹. The measured κ values approach κ_min above room temperature, as shown in Fig. 3. The origin of the low magnitude and anomalous temperature dependence of κ can be attributed to multiple factors, some of which are outlined above. Moreover, disorder can induce asymmetric bonding, as observed in other materials,^44–47 that can also introduce lattice anharmonicity and enhance phonon scattering. The phonon mean-free-path λ = 6 Å, estimated using the relationship κ = 1/3(C_vv_sλ),⁴⁸ is relatively short and confirms strong phonon scattering. Therefore, to gain further insight into the thermal properties and the inherently low κ values described above, C_p measurements were performed. Fig. 4 shows temperature-dependent C_p data. As seen in the figure, the data approach the Dulong–Petit limit at higher measured temperatures, suggesting excitation of all acoustic and optic phonon modes at these temperatures. The low-temperature data (inset of Fig. 4) include a fit of the form C_p = αT + αT³, where α and β correspond to the Sommerfeld and lattice contribution to C_p, respectively, and allows for an estimation of θ_D and v_s using the relations and υ_s = θ_D(k_B/ℏ)(6π²n)^1/3, where R is the molar gas constant, n is the number of atoms per formula unit and ℏ is the reduced Planck constant. The values for θ_D and v_s are 141 K and 1412 m s⁻¹, respectively. These θ_D and v_s values are low, significantly lower than those of analogous chalcogenides,^41,42,49 and support the ultralow κ for Zn₂GeSe₄ described above. Using these results we can also estimate the Grüneisen parameter, γ, employing the relation 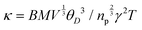, where B = 2.43 × 10⁻⁸/(1–0.514/γ + 0.228/γ²), M is the average mass of an atom in the crystal (amu), V is the volume per atom and n_p is the number of atoms per primitive cell.⁵⁰ The Grüneisen parameter (γ = 2) thus obtained indicates relatively large lattice anharmonicity further supporting the fact that Zn₂GeSe₄ possesses intrinsically very low κ.

Fig. 3 Temperature-dependent κ data.

Fig. 4 C _p/3nR versus T data, where a value of unity represents the Dulong–Petit limit. The inset shows C_p/T versus T² data at low temperatures with the solid line representing a fit of the data of the form C_p/T = α + βT².

Table 3 Band gap and κ for Zn₂GeSe₄ and related chalcogenides

Compound	Structure/space group	Band gap (eV), T = 300 K	κ (W m^−1 K^−1), T = 300 K
Cu3SbSe4 ^61,62	Tetragonal, I4̄2m	0.20	1.32
CuInSe2 ^40,63	Chalcopyrite, I4̄2d	0.96	1.70
CuInSnSe4 ^41	Defect chalcopyrite, I4̄2d	0.75	1.50
Cu2ZnSnSe4 ^42,64	Stannite, I4̄2m	1.20	1.25
CuZn2InS4 ^7	Sphalerite, F4̄3m	—	2.75
Zn2GeSe4 (this work)	Sphalerite, F4̄3m	1.85	0.57

---

The thermal properties revealed by our data and analyses warrant additional analysis of the C_p data. Fig. 5 shows C_p/T³versus T and indicates a relatively large deviation from Debye-like behavior that can be associated with low-frequency optic modes, which have been shown to directly affect κ in other materials.^{31,51–54,55–60} We therefore employed a phenomenological model that includes both Debye-like contributions and Einstein contributions to analyze the data. The solid line in Fig. 5 is a fit of the experimental data of the form⁴⁸

where the terms represent the electronic contribution, Debye contribution and Einstein contribution to C_p, respectively, and A and B are fitting parameters. From the data fit, α = 2.0 mJ mol⁻¹ K⁻², θ_D = 141 K, θ_E = 21 K, A = 0.075 and B = 34.3 were obtained. The value of θ_D is in agreement with that obtained from the low-temperature data fit as shown in the inset of Fig. 4. Furthermore, the very low value of θ_E indicates the existence of low frequency modes. These low-frequency modes contribute to the measured ultra-low κ value for Zn₂GeSe₄.

Fig. 5 C _p/T³versus T data illustrating deviations from the Debye behavior. The solid line represents a fit of the phenomenological model described in the text.

Conclusions

In this work we synthesized phase-pure polycrystalline Zn₂GeSe₄ in order to investigate the previously unexplored thermal properties of this material. UV–vis–NIR measurements revealed an indirect optical band gap of 1.85 eV, and analyses of the temperature-dependent κ and C_p data revealed very low κ over a large temperature range, as well as low θ_D and υ_s, attributable to the lattice anharmonicity resulting from structural disorder and low-frequency optic modes. These findings advance our understanding of the structure and physical properties of multinary chalcogenides and should facilitate further research and exploration on this and similar chalcogenides for applications of interest where low κ values are desirable.

Ethical statement

Certain commercial equipment, instrumentation, or materials are identified in this document to adequately specify the experimental procedures. Such identification does not imply recommendation or endorsement by the National Institute of Standards and Technology, nor does it imply that the materials or equipment identified are necessarily the best available for the purpose.

Author contributions

Oluwagbemiga P. Ojo: data curation, investigation, formal analysis, visualization, and writing – original draft. Wilarachchige D. C. B. Gunatilleke: data curation, investigation, formal analysis and visualization. Adam J. Biacchi: data curation, investigation, and visualization. Hsin Wang: data curation and investigation. George S. Nolas: conceptualization, investigation, supervision, writing – review & editing, and project administration.

Data availability

All data are provided and data are also available upon request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

H.W. acknowledges the support of the U.S. Department of Energy, Vehicle Technologies Office, Powertrain Materials Core Program and the International Energy Agency (IEA) Advanced Materials for Transportation (AMT) Technology Collaboration Programme (TCP). Oak Ridge National Laboratory is managed by UT-Battelle LLC under contract DE-AC05000OR22725.

References

1. R. Waser, R. Dittmann, M. Salinga and M. Wuttig, Int. J. Mater. Res., 2010, 101, 182–198.
2. J. M. Hodges, Y. Xia, C. D. Malliakas, G. C. B. Alexander, M. K. Y. Chan and M. G. Kanatzidis, Chem. Mater., 2018, 30, 7245–7254.
3. K. Ye, S. C. Siah, P. T. Erslev, A. Akey, C. Settens, M. S. B. Hoque, J. Braun, P. Hopkins, G. Teeter, T. Buonassisi and R. Jaramillo, Chem. Mater., 2019, 31, 8402–8412.
4. Y. Xu, X. Wang, W. Zhang, L. Schäfer, J. Reindl, F. vom Bruch, Y. Zhou, V. Evang, J.-J. Wang, V. L. Deringer, E. Ma, M. Wuttig and R. Mazzarello, Adv. Mater., 2021, 33, 2006221.
5. A. Giri, G. Park and U. Jeong, Chem. Rev., 2023, 123, 3329–3442.
6. G. S. Nolas, M. S. Hassan, Y. Dong and J. Martin, J. Solid State Chem., 2016, 242, 50–54.
7. O. P. Ojo, W. D. C. B. Gunatilleke, H. Poddig, H. Wang, J. Martin, D. J. Kirsch and G. S. Nolas, Dalton Trans., 2021, 50, 17611–17617.
8. D. Hobbis, K. Wei, H. Wang and G. S. Nolas, J. Alloys Compd., 2018, 743, 543–546.
9. D. Hobbis, W. Shi, A. Popescu, K. Wei, R. E. Baumbach, H. Wang, L. M. Woods and G. S. Nolas, Dalton Trans., 2020, 49, 2273–2279.
10. K. D. Profita and E. M. Heppke, Z. Naturforsch., B:J. Chem. Sci., 2024, 79(8–9), 489–496.
11. X. Yang, Y. Li and J. Chen, Miner. Eng., 2022, 183, 107596.
12. M. Ibáñez, R. Zamani, A. LaLonde, D. Cadavid, W. Li, A. Shavel, J. Arbiol, J. R. Morante, S. Gorsse, G. J. Snyder and A. Cabot, J. Am. Chem. Soc., 2012, 134, 4060–4063.
13. K. Wei, L. Beauchemin, H. Wang, W. D. Porter, J. Martin and G. S. Nolas, J. Alloys Compd., 2015, 650, 844–847.
14. S. Chen, A. Walsh, Y. Luo, J.-H. Yang, X. G. Gong and S.-H. Wei, Phys. Rev. B:Condens. Matter Mater. Phys., 2010, 82, 195203.
15. F.-J. Fan, L. Wu and S.-H. Yu, Energy Environ. Sci., 2014, 7, 190–208.
16. B. R. Pamplin, J. Phys. Chem. Solids, 1964, 25, 675–684.
17. C. H. L. Goodman, J. Phys. Chem. Solids, 1958, 6, 305–314.
18. G. S. Nolas, H. Poddig, W. Shi, L. M. Woods, J. Martin and H. Wang, J. Solid State Chem., 2021, 297, 122058.
19. C. K. Lowe-Ma and T. A. Vanderah, Acta Crystallogr., Sect. C:Cryst. Struct. Commun., 1991, 47, 919–924.
20. D. P. Kozlenko, V. V. Shchennikov, V. I. Voronin, V. P. Glazkov and B. N. Savenko, Phys. Solid State, 2002, 44, 1628–1631.
21. A. Tengå, F. J. García-García, A. S. Mikhaylushkin, B. Espinosa-Arronte, M. Andersson and U. Häussermann, Chem. Mater., 2005, 17, 6080–6085.
22. B. H. Toby and R. B. Von Dreele, J. Appl. Crystallogr., 2013, 46, 544–549.
23. H. Wang, W. D. Porter, H. Böttner, J. König, L. Chen, S. Bai, T. M. Tritt, A. Mayolet, J. Senawiratne, C. Smith, F. Harris, P. Gilbert, J. Sharp, J. Lo, H. Kleinke and L. Kiss, J. Electron. Mater., 2013, 42, 1073–1084.
24. J. Martin and G. S. Nolas, Rev. Sci. Instrum., 2016, 87, 015105.
25. J. Martin, S. Erickson, G. S. Nolas, P. Alboni, T. M. Tritt and J. Yang, J. Appl. Phys., 2006, 99, 044903.
26. J. Tauc, R. Grigorovici and A. Vancu, Phys. Status Solidi B, 1966, 15, 627–637.
27. P. Makuła, M. Pacia and W. Macyk, J. Phys. Chem. Lett., 2018, 9, 6814–6817.
28. G. S. Nolas, J.-M. Ward, J. Gryko, L. Qiu and M. A. White, Phys. Rev. B:Condens. Matter Mater. Phys., 2001, 64, 153201.
29. G. A. Lamberton Jr., R. H. Tedstrom, T. M. Tritt and G. S. Nolas, J. Appl. Phys., 2005, 97, 113715.
30. C. L. Condron, S. M. Kauzlarich and G. S. Nolas, Inorg. Chem., 2007, 46, 2556–2562.
31. T. Mori, J. Martin and G. Nolas, J. Appl. Phys., 2007, 102, 073510.
32. S. Stefanoski, J. Martin and G. S. Nolas, J. Phys.: Condens. Matter, 2010, 22, 485404.
33. O. Delaire, J. Ma, K. Marty, A. F. May, M. A. McGuire, M.-H. Du, D. J. Singh, A. Podlesnyak, G. Ehlers, M. D. Lumsden and B. C. Sales, Nat. Mater., 2011, 10, 614–619.
34. S. Stefanoski, C. D. Malliakas, M. G. Kanatzidis and G. S. Nolas, Inorg. Chem., 2012, 51, 8686–8692.
35. Y. Dong, H. Wang and G. S. Nolas, Inorg. Chem., 2013, 52, 14364–14367.
36. H. Wang, G. Qin, G. Li, Q. Wang and M. Hu, 2D Mater., 2017, 5, 015022.
37. G. Qin, Z. Qin, H. Wang and M. Hu, Phys. Rev. B, 2017, 95, 195416.
38. S. C. Rakesh Roshan, N. Yedukondalu, T. Pandey, L. Kunduru, R. Muthaiah, R. K. Rajaboina, L. Ehm and J. B. Parise, ACS Appl. Electron. Mater., 2023, 5, 5852–5863.
39. E. J. Skoug, J. D. Cain and D. T. Morelli, Appl. Phys. Lett., 2011, 98, 261911.
40. S. M. Wasim, Sol. Cells, 1986, 16, 289–316.
41. O. P. Ojo, L. Ma, W. D. C. B. Gunatilleke, A. F. May, L. M. Woods and G. S. Nolas, Inorg. Chem., 2023, 62, 16114–16121.
42. Y. Dong, H. Wang and G. S. Nolas, Phys. Status Solidi RRL, 2014, 8, 61–64.
43. D. G. Cahill, S. K. Watson and R. O. Pohl, Phys. Rev. B:Condens. Matter Mater. Phys., 1992, 46, 6131.
44. W. Lai, Y. Wang, D. T. Morelli and X. Lu, Adv. Funct. Mater., 2015, 25, 3648–3657.
45. Z. Wang, S. Liu, X. Zhang, Y. Gao and D. Tang, Int. J. Heat Mass Transfer, 2024, 218, 124753.
46. Z. Liu, W. Zhang, W. Gao and T. Mori, Energy Environ. Sci., 2021, 14, 3579–3587.
47. O. P. Ojo, W. D. C. B. Gunatilleke, H. Wang and G. S. Nolas, J. Alloys Compd., 2024, 1004, 175812.
48. C. Kittel, Introduction to solid state physics, John Wiley & Sons, Inc., 5th edn, 1976.
49. K. J. Bachmann, F. S. L. Hsu, F. A. Thiel and H. M. Kasper, J. Electron. Mater., 1977, 6, 431–448.
50. G. A. Slack, Solid State Phys., 1979, 34, 1–71.
51. S. Paschen, W. Carrillo-Cabrera, A. Bentien, V. H. Tran, M. Baenitz, Yu. Grin and F. Steglich, Phys. Rev. B:Condens. Matter Mater. Phys., 2001, 64, 214404.
52. B. C. Chakoumakos, B. C. Sales and D. G. Mandrus, J. Alloys Compd., 2001, 322, 127–134.
53. M. A. Avila, K. Suekuni, K. Umeo, H. Fukuoka, S. Yamanaka and T. Takabatake, Phys. Rev. B:Condens. Matter Mater. Phys., 2006, 74, 125109.
54. G. S. Nolas, G. Fowler and J. Yang, J. Appl. Phys., 2006, 100, 043705.
55. M. Beekman, W. Schnelle, H. Borrmann, M. Baitinger, Yu. Grin and G. S. Nolas, Phys. Rev. Lett., 2010, 104, 018301.
56. M. Beekman, R. P. Hermann, A. Möchel, F. Juranyi and G. S. Nolas, J. Phys.: Condens. Matter, 2010, 22, 355401.
57. W. D. C. B. Gunatilleke, A. F. May, H. Wang and G. S. Nolas, Appl. Phys. Lett., 2020, 117, 092101.
58. W. D. C. B. Gunatilleke, R. Juneja, O. P. Ojo, A. F. May, H. Wang, L. Lindsay and G. S. Nolas, Phys. Rev. Mater., 2021, 5, 085002.
59. W. D. C. B. Gunatilleke, M. Zhang, W. Wong-Ng, P. Zavalij, Y.-S. Chen and G. S. Nolas, J. Appl. Phys., 2023, 133, 095108.
60. K. S. Rana, D. Sarkar, Nidhi, A. Singh, C. Bera, K. Biswas and A. Soni, Phys. Rev. B, 2024, 109, 115202.
61. K. Tyagi, B. Gahtori, S. Bathula, V. Toutam, S. Sharma, N. K. Singh and A. Dhar, Appl. Phys. Lett., 2014, 105, 261902.
62. A. Moser, O. Yarema, G. Garcia, M. Luisier, F. Longo, E. Billeter, A. Borgschulte, M. Yarema and V. Wood, Chem. Mater., 2023, 35, 6323–6331.
63. J. L. Shay, B. Tell, H. M. Kasper and L. M. Schiavone, Phys. Rev. B, 1973, 7, 4485–4490.
64. K. Wei and G. S. Nolas, ACS Appl. Mater. Interfaces, 2015, 7, 9752–9757.

---