High-pressure phase transition and amorphization of BaV₂O₆

Abstract

The structural evolution of metavanadate compounds under high pressure offers valuable insights into phase transitions and changes in material properties. This study explores the structural behavior of BaV₂O₆ under pressures up to 12 GPa using powder X-ray diffraction and density-functional theory (DFT) simulations. The results indicate a phase transition from the ambient pressure orthorhombic phase (space group C222) to a monoclinic phase (space group C2) at 4 GPa, likely driven by the distortion of the vanadium oxide polyhedron. Above 10 GPa, the C2 phase undergoes amorphization, attributed to the breakdown of the infinite [VO₄] chains into [VO₃]⁻ units. Additionally, BaV₂O₆ exhibits anisotropic lattice contraction and a relatively low bulk modulus (B₀ ≈ 50 GPa). DFT calculations further explore the pressure dependence of enthalpy differences, Raman modes, and band structures, providing insights into the structural and electronic transformations of BaV₂O₆ under high pressure. This work deepens the understanding of the structural and band structure development of the metavanadate family under high pressure, contributing to advancements in materials science under extreme conditions.

---

I. Introduction

The family of metavanadate compounds, represented by the general formula MV₂O₆ (where M is a divalent cation), exhibits rich polymorphism.¹ They adopt structural types consisting of V–O polyhedral frameworks and interstitial M²⁺ ions. These structural types include the brannerite-type (space group C2/m, e.g. MgV₂O₆,² CaV₂O₆,³ and MnV₂O₆ ⁴), the pseudo-brannerite-type (space group C2/m, e.g. CdV₂O₆ and CdV₂O₆),³ the columbite-type (space group Pbcn, e.g. MnV₂O₆, CoV₂O₆, and NiV₂O₆),^5,6 and the NiV₂O₆-type (space group P1̄, e.g. NiV₂O₆ ⁷ and CoV₂O₆ ⁸). In contrast, BaV₂O₆ and SrV₂O₆ with a larger divalent metal atom adopt orthorhombic structures that differ from those above-mentioned, featuring [VO₆] octahedral or [VO₅] square pyramidal, and [VO₄] tetrahedral units.⁹ MV₂O₆ compounds also exhibit temperature- and pressure-dependent polymorphism with phase transitions.^10–13 Therefore, the polymorphism of MV₂O₆ offers a valuable framework for understanding the interplay between various factors, such as the ionic radius of the metal ion, and the influence of temperature and pressure on structural transformations. This diversity in crystal structures provides critical insights into how different physical conditions drive phase transitions and affect structural stability across this family of materials.

High-pressure (HP) studies of metavanadates have attracted extensive research interest due to the induced phase transitions and changes in physical properties.^11–16 For instance, brannerite-type MgV₂O₆ undergoes a phase transition from the C2/m phase to the C2 phase.¹¹ ZnV₂O₆ was predicted using a density-functional theory (DFT) study to undergo a transition from the brannerite-type phase to the columbite-type phase at 5.0 GPa, and then to the monoclinic ThTi₂O₆-type phase at 15.0 GPa.¹⁴ However, an HP X-ray diffraction (XRD) study of brannerite-type ZnV₂O₆ suggests a phase transition to a monoclinic C2 phase at 16.6 GPa.^12,13 For the orthorhombic Pnma structure of PbV₂O₆, no phase transition is observed up to 20.0 GPa. Still, it exhibits zero-linear compressibility along the b-axis, a property comparable to the compressibility of the diamond.¹⁵ This unique behavior is attributed to the pressure-induced transformation of all [VO₅] pyramids into [VO₆] octahedra, which enhances the structural rigidity along the b-axis. For BaV₂O₆ and SrV₂O₆ compounds, their HP Raman spectra indicate that a phase transition occurs at 4.3 and 3.9 GPa, respectively, and amorphization occurs around 10 GPa.¹⁶

In this study, the HP phase transition and amorphization of BaV₂O₆ are further explored using in situ powder XRD. The XRD data reveal a phase transition from the initial orthorhombic phase (space group C222) to a monoclinic phase (space group C2) at approximately 4 GPa, followed by amorphization at around 10 GPa. These findings align well with previous HP Raman studies on BaV₂O₆.¹⁶ Additionally, the HP XRD data were used to investigate the mechanical properties of BaV₂O₆, including its bulk modulus (B₀) and linear compressibility along the three crystallographic axes. Notably, BaV₂O₆ exhibits a significantly lower bulk modulus (50 GPa) compared to other MV₂O₆ compounds, such as ZnV₂O₆ (147 GPa) and PbV₂O₆ (86 GPa). DFT calculations, covering enthalpy, mechanical properties, and Raman spectra, also support the experimental findings. Furthermore, the band structure and pressure dependence of the band gap is provided to reveal the change in the electronic properties accompanied by the phase transition.

II. Methods

A. Synthetic procedures

Polycrystalline BaV₂O₆ was synthesized via a sol–gel chemical technique at low temperature.¹⁷ Ba(NO₃)₂ and NH₄VO₃ (Sigma-Aldrich, ACS grade) were used as the starting materials. Stoichiometric quantities of these materials were accurately weighed and individually dissolved in a minimal amount of pure water. Oxalic acid dihydrate (Scharlau, ACS grade), used as a complexing agent, was added to each solution to form intermediate precursors, maintaining a metal-to-oxalic acid molar ratio of 1 : 2. All reagents were used as received, without further purification. The two prepared solutions were combined by continuously stirring on a magnetic stirrer. The resulting mixture was slowly evaporated on a hot plate until a viscous gel formed. This gel was subsequently decomposed into a black solid mass and heated at 400 °C for 5 hours to remove any carbon residues. The resulting calcined powder was manually ground, pressed into a pellet and then heated at 600 °C for 10 hours to obtain the desired product. The final product was furnace-cooled and powdered. Subsequently, the orthorhombic structure¹⁸ of BaV₂O₆ was confirmed by powder XRD (CCDC number: 1641112).

B. Details of HP XRD experiments

HP powder XRD measurements were carried out using a membrane-type diamond anvil cell (DAC) fitted with diamond culets of 500 μm in diameter. A 200 μm thick Inconel gasket was pre-indented to a thickness of 50 μm, with a 250 μm diameter hole drilled in the center to serve as the pressure chamber. A 4 : 1 methanol–ethanol (ME) mixture was used as the pressure-transmitting medium (PTM) to achieve quasi-hydrostatic conditions. A Cu grain was loaded next to the sample in the DAC to determine pressure from the position of the Cu 111 reflection in the XRD pattern and the equation of state (EOS) of Cu.¹⁹ The experiments were conducted at the MSPD beamline of the ALBA synchrotron²⁰ using a monochromatic beam of wavelength 0.4246 Å. XRD patterns were collected on a Rayonix charge-coupled device detector and LaB₆ was applied to calibrate the geometry parameters. Dioptas software was used to reduce the collected data.²¹ Refinement and indexation were performed using Jana 2006 software, Material Studio, and PowderCell.^22,23

C. DFT calculations

All DFT calculations in this study were performed at 0 K. The crystal structure optimization and the calculation of enthalpy and mechanical properties were performed using the Vienna ab initio simulation package (VASP).^24,25 The generalized gradient approximation (GGA) using the Perdew–Burke–Ernzerhof for solids (PBEsol) functional was chosen in the calculations.²⁶ The valence electrons were treated as Ba 5s²5p⁶6s², V 3d³4s², and O 2s²2p⁴. The kinetic energy cutoff was set at 830 eV and Monkhorst–Pack 3 × 3 × 3 k-point meshes were used.²⁷

DFT calculations were also performed using the Cambridge Sequential Total Energy Package (CASTEP) module²⁸ in Material Studio to optimize the crystal structure and simulate Raman spectra,²⁹ band structures and densities of states. The GGA in the form of PBE³⁰ was employed and norm-conserving pseudopotentials with an 1170 eV energy cutoff were implemented with k-point sampling better than 2π × 0.06 A⁻¹. For the calculation of band structures and densities of states, the separation of the k-point path was 2π × 0.015 A⁻¹.

III. Results and discussion

A. High-pressure powder X-ray diffraction

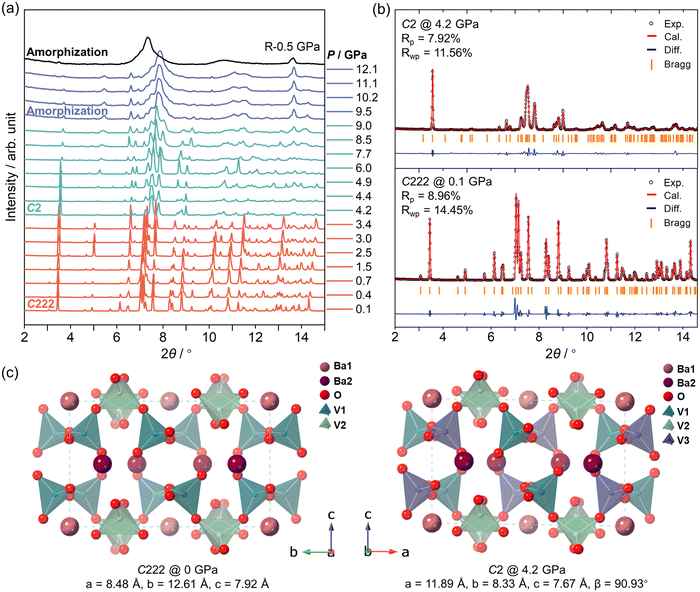
HP powder XRD measurements were performed up to 12.1 GPa with ME as a PTM. As shown in Fig. 1a and c, BaV₂O₆ maintains the orthorhombic phase (C222, a = 8.48 Å, b = 12.61 Å, and c = 7.92 Å) from ambient pressure to 3.4 GPa, and all Bragg diffraction peaks just shift toward higher angles upon compression in this pressure range, which is attributed to the pressure-induced lattice shrinkage. Above 4.2 GPa, the XRD pattern undergoes a significant change, especially between 7° and 8°, where some extra peaks appear. This undoubtedly indicates a phase transition, as previously reported in the HP Raman study, suggesting that the studied compound undergoes a phase transition at around 4 GPa.¹⁶ Under further compression, the XRD patterns maintain their profile up to 9.0 GPa. The HP phase begins to transform into an amorphous phase around 10 GPa, due to the progressive broadening of Bragg peaks and the eventual disappearance of most peaks, accompanied by the emergence of a diffuse scattering background.³¹ This signifies the loss of long-range structural order, which cannot be attributed to microstrain or local disorder alone. In contrast, microstrain or local disorder typically causes corresponding asymmetric peak broadening or shifts but retains identifiable diffraction peaks.³² This also agrees with the previous HP Raman study.¹⁶ After decompression to 0.5 GPa, the amorphous phase does not recover to the initial orthorhombic phase, indicating nonreversible amorphization at room temperature and high pressure.

Fig. 1 (a) Powder XRD patterns of BaV₂O₆ under high pressure. R denotes the process of decompression. (b) Selected Le Bail fit plots of the C222 phase at 0.1 GPa and the C2 phase at 4.2 GPa. The black circles, solid red lines, solid blue lines, and violet bars represent the experimental data, simulated data, difference, and Bragg positions, respectively. (c) Crystal structure of the C222 phase and the C2 phase.

Due to the influence of preferred orientation effects in the XRD patterns, the Le Bail method was used to analyze the data. As illustrated in Fig. 2b, the XRD pattern at 0.1 GPa corresponds to the initial orthorhombic phase. The orthorhombic structure depicted in Fig. 2c consists of crossed helical chains of [VO₄] tetrahedra running along the [120] directions in a zigzag manner and Ba atoms reside at two different sites surrounded by the chains of [VO₄] tetrahedra. However, at 4.2 GPa, the XRD pattern was successfully indexed and fitted to a monoclinic phase, consistent with the C2 space group, with parameters a = 11.89 Å, b = 8.33 Å, c = 7.67 Å and β = 90.93° (Fig. 2b and Table S1†). In comparison with the crystallographic axes of the initial orthorhombic phase, the monoclinic phase undergoes an a-axis and b-axis swap to align with the standard space group convention. This symmetry-reducing phase transition, from C222 to C2, is likely driven by the distortion of the vanadium oxide polyhedron. Similar behaviors have also been observed in the HP structural evolution of MV₂O₆ (M = Mg and Zn), where increased distortion of the [VO₆] octahedra induces the phase transformation from the C2/m phase to the C2 phase under high pressure.^11,12 Therefore, the C222 structure has two symmetrically independent V⁵⁺ cations/[VO₄] tetrahedral units, while the C2 structure has three symmetrically independent V⁵⁺ cations/[VO₄] tetrahedral units.

Fig. 2 (a) Pressure dependence of the unit cell parameters of BaV₂O₆. Symbols represent experimental results using ME as a PTM and solid lines are the results from DFT calculations. (b) Pressure-dependent compressibility of lattice axes of the C222 phase. The compressibility coefficients (K) were determined using the PASCal program.³³ (c) Connection and arrangement of [VO₄] units of C222 phase BaV₂O₆ at ambient pressure. (d) Pressure dependence of the volume of BaV₂O₆. Symbols represent experimental results and solid lines are the results from DFT calculations. Black dotted lines are the 2^nd-order BM-EOS fits of the experimental results. The data above 6.4 GPa were not used to fit the BM-EOS of the C2 phase due to the degradation of data quality. (e) Comparison of the bulk modulus (B₀) of different MV₂O₆ (M = Ba, Mg, Zn, and Pb) compounds and the Ba₃V₂O₈ compound in different pressure ranges.^{11,12,14,15,38}

As shown in Fig. 2a, the corresponding lattice parameters (symbols) obtained from Le Bail are in agreement with the DFT results (solid lines), and they indicate that the b-axis of the initial C222 phase (equivalent to the a-axis of the HP C2 phase) collapses after the phase transition. The pressure-dependent compressibility of the lattice axes of the C222 phase was further analyzed using the online PASCal program.³³ As shown in Fig. 2b, the C222 phase of BaV₂O₆ exhibits obvious anisotropic contraction under high pressure. It should be noted that [VO₄] tetrahedra are much less compressible than the coordination polyhedra of Ba and determine the evolution of the structure with pressure. By analyzing the connection and arrangement of [VO₄] units, we find that the empty space between vanadate layers along the c-axis makes this direction highly compressible. The changing alignment makes the a-axis less compressible than the b-axis. A tilting of [VO₄] units could also favor the collapse of the b-axis observed at the phase transition and the disorder of the chains, inducing the amorphization that happens at higher pressure. The amorphization can be understood in the concept of Zintl–Klemm extended to oxides.³⁴ The idea is that under compression the most electropositive atoms of Ba would give up their valence electrons to the skeleton vanadate forming anions [VO₃]⁻.¹⁶ This electron transfer leads to the disruption of the original crystalline structure, promoting the transition to an amorphous state as the material rearranges to accommodate the bonding environments. Similar behaviors have been reported in the HP studies of LiVO₃ and NaVO₃ and induce their structural transitions.^35,36

To analyze the pressure dependence of the volume, the P–V data were fitted with two 2^nd-order Birch–Murnaghan equations of state (BM-EOS)³⁷ with V₀ = 845.7(7) ų and B₀ = 50(1) GPa for the C222 phase and V₀ = 814 ų and B₀ = 50.4(8) GPa for the C2 phase (Fig. 2d). The volume collapse caused by the phase transition is about 4.5%. Compared with the experimental analysis results, the DFT calculation results show that the C222 phase has V₀ = 847.2(1) ų and B₀ = 57.2(2) GPa and the C2 phase has V₀ = 818.3(5) ų and B₀ = 58.6(5) GPa, and they slightly overestimate B₀. Both experimental and computational results indicate that B₀ changes very little during the phase transition. Interestingly, the B₀ of BaV₂O₆ is the smallest among the corresponding MV₂O₆ (M = Mg, Zn, and Pb) compounds, as well as compared to BaV₃O₈ (Fig. 2e and Table S2†).^{11,12,14,15,38} The compressibility of vanadium oxide polyhedra is mainly influenced by their type and connection. BaV₂O₆ has corner-sharing [VO₄] tetrahedra,¹⁸ MgV₂O₆ and ZnV₂O₆ feature edge-sharing [VO₆] octahedra,^2,39 PbV₂O₆ contains edge-sharing [VO₅] square pyramids⁴⁰ and Ba₃V₂O₈ has independent [VO₄] tetrahedra interspersed in the Ba–O network (Table S3†).⁴¹ [VO₄] tetrahedra, due to their smaller size and symmetry, are more easily deformed under pressure, making them highly compressible. [VO₆] octahedra are larger and more rigid, especially when connected by edges, which further reduces their compressibility. The compressibility of [VO₅] square pyramids is intermediate, depending on the connection. Among connection types, corner-sharing is much more compressible than edge-sharing. This is because polyhedra sharing one oxygen atom (corner-sharing) tend to have weaker inter-polyhedral interactions, resulting in larger distances between them and making the structure easier to compress. When polyhedra share two oxygen atoms, the connection becomes tighter, making the structure more rigid. The O–V–O bond angle becomes more resistant to changes, reducing compressibility.

B. Enthalpy and Raman mode calculations

The pressure dependence of the enthalpy (ΔH) difference between the C2 phase and the C222 phase was calculated to understand this phase transition from the energy perspective. As illustrated in Fig. 3, the C2 phase exhibits lower enthalpy above 4 GPa, reinforcing the phase transition from the C222 phase to the C2 phase observed in the HP XRD experiments.

Fig. 3 The pressure dependence of the enthalpy difference between the C2 phase and C222 phase in the range from 0 to 8 GPa.

The changes in Raman modes caused by phase transitions are also analyzed here. With six molecules in the primitive unit cell of both phases, BaV₂O₆ has a total of 78 Raman active modes, Γ_Raman = 18A + 19B₁ + 20B₂ + 21B₃ for the C222 phase and Γ_Raman = 39A + 39B for the C2 phase. The pressure-dependent evolution of Raman active modes is shown in Fig. 4 and S1,† which qualitatively agree with changes observed in the Raman experiments reported in the literature.¹⁶ Interestingly, the lowest frequency A and B modes of the C2 phase soften under compression, suggesting that the crystal structure becomes less stable, leading to a loss of long-range order. In this case, the softening of these Raman modes signals the breakdown of the ordered C2 phase, which aligns with the observed amorphization above 10 GPa in the experiments.

Fig. 4 Pressure dependence of the Raman A modes of the C222 phase and the C2 phase.

C. Band structure and band gap

The calculated band structure and partial density of states (PDOS) of the C222 phase at 0 GPa and the C2 phase at 4.2 GPa are shown in Fig. 5a and b. Both the C222 and the C2 phases of BaV₂O₆ are semiconductors, with indirect band gaps of 2.726 and 2.703 eV, respectively. The PDOS of both phases indicates that the states at the valence band maximum (VBM) are mainly contributed by the O 2p orbitals, and the conduction band minimum (CBM) consists of contributions from the V 3d and O 2p orbitals, with the V 3d orbital contributing the most. This is a typical feature of vanadates.⁴² Therefore, in both phases of BaV₂O₆, the band edges are predominantly governed by [VO₄] tetrahedra. This is comparable to CaV₂O₆ and ZnV₂O₆, where the band edges are primarily influenced by [VO₅] square pyramids and [VO₆] octahedra, respectively.^4,14 However, it differs from MnV₂O₆ or PbV₂O₆, where the band edges also receive a non-negligible contribution of Mn 3d or Pb 6s orbitals.^4,15 As shown in Fig. 5c, the pressure dependence of the calculated band gaps primarily reveals a closing of the gap, but there is also a slight reopening of the gap during the phase transition. In each phase, under high pressure, the average V–O length is continuously compressed, which could lead to enhanced hybridization and an increased crystal field effect (Fig. S2†). Enhanced hybridization between V 3d and O 2p orbitals could drive the band gap reduction, while crystal field splitting could lead to an energy difference between bonding and antibonding states, inducing the increase of the band gap. This subtle interplay between hybridization and crystal field effects could account for the observed narrowing and reopening of the band gap under high pressure. The pressure-induced band gap narrowing could improve the absorption capacity of photons and increase the number of photogenerated carriers, thereby enhancing the photocurrent.⁴³ In addition, the narrowing and reopening of the band gap may play an important role in the design of high-performance thermoelectric materials through the influence on carrier concentration, carrier mobility and thermal conductivity.⁴⁴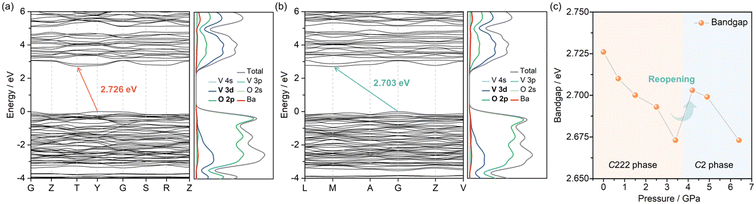

Fig. 5 Calculated band structures and PDOS of (a) the C222 phase at 0 GPa and (b) the C2 phase at 4.2 GPa. (c) Pressure dependence of the calculated band gaps of the C222 phase and the C2 phase.

IV. Conclusion

We investigated the HP phase transition and amorphization of BaV₂O₆ up to 12 GPa using synchrotron in situ powder XRD and systematic theoretical calculations. The ambient pressure orthorhombic phase (space group C222) transforms into a monoclinic phase (space group C2) at around 4 GPa, followed by amorphization above 10 GPa. BaV₂O₆ exhibits anisotropic contraction of the lattice axis and a lower bulk modulus B₀ ≈ 50 GPa due to the structural feature that the helical chains of [VO₄] tetrahedra run along the [120] direction in a zigzag manner. The DFT results of the pressure dependence of the enthalpy difference and Raman modes are also provided to support the phase transition from the C222 phase to the C2 phase at 4 GPa. The pressure dependence of the band structures of BaV₂O₆ is explored via DFT calculations, which reveals changes in its electronic structure due to the evolution of its crystal structure. Our work provides a valuable contribution to the fundamental research on metavanadate compounds and is expected to advance the development of these materials.

Author contributions

Conceptualization, P. Z. and D. E.; investigation, P. Z., P. B., N. B., J.-L. R., J. S.-M., D. V., and D. E.; methodology, C. P.; writing – original draft, P. Z.; writing – review & editing, D. E.; and funding acquisition, P. B., J. S.-M., C. P., and D. E. The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

Data availability

The authors confirm that the data supporting the findings of this study are available within the article and its ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the financial support from the Spanish Ministerio de Ciencia, Innovación y Universidades, MCIU, (https://doi.org/10.13039/501100011033) under projects PID2022-138076NB-C41 and RED2022-134388-T. They also acknowledge the financial support of the Generalitat Valenciana through grants PROMETEO CIPROM/2021/075 and MFA/2022/007. P. B. acknowledges funding from the Generalitat Valenciana for Postdoctoral Fellowship no. CIAPOS/2023/406. J. S.-M. acknowledges the Spanish MCIU for the PRE2020-092198 fellowship. C. P. recognizes the financial support from the Spanish Ministerio de Ciencia e Innovacion through project PID2021-125927NB-C21. This study is part of the Advanced Materials program and is supported by the MCIU with funding from the European Union Next Generation EU (PRTR-C17.I1) and by the Generalitat Valenciana. The authors thank ALBA for providing beamtime under experiment no. 2023087668. P. Z. thanks Dr Kuo Li from Center for High Pressure Science and Technology Advanced Research (HPSTAR) for providing the platform for theoretical calculations.

References

1. P. Garnier and D. Weigel, J. Solid State Chem., 1983, 47, 16.
2. H. N. Ng and C. Calvo, Can. J. Chem., 1972, 50, 3619.
3. J.-C. Bouloux, G. Perez and J. Galy, Bull. Soc. Fr. Mineral. Crystallogr., 1972, 95, 130.
4. M. S. Islam, H. Kabir, Y. Inagaki and A. R. Sarker, J. Alloys Compd., 2020, 829, 154499.
5. M. Gondrand, A. Collomb, J. C. Joubert and R. D. Shannon, J. Solid State Chem., 1974, 11, 1.
6. J. P. Peña, P. Bouvier, M. Hneda, C. Goujon and O. Isnard, J. Phys. Chem. Solids, 2021, 154, 110034.
7. A. Le Bail and M.-A. Lafontaine, Eur. J. Solid State Inorg. Chem., 1990, 27, 671.
8. H. Müller-Buschbaum and M. Kobel, J. Alloys Compd., 1991, 176, 39.
9. Y. Li, R. Tang, N. Li, H. Li, X. Zhao, P. Zhu and X. Wang, J. Appl. Phys., 2015, 118, 035902.
10. K. Mocala and J. Ziolkowski, J. Solid State Chem., 1987, 69, 299.
11. R. Tang, Y. Li, S. Xie, N. Li, J. Chen, C. Gao, P. Zhu and X. Wang, Sci. Rep., 2016, 6, 38566.
12. R. Tang, Y. Li, N. Li, D. Han, H. Li, Y. Zhao, C. Gao, P. Zhu and X. Wang, J. Phys. Chem. C, 2014, 118, 10560.
13. D. Díaz-Anichtchenko, D. Santamaria-Perez, T. Marqueño, J. Pellicer-Porres, J. Ruiz-Fuertes, R. Ribes, J. Ibañez, S. N. Achary, C. Popescu and D. Errandonea, J. Alloys Compd., 2020, 837, 155505.
14. A. Beltrán, L. Gracia and J. Andrés, J. Phys. Chem. C, 2019, 123, 3239.
15. J. Sanchez Martin, J. Pellicer-Porres, R. Turnbull, D. Diaz-Anichtchenko, S. Anzellini, A. Liang, C. Popescu, M. Bettinelli, P. Rodriguez-Hernandez, A. Munoz and D. Errandonea, Dalton Trans., 2024, 53, 11490.
16. Y. Li, R. Tang, N. Li, H. Li, X. Zhao, P. Zhu and X. Wang, J. Appl. Phys., 2015, 118, 035902.
17. T. Vaz and A. V. Salker, J. Adv. Sci. Res., 2021, 11, 107.
18. T. Yao, Y. Oka and N. Yamamoto, Inorg. Chim. Acta, 1995, 238, 165.
19. A. Dewaele, P. Loubeyre and M. Mezouar, Phys. Rev. B:Condens. Matter Mater. Phys., 2004, 70, 094112.
20. F. Fauth, I. Peral, C. Popescu and M. Knapp, Powder Diffr., 2013, 28, S360.
21. C. Prescher and V. B. Prakapenka, High Pressure Res., 2015, 35, 223.
22. V. Petříček, M. Dušek and L. Palatinus, Z. Kristallogr. – Cryst. Mater., 2014, 229, 345–352.
23. W. Kraus and G. Nolze, J. Appl. Crystallogr., 1996, 29, 301.
24. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15.
25. G. Kresse and J. Furthmüller, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 11169.
26. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406.
27. H. J. Monkhorst and J. D. Pack, Phys. Rev. B, 1976, 13, 5188.
28. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr. – Cryst. Mater., 2005, 220, 567.
29. S. Baroni, S. de Gironcoli, A. Dal Corso and P. Giannozzi, Rev. Mod. Phys., 2001, 73, 515.
30. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406.
31. T. Egami and S. J. L. Billinge., Underneath the Bragg Peaks: Structural Analysis of Complex Materials, Elsevier, 2nd edn, 2012.
32. B. E. Warren, X-ray Diffraction, Addison-Wesley, 1969.
33. M. Lertkiattrakul, M. L. Evans and M. J. Cliffe, J. Open Source Software, 2023, 8, 5556.
34. D. Santamaria-Perez and A. Vegas, Acta Crystallogr., Sect. B:Struct. Sci., 2003, 59, 305.
35. Z. X. Shen, C. W. Ong, M. H. Kuok and S. H. Tang, J. Phys.: Condens. Matter, 1995, 7, 939.
36. Z. X. Shen, C. W. Ong, S. H. Tang and M. H. Kuok, J. Phys. Chem. Solids, 1994, 55, 665.
37. F. Birch, Phys. Rev., 1947, 71, 809.
38. A. Grzechnik and P. F. McMillan, Physica B, 1998, 252, 268.
39. G. D. Andreetti, G. Calestani, A. Montenero and M. Bettinelli, Z. Kristallogr., 1984, 168, 53.
40. B. D. Jordan and C. Calvo, Can. J. Chem., 1974, 52, 2701.
41. P. Süsse and M. J. Buerger, Z. Kristallogr., 1970, 134, 161.
42. D. Errandonea and A. B. Garg, Prog. Mater. Sci., 2018, 97, 123.
43. N. Wang, G. Zhang, G. Wang, Z. Feng, Q. Li, H. Zhang, Y. Li and C. Liu, Small, 2024, 20, 2400216.
44. G. D. Mahan and J. O. Sofo, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 7436.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dt03091e

---