Evaluation of structurally related acyclic ligands OBETA, EHDTA, and EGTA for stable Mn²⁺ complex formation

Abstract

In recent years, significant research efforts have been dedicated to finding efficient and safe alternatives to the currently used gadolinium (Gd)-based MRI contrast agents. Among the most explored alternatives are paramagnetic chelates of the Earth-abundant Mn²⁺, which form a prominent class of metal complexes. The design of Mn²⁺ complexes with enhanced relaxation properties and improved safety profiles hinges on a delicate balance between thermodynamic and kinetic stability, as well as the presence of coordinated water molecules. In this study, we present a comprehensive investigation into the coordination chemistry of three structurally related polyetheraminocarboxylic chelating agents. Our aim is to elucidate the structural features, paramagnetic properties, and thermodynamic and kinetic inertness of the corresponding Mn²⁺ complexes. The most significant finding is the considerable difference in the dissociation rates of the complexes, with the octadentate EGTA complex being the most labile. The observed dissociation rates correlate well with the nitrogen inversion dynamics, as assessed through NMR spectral analysis of the analogous Zn²⁺ complexes.

---

Introduction

An intensive worldwide use of gadolinium-based chelates as MRI contrast agents (CAs) during the last 45 years led the scientific community to the awareness of specific problems and limitations of this fundamental class of metal complexes.^1,2 Administration of hundreds of millions of doses of Gd-based contrast agents (GBCAs) brought to light some concerns for their in vivo applications.^3–5 Moreover, GBCAs excreted by patients pass through wastewater treatments intact as evidenced by the presence of steadily increasing concentrations of anthropogenic Gd³⁺ in aquatic environments.^6–10

Recent years have seen significant research efforts aimed at finding efficient and safe alternatives to the currently used Gd-based MRI contrast agents. This includes the development of nanoparticles, stable organic radicals, and metal complexes with alternative paramagnetic metal ions.^11,12 Among these, paramagnetic chelates of the Earth-abundant Mn²⁺ stand out as one of the most extensively studied families of metal complexes.^13–15

The efficacy of MRI contrast agents is usually measured in terms of relaxivity, defined as the water proton relaxation rate variation observed in aqueous solution in the presence of a 1.0 mM concentration of the CA. The relaxivity of a paramagnetic metal complex depends on a complex interplay of different structural and dynamic parameters, such as the electronic relaxation rate, the rotational correlation time, and the presence of coordinated water molecules and their corresponding exchange lifetimes.¹⁶

The metal centre can accommodate coordinated water molecules depending on its coordination number and the steric hindrance created by the chelating agent. The coordination number of Mn²⁺ complexes is in the range of 6–8, and chelating agents with a denticity of 5–7 are usually employed to leave room for coordinated water molecules.¹³

However, maintaining the structural integrity of the metal complex under physiological conditions is crucial to prevent the release of free Mn²⁺ ions, which could disrupt delicate biochemical processes. High thermodynamic stability and kinetic inertness are critical prerequisites for resisting endogenous species that may compete with the ligand or metal ion. These properties are essential to prevent transchelation or transmetalation, processes where other biomolecules could displace the ligand or metal, potentially compromising the integrity and safety of the complex. The stability of metal complexes is generally associated with the denticity of the chelating agent: higher denticity provides better encapsulation of the metal ion, reducing its exposure to competing species.

The design of Mn²⁺-based contrast agents (MBCAs) involves balancing two opposing requirements: reducing the ligand denticity to increase the number of coordinated water molecules, which boosts relaxivity, while simultaneously increasing the denticity to ensure the complex's thermodynamic stability. Perhaps even more significant is the kinetic inertness, as demonstrated by Mn²⁺ complexes with bispidine ligands, whose kinetic stability far exceeds that of other Mn²⁺ complexes studied.¹⁷ It is important to highlight that kinetic inertness can be enhanced by increasing the stereochemical rigidity of the ligand's backbone, as observed with Mn-CDTA and Mn-PhDTA when compared to the parent Mn-EDTA complex.^18,19 Another well-known example is Mn-PyC3A, where an increase in kinetic inertness is achieved by introducing a 2-picolyl donor group in place of an acetate group in CDTA.¹⁵ More recently, the introduction of a propylene bridge onto the cyclohexane ring of CDTA has resulted in the Mn-BCN-DTA complex, which exhibits a marked increase in kinetic inertness.²⁰ Thus, even relatively minor structural modifications can lead to significant improvements in both the thermodynamic stability and/or kinetic inertness of these complexes.

Another feature of these complexes that shows significant dependence on small structural modifications of the chelating agents is the hydration state. In 2011, we were the first to highlight the presence of a mixture of coordination isomers in aqueous solution for Mn²⁺ complexes with the hexadentate ligand AAZ3A and its derivatives (Fig. 1). These isomers, seven-coordinate (q = 1) and six-coordinate (q = 0) species, differ in their hydration number q, with the population of each isomer appearing to correlate with the steric hindrance of the substituent.²¹ Subsequently, Mn²⁺ complexes with a homologous series of ligands based on cyclen, with denticity 5, 6, and 7 (DO3A, DO2A, DO1A; Fig. 1), were examined.²² In this case as well, the results did not show a clear predominance of the seven-coordinate species for Mn²⁺. Instead, equilibria between species with hydration numbers ranging from 0 to 1 were observed in aqueous media. Of particular interest is the significant difference in the hydration states between the isomeric complexes Mn(1,4-DO2A) and Mn(1,7-DO2A), for which q values were 0.87 and 0, respectively. All these examples highlight the often complex nature of Mn²⁺ chelates, where small modifications in the ligand backbone or the steric hindrance of the arms can significantly impact both the hydration state and the kinetic inertness of the complexes. Therefore, a more systematic and in-depth study is needed to understand how to modify the basic structure of a chelating agent to achieve a Mn²⁺ complex with a seven-coordinate ground state and one bound water molecule under fast exchange conditions.

Fig. 1 Chelating agents discussed and investigated in this work.

Some years ago, we reported a systematic investigation of lanthanoid (Ln³⁺) complexes of OBETA (Fig. 1).^23–25OBETA can be regarded as a structural analogue of EDTA, with an additional donor group provided by an ether oxygen, making it a potentially heptadentate chelating agent. It can also be considered a lower homologue of the more widely known octadentate ligand EGTA. While one would generally expect increased thermodynamic stability in Ln³⁺-OBETA complexes compared to their Ln³⁺-EDTA counterparts, it is quite surprising to observe that Ln³⁺-OBETA complexes not only exhibit greater stability than the corresponding Ln³⁺-EGTA complexes but also demonstrate significantly higher kinetic inertness.

Aiming at further improving the coordinating ability of OBETA, more recently we designed EHDTA, a rigidified derivative of OBETA, showing improved stability profiles while retaining the coordination behaviour observed with Ln³⁺-OBETA (Fig. 1).²⁶

The structural characteristics of OBETA and EHDTA are particularly well-suited to achieve the ideal balance of low denticity and high stability required to enhance the performance of Mn²⁺ in MBCAs. In this study, we systematically investigate the Mn²⁺ complexes of these two heptadentate chelating agents, comparing their properties with those of the octadentate analogue EGTA (Fig. 1)²⁷ to assess their potential as effective MBCAs.

Experimental

Materials

Solvents and chemicals were obtained from Carlo Erba (Milan, Italy) or BLD Pharm (Karlsruhe, Germany) and used as received. OBETA was prepared according to our previously reported procedure.²³ Aqueous solutions were prepared from ultrapure laboratory grade water (18 MΩ cm) obtained from a Millipore/Milli-Q purification system. ¹H and ¹³C NMR spectra were recorded on a Bruker Avance Neo 400 spectrometer operating at 9.4 T. Chemical shifts are reported in ppm with the protic impurities of the deuterated solvent as the internal reference. Mass spectra were obtained with a Thermo Finnigan LCQ-Deca XP-PLUS ion trap spectrometer equipped with an electrospray source. High resolution mass spectra were recorded on a Thermo Scientific Q-Exactive Plus spectrometer. TLC analyses were performed with silica gel (MN Kieselgel 60 F254) and visualized using UV light or sprayed with the Dragendorff reagent or alkaline KMnO₄. Column chromatography was carried out on Macherey–Nagel silica gel 60 (0.063–0.200 mm).

Solution thermodynamic studies

Materials. The chemicals used for the experiments were of the highest analytical grade. The concentration of the MnCl₂ solutions were determined by complexometric titration with standardized Na₂H₂EDTA and eriochrome black T as indicators. The concentration of EHDTA, OBETA and EGTA was determined by pH-potentiometric titration in the presence and absence of a large (40-fold) excess of CaCl₂. The pH-potentiometric titrations were made with standardized 0.2 M KOH.

pH-potentiometric measurements. The protonation constants of the EHDTA ligand, and the stability and protonation constant of the [Mn(EHDTA)]²⁻ complex were determined by pH-potentiometric titration. The metal-to-ligand concentration ratio was 1 : 1 (the concentration of the ligand was generally 0.002 M). For the pH measurements and titrations, a Metrohm 888 Titrando titration workstation Metrohm-6.0234.110 combined electrode was used. Equilibrium measurements were carried out at a constant ionic strength (0.1 M KCl) in 6 mL samples at 25 °C. The solutions were stirred, and N₂ was bubbled through them. The titrations were made in the pH range of 1.7–12.0. KH-phthalate (pH = 4.005) and borax (pH = 9.177) buffers were used to calibrate the pH meter For the calculation of [H⁺] from the measured pH values, the method proposed by Irving et al. was used as follows.²⁸ A 0.01 M HCl solution was titrated with standardized KOH solution at 0.1 M KCl ionic strength. The differences (A) between the measured (pH_read) and calculated pH (−log[H⁺]) values were used to obtain the equilibrium H⁺ concentration from the pH values measured in the titration experiments (A = 0.05). For the equilibrium calculations, the stoichiometric water ionic product (pK_w) was also needed to calculate [OH⁻] values under basic conditions. The V_KOH–pH_read data pairs of the HCl–KOH titration obtained in the pH range 10.5–12.0 were used to calculate the pK_w value (pK_w = 13.85). The protonation and stability constants were calculated with the PSEQUAD program.²⁹

Transmetallation studies

Rates of the metal exchange reactions of [Mn(EHDTA)]²⁻ and [Mn(OBETA)]²⁻ with Cu²⁺ were measured by spectrophotometry by following the formation of the related Cu²⁺ complexes at 295 nm with an Applied Photophysics DX-17MV stopped-flow instrument. The concentration of [Mn(EHDTA)]²⁻ and [Mn(OBETA)]²⁻ was 1.0 × 10⁻⁴ M, whereas the concentration of Cu²⁺ was 10–40 times higher in order to guarantee pseudo-first-order conditions. The temperature was maintained at 298 K and the ionic strength of the solutions was kept constant with 0.15 M NaCl. Rates of the exchange reactions with Cu²⁺ were studied in the pH range of ca. 3.3–4.9. To keep the pH values constant, monochloroacetic acid (pH range 2.0–3.3), 1,4-dimethylpiperazine (pH range 3.3–4.1) and N-methylpiperazine (pH range 4.1–5.0) buffers were used (0.01 M). The pseudo-first-order rate constants (k_d) were calculated by fitting the absorbance data to eqn (1).

A_t = (A₀ − A_p)e^−k_dt + A_p (1)

where A_t, A₀ and A_p are the absorbance values at time t, the start of the reaction and at equilibrium, respectively. The calculation of the kinetic parameters was performed by the fitting of the absorbance–time data pairs with the Micromath Scientist computer program (version 2.0, Salt Lake City, UT, USA).

NMR experiments

¹H and ¹³C NMR measurements were performed using a Bruker Avance III (9.4 T) spectrometer, equipped with a Bruker Variable Temperature Unit (BVT), a Bruker Cooling Unit (BCU) and a BB inverse z gradient probe (5 mm). VT-NMR spectra of [Zn(EHDTA)]²⁻, [Zn(OBETA)]²⁻ and [Zn(EGTA)]²⁻ were measured in 0.05 M samples prepared at pD = 7.40 in D₂O. The ¹H–¹H (COSY), ¹H–¹H (EXSY) and ¹H–¹³C (HSQC) correlation spectra were collected by using gradient pulses in the z direction with the standard Bruker pulse program. Band-shape analyses were performed by using the DNMR program included in the Bruker Topspin software package. Values of the chemical shift, the spin–spin coupling constants, intensity and LB without chemical exchange were fixed input parameters during the fitting procedure. Co-plotting the measured and calculated ¹H and ¹³C NMR spectra obtained at different temperature shows a similarity >92% in all cases.

Relaxometric measurements

The ¹H 1/T₁ NMRD profiles were obtained with a fast-field cycling Stelar SmartTracer relaxometer (Mede, Pavia, Italy) varying the magnetic-field strength from 0.00024 to 0.25 T (0.01–10 MHz range). The 1/T₁ values are measured with an absolute uncertainty of ±1%. Temperature was controlled with a Stelar VTC-91 airflow heater equipped with a calibrated copper–constantan thermocouple (uncertainty of ±0.1 K). Data at higher magnetic field strength values (0.5–3 T, corresponding to 20–120 MHz proton Larmor frequency) were collected with a high field relaxometer (Stelar) equipped with the HTS-110 3T metrology cryogen-free superconducting magnet. The measurements were performed with a standard inversion recovery sequence (20 experiments, 2 scans) with a typical 90° pulse width of 3.5 μs, and the reproducibility of the data was within ±0.5%. The exact concentration of Mn²⁺ was determined by measurement of bulk magnetic susceptibility shifts of a tBuOH signal.²³

¹⁷O NMR data were recorded on a Bruker Avance III spectrometer (11.7 T) using a 5 mm probe under temperature control. An aqueous solution of the complex was enriched to achieve 2.0% of the ¹⁷O isotope (Cambridge Isotope Laboratories). The transverse relaxation rates were measured from the signal width at half-height as a function of temperature in the 278–350 K range.

DFT studies

The geometries of the Mn²⁺ complexes were optimized using the Gaussian 16 program package (version C.01).³⁰ In these calculations we used the range-separated hybrid wB97XD³¹ functional (22% HF exchange) and the Def2-TZVPP³² basis set. All complexes were modelled in their sextet ground states using unrestricted wave functions. The stationary points obtained as a result of geometry optimization were characterised by frequency calculations. Solvent effects were incorporated using the integral equation formalism variant of the polarized continuum model (IEFPCM).³³ Spin restricted calculations were conducted for the Zn²⁺ analogues using the same methodology. A superfine integration grid was used throughout.

Results and discussion

Design and synthesis

The chelating agents OBETA and EHDTA share a common backbone represented by a 2,2′-oxybis(ethylamine) moiety, bearing the coordinating carboxymethyl arms on the distal nitrogen atoms. The backbone in EHDTA is embedded in a mesocyclic 5-membered tetrahydrofuran ring, with a cis-stereochemistry imperative to provide the correct convergent positioning of the whole donor atom set.

Straightforward functionalisation of the commercially available 2,2′-oxydiethylamine allows the easy preparation of OBETA.^24,34,35 Even if the parent diamine of EHDTA (cis-2,5-bis(amino-methyl)tetrahydrofuran, 6) is claimed to be a potential key biomass-derived starting material for the preparation of green polyamides and polyurethanes, large scale processes are still in their infancy and the commercial availability of this interesting diamine is limited to date to very small amounts.

The N–O–N donor set, endowed with a connectivity well suited for the formation of chelate rings and rigidified by the structural constraint imposed by the stereochemically defined oxolane ring, makes this diamine a preferred scaffold for coordination chemistry studies. This prompted us to explore in more detail alternative synthetic paths for this compound, along with the need for accessing multigram amounts for our purposes.

We recently reported a synthetic approach for the mesocyclic chelator EHDTA (Scheme 1, route A), starting from biomass-derived furfurylamine 1, initially protected as N-acetyl derivative 2. Tscherniak–Einhorn aminomethylation with N-hydroxymethylacetamide 3 generated the symmetrically difunctionalised furandiamide 4. Catalytic hydrogenation of the heterocyclic ring provided the stereochemically pure cis-diamide 5, which was then hydrolysed under acidic conditions to afford the desired diamine 6.

Scheme 1 Synthetic routes to EHDTA.

In this work, we report an alternative synthetic approach for diamine 6, outlined in Scheme 1 (route B), by starting from the well-known conversion of natural fructose to 5-hydroxymethylfurfural (HMF, 8). Catalytic hydrogenation of 8 selectively provides the cis-diol 9. Functional group interconversion was accomplished by O,O′-ditosylation (10), nucleophilic disubstitution (11), and hydrogenolysis, finally leading to the diamine 6.

For both routes, the synthesis of the chelating agent is completed by alkylating diamine 6 with t-butyl bromoacetate in acetonitrile, yielding tetraester 7, which is finally deprotected to give EHDTA.

The starting materials for both synthetic routes are commercially available in large amounts and are relatively cheap. Even if route A shows higher yield and a better atom economy with respect to route B, the availability of two distinct and proven synthetic approaches is extremely useful for the future preparation of lipophilic and bifunctional derivatives of EHDTA.

Solution thermodynamic studies

Protonation constants of EHDTA, OBETA and EGTA and stability constants of their [Mn(OBETA)]²⁻ and [Mn(EGTA)]²⁻ complexes were previously studied by our group.^24,26 However, the stability and protonation constants of [Mn(EHDTA)]²⁻ were not investigated before. Therefore, we decided to determine the stability and protonation constants of [Mn(EHDTA)]²⁻ by pH-potentiometry. The protonation constants (log K_i^H) of the EHDTA ligand defined by eqn (2) and obtained by pH-potentiometry are listed in Table 1 (standard deviations are shown in parentheses),where i = 1, 2…5. The stability and protonation constants of the Mn²⁺ complex with EHDTA, defined by eqn (3) and (4), were also determined by using pH-potentiometric titrations. The log K_MnL, log K_Mn(HiL) and pMn values of the [Mn(EHDTA)]²⁻ are listed and compared with those of [Mn(OBETA)]²⁻ and [Mn(EGTA)]²⁻ complexes in Table 1 (pMn = −log[Mn²⁺]_free, [Mn²⁺]_t = [L]_t = 10 μM, pH = 7.4).where i = 1 and 2. The stability and protonation constants listed in Table 1 show that log K_MnL values of [Mn(EHDTA)]²⁻ and [Mn(OBETA)]²⁻ are quite similar and about 0.9log K units higher than that of [Mn(EGTA)]²⁻. Although the ∑log K_i^H values of EHDTA, OBETA and EGTA are very similar, the presence of an additional ether donor atom in EGTA decreases the thermodynamic stability as compared to OBETA, while the incorporation of a rigid tetrahydrofuran ring in the backbone of OBETA to give EHDTA does not have a significant impact on the stability constants of the Mn²⁺ complexes. The higher Mn²⁺ affinity of EHDTA and OBETA compared to EGTA is also confirmed by their conditional stability constants (pMn) calculated at pH = 7.4 and 25 °C in the presence of 10 μM Mn²⁺ and ligand. Since the basicity of the three ligands are comparable (∑log K_i^H, Table 1) it is not surprising that the pMn values of [Mn(EHDTA)]²⁻ and [Mn(OBETA)]²⁻ are quite similar and somewhat higher than that of [Mn(EGTA)]²⁻, because of their higher stability constant. By taking into account the protonation constants of the ligands and the stability and protonation constants of the Mn²⁺ complexes, the speciation of the Mn²⁺-EHDTA, Mn²⁺-OBETA and Mn²⁺-EGTA systems have been calculated (Fig. S12–S14†). The stability trend observed is in agreement with the negative contributions to both log K_MnL and pMn provided by the incorporation of ether donor atoms.³⁶

Table 1 Protonation constants of the chelating agents, and stability and protonation constants of the corresponding Mn²⁺ complexes (25 °C)

	EHDTA		OBETA		EGTA
I	0.1 M KCl	0.1 M KCl^a	0.1 M KCl^b^,^c	0.1 M KNO3 ^d	0.1 M KCl^b^,^c	0.1 M KNO3 ^d
a Ref. 26. b Ref. 23. c Ref. 24. d Ref. 34. e Ref. 37. f pMn = −log[Mn^2+]free, [Mn^2+]t = [L]t = 10 μM, pH = 7.4.
log K1^H	9.37 (2)	9.40	9.34	9.39	9.43	9.47
log K2^H	8.75 (2)	8.70	8.62	8.75	8.82	8.85
log K3^H	3.25 (2)	2.84	3.19	2.76	2.77	2.66
log K4^H	2.21 (2)	2.11	2.19	1.80	2.06	2.00
log K5^H	2.01 (2)	1.30	1.77	—	1.88	—
∑log Ki^H	25.59	24.35	25.11	22.70	24.96	22.98
log KMnL	13.17 (1)		13.57	13.7^e	12.28	12.2^e
log KMnHL	3.98 (2)		3.45	—	4.43	—
log KMnH2L	3.73 (2)		—	—	—	—
pMn^f	7.42		7.69	7.67	6.91	6.84

---

Kinetic inertness of the Mn²⁺ complexes

To investigate the effect of substituting the oxyethylene bridge of EGTA with an ether oxygen atom or a five-membered tetrahydrofuran ring on the kinetic inertness of Mn²⁺ complexes, the transmetalation kinetics of [Mn(EHDTA)]²⁻ and [Mn(OBETA)]²⁻ were studied by monitoring their exchange reactions with Cu²⁺ in the pH range of 3.3–4.9. The mechanisms proposed for the transmetalation reactions of [Mn(EHDTA)]²⁻ and [Mn(OBETA)]²⁻ with Cu²⁺ are shown in Scheme 2. Experimental details and the equations used to evaluate the kinetic parameters are summarized in the ESI.† The rate and equilibrium constants that characterize the transmetalation reaction of [Mn(EHDTA)]²⁻ and [Mn(OBETA)]²⁻ are shown in Table 2.

Scheme 2 Proposed mechanism of the transmetalation reactions for [Mn(EHDTA)]²⁻ and [Mn(OBETA)]²⁻.

Table 2 Rate (k_i) and equilibrium (K_i) constants and half-life (t_1/2 = ln 2/k_d) values characterizing the transmetalation reactions of the Mn²⁺ complexes with EHDTA, OBETA and EGTA (25 °C)

	[Mn(EHDTA)]^2−	[Mn(OBETA)]^2−	[Mn(EGTA)]^2− ^a
I	0.15 M NaCl	0.15 M NaCl
a Ref. 27. b t 1/2 = ln 2/kd at pH = 7.4 and 25 °C in the presence of 10 μM Cu^2+. k1 = kMn(HL) × KMn(HL), k2 = k^HMn(HL) × KMn(HL) and k3^Cu = kMn(L)Cu × KMn(L)Cu.
k 0 (s^−1)	—	—	—
k 1 (M^−1 s^−1)	(2.8 ± 0.3) × 10^5	(1.3 ± 0.9) × 10^4	1.9 × 10^6
k 2 (M^−2 s^−1)	—	(8 ± 3) × 10^8	—
k 3 ^Cu (M^−1 s^−1)	(4.2 ± 0.9) × 10^3	(2.5 ± 0.2) × 10^3	5 × 10^3
log KMnHL	3.4 ± 0.1	3.2 ± 0.2	4.55
K MnLCu	—	44 ± 20	317
k d (s^−1) at pH = 7.4^b	5.0 × 10^−2	2.6 × 10^−2	0.13
t 1/2 (h) at pH = 7.4^b	3.8 × 10^−3	7.4 × 10^−3	1.5 × 10^−3

---

The k₀ rate constants obtained from the fitting procedure are very low and have a high error margin, confirming that the spontaneous dissociation pathway has no significant contribution to the dissociation rate of [Mn(EHDTA)]²⁻ and [Mn(OBETA)]²⁻ under our experimental conditions (pH 3.3–4.9). Comparing the k₁ rate constants of the Mn²⁺ complexes reveals that the proton-assisted dissociation of [Mn(EHDTA)]²⁻ and [Mn(OBETA)]²⁻ is approximately 7 and 146 times slower, respectively, than that of [Mn(EGTA)]²⁻. On the other hand, the k₃^Cu rate constant characterizing the Cu²⁺-assisted dissociation of [Mn(EHDTA)]²⁻ and [Mn(EGTA)]²⁻ is rather similar and about two times higher than that of [Mn(OBETA)]²⁻. Systematic kinetic studies of Mn²⁺ complexes with various open-chain amino-polycarboxylate ligands have shown that a longer ligand backbone increases complex lability and reduces kinetic inertness.²⁷ However, the kinetic inertness of the Mn²⁺ complexes can be improved by increasing the rigidity of the ligand backbone.^20,38 Conversely, the preorganization of iminodiacetate groups imposed by cyclobutyl and cyclopentyl rings in the ligand backbone reduces the kinetic inertness of Mn²⁺ complexes. This is due to the creation of a suboptimal coordination environment around the Mn²⁺ ion.^20,38 Based on the kinetic data summarized in Table 2, the most important pathway of the transmetalation reactions of [Mn(EHDTA)]²⁻, [Mn(OBETA)]²⁻ and [Mn(EGTA)]²⁻ is the proton assisted dissociation. Generally, the proton assisted dissociation of the Mn²⁺ complexes occurs through the formation of a labile protonated Mn(HL) intermediate. The protonation of the Mn²⁺ complexes takes place on the carboxylate group. The proton transfer from the carboxylate group to the nitrogen of the ligand backbone results in the dissociation of the Mn(HL) intermediate. The relatively fast proton-assisted dissociation of [Mn(EGTA)]²⁻ can be attributed to the greater flexibility of the oxyethylene bridge, which facilitates proton transfer from the carboxylate group to the nitrogen of the iminodiacetate group. Replacing the oxyethylene group in [Mn(EGTA)]²⁻ with an ether oxygen increases the rigidity of the complex, resulting in a slower proton-assisted dissociation of [Mn(OBETA)]²⁻. On the other hand, the incorporation of the ether oxygen in the tetrahydrofuran ring of OBETA leads to faster proton-assisted dissociation of [Mn(EHDTA)]²⁻ due to the unfavourable coordination environment of the Mn²⁺ ion. The dissociation rate (k_d) and half-life (t_1/2) values of the Mn²⁺ complexes have been calculated at pH = 7.4 in the presence of 10 μM Cu²⁺ (Table 2). The comparison of the k_d and t_1/2 values also reveals that the dissociation rate of [Mn(OBETA)]²⁻ is about 2 and 5 times lower than that of [Mn(EHDTA)]²⁻ and [Mn(EGTA)]²⁻, respectively.

¹H and ¹⁷O NMR relaxometric data¹⁶. Over the years, ¹H and ¹⁷O NMR relaxometric analysis has become a fundamental technique for the detailed and comprehensive characterization of paramagnetic metal ion complexes in aqueous solutions. Consequently, we examined the relaxometric properties of the [Mn(OBETA)]²⁻, [Mn(EGTA)]²⁻, and [Mn(EHDTA)]²⁻ complexes to determine their hydration state (q), stability with pH, and effectiveness as relaxation agents in magnetic fields typical of MRI. From the perspective of proton relaxometry, the key parameter is relaxivity, denoted as r₁, which measures the increase in the longitudinal nuclear magnetic relaxation rate of water protons scaled to a concentration of 1 mM of the paramagnetic ion.³⁹ The value of r₁, dependent on the observation frequency, is determined by interactions between the nuclear spins of the proton nuclei of water molecules and the unpaired electrons of the magnetic centre. These interactions can involve both water molecules present in number q within the inner coordination sphere of the metal ion (inner sphere contribution, IS) and water molecules freely diffusing in the outer coordination sphere (outer sphere contribution, OS).⁴⁰ The inner sphere contribution (r_1IS) holds greater importance due to its dependence on the structural properties of the complex. It can be enhanced through various strategies, including appropriate chelate design. The IS relaxivity values of Mn²⁺ complexes are anticipated to exhibit a linear correlation with the molecular weight of the complexes at high fields (>10 MHz), where rotational dynamics (τ_R) assume a dominant role over both the water exchange lifetime (τ_M) and the electronic relaxation times (T_ie,i = 1, 2). In addition, the value of r_1IS scales linearly with q, so as a first step, we measured the r₁ value of the complexes at 20 MHz and 298 K to estimate their hydration state by comparison with published data for related Mn²⁺ complexes with q = 1 and q = 0.²² From the plot of r₁versus molecular mass, it is evident that the relaxivity values for [Mn(EGTA)]²⁻ and [Mn(EHDTA)]²⁻ are comparable to those of other Mn²⁺ complexes with a hydration number q = 0 (Fig. 2).

Fig. 2 Plot of the relaxivity (20 MHz, 25 °C) of selected Mn²⁺ complexes with q = 1 (◆) and q = 0 (◊) as a function of the molecular mass. The linear correlations were calculated without the value of [Mn-OBETA]²⁻. The chemical structures of all ligands shown in the figure are provided in Scheme S1 of the ESI.†

Meanwhile, [Mn(OBETA)]²⁻ exhibits an r₁ value that is distinctly higher (ca. 25%), yet still below the level expected for a monohydrate complex. This suggests that [Mn(OBETA)]²⁻ likely exists in solution as a mixture of two species with differing populations and hydration states: zero and one.²²

pH dependency

The assessment of r₁ as a function of pH reveals a characteristic pattern observed in small polyamine carboxyl complexes of Mn²⁺, akin to [Mn(EDTA)]²⁻. Across a broad spectrum of pH values, the relaxivity remains constant, with a notable increase observed within the acidic pH range (Fig. 3).

Fig. 3 The relaxivity of the three Mn²⁺ complexes investigated in this study, measured at 20 MHz and 25 °C, measured as a function of pH.

This increase is likely due to a growing presence of the hexaaqua ions resulting from complex dissociation. Notably, complexes exhibiting greater stability display a wider pH range of constant r₁ values.

¹H NMRD profiles. An accurate evaluation of the structural and dynamic parameters governing the relaxivity of a paramagnetic compound requires measuring r₁ over a wide range of observation frequencies and temperatures. This is conveniently achieved through Fast Field-Cycling relaxometry (FFC-NMR), which involves determining the frequency dependence of the longitudinal proton relaxation rate of the solvent water to gather information about the solute.⁴¹ The r₁ data are plotted as a function of the proton Larmor frequency to generate the nuclear magnetic relaxation dispersion (NMRD) profile. Advanced instruments can measure data in the range of approximately 0–3 T, with higher magnetic field data obtainable using high-resolution NMR spectrometers. We measured the NMRD profiles of the three Mn²⁺ complexes at pH values of 7.2 and at four different temperature values, specifically 283, 288, 298, and 310 K. The results obtained are shown in Fig. 4.

Fig. 4 ¹H NMRD profiles at 283 (), 288 (), 298 (◆) and 310 K () (pH = 7.5) for [Mn(EGTA)]²⁻ (A), [Mn(EHDTA)]²⁻ (B) and [Mn(OBETA)]²⁻ (C).

All the NMRD profiles exhibit a very similar pattern characteristic of low molecular weight and low hydration state complexes, where the OS contribution to r₁ is predominant.¹³ A constant relaxivity region is observed between 0.01 and 1 MHz, followed by a broad dispersion in which r₁ decreases with increasing frequency. As typical for q = 0 complexes, the r₁ values decrease with increasing temperature following the trend of the solute–solvent diffusion coefficient (D) and the electronic relaxation times T_ie (i = 1 and 2). This is especially true for [Mn(EGTA)]²⁻ and [Mn(EHDTA)]²⁻ where the data can be very well reproduced based on the classic Freed model for outer sphere relaxation, obtaining the parameters reported in Table 3.^42,43 Given the very similar molecular sizes of the complexes, during the analysis we used standard values for the distance of the closest approach between the paramagnetic ion and the bulk water protons (a) and for the diffusion coefficient ²⁹⁸D. The small difference in relaxivity values observed at low frequencies is fully explainable based on a small difference in the values of the electronic relaxation parameters, Δ² and τ_V. On the other hand, in the case of [Mn(OBETA)]²⁻, the experimental data can be satisfactorily fitted only by considering the presence in solution of a small population of a species with q = 1. To proceed with this type of analysis, it is necessary to consider a number of additional parameters, such as the rotational correlation time τ_R, the distance between the Mn²⁺ ion and the protons of the coordinated water molecule, and the average lifetime τ_M. We then proceeded with the best-fit procedure, also using q as a variable parameter.^44–46 The result obtained is of excellent quality, as shown in Fig. 4, considering a population of 15% of the monohydrated species (q = 0.15 ± 0.01) characterized by a rotational correlation time of 71 ps (Table 3). An independent estimate of the hydration number of [Mn(OBETA)]²⁻ can be obtained using the approximate method proposed by J. Peters and C.F.G.C. Geraldes, based on the low-field (0.01 MHz) r₁ value and the molecular weight of the complexes.⁴⁷ The results confirm that [Mn(OBETA)]²⁻ is partially hydrated. The q value from this approach (q = 0.6 ± 0.4) is higher than the value obtained from the simultaneous analysis of ¹H NMRD and ¹⁷O NMR data (q = 0.15 ± 0.01). This discrepancy arises from the limited accuracy of the model, estimated at ±0.4. Nevertheless, this result provides further confirmation that the q value of [Mn(OBETA)]²⁻ is greater than that of [Mn(EGTA)]²⁻ (q = 0.4) and [Mn(EHDTA)]²⁻ (q = 0.4). For further verification of the plausibility of the approach and the results, we deemed it appropriate to proceed with a simultaneous fit of the ¹H NMR data with the ¹⁷O NMR data, fixing q at the value of 0.15.

Table 3 Best fit parameters of analysis of ¹H NMRD and ¹⁷O NMR data

Parameters	[Mn(OBETA)]^2−	[Mn(EGTA)]^2−	[Mn(EHDTA)]^2−
a Fixed in the fitting procedure. a and ^298D were fixed to 3.4 Å and 2.24 × 10^−5 cm^2 s^−1, respectively.
^22 r 1 (298 K) (mM^−1 s^−1)	2.0	1.7	1.7
Δ ^2/10^19 s^−2	4.4 ± 0.3	1.4 ± 0.2	2.6 ± 0.1
τ V/ps	20 ± 1	31 ± 2	30 ± 1
τ M/ns	6.7 ± 0.2	—	—
ΔHM/kJ mol^−1	31.5 ± 1.0	—	—
τ R/ps	71 ± 3	—	—
A O/h/10^6 rad s^−1	31.5 ± 1.0	—	—
q	0.15 ± 0.01	0^a	0^a
r/Å	2.83^a	—	—

---

¹⁷O NMR data

The optimal method for investigating the water exchange process in paramagnetic metal complexes involves measuring variable temperature ¹⁷O NMR transverse relaxation rates (R₂) and shift values (Δω) of ¹⁷O-enriched water molecules.⁴⁸ These measurements provide the exchange rate constant (k_ex = 1/τ_M) and the associated activation parameters. The resulting data can be analysed using the Swift–Connick equations.⁴⁹ For very fast exchange, R₂ decreases with increasing temperature, whereas for very slow exchange, R₂ increases with temperature. Often, there is a maximum in the curve, indicating the transition from the “slow exchange” to the “fast exchange” regime.³⁹ Finally, a global fitting of the shift and relaxation data is performed to obtain the kinetic parameters of the exchange. The R₂ values for the three complexes were measured over the temperature range of 275–355 K (Fig. S19†). For [Mn(EGTA)]²⁻ and [Mn(EHDTA)]²⁻, the data clearly indicate the absence of a water molecule in the inner coordination sphere of Mn²⁺, as the measured values deviate only slightly from those of pure solvent. In contrast, [Mn(OBETA)]²⁻ exhibits a profile with a maximum at low temperatures, indicative of a rapid exchange regime. However, the profile's amplitude is significantly reduced compared to that of a complex with q = 1, supporting the hypothesis that a species with q = 1 is present in solution, albeit with a relatively small population. Experimental data are typically reported as reduced relaxation rates (R_2r) and chemical shifts (Δω_r) following normalization to the mole fraction of the bound water molecule (Fig. 5).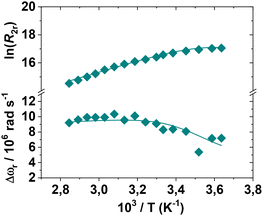

Fig. 5 Reduced transverse relaxation rates and chemical shifts for an aqueous solution of [Mn-OBETA]²⁻ at pH = 7.4 (11.7 T).

The R_2r values show a clear increase with decreasing temperature, a behaviour typical of complexes characterized by a fast exchange regime. The calculated τ_M value is approximately 7 ns, associated with a low activation enthalpy (ΔH_M). Additionally, the presence of two species in equilibrium with different q values implies a small energy difference between the corresponding hydration states, resulting in a high water exchange rate. Thus, despite the implicit approximation that q is temperature-independent, the ¹H and ¹⁷O NMR relaxometric data are well-reproduced using the parameters in Table 3, providing a detailed description of the behaviour of [Mn(OBETA)]²⁻ in aqueous solution.

Solution structure and dynamics

The X-ray diffraction analysis of single crystals of Sr[Mn(EGTA)]·7H₂O is reported in the literature, enabling detailed examination of the solid-state structure of the [Mn(EGTA)]²⁻ complex.²⁰ The Mn²⁺ ion (ionic radius 0.96 Å for CN 8)⁵⁰ is directly bound to the eight donor atoms of the ligand: two ether (O5, O6), four carboxylate oxygen (O1, O3, O7, O9) and two nitrogen atoms (N1, N2). The Mn²⁺ ion is situated within a distorted dodecahedral coordination polyhedron. This structure is characterized by a 1 : 4 : 3 arrangement, with the O1 atom at the top, followed by two nearly parallel pseudo-planes formed by atoms N1, N2, O6, and O7 in the first plane, and O3, O5, and O9 in the second (Fig. S39, ESI†). A similar coordination geometry was also identified around the larger Cd²⁺ ion (ionic radius: 1.10 Å for CN 8) in Sr[Cd(EGTA)]·7H₂O.⁵¹ The analysis of the bond distances in [Mn(EGTA)]²⁻ reveals that the Mn–O distances to ether oxygen atoms (Mn–O5: 2.495 Å, Mn–O6: 2.529 Å) are significantly longer than those involving the carboxylate oxygen donor atoms (2.21–2.29 Å). DFT calculations provide a geometry for the [Mn(EGTA)]²⁻ very similar to the X-ray structure (Table S3, ESI†), although it overestimates significantly the Mn–O6 distance involving one of the ether oxygen atoms. The DFT structure obtained for the [Zn(EGTA)]²⁻ complex shows a very similar wrapping of the ligand around the metal ion, with the Zn–O6 distance being further enlarged to 3.011 Å. Thus, the Mn²⁺ and Zn²⁺ complexes exhibit similar structures, with the metal ion weakening the interaction with the ether oxygen atoms as its ionic radius decreases. DFT calculations also provide very similar structures for the Mn²⁺ and Zn²⁺ complexes of OBETA and EHDTA (Fig. S43 and 44, ESI†). Thus, we investigated the dynamics of this family of Mn²⁺ complexes by performing multinuclear 1D and 2D NMR studies on the diamagnetic Zn²⁺ analogues.

The 1D (VT-¹H and VT-¹³C NMR) and 2D (¹H–¹H COSY, ¹H–¹H EXSY and ¹H–¹³C HSQC) NMR spectra of Zn²⁺ complexes with EHDTA, OBETA and EGTA measured in the temperature range 273–343 K are shown in Fig. 6 and 7, and S20–S34.† The chemical structure and the possible isomerization of [Zn(EHDTA)]²⁻, [Zn(OBETA)]²⁻ and [Zn(EGTA)]²⁻ with the assignment of the ¹H and ¹³C NMR signals are shown in Scheme 3.

Fig. 6 ¹H NMR spectra of [Zn(EHDTA)]²⁻ at 273 K and pH = 7.10 (A), [Zn(OBETA)]²⁻ at 298 K and pH = 7.01 (B) and [Zn(EGTA)]²⁻ at 343 K and pH = 7.04 (C) ([ZnL] = 50 mM, D₂O, 9.4 T).

Fig. 7 ¹³C NMR spectra of [Zn(EHDTA)]²⁻ (A) [Zn(OBETA)]²⁻ (B) and [Zn(EGTA)]²⁻ (C) complexes ([Zn(EHDTA)] = 50 mM, pH = 7.10; [Zn(OBETA)] = 50 mM, pH = 7.01; [Zn(EGTA)] = 50 mM, pH = 7.04; D₂O, 9.4 T, 273 K).

Scheme 3 Numbering scheme used for NMR spectral assignment and N inversion process in [Zn(EHDTA)]²⁻, [Zn(EGTA)]²⁻ and [Zn(OBETA)]²⁻. In [Zn(EHDTA)]²⁻ N inversion is likely assisted by the coordination of a water molecule (see text).

The ¹H NMR spectrum of [Zn(EGTA)]²⁻ at 273 K displays four broad signals that indicate a fluxional behaviour in solution. Based on 2D NMR experiments (Fig. S32–S34†), the two broad multiplets and two singlets at 3.45, 3.95, 4.05 and 3.80 ppm in the ¹H NMR spectra can be assigned to the 3H, 4H, 5H and 2,2′H methylene protons. The acetate methylene protons are magnetically equivalent due to the fast intramolecular acetate scrambling processes and the shortening of the lifetime of the Zn²⁺–O⁻ coordination bond on the actual NMR time scale at 273 K (Scheme 3, and Fig. 6). However, the 2,2′H methylene protons are observed as an AB spin system for [Zn(OBETA)]²⁻, a situation that indicates that the acetate groups are undergoing fast rotation in the NMR timescale leading to a δ ↔ λ change in the configuration of the corresponding five-membered chelate rings. This process can follow a concerted mechanism and does not require de-coordination of the acetate groups. This pathway does not exchange the geminal protons of the acetate groups in [Zn(EHDTA)]²⁻ due to the cis stereochemistry of the tetrahydrofuran ring, and thus the ¹H NMR spectrum shows two AB spin systems for 2,2′H methylene protons (Fig. 6A).^52,53

The ¹³C NMR spectra of [Zn(EGTA)]²⁻ and [Zn(EHDTA)]²⁻ recorded at 273 K (Fig. 7) show two signals for the magnetically non-equivalent carbons of the acetate groups (2,2′ and 1,1′, Fig. 7, S21 and S31†) bound to the same amine nitrogen atom. The VT-¹³C NMR spectra of [Zn(EGTA)]²⁻ and [Zn(EHDTA)]²⁻ reveal a progressive broadening and coalescence of the signals assigned to carbons of the acetate groups by increasing temperature, a situation that can be ascribed to intramolecular exchange between the acetate groups at the same nitrogen atom via inversion of the amine N atom, which requires de-coordination of the acetate group (Fig. S21 and S31,†Scheme 3). However, the ¹³C NMR spectra of [Zn(OBETA)]²⁻ consist of four signals, which are practically unchanged in the temperature range of 273–343 K (Fig. 7 and S26†), indicating that the inversion of the amine N atom is fast within the timescale of this experiment.

In order to calculate the rate and the activation parameters characterizing the N inversion processes of [Zn(EGTA)]²⁻ and [Zn(EHDTA)]²⁻, we performed a line-shape analysis of the 2,2′ ¹³C NMR signals in the temperature range 273–343 K. For [Zn(OBETA)]²⁻, this dynamic process was investigated using VT-¹H NMR spectra, which reveal a broadening and coalescence of the AB system by increasing the temperature (Fig. S25†). The ¹H and ¹³C NMR spectral parameters used for the calculations of the rate constants are summarized in Table S1.† Activation parameters for the N inversion process were estimated with the Eyring equation using the k_ex rate constant obtained in the line-shape analysis of the VT-¹H and VT-¹³C NMR spectra (Fig. S38† and Table 4).

Table 4 Rate constants and activation parameters of the isomerization processes for the Zn²⁺-complexes of EHDTA, OBETA and EGTA

	[Zn(EHDTA)]^2−	[Zn(OBETA)]^2−	[Zn(EGTA)]^2−
ΔH^‡/kJ mol^−1	36.0 ± 0.5	71 ± 3	59 ± 1
ΔS^‡/J mol^−1 K^−1	−90 ± 2	−7 ± 3	14 ± 4
ΔG^‡298/kJ mol^−1	62.8	72.8	55.5
k ^298ex/s^−1	57	1.1	1150

---

The comparison of the activation parameters shown in Table 4 reveals that the N inversion process of [Zn(EGTA)]²⁻ is characterized by a higher enthalpy (ΔH^‡) than that in [Zn(EHDTA)]²⁻, with the entropy (ΔS^‡) values having opposite signs. The relatively large negative value of the activation entropy for the N inversion in [Zn(EHDTA)]²⁻ suggests that this process may be assisted by the coordination of a water molecule. For instance, a pseudo-heptacoordinated [Zn(CDTA)(H₂O)]²⁻ complex with a partially open acetate arm was observed in the X-ray structure of [{Zn(H₂O)₄}{Zn(CDTA)(H₂O)}]·4H₂O.⁵⁴ The presence of the water molecule in the inner sphere of Zn²⁺ ion results in the weakening of the Zn²⁺–O⁻ and Zn²⁺–N bonds, which may facilitate the de-coordination of the acetate arm and the inversion of the N donor atom in [Zn(EHDTA)]²⁻. However, the N inversion process of [Zn(EGTA)]²⁻ cannot take place via the formation of a [Zn(EGTA)(H₂O)]²⁻ intermediate due to the presence of eight donor atoms in the flexible ligand backbone. Based on the relatively high enthalpy and small entropy values, it might be assumed that the N inversion process of [Zn(EGTA)]²⁻ occurs by the substitution in the inner sphere of the Zn²⁺ ion of the carboxylate–O atom by an otherwise weakly coordinated ether O atom. Because of the large negative value of the activation entropy, the N inversion of [Zn(EHDTA)]²⁻ is an entropy controlled process, which is characterized by significantly higher activation free energy (ΔG^‡₂₉₈) and lower exchange rate (k²⁹⁸_ex) than in [Zn(EGTA)]²⁻.

According to the parameters summarized in Table 4, the coordination/decoordination processes of the carboxylate oxygen atoms in [Zn(OBETA)]²⁻ is characterized by very high activation enthalpy and a slightly negative activation entropy, which is consistent with the formation of a temporarily ordered water shell in the transition state.

The dynamics of the N inversion in Zn²⁺ complexes correlate very well with the dissociation kinetics data of the Mn²⁺ analogues. In particular, complex dissociation following the acid-catalysed mechanism likely proceeds through the protonation of a negatively charged acetate group. This proton then triggers a cascade of processes involving carboxylate decoordination, transfer of the proton to an amine N atom and eventual complex dissociation. The NMR studies indicate that carboxylate decoordination is slower in [Zn(OBETA)]²⁻ than in [Zn(EHDTA)]²⁻and [Zn(EGTA)]²⁻, which correlates nicely with the kinetics of the complex dissociation summarized in Table 2.

Conclusions

In this study, we investigated the relaxometric, thermodynamic, and kinetic properties of three Mn²⁺ complexes with structurally related polyetheraminocarboxylate ligands. The potentially octadentate EGTA ligand and the heptadentate EHDTA form complexes that lack inner-sphere water molecules. However, it is somewhat surprising that a fraction of the OBETA complex contains an inner-sphere water molecule in aqueous solution. It remains unclear whether this results from the formation of an eight-coordinate complex or partial de-coordination of the ligand, allowing water coordination.

All three complexes exhibit comparable thermodynamic stability, although the inclusion of an additional ether donor atom in the ligand scaffold slightly reduces stability. The dissociation rates of these complexes differ significantly, with the EGTA complex being notably more labile. Interestingly, the observed dissociation rates correlate with the nitrogen inversion dynamics, as studied by NMR for their Zn²⁺ analogues. While studies on additional Mn²⁺/Zn²⁺ complexes are required to demonstrate this connection, the results reported here suggest that NMR studies on Zn²⁺ analogues are useful to assess the kinetic inertness of Mn²⁺ complexes.

The work reported here highlights how small structural changes may have a significant impact on the properties of Mn²⁺ complexes. The rigidification of the ligand scaffold of OBETA to give EHDTA does not result in an enhanced kinetic inertness, as it is generally observed. This structural modification does not hinder the dynamics of the complex, as shown by NMR studies on the Zn²⁺ analogue, and thus fails to slow down complex dissociation.

In summary, the lower stereochemical rigidity of OBETA not only promotes greater kinetic inertness, but also allows for the presence of a small population of monohydrated Mn²⁺ complexes (q = 1). This further confirms that, in the case of Mn²⁺ complexes, it is challenging to make accurate predictions based solely on the ligand's core structure. Significant variations in the hydration state and kinetic inertness can be induced by making slight modifications to the ligand backbone or altering the chemical nature of one or more pendant arms. We hope that by continuing in this direction, it will be possible to significantly increase the population of the q = 1 species without compromising—or even enhancing—kinetic inertness and thermodynamic stability by appropriately modifying [Mn(OBETA)]²⁻.

Author contributions

Conceptualization, project administration and supervision: M. B., G. B. G. and Z. B.; funding acquisition: M. B. and G. B. G.; preparation of the chelating agents and complexes: F. T., R. N. and F. C.; relaxometric studies: M. B. and F. C.; complexometric studies: F. K. and Z. B.; DFT studies: C.P.-I.; writing and finalization of the manuscript: all authors.

Data availability

The authors confirm that the data supporting the findings of this study are available within the article and its ESI.† Raw data that support the findings of this study are available from the corresponding author upon reasonable request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This publication is part of the project NODES which has received funding from the MUR – M4C2 1.5 of PNRR with grant agreement no. ECS00000036 (M. B., G. B. G., F. T.). C. P.-I. thanks Ministerio de Ciencia e Innovación (PID2022-138335NB-I00) and Xunta de Galicia (ED431C 2023/33) for generous financial support, as well as Centro de Supercomputación de Galicia (CESGA) for providing the computing facilities. The research was also partially funded by the Hungarian National Research, Development and Innovation Office (FK-134551) project, the New National Excellence Program ÚNKP-22-5 (F. K. K.). F. K. K. acknowledges financial support of the János Bolyai Research Scholarship of the Hungarian Academy of Sciences.

References

1. J. Wahsner, E. M. Gale, A. Rodríguez-Rodríguez and P. Caravan, Chem. Rev., 2019, 119, 957–1057.
2. M. Le Fur and P. Caravan, Metallomics, 2019, 11, 240–254.
3. H. Malikova, Quant. Imaging Med. Surg., 2019, 9, 1470474–1471474.
4. K. A. Layne, D. M. Wood and P. I. Dargan, Clin. Toxicol., 2020, 58, 151–160.
5. L. Yang, I. Krefting, A. Gorovets, L. Marzella, J. Kaiser, R. Boucher and D. Rieves, Radiology, 2012, 265, 248–253.
6. T. Wang, Q. Wu, Z. Wang, G. Dai, H. Jia and S. Gao, ACS Earth Space Chem., 2021, 5, 3130–3139.
7. V. Hatje, K. W. Bruland and A. R. Flegal, Environ. Sci. Technol., 2016, 50, 4159–4168.
8. R. Brünjes and T. Hofmann, Water Res., 2020, 182, 115966.
9. J. Rogowska, E. Olkowska, W. Ratajczyk and L. Wolska, Environ. Toxicol. Chem., 2018, 37, 1523–1534.
10. E. Perrat, M. Parant, J.-S. Py, C. Rosin and C. Cossu-Leguille, Environ. Sci. Pollut. Res. Int., 2017, 24, 12405–12415.
11. E. M. Snyder, D. Asik, S. M. Abozeid, A. Burgio, G. Bateman, S. G. Turowski, J. A. Spernyak and J. R. Morrow, Angew. Chem., Int. Ed., 2020, 59, 2414–2419.
12. Z. Baranyai, F. Carniato, A. Nucera, D. Horváth, L. Tei, C. Platas-Iglesias and M. Botta, Chem. Sci., 2021, 12, 11138–11145.
13. M. Botta, F. Carniato, D. Esteban-Gómez, C. Platas-Iglesias and L. Tei, Future Med. Chem., 2019, 11, 1461–1483.
14. A. Gupta, P. Caravan, W. S. Price, C. Platas-Iglesias and E. M. Gale, Inorg. Chem., 2020, 59, 6648–6678.
15. E. M. Gale, I. P. Atanasova, F. Blasi, I. Ay and P. Caravan, J. Am. Chem. Soc., 2015, 137, 15548–15557.
16. S. Aime, M. Botta, D. Esteban-Gómez and C. Platas-Iglesias, Mol. Phys., 2019, 117, 898–909.
17. D. Ndiaye, M. Sy, A. Pallier, S. Même, I. de Silva, S. Lacerda, A. M. Nonat, L. J. Charbonnière and É. Tóth, Angew. Chem., Int. Ed., 2020, 59, 11958–11963.
18. E. Molnár, B. Váradi, Z. Garda, R. Botár, F. K. Kálmán, É. Tóth, C. Platas-Iglesias, I. Tóth, E. Brücher and G. Tircsó, Inorg. Chim. Acta, 2018, 472, 254–263.
19. K. Pota, Z. Garda, F. K. Kálmán, J. L. Barriada, D. Esteban-Gómez, C. Platas-Iglesias, I. Tóth, E. Brücher and G. Tircsó, New J. Chem., 2018, 42, 8001–8011.
20. J. Martinelli, E. Romano, A. Laczovics, D. Horváth, E. Grattoni, Z. Baranyai and L. Tei, Chem. – Eur. J., 2024, 30, e202400570.
21. L. Tei, G. Gugliotta, M. Fekete, F. K. Kálmán and M. Botta, Dalton Trans., 2011, 40, 2025–2032.
22. G. A. Rolla, C. Platas-Iglesias, M. Botta, L. Tei and L. Helm, Inorg. Chem., 2013, 52, 3268–3279.
23. Z. Baranyai, M. Botta, M. Fekete, G. B. Giovenzana, R. Negri, L. Tei and C. Platas-Iglesias, Chem. – Eur. J., 2012, 18, 7680–7685.
24. R. Negri, Z. Baranyai, L. Tei, G. B. Giovenzana, C. Platas-Iglesias, A. C. Bényei, J. Bodnár, A. Vágner and M. Botta, Inorg. Chem., 2014, 53, 12499–12511.
25. R. Negri, F. Carniato, M. Botta, G. B. Giovenzana and L. Tei, ChemPlusChem, 2016, 81, 235–241.
26. F. Travagin, M. L. Macchia, T. Grell, J. Bodnár, Z. Baranyai, F. Artizzu, M. Botta and G. B. Giovenzana, Dalton Trans., 2024, 53, 1779–1793.
27. F. K. Kálmán and G. Tircsó, Inorg. Chem., 2012, 51, 10065–10067.
28. H. M. Irving, M. G. Miles and L. D. Pettit, Anal. Chim. Acta, 1967, 38, 475–488.
29. L. Zekany and I. Nagypal, in Computational Methods for the Determination of Formation Constants, ed. D. J. Leggett, Springer US, Boston, MA, 1985, pp. 291–353.
30. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. C.01, Wallingford, CT, 2016.
31. J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
32. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
33. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094.
34. J. L. Mackey, M. A. Hiller and J. E. Powell, J. Phys. Chem., 1962, 66, 311–314.
35. J. R. Geigy AG, GB Pat., GB695346, 1953.
36. R. Uzal-Varela, F. Pérez-Fernández, L. Valencia, A. Rodríguez-Rodríguez, C. Platas-Iglesias, P. Caravan and D. Esteban-Gómez, Inorg. Chem., 2022, 61, 14173–14186.
37. G. Anderegg, Helv. Chim. Acta, 1964, 47, 1801–1814.
38. R. Uzal-Varela, D. Lalli, I. Brandariz, A. Rodríguez-Rodríguez, C. Platas-Iglesias, M. Botta and D. Esteban-Gómez, Dalton Trans., 2021, 50, 16290–16303.
39. L. Helm, J. R. Morrow, C. J. Bond, F. Carniato, M. Botta, M. Braun, Z. Baranyai, R. Pujales-Paradel, M. Regueiro-Figuero, D. Esteban-Gómez, C. Platas-Iglesias and T. J. Scholl, in Contrast Agents for MRI: Experimental Methods, ed. V. C. Pierre and M. J. Allen, The Royal Society of Chemistry, 2017, ch. 2, pp. 121–242.
40. S. Aime, M. Botta and E. Terreno, in Advances in Inorganic Chemistry, Academic Press, 2005, vol. 57, pp. 173–237.
41. S. H. Koenig and R. D. Brown, Prog. Nucl. Magn. Reson. Spectrosc., 1990, 22, 487–567.
42. L. Hwang and J. H. Freed, J. Chem. Phys., 1975, 63, 4017–4025.
43. J. H. Freed, J. Chem. Phys., 1978, 68, 4034–4037.
44. I. Solomon, Phys. Rev., 1955, 99, 559–565.
45. N. Bloembergen, J. Chem. Phys., 1957, 27, 572–573.
46. N. Bloembergen and L. O. Morgan, J. Chem. Phys., 1961, 34, 842–850.
47. J. A. Peters and C. F. G. C. Geraldes, Inorganics, 2018, 6, 116.
48. D. H. Powell, O. M. N. Dhubhghaill, D. Pubanz, L. Helm, Y. S. Lebedev, W. Schlaepfer and A. E. Merbach, J. Am. Chem. Soc., 1996, 118, 9333–9346.
49. T. J. Swift and R. E. Connick, J. Chem. Phys., 1962, 37, 307–320.
50. R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767.
51. C. K. Schauer and O. P. Anderson, J. Am. Chem. Soc., 1987, 109, 3646–3656.
52. Y. Ba, R.-F. Song and Z.-W. Qiu, Magn. Reson. Chem., 1989, 27, 916–921.
53. J. Maigut, R. Meier, A. Zahl and R. van Eldik, Inorg. Chem., 2008, 47, 5702–5719.
54. A. Fuertes, C. Miravitlles, E. Escrivá, E. Coronado, D. Beltrán and L. Padel, J. Chem. Soc., Dalton Trans., 1989, 863–871.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dt02761b

---