Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Yb5Rh6Sn18: a valence fluctuating system with ultra-low thermal conductivity†
Oleksandr
Bolielyi
a,
Volodymyr
Levytskyi
 a,
Jörg
Wagler
a,
Jörg
Wagler
 b,
Kristina O.
Kvashnina
b,
Kristina O.
Kvashnina
 cd,
Bohdan
Kundys
cd,
Bohdan
Kundys
 e,
Andreas
Leithe-Jasper
e,
Andreas
Leithe-Jasper
 f and
Roman
Gumeniuk
f and
Roman
Gumeniuk
 *a
*a
aInstitut für Experimentelle Physik, TU Bergakademie Freiberg, Leipziger Straße 23, 09596 Freiberg, Germany. E-mail: roman.gumeniuk@physik.tu-freiberg.de
bInstitut für Anorganische Chemie, TU Bergakademie Freiberg, Leipziger Straße 29, 09599 Freiberg, Germany
cThe Rossendorf Beamline at ESRF, CS 40220, 38043 Grenoble Cedex 9, France
dHelmholtz-Zentrum Dresden-Rossendorf (HZDR), Institute of Resource Ecology, P.O. Box 510119, 01314 Dresden, Germany
eUniversité de Strasbourg, CNRS, Institut de Physique et Chimie des Matériaux de Strasbourg, UMR 7504, Strasbourg F-67000, France
fMax-Planck-Institut für Chemische Physik fester Stoffe, Nöthnitzer Straße 40, 01187 Dresden, Germany
First published on 22nd November 2024
Abstract
Yb5Rh6Sn18 crystallizes with a unique structural arrangement [space group P42/nmc, a = 9.6997(4) Å, c = 13.7710(7) Å], which is related with primitive cubic Yb3Rh4Sn13 and body-centered tetragonal (Sn1−xTbx)Tb4Rh6Sn18 types. X-ray absorption spectroscopy showed that Yb atoms exhibit temperature-dependent valence fluctuations (VF) (i.e., intermediate valence state). Its complex mechanism is corroborated by the fact that the well-pronounced maximum in magnetic susceptibility can only be fairly described by the Bickers–Cox–Wilkins model developed for a J = 3/2 multiplet, atypical for Yb ions. Both Hall and Seebeck coefficients revealed a switch of the sign, indicating the change of charge carrier type from electrons to holes between 120 and 220 K. Both these effects together with electrical resistivity and theoretical DFT calculations confirm Yb5Rh6Sn18 to be a metal, which disobeys the free electron gas theory. ‘Rattling’ motion of Sn1 atoms within the enlarged 16-vertices distorted Frank–Kasper polyhedra, concluded from the specific heat measurements, is argued to be the main reason for the appearance of a phonon resonance behavior, resulting in an ultra-low thermal conductivity in the studied stannide.
1 Introduction
Intermetallics containing 4f rare-earth elements are known to tend towards magnetically ordered states defined by the Ruderman–Kittel–Kasuya–Yosida (RKKY) interaction. Its strength depends on the number of 4f electrons (nf) as well as their position relative to the Fermi level (EF), which determines the degree of localization. The competing scenario is the formation of a non-magnetic Fermi liquid ground state commonly referred to as the Kondo effect. Obviously, the decisive role in such a competition is played by the level of hybridization of 4f electrons with the conduction band states. Frequently it results in some exciting features like heavy fermions, quantum criticality, non-Fermi liquid state, spin and valence fluctuations [i.e., intermediate valence state (IVS)], etc.1–4The latter effect is observed in intermetallics containing rare-earth ions, revealing both non-magnetic (e.g., Ce4+, Eu3+, and Yb2+) and magnetic (e.g., Ce3+, Eu2+, and Yb3+) states. In some cases, such an ion can switch between configurations, resulting in a non-integer valence that is usually temperature dependent.5,6 All these indicate the change of the ground state of the ion and its degeneracy (N), which is reflected in well-pronounced maxima in magnetic susceptibility and specific heat capacity. To simulate them, some theories, based on the Anderson and Kondo impurity models accounting for the hybridization strength,7,8 are normally applied. For instance, using a unified approach for the former one, which assumes a simplified concept of large angular momentum degeneracy, Bickers, Cox and Wilkins9 successfully simulated static properties. The Bethe ansatz, allowing determination of exact wave functions for quantum many-body models,10 is a powerful tool in the solution of both the abovementioned models. So, generalization of the Kondo impurity approach for an N-fold degenerate state and application of the Bethe ansatz allowed the solution of the SU (N) Coqblin–Schrieffer model, which described well the properties of such impurities in a metal as Ce3+ (N = 6) and Yb3+ (N = 8).11,12 Furthermore, it was extended to a complete range of temperatures and fields.13 However, despite all these successes, none of the discussed models accounts for crystal electric field (CEF) multiplets splitting at non-zero temperatures. Being in the order of a few eV,14 the splitting energy influences strongly the magnetic susceptibility and specific heat capacity. There is an attempt of theoretical simulation of such an effect; however, it is done only for the ions with a degeneracy of N = 4.15 Among the known examples, where the theories fail in the description of temperature dependence of magnetic susceptibilities, we would like to mention YbCuAl,16–18 YbB12,19 YbNi2Ge2 and YbPd2Si2.20
In the past decades, numerous compounds have been found to be isostructural to the primitive cubic Yb3Rh4Sn13 structure type discovered by Remeika and co-workers.21 Furthermore, several intermetallics are shown to be its distorted variants with the same composition (such a structural relationship is normally explained within the group–subgroup scheme22–27) or with a close composition.28–30 The majority of the latter compounds crystallize with the body-centered tetragonal (Sn1−xTbx)Tb4Rh6Sn18 type.28 Interestingly, among stannides of this series, mainly those containing non-magnetic Sc, Y or Lu attract much attention, which is due to their exciting superconducting properties.31–37 A further important observation is that such compounds are unknown with Ce, Eu or Yb, which could reveal VF. The only exceptions in this respect would be primitive tetragonal Yb6.6Ir6Sn16,29 face-centered cubic Yb5Pt6In16Bi2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 38 and body-centered tetragonal Yb5Ru6Sn18
38 and body-centered tetragonal Yb5Ru6Sn18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 39 revealing a mixed valence state (i.e., non-integer, but temperature independent) for Yb ions.
39 revealing a mixed valence state (i.e., non-integer, but temperature independent) for Yb ions.
Stannides with primitive tetragonal (a ≈ 9.7 Å, c ≈ 13.7 Å), face-centered cubic (a ≈ 13.7 Å) and distorted body-centered cubic (a ≈ 19.4 Å) structures and compositions close to 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 13 in the Yb–Rh–Sn system were reported to exist by Espinosa.40 However, in further studies,41,42 this information has not been confirmed. Furthermore, detailed single-crystal diffraction studies performed on SnM3Rh4Sn13 (M = La–Gd, Yb, Ca, Sr and Th) explained some earlier observed distortions by anomalous thermal displacements of Sn2-atoms and structural disorder.43 Finally, a face-centered cubic phase with a unit cell parameter a ≈ 13.7 Å and the (YbxSn1−x)Yb4Rh6Sn18 composition (no refinements were provided) was reported to exist in ref. 44. For unclear reasons, the same work claims Yb atoms to be in an intermediate valence state based on measurements of magnetic susceptibility (not presented) and room-temperature X-ray absorption spectra at the YbLIII edge. Considering this information and taking into account unusual valence fluctuations reported for Yb3Co4Ge13,45,46 we decided to shed more light on the properties of a stannide with a composition close to the Yb3Rh4Sn13,47 recently studied.
13 in the Yb–Rh–Sn system were reported to exist by Espinosa.40 However, in further studies,41,42 this information has not been confirmed. Furthermore, detailed single-crystal diffraction studies performed on SnM3Rh4Sn13 (M = La–Gd, Yb, Ca, Sr and Th) explained some earlier observed distortions by anomalous thermal displacements of Sn2-atoms and structural disorder.43 Finally, a face-centered cubic phase with a unit cell parameter a ≈ 13.7 Å and the (YbxSn1−x)Yb4Rh6Sn18 composition (no refinements were provided) was reported to exist in ref. 44. For unclear reasons, the same work claims Yb atoms to be in an intermediate valence state based on measurements of magnetic susceptibility (not presented) and room-temperature X-ray absorption spectra at the YbLIII edge. Considering this information and taking into account unusual valence fluctuations reported for Yb3Co4Ge13,45,46 we decided to shed more light on the properties of a stannide with a composition close to the Yb3Rh4Sn13,47 recently studied.
In this work, we show that Yb5Rh6Sn18 crystallizes with a unique structural arrangement, and investigate its magnetic, electrical and thermal transport properties. They reveal a complex temperature-dependent behavior of the Yb ion valence. The observed ‘rattling’ effect is found to result in a phonon resonance behaviour, resulting in ultra-low thermal conductivity.
2 Experimental
The Yb5Rh6Sn18 sample of a total mass of 1 g was prepared in a glassy carbon crucible by high-frequency melting from stoichiometric amounts of ytterbium (Ames, 99.95 wt%), rhodium granules (ChemPur, 99.9 wt%), and tin foil (ChemPur, 99.995 wt%). The total weight losses were <0.5 wt%. To avoid oxygen and moisture contaminations, all sample handling and manipulations were performed inside a glove box system under a protective argon atmosphere [p(H2O), p(O2) < 1 ppm]. To perform heat treatment, the obtained button was placed in a glassy carbon crucible, sealed in a Ta-tube and enclosed in an evacuated silica ampoule. Further, it was annealed at 1070 K for 720 hours and finally quenched in cold water.Powder X-ray diffraction (PXRD) was carried out on a Huber G670 Guinier camera (CuKα1 radiation, λ = 1.54056 Å). Phase analysis was performed using the WinXpow software package,48 and Rietveld refinement using WinCSD.49 Single-crystal diffraction (SCXRD, two-circle diffractometer Stoe IPDS-2T, MoKα1 radiation, λ = 0.71073 Å) was performed on a crystal mechanically extracted from the crushed sample. The obtained data were refined using the SHELXL-2019/3 program50 within the WinGX package.51
The Yb5Rh6Sn18 sample was embedded in a conductive resin and polished, and the surface was investigated with a scanning electron microscope (SEM) (Jeol JSM – 7800F) and its chemical composition Yb5.0(1)Rh5.9(1)Sn18.1(1) (in good agreement with the nominal and refined ones) was determined by the mapping procedure with energy dispersive X-ray spectroscopy (EDXS) (Quantax 400 EDXS system, Bruker). Interestingly, in the mapped surface (an area of ≈600 × 600 μm), no traces of Yb2O3 were detected (Fig. S1†). This finding confirms, if any, only minor quantities of such an impurity in the studied sample.
The X-ray absorption spectra (XAS) near the YbLIII edge of Yb5Rh6Sn18 were measured in fluorescence mode at 100 K and 293 K at the Rossendorf Beamline (BM20) of ESRF with the help of a Canberra photodiode.52 The spectra were recorded at a scattering angle of 90° in the horizontal plane.53 The XAS spectra were recorded in the energy region from 8920 to 9000 eV with a step size of 0.5 eV. The intensity was normalized to the incident flux. The standard normalization routines were applied to the spectra with the help of the PyMCA program.54
To investigate the temperature and field dependencies of magnetic susceptibility, specific heat capacity, electrical resistivity, Seebeck coefficient, thermal conductivity and Hall coefficients for Yb5Rh6Sn18 VSM, 4He heat capacity, TTO and Van der Pauw options of a DynaCool-12 instrument (Quantum Design) were used.
The electronic band structure and density of states were calculated with density functional theory (DFT) [local density approximation (LDA)] using the full-potential FPLO code (version 18.00–52.38).55 The exchange–correlation potential by Perdew and Wang56 was used to perform the scalar relativistic calculation. The k-mesh included 8000 points in the first Brillouin zone.
3 Results and discussion
3.1 Crystal structure
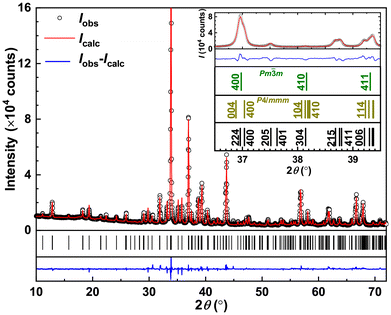
The single-crystal XRD (SCXRD) data set of Yb5Rh6Sn18 was collected from a crystalline shard of an approximate size of 0.01 × 0.02 × 0.03 mm3. The positions of the strongest reflections were in accordance with a cubic crystal system (cF, a ≈ 13.8 Å), but additional weak reflections indicated a superstructure (cP, a ≈ 13.8 Å or tP, a ≈ 9.7 Å, c ≈ 13.8 Å). As the intensities of symmetry-equivalent reflections did not adhere to cubic symmetry (shown in Fig. S2†), it was concluded that the diffraction pattern was produced by a three-domain twin of the tetragonal system with domains of noticeably different diffraction powers. [The twin domains are related to one another by 120° and 240° rotation about [0 1 2]; data of domains 2 and 3 are related to domain 1 according to (−0.5 0.5–0.5) (−0.5 0.5 0.5) (1 1 0) and (−0.5–0.5 0.5) (0.5 0.5 0.5) (−1 1 0), respectively.] For structure solution, the data set of the predominant domain was integrated, and the solution (intrinsic phasing method, ShelXT) was performed with the HKLF4 format data set obtained therefrom. For the final refinement, data integration was performed for all three domains to account for spot shape distortions of the overlapping reflections, and an HKLF5 format data set of all reflections of domain 1 (with overlaps of domains 2 and 3) was created. A numerical absorption correction (cylinder) was applied afterwards in WinGX. In the structure refinement, the population of the twin domains was refined to 0.635(6), 0.293(6), and 0.072(6) for domains 1, 2 and 3, respectively.In agreement with the model obtained from the refinement of SCXRD data, all peaks observed in the PXRD pattern of Yb5Rh6Sn18 could be indexed with the unit cell parameters presented in Table 1 (the difference in the given values obtained from SCXRD is due to diverse methods of their estimation and not due to a negative thermal expansion). The analysis of systematic absences (h + k = 2n, l = 2n and k = 2n for hk0, hhl, 00l and 0k0, respectively) confirmed the space group (SG) P42/nmc. Further refinement of atomic coordinates and thermal displacement parameters (Table 2 and 3) converged with low reliability factors (Table 1) confirming its correctness. The obtained profiles are depicted in Fig. 1. Noteworthily, the main peaks in the PXRD pattern of Yb5Rh6Sn18 could be indexed within a primitive cubic SG Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m with a ≈ 9.8 Å, whereas some of their splittings could be indexed within a primitive tetragonal SG P4/mmm with unit cell parameters a ≈ c ≈ 9.8 Å (inset in Fig. 1). These observations suggest a structural relationship of the herein studied phase with the Yb3Rh4Sn13 Remeika prototype.21 In this regard, we would like to refer to our previous discussions in ref. 23, 24 and 27.
m with a ≈ 9.8 Å, whereas some of their splittings could be indexed within a primitive tetragonal SG P4/mmm with unit cell parameters a ≈ c ≈ 9.8 Å (inset in Fig. 1). These observations suggest a structural relationship of the herein studied phase with the Yb3Rh4Sn13 Remeika prototype.21 In this regard, we would like to refer to our previous discussions in ref. 23, 24 and 27.
| a w = 1/σ2(Fo)2 + (0.0757p)2 with p = (Fo2 + 2Fc2)/3. | ||
|---|---|---|
| Temperature, T (K) | 200 | 293 |
| Method | Single crystal | Powder |
| Space group (No.) | P42/nmc (137) | |
| Formula per unit cell, Z | 2 | |
| Unit cell parameter: | ||
| a (Å) | 9.7018(5) | 9.6997(4) |
| c (Å) | 13.793(1) | 13.7710(7) |
| V (Å3) | 1298.3(2) | 1295.6(2) |
| Density, ρ (g cm−3) | 9.26(1) | 9.3(1) |
| Crystal size (mm3) | 0.03 × 0.02 × 0.01 | — |
| Abs. coef., μ (mm−1) | 38.4 | 203.3 |
| F(000) | 3040 | |
| Radiation | MoKα | CuKα1 |
| Diffractometer | STOE IPDS 2T | Huber G670 |
| 2θmax (°) | 58.0 | 105.5 |
(sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/λ)max θ/λ)max |
0.682 | 0.517 |
| Minimum h, k, l | −13, −13, −18 | 0, 0, 0 |
| Maximum h, k, l | 13, 13, 18 | 7, 9, 14 |
| Abs. correction | Numerical | — |
| Collected reflections | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 544 544 |
393 |
| Independent reflections | 961 (Rint = 0.070) | — |
| Refined parameters | 45 | 31 |
| Refl. with Ihkl ≥ 2σ(I) | 920 (Rσ = 0.027) | — |
| Refinement on | F 2 | — |
| R/wRa; RI/RP | 0.056/0.121 | |
| (I ≥ 2σ(I)) | 0.042/0.108 | |
| (All data) | 0.057/0.116 | — |
| Goodness of fit | 1.022 | 1.011 |
| Min. and max. residual | ||
| Resid. electr. density (e− Å−3) | −2.99; +2.04 | −1.12; +1.35 |
| Atom | Site | x | y | z | U eq/Uiso |
|---|---|---|---|---|---|
| 200 K | |||||
| Yb1 | 2b | 3/4 | 1/4 | 1/4 | 21.0(4) |
| Yb2 | 8g | 1/4 | 0.0255(1) | 0.38263(8) | 19.4(2) |
| Rh1 | 4c | 3/4 | 1/4 | 0.5060(2) | 15.8(6) |
| Rh2 | 8f | 0.4953(1) | −x + 1 | 1/4 | 17.2(4) |
| Sn1 | 4d | 1/4 | 1/4 | 0.0389(2) | 27.5(1) |
| Sn2 | 8g | 1/4 | 0.0999(1) | 0.7388(2) | 21.6(4) |
| Sn3 | 8g | 1/4 | 0.5787(2) | 0.1634(1) | 19.6(3) |
| Sn4 | 16h | 0.5758(2) | 0.0743(1) | 0.0737(1) | 22.9(3) |
| 293 K | |||||
| Yb1 | 2b | 3/4 | 1/4 | 1/4 | 29(6) |
| Yb2 | 8g | 1/4 | 0.0229(9) | 0.3826(7) | 31(4) |
| Rh1 | 4c | 1/4 | 1/4 | 0.5069(9) | 26(9) |
| Rh2 | 8f | 0.4970(9) | −x + 1 | 1/4 | 26(6) |
| Sn1 | 4d | 1/4 | 1/4 | 0.0354(9) | 39(7) |
| Sn2 | 8g | 1/4 | 0.0991(9) | 0.7404(9) | 20(6) |
| Sn3 | 8g | 1/4 | 0.5743(9) | 0.1643(9) | 29(5) |
| Sn4 | 16h | 0.5737(9) | 0.0744(9) | 0.0739(9) | 26(3) |
| Atom | U 11 | U 22 | U 33 | U 12 | U 13 | U 23 |
|---|---|---|---|---|---|---|
| Yb1 | 20.2(7) | U 11 | 23(1) | 0 | 0 | 0 |
| Yb2 | 18.4(5) | 19.9(5) | U 22 | 0 | −0.1(4) | 0 |
| Rh1 | 14(1) | 16(1) | 18(2) | 0 | 0 | 0 |
| Rh2 | 16.9(6) | U 11 | 18(1) | −0.4(4) | U 12 | 0.0(8) |
| Sn1 | 24(1) | 41(1) | 18(1) | 0 | 0 | 0 |
| Sn2 | 15.5(9) | 17.6(9) | 31.6(9) | −0.9(6) | 0 | 0 |
| Sn3 | 16.4(7) | 21.1(7) | 21.5(8) | 3.2(6) | 0 | 0 |
| Sn4 | 26.0(6) | 23.1(6) | 19.6(8) | 1.9(4) | −0.4(4) | −8.9(5) |
Interatomic distances in the crystal structure of Yb5Rh6Sn18 are presented in Table S2.† As for the majority of phases crystallizing in the Remeika type and derived arrangements,27 there are no Yb–Yb and Rh–Rh bonding contacts (i.e., these distances exceed the  limit, where rYb = 1.94 Å, rRh = 1.34 Å and rSn = 1.41 Å (ref. 57) are atomic radii of the elements) in the herein studied compound. Remarkable shortenings occur in Yb5Rh6Sn18 for Yb2–2Rh2 (8.0%) and Yb2–1Sn1 (8.5%) distances, whereas the Rh–Sn and Sn–Sn contacts are either slightly shrunk (e.g., Rh1–4Sn4 by 4.0%) or even longer than the corresponding sum (e.g., Sn4–1Sn4 by −2.6%).
limit, where rYb = 1.94 Å, rRh = 1.34 Å and rSn = 1.41 Å (ref. 57) are atomic radii of the elements) in the herein studied compound. Remarkable shortenings occur in Yb5Rh6Sn18 for Yb2–2Rh2 (8.0%) and Yb2–1Sn1 (8.5%) distances, whereas the Rh–Sn and Sn–Sn contacts are either slightly shrunk (e.g., Rh1–4Sn4 by 4.0%) or even longer than the corresponding sum (e.g., Sn4–1Sn4 by −2.6%).
Having a stoichiometry 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6
6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 18, the compound studied here is expected to be structurally related to the series of M5Rh6Sn18 (M = Y, Tb, Dy, Ho, Er, and Tm) stannides crystallizing with the (Sn1−xTbx)Tb4Rh6Sn18 type (SG I41/acd, atetr ≈ 13.8 Å, ctetr ≈ 27.5 Å),58 which is considered to be a derivative of the Yb3Rh4Sn13 Remeika prototype (SG Pm
18, the compound studied here is expected to be structurally related to the series of M5Rh6Sn18 (M = Y, Tb, Dy, Ho, Er, and Tm) stannides crystallizing with the (Sn1−xTbx)Tb4Rh6Sn18 type (SG I41/acd, atetr ≈ 13.8 Å, ctetr ≈ 27.5 Å),58 which is considered to be a derivative of the Yb3Rh4Sn13 Remeika prototype (SG Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, acub ≈ 9.7 Å). Indeed, comparing the unit cell parameters from Table 1 with the abovementioned observations, clear relations become visible:
m, acub ≈ 9.7 Å). Indeed, comparing the unit cell parameters from Table 1 with the abovementioned observations, clear relations become visible:  and
and  . Such a close relationship between UCPs is also reflected in the structural arrangements. As one can see from Fig. 2a, b and c, in all three types [for better visualization, we present Sc5Rh6Sn18 in Fig. 2c, which is an ordered variant of the (Sn1−xTbx)Tb4Rh6Sn18 type], an array of corner sharing [RhSn6] trigonal prisms (tan) with [YbSn12] cuboctahedra (gray) incorporated into the free space in-between occurs. In the case of the cubic Yb3Rh4Sn13 prototype, trigonal faces of prisms and cuboctahedra are shared with those of [SnSn12] icosahedra (cyan) (Fig. 2a), whereas for the tetragonally distorted 5
. Such a close relationship between UCPs is also reflected in the structural arrangements. As one can see from Fig. 2a, b and c, in all three types [for better visualization, we present Sc5Rh6Sn18 in Fig. 2c, which is an ordered variant of the (Sn1−xTbx)Tb4Rh6Sn18 type], an array of corner sharing [RhSn6] trigonal prisms (tan) with [YbSn12] cuboctahedra (gray) incorporated into the free space in-between occurs. In the case of the cubic Yb3Rh4Sn13 prototype, trigonal faces of prisms and cuboctahedra are shared with those of [SnSn12] icosahedra (cyan) (Fig. 2a), whereas for the tetragonally distorted 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6
6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 18 variants (Fig. 2b and c), the 16-vertices distorted Frank–Kasper [SnR2Sn14] polyhedra share these with only cuboctahedra. Additionally, the latter units in Sc5Rh6Sn18 are distorted in a different way due to diverse distributions of M atoms therein (Fig. 2c), which results in the shifted positions of centering Sn atoms (black connected with red zigzag). On the other hand, in the structures of Yb3Rh4Sn13 (Fig. 2a) and Yb5Rh6Sn18 (Fig. 2b), the Sn atoms centering the similar voids are along a straight line (red).
18 variants (Fig. 2b and c), the 16-vertices distorted Frank–Kasper [SnR2Sn14] polyhedra share these with only cuboctahedra. Additionally, the latter units in Sc5Rh6Sn18 are distorted in a different way due to diverse distributions of M atoms therein (Fig. 2c), which results in the shifted positions of centering Sn atoms (black connected with red zigzag). On the other hand, in the structures of Yb3Rh4Sn13 (Fig. 2a) and Yb5Rh6Sn18 (Fig. 2b), the Sn atoms centering the similar voids are along a straight line (red).
In Fig. 2d, e and f, we demonstrate the packing of [Yb4] tetrahedra (red) together with tetrahedral fragments (marked with thick blue lines) within the [SnSn12] icosahedra and 16-vertices distorted Frank–Kasper [SnM2Sn14] polyhedra (both units are given in cyan). These fragments consist of only Sn atoms in the case of Yb3Rh4Sn13 (Fig. 2d), whereas for Yb5Rh6Sn18 (Fig. 2e) and Sc5Rh6Sn18 (Fig. 2f), they contain 2Sn and 2M. Again, being nearly equally oriented in Yb-containing stannides, they reveal different distributions in the Sc5Rh6Sn18 type.
Similarly to Yb5Rh6Sn18, Yb6.6Ir6Sn16 crystallizes with the same space group, close unit cell parameters and even identical Wyckoff positions.29 The only difference between these structural arrangements is the appearance of an 8g site occupied by Yb (≈40%) in the Ir-containing stannide instead of Sn1 at the 4d position (Table 2), which results in various compositions.
All these let us to conclude that Yb5Rh6Sn18 crystallizes with a unique structural arrangement, which belongs to the family of derivatives of the Yb3Rh4Sn13 Remeika prototype.
3.2 X-ray absorption spectroscopy
The X-ray absorption spectra (XAS) of Yb5Rh6Sn18 measured at the YbLIII edge are presented in Fig. 3. They reveal two white lines, which are attributed to Yb-4f14 (≈8940.5 eV) and Yb-4f13 (≈8946 eV) configurations, respectively. Interestingly, the XAS measured here at room temperature are nearly identical to those reported for a (YbxSn1−x)Yb4Rh6Sn18 compound, which was believed to crystallize with the face-centered cubic structure (SG Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, a = 13.74 Å).44
m, a = 13.74 Å).44
 | ||
Fig. 3 Temperature-dependent X-ray absorption spectra of Yb5Rh6Sn18 at the YbLIII edge in comparison with the literature data for (YbxSn1−x)Yb4Rh6Sn18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 44 and the theoretically calculated Yb-5d density of states. 44 and the theoretically calculated Yb-5d density of states. | ||
A clear reduction of the intensity of the low-energy line (≈8940.5 eV) in the XAS of Yb5Rh6Sn18 with increasing temperature is observed. This is an indication of the fluctuating valence [i.e. intermediate valence state (IVS)] of ytterbium. Indeed, by deconvoluting the measured spectra, we obtain Yb2.59(1)+ and Yb2.62(1)+ at 100 K and 293 K, respectively. Interestingly, similar valence evolution is reported for the Yb3Co4Ge13 modulated Remeika phase46 and YbPtGe2: a multivalent charge-ordered system with an unusual spin pseudogap.59 The IVS in Yb5Rh6Sn18 is in contrast with the prevailing temperature-independent state of Yb-4f14 (i.e., Yb2+) observed in the weakly Pauli paramagnetic and superconducting Yb3Rh4Sn13 compound with a close composition.44,47
Furthermore, we compared the Yb-5d electronic density of states (DOS) obtained from the theoretical DFT calculations with the measured XAS. They are expected to reproduce the lower-energy feature in the spectra and therefore became shifted to ≈8940.5 eV. As one can see from Fig. 3, the Yb1-5d orbitals are mainly unoccupied (they are above the Fermi level EF) and nicely coincide with the position of the corresponding absorption maximum. However, unexpectedly, the 5d states of the Yb2 atom are found to be partially occupied. Also, these orbitals contribute remarkably to the higher-energy absorption maximum at ≈8946 eV corresponding to the Yb-4f13 configuration, which would assume an underestimation of the Yb2+ fraction in the valences obtained from the deconvolution of XAS. Since the temperature dependence of the Yb2-5d DOS cannot be simulated, its influence on the IVS behavior in Yb5Rh6Sn18 remains rather unclear.
3.3 Magnetic susceptibility
Temperature dependence of magnetic susceptibility [χ(T)] for Yb5Rh6Sn18 is depicted in Fig. 4. It obeys the Curie–Weiss (CW) law for 180 K < T < 350 K (inset in Fig. 4). The effective magnetic moment μeff = 2.94(5)μB deduced from such a fit is approximately by a factor of 3/2 smaller than 4.54μB – a value theoretically calculated for the Yb-4f13 configuration. A similar situation was observed in YbPtGe2, where the Yb atom in one of the crystallographic positions was shown to be non-magnetic (i.e., in the Yb-4f14 state),59,60 which resulted in the reduction of μeff by a factor of . Also, the performed CW fit indicated a large negative Weiss temperature of ΘP = −175(1) K, which can be explained by an enhanced characteristic energy (≈47 K) of valence fluctuations.
. Also, the performed CW fit indicated a large negative Weiss temperature of ΘP = −175(1) K, which can be explained by an enhanced characteristic energy (≈47 K) of valence fluctuations.
Below 180 K, the χ(T) of Yb5Rh6Sn18 deviates from the CW law, overcomes a maximum centered at Tχmax ≈ 47 K and finally reveals an upturn for T < 25 K (Fig. 4) due to a minor (invisible in XRD) paramagnetic impurity. Such a behavior of magnetic susceptibility is in line with the IVS observed in XAS. Noteworthily, Tχmax varies in a broad range for Yb-containing intermetallics, revealing the IVS [e.g., 25 K for YbPd2Si2,20 30 K for YbCuAl,18 150 K for Yb3Co4Ge13,46 240 K for Yb4Sb3,61 250 K for YbNi0.8Al4.2,62 250 K for YbPtGe2,59 400 K for YbNiAl4,63 500 K for Yb3Ge5,64etc.]. Such a behavior is expected to be universally described by a Coqblin–Schrieffer (CS) model proposed by Rajan for the whole Yb3+ multiplet J = 7/2 (i.e., degeneracy N = 2J + 1 = 8).13 However, since this model does not account for crystal electric field (CEF) effects, the low temperature lattice problem and the so-called Kondo limit (i.e., valence variation, 0.5 < nf < 1), it frequently fails in the description of the IVS, as it is the case for e.g., YbPd2Si2,20 YbCuAl,18 Yb3Co4Ge13,46etc.
A similar observation is made for the herein studied Yb5Rh6Sn18, where a good description for T > 100 K is obtained with J = 3/2 (N = 4) and the characteristic spin-fluctuation temperature T0 = 201 K. The situation can be somewhat improved while switching to the Anderson model developed for the same multiplet and nf = 1 by Bickers, Cox and Wilkins (BCW)9 (Fig. 4). From such a fit, we obtained a similar characteristic temperature T0 = 208 K. Using the Rajan prediction13 for the Sommerfeld coefficient of electronic specific heat, we calculated γ = 2JπkBNA/6T0 ≈ 63 mJ mol−1 K−2 (with kB = 1.38 × 10−23 J K−1 and NA = 6.022 × 10−23 mol−1 as Boltzmann and Avogadro constants, respectively) – a value that seems to be degeneracy-independent and would even be in fair agreement with the corresponding value obtained from cp-measurements (see below). However, implying the obtained T0 to be correct, we calculated a Kondo temperature: TK = 2πT0WJ(2J + 1)−1 ≈ 191 K (where W3/2 = 0.5843 is the Wilson number),65 which is in complete disagreement with the measured electrical resistivity, revealing no signature of any Kondo-like behavior at this TK.
In view of the complicated Yb valency situation (i.e., Yb2-5d states contribute to the Yb3+ fraction), it is not surprising that the classical CS and BCW models do not work well. Additionally, as it is shown in section 1.1 and Fig. S3 of the ESI,† the simplified two-level interconfigurational fluctuation model (ICF)66 fails in the description of the valence fluctuations in Yb5Rh6Sn18 as well, thus confirming the conclusion above.
3.4 Specific heat
The temperature dependence of specific heat capacity cp(T) of Yb5Rh6Sn18 reveals no anomalies for 3 K < T < 200 K (inset in Fig. 5) and reaches the Dulong–Petit limit cp = 3nR ≈ 723 J mol−1 K−1 (R = 8.31 J K−1 mol−1 is the gas constant) at ≈183 K. However, it reveals an anomaly at TN = 2.3 K (Fig. S4†). This is due to a minor (not detectable with XRD or EDX) Yb2O3 impurity ordering antiferromagnetically.67 The influence of such an impurity on the physical properties of the similar Yb3Pt4Ge13 is discussed in detail in ref. 22. Noteworthily, the cusp at the transition in the current case is by a factor of ≈3 smaller than that in ref. 22. Therefore, we further consider the specific heat of Yb5Rh6Sn18 in the cp/T(T2) presentation and assume it to follow an ansatz of cp = γT + βT3 in a temperature range of ≈4.5–6.1 K (Fig. S4†). This would indicate γ ≈ 55(5) mJ mol−1 K−2 and ΘD = 148(2) K – values that are very similar to those reported for non-magnetic Sc5Rh6Sn18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 34 and Lu5Rh6Sn18.68
34 and Lu5Rh6Sn18.68
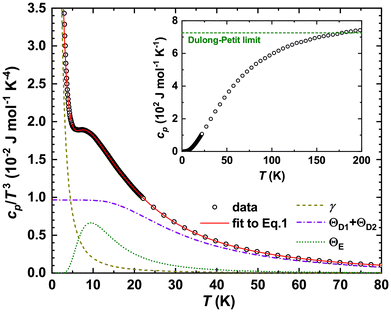 | ||
| Fig. 5 Specific heat for Yb5Rh6Sn18 in the cp/T3(T) presentation together with a fit to eqn (1) and Debye (ΘD1 + ΘD2), Einstein (ΘE) and electronic (γ) contributions. Inset: specific heat for Yb5Rh6Sn18. | ||
For T > 6 K, the cp(T) of Yb5Rh6Sn18 deviates from the above given ansatz, which is confirmed by a well-pronounced maximum centered at ≈8 K observed for the cp/T3(T) presentation (Fig. 5). It signals a contribution of low energy Einstein optical modes to the measured specific heat. One of the possible reasons of their appearance could be the so-called ‘rattling’ motion69 of Sn1 atoms within the enlarged 16-vertices distorted Frank–Kasper polyhedra (Fig. 2b). Such an effect is discussed for some Remeika phases.27 To describe it, a combined Debye–Einstein model is frequently used.70,71 It assumes as a first approximation72 the separation of phononic contributions originating from different types of sublattices (i.e., covalently and ionically bonded) and is given as follows:
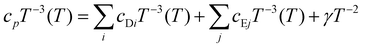 | (1) |
 | (2) |
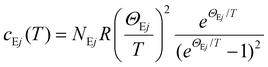 | (3) |
By fitting the cp(T) of Yb5Rh6Sn18 to eqn (1), the characteristic Debye and Einstein temperatures and number of modes were found to be ΘD1 = 300(2) K, ΘD2 = 134(2) K, and ΘE1 = 47(1) K and ND1 = 59(1), ND2 = 30(1), and NE1 = 4(1), respectively. Comparing this result with the Yb5Rh6Sn17Sn1 (Sn1 should remain for a possible ‘rattling’) stoichiometry, ND1 could be assumed to originate mainly from the covalently bonded Sn17 framework (i.e., theoretically expected number of Debye modes is 51). ND2 is then due to 5Yb and 6Rh atoms (theoretical value of 33) and finally NE1 is from 1Sn1 in the enlarged [Sn1M2Sn14] polyhedron (should be 3). In total, the abovementioned stoichiometry indicates 87 possible modes, whereas our fit results in Ntot = NDi + NEj = 93(1). The mismatches between the theoretical expectations and the experiment are not a rare case (here we would like to refer to ref. 47, 71, 73 and 74) and reflect the shortcomings of the simple model applied to the complex phononic spectra of compounds.
Interestingly, taking the thermal displacement parameter Biso = 8π2Uiso = 3.1(1) Å2 of the ‘rattling’ Sn1 atom refined from the powder XRD data at room temperature (Table 2) and implementing it into eqn (4), we obtained the Einstein temperature ΘBE = 55(1) K, which fairly agrees with the specific heat data. This is a rather unexpected result. As it has been shown for such well-established ‘rattling’ systems as filled skutterudites75,76 and the recently studied Yb3Rh4Sn13,47 if the atomic masses of the ‘rattling’ systems are comparable with those of the atoms forming the framework, ΘE and ΘBE differ strongly.
 | (4) |
The fit to eqn (1) also resulted in an enhanced Sommerfeld coefficient of the electronic specific heat γ = 196(1) mJ mol−1 K−2, which is by a factor of ≈4 larger than the values observed from the classical ansatz as well as for the non-magnetic Sc5Rh6Sn18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 34 or Lu5Rh6Sn18.68 This is again due to the enhancement of low-temperature cp(T) caused by the Yb2O3 impurity.
34 or Lu5Rh6Sn18.68 This is again due to the enhancement of low-temperature cp(T) caused by the Yb2O3 impurity.
3.5 Electrical transport
The temperature dependence of electrical resistivity ρ(T) for Yb5Rh6Sn18 is presented in Fig. 6. In contrast to that for Lu5Rh6Sn18 – a phonon reference compound77 – as well as Y5Rh6Sn18,78 Sc5Rh6Sn18,34,35 Y5Ir6Sn18,30 analogous intermetallics, etc., it increases with increasing temperature and is of the same order of magnitude as that of a metal.79 Furthermore, in the temperature range of ≈4–12 K, ρ(T) of Yb5Rh6Sn18 follows the Fermi-liquid behavior and fits well to ρ0 + AFLT2, with ρ0 = 61(1) μΩ cm and AFL = 0.13(1) μΩ cm K−2. However, this ρ(T) cannot be described by a Bloch–Grüneisen model (typical of metals)80 in the whole temperature range (for more details, see the discussions in section 1.2 of the ESI†), which is most probably due to the change of the scattering mechanism at T ≈ 100 K. Similar temperature dependencies of electrical resistivity were reported for such unusual IVS as CePt4Ge12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 81 and YbPtGe2.59
81 and YbPtGe2.59
Taking the values obtained from the Fermi-liquid fit, we estimated the residual resistance ratio RRR = ρ(300)/ρ0 ≈ 9.3, which indicates a fair quality of the studied sample. From the quadratic term, Kadowaki–Woods ratios82 (RKW = AFL/γ2) of 4.2 × 10−5 μΩ cm (mol K mJ−1)2 [for γ ≈ 55(5) mJ mol−1 K−2] and 3.4 × 10−6 μΩ cm (mol K mJ−1)2 [for γ ≈ 196(1) mJ mol−1 K−2] were obtained. Both the obtained values differ strongly from the RKW = 1.0 × 10−5 μΩ cm (mol K mJ−1)2 expected for a heavy fermion compound, which is in line with the IVS of Yb5Rh6Sn18.
Temperature dependence of the Hall coefficient RH(T) for Yb5Rh6Sn18 in different magnetic fields is presented in the inset of Fig. 6. Being nearly field independent, RH(T) mimics the behavior of the Seebeck coefficient (see below, Fig. 7), revealing a well-pronounced minimum at  and changing the sign from negative to positive at T ≈ 120 K. This latter observation confirms the switching of the conduction mechanism from electron- to hole-like type. By applying the one-band model [RH = (n|e|)−1 and μ = RH/ρ], we found that their charge carrier concentration n and mobility μ vary (with the exception of singularity at RH = 0) in the narrow ranges of 7.6–9.4 × 10−21 cm−3 and 1.1–2.1 cm2 V−1 s−1, respectively. Weak temperature dependence of both these characteristics and their order of magnitudes indicate Yb5Rh6Sn18 to be a metal.79 By further applying the free electron gas model, we calculated the Fermi energy EF = (ħ2/2m)(3π2n)2/3e−1 = 1.52(9) eV and the DOS at the Fermi level D(EF) = 3nV/2EF = 10.9(4) states eV−1 f.u.−1. The latter value is strongly underestimated in comparison with the theoretically calculated one, which is in line with a complex electronic band structure of Yb5Rh6Sn18 (see the discussion below).
and changing the sign from negative to positive at T ≈ 120 K. This latter observation confirms the switching of the conduction mechanism from electron- to hole-like type. By applying the one-band model [RH = (n|e|)−1 and μ = RH/ρ], we found that their charge carrier concentration n and mobility μ vary (with the exception of singularity at RH = 0) in the narrow ranges of 7.6–9.4 × 10−21 cm−3 and 1.1–2.1 cm2 V−1 s−1, respectively. Weak temperature dependence of both these characteristics and their order of magnitudes indicate Yb5Rh6Sn18 to be a metal.79 By further applying the free electron gas model, we calculated the Fermi energy EF = (ħ2/2m)(3π2n)2/3e−1 = 1.52(9) eV and the DOS at the Fermi level D(EF) = 3nV/2EF = 10.9(4) states eV−1 f.u.−1. The latter value is strongly underestimated in comparison with the theoretically calculated one, which is in line with a complex electronic band structure of Yb5Rh6Sn18 (see the discussion below).
 | ||
| Fig. 7 Temperature dependence of the Seebeck coefficient S(T) for Yb5Rh6Sn18 on a logarithmic scale together with the fit to eqn (5). Inset: temperature dependence of the Seebeck coefficient S(T) for Yb5Rh6Sn18 on a linear scale together with the linear fit as expected for a metallic system. | ||
Temperature dependence of the Seebeck coefficient of thermopower S(T) for Yb5Rh6Sn18 in logarithmic and linear scales is shown in Fig. 7 and the inset therein, respectively. It is negative in the LT range and decreases with increasing temperature, passing through a minimum centered at TSmin ≈ 41 K (in fair agreement with Tχmax). Furthermore, S(T) starts to increase steeply, becoming almost linear, and changes the sign to positive at T ≈ 220 K, which indicates the switch from n- to p-type conductivity.
Having two crystallographic positions for Yb atoms in the structure of Yb5Rh6Sn18, we assumed that the conduction electrons scattered on two independent 4f quasiparticle bands. This prompted us to try to describe S(T) using the model proposed by Bando et al.:83
 | (5) |
 | (6) |
 | (7) |
 | (8) |
The parameters obtained from the fit of S(T) of Yb5Rh6Sn18 to eqn (5) and the theory related to it are presented in Table 4. Knowing that the Yb valence is given as ν = 3 − z, we can state that from these calculations, it is ≈2.9 for both bands if one assumes the whole J = 7/2 (N = 8) multiplet for Yb ions. These values strongly deviate from those observed experimentally from XAS and can become somewhat improved (i.e., to ≈2.8) while taking into consideration the J = 3/2 (N = 4) multiplet applied for the description of temperature dependence of magnetic susceptibility. Such an inconsistency can be explained by the fact that the applied model is much too simple, which stresses again the fact that the Yb valence fluctuation in the studied stannide is of a very complex mechanism. Interestingly, the Yb-valences obtained here are in good agreement with those deduced from the ICF fit to the magnetic susceptibility of Yb5Rh6Sn18. With due caution, we thus conclude that the simplifications in both theories (i.e., electron scattering on two quasiparticle bands and valence fluctuations between two energetic levels, respectively) result in comparable values.
| i | Δ i (meV) | Γ i (meV) | z (N = 8) | z (N = 4) |
|---|---|---|---|---|
| N | −0.86(5) | 7.30(5) | 0.09(1) | 0.15(1) |
| W | −0.02(1) | 0.56(1) | 0.10(1) | 0.19(1) |
In the temperature range of 150–250 K, the Seebeck coefficient of Yb5Rh6Sn18 fits well to S(T) = AST + B (the inset in Fig. 7) with the carriers’ diffusion component AS = π2kB2/2eEF = 0.15(1) μV K−2 and the term due to the contribution of electronic interaction B = −32(1) μV K−2.85,86 Having these fit parameters, we calculated the Fermi energy EF = 1.64(9) eV, which is in good agreement with the value obtained from Hall effect measurements.
3.6 Thermal conductivity
The temperature dependence of the thermal conductivity [κtot(T)] of Yb5Rh6Sn18 is depicted in Fig. 8. It is very low and thus comparable with those of such well-established ‘rattling’ systems as intermetallic clathrates87–89 and filled skutterudites.90 To shed light on this behavior, we decomposed κtot(T) into its electronic (κel = [L(T)/ρ(T)]T) and phononic (κph = κtot − κel) parts. Knowing that the Lorenz number L0 = 2.44 × 10−8 W Ω K−2 is temperature dependent, we corrected it as proposed in:91 | (9) |
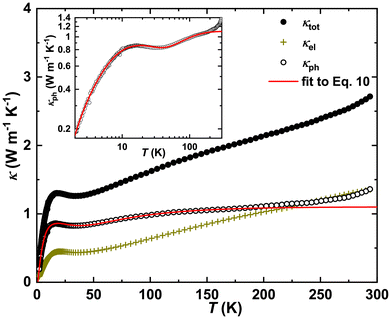 | ||
| Fig. 8 Temperature dependence of thermal conductivity and its electronic κel and phononic κph contributions for Yb5Rh6Sn18 together with the fit to eqn (10). For T > 250 K, κtot(T) and κph reveal an upturn following the ∝T3 law due to radiation heat losses. Inset: κph together with the fit to eqn (10) on a logarithmic scale for the better visualization of a minimum at Tmin ≈ 40 K. | ||
As one can see from Fig. 8, the phononic contribution to the thermal conductivity of Yb5Rh6Sn18 is larger than the electronic one, which is again similar to the situation in the abovementioned ‘rattling’ systems. Furthermore, the obtained κph(T) reveals a well-pronounced minimum at Tmin ≈ 40 K (inset in Fig. 8), which could be a signature of the so-called phonon resonance (PR).92 There are two known reasons for the appearance of such a phenomenon: (i) resonant interaction occurring between phonons and non-paramagnetic lattice point defects (reported for mixed halides93,94 and recently for natural galena95) and/or (ii) anticipated scattering of the phonons by the vibrations of a weakly bound cation incorporated inside an enlarged anionic void (i.e., ‘rattling’ effect).96 The modified Debye–Callaway model97 [eqn (10)] allows accounting for different scattering mechanisms of phonons (including PR) and to describe κph(T).
 | (10) |
In eqn (10), we used ΘD = 148(2) K, the average sound velocity vS = kBΘD/h(6π2nat)1/3 = 1435(1) m s−1 (with the concentration of atoms per unit cell volume nat = 4.48 × 1028 m−3) deduced from XRD refinement and x = ħω/kBT. The total relaxation time τtot−1 in the current case includes the following contributions: phonon scattering on (i) grain boundaries (τB−1) and (ii) point defects (τPD−1), (iii) normal (τN−1) and (iv) umklapp (τU−1) phonon processes and (v) τPR−1 due to phonon resonance:
| τtot−1 = τB−1 + τPD−1 + τN−1 + τU−1 + τPR−1 | (11) |
 | (12) |
Parameters obtained from the fit to eqn (10) are presented in Table 5. Interestingly, the observed C1 value is by 1–2 orders of magnitude smaller than those reported for the intermetallic ErPdSb98 or semiconducting PbS95 and In1−y@yIn2S4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 74 thermoelectric materials. This means that phonon scattering on the grain boundaries in Yb5Rh6Sn18 is rather weak. On the other hand, parameter C2, which is due to the point defects, is (for the stannide studied here) by a factor of 10–100 larger than the analogues in the abovementioned compounds. Thus, this scattering process is a dominating one in the low temperature regime. For T > 50 K, the dominance of normal and umklapp phonon–phonon processes is observed, which is reflected in the remarkable C3 and C4 parameters. Such a clear separation of both contributions is frequently not the case, especially for intermetallic systems. For instance, the normal processes seem to be completely screened by the umklapp ones in ErPdSb98 and as a result, no C3 parameter is obtained from the fit to the Debye–Callaway model. In concluding this discussion, we emphasize that the C1–4 parameters obtained for Yb5Rh6Sn18 are quite conventional and do not provide any insights into the ultra-low values of κ(T). Herein, it should be also noted that the applied model does not distinguish between three- and four-phonon decay mechanisms in umklapp processes, and as is known, the latter can lead to extremely low κ(T), as it is the case for PbCuSbS3.73 Obviously, to shed more light on this problem, inelastic neutron scattering on single-crystalline Yb5Rh6Sn18 combined with theoretical lattice dynamics studies would be required.
74 thermoelectric materials. This means that phonon scattering on the grain boundaries in Yb5Rh6Sn18 is rather weak. On the other hand, parameter C2, which is due to the point defects, is (for the stannide studied here) by a factor of 10–100 larger than the analogues in the abovementioned compounds. Thus, this scattering process is a dominating one in the low temperature regime. For T > 50 K, the dominance of normal and umklapp phonon–phonon processes is observed, which is reflected in the remarkable C3 and C4 parameters. Such a clear separation of both contributions is frequently not the case, especially for intermetallic systems. For instance, the normal processes seem to be completely screened by the umklapp ones in ErPdSb98 and as a result, no C3 parameter is obtained from the fit to the Debye–Callaway model. In concluding this discussion, we emphasize that the C1–4 parameters obtained for Yb5Rh6Sn18 are quite conventional and do not provide any insights into the ultra-low values of κ(T). Herein, it should be also noted that the applied model does not distinguish between three- and four-phonon decay mechanisms in umklapp processes, and as is known, the latter can lead to extremely low κ(T), as it is the case for PbCuSbS3.73 Obviously, to shed more light on this problem, inelastic neutron scattering on single-crystalline Yb5Rh6Sn18 combined with theoretical lattice dynamics studies would be required.
| τ −1 | Equation97 | C n |
|---|---|---|
| τ B −1 | v S/C1 | 4.0(1) × 10−7 m |
| τ PD −1 | C 2 x 4 T 4 | 4.0(1) × 105 s−1 K−4 |
| τ N −1 | C 3 x 3 T 4 | 1.5(1) × 103 s−1 K−4 |
| τ U −1 | C 4 x 2 T 2 e (−ΘD/3T) | 8.7(1) × 105 s−1 K−2 |
| τ PR −1 | C 5 | 5.1(1) × 1035 s−3 |
| C 6 | 2.1(1) | |
| ω PR | 5.8(1) THz |
The possible occurrence of phonon resonance in Yb5Rh6Sn18 could be the main reason for its ultra-low thermal conductivity. This phenomenon is usually described by a simple mechanical oscillator model given by eqn (12), where the half-width of the energy resonance curve is defined as Γ = ωPRC6/2 and a proportionality factor containing the concentration of oscillators is A = C5/Γ.92 Since a resonance interaction with a relaxation time τPR−1 is believed to occur between phonons and defects, the enhanced C2 parameter would nicely agree with this expectation. One of the central questions for such systems is the nature of the resonator. In early studies of mixed halides, this role was ascribed to the impurity non-magnetic ions,92–94 whereas in the cage compounds to ‘rattling’ atoms.96 However, the concept of inelastic resonance associated with energy dissipation of isolated ‘rattling’ atoms has been recently challenged99–101 by inelastic neutron scattering and lattice dynamics studies for clathrate- and skutterudite-based cage compounds. Since the value of the characteristic PR frequency ωPR, deduced for Yb5Rh6Sn18 from our fit, is comparable with that reported for the Sr8Ga16Ge30 clathrate,96 one could conclude on the same nature of the resonator (i.e., ‘rattling’ atoms) in both substances. Despite being less understood and its applicability to thermal properties of cage compounds is debated,72,102–104 PR would clearly contribute to a drastic reduction in κ(T). For instance, as it has been shown in ref. 95, its appearance in PbS leads to a decrease of κph(T) by ≈70% at a certain temperature. Thus, since the lattice contribution is a dominant one in the case of Yb5Rh6Sn18, its suppression plays a central role in the minimization of κtot(T).
Due to their ultra-low thermal conductivity, clathrates and filled skutterudites are known to be promising thermoelectric (TE) materials, which is reflected in their enhanced dimensionless figure of merit zT = S2T/ρκ > 1.87,90 In the case of Yb5Rh6Sn18, the highest zT = 5 × 10−3 is observed at 40 K. The poor TE performance of this stannide is explained by the negligibly small Seebeck coefficient due to its predominantly metallic behavior.79
3.7 Electronic band structure
The atomic- and orbital-resolved electronic densities of states (DOS) of Yb5Rh6Sn18 are presented in Fig. 9a and b, respectively. They show similar features to those reported earlier for the Yb3Rh4Sn13 Remeika prototype47 and the idealized structural model of Sc5Rh6Sn18.35 These are: (i) a low-lying energy band in the ≈−10.8 – ≈−5.8 eV range formed mainly by Sn-5s states, followed by (ii) an energy gap of ≈1 eV and (iii) a broad valence band extending from ∼−4.5 eV to the Fermi level EF dominated mainly by Rh-4d and Sn-5p electrons.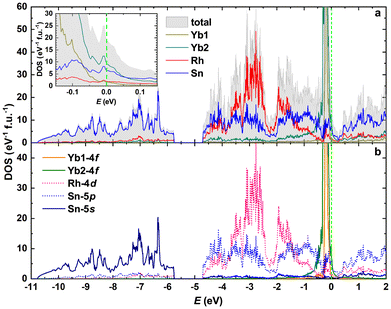 | ||
| Fig. 9 (a) Total and atomic resolved electronic density of states (DOS) for Yb5Rh6Sn18. Inset: DOS near the Fermi level EF. (b) Orbital resolved DOSs. EF is marked as a green dashed line. | ||
As one can see from the inset in Fig. 9a and b, the majority of the states at EF originate from Yb2-4f (≈41%), Sn-5p (≈29%), Yb1-4f (≈8%) and Rh-4d (≈9%) (the small admixture of Yb1,2-5d, Rh-5p, and Sn-5s together contributing ≈9% is not shown in the figures). Thus, in total, we obtain at the Fermi level a DOS of D(EF) = 18.8 states eV−1 f.u.−1, which can be recalculated in a Sommerfeld coefficient of the electronic specific heat γtheor = 44.5 mJ mol−1 K−1. This value would be in acceptable agreement with those approximately estimated from the experiment. Taking into account that four electronic bands, with a curvature revealing no similarities to a parabola (Fig. S6†), cross EF, one cannot expect that the simple free electron gas model would satisfactorily work in the case of Yb5Rh6Sn18. Indeed, as it has been shown above, the electrical conduction mechanisms are found here to be of a complex nature.
4 Conclusions
Yb5Rh6Sn18 crystallizes with a unique primitive tetragonal structural arrangement, which is closely related with the Yb3Rh4Sn13 Remeika and (Sn1−xTbx)Tb4Rh6Sn18 types. Such a relationship is reflected in the unit cell parameters which are derived from a ≈ 9.5 Å as well as in the common [RhSn6] corner sharing trigonal prismatic arrays with cuboctahedra incorporated into the free space in between. An important feature of the Yb5Rh6Sn18 crystal structure is that the relatively small Sn1 atoms reside inside enlarged 16-vertices distorted Frank–Kasper polyhedra thus possessing potential for a ‘rattling’ motion. This expectation is confirmed by the fitting of the temperature dependence of specific heat capacity to the combined Debye–Einstein model. The Einstein temperature deduced from the fit is in good agreement with the value obtained from the thermal displacement parameter of the Sn1 atom refined from the powder XRD data.The two white lines with temperature-dependent intensities in the X-ray absorption spectra (XAS) of Yb5Rh6Sn18 indicate that the Yb ions are in the intermediate valence state (IVS) switching between the 4f13 (Yb3+) and 4f14 (Yb2+) configurations. The latter one was simulated by quantum mechanical density functional theory (DFT) calculations, which showed that the Yb2-5d states are unexpectedly strong, contributing to the Yb3+ white line. This finding can explain why the known theories fail to describe the IVS in the new stannide.
Indeed, the well-established Coqblin–Schrieffer model fails, whereas the Bickers–Cox–Wilkins one fairly describes the maximum in the temperature dependence of the magnetic susceptibility of Yb5Rh6Sn18 only on the assumption of the J = 3/2 multiplet (degeneracy N = 4) which, however, is atypical for Yb atoms. Furthermore, the Kondo temperature of 191 K, obtained from such a fit, is much too low, which is not confirmed in further electrical transport studies.
Electrical resistivity, which increases with increasing temperature and fits well to the quadratic Fermi-liquid approach in the low-T regime, together with the observed small Seebeck coefficients as well as high charge carrier concentrations and their mobilities hints towards the metallic properties of Yb5Rh6Sn18. However, application of the free electron gas model failed in the description of electrical transport of this stannide. This fact is further ascribed to its complex electronic structure revealing four bands at the Fermi level (EF) as well as to the temperature-dependent domination of the type of charge carrier (i.e., electrons below ≈200 K and holes above).
A well-pronounced minimum in the T-dependent Seebeck coefficient is a feature indicating IVS. By applying a two-band theory, we found that the mean Yb valence is ν ≈ 2.8, if one assumes smaller degeneracy (N = 4), and it increases up to ≈2.9 for N = 8. Although both ν-values differ strongly from ν = 2.59 to 2.62 (deduced from XAS), the observed tendency is in line with those found for magnetic susceptibility (i.e., better description with models for smaller N).
Yb5Rh6Sn18 shows an ultra-low thermal conductivity dominated by phonons in the low-T range. The lattice contribution shows also a clear minimum, which (at the level of this investigation) most likely can be attributed to the appearance of phonon resonance due to the ‘rattling’ motion of Sn1 atoms in the structure of this new stannide. Indeed, by applying the Debye–Callaway model, we deduced the characteristic resonance frequency [5.81 THz], which is comparable with the values for such cage compounds as intermetallic clathrates. Therefore, it is argued that the phonon resonance can explain why the thermal conductivity of Yb5Rh6Sn18 becomes ultra-low.
Data availability
The data supporting this article are included as part of the ESI.†Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The DynaCool-12 system was acquired within the DFG project 422219907. VL is grateful to DFG for financial support within the project 467257848. The authors thank H. Borrmann for performing the powder XRD analysis. We are also grateful to U. Burkhardt, S. Kostmann and P. Scheppan for the microstructural and EDX studies.References
- S. Engel, E. C. J. Gießelmann, M. K. Reimann, R. Pöttgen and O. Janka, ACS Org. Inorg. Au, 2024, 4, 188–222 CrossRef CAS PubMed.
- P. S. Riseborough, Adv. Phys., 2000, 49, 257–320 CrossRef CAS.
- G. R. Stewart, Rev. Mod. Phys., 2001, 73, 797–855 CrossRef CAS.
- A. Georges, G. Kotliar, W. Krauth and M. J. Rozenberg, Rev. Mod. Phys., 1996, 68, 13–125 CrossRef CAS.
- C. M. Varma, Rev. Mod. Phys., 1976, 48, 219–238 CrossRef CAS.
- J. M. Lawrence, P. S. Riseborough and R. D. Parks, Rep. Prog. Phys., 1981, 44, 1–84 CrossRef.
- P. W. Anderson, Phys. Rev., 1961, 124, 41–53 CrossRef CAS.
- J. Kondo, Prog. Theor. Phys., 1964, 32, 37–49 CrossRef CAS.
- N. E. Bickers, D. L. Cox and J. W. Wilkins, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 36, 2036–2079 CrossRef.
- H. Bethe, Z. Phys., 1931, 71, 205–226 CrossRef CAS.
- B. Coqblin and J. R. Schrieffer, Phys. Rev., 1969, 185, 847–853 CrossRef CAS.
- A. M. Tsvelick and P. B. Wiegmann, J. Phys. C: Solid State Phys., 1982, 15, 1707 CrossRef CAS.
- V. T. Rajan, Phys. Rev. Lett., 1983, 51, 308–311 CrossRef CAS.
- A. Hewson, J. Rasul and D. Newns, Solid State Commun., 1983, 47, 59–61 CrossRef CAS.
- H.-U. Desgranges, Phys. B, 2015, 473, 93–100 CrossRef CAS.
- A. Hewson, D. Newns, J. Rasul and N. Read, J. Magn. Magn. Mater., 1985, 47–48, 354–356 CrossRef CAS.
- E. Cattaneo, Z. Phys. B: Condens. Matter, 1986, 64, 317–325 CrossRef CAS.
- H. Yamaoka, N. Tsujii, Y. Utsumi, H. Sato, I. Jarrige, Y. Yamamoto, J.-F. Lin, N. Hiraoka, H. Ishii, K.-D. Tsuei and J. Mizuki, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 205120 CrossRef.
- M. Kasaya, F. Iga, M. Takigawa and T. Kasuya, J. Magn. Magn. Mater., 1985, 47–48, 429–435 CrossRef CAS.
- H. Yamaoka, I. Jarrige, N. Tsujii, J.-F. Lin, N. Hiraoka, H. Ishii and K.-D. Tsuei, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 035111 CrossRef.
- J. Remeika, G. Espinosa, A. Cooper, H. Barz, J. Rowell, D. McWhan, J. Vandenberg, D. Moncton, Z. Fisk, L. Woolf, H. Hamaker, M. Maple, G. Shirane and W. Thomlinson, Solid State Commun., 1980, 34, 923–926 CrossRef CAS.
- R. Gumeniuk, L. Akselrud, K. O. Kvashnina, W. Schnelle, A. A. Tsirlin, C. Curfs, H. Rosner, M. Schöneich, U. Burkhardt, U. Schwarz, Y. Grin and A. Leithe-Jasper, Dalton Trans., 2012, 41, 6299–6309 RSC.
- R. Gumeniuk, M. Schöneich, K. O. Kvashnina, L. Akselrud, A. A. Tsirlin, M. Nicklas, W. Schnelle, O. Janson, Q. Zheng, C. Curfs, U. Burkhardt, U. Schwarz and A. Leithe-Jasper, Dalton Trans., 2015, 44, 5638–5651 RSC.
- R. Gumeniuk, M. Nicklas, L. Akselrud, W. Schnelle, U. Schwarz, A. A. Tsirlin, A. Leithe-Jasper and Y. Grin, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 224502 CrossRef.
- I. W. H. Oswald, B. K. Rai, G. T. McCandless, E. Morosan and J. Y. Chan, CrystEngComm, 2017, 19, 3381–3391 RSC.
- M. Feig, W. Carrillo-Cabrera, M. Bobnar, P. Simon, C. Curfs, V. Levytskyi, A. A. Tsirlin, A. Leithe-Jasper and R. Gumeniuk, Dalton Trans., 2022, 51, 4734–4748 RSC.
- R. Gumeniuk, in Handbook on the Physics and Chemistry of Rare Earths, ed. J.-C. G. Bünzli and V. K. Pecharsky, Elsevier, 2018, vol. 54, pp. 43–143 Search PubMed.
- S. Miraglia, J. L. Hodeau, F. de Bergevin, M. Marezio and G. P. Espinosa, Acta Crystallogr., Sect. B: Struct. Sci., 1987, 43, 76–83 CrossRef.
- S. C. Peter, U. Subbarao, S. Rayaprol, J. B. Martin, M. Balasubramanian, C. D. Malliakas and M. G. Kanatzidis, Inorg. Chem., 2014, 53, 6615–6623 CrossRef CAS.
- V. Levytskyi, W. Carrillo-Cabrera, L. Akselrud, B. Kundys, A. Leithe-Jasper and R. Gumeniuk, Dalton Trans., 2022, 51, 10036–10046 RSC.
- A. Bhattacharyya, D. T. Adroja, N. Kase, A. D. Hillier, A. M. Strydom and J. Akimitsu, Phys. Rev. B, 2018, 98, 024511 CrossRef CAS.
- N. Kase, K. Inoue, H. Hayamizu and J. Akimitsu, J. Phys. Soc. Jpn., 2011, 80, SA112 CrossRef.
- A. Bhattacharyya, D. Adroja, N. Kase, A. Hillier, J. Akimitsu and A. Strydom, Sci. Rep., 2015, 5, 12926 CrossRef CAS.
- M. Feig, W. Schnelle, A. Maisuradze, A. Amon, C. Baines, M. Nicklas, S. Seiro, L. Howald, R. Khasanov, A. Leithe-Jasper and R. Gumeniuk, Phys. Rev. B, 2020, 102, 024508 CrossRef CAS.
- M. Feig, L. Akselrud, W. Schnelle, V. Dyadkin, D. Chernyshov, A. Ormeci, P. Simon, A. Leithe-Jasper and R. Gumeniuk, Dalton Trans., 2020, 49, 6832–6841 RSC.
- D. Kumar, C. N. Kuo, F. Astuti, T. Shang, M. K. Lee, C. S. Lue, I. Watanabe, J. A. T. Barker, T. Shiroka and L. J. Chang, J. Phys.: Condens. Matter, 2018, 30, 315803 CrossRef CAS.
- V. Levytskyi, M. Feig, L. Akselrud, W. Schnelle, A. Leithe-Jasper, V. Dyadkin, D. Chernyshov and R. Gumeniuk, J. Phys.: Condens. Matter, 2019, 31, 445603 CrossRef CAS PubMed.
- E. G. Moshopoulou, M. F. Hundley, R. Movshovich, J. D. Thompson, J. L. Sarrao, Z. Fisk, E. Felder, M. Chernikov, D. Pushin and H. R. Ott, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 4096–4100 CrossRef CAS.
- A. D. Montero, G. T. McCandless, O. Oladehin, R. E. Baumbach and J. Y. Chan, Chem. Mater., 2023, 35, 2238–2247 CrossRef.
- G. Espinosa, Mater. Res. Bull., 1980, 15, 791–798 CrossRef CAS.
- G. Espinosa, A. Cooper and H. Barz, Mater. Res. Bull., 1982, 17, 963–969 CrossRef CAS.
- J. Hodeau, M. Marezio, J. Remeika and C. Chen, Solid State Commun., 1982, 42, 97–102 CrossRef CAS.
- S. Miraglia, J. Hodeau, M. Marezio, C. Laviron, M. Ghedira and G. Espinosa, J. Solid State Chem., 1986, 63, 358–368 CrossRef CAS.
- P. Bordet, J. Hodeau, P. Wolfers, G. Krill, F. Weiss and M. Marezio, J. Magn. Magn. Mater., 1987, 63–64, 524–526 CrossRef CAS.
- B. K. Rai, I. W. H. Oswald, J. Y. Chan and E. Morosan, Phys. Rev. B, 2016, 93, 035101 CrossRef.
- M. Feig, L. Akselrud, M. Motylenko, M. Bobnar, J. Wagler, K. O. Kvashnina, V. Levytskyi, D. Rafaja, A. Leithe-Jasper and R. Gumeniuk, Dalton Trans., 2021, 50, 13580–13590 RSC.
- R. Gumeniuk, V. Levytskyi, B. Kundys and A. Leithe-Jasper, Phys. Rev. B, 2023, 108, 214515 CrossRef CAS.
- STOE Powder Software, WinXPow (version 2), Darmstadt, STOE and Cie GmbH, 2001 Search PubMed.
- L. Akselrud and Y. Grin, J. Appl. Crystallogr., 2014, 47, 803–805 CrossRef CAS.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122 CrossRef CAS PubMed.
- L. J. Farrugia, J. Appl. Crystallogr., 2012, 45, 849–854 CrossRef CAS.
- A. C. Scheinost, J. Claussner, J. Exner, M. Feig, S. Findeisen, C. Hennig, K. O. Kvashnina, D. Naudet, D. Prieur, A. Rossberg, M. Schmidt, C. Qiu, P. Colomp, C. Cohen, E. Dettona, V. Dyadkin and T. Stumpf, J. Synchrotron Radiat., 2021, 28, 333–349 CrossRef CAS PubMed.
- K. O. Kvashnina and A. C. Scheinost, J. Synchrotron Radiat., 2016, 23, 836–841 CrossRef CAS PubMed.
- V. Solé, E. Papillon, M. Cotte, P. Walter and J. Susini, Spectrochim. Acta, Part B, 2007, 62, 63–68 CrossRef.
- K. Koepernik and H. Eschrig, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1743–1757 CrossRef CAS.
- J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244 CrossRef PubMed.
- J. Emsley, The Elements, Clarendon Press, Oxford, 1998 Search PubMed.
- J. Vandenberg, Mater. Res. Bull., 1980, 15, 835–847 CrossRef CAS.
- R. Gumeniuk, R. Sarkar, C. Geibel, W. Schnelle, C. Paulmann, M. Baenitz, A. A. Tsirlin, V. Guritanu, J. Sichelschmidt, Y. Grin and A. Leithe-Jasper, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 235138 CrossRef.
- R. Sarkar, R. Gumeniuk, A. Leithe-Jasper, W. Schnelle, Y. Grin, C. Geibel and M. Baenitz, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 201101 CrossRef.
- A. Ochiai, T. Suzuki and T. Kasuya, J. Phys. Soc. Jpn., 1990, 59, 4129–4141 CrossRef CAS.
- V. H. Tran, W. Miiller, A. Kowalczyk, T. Tolinski and G. Chelkowska, J. Phys.: Condens. Matter, 2006, 18, 10353 CrossRef CAS PubMed.
- A. Kowalczyk, M. Falkowski and T. Tolinski, J. Appl. Phys., 2010, 107, 123917 CrossRef.
- A. Grytsiv, D. Kaczorowski, A. Leithe-Jasper, P. Rogl, M. Potel, H. Noël, A. Pikul and T. Velikanova, J. Solid State Chem., 2002, 165, 178–181 CrossRef CAS.
- J. W. Rasul and A. C. Hewson, J. Phys. C: Solid State Phys., 1984, 17, 2555–2573 CrossRef.
- B. C. Sales and D. K. Wohlleben, Phys. Rev. Lett., 1975, 35, 1240–1244 CrossRef CAS.
- L. B. Farhat, M. Amami, E. Hlil and R. B. Hassen, J. Alloys Compd., 2009, 485, 701–705 CrossRef.
- A. Bhattacharyya, D. T. Adroja, J. Quintanilla, A. D. Hillier, N. Kase, A. M. Strydom and J. Akimitsu, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 060503 CrossRef.
- J. Wu, J. Xu and K. Tanigaki, J. Phys. Chem. Solids, 2024, 184, 111709 CrossRef CAS.
- Y. Ikeuchi, H. Takatsu, C. Tassel, C. M. Brown, T. Murakami, Y. Matsumoto, Y. Okamoto and H. Kageyama, Inorg. Chem., 2019, 58, 6790–6795 CrossRef CAS PubMed.
- M. Beekman, W. Schnelle, H. Borrmann, M. Baitinger, Y. Grin and G. S. Nolas, Phys. Rev. Lett., 2010, 104, 018301 CrossRef CAS.
- S. Pailhes, V. Giordano, S. Turner, P.-F. Lory, C. Candolfi, M. de Boissieu and H. Euchner, Results Phys., 2023, 49, 106487 CrossRef.
- E. Zuñiga-Puelles, R. Cardoso-Gil, A. Özden, N. Bulut, V. Svitlyk, C. Himcinschi, J. Kortus and R. Gumeniuk, Phys. Rev. B, 2022, 106, 195201 CrossRef.
- E. Zuñiga-Puelles, A. Özden, V. Pacheco, L. Akselrud, R. Cardoso-Gil, A. Straßheim, P. Wyżga, C. Himcinschi and R. Gumeniuk, J. Alloys Compd., 2024, 976, 173055 CrossRef.
- W. Schnelle, A. Leithe-Jasper, H. Rosner, R. Cardoso-Gil, R. Gumeniuk, D. Trots, J. A. Mydosh and Y. Grin, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 094421 CrossRef.
- M. M. Koza, A. Leithe-Jasper, H. Rosner, W. Schnelle, H. Mutka, M. R. Johnson, M. Krisch, L. Capogna and Y. Grin, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 014306 CrossRef.
- A. Wang, Z. Y. Nie, F. Du, G. M. Pang, N. Kase, J. Akimitsu, Y. Chen, M. J. Gutmann, D. T. Adroja, R. S. Perry, C. Cao, M. Smidman and H. Q. Yuan, Phys. Rev. B, 2021, 103, 024503 CrossRef CAS.
- Z. Zhang, Y. Xu, C. N. Kuo, X. C. Hong, M. X. Wang, P. L. Cai, J. K. Dong, C. S. Lue and S. Y. Li, Supercond. Sci. Technol., 2015, 28, 105008 CrossRef.
- R. Groos and A. Marx, Festkörperphysik, Oldenbourg Verlag München, 2012 Search PubMed.
- N. Mott and H. Jones, The Theory of the Properties of Metals and Alloys, Dover Publications, New York, 1958 Search PubMed.
- R. Gumeniuk, K. Kvashnina, W. Schnelle, M. Nicklas, H. Borrmann, H. Rosner, Y. Skourski, A. A. Tsirlin, A. Leithe-Jasper and Y. Grin, J. Phys.: Condens. Matter, 2011, 23, 465601 CrossRef CAS.
- K. Kadowaki and S. Woods, Solid State Commun., 1986, 58, 507–509 CrossRef CAS.
- Y. Bando, T. Suemitsu, K. Takagi, H. Tokushima, Y. Echizen, K. Katoh, K. Umeo, Y. Maeda and T. Takabatake, J. Alloys Compd., 2000, 313, 1–6 CrossRef CAS.
- U. Gottwick, K. Gloss, S. Horn, F. Steglich and N. Grewe, J. Magn. Magn. Mater., 1985, 47–48, 536–538 CrossRef CAS.
- P. M. Chaikin and G. Beni, Phys. Rev. B: Solid State, 1976, 13, 647–651 CrossRef CAS.
- J. F. Kwak and G. Beni, Phys. Rev. B: Solid State, 1976, 13, 652–657 CrossRef CAS.
- M. Baitinger, B. Böhme, A. Ormeci and Y. Grin, in Solid State Chemistry of Clathrate Phases: Crystal Structure, Chemical Bonding and Preparation Routes, ed. G. S. Nolas, Springer, Netherlands, Dordrecht, 2014, pp. 35–64 Search PubMed.
- D. O. Lindroth, J. Brorsson, E. Fransson, F. Eriksson, A. Palmqvist and P. Erhart, Phys. Rev. B, 2019, 100, 045206 CrossRef CAS.
- J. Shen, T. Xie, L. Zhang, P. Wang and Z. Fang, Sci. Rep., 2020, 10, 3068 CrossRef CAS.
- Recent Trends in Thermoelectric Materials Research I, ed. T. M. Tritt, Elsevier, 2001, vol. 69 of Semiconductors and Semimetals, pp. 139–253 Search PubMed.
- H.-S. Kim, Z. M. Gibbs, Y. Tang, H. Wang and G. J. Snyder, APL Mater., 2015, 3, 041506 CrossRef.
- R. O. Pohl, Phys. Rev. Lett., 1962, 8, 481–483 CrossRef CAS.
- F. C. Baumann, J. P. Harrison, R. O. Pohl and W. D. Seward, Phys. Rev., 1967, 159, 691–699 CrossRef CAS.
- R. F. Caldwell and M. V. Klein, Phys. Rev., 1967, 158, 851–875 CrossRef CAS.
- E. Zuñiga-Puelles, V. Levytskyi, A. Özden, T. Gürel, N. Bulut, C. Himcinschi, C. Sevik, J. Kortus and R. Gumeniuk, Phys. Rev. B, 2023, 107, 195203 CrossRef.
- J. L. Cohn, G. S. Nolas, V. Fessatidis, T. H. Metcalf and G. A. Slack, Phys. Rev. Lett., 1999, 82, 779–782 CrossRef CAS.
- T. M. Tritt, Thermal conductivity: theory, properties, and applications, Springer Science & Business Media, 2005 Search PubMed.
- K. Gofryk, D. Kaczorowski, T. Plackowski, J. Mucha, A. Leithe-Jasper, W. Schnelle and Y. Grin, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 224426 CrossRef.
- M. M. Koza, M. R. Johnson, R. Viennois, H. Mutka, L. Girard and D. Ravot, Nat. Mater., 2008, 7, 805–810 CrossRef CAS PubMed.
- M. Christensen, A. B. Abrahamsen, N. B. Christensen, F. Juranyi, N. H. Andersen, K. Lefmann, J. Andreasson, C. R. H. Bahl and B. B. Iversen, Nat. Mater., 2008, 7, 811–815 CrossRef CAS PubMed.
- A. Bhattacharya, J. Mater. Chem. C, 2019, 7, 13986–13992 RSC.
- E. S. Toberer, A. Zevalkink and G. J. Snyder, J. Mater. Chem., 2011, 21, 15843–15852 RSC.
- W. Li and N. Mingo, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 144304 CrossRef.
- M. Baggioli, B. Cui and A. Zaccone, Phys. Rev. B, 2019, 100, 220201 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2383845. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4dt02759k |
| This journal is © The Royal Society of Chemistry 2025 |