Bifunctional heterobimetallic 3d–4f [Co(II)-RE, RE = Dy, Eu, and Y] ionic complexes: modulation of the magnetic-luminescence behaviour

Abstract

This work reports the engineering and functional properties of an emerging class of heterobimetallic 3d–4f ionic complexes designed with cobalt and rare-earth (RE) metals. We present a comprehensive examination of the structural, magnetic, optical, and thermal properties of the heterobimetallic ionic complexes with the general formula [Co(hfa)₃]⁻[RE(hfa)₂tetraglyme]⁺ (RE = Dy, Eu, and Y), where the metal centres are coordinated by hexafluoroacetylacetonate (Hhfa = 1,1,1,5,5,5-hexafluoro-2,4-pentanedione), β-diketone and tetraglyme (2,5,8,11,14-pentaoxapentadecane) polyether. Structural analysis reveals an octahedral coordination geometry enveloping the cobalt(II) centre, characterized by inherent symmetry properties consistent across the derivatives, while a capped square-antiprism coordination polyhedron is observed for the RE ions. Electron paramagnetic resonance (EPR) spectroscopy confirms the constancy of the electronic structure of the cobalt(II) moiety and the significant contribution of the lanthanide ions to the magnetic properties of the compounds. The non-trivial single-ion magnetic properties of cobalt(II), dysprosium(III), and europium(III) centres, and the effect of their interactions are investigated by a detailed static and dynamic magnetic susceptibility study. Moreover, optical analyses have been carried out showing the π–π* intraligand (IL) transition of the β-diketonate ligand and the d–d cobalt(II) transitions. Luminescence characterization of dysprosium(III) and europium(III) derivatives exhibits their characteristic emission bands, indicative of the unique photophysical properties conferred by the lanthanide ions. Thermal studies using thermogravimetric analysis (TGA) and differential scanning calorimetry (DSC) reveal good thermal stability and volatility properties, underscoring the interesting nature of these ionic complexes for potential deposition on suitable substrates. In summary, these heterobimetallic complexes show intriguing optical and magnetic properties with potential implications across diverse scientific disciplines, including molecular magnetism, optoelectronics, and materials science.

---

1. Introduction

One of the primary objectives in the field of molecular magnetism is the synthesis of molecular complexes combining magnetism with properties that are typically not observed in bulk magnets, such as superconductivity or luminescence.^1–4 In this sense, compounds that contain trivalent lanthanide ions Ln(III), characterized by unique optical and magnetic properties, are particularly appealing. Indeed, Ln(III)-based compounds are actively investigated for a wide range of potential applications in diverse fields, including permanent magnets, telecommunication technologies, light-emitting devices, bioimaging, and sensing.⁵ In particular, the study of the magnetic properties of lanthanide based complexes has been boosted, in the past couple of decades,^6–9 after the report by Ishikawa and coworkers of slow relaxation of the magnetization in mononuclear lanthanide complexes of phthalocyanine.¹⁰ These systems were indeed proposed as molecular based magnetic memory units and thus with perspective applications in ultrahigh density magnetic information storage and molecular spintronics.^6,11–14 It was soon realized that, in close similarity to what is observed in polynuclear transition metal clusters,¹⁵ this peculiar behaviour is due to the large easy-axis magnetic anisotropy and large global angular momentum.^16,17 For these reasons, the overwhelming majority of the systems, reported up to now, incorporate dysprosium(III) or terbium(III).¹⁷ This subsequently led to the investigation of mononuclear transition element complexes based on metal ions with comparable features, among which cobalt has been by far the most investigated.^18–20 The hundreds of studies proposed since then have evidenced that for both these classes of systems, collectively named Single Ion Magnets (SIMs), the relaxation of the magnetization is often accelerated by concomitant processes, such as Raman and direct ones, and Quantum Tunnelling of the Magnetization (QTM).^21–23 A possible workaround to this issue has been proposed by several authors by using hybrid 3d–4f (and 4f–4f) systems, in which the exchange coupling between different spin carriers can lead to quenching of the detrimental quantum tunnelling of the magnetization.^24–27 This raises the issue of the tunability of exchange coupling involving Ln(III) ions, which is usually weak due to the inner nature of the 4f orbitals and difficult to assess due to competing magnetic anisotropy effects.²⁸ In this respect, the lowest approachable limit for the magnetic interaction in 3d–4f systems is the one where the two centres are only interacting via dipolar interactions. This has the advantage that the magnitude of the pairwise interaction can be in principle obtained by the simple point-dipole approximation. Such systems can be achieved by building up ionic lattices where the cation and anion are made up of molecules containing two different spin carriers. However, to the best of our knowledge, the magnetic response in such systems has been investigated only in bimetallic cobalt(II) complexes by Boča and coworkers,^29,30 and in a cobalt-radical(cation)–lanthanide(anion) pair,³¹ while no reports are present in the literature for ionic 3d–4f systems. At the same time, lanthanide compounds are also investigated for their distinctive metal-based luminescence due to 4f–4f intra-configurational radiative transitions for various applications such as biological sensing,^32,33 time-resolved fluoro-immunoassays,³⁴ time-resolved imaging,³⁵ optical amplifiers in telecommunications,³⁶ and OLED displays.^37,38 According to the Laporte principles, the emitting f excited states have very weak absorption coefficients and extended lifetimes.³⁹ Consequently, direct sensitization of the metal centre is inefficient for 4f luminescence, particularly in diluted solutions. To overcome this limit a variety of strategies,⁴⁰ which include singlet excited-state with intra-ligand charge transfer (ILCT),⁴¹ induced triplet metal-to-ligand charge transfer (MLCT) and the insertion of 3d metals in the system,⁴² have been developed. The heterobimetallic 3d–4f complexes^43–45 gained strong attention also in this framework. In these complexes, lanthanide luminescence is sensitized through antenna ligands or 3d complex antenna.^46–48 In order to have efficient energy transfer between the antenna ligand and the Ln(III) ion, the ligand triplet state should be at least 2000 cm⁻¹ higher in energy than the lanthanide ion emitting state.⁴⁹

With the aim of obtaining a complex simultaneously showing luminescence and slow relaxation of the magnetization and where the two centres are characterized by interionic dipolar interactions, we report in the following the one-pot synthesis of three isostructural novel heterobimetallic 3d–4f ionic fluorinated β-diketonate complexes with a polyether as a co-ligand. In particular, the 3d ion is cobalt(II), while the 4f unit is formed by dysprosium(III), europium(III) or yttrium(III). The fluorinated β-diketonate ligand is hexafluoroacetylacetonate, while the polyether, employed to complete the coordination sphere of the rare-earth cation, is the tetraglyme. The former ligand can promote efficient energy transfer toward the 4f ion, promoting its luminescence properties, while cations based on the latter ligand have been previously shown to present slow relaxation of the magnetization.⁵⁰ At the same time, the presence of a cobalt(II) octahedrally distorted anion could also contribute to slow relaxation of the magnetization of the compound, where the 3d and 4f paramagnetic centres only interact via dipolar interactions. A complete structural, magnetic and luminescence characterization study of the three isostructural derivatives is reported here. Furthermore, also thermal stability and volatility properties have been investigated as a proof of their suitability in a wide range of application fields.

2 Experimental section

2.1 Reagents

Commercial cobalt acetate tetrahydrate, dysprosium acetate hydrate, yttrium acetate hydrate, europium acetate hydrate, and Hhfa (1,1,1,5,5,5-hexafluoro-2,4-pentanedione) were purchased from STREM Chemicals Inc, while tetraglyme (2,5,8,11,14-pentaoxapentadecane) was purchased from Sigma-Aldrich. All chemicals were used without any further purification.

2.2 Synthetic procedures

The syntheses were performed under normal laboratory conditions.

Synthesis of [Co(hfa)₃]⁻[Dy(hfa)₂tetraglyme]⁺ (Dy-Co). 0.5281 g (2.1202 mmol) of Co(CH₃COO)₂·4H₂O and 0.7200 g (2.1202 mmol) of Dy(CH₃COO)₃·xH₂O were suspended in 50 ml of dichloromethane inside a flat bottom flask, and then 0.39 ml of tetraglyme (1.7668 mmol, d = 1.01 g ml⁻¹) were added. The suspension was vigorously stirred at room temperature for 10 minutes. Subsequently, 1.25 ml of Hhfa (8.8341 mmol, d = 1.47 g ml⁻¹) were added and the mixture was refluxed under magnetic stirring for 75 minutes. After filtration of the acetate excess, an orange product was obtained through evaporation of the solvent. The melting point of the obtained compound was 132–136 °C per 760 torr. Elemental analysis (C₃₅H₂₇F₃₀O₁₅DyCo): calc: C, 28.42; H: 1.84. Found: C, 27.98; H, 1.89. IR (Nujol; ν, cm⁻¹): 2895 (vs), 2721 (vw), 2665 (vw), 1655 (s), 1558 (m), 1530 (m), 1460 (vs), 1375 (vs), 1255 (s), 1202 (s), 1145 (s), 1058 (m), 1020 (w), 947 (m), 848 (s), 807 (s), 792 (s), 723 (s), 660 (s), 442 (vs).

Synthesis of [Co(hfa)₃]⁻[Eu(hfa)₂tetraglyme]⁺ (Eu-Co). The complex has been prepared using a procedure analogous to that described for the Dy-Co adduct, using 0.5283 g (2.1202 mmol) of Co(CH₃COO)₂·4H₂O, 0.6977 g (2.1202 mmol) of Eu(CH₃COO)₃·xH₂O, 0.39 ml of tetraglyme (1.7668 mmol, d = 1.01 g ml⁻¹) and 1.25 ml of Hhfa (8.8341 mmol, d = 1.47 g ml⁻¹). After filtration of the acetate excess, an orange product was obtained upon evaporation of the solvent. The melting point of the obtained compound was 145–150 °C per 760 torr. Elemental analysis (C₃₅H₂₇F₃₀O₁₅EuCo): calc: C, 28.63; H: 1.85. Found: C, 28.11; H, 1.90. IR (Nujol; ν, cm⁻¹): 2910 (vs), 2724 (w), 2669 (vw), 1653 (s), 1557 (m), 1530 (m), 1460 (vs), 1376 (vs), 1255 (s), 1205 (s), 1145 (s), 1102 (vw), 1060 (m), 1018 (vw), 947 (s), 848 (s), 807 (s), 792 (s), 767 (vw), 740 (vw), 723 (m), 670 (m), 660 (s), 585 (m), 442 (vs).

Synthesis of [Co(hfa)₃]⁻[Y(hfa)₂tetraglyme]⁺ (Y-Co). The adduct has been obtained using a procedure analogous to the synthesis of Dy-Co, using 0.4840 g (1.9431 mmol) of Co(CH₃COO)₂·4H₂O and 0.5170 g (1.9431 mmol) of Y(CH₃COO)₃·xH₂O, 0.39 ml of tetraglyme (1.7668 mmol, d = 1.01 g ml⁻¹) and 1.25 ml of Hhfa (8.8341 mmol, d = 1.47 g ml⁻¹). The acetate excess was filtered off and an orange colour product was obtained through solvent evaporation. The melting point of the obtained compound was 117–125 °C per 760 torr. Elemental analysis (C₃₅H₂₇F₃₀O₁₅YCo): calc: C, 29.92; H: 1.94. Found: C, 29.28; H, 1.99. IR (Nujol; ν, cm⁻¹): 2908 (vs), 2723 (vw), 2669 (vw), 1652 (s), 1615 (vw), 1560 (m), 1530 (m), 1460 (vs), 1376 (vs), 1250 (s), 1203 (s), 1140 (s), 1103 (vw), 1058 (m), 1020 (vw), 947 (s), 930 (w), 875 (w), 848 (s), 807 (s), 795 (s), 767 (w), 740 (m), 723 (m), 670 (m), 660 (m), 585 (s), 442 (vs).

2.3 Characterization

Fourier transform infrared spectra were recorded using a JASCO FT-IR-4600 spectrometer (Easton, MD, USA) in the wavenumber range 4000–400 cm⁻¹. Samples were prepared using a minor amount of complex powders finely ground in an agate mortar with two drops of nujol to produce mulls placed between NaCl plates. The instrumental resolution was 4 cm⁻¹. The melting points were measured in air with a Kofler microscope.

Elemental analyses were carried out using a EuroVector EA3100 elemental analyzer (CHNS).

Thermogravimetric analyses (TGA) were carried out using a Mettler Toledo TGA2 and STAR^e software with a heating rate of 5 °C min⁻¹ at atmospheric pressure under prepurified nitrogen flow, fed into the working chamber at 50 standard cubic centimetres per minute (sccm). The weights of the samples were between 11 and 14 mg.

Differential scanning calorimetry (DSC) analyses were performed using a Mettler Toledo Star System DSC 3 under prepurified nitrogen flow (50 sccm) at atmospheric pressure with a heating rate of 5 °C min⁻¹. The sample weights ranged from 8 to 10 mg.

Powder X-ray diffraction (PXRD) patterns were recorded using a SmartLab Rigaku diffractometer in the Bragg–Brentano mode, equipped with a rotating anode of Cu K_α radiation operating at 45 kV and 200 mA. The acquisition employed a 0.02° incremental step.

Energy dispersive X-ray (EDX) analysis was used to assess the atomic composition of the powders using an INCA-Oxford “windowless” detector with an electron beam energy of 15 keV, with a resolution of 127 eV evaluated as the full width half maximum (FWHM) of Mn K_α.

UV-vis spectroscopy analyses were carried out on the obtained complexes dissolved in dichloromethane to produce solutions at concentrations of 2.5 × 10⁻³ mol L⁻¹ and 2.5 × 10⁻⁶ mol L⁻¹. Measurements were carried out at room temperature with a scan speed of 40 nm min⁻¹, a bandwidth of 2 nm and a data pitch of 1 nm using a JASCO V650 spectrophotometer.

Fluorescence spectroscopy was carried out on the obtained complexes dissolved in dichloromethane to produce solutions at a concentration of 1 × 10⁻² mol L⁻¹, using a JASCO FP-8250 spectrofluorometer at room temperature. For the Y-Co and Dy-Co complexes emission spectra were recorded using a 310 nm xenon lamp as the excitation source, in the emission range of 350–650 nm, with an angle of 90°, a data interval of 1 nm and a scan speed of 20 nm min⁻¹. For the Eu-Co complex, emission spectra were recorded using a 390 nm xenon lamp as the excitation source, in the emission range of 450–750 nm, with an angle of 90°, a data interval of 1 nm and a scan speed of 20 nm min⁻¹.

X-ray crystallography. Single crystal X-ray diffraction data of Eu-Co and Y-Co were collected using a Bruker Apex-II diffractometer equipped with a CCD detector (T = 100 K), Mo-K_α radiation (λ = 0.71073 Å). For the data collection the APEX2 software was used,⁵¹ while data integration and reduction were performed with the Bruker SAINT software.⁵² The crystal structures were solved using the SIR-2004 package⁵³ and refined using full-matrix least squares against F2 using all data (SHELXL-2018/3).⁵⁴ In both structures, all the non-hydrogen atoms were refined with anisotropic displacement parameters, with the exception of the fluorine atoms bonded to the trifluoromethyl carbon atoms C4A, C4E and C5D, in Y-Co, which were in disordered positions. Such disorder was refined by using three models for every fluorine atom bonded to C4A and C5D (with occupancy factors of 0.5, 0.25, and 0.25) and two models for the fluorine atoms bonded to C4E (occupancy factors of 0.6 and 0.4), all these fluorine atoms were isotropically refined. All the hydrogen atoms were set in calculated positions and refined in accordance with the atoms to which they are bonded. Geometrical calculations were performed using PARST97⁵⁵ and molecular plots were produced using the program Mercury (v4.1.2)⁵⁶ and Discovery Studio Visualizer 2019.⁵⁷ Crystallographic data and refinement parameters are reported in Table 1.

Table 1 Crystallographic data and refinement parameters of Eu-Co and Y-Co

	Eu-Co	Y-Co
Empirical formula	[Co(hfa)3]^−[Eu(hfa)2·tetraglyme]^+	[Co(hfa)3]^−[Y(hfa)2·tetraglyme]^+
Formula weight	1468.45	1405.40
T (K)	100	100
Crystal system, space group	Monoclinic, P21/n	Monoclinic, P21/n
λ (Å)	0.71073	0.71073
Unit cell dimensions (Å, °)	a = 14.3491(9)	a = 14.2628(5)
	b = 23.324(1), β = 95.082(2)	b = 23.3033(8), β = 94.9670(10)
	c = 15.1101(10)	c = 15.0829(6)
V (Å^3)	5037.2(5)	4994.3(3)
Z, dcalc(g cm^−3)	4, 1.936	4, 1.869
μ (mm^−1)	1.736	1.663
F(000)	2868	2772
Reflections collected/unique	119 698/15 458	205 161/19 021
Data/parameters	15 458/739	19 021/751
Final R indices [I > 2σ(I)]	R 1 = 0.0359, wR2 = 0.0796	R 1 = 0.0565, wR2 = 0.1274
R indices all data	R 1 = 0.0535, wR2 = 0.0893	R 1 = 0.1113, wR2 = 0.1671
GooF	1.035	0.819

---

Magnetic characterization. Temperature and field-dependent direct current (DC) magnetic measurements were performed using a Quantum Design MPMS SQUID magnetometer. Raw data were processed to remove the sample holder contribution and corrected for sample diamagnetism using Pascal's constants.

Alternating current (AC) magnetic susceptibility characterization was conducted using Quantum Design PPMS and Quantum Design SQUID magnetometers, in the ranges of 10 Hz to 10 kHz and 0.02 Hz to 1 kHz, respectively. The AC data were analysed using a code that was previously described.⁵⁰ To prevent field-induced orientation of the crystallites, powders were analysed as pressed pellets.

Electron paramagnetic resonance (EPR) spectroscopy. X-band (ν ≈ 9.40 GHz) EPR spectra on microcrystalline powder samples of Y-Co, Eu-Co and Dy-Co were recorded using a Bruker Elexsys E500 spectrometer equipped with an SHQ cavity and an ESR900 continuous flow helium cryostat (Oxford Instruments) to achieve low temperatures.

3 Results and discussion

3.1 Synthesis

The three ionic complexes [Co(hfa)₃]⁻[Dy(hfa)₂tetraglyme]⁺, [Co(hfa)₃]⁻[Eu(hfa)₂tetraglyme]⁺ and [Co(hfa)₃]⁻[Y(hfa)₂tetraglyme]⁺ have been synthesized through a single step procedure using metal acetates in a ratio of 1 : 1, hexafluoroacetylacetone (Hhfa) and polyether tetraethylene glycol dimethyl ether (tetraglyme) as reagents, in dichloromethane following the general reaction (RE = Dy, Eu and Y):

This single step synthetic strategy uses commercially available chemicals and provides a reaction yield in the 80–88% range. Therefore, it represents an easy and low-cost strategy to produce this type of bimetallic complex. An excess of the two metal acetates promotes easy isolation of the adducts, as the acetate excess is insoluble and thus easily filterable. The obtained complexes present good solubility in acetone, dichloromethane and ethanol and are less soluble in non-polar solvents, such as pentane and hexane. The synthetic procedure described produces three water-free coordination compounds Dy-Co, Eu-Co and Y-Co.

3.2 XRD single-crystals of Eu-Co and Y-Co

Crystals of both complexes were grown through low temperature solvent evaporation of their own supersaturated solution. In Fig. 1 an Ortep-3 view of the asymmetric units of Eu-Co (top) and Y-Co (bottom) is reported.

Fig. 1 Ortep view of the asymmetric unit of Eu-Co (top) and Y-Co (bottom) and the corresponding labelling scheme of the metal cation and donor atoms. Thermal ellipsoids are shown at 30% probability. Hydrogen and fluorine atoms have been omitted for the sake of clarity.

In both structures the asymmetric unit contains one [Co(hfa)₃]⁻ anion and one [RE(hfa)₂tetraglyme]⁺ cation. In Table S1† the M–X distances and X–M–Y angles are reported. The two compounds are almost isomorphous (see Table 1) and isostructural (see Fig. 2 and Table S1†). The rare-earth metal ion in the [RE(hfa)₂·tetraglyme]⁺ cation is nine-coordinated, being the donor atoms the five oxygen atoms of one tetraglyme molecule and the oxygen atoms of two hfa⁻ anions. The coordination geometry around RE can be best described as a distorted capped square-antiprism,⁵⁸ with the oxygen atom O5 capping the face defined by the atoms O1D, O2E, O4 and O6 (see Fig. S1†). The tetraglyme molecule adopts a conventional geometry with anti and gauche relationships around C–O and C–C bonds, respectively. The cobalt(II) ion is hexacoordinated by the oxygen atoms of the three hfa⁻ anions and the resulting coordination polyhedron is an octahedron (see Fig. S2†).⁵⁹ This coordination geometry is typical for this anion as proved by the results of a search performed by using the Cambridge Structural Database,⁶⁰ where 12 structures containing the [Co(hfa)₃]⁻ anion, all with the same coordination geometry, have been found. The Co–O distances are in the 2.058(2)–2.074(2) Å range (see Table S1†) and no evidence of Jahn–Teller distortion is present. Finally, these distances were compared with the ones found in the above cited 12 structures. The analysis of the crystal packing of both compounds, shown in Fig. 3, evidences the presence of planes containing [RE(hfa)₂·tetraglyme]⁺ cations and perpendicular to the b axis, which are alternated to planes containing [Co(hfa)₃]⁻ anions. No close intermolecular contacts between the ions, within the plane or between planes, are observed.

Fig. 2 (a) Superimposition of the [Co(hfa)₃]⁻ anion in Eu-Co (ball and stick, pale blue) and Y-Co (stick, orange). (b) Superimposition of the [RE(hfa)₂·tetraglyme]⁺ cation in Eu-Co (ball and stick, pale blue) and Y-Co (stick, orange).

Fig. 3 Crystal packing of Y-Co view along the a (left) and the c (right) crystallographic axes. The [Y(hfa)₂·tetraglyme]⁺ cations are reported in blue, while the [Co(hfa)₃]⁻ anions are in magenta.

No single crystals were obtained for Dy-Co, and thus its powder X-ray diffraction (PXRD) pattern has been compared with the theoretical patterns derived from the refined structures of Eu-Co and Y-Co (Fig. 4). In addition, the powder pattern of Dy-Co has been compared with the Eu-Co and Y-Co experimental powder patterns (Fig. S3†). The good comparison among the patterns of the three compounds points to the isostructural nature of Dy-Co with respect to Eu-Co and Y-Co.

Fig. 4 PXRD patterns of Dy-Co (black, experimental), Eu-Co (red, simulated) and Y-Co (blue, simulated).

This observation is supported by similar FT-IR data (Fig. S4†) and the comparable thermal behaviour of the three complexes. FT-IR has been employed to evaluate the ligand and co-ligand coordination of the two metal centres. Fig. S4† shows the FT-IR spectra of the three complexes. In all the spectra, the nujol peaks are present at around 2923 cm⁻¹, 2854 cm⁻¹, 1461 cm⁻¹ and 1373 cm⁻¹. In addition, the 2900 cm⁻¹ peak is linked to the stretching of –CH groups of tetraglyme, but it is overlapped to the nujol band. Coordination of tetraglyme is supported by the peaks observed in the range 1000–800 cm⁻¹.⁵⁰ The peaks visible in the range 1580–1660 cm⁻¹ are due to the stretching of C=C and C=O. In the range 1350–1000 cm⁻¹ the peaks are caused by the stretching of carbon–fluorine bonds of the β-diketonate ligand, overlapped with other peaks related to the carbon–oxygen bonds of polyether.⁶¹

3.3 Magnetic and electron paramagnetic resonance (EPR) spectroscopy characterization

The determination of the relevant magnetic interactions in systems containing one or more paramagnetic centres with unquenched orbital angular momentum, such as lanthanide ions,⁶² high spin cobalt(II)⁶³ or low spin iron(III),⁶⁴ presents a major challenge since the use of a simple Heisenberg Hamiltonian to model the exchange-coupling and of a second order zero field splitting Hamiltonian to model anisotropy is usually not appropriate.⁶⁵ For these reasons, a semiquantitative approach is often pursued, wherein single ion anisotropy effects are evaluated in isostructural systems only containing a single anisotropic ion.^66,67 Following this approach we tried to rationalize the magnetic properties of Dy-Co and Eu-Co by comparing them to the single ion properties of cobalt(II) observed in Y-Co.

As a first step we performed low-temperature (T = 10 K) X-band (ν ≈ 9.40 GHz) EPR spectroscopy on powder samples of the three compounds, which can provide information on the ground state of the cobalt(II) moiety and on the validity of the assumption of the same electronic structure for this ion in the three different derivatives. Their EPR spectra (Fig. 5) are all characterized by a broad and partially structured absorption centred at around 175 mT and covering a similar field range. The Dy-Co spectrum is the broadest one, while Eu-Co and Y-Co are much more resolved, and very similar to each other. The broader line for the dysprosium(III) derivative can be attributed to the stronger dipolar interactions in this derivative than in the other two. Indeed, yttrium(III) is diamagnetic and europium(III) is only weakly paramagnetic (⁷F₀ ground multiplet) at low temperature, while dysprosium(III) is strongly paramagnetic (⁶H_15/2 ground multiplet). Thus, the comparison of the EPR spectra of the three derivatives confirms the invariance of the electronic structure of the cobalt(II) moiety in the three derivatives. Given the more resolved features of the Y-Co spectrum, we carried out a more detailed analysis on this one. The spectrum is typical of a rhombic effective doublet with a highly anisotropic g tensor, where each transition is split into two distinct components. This splitting can be attributed to the anisotropic dipolar interactions between nearest-neighbour cobalt centres. Following this interpretation, the spectrum was simulated⁶⁸ considering the spin-Hamiltonian reported in eqn (1).

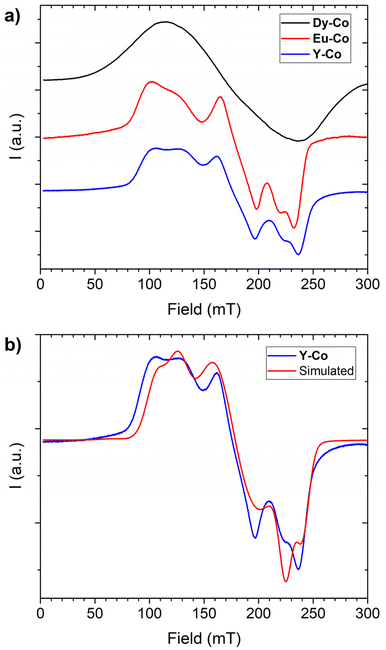Fig. 5 EPR spectra acquired at 10 K on powders of the three investigated derivatives (a). Comparison between the experimental spectrum of Y-Co and the one simulated using Hamiltonian shown in eqn (1) and best-fit parameters reported in the main text (b).

Here represents the components of the effective g tensor of the ground doublet S′ of the cobalt(II), arising as a combined effect of spin–orbit coupling and low-symmetry distortion of the ligand field, while J_α is the component of the effective dipolar interaction acting between two centres. For the sake of simplicity, we assumed the g tensors of the two interacting doublets to be collinear among them and with the dipolar interaction in principal directions. The best simulation of the experimental spectrum was obtained using anisotropic broadening of the linewidth and the following parameters:

The temperature dependence of χ_MT acquired at 0.1 T for all the investigated complexes is reported in Fig. 6a. At room temperature, the Y-Co complex exhibits a χ_MT value (∼3.4 emu K mol⁻¹) significantly higher than the spin-only expected value (∼1.875 emu K mol⁻¹ for an S = 3/2 with g = 2.00); this can be traced back to a large magnetic contribution of the unquenched orbital momentum of cobalt(II) in a pseudo-octahedral environment. Upon lowering the temperature, the χ_MT value monotonously decreases to reach 1.90 emu K mol⁻¹ at 2 K. This behaviour can be attributed to the thermal depopulation of the excited doublets of the cobalt(II) ions arising from the splitting of the ⁴T_1g ground state in octahedral geometry, induced by low symmetry components of the ligand field and spin–orbit coupling. We note here that the χ_MT values at both room and low temperatures are considerably higher than those previously reported for the same molecular unit in the Et₄N[Co^II(hfa)₃] complex (∼2.78 and ∼1.60 emu K mol⁻¹, respectively).⁶⁹ Furthermore, the rhombic g values of the Co(II) centre, derived from our comprehensive analysis of the low-temperature EPR spectrum of the Y-Co derivative, suggest an electronic structure different from the one previously reported for Et₄N[Co^II(hfa)₃].⁶⁹ Although the Co(II) distortions from the octahedron as calculated using SHAPE (see Table S2†) are similar for the two compounds, with values of 0.169 for Et₄N[Co^II(hfa)₃] and 0.181 for Y-Co, a comprehensive structural analysis of the coordination environments in the two complexes reveals significant differences (see Fig. S5 and Table S3†). In the case of the Et₄N[Co^II(hfa)₃] complex, a distinct compression of the octahedron is evident along the O3–Co1–O6 direction, with bond lengths being similar for Co–O bonds in trans positions (i.e. for oxygens belonging to different hfa⁻ ligands). In contrast, the Y-Co derivative does not exhibit a discernible compression direction, and the bond lengths are comparable for Co–O bonds in cis positions (i.e., for oxygens belonging to the same hfa⁻ ligand).

Fig. 6 (a) Experimental χ_MT vs. T curve of Y-Co, Dy-Co and Eu-Co and the best fit (continuous line) obtained for Y-Co using the parameters and model reported in the text. (b) Difference between the experimental χ_MT vs. T curve of Dy-Co and Eu-Co and the simulated one for Y-Co. The corresponding best fit to the Eu³⁺ single ion is reported as a continuous line.

The electronic structure of distorted octahedral Co(II) complexes can be described using the Figgis–Griffith Hamiltonian,⁷⁰ reported in eqn 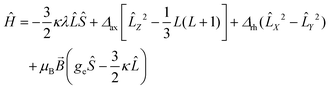(2).

In order to gain a deeper insight into the electronic structure of the Co(II) moiety, we simultaneously fitted the DC magnetometry data and the values of the g factor derived from the EPR analysis using eqn (2) leaving κ, λ, Δ_ax, and Δ_rh as free parameters. The fit was conducted using a custom-written MATLAB script based on the EASYSPIN toolkit and the fminuit minimization routine (see ESI, Note S1† for more details).^71,72 The best-fit parameters obtained are as follows: κ = 1.00 ± 0.01, λ = 122.6 ± 0.2 cm⁻¹, Δ_ax = 100.2 ± 0.1 cm⁻¹, and Δ_rh = 99.8 ± 0.1 cm⁻¹.

The simulated χ_MT for the Y-Co derivative is reported in Fig. 6 while the simulated values of the g factor are: g_x = 4.03, g_y = 5.81 and g_z = 2.87, in good agreement with the values obtained experimentally by EPR.

The magnetic properties of the cationic lanthanide component can be in principle determined from the Dy-Co and Eu-Coχ_MT curves by subtracting the magnetic signal due to the cobalt(II) unit, since we determined by EPR that the magnetic properties of the anion are essentially the same in the three complexes.

Fig. 6b displays the χ_MT curves of Dy-Co and Eu-Co after removing the simulated curve for the Co(hfa)₃⁻ unit. Notably, the resulting room temperature χ_MT value of Dy-Co is close to the expected free-ion value for a dysprosium(III) ion (⁶H_15/2, g_J = 4/3, and χ_MT_free-ion = 14.16 emu K mol⁻¹). Lowering the temperature induces a progressive depopulation of the highest lying levels in the J = 15/2 multiplet, split by the crystal field surrounding the dysprosium(III) centre.

As for the Eu-Co compound, the resulting curve aligns with the expectations for the dominant temperature-independent paramagnetism expected for a europium(III) ion. Additionally, the obtained experimental χ_MT curve for the europium(III) centre could be fairly well reproduced (see Fig. 6b) considering a spin–orbital coupling factor λ_Eu equal to 315 cm⁻¹, which is in line with expectations for Eu(III).¹

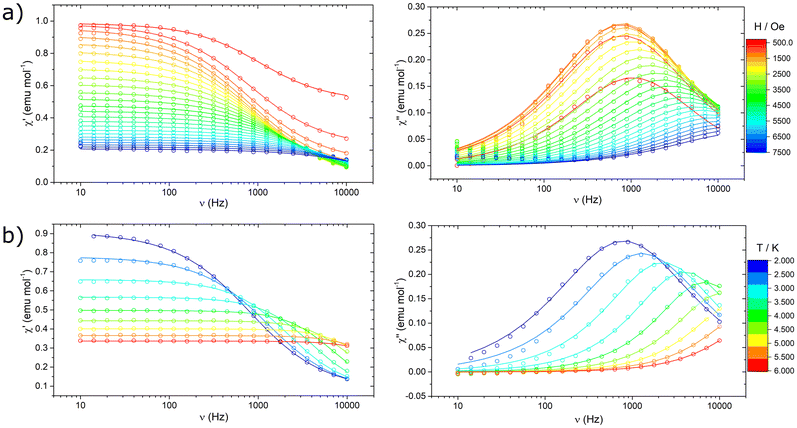
The Y-Co and Dy-Co derivatives were further characterized through ac susceptibility measurements to determine the role of the two coordination units, and possibly their interactions, in magnetization relaxation processes. Experiments were conducted (Fig. 7 and 8) with varying applied magnetic fields (0–7.5 kOe), temperatures (2–30 K), and frequencies (0.02 Hz–10 kHz). To investigate the relaxation dynamics of the cobalt(II) unit we began our investigation with the Y-Co complex. As already reported for the NEt₄⁺ derivative of Co(hfa)₃⁻, in the absence of an external magnetic field, no out-of-phase susceptibility signal (χ′′) could be detected for this complex. However, upon application of a dc magnetic field, a clear peak in the imaginary component of the susceptibility, plotted as a function of frequency, can be observed. As the strength of the applied magnetic field increases, the χ′′ value for the maximum of this peak increases, while remaining located at the same frequency, and reaches the highest value around 1.2 kOe (Fig. 7a). Upon further increasing the applied magnetic fields, the peak shifts towards higher frequencies and becomes unmeasurable for our setup for H > 7.5 kOe. The temperature dependence of this process was then measured at an optimal magnetic field of 1.2 kOe (Fig. 7b). The magnetization relaxation time was obtained by simultaneous fitting of the experimental data using a generalized Debye model with a single contribution.⁵⁰ The obtained field dependence of the relaxation time (Fig. 9a) was then rationalised by fitting the experimental data with eqn (3). This equation includes two field-assisted relaxation processes: the quantum tunnelling of magnetisation (QTM) and the direct process.⁷³ The field dependence of the direct process is modelled as a magnetic field phenomenological power law.

Fig. 7 Frequency dependence of the real (left) and the imaginary (right) component of the magnetic susceptibility for the Y-Co derivative: (a) as a function of the external magnetic field at a temperature of 2 K; (b) as a function of temperature in an external field of 1.2 kOe. Lines represent the best fit obtained through a generalized Debye model assuming a single contribution.

Fig. 8 Frequency dependence of the real (left) and the imaginary (right) component of the magnetic susceptibility for the Dy-Co derivative: (a) as a function of temperature in a zero-external field; (b) as a function of the external magnetic field at a temperature of 2 K; and (c) as a function of temperature in an external field of 2.1 kOe. Lines represent the best fit obtained using a generalized Debye model assuming one single contribution (a and 0 T data in b) and two different contributions (b, c).

Fig. 9 Extracted magnetic relaxation times of Y-Co (a and b) and Dy-Co (c and d). Lines represent the best fit curves using models reported in the text and best fit parameters of Table 2.

Table 2 reports the best-fit values, indicating dynamics characterized by a field-independent QTM process at very low fields and by a direct process in the high-field regime. The obtained exponential value m is consistent with the magnetic field dependence expected for a direct process.^73–75 The temperature dependence (Fig. 9b) was modelled by including a thermally-assisted Raman process in the previous model. In particular, a temperature dependent phenomenological power law (eqn (4)) was considered:

τ_RAMAN⁻¹ = CTⁿ (4)

Table 2 Best-fit parameters for magnetic relaxation times of Y-Co and Dy-Co. Parameters indicated with * have not been varied through the fitting procedure. (a), (b) and (c) refer to the panels of Fig. 9

		B 1 (s^−1)	B 2 (Oe^−2)	a (s^−1 Oe^−m K^−1)	m	C (s^−1 K^−n)	n
Y-Co	(a)	(6.2 ± 1.0) × 10^3	0	(1.5 ± 0.2) × 10^−10	3.78 ± 0.12	—	—
	(b)	6172*	0*	1.5 × 10^−10*	3.78*	50.9 ± 7.2	4.7 ± 0.1
Dy-Co	(c)	(24.3 ± 0.5) × 10^3	—	—	—	(2.5 ± 1.3) × 10^−9	9.4 ± 0.1

---

To prevent over-parametrization of the model due to the low number of experimental points, the parameters of QTM and the direct process were fixed to those obtained from the in-field dependence. Best-fit values are reported in Table 2. The Raman process for a half-integer spin is theoretically expected to follow a T⁹ power law.⁷⁶ However, experimental results for cobalt(II) complexes commonly show a much weaker dependence, with exponents ranging from 3 to 6.⁷⁷

We notice here that the observed field dependence of the magnetization relaxation rate is remarkably different, both qualitatively and quantitatively, from that reported for the same unit in ref. 69. Indeed, for the Et₄N[Co^II(hfa)₃] complex two distinct magnetic field dependent relaxation processes were distinguishable, whereas for Y-Co only one is detectable. This suggests that the counterion and the packing play a key role in defining the magnetic relaxation dynamics. Regarding the temperature dependence of the relaxation dynamics, it is important to note that the experiments on the two complexes were performed in different static magnetic fields (1 kOe for Et₄N[Co^II(hfa)₃] and 1.2 kOe for Y-Co), making a direct comparison not completely meaningful.

Nonetheless, the extracted experimental relaxation times are reasonably comparable in magnitude. On the other hand, at variance with the interpretation given in ref. 69, we did not include an Orbach process in our modelling. Indeed, using the Hamiltonian described in eqn (2) and the parameters obtained by the fitting procedure leads to a first excited state lying at approximately 195 cm⁻¹. At the low temperature investigated, such a high energy barrier hinders the Orbach process from actively contributing to relaxation. The Dy-Co complex exhibited a completely different behaviour. In zero external magnetic field and T = 2 K, a single peak centred around 3 kHz is observed in the χ(ν)′′ plot (Fig. 8a). This relaxation process is absent in the Y-Co derivative, and can be attributed unambiguously to the contribution of the dysprosium(III) containing cation. The position of the maximum is temperature-independent up to 10 K, but it becomes strongly temperature-dependent above this temperature (Fig. 8a). The application of an external magnetic field suppresses the aforementioned process, promoting the growth of a second process at lower frequencies (Fig. 8b); however, at intermediate fields, the relative contribution of the two processes cannot be disentangled. At fields higher than 2 kOe, two distinct processes can be identified: one occurring above 1 kHz and the other at frequencies lower than 10 Hz. The thermal dependence of these two processes (Fig. 8c) was studied in a range of 0.02 Hz to 10 kHz in an external magnetic field of 2.1 kOe. The fast relaxation process rapidly becomes unmeasurable with our experimental setup, while the slow relaxation process can be followed up to 30 K. In order to extract the magnetization relaxation time of the Dy-Co complex, the experimental data were fitted using a generalized Debye model including either a single contribution (thermal dependence in a zero field) or two different contributions (field dependence and thermal dependence in a non-zero field).⁵⁰

The resulting temperature and field dependencies of the relaxation times are reported in Fig. 9c and d, respectively. In zero-field, a field-independent QTM process (i.e. B₂ = 0 in eqn (3)) can successfully model the dynamics at low temperatures, while a Raman process can rationalize the observed behaviour at higher temperatures. The obtained best-fit values (Table 2) show a very strong temperature dependence for the Raman process (n ca. 9), in agreement with expectations for lanthanide-based systems.⁷⁸ Modelling the in-field thermal dependence of the two processes is far more challenging. In particular, the temperature dependence of the low frequency relaxation time τ₁ is, to the best of our knowledge, hitherto unreported for systems with S > 1/2,⁷⁹ with three regions of different slopes observed in the log–log plot of τ₁(T) (Fig. 9d). These different slopes suggest that the spin–lattice relaxation is dominated by different thermally assisted processes. Despite the difficulty in making a direct comparison between the in-field relaxation of the two complexes, due to the differing intensities of the applied static magnetic field, it is possible to exploit the comparison to gain some insight. As illustrated in Fig. S6,† the relaxation times extracted for Y-Co are found to be consistent with the relaxation times τ₂ extracted for Dy-Co. This result suggests that the two relaxation dynamics observed for Dy-Co may originate from the two magnetic centres, dysprosium(III) for τ₁ and cobalt(II) for τ₂. In this respect, the differences in the temperature dependent behaviour (Fig. S6†), observed for the cobalt(II) based processes in the two compounds could be related to different dipolar interactions. The high frequency relaxation, denoted as τ₂, exhibits two distinct linear trends that may suggest two different regimes. However, due to the limited number of temperature dependent data, it is not possible to obtain physically meaningful models for the two relaxation dynamics and thus derive more accurate information on the effect of dipolar interactions.

3.4 Optical properties

The optical properties of the adducts have been investigated through UV-Vis and photoluminescence spectroscopy. Solutions in dichloromethane of the three complexes at concentrations 2.5 × 10⁻⁶ mol L⁻¹ have been analysed in the range 200–700 nm at room temperature (Fig. 10). All the complexes present the same band at 300 nm (33 333 cm⁻¹), associated with the lowest energy spin-allowed π–π* intraligand (IL) transition of the hfa⁻ chelate rings.^80–82 In order to register the UV-Vis cobalt bands, more concentrated solutions, 2.5 × 10⁻³ mol L⁻¹, have been used and analysed in the range 450–650 nm. All the complexes present bands at 510 nm (19 607 cm⁻¹) and 550 nm (18 182 cm⁻¹). These findings are in accordance with the octahedral coordination of the [Co(hfa)₃]⁻ anion observed through single-crystal X-ray structure and magnetic characterization. The anionic part [Co(hfa)₃]⁻ belongs to the D₃ point group symmetry,^83,84 but considering strictly the immediate coordinating atoms, namely the six oxygens, O_h symmetry may be assumed. Considering the weak field type hfa ligand,^85–87 and the above-reported magnetic investigation which unequivocally points to a high-spin configuration, the left side of the Tanabe–Sugano diagram for a d⁷ ion has been used to interpret the spectra. Hence, the two bands at around 510 nm and around 550 nm may be assigned to the ⁴T_1g(F) → ⁴T_1g(P) and the ⁴T_1g(F) → ⁴A_2g(F) transitions. The very low ε values observed for these bands confirm the not allowed d–d transition nature of the bands, while the intra-ligand π–π* band has a very high ε value, as expected for this type of transition (Table 3).

Fig. 10 UV-Vis spectra of Dy-Co (a), Eu-Co (b) and Y-Co (c) complexes in CH₂Cl₂ at room temperature. Insets show the details of the region where the d–d transitions occur and their assignment.

Table 3 Data of the UV-Vis spectra of Dy-Co, Eu-Co and Y-Co

	Dy-Co	Eu-Co	Y-Co
	ε (L mol^−1 cm^−1)	ε (L mol^−1 cm^−1)	ε (L mol^−1 cm^−1)
λ = 510 nm	53.74	89.59	49.94
λ = 540–550 nm	45.64	74.53	41.58
λ = 300 nm	422 796	347 423	443 324

---

Luminescence spectra of the three complexes have been recorded at room temperature in dichloromethane solutions with 10⁻² mol L⁻¹ concentrations. For Y-Co and Dy-Co complexes emission spectra have been recorded using a 310 nm excitation source, in the emission range of 350–600 nm, while Eu-Co complex emission spectra have been recorded using a 390 nm excitation source, in the emission range of 450–750 nm.

In Fig. 11 the emission spectra of the complexes are shown. For the Dy-Co complex there are two emission bands of 4f dysprosium electrons,^50,88 the most intense is located in the yellow region of the spectrum at 575 nm (17 391 cm⁻¹) and is due to ⁵F_9/2 → ⁶H_13/2 transition, while the weaker one is in the blue region at 485 nm (20 619 cm⁻¹) and is due to ⁵F_9/2 → ⁶H_15/2 transition. Being the intensity of the solution emission spectrum of Dy-Co very low, the solid-state spectrum has been recorded. The luminescence spectra of the solution and solid state are quite similar except for the different intensities (Fig. S7†).

Fig. 11 Emission spectra obtained with the reported wavelength excitation for Dy-Co (a), Eu-Co (b) and Y-Co (c) complexes. Spectra recorded at room temperature in CH₂Cl₂ solutions.

For the Eu-Co complex there are five emission bands assigned to the following relaxation transitions of 4f europium electrons:⁸⁹ one low intensity band, in the green region at 537 nm (18 622 cm⁻¹), due to the ⁵D₁ → ⁷F₁ transition and two slightly more intense bands, in the yellow region at 580 nm (17 241 cm⁻¹) and 593 nm (16 863 cm⁻¹), due to the ⁵D₀ → ⁷F₀ and ⁵D₀ → ⁷F₁ transitions, respectively. The most intense band is located in the orange-red region at 615 nm (16 260 cm⁻¹) and is due to ⁵D₀ → ⁷F₂, while the weakest band, located in the red region at 654 nm (15 291 cm⁻¹), is due to ⁵D₀ → ⁷F₃.

The asymmetry ratio R, i.e. the ratio between the integrated areas of the ⁵D₀ → ⁷F₂ and ⁵D₀ → ⁷F₁ electronic transitions, with a value of 13.8, indicates that the Eu³⁺ ion occupies a low symmetry environment,⁸⁷ similarly to the coordination observed in [Eu(hfa)₃(1,10-phenanthroline)].⁹⁰ This feature is also supported by the presence of the band at 580 nm associated with the ⁵D₀–⁷F₀ singlet-to-singlet transition and it finds its counterpart in the Eu³⁺ coordination observed in single crystal X-ray diffraction, which points to a distorted capped square-antiprism, i.e. a highly asymmetric environment. As expected, Y-Co does not present any emission, since yttrium does not have 4f electrons.

3.5 Thermal properties

Good thermal properties in terms of thermal stability and volatility would allow the possibility of depositing these molecules through vapor phase processes on suited substrates.

Thus, the thermal behaviour of the three complexes has been studied by thermogravimetric analysis (TGA) and differential scanning calorimetry (DSC). Fig. 12 reports the overlap of TGA curves of the three complexes, evidencing that all the complexes present a similar thermal behaviour, characterized by a single step weight loss in the range 195–300 °C with a percentage residue lower than 8%.

Fig. 12 TGA curves of Dy-Co (black), Eu-Co (red) and Y-Co (blue) complexes.

In particular, the Dy-Co and Eu-Co complexes (black and red curves, respectively) present a single step weight loss in the range 200–300 °C with residue percentages of 7.4% and 6.9% at 350 °C, respectively. The Y-Co complex (blue curve) presents a single step weight loss in the range 195–280 °C, with a residue percentage of 2.1% at 350 °C. Fig. 13 reports the DSC analyses of the three complexes. The DSC curves of the complexes show two endothermic peaks. The first peak, occurring at 133 °C (Dy-Co), 147 °C (Eu-Co), and 123 °C (Y-Co), is attributed to the melting of the complex, matching the melting range observed for the three derivatives with a Kofler microscope. Finally, the second peak at 310 °C (Dy-Co), 307 °C (Eu-Co), and 311 °C (Y-Co) is assigned to the vaporization of the complexes.

Fig. 13 DSC curves of Dy-Co (black), Eu-Co (red) and Y-Co (blue) complexes.

In summary, all three heterobimetallic complexes under study have excellent properties in terms of thermal stability and volatility and this is a very intriguing issue considering their ionic nature.

4 Conclusions

In this comprehensive investigation, we have provided a detailed examination of heterobimetallic complexes featuring an ionic structure with cobalt(II) ions octahedrally coordinated by three hfa⁻ ligands and the dysprosium(III), europium(III) or yttrium(III) ions coordinated by two hfa⁻ and one tetraglyme ligands. Electron paramagnetic resonance (EPR) spectroscopy allowed us to characterize the magnetic ground state of the cobalt(II) anionic moiety, whereas temperature-dependent magnetic susceptibility measurements pointed out that the interionic magnetic interactions do not play a major role in determining the static properties of these complexes. In terms of the dynamic properties, the presence of more than one magnetic centre provided interesting results, with the dysprosium(III) derivative evidencing an extremely rich behaviour. Optical studies provided valuable insights into the electronic transitions within the complexes, with distinct UV-Vis absorption and luminescence emission bands observed. Luminescence spectra of dysprosium(III) and europium(III) derivatives exhibited characteristic emission bands in the yellow and red regions, respectively. The thermal analysis demonstrated exceptional thermal stability and volatility properties of the investigated compounds, suggesting potential applications in vapor-phase processes for depositing these molecules onto suitable substrates. These results not only broaden the understanding of the fundamental properties of heterobimetallic complexes, but also hold promise for applications in molecular magnetism, optoelectronics, and materials science. The intriguing behaviour observed in these ionic complexes offers opportunities for the development of novel functional materials and devices with tailored magnetic, optical, and thermal properties.

Author contributions

Matteo Bombaci: investigation, formal analysis and writing – original draft. Anna Lucia Pellegrino: validation, data curation, and writing – review and editing. Francesca Lo Presti: investigation and data curation. Martina Lippi: investigation. Patrizia Rossi: methodology and validation. Leonardo Tacconi: investigation, data curation, and writing. Lorenzo Sorace: methodology, validation, and writing – review and editing. Graziella Malandrino: supervision, funding acquisition and writing – review and editing.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

M. B., F. L. P. and G. M. thank the European Union (NextGeneration EU) for financial support through the MUR-PNRR project SAMOTHRACE (ECS00000022). A. L. P. thanks the Ministero dell'Università e della Ricerca within the PON “Ricerca e Innovazione” 2014-2020 Azioni IV.4 program. The authors thank Bionanotech Research and Innovation Tower (BRIT) Laboratory of the University of Catania (Grant no. PONa3_00136 financed by the Italian Ministry for Education, University and Research, MIUR) for the diffractometer facility. L. S. and L. T. acknowledge the support from MUR through Progetto Dipartimenti di Eccellenza 2023–2027 (CUP B97G22000740001–DICUS 2.0).

References

1. O. Kahn, Molecular magnetism, Wiley-VCH, New York (N.Y.), 1993.
2. M. Atzori and F. Artizzu, Functional Molecular Materials: An Introductory Textbook, Jenny Stanford Publishing, New York, 2018.
3. Multifunctional Molecular Materials, ed. L. Ouahab, Jenny Stanford Publishing, New York, 2013.
4. R. Marin, G. Brunet and M. Murugesu, Angew. Chem., Int. Ed., 2021, 60, 1728–1746.
5. J.-C. G. Bünzli, Trends Chem., 2019, 1, 751–762.
6. Lanthanides and Actinides in Molecular Magnetism, ed. R. A. Layfield and M. Murugesu, Wiley, 1st edn, 2015.
7. C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Nature, 2017, 548, 439–442.
8. F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Science, 2018, 362, 1400–1403.
9. C. A. Gould, K. R. McClain, D. Reta, J. G. C. Kragskow, D. A. Marchiori, E. Lachman, E.-S. Choi, J. G. Analytis, R. D. Britt, N. F. Chilton, B. G. Harvey and J. R. Long, Science, 2022, 375, 198–202.
10. N. Ishikawa, M. Sugita, T. Ishikawa, S. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694–8695.
11. A. Raza and M. Perfetti, Coord. Chem. Rev., 2023, 490, 215213.
12. D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110–5148.
13. C. Benelli and D. Gatteschi, Introduction to molecular magnetism: from transition metals to lanthanides, Wiley-VCH, Weinheim, 2015.
14. J. Tang and P. Zhang, Lanthanide Single Molecule Magnets, Springer, Berlin Heidelberg, 2015.
15. D. Gatteschi, R. Sessoli and J. Villain, Molecular Nanomagnets, 2006, vol. 376.
16. L. Sorace, C. Benelli and D. Gatteschi, Chem. Soc. Rev., 2011, 40, 3092–3104.
17. J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078–2085.
18. S. Tripathi, A. Dey, M. Shanmugam, R. S. Narayanan and V. Chandrasekhar, in Organometallic Magnets, ed. V. Chandrasekhar and F. Pointillart, Springer International Publishing, Cham, 2019, pp. 35–75.
19. Y. Rechkemmer, F. D. Breitgoff, M. van der Meer, M. Atanasov, M. Hakl, M. Orlita, P. Neugebauer, F. Neese, B. Sarkar and J. van Slageren, Nat. Commun., 2016, 7, 10467.
20. L. Rigamonti, N. Bridonneau, G. Poneti, L. Tesi, L. Sorace, D. Pinkowicz, J. Jover, E. Ruiz, R. Sessoli and A. Cornia, Chem. – Eur. J., 2018, 24, 8857–8868.
21. S. T. Liddle and J. van Slageren, Chem. Soc. Rev., 2015, 44, 6655–6669.
22. E. Lucaccini, L. Sorace, M. Perfetti, J.-P. Costes and R. Sessoli, Chem. Commun., 2014, 50, 1648–1651.
23. J. M. Zadrozny, M. Atanasov, A. M. Bryan, C.-Y. Lin, B. D. Rekken, P. P. Power, F. Neese and J. R. Long, Chem. Sci., 2012, 4, 125–138.
24. S. K. Singh, M. F. Beg and G. Rajaraman, Chem. – Eur. J., 2016, 22, 672–680.
25. T. Gupta, M. F. Beg and G. Rajaraman, Inorg. Chem., 2016, 55, 11201–11215.
26. A. Dey, J. Acharya and V. Chandrasekhar, Chem. - Asian J., 2019, 14, 4433–4453.
27. S. K. Langley, D. P. Wielechowski, V. Vieru, N. F. Chilton, B. Moubaraki, B. F. Abrahams, L. F. Chibotaru and K. S. Murray, Angew. Chem., Int. Ed., 2013, 52, 12014–12019.
28. D. Gatteschi, R. Sessoli and L. Sorace, in Handbook on the Physics and Chemistry of Rare Earths, ed. J.-C. G. Bünzli and V. K. Pecharsky, Elsevier, 2016, vol. 50, pp. 91–139.
29. F. Varga, C. Rajnák, J. Titiš, J. Moncol and R. Boča, Dalton Trans., 2017, 46, 4148–4151.
30. C. Rajnák, F. Varga, J. Titiš, J. Moncol and R. Boča, Inorg. Chem., 2018, 57, 4352–4358.
31. M. S. De Souza, M. Briganti, S. G. Reis, D. Stinghen, C. S. Bortolot, R. A. A. Cassaro, G. P. Guedes, F. C. Da Silva, V. F. Ferreira, M. A. Novak, S. Soriano, F. Totti and M. G. F. Vaz, Inorg. Chem., 2019, 58, 1976–1987.
32. J.-C. G. Bünzli, Chem. Rev., 2010, 110, 2729–2755.
33. R. M. Duke, E. B. Veale, F. M. Pfeffer, P. E. Kruger and T. Gunnlaugsson, Chem. Soc. Rev., 2010, 39, 3936–3953.
34. E. G. Moore, A. P. S. Samuel and K. N. Raymond, Acc. Chem. Res., 2009, 42, 542–552.
35. A. Beeby, S. W. Botchway, I. M. Clarkson, S. Faulkner, A. W. Parker, D. Parker and J. A. G. Williams, J. Photochem. Photobiol., B, 2000, 57, 83–89.
36. J.-C. G. Bünzli and S. V. Eliseeva, J. Rare Earths, 2010, 28, 824–842.
37. D. Kovacs and K. E. Borbas, Coord. Chem. Rev., 2018, 364, 1–9.
38. H. Xu, Q. Sun, Z. An, Y. Wei and X. Liu, Coord. Chem. Rev., 2015, 293–294, 228–249.
39. J. H. Van Vleck, J. Phys. Chem., 1937, 41, 67–80.
40. A. D'Aléo, F. Pointillart, L. Ouahab, C. Andraud and O. Maury, Coord. Chem. Rev., 2012, 256, 1604–1620.
41. F. Pointillart, B. le Guennic, O. Cador, O. Maury and L. Ouahab, Acc. Chem. Res., 2015, 48, 2834–2842.
42. H. Douib, J. F. Gonzalez, S. Speed, V. Montigaud, B. Lefeuvre, V. Dorcet, F. Riobé, O. Maury, A. Gouasmia, B. L. Guennic, O. Cador and F. Pointillart, Dalton Trans., 2022, 51, 16486–16496.
43. G. Novitchi, J. Costes and B. Donnadieu, Eur. J. Inorg. Chem., 2004, 2004, 1808–1812.
44. G. Novitchi, S. Shova, A. Caneschi, J.-P. Costes, M. Gdaniec and N. Stanica, Dalton Trans., 2004, 1194–1200.
45. S. Osa, T. Kido, N. Matsumoto, N. Re, A. Pochaba and J. Mrozinski, J. Am. Chem. Soc., 2004, 126, 420–421.
46. H.-B. Xu, Y.-T. Zhong, W.-X. Zhang, Z.-N. Chen and X.-M. Chen, Dalton Trans., 2010, 39, 5676.
47. X. Lü, W. Feng, Y. Hui, T. Wei, J. Song, S. Zhao, W. Wong, W. Wong and R. A. Jones, Eur. J. Inorg. Chem., 2010, 2010, 2714–2722.
48. S. Singaravadivel, E. Babu, M. Velayudham, K.-L. Lu and S. Rajagopal, J. Organomet. Chem., 2013, 738, 49–54.
49. M. Latva, H. Takalo, V.-M. Mukkala, C. Matachescu, J. C. Rodríguez-Ubis and J. Kankare, J. Lumin., 1997, 75, 149–169.
50. A. L. Pellegrino, C. Mezzalira, F. Mazzer, L. Cadi Tazi, A. Caneschi, D. Gatteschi, I. L. Fragalà, A. Speghini, L. Sorace and G. Malandrino, Inorg. Chim. Acta, 2022, 535, 120851.
51. Bruker, Bruker APEX2, Bruker AXS Inc., Madison, Wisconsin, USA, 2012.
52. Bruker, Bruker SAINT, Bruker AXS Inc., Madison, Wisconsin, USA, 2012.
53. M. C. Burla, R. Caliandro, M. Camalli, B. Carrozzini, G. L. Cascarano, L. De Caro, C. Giacovazzo, G. Polidori and R. Spagna, J. Appl. Crystallogr., 2005, 38, 381–388.
54. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8.
55. M. Nardelli, J. Appl. Crystallogr., 1995, 28, 659–659.
56. C. F. Macrae, I. J. Bruno, J. A. Chisholm, P. R. Edgington, P. McCabe, E. Pidcock, L. Rodriguez-Monge, R. Taylor, J. Van De Streek and P. A. Wood, J. Appl. Crystallogr., 2008, 41, 466–470.
57. Dassault Systèmes BIOVIA, Discovery Visualizer, v19.1.0.18287, Dassault Systèmes, San Diego, 2019.
58. L. J. Guggenberger and E. L. Muetterties, J. Am. Chem. Soc., 1976, 98, 7221–7225.
59. E. L. Muetterties and L. J. Guggenberger, J. Am. Chem. Soc., 1974, 96, 1748–1756.
60. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179.
61. M. L. Morris, R. W. Moshier and R. E. Sievers, Inorg. Chem., 1963, 2, 411–412.
62. J. Mayans, L. Tesi, M. Briganti, M.-E. Boulon, M. Font-Bardia, A. Escuer and L. Sorace, Inorg. Chem., 2021, 60, 8692–8703.
63. G. K. Gransbury, M.-E. Boulon, R. A. Mole, R. W. Gable, B. Moubaraki, K. S. Murray, L. Sorace, A. Soncini and C. Boskovic, Chem. Sci., 2019, 10, 8855–8871.
64. L. Sorace, C. Sangregorio, A. Figuerola, C. Benelli and D. Gatteschi, Chem. – Eur. J., 2009, 15, 1377–1388.
65. A. Palii, B. Tsukerblat, S. Klokishner, K. R. Dunbar, J. M. Clemente-Juan and E. Coronado, Chem. Soc. Rev., 2011, 40, 3130–3156.
66. J.-P. Costes, F. Dahan, A. Dupuis and J.-P. Laurent, Chem. – Eur. J., 1998, 4, 1616–1620.
67. M. L. Kahn, R. Ballou, P. Porcher, O. Kahn and J.-P. Sutter, Chem. – Eur. J., 2002, 8, 525–531.
68. S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178(1), 42–55.
69. A. V. Palii, D. V. Korchagin, E. A. Yureva, A. V. Akimov, E. Ya. Misochko, G. V. Shilov, A. D. Talantsev, R. B. Morgunov, S. M. Aldoshin and B. S. Tsukerblat, Inorg. Chem., 2016, 55, 9696–9706.
70. F. Lloret, M. Julve, J. Cano, R. Ruiz-García and E. Pardo, Inorg. Chim. Acta, 2008, 361, 3432–3445.
71. S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55.
72. F. James, MINUIT: Function Minimization and Error Analysis Reference Manual Version 94.1 (cern.ch).
73. F. S. Santana, M. Perfetti, M. Briganti, F. Sacco, G. Poneti, E. Ravera, J. F. Soares and R. Sessoli, Chem. Sci., 2022, 13, 5860–5871.
74. C. E. Jackson, I. P. Moseley, R. Martinez, S. Sung and J. M. Zadrozny, Chem. Soc. Rev., 2021, 50, 6684–6699.
75. H.-H. Cui, Y.-Q. Zhang, X.-T. Chen, Z. Wang and Z.-L. Xue, Dalton Trans., 2019, 48, 10743–10752.
76. M. Briganti, F. Santanni, L. Tesi, F. Totti, R. Sessoli and A. Lunghi, J. Am. Chem. Soc., 2021, 143, 13633–13645.
77. B. Yao, M. K. Singh, Y.-F. Deng, Y.-N. Wang, K. R. Dunbar and Y.-Z. Zhang, Inorg. Chem., 2020, 59, 8505–8513.
78. R. Orbach, Proc. R. Soc. London, Ser. A, 1961, 264, 458–484.
79. T. Yamabayashi, M. Atzori, L. Tesi, G. Cosquer, F. Santanni, M.-E. Boulon, E. Morra, S. Benci, R. Torre, M. Chiesa, L. Sorace, R. Sessoli and M. Yamashita, J. Am. Chem. Soc., 2018, 140, 12090–12101.
80. A. Strasser and A. Vogler, Inorg. Chem. Commun., 2004, 7, 528–530.
81. L. Bai, F. Wyrwalski, M. Safariamin, R. Bleta, J.-F. Lamonier, C. Przybylski, E. Monflier and A. Ponchel, J. Catal., 2016, 341, 191–204.
82. R. H. Holm and F. A. Cotton, J. Am. Chem. Soc., 1958, 80, 5658–5663.
83. S. Yamada and R. Tsuchida, Bull. Chem. Soc. Jpn., 1960, 33, 98–103.
84. D. Mandeep, A Textbook of Inorganic Chemistry – Volume 1, Dalal institute, vol. 1.
85. B. N. Figgis and M. A. Hitchman, Ligand field theory and its applications, Wiley-VCH, New York, 2000.
86. M. Q. Farooq, D. Chand, G. A. Odugbesi, M. Varona, Y. Mudryk and J. L. Anderson, New J. Chem., 2019, 43, 11334–11341.
87. N. Pernicone, J. Geri and J. York, J. Chem. Educ., 2011, 88, 1323–1327.
88. K. Krekić, D. Klintuch and R. Pietschnig, Chem. Commun., 2017, 53, 11076–11079.
89. K. Binnemans, Coord. Chem. Rev., 2015, 295, 1–45.
90. F. Fagnani, A. Colombo, G. Malandrino, C. Dragonetti and A. L. Pellegrino, Molecules, 2022, 27, 6990.

---

Footnote

† Electronic supplementary information (ESI) available: Single crystal XRD data of Eu-Co and Y-Co, IR spectra of the three complexes and relaxation data. CCDC 2361212 and 2361213. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4dt01693a

---