 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Efficient simulation of complex fluid phase diagrams with Bayesian optimization
Steven G. Arturo a,
Clyde Fare
a,
Clyde Fare d,
Kaoru Aou
d,
Kaoru Aou b,
Dan Dermodyc,
Will Edsallc,
Jillian Emersonc,
Kathryn Grzesiakc,
Arjita Kulshreshthab,
Paul Mwasamea,
Edward O. Pyzer-Knappe and
Jed Pitera
b,
Dan Dermodyc,
Will Edsallc,
Jillian Emersonc,
Kathryn Grzesiakc,
Arjita Kulshreshthab,
Paul Mwasamea,
Edward O. Pyzer-Knappe and
Jed Pitera *f
*f
aThe Dow Chemical Company, Northeast Technology Center, Collegeville, 400 Arcola Road, PA 19426, USA
bThe Dow Chemical Company, Texas Innovation Center, 220 Abner Jackson Parkway, Lake Jackson, TX 77566, USA
cThe Dow Chemical Company, Michigan Operations, 693 Washington Street, Midland, MI 48640, USA
dIBM Research UK, Hartree Centre, Keckwick Lane, Daresbury, Cheshire, Warrington, WA4 4AD, UK
eXyme, Botley Road, Oxford, OX2 0HA, England, UK
fIBM Research Almaden, 650 Harry Road, San Jose, CA 95120, USA
First published on 15th December 2025
Abstract
Phase diagrams of complex fluids are essential tools for understanding solubility and miscibility. Using a new objective function coupled with a constrained Bayesian optimization algorithm, we demonstrate the efficient location of phase boundaries in a sample two-phase ternary modeled using polymer self-consistent field theory, regularly seeing 50% fewer observations than an exhaustive search. Our approach is general, gradient-free, and can be applied to either simulation or experimental campaigns.
Complex polymer blends and solutions are essential to modern life, with examples ranging from paints to photoresists. These blends exhibit complex phase behavior, including both macro- and micro-phase separation. Understanding and controlling this phase behavior is essential to formulate both stable and functional polymer-based products. One challenge to this understanding in an industrial context is the sheer complexity of the compositions being considered, often on the order of ten majority and minority components mixed together. Even when considering just four majority components, a detailed phase diagram at 10 weight percent (wt%) resolution requires evaluation of 1001 different composition points. For six or eight components, the number grows exponentially to 8008 or 43
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 758, respectively.
758, respectively.
To address this combinatorial explosion and make high-dimensional phase diagrams tractable, we explored the use of an active learning approach based on Bayesian optimization.1–3 In such an approach, bulk composition points are sampled iteratively, and data from all prior observations inform the selection of each new point. A Bayesian optimization approach is particularly suited for this problem because it does not require gradients, just the value of the observation at each point in the domain. This allows the observation (simulation or experiment) to be treated as a “black box”, and even enables optimization using a mixed set of observation types.4,5 Recent studies have established the utility of such machine-learning methods to map phase diagrams. Kusne et al. used Bayesian optimization to realize a reduction of 90% in the number of experiments needed to map the phase diagram of solid-state materials with X-ray diffraction.6 Beaucage and Martin published a study on the design of an autonomous lab for formulation preparation using scattering, among other analytical tools, with AI/ML methods guiding formulation screening.7 Adams et al. considered human interaction with machine learning algorithms and showed a system that improves in phase-mapping performance for an inorganic material.8
The key challenge considered in this work is the design of the objective function.2 Each observation can tell whether a particular bulk composition is single- or multi-phase, but the real property of interest is the location of phase boundaries. The boundaries can be estimated by sampling points on either side and interpolating between them, but this requires a way to drive sampling toward regions near phase boundaries. A productive sampling strategy allows observations to be focused within regions that are maximally informative about the boundary and away from bulk compositions in the interior of a particular phase. We have developed a combination of objective function and constrained Bayesian optimization9,10 that, in the context of a model simulation problem, reduces the number of observations required to find useful phase boundaries by at least 50% and in one case over 90%.
Polymer self-consistent field theory (SCFT) is a well-established method for modeling phase behavior in complex fluids.11–13 SCFT calculations were performed with PolyFTS14 to compute density profiles of complex fluid mixtures, with results granted by this and other correctly-employed SCFT software. The parameters used in the SCFT calculations were regressed to reproduce the measured miscibility results of an industrially-relevant ternary mixture of polymeric fluids; therefore, the model in this work is considered ground-truth since it represents the experimental system at equilibrium and without error. Observations of the complex mixtures are either bulk immiscible or bulk miscible. The polymers are successfully modeled as incompressible unimodal linear homopolymers whose configurations are treated with Gaussian statistics. The SCFT calculation in PolyFTS simulated a one-dimensional domain of length 40 radii of gyrations of the reference unit using a canonical ensemble. Initial guesses for the volume density profiles assumed immiscibility. A calculation with PolyFTS at one composition point takes on the order of minutes to converge. The detailed phase diagram generated with SCFT in PolyFTS at 1 wt% resolution and the parameters used are shown in Fig. 1.
 | ||
| Fig. 1 Ternary phase diagram and parameters for the model mixture of polymers from SCFT at 1 wt% resolution. Compositions are computed to be either bulk miscible (green) or bulk immiscible (red). | ||
A systematic method is needed to relate results from PolyFTS or similar software to whether the state of the system is miscible or immiscible and, if immiscible, to quantify a magnitude of immiscibility from density profiles. A result in the miscible region from PolyFTS or similar software would show uniform density profiles throughout the system. A result from a composition in the immiscible region shows density profiles indicative of two phases, where one region is rich in some polymers and the other rich in the remaining polymers, as shown in Fig. 2. This work proposes a designed objective function that uses the differences in extrema in density profiles to give information regarding the relative distance of the bulk composition point from a region of miscibility. A partition ratio for a species accepts such information for compositions where immiscibility is seen and results in unity where miscibility is found.
 | ||
| Fig. 2 Density profile output from PolyFTS is indicative of two phases with one being A-rich and the other being B-rich. | ||
The partition ratio P for each polymer M is defined as the ratio of rich and lean concentrations
 | (1) |
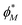 is indicative of the amount of polymer in the phase, the number of moles of material M in phase i, nM, i, can be approximated by
is indicative of the amount of polymer in the phase, the number of moles of material M in phase i, nM, i, can be approximated by
 | (2) |
 is the assumed composition M in phase i, ρM is the density of M, NM is the length of polymer M given as its number of monomeric segments, and MWsegment, M is the molar weight of a monomeric segment. The volume of each phase Vi can be approximated by the relative lengths of each phase li given by the distances between inflection points in the density profile multiplied by a constant cross-sectional area a for the system. Therefore, the concentration of polymer M in phase i can be approximated by the ratio of eqn (2) and the equation for Vi. Combining the definitions gives the approximation of the partition ratio in terms of computed results from PolyFTS or similar software
is the assumed composition M in phase i, ρM is the density of M, NM is the length of polymer M given as its number of monomeric segments, and MWsegment, M is the molar weight of a monomeric segment. The volume of each phase Vi can be approximated by the relative lengths of each phase li given by the distances between inflection points in the density profile multiplied by a constant cross-sectional area a for the system. Therefore, the concentration of polymer M in phase i can be approximated by the ratio of eqn (2) and the equation for Vi. Combining the definitions gives the approximation of the partition ratio in terms of computed results from PolyFTS or similar software
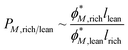 | (3) |
An objective function can be made by combining the partition ratios in eqn (3) with a weighting factor fM
 | (4) |
Each of the ratios in the summation is greater than 1 for bulk compositions in the immiscible region and will be equal to 1 for points in the miscible region of the phase diagram. An artificially high value of the objective function is given for points in the miscible region to create a valley of relative minima that exists at the boundary in the immiscible region. Due to the nature of the objective function, for all points in the immiscible region of a phase diagram, there exists a monotonically decreasing smooth curve that ends at a point on the phase boundary, resulting in no local minima within the immiscible region of a phase diagram.
Use of the designed objective function and a binary classifier objective function is explored with Bayesian optimization. The design objective function uses weighting factors equal to the overall composition of the components in the mixture. The binary classifier scores the system with either 0 or 1 for immiscible and miscible, respectively. For Bayesian optimization, both objective functions were modeled using Gaussian process regression with a Matern(5/2) kernel.15 The expected improvement acquisition function16 applying a contextual improvement parameter17 is used with the designed objective function while maximum entropy18 is used with the binary classifier.
A key aspect of the optimization procedure is the use of constraints when sampling, given already-made observations. A space-filling design of experiments, whether carried out with real-world experiments or with computation, has a resolution in the observations made. There is acceptance of some loss of precision with the choice of resolution. For instance, for a phase boundary search in a binary system, if a measurement indicates miscibility at 10 wt% and immiscibility at 20 wt%, then the boundary lies somewhere between 10 and 20 wt%, and no further search is warranted due to the accepted level of precision. The constraints on the search made by the sampling in this work replicates the example. Given a desired resolution of the phase diagram, each observation is used to exclude sampling in a neighborhood of points within a distance corresponding to that resolution. In addition, constraints are used to avoid sampling in regions where the surrogate model predicts miscibility, effectively focusing sampling on immiscible and boundary regions. The algorithm is illustrated in Fig. 3. For this work, sampling was initialized with one, four, or nine observations along each binary mixture as well as one interior point at A, B, C = 60, 20, 20 wt% where immiscibility is found.
 | ||
| Fig. 3 Algorithm used to initialize the constrained Bayesian optimization with a domain where points within the desired resolution of previous observations are removed. | ||
Fig. 4 shows the search trajectory and the assumed phase diagrams obtained using the designed objective function starting with one data point per binary mixture and requesting 10 wt% resolution. The plots in the left column show the values of the objective function where points of miscibility appear yellow due to their artificially assigned high values of 100. The plots on the right are constructed after each observation by determining which points are assumed immiscible (in red) or boundary points (in orange). Points assumed immiscible exist in triangles formed with observed immiscible points. Points assumed to contain the phase boundary lie outside the triangles but within the desired resolution, here 10 wt%. A search is considered complete when the phase boundary entirely exists within the orange region.
Early in the search, in iteration 2 shown in Fig. 4, the addition of the third observation allows an area of immiscibility to be set along with an assumed phase boundary. By iteration 10, a fuller space of immiscibility is assumed; the upper portion of the phase boundary has been found. Between iteration 10 and iteration 21 a productive search is done within the interior of the phase diagram, resulting in 98% of the immiscible region being contained within the red and orange points. Iteration 28 is when 100% of the boundary is contained within the orange points. Note that the constraints against sampling in the miscibility regions (yellow points in the left figures) and at points close to observed immiscible points are working to provide spaced sampling mostly within the immiscible region.
In general, the binary classifier objective function outperformed the designed objective function using partition ratios, although all showed savings over exhaustive search. Fig. 5 shows the progress in phase boundary coverage from both objectives with the binary model reaching completion earlier than the design objective. The savings to achieve 99% coverage of the phase boundary with the binary model at a 10 wt% resolution is 61–83%, improving to 66–93% for 5 wt% resolution. The results are shown in Table 1. At best, a ten-fold decrease in the cost of exploring a complex fluid phase diagram is found, substantially increases the utility and impact of the use of Bayesian optimization for active learning in industrial product formulation.
 | ||
| Fig. 5 Evolution of phase boundary coverage for both the designed objective function and the binary classifier objective with one initial data point per binary pair requesting 10 wt% resolution. | ||
| Objective function | No. of binary points/resolution | Iteration at completiona | Savingsb |
|---|---|---|---|
| a Completion is when 99% of the actual immiscible region is within the assumed immiscible region and the assumed boundary.b As compared to 36 interior points needed for 10% resolution and 190 interior points needed for 5% resolution. | |||
| Designed | 1/5% | 66 | 65% |
| Designed | 4/5% | 74 | 61% |
| Designed | 9/5% | 54 | 71% |
| Binary | 1/5% | 64 | 66% |
| Binary | 4/5% | 19 | 89% |
| Binary | 9/5% | 12 | 93% |
| Designed | 1/10% | 26 | 25% |
| Designed | 4/10% | 11 | 67% |
| Designed | 9/10% | 11 | 67% |
| Binary | 1/10% | 13 | 61% |
| Binary | 4/10% | 5 | 83% |
| Binary | 9/10% | 7 | 78% |
Conclusions
With this work, we have shown that Bayesian optimization, appropriately deployed, can significantly reduce the cost of determining phase diagrams for complex fluids. Further studies are needed to show if this benefit scales exponentially or linearly with the number of components. Since our approach is general-purpose, additional savings could likely be generated by heuristics that make assumptions about the structure (e.g. convexity) of phase boundaries for specific systems. Another area of research is the explicit combination of experimental and computational observations in this same Bayesian framework. Overall, this work shows how recent advances in machine learning and computation can significantly benefit the practice of modern polymer science.Author contributions
All authors contributed to the conceptualization and technical work in this study. AK, PM, and SGA carried out the PolyFTS simulations. SGA, CF, WE, EOPK, and JP developed the sampling algorithm and software infrastructure. SGA, CF, and JP wrote and edited the paper.Conflicts of interest
This work was supported directly by IBM Research and the Dow Chemical Company. There are no conflicts to declare.Data availability
Pseudocode and data are available at https://doi.org/10.5281/zenodo.17547303. Details to reproduce the work as described have been included in the text of the paper and in the Supporting Information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5dd00150a.Notes and references
- D. R. Jones, M. Schonlau and W. J. Welch, J. Glob. Optim., 1998, 13(4), 455, DOI:10.1023/A:1008306431147.
- B. Shahriari, K. Swersky, Z. Wang, R. P. Adams and N. De Freitas, Proc. IEEE, 2016, 104(1), 148, DOI:10.1109/JPROC.2015.2494218.
- Q. Liang, A. E. Gongora, Z. Ren, A. Tiihonen, Z. Liu, S. Sun, J. R. Deneault, D. Bash, F. Mekki-Berrada, S. A. Khan, K. Hippalgaonkar, B. Maruyama, K. A. Brown, J. Fisher III and T. Buonassisi, npj Comput. Mater., 2021, 7(1), 188, DOI:10.1038/s41524-021-00656-9.
- Y. Zhang, D. W. Apley and W. Chen, Sci. Rep., 2020, 10(1), 4924, DOI:10.1038/s41598-020-60652-9.
- P. Z. G. Qian, H. Wu and C. F. J. Wu, Technometrics, 2008, 50(3), 383, DOI:10.1198/004017008000000262.
- A. G. Kusne, H. Yu, C. Wu, H. Zhang, J. Hattrick-Simpers, B. DeCost, S. Sarker, C. Oses, C. Toher, S. Curtarolo, A. V. Davydov, R. Agarwal, L. A. Bendersky, M. Li, A. Mehta and I. Takeuchi, Nat. Commun., 2020, 11, 5966, DOI:10.1038/s41467-020-19597-w.
- P. A. Beaucage and T. B. Martin, Chem. Mater., 2023, 35(3), 846–852, DOI:10.1021/acs.chemmater.2c03118.
- F. Adams, A. McDannald, I. Takeuchi and A. G. Kusne, Matter, 2024, 7, 697, DOI:10.1016/j.matt.2024.01.005.
- J. M. Hernández-Lobato, J. Requeima, E. O. Pyzer-Knapp and A. Aspuru-Guzik, International Conference On Machine Learning, 2017, p. , p. 1470, PMLR, https://proceedings.mlr.press/v70/hernandez-lobato17a.html Search PubMed.
- D. Jasrasaria and E. O. Pyzer-Knapp, Intelligent Computing: Proceedings of the 2018 Computing Conference, Springer International Publishing, 2019, vol. 1, DOI:10.1007/978-3-030-01174-1_1.
- L. Leibler, Macromolecules, 1980, 13(6), 1602, DOI:10.1021/ma60078a047.
- M. W. Matsen and M. Schick, Phys. Rev. Lett., 1994, 72(16), 2660, DOI:10.1103/PhysRevLett.72.2660.
- M. W. Matsen, J. Phys. Condens. Matter, 2002, 14(2), R21, DOI:10.1088/0953-8984/14/2/201.
- K. T. Delaney and G. H. Fredrickson, Comput. Phys. Commun., 2013, 184(9), 2102, DOI:10.1016/j.cpc.2023.04.002.
- C. E. Rasmussen and C. K. I. Williams, Gaussian Processes for Machine Learning. The MIT Press, 2006 Search PubMed.
- J. Mockus, IFIP Technical Conference, 1974 Search PubMed.
- D. Jasrasaria and E. O. Pyzer-Knapp, arXiv, 2018, preprint, arXiv:1807.01279, DOI:10.48550/arXiv.1807.01279, Computing Conference, https://arxiv.org/pdf/1807.01279.
- P. Hennig and C. J. Schuler, J. Mach. Learn. Res., 2012, 13, 1809 Search PubMed.
| This journal is © The Royal Society of Chemistry 2025 |

