Evaluating the performance and robustness of LLMs in materials science Q&A and property predictions

Abstract

Large Language Models (LLMs) have the potential to revolutionize scientific research, yet their robustness and reliability in domain-specific applications remain insufficiently explored. In this study, we evaluate the performance and robustness of LLMs for materials science, focusing on domain-specific question answering and materials property prediction across diverse real-world and adversarial conditions. Three distinct datasets are used in this study: (1) a set of multiple-choice questions from undergraduate-level materials science courses, (2) a dataset including various steel compositions and yield strengths, and (3) a band gap dataset, containing textual descriptions of material crystal structures and band gap values. The performance of LLMs is assessed using various prompting strategies, including zero-shot chain-of-thought, expert prompting, and few-shot in-context learning. The robustness of these models is tested against various forms of “noise”, ranging from realistic disturbances to intentionally adversarial manipulations, to evaluate their resilience and reliability under real-world conditions. Additionally, the study showcases unique phenomena of LLMs during predictive tasks, such as mode collapse behavior when the proximity of prompt examples is altered and performance recovery from train/test mismatch. The findings aim to provide informed skepticism for the broad use of LLMs in materials science and to inspire advancements that enhance their robustness and reliability for practical applications.

---

1 Introduction

Large Language Models (LLMs) represent a significant advancement in the field of artificial intelligence and have been rapidly adopted for application in various scientific disciplines.^1–4 With their ability to process and generate natural language, LLMs are potent tools for tasks like information retrieval, question and answering (Q&A), and property predictions.^5–7 Similar to traditional ML models, LLMs can require extensive data processing, large volumes of data, and massive compute resources to train.⁸ Despite these limitations, pretrained LLMs can be adapted to new tasks with few-shot examples via in-context learning (ICL), making them both cost-effective and rapid to deploy.^9–11 In the context of materials science, where data acquisition can often be costly and time-consuming, leveraging ICL enables LLMs to efficiently prototype and generate predictive insights even in low-data settings.^12–14 Recent work has demonstrated that LLMs are capable of domain-specific Q&A,^15–17 materials property predictions,^18–20 and information extraction from complex datasets.^7,21 In addition, LLMs have been integrated into self-driving laboratories, where they assist in experiment planning, synthesis design, autonomous retrosynthetic workflows, and orchestration of multi-step experimental procedures.^3,22,23 These studies demonstrate LLMs' potential to serve as flexible and powerful analytical tools for advancing scientific discovery and generating new insights.

However, the robustness of LLMs is a critical factor in their practical deployment, yet it remains an underexplored area, particularly in domain-specific applications such as materials science. Previous studies have shown that LLMs struggle to maintain predictive accuracy when the input distribution shifts, exhibiting poor generalization to out-of-distribution (OOD) test data and vulnerability to adversarial attacks.^24–26 These challenges highlight the need for systematic robustness evaluations to ensure LLM reliability in real-world scenarios. A key aspect of the robustness of LLMs is their sensitivity to prompt changes either due to innocuous or adversarial reasons.^27,28 Variations in how a query or instruction is formulated may cause a response to factually change.²⁷ As an example, 0.1 nm and 1 Å are equivalent but switching them in a prompt could result in different LLM predictions for the same task. Alternatively, the response of the LLM can be deliberately altered through intentional misinformation or misleading inputs.²⁸ These attributes are not only theoretical concerns but are critical for the reliable usage of LLMs as they become integrated into the materials science research and development pipeline. Given that LLMs generate outputs with indifference to truth,²⁹ thoroughly probing LLM prompt sensitivity would allow us to critically evaluate model performance in practical situations; providing informed skepticism for the broad use of LLMs in materials science.

In this work, we conducted a holistic robustness analysis of commercial and open-source LLMs for materials science. While our primary analyses focus on pre-reasoning models due to their consistent single-pass inference structure, we also include a representative reasoning model (DeepSeek-R1 (ref. 30)) in both the initial benchmarking and the robustness evaluation. Reasoning models, such as DeepSeek-R1 and OpenAI-o1,³¹ incorporate intermediate reasoning steps during inference, which distinguish them from pre-reasoning models. Including DeepSeek-R1 allows us to assess whether such reasoning architectures improve overall performance and robustness under perturbed conditions. Three distinct datasets of domain-specific Q&A and materials property prediction were selected. First, we benchmarked LLMs of different sizes and release periods using prompt engineering to establish baseline and optimal performance boundaries. We then investigated the impact of various textual perturbations, ranging from realistic to adversarial, on LLM performance in materials science Q&A. We then used the matbench_steels dataset to investigate whether pretrained LLMs can move beyond simple interpolation of few-shot examples to capture deeper structure-property relationships. Without fine-tuning, pretrained LLMs demonstrated enhanced predictive ability through few-shot ICL when presented with similar examples to the prediction task. Conversely, when provided with dissimilar examples during few-shot ICL, mode collapse behavior was observed, where the model often generated identical outputs despite varying inputs, suggesting limited generalization capability in OOD settings. Furthermore, we also evaluated a fine-tuned LLM (LLM-Prop¹⁸) on a band gap prediction task to assess the robustness of task-specific models, which are increasingly adopted in materials science due to their strong performance on targeted problems.^32,33 Counterintuitively, supposedly adversarial perturbations like sentence shuffling enhanced LLM-Prop's predictive capability with significantly truncated prompts. This train/test mismatch behavior, absent in traditional ML models, highlights a potential direction for distilling LLM-based predictive models.

2 Methods

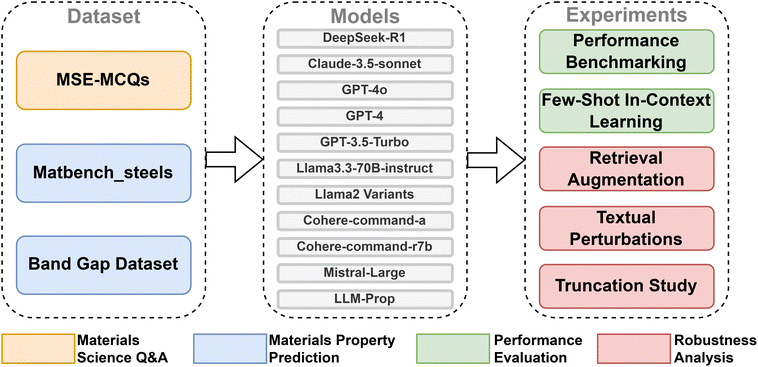
The methodology is divided into four subsections that cover the performance evaluation and robustness analysis of LLMs in materials science Q&A and property predictions. In each subsection, we will introduce the models, datasets used, prompting techniques, and evaluation criteria chosen for the specific study. All the evaluated models were set to their lowest temperature (typically 0) to minimize the non-determinism and maximize reproducibility. Fig. 1 illustrates the experimental framework for evaluating LLMs in materials science Q&A and materials property prediction. For performance evaluation and robustness analysis of materials science Q&A, we compiled the MSE-MCQs dataset, consisting of 113 multiple-choice questions specifically designed for this study. These questions are original and were created by faculty at the University of Toronto for a first-year introductory materials science and engineering course. The questions were designed to test students' understanding of materials science knowledge, including material mechanics, thermodynamics, crystal structures, materials properties, etc. For the performance evaluation of property prediction, we use matbench_steels, a subcategory of the Matbench test set originally proposed for benchmarking traditional machine learning (ML) models for materials property predictions.³⁴ The matbench_steels dataset has 312 pairs of material compositions (as chemical formula) and yield strength (in MPa). For the robustness analysis of property prediction, we use a band gap dataset, which comprises 10 047 descriptions of material crystal structures generated via Robocrystallographer, along with their corresponding band gap values from the Materials Project database.¹⁸

Fig. 1 Schematic representation of the experiment design for performance evaluation and robustness analysis of various LLMs. Yellow highlights the testing conducted in Q&A settings. Blue highlights the testing conducted in property prediction settings. Green represents the tests associated with performance evaluation. Red represents tests related to degradation and robustness analysis.

2.1 Performance evaluation of materials science Q&A

Using MSE-MCQs, we benchmarked a range of both commercial and open-source LLMs, including Anthropic's claude-3.5-sonnet-20240620,³⁵ OpenAI's gpt-4o-2024-11-20,³⁶ gpt-4-0613,³⁷ and gpt-3.5-turbo-0613,³⁸ alongside Meta AI's Llama variants – llama3.3-70B-instruct,³⁹ llama2-70b-chat, llama2-13b-chat, and llama2-7b-chat.⁴⁰ A reasoning model, DeepSeek-R1 (ref. 30) was also evaluated. Model suffixes indicate their key attributes: Claude-3.5-sonnet-20240620 refers to a balanced model variant from Claude 3.5 released in June 2024.³⁵ OpenAI's “0613” and “2024-11-20” indicate model version dates, and “4o” (“omni”) indicates its multimodal capability.³⁶ For the Llama models, “7b”, “13b”, and “70b” denote parameter count in billions, while “chat” or “instruct” refer to instruction tuning.^39,40 For DeepSeek-R1, “R1” indicates its first release of a reasoning model.³⁰ This study primarily utilized fixed-version and open-source models to enhance the reproducibility of the findings. To account for the inherent non-determinism in LLM outputs,⁴¹ we conducted three independent trials for each model under each prompting condition, allowing us to capture the variability in the responses.

The MSE-MCQs questions are manually categorized into easy (number of questions, n = 39), medium (n = 40), and hard levels (n = 34), based on a set of heuristics, including conceptual complexity, the level of reasoning required, and the presence and difficulty of the calculations. For example, “easy” questions primarily test factual recall or direct application of basic concepts, such as identifying the crystal structure of a material. “Medium” questions involve moderate reasoning or straightforward calculations, such as determining the stress in a material under specific conditions. “Hard” questions require multi-step reasoning or more complex calculations, such as deriving material properties from combined thermodynamic and mechanical data. Some examples are shown in Table 1.

Table 1 Examples of MSE-MCQs questions categorized by difficulty level

Difficulty	MSE-MCQsa question
Easy	Which of the following most closely describes the ductility of a sample?
	(a) The plastic strain at fracture
	(b) The elastic strain at fracture
	(c) The total strain at fracture
	(d) None of the above
Medium	An hypothetical FCC metal has a density of 7.4 g cm^−3 and a molar mass of 55.3 g mol^−1. Which of the following is the correct number of atom sites (that is, without any vacancies)?
	(a) 1.09 × 10^22 atoms per cm^3
	(b) 1.34 × 10^−1 atoms per cm^3
	(c) 6.80 × 10^−22 atoms per cm^3
	(d) 8.06 × 10^22 atoms per cm^3
Hard	A cylindrical sample of stainless steel having a Young's modulus of 204.3 GPa, a diameter of 12.0 mm, and initial length of 237.8 mm is loaded to a stress of 411.5 MPa. The sample is then completely unloaded. What will the elastic recovery of this sample be, in mm? The yield strength and ultimate tensile strength of this specific alloy are 292.0 MPa and 688.0 MPa, respectively
	(a) Possible to calculate from information provided, but none of these options are correct
	(b) 0.96
	(c) Not possible to calculate from information provided
	(d) 239.0
	(e) 0.24
	(f) 0.48

---

To evaluate the impact of prompt engineering on LLM performance in materials science Q&A tasks, we tested each model under two distinct conditions: (1) without expert prompt (no prompt engineering) – the model received only the multiple-choice question in the user message, with no system prompt or additional instruction, serving as a baseline to assess its default performance; and (2) with expert prompt – the model was provided with a structured system prompt instructing it to act as a domain expert and reason through the problem step-by-step, aiming to enable a direct assessment of how prompt engineering influences reasoning and answer accuracy.

The expert prompt incorporates both expert prompting and zero-shot chain-of-thought (CoT) strategies. Expert prompting involves instructing the LLM to adopt the role of a domain expert, which has been shown to guide responses toward more accurate and knowledge-aligned reasoning.⁴² Zero-shot CoT prompting complements this by encouraging the model to “think aloud” and generate step-by-step reasoning even without prior examples, potentially improving accuracy in problem-solving tasks.⁴³ These strategies were combined into a single structured system prompt used across all “With Expert Prompt” evaluations. In the Q&A evaluation, the expert prompt includes instructions to define the domain of study, introduces the settings of the questions, and emphasizes step-by-step reasoning and calculations. The goal is to improve the LLMs' ability to retrieve domain-specific knowledge, follow the instructions, and correctly perform reasoning and calculations. The expert prompt is shown below:

Given the lengthy reasoning in the answers and the potential for errors in manual verification, we used the gpt-4-0613 API in a separate client to extract and assess responses automatically. For each trial, the model compared the answer to the provided correct choice, generating a simple binary score (1 for correct, 0 for incorrect). While the evaluation focused on final answers, rare cases occurred where the model based its judgment on the reasoning rather than the final choice. These cases were manually reviewed and corrected when identified. Finally, the average accuracy and standard deviation of each category were calculated and plotted. When selectively compared to manual checks (>2000 answers), the method was found to be reliable, consistently identifying correct answers with over 95% accuracy. The prompt is shown below:

2.2 Performance evaluation of materials property prediction

This study used the matbench_steels dataset to assess whether pretrained LLMs can leverage few-shot ICL to infer deeper structure-property relationships for materials property prediction. We benchmarked claude-3.5-sonnet-20240620, gpt-4o-2024-11-20, gpt-3.5-turbo-1106 llama3.3-70B-instruct, mistral-large-2411,⁴⁴ Cohere's command-r7b-12-2024,⁴⁵ and command-a⁴⁶ on their abilities to predict the yield strengths given the steel compositions. In these model names, “large” in mistral-large-2411 indicates a large parameter size,⁴⁴ while “2411” and “12-2024” refer to the release dates (November 2024 and December 2024, respectively). Note that not all models evaluated in the Q&A tasks were reused in this study. This is due to differences in prompt window sizes: some LLMs lacked sufficient context capacity to support long few-shot inputs required in this property prediction task. To validate whether performance trends hold across LLMs released from different developers, we included newer models from Mistral and Cohere in this analysis.

Few-shot learning involves providing the LLM with a few examples of the task at hand, enabling it to learn the pattern and apply it to unseen questions or problems.⁴⁷ To use LLMs as predictive models, we fed the few-shot examples to the prompt windows of the LLMs. Starting with an instruction, compositions were restructured by separating each element with a space and then paired to their corresponding yield strengths. We varied the number of few-shot examples from 5 to 25 to observe how LLMs' prediction accuracy scales with data size. Beyond 25 points, some models suffered from limited prompt windows. An example of the prompt containing these few-shot examples is shown below.

To compare the predictive capabilities of LLMs and traditional ML models, k-nearest neighbors (KNN) and random forest regressor (RFR) models were also implemented. For direct comparison, each RFR model was trained using the exact same data points that were provided to the LLMs in each few-shot setting. Specifically, for every prediction target, if the LLM received 10 few-shot examples as prompt context, the corresponding RFR model was trained using those same 10 compositions as its training set. To enable a more direct comparison with LLMs, we implemented two variants of the RFR model: one trained directly on the elemental compositions, where each element was represented as a feature with its corresponding fractional value, and another trained on MAGPIE features⁴⁸ extracted from the compositions. The selected MAGPIE features are presented in the ESI.†

A retrieval-augmented method was used to evaluate the impact of the proximity of the few-shot examples on the predictive performance. Each composition was encoded using its elemental proportions and projected into a lower-dimensional space using principal component analysis (PCA). Given each prediction target, candidate few-shot examples were ranked based on their Euclidean distances (L2 norm) in the PCA-transformed space, enabling the selection of training examples with varying levels of similarity to the target composition. Three settings were chosen based on the distances: (1) random neighbors – few-shot examples were randomly sampled from the dataset without considering proximity; (2) nearest neighbors – examples closest to the prediction target in PCA space were selected to match its local distribution; (3) farthest neighbors – examples most dissimilar to the prediction target were selected to evaluate model generalization under distribution shift. The performance in each setting was evaluated using mean absolute error (MAE), which quantifies the average absolute difference between predicted and true yield strengths. These evaluations aim to probe the sensitivity of LLMs to the choice and proximity of few-shot examples.

2.3 Robustness analysis of materials science Q&A

To evaluate the robustness of LLMs for materials science Q&A, we continued using the MSE-MCQs dataset and selected three representative models: gpt-3.5-turbo-0613, gpt-4o-2024-11-20, and DeepSeek-R1. The two OpenAI models were chosen for a generational comparison within the same LLM family, minimizing variability introduced by differences in training objectives, model architectures, or prompting behavior across different developers. DeepSeek-R1 was chosen as a representative reasoning model to evaluate whether its iterative reasoning architecture offers enhanced robustness compared to the pre-reasoning models. In this study, no prompting strategy was implemented, and the questions were directly used as the user prompts to better isolate the models' inherent robustness and avoid introducing external guidance that could influence their sensitivity to perturbations. We identified different types of “noise” that can be introduced to the MCQs to evaluate the robustness of LLMs. As shown in Table 2, the textual inputs were modified systematically in five different ways, i.e., (1) unit mixing, (2) sentence reordering, (3) synonym replacement, (4) distractive info, and (5) superfluous info.

Table 2 Types and descriptions of textual degradation applied to LLMs

Degradation type	Description	Goal
Unit mixing	Mixing and converting the units	To test LLMs' interpretation of different unit systems and calculation abilities
Sentence reordering	Reordering the sentences in the questions	To assess LLMs' capability to maintain comprehension on varied sentence constructions and logical flow
Synonym replacement	Replacing technical nomenclature with their synonyms	To evaluate the semantic understanding and stability of LLMs
Distractive info	Adding non-materials-science-related distractive information to the questions	To test LLMs' ability to filter out irrelevant data
Superfluous info	Adding materials-science-related superfluous information containing numerical values to the questions	To challenge LLMs' ability to identify relevant data without being misled by additional numeric details

---

These modifications are expected to vary in their impact on the LLMs' performance, with some potentially degrading it due to their adversarial nature (such as reordering sentences and adding superfluous materials-science information) and others more realistically simulating conditions encountered in real-life scenarios. Considering the inherent variability due to the non-deterministic nature of LLMs, the test was repeated three times for the original, synonym replacement, and distractive info (same input texts). The unit mixing, sentence reordering, and superfluous info were randomized three times to introduce variability in the data for the evaluation. Finally, the accuracy of each category was calculated and reported.

2.4 Robustness analysis of materials property prediction

In materials property prediction, we selected the LLM-Prop model along with its associated band gap dataset. LLM-Prop is a fine-tuned T5 model, topped with a linear layer, designed to predict materials properties from crystal structure descriptions generated using Robocrystallographer.^18,49,50

The material descriptions underwent systematic modifications mirroring those applied in the Q&A evaluations, except for unit mixing and synonym replacement. Note that, because of the highly templated nature of crystal structure descriptions, superfluous information in this context is better characterized as misleading information rather than simply extraneous text. During data preprocessing for LLM-Prop, all numerical values and units, such as bonding distances and angles, are replaced with a [NUM] token, to emphasize the model's focus on text-based understanding.¹⁸ Unit mixing might disrupt the preprocessing algorithm, and thus was excluded from the analysis. Synonym replacement was excluded because the original terminology was already highly specific and lacked equivalent synonyms. Furthermore, we conducted a truncation study of textual degradation to examine the model's resilience against structural and length variations in the input data, as well as to explore which aspects of the descriptions the model relies on for predictions. We manipulated the order and fraction of sentences included, testing configurations including (1) original order, which prioritizes the initial information in a description, (2) reverse order, which prioritizes the sentences from the end of a description, (3) random order, shuffling the information, and (4) sides-to-middle, which deprioritized central information. The impact of these textual degradations was quantitatively assessed by measuring the resultant prediction error in MAE.

3 Results and discussion

3.1 Performance evaluation of materials science Q&A

The results of the performance evaluation of LLMs on the MSE-MCQs dataset are shown in Fig. 2. For each model and setting, three trials were conducted, and the error bars represent the inherent non-determinism in LLMs even at the lowest temperature settings (typically 0). This non-determinism may affect the reliability and reproducibility of the models⁴¹ and is likely a result of stochastic sampling during text generation.^51–53 We evaluated several advanced models released after late 2024 (i.e., DeepSeek-R1 (reasoning model), claude-3.5-sonnet-20240620, llama3.3-70B-instruct, and gpt-4o-2024-11-20), along with some older models (i.e., gpt-4-0613, gpt-3.5-turbo-0613, and the llama2 variants). Overall, the newer and larger models significantly outperform older models, highlighting substantial recent advancements in LLM capabilities.

Fig. 2 LLM performance evaluation and prompt engineering enhancement in materials science Q&A using MSE-MCQs dataset. On each bar, the lighter color represents the performance of those models when introduced with the expert prompt. Error bars represent the standard deviation due to LLMs' non-determinism.

Among the evaluated pre-reasoning models, claude-3.5-sonnet-20240620 achieved the highest accuracy across all difficulty levels with over 0.8 accuracy. Notably, the reasoning model, DeepSeek-R1, demonstrated competitive performance with over 0.85 accuracy across all difficulty levels, closely matching claude-3.5-sonnet-20240620 on easy and medium questions, and surpassing all models on hard questions with an accuracy of 0.93. The hard questions predominantly involve complex, multi-step reasoning or advanced mathematical calculations, tasks that typically present substantial challenges for single-pass pre-reasoning models. This superior performance by DeepSeek-R1's clearly highlights its inherent strength in tasks demanding deeper analytical and mathematical reasoning compared to the pre-reasoning models.

The older llama2 models performed at or slightly below the baseline score of 0.25, equivalent to random guessing, while the newer llama3.3-70B-instruct achieved comparable accuracy to gpt-4o-2024-11-20 on easy and medium questions with about 0.8 and 0.7 accuracy, respectively.

Upon implementing the expert prompt (see expert prompt), we observe consistent performance improvement across almost all models and question types. The improvement is more significant on the older models, suggesting that the expert prompt can enhance reasoning abilities with weaker baseline capabilities. However, the expert prompt provides minimal benefit for the newer pre-reasoning models on the easy questions, likely because the extensive reasoning process induced by the expert prompt contributes little to the performance on simple conceptual questions that rely primarily on factual recall. Interestingly, DeepSeek-R1 shows no performance improvement on hard questions upon implementing the expert prompt, suggesting that the reasoning capabilities of DeepSeek-R1 are already effectively saturated by its built-in iterative reasoning mechanism, such that additional explicit prompting does not further augment its performance.

We further investigated why the smaller llama2 models (llama-13b-chat and llama-7b-chat) scored lower than the baseline without the expert prompt. Despite being chat models, they sometimes failed to understand the intent when instructions were not provided. Instead of answering, they often attempted to “complete” the questions. Once the expert prompt was implemented, these smaller models could follow the instructions and attempt to solve the questions, in which case the performance improved to around and sometimes above the baseline scores. However, their overall performance remained weak due to their limited skill levels.

Overall, the observed performance trends align with expectations: more recent and larger models consistently demonstrate enhanced capabilities in domain-specific Q&A tasks compared to their predecessors. Additionally, prompt engineering demonstrated effectiveness as a strategy for enhancing model performance when handling more complex questions, especially for older or smaller models with limited baseline capabilities. On the other hand, the reasoning model, DeepSeek-R1, exhibits inherently superior performance in complex analytical and mathematical reasoning tasks, achieving high accuracy even without specialized prompting.

3.2 Performance evaluation of materials property prediction

Here, we investigate LLM materials property prediction with ICL, utilizing the matbench_steels dataset to predict the yield strength of steels. To explore how the selection of highly relevant few-shot examples can be used to enhance LLM performance in property prediction, we conduct a systematic study using nearest-neighbor-boosted ICL. The method developed here involves deliberately selecting data points based on their representational proximity, meaning that data points with material compositions most similar to the test sample are used as few-shot examples to enhance the model's performance. Fig. 3 shows the prediction performance when LLMs are tasked with predicting yield strength using (a) farthest neighbors, (b) random neighbors, and (c) nearest neighbors. For performance comparison, KNN and RFR models are also implemented. The RFR is explicitly trained using MAGPIE features⁴⁸ from the same data points used in ICL. While there is some correlation between material composition and yield strength, composition alone is not a strong predictor of yield strength. The KNN model serves as an additional baseline to demonstrate that the LLMs are not merely averaging or interpolating values from the selected examples but may be identifying implicit patterns in the data. The results are shown in Fig. 3.

Fig. 3 Prediction performance of various LLMs and traditional ML models under different training neighbor settings. Three panels compare the model performance across neighbor selection methods (left to right): (a) farthest neighbors, (b) random neighbors, and (c) nearest neighbors. The TPOT-Mat performance is indicated by a horizontal grey line for benchmarking.

When trained with farthest neighbors, models generally exhibit high MAE with no clear trend as the number of neighbors increases. Most models perform worse than the KNN and RFR models except for claude-3.5-sonnet-20240620, which slightly outperforms the RFR models but still exhibits high MAE. These results suggest that, when provided with distant data points, both LLMs and traditional ML models struggle to make valid predictions. This highlights a key challenge in OOD generalization, as training examples that are too dissimilar to the test sample prevent models from capturing meaningful structure-property relationships, leading to higher prediction errors.

For the random neighbors training set, the LLMs' performance consistently improves as the dataset size increases. This suggests that randomly composed few-shot examples offer a more balanced and diverse learning environment for these models, allowing models to develop more robust generalization. The claude-3.5-sonnet-20240620 and gpt-4o-2024-11-20 models consistently outperform the RFR models as the data size increases, indicating that their more sophisticated architectures and larger training corpora enhance their ability to analyze and interpret complex data relationships more effectively. On the other hand, the smaller and older LLMs (i.e., cohere-command-r7b-12-2024 and gpt-3.5-turbo-1106) exhibit higher MAE values throughout. The random neighbors setting appears to challenge these models to a greater degree, likely due to their smaller scale and pretraining, which limit their ability to generalize effectively to diverse inputs without fine-tuning or additional data processing. However, while their overall performance remains lower, their MAE decreases more significantly with more few-shot examples, suggesting that these LLMs can benefit from more context.

The nearest neighbors represent the most relevant data points in the compositional space to the test points. As expected, the KNN shows an increase in MAE as the number of neighbors grows, since additional neighbors are more distant from the prediction target. If LLMs rely solely on the provided information without additional internal computation, a similar performance decline would be expected. Contrastingly, as the data size increases, all the LLMs show a consistent decrease in MAE and outperform the KNN model after 5 points. Among traditional models, the RFR trained directly on elemental compositions outperforms the version trained on MAGPIE features. This observation is consistent with the training data selection strategy, which was based on compositional similarity to the prediction target and thus more aligned with raw compositions than with derived features. Nonetheless, claude-3.5-sonnet-20240620 still consistently outperforms both RFR models, suggesting that advanced LLMs can capture more complex relationships in the data rather than solely relying on interpolation from the provided examples. Notably, with 25 nearest neighbors, claude-3.5-sonnet-20240620 achieves an MAE of 80.5, nearly matching the best-performing ML model, TPOT-Mat, which achieves an MAE of 79.9 on the matbench_steels dataset.⁵⁴ However, it is important to note that this is not a direct comparison, as TPOT-Mat employs a 5-fold nested cross-validation method on Matbench datasets,³⁴ which uses 80% of the data and is likely to result in better performance. The results highlight the potential of LLMs in data-lean materials property prediction tasks without the need for feature engineering, particularly given their general-purpose design and lack of task-specific fine-tuning.

The results suggest that pretrained LLMs may exhibit adaptability to new predictive challenges using ICL, particularly when data availability is limited. While their ability to extract patterns from a small number of examples is promising, their performance remains task-dependent and may not generalize across all types of property predictions. A key insight is that LLMs can be potentially valuable in early-stage research or exploratory studies in materials science, where data may be scarce or costly to obtain. One potential use case is active learning, where LLMs help identify the most informative data points for experimental validation, optimizing the data acquisition process and reducing the number of required experiments while still achieving meaningful insights. However, as the number of data points increases, most LLMs suffer from limited prompt windows, which make such applications computationally expensive or impossible, in which case fine-tuned LLMs and traditional machine learning models with dedicated training may be more effective.

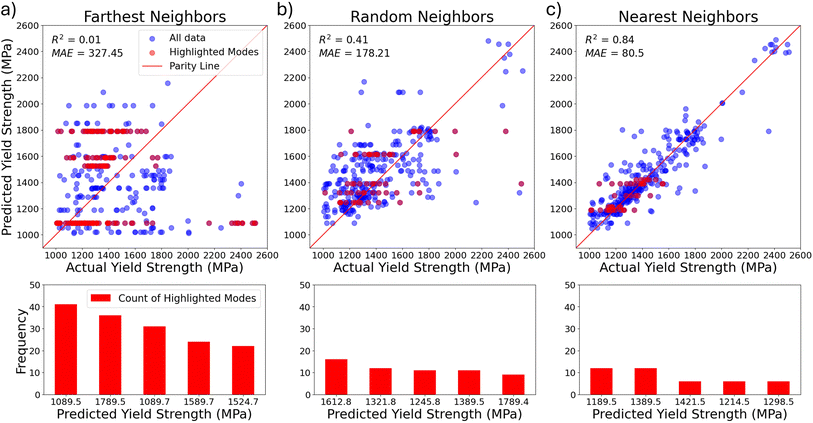
To investigate the model's predictive behaviors under these different settings, we analyzed the parity plots of the claude-3.5-sonnet-20240620's predictions when utilizing 25 neighboring data points, as shown in Fig. 4. A parity plot compares the predicted values against the ground truth values. Perfect predictions fall along the diagonal line while deviation from this line indicates prediction errors. Alongside these plots, the figure also includes histograms of the top five most frequently predicted yield strength values, to investigate whether the model is merely guessing a few commonly present values (shown as the red points in the parity plots). This behavior is known as “mode collapse”, whereby a generative model can favor a certain output due to overfitting to its pretraining data or lack of generalization capability.⁵⁵ Understanding mode collapse is crucial for evaluating the robustness of LLMs because it directly impacts the model's reliability and utility in practical applications. By identifying the mode collapse behavior, one can evaluate the validity of those predictions and potentially improve the performance.

Fig. 4 Parity plots (top) and associated histograms (bottom) of highlighted modes of claude-3.5-sonnet-20240620 with 25 neighboring data points under different training neighbor settings: (a) farthest neighbors, (b) random neighbors, and (c) nearest neighbors, from left to right.

In the farthest neighbors setting, the red points in the figure form horizontal lines, indicating that the model frequently predicts the same yield strength values regardless of composition. This suggests that it fails to capture the underlying relationship between composition and yield strength effectively. The histogram further reveals a strong mode collapse behavior, with the model repeatedly predicting a set of values. This suggests that the model may be defaulting to a “safe” prediction range when provided with less relevant examples. This aligns with the shortcut learning behavior observed in LLMs, where models rely on superficial correlations rather than learning meaningful patterns from the data.⁵⁶ Instead of extrapolating from compositional trends, the model may be leveraging spurious cues from its training distribution, leading to repetitive and less informative predictions. In the random neighbors setting, the model shows better overall performance and a reduced mode collapse behavior. This suggests that introducing more variability into the few-shot examples helps the model to better understand the underlying patterns that predict yield strength. The nearest neighbors setting exhibits the best performance, suggesting that higher proximity can lead to more accurate predictions. The mode collapse behavior is significantly reduced compared to the farthest neighbors and random neighbors, showing a greater diversity in the model's output.

The observations show varying degrees of mode collapse based on the proximity of prompt examples to the test point. For instance, when provided with more closely related few-shot examples, the model exhibits stronger predictive signals with fewer repeated outputs. The results from Fig. 3 and 4 suggest that LLMs do not appear to develop an intrinsic understanding of structure-property relationships but instead rely heavily on contextual information from the prompt. Pretrained LLMs are uncalibrated classifiers that can be overconfident in OOD scenarios, causing them to default to high-probability responses from their pretraining data and lead to repeated or generic outputs.^57–59 The mode collapse behavior and poor OOD generalization may be exacerbated by token frequency biases from overexposure to syntactic or uninformative data during pretraining,⁶⁰ as well as by LLMs' limited compositional reasoning capabilities, which hinder their ability to generalize from dissimilar few-shot examples.⁶¹ Although this limits the utility of LLMs in extrapolative property prediction tasks in OOD settings, the observed mode collapse can be repurposed as a proxy for epistemic uncertainty. In the context of active learning, the mode collapse behavior could serve as a self-diagnostic tool for guiding data acquisition – when a model repeatedly generates identical outputs across varied inputs, it may reflect a lack of confidence or failure to generalize. Such occurrences can be used to identify regions of high model uncertainty where additional experimental validation is most needed.

3.3 Robustness analysis of materials science Q&A

In Fig. 5, we present the outcomes of the robustness assessment of gpt-3.5-turbo-0613 and gpt-4o-2024-11-20 when confronted with different types of textual modifications to the MSE-MCQs (see Table 2), to evaluate its stability to various types of “noise”. The comparison of these two models further demonstrates how the evolution of LLMs has influenced their robustness, contextual understanding, and overall reliability in processing modified inputs.

Fig. 5 Robustness analysis of (a) gpt-3.5-turbo-0613, (b) gpt-4o-2024-11-20, and (c) DeepSeek-R1 in materials science Q&A using MSE-MCQs dataset. The error bars represent the standard deviation due to LLMs' non-determinism (original, synonym replacement, distractive info) and the randomness (sentence reordering, unit mixing, superfluous info) introduced to the questions.

Ranking by the degradation severity on the easy-level questions for gpt-3.5-turbo-0613, sentence reordering has the least performance drop, followed by synonym replacement, distractive info, unit mixing, and superfluous info. The performance on the hard-level questions is close to the baseline score, indicating that gpt-3.5-turbo-0613 struggles with complex queries regardless of textual modifications, and thus will not be discussed in detail. The larger error bars in medium and hard questions suggest that LLMs tend to generate more varied responses to complex and lengthy queries. In contrast, the newer and more advanced model, gpt-4o-2024-11-20, shows minimal degradation on the easy-level questions, maintaining an accuracy above 0.8, except for unit mixing. This suggests that the model is better at handling text changes and more robust than its predecessor. However, performance degradation becomes more noticeable on medium and hard questions. DeepSeek-R1, as a reasoning model, exhibits the strongest robustness among the three. Across all perturbation types and difficulty levels, it consistently achieves high accuracy, often above 0.9. Similar to gpt-4o-2024-11-20, unit mixing caused the most notable degradation, suggesting minor limitations in numerical reasoning and unit conversion. Nonetheless, its performance remains stable under all syntax-disrupting and distractive perturbations, demonstrating its strong parsing and reasoning capabilities overall.

Sentence reordering has little effect on the performance of all three models on easy-level questions, indicating that they can effectively parse and extract key information even when the natural flow of a question is altered. However, the impact becomes more significant on medium and hard-level questions, where reordering appears to disrupt comprehension more significantly. This suggests that while the models exhibit strong syntactic flexibility in simpler cases, they may rely more heavily on common question structures when dealing with more complex queries.

The slight performance drop with synonym replacement in gpt-3.5-turbo-0613 and gpt-4o-2024-11-20 suggests that both models are somewhat sensitive to changes in terminology, leading to inconsistencies in their responses. This reveals a reliance on specific wording for recognition and comprehension in materials science. Unlike humans, who can grasp the conceptual continuity behind varied expressions for flexible cognition, these models' struggles with synonym replacement emphasize the need for advanced training that prioritizes semantic networks over mere word recognition.⁶² Contrastingly, DeepSeek-R1 shows a slight improvement under synonym replacement, indicating that its reasoning-oriented architecture may better capture underlying semantic relationships and handle paraphrased inputs more effectively.

Introducing distractive information simulates a real-world scenario where irrelevant data often accompanies critical information, requiring sharp focus and analytical precision. Improving LLMs' ability to filter out irrelevant information is crucial for more effective information retrieval, problem-solving, and data interpretation.⁶³ While gpt-3.5-turbo-0613 shows slight degradation on easy-level questions, both gpt-4o-2024-11-20 and DeepSeek-R1 generally maintain or even improve their performance across difficulty levels. This suggests that the added information may inadvertently help the more advanced models by reinforcing key concepts or encouraging deeper contextual reasoning, aligning with the mechanisms of guided reasoning and selective attention.

Mixing and converting the units tests LLMs' abilities to perform numerical reasoning and apply mathematical concepts within a linguistic context. The added complexity introduced by unit mixing degraded the performance of all the models, indicating challenges in handling numerical transformations embedded in text. Although some state-of-the-art LLMs support multi-modal applications and function calls to perform calculations,⁶⁴ accurately identifying and converting units within large text can still be critical. Improving this ability could enhance LLMs' effectiveness in tasks such as information retrieval, data interpretation, and scientific analysis, where precise numerical reasoning is essential.

Superfluous information differs from distractive information in that it is more relevant to the questions themselves. The extent of performance degradation is likely influenced by the type and relevance of the superfluous information provided. The results show that gpt-3.5-turbo-0613 struggles significantly with superfluous information, experiencing the most severe performance degradation among all modifications. This suggests that it has difficulty filtering out non-essential details, leading to confusion or misinterpretation. In contrast, gpt-4o-2024-11-20 remains largely unaffected on easy and medium questions, but experiences moderate degradation on hard questions. Similarly, DeepSeek-R1 experiences a slight drop on medium and hard questions, though it still maintains high overall performance. These results suggest that while the more advanced models demonstrate stronger information selection capabilities, their ability to filter out unnecessary details weakens as question complexity increases. For LLMs, distinguishing the necessary information from merely relevant but non-essential details is a more challenging cognitive process, mirroring advanced human problem-solving. It requires an understanding of the problem's objective, prioritizing information based on the question, and applying only the information that will lead to the correct conclusion. This highlights a potential area for improvement in LLMs, particularly in their ability to assess and prioritize critical information in complex reasoning tasks.

3.4 Robustness analysis of materials property prediction

Table 3 shows the result of the degradation study on the LLM-Prop model, demonstrating how the LLM's performance on the band gap prediction is affected by various modifications to the textual descriptions of material crystal structures.

Table 3 Mean absolute error (MAE) under different conditions

	Original	Distractive info	Sentence reordering	Misleading info
MAE (eV)	0.286	0.287	0.323 ± 0.002	0.398 ± 0.005

---

After adding distractive information to the material descriptions, the LLM-Prop model showed negligible degradation, indicating this application-specific model can effectively differentiate relevant from irrelevant information. This resilience, likely due to the targeted training and fine-tuning on domain-specific texts, enables it to focus on key features for band gap prediction. This showcases the potential noise-filtering capabilities of the trained and fine-tuned transformer models, which traditional ML models may suffer from.

The impact of sentence reordering increased the MAE by 12.9%, suggesting the model's reliance on the structured descriptions for accurate predictions. From the previous study on MSE-MCQs degradation, the effect of sentence reordering was less significant, indicating that larger general LLMs, which are trained with more various texts, can exhibit better contextual understanding and are less prone to order changes.

The presence of misleading information, particularly an additional sentence from another material's description, leads to a 39% increase in MAE. This substantial degradation indicates that while the model can filter out irrelevant distractive noise, it struggles considerably when faced with data that is contextually relevant to the specific prediction task. Notably, this impact arises from the addition of just a single misleading sentence, highlighting the model's vulnerability to subtle contextual inconsistencies that misdirect its predictions.

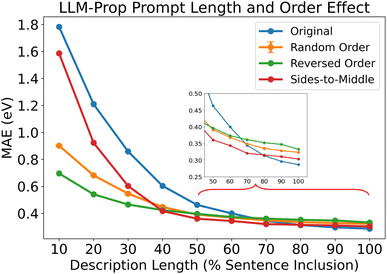
To further assess the model's robustness and determine which description elements are essential for prediction accuracy, we conducted a truncation study that involves altering the orders and lengths of the input description. As shown in Fig. 6, the description length is expressed as percent sentence inclusion, ranging from 10% to 100% and MAE is used as a measure of prediction accuracy.

Fig. 6 Order and length effect of LLM-Prop on prediction performance.

When the number of description sentences is incrementally increased, the MAE rapidly decreases and is minimized at 100% sentence inclusion. Interestingly, in the random order, reversed order, and sides-to-middle configurations, the initial MAE at 10% sentence inclusion is notably lower than in the original order, with some configurations achieving nearly double the performance of the original setting. This indicates that the initial sentences may not contain the most useful information for prediction. The MAEs begin to converge around 50% sentence inclusion, beyond which differences become statistically insignificant. Notably, in the random order setting, there is virtually no variation in the MAE when incorporating three different sentence shuffles. This suggests that LLM-Prop can effectively extract key information and deliver consistent predictions, despite variations in the sentence order.

By 40% sentence inclusion, the reversed order yields the lowest MAE, indicating that sentences at the end of descriptions contain crucial predictive information. However, by 50% sentence inclusion, the performance of the reversed order begins to align with that of the random order, suggesting that central information in the descriptions may not be as crucial for prediction accuracy. Since random order includes more initial sentences than reversed order, this suggests that the first sentences may contribute less relevant details, particularly at lower inclusion percentages. Based on these insights, we developed the sides-to-middle approach, aiming to prioritize information at the beginning and the end. This approach consistently outperforms other configurations between 40% and 70% sentence inclusion, achieving the lowest MAE in this range. The error continues to decrease and is optimized at full sentence inclusion being only 5.8% higher than the original setting in MAE. This result suggests that while the original order remains optimal, the contextual framing provided by the beginning and end of descriptions is particularly important for model accuracy.

This truncation study showcases that the fine-tuned model can perform effectively even when provided with significantly reduced prompts. We found that diverging from the training setup (i.e., changing the textual order of the prompt) can sometimes result in improved performance at truncated data volumes. This counterintuitive result suggests that highly templated training or fine-tuning data can lead to unexpected effects. Consequently, this implies two key considerations: (1) training templates should be diverse to prevent models from overfitting to unimportant patterns, and (2) when using a fine-tuned model trained on a specific template, it may not always be optimal to match the template during inference. These insights highlight the potential for optimizing training costs while maintaining performance.

4 Conclusions

The findings of this study offer crucial insights into the behaviors and limitations of LLMs in materials science domain-specific Q&A and materials property prediction. While the robustness analysis indicates that LLMs can manage certain types of noise with resilience, their performance is significantly challenged under more complex and deceptive conditions, such as when superfluous information is introduced. In Q&A tasks, prompting techniques (e.g., expert prompting, zero-shot chain-of-thought prompting) can sometimes improve the model performance in handling more complex queries, not by unlocking new capabilities, but by increasing the probability of following an expected format. In materials property predictions, we find that in-context learning allows pretrained LLMs to achieve relatively high accuracy in low-data settings when provided with few-shot examples with high proximity to the target material. However, the observed mode collapse behavior, where the model generates repeated outputs despite varying inputs, showcases that providing ineffective few-shot examples (i.e., out-of-distribution data points to the prediction target) can cause the model to default to a memorized response rather than conditioning its output on the provided prompt. Although this behavior reflects a limitation in model generalization, it could be repurposed as a useful diagnostic signal in active learning where repeated outputs across varied inputs may indicate regions of high uncertainty that require further experimental validation. This study also highlights that fine-tuned models can exhibit enhanced performance under truncated data conditions when diverging from the training setup, such as altering the textual order. While this suggests an unexpected level of robustness, it also exposes the risks associated with fixed templating during fine-tuning, suggesting that users should be cautious about strictly matching the training templates during inference. This study highlights the challenges and limitations of using LLMs in materials science, emphasizing the importance of better dataset curation, dynamic prompting techniques, and training strategies to enhance LLMs as reliable tools for materials discovery and scientific research.

Data and code availability

The datasets and code for the analyses and figure generations in this work are publicly available on GitHub at url: https://github.com/Toniaac/LLM-MSE-Eval-Robustness.git (DOI: https://doi.org/10.5281/zenodo.15330658). Detailed information on data and code access is provided in the README.md file in the GitHub repository.

Author contributions

H. W., E. K., and J. H. S. conceived and designed the project. E. K., and J. H. S. supervised the project. H. W. conducted the experiments. S. R. provided the dataset for materials science question & answering study. H. W., K. L., Y. F., E. K., and J. H. S. discussed the results. H. W. drafted the manuscript. All authors reviewed and edited the manuscript.

Conflicts of interest

The authors declare no conflicts of interest.

Acknowledgements

We acknowledge Andre Niyongabo Rubungo and Adji Bousso Dieng for providing the dataset and model for the LLM-Prop study. We thank Yingxi Wang for assistance with the table of contents artwork.

References

1. J. Clusmann, et al., Commun. Med., 2023, 3, 141.
2. T. Mishra, et al., Sci. Rep., 2024, 14, 31672.
3. D. A. Boiko, et al., Nature, 2023, 624, 570–578.
4. M. R. AI4Science and M. A. Quantum, The Impact of Large Language Models on Scientific Discovery: a Preliminary Study using GPT-4, arXiv, 2023, preprint, arxiv:2311.07361, https://arxiv.org/abs/2311.07361.
5. G. Lei, R. Docherty and S. J. Cooper, Materials science in the era of large language models: a perspective, arXiv, 2024, preprint, arxiv:2403.06949, https://arxiv.org/abs/2403.06949.
6. K. M. Jablonka, et al., Digital Discovery, 2023, 2, 1233–1250.
7. T. Gupta, et al., npj Comput. Mater., 2022, 8, 102.
8. H. Naveed et al., A Comprehensive Overview of Large Language Models, arXiv, 2024, preprint, arxiv:2307.06435, https://arxiv.org/abs/2307.06435.
9. Z. Wu et al., OpenICL: An Open-Source Framework for In-context Learning, arXiv, 2023, preprint, arxiv:2303.02913, https://arxiv.org/abs/2303.02913.
10. T. Z. Zhao et al., Calibrate Before Use: Improving Few-Shot Performance of Language Models, 2021, https://www.github.com/tonyzhaozh/few-shot-learning.
11. R. Vacareanu et al., From Words to Numbers: Your Large Language Model Is Secretly A Capable Regressor When Given In-Context Examples, arXiv, 2024, preprint, arxiv:2404.07544, https://arxiv.org/abs/2404.07544.
12. J. Schmidt et al., Recent advances and applications of machine learning in solid-state materials science, 2019.
13. P. Patwa et al., Enhancing Low-Resource LLMs Classification with PEFT and Synthetic Data, arXiv, 2024, preprint, arxiv:2404.02422, https://arxiv.org/abs/2404.02422.
14. J. Li et al., Large Language Models are In-Context Molecule Learners, arXiv, 2024, preprint, arxiv:2403.04197, https://arxiv.org/abs/2403.04197.
15. M. Zaki, et al., Digital Discovery, 2023, 3, 313–327.
16. L. S. Balhorn et al., What does ChatGPT know about natural science and engineering?, arXiv, 2023, preprint, arxiv:2309.10048, https://arxiv.org/abs/2309.10048.
17. A. Mirza et al., Are large language models superhuman chemists?, arXiv, 2024, preprint, arxiv:2404.01475, https://arxiv.org/abs/2404.01475.
18. A. N. Rubungo et al., LLM-Prop: Predicting Physical And Electronic Properties Of Crystalline Solids From Their Text Descriptions, arXiv, 2023, preprint, arxiv:2310.14029, https://arxiv.org/abs/2310.14029.
19. C. Qian et al., Can Large Language Models Empower Molecular Property Prediction?, arXiv, 2023, preprint, arxiv:2307.07443, https://arxiv.org/abs/2307.07443.
20. K. M. Jablonka, et al., Nat. Mach. Intell., 2024, 6, 161–169.
21. Y. Chiang et al., LLaMP: Large Language Model Made Powerful for High-fidelity Materials Knowledge Retrieval and Distillation, arXiv, 2024, preprint, arxiv:2401.17244, https://arxiv.org/abs/2401.17244.
22. K. Darvish, et al., Matter, 2025, 8, 101897.
23. T. Yin et al., Learning Advance: Robotics-LLM Guided Hypotheses Generation for the Discovery of Chemical Knowledge, 2025.
24. T. Niven and H.-Y. Kao, Probing Neural Network Comprehension of Natural Language Arguments, arXiv, 2019, preprint, arxiv:1907.07355, https://arxiv.org/abs/1907.07355.
25. P. A. Utama, N. S. Moosavi and I. Gurevych, Towards Debiasing NLU Models from Unknown Biases, arXiv, 2020, preprint, arxiv:2009.12303, https://arxiv.org/abs/2009.12303.
26. M. Du et al., Towards Interpreting and Mitigating Shortcut Learning Behavior of NLU Models, arXiv, 2021, preprint, arxiv:2103.06922, https://arxiv.org/abs/2103.06922.
27. Y. Zhao et al., Improving the Robustness of Large Language Models via Consistency Alignment, arXiv, 2024, preprint, arxiv:2403.14221, https://arxiv.org/abs/2403.14221.
28. J. Gu et al., Robustness of Learning from Task Instructions, arXiv, 2023, preprint, arxiv:2212.03813, https://arxiv.org/abs/2212.03813.
29. M. T. Hicks, J. Humphries and J. Slater, Ethics Inf. Technol., 2024, 26, 38.
30. DeepSeek-AI et al., DeepSeek-R1: Incentivizing Reasoning Capability in LLMs via Reinforcement Learning, arXiv, 2025, preprint, arxiv:, https://arxiv.org/abs/2501.12948.
31. T. Zhong et al., Evaluation of OpenAI o1: Opportunities and Challenges of AGI, arXiv, 2024, preprint, arxiv:2409.18486, https://arxiv.org/abs/2409.18486.
32. J. V. Herck, et al., Chem. Sci., 2025, 16, 670–684.
33. X. Jiang, et al., npj Comput. Mater., 2025, 11, 79.
34. A. Dunn, et al., npj Comput. Mater., 2020, 6, 138.
35. Anthropic, Introducing the next generation of Claude, 2024, https://www.anthropic.com/news/claude-3-family.
36. OpenAI et al., GPT-4o System Card, arXiv, 2024, preprint, arxiv:2410.21276, https://arxiv.org/abs/2410.21276.
37. OpenAI et al., GPT-4 Technical Report, arXiv, 2024, preprint, arxiv:2303.08774, https://arxiv.org/abs/2303.08774.
38. OpenAI, Introducing ChatGPT, 2022, https://openai.com/index/chatgpt/.
39. A. Grattafiori et al., The Llama 3 Herd of Models, arXiv, 2024, preprint, arxiv:2407.21783, https://arxiv.org/abs/2407.21783.
40. H. Touvron et al., Llama 2: Open Foundation and Fine-Tuned Chat Models, arXiv, 2023, preprint, arxiv:2307.09288, https://arxiv.org/abs/2307.09288.
41. B. Yu, Benchmarking Large Language Model Volatility, arXiv, 2023, preprint, arxiv:2311.15180, https://arxiv.org/abs/2311.15180.
42. C. Xu, Y. Wang and A. Barati Farimani, npj Comput. Mater., 2023, 9, 64.
43. J. Wei et al., Chain-of-Thought Prompting Elicits Reasoning in Large Language Models, arXiv, 2023, preprint, arxiv:2201.11903, https://arxiv.org/abs/2201.11903.
44. M. A. team, Large Enough, 2024, https://mistral.ai/en/news/mistral-large-2407.
45. A. Gomez, Introducing Command R7B: Fast and efficient generative AI, 2024, https://cohere.com/blog/command-r7b.
46. C. Team, Introducing Command A: Max performance, minimal compute, 2025, https://cohere.com/blog/command-a.
47. T. Gao, A. Fisch and D. Chen, Making Pre-trained Language Models Better Few-shot Learners, arXiv, 2021, preprint, arxiv:2012.15723, https://arxiv.org/abs/2012.15723.
48. L. Ward, et al., npj Comput. Mater., 2016, 2, 16028.
49. A. M. Ganose and A. Jain, MRS Commun., 2019, 9, 874–881.
50. C. Raffel et al., Exploring the Limits of Transfer Learning with a Unified Text-to-Text Transformer, 2020, http://jmlr.org/papers/v21/20-074.html.
51. E. Mitchell et al., DetectGPT: Zero-Shot Machine-Generated Text Detection using Probability Curvature, arXiv, 2023, preprint, arxiv:2301.11305, https://arxiv.org/abs/2301.11305.
52. K. Krishna et al., RankGen: Improving Text Generation with Large Ranking Models, arXiv, 2022, preprint, arxiv:2205.09726, https://arxiv.org/abs/2205.09726.
53. S. Ouyang et al., LLM is Like a Box of Chocolates: the Non-determinism of ChatGPT in Code Generation, arXiv, 2023, preprint, arxiv:2308.02828, https://arxiv.org/abs/2308.02828.
54. R. S. Olson and J. H. Moore, in TPOT: A Tree-Based Pipeline Optimization Tool for Automating Machine Learning, ed. F. Hutter, L. Kotthoff and J. Vanschoren, Springer International Publishing, Cham, 2019, pp. 151–160.
55. H. Thanh-Tung and T. Tran, On Catastrophic Forgetting and Mode Collapse in Generative Adversarial Networks, arXiv, 2020, preprint, arxiv:1807.04015, https://arxiv.org/abs/1807.04015.
56. M. Du et al., Shortcut Learning of Large Language Models in Natural Language Understanding, arXiv, 2023, preprint, arxiv:2208.11857, https://arxiv.org/abs/2208.11857.
57. M. Xiong et al., Can LLMs Express Their Uncertainty? An Empirical Evaluation of Confidence Elicitation in LLMs, arXiv, 2024, preprint, arxiv:2306.13063, https://arxiv.org/abs/2306.13063.
58. B. Wen et al., NeurIPS 2024 Workshop on Behavioral Machine Learning, 2024.
59. W. Shi et al., Trusting Your Evidence: Hallucinate Less with Context-aware Decoding, arXiv, 2023, preprint, arxiv:2305.14739, https://arxiv.org/abs/2305.14739.
60. E. Dohmatob, Y. Feng and J. Kempe, Model Collapse Demystified: The Case of Regression, arXiv, 2024, preprint, arxiv:2402.07712, https://arxiv.org/abs/2402.07712.
61. Z. Li et al., Understanding and Patching Compositional Reasoning in LLMs, arXiv, 2024, preprint, arxiv:2402.14328, https://arxiv.org/abs/2402.14328.
62. J. Ye et al., LLM-DA: Data Augmentation via Large Language Models for Few-Shot Named Entity Recognition, arXiv, 2024, preprint, arxiv:2402.14568, https://arxiv.org/abs/2402.14568.
63. S. Wu et al., How Easily do Irrelevant Inputs Skew the Responses of Large Language Models?, arXiv, 2024, preprint, arxiv:2404.03302, https://arxiv.org/abs/2404.03302.
64. C. Wang et al., MLLM-Tool: A Multimodal Large Language Model For Tool Agent Learning, arXiv, 2024, preprint, arxiv:2401.10727, https://arxiv.org/abs/2401.10727.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5dd00090d

---