Open Access Article
Open Access ArticleMachine learning-assisted profiling of a kinked ladder polymer structure using scattering†
Lijie
Ding
 a,
Chi-Huan
Tung
a,
Zhiqiang
Cao
a,
Zekun
Ye
b,
Xiaodan
Gu
a,
Chi-Huan
Tung
a,
Zhiqiang
Cao
a,
Zekun
Ye
b,
Xiaodan
Gu
 c,
Yan
Xia
c,
Yan
Xia
 b,
Wei-Ren
Chen
b,
Wei-Ren
Chen
 a and
Changwoo
Do
a and
Changwoo
Do
 *a
*a
aNeutron Scattering Division, Oak Ridge National Laboratory, Oak Ridge, TN 37831, USA. E-mail: doc1@ornl.gov
bDepartment of Chemistry, Stanford University, Stanford, CA 94305, USA
cSchool of Polymer Science and Engineering, Center for Optoelectronic Materials and Devices, The University of Southern Mississippi, Hattiesburg, MS 39406, USA
First published on 21st May 2025
Abstract
Ladder polymers consisting of fused rings in the backbone have very limited conformational freedom, which results in very different properties from traditional linear polymers. However, accurately determining their size and chain conformations from solution scattering remains a challenge. Their chain conformations of kinked ladder polymers are largely governed by the structures and relative orientations or configurations of the repeat units, unlike conventional polymer chains whose bending angles between repeat units follow a unimodal Gaussian distribution. Meanwhile, traditional scattering models for polymer chains do not account for these unique structural features. This work introduces a novel approach that integrates machine learning with Monte Carlo simulations to construct a model that can describe the geometry of a type of kinked CANAL ladder polymers. We first develop a Monte Carlo simulation model for sampling the configuration space of CANAL ladder polymers, where each repeat unit is modeled as a biaxial segment. Then, we establish a machine learning-assisted scattering analysis framework based on Gaussian Process Regression. Finally, we conduct small-angle neutron scattering experiments on a CANAL ladder polymer solution to apply our approach. Our method uncovers structural features of such ladder polymers that conventional methods fail to capture.
1 Introduction
Ladder polymers are a unique polymer architecture, consisting of continuously fused, conformationally restrictive rings.1–3 Such unique backbone structures result in many different properties from traditional linear polymers, which are desired in a range of applications ranging from electronics to membrane separations.1–3 In particular, non-conjugated ladder polymers are characteristic of their kinked rigid conformations.2,4 Xia and coworkers have developed a type of kinked ladder polymer via catalytic arene norbornene annulation (CANAL) using norbornadiene and aryl dibromides as monomers.5 The rigid and frequently kinked structures of CANAL polymers result in frustrated packing and high microporosity.5,6 Certain CANAL polymer films can exhibit strong size sieving effect and remarkable performance in gas separations.6 Probing the overall conformations and dimensional characteristics of CANAL ladder polymers is the first step toward understanding their macromolecular packing behavior. CANAL reaction results in norbornyl benzocyclobutene structures with exclusive exo-configuration.5 In CANAL polymerization, the bridge carbon of neighboring norbornyl units can orient to either the same or opposite side of the ladder chain, resulting in syn or anti-configuration, respectively, as shown in Fig. 1. The sequence and distribution of these configurations determine the overall ladder chain dimensions. Therefore, it is important to first develop a model that can describe the statistical distribution of the syn and anti-configurations in a CANAL ladder polymer chain.Small angle scattering experiments,7 including X-ray scattering8 and neutron scattering9,10 are often used to study the characteristics of polymer system, and to unveil the single polymer structure using dilute polymer solutions. The scattering data is often analyzed using various polymer models to extract the polymer parameters, e.g. contour length, radius of gyration and persistence length. However, traditional polymer models, such as Gaussian coils11 or worm-like chains12 are inadequate for capturing the distinctive features of ladder polymers since they are designed to model the single-stranded polymers and discard bending. These models do not fully represent the inherent rigidity and extended conformation of the ladder polymer, thus fail to provide an accurate depiction of the ladder polymers structure.
To overcome these challenges and provide an accurate description of the ladder polymer structure using scattering data, we build a new model for the simplest CANAL ladder polymer consisting only fused norbornyl and benzocyclobutene units, produced from norbornadiene and dibromo-p-xylene. This model accounts for the biaxial nature of it's monomer structure and inherent rigidity. Due to the complexity of this model, it is difficult to derive the analytical form of the scattering function, which is typically required for fitting scattering data using traditional approaches. To address this, we leverage the power of Machine Learning (ML)13 and Monte Carlo (MC)14 simulations.
The recent advancements in ML have enabled numerous applications in materials science, including the analysis of scattering data15 without knowing an explicit analytical form. This approach relies on large data sets that include scattering functions and corresponding polymer parameters, allowing ML to learn the relationship between them. Meanwhile, MC can be used to build such data sets. Given a set of polymer parameters, such as contour length and bending rigidity, we can use MC simulation to generate an ensemble of the polymer conformations and calculate the structure factor, or scattering function. This combination of ML and MC provides a powerful framework for analyzing complex polymer systems and has been proven useful for various single-stranded polymer systems16–19 and other soft matter system.20 Other works such as SCAN automates structural analysis using predefined particle shape models, while CREASE employs genetic algorithms and surrogate ML to reconstruct 3D features—such as domain size, shape, orientation, and spatial distributions—from scattering profiles.21–24 Other ML approaches have been used for particle tracking in soft materials25 and for surface scattering analysis.26 Nevertheless, these methods do not provide insight for the model-specific parameters for systems like the ladder polymer and can not capture the unique structural nuances of such systems.
In this paper, we present a framework for analyzing the scattering data of ladder polymer using ML. We firstly introduce a model of the ladder polymer where the biaxiality, inherent rigidity and arrangement of successive monomers all play crucial role in determining the polymer conformation. We then carry out MC simulation to generate a large data set of the scattering data and train a ML model of Gaussian process regression27 (GPR) to obtain the mapping between scattering data and polymer parameters. Finally, we synthesize ladder polymer samples and measure the scattering function using small-angle neutron scattering (SANS) experiment and apply out method to the extract important polymer parameters for the measured sample. In contrast to conventional Gaussian process-based data inversion approaches,28–30 our approach avoid the potentially large computational cost in posterior sampling and predict each polymer parameters separately.
2 Model
To capture the ladder shape and biaxiality of the polymer, we model each monomer unit of the polymer as a rectangular segment whose orientation is specified by two unit vectors, û and![[v with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0076_0302.gif) , where û is along the along axis of the segment, or the polymer tangent direction, and
, where û is along the along axis of the segment, or the polymer tangent direction, and ![[v with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0076_0302.gif) is along the segment short axis and perpendicular to û. A polymer is then modeled as a chain of L segments, where L is the contour length in unit of monomer length B.
is along the segment short axis and perpendicular to û. A polymer is then modeled as a chain of L segments, where L is the contour length in unit of monomer length B.
Unlike conventional polymer, the successive segments on the ladder polymer, i.e. catalytic arene-norbornene annulation (CANAL) polymer, tend to form a angle, as shown in Fig. 2(a and b). We introduce another two unit vectors, û′ and ![[v with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0076_0302.gif) ′, to represent this preferred orientation for the successive segment. For two connecting segments i and j, the angle between (û,
′, to represent this preferred orientation for the successive segment. For two connecting segments i and j, the angle between (û, ![[v with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0076_0302.gif) ) and (û′,
) and (û′, ![[v with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0076_0302.gif) ′) is the inherent bending and twisting. For this specific model we are concerned of, the
′) is the inherent bending and twisting. For this specific model we are concerned of, the ![[v with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0076_0302.gif) =
= ![[v with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0076_0302.gif) ′, and we denote the inherent bending cos(α) = û·û′. There is a energy cost when (ûi+1,
′, and we denote the inherent bending cos(α) = û·û′. There is a energy cost when (ûi+1, ![[v with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0076_0302.gif) i+1) tilt away from
i+1) tilt away from  , given polymer energy
, given polymer energy  , where the bending is
, where the bending is  , twisting is
, twisting is  , and Kt and Kb are the twisting and bending modulus, respectively.
, and Kt and Kb are the twisting and bending modulus, respectively.
Finally, the preferred orientation for successive segment at each segment may not stay on the same side. Comparing Fig. 2(a and b), when they stay on the same side, we call them connected by syn links, the polymer rolls up and become coil shape as shown in Fig. 2(c). On the contrary, if they flip side, or connected by anti links, the polymer tend to extend longer, as shown in Fig. 2(d). We define the probability of a link being a anti link as anti rate Ra.
Given a contour length L, inherent bending angle α, anti rate Ra, bending modulus Kt and twisting modulus Kb, the ensemble of ladder polymer configuration is determined. The configuration can be captured by the intra-polymer structure factor, given by:7,9
 | (1) |
 is the position vector of segment i and
is the position vector of segment i and  . In addition, we also calculate the radius of gyration
. In addition, we also calculate the radius of gyration  , with 〈⋯〉i,j denoting the average over all pairs of segments. We will use MC and ML to understand the relationship between structure factor S(QB) and other polymer parameters (Ra, α, L, Rg2, Kt, Kb).
, with 〈⋯〉i,j denoting the average over all pairs of segments. We will use MC and ML to understand the relationship between structure factor S(QB) and other polymer parameters (Ra, α, L, Rg2, Kt, Kb).
3 Method
3.1 Synthesis of CANAL ladder polymer
To a flame-dried 15 mL glass pressure tube was added 1,4-dibromo-2,5-diethylbenzene31 (584 mg, 2 mmol), Pd(OAc)2 (9 mg, 0.04 mmol), PPh3 (21 mg, 0.08 mmol) and butylated hydroxytoluene (1 mg). The tube was transferred into a nitrogen-filled glove box, and norbornadiene (220 μL, 2.2 mmol), Cs2CO3 (1.3 mg, 4 mmol) and THF (2 mL) was added. The tube was sealed with a Teflon cap and removed from the glovebox. The reaction mixture was heated to 150 °C for 24 h. The mixture was then cooled to room temperature and passed through Celite to remove inorganic salts. Chloroform (3 × 5 mL) was used to wash the residue. The filtrate was concentrated and dissolved in a minimum amount of chloroform, which was then precipitated into methanol. The precipitated polymer was collected by centrifugation, washed with methanol, and dried under vacuum. The obtained polymer were fractionated using Soxhlet Extractor to generate low molecular weight polymer fraction (washed down from ethyl acetate) and high molecular weight polymer fraction (washed down from choloroform).3.2 Small-angle neutron scattering
The extended Q-range small-angle neutron diffractometer (EQ-SANS) at the Spallation Neutron Source at the Oak Ridge National Laboratory was used to characterize the conformation of the ladder polymer.32,33 Low molecular weight CANAL ladder polymer was dissolved in deuterated 1,2-dichlorobenzene at 5 mg mL−1. Two sample-to-detector distances (2.5 m and 4 m) were used with two wavelength bands defined by the minimum wavelength of λmin = 2.5 Å and λmin = 10 Å, respectively, to cover scattering wave vectors ranging from 0.006 to 0.5 Å−1. The choppers were operated at 60 Hz. The ladder polymer solution was loaded in the quartz cell of 2 mm path length and measured at 25 °C, 75 °C and 125 °C. The measured data were corrected by detector sensitivity and background scattering from the empty cell and then converted into absolute scale intensities (cm−1) using a porous silica standard sample.34,35 Finally, scattering from the solvent was subtracted before the data is scaled into the unit-less QB axis using the monomer length B.3.3 Monte Carlo simulation
To calculate the intra-polymer structure factor of the polymer ensemble at various polymer parameters, we sample the configuration space of the polymer using direct sampling.14 For a given set of (Ra, α, L, Kt, Kb), we generate 2000 polymer configurations and calculate the averaged structure factor S(QB). The polymer configuration is determined by the link type li, relative bending and twisting angles {(li, θi, ϕi)}, letting li = 0 represent syn link and li = 1 denotes anti link, the li follows a Bernoulli distribution with probability P(li = 1) = Ra. In addition θi and ϕi follows the Gaussian distribution and
and  , as they are independent in the polymer energy
, as they are independent in the polymer energy  , which follow the Boltzmann distribution P(E) ∼ e−E/kBT. After sampling {(li, θi, ϕi)} for all segments based on their distribution, we calculate (ui, vi) and
, which follow the Boltzmann distribution P(E) ∼ e−E/kBT. After sampling {(li, θi, ϕi)} for all segments based on their distribution, we calculate (ui, vi) and  of each polymer segments, then check the self-avoidance criteria
of each polymer segments, then check the self-avoidance criteria  for all pairs of segments, only configurations satisfying these criteria are kept.
for all pairs of segments, only configurations satisfying these criteria are kept.
3.4 Gaussian process regression
Under the framework of GPR,27 the goal is to obtain the posterior p(Y*|X*, X, Y) of the function output y, where X = {ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S(QB)train}, X* = {ln
S(QB)train}, X* = {ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S(QB)test} are the training set and test set, Y and Y* are the corresponding polymer parameters (Ra, α, L, Rg2). In our case, we use 70% of the data set F = {ln
S(QB)test} are the training set and test set, Y and Y* are the corresponding polymer parameters (Ra, α, L, Rg2). In our case, we use 70% of the data set F = {ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S(QB)} as the training set, and the rest 30% as the test set. The joint distribution is for a Gaussian process is given by eqn (2)
S(QB)} as the training set, and the rest 30% as the test set. The joint distribution is for a Gaussian process is given by eqn (2) | (2) |
 are used, in which l is the correlation length, σ is the variance of observational noise and δ is the Kronecker delta function.
are used, in which l is the correlation length, σ is the variance of observational noise and δ is the Kronecker delta function.
4 Results
We prepare the data set F = {ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S(QB)} by generating conformations of ladder polymers using MC for 6000 random combination of (Ra, α, L, Kt, Kb) and calculate the corresponding Rg2 and S(QB). The S(QB) are calculated for 100 different QB ∈ [0.07, 3], such that the ln
S(QB)} by generating conformations of ladder polymers using MC for 6000 random combination of (Ra, α, L, Kt, Kb) and calculate the corresponding Rg2 and S(QB). The S(QB) are calculated for 100 different QB ∈ [0.07, 3], such that the ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) QB grid is uniformly placed in this interval. The polymer parameters are sampled as Ra ∼ U(0, 1),
QB grid is uniformly placed in this interval. The polymer parameters are sampled as Ra ∼ U(0, 1),  , L ∼ U(4, 50), Kt ∼ U(50, 100) and Kb ∼ U(50, 100), where U(a, b) is the uniform distribution in interval [a, b]. In practice, these simulations are carried out in parallel on different CPUs, and each simulation takes up to half hour to complete. Natural units are used, such that length are in unit of segment or monomer length B, and energy are measured in unit of thermal noise kBT. We firstly study the effect of polymer parameters on the structure factor, then validate the feasibility for ML inversion of each polymer parameter, train a GPR and test it using MC generated data. Finally, we carry out SANS experiment and applied the trained GPR to the experimentally obtained structure factor.
, L ∼ U(4, 50), Kt ∼ U(50, 100) and Kb ∼ U(50, 100), where U(a, b) is the uniform distribution in interval [a, b]. In practice, these simulations are carried out in parallel on different CPUs, and each simulation takes up to half hour to complete. Natural units are used, such that length are in unit of segment or monomer length B, and energy are measured in unit of thermal noise kBT. We firstly study the effect of polymer parameters on the structure factor, then validate the feasibility for ML inversion of each polymer parameter, train a GPR and test it using MC generated data. Finally, we carry out SANS experiment and applied the trained GPR to the experimentally obtained structure factor.
4.1 Intra-polymer structure factor of the ladder polymer
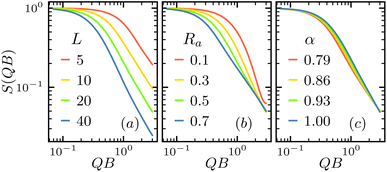
While the polymer energy is only directly related to the bending modulus Kb and twisting modulus Kt, these modulus are relative large as the segments are connected by strong chemical bonds, leaving the major conformation change determined by the inherent bending angle α, and anti rate Ra. These conformation change is captured by the structure factor. Fig. 3 shows the S(QB) at various contour length L, anti rate Ra and inherent bending angle α. As shown in Fig. 3(a), increasing the contour length lead to rapid decrease of S(QB), resulting from the extension of the polymer that increase the scattering at low Q. Fig. 3(b) shows that increasing anti rate Ra has similar effect of increasing L, as it also make the polymer extending longer. Increasing inherent bending angle α make the opposite effect and increase the S(QB) as it effectively make the polymer more straight.4.2 Feasibility of machine learning inversion
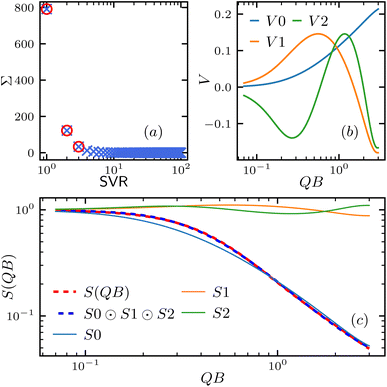
To access the feasibility of using GPR to map the structure factor F = {ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S(QB)} to polymer parameters Y = {(Ra, α, L, Rg2, Kt, Kb)}, following the similar ML inversion framework,15 we carry out principle component analysis of 6000 × 100 matrix F, by decomposing it into F = UΣVT using singular value decomposition (SVD), where U, Σ, and V are matrices of 6000 × 6000, 6000 × 100, and 100 × 100 sizes, respectively. V is consist of the singular vectors, and the entries of Σ2 are proportional to the variance of the projection of F onto corresponding principal vectors in V.
S(QB)} to polymer parameters Y = {(Ra, α, L, Rg2, Kt, Kb)}, following the similar ML inversion framework,15 we carry out principle component analysis of 6000 × 100 matrix F, by decomposing it into F = UΣVT using singular value decomposition (SVD), where U, Σ, and V are matrices of 6000 × 6000, 6000 × 100, and 100 × 100 sizes, respectively. V is consist of the singular vectors, and the entries of Σ2 are proportional to the variance of the projection of F onto corresponding principal vectors in V.
As shown in Fig. 4(a), the singular value decays rapidly with its rank, suggesting the projecting ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S(QB) ∈ F onto the space spanned by the high rank singular vectors manifest good approximation of the entire ln
S(QB) ∈ F onto the space spanned by the high rank singular vectors manifest good approximation of the entire ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S(QB). Fig. 4(b) shows the first three singular vectors (V1, V2, V3), and Fig. 4(c) demonstrate the projection of ln
S(QB). Fig. 4(b) shows the first three singular vectors (V1, V2, V3), and Fig. 4(c) demonstrate the projection of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S(QB) on to these top 3 singular vectors do recover the original ln
S(QB) on to these top 3 singular vectors do recover the original ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S(QB) very well.
S(QB) very well.
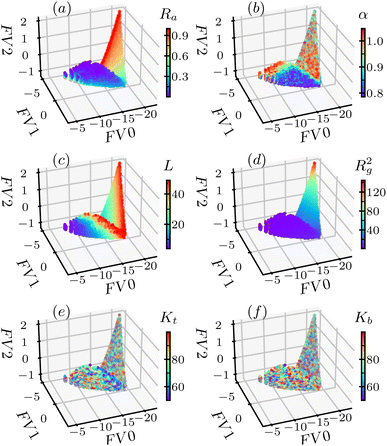
By projecting the F = {ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S(QB)} onto the singular vector space of (V0, V1, V2), each ln
S(QB)} onto the singular vector space of (V0, V1, V2), each ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S(QB) become a coordinate in the three dimensional space, (FV0, FV1, FV2), and the entire set of coordinates provides a good proxy of the raw data set F. By plotting the distribution of polymer parameters Y in the (FV0, FV1, FV2), Fig. 5 provide insight for the feasibility of ML inversion of each of the polymer parameter, int which the corresponding value are represented by color distribution.
S(QB) become a coordinate in the three dimensional space, (FV0, FV1, FV2), and the entire set of coordinates provides a good proxy of the raw data set F. By plotting the distribution of polymer parameters Y in the (FV0, FV1, FV2), Fig. 5 provide insight for the feasibility of ML inversion of each of the polymer parameter, int which the corresponding value are represented by color distribution.
As shown in Fig. 5(a–d), the polymer parameters (Ra, α, L, Rg2) are well spread out in the (FV0, FV1, FV2) space, indicating a good reversed mapping from ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S(QB) to these parameters, indicating they are good inversion targets. On the contrary, Fig. 5(e and f) show that the distribution of the bending and twisting modulus Kb and Kt are rather random, suggesting there they can not be easily extract from the ln
S(QB) to these parameters, indicating they are good inversion targets. On the contrary, Fig. 5(e and f) show that the distribution of the bending and twisting modulus Kb and Kt are rather random, suggesting there they can not be easily extract from the ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S(QB). This is in line with our expectation as the conformation of the ladder polymer is not sensitive to the wiggling around the inherent bending angle α since α is very large compare to the flexibility of the chemical bond.
S(QB). This is in line with our expectation as the conformation of the ladder polymer is not sensitive to the wiggling around the inherent bending angle α since α is very large compare to the flexibility of the chemical bond.
4.3 Machine learning inversion of simulation data
With the feasibility for ML inversion for (Ra, α, L, Rg2) from the ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S(QB) established, we test such inversion using simulation data. We divide the data set F = {ln
S(QB) established, we test such inversion using simulation data. We divide the data set F = {ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S(QB)} randomly into two parts, a training set {ln
S(QB)} randomly into two parts, a training set {ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S(QB)train} consisting 70% of F and a testing set {ln
S(QB)train} consisting 70% of F and a testing set {ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S(QB)test} made of the rest 30%. We optimize the hyperparameters of the GPR model using the training set for each polymer parameter and then extract the corresponding polymer parameters (Ra, α, L, Rg2) from the ln
S(QB)test} made of the rest 30%. We optimize the hyperparameters of the GPR model using the training set for each polymer parameter and then extract the corresponding polymer parameters (Ra, α, L, Rg2) from the ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S(QB) ∈ {ln
S(QB) ∈ {ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S(QB)test}. The scikit-learn Gaussian process library36 was used for the training. Table 1 shows the optimized hyperparameters for each polymer parameters, obtained by maximizing the log marginal likelihood27 as shown in Fig. 6.
S(QB)test}. The scikit-learn Gaussian process library36 was used for the training. Table 1 shows the optimized hyperparameters for each polymer parameters, obtained by maximizing the log marginal likelihood27 as shown in Fig. 6.
| l | σ | |
|---|---|---|
| R a | 6.497 × 10−1 | 6.301 × 10−4 |
| α | 3.570 × 10−1 | 1.585 × 10−2 |
| L | 1.043 | 4.442 × 10−3 |
| R g 2 | 3.843 | 1.447 × 10−7 |
Fig. 7 shows the comparison between the polymer parameters (Ra, α, L, Rg2)obtained from ML inversion and the corresponding MC references. The data agree very well, and lie closely to the diagonal line, with coefficient of determination r2 score close to 1. The high precision highlights the effectiveness of extracting key parameters from the structure factor and further confirms the robustness of our GPR model. These results also indicate that, for our model, these polymer parameter can be extracted from the scattering curve independently, whereas there may need to be additional constraints in some cases, e.g. charged polymer.18
 | ||
| Fig. 7 Comparison of polymer parameters in simulation and inverted by machine learning. (a) Anti rate Ra. (b) Inherent bending angle α. (c) Contour length L. (d) Radius of gyration Rg2. | ||
4.4 Analysis of experimental measurement
To put our ML inversion model into practice, we synthesize CANAL ladder polymer and carry out small-angle neutron scattering (SANS) experiment to measure it's form factor.
Fig. 8 shows normalized form factor measured from the SANS experiment and the ML implied curve. The SANS measured S(QB) shows good flat part in the low Q region in the log–log plot, allow us to fit for the normalization coefficient using Guinier approximation7,37S(QB) ∼ e−(QRg)2/3, and the monomer length B obtained by molecular structure optimization allow us to rescale the horizontal axis. By feeding the normalized experimental ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S(QB) to the trained GPR, we obtain the polymer parameters (Ra, α, L, Rg2), as shown in Table 2, and then run MC simulation with these parameters to reconstruct the ML implied S(QB). The SANS measured S(QB) and the Ml implied one agree closely. As shown in Fig. 8, the black line, which reproduced using the mean value of the GPR predicted polymer parameter agrees with the experimental data very well, and the gray region are reproduced by taking the extreme of the error bar of each polymer parameter. We note that although the experimentally measured SANS data show high noise at low Q range, it is a common issue due to low neutron counts and since it is known that the polymer structure factor has the universal Guinier form at low Q, we firstly fit for the Guinier region37 to find the normalization factor of the scattering density and replace the low Q data with smooth Guinier form before feeding in to the GPR. In addition, while the SANS measured S(QB) exhibit different noise levels at different Q due to neutron counting and instrument error, we only used the mean for the inversion as it is conventional for the SANS analysis, such impact can be minimized by taking longer and costly SANS experiment or use higher concentration of the sample to improve the signal. The current method cannot account for the error bar in the experimental data when applying the GPR, which can result in a larger uncertainty for the extracted parameters.
S(QB) to the trained GPR, we obtain the polymer parameters (Ra, α, L, Rg2), as shown in Table 2, and then run MC simulation with these parameters to reconstruct the ML implied S(QB). The SANS measured S(QB) and the Ml implied one agree closely. As shown in Fig. 8, the black line, which reproduced using the mean value of the GPR predicted polymer parameter agrees with the experimental data very well, and the gray region are reproduced by taking the extreme of the error bar of each polymer parameter. We note that although the experimentally measured SANS data show high noise at low Q range, it is a common issue due to low neutron counts and since it is known that the polymer structure factor has the universal Guinier form at low Q, we firstly fit for the Guinier region37 to find the normalization factor of the scattering density and replace the low Q data with smooth Guinier form before feeding in to the GPR. In addition, while the SANS measured S(QB) exhibit different noise levels at different Q due to neutron counting and instrument error, we only used the mean for the inversion as it is conventional for the SANS analysis, such impact can be minimized by taking longer and costly SANS experiment or use higher concentration of the sample to improve the signal. The current method cannot account for the error bar in the experimental data when applying the GPR, which can result in a larger uncertainty for the extracted parameters.
| R a | α | L | R g 2 | |
|---|---|---|---|---|
| a The atomistic structure of the ladder polymer with 4 monomer units were optimized using the Forcite Module with COMPASS force field in Materials Studio 8.0, BIOVIA. | ||||
| Machine learning inversion | 0.14 ± 0.07 | 0.89 ± 0.05 | 11.6 ± 2.8 | 2.07 ± 0.28 |
| Molecular structure optimizationa38 | N/A | 0.96 ± 0.08 | N/A | N/A |
| Flexible cylinder fitting12,39 | N/A | N/A | 12.0 ± 0.8 | N/A |
| Guinier approximation fitting7,37 | N/A | N/A | N/A | 1.82 ± 0.15 |
Table 2 shows the four GPR predicted polymer parameters of SANS our synthesized CANAL ladder polymer along with comparison with parameters obtained from other traditional methods. Note that our ML inversion method can extract all parameters simultaneously, and those parameters that the traditional method can extract, (α, L, Rg2), show strong agreement with its results. Moreover, due to the special monomer structure of the CANAL ladder polymer, the anti rate Ra is a unique parameter that only can be obtained using the ML inversion method. The ML inversion method suggest our sample is relative short, with only about 12 segments, and the radius of gyration is even just Rg2 ≃ 2, fairly small for such contour length comparing to semiflexible chains.40 This discrepancy is explained by the low anti rate Ra ≃ 0.14, which suggesting the monomers are most connected through syn link, making the polymer roll up, as shown in Fig. 9. The tendency to have more coiling structure of ladder polymers has also been observed from other systems.41
 | ||
| Fig. 9 Sample ladder polymer configurations generated using MC with (L, Ra, α) = (12, 0.14, 0.89) and Kt = Kb = 100. | ||
5 Conclusions
In this paper, we introduce an biaxial segmentation model for the ladder polymer, we use a ML inversion method to extract polymer parameters from the form factor of the polymer system, and apply such method on real scattering data of the CANAL ladder polymer. The segmentation model represent the ladder polymer as a chain of two dimensional rectangular segments whose orientation is given by two unit vectors corresponding to the long and short axis. We prepare a data set consisting of 6000 structure factor F = {S(QB)} and corresponding polymer parameters Y = {(Ra, α, L, Rg2)} including anti rate Ra, inherent bending angle α, contour length L, and radius of gyration Rg2. We train a GPR using part of data set as training set to achieve the mapping from F to Y, and show that the trained GPR achieves excellent mapping when applied on the rest of data set, i.e. test set. Given that, we apply the ML inversion analysis on real scattering data. We firstly synthesize a CANAL ladder polymer, and run SANS experiment for a dilute sample. We normalize the SANS measured S(QB) and feed it into the trained GPR. All four polymer parameters are successfully extracted and the consistent with other traditional method when applicable. The anti rate Ra is extracted from the scattering data for the first time, providing new insight for the understanding of ladder polymer. While in this work we used the GPR to achieve the inversion from scattering to polymer parameter due to the simplicity and interpretability of GPR, there are alternative approaches utilizing neural network19,42,43 can also be applied to our system.Using the ML extracted polymer parameters, we can regenerate sample configurations using MC. It is expected that the CANAL ladder polymer sample we synthesized roll up to a coil or ring shape due to it’s low anti rate. Further studies on single polymer imaging using scanning tunneling microscope44 (STM) or ultra resolution atomic force microscopy45 (AFM) would be highly beneficial. Moreover, the sample we used in this work only have inherent bending, application of this ML inversion method for other CANAL ladder polymers with both inherent bending and twisting can also be carried out in the future.
We also note that the CANAL ladder polymer structure we studied is dominated by the inherent bending angle and anti rate, the effect of bending modulus Kb and twisting modulus Kt are too weak to be extracted for this system. For the study of these Kb and Kt, ladder polymer whose monomers are connected in a flat manner are more suitable, as well as conjugated polymer46,47 whose twisting can be more significant due to the existent of single bond.
Data availability
The code and data for this work are available at the GitHub repository https://github.com/ljding94/Ladder_Polymer (https://doi.org/10.5281/zenodo.15318836) and Hugging Face repository https://huggingface.co/datasets/ljding94/Ladder_Polymer (https://doi.org/10.57967/hf/5316), respectively. The provided code was developed for internal use by the author to generate the results in this study. It is not optimized for general user-friendliness. For support or clarification on its implementation please contact the author.Author contributions
L. D. designed the model, carried out the MC simulation and ML analysis and draft the manuscript. C. H. T discussed the model and results, reviewed the manuscript. Z. C measured the SANS spectrum, discussed the results and reviewed the manuscript, Z. Y. synthesized the material, discussed the results and reviewed the manuscript, X. G. discussed the results and reviewed the manuscript. Y. X discussed the results and reviewed the manuscript. W. R. C discussed the results and reviewed the manuscript. C. D. conceived this work, discussed the model and results, and draft the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was performed at the Spallation Neutron Source and the Center for Nanophase Materials Sciences, which are DOE Office of Science User Facilities operated by Oak Ridge National Laboratory. This research was sponsored by the Laboratory Directed Research and Development Program of Oak Ridge National Laboratory, managed by UT-Battelle, LLC, for the U. S. Department of Energy. Monte Carlo simulations and computations used resources of the Oak Ridge Leadership Computing Facility, which is supported by the DOE Office of Science under Contract DE-AC05-00OR22725. Z. C. and X. G. acknowledge partial support from the U.S. Department of Energy under Award number DE-SC0022050 for the scattering experiments conducted in this work.Notes and references
- Y. Xia, M. Yamaguchi and T.-Y. Luh, Ladder Polymers: Synthesis, Properties, Applications and Perspectives, John Wiley & Sons, 2023 Search PubMed.
- Y. C. Teo, H. W. Lai and Y. Xia, Chem.–Eur. J., 2017, 23, 14101–14112 CrossRef CAS PubMed.
- J. S.-J. Yang and L. Fang, Chem, 2024, 10(6), 1668–1724 CAS.
- N. B. McKeown, P. M. Budd, K. J. Msayib, B. S. Ghanem, H. J. Kingston, C. E. Tattershall, S. Makhseed, K. J. Reynolds and D. Fritsch, Chem.–Eur. J., 2005, 11, 2610–2620 CrossRef CAS PubMed.
- S. Liu, Z. Jin, Y. C. Teo and Y. Xia, J. Am. Chem. Soc., 2014, 136, 17434–17437 CrossRef CAS PubMed.
- H. W. Lai, F. M. Benedetti, J. M. Ahn, A. M. Robinson, Y. Wang, I. Pinnau, Z. P. Smith and Y. Xia, Science, 2022, 375, 1390–1392 CrossRef CAS PubMed.
- P. Lindner and T. Zemb, Neutrons, X-rays and Light: Scattering Methods Applied to Soft Condensed Matter, Elsevier Science, 2002 Search PubMed.
- B. Chu and B. S. Hsiao, Chem. Rev., 2001, 101, 1727–1762 CrossRef CAS PubMed.
- S.-H. Chen, Annu. Rev. Phys. Chem., 1986, 37, 351–399 CrossRef CAS.
- M. Shibayama, Polym. J., 2011, 43, 18–34 CrossRef CAS.
- P. Debye, J. Phys. Chem., 1947, 51, 18–32 CrossRef CAS PubMed.
- J. S. Pedersen and P. Schurtenberger, Macromolecules, 1996, 29, 7602–7612 CrossRef CAS.
- K. P. Murphy, Machine learning: a probabilistic perspective, MIT press, 2012 Search PubMed.
- W. Krauth, Statistical mechanics: algorithms and computations, OUP Oxford, 2006, vol. 13 Search PubMed.
- M.-C. Chang, C.-H. Tung, S.-Y. Chang, J. M. Carrillo, Y. Wang, B. G. Sumpter, G.-R. Huang, C. Do and W.-R. Chen, Commun. Phys., 2022, 5, 46 CrossRef.
- C.-H. Tung, S.-Y. Chang, H.-L. Chen, Y. Wang, K. Hong, J. M. Carrillo, B. G. Sumpter, Y. Shinohara, C. Do and W.-R. Chen, J. Chem. Phys., 2022, 156, 13 CrossRef PubMed.
- L. Ding, C.-H. Tung, B. G. Sumpter, W.-R. Chen and C. Do, arXiv, 2024, preprint, arXiv:2410.05574, DOI:10.48550/arXiv.2410.05574.
- L. Ding, C.-H. Tung, J.-M. Y. Carrillo, W.-R. Chen and C. Do, arXiv, 2025, preprint, arXiv:2501.14647, DOI:10.48550/arXiv.2501.14647.
- L. Ding, C.-H. Tung, B. G. Sumpter, W.-R. Chen and C. Do, J. Chem. Theory Comput., 2025, 21, 4176–4182 CrossRef CAS PubMed.
- L. Ding, Y. Chen and C. Do, arXiv, 2024, preprint, arXiv:2412.07926, DOI:10.48550/arXiv.2412.07926.
- P. Tomaszewski, S. Yu, M. Borg and J. Rönnols, 2021 Swedish Workshop on Data Science (SweDS), 2021, pp. 1–6 Search PubMed.
- A. S. Anker, K. T. Butler, R. Selvan and K. M. Jensen, Chem. Sci., 2023, 14, 14003–14019 RSC.
- S. Lu and A. Jayaraman, Prog. Polym. Sci., 2024, 101828 CrossRef CAS.
- S. V. R. Akepati, N. Gupta and A. Jayaraman, JACS Au, 2024, 4, 1570–1582 CrossRef CAS.
- P. S. Clegg, Soft Matter, 2021, 17, 3991–4005 RSC.
- A. Hinderhofer, A. Greco, V. Starostin, V. Munteanu, L. Pithan, A. Gerlach and F. Schreiber, J. Appl. Crystallogr., 2023, 56, 3–11 CrossRef CAS PubMed.
- C. K. Williams and C. E. Rasmussen, Gaussian processes for machine learning, MIT press, Cambridge, MA, 2006, vol. 2 Search PubMed.
- M. Gu and L. Wang, SIAM/ASA J. Uncertain. Quantification, 2018, 6, 1555–1583 CrossRef.
- M. C. Kennedy and A. O'Hagan, J. Roy. Stat. Soc. B Stat. Methodol., 2001, 63, 425–464 CrossRef.
- A. M. Stuart, Acta Numer., 2010, 19, 451–559 CrossRef.
- K. Sugamata, S. Kobayashi, T. Iihama and M. Minoura, Eur. J. Inorg. Chem., 2021, 2021, 3185–3190 CrossRef CAS.
- J. K. Zhao, C. Y. Gao and D. Liu, J. Appl. Crystallogr., 2010, 43, 1068–1077 CrossRef CAS.
- W. T. Heller, M. Cuneo, L. Debeer-Schmitt, C. Do, L. He, L. Heroux, K. Littrell, S. V. Pingali, S. Qian, C. Stanley, V. S. Urban, B. Wu, W. Bras and IUCr, J. Appl. Crystallogr., 2018, 51, 242–248 CrossRef CAS.
- O. Arnold, J.-C. Bilheux, J. Borreguero, A. Buts, S. I. Campbell, L. Chapon, M. Doucet, N. Draper, R. F. Leal and M. Gigg, et al. , Nucl. Instrum. Methods Phys. Res., Sect. A, 2014, 764, 156–166 CrossRef CAS.
- W. T. Heller, J. Hetrick, J. Bilheux, J. M. B. Calvo, W.-R. Chen, L. DeBeer-Schmitt, C. Do, M. Doucet, M. R. Fitzsimmons, W. F. Godoy, G. E. Granroth, S. Hahn, L. He, F. Islam, J. Lin, K. C. Littrell, M. McDonnell, J. McGaha, P. F. Peterson, S. V. Pingali, S. Qian, A. T. Savici, Y. Shang, C. B. Stanley, V. S. Urban, R. E. Whitfield, C. Zhang, W. Zhou, J. J. Billings, M. J. Cuneo, R. M. F. Leal, T. Wang and B. Wu, SoftwareX, 2022, 19, 101101 CrossRef.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss and V. Dubourg, et al. , J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- A. Guinier, G. Fournet, C. B. Walker and K. L. Yudowitch, Small-angle Scattering of X-rays, Wiley, New York, 1955 Search PubMed.
- U. Shankar, R. Gogoi, S. K. Sethi and A. Verma, in Forcefields for atomistic-scale simulations: materials and applications, Springer, 2022, pp. 299–313 Search PubMed.
- W.-R. Chen, P. D. Butler and L. J. Magid, Langmuir, 2006, 22, 6539–6548 CrossRef CAS PubMed.
- L. Ding, C.-H. Tung, B. G. Sumpter, W.-R. Chen and C. Do, J. Chem. Theory Comput., 2024, 20, 10697–10702 CrossRef CAS PubMed.
- T. Ikai, T. Yoshida, K.-i. Shinohara, T. Taniguchi, Y. Wada and T. M. Swager, J. Am. Chem. Soc., 2019, 141, 4696–4703 CrossRef CAS PubMed.
- C.-H. Tung, L. Ding, G.-R. Huang, L. Porcar, Y. Shinohara, B. G. Sumpter, C. Do and W.-R. Chen, Appl. Crystallogr., 2025, 58, 523–534 CrossRef CAS PubMed.
- C.-H. Tung, L. Ding, M.-C. Chang, G.-R. Huang, L. Porcar, Y. Wang, J.-M. Y. Carrillo, B. G. Sumpter, Y. Shinohara, C. Do and W.-R. Chen, J. Chem. Phys., 2025, 162(7), 074106 CrossRef CAS PubMed.
- G. Binnig and H. Rohrer, Rev. Mod. Phys., 1987, 59, 615 CrossRef CAS.
- F. J. Giessibl, Rev. Mod. Phys., 2003, 75, 949 CrossRef CAS.
- X. Yin, K. Zheng, Z. Jin, M. Horst and Y. Xia, J. Am. Chem. Soc., 2022, 144, 12715–12724 CrossRef CAS PubMed.
- Z. Cao, S. A. Tolba, Z. Li, G. T. Mason, Y. Wang, C. Do, S. Rondeau-Gagné, W. Xia and X. Gu, Adv. Mater., 2023, 35, 2302178 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5dd00051c |
| This journal is © The Royal Society of Chemistry 2025 |