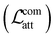ACES-GNN: can graph neural network learn to explain activity cliffs?

Abstract

Graph Neural Networks (GNNs) have revolutionized molecular property prediction by leveraging graph-based representations, yet their opaque decision-making processes hinder broader adoption in drug discovery. This study introduces the Activity-Cliff-Explanation-Supervised GNN (ACES-GNN) framework, designed to simultaneously improve predictive accuracy and interpretability by integrating explanation supervision for activity cliffs (ACs) into GNN training. ACs, defined by structurally similar molecules with significant potency differences, pose challenges for traditional models due to their reliance on shared structural features. By aligning model attributions with chemist-friendly interpretations, the ACES-GNN framework bridges the gap between prediction and explanation. Validated across 30 pharmacological targets, ACES-GNN consistently enhances both predictive accuracy and attribution quality for ACs compared to unsupervised GNNs. Our results demonstrate a positive correlation between improved predictions and accurate explanations, offering a robust and adaptable framework to better understand and interpret ACs. This work underscores the potential of explanation-guided learning to advance interpretable artificial intelligence in molecular modeling and drug discovery.

---

1 Introduction

In silico molecular property prediction, commonly known as quantitative structure–activity relationship modeling (QSAR), is one of the most important topics in the field of chemical science and drug discovery.^1–3 In recent years, the application of deep learning (DL) techniques,^4–6 especially graph neural networks (GNNs), has gained significant momentum in these domains.^7–10 GNNs autonomously learn optimal molecular graph representations from training data, allowing the modeling of complex nonlinear relationships between molecular structures and their properties. These models have been demonstrated to equal or even exceed the performance of conventional machine learning (ML) models in many QSAR tasks.^7,11

However, like other deep learning models, GNNs are often criticized for their “black-box” nature because their highly parameterized architectures obscure the reasoning behind predictions.^12–14 This opacity poses challenges for broader applications in scientific research, particularly in drug discovery, where understanding predictions is as important as achieving high accuracy. For instance, interpretable linear models, such as Free-Wilson models,¹⁵ are still valued in medicinal chemistry for providing actionable “rules of thumb” that correlate biological effects with physicochemical properties, despite their simplicity and limited accuracy.^16–18 Interpretable models not only validate hypotheses and guide research but also offer practical advantages:¹³ (1) improving the transparency of decision-making processes, (2) avoiding erroneous predictions caused by misleading correlations (commonly referred to as the “Clever Hans” effect¹⁹ or shortcut learning²⁰), (3) supplying chemists with insights that could spark new scientific discoveries, and (4) fostering stronger connections between ML and chemistry by uncovering meaningful correlations or causal relationships in data.

To address this limitation, many explainable artificial intelligence (XAI) methods have been developed to improve the interpretability of deep learning models, such as gradient-/feature-based methods, decomposition methods, surrogate methods, generation-based methods, and perturbation-based methods.^21,22 These approaches have been widely applied in drug discovery studies to elucidate important molecular substructures or chemical descriptors that drive a model's decision-making.^23,24 However, many of these attribution methods, originally developed for fields like natural language processing and image recognition, exhibit unexpected behaviors when applied to molecular interpretation tasks. For instance, perturbation-based methods such as GNNExplainer²⁵ may highlight important nodes or edges that do not form chemically meaningful fragments. Therefore, one line of improvement in molecular XAI is to make the XAI method speak the same language as a chemist, i.e., generate chemist-friendly interpretation, e.g., highlighting chemically meaningful fragments,²⁶ generating counterfactual molecules²⁷ and employing natural language-based descriptors.²⁸ While these methods improve the quality of explanations, they do not alter the internal decision-making logic of the model. Consequently, models remain susceptible to the “Clever Hans” effect, where correct predictions arise from erroneous reasoning. Furthermore, these flawed explanations are frequently encountered in XAI applications, with issues such as spurious correlations between molecular structure and property²⁹ and instability of attribution between closely related compounds.³⁰ To address these challenges, some molecular XAI research has focused on adjusting the explanations produced by the model.³¹ However, current methods fall short of directly correcting flawed explanation outputs or significantly improving overall predictive performance. This highlights the need for better alignment among predictions, explanations, and domain knowledge, which is a crucial yet open problem of XAI research.

Recent progress in explanation-guided learning shows promise for addressing these challenges.^32–34 By integrating human-provided explanations as priors, explanation-guided learning can not only adjust the rationale learned by models but also make models generate chemist-friendly explanations, enhancing both predictions and interpretability. However, obtaining high-quality ground-truth explanations remains challenging due to the reliance on expert knowledge, which is subjective and hard to quantify.^32,35 Herein, we introduce an Activity-Cliff-Explanation-Supervised GNN (ACES-GNN) framework that incorporates an activity-cliff (AC) explanation supervision into the GNN training objective. ACs are generally defined as pairs of structurally similar compounds that exhibit unexpectedly large differences in binding affinity for a given pharmacological target.^36,37 The presence of ACs indicates that small compound modifications can have large biological impacts. The ability to highlight such sensitive substructures in prediction attributions is critical for uncovering mechanisms of drug–target interactions and guiding compound optimization.^38,39 Consequently, explanations for ACs are frequently used as ground truth in benchmarks for evaluating explanation methods.^35,40,41 This AC explanation assumes that attributions for minor substructure differences between an AC pair should reflect corresponding changes in molecular properties (see Fig. 1 for an illustration). Furthermore, recent studies have highlighted that ML models, especially DL models, often struggle with predicting ACs, a challenge known as the “intra-scaffold” generalization problem,^8,42–44 and the poor performance of AC predictions can result from the models overemphasizing shared structural features between AC pairs.⁴⁵

Fig. 1 Illustration of non-cliff molecules and activity-cliff molecule pairs from the CHEMBL214 data set. For each pair of highly similar molecules, their differing substructures are highlighted. These substructure variations influence the negative logarithm of potency (pK_i). Molecule pairs with |ΔpK_i| < 1.0 are classified as non-cliff, with the differing substructures highlighted in grey. In contrast, pairs with |ΔpK_i| > 1.0 are classified as activity cliffs: substructures are colored red if their variation decreases pK_i and blue if it increases pK_i.

To address these issues, our approach supervises both predictions and model explanations for ACs in the training set, enabling the model to identify patterns that are both predictive and intuitive for chemists. Such a framework is adaptable to various GNN architectures, gradient-based attribution methods, and predictive tasks with established AC ground-truth explanations.

To validate our approach, we established the AC explanation ground truth using a previously benchmark AC dataset⁴⁰ encompassing 30 pharmacological targets. We then evaluated our training strategy using the widely adopted message-passing neural network (MPNN)⁴⁶ across these datasets. Our experiments demonstrated that 28 out of 30 datasets showed improved explainability scores, with 18 of these achieving improvements in both explainability and predictivity scores. We further analyze the impact of dataset characters and GNN backbones on such a training scheme. Our results indicate a positive correlation between the improvement of prediction of AC molecules and the explanation for AC molecules. Further analysis of the results provides deeper insights into the model-generated explanations and its prediction accuracy.

2 Experimental

2.1 Data sets and activity cliff definition

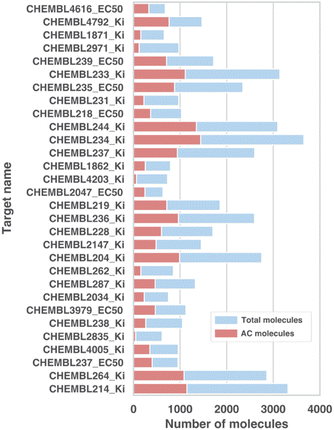
We use the recently proposed ACs dataset⁴² to construct ground-truth explanations for ACs and evaluate our ACES-GNN model. The ACs dataset comprises 30 datasets spanning various macromolecular targets from several target families relevant to drug discovery (e.g. kinases, nuclear receptors, transferases and proteases). This dataset, initially curated from ChEMBLv29,⁴⁷ contains a total of 48 707 organic molecules with sizes ranging from 13 to 630 atoms, of which 35 632 are unique. This diversity reflects the molecular variation commonly encountered in drug discovery datasets.⁴² The size of individual target datasets ranges from approximately 600 to 3700 molecules, with most containing fewer than 1000 molecules. This variation in dataset size mirrors the typical scope and scale of molecular collections used in the field.

For each macromolecular target, ACs are identified by considering pairwise structural similarities and differences in potency. Here, potency is the bioactivity reported on either inhibitory constant (K_i) or maximal effective concentration (EC₅₀) and is transformed using the negative base-10 logarithm to serve as the prediction target. Following the method outlined in the benchmark, the molecular similarity between any pairs of molecules within the same data set is quantified using three distinct approaches: substructure similarity, scaffold similarity and SMILES string similarity.⁴² Substructure similarity is assessed using the Tanimoto coefficient⁴⁸ on Extended Connectivity Fingerprints (ECFPs) of the whole molecule,⁴⁹ enabling the identification of shared radial, atom-centered substructures between molecule pairs. ECFPs are computed with a radius of 2 and a length of 1024 throughout this study. This method captured “global” molecular differences by considering all substructures present in a molecule. Scaffold similarity, on the other hand, is determined by computing ECFPs on atomic scaffolds⁵⁰ and calculating the Tanimoto similarity coefficient, thus identifying pairs of compounds with minor variations in their molecular cores or differences based on scaffold decoration. Lastly, the similarity of SMILES strings is gauged using the Levenshtein distance,⁵¹ a metric that detects character insertions, deletions, and translocations, offering a different perspective on molecular similarity.

These similarity measures encompass prevalent structural differences relevant to medicinal chemistry. Specifically, a pair of molecules is defined as ACs if they share at least one structural similarity exceeding 90% and exhibit a tenfold (10×) or greater difference in bioactivity. A molecule is labeled as an AC molecule if it forms an AC relationship with at least one other molecule in the data set. As shown in Fig. 2, the percentage of AC compounds identified using this approach varied from 8% to 52%, with most target datasets containing approximately 30% AC compounds.

Fig. 2 Overview of the activity cliff (AC) benchmark dataset. The dataset includes 30 target datasets, with names ending in “_K_i” or “_EC50,” indicating that potency is reported as the inhibitory constant (K_i) or the maximal effective concentration (EC₅₀), respectively. The number of total compounds and AC compounds is displayed for each protein target.

2.2 Ground-truth colors

Ground-truth atom-level feature attributions are determined via the concept of ACs. These attributions are often visualized through atom coloring, where structural patterns driving a prediction are highlighted on a two-dimensional molecular graph. Throughout this work, the terms “ground-truth coloring,” “ground-truth feature attributions,” and “ground-truth explanation” will be used interchangeably. The uncommon substructure(s) attached to the shared scaffold are assumed to explain the observed potency difference. Ground-truth explanations are defined such that the sum of the uncommon atomic contributions preserves the direction of the activity difference (as illustrated in Fig. 1). Specifically, if M^uncom_i and M^uncom_j are the uncommon atomic sets of AC molecular pair m_i and m_j with potency y_i and y_j, respectively (see Fig. 3 for an example), we check whether

(Φ(ψ(M^uncom_i)) − Φ(ψ(M^uncom_j)))(y_i − y_j) > 0. (1)

Here, represents an attribution method that assigns attribution values to each atom in the atomic set M, which contains n atoms, and is a sum function applied to the attributions assigned to the uncommon atomic sets. This definition of ground-truth colors was originally proposed by José Jiménez-Luna et al.⁴⁰ and further evaluated by Amara et al.³¹ The “global direction” metric³¹ is used to evaluate the explanation performance, defined as the number of correctly assigned attributions divided by the total number of ground-truth attributions in the test set. We maintain the same nomenclature in the following texts. The only difference between our “global direction” definition and the original one is that instead of using the average function as Φ, we used the sum aggregator to account for substructure contributions.

Fig. 3 Architecture of the proposed ACES-GNN framework. During training, molecules m_i without AC pairs follow the standard GNN training pipeline, optimizing the prediction loss . For a molecule with AC pairs, corresponding AC molecules (e.g. m_j) are sampled from the training set, and gradient-based attributions are computed for all molecules. These attributions are compared to the ground-truth explanations between AC molecules, which consist of uncommon and the common parts. The discrepancy between model-predicted and ground-truth attributions is quantified as an additional attribution loss, which, combined with the , is used in the joint optimization of the framework.

The previous study⁴⁰ obtained the ACs and their ground-truth explanation by computing the maximum common substructure (MCS) between each pair of molecules in the dataset. While identifying ACs via brute-force pairwise comparison has a nominal complexity of O(N²), we note that in practice, this computation is performed only once during preprocessing and can be substantially accelerated through threshold-based filtering and vectorized operations. In our case, we first apply the activity threshold and then the structural similarity threshold to efficiently identify candidate AC pairs before proceeding to MCS computation. FMCS algorithm,⁵² implemented in the RDKit rdFMCS module,⁵³ is employed to compute MCS. We allocate a patience duration of 1800 seconds for the matching process of each pair. Our post-analysis revealed that for each AC molecule, there is at least one substructure match. Furthermore, we configured the ‘matchValences’, ‘ringMatchesRingOnly’, and ‘completeRingOnly’ parameters to True. This configuration is set to ensure matches are more aligned with chemical or functional group logic. While this approach can yield smaller scaffolds and larger uncommon substructures (as shown in ESI Fig. S1†), the impact of this outcome on model training may vary depending on the specific context.

2.3 Graph neural networks

GNNs are utilized to train and predict compound activity against all dataset targets. Each molecule can be represented as a graph , where 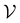is a set of nodes v and is a set of edges e_v,w, which defines the connections between nodes. A GNN takes in the graph-structured molecular data, where each node and edge are encoded with a feature vector. All atomic and bond encodings used in this work are summarized in ESI Tables S1 and S2,† respectively. GNN operates in two phases: a message-passing phase and a read-out phase. The message-passing phase consists of T steps. On each step t, hidden state h_v^t is updated by the update function U_t with message m_v^t+1. The message is aggregated by a message function M_t considering all the neighboring atoms and the connecting edges, according to

h_v^t+1 = U_t(h_v^t,m_v^t+1) (3)

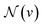where is the set of neighbors of v in graph G. The readout phase then uses a readout function R to compute a feature vector for the whole graph and make a property prediction based on the graph representation according toIn this study, we evaluated the ACES framework using several commonly used message-passing backbones including the edge-conditioned convolution,⁵⁴ also known as message-passing neural network (MPNN),⁴⁶ the graph isomorphism network (GIN)⁵⁵ and the graph attention network (GAT).⁵⁶ In our implementation of the readout function R, a global pooling layer (either mean or sum) is used to aggregate the final hidden states (h_v^T) of all nodes, and a 2-layer fully connected neural network is then connected to output the predicted potency.

2.4 Feature attribution

Feature/gradient-based attribution methods are functions that take a molecular graph and a trained GNN model to generate an attribution value for each atom in the graph. An ideal attribution value of an atom should be able to indicate the contribution of that atom to the predicted value(s). Thanks to the differentiable nature of such methods,⁵⁰ they can be directly supervised during model optimization. In this work, gradient-weighted Class Activation Mapping (GradCAM)⁵⁷ is used as the primary attribution method for explanation loss calculations considering its effectiveness and computational efficiency. Other attribution methods, including GradInput,⁵⁸ SmoothGrad,⁵⁹ Integrated Gradient (IG),⁶⁰ are used as contrastive methods. These types of methods were initially designed for convolutional neural networks (CNN) used for visual explanations of 2-dimensional images⁶¹ and are adapted for graph explanations.^35,62–64 Here, we follow the implementation of GradCAM to visualize atomic attributions in previous work.^31,40 Specifically, we used the following expression to account for the attribution of a node v:where A_v^k is the last message-passing layer activation of graph node v in channel k.

2.5 Activity-cliff explanation guided GNN

Building on the components defined in previous sections, we introduce the ACES-GNN framework, illustrated in Fig. 3. The proposed framework functions as a standard GNN architecture for non-AC molecules. For a molecule that forms AC pairs with others in the training set, its AC counterparts are sampled based on the previously defined criteria for ACs, and the ground-truth explanation for them is also computed. An additional explanation supervision loss is incorporated into the total loss function to guide the GNN to learn better representations for ACs. To do this, two notions need to be enforced: Notion 1: when visualizing the attribution of an AC molecule, the highlighted region should correspond to the uncommon substructure, and the attribution for the uncommon part should reflect the potency difference within the AC pair. Notion 2: the model's reliance on the common structure when predicting ACs should be minimized, which could be the reason for AC prediction failure.⁴⁵ To realize Notion 1, the trend of the potency y is aligned with the trend of the uncommon part, following the AC explanation ground truth defined in eqn (1). Such a constraint can be turned into a pairwise ranking loss, shown as follows, for efficient optimization:

To realize Notion 2, we can just minimize the magnitude of the saliency of the common parts with respect to the output:

The total explanation loss is calculated by summing these two components in eqn (6) and (7) across all AC pairs (m_j) of a molecule m_i in the training set. In all, for each molecule (m_i) in the dataset, the total training loss is calculated as

Here, λ is the scaling factor for the explanation loss. is the mean squared error (MSE) prediction loss between observed and predicted potency (in logarithmic scale).

2.6 Model training details

We followed the same splitting strategy employed in the benchmark study.⁴² Molecules are grouped according to their molecular structures, defined by ECFP, employing spectral clustering facilitated by scikit-learn.⁶⁵ This clustering approach made use of a Gaussian kernel alongside a precomputed affinity matrix based on Tanimoto distances. Following this, we applied a stratified splitting method within each cluster, allocating 80%, 10%, and 10% of the molecules to the training, validation, and test datasets, respectively. Stratification is determined by whether molecules are part of at least one AC pair, with labels designated as “yes” or “no”. For each target, the splitting is repeated for ten times using different seeds, and for each split, the hyperparameters of the GNNs are fine-tuned using Hyperopt,⁶⁶ and the optimal scaling factor λ for the explanation loss is determined through grid search (see detailed discussions about the impact of λ on the training dynamics in ESI Text S1 and Fig. S3†). Details on the use of Hyperopt and the search space are provided in the ESI Table S3.† Models underwent training for a maximum of 1000 epochs using the ADAM optimizer.⁶⁷ An early stopping scheme is applied if no validation performance improvement is observed in successive 150 epochs. A ‘ReduceLROnPlateau’ learning rate scheduler is employed, reducing the learning rate by 10% whenever the validation Root Mean Square Error (RMSE) ceased to improve over a span of 10 epochs, with the minimum learning rate set at 1 × 10⁻⁷. The implementation of the models is carried out using torch-geometric⁶⁸ with a PyTorch backend.⁶⁹

2.7 Representation–property relationship analysis

Representation–Property–Similarity Map (RPSMap) serves as a visualization tool to study the quality of molecular representations.⁷⁰ Following the classical QSAR layout,⁷⁰ the y-axis of RPSMap indicated the distance of properties d(y_i,y_j). Min-Max normalized Euclidean distance is used to quantify the distances between properties: d_norm(y_i,y_j) = (d_ij − d_min)/(d_max − d_min), where d_ij = ‖y_i − y_j‖, and d_min and d_max are the minimum and maximum distances across all pairs of data points. The x-axis of RPSMap indicates the representation similarity. We used a cosine similarity metric to quantify both fingerprints and GNN-generated representations: sim(z_i,z_j) = 〈z_i,z_j〉/‖z_i‖·‖z_j‖. Cosine similarity is widely adopted in cheminformatics and machine learning applications,⁷¹ due to its ability to capture directional alignment in high-dimensional spaces while being scale-invariant. This metric calculated the cosine of the angle between representations of two molecules, signifying the different combinations of structural characteristics. For a data set with N samples, N(N − 1)/2 points will be plotted in the RPSMap. We keep the consensus of ACs (a 10-fold potency difference and 0.9 of similarity) to set the thresholds for RPSMap.^40,42 Since the consensus 0.9 similarity is usually measured by Tanimoto similarity, we evaluated the difference between cosine similarity and Tanimoto similarity shown in ESI Fig. S2.† Our results indicate no significant difference between the two metrics for setting the 0.9 similarity threshold.

2.8 Statistical analysis

To determine whether performance differences across models are statistically significant, we used the Wilcoxon signed-rank test⁷² for each metric, leveraging the fact that all models were evaluated on the same datasets or splits, yielding paired observations. This non-parametric alternative to the paired t-test ranks within-pair score differences and tests whether their median deviates from zero, without assuming normality. We conducted two levels of analysis. First, across the 30 targets (n = 30), we compared the mean scores (averaged over 10 stratified splits per target) to evaluate whether the explanation-supervised model significantly differs from other models overall. Diagnostic plots of the 30 paired differences revealed skewness and deviations from normality (Fig. S11; Text S2†), supporting the use of the Wilcoxon test at this level. Second, to evaluate whether explanation supervision improved performance on a per-target basis, we tested differences in performance across the 10 splits before and after supervision. While a full distributional check was impractical across all 30 targets, visual inspection of the per-target score (Fig. S6†), together with the small sample size, also justified the continued use of the Wilcoxon signed-rank test. Although the paired t-test may offer greater power under normality, the Wilcoxon test provides robust control of type I error under the observed distributional irregularities with only a modest loss of power.⁷³

3 Results and discussion

3.1 Prediction and explanation performance

In the following sections, we analyze the performance of the ACES-GNN framework using the message-passing neural network (MPNN) as its backbone, referred to as ACES-MPNN. ACES-MPNN is assessed for its ability to predict the negative logarithm of potency (expressed as pEC₅₀ or pK_i) in the presence of ACs and the explainability for attributing important uncommon structure(s) between AC pairs. The performance of the prediction accuracy is quantified by two metrics in previous benchmark:⁴² (1) the root-mean-square error (RMSE_all) across all test set molecules, and (2) the RMSE specific to AC molecules in the test set (RMSE_cliff). As RMSE is sensitive to outliers and may amplify large error reduction associated with ACs, we added another two metrics as a reference point: (3) the mean absolute error (MAE_all) across all test set molecules, and (4) the MAE for AC molecules in the test set (MAE_cliff). The explainability is evaluated by the global direction metric,³¹ which assesses the consistency of attributions for test set molecules. Each target dataset is trained, validated and tested independently for 10 random stratified splits.

Fig. 4 summarizes the explainability performance for the 30 target datasets (see ESI Table S4 and Fig. S6† for the detailed per-target results). For AC molecules in each target test set, we evaluate the attribution performance of MPNN without explanation supervision combined with various gradient-based attribution methods, including GradCAM,⁵⁷ GradInput,⁵⁸ SmoothGrad⁵⁹ and IG,⁶⁰ and a perturbation-based atomic masking method for random forest combined with ECPF as a reference point.⁷⁴ Additionally, we assess ‘our method’ by applying GradCAM to ACES-MPNN.

Fig. 4 Performance of explainability in terms of global direction (higher values indicate better performance) for our method (GradCAM combined with ACES-MPNN) compared to other gradient-based attribution methods combined with MPNN (including GradCAM, GradInput, SmoothGrad and IG) and perturbation-based atomic mask method (RF combined with ECFP). For each target, the value is averaged across ten stratified splits. Statistical significance for pairwise comparison is indicated by asterisks (**** = p < 0.0001).

The masking approach applied to the Random Forest (RF) model with ECFP features on average still outperforms gradient-based attribution methods used with GNNs. This advantage can be partially attributed to the strong predictive performance of the RF + ECFP model itself (see Fig. 5 and Table S12†). Additionally, the performance gap may stem from fundamental differences between perturbation-based and gradient-based attribution methods.⁷⁵ Perturbation-based methods, such as masking, directly estimate the marginal effect of each atom by measuring output changes upon atom-level modifications. However, they are computationally expensive, as the number of perturbations scales with molecular size (see Fig. S12† for the scaling test), which make them extremely inefficient in dataset-wise explanation analysis.²⁶ In contrast, gradient-based methods are more computationally efficient, producing attributions in a single forward-backward pass, but their outputs are often less directly interpretable in terms of the model's output variation—highlighting a trade-off that leaves room for further methodological improvement.

Fig. 5 Prediction performance (lower values indicate better performance) of ACES-MPNN compared to MPNN and RF combine with ECFP across 30 binding potency prediction tasks. Performance on each dataset is averaged across ten stratified splits. (a) Violin plot of RMSE on the entire test set (RMSE_all) and RMSE on the AC molecules in each test set (RMSE_cliff) of the 30 target datasets. (b) Violin plot of MAE on the entire test set (MAE_all) and MAE on the AC molecules in each test set (MAE_cliff) of the 30 target datasets. Statistical significance is indicated by asterisks (** = p < 0.01, *** = p < 0.001, **** = p < 0.0001) or “ns” if not significant. Violin plots are ranked by mean.

Supervision of GradCAM explanations results in improvements in global direction accuracy on 28 out of 30 datasets (see Table S4†), with statistically significant gains observed on 18 of them (Fig. S6†). It is important to note that the validation process prioritizes minimizing RMSE during model training rather than optimizing explainability metric. As a result, not all GradCAM attributions after supervision achieve higher global direction accuracy. Nevertheless, as shown in Fig. 4, our method consistently achieves the highest global direction accuracy across all datasets compared to other gradient-based attribution methods.

For the prediction performance, Fig. 5 shows a consistently higher RMSE/MAE for predicting AC molecules (RMSE_cliff/MAE_cliff) than the overall average (RMSE_all/MAE_all) across models, reaffirming the challenge of accurately predicting AC molecules (see Table S5† for per-dataset performance). This observation aligns with prior findings in bioactivity prediction benchmarks.^8,42,76 By introducing explanation supervision via additional loss terms for AC molecules, the prediction of AC molecules (ACES-MPNN RMSE_cliff) can still have difficulty. However, it has been greatly improved across datasets (p < 0.01; Fig. 5). In contrast, MAE_all and MAE_cliff, do not show significant improvements. This suggests that explanation supervision helps the model reduce large prediction errors on ACs—which RMSE disproportionately penalizes—highlighting its effectiveness in mitigating the steep error gradients associated with activity cliffs.

To assess the robustness of each component of the explanation loss, we performed an ablation study on the 30 datasets, summarized in ESI Tables S6, S7 and Fig. S7.† The findings indicate that while incorporating each component of the explanation loss improves both prediction and explainability compared to the original MPNN, combining both the common and uncommon components of the loss yields the best overall performance. Using either component in isolation does not achieve comparable results. Specifically, the addition of either or 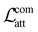to the loss function makes the model more sensitive to the existence of ACs, as indicated by the improvement over RMSE_cliff. The addition of contribute more than to the improvement over global direction accuracy as the uncommon part loss directly aligned with the definition of global direction metric. We further explored the possibility of replacing the GradCAM attribution function with a multi-layer perceptron (MLP), similar to a previous study.³¹ While this simplification avoids explicit gradient computation, replacing the GradCAM module with a MLP yields only marginal improvements in RMSE_cliff and attribution quality compared to using the explanation supervision loss alone. Unlike GradCAM, the MLP lacks a built-in attribution mechanism, limiting its ability to produce faithful explanations of the model's predictions. As a result, its effectiveness in both predicting and explaining activity cliffs is reduced, even when supervision is applied.

3.2 Potential factors influencing explanation supervision

Although the same explanation supervision is applied to all datasets, the resulting ML model performance improvement varies for different datasets. The improvement of prediction and global direction is significant for some datasets, but marginal for others. The explanation supervised model even exhibits degraded performance on a few datasets. To explore the potential factors that affect the result of explanation supervision, we investigate the Pearson correlation coefficient (PCC) between the improvements (measured by test set RMSE, RMSE_cliff and global direction) and the dataset characters. These characters include the data set size, the ratio of the number of AC molecules, scaffold diversity, scaffold Shannon entropy, substitution diversity and substitution Shannon entropy. Here, the scaffold is considered the Murcko scaffold.⁵⁰ Substitution takes into account all single-site substitutions of ground-truth uncommon substructures. The diversity of scaffolds and substitutions is calculated by the total types of scaffolds and substitutions divided by the total number of molecules in the dataset. Shannon entropy is used to describe the distribution of molecules over scaffolds and substitutions.⁷⁷ A Shannon entropy of 0 indicates that all compounds contain the same scaffold; a high Shannon entropy indicates that each scaffold represents the same number of molecules, and that the dataset is therefore evenly distributed over the represented scaffolds.

As shown in Fig. 6 (with full scatter plots in ESI Fig. S4†), a strong correlation is observed between the overall RMSE improvement and RMSE_cliff, as expected, given that RMSE_cliff is part of the overall RMSE. The PCC between RMSE_cliff improvement and global direction improvement is 0.56 (p-value = 0.001). This suggests that enhancing the explanation of ACs can simultaneously improve their predictions. Furthermore, this finding provides evidence that a model's decision-making rationale directly affects the prediction performance, implying that correcting a model's explanations can lead to better generalizability. Additionally, a negative correlation is found between RMSE_cliff improvement and both the ACs ratio in the dataset and the substructure diversity. This indicates that a higher proportion of ACs still impede the model from generalization. One possible explanation is that the ground-truth explanations for AC molecules serve only as proxies for the true underlying causal substructures, which may require detailed biophysical investigations to uncover. Hence, datasets with higher AC ratios may introduce noisier supervision labels. Additionally, the prevalence of highly diverse ACs in test sets inherently makes predictions more challenging.⁷⁸ As a result, explanation supervision proves to be more effective in enhancing prediction performance when AC explanations are not overly prevalent in the training data. Furthermore, a negative correlation can also be observed between explainability improvement and both scaffold Shannon entropy and scaffold diversity. This suggests that the ACES framework is particularly effective in improving the visualization of substituents attached to scaffolds in datasets with fewer analogue series. This makes ACES especially valuable in chemical optimization tasks, where analogue series are often investigated individually.⁷⁹

Fig. 6 Distributions of molecular representation similarities. (a) RPSMap of CHEMBL2835 test set, showing property distance versus representation similarity for different molecular representations (ECFP, MPNN, and ACES-MPNN). (b) An illustrative example demonstrating the use of RPSMap to identify activity cliffs (ACs) within specific quadrants.

3.3 Analysis by RPSMap

To investigate how the representation space changes after explanation supervision, we use the RPSMap (as described in the Experimental section) to visualize the representation distributions extracted by MPNN and ACES-MPNN, along with ECFP, for the CHEMBL2835 test set. A typical RPSMap can be divided into 4 regions based on the thresholds for the representation similarity and the property distance.⁷⁰ Region IV represents ACs, characterized by high representation similarity and high property distance (Fig. 7b). In this analysis, we used the consensus thresholds of a 10-fold potency difference and a 0.9 representation similarity (Fig. 7a).

Fig. 7 Pearson correlation coefficients between the improvement of the test set RMSE, RMSE_cliff and global direction score, number of molecules in the data set, the ratio of AC molecules in the data set, scaffold diversity, scaffold Shannon entropy, ground-truth substructure diversity and ground-truth substructure Shannon entropy across 30 target datasets.

An ideal representation-property relationship should have samples widely distributed in Regions II and III in the plot (Fig. 7b).⁸⁰ A significant presence of samples in Region IV indicates a pronounced AC problem. ECFP-derived representations are rather sparse and mainly occupy Region I and III, suggesting a minimal impact of ACs. In contrast, representations derived from MPNN tend to cluster on the right side of the RPSMap, where most molecules possess highly similar representations, even though they exhibit distinct bioactivities, highlighting a heightened susceptibility to ACs (see similar behaviors for other targets in ESI Fig. S5†). This observation, to some extent, explains the performance variation found in the ACs benchmark study, which stated that traditional ML approaches leveraging ECFP generally outperform graph-based deep learning methods in mitigating ACs.⁴²

Integrating explanation supervision into the GNN training forces the AC-prone molecules to disperse in the representation space. This adjustment has been depicted in the RPSMap (green points in Fig. 7a). Predominantly, molecule pairs in Region IV shift to Region III, indicating that molecules with significantly different potencies are given less similar representations. This adjustment increases the model's sensitivity to AC molecules, facilitating more accurate property predictions and enhancing overall performance. This trend is observed in other target datasets as well, which exhibited improved prediction performance with ACES-MPNN, demonstrating a consistent shift toward a more desirable representation-property relationship (see ESI Fig. S5†). To ensure the robustness of our analysis, we further examined how the choice of structural similarity metric affects RPSMap trends by generating visualizations using normalized Euclidean distance⁸⁰ (ESI Text S3 and Fig. S13†) and continuous Tanimoto similarity (ESI Fig. S14†). These alternative metrics yielded similar global trends, reinforcing the conclusion that explanation supervision leads to a more desirable representation–property relationship.

3.4 Explainability for individual molecules

To understand how explainability has been improved for individual molecules, we perform three case studies of AC molecules' heat map. As shown in Fig. 8, we present heat maps illustrating feature attributions for AC molecules from test sets, alongside their respective AC pair found either within the test or training set, across three distinct targets: Peroxisome proliferator-activated receptor alpha (CHEMBL239), Janus kinase 1 (CHEMBL2835), and Dopamine D4 receptor (CHEMBL219). The left column shows the ground-truth-coloring, which highlights the uncommon structures of each pair that lead to their drastically different experimental potency values (in pEC₅₀ or pK_i). As outlined in the Ground-truth colors section, an optimal attribution is desired to reproduce the ground-truth coloring. The column in the middle shows the GradCAM attribution results for the MPNN model without the explanation supervision. For the CHEMBL239 AC pair and the CHEMBL2835 AC pair, GradCAM tends to assign very similar attribution values to most substructures, neglecting the crucial ones that significantly influence molecular potency. This may contribute to the model's inadequate prediction performance for AC molecules. By treating all atomic attributions similarly, the model fails to predict the substantial potency variations induced by the key uncommon substructures. Although GradCAM performs better at distinguishing the attribution values of different substructures of the CHEMBL219 pair, it incorrectly assigns a more positive contribution to –NH₂ than –OH, failing to capture the correct global direction. In contrast, the right column shows GradCAM results for MPNNs trained with explanation supervision (i.e., ACES-MPNN). These models demonstrate improved sensitivity to critical uncommon substructures in AC pairs, with all important uncommon substructures aligning with the ground-truth colors. This improvement highlights the value of incorporating explainability priors into the model training process, enabling the model to better capture the key structural determinants of ACs.

Fig. 8 Exemplary explanations for test set molecules from CHEMBL239, CHEMBL2835 and CHEMBL219 datasets. The left, middle and right columns display the ground-truth colors, the attribution colors assigned by GradCAM for MPNN (without explanation supervision), and the attribution assigned by GradCAM for ACES-MPNN, respectively. All attribution values are normalized to [−1, 1] within each molecular pair.

3.5 Effect of various GNN backbones

To evaluate how various GNN backbones affect the performance of our ACES training strategy, we test the prediction and global direction performance of another two types of widely used GNN backbone, i.e. GIN⁵⁵ and GAT.⁵⁶ Table 1 summarizes the averaged performance across all target datasets for the three GNN backbones, with and without explanation supervision. The same metrics for prediction and explanation performance, as described earlier, are used for evaluation.

Table 1 Prediction and global direction performance of various GNN backbones (MPNN, GIN, GAT) combined with various feature-attribution methods. Results are reported as the mean score across 30 target datasets. For each backbone, performance with and without explanation supervision is reported. Prediction performance is measured using RMSE_all and MAE_all for the full test set and activity-cliff molecules in the test set (RMSE_cliff and MAE_cliff). Global direction scores are reported for Gradinput, SmoothGrad, GradCAM, and Integrated Gradients (IG)

Backbone	Explanation supervision	Prediction ↓				Global direction ↑
		RMSEall	RMSEcliff	MAEall	MAEcliff	GradInput	SmoothGrad	GradCAM	IG
MPNN	No	0.756	0.829	0.569	0.657	0.715	0.691	0.722	0.720
	Yes	0.752	0.814	0.568	0.649	0.734	0.700	0.765	0.741
GIN	No	1.136	1.146	0.907	0.936	0.596	0.570	0.667	0.637
	Yes	1.055	1.074	0.837	0.873	0.600	0.575	0.700	0.649
GAT	No	1.178	1.183	0.953	0.972	0.561	0.532	0.621	0.607
	Yes	1.082	1.084	0.870	0.883	0.566	0.541	0.672	0.634

---

Explanation supervision consistently improves both prediction accuracy and explanation performance across all GNN backbones (see results with statistical testing in ESI Fig. S8–S10†). However, the improvement's magnitude varies (dataset-specific results are available in ESI Tables S8–S11†). Relative to their unsupervised counterparts, ACES-MPNN, ACES-GAT, and ACES-GIN reduce RMSE_cliff by 1.8%, 6.3%, and 8.9%, respectively while increasing the GradCAM global-direction accuracy by 6.0%, 5.0% and 8.2%. Prediction errors on cliff molecules (RMSE_cliif and MAE_cliff) are consistently higher than the overall test RMSE and MAE but are consistently improved after explanation supervision. A notable pattern in global direction improvements is that the feature attribution method directly supervised during training (i.e., GradCAM) achieves the most significant enhancements, whereas other attribution methods (e.g., GradInput, SmoothGrad, IG) exhibit smaller improvements. This outcome aligns with our expectations, as all attribution methods approximate the model's decision-making mechanism. The method under direct supervision benefits the most, while other methods indirectly improve due to enhanced model generalizability. In contrast to previous feature-attribution benchmark studies, which often concluded that specific combinations of GNN backbones and attribution methods work best for particular tasks,^40,63 our training scheme makes the supervised method performance consistently better than others regardless of the GNN backbone being used. This finding highlights the versatility of the ACES framework for broader XAI applications.

4 Conclusions

In this study, we have introduced ACES-GNN as a novel approach to address the inherent explainability challenges in GNNs applied to ACs in drug discovery. By incorporating an explanation loss into the training of GNNs, ACES-GNN enhances both predictive performance and the interpretability of molecular structure–property relationships, compared to unsupervised GNNs, across all tested backbones. Notably, ACES-GNN enhances GNNs' ability to differentiate between structurally similar molecules with significant potency differences, a critical aspect in drug discovery. Our approach successfully aligns model attributions with chemists' interpretations of ACs, demonstrating that improved explainability can lead to better generalization across datasets. While the current GNN backbone does not outperform the RF + ECFP combination in predictive accuracy or attribution quality (using atomic masking) across all datasets, GNNs with gradient-based attribution methods offer far greater efficiency at scale. Incorporating geometric information into GNNs holds promise for further improvement—without requiring changes to the explanation supervision framework.

Furthermore, the results highlight that: (1) gradient-based attribution methods can effectively integrate human prior knowledge into GNN models; and (2) even in the absence of precise physics-based or human-labeled explanations, heuristic explanations for ACs can still contribute to improving model generalization. While this study employed GradCAM as the explanation method, future research could explore alternative gradient-based techniques, such as expected gradients,⁸¹ to reduce potential biases and further refine the model's decision-making transparency.

Additionally, the current approach to ground-truth coloring relies on fixed definition for AC molecules across all datasets. Some uncommon substructures between AC pairs may not be causative for potency changes. Future work could focus on developing methods to identify true causal substructures in ACs, e.g., by choosing suitable hyperparameters for determining ACs, thereby enhancing the effectiveness of explanation evaluation and guidance.

In conclusion, ACES-GNN represents a promising direction for improving both the predictivity and interpretability of GNN models in QSAR applications, with the potential to accelerate lead optimization in drug discovery.

Data availability

The data and source code used in this work are available at the GitHub repository (https://github.com/Liu-group/XACs) and Zenodo (https://doi.org/10.5281/zenodo.15558394).

Author contributions

Xu Chen: conceptualization (equal); data curation (lead); formal analysis (lead); investigation (lead); methodology (lead); software (lead); validation (lead); visualization (lead); writing – original draft (lead); writing – review and editing (equal). Dazhou Yu: writing – review and editing (supporting). Liang Zhao: writing – review and editing (equal). Fang Liu: conceptualization (equal); funding acquisition (lead); project administration (lead); resources (lead); supervision (lead); writing – review and editing (equal).

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

X. C. and F. L. supported by a DOE Office of Science Early Career Research Program Award, managed by the DOE BES CPIMS program under award number DE-SC0025345. This research used resources of the National Energy Research Scientific Computing Center, a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231 using NERSC award BES-ERCAP0033060. D. Y. and L. Z. acknowledge support from the NSF Grant No. 2007716, No. 2007976, No. 1942594, No. 1907805, Cisco Faculty Research Award, and NIH Grant No. R01AG089806.

Notes and references

1. E. N. Muratov, J. Bajorath, R. P. Sheridan, I. V. Tetko, D. Filimonov, V. Poroikov, T. I. Oprea, I. I. Baskin, A. Varnek and A. Roitberg, Chem. Soc. Rev., 2020, 49, 3525–3564.
2. A. Cherkasov, E. N. Muratov, D. Fourches, A. Varnek, I. I. Baskin, M. Cronin, J. Dearden, P. Gramatica, Y. C. Martin and R. Todeschini, J. Med. Chem., 2014, 57, 4977–5010.
3. X. Chen, P. Li, E. Hruska and F. Liu, Phys. Chem. Chem. Phys., 2023, 25, 13417–13428.
4. K. Choudhary, B. DeCost, C. Chen, A. Jain, F. Tavazza, R. Cohn, C. W. Park, A. Choudhary, A. Agrawal and S. J. Billinge, npj Comput. Mater., 2022, 8, 59.
5. G. B. Goh, N. O. Hodas and A. Vishnu, J. Comput. Chem., 2017, 38, 1291–1307.
6. J. A. Keith, V. Vassilev-Galindo, B. Cheng, S. Chmiela, M. Gastegger, K.-R. Muller and A. Tkatchenko, Chem. Rev., 2021, 121, 9816–9872.
7. P. Reiser, M. Neubert, A. Eberhard, L. Torresi, C. Zhou, C. Shao, H. Metni, C. van Hoesel, H. Schopmans and T. Sommer, Commun. Mater., 2022, 3, 93.
8. J. Deng, Z. Yang, H. Wang, I. Ojima, D. Samaras and F. Wang, Nat. Commun., 2023, 14, 6395.
9. J. Deng, Z. Yang, I. Ojima, D. Samaras and F. Wang, Briefings Bioinf., 2022, 23, bbab430.
10. H. Chen, O. Engkvist, Y. Wang, M. Olivecrona and T. Blaschke, Drug Discov. Today, 2018, 23, 1241–1250.
11. K. Yang, K. Swanson, W. Jin, C. Coley, P. Eiden, H. Gao, A. Guzman-Perez, T. Hopper, B. Kelley and M. Mathea, J. Chem. Inf. Model., 2019, 59, 3370–3388.
12. G. P. Wellawatte, H. A. Gandhi, A. Seshadri and A. D. White, J. Chem. Theory Comput., 2023, 19, 2149–2160.
13. J. Jiménez-Luna, F. Grisoni and G. Schneider, Nat. Mach. Intell., 2020, 2, 573–584.
14. F. Oviedo, J. L. Ferres, T. Buonassisi and K. T. Butler, Acc. Mater. Res., 2022, 3, 597–607.
15. S. M. Free and J. W. Wilson, J. Med. Chem., 1964, 7, 395–399.
16. M. Gupta, H. J. Lee, C. J. Barden and D. F. Weaver, J. Med. Chem., 2019, 62, 9824–9836.
17. Z. Rankovic, J. Med. Chem., 2017, 60, 5943–5954.
18. P. D. Leeson and R. J. Young, ACS Med. Chem. Lett., 2015, 6, 722–725.
19. S. Lapuschkin, S. Wäldchen, A. Binder, G. Montavon, W. Samek and K.-R. Müller, Nat. Commun., 2019, 10, 1096.
20. R. Geirhos, J.-H. Jacobsen, C. Michaelis, R. Zemel, W. Brendel, M. Bethge and F. A. Wichmann, Nat. Mach. Intell., 2020, 2, 665–673.
21. Z. Wu, J. Chen, Y. Li, Y. Deng, H. Zhao, C.-Y. Hsieh and T. Hou, J. Chem. Inf. Model., 2023, 63, 7617–7627.
22. H. Yuan, H. Yu, S. Gui and S. Ji, IEEE Trans. Pattern Anal. Mach. Intell., 2022, 45, 5782–5799.
23. P. E. Pope, S. Kolouri, M. Rostami, C. E. Martin and H. Hoffmann, Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 2019, pp. 10772–10781.
24. T. Harren, H. Matter, G. Hessler, M. Rarey and C. Grebner, J. Chem. Inf. Model., 2022, 62, 447–462.
25. Z. Ying, D. Bourgeois, J. You, M. Zitnik and J. Leskovec, Proceedings of the 33rd International Conference on Neural Information Processing Systems, Curran Associates Inc., Red Hook, NY, USA, 2019.
26. Z. Wu, J. Wang, H. Du, D. Jiang, Y. Kang, D. Li, P. Pan, Y. Deng, D. Cao and C.-Y. Hsieh, Nat. Commun., 2023, 14, 2585.
27. G. P. Wellawatte, A. Seshadri and A. D. White, Chem. Sci., 2022, 13, 3697–3705.
28. H. A. Gandhi and A. D. White, ChemRxiv, 2022, preprint,  DOI:10.26434/chemrxiv-2022-v5p6m-v3.
29. K. McCloskey, A. Taly, F. Monti, M. P. Brenner and L. J. Colwell, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 11624–11629.
30. J. Jiménez-Luna, M. Skalic, N. Weskamp and G. Schneider, J. Chem. Inf. Model., 2021, 61, 1083–1094.
31. K. Amara, R. Rodríguez-Pérez and J. Jiménez-Luna, J. Cheminf., 2023, 15, 67.
32. Y. Gao, T. Sun, R. Bhatt, D. Yu, S. Hong and L. Zhao, 2021 IEEE international conference on data mining (ICDM), 2021, pp. 131–140.
33. Y. Gao, S. Gu, J. Jiang, S. R. Hong, D. Yu and L. Zhao, ACM Comput. Surv., 2024, 56, 1–39.
34. D. Yu, B. Chen, Y. Li, S. Dhakal, Y. Zhang, Z. Liu, M. Zhang, J. Zhang and L. Zhao, Proceedings of the 2024 SIAM International Conference on Data Mining (SDM), Society for Industrial and Applied Mathematics, 2024, pp. 73–81.
35. J. Rao, S. Zheng, Y. Lu and Y. Yang, Patterns, 2022, 3(12) DOI:10.1016/j.patter.2022.100628.
36. M. Cruz-Monteagudo, J. L. Medina-Franco, Y. Pérez-Castillo, O. Nicolotti, M. N. D. Cordeiro and F. Borges, Drug Discov. Today, 2014, 19, 1069–1080.
37. D. Stumpfe, Y. Hu, D. Dimova and J. r. Bajorath, J. Med. Chem., 2014, 57, 18–28.
38. D. Stumpfe, H. Hu and J. r. Bajorath, ACS Omega, 2019, 4, 14360–14368.
39. H. Chen, M. Vogt and J. Bajorath, Digital Discovery, 2022, 1, 898–909.
40. J. Jiménez-Luna, M. Skalic and N. Weskamp, J. Chem. Inf. Model., 2022, 62, 274–283.
41. J. Park, G. Sung, S. Lee, S. Kang and C. Park, J. Chem. Inf. Model., 2022, 62, 2341–2351.
42. D. van Tilborg, A. Alenicheva and F. Grisoni, J. Chem. Inf. Model., 2022, 62, 5938–5951.
43. M. Dablander, T. Hanser, R. Lambiotte and G. M. Morris, J. Cheminf., 2023, 15, 47.
44. R. P. Sheridan, P. Karnachi, M. Tudor, Y. Xu, A. Liaw, F. Shah, A. C. Cheng, E. Joshi, M. Glick and J. Alvarez, J. Chem. Inf. Model., 2020, 60, 1969–1982.
45. T. Janela and J. r. Bajorath, J. Chem. Inf. Model., 2023, 63, 7032–7044.
46. J. Gilmer, S. S. Schoenholz, P. F. Riley, O. Vinyals and G. E. Dahl, International conference on machine learning, PMLR, 2017, pp. 1263–1272.
47. A. Gaulton, L. J. Bellis, A. P. Bento, J. Chambers, M. Davies, A. Hersey, Y. Light, S. McGlinchey, D. Michalovich, B. Al-Lazikani and J. P. Overington, Nucleic Acids Res., 2012, 40, D1100–D1107.
48. A. Cereto-Massagué, M. J. Ojeda, C. Valls, M. Mulero, S. Garcia-Vallvé and G. Pujadas, Methods, 2015, 71, 58–63.
49. D. Rogers and M. Hahn, J. Chem. Inf. Model., 2010, 50, 742–754.
50. G. W. Bemis and M. A. Murcko, J. Med. Chem., 1996, 39, 2887–2893.
51. L. Yujian and L. Bo, IEEE Trans. Pattern Anal. Mach. Intell., 2007, 29, 1091–1095.
52. A. Dalke and J. Hastings, J. Cheminf., 2013, 5, O6.
53. G. Landrum, Release, 2013, 1, 4.
54. M. Simonovsky and N. Komodakis, Proceedings of the IEEE conference on computer vision and pattern recognition, 2017, pp. 3693–3702.
55. K. Xu, W. Hu, J. Leskovec and S. Jegelka, arXiv, 2018, preprint, arXiv:1810.00826,  DOI:10.48550/arXiv.1810.00826.
56. P. Veličković, G. Cucurull, A. Casanova, A. Romero, P. Lio and Y. Bengio, arXiv, 2017, preprint, arXiv:1710.10903,  DOI:10.48550/arXiv.1710.10903.
57. R. R. Selvaraju, M. Cogswell, A. Das, R. Vedantam, D. Parikh and D. Batra, Proceedings of the IEEE international conference on computer vision, 2017, pp. 618–626.
58. A. Shrikumar, P. Greenside and A. Kundaje, International conference on machine learning, PMLR, 2017, pp. 3145–3153.
59. D. Smilkov, N. Thorat, B. Kim, F. Viégas and M. Wattenberg, arXiv, 2017, preprint, arXiv:1706.03825,  DOI:10.48550/arXiv.1706.03825.
60. M. Sundararajan, A. Taly and Q. Yan, International conference on machine learning, PMLR, 2017, pp. 3319–3328.
61. B. Zhou, A. Khosla, A. Lapedriza, A. Oliva and A. Torralba, Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 2921–2929.
62. C. Agarwal, O. Queen, H. Lakkaraju and M. Zitnik, Sci. Data, 2023, 10, 144.
63. B. Sanchez-Lengeling, J. Wei, B. Lee, E. Reif, P. Wang, W. Qian, K. McCloskey, L. Colwell and A. Wiltschko, Adv. Neural Inf. Process. Syst., 2020, 33, 5898–5910.
64. M. Liu, Y. Luo, L. Wang, Y. Xie, H. Yuan, S. Gui, H. Yu, Z. Xu, J. Zhang and Y. Liu, J. Mach. Learn. Res., 2021, 22, 1–9.
65. F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss and V. Dubourg, J. Mach. Learn. Res., 2011, 12, 2825–2830.
66. J. Bergstra, B. Komer, C. Eliasmith, D. Yamins and D. D. Cox, Comput. Sci. Discov., 2015, 8, 014008.
67. D. P. Kingma and J. Ba, arXiv, 2014, preprint, arXiv:1412.6980,  DOI:10.48550/arXiv.1412.6980.
68. M. Fey and J. E. Lenssen, arXiv, 2019, preprint, arXiv:1903.02428,  DOI:10.48550/arXiv.1903.02428.
69. A. Paszke, S. Gross, F. Massa, A. Lerer, J. Bradbury, G. Chanan, T. Killeen, Z. Lin, N. Gimelshein and L. Antiga, Proceedings of the 33rd International Conference on Neural Information Processing Systems, Curran Associates Inc., Red Hook, NY, USA, 2019.
70. J. Pérez-Villanueva, O. Méndez-Lucio, O. Soria-Arteche and J. L. Medina-Franco, Mol. Divers., 2015, 19, 1021–1035.
71. D. Bajusz, A. Rácz and K. Héberger, J. Cheminf., 2015, 7, 1–13.
72. F. Wilcoxon, Biometrics Bull., 1945, 1, 80–83.
73. P. Sedgwick, BMJ, 2015, 350.
74. R. P. Sheridan, J. Chem. Inf. Model., 2019, 59, 1324–1337.
75. M. Ancona, E. Ceolini, C. Öztireli and M. Gross, arXiv, 2017, preprint, arXiv:1711.06104,  DOI:10.48550/arXiv.1711.06104.
76. J. Xia, L. Zhang, X. Zhu, Y. Liu, Z. Gao, B. Hu, C. Tan, J. Zheng, S. Li and S. Z. Li, Adv. Neural Inf. Process. Syst., 2023, 36, 64774–64792.
77. S. R. Langdon, N. Brown and J. Blagg, J. Chem. Inf. Model., 2011, 51, 2174–2185.
78. M. Aldeghi, D. E. Graff, N. Frey, J. A. Morrone, E. O. Pyzer-Knapp, K. E. Jordan and C. W. Coley, J. Chem. Inf. Model., 2022, 62, 4660–4671.
79. J. J. s. Naveja, M. Vogt, D. Stumpfe, J. L. Medina-Franco and J. r. Bajorath, ACS Omega, 2019, 4, 1027–1032.
80. Z. Zhang, Y. Bian, A. Xie, P. Han and S. Zhou, J. Chem. Inf. Model., 2023, 64(7), 2921–2930.
81. G. Erion, J. D. Janizek, P. Sturmfels, S. M. Lundberg and S.-I. Lee, Nat. Mach. Intell., 2021, 3, 620–631.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5dd00012b

---