Active learning-guided exploration of thermally conductive polymers under strain

Abstract

Finding amorphous polymers with higher thermal conductivity (TC) is technologically important, as they are ubiquitous in applications where heat transfer is crucial. While TC is generally low in amorphous polymers, it can be enhanced by mechanical strain, which facilitates the alignment of polymer chains. However, using the conventional Edisonian approach, the discovery of polymers that may have high TC after strain can be time-consuming, with no guarantee of success. In this work, we employ an active learning scheme to speed up the discovery of amorphous polymers with high TC under strain. Polymers under 2× strain are simulated using molecular dynamics (MD), and their TCs are calculated using non-equilibrium MD. A Gaussian process gegression (GPR) model is then built using these MD data as the training set. The GPR model is used to screen the PoLyInfo database, and the predicted mean TC and uncertainty are used towards an acquisition function to recommend new polymers for labeling via Bayesian optimization. The TCs of these selected polymers are then labeled using MD simulations, and the obtained data are incorporated to rebuild the GPR model, initiating a new iteration of the active learning cycle. Over a few cycles, we identified ten strained polymers with significantly higher TC (>1 W mK⁻¹) than the original dataset, and the results offer valuable insights into the structural characteristics favorable for achieving high TC of polymers subject to strain.

---

1. Introduction

Bulk amorphous polymers are used extensively in many industrial and household applications¹ because of their outstanding properties, such as light weight, corrosion resistance, electrical insulation, and low cost.^2,3 Traditional polymers are poor conductors of heat, generally attributed to their amorphous nature and disordered molecular arrangement,^4,5 with thermal conductivity (TC) values typically in the range of 0.1–0.4 W m⁻¹ K⁻¹, which is substantially lower than those of metals and semiconductors. Nevertheless, certain mechanisms, such as strain, can significantly change this inherent property.^6–8 Mechanical strain can affect the chain orientation, crystallinity,⁹ and defect density of many polymers, which are shown to greatly enhance TC by improving phonon transport along the polymer chains.^10–13 Nonetheless, the extent of improvement in TC of stretched polymers depends on various factors, including the type of polymer, the method of stretching, and the degree of strain applied.^14,15 Strained polymers can be integrated into flexible printed circuit boards, wearable devices, and bendable displays. Their improved TC helps with efficient heat dissipation, extending the lifespan of components. Additionally, in devices like LEDs, transistors, or CPUs, strained polymers with high TC could be incorporated into heat sinks, heat spreaders, and thermal interface materials to manage heat flow.

For many polymers, it is time-consuming to synthesize or measure their properties in the laboratory, but molecular dynamics (MD) simulations offer a viable alternative for calculating TC. However, employing MD simulations for exhaustive screening can still be prohibitively expensive due to the computational resources required to simulate a large number of polymers. Recently, data-driven approaches utilizing machine learning have been developed to establish structure-property relationships for different materials.^16–19 These methods allow for the fast screening of vast numbers of polymers to identify promising candidates efficiently.^20–24 Data-driven machine learning tasks, however, require large labeled datasets that adequately cover the chemical space, but acquiring such datasets can be costly and time-consuming. To address this problem, active learning has been utilized,^25–29 which can raise dynamic queries or make suggestions to guide the learning process itself. For instance, when the training dataset is sparse or labeling is arduous, acquisition functions will identify and suggest the most informative data points from the unlabeled pool to label and incorporate them into the training set to improve the model's performance.^30–33 This approach effectively minimizes computational costs and accelerates material discovery.

In this study, we employ an active learning framework to explore the chemical space for promising high TC polymers under strain. We begin with a sparse initial dataset of 36 MD-labeled polymers, containing both chemistry information and TC values under strain, and build a surrogate Gaussian process regression (GPR) model to describe their relationship. Utilizing the expected improvement (EI) acquisition function, which assesses both the mean predicted values and the associated uncertainties, enables dynamic recommendations for the most promising candidates. By incorporating the most informative data into the dataset and repeating the iterative active learning cycles seven times, our updated GPR model successfully identifies 30 strained polymers with MD-labeled TC above 0.8 W m⁻¹ K⁻¹, among which ten polymers have TC exceeding 1.0 W m⁻¹ K⁻¹. This study demonstrates a powerful approach to discovering high TC polymers, which may significantly enhance the development of advanced thermal management materials for electronics and other heat transfer applications.

2. Methods

In many machine learning tasks, there is an abundance of unlabeled data, but the process of labeling can be prohibitively expensive. To address this challenge, we adopt active learning, a semi-supervised technique that enhances learning efficiency by involving the model in selecting the data from which it learns. Unlike traditional supervised learning approaches where the model is trained on a pre-labeled dataset, active learning enables the model to identify and select the most informative examples for labeling,^34–36 thereby optimizing the use of both labeled and unlabeled data and minimizing the amount of labeled data required. This approach aims to maximize performance gains with respect to the target property with a minimal number of labeled instances. In traditional supervised learning, a model is trained on a large set of labeled examples, which are often costly to label in terms of time and computational resources. For instance, in our study, MD simulation of each polymer requires approximately 100 hours on a 24-core CPU, which makes it challenging to label a large dataset. The specific active learning workflow is shown in Fig. 1, which follows 5 steps:

Fig. 1 Schematics of active learning. This workflow is implemented in five iterative steps: (1) data preparation and GPR model training; (2) prediction via GPR; (3) instance selection through acquisition functions; (4) MD labeling; (5) GPR model updating.

Step 1: the first step involves building and training a base GPR model on a small dataset of MD-labeled samples. These samples are usually drawn randomly from a larger, mostly unlabeled dataset. We choose the GPR model as the surrogate model since its posterior is easily accessible to evaluate and it has the ability to provide uncertainty estimates.

Step 2: this GPR model is then utilized to screen the unlabeled database with predicted mean TC and uncertainty.

Step 3: guided by the model's predictive output (mean and uncertainty), the most informative instances are sampled from the unlabeled database through a query strategy governed by an acquisition function through Bayesian optimization (BO).

Step 4: these sampled polymer candidates are then subjected to labeling by our MD simulation, with the MD labels used as the ground truth.

Step 5: these MD-labeled polymers are then integrated into the dataset, and the GPR model is accordingly updated for a new round of ML-MD iteration.

For the query strategy, we use the EI acquisition function, which is given by eqn (1),

(EI(x) = [max(f(x_*) − f(x⁺),0)]) (1)

where f(x) is the output of the surrogate model at location x. f(x⁺) is the value of the best output of the GPR model so far, and x⁺ is the location of that sample.

When using the GPR model, the above equation for EI can be evaluated analytically using eqn (2) and (3),

where μ_*(x_*) and σ_*(x_*) are the predicted mean and the standard deviation of the GPR posterior prediction at x_*, respectively. Φ(z(x_*)) and ϕ(z(x_*)) are, respectively, the cumulative distribution function and probability density function of the standard normal distribution. ξ is a hyperparameter that balances the level of exploration and exploitation. With an increasing ξ value, the weight of exploitation decreases, and exploration is encouraged.

3. MD simulations

In the high-throughput MD simulation procedure, we first manually collected 12 777 homopolymer structures from the PoLyInfo³⁷ database, storing their monomers in SMILES strings^38,39 (simplified molecular input line entry system). Then, a Python pipeline based on PYSIMM⁴⁰ was used to facilitate the creation of amorphous polymer structures using the SMILES strings of monomers as the input. In Fig. 2a, the pipeline polymerized the monomer into a polymer chain, and simultaneously, the general AMBER force field 2 (GAFF2)⁴¹ forcefield parameters were assigned to the polymer by PYSIMM, which also created input scripts for MD simulations using the large-scale atomic-molecular massively parallel simulator (LAMMPS).⁴² During the data generation process, polymers that lack GAFF2 forcefield parameters were excluded from the MD simulations. Each polymer chain was duplicated by six copies and put in a simulation box, followed by optimization through several stages. In all simulations, we utilized periodic boundary conditions in all spatial dimensions. The details are described in ESI Note 1.†

Fig. 2 Scheme of amorphous polymer generation and NEMD simulation. (a) Diagram of amorphous polymer generation and TC calculation using MD simulations: the amorphous polymer generation includes the polymerization of monomers, chain replication, structural relaxation, application of strain, and TC calculation using NEMD via Fourier's law. (b) An example of energy added to or subtracted from the thermostated regions (i.e., heat source and sink) in the NEMD simulation. (c) An example of the steady-state temperature profile of the polymer system in the NEMD simulation.

Each relaxed cubic box of amorphous polymer structure was duplicated into eight copies to assemble a larger cubic simulation domain. The resulting cubes, slightly varied in size due to the differing densities of the polymers, typically measured ∼6.6 × 6.6 × 6.6 nm³. To mimic the strain, this expanded system was subsequently elongated in one direction by a factor of two, while the other two directions shrunk in the meantime to ∼4.7 nm, thus forming a cuboid of 13.2 × 4.7 × 4.7 nm³. This reshaped cuboid was employed for TC calculations through non-equilibrium molecular dynamics (NEMD) simulations. In the NEMD simulation, the system was run in an NVE (constant number of atoms, volume, and energy) ensemble for 5 ns. A 0.25 fs time step size was used to capture the vibrational dynamics of the light hydrogen atoms. Thermal gradients were established by placing Langevin thermostats at either end of the system, set at 320 K for the heat source and 280 K for the sink, with each thermostated region having a thickness of 0.5 nm (Fig. 2a). The heat flux, calculated from the energy exchanged with these Langevin heat baths (Fig. 2b), along with the temperature distribution (Fig. 2c), was averaged over the last 4 ns of the run. These values were then applied to Fourier's law to determine the TC,

where κ is TC, ∇T is the temperature gradient calculated by the linear fit of the temperature profile (Fig. 2c), and J is heat flux (Fig. 2b). While simulation domain size was found to have some impact in polymer TC,⁴³ such an influence is relatively small and less than the inherent uncertainty of our NEMD calculations.⁴⁴ Since all our simulations have similar domain sizes, the calculated TC will offer a fair comparison of different polymers.

4. Dataset

PoLyInfo, the largest polymer database, contains over 13 000 homopolymers. Despite its extensive inventory, the database contains limited values of pure polymer TC, and these reports are found to have significant noise due to variability in experimental conditions, polymer synthesis methods, and measurement techniques. Ma et al.⁴⁴ verify that the experimental TC values of the polymers recorded in PoLyInfo and the MD-labeled TC values are in reasonable agreement. Therefore, in this work, we use MD for data generation and active learning labels to ensure all data are consistently produced with the same standard. We first randomly select 36 polymers from PoLyInfo to label using MD as the initial dataset. Fig. 3a and b show the distribution of the 36 randomly selected polymers' MD-labeled TC before and after strain, respectively. For all polymers, their TC (Fig. 3c) increases under strain. Notably, after strain, those high TC polymers generally show greater increases in TC than low TC polymers. The mean TC of these 36 polymers increased by around 50% under the 2× strain.

Fig. 3 MD results of the 36 initial polymers. Distribution of the MD-labeled TC values for (a) un-strained and (b) strained polymers in the initial dataset. (c) Comparison between TC of un-strained and strained polymers and the increase in TC shown as the yellow shadow.

5. Machine learning model and results

With the initial dataset, we constructed a GPR model (the details are shown in ESI Note 2†) to establish a correlation between polymer structure and TC. This model was then used to screen the entire PoLyInfo database. Each polymer was first encoded using an ML-based representation, polymer embedding, trained from both the PoLyInfo and the PI1M⁴⁵ database—a virtual library generated by a recurrent neural network (RNN) trained on the PoLyInfo database that constitutes polymer SMILES. The embedding converted SMILES into a continuous-valued vector with a length of 300. However, this dimensionality was too large for efficient GPR model prediction. To address this issue, we employed principal component analysis (PCA)⁴⁶ to reduce the dimensionality of the input from 300 to 6 (the dimensionality that can produce the optimal R² for predicting TC) in the first round. Subsequently, the surrogate GPR model was trained using 5-fold cross-validation with the 36 initial strained polymers' TC. Fig. 4a indicates their location in the two-dimensional PoLyInfo chemical space using t-SNE,⁴⁷ which is an ML algorithm for dimensionality reduction and visualization by embedding high-dimensional data into two dimensions. The predictive accuracy of the GPR model, measured by R², is 0.82 on the validation sets, and the parity plot between predicted TC and MD-labeled TC is shown in Fig. 4b.

Fig. 4 GPR model performance and suggestions of EI acquisition functions in iteration 1. (a) t-SNE plot of the 36 polymers in the PoLyInfo chemical space. (b) Parity plot between GPR-predicted TC and MD-labeled TC, where R² is 0.82 and the mean-square error (MSE) is below 0.05. (c) GPR-predicted TC of each polymer in the PoLyInfo database and its uncertainty. (d) GPR-predicted TC values and (e) uncertainties of the PoLyInfo database. (f) The EI metric for all polymer candidates in PoLyInfo based on the GPR-predicted TC means and uncertainties. The five grey dashed lines indicate the polymers with the five highest EI acquisition functions, which are selected for MD labeling (note: two polymers have very close EIs). For better visualization, the EI metric shown is after logarithmic transformation because of the relatively small magnitude of the EI values.

This GPR model was then used to screen the PoLyInfo database to predict TC mean and uncertainty. Fig. 4c illustrates the TC values predicted by the GPR model for each polymer, along with their uncertainties. In this iteration, the highest GPR-predicted TC is 0.67 W m⁻¹ K⁻¹, with only 325 polymers exhibiting TC values exceeding 0.6 W m⁻¹ K⁻¹. The mean (Fig. 4d) and uncertainty (Fig. 4e) were used to calculate the EI acquisition function, shown in Fig. 4f, which guided the selection of the next optimal candidates for MD simulation. Due to the relatively small magnitude of the EI values, logarithmic transformation was applied to improve the visualization in Fig. 4f. Five polymers with the highest EI values were selected for further MD labeling to produce new data integrated into the next iteration. Since polymers lacking GAFF2 forcefield parameters could not be simulated in our MD pipeline, these polymers were excluded from the study, and the process moved on to the next polymer in the EI rank that could be simulated.

To evaluate the efficacy of BO versus random sampling, we randomly selected five polymers from the PoLyInfo database to label via MD simulation, and the data was then integrated into the initial dataset to update the GPR model to screen the whole PoLyInfo database. The performance of the GPR model, incorporating these five randomly sampled polymers, is shown in Fig. 5a. Using this new GPR model to screen the PoLyInfo database, we found that the distribution polymer TC (Fig. 5b) remained largely unchanged compared to those predicted by the initial GPR. In contrast, by incorporating the five EI-samples' data (Fig. 5c) into the initial dataset, the BO-guided strategy demonstrated significant improvements (Fig. 5d) over the initial dataset, with 962 polymers having GPR-predicted TC greater than 0.6 W m⁻¹ K⁻¹ and 306 polymers exceeding 0.7 W m⁻¹ K⁻¹. Under the framework of active learning, we performed eight iterations in total, and 35 polymers in total were labeled by MD in these rounds. For each iteration, as new data was incorporated, the PCA-reduced input dimensionality varied based on the best model R². Iterations 3–8 are shown in Fig. S1,† and the 35 EI-sampled polymers are listed in Table S1.†

Fig. 5 GPR model performances of random round and iteration 2. (a) Parity plot between GPR-predicted TC and MD-labeled TC in the random round, with five new randomly selected data points marked by red circles. (b) GPR-predicted TC and the uncertainty of each polymer in the PoLyInfo database in the random round. (c) Parity plot between GPR-predicted TC and MD-labeled TC in iteration 2, with five new BO-guided data points marked by red circles. (d) GPR-predicted TC of each polymer in the PoLyInfo database and its uncertainty in iteration 2.

In Fig. 6a, we utilized a t-SNE plot to visualize the spatial distribution of the initial 36 data points (blue) and the subsequent 35 BO-suggested data points (red) within the two-dimensional chemical space of the PoLyInfo database (depicted in grey). It was found that around 60% of the BO-suggested data clustered in the upper left corner, a region associated with polymers exhibiting high TC. This clustering represents a strategic exploitation aimed at identifying high TC polymers. The remaining points are more dispersed across the chemical space, reflecting an exploratory strategy to identify polymers with different structures for our model. Fig. 6b shows the distribution of TC values for the 36 polymers in the initial training set (blue) and the 35 EI-sampled polymers (red). It is apparent that the TC of the EI-sampled polymers significantly shifted to the higher TC end compared to the initial random samples, indicating the effectiveness of our active learning strategy.

Fig. 6 The changes of training set through the eight iterations. (a) t-SNE plot of the initial 36 data points (blue) and the subsequent 35 BO-suggested data points (red) in the PoLyInfo chemical space (grey). (b) Distribution of the initial 36 polymers (blue) and the EI-sampled 35 polymers (red).

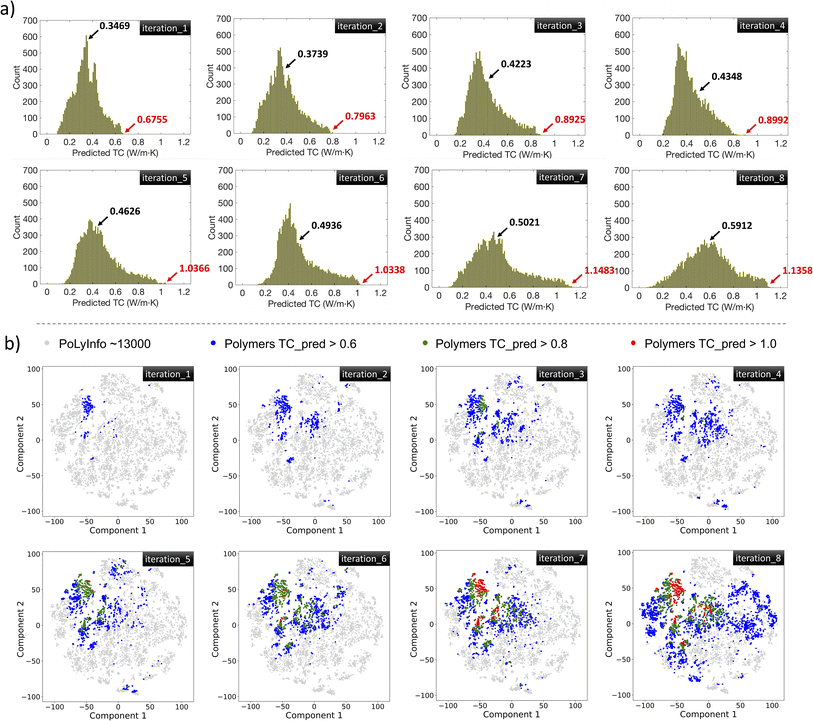
Fig. 7a shows the distributions of GPR-predicted TC values of all polymers in the PoLyInfo database in each iteration. Although there are some flat parts or a slight decrease in the upper-bound TC, both the average and boundary values are trending upward. Notably, the upper-bound TC has increased significantly from 0.6755 W m⁻¹ K⁻¹ to 1.1358 W m⁻¹ K⁻¹ after seven iterations. Fig. 7b presents a t-SNE visualization of the GPR-predicted TC values for the polymers in the PoLyInfo database at each iteration. The analysis indicates that polymers with GPR-predicted TC > 0.8 W m⁻¹ K⁻¹ and GPR-predicted TC > 1.0 W m⁻¹ K⁻¹ emerge in iteration 3 and iteration 5, respectively. With the model being continuously updated, an increasing number of polymers with high TC values are identified, culminating in iteration 8, where 485 polymers are found to have GPR-predicted TC values above 1.0 W m⁻¹ K⁻¹. Most of these high TC polymers are concentrated in the upper left corner of the plot, while the sparsely distributed points outside this high-density area reflect the exploration efforts. To compare the performance of the GPR model, we test two other popular ML models: random forest (RF) and gradient boosting regressor (GBR). The results show that both RF and GBR models underestimate the strained polymers' TC to some extent (Fig. S2†).

Fig. 7 The changes of GPR-predicted TC of all polymers in PoLyInfo from iteration 1 to iteration 8. (a) Distributions of GPR-predicted TC values of all polymers in PoLyInfo from iteration 1 to iteration 8. (b) t-SNE plots of GPR-predicted TC of all polymers in PoLyInfo from iteration 1 to iteration 8.

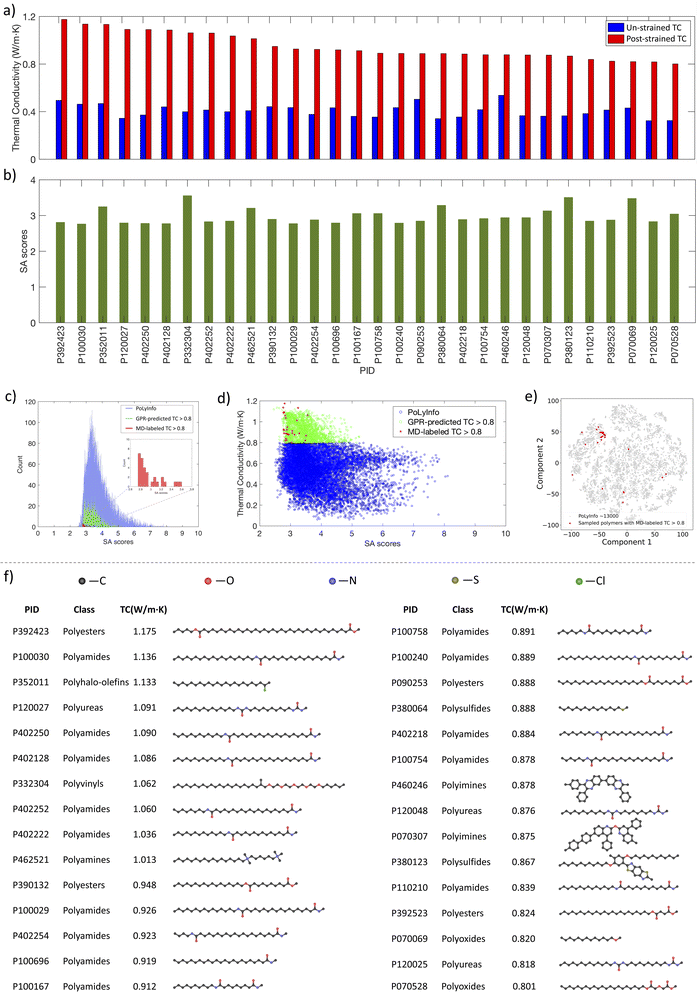
Subsequently, from the eight BO iterations, we selected 30 polymers with the highest GPR-predicted TC values and labeled their un-strained TC and strained TC using our MD pipeline, as shown in Fig. 8a. The results revealed that all these polymers exhibit MD-labeled TC values above 0.8 W m⁻¹ K⁻¹, with 10 polymers exceeding 1.0 W m⁻¹ K⁻¹, which indicated a strong correlation between the GPR predictions and the actual MD results, affirming the robustness of our active learning approach.

Fig. 8 MD simulation results and SA scores of the 30 polymers with structural visualization. (a) MD-labeled TC of the sampled 30 polymers prior to and after strain. (b) SA scores of the sampled 30 polymers. (c) SA scores distributions of all polymers in the PoLyInfo database (blue), polymers with GPR-predicted TC values >0.8 W m⁻¹ K⁻¹ (green) and the 30 polymers having MD-labeled TC > 0.8 W m⁻¹ K⁻¹ (red). (d) Scatter plot of the relationship between SA score and TC for polymers with GPR-predicted TC values <0.8 W m⁻¹ K⁻¹ (blue) and GPR-predicted TC values >0.8 W m⁻¹ K⁻¹ (green), as well as the 30 polymers that have MD-labeled TC > 0.8 W m⁻¹ K⁻¹ (red). (e) t-SNE visualization of the sampled 30 polymers. (f) Structural visualization of the 30 polymers.

We also evaluated if these high TC polymers can be easily synthesized for their potential practical use. Fig. 8b shows the synthetic accessibility (SA)⁴⁸ scores of these 30 polymers. Originally developed to assess the synthetic feasibility of drug-like molecules by evaluating molecular complexity and fragment contributions, the SA scoring system has been adapted for polymers.^24,49–52 The SA scores range from 1 to 10, with higher scores indicating increased synthetic difficulty. Fig. 8c shows the SA scores histograms of the MD-labeled 30 high TC polymers (red), polymers with GPR-predicted TC > 0.8 W m⁻¹ K⁻¹ (green), and their distributions relative to all polymers in PoLyInfo (blue). For these 30 MD-labeled polymers and the polymers with high GPR-predicted TC, they all have relatively low SA scores below 4, indicating that these high TC materials should not be difficult to synthesize. This relationship between SA score and TC for polymers is shown in Fig. 8d. Most of these high TC polymers concentrate within the upper left corner of the PoLyInfo chemical space (Fig. 8e), while the rest scattered in the entire space. The structures of these polymers are visualized in Fig. 8f, and their categories are summarized in Fig. S3.† Notably, the majority of these polymers are polyamides, a class of polymers characterized by amide bonds (–CONH–) linking monomers, which can be formed by the condensation reaction between an amine group (–NH₂) and a carboxylic acid group (–COOH).⁵³ The amide linkages can form hydrogen bonds between the polymer chains,^54,55 potentially enhancing inter-chain thermal transport.⁵⁶

As shown in Fig. 8f, linear chain structures are the majority of the identified high TC polymers because polymers with simple and long backbones can be strained to align the chain orientation relatively easily.^7,8,12,57 This alignment facilitates heat conduction by allowing phonons to travel more efficiently along the chain.^4,10,13

To examine the strain effect on the chain orientation, we characterize the orientation of the chain segments using Herman's orientation factor (f)^58,59 along different directions (see Fig. S4a in the ESI†) and find that f increases in the direction of alignment while decreasing in the perpendicular directions. Such observation is consistent with the anisotropic TC, which exhibits higher values in the aligned direction and lower values in the perpendicular directions (Fig. S4b†). Furthermore, it is generally easier to form crystalline domains for polymers with simple linear backbones^60–62 (e.g., see Fig. S4c†). Crystalline regions conduct heat better than amorphous regions due to the orderly arrangement that allows phonons to travel with less disorder scattering.^63–66 For instance, polymers with a simple linear chain structure have higher TC and f than those with bulkier side chain polymers. This comparison is shown in Fig. S5.†

To quantify the accuracy of our model, we analyzed the GPR predictions in different stages (iteration 1, iteration 2, the random round, and iteration 8) against MD labels for the 30 MD-labeled high TC polymers (Fig. 9a). The MD-labeled TCs for these 30 polymers all fell within the standard deviation of the eighth iteration, indicating that our model and its uncertainty reliably capture the TC values of these polymers. This plot also shows how these final identified high TC polymers are outside the uncertainty ranges of GPR prediction of earlier rounds, suggesting the extrapolatability of the active learning scheme. Fig. 9b illustrates the progressive refinement of our model. As the number of iterations increased, the MSE between the GPR predictions and the MD labels significantly decreased, from 14.68% in iteration 1 to 1.96% by iteration 8, indicating that actively learning not only helps find better candidates but also improves surrogate model accuracy over time. The criteria to determine when the iteration has converged are usually not absolute. However, they can be inferred from several key indicators. First, the MSE between the GPR model and MD simulation results gradually declines and reaches a plateau during the final two iterations (Fig. 9b), and the GPR-predicted TC's upper bound stops growing (Fig. 7a). Additionally, polymers with MD-labeled TC values exceeding 1 W m⁻¹ K⁻¹ first appear in iteration 3, while those with GPR-predicted TC values above this threshold do not emerge until iteration 5 (Fig. 7b). By iteration 8, the GPR-predicted TC values for the 10 polymers that have MD-labeled TC > 1 W m⁻¹ K⁻¹ agree with the MD simulation results, further confirming a converging trend.

Fig. 9 Improvement of the GPR model through the eight iterations. (a) Comparison of GPR-prediction in iteration 1, iteration 2, random round, iteration 8 and MD-labeled TC values for the final identified 30 high TC polymers. (b) MSE of the GPR prediction with respect to the MD labels in the eight iterations.

6. Conclusion

In summary, this study showed the effectiveness of an active learning framework in accelerating the discovery of thermally conductive strained polymers. By combining ML techniques with MD simulations, we efficiently identified strained polymers with high TC. Despite the initial sparsity of our initial dataset, the active learning algorithm dynamically identified the most informative data points for further consideration. By continuously integrating these points into the training dataset, we progressively enhanced the performance of the surrogate GPR model. After eight rounds of active learning, we discovered 30 polymers that have MD-labeled TC above 0.8 W m⁻¹ K⁻¹, among which 10 polymers have TC greater than 1.0 W m⁻¹ K⁻¹. Our analysis of selected high TC polymer revealed that polymers with simple linear chain structures can have enhanced chain alignment after strain, which helps increase TC. Additionally, these high TC polymers are promising candidates for synthesis, as indicated by their relatively low SA scores, suggesting their practical feasibility. This study may provide insights into the structural characteristics favorable for achieving high TC in strained polymers and demonstrates the considerable potential of an active learning based GPR model in expediting the discovery of advanced thermal materials.

Data availability

The code for the paper active learning-guided exploration of thermally conductive polymers under strain can be found at [https://github.com/REINEDSFS/Active-Learning-Guided-Exploration-of-Thermally-Conductive-Polymers-Under-Strain]. The repository includes all scripts and instructions necessary to reproduce the results presented in this work.

Author contributions

Renzheng Zhang: methodology, software, data production, manuscript writing. Jiaxin Xu: data production, software. Hanfeng Zhang: software. Guoyue Xu: data production. Tengfei Luo: conceptualization, methodology, writing – reviewing and editing, supervision, project administration, funding acquisition.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

This work is supported in part by the University of Notre Dame, Center for Research Computing, and National Science Foundation (grant number 2102592 and 2332270).

References

1. X. Chen, Y. Su, D. Reay and S. Riffat, Recent research developments in polymer heat exchangers – a review, Renewable Sustain Energy Rev., 2016, 60, 1367–1386.
2. D. W. van Krevelen and K. te Nijenhuis, Properties of Polymers: Their Correlation with Chemical Structure; Their Numerical Estimation and Prediction from Additive Group Contributions, Elsevier, San Diego, 4th edn, 2009.
3. N. Mehra, L. Mu, T. Ji, X. Yang, J. Kong, J. Gu and J. Zhu, Thermal transport in polymeric materials and across composite interfaces, Appl. Mater. Today, 2018, 12, 92–130.
4. X. Wei, Z. Wang, Z. Tian and T. Luo, Thermal transport in polymers: a review, J. Heat Transf., 2021, 143, 072101.
5. A. Henry, Thermal transport in polymers, Annu. Rev. Heat Transf., 2014, 17, 485–520.
6. S. Shen, A. Henry, J. Tong, R. Zheng and G. Chen, Polyethylene nanofibres with very high thermal conductivities, Nat. Nanotechnol., 2010, 5, 251–255.
7. J. Liu and R. Yang, Tuning the thermal conductivity of polymers with mechanical strains, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 174122.
8. V. Singh, T. L. Bougher, A. Weathers, Y. Cai, K. Bi, M. T. Pettes, S. A. McMenamin, W. Lv, D. P. Resler, T. R. Gattuso, D. H. Altman, K. H. Sandhage, L. Shi, A. Henry and B. A. Cola, High thermal conductivity of chain-oriented amorphous polythiophene, Nat. Nanotechnol., 2014, 9(5), 384–390.
9. R. Shrestha, P. Li, B. Chatterjee, T. Zheng, X. Wu, Z. Liu, T. Luo, S. Choi, K. Hippalgaonkar, M. P. de Boer and S. Shen, Crystalline polymer nanofibers with ultra-high strength and thermal conductivity, Nat. Commun., 2018, 9(1), 1664–1669.
10. J. Liu and R. Yang, Length-dependent thermal conductivity of single extended polymer chains, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 104307.
11. K. Kurabayashi, Anisotropic thermal properties of solid polymers, Int. J. Thermophys., 2001, 22(1), 277–288.
12. X. Pan, M. G. Debije and A. P. H. J. Schenning, High thermal conductivity in anisotropic aligned polymeric materials, ACS Appl. Polym. Mater., 2021, 3(3), 578–587.
13. X. Li, K. Maute, M. L. Dunn and R. Yang, Strain effects on the thermal conductivity of nanostructures, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 245318.
14. J. Shen, J. Liu, Y. Gao, X. Li and L. Zhang, Elucidating and tuning the strain-induced non-linear behavior of polymer nanocomposites: a detailed molecular dynamics simulation study, Soft Matter, 2014, 10, 5099–5113.
15. A. Henry and G. Chen, High thermal conductivity of single polyethylene chains using molecular dynamics simulations, Phys. Rev. Lett., 2008, 101, 235502.
16. S. Wu, H. Yamada, Y. Hayashi, M. Zamengo and R. Yoshida, Potentials and challenges of polymer informatics: exploiting machine learning for polymer design, arXiv, 2020, preprint, arXiv:2010.07683,  DOI:10.48550/arXiv.2010.07683.
17. L. Chen, G. Pilania, R. Batra, T. D. Huan, C. Kim and C. Kuenneth, et al., Polymer informatics: current status and critical next steps, Mater. Sci. Eng., R, 2021, 144, 100595.
18. J. Yang, L. Tao, J. He, J. R. McCutcheon and Y. Li, Machine learning enables interpretable discovery of innovative polymers for gas separation membranes, Sci. Adv., 2022, 8(29), eabn9545.
19. D. J. Audus and J. J. De Pablo, Polymer informatics: opportunities and challenges, ACS Macro Lett., 2017, 6(10), 1078–1082.
20. R. Ma, Z. Liu, Q. Zhang, Z. Liu and T. Luo, Evaluating polymer representations via quantifying structure–property relationships, J. Chem. Inf. Model., 2019, 59(7), 3110–3119.
21. X. Huang, S. Ma, C. Y. Zhao, H. Wang and S. Ju, Exploring high thermal conductivity polymers via interpretable machine learning with physical descriptors, npj Comput. Mater., 2023, 9, 191.
22. H. Yamada, et al., Predicting materials properties with little data using shotgun transfer learning, ACS Cent. Sci., 2019, 5, 1717–1730.
23. Y. Huang, et al., Structure–property correlation study for organic photovoltaic polymer materials using data science approach, J. Phys. Chem. C, 2020, 124, 12871–12882.
24. X. Huang, C. Y. Zhao, H. Wang and S. Ju, AI-assisted inverse design of sequence-ordered high intrinsic thermal conductivity polymers, Mater. Today Phys., 2024, 44, 101438.
25. M. K. Warmuth, et al., Active learning with support vector machines in the drug discovery process, J. Chem. Inf. Comput. Sci., 2003, 43, 667–673.
26. C. Kim, A. Chandrasekaran, A. Jha and R. Ramprasad, Active-learning and materials design: the example of high glass transition temperature polymers, MRS Commun., 2019, 9, 860–866.
27. O. L. Bassman, et al., Active learning for accelerated design of layered materials, npj Comput. Mater., 2018, 4, 74.
28. P. V. Balachandran, Adaptive machine learning for efficient materials design, MRS Bull., 2020, 45, 579–586.
29. K. Wang and A. W. Dowling, Bayesian optimization for chemical products and functional materials, Curr. Opin. Chem. Eng., 2022, 36, 100728.
30. K. M. Jablonka, G. M. Jothiappan, S. Wang, B. Smit and B. Yoo, Bias free multiobjective active learning for materials design and discovery, Nat. Commun., 2021, 12, 2312.
31. W. Shang, et al., Hybrid data-driven discovery of high-performance silver selenide-based thermoelectric composites, Adv. Mater., 2023, 35, 2212230.
32. K. Wang, et al., When physics-informed data analytics outperforms black-box machine learning: a case study in thickness control for additive manufacturing, Digit Chem. Eng., 2023, 6, 100076.
33. A. M. Gopakumar, P. V. Balachandran, D. Xue, J. E. Gubernatis and T. Lookman, Multi-objective optimization for materials discovery via adaptive design, Sci. Rep., 2018, 8, 3738.
34. B. Shahriari, K. Swersky, Z. Wang, R. P. Adams and N. De Freitas, Taking the human out of the loop: a review of Bayesian optimization, Proc. IEEE, 2016, 104, 148–175.
35. A. Sóbester, A. I. J. Forrester, D. J. J. Toal, E. Tresidder and S. Tucker, Engineering design applications of surrogate-assisted optimization techniques, Optim. Eng., 2014, 15, 243–265.
36. B. Rouet-Leduc, C. Hulbert, K. Barros, T. Lookman and C. J. Humphreys, Automatized convergence of optoelectronic simulations using active machine learning, Appl. Phys. Lett., 2017, 111, 043506.
37. S. Otsuka, I. Kuwajima, J. Hosoya, Y. Xu and M. Yamazaki. PoLyInfo: polymer database for polymeric materials design, in 2011 International Conference on Emerging Intelligent Data and Web Technologies, IEEE, 2011, pp. 22–29.
38. D. Weininger, SMILES, a chemical language and information system. 1. Introduction to methodology and encoding rules, J. Chem. Inf. Comput. Sci., 1988, 28, 31–36.
39. D. Weininger, A. Weininger and J. L. Weininger, SMILES. 2. Algorithm for generation of unique SMILES notation, J. Chem. Inf. Comput. Sci., 1989, 29, 97–101.
40. A. G. Demidov, B. L. A. Perera, M. E. Fortunato, S. Lin and C. M. Colina, Update 1.1 to “pysimm: a python package for simulation of molecular systems” (PII: S2352711016300395), SoftwareX, 2021, 15, 100749.
41. D. Vassetti, M. Pagliai and P. Procacci, Assessment of GAFF2 and OPLS-AA general force fields in combination with the water models TIP3P, SPCE, and OPC3 for the solvation free energy of druglike organic molecules, J. Chem. Theory Comput., 2019, 15, 1983–1995.
42. S. Plimpton, Fast parallel algorithms for short-range molecular dynamics, J. Comput. Phys., 1995, 117, 1–19.
43. T. Feng, et al., Size effects in the thermal conductivity of amorphous polymers, Phys. Rev. Appl., 2020, 14, 044023.
44. R. Ma, et al., Machine learning-assisted exploration of thermally conductive polymers based on high-throughput molecular dynamics simulations, Mater. Today Phys., 2022, 28, 100850.
45. R. Ma and T. Luo, PI1M: a benchmark database for polymer informatics, J. Chem. Inf. Model., 2020, 60, 4684–4690.
46. K. L. I. I. I. Pearson, On lines and planes of closest fit to systems of points in space, Lond. Edinburgh Dublin Philos. Mag. J. Sci., 1901, 2, 559–572.
47. L. V. D. Maaten and G. E. Hinton, Visualizing data using t-SNE, J. Mach. Learn. Res., 2008, 9, 2579–2605.
48. P. Ertl and A. Schuffenhauer, Estimation of synthetic accessibility score of drug-like molecules based on molecular complexity and fragment contributions, J. Cheminform., 2009, 1, 8.
49. F. M. A. Alzahrani, et al., Computational design of new polymers having low exciton binding energy for organic solar cells fabrication: chemical generation and visualization, J. Photochem. Photobiol. A Chem., 2024, 450, 115457.
50. M. Ishfaq, et al., Data mining and library generation to search electron-rich and electron-deficient building blocks for the designing of polymers for photoacoustic imaging, Heliyon, 2023, 9, e21332.
51. M. Ishfaq, et al., Generation of chemical space of compounds for prostate cancer treatment: biological activity prediction, clustering, and visualization of chemical space, ACS Omega, 2023, 8, 39408–39419.
52. Z. Long, H. Lu and Z. Zhang, Large-scale glass-transition temperature prediction with an equivariant neural network for screening polymers, ACS Omega, 2024, 9, 5452–5462.
53. Z. Wang, et al., Copolymerization-regulated hydrogen bonds: a new routine for high-strength copolyamide 6/66 fibers, Polymers, 2022, 14, 3517.
54. C. Tang, X. Li, Z. Li and J. Hao, Interfacial hydrogen bonds and their influence mechanism on increasing the thermal stability of nano-SiO₂-modified meta-aramid fibres, Polymers, 2017, 9, 504.
55. J. Reglero Ruiz, M. Trigo-López, F. García and J. García, Functional aromatic polyamides, Polymers, 2017, 9, 414.
56. G. H. Kim, et al., High thermal conductivity in amorphous polymer blends by engineered interchain interactions, Nat. Mater., 2015, 14, 295–300.
57. T. Zhang and T. Luo, High-contrast, reversible thermal conductivity regulation utilizing the phase transition of polyethylene nanofibers, ACS Nano, 2013, 7, 7592–7600.
58. T. Zhang and T. Luo, Role of chain morphology and stiffness in thermal conductivity of amorphous polymers, J. Phys. Chem. B, 2016, 120(4), 803–812.
59. S. Pal, G. Balasubramanian and I. K. Puri, Modifying thermal transport in electrically conducting polymers: effects of stretching and combining polymer chains, J. Chem. Phys., 2012, 136, 044901–044907.
60. S. Basak and K. A. Cavicchi, Structure–property relationships of shape memory, semicrystalline polymers fabricated by in situ polymerization and crosslinking of octadecyl acrylate/polybutadiene blends, Macromol. Rapid Commun., 2023, 44, 2200404.
61. F. Liu, T. Sun, P. Tang, H. Zhang and F. Qiu, Understanding chain folding morphology of semicrystalline polymers based on a rod–coil multiblock model, Soft Matter, 2017, 13, 8250–8263.
62. C. Y. Li, The rise of semicrystalline polymers and why are they still interesting, Polymer, 2020, 211, 123150.
63. V. M. Nazarychev and S. V. Lyulin, The effect of mechanical elongation on the thermal conductivity of amorphous and semicrystalline thermoplastic polyimides: atomistic simulations, Polymers, 2023, 15, 2926.
64. Y. Oh, K. J. Bae, Y. Kim and J. Yu, Analysis of the structure and the thermal conductivity of semi-crystalline polyetheretherketone/boron nitride sheet composites using all-atom molecular dynamics simulation, Polymers, 2023, 15, 450.
65. L. Bai, et al., Effect of temperature, crystallinity and molecular chain orientation on the thermal conductivity of polymers: a case study of PLLA, J. Mater. Sci., 2018, 53, 10543–10553.
66. Y. Jia, Z. Mao, W. Huang and J. Zhang, Effect of temperature and crystallinity on the thermal conductivity of semi-crystalline polymers: a case study of polyethylene, Mater. Chem. Phys., 2022, 287, 126325.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00267a

---