Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Embedded machine-readable molecular representation for resource-efficient deep learning applications†
Emilio
Nuñez-Andrade
*a,
Isaac
Vidal-Daza
ab,
James W.
Ryan
 ac,
Rafael
Gómez-Bombarelli
ac,
Rafael
Gómez-Bombarelli
 d and
Francisco J.
Martin-Martinez
d and
Francisco J.
Martin-Martinez
 *ae
*ae
aDepartment of Chemistry, Swansea University, Singleton Park, Sketty, SA28PP, Swansea, UK. E-mail: 2132253@swansea.ac.uk
bGrupo de Modelización y Diseño Molecular, Departamento de Química Orgánica, Facultad de Ciencias, Universidad de Granada, 18071 Granada, Spain
cCentre for Integrative Semiconductor Materials (CISM), Swansea University, Swansea SA1 8EN, UK
dDepartment of Materials Science and Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
eDepartment of Chemistry, Faculty of Natural, Mathematical & Engineering Sciences, King’s College London, London, UK. E-mail: francisco.martin-martinez@kcl.ac.uk
First published on 3rd February 2025
Abstract
The practical implementation of deep learning methods for chemistry applications relies on encoding chemical structures into machine-readable formats that can be efficiently processed by computational tools. To this end, One Hot Encoding (OHE) is an established representation of alphanumeric categorical data in expanded numerical matrices. We have developed an embedded alternative to OHE that encodes discrete alphanumeric tokens of an N-sized alphabet into a few real numbers that constitute a simpler matrix representation of chemical structures. The implementation of this embedded One Hot Encoding (eOHE) in training machine learning models achieves comparable results to OHE in model accuracy and robustness while significantly reducing the use of computational resources. Our benchmarks across three molecular representations (SMILES, DeepSMILES, and SELFIES) and three different molecular databases (ZINC, QM9, and GDB-13) for Variational Autoencoders (VAEs) and Recurrent Neural Networks (RNNs) show that using eOHE reduces vRAM memory usage by up to 50% while increasing disk Memory Reduction Efficiency (MRE) to 80% on average. This encoding method opens up new avenues for data representation in embedded formats that promote energy efficiency and scalable computing in resource-constrained devices or in scenarios with limited computing resources. The application of eOHE impacts not only the chemistry field but also other disciplines that rely on the use of OHE.
1 Introduction
The rapid advancement of Deep Learning (DL) models and algorithms has ushered in an unprecedented era of possibilities for analyzing and leveraging chemical data. This revolution covers molecular discovery,1,2 chemical synthesis,3,4 and property prediction,5,6 among other diverse domains.The practical implementation of DL models in chemistry relies on encoding chemical structures into machine-readable formats for computational tools. Among the machine-readable molecular representations used in cheminformatics,7,8 this work focuses on the use of three widely used string-based molecular graph representations, and particularly their use in the context of generative models: the Simplified Molecular Input Line Entry System (SMILES),9,10 which facilitates the specification of molecular structures through simple rules, DeepSMILES,11,12 which addresses syntax issues that SMILES present in generative models, and the SELF-referencing Embedded Strings (SELFIES),12 which was developed more recently to address some invalid molecular structures generated by SMILES and DeepSMILES, even when specific models were used ad hoc to avoid such molecule invalidity.13,14
SMILES, DeepSMILES and SELFIES need further encoding into numerical representations understandable by DL algorithms. Codification methods like One Hot Encoding (OHE), Ordinal Encoding (OE),15 or Morgan fingerprints (MFP)16 simplify these N-sized alphanumeric representations into simpler numerical matrices. OHE treats all variables as independent, OE considers correlations between variables,17 while MFP captures structural and chemical features. Because of its simplicity, OHE has been especially popular and commonly applied across models. OHE represents each category in an orthogonal dimension of a vector space, avoiding any ambiguity between categories. There are already some alternative methods for embedded data representation, such as torch.nn.Embedding, but this approach requires a training phase and does not allow direct interpretability of the data. Regardless of its applicability, OHE comes with some drawbacks, including the need of a dictionary for mapping categorical features into vector indices, the inability to handle new and unseen categories, the potential for a significant increase in dimensionality, and the creation of sparse vectors containing mostly zero values, which can lead to large memory usage (both vRAM and disk memory) and slower computation.18 To address some of the OHE's pitfalls, we propose an embedded OHE (eOHE), a conceptually different interpretable representation19 that concentrates rather than expanding the machine-readable data, i.e., embedding, while preserving data integrity. Similar to OHE, this eOHE captures the chemical characteristics of molecular graphs, but it decreases the OHE dimensionality while addressing issues related to highly sparse arrays. The interconversion between OHE and eOHE is possible, thus maintaining the structure and meaning of the data. This bidirectional conversion ensures that the interpretability of the data is preserved, as the transformation process is straightforward and based on well-defined rules and equations given in the Methods section. It also opens new avenues within the community to develop embedded representations that increase the computational efficiency without compromising the performance.
To demonstrate our concept, we have tested two DL models, a variational autoencoder (VAE)12 and a recurrent neural network (RNN).2 VAEs1 transform discrete molecular graphs into a continuous representation of molecules, commonly referred to as the latent space. The entire training process is optimized using Bayesian methods,20,21 and navigating this latent space enables the discovery of new molecules.22–26 A decoder learns how to translate the continuous representation of the latent space back into discrete molecules. RNNs27,28 are sequential DL models in which the output of the previous step is used as an input for the current step. RNNs have been extensively used in predicting chemical properties29–31 and in generative models.2,12 While several generative models, such as Generative Adversarial Networks (GANs),32–34 diffusion models35,36 and normalized flow models,37 have found application in generating new molecules as well, we believe that VAE's and RNN's proven effectiveness for molecular discovery and property prediction make them ideal benchmarks for testing the performance of eOHE.
We have adopted the work of Krenn et al.12 on VAEs and Skinnider et al.2 on RNNs as our benchmark, which allow us to leverage their code availability for performing this eOHE feasibility study. Nevertheless, eOHE could be tested in the future in a larger range of model architectures. To maintain the integrity of the models and to enable a fair evaluation of the proposed eOHE, we have chosen not to modify the hyperparameters of the original benchmark studies taken as reference, as well as the proportion of data splitting for training and testing, choosing instead to rely on their original configurations. This decision is rooted in our explicit aim to isolate the effect of eOHE. By doing so, we ensure that the observed differences in performance are a direct consequence of the encoding method itself, rather than any adjustments in the models' hyperparameter optimization. While further improvement on the performance of VAEs and RNNs is possible if hyperparameters are optimized alongside the implementation of eOHE, such optimization is outside the scope of our current investigation, which is focused solely on the impact of eOHE.
The implementation of eOHE reduces the use of computational resources, particularly the vRAM memory allocated per GPU with the VAE model. We believe that the implementation of eOHE opens up new avenues for data representation in embedded formats that promote energy efficiency and scalable computing in resource-constrained devices or in scenarios with limited computing resources. The application of eOHE impacts not only the chemistry field but also other disciplines that rely on the use of OHE to encode categorical data. It is important to highlight that eOHE is an encoding method specially designed to handle categorical data and is not intended for continuous or numerical data.
2 Methods
2.1 Embedding One Hot Encoding
The general idea of eOHE is to encode each discrete alphanumeric token of an![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) -sized alphabet into a few real numbers instead of sparse vectors of dimension
-sized alphabet into a few real numbers instead of sparse vectors of dimension ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) .
.
The ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) dimensions of the OHE dictionary of alphanumeric tokens, which usually constitute the x-axis of the OHE matrix representation, are reduced by a factor of q as a result of this embedding. A reduced dictionary of tokens with p elements instead of
dimensions of the OHE dictionary of alphanumeric tokens, which usually constitute the x-axis of the OHE matrix representation, are reduced by a factor of q as a result of this embedding. A reduced dictionary of tokens with p elements instead of ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) is produced according to eqn (1),
is produced according to eqn (1),
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = p × q = p × q | (1) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) is the length of the OHE dictionary of tokens, p is the length of the reduced eOHE dictionary after embedding, and q is the reduction factor. Based on eqn (1),
is the length of the OHE dictionary of tokens, p is the length of the reduced eOHE dictionary after embedding, and q is the reduction factor. Based on eqn (1), ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) needs to be factorizable by p and q. When this is not the case, we increase the number of tokens in the OHE dictionary by 1 until
needs to be factorizable by p and q. When this is not the case, we increase the number of tokens in the OHE dictionary by 1 until ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) becomes factorizable. A deeper discussion on the addition of extra elements to the OHE dictionary, as well as on the dependency of learning outcomes with the order in which the tokens are organized within the dictionary, is available in the ESI.† Furthermore, from all the possible pairs of p and q, we always select the pair with the smallest p value to achieve the highest dimensionality reduction possible. The feasible values for the pair p–q vary depending on the database and the subsequent subsets because the set of molecules being considered determines the size of OHE dictionary of tokens,
becomes factorizable. A deeper discussion on the addition of extra elements to the OHE dictionary, as well as on the dependency of learning outcomes with the order in which the tokens are organized within the dictionary, is available in the ESI.† Furthermore, from all the possible pairs of p and q, we always select the pair with the smallest p value to achieve the highest dimensionality reduction possible. The feasible values for the pair p–q vary depending on the database and the subsequent subsets because the set of molecules being considered determines the size of OHE dictionary of tokens, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) . More details about feasible values for p and q, as well as all the values for the selected data sets considered in this work, are provided in the ESI.†
. More details about feasible values for p and q, as well as all the values for the selected data sets considered in this work, are provided in the ESI.†
This dimensionality reduction implies that the positions of the tokens in the OHE dictionary, k, are embedded into a new key ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) , which determines the matching positions of each token in the eOHE representation.
, which determines the matching positions of each token in the eOHE representation. ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) values are generated by eqn (2)
values are generated by eqn (2)
 | (2) |
![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) range in the interval [0, p − 1], and each u-th
range in the interval [0, p − 1], and each u-th ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) compresses a range of keys from uq to (u + 1)q − 1, as presented by the equation:
compresses a range of keys from uq to (u + 1)q − 1, as presented by the equation:| k = {uq, (u + 1)q − 1} | (3) |
![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) takes values u = 0, 1, 2, …, p − 1, as mentioned previously.
takes values u = 0, 1, 2, …, p − 1, as mentioned previously.
For instance, if p = 3, q = 8 and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 24, values from k = {0, …, 7} are compressed in
= 24, values from k = {0, …, 7} are compressed in ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) = 0, values from k = {8, …, 15} are compressed in
= 0, values from k = {8, …, 15} are compressed in ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) = 1, values from k = {16, …, 23} are compressed in
= 1, values from k = {16, …, 23} are compressed in ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) = 2, and so on, according to eqn (1)–(3).
= 2, and so on, according to eqn (1)–(3).
Once the fundamental reduction factor is set and the positions of the tokens in the OHE dictionary, k, are embedded into ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) , we proceed with data embedding. In this work, we have explored two different versions of data embedding to demonstrate the impact of eOHE.
, we proceed with data embedding. In this work, we have explored two different versions of data embedding to demonstrate the impact of eOHE.
Version 1 (eOHE-v1) applies a linear dimensionality reduction of data, following eqn (4),
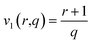 | (4) |
![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) ) following eqn (5).
) following eqn (5). | (5) |
Version 2 of eOHE (eOHE-v2) applies a power-of-2 data dimensionality reduction. We have selected 2 as the base value for the dimensionality reduction, since higher values for the base would output embedded results too close to each other and to zero, losing resolution. Eqn (6) defines eOHE-v2,
 | (6) |
Additional scaling methods for dimensionality reduction are equally applicable beyond the linear and the power-of-2 methods used here. Nevertheless, we have restricted this work to the use of eqn (4) and (6), leaving open the possibility of other functions for dimensionality reduction in future research.
To illustrate the implementation of eOHE, the SMILE encoding of a randomly selected molecule from the QM9 database,38,39i.e., 4-nitro-1H-pyrrol-2-ol displayed in Fig. 1(a), is used as a case study. Nevertheless, the same approach applies to DeepSMILES and SELFIES and to any molecule from any other database under consideration.
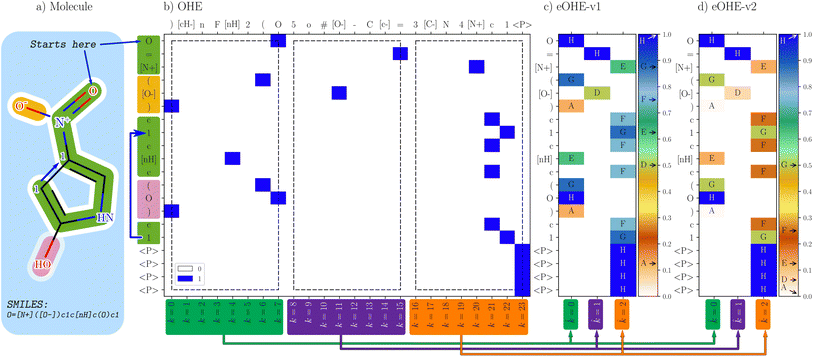 | ||
Fig. 1 Comparison of OHE representation and the two embedded methods, eOHE-v1 and eOHE-v2. (a) A SMILES representation of the 4-nitro-1H-pyrrol-2-ol sample molecule. (b) OHE, where each token considered in the SMILES (y-axis) finds its match in the dictionary of tokens (top x-axis) and is assigned a value of 1, highlighted in blue. The lower x-axis shows the position of the token in the OHE dictionary of tokens, k. The arrows (green, purple and orange) at the bottom of the figure indicate the reduction from k = {0, …, 7}, k = {8, …, 15} and k = {16, …, 23} to ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) = 0, = 0, ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) = 1 and = 1 and ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) = 2, respectively. The three black rectangles (dashed lines) highlight the eight tokens from the dictionary that are embedded for p = 3 and q = 8. (c) eOHE-v1, the y-axis displays the same SMILES, while the x-axis shows the reduced index = 2, respectively. The three black rectangles (dashed lines) highlight the eight tokens from the dictionary that are embedded for p = 3 and q = 8. (c) eOHE-v1, the y-axis displays the same SMILES, while the x-axis shows the reduced index ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) . The normalized values for v1(r, q = 8) are labeled A to H and displayed within the color bar. (d) eOHEv2, the y-axis displays the same SMILES, while the x-axis shows the reduced index . The normalized values for v1(r, q = 8) are labeled A to H and displayed within the color bar. (d) eOHEv2, the y-axis displays the same SMILES, while the x-axis shows the reduced index ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) . The normalized values for v2(r, q = 8) are labeled A to H and displayed within the color bar. Table S1 in the ESI† shows the exact values of A–H for each case. . The normalized values for v2(r, q = 8) are labeled A to H and displayed within the color bar. Table S1 in the ESI† shows the exact values of A–H for each case. | ||
Fig. 1 displays the OHE representation together with eOHE-v1 and eOHE-v2 for 4-nitro-1H-pyrrol-2-ol. As is seen in Fig. 1(b) the specific SMILES representation (y-axis) is determined by the molecule being considered, while the OHE dictionary of tokens (top x-axis) is determined by the database, e.g., QM9. Additionally, the labels on the bottom x-axis represent the position of each element in the dictionary, labeled as k = n, where n is a positive integer number, starting from 0. The resulting OHE representation depicted in Fig. 1(b) is calculated by matching each token on the SMILES axis with its corresponding position on the OHE dictionary axis. A value of 1 is assigned when there is matching (highlighted in blue) and 0 when there is no matching (highlighted in white). eOHE-v1 and eOHE-v2 are displayed in Fig. 1(c), (d), respectively. The color bars indicate the range of values for v1(r, q = 8) and v2(r, q = 8), while the exact values from the model molecule are labeled A to H and located by arrows within the color bar for display purposes. As a result of the embedding process, the length of the OHE dictionary for QM9, which consists of 24 elements (![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 24), is reduced to p = 3. Therefore, dimensionality reduction by a factor of q = 8 is achieved, in accordance with eqn (1). The three white rectangles in Fig. 1(b) highlight the three groups of eight tokens from the OHE dictionary that are embedded, for p = 3 and q = 8.
= 24), is reduced to p = 3. Therefore, dimensionality reduction by a factor of q = 8 is achieved, in accordance with eqn (1). The three white rectangles in Fig. 1(b) highlight the three groups of eight tokens from the OHE dictionary that are embedded, for p = 3 and q = 8.
While eOHE-v1 scales linearly from 0 to 1, eOHE-v2 scales as an exponentially normalized function by a power of 2. Table S1 in the ESI† summarizes the values for r(q = 8, k), v1(r, q = 8) and v2(r, q = 8). A deeper discussion can be found in the ESI,† where Fig. S1(a)† shows the values of r for all the k – indexes in the dictionary of tokens (![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 24) for 4-nitro-1H-pyrrol-2-ol, in accordance with eqn (5), while Fig. S1(b)† shows the embedded values, v1(r, q) and v2(r, q), resulting from applying the eOHE-v1 method with eqn (4), or the eOHE-v2 method with eqn (6) and q = 8 for 4-nitro-1H-pyrrol-2-ol.
= 24) for 4-nitro-1H-pyrrol-2-ol, in accordance with eqn (5), while Fig. S1(b)† shows the embedded values, v1(r, q) and v2(r, q), resulting from applying the eOHE-v1 method with eqn (4), or the eOHE-v2 method with eqn (6) and q = 8 for 4-nitro-1H-pyrrol-2-ol.
2.2 Workflow for training deep learning models
The workflow employed to benchmark the performance of using eOHE of SMILES, DeepSMILES and SELFIES for training VAE and RNN models encompasses six sequential steps, adopting a similar approach to the one provided by Skinnider et al.2 for RNN training and validation. Fig. 2 shows a flowchart with these steps, including data selection and cleaning, model training and analysis. Additional details on VAE and RNN model architectures are provided in the ESI.†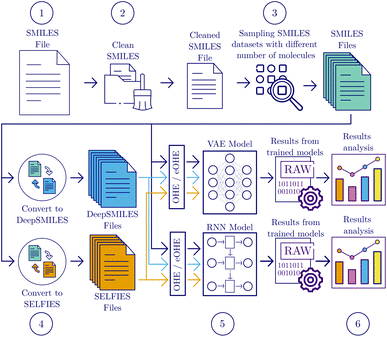 | ||
| Fig. 2 Flowchart of the methodology followed to train the VAE and RNN models for testing the effectiveness of eOHE-v1 and eOHE-v2 against OHE. | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 SMILES are sampled from the QM9, GDB-13, and ZINC databases. Since the QM9 database only contains roughly 134 × 103 molecules, subsets with 250 × 103 and 500 × 103 molecules are omitted for this case, and a subset with 125 × 103 SMILES is sampled instead. However, because such dataset with 125 × 103 items was not originally considered in the benchmark study by Skinnider et al. for GDB-13 and ZINC databases, this subset is omitted for the case of GDB-13 and ZINC databases, to be consistent with our selected reference benchmark.
000 SMILES are sampled from the QM9, GDB-13, and ZINC databases. Since the QM9 database only contains roughly 134 × 103 molecules, subsets with 250 × 103 and 500 × 103 molecules are omitted for this case, and a subset with 125 × 103 SMILES is sampled instead. However, because such dataset with 125 × 103 items was not originally considered in the benchmark study by Skinnider et al. for GDB-13 and ZINC databases, this subset is omitted for the case of GDB-13 and ZINC databases, to be consistent with our selected reference benchmark.
2.3 Evaluation metrics
In both models, we have monitored vRAM memory usage during the training, disk space utilization, and training time. We have also monitored the number of parameters used when training the VAE (both the encoder and decoder) and RNN models. vRAM memory usage is measured using a function from Python's PyTorch package called torch.cuda.max_memory_allocated, disk space utilization is measured by looking at the model size in the hard drive, while training time is considered from the moment the OHE and eOHE vectors are calculated until the end of the training.To evaluate model's performance, we have evaluated the following metrics:
• Validity, which evaluates model's learning of SMILES syntax and its capacity to generate valid molecules.
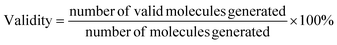 | (7) |
• Diversity and uniqueness, which evaluate the percentage of correct, diverse and unique molecules generated in a sample of molecules from the latent space of the model, e.g., a high value indicates that the model understood the complexity of the chemical space, and it is able to generate a diverse and unique variety of molecules.
The sampling of the VAE's latent space is based on the diversity of points within the latent space, while the RNN introduces variation through probabilistic sampling at each step of sequence generation
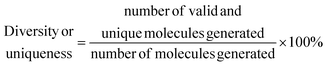 | (8) |
• Reconstruction rate, which evaluates the quality of the encoding–decoding process in the VAE by measuring the percentage of valid molecules recovered by the model in the validation data related to the number of molecules encoded.
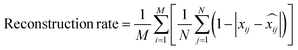 | (9) |
 is the i-th decoded label of the j-th molecule.
is the i-th decoded label of the j-th molecule.
• Novelty, which quantifies the proportion of valid molecules generated by the model that is not included in the training data.
 | (10) |
• Internal diversity I(A), defined for a set of molecules A with size |A| as the mean of the Tanimoto distance Td of molecules of A with respect to each other, following the expression:43
 | (11) |
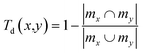 | (12) |
• External diversity E(A1, A2), defined by the training set A1 and the generated set of molecules A2 given by
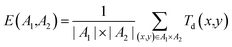 | (13) |
Validity is monitored for both models. Diversity and the reconstruction rate are monitored only for the VAE model, while the uniqueness, novelty, internal diversity and external diversity are considered for the RNN model, following reference benchmarks. This benchmarking does not aim to homogenize the metrics used, but rather compares the proposed technique performance on different models.
3 Results and discussion
In the sections below, we discuss the memory usage (both vRAM and disk) and training time, as well as the validity, diversity, and uniqueness of molecules for both the VAE and RNN models. The reconstruction rate is discussed for the VAE model, while molecular novelty, internal and external diversity are discussed for the RNN one, following our reference benchmarks.All figures show results for the three molecular string representations, i.e., SMILES on top, DeepSMILES in the middle, and SELFIES at the bottom.
3.1 Memory results
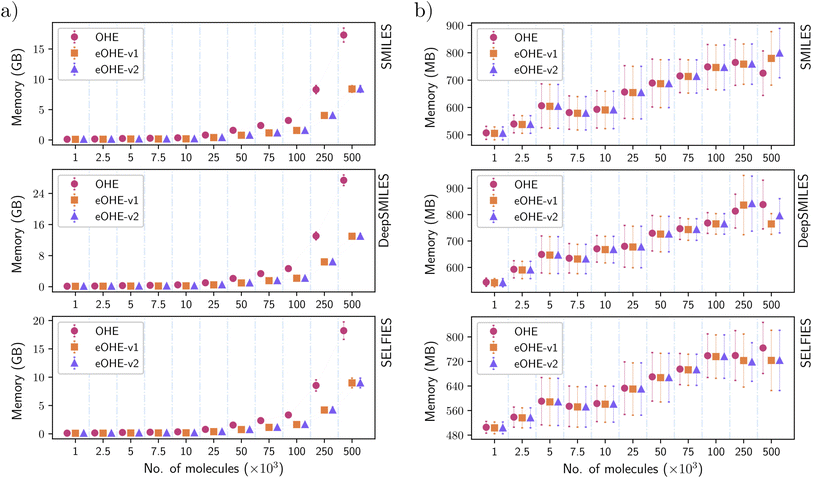
Fig. 3(a) and (b) show the amount of vRAM memory used by a single GPU during training of the VAE and RNN models, respectively, for different ZINC subsets with increasing number of molecules for SMILES, DeepSMILES and SELFIES codified with both OHE and eOHE. Similar results for the QM9 and GDB-13 datasets are available in Fig. S2 and S4 in the ESI,† respectively.Training a VAE model with eOHE of DeepSMILES of 500 × 103 molecules from the ZINC database demands almost 50% less vRAM memory allocation than the use of OHE, i.e., 12.97 GB for eOHE instead of 27.38 GB for OHE.
In a more general view, the use of vRAM memory increases with the size of the subset, but it is always lower when eOHE is implemented. This reduction in the amount of vRAM memory required is a direct consequence of embedding because it reduces the size of the data input that enters the first layer of the models. In the VAE model, such vRAM memory usage with eOHE is significantly lower than that with OHE and even more remarkable as the size of molecular subsets increases for all the molecular string representations encoded. In the case of the RNN model, the vRAM memory usage is also lower in most cases, with some exceptions at larger datasets but still within the error bars, e.g., SMILES encoding for subsets with 500 × 103 (Fig. 3(b)).
The lower impact of embedding in the use of vRAM memory by the RNN is due to the higher number of parameters of this model compared to the VAE and to the distribution of these parameters across the different layers of the models' architecture. For instance, the VAE model with SMILES encoded by OHE has a total number of 268![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 725 training parameters for a ZINC subset with 7500 molecules, with an input size of 2610 elements, which is the result of a dictionary with 29 tokens and the largest SMILES string size of 90 tokens for this subset. For this VAE architecture, around 84% of these training parameters belong to the first layer. Implementing the eOHE reduces the input size to 270 elements, and the total number of training parameters in the model decreases to 75
725 training parameters for a ZINC subset with 7500 molecules, with an input size of 2610 elements, which is the result of a dictionary with 29 tokens and the largest SMILES string size of 90 tokens for this subset. For this VAE architecture, around 84% of these training parameters belong to the first layer. Implementing the eOHE reduces the input size to 270 elements, and the total number of training parameters in the model decreases to 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 855 (35% on them in the first layer), which is a reduction of 76%. Similarly, a RNN model for the same QM9 subset with 7500 molecules has a total number of 4
855 (35% on them in the first layer), which is a reduction of 76%. Similarly, a RNN model for the same QM9 subset with 7500 molecules has a total number of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 004
004![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 895 training parameters with an input size of 31 elements, because only the size of the OHE dictionary of tokens is considered. For the RNN architecture, only 20% of the training parameters are in the first layer. The implementation of eOHE reduces the input size to 4 elements, and the total number of training parameters decreases to 3
895 training parameters with an input size of 31 elements, because only the size of the OHE dictionary of tokens is considered. For the RNN architecture, only 20% of the training parameters are in the first layer. The implementation of eOHE reduces the input size to 4 elements, and the total number of training parameters decreases to 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 963
963![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 423 (20% in the first layer), which is less than 1% reduction, given the lower relevance that the first layer has in the total of the model. Thus, the impact of eOHE is diluted. An additional reason for a different order of magnitude in the vRAM memory mobilized by the VAE and the RNN is their different procedure for loading training data. While the VAE loads the fully encoded dataset into memory during training, which is inherited from the original VAE code used for benchmarking, the RNN only loads each batch being used. Thus, we report vRAM memory usage for the same subsets in GB for the VAE and MB for the RNN.
423 (20% in the first layer), which is less than 1% reduction, given the lower relevance that the first layer has in the total of the model. Thus, the impact of eOHE is diluted. An additional reason for a different order of magnitude in the vRAM memory mobilized by the VAE and the RNN is their different procedure for loading training data. While the VAE loads the fully encoded dataset into memory during training, which is inherited from the original VAE code used for benchmarking, the RNN only loads each batch being used. Thus, we report vRAM memory usage for the same subsets in GB for the VAE and MB for the RNN.
Fig. 4 shows the disk space utilization during training of the VAE and RNN models, respectively, for different ZINC subsets with increasing number of molecules for SMILES, DeepSMILES and SELFIES codified with both OHE and eOHE. Fig. 5 shows the disk MRE of using eOHE compared to OHE for the same subsets. Similar results of both disk space utilization and MRE are provided in the ESI for the QM9 and GDB-13 datasets in Fig. S5 and S5,† respectively. MRE percentages are obtained following the equation:
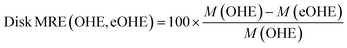 | (14) |
 | ||
| Fig. 5 Disk MRE for (a) the VAE model and (b) the RNN model for ZINC subsets; the disk MRE is calculated using eqn (14). Each data point represents the mean value of ten independent replicates, and the error bars are the standard deviations. The x-axis displays the amount of molecules used for training the models. Every subplot displays the results of training with a different molecular string representation: SMILES (top), DeepSMILES (middle) and SELFIES (bottom). | ||
Training the VAE with eOHE of DeepSMILES of 500 × 103 molecules from the ZINC database reduces disk space utilization from 2.21 MB to 0.25 MB, while the disk Memory Reduction Efficiency (MRE) increases up to 88%. Overall, the disk MRE ranges between 80% and 88% for the VAE model when it is trained with SMILES, from 85% to 92.5% when it is trained with DeepSMILES, and from 84% to 87.2% when it is trained with SELFIES, all of them from ZINC subsets. For the RNN model, disk MRE values are significantly lower than those for the VAE, always in a 1–2% range, which can also be observed in the small variation of the y-axis values in Fig. 4(b) due to the distinct memory usage patterns of each model. This reduction in disk space utilization and increase of MRE save the storage space and improve the efficiency of model implementation and execution, which facilitate model deployment in resource-constrained environments, such as mobile devices or embedded systems. It also bears direct implications for energy consumption. Lannelongue et al.44 reported that energy consumption is proportional to the process time of computing cores, vRAM memory mobilization, and power drawn by the resources. To quantify the impact of eOHE on CO2 emissions, we computed the estimated energy consumption for each model, dataset, and encoding scheme following the green algorithm calculator website provided by Lannelongue et al.44 We have included a Power Usage Effectiveness (PUE) of 1.67, a core power draw (cp) of 250 W for a NVIDIA A100 GPU, a number of cores (nc) of 1, a memory power draw (mp) of 4.3 W GB−1, and an average carbon intensity of electricity (CI) of 231.12 gCO2 per kW h. We have also utilized the specific memory (Pm) and runtime (t) values from the training of our models. This runtime is calculated dividing the total training time by the number of epochs, because every model stops its training at a different number of epochs, depending on the stop criteria. Finally, we used the following equation:
| CO2 emission = CI × t × PUE × (nc × cp+ × Pm × mp) | (15) |
| Database | Molecular string representation | CO2 emission VAE (g per epoch) | CO2 emission RNN (g per epoch) | ||
|---|---|---|---|---|---|
| OHE – eOHE-v1 | OHE – eOHE-v2 | OHE – eOHE-v1 | OHE – eOHE-v2 | ||
| QM9 | SMILES | −0.514 | 0.336 | 22.785 | 14.049 |
| DeepSMILES | 0.188 | −0.930 | 18.487 | 14.084 | |
| SELFIES | −0.999 | −0.668 | 13.205 | 14.738 | |
| GDB-13 | SMILES | 18.626 | 8.604 | 72.939 | 70.036 |
| DeepSMILES | 23.650 | 15.098 | 107.171 | −93.745 | |
| SELFIES | 54.950 | 40.210 | 8.785 | 62.134 | |
| ZINC | SMILES | 144.703 | 11.338 | 115.341 | 207.246 |
| DeepSMILES | 95.920 | 65.833 | 182.601 | 226.479 | |
| SELFIES | 179.624 | 147.992 | 89.519 | 154.454 | |
3.2 Training time results
Fig. 6(a) and (b) show the time utilised by a single NVIDIA A100 Tensor Core GPU during training of the VAE and RNN models, respectively, with OHE or eOHE for different GDB-13 subsets. Similar values for the ZINC and QM9 databases are provided in Fig. S6 and S8 in the ESI,† respectively. The implementation of eOHE leads to a similar training time for both models. In fact, the small differences observed for the case of SELFIES with the VAE model, with a lower training time for OHE, are due to a programmed training stop when the reconstruction rate does not improve for 20 epochs. Similar behavior is observed with SELFIES in the VAE model for the ZINC database (see ESI Fig. S6†).Because of the benchmarks chosen to validate eOHE, we did not modify the set of hyperparameters. We believe, however, that using an optimized set of hyperparameters, e.g., increasing the batch size, for each encoding method and molecular string representation could lead to an even faster performance of eOHE-driven models.
3.3 Validity of molecules
Fig. 7(a) and (b) show the percentage of valid molecules generated by the VAE and RNN models, respectively, using the GDB-13 subsets. Similar results are shown in the ESI for the QM9 and ZINC subsets in Fig. S2 and S6† with the VAE and Fig. S8 and S12† with the RNN.For both models, SELFIES produce a higher percentage of valid molecules, regardless of the encoding method implemented, which reaches 100% in the case of the VAE model for both OHE and eOHE.
SMILES and DeepSMILES follow similar trends in the percentage of valid molecules for the VAE with both OHE and eOHE and higher percentages for the OHE implementation, when the RNN model is adopted. The lower performance of the RNN model with eOHE, compared to OHE implementation, is attributed to the intrinsic characteristics of this encoding in connection to the RNN architecture. As we have discussed in Section 3.1, the implementation of eOHE only affects the first layer of the RNN model and reduces the number of parameters by 1%. Thus, the poor improvement in validity of molecules by the use of eOHE must be related to the struggling of the first layer to learn the complexity of this encoding. Differently, we believe that the presence of an encoder–decoder in the VAE assists with better learning of the eOHE complexity. This issue is particularly evident in the RNN model for all three representations, as shown in Fig. 7(b), whereas SELFIES, possibly due to their derivation rules lead to known robustness when generating valid structures.12
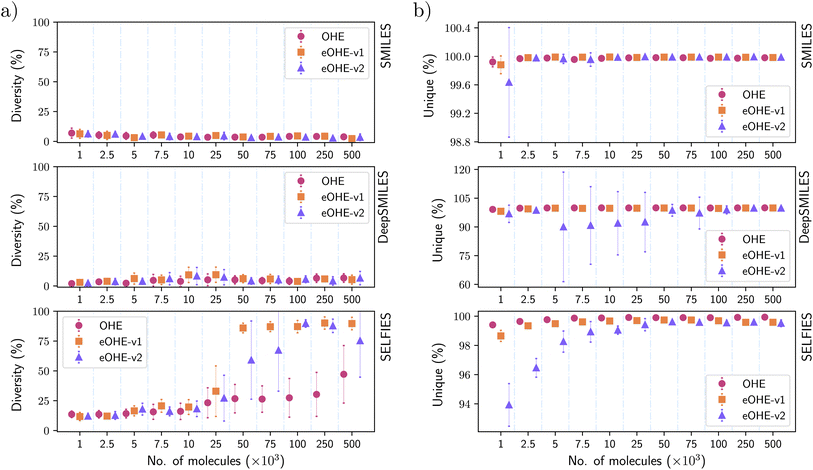
3.4 Diversity and uniqueness of molecules
Fig. 8(a) and (b) show the diversity of molecules generated by the VAE model, and the uniqueness of molecules generated by the RNN model, respectively, for subsets of the ZINC database. Similar results are shown in the ESI for the QM9 and GDB-13 subsets in Fig. S2 and S4† with the VAE and Fig. S9 and S11† with the RNN.For the VAE model, the implementation of eOHE achieves similar performance to OHE when SMILES and DeepSMILES are encoded, with a couple of exceptions. By contrast, SELFIES achieves higher diversity of molecules in all cases, and especially for subsets with more than 25 × 103 molecules if eOHE is implemented. In fact, eOHE improves the diversity of molecules generated by the VAE by up to 55% while reducing the memory usage, decreasing the number of training parameters, and keeping the training time, as discussed before. This behavior is caused because the VAE model stops its training for those subsets using OHE since there is no improvement in the reconstruction rate for 20 epochs. Additionally, since the training stops in an early stage, the VAE model is unable to learn and recognize broader diversity of molecules, when the molecules were encoded with OHE; however, when the molecules are encoded with eOHE, the VAE model continues its training to more advanced stages for the same subsets allowing eOHE to outperform OHE. This behavior could be attributed to the more compact and less sparse nature of eOHE, which works better with the fixed learning rate, enabling continued improvements over epochs compared to OHE.
It is especially noticeable that the 80% diversity plateau is reached by eOHE-v1 for subsets with more than 50 × 103 molecules and is maintained up to 500 × 103 molecules with very small error bars. This result points out eOHE-v1 as an especially useful encoding method for efficient generation of diverse molecules using a VAE.
In the case of the RNN, the uniqueness of molecules for SMILES is similar for both OHE and eOHE and always close to 100% in all cases. When eOHE-v2 is implemented, the uniqueness for subsets with 1 × 103 molecules is a bit lower but still within the error bars. A similar trend is observed for DeepSMILES for subsets with less than 100 × 103 molecules. For SELFIES, the percentage of unique molecules increases with the number of molecules in the training subset for all cases, with the lowest percentage of unique molecules of ≈94% for eOHE-v2. OHE always achieves the best percentage of unique molecules, followed very closely by eOHE-v1.
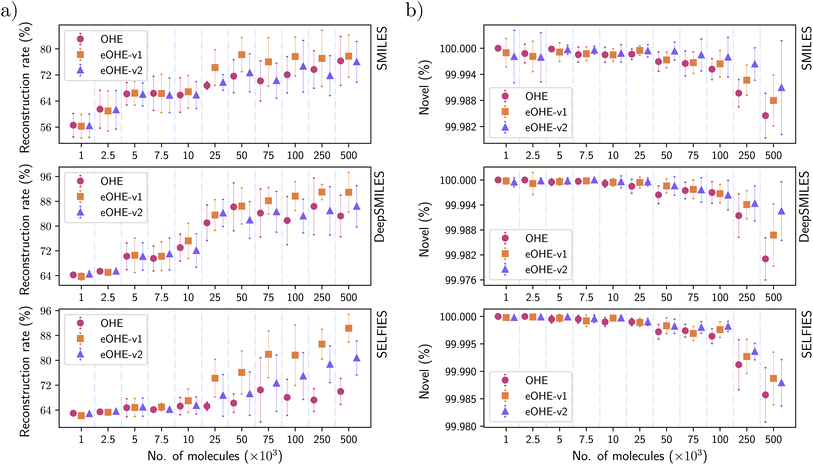
3.5 Reconstruction rate of the VAE model
Fig. 9(a) shows the reconstruction rate of the VAE model for the GDB-13 subsets. Similar results are shown in the ESI for the QM9 and ZINC subsets in Fig. S2 and S6.†eOHE performs better than OHE in all cases. For SMILES representation, eOHE-v1 achieves a better reconstruction rate than the OHE for subsets with more than 25 × 103 molecules, while eOHE-v2 reaches approximately the same reconstruction rate as the OHE, but using less training parameters. Similar behavior is observed for DeepSMILES representation, with a slightly lower reconstruction rate for eOHE-v2 compared to OHE, although within the error bars.
SELFIES achieves the best performance in the reconstruction rate for eOHE, compared to other molecular string representations. While OHE achieves reconstruction rates of 76%, 83% and 70% for SMILES, DeepSMILES, and SELFIES, eOHE-v1 reaches almost 77%, 91% and 90%, and eOHE-v2 reaches 76%, 86% and 81%, respectively. This implies a 10% improvement in the reconstruction rate for eOHE-v1 and 5% improvement for eOHE-v2, in addition to the lower memory usage, in the same training time.
A consequence of SELFIES achieving such a small reconstruction rate for OHE compared with eOHE-v1 and eOHE-v2 is that the training time is small, which can be observed in Fig. 6(a) for the case of VAE model and SELFIES. The model stops training if the reconstruction rate does not improve in 20 epochs.
3.6 Novelty of molecules from the RNN model
Fig. 9(b) shows the novelty of the molecules from the RNN model for all GDB-13 subsets. Similar results are shown in the ESI for the QM9 and ZINC subsets in Fig. S8 and S12.†For all the molecular string representations, eOHE implementation performs better than OHE, and the novelty of the molecules is above 99% in all cases. eOHE-v2 shows the best performance for subsets with more than 7.5 × 103 molecules. In subsets with more than 100 × 103 molecules, the novelty of molecules decreases at a higher rate for all the molecular representations regardless of the codification method. This behavior is also observed for subsets of the QM9 and ZINC databases (see Fig. S8 and S12 in the ESI†).
3.7 Internal and external diversity of molecules from the RNN model
Fig. 10(a) and (b) show the internal and external diversity of molecules, respectively, from the RNN model for ZINC subsets. Similar results are shown in the ESI† for the QM9 and GDB-13 subsets in Fig. S9 and S11.†These are the only metrics in which OHE clearly outperforms eOHE but only for SELFIES representation with an average improvement in the order of 10−3 for the internal diversity coefficient. For SMILES and DeepSMILES, eOHE matches the performance of OHE for both internal and external diversity.
When the training is performed with DeepSMILES, the internal diversity is constant for both OHE and eOHE; in the case of external diversity, OHE performs better for subsets with lower than 2.5 × 103 molecules. In fact, eOHE-v2 undergoes a reduction in external diversity for subsets between 5 × 103 and 75 × 103 molecules but recovers as the size of the subset increases.
The reduction in internal and external diversity observed with SELFIES is attributed to the low structural variability of the generated molecules. While SELFIES ensures a high percentage of valid molecules, the uniqueness and novelty metrics assess the differences at the token level in the molecular representations. Additionally, internal and external diversity metrics evaluate the structural variability of the molecules using MFP to capture structural features, as defined in eqn (11) and (13)
4 Conclusions
We have developed an embedded alternative to OHE that encodes discrete alphanumeric tokens of an![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) -sized alphabet into a few real numbers that constitute a simpler matrix representation of chemical structures. The implementation of this eOHE maintains model performance while significantly reducing memory usage (both vRAM and disk) and the number of training parameters.
-sized alphabet into a few real numbers that constitute a simpler matrix representation of chemical structures. The implementation of this eOHE maintains model performance while significantly reducing memory usage (both vRAM and disk) and the number of training parameters.
This embedding is highly customizable depending on the degree of compression required. We have explored two different embedding versions. eOHE-v1 applies a linear data dimensionality reduction, while eOHE-v2 applies a power-of-2 dimensionality reduction.
We have conducted a series of benchmark studies with VAE and RNN models for QM9, GDB-13 and ZINC databases, evaluating memory usage, training time, number of training parameters, and reconstruction rates, as well as molecular validity, diversity, uniqueness, novelty, internal and external diversity.
The use of eOHE outperforms OHE in most cases, the combination of SELFIES, VAE, and eOHE being an optimal configuration for efficient training and generation of molecular structures.
By using eOHE, the number of VAE training parameters is reduced by 50%. It also reduces vRAM memory allocated by 50%, and it increases the disk MRE to 80% on average. This notable decrease in memory utilization not only enhances storage efficiency but also reduces energy consumption, with direct consequences on the environmental impact of a computational facility.
For both VAE and RNN models, eOHE of SELFIES representation produces 100% of valid molecules, achieves higher diversity of molecules in all cases, and improves the diversity of molecules generated by the VAE by up to 55%. eOHE of SELFIES representation also achieves the best performance in the reconstruction rate, with an average improvement of 10% for eOHE-v1 and 5% for eOHE-v2. eOHE implementation also outperforms OHE in the novelty of molecules that reaches above 99%, for all the molecular string representations.
We consider it worthwhile to investigate the impact of eOHE in other areas beyond chemistry, especially in any ML application where categorical data are usually encoded with OHE. Future work could also benchmark eOHE with different data encoding methods, such as sparse encodings. It opens up new avenues for data representation in embedded formats to achieve better energy efficiency and scalable computing in resource-constrained devices or in scenarios with limited access to computational resources.
Data availability
This study was carried out using publicly available data from the QM9 database: https://figshare.com/collections/Quantum_chemistry_structures_and_properties_of_134_kilo_molecules/978904, and ZINC and GDB13 databases: https://zenodo.org/records/4641960. The code repositories are available in the following links: https://doi.org/10.5281/zenodo.14651123 and https://doi.org/10.5281/zenodo.14651290.Author contributions
Emilio Nuñez-Andrade: conceptualization (lead), software (lead), investigation (lead), formal analysis (equal), visualization (equal), writing – original draft (equal). Isaac Vidal-Daza: software (supporting), investigation (supporting), writing – review and editing (supporting). James W. Ryan: writing – review and editing (supporting), funding acquisition (supporting). Rafael Gómez-Bombarelli: conceptualization (supporting), writing – review and editing (supporting). Francisco J. Martin-Martinez: conceptualization (equal), software (supporting), investigation (supporting), formal analysis (equal), visualization (equal), supervision (lead), project administration (lead), funding acquisition (lead).Conflicts of interest
The authors declare no competing interests.Acknowledgements
This work was supported by the Engineering and Physical Sciences Research Council (EPSRC) Program Grant EP/T028513/1 “Application Targeted and Integrated Photovoltaics”, the Royal Society of Chemistry (RSC) Enablement Grant (E21-7051491439), and the RSC Enablement Grant (E21-8254227705). The authors also acknowledge the support from the Google Cloud Research Credits program with the award GCP19980904 and the support from the Supercomputing Wales project. E. N.-A. acknowledges support from the EPSRC PhD scholarship ref. 2602452 and the Consejo Nacional de Humanidades, Ciencias y Tecnologías (CONAHCYT) PhD scholarship ref. 809702. F. J. M.-M. acknowledges the Google Cloud Research Innovators program.Notes and references
- R. Gómez-Bombarelli, J. N. Wei, D. Duvenaud, J. M. Hernández-Lobato, B. Sánchez-Lengeling, D. Sheberla, J. Aguilera-Iparraguirre, T. D. Hirzel, R. P. Adams and A. Aspuru-Guzik, ACS Cent. Sci., 2018, 4, 268–276 CrossRef PubMed.
- M. A. Skinnider, R. G. Stacey, D. S. Wishart and L. J. Foster, Nat. Mach. Intell., 2021, 3, 759–770 CrossRef.
- W. Zhong, Z. Yang and C. Y.-C. Chen, Nat. Commun., 2023, 14, 3009 CrossRef CAS.
- Y. Wang, C. Pang, Y. Wang, J. Jin, J. Zhang, X. Zeng, R. Su, Q. Zou and L. Wei, Nat. Commun., 2023, 14, 6155 CrossRef CAS PubMed.
- J. Born, G. Markert, N. Janakarajan, T. B. Kimber, A. Volkamer, M. R. Martínez and M. Manica, Digital Discovery, 2023, 2, 674–691 RSC.
- X. Li and D. Fourches, J. Cheminf., 2020, 12, 27 CAS.
- V. Hähnke, S. Kim and E. Bolton, J. Cheminf., 2018, 10, 36 Search PubMed.
- L. David, A. Thakkar, R. Mercado and O. Engkvist, J. Cheminf., 2020, 12, 56 CAS.
- D. Weininger, J. Chem. Inf. Comput. Sci., 1988, 28, 31–36 CrossRef CAS.
- D. Weininger, A. Weininger and J. L. Weininger, J. Chem. Inf. Comput. Sci., 1989, 29, 97–101 CrossRef CAS.
- N. O'Boyle and A. Dalke, ChemRxiv, 2018, preprint, DOI:10.26434/chemrxiv.7097960.v1.
- M. Krenn, F. Häse, A. Nigam, P. Friederich and A. Aspuru-Guzik, Mach. Learn.: Sci. Technol., 2020, 1, 045024 Search PubMed.
- L. Schoenmaker, O. J. M. Béquignon, W. Jespers and G. J. P. van Westen, J. Cheminf., 2023, 15, 22 Search PubMed.
- Q. Liu, M. Allamanis, M. Brockschmidt and A. L. Gaunt, Proceedings of the 32nd International Conference on Neural Information Processing Systems, 2018, pp. 7806–7815 Search PubMed.
- K. Potdar, T. Pardawala and C. Pai, Int. J. Comput. Appl., 2017, 175, 7–9 Search PubMed.
- D. Rogers and M. Hahn, J. Chem. Inf. Model., 2010, 50, 742–754 CrossRef CAS.
- P. Rodríguez, M. A. Bautista, J. Gonzàlez and S. Escalera, Image Vision Comput., 2018, 75, 21–31 CrossRef.
- A. Slakey, D. Salas and Y. Schamroth, arXiv, 2019, preprint, DOI:10.48550/arXiv.1904.13001.
- M. Weckbecker, A. Anžel, Z. Yang and G. Hattab, Comput. Struct. Biotechnol. J., 2024, 23, 2326–2336 CrossRef CAS.
- D. P. Kingma and M. Welling, arXiv, 2013, preprint, DOI:10.48550/arXiv.1312.6114.
- C. Doersch, arXiv, 2016, preprint, DOI:10.48550/arXiv.1606.05908.
- V. Kondratyev, M. Dryzhakov, T. Gimadiev and D. Slutskiy, J. Cheminf., 2023, 15, 11 CAS.
- M. J. Kusner, B. Paige and J. M. Hernández-Lobato, arXiv, 2017, preprint, DOI:10.48550/arXiv.1703.01925.
- Z. Mao, Y. Matsuda, R. Tamura and K. Tsuda, Digital Discovery, 2023, 2, 1098–1103 RSC.
- C. Hu, S. Li, C. Yang, J. Chen, Y. Xiong, G. Fan, H. Liu and L. Hong, J. Cheminf., 2023, 15, 91 Search PubMed.
- R. Bajpai, A. Shukla, J. Kumar and A. Tewari, Comput. Mater. Sci., 2023, 230, 112525 CrossRef CAS.
- J. Chung, C. Gulcehre, K. Cho and Y. Bengio, arXiv, 2014, preprint, DOI:10.48550/arXiv.1412.3555.
- Z. C. Lipton, J. Berkowitz and C. Elkan, arXiv, 2015, preprint, DOI:10.48550/arXiv.1506.00019.
- M. H. S. Segler, T. Kogej, C. Tyrchan and M. P. Waller, ACS Cent. Sci., 2018, 4, 120–131 CrossRef CAS.
- O. Méndez-Lucio, B. Baillif, D.-A. Clevert, D. Rouquié and J. Wichard, Nat. Commun., 2020, 11, 10 CrossRef.
- M. Jiao, D. Wang and J. Qiu, J. Power Sources, 2020, 459, 228051 CrossRef CAS.
- N. De Cao and T. Kipf, arXiv, 2022, preprint, DOI:10.48550/arXiv.1805.11973.
- O. Prykhodko, S. V. Johansson, P.-C. Kotsias, J. Arús-Pous, E. J. Bjerrum, O. Engkvist and H. Chen, J. Cheminf., 2019, 11, 74 Search PubMed.
- B. Sanchez-Lengeling, C. Outeiral, G. L. Guimaraes and A. Aspuru-Guzik, ChemRxiv, 2017, preprint, DOI:10.26434/chemrxiv.5309668.v3.
- M. Xu, A. S. Powers, R. O. Dror, S. Ermon and J. Leskovec, Proceedings of the 40th International Conference on Machine Learning, 2023, pp. 38592–38610 Search PubMed.
- C. Shi, S. Luo, M. Xu and J. Tang, arXiv, 2021, preprint, DOI:10.48550/arXiv.2105.03902.
- C. Zang and F. Wang, Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, 2020, pp. 617–626 Search PubMed.
- R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. von Lilienfeld, Sci. Data., 2014, 1, 140022 CrossRef CAS PubMed.
- L. Ruddigkeit, R. van Deursen, L. C. Blum and J.-L. Reymond, J. Chem. Inf. Model., 2012, 52, 2864–2875 CrossRef CAS.
- J. Arús-Pous, T. Blaschke, S. Ulander, J.-L. Reymond, H. Chen and O. Engkvist, J. Cheminf., 2019, 11, 20 Search PubMed.
- L. C. Blum and J.-L. Reymond, J. Am. Chem. Soc., 2009, 131, 8732–8733 CrossRef CAS.
- J. J. Irwin and B. K. Shoichet, J. Chem. Inf. Model., 2005, 45, 177–182 CrossRef CAS PubMed.
- M. Benhenda, bioRxiv, 2018, preprint, DOI:10.1101/292177.
- L. Lannelongue, J. Grealey and M. Inouye, Adv. Sci., 2021, 8, 2100707 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00230j |
| This journal is © The Royal Society of Chemistry 2025 |