Time-resolved solvation dynamics of Li+, Na+ and K+ ions in liquid helium nanodroplets
Jeppe K.
Christensen
 a,
Simon H.
Albrechtsen
a,
Simon H.
Albrechtsen
 a,
Christian E.
Petersen
a,
Christian E.
Petersen
 b,
Constant A.
Schouder
b,
Constant A.
Schouder
 c,
Iker
Sánchez-Pérez
c,
Iker
Sánchez-Pérez
 d,
Pedro Javier
Carchi-Villalta
d,
Pedro Javier
Carchi-Villalta
 d,
Massimiliano
Bartolomei
d,
Massimiliano
Bartolomei
 d,
Fernando
Pirani
d,
Fernando
Pirani
 e,
Tomás
González-Lezana
e,
Tomás
González-Lezana
 d and
Henrik
Stapelfeldt
d and
Henrik
Stapelfeldt
 *a
*a
aDepartment of Chemistry, Aarhus University, Langelandsgade 140, DK-8000 Aarhus C, Denmark. E-mail: henriks@chem.au.dk
bDepartment of Physics and Astronomy, Aarhus University, Ny Munkegade 120, DK-8000 Aarhus C, Denmark
cUniversité Paris-Saclay, CNRS, Institut des Sciences Moléculaires d'Orsay, 91405 Orsay, France
dInstituto de Física Fundamental, CSIC (IFF-CSIC), Serrano 123, 28006 Madrid, Spain
eDipartimento di Chimica, Biologia e Biotecnologie, Universitá di Perugia, 06123 Perugia, Italy
First published on 4th November 2025
Abstract
In 2023, ultrafast pump–probe spectroscopy was used to record the solvation dynamics of a single Na+ ion in a liquid helium droplet, atom-by-atom and with femtosecond time resolution [Albrechtsen et al., Nature, 2023, 623, 319]. Subsequently, theoretical studies showed that other alkali ions solvate in a similar manner but no experimental results have been reported so far. Here, we extend the previous measurement on Na+ to Li+ and K+ ions. A pump pulse selectively ionizes an alkali atom, initially residing at the droplet surface, and the ensuing solvation dynamics of the formed alkali cation, Ak+, is followed by ionizing a Xe atom, located in the droplet interior, and recording the yields of Ak+Hen ions expelled from the droplet as a function of the pump–probe pulse delay. We found that Li+, Na+ and K+ ions solvate with a binding rate of 1.8 ± 0.1, 1.8 ± 0.1 and 1.7 ± 0.1 He per ps, respectively. Furthermore, by comparing the number distribution of the Ak+Hen ion yields with the evaporation energies of these ion–He complexes, obtained by Path Integral Monte Carlo calculations, we identify signatures of the first solvation shells of Li+, Na+ and K+. Lastly, we determine the time-dependent dissipation of the solvation energy from the vicinity of the three alkali ion species and found that the rate is the highest (lowest) for Li+ (K+).
Introduction
Ions and their solvation structures play a crucial role in both chemical and biological systems,1 where an important elemental group is the alkali metal ions.2 The solvation structure of Li+ ions in Li-ion batteries is important for battery efficiency,3 the hydration number of the Na+ ion significantly changes its transport properties4 and the solvation and desolvation dynamics of the K+ ion are central to the functioning of cellular potassium channels.5 It is therefore of significant interest to understand the fundamentals of the cation solvation process and how this depends on different alkali species. In practice, this requires experiments capable of following the transfer of an ion from an initial unsolvated state to a (fully) solvated state in a liquid, i.e., the process where solvent molecules – or atoms – are attracted to and bind to the ion. This is an experimentally challenging task due to the need for methods sensitive to the instantaneous solvation state,6 namely how many solvent particles the ion has bound at a particular time. Furthermore, the experiment should operate with picosecond or even sub-picosecond time resolution to capture the binding dynamics of individual solvent particles.A model system useful for addressing these experimental challenges is superfluid liquid helium droplets. Liquid helium can readily dissolve cations including the alkali metal ions7–9 and nanoscopic droplets of liquid helium have been used extensively to host single atoms, molecules, clusters or complexes in a cold, weakly perturbing environment.10–13 In particular, neutral alkali metal atoms are known to be weakly bound on the surface of the droplets,14,15 from which they solvate and move into the droplet upon ionization16–21 – an example of ion solvation in an atomic bath.22 During the solvation, the ion breaks the local superfluidity of the droplet by forming a solvation shell,23–25 where the charge density and ionic size of the alkali metal ion play important roles in the size and structure of the shells. Thus, ionization of an alkali atom at the droplet surface with a femtosecond laser pulse opens unique opportunities for real-time exploration of the solvation process of the corresponding alkali ion as it starts essentially from a gas phase, i.e. the unsolvated state. Since helium is transparent well into the deep UV, the laser pulse does not perturb the surrounding environment.
Alkali metal ions solvated in liquid helium droplets have been extensively studied using static and dynamic measurements. For instance, both electron impact ionization26 and femtosecond photoionization27 of surface-located alkali metal atoms were used to measure mass spectra of Ak+HeN clusters, revealing particularly stable structures that are interpreted as closed solvation shells. Theoretical studies23,28 have also shown how the binding energy of individual helium atoms changes as a function of the number of helium atoms attached to the Ak+HeN ion. Here, steep decreases in the binding energy have been observed at specific values of N indicating the closure of solvation shells. Concerning the solvation dynamics of alkali ions, several results were reported using different methods.18,29–33 Time-dependent liquid4 He density-functional theory predicts that all alkali metal species, Li through Cs, solvate into the helium droplet upon ionisation.18,31 For Li+, a binding rate of 1.46 He per ps was observed,18 while Na+ and K+ were found to bind with a rate of 1.3 and 1.0 He per ps.31 These studies also indicate that the solvation process can be described as Poissonian for the first several helium atoms. Another approach,32 utilising ring-polymer molecular dynamics, has similarly been employed to show how Na+ solvates into the droplet upon ionisation. The ring-polymer molecular dynamics simulations are atomistic, so the coordination number of He around Na+ can be followed as a function of time, where a stable structure of N = 10 was found, interpreted as the first solvation shell.
Recently, we showed experimentally that the initial solvation dynamics of a Na+ ion sinking into a helium droplet can be monitored on the femtosecond timescale by using a pump–probe laser scheme.34,35 In this work, a helium droplet was doubly doped with a Na atom at the surface and a Xe atom at the center of the droplet. The pump laser pulse selectively ionised the Na atom, thereby initiating solvation of Na+. At a well-defined time delay, the probe pulse ionised Xe, which repels Na+ and any He atoms attached. Detection of these Na+Hen ions, as a function of time delay between the two laser pulses, allowed us to determine the solvation dynamics atom-by-atom. We found that the solvation process for the first five He atoms can be described as Poissonian with a binding rate that depends on the droplet size and is ∼1.8 atoms per ps for a droplet containing 5200 atoms. Using evaporation energies obtained by Path Integral Monte Carlo (PIMC) simulations on a specifically calculated new potential energy surface (PES) describing the interactions between the atoms in the Na+Hen ions, the time-dependent dissipation of energy from the region around the sodium ion was determined. Here, we extend the studies to two other alkali metals, Li and K. The purpose of this work is two-fold: first, to establish the pump–probe technique developed for Na+ as a more general method for monitoring solvation dynamics of surface-bound species on helium droplets. Secondly, to investigate how the solvation dynamics of Li+ and K+ ions differ from that of Na+ and how these results compare to theoretical results.
Methods
Experiment
The experimental setup has previously been explained in detail35 and will be briefly stated here with changes between the alkali species noted. A beam of liquid helium droplets is formed by expanding 50 bar of 99.9999% purity He gas through a 5 μm round orifice into vacuum. The expansion nozzle is cooled to 18 K in all measurements, resulting in a distribution of helium droplet sizes with an average number of helium atoms 〈ND〉 = 5200. The helium droplets have an expected temperature of 0.37 K.36 The helium droplet beam enters a second vacuum chamber through a 2 mm-diameter skimmer, where the droplets are doubly doped with a single xenon atom and a single alkali atom (Li, Na or K). The gaseous Xe sample is introduced through a leak valve, while the alkali metal vapor is formed by heating a sample of the metal. The alkali metal samples are heated to 400 °C, 180 °C and 75 °C for Li, Na and K, respectively. The vapor pressures of both elements are optimized for single doping of the helium droplets, but the formation of some larger clusters is unavoidable due to the statistical nature of the doping process.10 The doped droplet beam passes through another 2 mm-diameter skimmer into a target vacuum chamber, where it is crossed by two focused laser beams in the center of a velocity map imaging (VMI) spectrometer.37,38The results on Li and Na were obtained using laser pulses from a Spectra-Physics Spitfire Ace (800 nm, 50 fs, 4 mJ, 1 kHz) laser system and the results on K were obtained using a Coherent Astrella HE (800 nm, 35 fs, 2 mJ, 5 kHz) laser system with specific parameters shown in Table 1.
| Alkali | λ (nm) | E pulse (μJ) | τ (fs) | w 0 (μm) | I 0 (W cm−2) |
|---|---|---|---|---|---|
| Pump pulse | |||||
| Li | 400 | 25 | 100 | 24 | 2.6 × 1013 |
| Na | 800 | 35 | 65 | 24 | 5.8 × 1013 |
| K | 800 | 6 | 41 | 44 | 4.5 × 1012 |
| Probe pulse | |||||
| Li | 800 | 25 | 63 | 21 | 1.2 × 1014 |
| Na | 400 | 35 | 100 | 16 | 9.1 × 1013 |
| K | 400 | 26 | 51 | 16 | 1.0 × 1014 |
The color and intensity of the pump pulse were chosen to efficiently ionize the alkali metal atom while avoiding ionization of Xe. The probe pulse intensity was chosen to efficiently ionize Xe to Xe+ while avoiding double ionization of Xe and saturation of the detector from Xe+Hek ions. Both laser pulses were linearly polarized in the plane of the position-sensitive detector at the end of the VMI spectrometer. The detector consists of a pair of microchannel plates backed by a P47 phosphor screen, which is imaged using a TPX3Cam.39–41 The TPX3Cam records the position and time-of-arrival for each lit up pixel independently and these values are converted to a time-of-flight (ToF) and a pair of coordinates, (x,y), representing the pixel. The conversion includes correcting for time-walk effects,42,43 clustering and centroiding the data using the DBSCAN algorithm. The ToF values are calibrated using known molecular species to mass-over-charge, m/q, values and the (x,y) coordinates are calibrated to the projected (vx,vy) velocities using the known velocities of the Ak+ ions originating from the laser-induced Coulomb explosion of the relevant Ak2 dimer.44,45
Data analysis
The purpose of the data analysis is to extract the yields of the Ak+Hen ions as a function of the delay, t, between the pump and the probe pulse. Here, n denotes the number of He atoms attached to the Ak+ ion when it hits the detector. This is achieved by first identifying the peaks in the m/q-spectrum corresponding to the masses of Ak+Hen ions, i.e., m/q= (mAk + n·4)u/e. The ions in each peak are binned together and a VMI image is generated using their (vx,vy) values. The VMI image contains the projected velocity components and the full three-dimensional velocity distribution is retrieved using the MEVIR algorithm.46 From this distribution, the yield of the Ak+Hen ions, Yn, is obtained by summing all ions inside a restricted velocity range, see the Methods section in ref. 34 for details. This process is repeated for all delays measured between 0.2 ps and 20 ps, resulting in the main observable, Yn(t), called the time-dependent yield.Computational details
As in our previous investigation on the Na+-doped helium clusters,35 we have built the global PESs describing both the two-body (2B) interactions between the alkali ion Ak+ and the He atoms and the corresponding three-body (3B) non-covalent contributions, whereas for describing the 2B He–He interaction we have employed the potential reported by Aziz.47 The 2B Li+–He and Na+–He interactions were already reported in ref. 28 and 35, respectively. In the case of the 2B K+–He interaction, reference ab initio energies have been here computed for a series of interparticle distances at the coupled cluster with single, double and perturbative triple excitation [CCSD(T)] levels, obtained using the Molpro2012.1 package.48In particular, accurate counterpoise corrected K+–He interaction energies have been computed by using the def2-AQZVPP49 and d-aug-cc-pV6Z50 basis sets for K+ and He, respectively. We have checked that the computed interaction energies are well-converged by verifying that they differ by less than 1% from those obtained in the minimum region with the def2-AQZVPP/d-aug-cc-pV5Z set.
The obtained ab initio results have been represented by the analytical improved Lennard-Jones (ILJ) formulation:51
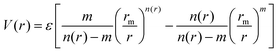 | (1) |
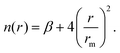 | (2) |
A fine tuning of the parameters of the ILJ expression has been carried out by exploiting the comparison with the reference CCSD(T) interaction energies, as shown in Fig. S1 included in the SI, where quite good agreement between the ab initio estimations and their analytical representation is seen. Such parameters are reported in Table 2 in comparison with the values corresponding to the Li+–He28 and Na+–He35 cases. It is of relevance to note that, for all three Ak+–He systems, the adopted parameters are in very good agreement with those predicted by correlation formulas (see the study by Cappelletti et al.52), given in parenthesis in Table 2, that exclusively exploit polarizability and charge of the interacting partners. This finding confirms the pure non-covalent nature of the interaction, being only determined by the balance of exchange (size) repulsion with induction plus dispersion attraction. Moreover, the smaller stability of K+–He is mostly determined by the largest exchange repulsion.
Our investigation also comprises the description of the 3B non-covalent interaction to be added to the pairwise 2B contributions from the He–He and Ak+–He terms. In this work, we have followed the same procedure as in previous studies of similar systems28,35 given by:
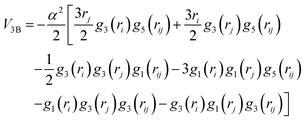 | (3) |
 | (4) |
With the above described PESs, we have employed a PIMC method53 to calculate: (i) evaporation energies, defined as Eevap(N) =Ebind(N) − Ebind(N − 1), where Ebind(N) stands for the binding energy of the Ak+HeN cluster, and (ii) the structures for clusters of different sizes. The PIMC method has already been described many times before in previous applications;28,35,53,54 so here, we just mention that a thermodynamic estimator53 has been used and a variable number of quantum beads between 600 and 1200 have been considered in the calculations. The PIMC simulations are initiated from either classically optimized or selected configurations.
Results and discussion
First, we present the theoretical results, which both motivate the subsequent analysis of the experimental Ak+Hen yields and help interpret the observed differences between the three alkali ion species.Evaporation energies and characteristics of Ak+HeN complexes
Fig. 1 shows the calculated evaporation energies, Eevap, of Li+HeN, Na+HeN and K+HeN for the first 30, 34 and 33 He atoms, respectively. Here, we use N for the number of He atoms bound to the Ak+ ion to make a distinction from the Ak+Hen ions recorded using the detector in the experiment. | ||
| Fig. 1 The evaporation energy, Eevap(N), of the Ak+HeN complexes calculated by PIMC. Results for Li+ (red), Na+ (blue) and K+ (green) are shown as filled dots. Values for Li+ are from ref. 28, values for Na+ are from ref. 35 and K+ values are from this paper. | ||
The evaporation energies for all three alkali ions are the largest for the first few helium atoms and then decrease at larger values of N. Li+ has the highest evaporation energies for the first helium atoms followed by Na+ and then K+, i.e. a trend that reflects the binding energies for the corresponding Ak+–He pair potentials, see Table 2. Significant features are found at N = 6 for Li+ and Na+. Beyond this size, a steep decrease in Eevap is observed for Li+ while Na+ exhibits a gradual reduction reaching a plateau at N = 10. For K+, the first 12 He attachments have a similar Eevap before decreasing.
For Na+, the evaporation energy exhibits a local maximum at N = 12. This particular size has been found to correspond to a stable configuration in other systems as well as Ca2+He12,55 Ar+He12,56,57 Ho2+He1258 or Ag+He12.59 Previous theoretical investigations on Na+HeN complexes concluded that the closure of the first solvation shell of He atoms around the ion actually occurs for N = 12.60–65 The only exception of this apparent overall agreement comes from the estimate by integration of the radial density profile performed by Galli et al.66 and the abrupt drop of the experimental ion yield of the work by An der Lan et al.,26 which may suggest the relevance of N = 9. In this sense, one might argue that the decrease seen at N = 9 of Eevap shown in Fig. 1 could be understood as a special feature for such a configuration. In the case of K+, there is general agreement that there are 14 He atoms in the first solvation shell,26,60,66 although Galli et al.61 and Rossi et al.64 suggest that the number could be 15. Recent density functional theory calculations in helium nanodroplets by García-Alfonso et al.31 systematically predict a larger number of He atoms for the first solvation shell for all the alkali ions than those reported in the rest of the literature.
For all Ak+HeN complexes with N > 12, subsequent helium attachments exhibit roughly a constant evaporation energy (<5 meV) independent of the alkali species. This is ascribed to the shielding effect of the first solvation shell of helium atoms around the ion. This shielding causes the next helium atoms to experience a similar ionic attraction irrespective of the ion species. This makes the first helium attachments particularly important for observing differences between the solvation of the alkali species.
To further corroborate this analysis, we consider the structures of the Ak+HeN complexes for the values of N where a significant change in the evaporation energy is observed. These are displayed in Fig. 2. The structures show an important interplay between charge density and ion size. Li+ is the smallest ion with the highest charge density and will therefore bind the strongest to helium, but due to the small size, only a few helium atoms can bind independently before He–He repulsion becomes noticeable. For K+, a lot of helium atoms can attach before any strong repulsion between the He atoms is observed. However, due to the smaller charge density, these helium atoms are not very strongly bound. Na+ places somewhere between these two systems. From a static point of view, we can then already see significant differences in the helium solvation properties of the three alkali ions, which then become less pronounced as the clusters grow in size. From Fig. 2, it is clear that only the structures for Na+He12 and K+He12, in the bottom panels (e) and (f), exhibit a closed, well-ordered icosahedral geometry.
 | ||
| Fig. 2 Structures of relevant solvation complexes with evaporation energies shown in Fig. 1 and obtained by considering either an average (Li+) or a limited value (Na+ and K+) of quantum beads for a better illustration. (a) and (b) PIMC results adapted from ref. 28 for Li+He6 and Li+He8, respectively; (c)–(e) estimated from the calculation reported in ref. 35 for Na+He6 and Na+He12, respectively, and finally (f) the structure from the present PIMC calculation for K+He12. | ||
Experimental time-dependent ion yields
Fig. 3 displays the Ak+Hen yields as a function of time for the three alkali species. For Li+ (first column) and Na+ (second column), Yn(t) values are shown for 0 ≤ n ≤ 10 but data were recorded up to nmax = 29 (Li+) and nmax = 25 (Na+), with the maximum value of n being limited by overlap with Xe+Hek ions in the m/q-spectrum. In the case of K+, all Yn(t) values up to nmax = 21 are displayed (third and fourth columns). The Yn(t) traces show a similar trend for the three alkali species. Notably, Y0(t), i.e. the yield of the bare alkali ions [panels (a0), (b0) and (c0)] gradually decreases whereas, for n ≥ 1, the ion yields reach a maximum followed by a gradual decrease. The progressive shifting of the maximum to larger times for increasing n illustrates directly that He atoms gradually bind to the alkali ions. | ||
| Fig. 3 Time-dependent ion yields, Yn(t). Left column of panels (red): Li+Hen. Second left column of panels (blue): Na+Hen. Two rightmost columns of panels (green): K+Hen. Black dots are experimental data, full lines are the results from a fit to eqn (5) and dashed lines are extrapolated values of the fit beyond the fitted range. | ||
Motivated by theoretical simulations18 and our previous work,35 we employ a Poissonian model to fit Yn(t) for the three alkali ions:
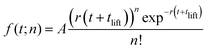 | (5) |
The result of the fit of eqn (5) to each alkali ion measurement is shown by the full lines in Fig. 3 and the fit parameters are given in Table 3. The dashed lines in Fig. 3 illustrate the result of the fit beyond the range included in the fit (t > 10 ps and the alkali-specific n-ranges).
| Alkali | n inc (min–max) | r (He ps−1) | t lift (ps) |
|---|---|---|---|
| Li | 0–3 | 1.8 ± 0.2 | 0.09 ± 0.09 |
| Na | 0–5 | 1.8 ± 0.1 | 0.24 ± 0.06 |
| K | 1–11 | 1.7 ± 0.1 | 0.08 ± 0.08 |
First, we note that the Poissonian model agrees well with the experimental results in the respective fitting ranges for the three ions. Going beyond these ranges, the Yn(t) curves deviate significantly from the corresponding Poisson curves, as seen in the case of Li+, Fig. 3(a4)–(a10), Na+, Fig. 3(b6)–(b10), and K+, Fig. 3(c12)–(c21). The reasons for the deviations were already discussed for Na+ in the two previous works, ref. 34 and 35. Here, we briefly account for the Li+ and K+ results.
In the Li+ case, Fig. 3(a4) shows that Y4(t) is significantly higher than the Poisson curve. In line with the discussions in ref. 34 and 35, we ascribe this to dissociation of Li+Hen with n ≥ 5 because of the drop in Eevap from n = 4 to 5, see Fig. 1. This effect is even more pronounced for Y6(t) where the maximum is almost a factor of 4 higher than the maximum in the Poisson curve. The explanation is found in the strong drop of Eevap (55 to 18 meV) from N = 6 to 7, Fig. 1, that causes Li+He7 or larger complexes leaving from the droplet to likely lose a He atom (or more He atoms) and thus be detected as a Li+He6 ion. Note that the position of the maximum of Y6(t) appears later than the maximum of the corresponding Poisson curve corroborating that the Li+He6 ions originate from larger complexes that were formed later but lost He atoms after departing from the droplet surface. The strong Y6(t) signal indicates that Li+He6 most likely is a filled solvation shell or, at least, a significantly stable structure compared to larger complexes as predicted by theory.
In the K+ case, the Yn(t) and Poisson curves agree quite well in the fitting range, i.e. up to n = 11. This reflects, we believe, that Eevap is essentially constant in the range N = 1–12. The slightly less good agreement between the Yn(t) and Poisson curves compared to the Li+ an Na+ cases is likely a result of the significantly lower Eevap, which could causes some dissociation to occur in the fitted n-range. For Y12(t), the maximum rises above that of the Poisson curve, whereas for Y13(t) the maximum falls much below that of the Poisson curve. This behavior, caused by the drop in Eevap from ∼12 meV at N = 12 to 3 meV at N = 13, is similar to that seen in the Li+ data from Y6(t) to Y7(t) and in the Na+ data from Y9(t) to Y10(t). In the Li+ and Na+ cases, the drop in Eevap means that one or more He atoms evaporate from K+Hen with n > 12, leading to a depletion of Yn(t) and a corresponding pile-up in Y12(t).
Table 3 shows that the He binding rate, r, is about the same for the three alkali species with a value of ∼1.7–1.8 ± 0.1 He per ps. Regarding comparison to theoretical calculations, we refer to the very recent work of García-Alfonso et al. where time-dependent density-functional theory was used to simulate the alkali ion solvation in nanodroplets consisting of 2000 He atoms.31 The simulations were carried out for Na+, K+, Rb+ and Cs+ and thanks to a smaller space step in the simulation grid, the results are expected to be more accurate than previous findings.18 In the case of Na+ and K+, the theoretical results confirmed that the binding of the first five He atoms to the alkali ions occurs at a constant rate. Furthermore, r values were found to be 1.3 and 1.0 He per ps for Na+ and K+, respectively. In our previous work on Na+, r-values of 2.04 ± 0.13, 1.84 ± 0.09 and 1.65 ± 0.09 were determined for droplets with an average number of 9000, 5200, and 3600 He atoms, respectively. This decreasing trend of r with the droplet size indicates good agreement between the experimental values and the simulated result obtained for 2000 He atom droplets. For K+, we also measured the binding rate for other droplet sizes namely droplets with an average number of 9000, 5200 and 3600 He atoms. Here, we found a similar trend with an obtained binding rate of 1.9 ± 0.1, 1.7 ± 0.1 and 1.6 ± 0.1 He per ps, again pointing to good agreement between the experimental and simulated binding rates.
Number distribution of ions
From the time-dependent ion yields, Yn(t), we conversely determine a distribution of ion yields, Yt(n) at each time delay, t. From this, we calculate the normalized number distribution, Pexp(n;t), as: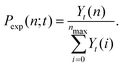 | (6) |
Fig. 4 displays Pexp(n;t) at nine selected times for Li+, Na+ and K+. In common for the three ion species, it is seen that at the earliest times, Ak+ and Ak+He dominate Pexp(n;t). This observation is expected since the alkali ion has not had much time to interact with and effectively bind He atoms. At longer times, the number distributions broaden and their weights displace to larger n values. This behavior illustrates that the solvation process of the Ak+ ions, i.e. the gradual binding of He atoms, is stochastic.
Fig. 4 also depicts the outcome of the fit applied to Pexp(n;t), i.e.eqn (5) using the parameters listed in Table 3. The fitted results (full black curves) agree well with the experimental data in the fitting ranges and, similar to the Yn(t) curves in Fig. 3, deviations appear beyond these ranges, where the fit is extrapolated (black dotted curves). In the Li+ case, we observe that the amplitudes of Pexp(4), Pexp(5) and Pexp(6) at early times, t = 0.8 ps–3.0 ps, are significantly larger than the Poisson curves, see Fig. 4(a2)–(a5). Equivalently, the Y4(t), Y5(t) and Y6(t) curves lie significantly above the Poisson curves, see Fig. 3(a4)–(a6). These observations could be due to many-body binding processes where several He atoms attach to the ion simultaneously. Such non-Poissonian processes may be particularly important for the solvation of the Li+ ion because the interaction with the He atoms is the largest of the three alkali ions. Finally, for all three ion species, we see a clear edge in the number distributions, i.e. a n-value after which the amplitude significantly decreases. For Li+, the n-value is 6 observed when t ≥ 1.4 ps, for Na+ it is 9 observed when t ≥ 2.0 ps and for K+ it is 12 observed when t ≥ 3.0 ps. These numbers reflect the N-values where Eevap(N) makes a steep drop, Fig. 1, as mentioned in the discussion of the Yn(t) curves.
Energy dissipation
When the Ak+ ions solvate in the helium droplets, energy is removed from the local region around Ak+. Once the solvation is complete, an energy of 604 meV for Li+, 385 meV for Na+ and 287 meV for K+ has been dissipated.18 This energy, termed as the sinking energy, Esink in ref. 18, is the energy difference between Ak+ at its initial position at the surface and when it is fully solvated in the droplet interior. In our two previous works,34,35 we showed that the mean energy dissipated at time t, 〈Edisp〉(t), can be determined from the distribution of the Ak+Hen ions recorded at t, Fig. 4, and the binding energy of each Ak+Hen ion, Ebind(n):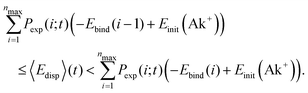 | (7) |
The outcome of applying eqn (7) to the experimental data, displayed in Fig. 5, shows a similar trend of 〈Edisp〉(t) for the three ion species. Initially, 〈Edisp〉(t) rises steeply after which it flatten off and asymptotically reaches a maximum value. Similar to previous work,35 we fit the following function to the experimental results:
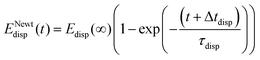 | (8) |
 | ||
| Fig. 5 Mean dissipated energy as a function of time for Li+ (red), Na+ (blue) and K+ (green). The dark-colored regions indicate the values included in the fit of eqn (8). The fit is shown as the full colored lines, while the dashed colored lines represent the fit extrapolated beyond the fitted time ranges. | ||
Fig. 5 shows that the fits of eqn (8) agree well with the experimental data in the time ranges selected. For K+, there is a minor deviation during the first ps, which we believe is caused by a small contribution to the K+ and K+He signals from dissociative ionization of K2.
The parameters of the fits are given in Table 4. Firstly, the decreasing value of τdisp as the alkali ions become larger reflects the obvious fact from the experimental curves in Fig. 5, that energy dissipates fastest in the Li+ case followed by Na+ and then K+. This observation makes sense because we found that the helium binding rates were similar for the three alkali ions and since the order of the total energy released in the solvation process, i.e. Esink, is Esink (Li+) > Esink (Na+) > Esink (K+), then the energy dissipation rate must be in the same order. Secondly, the values of Edisp(∞) are ∼57%, ∼59% and ∼65% of the values of Esink given above. This experimental underestimate reflects the limitation of the experiment in terms of not being able to measure Ak+Hen ions with n > nmax when a Xe atom is used as the interior dopant to create the repeller ion. It may be possible to lift this limitation and extend the range of Ak+Hen ions detected to larger n-values by choosing another interior dopant. For instance, SF6 is a possible candidate.
| Alkali | τ disp(ps) | Δtdisp (ps) | E disp(∞) (meV) |
|---|---|---|---|
| Li | 1.5 ± 0.1 | 0.01 ± 0.05 | 344 ± 7 |
| Na | 2.1 ± 0.2 | −0.15 ± 0.04 | 229 ± 8 |
| K | 4.9 ± 3.7 | −0.55 ± 0.25 | 187 ± 92 |
Conclusions
We investigated the solvation dynamics of single Li+, Na+ and K+ ions in helium nanodroplets, on the natural femto- and picosecond timescale and with atomic number-resolution. A fs pump pulse initiated solvation by ionizing the alkali atom, residing at the droplet surface, and the ensuing dynamics was inferred by ionizing a Xe atom in the center of the droplet, by a delayed fs probe pulse, and recording the yield of Ak+Hen ions repelled from the droplet, as a function of time. We found that the binding of individual He atoms to the alkali ions is well-described by a Poisson process for the first 3, 5 and 11 He atoms for Li+, Na+ and K+, respectively. From the Poisson analysis of the time-dependent Ak+Hen ion yields, we determined a binding rate of 1.8 ± 0.1, 1.8 ± 0.1 and 1.7 ± 0.1 He per ps, respectively, for the three ions. For Na+ and K+, these values could be compared to very recent results from time-dependent density functional simulations, revealing good agreement when accounting for differences in the droplet sizes explored experimentally and theoretically. Furthermore, in the number distributions of the Ak+Hen ions, we observe pronounced edge effects at n = 6 for Li+, n = 9 for Na+ and n = 12 for K+. These numbers correspond to the values where the evaporation energy of the Ak+Hen ion makes a steep drop as predicted by our Path Integral Monte Carlo calculations.We also determined the average energy dissipated from the local region of the Ak+ ions as a function of time. The energy dissipation follows Newton's law of cooling for the first ∼5 ps. The cooling was observed to occur fastest (slowest) for Li+ (K+), which is also the ion that needs to dissipate the largest (smallest) amount of energy in the solvation process. Our method paves the way for similar studies of the singly as well as doubly charged alkaline-earth cations, which are still unexplored.
Author contributions
Jeppe K. Christensen: conceptualization, formal analysis, investigation, methodology, validation, writing – original draft, and writing – review and editing. Simon H. Albrechtsen: conceptualization, formal analysis, investigation, methodology, visualization, and writing – review and editing. Christian E. Petersen: formal analysis, investigation, methodology, and writing – review and editing. Constant A. Schouder: conceptualization, investigation, methodology, and writing – review and editing. Iker Sánchez-Pérez: investigation and methodology. Pedro Javier Carchi-Villalta: investigation and methodology. Massimiliano Bartolomei: investigation, methodology, and writing – review and editing. Fernando Pirani: investigation and methodology. Tomás González-Lezana: funding acquisition, investigation, methodology, project administration, supervision, writing – original draft, and writing – review and editing. Henrik Stapelfeldt: conceptualization, formal analysis, funding acquisition, investigation, methodology, supervision, writing – original draft, and writing – review and editing.Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting this article have been included as part of the supplementary information (SI). Supplementary information: data for this article, including the K+–He potential as Fig. S1, calculated evaporation energies shown in Fig. 1, Yn(t) traces shown in Fig. 3, Pexp(n;t) distributions shown in Fig. 4 and mean dissipated energies shown in Fig. 5. See DOI: https://doi.org/10.1039/d5cp03894d.Acknowledgements
We thank Jan Thøgersen for his expert help in keeping the laser system under optimal conditions. H. S. acknowledges the support from Villum Fonden through a Villum Investigator Grant No. 25886. This work has been supported by Grant No. MICIU/AIE/10.13039/501100011033 PID2024-155666NB-I00.References
- Y. Marcus, Ions in Solution and their Solvation, Wiley, 1st edn, 2015 Search PubMed.
- S. Astrid, H. Sigel and R. K. O. Sigel, The Alkali Metal Ions: Their Role for Life, Springer Charm, 1st edn, 2016 Search PubMed.
- Z. Wang, H. Wang, S. Qi, D. Wu, J. Huang, X. Li, C. Wang and J. Ma, EcoMat, 2022, 4, e12200 CrossRef CAS.
- J. Peng, D. Cao, Z. He, J. Guo, P. Hapala, R. Ma, B. Cheng, J. Chen, W. J. Xie, X.-Z. Li, P. Jelínek, L.-M. Xu, Y. Q. Gao, E.-G. Wang and Y. Jiang, Nature, 2018, 557, 701–705 CrossRef CAS.
- J. H. Morais-Cabral, Y. Zhou and R. MacKinnon, Nature, 2001, 414, 37–42 CrossRef CAS.
- M. Yu, C. Chen, J. Wu, J. Deng, B. Li and Z. Li, Int. J. Hydrogen Energy, 2025, 136, 413–426 CrossRef CAS.
- W. I. Glaberson and W. W. Johnson, J. Low Temp. Phys., 1975, 20, 313–338 CrossRef CAS.
- K. R. Atkins, Phys. Rev., 1959, 116, 1339–1343 CrossRef CAS.
- B. Tabbert, H. Günther and G. Z. Putlitz, J. Low Temp. Phys., 1997, 109, 653–707 CAS.
- J. P. Toennies and A. F. Vilesov, Angew. Chem., Int. Ed., 2004, 43, 2622–2648 CrossRef CAS.
- M. Y. Choi, G. E. Douberly, T. M. Falconer, W. K. Lewis, C. M. Lindsay, J. M. Merritt, P. L. Stiles and R. E. Miller, Int. Rev. Phys. Chem., 2006, 25, 15 Search PubMed.
- A. Mauracher, O. Echt, A. M. Ellis, S. Yang, D. K. Bohme, J. Postler, A. Kaiser, S. Denifl and P. Scheier, Phys. Rep., 2018, 751, 1–90 CrossRef CAS.
- M. Stadlhofer, B. Thaler, P. Heim, J. Tiggesbäumker and M. Koch, Commun. Chem., 2025, 8, 165 CrossRef CAS.
- F. Stienkemeier, J. Higgins, C. Callegari, S. I. Kanorsky, W. E. Ernst and G. Scoles, Z. Phys. D: At., Mol. Clusters, 1996, 38, 253–263 CrossRef CAS.
- M. Barranco, R. Guardiola, S. Hernández, R. Mayol, J. Navarro and M. Pi, J. Low Temp. Phys., 2006, 142, 1–81 CrossRef CAS.
- M. Theisen, F. Lackner and W. E. Ernst, Phys. Chem. Chem. Phys., 2010, 12, 14861–14863 RSC.
- X. Zhang and M. Drabbels, J. Chem. Phys., 2012, 137, 051102 CrossRef.
- E. García-Alfonso, M. Barranco, N. Halberstadt and M. Pi, J. Chem. Phys., 2024, 160, 164308 CrossRef PubMed.
- F. Lackner, G. Krois and W. E. Ernst, J. Chem. Phys., 2017, 147, 184302 CrossRef PubMed.
- M. Theisen, F. Lackner and W. E. Ernst, J. Chem. Phys., 2011, 135, 074306 CrossRef.
- M. Theisen, F. Lackner, G. Krois and W. E. Ernst, J. Phys. Chem. Lett., 2011, 2, 2778–2782 CrossRef CAS.
- S. Chowdhury and J. Perez-Ríos, Nat. Sci., 2024, 4, e20240006 CrossRef.
- T. González-Lezana, O. Echt, M. Gatchell, M. Bartolomei, J. Campos-Martínez and P. Scheier, Int. Rev. Phys. Chem., 2020, 39, 465–516 Search PubMed.
- J. C. A. Matos, P. Giannakeas, M. Ciardi, T. Pohl and J. M. Rost, Phys. Rev. Lett., 2025, 134, 186001 CrossRef CAS.
- R. Yanes-Rodríguez, P. Villarreal and R. Prosmiti, Phys. Chem. Chem. Phys., 2025, 27, 8259–8266 RSC.
- L. An der Lan, P. Bartl, C. Leidlmair, R. Jochum, S. Denifl, O. Echt and P. Scheier, Chem. – Eur. J., 2012, 18, 4411–4418 CrossRef CAS.
- S. Müller, M. Mudrich and F. Stienkemeier, J. Chem. Phys., 2009, 131, 044319 CrossRef PubMed.
- M. Rastogi, C. Leidlmair, L. A. D. Lan, J. O. D. Zárate, R. P. D. Tudela, M. Bartolomei, M. I. Hernández, J. Campos-Martínez, T. González-Lezana, J. Hernández-Rojas, J. Bretón, P. Scheier and M. Gatchell, Phys. Chem. Chem. Phys., 2018, 20, 25569–25576 RSC.
- A. Leal, D. Mateo, A. Hernando, M. Pi, M. Barranco, A. Ponti, F. Cargnoni and M. Drabbels, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 224518 CrossRef.
- A. Leal, X. Zhang, M. Barranco, F. Cargnoni, A. Hernando, D. Mateo, M. Mella, M. Drabbels and M. Pi, J. Chem. Phys., 2016, 144, 094302 CrossRef.
- E. García-Alfonso, M. Barranco, M. Pi and N. Halberstadt, J. Chem. Phys., 2025, 163, 144309 CrossRef.
- F. Calvo, J. Chem. Phys., 2024, 161, 121101 CrossRef CAS PubMed.
- F. Calvo, Low Temp. Phys., 2025, 51, 453–459 CrossRef CAS.
- S. H. Albrechtsen, C. A. Schouder, A. Viñas Muñoz, J. K. Christensen, C. Engelbrecht Petersen, M. Pi, M. Barranco and H. Stapelfeldt, Nature, 2023, 623, 319–323 CrossRef CAS.
- S. H. Albrechtsen, J. K. Christensen, C. E. Petersen, C. A. Schouder, P. J. Carchi-Villalta, I. Sánchez-Pérez, M. Bartolomei, T. González-Lezana, F. Pirani and H. Stapelfeldt, J. Chem. Phys., 2025, 162, 174309 CrossRef CAS PubMed.
- M. Hartmann, R. E. Miller, J. P. Toennies and A. Vilesov, Phys. Rev. Lett., 1995, 75, 1566–1569 CrossRef CAS PubMed.
- D. W. Chandler and P. L. Houston, J. Chem. Phys., 1987, 87, 1445–1447 CrossRef CAS.
- A. T. J. B. Eppink and D. H. Parker, Rev. Sci. Instrum., 1997, 68, 3477–3484 CrossRef CAS.
- M. Fisher-Levine and A. Nomerotski, J. Instrum., 2016, 11, C03016 CrossRef.
- A. Zhao, M. van Beuzekom, B. Bouwens, D. Byelov, I. Chakaberia, C. Cheng, E. Maddox, A. Nomerotski, P. Svihra, J. Visser, V. Vrba and T. Weinacht, Rev. Sci. Instrum., 2017, 88, 113104 CrossRef PubMed.
- A. Nomerotski, Nucl. Instrum. Methods Phys. Res., Sect. A, 2019, 937, 26–30 CrossRef CAS.
- H. Bromberger, C. Passow, D. Pennicard, R. Boll, J. Correa, L. He, M. Johny, C. C. Papadopoulou, A. Tul-Noor, J. Wiese, S. Trippel, B. Erk and J. Küpper, J. Phys. B: At., Mol. Opt. Phys., 2022, 55, 144001 CrossRef CAS.
- F. Pitters, N. A. Tehrani, D. Dannheim, A. Fiergolski, D. Hynds, W. Klempt, X. Llopart, M. Munker, A. Nürnberg, S. Spannagel and M. Williams, J. Instrum., 2019, 14, P05022 CrossRef CAS.
- H. H. Kristensen, L. Kranabetter, C. A. Schouder, C. Stapper, J. Arlt, M. Mudrich and H. Stapelfeldt, Phys. Rev. Lett., 2022, 128, 093201 CrossRef CAS.
- H. H. Kristensen, L. Kranabetter, C. A. Schouder, J. Arlt, F. Jensen and H. Stapelfeldt, Phys. Rev. A, 2023, 107, 023104 CrossRef CAS.
- B. Dick, Phys. Chem. Chem. Phys., 2014, 16, 570–580 RSC.
- R. A. Aziz and M. J. Slaman, J. Chem. Phys., 1991, 94, 8047–8053 CrossRef CAS.
- H.-J. Werner, P. J. Knowles, R. Lindh, F. R. Manby, M. Schütz, P. Celani, T. Korona, G. Rauhut, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, C. Hampel, G. Hetzer, A. W. Lloyd, S. J. McNicholas, W. Meyer, M. E. Mura, A. Nicklass, P. Palmieri, R. Pitzer, U. Schumann, H. Stoll, A. J. Stone, R. Tarroni and T. Thorsteinsson, MOLPRO, Version 2012.1, a Package of Ab Initio Programs, 2012, see https://www.molpro.net Search PubMed.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- F. Pirani, S. Brizi, L. F. Roncaratti, P. Casavecchia, D. Cappelletti and F. Vecchiocattivi, Phys. Chem. Chem. Phys., 2008, 10, 5489–5503 RSC.
- D. Cappelletti, G. Liuti and F. Pirani, Chem. Phys. Lett., 1991, 183, 297–303 CrossRef CAS.
- R. Rodríguez-Cantano, T. González-Lezana and P. Villarreal, Int. Rev. Phys. Chem., 2016, 35, 37–68 Search PubMed.
- R. Rodríguez-Cantano, T. González-Lezana, P. Villarreal and F. A. Gianturco, J. Chem. Phys., 2015, 142, 104303 CrossRef.
- E. Zunzunegui-Bru, E. Gruber, T. Lázaro, M. Bartolomei, M. I. Hernández, J. Campos-Martínez, T. González-Lezana, S. Bergmeister, F. Zappa, P. Scheier, R. Pérez de Tudela, J. Hernández-Rojas and J. Bretón, J. Phys. Chem. Lett., 2023, 14, 3126–3131 CrossRef CAS PubMed.
- F. Tramonto, P. Salvestrini, M. Nava and D. E. Galli, J. Low Temp. Phys., 2015, 180, 29–36 CrossRef CAS.
- P. Bartl, C. Leidlmair, S. Denifl, P. Scheier and O. Echt, J. Phys. Chem. A, 2014, 118, 8050–8059 CrossRef CAS.
- F. Foitzik, M. Bartolomei, J. Campos-Martínez, F. Pirani, S. Bergmeister, L. Ganner, I. Stromberg, F. Zappa, M. Mahmoodi-Darian, T. González-Lezana and E. Gruber, Small Struct., 2025, 2500094 CrossRef CAS.
- T. Döppner, T. Diederich, S. Göde, A. Przystawik, J. Tiggesbäumker and K.-H. Meiwes-Broer, J. Chem. Phys., 2007, 126, 244513 CrossRef PubMed.
- E. Coccia, E. Bodo, F. Marinetti, F. A. Gianturco, E. Yildrim, M. Yurtsever and E. Yurtsever, J. Chem. Phys., 2007, 126, 124319 CrossRef CAS.
- D. E. Galli, D. M. Ceperley and L. Reatto, J. Phys. Chem. A, 2011, 115, 7300–7309 CrossRef CAS PubMed.
- N. Issaoui, K. Abdessalem, H. Ghalla, S. J. Yaghmour, F. Calvo and B. Oujia, J. Chem. Phys., 2014, 141, 174316 CrossRef PubMed.
- N. Issaoui, K. Abdessalem, H. Ghalla, S. J. Yaghmour, F. Calvo and B. Oujia, Theor. Chem. Acc., 2020, 139, 40 Search PubMed.
- M. Rossi, M. Verona, D. E. Galli and L. Reatto, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 212510 CrossRef.
- S. Paolini, F. Ancilotto and F. Toigo, J. Chem. Phys., 2007, 126, 124317 CrossRef PubMed.
- D. E. Galli, M. Buzzacchi and L. Reatto, J. Chem. Phys., 2001, 115, 10239–10247 CrossRef CAS.
| This journal is © the Owner Societies 2025 |

