Resolving ionization-induced distortions in 2,5-difluoropyridine: influences of meta-fluorination on electronic and vibrational structures

Abstract

We conduct a high-resolution vacuum ultraviolet mass-analyzed threshold ionization spectroscopic study of 2,5-difluoropyridine (2,5-DFP), supported by Franck–Condon (FC) simulation and natural bond orbital analysis, to investigate the stereoelectronic influences of ortho- and meta-fluorination on ionization dynamics. The adiabatic ionization energy (AIE) is precisely determined as 77 760 ± 3 cm⁻¹, which is lower than those of other DFP isomers owing to the reduced stabilization of the highest occupied molecular orbital (HOMO) by meta-substituted F. The mass-analyzed threshold ionization spectrum reveals well-resolved vibrational progressions and weak out-of-plane modes, indicating slight nonplanarity in the cationic D₀ state. These features are successfully reproduced by FC simulations incorporating minor dihedral distortions, confirming the subtle symmetry breaking upon ionization. A second AIE of 78 227 ± 3 cm⁻¹ is assigned to the D₁ state, corresponding to ionization from a lower-lying nonbonding orbital (HOMO−1). Compared to that of 2,3-DFP, 2,5-DFP exhibits less extensive geometric reorganization upon ionization, reflecting the π-character of its singly occupied molecular orbital and its more delocalized charge distribution. These results demonstrate how meta-fluorination on the opposite side modulates the cationic geometry and frontier orbital energetics, offering fresh insights into the substitution-dependent ionization behavior of fluorinated heteroaromatics.

---

Introduction

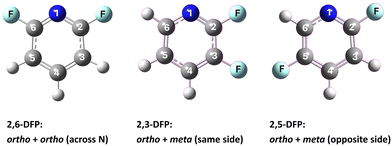
Fluorinated pyridines provide electronically versatile frameworks for use in elucidating how substituent geometry modulates the ionization dynamics, molecular orbital energetics, and cationic structures of N-containing aromatic systems.^1–6 Owing to its strong electronegativity and small size, F exerts pronounced inductive and hyperconjugative effects while introducing minimal steric distortion, and these characteristics render F an ideal probe for use in disentangling stereoelectronic influences in isomeric systems.^3–6 The positional variation of F substitution—at the ortho, meta, or para position relative to the N atom—profoundly alters the frontier orbital landscape and symmetry properties of the resulting molecular ion.^2,6–10

Previous high-resolution photoionization studies report that ortho-fluorination adjacent to pyridine N effectively stabilizes the nonbonding orbitals via hyperconjugative interactions. Compounds such as 2-fluoropyridine (2-FP)⁷ and symmetrically substituted 2,6-difluoropyridine (2,6-DFP),^2,6,8 in particular, exhibit pronounced orbital reordering and significantly nonplanar cationic geometries caused by the strong stabilization of their highest occupied molecular orbitals (HOMOs). In contrast, 2,3-difluoropyridine (2,3-DFP), which features ortho- and meta-F atoms positioned on the same side of the ring, displays π-to-n orbital switching, a slightly distorted D₀-state geometry, and an oblate cationic D₁-state structure upon ionization.¹⁰ Collectively, these observations underscore the decisive influences of the topology of substitution on ionization-induced structural distortion and electronic reconfiguration.

Despite this progress, the stereoelectronic effects associated with the fluorination of the opposite side, where ortho and meta substituents occupy trans positions across the ring, remain underexplored. 2,5-Difluoropyridine (2,5-DFP) represents a key isomeric structure in addressing this. Although it contains the same F substituents as those of 2,3-DFP,¹⁰ its trans–meta arrangement introduces markedly different spatial and electronic contexts. This topology should weaken the through-bond and -space interactions between the F atoms and N lone pair, leading to reduced HOMO stabilization and potentially less pronounced ionization-induced structural distortion; however, these predictions have not been experimentally verified or theoretically quantified.

In this study, we investigate the ionization behavior, cationic structure, and vibrational characteristics of 2,5-DFP using vacuum ultraviolet mass-analyzed threshold ionization (VUV-MATI) spectroscopy,¹¹ supported by Franck–Condon (FC) simulations¹² and natural bond orbital (NBO) analysis.¹³ The adiabatic ionization energies (AIEs) of both the ground (D₀) and excited (D₁) cationic states are accurately determined, and the effects of fluorine substitution on opposite sides of the ring are examined in terms of charge delocalization, vibrational activation, and ionization-induced structural reorganization. To contextualize these results, we compare 2,5-DFP with its regioisomers 2,3- and 2,6-DFP,^8,10 which share the same molecular formula but differ in fluorine substitution patterns, as illustrated in Fig. 1. This comparison reveals how substitution geometry modulates orbital energy levels, HOMO–HOMO−1 spacing, and vibrational coupling. The results demonstrate that fluorine positioning influences not only the ground-state electronic configuration but also the symmetry and delocalization properties of the cationic states. These findings underscore the utility of VUV-MATI spectroscopy for resolving subtle stereoelectronic effects in closely related heteroaromatic isomers.

Fig. 1 Molecular structures of 2,3-, 2,5-, and 2,6-DFP, highlighting the relative positioning of the F atoms with respect to their N atoms. The schematic emphasizes whether the F atoms are positioned on the same side (cis/meta) or opposite sides (trans/meta) of the ring.

Experimental methods

The vibrationally resolved cation spectrum of 2,5-DFP was acquired using a custom-built VUV-MATI mass spectrometer designed for use in high-resolution photoionization analysis.¹¹ The apparatus integrated four-wave difference frequency mixing (FWDFM) for tunable vacuum ultraviolet (VUV) generation, a dual-chamber assembly, and an 80 cm time-of-flight tube equipped with a multichannel plate (MCP) ion detector.

Sample introduction and molecular beam formation

Commercially available 2,5-DFP (95%, Tokyo Chemical Industry, Tokyo, Japan) was introduced without further purification. It was seeded in Ar at 5 atm and expanded into a vacuum through a pulsed nozzle (orifice of 500 µm, Parker Hannifin, Cleveland, OH, USA). This supersonic expansion ensured effective vibrational and rotational cooling. Based on the intensity ratio of the 0–0 and 27¹₁ hot bands in 2,3-DFP under similar conditions,¹⁰ the vibrational temperature was previously estimated to be approximately 49 K. Given the similarity in beam conditions, 2,5-DFP is expected to exhibit a comparable degree of vibrational cooling. The narrow linewidths and absence of discernible hot bands further support a vibrational temperature below 50 K. Although rotational temperature could not be directly extracted due to unresolved rotational contours, the spectral sharpness suggests substantial rotational cooling. The molecular beam passed through a 1.5 mm skimmer (Beam Dynamics, Dallas, TX, USA) and entered the photoionization chamber, which was maintained at ∼10⁻⁷ Torr and operated at 10 Hz. A weak DC field (∼0.1 V cm⁻¹) was applied to remove prompt ions and favor the formation of long-lived zero-kinetic-energy (ZEKE) Rydberg states.¹⁴ Field-induced enhancement of these states was further supported by electric jitter arising from the voltage drop of the high-voltage pulse.¹¹

VUV generation and photoionization

Tunable VUV light (123.7–129.3 nm) was generated by FWDFM within Kr, targeting the 4p⁶–5p[1/2]₀ or 4p⁶–5p[5/2]₂ transition to ensure phase matching. Ultraviolet (UV) pulses of 212.556 or 216.667 nm (∼0.8 mJ per pulse), which were required for each Kr transition, were produced via mixing after doubling the 637.668 or 650.002 nm light from a Continuum ND 6000 dye laser pumped using a Nd:YAG laser (Continuum Surelite II). Another Nd:YAG pumped dye laser (Lambda Physik Scanmate 2E, or Sirah PrecisionScan-LG) provided visible (VIS) light in the wavelength range 618.0–755.0 or 645.0–760.0 nm (∼10 mJ per pulse). These beams were spatiotemporally overlapped within the Kr cell (1–5 Torr) to optimize the VUV pulse yield. Residual UV and VIS radiations were separated from the VUV pulse using a MgF₂ lens, and the wavelength was calibrated using a WS5 wavemeter (HighFinesse, Tübingen, Germany) with an accuracy of 0.1 cm⁻¹.

MATI detection and signal optimization

A pulsed-field ionization (PFI) field (5 V cm⁻¹), applied ∼15 µs after VUV excitation, was used to ionize the neutral molecules in the long-lived ZEKE states into mass-selected MATI ions,¹⁵ which were then accelerated under space-focusing conditions and detected using the MCP. This intentional delay allowed sufficient time for the decay of prompt ions in the ionization region, enabling selective field ionization of the high-n Rydberg states and thereby enhancing spectral resolution. Under these conditions, the spectral resolution was approximately 7 cm⁻¹, determined from the full width at half maximum of the sharpest peaks in the MATI spectrum. This value was extracted by fitting individual peaks with analytical line-shape functions.

The uncertainty in the AIE determination was estimated to be ±3 cm⁻¹, primarily arising from two sources: the wavelength calibration accuracy of the VUV laser (∼0.3 cm⁻¹), determined through the four-wave mixing process using UV and VIS lasers, and the extrapolation of the 0–0 band position under varying PFI conditions, which introduced a reproducible spread of ±2.5–3.0 cm⁻¹. All peak intensities were normalized to the VIS laser pulse energy.

A shallow dip observed near 78 800 cm⁻¹ in the PIE curve is attributed to partial VUV attenuation caused by krypton reabsorption during four-wave mixing, a known artifact also reported in prior studies on 2-FP⁷ and 2,3-DFP.¹⁰ This is not a spectral feature of the sample itself. No corresponding MATI peak was observed in this region, allowing the Kr pressure to remain at 4 Torr for optimal VUV generation.

Computational methodology

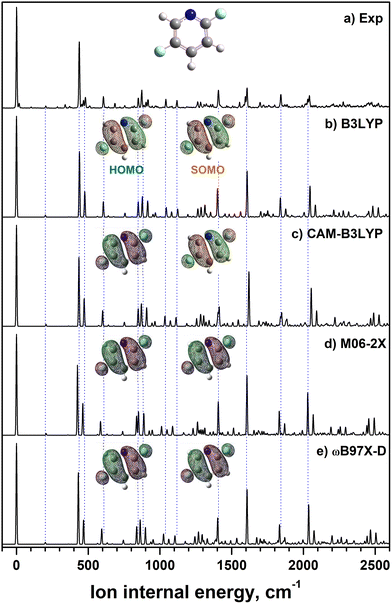
Electronic structure calculations were conducted using Gaussian 16 (Gaussian, Wallingford, CT, USA).¹⁶ The ground and cationic state geometries were optimized using density functional theory (DFT) at the B3LYP, CAM-B3LYP, M06-2X, and ωB97X-D levels with the cc-pVTZ basis set, and C_S symmetry was enforced during optimization.^17–20 FC simulations were conducted using the vibrational overlap integrals computed between the neutral (S₀) and D₀ states.¹² Time-dependent DFT (TD-DFT) calculations (root = 1, NStates = 3) were performed at the B3LYP/cc-pVTZ level to simulate D₁-state vibronic transitions.

To correct for anharmonic and basis set effects, empirical scaling factors were applied to the harmonic vibrational frequencies. These factors—0.983 for the D₀ state and 0.935 for the D₁ state—were derived using a least-squares fitting procedure based on the experimental peak positions observed in the MATI spectrum.^21,22 Additionally, the AIEs of related compounds, including 2,3-, 2,5-, and 2,6-DFP, were calculated with zero-point energy corrections to enable comparison with the experimental results. The experimental and theoretical AIEs (in wavenumbers) for the S₀ → D₀ transitions of 2,3-, 2,5-, and 2,6-DFP, as calculated at various DFT levels using the cc-pVTZ basis set, are listed in Table 1.

Table 1 AIEs (in wavenumbers) for the S₀ → D₀ transitions of 2,3-, 2,5-, and 2,6-DFP, as calculated using various DFT functionals with the cc-pVTZ basis set. The AIEs for the S₀ → D₁ transitions were calculated at the TD-DFT B3LYP/cc-pVTZ level. All values include zero-point energy corrections, and the experimental AIEs are provided for comparison

		VUV-MATI	B3LYP	CAM-B3LYP	M06-2X	ωB97X-D
a Ref. 10. b This work. c Ref. 8.
2,3-DFP	D0	78 202^a	76 018	76 418	77 716	75 696
	D1	78 754	82 136	—	—	—
2,5-DFP	D0	77 760^b	75 598	75 994	77 281	75 265
	D1	78 227	81 472	—	—	—
2,6-DFP	D0	78 365^c	76 344	76 725	78 152	76 035

---

Results and discussion

AIE of 2,5-DFP

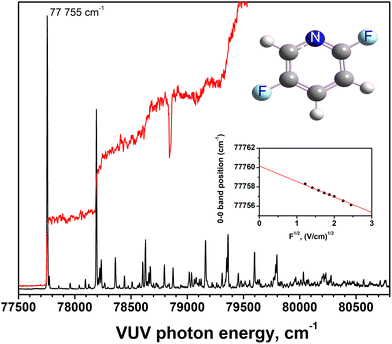
VUV-MATI spectroscopy was used to determine the AIE of 2,5-DFP with high precision. A four-electrode pulsed field ionization scheme selectively ionized high-n Rydberg states following a nanosecond-scale delay, effectively suppressing low-n Rydberg interferences that commonly affect traditional photoionization efficiency (PIE) curves.¹¹

The PIE curve obtained by monitoring the signal of the C₅H₃NF₂⁺˙ ion as a function of photon energy reveals a clear onset at 77 748 cm⁻¹, and the corresponding MATI spectrum (Fig. 2) displays a sharp 0–0 transition at 77 755 cm⁻¹. This band was extrapolated under varied pulsed field strengths to the zero field to accurately extract the field-free ionization energy. The inset shown in Fig. 2 depicts this procedure, and the AIE of 2,5-DFP is 77 760 ± 3 cm⁻¹ (9.6410 ± 0.0004 eV), based on this extrapolation.

Fig. 2 Delayed VUV-PIE curve (red trace) and high-resolution MATI spectrum (black trace) of 2,5-DFP. The ionization onset is observed at 77 748 cm⁻¹, with the 0–0 band observed at 77 755 cm⁻¹. Extrapolation to the zero-field limit yields an AIE of 77 760 ± 3 cm⁻¹ (9.6410 ± 0.0004 eV), which is lower than those of 2,3- (78 202 ± 3 cm⁻¹) and 2,6-DFP (78 365 ± 3 cm⁻¹), reflecting the weaker HOMO stabilization upon meta-fluorination. Inset: AIE determination via the linear extrapolation of the 0–0 band positions in the VUV-MATI spectra.

This value is lower than that of 2,6-DFP (78 365 ± 3 cm⁻¹)⁸ and 2,3-DFP (78 202 ± 3 cm⁻¹),¹⁰ suggesting relatively reduced HOMO stabilization in 2,5-DFP. The observed AIE is consistent with DFT predictions using various functionals (Table 1). While such isomer-dependent shifts in ionization energy are commonly observed in substituted heteroaromatic systems, this trend reflects the influence of fluorine positioning on orbital interactions—specifically, the diminished hyperconjugative coupling between the nitrogen lone pair and the meta-positioned F atom in 2,5-DFP, compared to the more effective overlap in ortho-substituted systems like 2,6-DFP.¹⁰ To assess this trend quantitatively, we performed second-order perturbation analysis within the NBO framework, as discussed in the next section and summarized in Table 2.

Table 2 NBO analysis, based on second-order perturbation theory, of the hyperconjugative stabilization energies (in kilocalories per mole) of 2,3-, 2,5-, and 2,6-DFP calculated at the B3LYP/cc-pVTZ level. The analysis includes the donor–acceptor NBO interactions involving the lone pair electrons of the N and F atoms

	S0	E rel	D0	E rel
a Difference in the stabilization energy of each DFP isomer relative to that of 2,6-DFP.
2,3-DFP	141.8	−7.5	82.2	−7.4
2,5-DFP	137.7	−11.6	79.2	−10.4
2,6-DFP	149.3	0	89.6	0

---

Electronic structure and hyperconjugative stabilization: NBO analysis

We conducted NBO¹³ analysis to quantify the hyperconjugative interactions across the DFP isomers to elucidate the electronic origin of the reduced ionization energy of 2,5-DFP. All calculations were performed at the B3LYP/cc-pVTZ level to maintain consistency with the FC simulations and TD-DFT results for the D₁ cationic state.

As shown in Fig. S1, the HOMO of 2,5-DFP is a delocalized π orbital that spans the pyridine ring but exhibits limited spatial overlap with the lone pairs of F at the meta position. This geometry significantly reduces the hyperconjugative stabilization compared to that of 2,6-DFP, where the ortho-F atoms are optimally positioned to interact with the lone pair of N. Quantitative analysis, as shown in Table 2, supports this trend. The total hyperconjugative stabilization energy involving lone pair donation from the F atoms to the π* and σ* acceptor orbitals is 7.5 kcal mol⁻¹ (0.3252 eV) lower in 2,3-DFP than in 2,6-DFP, and even more substantially reduced in 2,5-DFP by 11.6 kcal mol⁻¹ (0.5030 eV). These differences indicate a fundamental weakening of lone pair–orbital coupling due to the opposite-side fluorine substitution in 2,5-DFP, consistent with its experimentally observed lower AIE.

Further insights into orbital energetics are provided by comparing the HOMO–HOMO−1 energy separation (ΔE₁). The ΔE₁ of 2,5-DFP is 0.7538 eV, which is smaller than the separation of 2,6-DFP of 1.1448 eV and marginally larger than the separation of 2,3-DFP of 0.7148 eV.

Therefore, in 2,5-DFP, the HOMO is less stabilized and the HOMO−1 is more stabilized than in 2,3-DFP, reflecting the more effective relaxation of the nonbonding orbital induced by meta-fluorination on the opposite side of the ring.

The particularly strong stabilization of the lone-pair orbital of the N of 2,6-DFP is due to cooperative hyperconjugative and inductive effects afforded by symmetric ortho-F substitution, which enhances orbital relaxation and the electron correlation effects.⁸ In contrast, the meta-F atom of 2,5-DFP is less electronically coupled, resulting in the diminished overall orbital stabilization.

We examined the singly occupied molecular orbitals (SOMOs) in the D₀ and D₁ states to assess the structural consequences of ionization. Whereas 2,3-DFP exhibits localized nonbonding SOMOs consistent with its pronounced post-ionization distortion,¹⁰ 2,5-DFP maintains π-delocalized SOMOs in both states. This distinction supports the observed decreases in symmetry breaking and vibrational activation in 2,5-DFP. Comparing the hyperconjugative stabilization energies of the S₀ and D₀ states further reinforces this conclusion: upon ionization, the difference in the stabilization energies of 2,5- and 2,3-DFP decreases by 1.1 kcal mol⁻¹, indicating more efficient charge delocalization in the cationic form of 2,5-DFP.

Finally, the calculated energy separation between the D₀ and D₁ states of 2,5-DFP is 0.7281 eV, slightly smaller than the corresponding gap in 2,3-DFP (0.7586 eV).¹⁰ Despite the modest separation, the two cationic states remain electronically well-defined, supporting the applicability of the harmonic approximation in the FC simulations. While weak vibronic coupling may contribute to minor deviations in vibrational structure, no significant vibronic coupling was observed. These findings demonstrate that the spatial arrangement of fluorine substituents in DFPs directly modulates the extent of hyperconjugative stabilization and the delocalization of electronic density in the cationic states. In particular, NBO analysis reveals that 2,5-DFP exhibits markedly lower second-order perturbation energies compared to 2,6-DFP (Table 2), reflecting diminished lone pair–π* and lone pair–σ* interactions. This variation in orbital coupling accounts for the observed differences in HOMO energy levels, AIE values, and vibrational activation across the isomeric series.

Cationic structure and vibrational analysis of the D₀ state

The MATI spectrum of 2,5-DFP reveals the dominance of the 0–0 band and intense vibrational peaks, suggesting that ionization induces structural distortions along specific normal modes. FC simulations, based on the DFT-optimized geometries and scaled frequencies, reproduce the major vibrational features and validate the planar C_S geometry of the cationic state (Fig. 3b–e). However, weak experimental peaks at approximately 103, 285, and 371 cm⁻¹ (assigned to a″ out-of-plane modes ν₂₇, ν₂₆, and ν₂₅) are absent from the C_S-constrained simulations, indicating minor symmetry breaking upon ionization, as in 2,3-DFP.¹⁰ Although vibronic coupling can contribute in activating these modes, their manifestation may also be rationalized by unique geometrical distortions induced by electron removal from the HOMO, which relaxes the symmetry restrictions and activates nominally forbidden transitions within the harmonic approximation. These findings suggest that the experimental cationic geometry deviates slightly from the computed minimum-energy structure, which is consistent with prior observations for 2,6-DFP.⁸ Nevertheless, the optimized geometry of neutral 2,5-DFP is highly consistent with the results of microwave spectroscopy (Table 3). Furthermore, as shown in Table S1, the structural parameters obtained using three other DFT functionals remain consistent with those obtained using the B3LYP functional, and thus, the optimized structure is largely independent of the functional employed.

Fig. 3 (a) Experimental VUV-MATI spectrum of 2,5-DFP. (b)–(e) Simulated spectra based on the FC factors and vibrational frequencies calculated using the optimized geometries of 2,5-DFP in the S₀ and D₀ states at various DFT levels with the cc-pVTZ basis set: (b) B3LYP, (c) CAM-B3LYP, (d) M06-2X, and (e) ωB97XD. NBO analysis was performed at each level to examine the natures of the HOMOs and SOMOs. The blue dotted lines indicate peaks assigned to vibrational transitions in the D₀ cationic state.

Table 3 Geometrical parameters (bond lengths in angstroms and bond and dihedral angles in degrees) of 2,5-DFP in the neutral (S₀) and cationic (D₀ and D₁) states, as calculated at the B3LYP/cc-pVTZ level. The experimental data for the S₀ state are included for comparison

Parameter	2,5-DFP
	S0		D0		D1
	MW^a	Cal^b	Opt (Cs)^b	Fit (C1)^c	Opt (Cs)^b
a Previously reported experimental geometrical parameters determined via microwave spectroscopy.^5 b Geometrical parameters of 2,5-DFP with Cs symmetry in the S0 and D0 states, as calculated at the B3LYP/cc-pVTZ level. The numbers in parentheses indicate the changes upon ionization relative to the neutral geometry. c Geometries obtained following refinement of the D0-state cation under C1 symmetry to yield quantitative agreement with the experimental spectrum.
Bond length (Å)
1N–2C	1.310	1.307	1.328 (0.021)	1.329	1.320
2C–3C	1.398	1.390	1.435 (0.045)	1.435	1.386
3C–4C	1.382	1.385	1.366 (−0.019)	1.366	1.386
4C–5C	1.389	1.386	1.404 (0.018)	1.404	1.392
5C–6C	1.388	1.382	1.444 (0.062)	1.444	1.391
1N–6C	1.335	1.336	1.307 (−0.029)	1.307	1.301
2C–7F		1.341	1.290 (−0.051)	1.290	1.292
3C–8H		1.080	1.082 (0.002)	1.082	1.084
4C–9H		1.081	1.081 (0.000)	1.081	1.082
5C–10F		1.346	1.294 (−0.052)	1.294	1.312
6C–11H		1.082	1.085 (0.003)	1.085	1.086
Bond angle (°)
6C–1N–2C	117.1	117.6	116.9 (−0.7)	116.9	132.0
1N–2C–3C	126.1	125.5	126.2 (0.7)	126.2	113.8
2C–3C–4C	116.9	117.1	117.7 (0.6)	117.7	120.1
3C–4C–5C	117.5	117.8	116.4 (−1.4)	116.4	120.2
4C–5C–6C	120.9	120.5	121.5 (1.0)	121.5	119.1
1N–6C–5C	121.5	121.5	121.3 (−0.2)	121.3	114.8
3C–2C–7F		118.2	117.4 (−0.8)	117.4	126.0
6C–5C–10F		119.6	117.8 (−1.8)	117.8	118.8
Dihedral angle (°)
1N–2C–3C–4C		0.0	0.0	−0.8	0.0
3C–2C–1N–6C		0.0	0.0	1.0	0.0

---

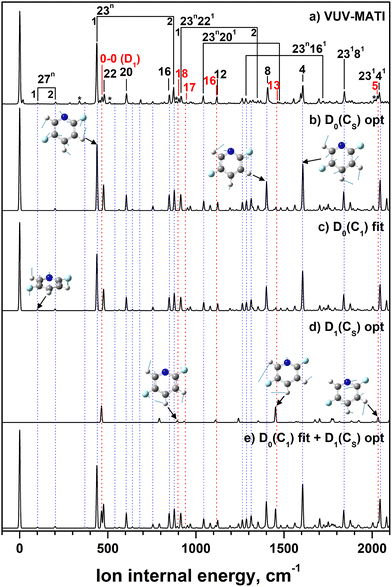
We applied constrained-geometry refinement using FC fitting to capture these features.^23,24 We selectively constrained the dihedral angles 1N–2C–3C–4C and 3C–2C–1N–6C, which significantly influence ring-bending motions, during re-optimization and recalculated the vibrational frequencies and FC factors based on the refined structure. The resulting nonplanar geometry corresponds to a true local minimum on the potential energy surface, confirmed by the absence of imaginary frequencies and any convergence warnings.

Although it lies only 2 cm⁻¹ higher in energy than the fully optimized planar C_S structure, this small difference is within the range of zero-point vibrational energy for out-of-plane modes (typically >100 cm⁻¹). Therefore, we do not interpret the nonplanar geometry as an alternative stable minimum under the harmonic approximation, but rather as a refined geometry that effectively captures ionization-induced displacement along symmetry-forbidden a″ vibrational coordinates. This approach aligns with prior observations in 2-FP, 3-chloropyridine, and 3-FP,^7,25,26 where activation of out-of-plane ring-bending modes was attributed to vibronic coupling and subtle symmetry lowering. In this context, the geometry derived from FC fitting is best viewed as a spectroscopically validated model that reproduces the weak vibrational bands and reflects vibronically allowed transitions rather than a separate energetic minimum.

The refined geometry improves reproduction of weak FC-inactive vibrational bands, particularly those observed in the low-frequency region above the 0-0 transition (Fig. 4c), and better reflects the symmetry-lowering effects associated with ionization-induced ring distortion. The adjusted dihedral angles were −0.8° (1N–2C–3C–4C) and 1.0° (3C–2C–1N–6C), and the full set of refined geometrical parameters is provided in Table 3. The refined geometry reveals that the geometric distortion upon the ionization of 2,5-DFP is reduced relative to those (−1.5° and 1.8°, respectively) of 2,3-DFP. Comparing the 6C–1N–2C bond angle across the isomers (2-FP⁷: 116.1°; 2,3-DFP¹⁰: 117.0°, 2,5-DFP: 116.9°; 2,6-DFP⁸: 115.4° in their cationic forms) highlights the means whereby the number and positions of the F substituents modulate the electronic structure and stability of the pyridine derivative. This effect indicates that F placement in the meta position slightly destabilizes the nonbonding orbital of N via interactions with the lone-pair orbitals of F, influencing the electronic properties of the pyridine derivative.

Fig. 4 (a) Experimental VUV-MATI spectrum of 2,5-DFP. Simulated spectra based on FC analysis of: (b) the D₀-state cation with C_S symmetry; (c) a slightly distorted D₀-state cation with a 3C–2C–1N–6C dihedral angle of 1.0°, as optimized at the B3LYP/cc-pVTZ level; and (d) the D₁-state cation optimized at the TD-DFT/B3LYP/cc-pVTZ level. (e) Combined spectrum generated by summing (c) and (d), with each 0–0 band normalized to match the experimental peaks at 0 and 467 cm⁻¹. The blue and red dotted lines indicate transitions originating from the D₀ and D₁ states, respectively, the mode eigenvectors associated with key vibrational transitions are displayed alongside each spectrum, and the asterisks denote weak peaks caused by a 3,5-DFP impurity.

D₁ state and secondary ionization features

In addition to the well-resolved vibrational bands assigned to the D₀ cationic state, the MATI spectrum of 2,5-DFP displays several higher-energy features at 467, 903, 946, 1119, 1466, and 2031 cm⁻¹ (indicated by the red dotted lines shown in Fig. 4). These features cannot be accounted for by the vibrational modes within the D₀ manifold, even after extensive FC simulation and spectral fitting. These features are thus attributed to ionization into the first electronically excited cationic state, i.e., D₁, analogous to previous observations for 2-FP and 2,3-DFP.^7,10

The D₁ 0–0 transition is observed at 467 cm⁻¹ above the D₀ origin, corresponding to an AIE of 78 227 ± 3 cm⁻¹ (9.6989 ± 0.0004 eV). This value is slightly lower than the corresponding D₁ AIE of 2,3-DFP, which is a trend that is consistent with the calculated AIEs summarized in Table 1. The additional bands at 903, 946, 1119, 1466, and 2031 cm⁻¹ are assigned to vibrational excitations in the D₁ state, corresponding to fundamental modes at 436, 479, 652, 999, and 1564 cm⁻¹ (modes 18, 17, 16, 13, and 5, respectively).

To validate these assignments, the D₁-state vibrational spectrum was constructed using FC-simulated spectra and convolved with Gaussian line shapes, then combined with the D₀-state spectrum and normalized to the respective intensities of the origin bands (at 0 and 467 cm⁻¹). The resulting simulated composite spectrum (Fig. 4e) closely reproduces the experimentally observed MATI profile, including the D₁-state progression, and thus, this analysis supports the assignment of the higher-energy spectral features to the HOMO−1 ionization pathway.

The optimized geometry of the D₁ state, as determined via TD-DFT (B3LYP/cc-pVTZ), retains the C_S symmetry, with a slightly oblate ring structure. Overall, the structural parameters of two cationic states and the corresponding vibrational assignments are presented in Tables 3 and 4, respectively. The retention of planarity and moderate geometrical change relative to the neutral structure reflect the π-character of the D₁-state SOMO and weaker influences of the lone pairs of F compared to those within the ortho-substituted isomer. These features are consistent with the reduced geometric distortion upon ionization, as established earlier in the D₀-state analysis.

Table 4 Experimental and calculated vibrational frequencies (in wavenumbers) and intensities of the 2,5-DFP cation (D₀ state), along with the corresponding assigned vibrational modes

Mode^a (C1/Cs)	Neutral (S0)	Cation (D0)
	Calc^b	VUV-MATI		Opt (Cs)^b		Fitting (C1)^c
		Freq	Int^d	Freq	Int^d	Freq	Int^d
a The vibrational assignments are provided for the 2,5-DFP cation in the Mulliken notation. b Calculated frequencies and FC factors obtained using the optimized structures of 2,5-DFP in the S0 and D0 states. c The adjusted frequencies and FC factors reflect quantitative agreement with the experimental results following the refinement of the geometrical parameters of the 2,5-DFP cation with C1 symmetry. d The intensities are normalized to the intensity of the 0–0 band in the experimental spectrum. e The frequencies represent the ion internal energy relative to the origin band of the D0 state. f The numbers in parentheses indicate the internal energies of the 2,5-DFP cations relative to the origin band of the D1 state.
Fundamentals
27/27 (a″)	150	103	0.012	101		101	0.011
26/26 (a″)	376	285	0.015	282		282	5 × 10^−4
25/25 (a″)	444	371	0.018	378		365	0.002
23/18 (a′)	447	437	0.658	439	0.651	438	0.652
22/17 (a′)	487	480	0.107	476	0.255	476	0.249
20/16 (a′)	638	606	0.116	605	0.155	605	0.157
18/15 (a′)	748	754	0.027	756	0.038	756	0.037
16/14 (a′)	872	850	0.100	848	0.154	848	0.154
14/13 (a′)	1019	970	0.021	968	0.044	968	0.045
12/12 (a′)	1112	1119	0.078	1124	0.081	1124	0.080
11/11 (a′)	1233	1263	0.063	1264	0.083	1264	0.087
8/8 (a′)	1291	1407	0.178	1401	0.277	1400	0.274
6/6 (a′)	1492	1466	0.025	1455	0.013	1455	0.014
4/4 (a′)	1612	1607	0.200	1607	0.452	1606	0.449
Overtones and combinations
27^2		204	0.023	201	0.021	201	0.019
27^223^1		642	0.015	640	0.014	640	0.012
27^222^1		686	0.048	677	0.005	677	0.005
27^220^1		806	0.013	806	0.003	806	0.003
23^2		872	0.181	877	0.205	877	0.205
23^122^1		917	0.084	914	0.162	914	0.158
23^120^1		1042	0.089	1044	0.096	1044	0.097
22^120^1		1084	0.020	1081	0.051	1081	0.050
23^118^1		1181	0.016	1194	0.025	1194	0.024
23^116^1		1285	0.061	1287	0.099	1287	0.099
23^3		1310	0.037	1316	0.042	1315	0.042
23^222^1		1354	0.036	1353	0.050	1353	0.049
23^220^1		1477	0.016	1482	0.028	1482	0.029
23^122^120^1		1521	0.016	1519	0.031	1519	0.031
23^112^1		1555	0.059	1562	0.053	1562	0.052
23^218^1		1627	0.019	1633	0.008	1633	0.008
23^111^1		1698	0.058	1703	0.055	1703	0.057
23^216^1		1722	0.031	1725	0.031	1725	0.031
23^18^1		1842	0.135	1839	0.188	1839	0.185
22^18^1		1886	0.036	1876	0.078	1876	0.076
23^16^1		1901	0.020	1893	0.008	1893	0.009
23^212^1		1991	0.030	2001	0.017	2001	0.017
23^14^1		2041	0.126	2045	0.303	2045	0.301
22^14^1		2087	0.028	2083	0.119	2082	0.116
23^211^1		2132	0.020	2141	0.018	2141	0.018
23^28^1		2278	0.063	2278	0.061	2277	0.061
23^122^18^1		2320	0.036	2315	0.052	2314	0.050
23^24^1		2477	0.060	2484	0.098	2483	0.098
23^122^14^1		2523	0.050	2521	0.078	2520	0.076
8^2		2812	0.036	2801	0.051	2800	0.050
8^14^1		3009	0.033	3007	0.125	3006	0.122

---

		Cation (D1)
		VUV-MATI		TD-DFT (Opt)
0–0		467^e (0)^f	0.078	0	0.078
18^1 (a′)		903 (436)	0.060	428	0.011
17^1 (a′)		946 (479)	0.022	476	0.008
16^1 (a′)		1119 (652)	0.078	644	0.019
13^1 (a′)		1466 (999)	0.025	998	0.077
5^1 (a′)		2031 (1564)	0.090	1571	0.060

---

Notably, a faint peak at 19 cm⁻¹ above the D₀ 0–0 transition remains unassigned, and it does not correspond to an expected fundamental or hot band transition. It may reflect a low-frequency vibronic feature caused by subtle coupling between the two closely spaced electronic states (D₀ and D₁), despite the general validity of the harmonic approximation used throughout FC analysis.

In combination, the well-resolved spectral features and distinct vibrational progressions of the D₀ and D₁ states provide strong evidence that 2,5-DFP undergoes less pronounced structural reorganization upon ionization than its 2,3-substituted analog. This behavior is consistent with the π-delocalized natures of the SOMOs and less-distorted dihedral angles of 2,5-DFP, reinforcing the broader conclusion that meta-fluorination leads to a shallower ionization-induced distortion profile while still activating low-frequency symmetry-breaking vibrational modes.

Conclusions

In this study, we investigated the ionization-induced structural dynamics of 2,5-DFP using high-resolution VUV-MATI spectroscopy, FC simulation, and NBO analysis. A precise AIE of 9.6410 ± 0.0004 eV was determined, which is notably lower than those of 2,3- and 2,6-DFP. This difference highlights the weaker stabilizing effect of meta-F substitution on the HOMO compared to that of ortho-substitution.

The VUV-MATI spectrum of 2,5-DFP revealed well-resolved vibrational progressions, including weak out-of-plane modes not captured by C_S-symmetric simulations. A refined FC-fitting approach incorporating slight dihedral distortion successfully reproduced these symmetry-breaking features, indicating a subtle nonplanarity in the cationic D₀ state. Additionally, a second AIE of 9.6989 ± 0.0004 eV was assigned to the D₁ state, corresponding to ionization from a nonbonding orbital. The D₁-state spectrum displayed characteristic vibrational transitions, and it was consistent with an oblate cationic geometry.

Compared to that of 2,3-DFP, 2,5-DFP exhibited reduced geometric reorganization upon ionization, as reflected in its vibrational structure and orbital character. This comparative behavior underscores how F positioning governs the electronic structure, stability, and vibronic activity of a pyridine cation. The results provide a detailed framework for use in understanding substitution-dependent stereoelectronic effects in hetero-aromatic systems, and they support the broader application of VUV-MATI spectroscopy in isomer-resolved ionization studies.

These findings are further supported by NBO analysis, which revealed that the hyperconjugative stabilization energy in 2,5-DFP is reduced by 11.6 kcal mol⁻¹ compared to 2,6-DFP, affirming the diminished donor–acceptor interactions arising from opposite-side fluorine substitution.

Author contributions

Hyojung Kim: conceptualization; data curation; formal analysis; investigation; methodology; resources; software; visualization. Sung Man Park: conceptualization; data curation; formal analysis; investigation; methodology; resources; software; visualization. Chan Ho Kwon: conceptualization; data curation; formal analysis; investigation; methodology; resources; software; visualization; funding acquisition; project administration; supervision; validation; writing – original draft; writing – review and editing.

Conflicts of interest

There are no conflicts to declare.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Supplementary information (SI) is available. Table S1: Optimized geometries of neutral and cationic 2,5-DFP obtained using various DFT functionals with the cc-pVTZ basis set, highlighting the influence of functional choice on predicted structural parameters. Fig. S1: Energy diagram illustrating the correlations between the valence molecular orbitals of pyridine, 2,3-DFP, 2,5-DFP, and 2,6-DFP, including the electronic transitions leading to their D₀ and D₁ cationic states. See DOI: https://doi.org/10.1039/d5cp03099d.

Acknowledgements

This work was supported by the National Research Foundation of Korea (2023R1A2C2002749 and RS-2024-00348644).

References

1. S. L. Wallace, A. Castellan, D. Muller and J. Michl, J. Am. Chem. Soc., 1978, 100, 6828–6834.
2. V. E. Bondybey, J. H. English and R. H. Shiley, J. Chem. Phys., 1982, 77, 4826–4831.
3. T. Itoh, Chem. Phys. Lett., 2010, 491, 29–32.
4. P. Boopalachandran, S. Kim, J. Choo and J. Laane, Chem. Phys. Lett., 2011, 514, 214–219.
5. C. W. van Dijk, M. Sun and J. van Wijngaarden, J. Mol. Spectrosc., 2012, 280, 34–41.
6. H. Sheu, S. Kim and J. Laane, J. Phys. Chem. A, 2013, 117, 13596–13604.
7. Y. R. Lee and C. H. Kwon, J. Chem. Phys., 2022, 157, 154306.
8. S. M. Park, H. Kim and C. H. Kwon, Phys. Chem. Chem. Phys., 2024, 26, 29805–29812.
9. H. Kim, S. M. Park and C. H. Kwon, Phys. Chem. Chem. Phys., 2025, 27, 5296–5304.
10. H. Kim, S. M. Park and C. H. Kwon, Phys. Chem. Chem. Phys., 2025, 27, 17399–17406.
11. Y. R. Lee and C. H. Kwon, J. Chem. Phys., 2021, 155, 164203.
12. T. E. Sharp and H. M. Rosenstock, J. Chem. Phys., 1964, 41, 3453–3463.
13. A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926.
14. R. Lindner, H. Dietrich and K. Müller-Dethlefs, Chem. Phys. Lett., 1994, 228, 417–425.
15. L. Zhu and P. Johnson, J. Chem. Phys., 1991, 94, 5769–5771.
16. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgometry, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Gaussian Inc., Wallingford CT, 2016.
17. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
18. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
19. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
20. J. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
21. P. Sinha, S. E. Boesch, C. Gu, R. A. Wheeler and A. K. Wilson, J. Phys. Chem. A, 2004, 108, 9213–9217.
22. J. P. Merrick, D. Moran and L. Radom, J. Phys. Chem. A, 2007, 111, 11683–11700.
23. P. Imhof, D. Krügler, R. Brause and K. Kleinermanns, J. Chem. Phys., 2004, 121, 2598–2610.
24. S. Leśniewski, P. Kolek, K. Pirowska, A. L. Sobolewski and J. Najbar, J. Chem. Phys., 2009, 130, 054307.
25. N. Helle, T. Raeker and J. Grotemeyer, Phys. Chem. Chem. Phys., 2021, 23, 17917–17928.
26. N. Helle, T. Raeker and J. Grotemeyer, Phys. Chem. Chem. Phys., 2022, 24, 2412–2423.

---

Footnote

† These authors contributed equally to this work.

---