 Open Access Article
Open Access ArticleModeling CH3SOH–aromatic complexes to probe cysteine sulfenic acid–aromatic interactions in proteins
Esam A.
Orabi
 ab and
Ann M.
English
ab and
Ann M.
English
 *a
*a
aCenter for Research in Molecular Modeling (CERMM), Quebec Network for Research on Protein Function, Engineering, and Applications (PROTEO), and Department of Chemistry and Biochemistry, Concordia University, 7141 Sherbrooke Street West, Montreal, Quebec H4B 1R6, Canada. E-mail: ann.english@concordia.ca; Tel: +1-514-848-2424ext3378
bCurrent address: Laboratory of Membrane Proteins and Structural Biology, Biochemistry and Biophysics Center, National Heart, Lung, and Blood Institute, National Institutes of Health, Bethesda, MD, USA
First published on 18th September 2025
Abstract
Cysteine sulfenic acid (CysOH), formed on oxidation of Cys residues, is an intermediate in the catalytic cycles of numerous antioxidant enzymes and participates in oxidative-stress sensing and redox signaling. Proteins control CysOH reactivity in part by its interactions with aromatic residues. To characterize such interactions, we performed extensive ab initio quantum mechanical calculations with MP2(full)/6-311++G(d,p) on complexes of CH3SOH as a CysOH model with side-chain models for Phe (toluene), Trp (3-methylindole), Tyr/Tyr− (4-methylphenol/4-methylphenolate) and His/HisH+ (4-methylimidazole/4-methylimidazolium) residues. The gas-phase global minima conformers extracted from the 67 aromatic complexes found exhibit binding energies of ∼−5 to −25 kcal mol−1. In the neutral CH3SOH–aromatics, the center oxidized is the stronger H-bond donor, which varies with the geometry of the complex as does the ionization potential (IPV). While CH3SOH (IPV = 9.20 eV) is exclusively oxidized when complexed to 4-methylimidazolium (IPV = 14.64 eV), the phenol ring is oxidized in all CH3SOH complexes with 4-methylphenolate (IPV = 3.31 eV). To perform molecular dynamics (MD) simulations of the aqueous complexes, a potential model was optimized for CH3SOH and calibrated for its interactions with the aromatic ions. The MD simulations reveal that in bulk water the S atom preferentially adopts en-face or intermediate binding geometry with binding free energies of ∼−0.6, −2.5 and −5 kcal mol−1 for the neutral, imidazolium and phenolate complexes, respectively. Overall, the gas-phase and aqueous CH3SOH complexes are 40–170% more stable and 0–40% less stable, respectively, than their CH3SH counterparts. Exceptionally, aqueous 4-methylphenolate binds CH3SOH ∼50% more tightly than CH3SH due to strong σ-type O–H⋯Oar H-bond bonding. Examination of a subset of CysOH–aromatics from the Protein Data Bank highlight their role in CysOH formation and stabilization in proteins.
Introduction
Although Cys comprises only ∼2% of all residues in proteins,1 its versatile redox chemistry is crucial for function. The oxidation number of the S atom can vary between −2 and +6 allowing the thiol group to be converted to a sulfenic, sulfinic and sulfonic acid, a sulfenamide, persulfide, disulfide, and S-nitrosothiol. These redox changes are induced by reactive nitrogen, oxygen, or sulfur species, making Cys residues key regulators in redox homeostasis and signaling.2,3Cys sulfenic acid (CysOH) is among the redox-reversible Cys oxoforms. In fact, the reversible oxidation of Cys to CysOH commonly regulates protein function, catalysis and signalling.2 For example, CysOH is involved in protein tyrosine phosphatase (PTP) signal transduction pathways,4 activation and function of T-cells,5 and redox-switching to regulate kinase activity.6
Under oxidative stress, which is linked to neurodegeneration and cancer pathogenesis,7 CysOH is often the first Cys oxidation product detected. Its susceptibility to further oxidation and the end products formed depend not only on the oxidant but also on the protein microenvironment such as the polarity of neighbouring residues and solvent accessibility.2 Furthermore, we have reported previously that charge transfer between aromatic residues and Cys (or Met) also impacts the redox properties of both.8,9 In fact, recurrent noncovalent S–aromatic interactions between Cys or Met and Phe, Tyr, Trp or His contribute significantly to protein stability and function.10–15 Towards characterizing CysOH–aromatic interactions and their influence on CysOH redox properties, here we investigate gas-phase and aqueous model complexes of methanesulfenic acid (CH3SOH) with toluene, 3-methylindole, 4-methylphenol/4-methylphenolate and 4-methylimidazole/4-methylimidazolium as proxies for the side chains of Phe, Trp, Tyr/Tyr− and His/HisH+ residues, respectively.
We performed ab initio quantum mechanical (QM) calculations to obtain geometries and interaction energies of the gas-phase CH3SOH–aromatic and CH3SOH–H2O complexes. A new additive potential model was developed for CH3SOH and used together with the CHARMM36 all-atom additive force field (FF)16 for the aromatic residues and the CHARMM-compatible TIP3P model for water17,18 in molecular dynamics (MD) simulations to evaluate the geometry and stability of the CH3SOH–aromatics in bulk water. Our detailed analysis of the properties of the CH3SOH–aromatic complexes provides a comprehensive data set that expands our profiling of the S–aromatic motif in proteins. Comparison with our previous investigations on Cys–aromatic interactions8,9 sheds new light on how S-aromatic interactions influence CysOH formation and redox stability and thereby the impact of Cys oxidation on protein structure and function.
Computational methods
Ab initio calculations
QM calculations were performed with the Gaussian 09 program.19 The geometry of methanesulfenic acid (CH3SOH) and a relaxed scan of its CSOH dihedral angle φCSOH between 0° and 180° in 5°-increments were calculated with MP2(full)/6-311++G(d,p) and MP2(full)/6-311++G(3df,3pd). The geometry of CH3SOH complexes with water, toluene, 3-methylindole, 4-methylphenol, 4-methylphenolate, 4-methylimidaole and 4-methylimidazolium were optimized with MP2(full)/6-311++G(d,p) without constraints by initially placing the interacting ligands at various relative orientations while considering all possible σ- and π-type H-bonding as well as S–π and O–π interactions. For the 7 binary complexes examined, over 300 structures were optimized and these converged to 69 energy minima structures (no imaginary frequencies). The coordinates of the 69 unique structures are provided in the SI and their geometries are reported in Fig. 2 and SI Fig. S1–S7. The counterpoise (CP) procedure of Boys and Bernardi20 was used to correct the interaction energies for basis set superposition error (BSSE) and both uncorrected (E) and corrected values (ECP) are reported. However, to benchmark the results reported here, interaction energies of the seven global minimum conformers were also calculated at their MP2(full)/6-311++G(d,p) geometries using the B3LYP21 and M06-2X22 density functional and the MP2(full) and CCSD(T) methods with the 6-311++G(d,p), 6-311++G(3df,3pd), and aug-ccpVQZ basis sets.The impact of complexation on the redox properties of the interacting ligands is investigated by comparing the calculated vertical ionization potentials (IPV) of the isolated ligands and the complexes, measuring the degree of charge transfer between the ligands by natural bond order (NBO) analysis, and localizing radical sites in the complexes following electron loss.9,23,24
The default FF described below underestimates the interaction energies of the charged aromatics relative to the MP2(full)/6-311++G(d,p) values. Hence, rigid-monomer potential energy curves (PECs) were generated for two conformers of CH3SOH–4-methylimidazolium and CH3SOH–4-methylphenolate by scanning the distance from 3.0 to 10.0 Å between the S atom and the aromatic ring centroid in 0.1-Å increments. The geometry of the interacting fragments and their relative orientations are fixed to those of the optimized conformers and the PECs are corrected for BSSE and later used to calibrate the FF for the ionic complexes.
Molecular mechanics (MM) calculations
Small CH3SOH–aromatic complexes are amenable to high-level QM calculations in the gas phase, but such calculations become prohibitive for the solvated complexes. MM calculations are typically performed instead and were implemented here with CHARMM25 using the CHARMM36 all-atom additive FF16 for the aromatic compounds, the CHARMM-compatible TIP3P model for water,17,18 and our new model developed in the next section for CH3SOH. Interaction energies of the CH3SOH complexes (EMM and EMM,opt) at various points along the PECs were calculated with the FF as the difference in energy between the complex and its isolated constituents while maintaining their ab initio geometries. | (1) |
 in the LJ potential are determined from individual LJ parameters for atoms i and j using the Lorentz–Berthelot combination rules:
in the LJ potential are determined from individual LJ parameters for atoms i and j using the Lorentz–Berthelot combination rules: | (2) |
An initial guess of the FF parameters of CH3SOH was performed using the CHARMM general FF (CGenFF) online tool.26 Except for the LJ parameters, other parameters were refined to reduce large deviations from ab initio calculations or large penalties assigned by the CGenFF. Parameters b0, θ0, S0 and Φ0 were obtained from geometry optimization of CH3SOH with MP2(full)/6-311++G(3df,3pd); Kr, Kθ, KS and KΦ are adjusted to reproduce the vibrational frequencies calculated at the same level and scaled by 0.945. Partial charges on the CH3 atoms (qH = 0.09e and qC = −0.15e) are set to those of dimethyl sulfoxide (CH3SOCH3) in the CGenFF and qS is set to −0.12e to give a neutral CH3S fragment. To maintain a neutral OH group, qH is set to −qO with charges set to reproduce the dipole moment of gaseous CH3SOH calculated at the same level. The dihedral parameters n and δ for the HCSO angle are assigned the values predicted by the CGenFF while those of the CSOH angle are set to yield torsional potentials in good agreement with the QM calculations. Our optimized FF for CH3SOH is reported in the SI.
FF optimization for CH3SOH interactions
The default FF gives interaction energies for the CH3SOH complexes of the four neutral aromatics and H2O in good agreement with the ECP values calculated with MP2(full)/6-311++G(d,p) but significantly underestimates the stabilities of the charged complexes. Optimization of the FF for CH3S–4-methylimidazolium and CH3SOH–4-methylphenolate follows previously reported procedures.8,9,23,24,27–32 In particular,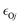 and Rmin,Oj, the pair-specific LJ parameters referring to the O atom of CH3SOH (O) and an imidazolium N or the phenolate O atom (j) in the nonbonded van der Waals energy term, are optimized to reproduce the ten lowest ECP values covering a range of 0.9 Å in 0.1-Å increments in the PEC of each complex. The optimized LJ parameters were input in the NBFIX section of the CHARMM parameter file to override the default values from the Lorentz–Berthelot combination rules.
and Rmin,Oj, the pair-specific LJ parameters referring to the O atom of CH3SOH (O) and an imidazolium N or the phenolate O atom (j) in the nonbonded van der Waals energy term, are optimized to reproduce the ten lowest ECP values covering a range of 0.9 Å in 0.1-Å increments in the PEC of each complex. The optimized LJ parameters were input in the NBFIX section of the CHARMM parameter file to override the default values from the Lorentz–Berthelot combination rules.
We have previously shown that the default FF reasonably reproduces the properties of H2O–aromatics except for overestimating the stability of H2O–4-methylphenolate.8,9 Thus, previously optimized pair-specific LJ parameters8 were used in MD simulations of this complex in water.
Investigating the CH3SOH–aromatics in bulk water
The bonding interactions and complexation geometry were investigated for each CH3SOH–aromatic in bulk water using 100-ns MD simulations (200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 frames) in 500 water molecules. Oar–H/Nar–H⋯O/S and O–H⋯Oar/Nar σ-type H-bonding (where the ar subscript indicates an aromatic N or O atom) between CH3SOH and the aromatics was investigated using a cut-off of 2.5 Å for H⋯O/N and 2.8 Å for H⋯S H-bonds.9,23,24,40 The rSX values (Fig. 2B) were binned and the percentage of H-bonded structures plotted vs. rSX9,23,24 for the 200
000 frames) in 500 water molecules. Oar–H/Nar–H⋯O/S and O–H⋯Oar/Nar σ-type H-bonding (where the ar subscript indicates an aromatic N or O atom) between CH3SOH and the aromatics was investigated using a cut-off of 2.5 Å for H⋯O/N and 2.8 Å for H⋯S H-bonds.9,23,24,40 The rSX values (Fig. 2B) were binned and the percentage of H-bonded structures plotted vs. rSX9,23,24 for the 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 structures analyzed for each complex. Contributions of π-type H-bonding (C–H/O–H⋯πar) or O/S⋯πar interactions to complex stability in bulk water were evaluated from the gZX(r) radial distribution functions representing the probability of finding any atom Z (H, C, O, S) of CH3SOH at a distance r from the aromatic ring centroid X.
000 structures analyzed for each complex. Contributions of π-type H-bonding (C–H/O–H⋯πar) or O/S⋯πar interactions to complex stability in bulk water were evaluated from the gZX(r) radial distribution functions representing the probability of finding any atom Z (H, C, O, S) of CH3SOH at a distance r from the aromatic ring centroid X.
Geometries of the aqueous complexes were investigated by binning the θSXY angles at each rSX (Fig. 2B). The number of structures in each bin ρ(rSX, θSXY) were counted and plots of the 2D PMF function,
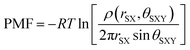 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θSXY and rSX
θSXY and rSX![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θSXY reveal the preference of the S atom for the face or the edge of the aromatic moiety, giving rise to en-face or edge-on geometry, respectively.8,9,23,24
θSXY reveal the preference of the S atom for the face or the edge of the aromatic moiety, giving rise to en-face or edge-on geometry, respectively.8,9,23,24
Results
Geometry and electrostatic potential map of free CH3SOH
Geometry optimization of CH3SOH with MP2(full)/6-311++G(3df,3pd) yields a minimum energy structure with a dihedral angle ϕCSOH = 92.8° and a dipole moment of 2.14 D. Conformers with ϕCSOH = 0° and 180° are transition state (TS) structures lying 6.5 and 3.6 kcal mol−1, respectively, above the most stable structure (Fig. 1A). MP2(full)/6-311++G(d,p) calculations predict ϕCSOH = 93.5° and a dipole moment of 2.38 D for the stable structure of CH3SOH and TS structures at 6.8 and 3.4 kcal mol−1 (Fig. 1A).Examination of the electrostatic potential surface map calculated with MP2(full)/6-311++G(d,p) (Fig. 1B) sheds light on the reactivity of CH3SOH. Its methyl and hydroxyl H atoms are characterised by maximum electropositive potentials (Vs,max) of 10–16.2 and 38.3 kcal mol−1, respectively. Additionally, CH3SOH possess a positive σ-hole (electron-deficient outer lobes of a bonding p orbital)23 with Vs,max = 17 kcal mol−1 extending from the S atom along the S–O bond. Minimum electronegative potentials (Vs,min) are centred on the O (−32.9 kcal mol−1) and S (−10.5 and −14.4 kcal mol−1) atoms. Note that the S lone pairs are well separated in space9,23,41 resulting in two distinct regions of Vs,min whereas the overlapping electron density of the O lone pairs results in a single electronegative site on this atom.15,42
Our previous calculations on CH3SH at the same level9 revealed electrostatic potentials of 12.2, 15.3 and −18.4 kcal mol−1 on its methyl H, thiol H, and S atoms, respectively. Thus, Cys oxidation to CysSOH should generate a better H-bond donor and a better H-bond acceptor at the sulfenic O but not S atom.
Gas-phase geometries and interaction energies of the CH3SOH–aromatics calculated with MP2(full)/6-311++G(d,p)
Fig. 2 shows the geometries of the global minimum energy gas-phase CH3SOH complexes while Table 1 summarizes their key inter-fragment structural parameters (rSX and θSXY, Fig. 2B) and interaction energies. Fig. S1–S7 and Tables S1–S7 of the SI present the corresponding properties of local-minimum conformers of the seven complexes. The large BSSE values observed in Table 1 and Tables S1–S7 are consistent with those we found previously for noncovalent interactions using the same level of theory.9,23 Although no experimental data are available for the systems examined in this study, the BSSE-corrected (ECP) interaction energies are expected to be reliable as demonstrated for other noncovalent complexes.32 Based on their θSXY values, the complexes are assigned en-face/distorted en-face (<30°), intermediate (30–60°) and edge-on (>60°) geometries.| Ligand (aab, complex)a | r SX , Å | θ SXY degrees | E , kcal mol−1 |
E
CP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c, kcal mol−1 c, kcal mol−1 |
E
MM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d, kcal mol−1 d, kcal mol−1 |
E
MM,opt![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d, kcal mol−1 d, kcal mol−1 |
CH3SOH chargee | IPVf, eV | CH3SOH spin densityg |
|---|---|---|---|---|---|---|---|---|---|
| a See structures of complexes in Fig. 2A; rSX and θSXY are defined in Fig. 2B. The CH3SOH–H2O complex 1g is included for reference and rSX corresponds to the S–O(H2O) distance. b Amino acid (aa) side chain modelled by the aromatic ligand. c BSSE-uncorrected (E) and corrected (ECP) ab initio gas-phase interaction energies calculated with MP2(full)/6-311++G(d,p). d Interaction energies calculated with the default (EMM) and optimized (EMM,opt) force field (FF) where necessary. e Net charge (e) of CH3SOH in the complex. f Vertical ionization potentials (IPV) from the ab initio calculations. The range of IPV values for the local minima conformers (SI Fig. S1–S7 and Tables S1–S7) is given in brackets. Calculated IPVs (eV) of the free ligands: CH3SOH (9.20; this work), toluene (9.45),9 3-methylindole (7.88),9 4-methylphenol (8.77),9 4-methylimidazole (8.78),9 4-methylimidazolium (14.64),24 4-methylphenolate (3.31),24 and H2O (12.60).9 g Spin density on CH3SOH ligand following loss of one electron from the complex; a value of 1.0 indicates CH3SOH oxidation and 0.0 aromatic oxidation. | |||||||||
| Toluene (Phe, 1a) | 3.93 | 27 | −9.77 | −4.85 | −5.00 | — | 0.009 | 8.48 (8.45–8.98) | 1.0 |
| 3-Methylindole (Trp, 1b) | 4.06 | 30 | −13.05 | −6.99 | −6.40 | — | −0.002 | 8.27 (7.65–8.90) | 0.6 |
| 4-Methylphenol (Tyr, 1c) | 4.40 | 48 | −12.41 | −7.16 | −5.95 | — | 0.024 | 8.60 (8.29–9.12) | 0.0 |
| 4-Methylimidazole (His, 1d) | 4.45 | 87 | −13.67 | −10.26 | −9.06 | — | −0.038 | 8.02 (7.93–8.64) | 1.0 |
| 4-Methylimidazolium (HisH+, 1e) | 4.64 | 82 | −21.40 | −16.86 | −8.75 | −15.14 | 0.059 | 12.6 (11.9–12.8) | 1.0 |
| 4-Methylphenolate (Tyr−, 1f) | 5.09 | 83 | −31.05 | −25.86 | −18.84 | −24.70 | −0.122 | 4.15 (3.66–4.21) | 0.0 |
| H2O (1g) | 3.27 | — | −8.40 | −5.87 | −5.27 | — | −0.013 | 8.64 (9.38) | 1.0 |
The optimized toluene complexes are characterized by O–H⋯πar (1a, S1g–S1i) or C–H⋯πar (S1a–S1f) π-type H-bonding, which accounts for their distorted en-face or borderline intermediate geometry (θSXY = 21–36°; Fig. 2, Table 1 and Fig. S1, Table S1). The significantly larger electropositive potential of the CH3SOH hydroxyl vs. methyl H (Fig. 1B) explains the greater stability of 1a and S1g–S1i (ECP = −4.3 to −4.9 kcal mol−1) vs. S1a–S1f (ECP = −2.2 to −3.6 kcal mol−1) (Table 1 and Table S1).
The 3-methylindole complexes are also stabilized by π-type H-bonding with distorted en-face or intermediate geometry (θSXY = 28–49°; Fig. 2, Table 1 and Fig. S2, Table S2). The larger electronegative potential of the indole C6 ring vs. the phenyl ring42 plus its simultaneous accommodation of two π-type H-bonds (1b) accounts for the greater stability of the methylindole vs. the toluene complexes (ECP values, Table 1 and Table S1, S2). Furthermore, C–H⋯O/S (S2a, S2b) and Nar–H⋯O S2f, S2h) σ-type H-bonds contribute to the stability of four of the ten optimized 3-methylindole complexes. Notably, the strong Nar–H⋯O σ-type H-bond present in both S2f and S2h shifts their θSXY values (47–49°, Table S2) towards the intermediate geometry (30–60°) midpoint.
Like the toluene and indole complexes, all 17 of the 4-methylphenol complexes are stabilized by π-type H-bonding (Fig. 2 and Fig. S3). Notably, 15 are additionally stabilized by σ-type H-bonds, resulting in distorted en-face and intermediate geometry (θSXY = 25–48°; Fig. 2 and Table 1, Fig. S3, Table S3). The two 4-methylphenol complexes S3h and S3k stabilized by π-type H-bonds only possess distorted en-face geometry (θSXY = 28 and 26°) and are essentially isoenergetic with toluene complex 1a, reflecting the similar electrostatic surface of the phenol and benzene aromatic rings.42 On the other hand, strong Oar–H⋯O σ-type H-bond explains the considerably higher stability and greater θSXY of 1c and 3Spvs.1a (Table 1 and Table S3). Also, the 0.5–1.1 kcal mol−1 higher stability of 1c and S3p relative to S3m and S3o with Oar⋯H–O σ-type H-bonding reveal that 4-methylphenol is a better H-bond donor than acceptor when interacting with CH3SOH. Finally, the Oar–H⋯S σ-type H-bond stabilizes the intermediate geometry of S3f, S3g, S3j, S3l and S3n (Table S3).
CH3SOH preferentially donates a H-bond to the pyridine-type N of 4-methylimidazole consistent with the electronegative potential of imidazole being centred over this atom.42 Hence, the most stable 4-methylimidazole complexes (1d, S4i, S4h) exhibit edge-on geometry (θSXY = 71–87°; Table S4) due to strong O–H⋯Nar σ-type H-bonding with the pyridine-type N (Fig. 1 and Fig. S4). The strength of this H-bonding is underscored by the significantly higher gas-phase affinity of CH3SOH for 4-methylimidazole vs. the other neutral aromatics (ECP values, Table 1). Conformers S4f and S4g also possess strong O–H⋯Nar σ-type H-bonding but are additionally stabilized by π-type H-bonding, accounting for their intermediate geometry (θSXY = 41–42°; Table S4). In fact, seven (S4a–S4g) of the 10 optimized 4-methylimidazole complexes exhibit π-type H-bonding and the weakest (S4a–S4c) exhibit en-face geometry (θSXY = 6–22°; Table S4). These three complexes also exhibit weak σ-type C–H⋯Nar H-bonding whereas stronger σ-type Nar–H⋯O H-bonding increases both the stability and θSXY (42–43°) of S4d–S4e (Table S4).
Imidazolium possesses an entirely electropositive surface (Vs,max = 84 to 138 kcal mol−1).24 Hence, all but three (S5b–S5d) of the 14 optimized 4-methylimidazolium conformers are stabilized by strong σ-type H-bond donation from a ring N to the O or S atom of CH3CSOH (Nar–H⋯O/S) (Fig. 1 and Fig. S5). S5b–S5d are also stabilized by strong Car–H⋯O/S σ-type H-bond donation from the C atoms of 4-methylimidazolium. Given their σ-type H-bonding, all but one (S5e) of the cationic complexes exhibit edge-on geometry (θSXY = 61–90°; Table S5). S5e adopts intermediate geometry (θSXY = 35°; Table S5) since, in addition to σ-type Nar–H⋯S H-bonding, it is also stabilized by electrostatic attraction between the O lone pairs and the electropositive surface of the imidazolium ring. Finally, we note that 1e with a single Nar–H⋯O σ-type H-bond is ∼8 kcal mol−1 more stable than S5a with a single Nar–H⋯S σ-type H-bond (Table S5 and Fig. 1, Fig. S5) due to the considerably larger Vs,min at the O vs. S atom of CH3SOH (Fig. 1B).
Phenolate possesses an entirely electronegative surface (Vs,min = −60 to −131 kcal mol−1).24 The global minimum CH3SOH–4-methylphenolate complex 1f, the most stable by far of the gas-phase CH3SOH complexes (Ecp ∼ −26 kcal mol−1; Table 1), possesses a single very strong O–H⋯Oar σ-type H-bond and exhibits edge-on geometry (Fig. 2A). In contrast, the five local minimum phenolate conformers all possess π-type C/O–H⋯πar H-bonding and four S6a–S6d adopt en-face geometry (θSXY = 15–29°; Fig. S6 and Table S6). Also, the high stability of S6b, S6c (Ecp ∼ −13 kcal mol−1; Table S6) with just C/O–H⋯πar H-bonding (Fig. S6) underscores the strength of π-type H-bonding with the phenolate ring.
Two stable structures were optimized for the CH3SOH–H2O complex with CH3SOH acting as a H-bond donor (1g, ECP = −5.87 kcal mol−1) or acceptor (S7a, ECP = −4.94 kcal mol−1). The ∼1 kcal mol−1 higher stability of 1g indicates that CH3SOH is a slightly better H-bond donor than H2O.
Benchmarking the MP2(full)/6-311++G(d,p) calculations
Before examining the redox properties of the complexes, we evaluated the performance of the MP2(full)/6-311++G(d,p) calculations by comparing the ECP interaction energies of the global minimum conformers (Table 1) against those obtained using DFT (B3LYP, M062X) or CCSD(T) methods, combined with the same [6-311++G(d,p)] or larger basis sets [6-311++G(3df,3pd) and aug-cc-pVQZ]. Due to its failure to account for dispersion interactions,43 B3LYP underestimates the stability of 1a–c, which are largely stabilized by dispersive π-type44vs. coulombic σ-type H-bonding in complexes 1d–g (Fig. 2A). Results using the M062X, MP2(full) and CCSD(T) functionals are closer (Fig. 3), in particular the ECP values calculated with MP2(full)/6-311++G(d,p) fall within an average unsigned deviation of only 1 kcal mol−1 from those obtained using CCSD(T)/6-311++G(d,p), the most computationally expensive model chemistry examined here. Thus, we conclude that MP2(full)/6-311++G(d,p) is an excellent compromise between accuracy and computational cost in modelling the CH3SOH–aromatics, which justifies its use in this study. In addition, the MP2(full)/6-311++G(d,p) method is chosen here as it was shown to yield interaction energies in good agreement with experiment for other noncovalent interactions32 and to allow direct comparison with the sulfur–aromatic interactions we investigated previously using this method.8,9 | ||
| Fig. 3 Benchmarking the MP2(full)/6-311++G(d,p) calculations (solid blue line) for the global minimum conformers of the CH3SOH–aromatic and CH3SOH–H2O complexes. The BSSE-corrected interaction energies ECP of the global minimum conformers (Fig. 2A) calculated with the B3LYP (black), M062X (red), MP2(full) (blue) and CCSD(T) (green) functionals using the 6-311++G(d,p) (triangles, solid lines), 6-311++G(3df,3pd) (circles, dashed lines) and aug-cc-pVQZ (squares, dotted lines) basis sets. Note that the B3LYP (black) and M062X (red) functionals yield ECP values that are essentially basis-set independent. Also, due to their high computational cost, we did not perform MP2(full)/aug-cc-pVQZ, CCSD(T)/6-311++G(3df,3pd) or CCSD(T)/aug-cc-pVQZ calculations. | ||
Redox properties of the gas-phase CH3SOH–aromatics
To predict the impact of complexation on the redox behaviour of CH3SOH, we calculated at the MP2(full)/6-311++G(d,p) level the IPV of the 69 stable complexes found here plus the charge on the CH3SOH ligand and its spin density following loss of an electron from each complex (Table 1 and Tables S1–S7). As we noted previously,9,23,24 the ligand with the smaller IPV gets oxidized when the free ligands exhibit considerably different IPVs (footnote f, Table 1). Thus, CH3SOH (9.20 eV) is the centre oxidized in all the 4-methylimidazolium (14.64 eV) complexes (Table S5) while the phenolate (3.31 eV) is oxidized in all the 4-methylphenolates (Table S6). Strong σ-type H-bonding promotes transfer of ∼0.1e from CH3SOH to 4-methylimidazolium (Table S5) and from 4-methylphenolate to CH3SOH in the most stable complexes (Table S6). Consequently, the IPVs of imidazolium complexes are up to 3.6 eV higher than that of free CH3SOH (Table S5) and the IPVs of the phenolates are up to 0.9 eV higher than that of free 4-methylphenolate (Table S6).In the toluene complexes, π-type H-bond donation to the ring results in charge transfer to CH3SOH (Fig. 1 and Fig. S1). However, the small positive charge on CH3SOH in all the toluene complexes except S1c (Table S1) suggests that weak long-range S–aromatic interactions counteract charge transfer from the ring. Nonetheless, CH3SOH is the center oxidized and the IPVs of the complexes lie ≤0.75 eV below that of free CH3SOH (Table S1). CH3SOH also acts as an H-bond donor and is the center oxidized in most of the 4-methylimidazole complexes (Table S4). Strong σ-type O–H⋯Nar H-bonding promotes the transfer of up to 0.04 e to CH3SOH and the IPVs of the complexes are up to 1.3 eV lower than that of free CH3SOH (Table S4).
CH3SOH is oxidized in only four of its ten 3-methylindole complexes, including its most stable complexes, 1b and S2i (Table S2) with exclusively π-type O–H⋯πar H-bonding. In contrast, CH3SOH is oxidized in 11 of its 17 complexes with 4-methylphenol but not in 1c and S3p, the two most stable complexes (Table S3). Transfer ∼0.02e to the aromatic via strong σ-type Oar–H⋯O H-bond donation precipitates ring donation in 1c and S3p (Table S3). The centre oxidized switches to CH3SOH in S3o and S3m (Table S3) with σ-type O–H⋯Oar H-bonding (Fig. 1 and Fig. S3). Since S3o and S3m are slightly less stable than 1c and S3p (ECP, Table S3), the O atom of CH3SOH is a slightly better H-bond acceptor than that of 4-methylphenol.
Free CH3SOH (9.20 eV) has significantly smaller IPV than H2O (12.60 eV) so CH3SOH is the centre oxidized in the two H2O complexes, 1g and S7a (Table S7). Nonetheless, these complexes exhibit IPVs ∼0.6 eV lower (1g) and ∼0.2 eV higher (S7a) than free CH3SOH (Table S7) since H2O is a H-bond acceptor in the former and donor in the latter (Fig. 1 and Fig. S7).
Optimized force field (FF) for CH3SOH and its interaction with the aromatic ions
To perform MD simulations in bulk water, a new potential model was optimized for CH3SOH and calibrated for its interactions with the aromatic ions. The optimized FF is reported in the SI. Our additive model yields an equilibrium geometry for CH3SOH characterized by ϕCSOH = 93.2° and a dipole moment of 2.11 D, in good agreement with the MP2(full)/6-311++G(3df,3pf) values (92.8° and 2.14 D). The model also finds TS conformers with ϕCSOH = 0° and 180° at 7.0 and 5.6 kcal mol−1 above the ground state vs. 6.5 and 3.6 kcal mol−1 for the ab initio values (Fig. 1A). The model also reproduces the shape of the ϕCSOH potential energy surface within ∼2 kcal mol−1 over the minimum energy region (ϕCSOH = 60–130°, Fig. 1A), thereby capturing the equilibrium geometry while still allowing the conformational flexibility relevant to ambient fluctuations.The default FF interaction energies (EMM) underestimate ECP of the CH3SOH–4-methylimidazolium and CH3SOH–4-methylphenolate complexes by an average of 5.4 and 3.2 kcal mol−1, respectively. In comparison, EMM for the neutral aromatic and H2O complexes deviate from ECP by an average unsigned error of only 0.7 kcal mol−1 (Table 1 and Tables S1–S7). Optimization of the O–N and O–O pair-specific LJ parameters allows calibration of the model vs. the ab initio PECs (Fig. 4) to give EMM,opt that deviate from ECP by average unsigned errors of 1.9 and 1.1 kcal mol−1 (Tables S5 and S6). Hence, adoption of the optimized pair-specific LJ parameters ( , Rmin,ON = 2.865 Å for 4-methylimidazolium;
, Rmin,ON = 2.865 Å for 4-methylimidazolium;  , Rmin,OO = 2.750 Å for 4-methylphenolate) ensures that interactions of CH3SOH with the charged aromatics are adequately described.
, Rmin,OO = 2.750 Å for 4-methylphenolate) ensures that interactions of CH3SOH with the charged aromatics are adequately described.
 | ||
| Fig. 4 Potential energy curves for selected CH3SOH complexes of 4-methylimidazolim (A and B) and 4-methylphenolate (C and D) from ab initio calculations with MP2(full)/6-311++G(d,p) (solid black lines), the default FF model (dotted red lines), and the optimized model (solid red lines). PEC were calculated by scanning the selected intermolecular coordinate rSX (Fig. 2B) shown for each structure as detailed under Computational methods. | ||
Stability and bonding of the CH3SOH–aromatics in bulk water
The affinity of CH3SOH for the aromatics was investigated in bulk water using PMF calculations (Fig. 5 and Table 2). Solute–solute interactions are usually weaker in bulk water vs. the gas phase due to competition from H2O–solute interactions.8,9,23,24,27–32 The CH3SOH complexes of the neutral aromatics display binding free energy minima in bulk water (∼−0.6 kcal mol−1; Table 2) 7–20-fold less than those in the gas phase (ECP values; Table 1). However, ionization of the aromatic greatly increases its affinity for CH3SOH in bulk water (Fig. 5) such that CH3SOH has only ∼5-fold less affinity for the aqueous vs. gaseous charged aromatics (Tables 1 and 2). | ||
| Fig. 5 Potentials of mean force (PMFs) between the S atom of CH3SOH and the ring centroid of (A) toluene (black), 3-methylindole (red), 4-methylphenol (blue), 4-methylimidazole (green); and (B) 4-methylimidaolium (pink), and 4-methylphenolate (cyan). The pair-specific LJ parameters optimized in this work for CH3SOH interaction with the aromatic ions and those optimized previously for H2O–phenolate interaction8 were used to derive the PMFs for the aromatic ion complexes. | ||
To characterize bonding in the aqueous complexes, we next examine the probability of finding atom Z (H, C, O or S) of CH3SOH at a distance rZX from the aromatic ring centroid X (Fig. 2B; C6 ring of indole). This probability is determined from the 100-ns MD simulations and expressed as radial distribution function, gZX(r). Notably, gHX(r) displays a peak centred at ∼5.0 Å for the toluene, 3-methyindole and 4-methylphenol complexes but at ∼4.3 Å for complexes of the smaller 4-methylimidazole ring (Fig. 6A–D). Also, the high electrostatic potentials at the hydroxyl atoms (Fig. 1B) results in higher intensities of the hydroxyl gHX(r) peak centred at rHX = 2.3 Å and the gOX(r) shoulder at rOX = 3.2 Å vs. the methyl gHX(r) peak and gCX(r) shoulder at rHX = 2.3 Å and rCX < 3.5 Å, respectively (Fig. 6A–D). Finally, we note that gSX(r) is less intense than gCX(r) or gOX(r) at rZX < 4.0 Å (Fig. 6A–D), mirroring the lower frequency of S⋯πarvs. C–H⋯πar or O–H⋯πar interactions in the gas-phase (Fig. S1–S6).
Based on the MD simulations, ∼10–17% of the 4-methylimidazole complexes are stabilized by O–H⋯Nar σ-type H-bonding at rSX = 3.2–4.1 Å (Fig. 7A). N–Har⋯O bonding is present in ∼2% of these complexes (Fig. 7A), confirming that CH3SOH is a better H-bond donor than acceptor in its 4-methylimidazole complexes as seen in the gas phase (Fig. 2A and Fig. S4). In the 4-methylphenol complexes, both O–H⋯Oar and O–Har⋯O σ-type H-bonding is ≤2% as is N–Har⋯O σ-type H-bonding in 3-methylindole (Fig. 7A). Note that N/O–Har⋯S σ-type H-bonded structures are <2% and their percentages are not plotted in Fig. 7A.
 | ||
| Fig. 7 Percentages of N/O–Har⋯O (solid lines) and O–H⋯Nar/Oar (dotted lines) σ-type H-bonded structures in the (A) neutral and (B) charged CH3SOH–aromatics in bulk water at 298.15 K as a function of rSX, the distance between the S atom of CH3SOH and the ring centroid X (C6 ring of indole; see Fig. 2B). Plots were constructed from the 100-ns MD simulations of the complexes and the H-bonded and aromatic (ar subscript) atoms are indicated in the panels. Less than 2% of the complexes possess N/O–Har⋯S σ-type H-bonds so their percentages are not plotted. | ||
Intense gOX(r) peaks at rOX = 3.0 and 3.8 Å plus the hydroxyl gHX(r) peak at rHX = 3.3 Å signal strong Nar–H⋯O H-bonding in CH3SOH–4-methylimidazolim (Fig. 6E). Likewise, the sharp gSX(r) peak at rSX = 4.4 Å suggests a sizable contribution from Nar–H⋯S σ-type H-bonding whereas the weak gCX(r) peaks at rCX = 4.5 and 5.3 Å combined with negligible methyl gHX(r) intensity are consistent with repulsive interactions between the aromatic cation and the electropositive methyl H atoms (Fig. 6E). The CH3SOH–4-methylphenolate complex (Fig. 6F) exhibits dominant hydroxyl gHX(r) peaks at rHX = 2.1 and 3.5 Å plus gOX(r) peaks at rOX = 3.1 and 4.3 Å. These peaks signal strong O–H⋯πar and O–H⋯Oar H-bonding whereas the baseline intensity of gHX(r) indicates negligible C–H⋯Oar H-bonding.
Again, mirroring the gas phase, σ-type H-bonding is dominant in the charged aqueous CH3SOH complexes (Fig. 7B). Approximately 35% of the 4-methylimidazolium complexes are stabilized by N–Har⋯O H-bonding at rSX = 4.8 Å while 25% and 75% of the 4-methylphenolate complexes are stabilized by O–H⋯Oar H-bonding at rSX = 3.5 and 4.7–6.1 Å, respectively, (Fig. 7B). Thus, the greater percentage of σ-type H-bonding in the anionic complexes explains their greater stability vs. the cationic complexes (Fig. 5B).
Geometry of the CH3SOH–aromatics in bulk water
The stabilities of the aqueous complexes vs. geometry are plotted in Fig. 8.8,9,23,24 The 2D plots of the PMF dependence on θSXY and rSX (Fig. 2B) reveal that the most stable neutral and cationic complexes are characterized by en-face binding (θSXY < 30°; Fig. 8A–E) whereas stable anionic 4-methylphenolate complexes adopt both en-face and intermediate geometry (θSXY = 10–60°; Fig. 8F). The relative stability of the latter over a wide range of θSXY values (Fig. 8F) is likely a consequence of H-bonding over an also wide range of rSX (Fig. 7B). | ||
| Fig. 8 Variation in stability of the aqueous CH3SOH–aromatics with geometry. The 2D heat maps show the potential of mean force (PMF, kcal mol−1) for the CH3SOH complex of (A) toluene, (B) 3-methylindole, (C) 4-methylphenol, (D) 4-methylimidazole, (E) 4-methylimidazolium, and (F) 4-methylphenolate from the 100-ns MD simulations in bulk water at 298.15 K. The PMF is given by eqn (3); rSX and θSXY are defined in Fig. 2B. The PMF value for idealized en-face geometry θSXY = 0°) falls on the x-axis and that for edge-on geometry (θSXY = 90°) falls on the y-axis. | ||
Discussion
In the present study, we have characterized both the gas-phase and aqueous complexes of CH3SOH, a model of CysOH, with toluene, 3-methylindole, 4-methylphenol, 4-methylphenolate, 4-methylimidazole, and 4-methylimidazolium, models of Phe, Trp, the neutral and charged side chains of Tyr and His, and with H2O. We identified a total of 69 stable gas-phase structures and investigated their interaction energies with MP2(full)/6-311++G(d,p). The global minimum-energy conformers display interaction energies in the range −4.9 to −25.9 kcal mol−1 (Table 1). Using the new additive FF model developed for CH3SOH and the CHARMM36 FF for the aromatics, the stability of the CH3SOH–aromatic complexes in water was measured. The model predicts maximum binding free energies of −0.55 to −0.65 for the neutral aqueous complexes, and values of −2.5 and −4.9 kcal mol−1 for the cationic and anionic complexes, respectively (Table 2). We previously reported that imidazolium possesses an entirely electropositive (Vs,max = +84 to +138 kcal mol−1) surface and phenolate an entirely electronegative surface (Vs,mjn = −60 to −131 kcal mol−1) surface.24 Thus, these ligands form strong ion–dipole and H-bonding interactions, as reflected here in higher stabilities for the charged CH3SOH vs. neutral aqueous complexes (Tables S1–S6).Nature of H-bonding controls the geometry of the complexes
CH3SOH binds toluene strictly by π-type H-bonding (O/C–H⋯πar) leading to distorted en-face or borderline intermediate geometry for the optimized CH3SOH–toluene structures (θSXY = 21°–36°; Fig. 2, Table 1 and Fig. S1, Table S1). Both π- and σ-type H-bonding is present in the 3-methylindole and 4-methylphenol complexes, which consequently adopt highly distorted en-face or intermediate geometry (θSXY = 28°–49°; Fig. 2, Table 1 and Fig. S2, S3, Tables S2, S3). Likewise, σ-type H-bonding is responsible for edge-on CH3SOH binding to 4-methylimidazole and 4-methylphenolate (O–H⋯Nar/O), which additionally exhibit π-type H-bonding and a broad range of θSXY values (6°–87°; Fig. 2 and Fig. S4, S6, Tables S4, S6). CH3SOH binds 4-methylimidazolium strictly edge-on (θSXY = 60°–90°) via σ-type H-bonding (N–Har⋯O/S) with the sole exception of S5e (θSXY = 35°), which is stabilized by electrostatic attraction between the O and S lone pairs and the electron-deficient surface of the imidazolium ring (Fig. 1 and Fig. S5).Nature of H-bonding controls the redox properties of the complexes
Computational9,23,24 and experimental45–48 investigations reveal that noncovalent interactions can significantly alter the redox properties of interacting fragments. Both the difference in IPV of the fee ligands and the geometry of the complex determine the centre oxidized. Notably, H-bond donation renders the donor more electron-rich and the acceptor more electron poor. Thus, in complexes between fragments of similar IPV, the fragment that H-bond donates often gets oxidized, especially if the H-bond is strong (Fig. S1–S4).9,23,24Focusing just on the five most stable complexes for each of the four neutral aromatics reveals that CH3SOH functions as a H-bond donor 15 out of 20 times and is the centre oxidized (Tables S1–S4). Furthermore, the IPV values of the most stable complexes are ∼1 eV lower than that of free CH3SOH indicating that strong H-aromatic interactions render CH3SOH more oxidizable. The aromatic is oxidized in the 4-methylphenol (Tyr) and 3-methylindole (Trp) complexes where the phenol O (1c, S3p) and indole N (S2h, S2f) act as H-bond donors (Tables S2 and S3). Presumably, H-bond donation by CH3SOH is insufficient to depress its IPV and become the centre oxidized in S2g. In fact, weaker CH3SOH H-bond donation in S2gvs.S2i is reflected in the relative lengths of the π-type O–H⋯πa H-bonds in these complexes (2.41 vs. 2.30 Å; Fig. S2).
Free 4-methylimidazolium (14.64 eV)24 and 4-methylphenolate (3.31 eV)24 have IPV values much greater and smaller, respectively, than free CH3SOH (9.20 eV, Table 1). Hence, the sulfenic acid is the centre oxidized in all complexes of the former and the aromatic in all complexes of the latter (Tables S5 and S6).
Affinity of CH3SOH vs. CH3SH for the aromatics
We previously reported ECP values (kcal mol−1) at the MP2(full)/6-311++G(d,p) level for the gas-phase CH3SH complexes,8,9 and Table 3 shows that their global minimum conformers are 1.4–2.7-fold weaker than the CH3SOH analogues. This arises because the electrostatic potentials (Vs,max, Vs,min; kcal mol−1) on the H (15.3) and S (−18.4) atoms of CH3SH15 are considerably smaller than those of the H (38.3) and O (−32.9) atoms of CH3SOH (Fig. 1B), rendering the latter a stronger H-bond donor and acceptor.| Aromatic (complex)a | CH3SOH–aromatic | CH3SH–aromatic | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| r SX, Åa |
E
CP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a, kcal mol−1 a, kcal mol−1 |
r SX (aq), Å | PMF (aq)b, kcal mol−1 | IPVa, eV | r SX, Å | E CP kcal mol−1 | r SX (aq)d, Å | PMF (aq)d, kcal mol−1 | IPV, eV | |
| a From Table 1 this work. b From Table 2 this work. c From Table 5 of ref. 9. d From Table 7 of ref. 9 (note average rSX values given here). e From Table 6 of ref. 9. f From Table S3 of ref. 8. g From Table S7 of ref. 8. h From Fig. S8 this work. i Calculated with MP2(full)/6-311++G(d,p) this work. | ||||||||||
| Toluene (1a) | 3.93 | −4.85 | 5.3 | −0.65 | 8.48 | 3.66c | −3.14c | 5.0d | −0.7d | 8.69e |
| 3-Methylindole (1b) | 4.06 | −6.99 | 5.3 | −0.65 | 8.27 | 4.01c | −5.04c | 5.1d | −0.6d | 9.02e |
| 4-Methylphenol (1c) | 4.40 | −7.16 | 5.3 | −0.65 | 8.60 | 4.11c | −5.12c | 5.0d | −1.0d | 8.81e |
| 4-Methylimidazole (1d) | 4.45 | −10.26 | 4.8 | −0.55 | 8.02 | 4.42c | −3.80c | 4.4d | −0.9d | 8.64e |
| 4-Methylimidazolium (1e) | 4.64 | −16.86 | 4.8 | −2.50 | 12.6 | 4.37f | −11.44f | 4.0h | −4.7h | 13.26i |
| 4-Methylphenolate (1f) | 5.09 | −25.86 | 5.0 | −4.90 | 4.15 | 4.41g | −12.84g | 3.5h | −3.2h | 4.58i |
CH3SH (9.17 eV)9 and CH3SOH (9.20 eV, Table 1) possess similar IPVs, explaining why Cys to CysOH oxidation is reversible. Table 3 reveals that the IPVs of the CH3SOH–aromatics are 0.2 to 0.75 eV lower than those of the CH3SH–aromatics, which should attenuate spontaneous reduction of the sulfenic acid back to the thiol and thereby serve to stabilize the former.
Before comparing the aqueous aromatic complexes, it is salient to compare their H2O complexes. Two stable structur were optimized here for the CH3SOH–H2O complex (Table S7) with CH3SOH as a H-bond donor (1g, ECP = −5.87 kcal mol−1) and acceptor (S7a, ECP = −4.94 kcal mol−1). CH3SOH is a better H-bond donor than H2O since 1g is ∼1 kcal mol−1 more stable than S7a, whereas H2O is a better H-bond donor than CH3SH. Furthermore, the global minimum conformer of CH3SH–H2O with S as an H-bond acceptor (ECP = −3.01 kcal mol−1)8 is ∼2 kcal mol−1 less stable than S7a, reflecting the magnitude of Vs,min (kcal mol−1) on the thiol S (−18.4)15 and the sulfenic O (−32.9; Fig. 1b).
Strong H-bonding between CH3SOH and H2O leads to ∼0–40% lower PMFs for the aqueous CH3SOH–aromatics vs. their CH3SH analogues (Table 3).8,9 However, 4-methylphenolate is a better H-bond acceptor than H2O so its CH3SOH complex is ∼1.5-fold more stable than its CH3SH complex (Table 3) due to the greater strength of O–H⋯Oarvs. S–H⋯Oar H-bonding. Finally, we note that the CH3SH–aromatics,8,9,23,24 like the CH3SOH–aromatics (Fig. 8), favour en-face and intermediate association in water.
CysOH–aromatic motifs in proteins
To examine cysteine sulfenic acid–aromatic interactions in proteins, the Protein Data Bank (PDB) was queried on 15 June 2025 using the keyword “sulfenic” as a search term. This search retrieved 86 protein structures with 29 nonredundant structures containing a CysOH. The remaining 57 structures were either redundant or included a ligand with a sulfenic acid group. Markedly, in 15 of the 29 nonredundant structures an aromatic ring is within 5 Å of the CysOH side chain (Fig. 9). A recent survey49 of Cys oxidation in proteins revealed that the probability of finding His close to non-oxidized Cys corresponds to the average prevalence of His in proteins but jumps ∼3-fold around CysOH. His can act as proton acceptor from Cys,9 lowering its pKa and rendering the thiol more oxidizable.49 Earlier protein profiling also identified His as a key residue in the modification of Cys to CysOH.50 Furthermore, strong σ-type H-bonding would significantly stabilize the nascent CysOH–His relative to Cys–His (Table 3), making the latter more prone to oxidation, while stabilizing CysOH, which is susceptible to further reaction.2 We note the presence of His near CysOH in 7 of the 15 structures in Fig. 9 with rsx values of 4.5–5.1 Å close to those of 1d and 1e in 6 of these 7 structures (Table 3). Additionally, a Tyr with a rsx value of 4.7–5.5 Å similar to those of 1c and 1f (Table 3) is found in 5 structures in Fig. 9, again signalling possible strong σ-type H-bonding. | ||
| Fig. 9 CysOH–aromatic interactions retrieved from the Protein Data Bank. PDB protein IDs are labelled in red and their backbones represented as ribbons. The CysOH (C) and aromatic residues within 5 Å are represented as sticks with CPK atom colouring. The dotted lines indicate the rsx values (Å) defined in Fig. 2B. The 15 structures presented here were retrieved from the PDB as outlined in section “CysOH–aromatic motifs in proteins” of the Discussion. | ||
The literature survey49 also revealed a ∼2-fold greater probability of finding crystallographic H2O in the proximity of CysOH than Cys. This is consistent with stronger H-bonding of CH3SOH vs. CH3SH to H2O, which accounts for the relative stability of their complexes in bulk water (Table 3) as discussed in the previous section. However, deprotonation of a neighbouring Tyr or protonation of a neighbouring His in a solvent-exposed protein region may favour and supress CysOH formation, respectively, based on the data for the ionized aromatics in bulk water in Table 3).
Given that reversible oxidation of Cys to CysOH is key in regulating function, catalysis and signalling of many proteins,2 control of the redox activity of protein-based Cys residues by their protein microenvironment is of vital importance in biology. Therefore, an in-depth survey of S–aromatic interactions in the PDB is warranted considering the data summarized in Table 3 but outside the scope of the current work.
Conflicts of interest
There are no conflicts to declare.Data availability
All data are presented in the main text and the SI. Supplementary information: 7 figures showing the optimized geometry of local minima conformers of all complexes, 7 tables showing the structural and energetic properties of these conformers, atomic coordinates of all (local + global) optimized geometries, force field parameters for CH3SOH, and the PMFs calculated for MeSH-aromatic ions complexes in water. See DOI: https://doi.org/10.1039/d5cp02976g.Acknowledgements
This work was supported by a research grant from the Natural Sciences and Engineering Research Council (NSERC) of Canada awarded to AME.References
- A. Miseta and P. Csutora, Relationship Between the Occurrence of Cysteine in Proteins and the Complexity of Organisms, Mol. Biol. Evol., 2000, 17(8), 1232–1239, DOI:10.1093/oxfordjournals.molbev.a026406.
- L. J. Alcock, M. V. Perkins and J. M. Chalker, Chemical methods for mapping cysteine oxidation, Chem. Soc. Rev., 2018, 47(1), 231–268, 10.1039/C7CS00607A.
- H. J. Forman, J. M. Fukuto and M. Torres, Redox signaling: thiol chemistry defines which reactive oxygen and nitrogen species can act as second messengers, Am. J. Physiol.: Cell Physiol., 2004, 287(2), C246–C256, DOI:10.1152/ajpcell.00516.2003.
- J. M. Denu and K. G. Tanner, Specific and Reversible Inactivation of Protein Tyrosine Phosphatases by Hydrogen Peroxide:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Evidence for a Sulfenic Acid Intermediate and Implications for Redox Regulation, Biochemistry, 1998, 37, 5633–5642, DOI:10.1021/BI973035T.
Evidence for a Sulfenic Acid Intermediate and Implications for Redox Regulation, Biochemistry, 1998, 37, 5633–5642, DOI:10.1021/BI973035T. - R. D. Michalek, K. J. Nelson and B. C. Holbrook, et al., The Requirement of Reversible Cysteine Sulfenic Acid Formation for T Cell Activation and Function, J. Immunol., 2007, 179(10), 6456–6467, DOI:10.4049/JIMMUNOL.179.10.6456.
- J. D. Keyes, D. Parsonage and R. D. Yammani, et al., Endogenous, regulatory cysteine sulfenylation of ERK kinases in response to proliferative signals, Free Radical Biol. Med., 2017, 112, 534–543, DOI:10.1016/J.FREERADBIOMED.2017.08.018.
- T. F. Brewer, F. J. Garcia, C. S. Onak, K. S. Carroll and C. J. Chang, Chemical Approaches to Discovery and Study of Sources and Targets of Hydrogen Peroxide Redox Signaling Through NADPH Oxidase Proteins, Annu. Rev. Biochem., 2015, 84(1), 765–790, DOI:10.1146/annurev-biochem-060614-034018.
- E. A. Orabi and A. M. English, Sulfur-Aromatic Interactions: Modeling Cysteine and Methionine Binding to Tyrosinate and Histidinium Ions to Assess Their Influence on Protein Electron Transfer, Isr. J. Chem., 2016, 56(9–10), 872–885, DOI:10.1002/ijch.201600047.
- E. A. Orabi and A. M. English, Modeling Protein S–Aromatic Motifs Reveals Their Structural and Redox Flexibility, J. Phys. Chem. B, 2018, 122(14), 3760–3770, DOI:10.1021/acs.jpcb.8b00089.
- D. Pal and P. Chakrabarti, Non-hydrogen Bond Interactions Involving the Methionine Sulfur Atom, J. Biomol. Struct. Dyn., 2001, 19(1), 115–128, DOI:10.1080/07391102.2001.10506725.
- M. Iwaoka, S. Takemoto, M. Okada and S. Tomoda, Weak Nonbonded S⋯X (X = O, N, and S) Interactions in Proteins. Statistical and Theoretical Studies, Bull. Chem. Soc. Jpn., 2002, 75(7), 1611–1625, DOI:10.1246/bcsj.75.1611.
- C. C. Valley, A. Cembran and J. D. Perlmutter, et al., The methionine-aromatic motif plays a unique role in stabilizing protein structure, J. Biol. Chem., 2012, 287(42), 34979–34991, DOI:10.1074/jbc.M112.374504.
- A. R. Viguera and L. Serrano, Side-chain interactions between sulfur-containing amino acids and phenyalanine in α-helixes, Biochemistry, 1995, 34(27), 8771–8779, DOI:10.1021/bi00027a028.
- B. J. Stapley, C. A. Rohl and A. J. Doig, Addition of side chain interactions to modified Lifson-Roig helix-coil theory: application to energetics of Phenylalanine-Methionine interactions, Protein Sci., 1995, 4(11), 2383–2391, DOI:10.1002/pro.5560041117.
- C. D. Tatko and M. L. Waters, Investigation of the nature of the methionine-π interaction in β-hairpin peptide model systems, Protein Sci., 2004, 13(9), 2515–2522, DOI:10.1110/ps.04820104.
- R. B. Best, X. Zhu and J. Shim, et al., Optimization of the additive CHARMM all-atom protein force field targeting improved sampling of the backbone φ, ψ and side-chain χ(1) and χ(2) dihedral angles, J. Chem. Theory Comput., 2012, 8(9), 3257–3273, DOI:10.1021/ct300400x.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, Comparison of simple potential functions for simulating liquid water, J. Chem. Phys., 1983, 79(2), 926–935, DOI:10.1063/1.445869.
- A. D. MacKerell, D. Bashford and M. Bellott, et al., All-Atom Empirical Potential for Molecular Modeling and Dynamics Studies of Proteins, J. Phys. Chem. B, 1998, 102, 3586–3616, DOI:10.1021/jp973084f.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng and D. J. Sonnenb, Gaussian 09, Revision B.01, 2010 Search PubMed.
- S. F. Boys and F. Bernardi, The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors, Mol. Phys., 1970, 19(4), 553–566, DOI:10.1080/00268977000101561.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields, J. Phys. Chem., 1994, 98(45), 11623–11627, DOI:10.1021/j100096a001.
- Y. Zhao and D. G. Truhlar, The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals, Theor. Chem. Acc., 2008, 120(1–3), 215–241, DOI:10.1007/s00214-007-0310-x.
- E. A. Orabi and A. M. English, Predicting structural and energetic changes in Met–aromatic motifs on methionine oxidation to the sulfoxide and sulfone, Phys. Chem. Chem. Phys., 2018, 20(35), 23132–23141, 10.1039/C8CP03277G.
- E. A. Orabi and A. M. English, Expanding the range of binding energies and oxidizability of biologically relevant S–aromatic interactions: imidazolium and phenolate binding to sulfoxide and sulfone, Phys. Chem. Chem. Phys., 2019, 21(27), 14620–14628, 10.1039/C9CP02332A . Accessed October 10, 2019.
- B. R. Brooks, C. L. Brooks and A. D. Mackerell, et al., CHARMM: the biomolecular simulation program, J. Comput. Chem., 2009, 30(10), 1545–1614, DOI:10.1002/jcc.21287.
- K. Vanommeslaeghe, E. Hatcher and C. Acharya, et al., CHARMM general force field: a force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields, J. Comput. Chem., 2010, 31(4), 671–690, DOI:10.1002/jcc.21367.
- G. Lamoureux and E. A. Orabi, Molecular modelling of cation–π interactions, Mol. Simul., 2012, 38(8–9), 704–722, DOI:10.1080/08927022.2012.696640.
- C. R. Rupakheti, B. Roux, F. Dehez and C. Chipot, Modeling induction phenomena in amino acid cation–π interactions, Theor. Chem. Acc., 2018, 137(12), 174, DOI:10.1007/s00214-018-2376-z.
- E. A. Orabi and G. Lamoureux, Cation–π and π–π Interactions in Aqueous Solution Studied Using Polarizable Potential Models, J. Chem. Theory Comput., 2012, 8(1), 182–193, DOI:10.1021/ct200569x.
- S. Wang, E. A. Orabi, S. Baday, S. Bernèche and G. Lamoureux, Ammonium transporters achieve charge transfer by fragmenting their substrate, J. Am. Chem. Soc., 2012, 134(25), 10419–10427, DOI:10.1021/ja300129x.
- E. A. Orabi and G. Lamoureux, Cation–π Interactions between Quaternary Ammonium Ions and Amino Acid Aromatic Groups in Aqueous Solution, J. Phys. Chem. B, 2018, 122(8), 2251–2260, DOI:10.1021/acs.jpcb.7b11983.
- E. A. Orabi, R. Davis and G. Lamoureux, Drude polarizable force field for cation–π interactions of alkali and quaternary ammonium ions with aromatic amino acid side chains, J. Comput. Chem., 2020, 41, 472–481, DOI:10.1002/jcc.26084.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, A smooth particle mesh Ewald method, J. Chem. Phys., 1995, 103(19), 8577–8593, DOI:10.1063/1.470117.
- W. G. Hoover, Canonical dynamics: Equilibrium phase-space distributions, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31(3), 1695–1697 CrossRef PubMed Accessed June 14, 2017.
- G. J. Martyna, D. J. Tobias and M. L. Klein, Constant pressure molecular dynamics algorithms, J. Chem. Phys., 1994, 101(5), 4177–4189, DOI:10.1063/1.467468.
- G. J. Martyna, M. E. Tuckerman, D. J. Tobias and M. L. Klein, Explicit reversible integrators for extended systems dynamics, Mol. Phys., 1996, 87(5), 1117–1157, DOI:10.1080/00268979600100761.
- S. Kumar, J. M. Rosenberg, D. Bouzida, R. H. Swendsen and P. A. Kollman, THE weighted histogram analysis method for free-energy calculations on biomolecules. I. The method, J. Comput. Chem., 1992, 13(8), 1011–1021, DOI:10.1002/jcc.540130812.
- M. Souaille and B. Roux, Extension to the weighted histogram analysis method: combining umbrella sampling with free energy calculations, Comput. Phys. Commun., 2001, 135(1), 40–57, DOI:10.1016/S0010-4655(00)00215-0.
- I. V. Khavrutskii, J. Dzubiella and J. A. McCammon, Computing accurate potentials of mean force in electrolyte solutions with the generalized gradient-augmented harmonic Fourier beads method, J. Chem. Phys., 2008, 128(4), 044106, DOI:10.1063/1.2825620.
- E. A. Orabi and G. Lamoureux, Simulation of liquid and supercritical hydrogen sulfide and of alkali ions in the pure and aqueous liquid, J. Chem. Theory Comput., 2014, 10(8), 3221–3235, DOI:10.1021/ct5002335.
- E. A. Orabi and G. H. Peslherbe, Computational insight into hydrogen persulfide and a new additive model for chemical and biological simulations, Phys. Chem. Chem. Phys., 2019, 21(29), 15988–16004, 10.1039/C9CP02998B.
- S. Mecozzi, A. P. West and D. A. Dougherty, Cation-pi interactions in aromatics of biological and medicinal interest: electrostatic potential surfaces as a useful qualitative guide, Proc. Natl. Acad. Sci. U. S. A., 1996, 93(20), 10566–10571, DOI:10.1073/pnas.93.20.10566.
- R. Peverati and D. G. Truhlar, Quest for a universal density functional: the accuracy of density functionals across a broad spectrum of databases in chemistry and physics, Philos. Trans. R. Soc., A, 2014, 372(2011), 20120476, DOI:10.1098/rsta.2012.0476.
- M. Nishio, The CH/π hydrogen bond in chemistry. Conformation, supramolecules, optical resolution and interactions involving carbohydrates, Phys. Chem. Chem. Phys., 2011, 13, 13873–13900 RSC.
- W. J. Chung, M. Ammam and N. E. Gruhn, et al., Interactions of Arenes and Thioethers Resulting in Facilitated Oxidation, Org. Lett., 2009, 11(2), 397–400, DOI:10.1021/ol802683s.
- N. P.-A. Monney, T. Bally, G. S. Bhagavathy and R. S. Glass, Spectroscopic Evidence for a New Type of Bonding between a Thioether Radical Cation and a Phenyl Group, Org. Lett., 2013, 15(19), 4932–4935, DOI:10.1021/ol402126f.
- J. C. Aledo, F. R. Cantón and F. J. Veredas, Sulphur Atoms from Methionines Interacting with Aromatic Residues Are Less Prone to Oxidation, Sci. Rep., 2015, 5, 16955, DOI:10.1038/srep16955.
- S. R. Lee, K. S. Kwon, S. R. Kim and S. G. Rhee, Reversible inactivation of protein-tyrosine phosphatase 1B in A431 cells stimulated with epidermal growth factor, J. Biol. Chem., 1998, 273(25), 15366–15372, DOI:10.1074/jbc.273.25.15366.
- D. G. Ruiz, A. Sandoval-Perez, A. V. Rangarajan, E. L. Gunderson and M. P. Jacobson, Cysteine Oxidation in Proteins: Structure, Biophysics, and Simulation, Biochemistry, 2022, 61, 2165–2176, DOI:10.1021/acs.biochem.2c00349.
- F. R. Salsbury Jr, S. T. Knutson, L. B. Poole and J. S. Fetrow, Functional site profiling and electrostatic analysis of cysteines modifiable to cysteine sulfenic acid, Protein Sci., 2008, 17, 299–312, DOI:10.1110/ps.073096508.
| This journal is © the Owner Societies 2025 |



