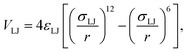A coarse-grained simulation toolkit for metal–organic framework synthesis

Abstract

To gain a better understanding of the processes with which metal–organic frameworks (MOFs) self-assemble, we construct a coarse-grained simulation toolkit to model the growth of a wide variety of MOF structure types. We employ the topology and symmetry of the underlying net of the framework structure to design building blocks that correspond to MOF components. Sphere-union polyhedra are constructed to model MOF nodes by choosing the types and positions of simulation beads, as well as the specific interactions between them, to correspond to the node coordination and local symmetry. The simulated linkers are composed of a shape defined by their coordination environment, combined with linker-end facets that allow for chemically and orientationally specific binding with the node. We compile a modular self-assembly model simulation kit and we implement the successful computational self-assembly of 34 MOF nets.

---

Metal–organic frameworks (MOFs) have broad applications in chemical separations,^1,2 gas storage^3,4 and delivery,⁵ catalysis,^6–8 adsorption,⁹ chemical sensing,¹⁰ and drug delivery.^11,12 The structures of MOFs are highly modular, which results in a wealth of discovered MOF structures: the number of new MOF entries in the Crystal Structure Database exceeded 1000 accepted structures per year for the last 15 years.¹³ Due to reticular chemistry, MOF components can be interchanged while retaining the same building block connectivity and framework topology,^14,15 which can allow for a combinatorial approach to MOF structure discovery^16–19 and add to the ever expanding catalog of reported MOF compounds. The investigation of MOF growth and structural transitions remain challenging, however, and databases of constructed MOFs do not currently incorporate kinetic factors.²⁰ While early stages of nucleation have been successfully reproduced in simulation,^21,22 and a “breathing” transition has been studied by combining experiments with ab initio calculations,²³ the complexity of MOFs prevents a representation of the kinetic processes involved if a model is built to represent these systems in full chemical detail.

Coarse-grained modeling enables the representation of MOF crystal growth with present computational capabilities, while putting aside chemical properties that need not be included in a study of the assembly process on a kinetic level. We previously used a coarse-grained model to simulate the defect-engineering of a two-dimensional MOF, mimicking the self-assembly process of coarse-grained, rigid-body building blocks with specific interactions.²⁴ Others used patchy particles previously to simulate the ordered assembly of porous organic cages.²⁵

To construct rigid-body models of a variety of three-dimensional MOFs, we use the topological and symmetry information available in the Reticular Chemistry Structure Resource (RCSR).²⁶ We generate a coarse-grained molecular dynamics (MD) model kit composed of linkers and nodes, which captures the necessary structural symmetry to allow for ordered simulated assembly of synthesized MOF structures. In addition to creating models for dozens of MOFs with distinct topological nets, we demonstrate the versatility of this approach by simulating equivalents to hierarchical MOF families such as UiO-66, -67, and -68 (UiO = Universitetet i Oslo), which combine linear organic linkers of increasing length with the same Zr₆O₈ node and connectivity, resulting in the same topological net (fcu).²⁷ We also simulate the three-dimensional assembly of layered MOFs (PPF-1)²⁸ and the conformations of the “breathing” MIL-53 framework (MIL = Matériaux de l′Institut Lavoisier).^23,29 Our computational models offer a means to simulate the ordered assembly of MOFs with possible applications in determining synthesis-relevant design properties such as the relative linker length before the onset of interpenetration, the effect of modulators and their properties on MOF crystallization, and reagent screening for defect engineering.

Methods

We simulate the self-assembly of common MOF structures with coarse-grained models, which we construct based on the different MOF nets (see Fig. 1). The net—obtained from the RCSR²⁶—provides essential information to construct a self-assembly model: the space group, the number of edges that connect to each vertex, and the coordination number and symmetry of each vertex and symmetry of each edge (see Table 1). The node is designed based on the symmetry of the respective vertex. The linker is designed based on the symmetry of the edge for linear linkers and on the symmetry of a second vertex for other linker topologies.

Fig. 1 Model design (demonstrated on the fcu net): (a) MOF, (b) its topological net, (c) the net's space group symmetry, the symmetry of the net components (node, linker, and linker end), and the crystallographic positions at which the components are located. (d) The coarse-grained building blocks are then used to (e) perform self-assembly simulations, and (f) the desired MOF topology crystallizes.

Table 1 Nets of MOFs characterized by their space groups, degrees of freedom (DOFs), the coarse-grained building blocks (nodes and linkers) used to simulate their self-assembly (defined by coordination number (CN), symmetry, Wyckoff positions), and example MOF structures that adopt the respective nets. MOF topologies: fcu = face-centered cubic; bcu = body-centered cubic; pcu = primitive cubic; dia = diamond; bnn = boron nitride; reo = ReO₃; crs = cristobalite; nbo = NbO; acs = Andrea C. Sudik; srs = SrSi₂; rtl = rutile; ant = anatase; spn = spinel; tbo = twisted boracite; bor = boracite; she = square and hexagon; soc = square and octahedron; csq = cube and square; shp = square and hexagonal prism; scu = square and cube; stp = square and trigonal prism; ith = icosahedron and tetrahedron; gar = garnet; flu = fluorite (CaF₂); dia-b = sphalerite; pts = platinum sulfide (PtS); sra = SrAl₂. MOF name acronyms: UiO = Universitetet i Oslo; PCN = Porous Coordinated Network; DUT = Dresden University of Technology; BIF = boron imidazolate framework; CTH = Chalmers Tekniska Högskola; BUT = Beijing University of Technology; HKUST = Hong Kong University of Science and Technology; NU = Northwestern University; BCN = Barcelona Material; UTSA = University of Texas San Antonio; ZIF = zeolitic imidazolate framework. Chemical reagents: BTC = benzene-1,3,5 -tricarboxylate; TPB = 3,3′,5,5′-tetrakis(4-pyridyl)bimesityl

Net	Space group	DOF	Node			Linker			Linker end	Example MOF
			CN	Wyckoff	Symmetry	CN	Wyckoff	Symmetry	Symmetry	Name
Linear linkers
fcu	Fm3̄m, 225	1	12	4a	m3̄m	2	24d	mmm	mm2	UiO-66^27
bcu	Im3̄m, 229	1	8	2a	m3̄m		8c	3̄m	3m	PCN-700^30
pcu	Pm3̄m, 221	1	6	1a	m3̄m		3c	4/mmm	4mm	MOF-5^31
dia	Fd3̄m, 227	1	4	8a	4̄3m		16c	3̄m	3m	MOF-31^32
bnn	P6/mmm, 191	2	5	2c	6̄m2		3f	mmm	mm2	MOF-74^33
crs	Fd3̄m, 227	1	6	16c	3̄m		48f	mm2	m2	MOF-500^34
reo	Pm3̄m, 221	1	8	3d	4/mmm		8c	mm2	mm2	DUT-67^35
nbo	Im3̄m, 229	1	4	6b	4/mmm		12d	4̄m2	mm2	MOF-101^36
acs	P63 /mmc, 194	2	6	1b	6̄m2		6g	2/m	m2	MOF-235^37
srs	I4132, 214	1	3	8a	32		12c	222	2	BIF-8^38
Trigonal linkers
llj	I4/mmm, 139	3	12	2a	4/mmm	3	8h	mm2	mm2, m	DUT-98^39
rtl	P42/mmm, 136	3	6	2a	mmm		4j	mm2	mm2, m	CTH-6^40
ant	I41/amd, 141	3	6	4a	4̄m2		8e	mm2	mm2, m	UTSA-16^41
spn	Fd3̄m, 227	2	6	16c	3̄m		32e	3m	m	MOF-808^9
the	Pm3̄m, 221	2	8	3d	4/mmm		8g	3m	m	BUT-12^10
tbo	Fm3̄m, 225	2	4	24d	mmm		32f	3m	m	HKUST-1^42
bor	P4̄3m, 215	2	4	3d	4̄m2		4e	3m	m	Cd3Na6 (BTC)4^43
srs-b	P4332, 212	1	3	4a	32		4b	32	2	NU-1301-C^44
Tetragonal linkers
ftw	Pm3̄m, 221	1	12	1a	m3̄m	4	3c	4/mmm	mm2	MOF-525^45
she	Im3̄m, 229	1	6	8c	3̄m		12d	4̄m2	2	PCN-224^46
soc	Im3̄m, 229	2	6	8c	3̄m		12e	4mm	m	Al-soc-MOF-1^4
nbo-b	Pm3̄m, 221	1	4	3c	4/mmm		3d	4/mmm	mm2	BCN-348^47
csq	P6/mmm, 191	3	8	3f	mmm		6m	mm2	1	PCN-222^7
shp	P6/mmm, 191	2	12	1a	6/mmm		3g	mmm	m	PCN-223^48
scu	P4/mmm, 123	2	8	1a	4/mmm		2e	mmm	m	UTSA-57^49
stp	P6/mmm, 191	2	6	2c	6̄m2		3g	mmm	m	PCN-600^50
Tetrahedral linkers
ith	Pm3̄n, 223	1	12	2a	m3̄	4	6c	4̄m2	m	MOF-812^9
gar	Ia3̄d, 230	1	6	16a	3̄		24d	4̄	1	ZIF-5^51
iac	Ia3̄d, 230	1	6	16a	3̄		24c	222	1	Cd(TPB)1.5 (ClO4)2^52
flu	Fm3̄m, 225	1	8	4a	m3̄m		8c	4̄3m	3m	MOF-841^9
dia-b	F4̄3m, 216	1	4	4a	4̄3m		4c	4̄3m	3m	MOF-32^32
pts	P42/mmc, 131	2	4	2c	mmm		2e	4̄m2	m	MOF-11^53
Tetragonal linkers (and secondary node–linker binding)
PPF-1	I4/mmm, 139	3	6	2a	4/mmm	6	2b	4/mmm	mm2	PPF-1^28
Linear linkers (and secondary node–node binding)
sra	Imma, 74	2	6	4c	2/m	2	8f	2	m	MIL-53^29

---

The node designs, linker shapes, and specific linker ends are combined to assemble a wide variety of MOF nets. Table 1 also lists example MOF compounds that have been reported to adopt the investigated nets, almost all of which have been experimentally observed (with the exceptions of both diamond-type nets dia and dia-b, which have been theoretically proposed as topologies of MOF-31 and MOF-32 but have not been synthesized so far).

Different MOF nets possess different numbers of degrees of freedom (DOFs), as specified in Table 1. One degree of freedom encodes the type of connection between nodes and linkers (shape/symmetry). Additional degrees of freedom are present if binding angles between building blocks represent free parameters or if node-to-linker connections are made through more than one type of facet. The fcu net, for example, features one type of linker end (mm2 symmetry), and the node exhibits only one type of rhombic facet, while all binding angles are fixed due to the cubic net symmetry—this corresponds to a single DOF. All tetragonal and hexagonal nets have at least two DOFs due to the free parameter represented by the c/a aspect ratio of the structures' unit cells. The llj and rtl nets require two types of facets, and the tilt angle of the linker ends encodes an additional degree of freedom—corresponding to three DOFs in both cases. The csq net exhibits three DOFs, as well, due to the node featuring both enantiomorphs of the triangular facet, as well as a tilt angle of the linker.

Self-assembly simulations

Simulations are performed using the molecular dynamics algorithm implemented in the HOOMD-blue software package.⁵⁴ An NVT canonical ensemble is simulated with a constant total system size (a total of 2000 to 6000 nodes and linkers combined), employing a Langevin integrator and a Nosé–Hoover thermostat. The signac framework was used for simulation production and data management.^55,56

Visualizations of idealized crystal structures and coarse-grained building blocks are generated with CrystalMaker®.⁵⁷ A prototypical model of each net is generated using the Wyckoff positions and the aspect ratio of the unit cell, allowing us to determine the angles between nodes and linkers, as well as potential building block shapes that conform with the coordination number and the bond arrangements of the nodes. Simulation trajectories and products are visualized with OVITO.⁵⁸

The simulations are initialized with periodic boundary conditions at a high starting temperature (2.6–0.9 kT) and cooled to a low final temperature (1.0–0.2 kT) over 10⁸ molecular dynamics time steps, with a step size of δτ = 0.005. Varying temperature ranges are needed due to the varying sizes, symmetries, and interaction patterns of the simulated MOF components. Center-of-mass particles are initialized on a simple cubic lattice, and the identity of the particles is assigned at random based on the node-to-linker ratio corresponding to the ideal stoichiometry of each MOF. With their identities assigned, particles are added to the center-of-mass particles to define the intended shape and interactions of each node or linker building block.

Only the molecular interaction between the node and the linker's functional group—i.e., carboxylate and amine at the end of each linker's arm—are modeled, while disregarding the electrostatic interactions resulting from conjugation and aromatic functionality within the linker's molecular structure. Attractive interactions are modeled with Lennard-Jones (LJ) potentials:^59,60

and repulsive interactions are modeled with Weeks–Chandler–Andersen (WCA) potentials:^61,62

Attractive interactions model node–linker bonds, while repulsive interactions are employed to model the sterics of the system.

The node–linker connections are designed with patterns composed of differently functionalized beads that impose an energetic penalty for misalignment: attractive beads selectively link to their counterparts in the intended arrangements of nodes and linker ends. The vertices and edges defining the shape of the linker ends must connect with the specific corresponding vertices and edges of the node within a tolerance radius defined by σ for the repulsive WCA potential (Table 2).

Table 2 Values for the pair-potential parameters used for the coarse-grained simulation

	Pair potential parameters
	εLJ	σLJ	εWCA	σWCA
Node–linker end	2.0–4.0	1.4	1.0	1.6
Node–node	1.0	1.4	1.0	4.5
Linker–linker	1.0	1.4	1.0	4.5

---

Component design

The design of the coarse-grained building blocks for our self-assembly simulations is guided by the symmetry of the nets (according to the RCSR), as well as the representation of MOF structures in the literature.⁶³ MOF components are typically represented by geometrical building blocks with the vertex-linked polygons or polyhedra (VLPP) method, and these same shapes also regularly define the name of the ascribed MOF net: the soc net can be represented by a s̲quare for the linker and o̲c̲tahedron for the node, and the scu net can be represented by a s̲quare for the linker and c̲u̲be for the node.

Nodes

The design of coarse-grained building blocks for the node is based on the coordination environment and symmetry of the corresponding vertex listed for the net in the RCSR (see Table 1). For many nets, the node geometry corresponds to a Platonic, Catalan, or Johnson solid, and their decoration with beads corresponding to different selective interactions is chosen according to the local environment of the node in the net (see Fig. 2).

Fig. 2 (a) Node polyhedra are constructed from coarse-grained beads to simulate MOF self-assembly (with different building block symmetries and coordination numbers CN): (b) rhombic dodecahedron (m3̄m, CN = 12), (c) modified rhombic dodecahedron (3̄m, CN = 6), (d) modified rhombic dodecahedron (3̄m, CN = 6), (e) modified rhombic dodecahedron/tetragonal bipyramid (4/mmm, CN = 8), (f) augmented hexagonal prism/bipyramid (6/mmm, CN = 12), (g) octahedron (m3̄m, CN = 8), (h) tetragonal bipyramid (4/mmm, CN = 8), (i) modified tetragonal bipyramid (mmm, CN = 4), (j) modified tetragonal bipyramid (4̄m2, CN = 4), (k) tetragonal bipyramid (4/mmm, CN = 8), (l) cube (m3̄m, CN = 6), (m) rectangular prism (mmm, CN = 6), (n) rectangular prism (4̄m2, CN = 6), (o) truncated elongated square bipyramid (4/mmm, CN = 4), (m) elongated square bipyramid (4/mmm, CN = 12), (q) tetrahedron (4̄3m symmetry, CN = 4), (r) trigonal bipyramid (6̄m2, CN = 6), (s) augmented triangular prism/bipyramid composed of 6 rhombic facets (6̄m2, CN = 6), (t) augmented triangular prism (6̄m2, CN = 5), (u) modified rhombic dodecahedron (32, CN = 3), (v) modified pyritohedron (m3̄, CN = 12), (w) modified pyritohedron (3̄, CN = 6), (x) modified pyritohedron (3̄, CN = 6), (y) tetragonal bipyramid (mmm, CN = 8).

The VLPP representations of nodes with polyhedra need to be “translated” for use in our simulations: while the symmetry of the nodes is maintained, the dual polyhedra of the VLPP polyhedra allow for the design of self-assembling node building blocks with selective binding sites.¹⁴ For example, the octahedron is used to describe the node connectivity of the spn net, but its dual (the cube) is used to simulate this MOF's self-assembly, such that the 6-fold connectivity of the node—expressed by bonds with the VLPP shape's vertices—can be translated to node-to-linker bonds in our coarse-grained models, which are realized by facet-to-facet bonding between nodes and linker-arm ends. Similarly, the fcu and the ftw nets are represented with a rhombic dodecahedral vertex, but their self-assembly models use the dual shape (the cuboctahedron) to represent the nodes of these MOFs. More generally, nodes are generated by positioning facets at angles to the vertices of the VLPP representation's node polyhedron; for example, the stp net (PCN-600⁵⁰) is represented by a triangular prism, and its node building block is constructed by placing rhombic facets perpendicularly to the node–linker bonds (see Fig. 2p). Further modifications to the basic layout of the nodes—to reduce the symmetry or to change the number of binding facets—define select vertices or edges to be entirely repulsive or add repulsive beads to polyhedral facets to impose additional steric interactions.

The node of the fcu and ftw nets is represented with the rhombic dodecahedron, which exhibits the correct symmetry (m3̄m) and number of polyhedral facets (CN = 12) to bind to the linker ends (Fig. 2b). The beads that compose the node are functionalized with attractive interactions in a manner that retains the m3̄m symmetry. To produce a node with CN = 6 to simulate the she net, the rhombic dodecahedron's symmetry is reduced: two beads are modified to repel the attractive ends of the linker (Fig. 2c). While the nodes of the soc and spn nets possess the same 3̄m symmetry and CN = 6, their coordination environment differs. Three unique attractive potentials are used for the beads of the simulated nodes to produce the modified rhombic dodecahedron with 3̄m symmetry, and six additional beads that repel the linker are placed at 6 facets of the simulated node (Fig. 2d). The rhombic dodecahedron's symmetry is reduced to 4/mmm to simulate the node of the reo net, by placing repulsive beads at 4 facets in the same plane (Fig. 2e) resulting in CN = 8 and producing a tetragonal bipyramid with isosceles triangular facets. The rhombic dodecahedron and its modified forms are used to simulate the Zr₆O₈ node in many of the example MOFs (Table 1): UiO-66²⁷ and MOF-525⁴⁵ with CN = 12, DUT-67³⁵ with CN = 8, and MOF-808⁹ and PCN-224⁴⁶ with CN = 6.

To simulate the shp net, an augmented hexagonal prism (i.e., a bipyramid) with 6/mmm symmetry and CN = 12 was used as the node (Fig. 2f).

The octahedron is used to simulate the node of the bcu and flu nets with symmetry m3̄m and CN = 8 (Fig. 2g). The octahedron is reduced in symmetry by a different patterning with the two distinct attractive interactions to produce a tetragonal bipyramid (4/mmm) to simulate the the net (Fig. 2h). By placing four repulsive beads at the facets of the tetragonal bipyramid, the coordination number is reduced—as is the symmetry (mmm and 4̄m2)—for the simulation of the tbo and bor nodes (Fig. 2i and j). Another tetragonal bipyramid is generated by using 4 different bead types to simulate the assembly of the scu net (Fig. 2i).

A cube is used to model the pcu net (CN = 6) with symmetry m3̄m (Fig. 2j). To model the rtl net, the node symmetry is reduced to mmm by modifying the cube beads' interaction pattern to generate a rectangular prism (Fig. 2m). Another rectangular prism (Fig. 2n) is generated by modifying the interaction pattern to reduce the node's symmetry to 4̄m2. To model the node of the nbo and nbo-b nets, a cube is augmented to become a truncated elongated tetragonal bipyramid with 4/mmm symmetry (Fig. 2o): 4 repulsive beads each attached to a pair of opposite facets reduce the node coordination to CN = 4. This polyhedral shape is further augmented to generate an elongated tetragonal bipyramid with CN = 12 and 4/mmm symmetry to model the llj net (Fig. 2p).

A tetrahedron (i.e., with CN = 4 and symmetry 4̄3m) is used as the node shape to assemble the dia and dia-b nets (Fig. 2q). The acs and stp net nodes are modeled with a trigonal bipyramid (with CN = 6 and symmetry 6̄m2)—effectively a combination of two tetrahedra with a shared facet—(Fig. 2r). An augmented triangular bipyramid (or alternatively: an augmented triangular prism) composed of 6 rhombic facets is used to model the stp net (Fig. 2s).

The node in the bnn net binds to three linkers and to two other nodes, resulting in an overall CN = 5. To generate a node for this net, building-block components for each of these separate bonds are constructed individually and effectively joined together into one rigid geometry: an augmented triangular prism is used for node–linker attraction and two additional triangular facets are used to model the node–node attraction (Fig. 2t).

A modified rhombic dodecahedron with 32 symmetry is used as the node shape to simulate the srs and srs-b nets with CN = 3 (Fig. 2u). The facets of this shape are rhombuses with symmetry 2, which are rotated relative to each other by an angle that was also chosen as the internal angle of the rhombus (≈70.1°).

To simulate the ith net, a pyritohedron is used—a 12-faceted polyhedron derived from the pentagonal dodecahedron, which has m3̄ symmetry. To avoid competing binding motifs, additional attractive beads are placed at the center of each facet, retaining the m3̄ symmetry, (Fig. 2v). To simulate the gar net, the pyritohedron's symmetry is reduced to 3̄ by changing some of the beads to distinct attractive interactions and others to be repulsive, resulting in CN = 6 (Fig. 2w). To simulate the iac net, the pyritohedron's symmetry is reduced to 3̄ by changing six of the beads at the facets' centers to be repulsive, resulting in CN = 6 (Fig. 2x).

A tetragonal bipyramid with isosceles triangular facets is used to simulate the csq net, with a reduced node symmetry of mmm (Fig. 2y).

Linkers

The coordination number and the angles between linker arms, as well as the linker symmetry, are used to design the layout of the linker building blocks (see Fig. 3). A minimum of three beads is used to produce the linker's arms, using increasing numbers as needed, e.g., for models with larger nodes (Fig. 2k and p). Ditopic linkers presented in this work are all treated as being linear. To produce planar linkers, a row of beads representing one arm is generated, and the symmetry operations of the linker are applied to generate all linker arms, i.e., linear linkers with a 180° rotation (Fig. 3a), trigonal linkers with 120° rotations (Fig. 3b), and tetragonal planar linkers with 90° rotations (Fig. 3c).

Fig. 3 Coarse-grained linker designs, and example carboxylate linkers with (a) linear, (b) trigonal planar, (c) tetragonal planar, (d) tetrahedral (4̄3m), and (e) reduced-symmetry tetrahedral (4̄m2) symmetries.

The tetratopic linker with tetrahedral symmetry (4̄3m) is generated with ≈109.5° angles (Fig. 3d), and a tetratopic linker with reduced tetrahedral symmetry (4̄m2) is constructed with out-of-plane angles of (Fig. 3e). (The tetrahedral linker with full 4̄3m symmetry can exhibit out-of-plane angles of .)

Node–linker connectivity

The linker's binding functional group (carboxylate or amine) is represented by several beads at the end of the linker arm, which mirror the shape of the node's binding facets (e.g., see Fig. 1d). The specific interactions between each bead of the “linker end” and the corresponding bead in the node are determined by the linker symmetry (listed in Table 1). The relative angle between the linker end and the plane normal to the linker arm varies depending on the topology and geometry of the simulated MOF net. All linker arm end shapes employed are shown in Fig. 4.

Fig. 4 (a) Coarse-grained linker-end designs with rhombic, triangular, square, and pentagonal geometries, chosen according to the node facet shapes. Functionalizations of the linker-arm ends with specific bead–bead interactions: rhombic facets with (b) mm and (c) and (d) m2 symmetry; (e) a modified rhombic (parallelogram) facet with 2 symmetry; triangular facets with (f) 3m and (g) and (h) m symmetry, and (i) and (j) isosceles triangular facets with 1 symmetry; square facets with (k) 4mm, (l) and (m) mm2, and (n) and (o) m symmetry; pentagonal facets with (p) m and (q) 1 symmetry.

Linkers to connect nodes that are modeled with rhombic dodecahedra and a few other node shapes (Fig. 2b, c, s and t) use rhombic linker ends with mm2 symmetry (Fig. 4b)—for the fcu, she, stp, and bnn nets. The modified rhombic dodecahedron (Fig. 2d) uses rhombic linker ends with m2 symmetry (Fig. 4c) to simulate the soc net. The modified rhombic dodecahedron (Fig. 2e) and augmented hexagonal prism use rhombic linker ends with m2 symmetry (Fig. 4d) to simulate the reo and shp nets. Assembly of the srs and srs-b nets is accomplished with a modified rhombic dodecahedron (Fig. 2u) and a parallelogram linker end with symmetry 2 (Fig. 4e).

Linkers to connect nodes that are modeled with octahedra or tetrahedra (Fig. 2g and q) use triangular linker ends with 3m symmetry (Fig. 4f)—e.g., for the bcu and dia nets. Linkers to connect nodes that are modeled with tetragonal or trigonal bipyramids with equilateral triangular facets (Fig. 2h–j and r) use triangular linker ends with m symmetry (Fig. 4g)—e.g., for the the, tbo, bor, acs, and stp nets. A triangular facet with m, using 4 different interaction types, is employed for the scu net linker and two linker arms for the llj net's trigonal planar linker (Fig. 4h). Enantiomorphic isosceles triangular facets are used to connect linkers to nodes in the csq net (Fig. 4i and j).

Beads are arranged in a square with 4mm symmetry (Fig. 4j) to generate the linker ends of a linear linker to connect the cubic nodes of the pcu net (Fig. 2k). Square facets with mm2 symmetry (Fig. 4m) and m symmetry (Fig. 4n) form the linker ends of the trigonal planar linker to connect cube-shaped rectangular prism nodes of the rtl net (Fig. 2m). A different square facet (Fig. 4o) with m symmetry is used to connect two facets of the cube-shaped rectangular prism nodes of the ant net (Fig. 2n). Square facets with mm2 symmetry (Fig. 4l) form the linker ends of the linear and tetragonal planar linkers connecting the truncated elongated tetragonal bipyramid nodes (Fig. 2o) of the nbo and nbo-b nets, as well as one linker arm of the trigonal planar linkers for the ant and llj nets, connecting to the rectangular prism (Fig. 2n) and elongated square bipyramid (Fig. 2p) nodes, respectively.

Pentagonal facets, with m symmetry, allowing linker connection to the pyritohedron node (Fig. 2v) are constructed from beads at the vertices, as well as on the facets (at the center, intersected by the mirror plane) to prevent unphysical steric hindrance (Fig. 4p). For the gar and iac nets, the pentagonal facet's symmetry is reduced to 1 (Fig. 4q).

Results and discussion

The MOF building-block components detailed above were combined to rationally design systems that would self-assemble into the nets listed in Table 1. To assemble the parts of the MOF model kit into different framework topologies, we broadly explored the diversity of possible MOF nets, targeting various symmetries and coordination environments. Nets with lower-symmetry components tended to be more difficult to simulate. The formation of the correct MOF net structures was verified by visual inspection with CrystalMaker®.⁵⁷ The specific components used to construct each net are listed in the ESI.†

In most MOF nets, the linker ends are positioned perpendicular to the linker arms. Some nets exhibit additional degrees of freedom that can correspond to parameters such as the angle between linker arm and linker-arm ends.

MOF nets with linear linkers

The fcu, bcu, pcu, dia, bnn, crs, reo, nbo, acs, and srs nets are assembled with coarse-grained models composed of linear linkers and various nodes (see Fig. 5). For all nets simulated with linear linkers—except for the acs net—the linker ends are positioned perpendicular to the linker arms. The rhombic and square linker ends for the fcu, pcu, bnn, crs, and reo nets are positioned in an eclipsed configuration. A staggered configuration of triangular linker ends is used for the bcu, dia, and acs nets, and the square linker ends for the nbo net and the parallelogram linker ends for the srs net are oriented in a staggered manner, as well.

Fig. 5 Self-assembled MOF nets with linear linkers: (a) fcu, (b) bcu, (c) pcu, (d) dia, (e) bnn, (f) crs, (g) reo, (h) nbo, (i) acs and (j) srs.

The only net to combine a linear linker with a Catalan polyhedron as a node is the fcu net simulated with a rhombic dodecahedral node with m3̄m symmetry (Fig. 5a). The nets combining linear linkers with Platonic polyhedra as nodes are: the bcu net, simulated with an octahedral node with m3̄m symmetry (Fig. 5b); the pcu net, simulated with a cubic node with m3̄m symmetry (Fig. 5c); and the dia net, simulated with a tetrahedral node with 4̄3m symmetry (Fig. 5d).

Another set of nets is constructed with modified polyhedra (Fig. 5e–i). An augmented triangular prism with rhombic facets is combined with a pair of additional triangular facets to model the independent bonds in crystallographically distinct directions in the bnn net (Fig. 5e): the rhombic facets of the node connect with the rhombic facets of the linker, and the triangular facets connect to other nodes, resulting in the rod-like nodes observed in MOF-74.³³ To simulate the crs net, a rhombic dodecahedral node is reduced to symmetry 3̄m and to CN = 6 (Fig. 5f) and a different symmetry reduction, to 4/mmm symmetry, is applied to a rhombic dodecahedral node to simulate the reo net with CN = 8 (Fig. 5g). The modified rhombic dodecahedra with reduced CN used for crs, reo, srs, and srs-b share the same underlying geometry as the fcu net, but they exhibit periodic linker vacancies. The relationship between the simulated fcu and reo nets corresponds with the use of Zr₆O₈ as the node for both UiO-66²⁷ and DUT-67.³⁵ To simulate the nbo net, the cubic node's coordination is reduced to CN = 4 (Fig. 5h). The nbo net exhibits the same pore structure as the pcu net, with a set of nodes and linkers missing. The blocking of facets to derive new nets corresponds to the use of “net-clipping” as a means of net discovery.⁶⁴

MOF nets with planar trigonal linkers

The llj, rtl, ant, spn, the, tbo, bor, and srs-b nets are assembled with coarse-grained models composed of triangular linkers and various nodes (see Fig. 6).

Fig. 6 Self-assembled MOF nets with trigonal planar linkers: (a) llj, (b) rtl, (c) ant, (d) spn, (e) the, (f) tbo, (g) bor, and (h) srs-b.

The llj net uses two different types of linker ends to connect the elongated square bipyramids that represent the nodes—two triangles and one square (Fig. 6a). The modified square linker end (with mm2 symmetry) lies in the plane normal to the linker arm, whereas the triangular linker ends (with m symmetry) are tilted out of the plane normal to the linker arms by ≈24.7°. For both the rtl and ant nets, two types of square linker ends are attached to the trigonal planar linker arms at a tilt of 15° and −45°, respectively (Fig. 6b and c). The spn net is simulated with the same modified rhombic dodecahedron used for the crs net (Fig. 6d).

The the, tbo, and bor nets use the same linker with only triangular linker ends, combined with varying node shapes, and the linker ends are tilted to align with the facets of the octahedral and modified octahedral nodes, respectively (Fig. 6e–g). To assemble the tbo and bor nets, repulsive beads are placed at four of the eight octahedral facets of the node resulting in a periodic suppression of linker binding at those facets. The srs-b net is simulated using the same node as the srs net, and the linker is also constructed with parallelogram linker ends, arranged to have the same 32 symmetry as the node (Fig. 6h).

MOF nets with planar tetragonal linkers

The ftw, she, soc, nbo-b, csq, shp, scu, and stp nets are assembled with coarse-grained models composed of planar 4-coordinated—tetragonal—linkers and various nodes (see Fig. 7). For the nets simulated with planar tetragonal linkers, we look beyond the prescribed symmetries of the RCSR and instead employ the symmetry of the actual MOF reagents. For example, the porphyrin linker for MOF-525,⁴⁵ PCN-224,⁴⁶ and PCN-600⁵⁰ has 4/mmm symmetry, which is therefore used to simulate the corresponding MOF nets—ftw, she, and stp.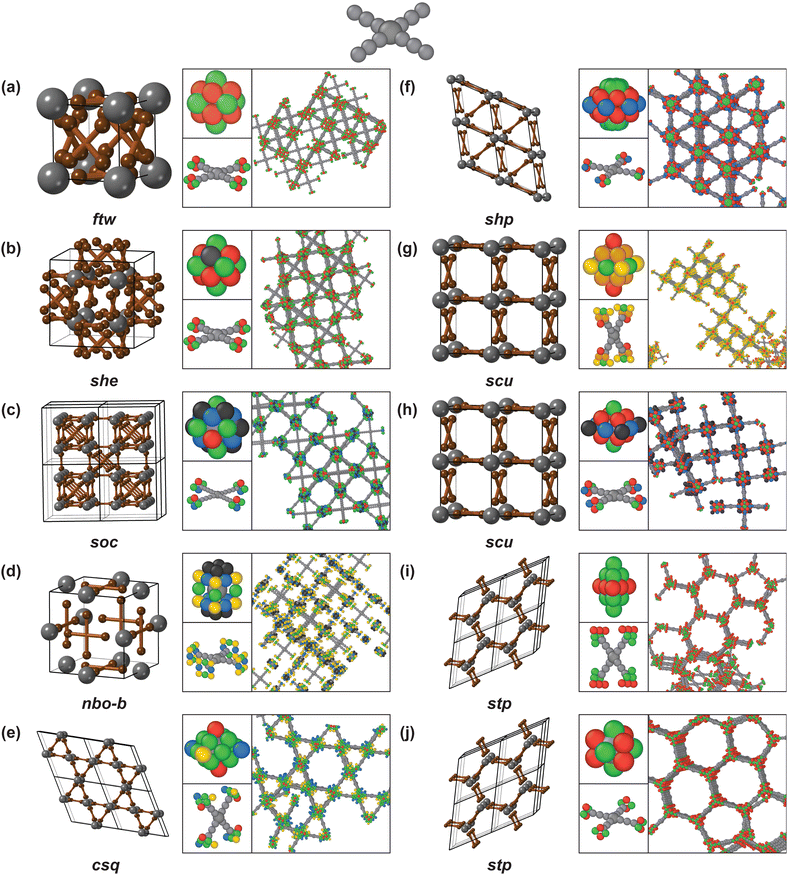

Fig. 7 Self-assembled MOF nets with planar 4-coordinated, tetragonal linkers: (a) ftw, (b) she, (c) soc, (d) nbo-b, (e) csq, (f) shp, (g) and (h) scu, and (i) and (j) stp.

The ftw net is simulated using the rhombic dodecahedron node and the linker is constructed from the tetragonal planar linker and the rhombic linker end (Fig. 7a). Modifying the rhombic dodecahedron node to exhibit six instead of twelve binding sites allows for the simulation of the she net (Fig. 7b). To simulate the soc net, a different modification to the rhombic dodecahedron node is made to yield six different binding sites that are complementary to the binding sites for the node used to simulate the she net (Fig. 7c). The planar 4-coordinated linker for the soc net also uses longer linker arms to prevent trapping of the larger nodes used.

The nbo-b net is simulated with a truncated elongated square bipyramid and the tetragonal linker with square linker ends (Fig. 7d). The csq net is simulated using a tetragonal bipyramid and with triangular linker ends that are tilted 15° (Fig. 7e). The node and linker for the csq net possess two enantiomorphic facets and linker ends, effectively constituting an additional building-block species and reducing the probability of correct binding. The shp net is simulated using an augmented hexagonal prism/bipyramid and the linker has rhombic linker ends (Fig. 7f). Since the apices of the shape feature a cluster of 6 overlapping beads of the same attractive potential, which leads to a corresponding amplification of their effective interaction strength, these beads are assigned interactions with lowered attractive strength.

The scu net is simulated using a tetragonal bipyramid and the linker has triangular linker ends (Fig. 7g). A second scu net model is constructed from a modified rhombic dodecahedron and with rhombic linker ends (Fig. 7h).

The stp net is simulated using a triangular bipyramid as a node, and the linker's overall symmetry is reduced to mmm (Fig. 7i). A second stp model is constructed with a node shape composed of 6 rhombic facets and with rhombic linker ends placed perpendicular to the linker arms (Fig. 7j).

For the ftw, she, soc, shp nets, as well as one implementation each of the scu and stp nets, the rhombic linker ends are positioned perpendicular to linker arms (Fig. 7a–c, f, h and j). The square linker ends with mm2 are also positioned perpendicular to the linker arms for the nbo-b net (Fig. 7d). For the scu and stp nets simulated with bipyramid node shapes, the triangular linker ends are tilted 19.5° (Fig. 7g and i).

MOF nets with tetrahedral linkers

The ith, gar, iac, flu, dia-b, and pts nets are assembled with coarse-grained models composed of tetrahedral 4-coordinated linkers and various nodes (see Fig. 8). The linker arm ends in all of the respective tetrahedral linkers are oriented perpendicular to the respective linker arms.

Fig. 8 Self-assembled MOF nets with tetrahedral 4-coordinated linkers: (a) ith, (b) gar, (c) iac, (d) flu, (e) dia-b, and (f) pts.

For the simulation of the ith net, the pyritohedron is used as the node shape and the linker ends are pentagonal (Fig. 8a). The symmetry-reduced tetrahedral linker—with 126.9° and 101.5° angles between linker arms—is used to simulate the ith net; it is designed to have longer linker arms to compensate for the larger pyritohedron node. The gar and iac nets are simulated with modified pyritohedron nodes to reduce the node's coordination number and change the symmetry from m3̄ to 3̄ (through different modifications for gar vs. iac, see Fig. 2v–x). Some of the pyritohedron beads are changed to repulsive interactions—in facet centers for both gar and iac, and additionally at some vertices for gar—to reduce the CN and change the coordination environment of the nodes. The average structure of the ith, gar, and iac nets is identical, with the modifications to the node and linker symmetry resulting in periodic missing linkers and therefore different net topologies.

The flu and dia-b nets are simulated with triangular linker ends with different linker-end orientations: for the flu net, the edges of the triangular linker ends are aligned in parallel (Fig. 8d), while for the dia-b net, the vertices of the triangular linker ends point toward one another (Fig. 8e).

To assemble the pts net, tetragonal bipyramid nodes with reduced 4̄m2 symmetry are combined with the triangular linker end with m symmetry (Fig. 8f).

Simulating the isoreticular relationship of UiO-66/67/68

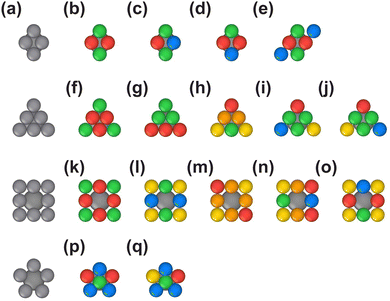
The isoreticular nature of MOFs is exemplified by the UiO-66/67/68 family of MOFs.²⁷ With progressively longer linkers, the same net structure is observed with increasingly larger pores (Fig. 9). In our self-assembly simulations, the same building blocks—node, linker, and linker ends (Fig. 9a)—and interaction parameters are used to construct models for all of these structures, simply by increasing the linker arm length (from 3 to 5 or 7 coarse-grained beads) (Fig. 9b–d). This demonstrates that the here-presented modular self-assembly model framework can be used to mimic the growth of isoreticular MOFs. Follow-up studies conducted with such a family of structures will be able to provide insight into how linker length may impact self-assembly efficiency.

Fig. 9 Self-assembled MOFs with the fcu net, with increasing linker arm length: (a) the rhombic dodecahedron node and the rhombic linker-arm ends are combined with linkers with varying arm lengths, consisting of 3, 5, and 7 coarse-grained beads. Self-assembled structures correspond to (b) UiO-66, (c) UiO-67, (d) and UiO-68.

Simulating PPF-1 assembly in 3D

Having previously simulated the self-assembly of defect-engineered PPF-1 in two dimensions,²⁴ we now expand this self-assembly to be three-dimensional (Fig. 10). The MOF's symmetry is I4/mmmm due to the stacking of the planar sql-b layers (Fig. 10a) in a staggered ABAB pattern (Fig. 10b). The attraction between the Zn-node and the carboxylate linkers, as well as between the porphyrin ring at the center of the linker and the node, are both modeled to simulate PPF-1 self-assembly. The simulated node is designed with four binding facets, related by a 4-fold rotation axis, to connect with the rhombic linker ends (Fig. 10c and d). To simulate the attraction between the center of the linker and the node, square binding facets are added perpendicular to the 4-fold rotation axis of the node (Fig. 4g and 10c). The specific arrangement of beads on the node is mirrored in a square pattern of beads at the center of the simulated linker (Fig. 10d).

Fig. 10 PPF-1 self-assembly model. (a) A layer of PPF-1 with nodes (light blue) connected to linkers through carboxylates and porphyrin rings. (b) A representative net (I4/mmm) showing the connectivity between nodes and linkers. (c) Node with rhombic facets (red and green beads) and square rings (orange and blue beads). (d) Simulated linker with rhombic linker ends (red and green beads) and square linker center (orange and blue beads). Different relative degrees of linker–linker vs. node–linker bonding strength lead to different self-assembled MOF aspect ratios: (e)–(f) faster in-plane than out-of-plane growth, resulting in platelet-shaped crystallites, vs. (g)–(h) comparable in-plane and out-of-plane growth rates, resulting in more globular crystallites.

Simulations are conducted with varying node-to-linker-end attraction (ε_{node facet–linker end} = 3.0–3.5) and node-to-linker-center attraction (ε_{node ring–linker center} = 1.5–2.5) defined by LJ potentials. MOF planes observed in the two-dimensional simulations²⁴ are now stacked into crystals with tunable aspect ratios (Fig. 10e–h). The resulting crystallites are platelet-shaped, with few layers stacked, if the node-to-linker attraction is simulated to be weaker in the out-of-plane than in the in-plane direction. More layers are stacked—relative to the progression of in-plane growth—when the attraction between the node's facets and linker ends is approximately equal to the attraction between the node's square rings and linkers' centers, i.e., ε_{node facet–linker end} = 3.0 and ε_{node ring–linker center} = 2.5. The tunable aspect ratios of the resulting MOF crystallites demonstrate that this model can be used to flexibly simulate the 3D self-assembly of 2D MOFs, which are of growing importance for chemiresistive sensing and electrocatalysis.^65,66

Simulating the assembly of MIL-53

MIL-53, which exhibits the sra net can possess various pore geometries²³—a product of varying node–linker–node angles due to its flexibility. Based on the initial report of MIL-53,²⁹ we use the Wyckoff positions for an orthorhombic space group symmetry (Imma) for the nodes and linkers. Triangular node facets with m symmetry are used for the node–linker attraction to produce a structure similar to the octahedral nodes used for the the and tbo nets (Fig. 6b and c), and square facets with mm2 symmetry are used for the node–node attraction (Fig. 11a and b) (similar to the triangular assembly used for node–node attraction in simulating the bnn net, see Fig. 5e).

Fig. 11 Self-assembly model for MIL-53: (a) nodes for square pores and (b) for rhombic pores; (c) node facet geometry at varying angles between node facets and with a constant node-facet perimeter; (d) linkers for square pores and (e) for rhombic pores. MIL-53 was self-assembled (f) with square pores (θ = 90°) and (g) with rhombic pores (θ = 150°).

For the angle between triangular nodes facets (θ) to be a continuous simulation variable, the triangular node facets sharing vertices and edges are defined to have a constant perimeter (Fig. 11c). The x- and y-coordinates of the bead positions of the triangular facets are scaled by cos(θ/2) and sin(θ/2), respectively. The angle between linker arm and linker end is θ/2–90° (Fig. 11d and e). MIL-53 simulations are performed with values of θ = 90°, 120°, and 150° (Fig. 11f and g).

If dynamic rotation of linker ends relative to linker arms and breathing between node facets were integrated into the simulation model for MIL-53, it could be possible to investigate the synthesis conditions, i.e., the presence of guest molecules or spectator ions, of the MOF that lead to the varying pore structures. Previously, the varying pore structures were simulated with an already assembled MIL-53 structure.²³ Therefore, the here-developed model can serve as a starting point to simulate the responsive and flexile assembly of MIL-53, since we have demonstrated that different sheared versions of the same net are accessible through a simple adjustment of the angles with which its components are constructed.

Summary and conclusions

We designed node and linker building blocks for coarse-grained molecular dynamics simulations of MOF self-assembly using symmetry and topology. The nodes are represented by polyhedra that mimic the coordination environments in a MOF structure—i.e., coordination numbers and angles between linkers—and these nodes are bonded to linkers using linker-end polygons that mirror the facets of the node and encode the bonding angles between nodes and linkers. As a result, we create a modular toolkit of MOF building blocks and demonstrate a multitude of combinations that simulate the growth of 34 network structures. Among those 34 nets are the top 5 most common non-interpenetrated MOF topologies (pcu, dia, bcu, pts, and rtl, respectively^67,68), or in other terms: the most common MOFs that have building blocks with unique connectivities—triangular (srs), tetrahedral (dia), square-shaped (nbo), square-shaped and tetrahedral (pts), five-coordinated (bnn), or octahedral (pcu).⁶⁹ A much wider range of structures can theoretically be assembled with this approach, both with the here-presented 24 node shapes (Fig. 2), 5 linker geometries (Fig. 3), and 16 linker-arm ends (Fig. 4), as well as by constructing equivalent building blocks with the principles applied here.

In addition to building models for this wide variety of topologies and symmetries, we demonstrated the implementation of self-assembly models for (i) isoreticular compounds with increasing pore size, (ii) layered compounds forming crystallites with varying aspect ratios (from platelet-like to globular structures), and (iii) different configurations of MOFs that exhibit “breathing modes”. Rather than construct the complete, crystalline structure of a MOF to explore possible geometries, as was demonstrated successfully elsewhere,¹⁶ here we simulated the crystal growth and assembly of these framework structures. Modeling the self-assembly pathways is crucial in determining which crystal structures are kinetically accessible and therefore synthesizable, and we believe that our coarse-grained approach will help explore MOF growth in future studies.

Based on these coarse-grained models, more chemically detailed MOF analogs can be built that take specific features of the building blocks and the final structures into account, e.g., aromatic rings and conjugation, electrostatic interactions, sterics, interpenetration and concatenation. As a result, the influence of these phenomena on the crystal-growth process can be probed in a computationally efficient way, while minimizing the model complexity to the physically most meaningful parameters.

Author contributions

All authors designed the study and wrote the manuscript. R. N. S. designed the computational models, performed the molecular dynamics simulations, and analyzed the assembled structures. J. D. and P. J. M. supervised the research.

Conflicts of interest

There are no conflicts to declare.

Data availability

Data supporting this article have been included as part of the ESI.† Additional data, including simulation trajectories, are available at the Materials Data Facility⁷⁰ at https://doi.org/10.18126/75tn-px24.⁷¹

Acknowledgements

We thank Michael O'Keeffe and Frank Hoffmann for helpful discussions about net nomenclature, naming conventions, assignment, and origins. This material is based upon work supported by the National Science Foundation MPS-Ascend Postdoctoral Research Fellowship under Grant No. DMR-2139237. This work was supported by the donors of ACS Petroleum Research Fund under Grant 66310-DNI10. P. J. M. acknowledges support from the National Science Foundation (CBET-2047627). We gratefully acknowledge additional support from a SPROUT award from Cornell Engineering.

References

1. X. Lin, I. Telepeni, A. J. Blake, A. Dailly, C. M. Brown, J. M. Simmons, M. Zoppi, G. S. Walker, K. M. Thomas, T. J. Mays, P. Hubberstey, N. R. Champness and M. Schröder, J. Am. Chem. Soc., 2009, 131, 2159–2171.
2. J.-R. Li, J. Sculley and H.-C. Zhou, Chem. Rev., 2012, 112, 869–932.
3. R. E. Morris and P. S. Wheatley, Angew. Chem., Int. Ed., 2008, 47, 4966–4981.
4. D. Alezi, Y. Belmabkhout, M. Suyetin, P. M. Bhatt, J. Weselinski, V. Solovyeva, K. Adil, I. Spanopoulos, P. N. Trikalitis, A.-H. Emwas and M. Eddaoudi, J. Am. Chem. Soc., 2015, 137, 13308–13318.
5. R. M. Mandel, P. S. Lotlikar, K. T. Keasler, E. Y. Chen, J. J. Wilson and P. J. Milner, Chem. – Eur. J., 2024, 30, e202402163.
6. J. Lee, O. K. Farha, J. Roberts, K. A. Scheidt, S. T. Nguyen and J. T. Hupp, Chem. Soc. Rev., 2009, 38, 1450–1459.
7. D. Feng, Z.-Y. Gu, J.-R. Li, H.-L. Jiang, Z. Wei and H.-C. Zhou, Angew. Chem., Int. Ed., 2012, 51, 10307–10310.
8. Y. Lai and P. J. Milner, Angew. Chem., Int. Ed., 2024, 63, e202408834.
9. H. Furukawa, F. Gándara, Y.-B. Zhang, J. Jiang, W. L. Queen, M. R. Hudson and O. M. Yaghi, J. Am. Chem. Soc., 2014, 136, 4369–4381.
10. B. Wang, X.-L. Lv, D. Feng, L.-H. Xie, J. Zhang, M. Li, Y. Xie, J.-R. Li and H.-C. Zhou, J. Am. Chem. Soc., 2016, 138, 6204–6216.
11. S. He, L. Wu, X. Li, H. Sun, T. Xiong, J. Liu, C. Huang, H. Xu, H. Sun, W. Chen, R. Gref and J. Zhang, Acta Pharm. Sin. B, 2021, 11, 2362–2395.
12. R. M. Mandel, P. S. Lotlikar, T. Runčevski, J.-H. Lee, J. J. Woods, T. A. Pitt, J. J. Wilson and P. J. Milner, J. Am. Chem. Soc., 2024, 146, 18927–18937.
13. L. T. Glasby, J. L. Cordiner, J. C. Cole and P. Z. Moghadam, Chem. Mater., 2024, 36, 9013–9030.
14. Z. Chen, S. L. Hanna, L. R. Redfern, D. Alezi, T. Islamoglu and O. K. Farha, Coord. Chem. Rev., 2019, 386, 32–49.
15. H. Jiang, S. M. Moosavi, J. Czaban-Józwiak, B. Torre, A. Shkurenko, Z. O. Ameur, J. Jia, N. Alsadun, O. Shekhah, E. Di Fabrizio, B. Smit and M. Eddaoudi, Matter, 2023, 6, 285–295.
16. C. E. Wilmer, M. Leaf, C. Y. Lee, O. K. Farha, B. G. Hauser, J. T. Hupp and R. Q. Snurr, Nat. Chem., 2012, 4, 83–89.
17. M. A. Addicoat, D. E. Coupry and T. Heine, J. Phys. Chem. A, 2014, 118, 9607–9614.
18. O. M. Yaghi, J. Am. Chem. Soc., 2016, 138, 15507–15509.
19. X. Yin and C. E. Gounaris, Comput. Chem. Eng., 2022, 167, 108022.
20. P. G. Boyd, Y. Lee1 and B. Smit, Nat. Rev. Mater., 2017, 2, 17037.
21. L. Kollias, D. C. Cantu, M. A. Tubbs, R. Rousseau, V.-A. Glezakou and M. Salvalaglio, J. Am. Chem. Soc., 2019, 141, 6073–6081.
22. L. Kollias, R. Rousseau, V.-A. Glezakou and M. Salvalaglio, J. Am. Chem. Soc., 2022, 144, 11099–11109.
23. L. Chen, J. P. S. Mowat, D. Fairen-Jimenez, C. A. Morrison, S. P. Thompson, P. A. Wright and T. Düren, J. Am. Chem. Soc., 2013, 135, 15763–15773.
24. R. N. Scott, C. E. Frank, M. M. Martirossyan, P. J. Milner and J. Dshemuchadse, Chem. Mater., 2023, 35, 10050–10059.
25. E. H. Wolpert and K. E. Jelfs, Chem. Sci., 2022, 13, 13588–13599.
26. M. O'Keeffe, M. A. Peskov, S. J. Ramsden and O. M. Yaghi, Acc. Chem. Res., 2008, 41, 1782–1789.
27. J. H. Cavka, S. Jakobsen, U. Olsbye, N. Guillou, C. Lamberti, S. Bordiga and K. P. Lillerud, J. Am. Chem. Soc., 2008, 130, 13850–13851.
28. E.-Y. Choi, C. A. Wray, C. Hu and W. Choe, CrystEngComm, 2009, 11, 553–555.
29. F. Millange, C. Serre and G. Férey, Chem. Commun., 2002, 822–823.
30. S. Yuan, W. Lu, Y.-P. Chen, Q. Zhang, T.-F. Liu, D. Feng, X. Wang, J. Qin and H.-C. Zhou, J. Am. Chem. Soc., 2015, 137, 3177–3180.
31. H. Li, M. Eddaoudi, M. O'Keeffe and O. M. Yaghi, Nature, 1999, 402, 276–279.
32. J. Kim, B. Chen, T. M. Reineke, H. Li, M. Eddaoudi, D. B. Moler, M. O'Keeffe and O. M. Yaghi, J. Am. Chem. Soc., 2001, 123, 8239–8247.
33. N. L. Rosi, J. Kim, M. Eddaoudi, B. Chen, M. O'Keeffe and O. M. Yaghi, J. Am. Chem. Soc., 2005, 127, 1504–1518.
34. A. C. Sudik, A. P. Côté, A. G. Wong-Foy, M. O'Keeffe and O. M. Yaghi, Angew. Chem., Int. Ed., 2006, 45, 2528–2533.
35. V. Bon, I. Senkovska, I. A. Baburin and S. Kaskel, Cryst. Growth Des., 2013, 13, 1231–1237.
36. M. Eddaoudi, J. Kim, M. O'Keeffe and O. M. Yaghi, J. Am. Chem. Soc., 2002, 124, 376–377.
37. A. C. Sudik, A. P. Côté and O. M. Yaghi, Inorg. Chem., 2005, 44, 2998–3000.
38. J. Zhang, T. Wu, C. Zhou, S. Chen, P. Feng and X. Bu, Angew. Chem., Int. Ed., 2009, 48, 2542–2545.
39. S. Krause, V. Bon, U. Stoeck, I. Senkovska, D. M. Többens, D. Wallacher and S. Kaskel, Angew. Chem., Int. Ed., 2017, 56, 10676–10680.
40. F. M. Amombo Noa, E. Svensson Grape, S. M. Brülls, O. Cheung, P. Malmberg, A. K. Inge, C. J. McKenzie, J. Mårtensson and L. Öhrström, J. Am. Chem. Soc., 2020, 142, 9471–9481.
41. S. Xiang, X. Wu, J. Zhang, R. Fu, S. Hu and X. Zhang, J. Am. Chem. Soc., 2005, 127, 16352–16353.
42. S. S. Y. Chui, S. M. F. Lo, J. P. H. Charmant, A. G. Orpen and I. D. Williams, Science, 1999, 283, 1148–1150.
43. Y. Fu, J. Su, Z. Zou, S. Yang, G. Li, F. Liao and J. Lin, Cryst. Growth Des., 2011, 11, 3529–3535.
44. A. S. Plaman, J. G. Knapp, H. Xie, K. O. Kirlikovali and O. K. Farha, ACS Mater. Lett., 2024, 6, 4889–4896.
45. W. Morris, B. Volosskiy, S. Demir, F. Gándara, P. L. McGrier, H. Furukawa, D. Cascio, J. F. Stoddart and O. M. Yaghi, Inorg. Chem., 2012, 51, 6443–6445.
46. D. Feng, W.-C. Chung, Z. Wei, Z.-Y. Gu, H.-L. Jiang, Y.-P. Chen, D. J. Darensbourg and H.-C. Zhou, J. Am. Chem. Soc., 2013, 135, 17105–17110.
47. B. Ortn-Rubio, C. Perona-Bermejo, J. Suárez del Pino, F. J. Carmona, F. Gándara, J. A. R. Navarro, J. Juanhuix, I. Imaz and D. Maspoch, Chem. Commun., 2023, 59, 7803–7806.
48. D. Feng, K. Wang, J. Su, T.-F. Liu, J. Park, Z. Wei, M. Bosch, A. Yakovenko, X. Zou and H.-C. Zhou, Angew. Chem., Int. Ed., 2015, 54, 149–154.
49. Z. Guo, D. Yan, H. Wang, D. Tesfagaber, X. Li, Y. Chen, W. Huang and B. Chen, Inorg. Chem., 2015, 54, 200–204.
50. K. Wang, D. Feng, T.-F. Liu, J. Su, S. Yuan, Y.-P. Chen, M. Bosch, X. Zou and H.-C. Zhou, J. Am. Chem. Soc., 2014, 136, 13983–13986.
51. K. S. Park, Z. Ni, A. P. Côté, J. Y. Choi, R. Huang, F. J. Uribe-Romo, H. K. Chae, M. O'Keeffe and O. M. Yaghi, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 10186–10191.
52. R. Natarajan, G. Savitha, P. Dominiak, K. Wozniak and J. N. Moorthy, Angew. Chem., Int. Ed., 2005, 44, 2115–2119.
53. B. Chen, M. Eddaoudi, T. M. Reineke, J. W. Kampf, M. O'Keeffe and O. M. Yaghi, J. Am. Chem. Soc., 2000, 122, 11559–11560.
54. J. A. Anderson, J. Glaser and S. C. Glotzer, Comput. Mater. Sci., 2020, 173, 109363.
55. C. S. Adorf, P. M. Dodd, V. Ramasubramani and S. C. Glotzer, Comput. Mater. Sci., 2018, 146, 220–229.
56. V. Ramasubramani, C. S. Adorf, P. M. Dodd, B. D. Dice and S. C. Glotzer, Proceedings of the 17th Python in Science Conference, 2018.
57. D. Palmer, A. Fernandez, M. Gao, L. Rimmer and E. Palmer, CrystalMaker, 2024.
58. A. Stukowski, OVITO, https://www.ovito.org, accessed 2023-06-19.
59. J. E. Jones, Proc. R. Soc. London, Ser. A, 1924, 106, 441–462.
60. J. E. Jones, Proc. R. Soc. London, Ser. A, 1924, 106, 463–477.
61. J. D. Weeks, D. Chandler and H. C. Andersen, J. Chem. Phys., 1971, 54, 5237–5247.
62. D. Chandler, J. D. Weeks and H. C. Andersen, Science, 1983, 220, 787–794.
63. M. O'Keeffe and O. M. Yaghi, Chem. Rev., 2012, 112, 675–702.
64. B. Ortn-Rubio, H. Ghasempour, V. Guillerm, A. Morsali, J. Juanhuix, I. Imaz and D. Maspoch, J. Am. Chem. Soc., 2020, 142, 9135–9140.
65. C. Park, J. W. Baek, E. Shin and I.-D. Kim, ACS Nanosci. Au, 2023, 3, 353–374.
66. G. Benedetto and K. A. Mirica, Acc. Chem. Res., 2024, 57, 2775–2789.
67. E. V. Alexandrov, V. A. Blatov, A. V. Kochetkova and D. M. Proserpio, CrystEngComm, 2011, 13, 3947–3958.
68. S. V. Krivovichev, CrystEngComm, 2024, 26, 1245–1251.
69. N. W. Ockwig, O. Delgado-Friedrichs, M. O'Keeffe and O. M. Yaghi, Acc. Chem. Res., 2005, 38, 176–182.
70. B. Blaiszik, K. Chard, J. Pruyne, R. Ananthakrishnan, S. Tuecke and I. Foster, JOM, 2016, 68, 2045–2052.
71. R. N. Scott, P. J. Milner and J. Dshemuchadse, A Coarse-Grained Simulation Toolkit for Metal-Organic Framework Synthesis, ChemRxiv, 2025 DOI:10.26434/chemrxiv-2025-50s8.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp02121a

---