Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Coupling and decoupling of molecular reorientation and charge transport in Li-salt-doped cycloalcohol ion conductors†
Sofiane
Lansab
 a,
Yannik
Hinz
a,
Yannik
Hinz
 a,
Bastian
Grabe
a,
Bastian
Grabe
 b,
Peter
Lunkenheimer
b,
Peter
Lunkenheimer
 c and
Roland
Böhmer
c and
Roland
Böhmer
 a
a
aFakultät Physik, Technische Universität Dortmund, D-44221 Dortmund, Germany
bFakultät für Chemie und Chemische Biologie, Technische Universität Dortmund, D-44221 Dortmund, Germany
cExperimental Physics V, Center for Electronic Correlations and Magnetism, University of Augsburg, 86159 Augsburg, Germany
First published on 16th July 2025
Abstract
Using broadband impedance spectroscopy and conductometry, we study the phase behavior and the reorientational and translational dynamics of cycloalcohols doped with 1 to 20 mol% of Li salt. At low salt concentrations, a plastically crystalline state is stable. In this regime, the dielectric spectra of the cycloalcohols reveal two relaxation processes. One of them originates from the α-relaxation and indicates an orientational glass transition. The other, much slower process, is related to ionic hopping. By comparing reorientation times with electrical conductivities, for 1 mol% Li doping, previous studies suggested an only weak decoupling of rotational and translational motions. Rather than analyzing disparate quantities, the present work directly compares peak frequencies corresponding to reorientational and translational rates. This approach allows one to resolve the mild, yet significant divergence of the two rates, i.e., a dynamic decoupling, also for higher doping levels and for different Li salts. The electrolytes that form at Li salt concentrations of 5 mol% and more display a qualitatively different behavior. In this compositional regime, a liquid-to-glass transition arises and the ion hopping time that we probe using lithium nuclear magnetic resonance and proton-detected diffusometry is compatible with the reorientational time scales. This observation implies a close coupling of both underlying degrees of freedom.
1. Introduction
The quest for batteries with solid or solid-like electrolytes drives intensive research across a host of different materials, including polymer- and ionic-liquid-based electrolytes,1–5 superionic crystals,6 and not the least in the field of plastic crystalline solids (PCs).7,8 Here, molecules or molecular ions are placed on a well-defined center-of-mass lattice where they can perform fast reorientational motions. Therefore, the mobile species experience a kind of liquid-like environment. With a rotation-translation coupling present in various PCs, the fast reorientational motion in such crystals is a good candidate to enable efficient translational mobility as well. Often, the so-called “paddle-wheel” or “revolving-door” mechanism is found to facilitate the motion of intrinsic charge carriers as well as that of intentionally added ions.9Among the rotator crystals that hold promise for energy storage applications are (i) molecular PCs that are doped with suitable salts10–12 or (ii) ionic PCs,13–17i.e., solid solutions composed of cationic and anionic constituents. In the ionic PCs, one or both of the constituents can sustain fast reorientational motions. For these electrolytes, the large charge number density and the consequent presence of strong Coulombic interactions require dedicated strategies so that an efficient ionic transport still arises. To fine-tune the overall strength of the Coulombic interactions, it can be advantageous to resort to molecular PCs (composed of uncharged species) and to dope them with an optimum amount of salt. A particularly promising approach is to combine the ideas behind scenarios (i) and (ii), so that one arrives at ionic PCs with additional salt dopants. In some examples, the plastic phase can thus be maintained to even roughly 10 mol% of added salt.18–21
Nevertheless, many studies focus on the doping range of only a few percent of salt, sometimes in conjunction with blending in a second, structurally related plastic crystal. In this context, Li doped mixed dinitrile-,22–24 cycloalcohol-,25 pyrrolidinium-,26 and adamantane-based27 and other28 PCs were exploited to achieve further enhanced conductivity. Several of these mixtures were investigated using dielectric spectroscopy with the goal to sense the reorientational dynamics and using conductivity spectroscopy which probes the charge dynamics.24,25,27 The latter method provides access to transport quantities from which, in favorable cases, the often sought translational correlation times can be inferred. In this vein, the increased defect density that was reported to occur in Li doped adamantane-based PCs was conjectured to govern their electrical conductivity.27 Conversely, the paddle-wheel mechanism was directly demonstrated to be operative in Li doped dinitrile mixtures.29 This became possible by complementing dielectric spectroscopy by using nuclear magnetic resonance (NMR) techniques. The time scales describing the molecular reorientation of the different constituents within various dinitrile mixtures were accessed using protons, deuterons, and carbons as nuclear probes; the time scales that refer to the translational cationic motions were directly determined by means of 7Li NMR.29,30
The aforementioned dinitrile-, adamantane-, cycloalcohol-, and pyrrolidinium-based crystal alloys are miscible over the full compositional range. This situation is advantageous when studying the impact of effects related to the internal volume that is available to the charge carriers on the coupling of the orientational and translational degrees of freedom. However, it turned out that using the same type and concentration of (1 mol% LiPF6) doping, the mixed crystals formed by cyclohexanol (HEX) and cyclooctanol (OCT) display much higher conductivities than the adamantane-based rotator phases.25,27 This finding renders the HEX1−xOCTx matrix, to which Li salt is added, particularly attractive for study.
For different OCT concentrations x, this salt-doped molecular plastic crystal system displays similar dynamical behaviors. Particularly for (HEX0.6OCT0.4)0.99(LiPF6)0.01, significant, yet relatively mild deviations from rotation-translation coupling were reported.25 Assuming that the situation remains similar when doping with other Li-salts such as lithium bis(trifluoromethylsulfonyl)imide (LiTFSI), we chose HEX0.6OCT0.4 as a starting point for the present study. Our initial goal was to explore whether an increased Li doping to about 10 mol% and beyond would lead to a conductivity enhancement, similar to observations reported for various non-crystalline electrolytes.21,31,32
To anticipate some of our results, for mole fractions c ≥ 5 mol% of Li salt, it turned out that unlike, e.g., for the dinitrile-based alloys, the rotator phase of the cycloalcohol host matrix is less stable than the liquid phase. Thus, we find that at c ≥ 5 mol% of LiTFSI, crystallization is suppressed and liquid-to-glass transitions emerge when the sample approaches low temperatures. This situation resembles that of deep eutectic solvents. Typically, such solvents are formed when a molecular (usually hydrogen-bond sustaining) constituent and an ionic species such as LiTFSI are mixed over wide compositional ranges.21,31,33
Previously, HEX and OCT were studied as neat crystals using various techniques involving dielectric spectroscopy,34–36 NMR spectroscopy,37–40 and neutron scattering.41,42 Some cycloalcohols were also studied in salt-doped form, but as far as we know only up to the 1% level.27 To gain insights into the interplay of plastically crystalline and supercooled liquid phases, we aim at finding out whether or not, at higher doping levels, HEX1−cLiTFSIc and OCT1−cLiTFSIc may show deep-eutectic-like behavior. Therefore, by examining samples with salt concentrations as large as c = 20 mol%, a major objective of the present work is to explore the dynamic coupling, or decoupling, of the various degrees of freedom. To reach this goal, the different NMR techniques that we exploit play an important role.
After briefly presenting the experimental details, in Section 3, we focus on the regime of weak (c ≤ 3 mol%) Li doping in which plastically crystalline low-temperature phases are stable. Subsequently, stronger Li-doped, deep-eutectic-like glass formers are studied where the ions are dissolved in pure and in mixed cycloalcohol matrices. The interplay of the reorientational dynamics and translational mobility as probed by conductivity measurements is the focus of Section 4. Finally, we discuss the present results in the context of other electrolytes, before summarizing our findings in Section 5.
2. Experimental details
Protonated HEX, protonated OCT, LiTFSI salt (all with a purity of 99%), as well as C–D deuterated cyclohexanol (HEX-d11, degree of deuteration 98%) were purchased from Sigma-Aldrich (while deuterated OCT is apparently commercially not available). Upon cooling, HEX and OCT solidify near 270 and 280 K, respectively,25 so that at room temperature also their mixtures are liquid. The preparation of the salt doped samples with LiTFSI fractions c = 1, 3, 5, 8, 10, 15, and 20 mol% closely followed the procedure described in detail for other solutions that form PCs29 or deep eutectic solvents.31 Dielectric and conductivity experiments were carried out using a Novocontrol system. The samples were placed in a parallel-plate invar-sapphire capacitor43 that features an electrode gap of 50 μm. Typically, ac voltages of 1 Vrms were applied during the frequency sweeps. With a focus on the spectral shape, the dielectric function is usually given after normalization by the high-frequency dielectric constant, ε∞. Like in ref. 29, 2H and 7Li NMR relaxometry was applied using home-built spectrometers that were operated at Larmor frequencies of 46.5 and 116.9 MHz, respectively. Details of the proton-detected diffusion measurements are given elsewhere.293. Results and analyses
Weak Li doping: plastic-crystal regime
Fig. 1 shows frequency-dependent dielectric and conductivity results for (HEX0.6OCT0.4)0.97(LiTFSI)0.03. Frame (a) displays the real part ε′ of the complex dielectric constant ε* = ε′ − iε′′ from which a clear double step is seen. Such a somewhat uncommon behavior was previously reported for Li-doped adamantane-based crystals.27 Faint indications for such a feature were noted for dinitriles devoid of added salt.44 For (HEX0.6OCT0.4)0.99(LiPF6)0.01, i.e., for a PC with a different OCT concentration, some hints of a second low-frequency relaxation step are noted in ref. 25, but not analyzed in any detail.For (HEX0.6OCT0.4)0.97(LiTFSI)0.03, the Li salt generates strong electrical conductivity, which overlays any dielectric loss peaks. Fig. 1(b) shows an example for T = 233 K. The derivative45,46
 | (1) |
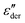 . The high-frequency peaks are narrower than the low-frequency loss peaks. Their line shape is, however, hard to define because at the lowest frequencies, an upturn is found in
. The high-frequency peaks are narrower than the low-frequency loss peaks. Their line shape is, however, hard to define because at the lowest frequencies, an upturn is found in  . This upturn, like the corresponding feature in ε′, arises as a consequence of electrode polarization effects. Roughly two decades above the peak frequency, the high-frequency flanks of
. This upturn, like the corresponding feature in ε′, arises as a consequence of electrode polarization effects. Roughly two decades above the peak frequency, the high-frequency flanks of  exhibit a crossover to a weaker frequency dependence. This may well indicate the presence of a secondary relaxation process, as reported for HEX0.6OCT0.4 doped with LiPF6.25 A close inspection of
exhibit a crossover to a weaker frequency dependence. This may well indicate the presence of a secondary relaxation process, as reported for HEX0.6OCT0.4 doped with LiPF6.25 A close inspection of  reveals that the low-frequency peaks are slightly more temperature dependent than the high-frequency peaks. In other words, the two peaks are somewhat more separated at lower temperatures than they are at higher temperatures.
reveals that the low-frequency peaks are slightly more temperature dependent than the high-frequency peaks. In other words, the two peaks are somewhat more separated at lower temperatures than they are at higher temperatures.
The representations in Fig. 1(a) and (b) clearly resolve dielectric relaxation steps and peaks. Fig. 1(c) shows the evolution of the real part, σ′(ν), of the complex, frequency-dependent electrical conductivity, σ*(ν) = iωε0ε*(ν), where ε0 designates the electrical field constant. The dc conductivity can easily be identified from the plateau σdc = σ′(ν→0). In the representation of Fig. 1(c), only the high-frequency relaxation process is evident, showing up as a shoulder, while the low-frequency process is superimposed by the dc contribution.
Before discussing corresponding relaxation times and conductivities for a doping level of 1 mol% and analyzing them in Section 4, in Fig. 2, we plot the dielectric loss as a function of temperature for several Li salt concentrations and several frequencies. When comparing the cooling with the heating runs for (HEX0.6OCT0.4)0.99(LiTFSI)0.01 (see Fig. 2(a)), a well-developed hysteresis is seen to occur at temperatures between 265 and 278 K. Similar effects, yet with a less pronounced hysteresis, were obtained for c = 3 and 5 mol%, as shown in Fig. 2(b) and (c), respectively. For the 1% sample, a well-defined discontinuity shows up in ε′′ which signals the presence of a phase transition, while for the 3% sample, the dielectric loss displays only a mild change of slope. For 5 mol%, hardly any such feature is discernible. Furthermore, for higher Li concentrations, clear signatures for liquid-to-crystal transitions are typically lacking.
For the 1% sample, the frequency and temperature dependent dielectric losses clearly reveal the presence of a relaxation process, showing up as a peak in ε′′(T), as seen in Fig. 2(a). Indications for a relaxation process are also visible for (HEX0.6OCT0.4)0.97(LiTFSI)0.03, as shown in Fig. 2(b). However, here the double peak structure in  that is clearly resolved from Fig. 1(b) is obviously obscured by the electrical conductivity.
that is clearly resolved from Fig. 1(b) is obviously obscured by the electrical conductivity.
Stronger Li doping: deep-eutectic regime
 | ||
Fig. 3 (a) Real part, ε′, and (b) imaginary part (ε′′, triangles;  , crosses) of the normalized complex permittivity of (HEX0.6OCT0.4)1−c(LiTFSI)c for c = 5 mol%. (c) Normalized dielectric loss of a sample with c = 20 mol%. With the intention to highlight the differences between the dielectric spectra of the 3 mol% and 5 mol% samples, the ε′ scale in frame (a) is chosen similar to that in Fig. 1(a). , crosses) of the normalized complex permittivity of (HEX0.6OCT0.4)1−c(LiTFSI)c for c = 5 mol%. (c) Normalized dielectric loss of a sample with c = 20 mol%. With the intention to highlight the differences between the dielectric spectra of the 3 mol% and 5 mol% samples, the ε′ scale in frame (a) is chosen similar to that in Fig. 1(a). | ||
Different from the loss curves seen for the plastic (HEX0.6OCT0.4)0.97(LiTFSI)0.03 crystal in Fig. 2(b), those seen in Fig. 3(b) for (HEX0.6OCT0.4)0.95(LiTFSI)0.05 display a clearly asymmetric shape that is rather expected for a supercooled liquid. From the high-frequency flanks of these asymmetric loss peaks, one recognizes that they become less steep and thus the spectra broader, as the sample is cooled. From Fig. 3(a), a Curie-type behavior is seen for the dielectric constant, i.e., the relaxation steps increase somewhat with decreasing temperature.
The pattern observed for c = 5 mol% is similarly also found for higher Li salt concentrations. In particular for c ≥ 5 mol%, there are no indications of double steps or peaks, nor do we observe compelling indications for structural phase transformations that would take place upon cooling. Fig. 3(c) shows the dielectric loss for (HEX0.6OCT0.4)0.80(LiTFSI)0.20, i.e., for a liquid with a much larger salt content. The ESI† provides a comparison with measurements for (binary) HEX0.80LiTFSI0.20 and OCT0.80LiTFSI0.20 mixtures. The relaxation times and the dc conductivities extracted from the various spectra will be discussed in Section 4.
Using standard inversion or saturation procedures, we recorded the time evolution of the longitudinal magnetization recovery, Mz(t). To determine the spin–lattice relaxation time T1, we parameterized Mz(t) using the stretched exponential function
| Mz(t) = M0 + (Mi − M0)exp[−(t/T1)μ]. | (2) |
At the temperatures of the T1 minima, motional correlation times τc can be estimated from the relation ωLτc = 0.62.47 This relation rationalizes, at least partially, why for 7Li (for which the Larmor frequency ωL is about 2.5 times greater than for 2H), the T1 minimum appears at a temperature that is larger than it is for the deuterons. A discussion of the resulting correlation times, also in relation to the ones from dielectric spectroscopy, will be given in Section 4.
Fig. 4(a) presents the Kohlrausch exponents that characterize the magnetization curves, however, only if the exponents differ markedly from μ = 1. As one infers from Fig. 4(a), this is the case only for the 2H spin–lattice relaxation at T < 220 K. In that range, μ decreases upon cooling, indicating an increasingly wider distribution of T1 times. Since here we are in the slow-motion regime, ωLτc ≫ 1, this increase indicates that the τc distribution broadens. This observation is compatible with the broadening of the ε′′ spectra of (HEX0.6OCT0.4)0.95(LiTFSI)0.05 that was noted in the context of Fig. 3(b).
4. Discussion
With the goal to map out the phase behavior of the (HEX0.6OCT0.4)1−c(LiTFSI)c system, Fig. 5(a) compiles the temperatures that were inferred from the hysteretic behavior in ε′′ such as shown in Fig. 2. For salt concentrations c < 5 mol%, the crystallization and melting temperatures of the mixtures strongly decrease as c increases. Furthermore, for the two Li-doped PCs (with c = 1 mol% and 3 mol%) that we measured in this low-c regime, the orientational freezing on the 100 s scale is independent of c. By contrast, for larger salt concentrations, the (HEX0.6OCT0.4)1−c(LiTFSI)c samples do not crystallize upon cooling. Hence, the 100 s-freezing, now corresponding to a liquid-to-glass transition, takes place at successively higher temperatures as c increases. This T(c) behavior resembles the one reported for other structural glass formers that contain a substantial amount of LiTFSI.21,29The weak hysteretic behavior observed for some mixtures with c ≥ 5 mol%, in Fig. 5(a) highlighted by hatching, calls for particular consideration. Fig. 2(c) shows that the dielectric loss of (HEX0.6OCT0.4)0.95(LiTFSI)0.05 evolves smoothly upon cooling, Yet, as expected from so-called two-step crystallization experiments,48 the nucleation propensity is generally increased by deep prior undercooling. Hence, in reheating runs, crystallization becomes more likely, in harmony with the observations made from Fig. 2(c) for the 5 mol% sample. The hatching marks the hysteretic range also for (HEX0.6OCT0.4)0.85(LiTFSI)0.15. The ESI† shows that HEX1−cLiTFSIc and OCT1−cLiTFSIc with c = 15 and 20 mol% display similar effects.
Interestingly, the phase diagram shown in Fig. 5(a) resembles those of some LiTFSI-dinitrile systems.21 For the doped cycloalcohols, this observation suggests that near c ≈ 10 mol%, the presumed eutectic point is so low that crystallization is effectively inhibited also upon reheating.
It is not only instructive to plot isochronal quantities such as in Fig. 5(a), but it is also revealing to consider the concentration dependence of the time scales τ as well as of the electrical conductivities σdc in an isothermal fashion. This is shown in Fig. 5(b). Here, one recognizes that at 275 K, i.e., above the temperatures at which even the neat cycloalcohols become solid, the ionic conductivity σdc displays a maximum near c = 10 mol%. This σdc maximum, appearing at a molarity of about 1 M, is a remarkable finding. It is not completely unexpected, though, since numerous other liquid electrolytes also exhibit a σdc maximum near 1 M salt concentrations.21,29,32,49,50 Our σdc data at 236 K are not incompatible with such a feature, but also not fully compelling in that respect.
Recalling that the PC state is stable for c < 5 mol%, it is seen that σdc is significantly lower in the crystalline solid than the value extrapolated from the liquid (i.e., from the data for c ≥ 5 mol%). For 206 K, σdc of (HEX0.6OCT0.4)0.97(LiTFSI)0.03 is again relatively small; for the 1 mol% sample, it is about 2 × 10−14 S cm−1, i.e., too low to be within the range shown in Fig. 5(b).
The isothermal relaxation times (at T = 206 K), shown in Fig. 5(b), and the isochronal relaxation times (at τ = 102 s), shown in Fig. 5(a), indicate the same trend as a function of the molar salt fraction c: for c < 5 mol%, τ, and correspondingly Tg, do not significantly change with c, while for larger salt concentrations, an increase of τ and of Tg is seen to emerge.
To obtain an overview regarding the translational and reorientational dynamics in a large temperature range, Fig. 6 presents the relaxation times and the inverse conductivity, i.e., the dc resistivity ρdc = 1/σdc, in an Arrhenius fashion. Frame (a) focuses on samples with c < 5 mol%. Including data also for undoped HEX0.6OCT0.4 and for LiPF6 doping,25 it is seen that the presence of Li salt leads to only mild changes in the reorientational dynamics. In ref. 25, the latter was identified as the so-called α-dynamics. It is important to realize that we determined τα from the high-frequency peaks of the double-peak structures that are seen for (HEX0.6OCT0.4)0.97(LiTFSI)0.03 in Fig. 1(b).
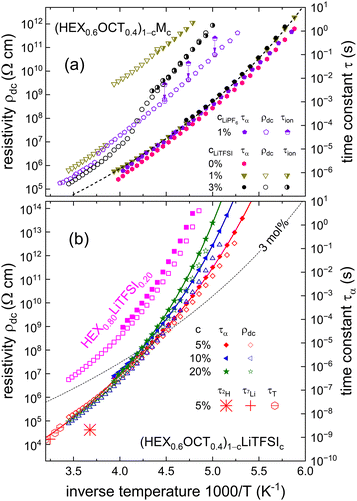 | ||
| Fig. 6 Arrhenius plot of resistivity ρdc (open symbols) and relaxation times (τα as filled symbols and τion as half-filled symbols, both derived from inverse circular peak frequencies) for HEX0.6OCT0.4 doped (a) at mole fractions (a) of c < 5 mol% and (b) at larger levels. Frame (a) features data relating to LiTFSI doping as well as results of a sample devoid of added salt. The purple pentagons represent data (based on ref. 25) for a crystal doped with 1 mol% of LiPF6. In frame (a), the ordinate axes are shifted so that for (HEX0.6OCT0.4)0.97(LiTFSI)0.03 the τion and the ρdc data overlap. Frame (b) shows ρdc and τα for (HEX0.6OCT0.4)1−c(LiTFSI)c with c = 5, 10, and 20 mol% as well as for HEX0.80LiTFSI0.20. For visual clarity, the latter data are shifted upward by 2 decades. Also included are NMR-based motional times inferred from the 2H (asterisk) and 7Li (plus sign) T1 minima reported in Fig. 4, as well as the diffusion-based translational times τT (hexagons with horizontal bars). All lines in the present figure are guides to the eye. In both frames, the y-axes are adjusted so that all decade ticks are spaced equally. Thus, by construction, the relative shift of the ρdc and the τ axes in frame (a) differs from that chosen for frame (b). | ||
To elucidate the nature of the low-frequency peaks, the corresponding time scales, that will be called τion, are also included in Fig. 6(a). One recognizes that they display a somewhat stronger temperature dependence than τα, which, however, matches that of the dc resistivity very well. To emphasize this coincidence, the resistivity and the relaxation ordinate axes were shifted accordingly. The striking similarity to the behavior seen for LiTFSI-doped adamantane-based PCs27 strongly suggests that the slower-than-α process is also here due to the ion transport. This is why, like in ref. 27, the corresponding relaxation time are designated τion. Ref. 27 points out that in most ion conductors the observation of this feature is hampered by the presence of spectrally close reorientational contributions. In the ESI,† the dielectric spectra of (HEX0.6OCT0.4)0.99(LiTFSI)0.01 are also seen to display a double-peak structure and for this sample, Fig. 6(a) reveals a close thermal evolution of τion and ρdc as well. Hence, one may ask whether the observation of an ion-transport dielectric loss peak in PCs is particularly facilitated by the presence of the LiTFSI salt.
To address this question, we analyzed unpublished raw data25 for (HEX0.6OCT0.4)0.99(LiPF6)0.01, a cycloalcohol mixture featuring another Li salt. For that sample, careful scrutiny also reveals a double-peak structure in  , implying that this feature may be more general than previously thought. The temperature dependence of the corresponding slower-than-α time scale, τion, is included in Fig. 6(a). It matches the temperature dependence of the electrical resistivity excellently. However, the relative shift of the ordinate axes (chosen to lead to an overlap of τion and ρdc for the LiTFSI based PCs) does not apply for the LiPF6-based electrolytes. Here, overlap with ρdc is achieved by shifting the τion symbols downward by an additional factor of 5 (see the arrows in Fig. 6(a)).
, implying that this feature may be more general than previously thought. The temperature dependence of the corresponding slower-than-α time scale, τion, is included in Fig. 6(a). It matches the temperature dependence of the electrical resistivity excellently. However, the relative shift of the ordinate axes (chosen to lead to an overlap of τion and ρdc for the LiTFSI based PCs) does not apply for the LiPF6-based electrolytes. Here, overlap with ρdc is achieved by shifting the τion symbols downward by an additional factor of 5 (see the arrows in Fig. 6(a)).
The necessity to use different sample-dependent shift factors, in order to generate an overlap of the ρdc and the τ data in Fig. 6(a), reminds one of the fact that ρdc and τ are rather disparate quantities. Hence, a comparison between them is necessarily indirect. Relations among the conductivity relaxation time τD and ρdc = 1/σdc have variously been formulated, e.g., as σdcτD = ε0ε∞ or in terms of the empirical Barton-Nakajima-Namikawa rule, σdcτD = pε0(εs−ε∞), where p is a constant close to 1 and εs is the static dielectric constant.51,52 There is some debate regarding the assignment of εs in ionic systems.53 It is clear, however, that the proportionality constants between τD and ρdc can vary quite a bit and that they can be (weakly) temperature dependent as well. Furthermore, it has been asserted that “the conductivity relaxation time τD is proportional to, not equal to, the ionic hopping correlation time”.54 Thus, in order to enable a direct, quantitative comparison of translational with reorientational or structural time scales, all these circumstances suggest to employ τion based, rather than σdc based measures, whenever possible.
For (HEX0.6OCT0.4)0.97(LiTFSI)0.03, Fig. 6(a) indicates that τα and τion share similar temperature dependences. A closer look reveals, however, an increasing dynamic decoupling between these quantities as the sample is cooled. In Fig. 6(a), the decoupling for this crystal is seen to be considerably more pronounced than it is for 1 mol%. This becomes particularly clear, if one observes that for c = 1 and 3 mol% of LiTFSI doping, the temperature dependences of τα are practically identical. At the same time, for c = 3 mol%, the temperature dependence of τion is significantly steeper than that for the 1 mol% sample.
However, the dynamic decoupling, even for the 3 mol% crystal, is still much less pronounced than that reported for LiTFSI-doped adamantane.27 There, τα shows only minor deviations from an Arrhenius temperature dependence, while τion displays a pronounced super-Arrhenius behavior. The latter has been taken to indicate an appearance of glassy dynamics in the ionic subsystem which has been rationalized within various approaches.55–58 Significant deviations from thermally activated behavior are not obvious in the relatively small range in which τion could be detected for the 3 mol% sample. Yet, for (HEX0.6OCT0.4)0.97(LiTFSI)0.03, an Arrhenius-based extrapolation of τion toward high temperatures yields an attempt frequency in excess of 1020 Hz. Such “unrealistically” large values are usually considered as a smoking gun for non-Arrhenian behavior. The presently discussed 1 mol% samples, i.e., (HEX0.6OCT0.4)0.99(LiPF6)0.01 and (HEX0.6OCT0.4)0.99(LiTFSI)0.01, display less pronounced decoupling effects, as shown in Fig. 6(a).
In the c ≥ 5 mol% regime, i.e., for higher doping levels, Fig. 6(b) reveals a different kind of behavior. Here, the reorientational dynamics within the matrix, i.e., the α relaxation time, does significantly depend on the salt content as the glass transition is approached. Conversely, for higher temperatures, τα depends little on c. As representative examples, Fig. 6(b) comprises τα data for samples with c = 5, 10, and 20 mol% (also data for HEX0.80LiTFSI0.20 are included; for additional compositions, see the ESI†). To examine the relation of τα and the ion hopping times, the time constant τLi extracted from the 7Li T1 minimum is added to Fig. 6(b). One recognizes that τLi smoothly lines up with τα, strongly suggesting a coupling of reorientational and translational time scales. Using this finding, in Fig. 6(b), the ρdc axis was adjusted (relative to the τα axis) accordingly. The common representation of τα and ρdc that is embodied in this figure shows that toward lower temperatures, a rather weak decoupling of the rotational from the translational degrees emerges, which remains much smaller than in the plastic-crystal regime.
A more succinct and more common way to check for a possible (de-) coupling of conductivity and reorientational dynamics is to plot the dc resistivity ρdcversus the dipolar relaxation time τ in a double-logarithmic representation.59–62 If the two dynamics are coupled, in the sense that they display the same temperature dependence, a power law ρdc ∝ τξ with an exponent ξ = 1 is expected. Indeed, for a host of cholinium-chloride and Li-salt based deep eutectic solvents, the experimentally determined exponents are in the range 0.9 < ξ < 1.1.63Fig. 7 shows that such a power-law behavior, with ξ = 0.92, is found for the c = 5 mol% electrolyte, i.e., in the deep-eutectic-solvent regime. Conversely, for c = 3 mol%, we find ξ = 1.8. This result confirms the observation made from Fig. 6(a) that severe deviations from rotation-translation coupling emerge when transitioning from the glass-forming to the PC regime.
Returning to the deep-eutectic-solvent regime, in the present work, we employ proton-detected diffusometry to trace the translational motions of the cycloalcohol molecules within the 5 mol% sample. To directly compare the self-diffusion coefficients Dtrans (tabulated in the ESI†) with the time constants in Fig. 6(b), we exploit the Stokes–Einstein-Debye relation. This involves the solution of the rotation diffusion equation in terms of the Legendre polynomials P![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) . In the NMR context, the correlation times refer to polynomials of rank
. In the NMR context, the correlation times refer to polynomials of rank ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) = 2. The resulting Stokes–Einstein-Debye relationship implies a coupling of the rotational diffusion coefficient64,65
= 2. The resulting Stokes–Einstein-Debye relationship implies a coupling of the rotational diffusion coefficient64,65
 | (3) |
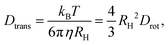 | (4) |
 | (5) |
To achieve coincidence of τT with the other translational time scales appearing in Fig. 6(b), we assumed a hydrodynamic radius of RH = 2.1 Å. Often RH is close to the molecular van der Waals radius RvdW.64 From ref. 68, the latter quantity can be estimated to be 2.97 Å for HEX and 3.25 Å for OCT so that RvdW for HEX0.6OCT0.4 amounts to about 3.1 Å. The finding that Rtrans < RvdW for most liquids, in particular for those formed by internally flexible molecules, is well known.64,65 It has also been pointed out65 that the use of slip boundary conditions is “resulting in RH values larger by a factor of 1.5.”
Initially, we expected that the deuteron NMR measurements of the HEX-d11 molecules, that we carried out for the 5 mol% sample, are most sensitive to their overall reorientational dynamics. Viewed from that perspective, it is somewhat surprising that the deuteron T1 minimum implies a time scale that is much shorter than expected from the dielectric τα times, as shown in Fig. 6(b). This observation thus hints at the importance of other (faster) motional processes with conformational modulations of the molecules as a potential candidate.69–71 The most likely scenario is indicated by proton and carbon T1 measurements of neat HEX crystals.39 These experiments revealed a type of motion that was described as a “uniaxial internal rotation of the cyclohexyl ring about the CO bond, with the COH group remaining stationary,”39 so that this process was concluded to display an, at best, weak dielectric signature. Hence, the dielectric response is governed by the collective reorientational molecular motions (i.e., the α-process).25 Thus, similar to previous work,7,11,23 the charge motions are envisioned to be facilitated by the global reorientational motions of the whole molecules.
As we have seen, for the glass forming liquids studied in this work, a double-peak in their dielectric dispersion, i.e., a resolved translational loss peak is not detected. This contrasts with the findings for the previously27 and the presently studied salt-doped PCs. The observation of a translational loss peak is, however, not generally restricted to PCs. It is for instance also observable for ionic glass formers devoid of constituents which by symmetry lack electrical dipole moments. Some molten salts like 2Ca(NO3)2-3KNO372 and other glassy electrolytes73–76 fall within this category. Interestingly, also for an ionic liquid composed solely of symmetric ions, the dielectric loss peaks were “ascribed to the frequency-dependent translational motion of ions, rather than the coupling with the reorientational relaxation.”77
5. Conclusions
In the present work, we studied the relationship of reorientational dynamics and charge transport in LiTFSI-doped cycloalcohols. Dielectric and conductivity measurements were carried out for salt concentrations ranging from 1 to 20 mol%. Close to room temperature, a conductivity maximum exists near the 1 M molarity, corresponding to about 10 mol% of salt doping. Upon cooling, a more complex behavior emerges. It is found that for c < 5 mol% at low temperatures, orientationally disordered crystals are stable. For them, we observe a two-step dielectric function. In harmony with previous work, also on undoped cycloalcohols, the high-frequency process is identified as the one which drives orientational freezing. By contrast, the low-frequency process corresponds to the ion transport. Its observation is not unprecedented (see ref. 27), but somewhat uncommon, and the present work reveals that it may be more abundant than previously thought. A prerequisite for its unambiguous detection is that reorientational processes must not overshadow nearby ionic relaxations. Promising for their observation is thus the study of strongly decoupled ion conductors and ion conductors for which the reorientation related contributions are small or even absent. This is not only the case for the presently studied crystals, but, as discussed, also for some molten salts and various glassy electrolytes.For the reorientational and the translational degrees of freedom of lightly Li-doped HEX0.6OCT0.4, we detected weak but significant differences of their temperature dependences. This is similar to the findings for some other Li-doped cycloalcohol mixtures that are based on comparing conductivities and motional time scales.25 Reorientational and translational time scales that evolve differently with temperature point to a decoupling of the underlying degrees of freedom. The observation of different thermal evolutions precludes a perfect one-to-one coupling as expected if a “revolving-door” mechanism would dominate the ionic conductivity of these systems. However, as we pointed out, any comparison between time scales and conductivities is necessarily indirect. Conversely, following ref. 27, here, based on the directly determined time constant τion, we were able to perform a more direct comparison of the ionic and structural time scales. The degree of decoupling that we thus find in the Li-doped cycloalcohols is certainly much less pronounced than in Li-doped adamantane-based PCs,27 a finding which in ref. 27 was rationalized by the more globular shape of the molecules in those systems.
The situation is different for salt concentrations of 5 mol% and more. Here, all the samples display a liquid-to-glass transition rather than an orientational glass transition. The overall phase behavior reveals a concentration-temperature pattern that resembles the one known from deep eutectic solvents.
For (HEX0.6OCT0.4)0.95(LiTFSI)0.05, we combined dielectric spectroscopy to probe the reorientational motions with 7Li NMR as well as diffusometry to probe the cationic and molecular (cycloalcohol) transport, respectively. At least near room temperature, where the NMR results were exploited to obtain absolute translational time scales, τT, we demonstrated a close coupling of the reorientational and translational dynamics. In addition, the comparison with the conductivity of the glass forming samples also indicates that towards lower temperature, the coupling of reorientations and translations remains relatively close. As discussed, e.g., in ref. 61 for particles moving within a viscous liquid, such a behavior is predicted by the combined Stokes–Einstein, Stokes–Einstein-Debye, and Nernst–Einstein relations. Within this framework, the observed rotation-translation coupling arises from the direct relation of both the rotational and the translational diffusion times, cf.eqn (3) and (4), to the viscosity. In contrast, for the plastic-crystalline states found at low salt concentrations in the present work, such viscosity-mediated coupling is excluded and a different type of rotation-translation coupling, most likely via the “revolving-door” mechanism, has to be invoked. Our results show that in the investigated cycloalcohol PCs with low salt content, this mechanism leads to less perfect coupling than for the samples with high salt content, where the viscosity-mediated mechanism is active. To summarize, our study reveals how small compositional changes can be exploited to tune a transition of Li-doped cycloalcohols from PCs with less coupled dynamics to glass forming liquids with largely coupled motions.
Conflicts of interest
There are no conflicts of interest to declare.Data availability
The data presented in this article are all given in the manuscript figures. Data supporting this article are part of the ESI† and are shown there as figures and tables.Acknowledgements
This work was financially supported by the Deutsche Forschungsgemeinschaft under Project No. 429918288 and 444797029.References
- N. S. Grundish, J. B. Goodenough and H. Khani, Designing composite polymer electrolytes for all-solid-state lithium batteries, Curr. Opin. Electrochem., 2021, 30, 100828 CrossRef CAS.
- S. Kundu and Y. Ein-Eli, A review on design considerations in polymer and polymer composite solid-state electrolytes for solid Li batteries, J. Power Sources, 2023, 553, 232267 CrossRef CAS.
- G. P. Pandey, T. Liu, C. Hancock, Y. Li, X. S. Sun and J. Li, Thermostable gel polymer electrolyte based on succinonitrile and ionic liquid for high-performance solid-state supercapacitors, J. Power Sources, 2016, 328, 510–519 CrossRef CAS.
- Q. Li, F. Yan and J. Texter, Polymerized and Colloidal Ionic Liquids–Syntheses and Applications, Chem. Rev., 2024, 124, 3813–3931 CrossRef CAS PubMed.
- J. Hwang, K. Matsumoto, C.-Y. Chen and R. Hagiwara, Pseudo-solid-state electrolytes utilizing the ionic liquid family for rechargeable batteries, Energy Environ. Sci., 2021, 14, 5834–5863 RSC.
- Y. Kato, S. Hori, T. Saito, K. Suzuki, M. Hirayama, A. Mitsui, M. Yonemura, H. Iba and R. Kanno, High-power all-solid-state batteries using sulfide superionic conductors, Nat. Energy, 2016, 1, 16030 CrossRef CAS.
- E. I. Cooper and C. A. Angell, Ambient temperature plastic crystal fast ion conductors (PLICFICS), Solid State Ionics, 1986, 18–19, 570–576 CrossRef CAS.
- T. Bauer, M. Köhler, P. Lunkenheimer, A. Loidl and C. A. Angell, Relaxation Dynamics and Ionic Conductivity in a Fragile Plastic Crystal, J. Chem. Phys., 2010, 133, 144509 CrossRef PubMed.
- Z. Zhang and L. F. Nazar, Exploiting the paddle-wheel mechanism for the design of fast ion conductors, Nat. Rev. Mater., 2022, 7, 389–405 CrossRef.
- P.-J. Alarco, Y. Abu-Lebdeh, A. Abouimrane and M. Armand, The plastic-crystalline phase of succinonitrile as a universal matrix for solid-state ionic conductors, Nat. Mater., 2004, 3, 476–481 CrossRef CAS PubMed.
- D. R. MacFarlane and M. Forsyth, Plastic crystal electrolyte materials: New perspectives on solid state ionics, Adv. Mater., 2001, 13, 957–966 CrossRef CAS.
- A. Abouimrane and I. J. Davidson, Solid Electrolyte Based on Succinonitrile and LiBOB: Interface Stability and Application in Lithium Batteries, J. Electrochem. Soc., 2007, 154, A1031–A1034 CrossRef CAS.
- H. Zhu, D. R. MacFarlane, J. M. Pringle and M. Forsyth, Organic Ionic Plastic Crystals as Solid-State Electrolytes, Trends Chem., 2019, 1, 126–140 CrossRef CAS.
- I. S. Klein, Z. Zhao, S. K. Davidowski, J. L. Yarger and C. A. Angell, A New Version of the Lithium Ion Conducting Plastic Crystal Solid Electrolyte, Adv. Energy Mater., 2018, 8, 1801324 CrossRef.
- S. Tian, B. Shao, Z. Wang, S. Li, X. Liu, Y. Zhao and L. Li, Organic ionic plastic crystal as electrolyte for lithium-oxygen batteries, Chin. Chem. Lett., 2019, 30, 1289–1292 CrossRef CAS.
- H. Zhou, S. Sato, Y. Nishiyama, G. Hatakeyama, X. Wang, Y. Murakami and T. Yamada, Molecular Design of Organic Ionic Plastic Crystals Consisting of Tetracyanoborate with Ultralow Phase Transition Temperature, J. Phys. Chem. Lett., 2023, 14, 9365–9371 CrossRef CAS PubMed.
- W. S. Tang, M. Matsuo, H. Wu, V. Stavila, W. Zhou, A. A. Talin, A. V. Soloninin, R. V. Skoryunov, O. A. Babanova, A. V. Skripov, A. Unemoto, S. I. Orimo and T. J. Udovic, Liquid-Like Ionic Conduction in Solid Lithium and Sodium Monocarba-closo-Decaborates Near or at Room Temperature, Adv. Energy Mater., 2016, 6, 1502237 CrossRef.
- L. Jin, P. C. Howlett, J. M. Pringle, J. Janikowski, M. Armand, D. R. MacFarlane and M. Forsyth, An organic ionic plastic crystal electrolyte for rate capability and stability of ambient temperature lithium batteries, Energy Environ. Sci., 2014, 7, 3352–3361 RSC.
- Y. Hirotsu, R. Sekiguchi, Y. Takeoka, M. Rikukawa and M. Yoshizawa-Fujita, Phase transition and ionic conductivity of pyrrolidinium-based ionic plastic crystals with magnesium salts, Bull. Chem. Soc. Jpn., 2024, 97, uoae101 CrossRef CAS.
- P. S. Whitfield, A. Abouimrane and I. J. Davidson, In situ XRD study of the succinonitrile–lithium bis(trifluoromethylsulfonyl) imide (LiTFSI) phase diagram, Solid State Ionics, 2010, 181, 740–744 CrossRef CAS.
- Y. Ugata, R. Tatara, K. Ueno, K. Dokko and M. Watanabe, Highly concentrated LiN(SO2CF3)2/dinitrile electrolytes: Liquid structures, transport properties, and electrochemistry, J. Chem. Phys., 2020, 152, 104502 CrossRef CAS PubMed.
- M. Zachariah, M. Romanini, P. Tripathi, J. L. Tamarit and R. Macovez, Molecular diffusion and dc conductivity perfectly correlated with molecular rotational dynamics in a plastic crystalline electrolyte, Phys. Chem. Chem. Phys., 2015, 17, 16053–16057 RSC.
- K. Geirhos, P. Lunkenheimer, M. Michl, D. Reuter and A. Loidl, Communication: Conductivity enhancement in plastic-crystalline solid-state electrolytes, J. Chem. Phys., 2015, 143, 081101 CrossRef CAS PubMed.
- D. Reuter, P. Lunkenheimer and A. Loidl, Plastic-crystalline solid-state electrolytes: Ionic conductivity and orientational dynamics in nitrile mixtures, J. Chem. Phys., 2019, 150, 244507 CrossRef CAS PubMed.
- D. Reuter, C. Geiß, P. Lunkenheimer and A. Loidl, Variation of ionic conductivity in a plastic-crystalline mixture, J. Chem. Phys., 2017, 147, 104502 CrossRef CAS PubMed.
- S. Abeysooriya, F. Makhlooghiazad, J.-N. Chotard, L. A. O’Dell and J. M. Pringle, Investigation of the Physicochemical Properties of Pyrrolidinium-Based Mixed Plastic Crystal Electrolytes, J. Phys. Chem. C, 2023, 127, 12304–12320 CrossRef CAS.
- D. Reuter, K. Seitz, P. Lunkenheimer and A. Loidl, Ionic conductivity and relaxation dynamics in plastic crystals with nearly globular molecules, J. Chem. Phys., 2020, 153, 014502 CrossRef CAS PubMed.
- A. Dorai, S. Kim, N. Kuwata, J. Kawamura, K. Kisu and S.-I. Orimo, Understanding Ion Dynamics in Closoborate-Type Lithium-Ion Conductors on Different Time-Scales, J. Phys. Chem. Lett., 2024, 15, 4864–4871 CrossRef CAS PubMed.
- S. Lansab, B. Grabe and R. Böhmer, Paddle-wheel mechanism in doped succinonitrile-glutaronitrile plastic electrolytes: A joint magnetic resonance, dielectric, and viscosimetry study of Li ion translational and molecular reorientational dynamics, Phys. Chem. Chem. Phys., 2023, 25, 9382–9393 RSC.
- S. Davidowski, A. R. Young-Gonzales, R. Richert, J. Yarger and C. A. Angell, Relation of Ionic Conductivity to Solvent Rotation Times in Dinitrile Plastic Crystal Solvents, J. Electrochem. Soc., 2020, 167, 070553 CrossRef.
- S. Lansab, T. Schwan, K. Moch and R. Böhmer, Shear rheology senses the electrical conductivity optimum in highly Li doped dinitrile electrolytes, J. Chem. Phys., 2024, 160, 084503 CrossRef CAS PubMed.
- C. J. Franko, C.-H. Yim, F. Aren, G. Avall, P. S. Whitfield, P. Johansson, Y. A. Abu-Lebdeh and G. R. Goward, Concentration Dependent Solution Structure and Transport Mechanism in High Voltage LiTFSI-Adiponitrile Electrolytes, J. Electrochem. Soc., 2020, 167, 160532 CrossRef CAS.
- B. B. Hansen, S. Spittle, B. Chen, D. Poe, Y. Zhang, J. M. Klein, A. Horton, L. Adhikari, T. Zelovich, B. W. Doherty, B. Gurkan, E. J. Maginn, A. Ragauskas, M. Dadmun, T. A. Zawodzinski, G. A. Baker, M. E. Tuckerman, R. F. Savinell and J. R. Sangoro, Deep Eutectic Solvents: A Review of Fundamentals and Applications, Chem. Rev., 2021, 121, 1232–1285 CrossRef CAS PubMed.
- Gangasharan and S. S. N. Murthy, Study of α-, β-, and γ-relaxation processes in some supercooled liquids and supercooled plastic crystals, J. Chem. Phys., 1993, 99, 9865–9873 CrossRef CAS.
- D. L. Leslie-Pelecky and N. O. Birge, Dielectric measurement of the model glass transition in orientationally disordered cyclo-octanol, Phys. Rev. B: Condens. Matter, 1994, 50, 13250–13258 CrossRef CAS.
- R. Brand, P. Lunkenheimer and A. Loidl, Relaxations and fast dynamics of the plastic crystal cyclo-octanol investigated by broadband dielectric spectroscopy, Phys. Rev. B: Condens. Matter, 1997, 10, R5713–R5716 CrossRef.
- T. Eguchi, G. Soda and H. Chihara, Molecular motion and polymorphic forms in cyclohexanol as studied by nuclear magnetic resonance, J. Magn. Reson., 1976, 23, 55–65 CAS.
- A. Dworkin, A. H. Fuchs, M. Ghelfenstein and H. Szwarc, Cristaux vitreux. I: RMN large bande, thermocourants de dépolarisation et analyse enthalpique dans quelques cycloalcools, J. Phys. Lett., 1982, 43, 21–27 CrossRef CAS.
- P. L. Kuhns and M. S. Conradi, NMR study of molecular motions in cyclohexanol, a glass-forming rotor crystal, J. Chem. Phys., 1984, 80, 5851–5858 CrossRef CAS.
- S. Stapf and R. Kimmich, Translational versus rotational molecular dynamics in plastic crystals studied by NMR relaxometry and diffusometry, Mol. Phys., 1997, 92, 1051–1060 CrossRef CAS.
- O. Yamamuro, H. Yamasaki, Y. Madokoro, I. Tsukushi and T. Matsuo, Calorimetric and neutron scattering studies of plastically crystalline cyclooctanol, J. Phys.: Condens. Matter, 2003, 15, 5439–5450 CrossRef CAS.
- E. Novak, N. Jalarvo, S. Gupta, K. Hong, S. Förster, T. Egami and M. Ohl, Dynamics in the Plastic Crystalline Phases of Cyclohexanol and Cyclooctanol Studied by Quasielastic Neutron Scattering, J. Phys. Chem. B, 2018, 122, 6296–6304 CrossRef CAS PubMed.
- H. Wagner and R. Richert, Equilibrium and non-equilibrium type β-relaxations: D-sorbitol versus o-terphenyl, J. Phys. Chem. B, 1999, 103, 4071–4077 CrossRef CAS.
- S. Lansab, P. Münzner, H. Zimmermann and R. Böhmer, Deuteron nuclear magnetic resonance and dielectric studies of molecular reorientation and charge transport in succinonitrile-glutaronitrile supercooled plastic crystals, J. Non-Cryst. Solids X, 2022, 14, 100097 CAS.
- P. Steeman and J. van Turnhout, Fine Structure in the Parameters of Dielectric and Viscoelastic Relaxations, Macromolecules, 1994, 27, 5421–5427 CrossRef CAS.
- M. Wübbenhorst and J. van Turnhout, Analysis of complex dielectric spectra. I. One dimensional derivative techniques and three-dimensional modelling, J. Non-Cryst. Solids, 2002, 305, 40–49 CrossRef.
- N. Bloembergen, E. M. Purcell and R. V. Pound, Relaxation Effects in Nuclear Magnetic Resonance Absorption, Phys. Rev., 1948, 73, 679–712 CrossRef CAS.
- R. K. Kadiyala and C. A. Angell, Separation of nucleation from crystallization kinetics by two step calorimetry experiments, Colloids Surf., 1984, 11, 341–351 CrossRef CAS.
- D. Farhat, Etude d’électrolytes à base de dinitriles aliphatiques pour des batteries Li-ion, PhD Dissertation, Université de Tours, 2017, https://www.theses.fr/2017TOUR4035/document.
- T. R. Kartha and B. S. Mallik, Molecular Dynamics and Emerging Network Graphs of Interactions in Dinitrile-Based Li-Ion Battery Electrolytes, J. Phys. Chem. B, 2021, 125, 7231–7240 CrossRef CAS PubMed.
- C. T. Moynihan, N. Balitactac, L. Boone and T. A. Litovitz, Comparison of Shear and Conductivity Relaxation Times for Concentrated Lithium Chloride Solutions, J. Chem. Phys., 1971, 55, 3013–3019 CrossRef CAS.
- J. C. Dyre, On the mechanism of glass ionic conductivity, J. Non-Cryst. Solids, 1986, 88, 271–280 CrossRef CAS.
- P. Sippel, S. Krohns, D. Reuter, P. Lunkenheimer and A. Loidl, Importance of reorientational dynamics for the charge transport in ionic liquids, Phys. Rev. E, 2018, 98, 052605 CrossRef CAS.
- I. M. Hodge, K. L. Ngai and C. T. Moynihan, Comments on the electric modulus function, J. Non-Cryst. Solids, 2005, 351, 104–115 CrossRef CAS.
- K. L. Ngai and A. K. Rizos, Parameterless explanation of the non-Arrhenius conductivity in glassy fast ionic conductors, Phys. Rev. Lett., 1996, 76, 1296–1299 CrossRef CAS PubMed.
- F. Mizuno, J.-P. Belieres, N. Kuwata, A. Pradel, M. Ribes and C. A. Angell, Highly decoupled ionic and protonic solid electrolyte systems, in relation to other relaxing systems and their energy landscapes, J. Non-Cryst. Solids, 2006, 352, 5147–5155 CrossRef CAS.
- M. Aniya and M. Ikeda, A Model for Non-Arrhenius Ionic Conductivity, Nanomaterials, 2019, 9, 911 CrossRef CAS PubMed.
- C. Bischoff, K. Schuller, S. P. Beckman and S. W. Martin, Non-Arrhenius Ionic Conductivities in Glasses due to a Distribution of Activation Energies, Phys. Rev. Lett., 2012, 109, 075901 CrossRef CAS PubMed.
- G. P. Johari and O. Andersson, On the nonlinear variation of dc conductivity with dielectric relaxation time, J. Chem. Phys., 2006, 125, 124501 CrossRef CAS PubMed.
- C. M. Roland, S. H. Bielowka, M. Paluch and R. Casalini, Supercooled dynamics of glass-forming liquids and polymers under hydrostatic pressure, Rep. Prog. Phys., 2005, 68, 1405–1478 CrossRef CAS.
- D. Reuter, P. Münzner, C. Gainaru, P. Lunkenheimer, A. Loidl and R. Böhmer, Translational and reorientational dynamics in deep eutectic solvents, J. Chem. Phys., 2021, 154, 154501 CrossRef CAS PubMed.
- A. Schulz, P. Lunkenheimer and A. Loidl, Lithium-salt-based deep eutectic solvents: Importance of glass formation and rotation-translation coupling for the ionic charge transport, J. Chem. Phys., 2021, 155, 044503 CrossRef CAS PubMed.
- A. Schulz, K. Moch, Y. Hinz, P. Lunkenheimer and R. Böhmer, Translational and reorientational dynamics in carboxylic acid-based deep eutectic solvents, J. Chem. Phys., 2024, 160, 074503 CrossRef CAS PubMed.
- H. J. V. Tyrrell and K. R. Harris, Diffusion in Liquids: a theoretical and experimental study, Butterworths, London, 1984 Search PubMed.
- I. Chang and H. Sillescu, Heterogeneity at the Glass Transition: Translational and Rotational Self-Diffusion, J. Phys. Chem. B, 1997, 101, 8794–8801 CrossRef CAS.
- F. Qi, K. U. Schug, A. Döβ, S. Dupont, R. Böhmer, H. Sillescu, H. Kolshorn and H. Zimmermann, Structural relaxation of the fragile glass-former propylene carbonate studied by nuclear magnetic resonance, J. Chem. Phys., 2000, 112, 9455–9462 CrossRef CAS.
- R. Meier, E. Schneider and E. A. Rössler, Change of translational-rotational coupling in liquids revealed by field-cycling 1H NMR, J. Chem. Phys., 2015, 142, 034503 CrossRef CAS PubMed.
- J. T. Edward, Molecular Volumes and Stokes-Einstein Equation, J. Chem. Educ., 1970, 47, 261–270 CrossRef CAS.
- M. J. Lizak, R. C. Keller, M. S. Coffey, M. S. Conradi and W. Bunnelle, Rotation and pseudorotation in solid cyclooctane, J. Phys. Chem., 1990, 94, 992–994 CrossRef CAS.
- C. A. Stortz, Conformational pathways of simple six-membered rings, J. Phys. Org. Chem., 2010, 23, 1173–1186 CrossRef CAS.
- I. Kishimoto, J. J. Pinvidic, T. Matsuo and H. Suga, Phase Transition and Glass Transitions in Isocyanocyclohexane Studied by a Polaro-Calorimeter, Proc. Jpn. Acad., Ser. B, 1991, 67, 66–71 CrossRef CAS.
- F. S. Howell, R. A. Bose, P. B. Macedo and C. T. Moynihan, Electrical Relaxation in a Glass-Forming Molten Salt, J. Phys. Chem., 1974, 78, 639–648 CrossRef CAS.
- A. Pimenov, P. Lunkenheimer, M. Nicklas, R. Böhmer, A. Loidl and C. A. Angell, Ionic transport and heat capacity of glass-forming metal-nitrate mixtures, J. Non-Cryst. Solids, 1997, 220, 83–101 CrossRef.
- B. Roling, Scaling properties of the conductivity spectra of glasses and supercooled melts, Solid State Ionics, 1998, 105, 185–193 CrossRef CAS.
- J. Habasaki, C. León and K. L. Ngai, Dynamics of Glassy, Crystalline and Liquid Ionic Conductors: Experiments, Theories, Simulations, Springer, Switzerland, 2017 Search PubMed.
- J. Beerwerth, S. P. Bierwirth, J. Adam, C. Gainaru and R. Böhmer, Local and global dynamics of the viscous ion conductors 2Ca(NO3)2–3KNO3 and 2Ca(NO3)2–3RbNO3 probed by 87Rb nuclear magnetic resonance and shear rheology, J. Chem. Phys., 2019, 150, 194503 CrossRef PubMed.
- T. Yamaguchi and S. Koda, Dielectric and shear relaxations of ionic liquid composed of symmetric ions, J. Chem. Phys., 2014, 141, 144503 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp02003d |
| This journal is © the Owner Societies 2025 |