Quantum-chemical molecular dynamics study of polaron formation in perovskite NaTaO₃ as a water-splitting photocatalyst

Abstract

The water splitting reaction mediated by photocatalysts is attracting much interest in the context of solar energy utilization. However, our understanding of the charge carrier dynamics underlying the photocatalytic water splitting reaction is still limited. Here, focusing on the perovskite-type oxide NaTaO₃, which is an archetypical heterogeneous photocatalyst for the water splitting reaction, the charge carrier dynamics were investigated by a computational approach, i.e., molecular dynamics simulations based on quantum chemical calculations. In particular, the present study sheds light on the formation process of polaron, which is a charge carrier dressed by lattice distortion in its surroundings induced to stabilize the charge carrier itself. The results suggested that the charge carriers are weakly localized and maintain the nanoscale spatial distribution of the charge density, and the change in O–Ta bond lengths is the primary factor in the polaron stabilization. In addition, the structural deformation and the resulting polaron stabilization was observed to be stronger in positive (hole) polarons than negative (electron) polarons.

---

Hydrogen production via the photocatalytic water splitting reaction is one of the potentially game-changing technologies, as it provides a way to utilize solar power as an alternative, carbon-free, energy source to fossil fuels.¹ Historically, the water splitting reaction has been investigated actively in the communities of both homogeneous² and heterogeneous catalysts.^3,4 In the heterogeneous photocatalysts, which are composed of semiconductors including metal oxides⁵ or oxinitrides,⁶ the exciton formed by light absorption is split into a pair of a hole and an electron, which populate on the valence and conduction bands, respectively. The oxidative and reductive potentials provided by the hole and the electron, respectively, serve as the driving forces for the water splitting reaction. A crucial requirement for achieving high photocatalytic activity is that the charge carriers should have lifetimes long enough to arrive at the semiconductor surface while maintaining the reactivity.⁷ Recent experimental and theoretical evidence suggest that formation of polarons may play a key role in this context.^8–13 The word polarons refers to charge carriers in solid materials dressed by lattice distortion induced by the charge carriers themselves.¹⁴ However, detailed structural, electronic, and dynamic characteristics of polarons in photocatalysts are scarcely understood, especially in terms of their formation process. A major difficulty for understanding the polaron formation process is that it necessitates access to atomistic yet ultrafast-time-resolved information, while it is formidably challenging to realize such an observation experimentally.

Here, a computational approach was employed to track the ultrafast process of polaron formation in the perovskite-type oxide NaTaO₃, an archetypical compound that serves as a homogeneous catalyst for the water splitting reaction.¹⁵ While NaTaO₃ is studied frequently in the presence of dopants in photocatalytic applications,^16,17 the present study focuses on the fundamental character of pristine NaTaO₃. The calculations were conducted based on the combined method of quantum chemical calculations and molecular dynamics simulations, which enables us to develop the real-time simulations of atomic dynamics and the associated change in electronic structures simultaneously.

The structural model for the present simulations was constructed as follows. Using the geometry-optimized cubic unit cell of NaTaO₃ (Pm3̄m) as the starting point, an orthorhombic unit cell was constructed by rotating the unit cell by 45° around an (a or b or c) axis and repeating the cell twice along that axis. The structural model for the formation of polarons was constructed by further repeating the cell by four times for each axis, resulting in the model containing 256 units of NaTaO₃ (Fig. 1).

Fig. 1 Structural model of NaTaO₃ for simulating polaron formation (after thermalization). The yellow and red spheres represent Na and O ions, respectively. A sphere located at the center of each octahedron represents a Ta ion. VESTA program¹⁸ was used for visualization.

All the calculations, unless otherwise noted, were conducted with the self-consistent-charge density-functional tight binding (simply denoted as DFTB in the rest of the present paper) method,¹⁹ which is an approximate analog of density-functional theory (DFT) based on the tight-binding model with the introduction of empirical parameters to replace the computationally costly part of the standard DFT calculations. Since the accuracy of the DFTB results depend on the employed parameters, these were optimized using the ADPT program²⁰ to reproduce the DFT (GGA-PBE²¹) level electronic structure and structural dynamics calculated using the VASP program package.^22,23 Further details of the parameter optimization and the benchmark results are presented in ESI.† While the DFTB offers an orders-of-magnitude acceleration compared to the standard DFT calculations, the computational cost is still a bottleneck when treating the systems including thousands of atoms, because in principle the computational cost for the DFTB increases proportionally to the cube of the number of atoms. To treat the nanoscale model system within a reasonable computational time, an acceleration technique called divide-and-conquer (DC)²⁴ was employed in combination with the DFTB. In the DC approach, the system is spatially divided into a set of small subsystems, and the quantum chemical calculation is performed for each subsystem with the inclusion of the neighbouring subsystems (“buffer region”) to mitigate the error originating from the spatial fragmentation. The subsystem electronic structures are summed up to reproduce the electronic structure of the entire system. In the present study, each orthorhombic unit cell was assigned as a subsystem, and the radius of the buffer region was set to 8 Å. The DC-DFTB calculations were performed under the periodic boundary condition using the DCDFTBMD program package.^25,26

To simulate the polaron formation process, the Born–Oppenheimer molecular dynamics (BOMD) calculations were performed at the DC-DFTB level. In BOMD simulations, the atomic dynamics is propagated by integrating Newton's equation of motion step-by-step with a sufficiently small time interval Δt, where the force acting on atoms is obtained according to the electronic structure based on the DFTB calculations at each time step.²⁷ Importantly, the BOMD simulations can capture the change in electronic structure, e.g., the fluctuation of electron density, and the dependence of atomic dynamics on that, both of which are key physics of polaron formation. In fact, the DC-DFTB-based BOMD simulation has been employed to study the polaron formation process in other solid-state systems and successfully provided detailed information on atomistic dynamics and electronic structure involved in the polaron formation.²⁸ The present study follows the approach established in ref. 28 with necessary adjustment for NaTaO₃. The simulations were conducted in the protocol as indicated below. First, to thermalize the system, the BOMD simulations were performed for 5 ps with rescaling the atomic velocity every 400 fs to set the temperature to 298.15 K. From the last 4 ps of the obtained trajectory, 81 snapshots were extracted every 50 fs. Using the each snapshot as the initial geometry and velocity, 81 runs of BOMD simulations were performed to simulate the formation of the hole polaron, and another 81 runs were performed for the electron polaron as well. The simulations of polaron formation were conducted by restarting the BOMD under the NVE ensemble starting from each snapshot with the total number of electrons in the system modified such that the total charge is +1 for hole polarons and −1 for electron polarons. For the simulations of polaron formation, the DC-DFTB calculations were performed in the spin-polarized manner.²⁹ All the BOMD simulations were conducted with fixed lattice parameters. The time interval Δt was set to be 1 femtosecond.

Fig. 2 presents the spatial distributions of charge carrier densities for holes (yellow) and electrons (blue) at t = 0 and 500 fs in the simulations of polaron formation. As the charge carriers are represented by removal of an unpaired electron from, or, addition of it to, the neutral and spin-unpolarized NaTaO₃ system, the charge carrier densities are represented by the total spin densities of the system. As shown in Fig. 2, the charge carriers are weakly localized; they have spatially inhomogeneous distributions, but are not completely localized to specific atoms or unit cells. Notably, Fig. 2 suggests that the nanoscale model structure employed here (Fig. 1) played a crucial role in observing the weak localization, because such long-range inhomogeneity in charge density cannot be properly described within smaller unit cells. The weakly localized distributions are attributed to the disorder in the structure arising from thermal fluctuations. Fig. 2 also indicates that the electrons delocalized more than the holes, being consistent with the fact that CBM of NaTaO₃ has the larger band curvature than the VBM,³⁰ making the effective mass of electrons less than that of holes. Note that the delocality of an electron observed here should be considered as an upper limit, because the DFTB tends to systematically overestimate the delocalization of electrons,³¹ due to the approximation in its theoretical backbone; the DFTB is grounded on the generalized gradient approximation, which is known to systematically overestimate the delocalization of polaron charge density because of the self-interaction error.^9,32–34

Fig. 2 Hole (yellow) and electron (blue) densities at t = 0 and 500 fs from representative trajectories of the simulations of polaron formation.

The polaron formation induces spatial localization of charge carrier densities. The degrees of locality, i.e., radii of the hole and electron, were quantified by following the previously proposed approach by one of the authors.²⁸ In this approach, the number of atoms over which the charge density is delocalized, d, is evaluated as where s_A is the number of unpaired electrons populated on atom A evaluated with Mulliken population analysis. The index A runs over all atoms in the simulation cell, and s_A is normalized as . The number of atoms d can be translated into the total effective volume of the charge carrier density, V, as V = V_celld/n where V_cell is the volume corresponding to a single formula of NaTaO₃, i.e., 1/256 of the total volume of the simulation cell employed. For the cases of holes and electrons, n = 1 and 3, respectively, where n = 1 and 3 denotes the number of Ta and O atoms within a unit cell, respectively. The meaning of the definition of V can be interpreted as follows. Because of the characters of valence band maximum (VBM) and the conduction band minimum (CBM) of NaTaO₃, holes and electrons in NaTaO₃ are predominantly populated on O and Ta, respectively. Hence, d/n corresponds to “the number of unit cells” over which the charge carrier delocalizes, and the total “volume” of the charge carrier is obtained by multiplying it by the volume of the unit cell. Finally, the volume V can be translated into the effective radii r by treating the charge carriers as spheres, i.e., r = (3V/4π)^1/3. Fig. 3 presents the timetraces of the charge carrier radii, indicating that the radii have significant fluctuations associated with the structural dynamics. The mean radii can be estimated as 0.49 and 1.14 nm for holes and electrons, respectively, quantitatively supporting the observation that the electron is more strongly delocalized than the hole.

Fig. 3 Timetraces of hole (red) and electron (blue) radii. Dashed lines indicate the mean values.

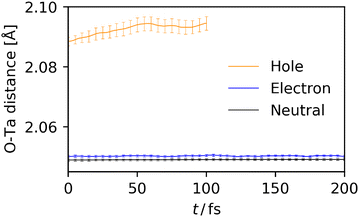
In general, polaron formation is characterized by structural deformation induced by the charge carrier in its surroundings. Here, from the BOMD trajectories, the structural deformation was characterized by approach reported in ref. 28. Because the VBM and CBM of the present system are primarily located on the framework composed of B and C sites, i.e., Ta and O, we focused on the change in O–Ta bond lengths. In this approach, the bond length around the charge carrier r^pol, which is considered to be involved in the polaron formation, is evaluated as the weighted-averaged bond length by the spin population of each atom. For instance, in the case of holes, where the charge carrier is considered populated on O atoms, where r^A_O–Ta denotes the bond length between the atom A, which is here assumed to be O atom, and the nearest-neighbor Ta atom. In the case of electrons, the same procedure as above was applied with swapping O and Ta. To clarify the effect of charge carriers on the structural deformation, “control experiments,” i.e., the BOMD simulations for a charge neutral system starting from the same initial geometry and velocity as the simulations of polaron formation, were also conducted. Fig. 4 shows the timetrace of O–Ta distance (r^pol_O–Ta) around holes (orange) and electrons (blue), and for comparison, the averaged O–Ta distance calculated for the charge-neutral BOMD simulations (black). Each result was averaged over the set of 81 trajectories starting from different initial geometries and velocities, and the error bars indicate 95% confidence interval of the averaged value. As indicated in Fig. 4, in the case of holes, the charge-weighted average was significantly longer than the neutral average at t = 0, and the charge-weighted average further increased for t > 0, finally arriving at a plateau at t = 50 fs. This behavior implies that the hole polaron forms by the following steps: the generated charge carrier is first localized to the region where the Ta–O bonds are long because of the thermal fluctuation, and then, relaxation of the localized charge carrier further increases the bond length. On the other hand, the O–Ta distance around electrons (blue) is only slightly longer than the charge-neutral result. Furthermore, the O–Ta distance around electrons did not increase with time, suggesting that in the present simulations the localization of electrons is dominated by thermal fluctuation and the additional structural deformation induced by the electron is insignificant compared to the thermal fluctuation. One of the reasons for this difference may be the different degree of spatial locality of holes and electrons, i.e., electrons are tend to be delocalized compared to holes (Fig. 3), weakening the local change in O–Ta bond lengths induced by electrons.

Fig. 4 Timetraces of O–Ta distance around holes (orange) and electrons (blue), averaged over 81 BOMD trajectories. The averaged O–Ta distance at the charge-neutral state (black) is also shown. Error bars indicate 95% confidence intervals.

Note that in the previous study of polarons in a lead iodide perovskite (CH₃NH₃PbI₃),²⁸ the structural deformation induced by polaron relaxation was observed for both holes and electrons, while the reported radius of electrons (1.1 nm) was close to that in NaTaO₃ (1.14 nm) estimated in the present study. The difference in the structural dynamics of electron polarons between CH₃NH₃PbI₃ and NaTaO₃ may be attributed to the difference in the nature of Pb–I and Ta–O bonds. Pb–I bonds in CH₃NH₃PbI₃ have a partially covalent nature and the CBM of CH₃NH₃PbI₃ is composed of antibonding orbitals between Pb and I,³⁵ suggesting that the change in the Pb–I bond length strongly influences the spatial distribution and energy levels of the CBM orbital. On the other hand, Ta–O bonds in NaTaO₃ are considered predominantly ionic, suggesting that such effects of structural deformation are weaker than in the case of CH₃NH₃PbI₃.

The polaron formation is a relaxation process that induces the stabilization of a charge carrier owing to the structural deformation in its surrounding area. Fig. 5 indicates the timetraces of hole and electron energies. The hole energy (E^h) and the electron energy (E^e) are defined as the differences in electronic energy E of charged and neutral states at the same geometry R, i.e., E^h/e(R) = E(R, N ± 1) − E(R, N) where N is the total number of electrons in the system at the charge-neutral state. As shown in Fig. 5a, holes underwent a rapid and significant stabilization, where the hole energy reached a plateau after t = 50 fs. This is a qualitatively similar behavior to the timetrace of O–Ta distance around holes (Fig. 4), where the structural deformation was completed at t = 50 fs, suggesting that the relaxation of hole polarons is dominated by the elongation of Ta–O bond lengths. The hole polaron stabilization can be quantified to be ∼70 meV as the difference between the hole energy at t = 0 and that after t = 50 fs. On the other hand, the electron polaron energy (Fig. 5b) did not show a significant change with time, suggesting that the stabilization of electron polarons is not substantial. This result is consistent with the fact that the structural deformation associated with electron polaron formation was insignificant (Fig. 4).

Fig. 5 Timetraces of hole (a) and electron (b) energies averaged over 81 BOMD trajectories. Error bars indicate 95% confidence intervals.

The previous time-resolved (TR) infrared (IR) spectroscopy by Yamakata and co-workers³⁶ suggests that the excited electrons in NaTaO₃ have IR absorption ranging from 4000 to 1200 cm⁻¹. They assigned the absorption to the excited electrons trapped in mid-gap states beneath the conduction bands, which are shallow enough to allow thermal excitation of trapped electrons to the conduction bands. Within the timescale of their measurements, trapping to the mid-gap states are suggested to occur instantaneously. They also found that the hole-originated absorption is absent, suggesting that the holes are also trapped to deep mid-gap states where thermal excitation of holes to valence bands is essentially not possible. Notably, Onishi and co-workers suggested the possibility that these mid-gap states originate from polaron self-trapping.³⁷ While the underestimation of polaron binding energy is inevitable due to the methodological limitations of the DFTB, our results (Fig. 5) suggests that the hole polaron is more strongly self-trapped (i.e., having the higher polaron stabilization energy) than the electron polaron, which is qualitatively consistent with the above-mentioned experimental observation. Note that the polaron binding energies in NaTaO₃ have been also calculated at the level of DFT with the hybrid exchange–correlation functional,⁹ providing binding energy values that are comparable to experimentally observed IR absorption energies. In addition, our simulation results suggested the polaron formation completes within 10² fs, which is consistent with the “instantaneous” formation of trapped electrons in the timescale of the TR–IR measurements, given that they originate from polaron self trapping.

In summary, quantum-chemistry-based MD simulations were employed to characterize the polaron formation process in perovskite-type oxide NaTaO₃ from the viewpoints of charge density distribution, structural deformation, and energetics. In terms of charge density distribution, it was found that the charge carriers show weak localization to nanoscale spatial regions, which is attributed to the structural disorder induced by thermal fluctuation. The result also suggested that the localization of electrons is weaker than that of holes. The structural deformation was analyzed focusing on the change in O–Ta bond lengths associated with polaron formation. In the case of holes, the O–Ta bond lengths tended to be longer than average even at t = 0, and increased for t > 0, suggesting a two-step process of hole polaron formation; the hole is first localized to the region where the O–Ta bond lengths are incidentally long due to thermal fluctuations, and the localized hole further elongates the O–Ta bonds in its relaxation process. On the other hand, the O–Ta bond lengths around electrons were only slightly longer than average, and did not increase with time, suggesting that the electron polaron character is dominated by thermal structural fluctuations, and the additional structural deformation induced by polaron relaxation is insignificant. The difference in the structural dynamics of the electron polaron in NaTaO₃ and in lead iodide perovskite (CH₃NH₃PbI₃)²⁸ implies that the nature of bonding between B-site and C-site ions critically influences the polaron dynamics. Finally, the observed polaron energetics were consistent with those expected from the above-mentioned discussion on the charge density distribution and the structural deformation. Holes underwent a relaxation of ∼70 meV, with a time trace approximately synchronized with that of the O–Ta bond length around holes. In contrast, the relaxation of electrons was insignificant, reflecting the fact that no substantial structural deformation was observed associated with the electron polaron relaxation process; however some attention should be paid to the overestimation of electron delocalization originating from the theoretical limitations of the DFTB technique.

This study was supported by JSPS KAKENHI Grant No. 22H00344 and 25H00902. H. U. is also grateful to JST PRESTO Grant No. JPMJPR23Q2 and JSPS KAKENHI Grant No. 21H05407 and 23H03976.

Conflicts of interest

There are no conflicts to declare.

Data availability

The data supporting the findings of this study are presented in the main text and ESI.†

Notes and references

1. W. Lubitz and W. Tumas, Chem. Rev., 2007, 107, 3900–3903.
2. S. Fukuzumi and D. Hong, Eur. J. Inorg. Chem., 2013, 645–659.
3. K. Maeda and K. Domen, J. Phys. Chem. Lett., 2010, 1, 2655–2661.
4. Z. Wang, C. Li and K. Domen, Chem. Soc. Rev., 2019, 48, 2109–2125.
5. H. Kato, K. Asakura and A. Kudo, J. Am. Chem. Soc., 2003, 125, 3082–3089.
6. K. Maeda, K. Teramura, D. Lu, T. Takata, N. Saito, Y. Inoue and K. Domen, Nature, 2006, 440, 295.
7. P. Zhang, T. Wang, X. Chang and J. Gong, Acc. Chem. Res., 2016, 49, 911–921.
8. Z. Fu, T. Hirai and H. Onishi, J. Phys. Chem. C, 2021, 125, 26398–26405.
9. H. Ouhbi and J. Wiktor, Phys. Rev. B: Condens. Matter Mater. Phys., 2021, 104, 235158.
10. X. Chi, L. Mandal, C. Liu, A. D. Fauzi, A. Chaudhuri, T. J. Whitcher, H. K. Jani, Z. Chen, S. Xi, C. Diao, M. A. Naradipa, X. Yu, P. Yang, A. H. Castro-Neto, M. B. H. Breese, K. P. Loh, T. V. Venkatesan and A. Rusydi, NPG Asia Mater., 2022, 14, 19.
11. A. J. Tanner and G. Thornton, J. Phys. Chem. Lett., 2022, 13, 559–566.
12. C. Cheng, Z. Zhou and R. Long, J. Phys. Chem. Lett., 2023, 14, 10988–10998.
13. Y. Xu, Z. Wang and Y. Weng, J. Phys. Chem. C, 2024, 128, 16275–16290.
14. G. D. Mahan, Many-Particle Physics, Plenum Press, New York, 1990.
15. H. Onishi, ChemSusChem, 2019, 12, 1825–1834.
16. S. Li, H. Qiu, C. Wang, Y. Sun, X. Du and J. Zhao, Sol. Energy Mater. Sol. Cells, 2016, 149, 97–102.
17. Z.-K. Tang, C. Di Valentin, X. Zhao, L.-M. Liu and A. Selloni, ACS Catal., 2019, 9, 10528–10535.
18. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.
19. M. Elstner, D. Porezag, G. Jungnickel, J. Elsner, M. Haugk, T. Frauenheim, S. Suhai and G. Seifert, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 7260–7268.
20. C.-P. Chou, Y. Nishimura, C.-C. Fan, G. Mazur, S. Irle and H. A. Witek, J. Chem. Theory Comput., 2016, 12, 53–64.
21. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
22. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269.
23. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
24. H. Nakai, M. Kobayashi, T. Yoshikawa, J. Seino, Y. Ikabata and Y. Nishimura, J. Phys. Chem. A, 2023, 127, 589–618.
25. Y. Nishimura and H. Nakai, J. Comput. Chem., 2019, 40, 1538–1549.
26. Y. Nishimura and H. Nakai, J. Comput. Chem., 2020, 41, 1759–1772.
27. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
28. H. Uratani, C.-P. Chou and H. Nakai, Phys. Chem. Chem. Phys., 2020, 22, 97–106.
29. C. Köhler, G. Seifert, U. Gerstmann, M. Elstner, H. Overhof and T. Frauenheim, Phys. Chem. Chem. Phys., 2001, 3, 5109–5114.
30. G. A. S. Alves, H. A. Centurion, J. R. Sambrano, M. M. Ferrer and R. V. Gonçalves, ACS Appl. Energy Mater., 2021, 4, 671–679.
31. A. Heck, J. J. Kranz, T. Kubař and M. Elstner, J. Chem. Theory Comput., 2015, 11, 5068–5082.
32. P. Deák, B. Aradi and T. Frauenheim, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 155207.
33. S. Falletta and A. Pasquarello, Phys. Rev. B: Condens. Matter Mater. Phys., 2022, 106, 125119.
34. E. Ghorbani, L. Villa, P. Erhart, A. Klein and K. Albe, Phys. Rev. Mater., 2022, 6, 074410.
35. M. G. Goesten and R. Hoffmann, J. Am. Chem. Soc., 2018, 140, 12996–13010.
36. A. Yamakata, T.-a Ishibashi, H. Kato, A. Kudo and H. Onishi, J. Phys. Chem. B, 2003, 107, 14383–14387.
37. R. Konno, S. Maruyama, T. Kosaka, R. Katoh, R. Takahashi, H. Kumigashira, N. Ichikuni, H. Onishi and Y. Matsumoto, Chem. Mater., 2021, 33, 226–233.

---

Footnote

† Electronic supplementary information (ESI) available: Detailed procedure and testing results of the DFTB parameter optimization. See DOI: https://doi.org/10.1039/d5cp01859e

---