Polytype family representations of octahedrally coordinated adaptive structures in Ta₂O₅: energetic and dynamic stability from first principles

Abstract

This study broadens the understanding of the crystalline structures of Ta₂O₅, renowned for its inherent adaptive characteristics, by a unified and systematic approach to reconstruct crystalline structures as polytypes. This approach is applied to the layered adaptive structure and the Wadsley–Roth crystallographic shear (CS) adaptive structure, which were conventionally considered separately. The λ phase and the γ phase are investigated as representative phases of each type of adaptive structure, respectively, and the newly proposed Pmma phase is also examined. Using glide or screw symmetry operations, the individual phase is decomposed into smaller structural units, enabling the construction of an infinite number of polytypic variants. These variants are categorized into distinct polytype families and integrated into a single schematic encompassing both layered and CS adaptive structures. First principles calculations reveal that energy differences between the polytypic variants are generally smaller than the thermal energy at ambient temperature, suggesting that various stacking sequences can appear experimentally. Dynamically, on the other hand, polytypic variants with regular and frequent alternations of the structural units are favorable. These theoretical predictions are supported by previous experimental observations of the orthorhombic low-temperature phase (L-Ta₂O₅) with various periodicities. The high-symmetry λ and γ phases are corroborated as benchmark phases within their respective polytype families.

---

Introduction

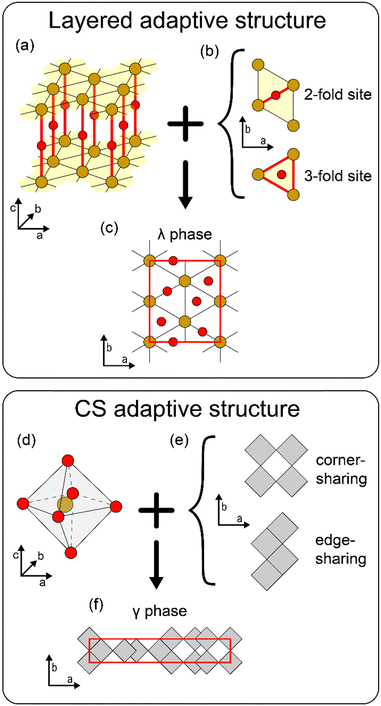
Identifying the crystalline phases of tantalum oxide has been under long-lasting debate.¹ The Ta–O system exists as a single stable stoichiometry of Ta₂O₅, and the phase transition from the orthorhombic low-temperature phase (L-Ta₂O₅) to the tetragonal high-temperature phase (H-Ta₂O₅) occurs at 1550 K.² Both L-Ta₂O₅ and H-Ta₂O₅ have their own structural varieties in ionic configurations, leaving their detailed ionic configurations ambiguous. The crystal characteristic that one composition can have multiple related structures is defined as an ‘adaptive structure’,³ and Ta₂O₅ is one of the representative systems that shows this structural adaptivity.

Fig. 1 shows the two types of adaptive structures of Ta₂O₅ currently recognized, which have their own invariant and variant characteristics. Fig. 1(a)–(c) depict a layered adaptive structure. Fig. 1(a) shows the invariant characteristic, which consists of each layer (yellow shade) of a triangular lattice of Ta ions (brown circles) and interlayer O ions (red circles) vertically connecting them. These form the Ta–O chains along the layer-normal c-direction, resulting in the Ta₂O₂ stoichiometry. Experimentally, transmission electron microscopy (TEM) or X-ray diffraction (XRD) analysis indicates the existence of the layers with a triangular lattice of Ta ions in the L-Ta₂O₅ phase.^4–10 Fig. 1(b) shows a variant characteristic where the O ions can possess either 2-fold or 3-fold coordinated intralayer sites within the Ta lattice. By partially filling the available sites for the layer to have Ta₂O₃ stoichiometry, the overall stoichiometry of Ta₂O₅ can be achieved. The occupation configuration of O ions is not uniquely determined, distinguishing each phase within the layered adaptive structure. Due to the difficulty of its direct observation even with the high-resolution TEM, the exact occupation configuration of the intralayer O ions has not been elucidated, and many theoretical phases have been proposed. The current representative phase within the layered adaptive structure is the orthorhombic λ phase,¹¹ presented in Fig. 1(c), which is calculated to be energetically sufficiently stable and have a small unit cell (red rectangular box) with high symmetry. However, observations so far have not been able to distinguish this specific configuration of the λ phase.

Fig. 1 Two types of adaptive structures of crystalline Ta₂O₅ composed of invariant and variant characteristics. Brown and red circles correspond to Ta and O ions, respectively. The red solid box represents the conventional unit cell throughout this paper. (a)–(c) Layered adaptive structure. (a) The triangular lattice of Ta–O chains is invariant, and (b) the occupation configuration of intralayer O ions is variant. The Ta layers are shaded in yellow in (a) and (b). This context is used to explain the (c) λ phase. (d)–(f) CS adaptive structure. (d) The local environment of the TaO₆ octahedron is invariant, and (e) the sharing arrangement, either corner- or edge-sharing, is variant. TaO₆ octahedra at the top view are represented as gray squares. This context is used to explain the (f) γ phase.

Fig. 1(d)–(f) shows another type of adaptive structure, the Wadsley–Roth crystallographic shear (CS) structure.^12–14 Fig. 1(d) presents TaO₆ octahedra with a Ta ion at the center and O ions at the vertices, constituting an invariant characteristic. Fig. 1(e) shows that the variant characteristic of this adaptive structure is related to the interconnection between the octahedra, either corner- or edge-sharing. The octahedra are represented as gray squares in the top view without explicitly showing the position of the ions. If a pair of octahedra shares a corner, the connection involves a 2-fold coordinated O ion, whereas if a pair shares an edge, the connection consists of two 3-fold coordinated O ions. The cubic TaO₃ is formed if all the octahedra share corners, while TaO₂ (e.g., anatase or rutile structure) emerges if all octahedra share edges. Starting from the cubic TaO₃, the stoichiometry can be tuned between TaO₃ and TaO₂ by gradually increasing the portion of the edge-sharing octahedra. Nb₂O_5−x also adopts the CS structure characteristics to tune the stoichiometry.^12–15 This adjustment involves the shearing operation along a shear plane, which is the origin of the term ‘CS’. The concept of shearing can also be applied to the Magneli (M_nO_2n−1) phases, whose base structure is rutile MO₂.¹⁶ In the Ta₂O₅ context, the CS adaptive structure usually explains the H-Ta₂O₅ phases,¹⁷ which are less studied than L-Ta₂O₅. The representative phase within the CS adaptive structure is the tetragonal γ phase,¹⁸ presented in Fig. 1(f), where the red rectangular box represents the conventional unit cell. The overlapped squares indicate the edge-sharing pair of octahedra stacked along the c-direction. Currently, the γ phase is the most computationally stable among the proposed phases of Ta₂O₅; however, this phase also has not yet been experimentally validated.

The number of possible structures within these two types of adaptive structures is infinite, making the theoretical and experimental understanding of the Ta₂O₅ structure challenging. It requires extensive theoretical costs to find the candidate structures that can be observed experimentally. This problem may have limited the studies on crystalline Ta₂O₅ within each distinct phase without considering the adaptivity in depth. A reasonable starting point for understanding the adaptive structure could be constructing the structural variants of the well-established stable phases based on their configuration. Lee et al., who first modeled the λ phase, provided several examples of the structural variants of the λ phase.¹¹ These consist of the same ‘structural motif’ as the λ phase to have similar configurations to the λ phase, and the calculated energies of these variants were also claimed to be similar within ±0.1 eV f.u.⁻¹ difference to the λ phase.¹¹ This theoretical suggestion on the structural variants motivates further studies on the variants of other phases. Nevertheless, systematic explanations of how to construct these variants are still lacking.

Therefore, this study suggests a unified and systematic procedure to construct the structural variants of several stable phases of Ta₂O₅ using the polytype concept and investigates their structural and energetic properties. A ‘polytype’ is defined as a structure consisting of stacks of (almost) identical unit layers, and the structure of polytypes depends only on the stacking sequence.¹⁹ The ‘structural motif’ of the structural variants of the λ phase¹¹ aforementioned corresponds to the unit layer of a polytype. Keeping the structure of the unit layer invariant, the stacking sequence of these unit layers is the only variable that can generate the structural variants from the original structure. These structural variants are named ‘polytypic variants’ in this study. By designing the polytypes from the structure of stable phases, the search field on the feasible low-energy structures can be effectively narrowed down while maintaining the infinite nature of the adaptive structure. The fundamental properties that enable the reconstruction of a structure as a polytype are the symmetry operations of the original phase. After reconstructing the various phases of Ta₂O₅ into the polytypes, the polytypic variants can be grouped into distinct ‘polytype families’ that enable the systematic analysis of the structures.

Calculation method

The density functional theory (DFT) calculations were performed using the Vienna ab initio simulation package (VASP).^20,21 The PBE exchange–correlation functional was used²² under the projected augmented wave (PAW) potential.^23,24 The Monkhorst–Pack k-point meshes with the spacing of 0.03 × 2π Å⁻¹ were sampled, which were generated by the vaspkit package.²⁵ The energy cutoff was set to 500 eV for the plane-wave basis set, and the self-consistency was met when the energy differences were below 10⁻⁶ eV. Gaussian smearing was applied with the smearing width of 0.01 eV. For the ionic relaxation, the cells were relaxed until the Hellmann–Feynman forces were below 0.02 eV Å⁻¹.

The two-step optimization procedure was employed to obtain the polytypic structures, ensuring the highest possible symmetry for a given stacking sequence. For example, a polytypic variant may prefer to be monoclinic, although the initial structure possesses higher symmetry, such as orthorhombic. In the first step, the initial structure is freely relaxed without imposing symmetry constraints. The initial structure is generated from the relaxed positions of selected stable phases of Ta₂O₅, as detailed in Section A of Results and discussion. The second step involves re-symmetrizing the relaxed structure, which might have minor ionic displacements away from symmetry positions. During this process, ions are repositioned with a loose tolerance value of 0.1 Å to align with higher symmetry. This is followed by a brief re-relaxation for fine adjustments, typically requiring only a few steps that do not change the space group symmetry. Most structural relaxation and energy minimization occur in the first step, while the second step fine-tunes the structure. Finally, the dynamic stability of the optimized structures was investigated via the finite displacement method in phonon calculations using phonopy^26,27 and vaspkit²⁵ packages.

Results and discussion

A. Polytypic variants of adaptive Ta₂O₅ structures

This section introduces a procedure to construct polytypic variants from the stable phases of adaptive Ta₂O₅ structures. This approach introduces constraints within the adaptive structure by defining the smaller unit layer of the structure which remains invariant. However, the stacking sequence can still vary, preserving the structural adaptivity. Although the procedure can be applied to any suitable structure, phases consisting solely of TaO₆ octahedra were selected for simplicity. This octahedral local ionic environment is known to be the preferred configuration in Ta₂O₅.²⁸ By applying this procedure, selected phases of Ta₂O₅ and their polytypic variants are integrated into a single schematic encompassing both layered and CS adaptive structures, which were conventionally considered separately. The procedure is first applied to the λ phase step-by-step as an example and then generalized into other Ta₂O₅ phases. It is worth noting that this procedure is related to the order–disorder (OD) theory^29–34 in the perspective of utilizing the partial symmetries, and details on similarities and differences with this study are summarized in Note S1 (ESI†).

For a structure to be a polytype, it should contain layers with identical structures repeating translationally, while the relationship between the adjacent layers can vary. Fig. 2(a) shows that the unit cell of the λ phase is orthorhombic (enclosed with a red solid box) and consists of two formula units (Ta₄O₁₀). Although it is a layered adaptive structure where the layers (yellow shade) repeat along the c-direction, the occupation configuration of the intralayer O ions is set to be invariant throughout the layers. Instead, the configuration itself can be decomposed into repeating structural units stacked along the b-direction (green shade). The unit cell is halved into one formula unit (Ta₂O₅), which cannot be further divided. From now on, the term ‘structural unit’ will be used to describe the unit layer of the polytypic variant to prevent confusion with the ‘layer’ (for example, the yellow shade) of the layered adaptive structure.

Fig. 2 λ_b polytype family. (a) Comparison between the conventional understanding of the layered adaptive structure (left) and the polytypic interpretation of the occupation configuration (right). (b) Ionic positions in a perfect triangular lattice and symmetry elements overlaid. Cyan and magenta circles correspond to the intralayer O ions with 2-fold and 3-fold coordination, respectively. (c) b-Glide symmetry operation. (d) λ phase having alternating (LR) stacking and two types of rhombi constituting the λ phase. (e) Cmmm phase having parallel (LL) stacking.

The key property that can provide the information for understanding how to divide a unit cell is the symmetry operations including translation. The space group of the λ phase is Pbam (No. 55), and all the symmetry elements of this space group are imposed on the ionic positions in Fig. 2(b). Along the b-direction, there exists b-glide symmetry (dotted vertical line), which is the combination of a halfway translation along the b-direction and a mirror operation by the bc-plane, described in Fig. 2(c) using the red markers. The halfway translation indicates the repetition of the halved unit cell (each rectangular box of Fig. 2(c)), while the mirror operation is the symmetry relationship between the halved unit cells. These halved cells correspond to the structural units of a polytype. Fig. 2(d) explicitly shows the constituent ions of each structural unit forming the λ phase. The structural units are represented by triangles with Ta ions at the vertices to make the schematic diagram comprehensive. The intralayer O ions are color-coded based on the coordination with Ta ions (cyan for 2-fold coordination and magenta for 3-fold coordination). The thick green solid lines distinguish each structural unit in a zigzag shape. Each structural unit consists of one pair of rhombi shown in the lower box, where one contains two 3-fold O ions and the other contains one 2-fold O ion at the center. The rhombi represent TaO₃ and TaO₂ stoichiometries, respectively, including the interlayer oxygens not shown. Placing these rhombi in equal amounts results in an overall stoichiometry of Ta₂O₅.

The structural units are denoted by L (light shade) and R (dark shade), respectively, following the mirror relationship as a handedness of left and right. As a result, the λ phase has the alternating stacking sequence of ‘LR’ along the b-direction. In contrast, the theoretical LL stacking in Fig. 2(e) does not mirror the L unit during stacking. Since this parallel stacking preserves the invariant characteristics of the layered adaptive structure, any stacking sequence consisting of L and R constructs feasible structures. This procedure constructs a ‘polytype family,’ a group of polytypes whose structural units are identical and have the same set of possible stacking relationships between adjacent units, related to the original stable phase (λ phase in this example). The polytype family described above is denoted by λ_b, indicating the name of the original phase (λ) and the symmetry operation (b) that divides the original phase. Each polytypic variant within a polytype family is distinguished by its stacking sequence. For example, the original λ phase is named λ_b-LR polytype in the context of the λ_b polytype family.

The approach described above can be generalized and adapted to construct other polytype families of Ta₂O₅. Fig. 3 depicts the overview of the polytype families defined and analyzed in this study. The first step to construct a polytype family is to select an energetically feasible phase with high symmetry. It is referred to as the ‘primary phase’ in this study. The selected primary phases are λ, γ, and Pmma phases illustrated in Fig. 3(a). The λ and γ phases are the representative phases of layered and CS adaptive structures, respectively, whose structures were taken from previous studies.^11,18 The Pmma phase, on the other hand, is newly proposed in this study and is named after its space group. The structural and energetic characteristics of these primary phases are listed in Table 1. Note that the ionic positions depicted in Fig. 3 are described within the context of both layered and CS adaptive structures, and the ionic configurations of each pair are identical. Under the particular condition present in the Ta₂O₅ system, these structures can be interpreted through either type of adaptive structure by allowing some leniency to the conventional schematic. For example, the λ phase consists of TaO₆ octahedra, similar to the CS adaptive structure. However, it has specific corner-edge-sharing arrangements, which results in the octahedra being slanted relative to each other. In the γ phase, on the other hand, the layer-normal direction (direction of the corner-sharing Ta–O chain) of all Ta ions can be defined as in the layered adaptive structure, but this direction alternates. The details are provided in Fig. S1 (ESI†).

Fig. 3 Overall schematics of the polytype family representation of octahedrally coordinated adaptive structures. (a) Selected primary phases and their space groups. Ionic positions are depicted within the context of both layered and CS adaptive structures. (b) Relationship between the selected polytype families. (c) Common parallel phase having either P2/m or Cmmm symmetry.

Table 1 Crystallographic data and energetics of the three primary phases and two parallel phases. The space group (short symbol) in the second row follows the conventional standard notation. However, the full symbols in the third row and lattice parameters are adjusted to match the structures in Fig. 3. The angle between a and b axes of the P2/m phase is calculated to be 84.35°, but this can vary around 90° depending on the criteria or procedure of the calculation. Some of the energies of previous studies are not available (N/A)

	λ phase	Pmma phase	γ phase	Cmmm phase	P2/m phase
Space group [number]	Pbam [55]	Pmma [51]	I41/amd [141]	Cmmm [65]	P2/m [10]
Full symbol	P21/b21/a2/m	P21/m2/a2/m	I41/b2/m2/d	C2/m2/m2/m	P112/m
Crystal system	Orthorhombic	Orthorhombic	Tetragonal	Orthorhombic	Monoclinic
a [Å]	6.258	6.180	26.272	13.143	13.139
b [Å]	7.411	8.261	3.883	3.871	3.851
c [Å]	3.826	3.842		3.890	3.876
Number of F. U. per unit cell	2	2	4	2	2
Density [g cm^−3]	8.271	7.482	7.410	7.415	7.518
Volume [Å^3 f.u.^−1]	88.72	98.07	99.03	98.96	97.60
Energy [eV per atom] (this work)	+0.038	+0.033	0	+0.012	+0.036
Energy [eV per atom]^18	+0.03	N/A	0	+0.01	N/A
Energy [eV per atom]^35	+0.035	N/A	0	+0.013	N/A

---

The second step to construct a polytype family is to identify the symmetry operation of the selected primary phase, which defines the relationship between adjacent structural units. This confirms that the unit cell can be divided into repeating structural units. The corresponding symmetry operation can be a glide or screw, which is the combination of translation and mirror or rotation, respectively. The third step is to define the structural units to construct the polytypic variants. As described above for the λ_b polytype family, the structural unit should be stackable in various orientations. In this study, the structural units are carefully defined to maintain the TaO₆ coordination throughout the entire polytypic variants to ensure energetic stability.

Fig. 3(b) summarizes the polytype family representations of octahedrally coordinated adaptive structures in Ta₂O₅, which will be discussed in detail. From the λ phase, two polytype families can be constructed from the a- and b-glides. The b-glide derives the λ_b polytype family (green shade) aforementioned, while the a-glide constructs another family named the λ_a polytype family (red shade). The polytype family of the Pmma phase (space group Pmma, No. 51) is derived from the a-glide operation, constructing the Pmma_a polytype family (orange shade). The γ₄ polytype family (blue shade) is constructed from the γ phase (space group I4₁/amd, No. 141), where the 4₁-screw symmetry along the long axis of the unit cell defines the repeating structural units. The use of rotational stacking of the 4₁-screw further differentiates the γ₄ polytype family from other polytype families, emphasizing its distinctive crystallographic characteristics. The notation of stacking sequences is also set to be different using B and C, which will be explained later. For simplicity, the subscript 1 in the 4₁-screw symmetry is omitted from the name of the γ₄ polytype family.

As a measure of the similarity of a polytypic variant to the primary phase, the alternation ratio (r_alt) is defined to indicate the degree of alternation within the polytypic variant. r_alt is calculated as the ratio of the number of adjacent XY or YX pairs to the total number of layers in the sequence, where X and Y correspond to either L and R, or C and B. This parameter is analogous to the hexagonality of the SiC-type polytypes. The range of r_alt spans from zero (when all the structural units are stacked in parallel, i.e., XXXX…) to one (when every adjacent structural unit is alternating, i.e., XYXY…), serving as the mixing parameter between these two extremes. Since the simplest stacking sequence with glide or screw operation is XY with r_alt = 1, it is natural for the primary phases to have this sequence. At the opposite extreme of r_alt = 0, it is intriguing that the polytype families presented in this study have one common phase with the same configuration of ions. The symmetry of this common phase converges to either monoclinic P2/m (No. 10) or orthorhombic Cmmm (No. 65) symmetry depending on the degree of symmetrization applied during structure optimization, as shown in Fig. 3(c). These two different lattices can be transformed into each other by shearing deformation of the 2-fold rhombi illustrated in Fig. S2 (ESI†). The structure of the P2/m phase has a more triangular-shaped Ta lattice, consistent with the layered adaptive context, whereas the Cmmm phase has some area of a square Ta lattice, consistent with the CS adaptive context. In this study, the P2/m or Cmmm phase is named the ‘parallel phase’ where every stacking sequence aligns in parallel, hence r_alt = 0. The characteristics of the parallel phases are also listed with those of the primary phases in Table 1.

Each polytype family of Fig. 3 is explained in detail below. Fig. 4 illustrates the structural relationship within the λ_a and Pmma_a polytype families. Fig. 4(a) and (b) describe the symmetry of the two primary phases of λ and Pmma, respectively. Note that Fig. 4(a) is identical to Fig. 2(b) but is presented again for clarity. Fig. 4(c) and (d) show the structural units of the λ_a and Pmma_a polytype families, respectively. The structural units are identical and can be described using a single pair of rhombi in Fig. 2(d), similar to the λ_b polytype family. Unlike the zigzag boundaries between the structural units in the λ_b polytype family in Fig. 2(d) and (e), boundaries between the structural units in the λ_a and Pmma_a phases are straight and repeat along the a-direction, as highlighted with thick vertical solid lines.

Fig. 4 λ_a and Pmma_a polytype families. (a) and (b) Ionic positions of the primary (a) λ and (b) Pmma phases and their symmetry elements. Panel (a) is identical to Fig. 2(b) and is repeated for clarity. (c) and (d) Alternating stacking of the structural units (LR) of the (c) λ and (d) Pmma phases. The stacking positions are heterogeneous (different rhombus types across the boundaries) in the λ phase, while homogeneous (identical rhombus types across the boundaries) in the Pmma phase. Likewise, the parallel stacking (LL) can have two possible stacking positions with (e) parallel and heterogeneous stacking in the β phase, and (f) parallel and homogeneous stacking in the P2/m form of the Cmmm phase, which is set to be the common parallel phase.

Due to the straight boundaries, the stacking relationships become more diverse, resulting in four possible distinct types. They are classified based on the boundary characteristics (heterogeneous or homogeneous, as shown in the columns of Fig. 4) and the stacking characteristics (alternating or parallel, as shown in the rows of Fig. 4). The heterogeneous boundaries feature different rhombus types across the boundaries (Fig. 4(c) and (e)), while homogeneous boundaries have identical rhombus types across the boundaries (Fig. 4(d) and (f)). The primary λ and Pmma phases exhibit heterogeneous and homogeneous boundaries, respectively, but both have alternating stacking (r_alt = 1). For r_alt = 0 at the other extreme, the phases with heterogeneous and homogeneous boundaries correspond to the β³⁶ and Cmmm³⁷ phases, respectively. Although the β phase was once regarded as the representative phase of L-Ta₂O₅, it has been disregarded due to its significantly lower energetic stability than the λ phase.³⁸ Therefore, this study focuses solely on the Cmmm phase as the parallel phase with homogeneous boundaries and r_alt = 0. Meanwhile, the potential polytype family between the λ and Pmma phases was not considered due to the absence of a mirror relationship between adjacent layers, rendering it impossible to describe under the approach proposed in this study.

Fig. 5 describes the γ₄ polytype family. Since this polytype family is constructed based on the 4₁-screw symmetry which alters the layer-normal direction, the interlayer O ions between the layers (2-fold O ions at the opposite direction of TaO₆ octahedra) are revealed and colored yellow in Fig. 5(a). Each structural unit is defined as having a single common layer-normal direction, as marked by the red arrows in Fig. 5(b) and (c). This direction denotes each structural unit, B (dark blue shade) and C (light blue shade). Fig. 5(d) and (e) show the alternating and parallel stackings, respectively. The structure of the γ₄ polytype family consists of the triangular lattice composed of the 3-fold rhombi plus the cubic lattice derived from the deformation of the 2-fold rhombi like in the parallel Cmmm phase, described in Fig. S2 (ESI†). Although the 4₁-screw symmetry divides the (conventional) unit cell of the γ phase into four volumes, each next-nearest structural unit is equivalent due to the symmetry of the structural unit. Thus, the unit cell of the γ phase has a stacking sequence of γ₄-CBCB, which is equivalent to γ₄-CB in brief, like other primary phases.

Fig. 5 γ₄ polytype family. (a) Ionic positions of the primary γ phase and the 4₁-screw axis to construct the γ₄ polytype family. The symmetry elements are not overlaid due to their abundance. (b) and (c) Each structural unit, B and C respectively. The layer-normal direction of each structural unit is marked by red arrows. (d) Alternating (CB) and (e) parallel (CC) stacking of the γ₄ polytype family, where the boundaries between the structural units are denoted by the thick blue lines. The parallel stacking derives the Cmmm phase.

From the four polytype families (λ_b, λ_a, Pmma_a, γ₄) defined, Fig. 6 presents several examples of the polytypic variants (XY, XXY, XXYY, X) derived from these polytype families and their space groups after structural relaxation. Since the TaO₆ octahedra are maintained in all the polytype families discussed, all polytypic variants can be visually described within the representation of the CS adaptive structure of Fig. 1(b). The structural units in Fig. 6 are indicated with (distorted) squares (TaO₆ octahedra) enclosed with bold lines. This representation can efficiently show the sharing arrangements between the octahedra and derive the identical polytypic variants to those of Fig. 2, 4, and 5. The λ_b and λ_a polytype families should involve distortions in the octahedral shapes to achieve their corner-edge-sharing arrangements, whereas the Pmma_a and γ₄ polytype families involve only corner- and edge-sharing without such distortions in the schematic. Meanwhile, even if the input structure before relaxation is orthorhombic, the polytypic variants with stacking sequences that have unequal numbers of Xs and Ys, such as XXY, tend to adopt a monoclinic unit cell rather than an orthorhombic one. This characteristic requires the desymmetrization step in the two-step structure optimization process to construct the polytypic variants accurately.

Fig. 6 Selected polytypic variants (XY, XXY, XXYY, and X) illustrated in the context of the CS adaptive structure. In the column of XY polytype (primary phase), the thick black arrows indicate the stacking direction, and the thick black solid boxes enclose one structural unit of each polytype family. The structural units may be different from those in Fig. 2–5 for comprehensibility in the CS adaptive context. All the thick red solid boxes indicate the conventional unit cell of each polytypic variant. The parallel lines in the background are the guidelines to distinguish each adjacent structural unit. X and Y correspond to either L and R, or C and B.

Table S1 (ESI†) defines each structural unit and the relationship between adjacent structural units, in the layered adaptive structure context. The positions of the O ions are defined relative to the triangular lattice of Ta ions, like in the layered adaptive context. The ionic relaxation may induce the ionic positions to shift off-center, depending on the polytype family and the stacking sequence.

In summary, this section provides an approach for dividing a crystal structure into smaller structural units and constructing polytypic variants. This concept is particularly effective for explaining adaptive structures, such as Ta₂O₅, which inherently possess an infinite number of ionic configurations. It can also be extended to existing polytype systems such as SiC, and is expected to provide even greater versatility since the approach presented in this work can manipulate certain polytype systems beyond the scope of OD theory. Moreover, this approach may apply to the structures previously recognized as non-adaptive, depending on the symmetry of the structural unit. While it may not generate an entirely new structure, it can provide insights into imperfections in the crystal that could lead to deviations from the ideal high-symmetry structures. For example, the high-pressure B phase of Ta₂O₅ (space group C2/c, No. 15),³⁹ an energetically stable phase consisting of TaO₆ octahedra with complex sharing arrangements, also exhibits the c-glide symmetry. This symmetry element makes it a pertinent case for such analysis, potentially leading to the development of the theoretical B_c polytype family.

B. Energetic and dynamic stability of the polytypes

This section analyzes the stability of the polytypic variants to assess the experimental feasibility. Since the polytypes in this study consist of similar local environments of TaO₆ octahedra, their energies are generally calculated to be similar. However, the dynamic stability varies depending on the stacking sequence. This section aims to show that the energy differences between these variants are so marginal that it is innately difficult to discriminate these structures energetically. Thus, the primary phases with high symmetry and small unit cells can serve as the representatives of their polytypic variants, eliminating the need to deal with computationally challenging phases.

Fig. 7(a) shows the calculated energies of the several polytypic variants of the four polytype families (λ_b, λ_a, Pmma_a, γ₄) listed in Table 2. The polytypic variants with stacking sequence lengths up to 6 are considered. Table 2 summarizes the r_alt values and the resulting space groups, and Table S2 (ESI†) provides additional information, including lattice parameters. The x-axis indicates the r_alt value, ranging from 1 on the left to 0 on the right. The three primary phases, γ, Pmma, and λ, are located at r_alt = 1, while the parallel Cmmm and P2/m phases are located at r_alt = 0. The stacking sequences of the polytypic variants are explicitly shown under the x-axis. The energy of the γ phase was used as a reference, which is currently reported to be the lowest. Three tie lines were drawn from γ to Cmmm, from Pmma to Cmmm, and from λ to P2/m, and the energies of their polytypic variants are shown along and around the tie lines. Generally, the energies of the polytypic variants do not deviate significantly from that of their primary phase, with only the marginal differences observed. The energy scale of the y-axis is smaller than the thermal energy (kT ∼ 26 meV at T = 300 K) or even comparable to the accuracy limit of the DFT calculations (∼10 meV per atom). Thus, it is plausible that any polytypic variant could appear experimentally in terms of energetic stability.

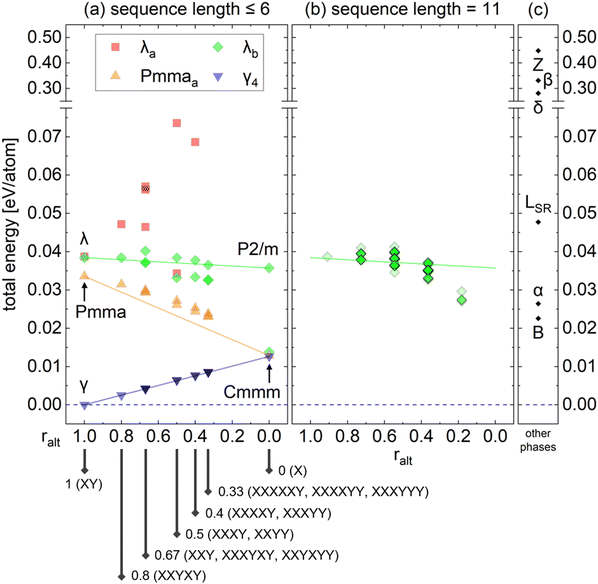Fig. 7 Calculated energies of (a) polytypic variants with sequence lengths up to 6. The complete list of the polytypic variants is available in Table 2. (b) λ_b polytype family with sequence length 11 for the direct comparison with the L_SR phase. Opacity increases when multiple data points overlap. (c) Other crystalline phases for comparison.

Table 2 Calculated polytypic variants and their space groups in Fig. 7(a). The polytypic variants are listed in the order of decreasing r_alt value. The asterisks in polytypic variants of the λ_a polytype family represent the cases where the relaxed structure after the two-step structure optimization resulted in different ionic configurations or failed to achieve the desired symmetry, and details of these structures are provided in Table S2 (ESI). The desired symmetry of the λ_a polytype family should be identical to the λ_b polytype family with the same stacking sequence. In contrast, the polytypes optimized using the LDA functional successfully reached the desired configurations and symmetries

Index	Stacking sequence	ralt	λb	λa	Pmmaa	γ4
1	XY	1	Pbam		Pmma	I41/amd
2	XXYXY	0.8	P2/m	P2/m	P2/m	Cmmm
3	XXY	0.67	P2/m	P2/m*	P2/m	Cmmm
4	XXYXYY	0.67	Pmc21	Pmc21	Pmm2	I4̄m2
5	XXXYXY	0.67	P2/m	P2/m	P2/m	Pmma
6	XXYY	0.5	Pbam	Pbam	Pmma	P42/mmc
7	XXXY	0.5	P2/m	P2/m	P2/m	Imma
8	XXXYY	0.4	P2/m	P2/m*	P2/m	Cmmm
9	XXXXY	0.4	P2/m	Pm*	P2/m	Cmmm
10	XXXYYY	0.33	Pbam	Pmma*	Pmma	I41/amd
11	XXXXYY	0.33	P2/m	P2/m*	P2/m	Pmmm
12	XXXXXY	0.33	P2/m	Pm*	P2/m	Imma
13	X	0	P2/m or Cmmm

---

The energy trends concerning r_alt reflect the interaction range of the structural units. The energies of the γ₄ polytype family (blue) show strong linearity lying on the tie line, showing that the energy is solely dependent on the interaction between very adjacent structural units. In contrast, the Pmma_a (orange) and λ_b (green) polytype families have weaker linearity, and the λ_a polytype family (red) forms a large concave hull above the tie line, indicating long-range interaction within the layer. The stacking sequence may significantly affect ionic displacements within the structural units, particularly in the λ phase and its polytypic variants, where substantial distortion of the TaO₆ octahedra occurs due to corner-edge-sharing. This effect is more pronounced in the λ_a polytype family, where several stacking sequences fail to maintain the initial configuration or the desired symmetries (defined by Table S1, ESI†) during the structure relaxation, as shown in Table 2.

The interaction range can be further inferred by the functional selection of the DFT calculations. The calculated energies of the same set of polytypes shown in Fig. 7(a) were also obtained using the local density approximation (LDA) functional^40,41 and plotted in Fig. S3 (ESI†). The relative energies of γ₄ and Pmma_a polytype families show minimal changes between the PBE and LDA calculations. In contrast, those of λ_a and λ_b polytype families exhibit slight differences, with the LDA results indicating higher stability than the PBE results. Moreover, the linearity in the λ_b polytype family becomes more substantial with the LDA functional, presumably due to the reduced influence of long-range interactions. In the λ_a polytype family, all 13 polytypic variants calculated using the LDA functional maintained their initial configurations after the relaxation steps, unlike some of those in PBE calculations. However, the linearity of the λ_a polytype family remains weak since the structure inherently has slanted arrangements of TaO₆ octahedra that require distortions. This result implies that the more spatially localized nature of the LDA functional may lead to an incomplete consideration of long-range interactions in the λ phase and its polytypic variants. Moreover, the HSE06 hybrid functional⁴² was also tested on the primary and parallel phases, and yielded the same energetic order (λ > Pmma > Cmmm > γ) and more consistent relative energy differences with the PBE results than the LDA ones. This indicates that the use of the PBE functional is adequate, balancing accuracy and computational efficiency.

Experimentally, the most commonly reported crystalline phases show a layered adaptive structure characterized by the triangular lattice of Ta ions. However, the occupation configuration of intralayer O ions is still unclear. One of the earliest models of the L-Ta₂O₅ structure, known as the L_SR phase (space group Pm, No. 6), features a long periodicity of 11 formula units to match the weak superstructure peaks in the X-ray diffraction patterns.⁴³ This early model can be interpreted as an energetically suboptimal version of the λ_b polytypic variants with an 11-unit sequence length, wherein some TaO₇ pentagonal bipyramids replace the typical TaO₆ octahedra. Fig. 7(b) shows the energies of all λ_b polytypes with a sequence length of 11 (total of 93 cases), which are generally more stable than the L_SR phase in Fig. 7(c). This is because the λ_b polytype family consists solely of TaO₆ octahedral coordination. Among the λ_b polytype family with a sequence length of 11, those with r_alt = 0.18 (2 alternations over a total sequence length of 11, e.g., λ_b-LLLLLLLLLRR) were found to be the most stable. However, polytypic variants with other stacking sequences could also appear since the energy difference is smaller than the thermal energy. Experimental observations reported the orthorhombic cell,^4–10 corresponding to a more balanced number of L and R units within the polytype family which is dynamically more stable, which will be discussed later. However, less alternation between L and R units is energetically more stable, leading to more monoclinic cells. Due to the ambiguity between experiments and calculations, adopting the polytype concept may help systematically analyze the L_SR phase, and more broadly, the structure of L-Ta₂O₅.

There have been several challenges in utilizing the L_SR phase in calculations. The L_SR phase was derived from the experimental data on the Ta₂O₅–WO₃ system, where the presence of W helped stabilize the structure.⁴³ Thus, it includes partial occupations of O ions due to the different oxidation states of Ta and W, which leads to structural ambiguity. Additionally, the L_SR phase has a large unit cell consisting of 77 atoms, making it computationally demanding. These challenges have led to the development of simplified models, such as Ta₆O₁₅ with the space group of Pm⁴⁴ and β_R phase,⁴⁵ though these models remain energetically less optimized presumably due to the presence of TaO₇ coordination. Moreover, the model should account for the existence of long-period orthorhombic L-Ta₂O₅ phases with different periodicities such as 13 or 19,⁷ and previous models proposed^7,43 are still energetically less optimized. In contrast, the λ_b polytype family offers a more robust model to describe the long-period orthorhombic L-Ta₂O₅ phases. Within this family, the primary λ phase, characterized by its small unit cell and high symmetry, serves as a benchmark phase for systematic analysis.

Fig. 7(c) compares the calculated energies of historically proposed phases of Ta₂O₅. The Z (space group C2, No. 5)⁴⁶ and δ (space group P6/mmm, No. 191)⁴⁷ phases exhibit high energies due to their significant portion of non-TaO₆ coordination. The β (space group Pmmm, No. 47)³⁶ phase of Fig. 4(e), once the representative phase of L-Ta₂O₅, consists only of TaO₆ octahedra. However, its calculated energy is relatively high due to the substantial distortion of the octahedra. The L_SR phase⁴³ and α phase⁴⁸ (space group I4₁/amd, No. 141) can be interpreted as the deviated versions of λ and γ phases, respectively, containing TaO₇ coordination. The B phase^39,46 (space group C2/c, No. 15) is the stable high-pressure phase, composed of TaO₆ octahedra. However, its complex sharing arrangements of the TaO₆ octahedra make it difficult to interpret within the conventional layered or CS adaptive contexts. Due to this structural complexity and the lack of straightforward correspondence to the adaptive contexts, the B phase is not considered in this study.

Since the energy differences between the polytypes are marginal, dynamic stability may play a major role in determining the existence of a specific crystalline structure of Ta₂O₅. The dynamic stability varies depending on the polytype families and the stacking sequence, with distinct characteristics observed between the fully layered λ_a, λ_b, and Pmma_a polytype families and the screw-type γ₄ polytype family.

Fig. 8 shows the phonon band diagrams of the selected polytypic variants (stacking sequences of XY, XXY, XXYY, and X) of λ_b and γ₄ polytype families, and Fig. S4 (ESI†) contains those of the λ_a and Pmma_a polytype families. The dynamic instability comes from the imaginary phonon frequencies, shaded gray in the figures. All the primary phases with the XY stacking sequence are dynamically stable, exhibiting no or only marginal imaginary frequencies, while the parallel Cmmm phase (stacking sequence X) is not. For the fully layered polytype families (λ_b, λ_a, and Pmma_a), the stacking sequences of XXYY also show dynamic stability. However, the polytypic variants of the γ₄ polytype family, except for the primary phase, are dynamically unstable. That is, the polytypic variants with the stacking sequence XXY are dynamically unstable, regardless of their polytype family.

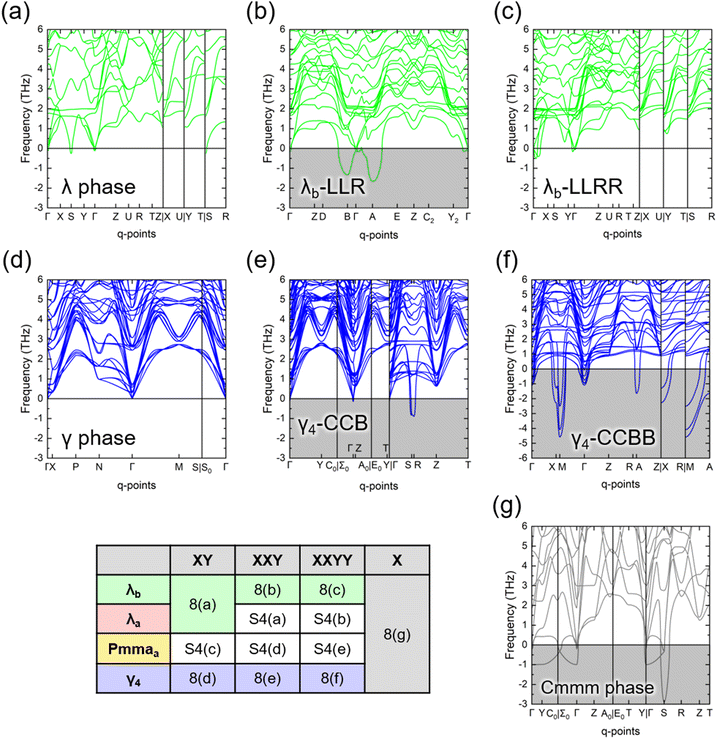Fig. 8 Phonon band diagrams of selected polytypic variants of λ_b and γ₄ polytype families in Fig. 6. Stacking sequences are (a) primary λ_b-LR (λ phase), (b) λ_b-LLR, (c) λ_b-LLRR. (d) primary γ₄-CB (γ phase), (e) γ₄-CCB, (f) γ₄-CCBB, and (g) parallel Cmmm phase. Those of other polytype families are available in Fig. S4 (ESI†). The gray shade indicates a significant imaginary frequency, and (f) γ₄-CCBB has a different y-axis setting presenting pronounced dynamic instability. The indexing table below briefly shows which figure each polytypic variant is located in.

The dynamic instability of some polytypic variants comes from the parallel Cmmm phase. As demonstrated in Fig. 3, the Cmmm phase has its low-symmetry form, P2/m phase, which implies its dynamic instability. The bc-plane with only corner-sharing (2-fold) bonds, the cyan-shaded region demonstrated in Fig. S2 (ESI†), acts as a source of structural weakness. This characteristic also leads to the low shear strength of the Cmmm phase.⁴⁹ For this reason, the polytypic variants with r_alt < 1 contain the Cmmm-like structure and are likely to be dynamically unstable. The γ₄ polytype family of Fig. 8(d)–(f) clearly shows this tendency. Only the primary γ phase is dynamically stable, and the other polytypic variants containing the parallel stacking (XX) are unstable. Although the primary γ phase also has the bc-plane with only corner-sharing (2-fold) bonds, the layer-normal direction across the bc-plane is altered. This structural characteristic may help prevent shearing deformation since the preferential shearing directions are oriented perpendicular to each other, providing mutual stabilization.

In contrast, the fully layered polytype families (λ_b, λ_a, and Pmma_a) show different trends. In these polytype families, the intralayer atomic positions can deviate from the perfect grid of Table S1 (ESI†), while maintaining the intralayer bonding configuration. This intralayer atomic interaction can dynamically stabilize the Cmmm-like structure, seemingly when the stacking sequence alternates regularly (i.e., XXYY), forming orthorhombic structures. In contrast, an imbalance between the numbers of the two structural units, X and Y, results in dynamic instability, leading to the formation of a monoclinic cell with the symmetry of P2/m or Pm. It is worth noting that the balanced stacking sequence XXXYYY in the λ_a polytype family fails to maintain the intralayer configuration (Table 2) since it requires a larger distortion of the intralayer positions compared to the XXYY, showing the limit of the intralayer dynamic stabilization. Moreover, small but negligible imaginary phonons in the ‘dynamically stable’ polytypic variants originate from the interlayer O ions between the adjacent layers, forming a plane composed only of corner-sharing (2-fold) bonds, which also acts as a source of structural weakness.

While the parallel Cmmm phase is energetically the most stable among the fully layered λ_a, λ_b, and Pmma_a polytype families, it is dynamically the least stable. Therefore, the energetic and dynamic stability compete and these polytype families should find an optimal balance between the two extremes, which led to the observation of the L_SR phase and its variants. However, the γ phase is energetically and dynamically most stable within the γ₄ polytype family. Therefore, it can be considered as the true ground state phase, as suggested by the previous study.^18,50 However, this γ phase is rarely observed experimentally, presumably due to the kinetic accessibility.

The historically proposed phases of L-Ta₂O₅ (L_SR, δ, β, λ, etc.) belong to the layered adaptive structures and are distinguished by their varying intralayer occupation configurations. In situ TEM analysis has revealed the layer-by-layer growth of L-Ta₂O₅ crystals within a thin amorphous film of Ta₂O₅.⁶ This growth mode likely inhibits the formation of the γ phase or its polytypic variants, assuming that the layer-normal direction remains consistent within a grain during crystallization. However, controlling the intralayer configuration is challenging due to the similar energetic and physical properties among the polytypic variants. For the Pmma phase, the newly proposed layered phase in this work, synthesis may need interface engineering, considering its distinct a/b ratio compared to the λ phase. Meanwhile, H-Ta₂O₅ is commonly considered to be tetragonal, and historically the α phase⁴⁸ was recognized as the representative. The α phase is a CS adaptive structure with TaO₇ coordination involved and has regularly alternating layer-normal directions similar to the γ phase. This suggests the hypothesis that the γ phase represents the ground state of H-Ta₂O₅, rather than L-Ta₂O₅ as previously proposed.⁴⁸ Note that the γ phase had been predicted as a form of H-Ta₂O₅ in the earlier study¹⁷ exploring other phases within the CS adaptive structure, and re-discovered by subsequent researchers.^18,35,51

Conclusion

This work establishes a comprehensive and generalized procedure for constructing and analyzing polytypic variants of octahedrally coordinated Ta₂O₅, providing new insights into its energetic and dynamic stability. Two types of adaptive structures previously recognized in Ta₂O₅, layered and CS, are interpreted in a unified context. As primary phases to be reconstructed into polytypes, not only the well-known λ and γ phases but also the newly proposed Pmma phase is selected in this work. From the glide or screw symmetry of the primary phases, the λ_a, λ_b, γ₄, and Pmma_a polytype families are constructed. These four polytype families have a common parallel configuration of the Cmmm (or P2/m with lower symmetry) phase. This structural reconstruction into polytype families enables systematic analysis of the adaptive structures. The energy calculations reveal that polytypic variants typically exhibit energies close to the tie line between the primary and parallel phases, and the energy differences are small enough, suggesting the experimental feasibility of various polytypic variants. The stacking sequences in each polytype family significantly affect dynamic stability, where regular and frequent alternations are generally favored. As a result, the primary phases with sufficiently low energies and high dynamic stability can serve as benchmarks for their respective polytype families, with potential extension to non-octahedral variants such as the L_SR or α phase. This study advances the understanding of the adaptive structural behavior in Ta₂O₅ and provides a unified perspective on its polytypic diversity, bridging theoretical predictions with experimental possibilities.

Author contributions

Dohyun Kim: formal analysis, investigation, methodology, writing – original draft; Kun Hee Ye: formal analysis, writing – review & editing; Taeyoung Jeong: formal analysis, writing – review & editing; Seungjae Yoon: formal analysis, writing – review & editing; Yunjae Kim: formal analysis, writing – review & editing; Cheol Seong Hwang: supervision, writing – review & editing; Jung-Hae Choi: conceptualization, funding acquisition, project administration, supervision, writing – review & editing.

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Data availability

The data that support the findings of this study are available within the article and its ESI.†

Acknowledgements

J.-H. C. was supported by the National Research Foundation of Korea (NRF) grant by MSIT [Next Generation Intelligence Semiconductor Foundation 2022M3F3A2A01076569], the National Research Council of Science & Technology (NST) grant by MSIT [No. GTL24041-000] and the Institutional Research Program of Korea Institute of Science and Technology (KIST) [2E33873].

References

1. C. Han and T. Wang, Energy Fuels, 2023, 37, 13624–13644.
2. S. Garg, N. Krishnamurthy, A. Awasthi and M. Venkatraman, J. Phase Equilib., 1996, 17, 63–77.
3. J. S. Anderson, J. Chem. Soc., Dalton Trans., 1973, 1107–1115.
4. K. Lehovec, J. Less-Common Met., 1964, 7, 397–410.
5. C. Askeljung, B.-O. Marinder and M. Sundberg, J. Solid State Chem., 2003, 176, 250–258.
6. K.-H. Min, R. Sinclair, I.-S. Park, S.-T. Kim and U.-I. Chung, Philos. Mag., 2005, 85, 2049–2063.
7. I. E. Grey, W. Mumme and R. S. Roth, J. Solid State Chem., 2005, 178, 3308–3314.
8. R. S. Devan, J.-H. Lin, W.-D. Ho, S. Y. Wu, Y. Liou and Y.-R. Ma, J. Appl. Crystallogr., 2010, 43, 1062–1067.
9. M. Audier, B. Chenevier, H. Roussel and A. L. Salaün, J. Solid State Chem., 2010, 183, 2068–2076.
10. E. Stavrou, J. M. Zaug, S. Bastea and M. Kunz, J. Appl. Phys., 2017, 121, 175901.
11. S.-H. Lee, J. Kim, S.-J. Kim, S. Kim and G.-S. Park, Phys. Rev. Lett., 2013, 110, 235502.
12. A. Wadsley, Acta Crystallogr., 1961, 14, 660–664.
13. R. Roth and A. D. Wadsley, Acta Crystallogr., 1965, 19, 38–42.
14. S. Andersson and A. Wadsley, Nature, 1966, 211, 581–583.
15. Y. Yang and J. Zhao, Adv. Sci., 2021, 8, 2004855.
16. J. Anderson and B. Hyde, J. Phys. Chem. Solids, 1967, 28, 1393–1408.
17. N. Stephenson and R. Roth, J. Solid State Chem., 1971, 3, 145–153.
18. J. H. Yuan, K. H. Xue, Q. Chen, L. R. Fonseca and X. S. Miao, Ann. Phys., 2019, 531, 1800524.
19. A. Guinier, G. Bokij, K. Boll-Dornberger, J. Cowley, S. Ďurovič, H. Jagodzinski, P. Krishna, P. De Wolff, B. Zvyagin and D. Cox, Acta Crystallogr., Sect. A: Found. Crystallogr., 1984, 40, 399–404.
20. G. Kresse and J. Furthmüller, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 11169.
21. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
22. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
23. P. E. Blöchl, Phys. Rev. B:Condens. Matter Mater. Phys., 1994, 50, 17953.
24. G. Kresse and D. Joubert, Phys. Rev. B:Condens. Matter Mater. Phys., 1999, 59, 1758.
25. V. Wang, N. Xu, J.-C. Liu, G. Tang and W.-T. Geng, Comput. Phys. Commun., 2021, 267, 108033.
26. A. Togo, L. Chaput, T. Tadano and I. Tanaka, J. Phys.: Condens. Matter, 2023, 35, 353001.
27. A. Togo, J. Phys. Soc. Jpn., 2023, 92, 012001.
28. D. Waroquiers, X. Gonze, G.-M. Rignanese, C. Welker-Nieuwoudt, F. Rosowski, M. Gobel, S. Schenk, P. Degelmann, R. André and R. Glaum, Chem. Mater., 2017, 29, 8346–8360.
29. K. Dornberger-Schiff, Acta Crystallogr., 1956, 9, 593–601.
30. K. Dornberger-Schiff and H. Grell-Niemann, Acta Crystallogr., 1961, 14, 167–177.
31. S. Ďurovič and Z. Weiss, Bull. Mineral., 1986, 109, 15–29.
32. B. Zvyagin, Crystal Symmetries, Elsevier, 1988, pp. 569–591.
33. S. Ďurovič, P. Krishna and D. Pandey, Int. Tables Crystallogr., 2006, 752–773.
34. S. Merlino, Z. Kristallogr., Kristallgeom., Kristallphys., Kristallchem., 2009, 224, 251–260.
35. Y. Tong, H. Tang and Y. Yang, Comput. Mater. Sci., 2023, 230, 112482.
36. L. Aleshina and S. Loginova, Crystallogr. Rep., 2002, 47, 415–419.
37. J. Y. Kim, B. Magyari-Köpe, K. J. Lee, H. S. Kim, S. H. Lee and Y. Nishi, Phys. Status Solidi RRL, 2014, 8, 560–565.
38. M. C. Brennan, D. A. Rehn, L. Q. Huston and B. T. Sturtevant, J. Phys.: Condens. Matter, 2024, 36, 275401.
39. F. Izumi and H. Kodama, J. Less-Common Met., 1979, 63, 305–307.
40. D. M. Ceperley and B. J. Alder, Phys. Rev. Lett., 1980, 45, 566.
41. J. P. Perdew and A. Zunger, Phys. Rev. B:Condens. Matter Mater. Phys., 1981, 23, 5048.
42. A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106.
43. N. Stephenson and R. Roth, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1971, 27, 1037–1044.
44. H. Sawada and K. Kawakami, J. Appl. Phys., 1999, 86, 956–959.
45. R. Ramprasad, J. Appl. Phys., 2003, 94, 5609–5612.
46. I. Zibrov, V. Filonenko, M. Sundberg and P.-E. Werner, Acta Crystallogr., Sect. B: Struct. Sci., 2000, 56, 659–665.
47. A. Fukumoto and K. Miwa, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 11155.
48. X. Liu, X. Han, Z. Zhang, L. Ji and Y. Jiang, Acta Mater., 2007, 55, 2385–2396.
49. Y. He and H. Sun, J. Appl. Phys., 2023, 133, 095103.
50. A. Pedrielli, N. M. Pugno, M. Dapor and S. Taioli, Comput. Mater. Sci., 2023, 216, 111828.
51. Y. Yang and Y. Kawazoe, Phys. Rev. Mater., 2018, 2, 034602.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp01821h

---