Water desorption from microcline (001): insights into the first water layer

Abstract

Feldspar minerals constitute an abundant group of tectosilicates in the Earth's crust. Consequently, feldspars play a significant role in a plethora of geochemical processes, including weathering, which results in carbon dioxide removal from the atmosphere by the formation of carbonates. Moreover, feldspar dusts are known as highly efficient ice nucleating particles, having a significant impact on the physical properties of mixed-phase clouds. For these processes, the interaction of water with the feldspar surface is decisive. However, little is known about the interaction of water with feldspar surfaces. More specifically, experimental data addressing the binding and in particular the desorption of the first water layer are sparse. Here, we present temperature-programmed desorption (TPD) experiments of water desorbing from the thermodynamically most stable cleavage plane of potassium-rich feldspar, microcline (001). From the interplay of these experimental data with density-functional theory (DFT) results we shed light onto the binding of the first water layer on microcline (001). The coverage-dependent TPD spectra reveal a gradual shift of the peak position from initially 235 K for low coverages towards lower temperatures until a coverage of four water molecules per primitive unit cell is reached. Above this coverage, the peak position remains fixed at about 180 K, even for high coverages. These results are in perfect agreement with DFT simulations, revealing a decrease in the adsorption energy with increasing coverage. When four water molecules per primitive unit cell are reached, the first layer is saturated and further water starts occupying the second layer. Our work confirms previous theory results from the literature and provides molecular-scale insights into the binding of water onto microcline (001).

---

1. Introduction

Feldspar minerals are a group of tectosilicates that account for 50 to 60% of the Earth's crust by volume.^1,2 Common feldspars are solid solutions of three components, namely the sodium, potassium and calcium end-members albite (NaAlSi₃O₈), orthoclase (KAlSi₃O₈) and anorthite (CaAl₂Si₂O₈). Being the most abundant constituent in rocks, feldspars are pivotal in many geochemical processes, including silicate weathering, which results in the sequestration of atmospheric carbon dioxide.³ Moreover, feldspar minerals have been shown to exhibit excellent ice nucleation abilities,⁴ with alkali feldspars (solid solution between albite and orthoclase) being more efficient than plagioclase feldspars (solid solution between albite and anorthite) both in immersion and in deposition modes.^4–10 Structurally, feldspar minerals exhibit a three-dimensional network of AlO₄ and SiO₄ tetrahedra, the so-called aluminosilicate framework. Interestingly, besides the chemical composition, also the order of the aluminium atoms inside this aluminosilicate network has been reported to correlate with the ice nucleation efficiency, as microcline (potassium-rich feldspar with high Al–Si order) has been shown to be more ice nucleation active than sanidine (potassium-rich feldspar with low Al–Si order).¹¹ So far, the reason for the exceptional ice nucleation ability of feldspars – and in particular alkali feldspars – compared to other minerals remains elusive. A lattice match between the thermodynamically unstable (100) plane and the ice I_h has been put forward based on scanning electron microscopy experiments.¹² Given the close structural similarity of alkali and plagioclase feldspars, these experiments, however, do not explain the superior ice nucleation efficiency of potassium-rich feldspars. It has been argued that the specific micro-texture of the minerals is important, which originates from an exsolution of sodium and potassium-rich regions.¹³ Triggered by these experimental findings, several theoretical studies have tried to elucidate the origin of the ice nucleation efficiency of feldspars.^14,15 Interestingly, molecular dynamics (MD) simulations of supercooled water on the (001), (010) and (100) planes of microcline have not observed ice nucleation.¹⁴ In contrast to this observation, density functional theory (DFT) simulations have suggested that an ice-like overlayer might form on an unordered first water layer on microcline (001).¹⁵ In view of these results, it is particularly interesting to elucidate the molecular structure of the K-feldspar cleavage plane in contact with water. To this end, the thermodynamically most stable cleavage plane of microcline, the (001) plane, has been investigated by atomic force microscopy both in ultrahigh vacuum^16,17 and at the solid–water interface.¹⁶ These studies have consistently revealed that the as-cleaved surface is terminated by hydroxyl groups, even in ultrahigh vacuum. These hydroxyl groups act as binding sites for water adsorption onto the hydroxylated surface as predicted by DFT.¹⁵ Due to the complexity of the surface, several different chemical binding sites are exposed, e.g., water binds more strongly towards the surface aluminol groups as compared to the silanol groups. Moreover, the potassium cations allow coordinative bond formation, albeit weaker than the hydrogen bonds towards the hydroxyl groups.¹⁵ So far, however, these insights are mainly based on DFT results, while direct experimental evidence for the binding of water in the first layer is largely lacking.

Here, we present temperature-programmed desorption (TPD) experiments of water desorbing from the microcline (001). Our TPD results reveal a gradual shift of the peak maximum temperature towards lower temperatures from about 235 K at low coverages to 180 K for coverages above about four molecules per primitive unit cell. From this coverage onwards, the peak remains at 180 K. These results can be understood by a comparison with DFT simulations. While a single molecule in the primitive unit cell can adopt the most favourable adsorption site forming a hydrogen bond towards the surface aluminol (as the donor) and silanol (as the acceptor) group, other molecules arriving at the surface need to arrange at less favourable sites. This situation results in a reduction of the adsorption energy per water molecule upon increasing the coverage, explaining the gradual shift of the peak maximum in TPD towards lower temperatures. Moreover, the fourth molecule added to the primitive unit cell fills the first layer, explaining the fact that the peak maximum temperature remains constant from this coverage onwards. Thus, our work provides a consistent picture of the binding of the first water layer onto microcline (001), which confirms previous theoretical predictions.

2. Experimental and theoretical methods

2.1. Experimental methods

2.1.1. Temperature-programmed desorption (TPD). Experiments were carried out under ultrahigh (UHV) vacuum conditions with base pressures in the low 10⁻¹⁰ mbar region. Feldspar samples (SurfaceNet, Germany) were introduced into the chamber via a load lock and degassed for around 3.5 hours at increasing temperatures up to 750 K. The samples were held at the highest temperature of 750 K for 50 minutes. During degassing, the degassing species were confirmed to be mainly water by mass spectrometry. Prior to the TPD experiments, the samples were cleaved in situ with a degassed tungsten carbide blade parallel to the (001) lattice plane to obtain a pristine (001) surface. Due to the hardness of feldspar, the sample did not cleave with just one pass of the cleaving blade but required multiple attempts. As only the very tip of the cleaving blade touched the side of the sample during these cleaving attempts, it is not to be expected that this cleaving procedure introduced contaminations. Upon cleavage, the water pressure in the chamber increased suddenly before decreasing again. The samples were mounted on a liquid nitrogen cooled manipulator. Sample temperatures were measured with a K-type thermocouple fixed at the tantalum sample holder as close to the sample as possible. Depending on the quality of the thermal contact upon mounting the sample, a minimum temperature of about 120 K can be reached. The temperature error within one session with the same sample holder and sample is ±1.2 K. The temperature variation between different sessions is ±17 K at 270 K due to differences in the thermal coupling between the sample holder and the sample. Water (Stakpure, resistance 18.2 MΩ) was purified with multiple freeze–pump–thaw cycles and dosed via backfilling the chamber through a leak valve. A resistive heater was used to heat the sample with a constant heating rate of β = 1 K s⁻¹. The desorbing water molecules (molecule ion peak at m/z 18) were monitored with a quadrupole mass spectrometer (Hiden HAL 511 3F RC PIC, Hiden Analytical, Great Britain) shielded in a glass shroud. For the TPD measurements, the entrance aperture of the mass spectrometer can be approached towards the sample surface to less than 1 mm. A second, unshielded quadrupole mass spectrometer (Hiden HAL 511 3F RC PIC, Hiden Analytical, Great Britain) mounted to the main part of the chamber was used to simultaneously monitor the background pressure. For the TPD measurements, the sample was first cooled below 130 K before dosing water onto the surface. The water dosage was adjusted by varying the exposure time and pressure. TPD measurements were started after the water pressure in the chamber had decreased again. TPD curves were recorded up to 600 K, well above the temperature range of interest, to ensure that all residual water had been desorbed from the sample and manipulator. The first measurement each day was a TPD measurement without water dosage to ensure a clean and consistent surface for the following measurements. These clean TPD measurements were compared to confirm that the sample was still contamination free. Desorption rates were background corrected with the background pressure measured in the chamber and calibrated based on the known desorption curves of water desorbing from calcite (10.4).^18,19 After background correction, a small peak at around 300 K remained from the background signal for desorption curves with a high initial coverage. We expect that this remaining peak does not interfere with our data analysis, because it is well-separated from the main desorption peaks and only has a very small relative intensity.

2.1.2. Atomic force microscopy (AFM). After performing all TPD experiments, the sample was locked out of the UHV chamber and inspected using an atomic force microscope from Oxford Instruments (Cypher VRS1250) operated in the dynamic mode at the feldspar–water interface. To this end, the sample was cleaned with gaseous nitrogen and a water droplet (stakpure, resistance 18.2 MΩ) was placed on the sample surface within one hour after the removal of the sample from the UHV chamber. Silicon cantilevers (TAP300GD-G, Budget Sensors, Bulgaria) with a gold coated back side were used, having an eigenfrequency between 115 and 140 kHz, a quality factor of approximately 7.5 and a nominal spring constant of 40 N m⁻¹ in water. In all AFM images, the recorded channel (z_p: z-piezo displacement, Δν_exc: excitation frequency shift) and the fast and slow scan direction are given.

2.1.3. Elemental analysis. Elemental analysis of a sample cut from the same base crystal as the microcline samples used in this study has been commissioned from Mikroanalytisches Laboratorium Kolbe (Germany). Cation mass fractions in our samples have been determined to be: K (12.87 wt%), Na (0.32 wt%), Ca (172 ppm), Ba (32 ppm), Sr (<5 ppm), Rb (12 ppm), Cu (119 ppm), Fe (0.10 wt%) and Pb (<5 ppm).

2.1.4. X-ray diffraction (XRD). X-ray diffraction (XRD) data of a sample also cut from the same base crystal has been reported previously by T. Dickbreder and F. Sabath et al.¹⁶

2.2. Theoretical methods

All first-principles calculations in this work were performed using the periodic plane-wave basis VASP code^20,21 implementing density functional theory. To accurately include van der Waals interactions for this system, we further used the Tkatchenko–Scheffler method with iterative Hirshfeld partitioning,²² shown to be best suited for ionic systems.^23,24 Note that this is a systematic improvement in accuracy compared to earlier work,¹⁵ but we generally agree with that work. Projected augmented wave potentials were used to describe the core electrons²⁵ with a kinetic energy cutoff of 500 eV (with PREC = accurate). Systematic k-point convergence was checked for all systems with sampling chosen according to the system size. This approach converged the total energy of all the systems to the order of 1 MeV. For calculations of the feldspar surface, we used a 2 × 1 × 1 supercell (208 atoms total), a vacuum gap of at least 1.5 nm and a 3 × 3 × 1 k-point grid. The upper four layers of the surface were allowed to relax to a force of less than 0.01 eV Å⁻¹. Water adsorption energies were calculated as the total energy difference per water molecule between the relaxed combined system and the isolated surface and water molecules. In total, we considered 23 different configurations of water on the microcline (001) surface, of which the five configurations with the lowest energy are shown.

3. Results and discussion

In this study, we investigated samples of the potassium-rich feldspar microcline. Microcline is characterized by a high potassium content and a high Al–Si order in its aluminosilicate framework.^1,2 However, the specific chemical composition and Al–Si order can vary between different samples. To characterize the chemical composition and crystal structure of the microcline samples used in this study, samples cut from the same base crystal were analysed by means of chemical analysis and X-ray diffractometry (XRD). Chemical analysis reveals that our samples consist mainly of potassium feldspar with a potassium mole fraction of 0.958 regarding the other series elements sodium and calcium. Moreover, our samples contain a small amount of sodium feldspar (sodium mole fraction 0.041) and almost no calcium feldspar (calcium mole fraction 0.001). Trace elements confirmed in our samples are iron (0.1 wt%), copper (119 ppm), barium (32 ppm) and rubidium (12 ppm). From the XRD measurements, we can assess the Al–Si order of our microcline samples. For a fully ordered, so-called maximum microcline, all aluminium atoms are situated in one of four tetrahedral sites.¹ This tetrahedral site is referred to as the T_1(o) site.¹ The XRD measurements of our samples reveal a triclinic crystal structure with about 80% of all aluminium atoms positioned in T_1(o) sites.¹⁶ Hence, our samples are, indeed, rather well ordered as expected for microcline.

The most easily cleaved surface of microcline is the (001) crystallographic plane. For one of the crystals used here, a view of this surface is given in Fig. 1a, presenting an AFM image that was acquired at the solid–liquid interface. In this image, flat terraces can be identified that are separated by single step edges or multiples thereof (see the ESI†), whose heights are in perfect agreement with the expected height for one atomic layer of 0.649 nm. In addition to the flat areas accessible by AFM, our samples exhibit cracks and pores visible in the optical microscope of our AFM. On the flat terraces, atomic resolution images can be achieved at the interface to water as presented in Fig. 1b. From the corresponding series of drift-corrected²⁶ images, we can extract average primitive unit cell dimensions (a = (0.78 ± 0.02) nm, b = (0.81 ± 0.02) nm, γ = (68 ± 2)°), which are in accordance with the bulk-truncated primitive unit cell dimensions (a = 0.765 nm, b = 0.790 nm, γ = 66.8°) expected based on XRD.¹⁶ The observed contrast and lattice parameters are in perfect agreement with our previous work,¹⁶ confirming the cleanliness and surface structure of the investigated microcline samples. The surface unit cell exhibits a centred lattice of potassium ions nested in the cavities formed by the aluminosilicate tetrahedra as shown in the top view in Fig. 1c. The centred unit cell (marked in black) contains two potassium ions and four hydroxyl groups, while the primitive unit cell (marked in blue) contains one potassium ion and two hydroxyl groups. Upon cleavage, both protruding oxygen atoms and dangling bonds are formed. The dangling bonds are, however, immediately saturated by water molecules, which results in a fully hydroxylated surface. The latter is true even for a UHV environment.¹⁶ Note that for the maximum microcline considered here, the positions of aluminium atoms in the surface are well defined, such that the primitive unit cell always contains one silanol and one aluminol group (see Fig. 1c).

Fig. 1 (a) Large-scale AFM image of the microcline sample investigated in this work. The image was taken at the solid–liquid interface after the TPD experiments have been completed. Flat areas separated by step edges can be seen. (b) Drift-corrected²⁶ AFM image revealing unit cell dimensions in accordance with the bulk-truncated microcline (001) surface. (c) Top and side view of the surface structure of microcline (001) as obtained by DFT (adapted from ref. 16). The potassium ions form a centred lattice. The protruding oxygen atoms and the dangling bonds formed upon cleavage are saturated by hydroxyl groups. The position of the aluminol groups is ordered as maximum microcline is shown here.

Prior to the TPD experiments, the microcline sample was cleaved in situ at room temperature. During cleavage, a steep rise in the water background signal was observed (see Fig. S5, ESI†), which points towards water contained within our sample. A similar increase in the water background upon cleaving has been reported previously by G. Franceschi et al., who attributed it to clay minerals or micro- to nanometre-sized fluid inclusions within their samples.¹⁷ After cleaving, the sample was immediately cooled down. Subsequently, several TPD curves without dosing any water were recorded, which show a desorption peak at around 235 K (see Fig. 2). Moreover, we observe an increase in the desorption rate towards the end of the TPD curve starting above 450 K for one of our samples (see Fig. S6, ESI†). This observation suggests that our sample was still degassing considerable amounts of water during the experiments. Since this signal increase above 450 K did not deplete significantly during our TPD experiments, we suspect that our sample exhibits microporosity, which allows for the continuous degassing of water from liquid inclusions in the bulk of our sample. However, degassing from the bulk only gets significant at 500 K, well above the desorption peak from the surface. Thus, we expect that degassing from the bulk does not interfere with our measurements. Furthermore, the absence of additional peaks in the low coverage desorption curves suggests that the (sub)monolayer desorption on microcline (001) does not overlap with desorption from defect states.

Fig. 2 (a) Coverage-dependent TPD curves of water desorbing from microcline (001). Shown is the calibrated and background corrected signal at m/z 18 as a function of temperature. Curves with an initial coverage below one molecule per primitive unit cell are drawn in red, curves with an initial coverage between one and five molecules per primitive unit cell in blue and all curves with coverages above five molecules per primitive unit cell are shown in black. For low coverages, the peak maximum is observed at about 235 K. With increasing coverage, the peak maximum shifts towards lower temperatures. At a coverage of about four water molecules per primitive unit cell, the peak maximum remains at a fixed temperature of about 180 K. Interestingly, a small initial peak at 150 K is observed for coverages larger than about five molecules per primitive unit cell. The inset shows a detailed view of the low coverage desorption curves. The small peak visible in the high-coverage desorption curves at around 300 K is an artefact from an incomplete background subtraction. (b) Change in surface coverage corresponding to the desorption curves shown in (a). The absolute coverage is obtained by integrating the TPD curves and calibrating against the known TPD curves of water desorbing from calcite (10.4).^18,19 (c) Peak maximum temperature as a function of the coverage for the peak initially situated at 200 K (marked in blue), revealing the shift of the peak maximum towards smaller temperatures for small coverages and a fixed temperature for coverages larger than four water molecules per primitive unit cell. For coverages larger than five molecules per primitive unit cell, we observe an initial peak at 150 K in addition. The coverage error corresponds to the error of the calibration (see ESI†), and the temperature error shown is the temperature error within one session of ±1.2 K.

Then, water was dosed from a leak valve to arrive at a controlled water coverage for collecting coverage-dependent TPD curves. The resulting TPD curves in the temperature range below 400 K are shown in Fig. 2a. Here, we show the calculated desorption rates after subtraction of the background signal, and calibration based on the known desorption curves of water desorbing from calcite (10.4).^18,19 The corresponding surface coverage obtained from integrating the peaks is given in Fig. 2b. For the smallest coverage investigated, a single peak is observed in the TPD spectrum at about 235 K (see the smallest red curve in Fig. 2a). With increasing coverage, this peak shifts its maximum position towards lower temperatures (red and blue curves). At a coverage of about four water molecules per primitive unit cell, this peak no longer shifts position but remains at a temperature of about 180 K with increasing coverage (black curves). Moreover, a small initial peak is observed at about 150 K for coverages higher than around five molecules per primitive unit cell (black curves). Since DFT predicts the saturation of the first water layer for four molecules per primitive unit cell,¹⁵ this coverage corresponds to slightly more than one water layer on the microcline (001) surface. This initial peak is very interesting as it seems very similar to the crystallization peak observed by B. D. Kay et al.^27,28 Thus, it can be speculated that an initially amorphous water layer rearranges into an ordered crystal lattice at this temperature. Note, however, that we already observe this second peak for coverages slightly above one monolayer of water on microcline, while B. D. Kay et al. studied thick water layers of several hundred monolayers.^27,28 In view of the excellent ice nucleation abilities of microcline, this peak deserves particular attention. However, here we want to focus on another aspect of the spectra, namely the initial shift of the maximum peak position upon increasing the coverage.

The specific peak shape and maximum temperature in TPD are associated with the molecular-scale details of the desorption process (e.g., the desorption order) and the transition state energy and entropy changes. On the hydroxylated microcline (001) surface, water is adsorbed non-dissociated,^15,17 which is why it is reasonable to assume first-order desorption. In this case, the change in peak temperature can be correlated with a change in desorption energy. Thus, the herein observed shift in the peak maximum is ascribed to a decrease in the desorption energy with increasing coverage. To unravel this evolution, we plot the peak maximum temperature as a function of surface coverage in Fig. 2c. Here, an initial strong decrease in desorption peak temperature from 235 K to 200 K for coverages below one molecule per primitive unit cell (red points) can be seen. Then, the peak temperature decreases less strongly to 190 K until about four molecules per primitive unit cell are reached (blue points). Above this coverage, the peak temperature remains constant at about 180 K (black points). Thus, from the TPD data we deduce that the first water molecule has the highest energy barrier for desorption, i.e., it is adsorbed at the most stable adsorption site in the primitive unit cell. For the second molecule in the primitive unit cell, a significantly weaker binding is revealed, indicating that the adsorption position differs from the one of the first molecule. For the second to fourth water molecule per primitive unit cell, the desorption energy appears to stay at a more or less constant value. A further slight decrease in desorption energy is revealed for more than four molecules per primitive unit cell. The latter observation is most easily explained by molecules now occupying the second layer, i.e., they all interact with water molecules and no longer experience the different chemical sites of the feldspar surface. Moreover, the peak temperature of 180 K suggests that desorption from the second water layer on the microcline (001) is still significantly different from multilayer water desorption, which is expected to set in between 150 K and 160 K in a typical TPD experiment.²⁹

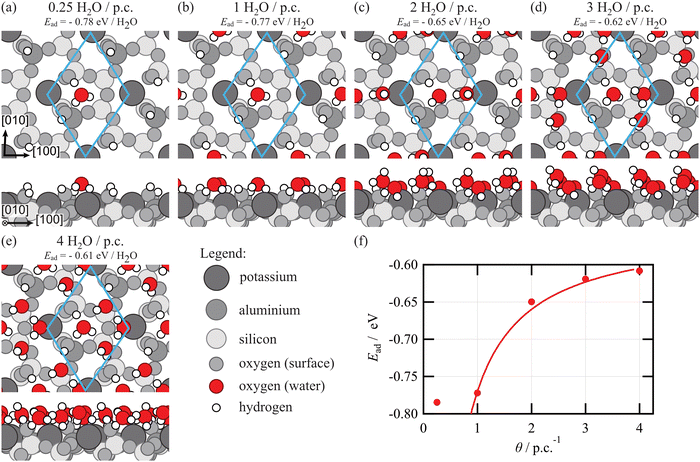
To shed light on the experimental findings, we performed coverage-dependent DFT simulations (Fig. 3). Due to the complex nature of the feldspar surface, several interaction motifs with water can be envisioned. As has been discussed in a comprehensive DFT study,¹⁵ water can form hydrogen bonds with the surface silanol and aluminol groups both as the donor and acceptor. Moreover, water can bind to the surface potassium cations. Finally, water can also bind to the bridging oxygen atoms of the surface, acting as a hydrogen bond donor. In agreement with the findings by P. Pedevilla et al.,¹⁵ the most stable geometry is found for a water molecule forming hydrogen bonds with the neighbouring aluminol (as hydrogen donor) and silanol (as hydrogen acceptor) groups. Additionally, the water molecule binds to a bridging oxygen atom as the hydrogen donor (Fig. 3a). In this configuration, an adsorption energy of about −0.78 eV per water molecule is obtained for both an isolated water molecule (Fig. 3a) and one water per primitive cell (Fig. 3b). For the next water molecule added to the primitive unit cell, the binding is already less attractive. We find several configurations with similar adsorption energies, where the second water molecule forms hydrogen bonds with the surface hydroxyl groups and the first water molecule or interacts with the potassium ion. In the most stable configuration shown in Fig. 3c, the second water molecule forms two bonds: one hydrogen bond with the first water molecule (as a hydrogen donor) and a second bond with the cation (with the oxygen). To accommodate this configuration, the hydrogen bond between the first water molecule and the bridging oxygen atom is broken. The second hydrogen atom of the second water molecule is not forming any bonds, but it is pointing away from the surface (Fig. 3c). This configuration is less favoured as compared to the situation of a single molecule, resulting in an adsorption energy of −0.64 eV per molecule when two molecules are situated in the primitive unit cell. The average adsorption energy continues to decrease for the third (Fig. 3d) and fourth (Fig. 3e) molecule added to the primitive unit cell. Note that the latter molecule adopts a position close to the surface cation, which is less favoured as compared to binding to the surface hydroxyl groups for an isolated water molecule. For the fourth water molecule, however, this is different as it can form hydrogen bonds with deposited water molecules. These findings are in general agreement with what has been obtained before³⁰ in the literature by P. Pedevilla et al.,¹⁵ showing that the average adsorption energy per water molecule decreases with increasing coverage of water molecules (see Fig. 3f). Interestingly, we find that the average adsorption energies can be described excellently with a simplified model assuming an adsorption energy of −0.77 eV for the first water molecule per primitive cell and −0.55 eV for all subsequent water molecules (solid line in Fig. 3f).

Fig. 3 DFT simulations of coverage-dependent water adsorption onto microcline (001). (a) A single water molecule on the surface and a coverage of (b) one, (c) two, (d) three and (e) four water molecules per primitive unit cell are considered. In all cases, the underlaying microcline surface is shown in grayscale and the adsorbed water molecules in colour. (f) Average adsorption energy per water molecule E_ad as a function of water coverage. The obtained average adsorption energy per molecule decreases from −0.78 eV for a single molecule to −0.61 eV per molecule for four molecules per unit cell. The solid line shows the average adsorption energy expected if the first water molecule binds with −0.77 eV and all subsequent water molecules bind with −0.55 eV per water molecule for coverages above one water molecule per primitive cell.

Further molecules added to this situation are known to bind in the second layer,¹⁵ i.e., they now experience a rather similar binding configuration as they interact with the adsorbed water rather than specific sites on the feldspar surface. The adsorption energy of these molecules has been calculated to be about −0.6 eV per molecule,¹⁵ with minor differences depending on the specific overlayer structure considered. These differences are, however, small compared to the accuracy of DFT. In essence, we expect the adsorption energy per molecule to decrease upon increasing the coverage until the first layer is filled by four molecules per primitive unit cell. On further increasing the coverage, the second layer is occupied. In this layer and all layers above, molecules bind to the water molecules in the layer underneath, which explains why the adsorption energy per molecule now remains constant. Note, however, that the adsorption energy of the second layer calculated by DFT¹⁵ (−0.6 eV) is still higher than the heat of sublimation of ice²⁹ (−0.5 eV), which implies that adsorption in the second layer is still influenced by the microcline surface underneath.

To compare our DFT results with the TPD experiments, we estimate desorption energies ΔE_d from the average adsorption energies E_ad obtained by DFT. This conversion is necessary, because desorption kinetics depend on the adsorption energy of the desorbing molecule rather than the average adsorption energy over all molecules. Assuming a desorption process without an additional energy barrier for adsorption as commonly discussed in the literature,³¹ the desorption energy ΔE_d is given by the derivative of the combined adsorption energy of all water molecules with respect to the number of molecules (see the ESI†). Fig. 4a shows that the desorption energy is approximately constant at around 0.77 eV up to one water molecule per unit cell. Then, the desorption energy drops and is again approximately constant at around 0.55 eV for the second to the fourth water molecule per unit cell. This decrease in desorption energy is in good agreement with the strong decrease in the experimental α peak temperature from 235 K to around 200 K for coverages below one water molecule per primitive cell (see Fig. 4b). The fact that we only observe one desorption peak with a gradually shifting peak temperature rather than two separated desorption peaks corresponding to 0.77 eV and 0.55 eV suggests a desorption mechanism with partial site occupation and exchange between the different adsorption sites.^18,32 For coverages between one and four to five water molecules per primitive cell, the α peak temperature only decreases slightly to around 190 K. This fits well with the desorption energy being approximately constant for the second to fourth water molecule per primitive unit cell.

Fig. 4 Comparison between DFT and TPD results. Shown are (a) the desorption energy ΔE_d estimated by DFT calculations and (b) the peak temperature T_max of the α peak from the TPD experiments as functions of water coverage.

4. Conclusions

In summary, we present temperature-programmed desorption experiments of water desorbing from the microcline (001) surface. For coverages below one molecule per primitive unit cell, a single desorption peak with a peak maximum at about 235 K is revealed. When increasing the coverage, the peak maximum shifts towards lower temperatures. For a coverage of about four molecules per primitive unit cell, a peak maximum of 180 K is obtained. When further increasing the coverage, the peak maximum does not shift any longer, but the peak increases in height. These findings are corroborated by density functional theory simulations that elucidate the binding configuration for water molecules in the first water layer. Due to the complex nature of the microcline (001) surface, several binding motifs for water adsorbing on this surface exist. While a single molecule in the primitive unit cell can form hydrogen bonds towards neighbouring aluminol and silanol groups simultaneously, further molecules added to the unit cell cannot attain a binding configuration with the same binding strength. Consequently, the absolute adsorption energy per molecule decreases upon increasing the coverage. When a coverage of four molecules is reached, the first layer is saturated and further molecules will occupy the second layer and multilayers. As the binding of these molecules is rather similar, the adsorption energy per molecule remains constant from this coverage on. As an interesting side note, we observe a small peak at 150 K for coverages larger than about five molecules per unit cell. This peak is rather similar to what has been observed before as a crystallization peak. Given the importance of microcline in ice nucleation, this observation deserves a more comprehensive investigation that is beyond the scope of this work.

Abbreviations

TPD	Temperature-programmed desorption
AFM	Atomic force microscopy
DFT	Density functional theory
UHV	Ultrahigh vacuum

Author contributions

TD, FSc and LK carried out the TPD experiments and analysed the experimental data. KND, TD and FS performed the AFM experiments. ASF performed the DFT simulations. AK wrote the first draft of the manuscript with contributions from TD and ASF. The manuscript was written through contributions of all authors. TD prepared the ESI† with contributions from KND and FSc. TD, RB and AK conceptualized the study. All authors have given approval to the final version of the manuscript.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank Annamaria Latus for support in organizing the elemental analysis of feldspar samples. AK acknowledges support from the Deutsche Forschungsgemeinschaft through grant KU 1980/18-1. ASF acknowledges support from the Research Council of Finland (project no. 347319 and 346824). Computing resources from the Aalto Science-IT project and CSC, Helsinki are gratefully acknowledged.

References

1. W. A. Deer, R. A. Howie and J. Zussman, An introduction to the rock-forming minerals, Longman Scientific & Technical, 1992.
2. M. Okrusch and H. E. Frimmel, Mineralogy: An Introduction to Minerals, Rocks, and Mineral Deposits, Springer Nature, Berlin, 2020.
3. R. A. Berner, Weathering, plants, and the long-term carbon cycle, Geochim. Cosmochim. Acta, 1992, 56, 3225–3231.
4. J. D. Atkinson, B. J. Murray, M. T. Woodhouse, T. F. Whale, K. J. Baustian, K. S. Carslaw, S. Dobbie, D. O’Sullivan and T. L. Malkin, The importance of feldspar for ice nucleation by mineral dust in mixed-phase clouds, Nature, 2013, 498, 355–358.
5. A. D. Harrison, T. F. Whale, M. A. Carpenter, M. A. Holden, L. Neve, D. O'Sullivan, J. Vergara Temprado and B. J. Murray, Not all feldspars are equal: a survey of ice nucleating properties across the feldspar group of minerals, Atmos. Chem. Phys., 2016, 16, 10927–10940.
6. A. Peckhaus, A. Kiselev, T. Hiron, M. Ebert and T. Leisner, A comparative study of K-rich and Na/Ca-rich feldspar ice-nucleating particles in a nanoliter droplet freezing assay, Atmos. Chem. Phys., 2016, 16, 11477–11496.
7. T. Zolles, J. Burkart, T. Häusler, B. Pummer, R. Hitzenberger and H. Grothe, Identification of Ice Nucleation Active Sites on Feldspar Dust Particles, J. Phys. Chem. A, 2015, 119, 2692–2700.
8. J. D. Yakobi-Hancock, L. A. Ladino and J. P. D. Abbatt, Feldspar minerals as efficient deposition ice nuclei, Atmos. Chem. Phys., 2013, 13, 11175–11185.
9. F. Zimmermann, S. Weinbruch, L. Schütz, H. Hofmann, M. Ebert, K. Kandler and A. Worringen, Ice nucleation properties of the most abundant mineral dust phases, J. Geophys. Res.: Atmos., 2008, 113, D23204.
10. L. Kaufmann, C. Marcolli, J. Hofer, V. Pinti, C. R. Hoyle and T. Peter, Ice nucleation efficiency of natural dust samples in the immersion mode, Atmos. Chem. Phys., 2016, 16, 11177–11206.
11. A. Welti, U. Lohmann and Z. A. Kanji, Ice nucleation properties of K-feldspar polymorphs and plagioclase feldspars, Atmos. Chem. Phys., 2019, 19, 10901–10918.
12. A. Kiselev, F. Bachmann, P. Pedevilla, S. J. Cox, A. Michaelides, D. Gerthsen and T. Leisner, Active sites in heterogeneous ice nucleation—the example of K-rich feldspars, Science, 2017, 355, 367–371.
13. T. F. Whale, M. A. Holden, A. N. Kulak, Y.-Y. Kim, F. C. Meldrum, H. K. Christenson and B. J. Murray, The role of phase separation and related topography in the exceptional ice-nucleating ability of alkali feldspars, Phys. Chem. Chem. Phys., 2017, 19, 31186–31193.
14. A. Soni and G. N. Patey, Simulations of water structure and the possibility of ice nucleation on selected crystal planes of K-feldspar, J. Chem. Phys., 2019, 150, 214501.
15. P. Pedevilla, S. J. Cox, B. Slater and A. Michaelides, Can Ice-Like Structures Form on Non-Ice-Like Substrates? The Example of the K-feldspar Microcline, J. Phys. Chem. C, 2016, 120, 6704–6713.
16. T. Dickbreder, F. Sabath, B. Reischl, R. V. E. Nilsson, A. S. Foster, R. Bechstein and A. Kühnle, Atomic structure and water arrangement on K-feldspar microcline (001), Nanoscale, 2024, 16, 3462–3473.
17. G. Franceschi, A. Conti, L. Lezuo, R. Abart, F. Mittendorfer, M. Schmid and U. Diebold, How Water Binds to Microcline Feldspar (001), J. Phys. Chem. Lett., 2024, 15, 15–22.
18. T. Dickbreder, D. Lautner, A. Köhler, L. Klausfering, R. Bechstein and A. Kühnle, How water desorbs from calcite, Phys. Chem. Chem. Phys., 2023, 25, 12694–12701.
19. T. Dickbreder, R. Bechstein and A. Kühnle, in preparation, 2025.
20. G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50.
21. G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
22. T. Bučko, S. Lebègue, J. Hafner and J. G. Ángyán, Improved Density Dependent Correction for the Description of London Dispersion Forces, J. Chem. Theory Comput., 2013, 9, 4293–4299.
23. A. Tkatchenko and M. Scheffler, Accurate Molecular van der Waals Interactions from Ground-State Electron Density and Free-Atom Reference Data, Phys. Rev. Lett., 2009, 102, 073005.
24. T. Bučko, S. Lebègue, J. G. Ángyán and J. Hafner, Extending the applicability of the Tkatchenko-Scheffler dispersion correction via iterative Hirshfeld partitioning, J. Chem. Phys., 2014, 141, 034114.
25. P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
26. T. Dickbreder, F. Sabath, L. Höltkemeier, R. Bechstein and A. Kühnle, unDrift: A versatile software for fast offline SPM image drift correction, Beilstein J. Nanotechnol., 2023, 14, 1225–1237.
27. R. J. Speedy, P. G. Debenedetti, R. S. Smith, C. Huang and B. D. Kay, The evaporation rate, free energy, and entropy of amorphous water at 150 K, J. Chem. Phys., 1996, 105, 240–244.
28. R. S. Smith, J. Matthiesen, J. Knox and B. D. Kay, Crystallization Kinetics and Excess Free Energy of H₂O and D₂O Nanoscale Films of Amorphous Solid Water, J. Phys. Chem. A, 2011, 115, 5908–5917.
29. P. A. Thiel and T. E. Madey, The Interaction of Water with Solid-Surfaces - Fundamental-Aspects, Surf. Sci. Rep., 1987, 7, 211–385.
30. Note that P. Pedevilla and coworkes use a different unit cell than we do. As their unit cell is twice as large as ours, eight molecules per unit cell form a first layer in their work, while we refer to four molecules per unit cell in the first layer.
31. C. T. Campbell and J. R. V. Sellers, The Entropies of Adsorbed Molecules, J. Am. Chem. Soc., 2012, 134, 18109–18115.
32. T. Dickbreder, R. Bechstein and A. Kühnle, Crucial impact of exchange between layers on temperature programmed desorption, Phys. Chem. Chem. Phys., 2021, 23, 18314–18321.

---

Footnotes

† Electronic supplementary information (ESI) available: Additional AFM data on microcline (001), mass spectra during degassing and sample cleavage, details of the TPD calibration and full TPD curves for water desorbing from microcline (001). A zip archive containing csv files with the raw data acquired by the mass spectrometers during TPD experiments and a text file with parameters used for data analysis. A zip archive containing cif files corresponding to the DFT structures shown in Fig. 1 and 3. See DOI: https://doi.org/10.1039/d5cp01796c

‡ Present address: Max Planck Institute for Polymer Research, 55128 Mainz, Germany.

---