Molecular dynamics simulations of discotic ionic liquid crystals: comparison of a full-charge and a scaled-charge force field

Abstract

We investigated the effect of using either a full-charge force field (FF) or a scaled-charge FF in the classical non-polarizable molecular dynamics (MD) simulation of discotic ionic liquid crystals (ILCs). We considered the tetrafluoroborate salts of three different gallic acid derivatives, namely, 3,4,5-tris(dodecyloxy)-N,N,N-trimethylbenzenamonium (1[BF₄]), 3,4,5-tris(dodecyloxy) benzyltrimethylammonium (2[BF₄]) and 3,4,5-tris(dodecyloxy)benzyltriethylammonium (3[BF₄]), also experimentally investigated in the literature, to prepare polymeric membranes for water desalination. The three cations all possess three alkyl chains, each containing 12 carbon atoms, attached to the phenyl ring via an ether linkage, making the hydrophobic part of the ion pair very significant. It is now well accepted that for simple ionic liquids (ILs), normally possessing one short alkyl chain on the ionic core, scaled-charge FFs perform much better than full-charge FFs in classical non-polarizable MD simulations by partly recovering the missing polarizability and charge transfer effects (which lowers the effective charge). However, it is unclear whether the same beneficial effect can also be found in ILCs, particularly discotics, which normally bear several and much longer alkyl chains. Therefore, it might be expected that the electrostatic contribution to phase stability is weaker for such systems and, as a consequence, the effect of charge scaling is less important. The results of our simulations clearly show that the scaling of charge instead has a very significant and favourable effect for the simulations of ILCs, although the volume fraction of the hydrophobic regions in discotic systems (hardly affected by the scaling) is significantly larger than that of the ionic region.

---

Introduction

Ionic liquid crystals (ILCs) are materials formed of molecules with the same functional groups found in ionic liquids (ILs) and exhibit mesomorphism, i.e. liquid crystal (LC) phases.^1–4 Typical examples include imidazolium, pyridinium, and ammonium cations paired with inorganic anions such as halides, tetrafluoroborate, and hexafluorophosphate. However, when compared with ILs, there is the additional requirement for one or more relatively long alkyl chains (typically in the cation) in order to induce microphase segregation, which is ultimately responsible for the induction of liquid crystalline behaviour.⁵ For this reason, ILCs normally exhibit positionally ordered LC phases, while nematic phases are extremely rare. This holds true for rod-like molecules, e.g. 1-alkyl-3-methylimidazolium salts, thus often forming ionic smectic A phases, and for discotic molecules, e.g. 3,4,5-trisalkoxyphenyl derivatives, which often form ionic columnar phases.

ILCs are exploited in various fields where an ordered transport of mass/charge is sought, for example, in separation technology⁶ or as electrolytes in energy storage devices.⁷ They are also used as lubricants⁸ and ordered reaction media.⁹ For example, 3,4,5-trisalkoxyphenyl-guanidinium-based ILCs showed a strong dependence of thermal behaviour on counteranions.¹⁰ However, pairing the guanidinium cation with an anionic phosphorescent metal cluster of molybdenum turned the LC phase into a smectic A phase with near-infrared emission properties, as a first example of an emitting clustomesogen.¹¹ Furthermore, coarse-grained MD simulations of the structural properties of such systems have been recently reported.¹² Among the many examples that can be found in the literature, very interesting applications of ILCs have been proposed by Kato's group as membranes for water desalination using disk-like ILCs forming either columnar or cubic phases.¹³ One such example is the gallic acid (GA) derivatives shown in Fig. 1, which are also based on the 3,4,5-trisalkoxyphenyl moiety.

Fig. 1 Chemical structure of the studied gallic acid derivatives. Y = NMe₃⁺: 3,4,5-tris(dodecyloxy)-N,N,N-trimethylbenzenamonium, 1[BF₄] salt; Y = CH₂NMe₃⁺: 3,4,5-tris(dodecyloxy) benzyltrimethylammonium, 2[BF₄] salt; Y = CH₂NEt₃⁺: 3,4,5-tris(dodecyloxy)benzyltriethylammonium, 3[BF₄] salt.

The phase behaviour of these systems has been experimentally investigated in ref. 14 (for compound 1[BF₄]) and in ref. 15 (for compounds 2[BF₄] and 3[BF₄]). The three tetrafluoroborate salts all exhibit a columnar hexagonal (Col_h) phase before the clearing point. The transition temperatures and phases are summarized in Table 1.

Table 1 Experimental transition temperatures (K) of the investigated systems. Data from Rref. 14 and 15

		T (Cr–P)^a		T (P–Colh)		T (Colh–Iso)
a P represents the intermediate phase before the hexagonal columnar phase investigated here.
1[BF4]	Cr	316	Colr1/r2	413	Colh	469	Iso
2[BF4]	Cr	317	Cr	333	Colh	479	Iso
3[BF4]	Cr	305	Cubbi	322	Colh	399	Iso

---

These molecules, composed of a wedge-shaped cation (see Fig. 2(a)), self-assemble into ionic discotic liquid crystal phases through the formation of a discotic unit formed by four ion pairs (see Fig. 2(b)). Then, the disks stack on top of each other to form columns (Fig. 2(c)). The discotic columns have an interior ionic channel (the red part in Fig. 2) and an external hydrophobic matrix (the green part in Fig. 2). We anticipate here that due to the presence of three alkoxy chains, the hydrophobic part of the molecule is relatively large compared to other ILCs, such as imidazolium salts bearing only a single alkyl chain attached to the ionic core of the cation and forming ionic smectic phases. It is also significantly larger than the hydrophobic part of simpler ILs which, by definition and exactly because the alkyl chain is short, do not form ionic mesophases.

Fig. 2 Schematic representation of the self-assembly of the 4 wedge-shaped cation–anion pairs (a), producing a disk-like structure (b), which stacks with other disks to form columns (c). The so-formed column has a conductive ionic channel in the middle (red) isolated by a hydrophobic sheath (green).

In this work, by means of fully atomistic MD simulations, we are interested in investigating the microscopic structural and dynamic details of the systems shown in Fig. 1 in their hexagonal columnar and isotropic phases. MD simulations of ILCs are becoming a useful tool for improving our understanding of the many factors affecting the stability of ionic mesophases, which include van der Waals interactions, electrostatic forces, and hydrophobic effects.¹⁶ We will compare the results of the simulations with the available experimental data in order to assess the performance of the force field (FF) used, either in a full-charge or scaled-charged version. A system analogous to 3[BF₄], but having a final butadiene moiety in two of the three alkoxy chains (instead of a CH₃(CH₂)₃-group), has been investigated by Washizu et al. using MD simulations.^17,18 The authors used a scaled-charge FF for these systems, as it is now well-known that full-charge FFs for ionic fluids overestimate the electrostatic interactions.^19,20 This is a consequence of the fact that in condensed phases of ionic fluids, there are large polarizability and charge-transfer effects that reduce the effective charge of the ions. In fact, in such kind of molecules, both effects are important since anions are highly polarizable and they are good charge donors. In contrast, cations normally have π systems with empty low-energy orbitals, which render them polarizable and good charge acceptors. The partial charges of the various atom types of the molecules, as well as the total charge of the ions, are clearly a key parameter of the classical FF, as for the isotropic ILs. Furthermore, a consensus is emerging about the use of scaled instead of full charges to approximately account for charge transfer and polarization effects.¹⁶ Clearly, scaling the fixed partial charges of the atoms is a quick and effective way to account for charge fluctuations in the bulk, while a more correct approach would be to recur to polarizable FFs. Recently, several groups have proposed polarizable FF for ILs. For example, Wang and Maginn presented a GAFF-based FF (general amber force field) for imidazolium and pyrrolidinium ILs of bistriflimide, dicyanamide, hexafluorophosphate, tetrafluoroborate and chloride.²¹ The well-known CL&P FF by Canongia-Lopes and Padua^22,23 was also recently recast into a polarizable version with the addition of Drude dipoles determined from atomic polarizability for a large collection of cation–anion pairs, including imidazolium, pyrrolidinium, pyridinium and tetraalkylammonium and dicyanamide, tetrafluoroborate, hexafluorophosphate, triflate, tosylate, acetate and bistriflimide.²⁴ Indeed, using polarizable FFs significantly improves the description of the structural and especially dynamic properties of ILs. However, this occurs at a cost, as reported in ref. 21, of an order of magnitude increase in the computational time. Since ILs are particularly slow, this is still a major drawback in the capillary diffusion of polarizable FF for their simulation.

Conversely, FFs for ILs obtained from machine-learning (ML) algorithms have recently appeared in the literature (for example, for ethylammonium nitrate²⁵ and [C₂C₁im][EtSO₄]),²⁶ although a general and transferable ML FF has not yet been developed to the best of our knowledge.

Despite the large body of literature concerning ILs, the impact of using a full-charge vs. a scaled-charge FF in predicting the phase behaviour of ionic liquid crystals systems remains unclear. In particular, since it is well-established that ILCs are formed mostly because of nano-segregation of the long alkyl chains (which separate from the ionic parts), it might be expected that scaling the charge of a FF when simulating ILCs will have a smaller or no effect compared to the simulation of an IL, where the alkyl chains are normally much smaller and the electrostatic terms dominate the intermolecular interactions and microscopic organization of the phase. In fact, as we will show, the volume fraction of the hydrophobic region in discotic ILC systems is much larger than the volume fraction of the ionic region. Therefore, it is with the aim of answering the above question that we present here the results of full-charge and scaled-charge atomistic MD simulations of the three tetrafluoroborate salts of Fig. 1, and compare them with experimental data. It is also important to recall that the drawbacks mentioned above concerning the use of polarizable ILs are particularly more burdensome for ILCs which, because of the long-range order, are generally even slower in dynamics and they require relatively large boxes to accommodate an appropriate number of repeating units (layers, columns, etc.).

Computational details

The initial parameters of the FF employed were generated using the tools of the LigParGen website;^27–29 therefore, they are based on the OPLS-AA general FF.³⁰ However, the partial charges of the aromatic ring and of the ammonium substituents were calculated with the CHELPG method³¹ using Gaussian16³² and using a small model of the cation; that is, the 3,4,5-trimethoxyammonium cations analogous to 1, 2 and 3, respectively. The level of theory used was MP2/cc-pVTZ(-f)//HF/6-31G(d). Together with the fully charged systems, we also adopted a scaled-charge FF where the partial charges were scaled by a factor of 0.831, as suggested by Washizu et al.^17,18 for an analogous gallic acid derivative. This value of the scaling parameter is quite close to the empirical scaling factor of 0.8 recommended by Sun et al.¹⁹ for ionic liquids, and also used in our previous simulations of smectic ionic liquid crystals.³³ The Lennard-Jones parameters and partial charges (for the full-charge case) are reported in ESI† in Table S1, together with a reference pdb structure of the cation 2.

A first set of simulations was run for relatively small systems made of 320 ion pairs (ca. 45k atoms, depending on the system) in the columnar hexagonal phase (Col_h), taken as the starting point, to assess how accurately the two FFs (full-charge and scaled-charge) reproduce the clearing temperature of the LC phase. Initial configurations of the boxes were prepared as follows: the discotic unit made by four cation–anion pairs was first assembled by replicating the single ion pair coordinates in the xy plane. Two disks were then stacked on top of each other with staggered units of gallic acid derivatives and anions, and then replicated along the z direction to form a column. Finally, four columns were replicated and arranged in a hexagonal fashion. The process is shown schematically in Fig. S1 in ESI.† All the simulations were performed in a rectangular box whose dimensions in the xy plane perpendicular to the column direction (which are along the z axis, which is also the director of the LC phase) are in the ratio of to allow for the hexagonal symmetry. Semi-isotropic pressure coupling was used to decouple the xy box fluctuations from the ones in the z direction, and periodic boundary conditions were applied in the three dimensions. The software package GROMACS version 2020.6 was used.^34–37

The initial boxes, having a relatively low density, were first energy minimized and then relaxed at 200 K and 15 bar (using a Berendsen thermostat and barostat) with 2.5 ns of NpT simulation. The timestep was set to 1 fs and the leap-frog algorithm was employed. The cut-off radii were set to 1 nm for both the van der Waals and electrostatic short-range interactions. The particle mesh Ewald technique was employed to account for long-range electrostatic interactions.

Then, a series of simulations with increasing temperature were carried out. Starting from 300 K and increasing the temperature in steps of 50 K, the systems were brought up to 600 K (well above the experimental clearing point). Then, starting from the high temperature final structure, a cooling run was used to bring the systems back to the ambient temperature with temperature steps of 25 K. For each temperature, the systems were simulated for 10⁸ time-steps. Trajectories of 100 ns were produced, of which the last 50 ns were used for the analysis, sampling the trajectory every 100 ps. For these production runs, the cut-off values for the van der Waals and electrostatic interactions were increased to 1.4 nm. X–H bonds were constrained using the LINCS algorithm.

Using the configurations previously obtained at 400 K in heating, larger systems were built by replicating the box twice along the x and y directions, thus resulting in initial configurations with 16 independent columns (1280 ion pairs, approximately 180k atoms). These larger boxes were equilibrated for 100 ns at 400 K using the same parameters mentioned above, and only considering the case of a scaled-charge FF. The common temperature of 400 K was selected in order to highlight the structural differences related only to the different chemical structure of the cationic head. In addition to this, starting from the final configurations at 400 K, we further equilibrated each system for 20 ns, followed by 40 ns of production run, at three specific temperatures near 400 K, where the cell parameters have been previously measured by X-ray scattering (433 K, 423 K and 393 K, for 1[BF₄],¹⁴2[BF₄]¹⁵ and 3[BF₄],¹⁵ respectively), for a direct comparison of structural data.

Radial distribution functions (RDF) or g(r), representing the probability density to find two atoms at a distance r, and the mean squared displacements (MSD), were evaluated using GROMACS built-in routines. Diffusion coefficients D were then obtained from the time dependence of the MSD as MSD(t) = 2dDt, where d is the dimensionality; that is, d = 1 for linear diffusion, d = 2 for diffusion in a plane, and d = 3 for a diffusion in a full tridimensional space. The orientational order parameter 〈P₂〉 of the vector normal to the benzene ring plane was calculated using home-made Fortran and Python codes following the procedure described in the literature.³⁸ 〈P₂〉 represents the average orientation of an ensemble of vectors, and it equals unity for the ideal case of vectors perfectly aligned along a common direction. Meanwhile, it is zero for a random distribution of orientations. Bidimensional probability density maps were calculated with MDanalysis.³⁹

Results

Evaluation of the phase behaviour: scaled-charge vs. full-charge FF

The 2[BF₄] system is presented here in detail as an example to test the FF in replicating the clearing point. Additional data for the other systems can be found in ESI.† In Fig. 3, we show the temperature dependence of the orientational order parameter 〈P₂〉. It is clear that the scaled-charge system melts into the isotropic phase just above 500 K (red filled circles). More importantly, the system undergoes a transition back into the LC phase with relatively little hysteresis in the cooling run. The clearing point is somewhat higher than the experimental value (479 K, see Table 1). However, the agreement is satisfactory from a qualitative point of view. In contrast, using the full-charge system, we do not observe a melting even at the higher studied temperature of 600 K. Moreover, as might be expected, the full-charge systems exhibit a higher orientational order related to the increased electrostatic interaction in the bulk.

Fig. 3 Temperature dependence of the orientational order parameter, 〈P₂〉, of 2[BF₄] (small box systems). (Large red circles): scaled-charge FF, heating run; (large blue circles): scaled-charge FF, cooling run; (small red circles): full-charge FF, heating run. The experimental clearing point of 2[BF₄] is 479 K. The standard deviation of the values reported in Fig. 3 is ±0.03, while the error on the mean calculated as a block average is ±0.006. Based on the temperature steps in the cooling run, the clearing point can be estimated to be 500 ± 12 K.

Visual inspection of the snapshots confirms the results obtained from the temperature dependence of the order parameter. The columns of the hexagonal columnar liquid crystal structure are composed of ionic channels, made of the [BF₄] anions and cations’ heads, separated by the hydrophobic alkyl chains that create a matrix hosting the hexagonal arrangement of ionic channels. Fig. 4 shows the snapshots viewed along the columns, i.e. along the director, of the Col_h phase at 350 K (start of the heating run), 600 K after the melting step, and again at 350 K after the cooling run starting from the previous isotropic phase for the scaled-charge FF. We clearly see that the initial columns are completely lost in the isotropic phase. Then, on cooling down, the columns are reformed. However, they are not in the same orientation as originally found, with respect to the box frame. This confirms that the system in the isotropic melt has completely lost the memory of the previous state (see also Fig. S2 and S3 in ESI,† where we also report the temperature dependence of the orientational order parameters of all of the systems). In contrast, the snapshot of the full-charge system at 600 K clearly reveals that the columnar ordering is still present (see Fig. S4 in ESI,† where the final configuration at 600 K for all three salts is shown), clearly exhibiting a hexagonal packing and no melting.

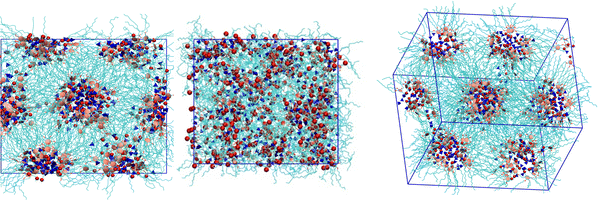Fig. 4 Snapshots of the simulation box of 2[BF₄] (small box systems) obtained using the scaled-charge FF, showing the (left) Col_h phase viewed along the column at 350 K, at the start of the heating run; (middle) at 600 K, at the end of the heating run; (right) at 350 K, at the end of the cooling run. Alkyl chains are colored in cyan, the anions in blue, the N atoms of the cation in red and the aromatic rings in pink. More snapshots of this heating–cooling run can be found in the ESI,† Fig. S3.

Although a remarkable improvement is obtained using the scaled-charge FF, the agreement of the clearing temperature between the simulations and experiments is still not quantitative. This contrasts with the prediction of the transition temperatures of typical non-ionic LCs, like cyanobiphenyls, which have been extensively studied using MD simulations by Zannoni and co-workers.^40,41 After an appropriate fine tuning of the force field, the Authors were able to reproduce the nematic–isotropic transition temperatures as a function of the alkyl chain length in n-cyanobiphenyls (with n = 4–8) within just 4 K.⁴¹ Meanwhile, for pentylcyanobiphenyl as an example, the original AMBER parameterization resulted in a clearing point that was 120 K higher than the experimental value. Thus, the key step was a fine-tuning of the FF parameters. In particular, the Lennard-Jones parameters ε and σ, representing the well-depth and contact distance, were found to strongly affect the clearing point. The authors had to vary both parameters in small increments, running equilibration and production runs for each case, searching for the optimal combination. Herein, we have not attempted a similar time-consuming approach because the scaling of the charge is a very drastic approximation that is used to partially recover the large polarizability and charge transfer effects. These effects are strong in these systems, but probably less important in neutral molecules such as cyanobiphenyls. We are therefore satisfied with the qualitative good agreement obtained from the scaled-charge FF without any additional tuning of the interaction parameters. Indeed, it is expected that further refining ε and σ, or a different charge-scaling procedure that is specifically tuned to reproduce the structural properties of these systems, will indeed improve the final results up to a quantitative agreement. However, such improvement would be at the cost of a loss of generality.

It is also useful to compare the structural arrangement of the scaled-charge and full-charge FF to see whether or not there are strong differences in the local structure. In Fig. 5, we report the RDF of the distance between the cation pairs (nitrogen atoms), anion pairs (boron atoms) and cation–anion pairs (nitrogen–boron atoms). The profiles show the typical alternation of peaks with the cation–anion RDF, having a minimum roughly corresponding to the maximum of the cation–cation and anion–anion RDF. As expected, the RDF obtained using the full-charge FF are more peaked, especially for the cation–anion case, reflecting the stronger Coulombic attraction. Apart from this, however, the general features are very similar. Therefore, the use of a scaled-charge FF does not introduce significant changes in the structure at a qualitative level.

Fig. 5 Radial distribution functions of 2[BF₄], small box systems, at T = 400 K, obtained with the full-charge (left) and scaled-charge (right) FF.

In contrast, the dynamic behaviour is more sensitive to the effects of polarizability and charge transfer. In Fig. 6, we show the diffusion coefficients obtained using the scaled-charge and full-charge FFs during the heating runs. For the full-charge systems, it was difficult in some cases to estimate the diffusion coefficient in the plane perpendicular to the columns (that is, in the xy plane) because the MSD did not have a clear linear trend. Therefore, we only report the full 3D diffusion and that one along the z-axis direction (along which, the columns are aligned during the heating run).

Fig. 6 Diffusion coefficients for the B atom of the anion (blue curves) and the N atom of the cations (red curves) as a function of temperature of 2[BF₄], small box systems. The in-plane anion diffusion for the full-charge system are omitted owing to a poor linear fitting of the MSD. (Top): Scaled-charge; (bottom): full-charge.

First, we observe a very large anisotropy of the diffusion coefficients in the LC phase. The mobility along the columns (z axis) is faster than the mobility in the direction perpendicular to the columns (that is, in the xy plane). The two diffusion coefficients converge to the same value in the isotropic phase of the scaled-charge model system. Moreover, at the same temperature, the anion is faster than the cation. However, the most striking difference is that the diffusion coefficients of the full-charge model are significantly lower than the ones obtained with the scaled-charge model. Unfortunately, there are no experimental data available for these systems. However, diffusion coefficients obtained with scaled-charge FF generally are in much better agreement with the experiments than the ones obtained with the full-charge FF.³³

Altogether, these results strongly suggest that a scaled-charge FF is much more accurate than a full-charge FF, concerning all properties related with the ion mobility (i.e., diffusion and melting transitions), which is in agreement with the literature concerning MD simulations of ILs¹⁹ and ILCs.¹⁶

Structure of the Col_h phase of [BF₄] salts

We will now discuss the structural properties of the three tetrafluoroborate salts 1[BF₄], 2[BF₄], 3[BF₄] in more detail, using the results of the scaled-charge FF. These systems were first simulated and compared at 400 K using large boxes having 16 independent columns in the simulation box (see the Computational details section). Then, while still using the large boxes, each one has been simulated at a specific temperature to compare the cell parameters with the experimental values. As an example, one snapshot of the large simulation box of 2[BF₄] is shown in Fig. 7.

Fig. 7 Perspective view along the director of the phase (z axis) of the simulation box obtained by replicating twice in the x and y direction of the small box of 2[BF₄] at 400 K. The new box contains 16 independent columns. Alkyl chains are colored in cyan, the anions in blue, the N atoms of the cation in red and the aromatic rings in pink.

A different view is given in Fig. 8, where we show a snapshot of the system with the alkyl chains forming the hydrophobic region, and two discotic units (one on top of the other) with each one formed by four molecules. The ionic channels are also clearly visible in Fig. 8 as an empty space since the tetrafluoroborate anions are not shown for clarity.

Fig. 8 Example of the arrangement of the discotic units formed by the four wedge-shaped cations of 2[BF₄] assembled to form a disk (see Fig. 2 for comparison). Yellow molecules: top discotic unit. Cyan molecules: lower discotic unit. Alkyl chains are indicated in grey, while the anions are omitted for clarity.

The existence of independent discotic units formed by four molecules is confirmed by the inspection of the RDF of the distance between the geometric centers of the phenyl rings projected along the axis of each column and considering only the pair of phenyl rings belonging to the same column. This RDF is shown in Fig. 9, and it clearly exhibits a strong modulation with a periodicity of approximately 4.7 Å. Moreover, there is zero probability to find two phenyl rings of the cation having a distance, projected along the column axis, shorter than 2.5 Å. This strongly indicates that the position of the four molecules forming each discotic unit is approximately co-planar.

Fig. 9 RDF of the distance between the geometric centers of the phenyl rings measured along the column axis (director of the phase) for 2[BF₄] at 400 K. Only pairs of phenyl rings belonging to the same column are considered.

In Fig. 10, we show the full anion–anion, cation–cation and anion–cation RDFs at 400 K for the three tetrafluoroborate salts. As noted already, they display the typical structure of ionic liquids where the cation–cation and anion–anion RDFs have a maximum in correspondence of the minimum of the cation–anion pairs. 1[BF₄] and 2[BF₄] have a very similar profile, while 3[BF₄] shows some differences from the other two. In fact, the cation RDFs show a first peak at 0.63 nm for both the trimethylated species, while the triethyl ammonium derivative exhibits the first peak at a slightly higher distance (0.74 nm) due to the presence of the additional CH₂ group in the three alkylammonium chains. The second peak is around 1.0 nm for all systems. However, it appears well defined only in 1[BF₄] and 2[BF₄], while it is a shoulder in 3[BF₄]. A third broad peak can be observed at around 1.36 nm in all systems.

Fig. 10 Radial distribution functions of 1[BF₄], 2[BF₄] and 3[BF₄]. (Left): Cation–cation, using the N atom as a reference. (Middle) anion–anion, using the B atoms as a reference. (Right) anion–cation. T = 400 K.

The first peak represents the average distance between the nitrogen atom of the two adjacent GA units laying on the same plane and constituting the same disk resulting from the assembly of four GA cations. This information is clearly depicted in Fig. 11. The second peak at around 1 nm corresponds to the N–N distance of the gallic acid units on the opposite side of the same discotic unit, as can be seen in Fig. 11 (right panel).

Fig. 11 Example of the in-plane organization of GA units of 2[BF₄] forming a disk with the distance of two adjacent N atoms (left) or two opposite N atoms (right) indicated in Å.

Concerning the anions (B–B) RDFs (middle panel in Fig. 10), an analogous behaviour is observed as for the cation RDFs. The shape of the RDFs for both trimethylated systems is similar with the first peak at 0.72 nm, a second peak at around 1.0 nm, and a third broad peak at 1.35 nm. The triethyl ammonium derivative system lacks the peak at around 1.0 nm, which appears as a side shoulder of the first one. Moreover, the first peak of the anion–anion RDF is shifted to larger distances (0.79 nm), compared to the previous two systems. This is again due to the hindrance of the additional CH₂ group in 3[BF₄] since the second peak of the anion–anion RDF corresponds (on average) to two anions separated by a cation.

The mixed anion–cation RDFs, N–B (right panel in Fig. 10), are similar for all three systems. They present a first sharp peak at 0.5 nm, and a second peak at around 1.0 nm and at 1.10 nm for the trimethylated and triethylated systems, respectively.

An interesting view of the structure is provided by the bidimensional density plots of the probability to find a given atom in a region of space projected on the plane perpendicular to the phase director. These are shown in Fig. 12. The alkyloxy chains in positions 3, 4, and 5 of the benzene ring act as spacers between the charges due to their hydrophobicity. Thus, they segregate ionic regions and, in turn, promote the liquid-crystalline organization of the bulk phase. Instead, the cationic heads and anions form the ionic channels. From the 2D maps in Fig. 12, we can see that the phenyl rings can be considered as defining a sort of internal wall of the ionic channels, while the cations’ heads and anions are contained within the channels.

Fig. 12 2D density maps projected in the xy plane perpendicular to the director of the phase for the system 2[BF₄] at T = 400 K representing the probability density to find (top) the center-of-geometry of the phenyl ring, (middle) the nitrogen atom of the cation's head, and (bottom) the boron atom of the anion at that given (x, y) coordinate.

Finally, some more quantitative structural parameters can be obtained from the planar RDF; specifically, the RDF of the distance resolved along the direction perpendicular to the director of the phase, labeled as g_xy(r). These have been calculated for each system at three different temperatures where X-ray scattering data are available (see Table 2), and they are shown in Fig. 13.

Table 2 Some structural parameters at T = 433 K for 1[BF₄], T = 423 K for 2[BF₄] and T = 393 K for 3[BF₄]. Data are obtained from the in-plane radial distribution functions of Fig. 13. Values are in nm

System	RDF	Col–Col distance α	Ionic radius ri	d 10 (simul)	d 10 (expt)	% Vol. hydrophobic^a	% Vol. ionic^a
a The volume fractions of the hydrophobic and ionic regions in the bulk phases are calculated as described in the main text. b From ref. 14. c From ref. 15.
1[BF4]	N–N	3.53	0.78	3.06	2.93^b	85.0	15.0
	B–B	3.57	0.78	3.09		85.2	14.8
2[BF4]	N–N	3.82	0.79	3.31	3.02^c	86.6	13.4
	B–B	3.79	0.82	3.28		85.5	14.5
3[BF4]	N–N	3.93	0.85	3.40	3.07^c	85.5	14.5
	B–B	3.86	0.85	3.34		85.0	15.0

---

Fig. 13 Radial distribution function of the distance measured in the xy plane, perpendicular to the director of the phase (z axis). (Left): cation–cation, using the N atom as a reference. (Right) anion–anion, using the B atoms as a reference. Temperatures are indicated in Table 2.

These distribution functions can be used to measure the inter-column (inter-channel) distance by measuring the distance of the first peak from the origin (approximately 3.5–4.0 nm), and the radii of the ionic channels by measuring the width at half height of the same peak. The results are reported in Table 2.

The intercolumn distance is basically the same either using the anion or cation peaks for all of the systems. This geometrical parameter corresponds to the cell parameter α, which is related to the d₁₀ reflection in the X-ray scattering by simply d₁₀ = α cos(30°). For 1[BF₄], 2[BF₄] and 3[BF₄], the results obtained from the simulations are therefore d₁₀ = 3.075, 3.30 and 3.37 nm, respectively, to be compared with the experimental values of 2.93,¹⁴ 3.02¹⁵ and 3.07¹⁵ nm for 1, 2 and 3, at 433, 423 and 393 K, respectively. The results of the simulations appear to be only about 10% larger than the experimental value. The difference is acceptable considering that the FF was not accurately tuned to reproduce the experimental data, except for an empirical scaling of the charge. Moreover, the qualitative trend of the cell parameters, in the order 1 < 2 < 3, is correctly reproduced by the simulations. This trend can be traced back to the increased size of the cationic head in going from 1 (phenyltrimethylammonium), to 2 (benzyltrimethylammonium) and finally 3 (benzyltriethylammonium). Also, the radius of the ionic channels (measured either from the B–B in plane RDF or the N–N in plane RDF) increases slightly with the larger size of the cationic head.

Finally, as mentioned in the Introduction, we are interested in the effect of charge scaling. This effect is expected to be relevant only for the atoms bearing a significant partial charge. Therefore, we do not expect it to be important for the methylene and methyl groups of the alkyl chains (see Table S1 in ESI†). It is thus useful to estimate the volume fraction of the hydrophobic and ionic regions in the bulk phase. These fractions are the same as the relative areas of hydrophobic and ionic regions in the plane perpendicular to the phase director. Using the distances reported in Table 2 (the Col–Col distance α, which is the “side” of a hexagon representing the hexagonal cell and the radius r_i of the circle representing the ionic channel), we obtain the corresponding areas as α² × 2.598 and 3πr_i², respectively (the coefficient 3 for the ionic area counts the three ionic channels fully included within one hexagonal cell, with one in the center and 1/3 of the six channels at the corners). The so-calculated volume fractions are also reported in Table 2. As we can see, the volume of the hydrophobic regions is much larger than the volume of the ionic regions.

Conclusions

In summary, we have investigated the structural and dynamic properties of three tetrafluoroborate salts of derivatives of gallic acid which form hexagonal columnar ionic liquid crystal phases by classical atomistic MD simulations. We have compared the performance of two OPLSAA-based force fields, one using full-charge and the second one using a charged scaled by a factor of 0.831.

The scaled-charge FF shows a significantly improved performance compared to the full-charge FF since (i) it exhibits a semiquantitative agreement with the clearing points; (ii) it provides a better description of the dynamics; and (iii) it is also in good agreement with the structural parameters obtained from scattering experiments. The full-charge FF overestimates the electrostatic interaction, a phenomenon which is well known when dealing with small ions (e.g., systems forming ionic liquids).¹⁹ For compounds forming only ionic liquid phases (besides the crystal phase, e.g., non-mesogenic ILs), the alkyl chains are usually short (1–10 carbon atoms, but the most common ILs have alkyl chains of 2–5 carbon atoms). Therefore, the electrostatic interaction is expected to be very important and scaling the charge of a FF is expected (and indeed observed) to have a significant impact on the properties of the isotropic phase as obtained from the simulations.¹⁹ However, ionic liquid crystals differ from ILs mainly because the alkyl chains are relatively long. In fact, it is the hydrophobicity of the alkyl chains that drives the long-range nano-segregation, ultimately leading to the formation of the mesophase. Thus, it might be expected that the electrostatic interaction in ILCs, playing a minor role compared to ILs, might also be less affected or even unaffected by the scaling the charge.

In this work, we have clearly shown that this is not the case. We should note that the partial volume of the alkyl chains represents a very large fraction (no less than 85%) of the total volume (see Table 2). However, despite this large difference in the partial volumes of hydrophobic (almost not affected by charge rescaling) and ionic parts, the total amount of the charge strongly influences the dynamic properties. Most importantly, it impacts the clearing point in the simulations. Thus, using a full-charge FF, once the system is nano-segregated, the high electrostatic interaction that takes place within the ionic channels is sufficient to over-stabilize the ordered phase with respect to the isotropic melt even if the effect is highly localized in space. In fact, it is exactly because the ionic parts and hydrophobic parts are nano-segregated that the scaling has a significant effect on the overall thermal stability of the columnar phase. We might look at the ionic channels as a sort of iron wires in reinforced concrete, slowing down the dynamics of the whole phase when using the full-charge FF, where the electrostatic interactions are not properly dumped by polarizability and charge transfer effects, as in real systems.

Conversely, the microscopic structural properties of the columnar phases studied with the scaled-charge FF agree well with the available experimental data. This suggests that, while scaling the charge indeed improves the dynamic properties and the melting temperature (which is also related to the mobility of the ions), it does not have any negative repercussion on the structural properties. Therefore, we recommend using scaled-charge versions of classical non-polarizable force fields for the simulation of ionic liquid crystals in cases when polarizable FFs are not available or too computationally demanding.

Conflicts of interest

There are no conflicts of interest to declare.

Data availability

The data supporting this article have been included as part of the ESI.†

Acknowledgements

Calculations were run in part on the Linux cluster of the Computational Chemistry Community, the Department of Chemical Sciences, the University of Padova (C3P). We also thank CINECA (Bologna) for the allocation of computing time through the Class B ISCRA project no. HP10B8AOVV and Class C ISCRA project no. HP10CUC24I. We are grateful to the Department of Chemical Sciences and Technology of Materials (DSCTM) of CNR and the Institute on Membrane Technology of CNR for sponsoring a PhD Scholarship to VM.

References

1. K. Goossens, K. Lava, C. W. Bielawski and K. Binnemans, Chem. Rev., 2016, 116, 4643–4807.
2. G. Saielli, Crystals, 2019, 9, 274.
3. N. Kapernaum, A. Lange, M. Ebert, M. A. Grunwald, C. Haege, S. Marino, A. Zens, A. Taubert, F. Giesselmann and S. Laschat, ChemPlusChem, 2022, 87, e202100397.
4. K. Salikolimi, A. A. Sudhakar and Y. Ishida, Langmuir, 2020, 36, 11702–11731.
5. G. Saielli, A. Bagno and Y. Wang, J. Phys. Chem. B, 2015, 119, 3829–3836.
6. J. Kloos, N. Joosten, A. Schenning and K. Nijmeijer, J. Membr. Sci., 2021, 620, 118849.
7. Q. Ruan, M. Yao, D. Yuan, H. Dong, J. Liu, X. Yuan, W. Fang, G. Zhao and H. Zhang, Nano Energy, 2023, 106, 108087.
8. M. D. Avilés, C. Sánchez, R. Pamies, J. Sanes and M. D. Bermúdez, Lubricants, 2019, 7, 72.
9. D. W. Bruce, Y. Gao, J. N. C. Lopes, K. Shimizu and J. M. Slattery, Chem. – Eur. J., 2016, 22, 16113–16123.
10. M. Ebert, A. Lange, M. Müller, E. Wuckert, F. Gießelmann, T. Klamroth, A. Zens, A. Taubert and S. Laschat, Phys. Chem. Chem. Phys., 2024, 26, 11988–12002.
11. M. Ebert, I. Carrasco, N. Dumait, W. Frey, A. Baro, A. Zens, M. Lehmann, G. Taupier, S. Cordier, E. Jacques, Y. Molard and S. Laschat, Chem. – Eur. J., 2022, 28, e202103446.
12. M. A. Kolmangadi, Y. M. Wani, A. Schönhals and A. Nikoubashman, J. Phys. Chem. B, 2024, 128, 8215–8222.
13. T. Ichikawa, T. Kato and H. Ohno, Chem. Commun., 2019, 55, 8205–8214.
14. B. Soberats, M. Yoshio, T. Ichikawa, X. Zeng, H. Ohno, G. Ungar and T. Kato, J. Am. Chem. Soc., 2015, 137, 13212–13215.
15. T. Ichikawa, M. Yoshio, A. Hamasaki, S. Taguchi, F. Liu, X. Zeng, G. Ungar, H. Ohno and T. Kato, J. Am. Chem. Soc., 2012, 134, 2634–2643.
16. G. Saielli, in Comprehensive Computational Chemistry, ed. A. Laaksonen and F. Mocci, Elsevier, 2024, pp. 723–761.
17. Y. Ishii, N. Matubayasi and H. Washizu, J. Phys. Chem. B, 2022, 126, 4611–4622.
18. Y. Ishii, N. Matubayasi, G. Watanabe, T. Kato and H. Washizu, Sci. Adv., 2021, 7, eabf0669.
19. Z. Sun, Z. Gong, L. Zheng, P. Kalhor, Z. Huai and Z. Liu, J. Ion. Liq., 2022, 2, 100043.
20. V. Chaban, Phys. Chem. Chem. Phys., 2011, 13, 16055–16062.
21. N. Wang and E. J. Maginn, J. Phys. Chem. B, 2024, 128, 871–881.
22. J. N. Canongia Lopes, J. Deschamps and A. A. H. Pádua, J. Phys. Chem. B, 2004, 108, 2038–2047.
23. J. C. Lopes, J. Deschamps and A. A. H. Padua, J. Phys. Chem. B, 2004, 108, 11250.
24. K. Goloviznina, J. N. Canongia Lopes, M. Costa Gomes and A. A. H. Pádua, J. Chem. Theory Comput., 2019, 15, 5858–5871.
25. H. Montes-Campos, J. Carrete, S. Bichelmaier, L. M. Varela and G. K. H. Madsen, J. Chem. Inf. Model., 2022, 62, 88–101.
26. R. Islam, M. F. Kabir, S. R. Dhruba and K. Afroz, Comput. Mater. Sci., 2021, 200, 110759.
27. L. S. Dodda, I. de Vaca, J. Tirado-Rives and W. L. Jorgensen, Nucleic Acids Res., 2017, 45, W331–W336.
28. W. L. Jorgensen and J. Tirado-Rives, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 6665–6670.
29. L. S. Dodda, J. Z. Vilseck, J. Tirado-Rives and W. L. Jorgensen, J. Phys. Chem. B, 2017, 121, 3864–3870.
30. W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236.
31. C. M. Breneman and K. B. Wiberg, J. Comput. Chem., 1990, 11, 361–373.
32. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. J. Montgomery, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision B.01, Gaussian, Inc., Wallingford CT, 2016.
33. G. Saielli, Phys. Chem. Chem. Phys., 2021, 23, 24386–24395.
34. S. Páll, M. J. Abraham, C. Kutzner, B. Hess and E. Lindahl, in Solving Software Challenges for Exascale, ed. S. Markidis and E. Laure, 2015, pp. 3–27.
35. M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25.
36. H. J. C. Berendsen, D. van der Spoel and R. van Drunen, Comput. Phys. Commun., 1995, 91, 43–56.
37. S. Páll, A. Zhmurov, P. Bauer, M. Abraham, M. Lundborg, A. Gray, B. Hess and E. Lindahl, J. Chem. Phys., 2020, 153, 134110.
38. V. Mazzilli, K. Satoh and G. Saielli, Soft Matter, 2023, 19, 3311–3324.
39. N. Michaud-Agrawal, E. J. Denning, T. B. Woolf and O. Beckstein, J. Comput. Chem., 2011, 32, 2319–2327.
40. R. Berardi, L. Muccioli and C. Zannoni, Chem. Phys. Chem., 2004, 5, 104–111.
41. G. Tiberio, L. Muccioli, R. Berardi and C. Zannoni, Chem. Phys. Chem., 2009, 10, 125–136.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp01726b

---