Open Access Article
Open Access ArticleUnderstanding the destruction of CH+ with atomic hydrogen at low temperatures: a non-adiabatic dynamical study†
Pablo del Mazo-Sevillano a,
Alfredo Aguado
a,
Alfredo Aguado a,
François Lique
a,
François Lique b,
Rafael A. Jara-Torob and
Octavio Roncero
b,
Rafael A. Jara-Torob and
Octavio Roncero *c
*c
aDepartamento de Química Física Aplicada (UAM), Unidad Asociada a IFF-CSIC, Facultad de Ciencias Módulo 14, Universidad Autónoma de Madrid, 28049, Madrid, Spain
bUniv Rennes, CNRS, IPR (Institut de Physique de Rennes), UMR 6251, F-35000, Rennes, France
cInstituto de Física Fundamental (IFF-CSIC), C.S.I.C., Serrano 123, 28006, Madrid, Spain. E-mail: octavio.roncero@csic.es
First published on 26th June 2025
Abstract
Carbon hydrides play a crucial role in the formation of complex organic molecules in highly UV illuminated regions of the interstellar medium (ISM). The formation of CH+ is the first step in the reactions leading to the formation of various carbon hydrides. CH+ formation is relatively well understood with strong agreement between theoretical and experimental results. However, its destruction by collision with the H atom, at low temperatures of interest in the ISM, is in contrast still not well understood and there is a large discrepancy between theoretical and experimental data [R. Plasil et al., AstroPhys. J., 2011, 737, 1], which are almost an order of magnitude smaller than various classical and quantum mechanical calculations. In this work we have computed and fitted a new set of non-adiabatic potential energy surfaces (PES) for the title system, including the three lower adiabatic states. We then investigate three possible sources of disagreement with the experimental results: non-adiabatic effects from regions near the conical intersections, and rotational and vibrational excitation of the CH+ molecule. We conclude that vibrational excitation of the CH+ plays a major role in reducing the reactivity at low temperatures, and we raise the question of whether vibrational thermalization of the CH+ is not fully achieved in the experiment. Such non-thermalized conditions could explain the decrease of the measured reaction rate constant.
1. Introduction
Carbon plays a pivotal role in the formation of biomolecules and, in the interstellar medium (ISM) all the molecules with more than 6 atoms, known as complex organic molecules (COMs), have at least one carbon atom. Ionized carbon hydrides are the first steps in forming such molecules in strongly UV illuminated gas,1,2 such as the fronts of molecular clouds (also called photodissociation regions, PDRs) or protoplanetary disks (PPDs), and are formed through sequential hydrogen addition3 starting from the C+ cation as
 | (1) |
This sequence stops with the formation of CH3+ because its reaction with a hydrogen molecule is very slow, and different experimental studies did not observe the formation of CH4+ or CH5+ in these reactions at low temperatures.4–6 CH3+ in the ISM then reacts with other atoms and molecules, initiating the formation of a great variety of organic molecules observed in space. These CHn+ (n = 1–5) carbon cations have anomalous properties and have opened the field of carbocation chemistry,7,8 where the spectroscopic study of these species, pioneered by Oka and co-workers,9–12 is extremely important to characterize these intermediates in astrochemistry.
CH+ was one of the first molecules observed in space13 and it has been observed in many different environments of the ISM since then. However, CH2+ has not been observed yet, and CH3+ was only observed in 202314 using the James Webb space telescope (JWST). Very recently, vibrationally excited CH+ and CH3+ were observed in emission using the JWST in the Orion bar and the protoplanetary disk d203-506.15 The simulation of the abundance of these species in different rovibrational states requires the knowledge of state-to-state rate constants to consider the chemical excitation in radiative transfer models.
The formation of CH+ in reaction (1) is reasonably well known. The reaction is endothermic by 0.393 eV (ref. 16) and presents a deep well of ≈4.5 eV. The integral cross-sections and thermal rate constants have been extensively studied experimentally.16–24 Many theoretical studies have been carried out using quasi-classical trajectory (QCT)25–28 and phase space and transition state theory.16,23,29 Also, quantum mechanical state-to-state rate constants have been obtained,30,31 which have been widely used in radiative transfer models.
However, the reverse reaction in reactions leading to the destruction of CH+ with atomic hydrogen is less understood. Federer and co-workers32 first measured the thermal reaction rate constant of 7.5 × 10−10 cm3 s−1 at 300 K, and later at higher temperatures.33 These values are about 2–3 times lower than the Langevin limit. New surprising experimental results were measured more recently in an ion trap combined with a cold effusive H-atom beam,34 revealing a one order of magnitude drop in the reaction rate constant below 60 K, while for higher temperatures, the values are consistent with those measured by Federer et al.32,33 This decrease at lower temperatures was initially interpreted as a decrease of the efficiency of the reaction with decreasing rotational state (j) of the CH+. There are two different families of theoretical calculations based on different families of ground adiabatic potential energy surfaces (PES's). Warmbier and Schneider35 and Bovino et al.,36 using close coupling in hyperspherical coordinates and negative imaginary potentials, respectively, reported a decrease of the reactive rate constant below 100 K. However, detailed theoretical studies27,37,38 performed accurate time-independent close coupling calculations on the ground adiabatic PES, and found the thermal rate constant to be nearly constant below 100 K, with a value of ≈10−9 cm3 s−1, far higher than that measured by Plasil et al.34 Moreover, Werfelli et al.38 found that the state-dependent rate constant decreases with an increase in the rotational excitation j, contradicting the initial interpretation of the experimental measurement.
A recent work39 considered the participation of other processes not included by Plasil et al.,34 such as the stabilization of ions by collisions with the He atoms used in the experiment as a buffer to thermalize CH+ in the ion trap, to model the kinetics and compare with the measured abundances of C+, CH+, CH2+ and CH3+. No appreciable difference was found in the abundances with or without including these extra processes, and the possibility of non-adiabatic effects was proposed as responsible for the reduction of reactivity at low temperatures. Indeed, it is important to note that in the H + CH+ linear approach, there is a conical intersection (CI), which was discussed in detail when constructing the ground electronic adiabatic PES.27,37,38 This PES was able to reproduce the cusp introduced by this CI rather satisfactorily. The question is then how non-adiabatic transitions affect the reaction dynamics? This is one of the objectives of this study.
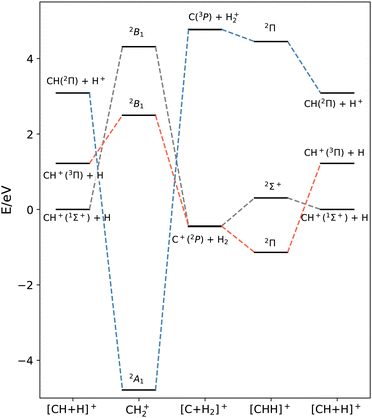
The crossings in the CH2+ system are not limited to this crossing, but instead are far more complicated as found by Liskow et al.,40 and the deep well describing CH2+(2A′) arises from a series of crossings involving C+(2P) + H2, C(3P) + H2+ and C(1D) + H2+, as represented in Fig. 1. In ref. 39 a simple energy-based diabatization model41 was applied to some fixed configurations, showing that it was able to reproduce the crossings occurring at relatively long distances, but failed to reproduce some intruder electronic states giving rise to the CH2+(2A′) well. Note that very recently, a 2 × 2 diabatic model has been developed for the two lower adiabatic states of CH2+, considering the 1Σ+ and 3Π states on the CH+ + H2 asymptote and the 2P states on the C+ + H2 asymptote. The formation of CH+ was studied using a wave packet method.42
In this work, we include a third state in the diabatization to account for the intruder state originating from the C(3P) + H2+ asymptote and giving rise to the deep CH2+(2A′) well, using a neural network method guided by symmetry considerations, as described in Section 2. We then study the destruction of CH+ by hydrogen atoms using quantum wave packet (WP), adiabatic statistical (AS) and quasi-classical (QCT) methods to obtain physical insight into the reaction, showing the impact of non-adiabatic dynamics in the reactive cross-section and state-dependent rate constants, as well as the effect of rotational and vibrational excitation of the CH+ reactant, as described in Section 3. Finally Section 4 is devoted to extracting some conclusions.
2. Coupled diabatic potentials
Using an adiabatic representation in dynamical calculations with several electronic states requires the inclusion of non-adiabatic couplings, which are very localized near avoided crossings and diverge at conical intersections. To avoid this, a unitary transformation is often done to a so-called diabatic representation,43 in which the non-adiabatic couplings are negligible and the couplings between diabatic states arise from the potential. However, a strict diabatic electronic basis does not exist in general, other than for diatomic states. Hence it is not possible to simultaneously remove all the components of the nuclear momentum coupling.44,45 Still, the diabatic states remove the divergence near conical intersections, leaving residual non-adiabatic couplings, introducing the so-called regularized diabatic representations.46There is no general method to build the unitary diabatization transformation and it is very system dependent. Traditionally, the methods are classified as derivative-based, energy-based and property-based methods.47 The complexity increases with the number of atoms and the number of states that need to be included. Diabatization localized in the Franck–Condon region using the linear couplings in the Hamiltonian has shown great success in the photodissociation of polyatomic systems.48 Also, in the fewest switching surface hopping method49 used in classical trajectory methods, a local diabatization along each individual trajectories can help to overcome the difficulties.
However, the description of the whole configuration space, from reactants to products along the reaction path, becomes very complex, especially when more than two electronic states are involved. Many different approaches have been used as recently reviewed.50 An energy-based method using a model Hamiltonian based on the inclusion of three states correlating to C+(2P) was explored39,41 yielding excellent results in the asymptotic regions. However, this method is not adequate when higher “intruder” electronic states appear in the interaction region, producing a disruption. In the field of neural networks, PES several automatic and semiautomatic methods exist to produce a diabatic potential energy matrix (PEM) depending on whether diabatic information is required in the procedure. Automatic methods have been successfully applied to treat two state systems.42,51 However, they are not directly applicable to more states since unexpected state crossings appear. Semiautomatic methods such as diabatization by deep neural network (DDNN)52,53 incorporate some diabatic information to the fit, aiming to govern the order of the diabatic states across the configuration space. In this work, we employ a version of the DDNN method where the diabatic dataset is generated from highly symmetric configurations (SDDNN). The steps to apply the SDDNN method are: (I) identify the correlation diagram between diabatic states, (II) compute the adiabatic and diabatic datasets and (III) fit the PEM with a feed-forward neural network.
2.1. Correlation diagram and ordering of diabatic states
Prior to the production of a diabatic set of potential energy surfaces, it is crucial to understand how the various diabatic states interact in the different regions of the configuration space. While in the adiabatic representation, the order of the electronic energies can be trivially assigned by the energy values, this is not the case in the diabatic representation, where the order of the different states usually changes. Probably, the simplest regions to identify are the asymptotic reactants and products where the couplings between the diabatic states tend to zero, making them coincide with the adiabatic states.In this work, we treat three lower A′ adiabatic states: CH+(1Σ+) + H, CH+(3Π) + H and CH(2Π) + H+ on the reactant side, and C+(2P) + H2 and C(3P) + H2+ on the product side. The criteria to identify the correlation diagram between diabatic states are as follows: (i) preserve the Λ projection of the electronic wavefunctions in the C∞v configurations and (ii) an ab initio analysis of highly symmetric configurations (i.e. C2v). There is one Σ state which correlates CH+(1Σ+) + H with C+(2P) + H2(1Σg+) through CH2+ (2B1), and two Π states which correlate CH+(3Π) + H with C+(2P) + H2(1Σg+) through CH2+ (2B1), and CH(2Π) + H+ with C(3P) + H2+ through CH2+ (2A1). In the following we refer to these diabatic states as Σ, Π1 and Π2.
These three states cross in various regions of the PES as sketched in Fig. 1 producing three relevant conical intersections for the collinear CH+ + H approach on both the C and H sides and a third one as C approaches perpendicularly the H2 in Jacobi coordinates. In these C2v configurations, some of the couplings vanish, making these highly symmetric geometries a perfect choice from which to generate the diabatic dataset employed in the training process.
2.2. Ab initio calculations
The ab initio calculations have been performed at the state averaged CASSCF level of theory followed by an MRCI-F12 calculation with the cc-pVTZ-F12 basis set with MOLPRO 2012.1. The core electrons of the C are closed while the active space consists of six orbitals. The four lower A′ and A′′ adiabatic states are computed. Similar to the DDNN method, in the SDDNN method, two datasets are required, which we will refer to as adiabatic and diabatic datasets. The specific grids employed to obtain the points are indicated in the ESI.†The adiabatic dataset consists of a set of all geometries with their respective adiabatic energies ordered by increasing energy. It is prepared by computing the ab initio energy of a grid of geometries in terms of the coordinates presented in the inset of Fig. 2 in the Cs symmetry group. A total of ≈58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 ab initio are included in the adiabatic dataset. About 85% of them have an energy lower than 5 eV with respect to the CH+ + H asymptote. The specific grids employed to computed these points can be found in the ESI.†
500 ab initio are included in the adiabatic dataset. About 85% of them have an energy lower than 5 eV with respect to the CH+ + H asymptote. The specific grids employed to computed these points can be found in the ESI.†
The diabatic dataset is required in the SDDNN method to enforce a specific ordering of the diabatic states. It is formed by a smaller set of points calculated at the higher symmetry C2v which allows identifying the diabatic states. In this case we select the geometries with θ = 0°, θ = 180° and γ = 90°. In this group, the A′ states split into the A1 and B1 representations. However, two B1 states appear, and its order must be assigned “by hand” according to the correlation scheme presented above. A total of ≈1500 geometries are included in this dataset.
2.3. Diabatic potential energy matrix
The diabatic potential energy matrix employed in this work is represented as:
 | (2) |
The diagonal elements represent the diabatic energies of each state, and the non-diagonal elements their couplings.
| Ui = ViNN + VLR,i (i = Σ, Π1, Π2) | (3) |
 | (4) |
 | (5) |
The adiabatic energies are the eigenvalues of the diabatic matrix in eqn (2). The charge transfer in the adiabatic states is implicitly associated with the transfer between the different diabatic states.
VNN is fitted with a FI-NN54 with 5 input neurons, three hidden layers of 40 neurons each, and an output layer with 6 elements—three diagonal and three non-diagonal elements in eqn (2). Hyperbolic tangent activation functions are applied between hidden layers except for the last output layer. The FIs are computed with the negative exponential of the interatomic distances (exp(−αd)), with α = 0.5a0−1.
The loss function to minimize during the training process is:
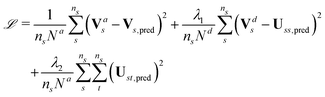 | (6) |
In summary, the key points to achieve a successful diabatic potential energy matrix are: (1) the diabatic dataset which governs the order of the diabatic states for highly symmetric geometries according to the correlation diagram proposed for the system, (2) the functional form to describe the couplings, which vanish for highly symmetric configurations, and (3) the minimization of the diabatic couplings, avoiding spurious state flips.
2.4. Long-range interactions
The long-range interactions are included at the diabatic level as expressed in eqn (3). In this work they have only been considered for the CH+(1Σ)+H and C+(2P) + H2(1Σg+) asymptotes, that is, the reactant and product sides of the Σ diabatic state, and the product side of the Π1 diabatic state.For the CH+ + H rearrangements we consider charge–induced dipole, dipole–induced dipole and dispersion. For the C+ + H2 rearrangement charge–quadrupole and charge–induced dipole are considered:
 | (7) |
 | (8) |
![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) = R + Rlim·exp(−(R − Re)) (Rlim = 100.0a0 and Re = 2.5a0) cancels out the long-range terms as R – the distance between the atom and the diatom's center of mass—approaches zero. This term has a two-fold purpose. First, it avoids the divergence of the long-range term at R → 0 and second, it allows a smooth transition between the long-range terms of the various rearrangement channels. Its effect, together with the accuracy of the long-range term is exemplified in the ESI.† ϕ is the angle between the diatomic bond and
= R + Rlim·exp(−(R − Re)) (Rlim = 100.0a0 and Re = 2.5a0) cancels out the long-range terms as R – the distance between the atom and the diatom's center of mass—approaches zero. This term has a two-fold purpose. First, it avoids the divergence of the long-range term at R → 0 and second, it allows a smooth transition between the long-range terms of the various rearrangement channels. Its effect, together with the accuracy of the long-range term is exemplified in the ESI.† ϕ is the angle between the diatomic bond and ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) . There are three possible rearrangement channels in the long-range, two for CH+ + H, depending on which hydrogen is bonded to the C atom, and C+ + H2. For each diabatic state, we can compute the long-range energy in every possible arrangement:
. There are three possible rearrangement channels in the long-range, two for CH+ + H, depending on which hydrogen is bonded to the C atom, and C+ + H2. For each diabatic state, we can compute the long-range energy in every possible arrangement:| WLR,Σ = (Vlr,CH++H, Vlr,CH++H, Vlr,C++H2) | (9) |
| WLR,Π1 = (0, 0, Vlr,C++H2) | (10) |
| WLR,Π2 = (0, 0, 0) | (11) |
| Wd = (σ(rCH1), σ(rCH2), σ(rHH)) | (12) |
| s = argmin(Wd) | (13) |
| VLR,χ = (WLR,χ)s | (14) |
Note that there is no continuity issues since the index s will only change upon reaction, when the three particles are close together and all of the long-range interactions are canceled due to the change of independent variable to ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) . In fact, the parameters Rlim and Re can be tuned in order to guarantee the energy conservation, by turning off the long-range contributions at larger or shorter distances.
. In fact, the parameters Rlim and Re can be tuned in order to guarantee the energy conservation, by turning off the long-range contributions at larger or shorter distances.
During the training process, these long-range contributions are included in the diagonal elements of the PEM in eqn (3). Therefore the VNN terms are effectively fit to the difference between the ab initio and the long range energies. At long distances between the reactants or products the only remaining interaction energy is the long-range term, without the need to use a switching function.
2.5. Features of the diabatic PES
As mentioned previously, the order of the diabatic states is governed by the inclusion of a rather small dataset of geometries with C2v symmetry. This scarcity of data raises the question of how well does the PEM extend to other geometries belonging to the less symmetric Cs group. In Fig. 2 the interaction of the CH+ + H and C+ + H2 systems is presented for different angles. In all cases, the diabatic description is smooth, and we do not observe any unexpected spurious state flip. It is interesting to note that for the CH+ + H approach at θ = 180°, the model automatically finds that the two states correlating to Π states have to exchange in order for the PEM to be smooth elsewhere.Fig. 2 also presents the three relevant CIs in the system. Two of them appear in the CH+ + H approach for θ = 0° and θ = 180°. The third CI is found in the C+ + H2 approach with γ = 90°. These CIs no longer appear once the system moves away from these highly symmetric configurations. Fig. 2 also shows the deepest well describing the CH2+ system in the bottom right panel. In all cases, the points are the ab initio points, and the solid lines are the adiabatic eigenvalues obtained in the diabatic fit, whose diagonal elements are shown by dashed lines, showing excellent agreement.
Fig. 3 presents the minimum energy paths for each of the diabatic states in terms of the H–H–C angle, showing the main features of the diabatic states. In the bottom panels, for large α angles near the H–H–C linear configuration, the two lower diabatic states, Σ and Π, are well separated from the third one, which causes the appearance of the CH2+ well at α = 30°. The Σ diabatic state is repulsive in the two rearrangement channels, with a maximum at rCH − rHH = 0. In contrast, the Π diabatic state is attractive in the two rearrangement channels showing a shallow well at rCH − rHH = 0. The Π state correlates with the excited CH+(3Π) and and it crosses the Σ before its minimum, giving rise to the CI. In the top panels, at bent geometries, α = 30 and 80°, the third diabatic state is strongly established, crossing the other two diabatic states to form the CH2+ well.
For α = 180° a direct mechanism can be found where the H atom approaches CH+ from the H side. For this linear approach, we do not find a deep well. For the reaction to occur in the ground electronic state, the system has to go through a CI, changing from the Σ state to the low lying Π state. On the other hand, as α tends to 0°, the first Π state becomes repulsive and the second Π state is highly attractive. The deeper well of this Π state corresponds to the equilibrium geometry of CH2+. When the system proceeds from this side, the process is expected to become statistical.
Finally, we investigate the accuracy of the non-adiabatic coupling matrix elements (NACMEs). The analytical NACMEs in the PES are computed as explained in ref. 55:
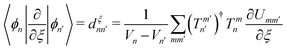 | (15) |
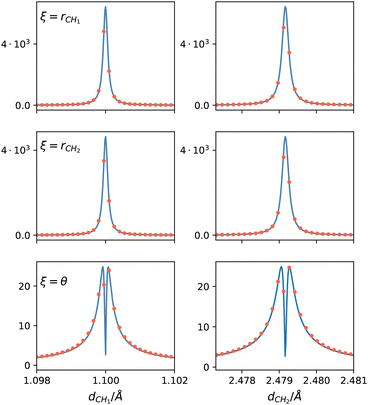 | ||
| Fig. 4 Comparison of the NACMEs along the two C–H distances computed in the PES (blue line) and ab initio at a CASSCF level (red dots) close to the CI, at θ = 0.01°. ξ indicates the coordinate with respect to which the NACME is computed as indicated in eqn (15). | ||
Finally, Table 1 presents the RMSE of the fitted potential energy surface for the range of energies of interest.
| E/eV | State ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) |
State à | State ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) |
|---|---|---|---|
| −4.0 | 35.7 (404) | — | — |
| −3.0 | 30.0 (1090) | — | — |
| −2.0 | 27.7 (2029) | — | — |
| −1.0 | 29.0 (4677) | 33.3 (41) | — |
| 0.0 | 26.0 (13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 782) 782) |
17.2 (3743) | — |
| 1.0 | 23.6 (24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800) 800) |
21.9 (11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 140) 140) |
— |
| 2.0 | 23.3 (32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 001) 001) |
26.1 (24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 192) 192) |
— |
| 3.0 | 22.7 (39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 324) 324) |
26.6 (34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 563) 563) |
35.9 (4967) |
| 4.0 | 22.0 (49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 113) 113) |
25.3 (46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 307) 307) |
33.0 (27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 491) 491) |
3. Reaction dynamics
3.1. Quantum wave packet dynamics
The study of the low energy quantum dynamics of the CH+ (v = 0, j = 0) + H → C+ + H2 reaction is challenging since it presents a deep well and several non adiabatic crossings. In this work, we use a time dependent wave packet approach, requiring a careful convergence study, especially of the absorption at the edges of the radial grids. The parameters used in the code are listed in the ESI.† The quantum dynamical calculations are performed with the MADWAVE3 program,56 using a modified Chebyshev propagator,57–62 representing the Hamiltonian in reactant Jacobi coordinates in a body-fixed frame, using grids for the internal coordinates (the distances r and R, associated to the CH internuclear vector, and the vector joining CH+ center of mass and the H atom), and a basis for the electronic coordinates and total angular momentum J, with modulus J and projections M and Ω, on the z-axis of the space-fixed and body-fixed frames, respectively. The flux on individual final states of the H2(v′, j′) products is evaluated by a reactant-to-product coordinate transformation method.63Two sets of calculations are performed, one including the three coupled diabatic states and the second with only the ground adiabatic potential obtained after diagonalization of the 3 × 3 electronic Hamiltonian developed above. The converged results for J = 0 and initial CH+(v = 0, j = 0) are shown in Fig. 5. In both cases, the reactivity presents rapid oscillations with energy, associated with resonances corresponding to the CH2+ complex in the deep well. At higher energies, the reaction probability in the 3 × 3 diabatic model is larger, by approximately a factor of 2. This increase is attributed to the increase of density of states in the C+ + H2 asymptote, to which two electronic states correlate in the diabatic representation, while only one correlates to the CH+ + H products. At low energies, the adiabatic and 3 × 3 diabatic are in general closer, simply because the number of open channels in the C+ + H2 side is already considerably higher even in the adiabatic model. All this indicates that the inclusion of the electronic couplings does not reduce the reactivity under this regime.
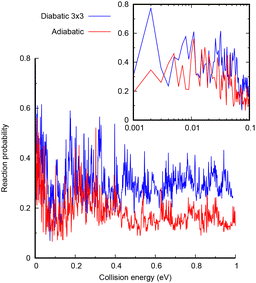 | ||
| Fig. 5 Total reaction probability for CH+ (v = 0, j = 0) + H → C+ + H2 reaction as a function of translational energy for the adiabatic (red) and 3 × 3 diabatic model (blue). | ||
The presence of resonances, especially at low energies, requires very long propagations to achieve convergence, typically of the order of 105 Chebyshev iterations. In addition, for insertion reactions presenting deep wells, it is important to include many Ω projections to obtain the appropriate density of states and properly describe the reaction dynamics. All this together, makes the calculation of all J values computationally very demanding. Up to J = 90 is required to converge the partial wave summation to obtain the reaction cross-section. In this study, we use Ωmax = min(J, 15) and we limit the calculations to J = 0, 5, 10, 15, 20, 25, 30, 40, 50 and 60. For intermediate J values, the state-2-state reaction probabilities are obtained with the J-shifting interpolation method,64 as successfully applied to the reverse reaction.30
The total reactive cross-section obtained for the adiabatic and the 3 × 3 diabatic PESs is shown in Fig. 6. The cross-section obtained in the 3 × 3 diabatic case is slightly larger than that for the single adiabatic PES (below 4 meV and above 0.1 eV) or very close. Above 0.1 eV and below 5 meV, the ratio between the 3 × 3/adiabatic cross-section is lower than 1.2, and this may be explained by the higher density of states of C+ + H2 products in the 3 × 3 case, because two electronic states correlate to this limit.
 | ||
| Fig. 6 Total CH+ (v = 0, j = 0) + H → C+ + H2 reaction cross-section for the adiabatic and 3 × 3 diabatic model obtained by WP and AS methods, as indicated in the caption. | ||
The continuous decreasing slope of the two cross-sections above 7–9 meV is consistent with the Langevin behavior for charge–induced dipole long-range interactions in CH+ + H. The change in the behavior below 4–5 meV is attributed to the cusp introduced by the electronic crossing at some configurations and could explain a slight decrease of the corresponding rate coefficients compared to the Langevin model.
3.2. Statistical versus direct mechanisms
To further analyze the reaction dynamics, in Fig. 6, the results obtained with the adiabatic statistical (AS) approach65 are also shown, which were obtained with the implementation recently done for the N+ + H2 reaction,66 and details are shown in the ESI.† Two cases are also considered, one with only one electronic state in each rearrangement and the case in which there are three electronic states in the C+ + H2 asymptote.The difference between the two AS results is similar to that obtained with the exact wave packet treatment, but larger, with a ratio of ≈1.5 instead of 1.2. The AS results are in general larger than the wave packet results, but very close in the 3–100 meV interval. This slight overestimation is attributed to the presence of an alternative direct reactive and non reactive routes, as it was recently found,39 which in the exact calculations may reduce the reactivity. These alternative routes can be seen in Fig. 3, especially in the diabatic MEP for α = 180° which shows a direct connection between reactants and products, with a rather low barrier with no entrance to the deep insertion well. The diabatic barrier at this angle is of 0.26 eV, which gets even lower in the adiabatic representation. Therefore, this direct route reduces the flux through the deep insertion well, and it is the reason for the difference between the wave packet and statistical methods.
The two AS results continue increasing with decreasing energy below 3 meV. The reason is that the effective adiabatic potential curves do not show any maxima because the average of the potential matrix elements somehow washes out the cusp introduced by the electronic crossing at some (linear) configurations. The fast decrease of the AS results above 0.5 eV corresponds to the disappearance of the well in the effective adiabatic potentials for J > 65. Thus, for J > 65 the reaction to form C+ + H2 is closed in the AS treatment, and only lower partial waves contribute to the reactive cross-section.
The structures of the AS cross-sections with energy are associated with the opening of C+ + H2 (N(H2), producing a relative increase in reactive probabilities) and CH+ + H (N(CH+), producing a decrease) channels. The N(CH+)/N(H2) ratio continuously increases with energy, and becomes 1 at approximately 0.1 eV, where the AS cross-sections show a change of slope (see Fig. 1 in the ESI†).
3.3. Quantum reactive rate constants
The total reaction rate is obtained by numerical integration of the reactive cross-section with a Boltzmann distribution.30 104 extra points are added in the 10−4–10−3 eV interval to obtain reliable results at low temperatures such as 10 K. These extra points are extrapolated with a constant value, because of the nearly constant, or slightly decreasing, behavior of the reactive cross-section below 5 meV. Therefore, the rate constant around 10 K is slightly overestimated, but the effect is very small and cannot be noticed in the scale of the figure.The results obtained with the 3 × 3 and adiabatic electronic models are shown in Fig. 7, and are compared with the state-selected rate constant for j = 0 obtained by Werfelli et al.38 using an accurate time-independent hyperspherical close coupling method with a fit of an adiabatic PES. The 3 × 3 results are in very good agreement in the interval 50–500 K with respect to that of Werfelli et al.,38 and the present results are slightly smaller. The two present results show a weak decrease below 30 K, far from that of the experimental results by Plasil et al.34
 | ||
| Fig. 7 Total CH+ (v = 0, j = 0) + H → C+ + H2 reaction rate constant for the adiabatic (red) and 3× 3 diabatic model (blue). The results in black lines with points correspond to the state selected rate constant of Werfelli et al.38 for j = 0. The experimental results are taken from Plasil et al.34 and Federer et al.32 | ||
3.4. Rotational effects on rate constants
The WP state-selected simulated rate constants for j = 0 are in reasonable agreement with experimental results above 100 K, considering the error bars, but they are systematically above the experimental results below 60 K. The theoretical state-selected rate constants decrease with increasing j, as shown by Werfelli et al.38 To check this, quasi-classical calculations including surface hopping using the fewest switches method of Tully49 have been performed using the MDwQT code55 (details are shown in the ESI†). Initial quantum conditions for the CH+ (v = 0) state are given by the adiabatic switching method,67,68 and all reactive trajectories are considered because the reaction is exoergic and very long-lived complexes are formed in the deep well of the CH2+ system.In Fig. 8 QCT and AS reaction rate constants for different j rotational levels are presented. The QCT result for j = 0 is about a factor of two lower than the WP result while the 3 × 1 AS presents much better agreement. Moreover, the QCT calculations do not show a marked dependence of the reaction rate constant with the rotational level, in contrast to the statistical results and those previously reported by Werfelli et al.,38 which are in good agreement. All these arguments yield to the conclusion that the QCT approach fails to accurately describe the reactive rate constant, loosing the memory of the initial state when forming long-lived complexes. QCT and AS results present lower and upper limits to the quantum Wave packet results, which are computationally more demanding. However, this mild effect of the initial rotational state is not sufficient to explain the huge decrease of the reactive rate constant found experimentally.
 | ||
| Fig. 8 Total CH+ (v = 0, j = 0, 1, 2, 3, 4, and 5) + H → C+ + H2 reaction rate constants obtained with QCT calculations including surface hopping (left panel) and the AS 3 × 1 method (right panel). The experimental results are taken from the studies by Plasil et al.34 and Federer et al.32 | ||
Therefore the origin of the decrease of the experimental rate constants below 50 K is not attributed to either non-adiabatic effects or the rotational excitation of CH+. The present 3 × 3 diabatic model includes the three relevant electronic states participating in the dynamics. It is rather accurate in the reproduction of the high level ab initio adiabatic calculations and the non-adiabatic couplings as shown above. We can therefore conclude that the crossings occurring among these electronic states are not responsible for the reduction of the rate constant at low temperatures.
There are other electronic mechanisms not considered in this model. First, the Renner–Teller couplings with the A′′ states. It has been argued that including this effect can reduce the reactivity.69 However, in this case, the A′′ states correlate only with C+ + H2 asymptote, but through the excited electronic states of CH+ products, not accessible at the energies considered here. Therefore, in the present case, it is expected that the inclusion of Renner–Teller couplings cannot reduce the reactivity, even more, it could increase it.
Also, the spin–orbit couplings are not considered here. The inclusion of spin–orbit sublevels would lead to the increase of C+(2P) + H2 density of states, while weakly affecting the CH+(1Σ+) + H(2S), whose degeneracy would be multiplied by a factor of two. Again, this would favor the reaction towards C+ formation.
Finally, in this work we study yet another possible source of reduction of reactivity at low temperatures, which is the potential excitation of the CH+ vibration during its generation in the experiments.
3.5. CH+ vibration
In the experimental work, the CH+ reactants were obtained via electron bombardment of methane, and confined in an ion trap,34 where the CH+ were thermalized in a gas of cold He atoms. It was then assumed that CH+ reactants cooled down to a Boltzmann distribution of rovibrational states. Vibrational cooling by the light and cold He atoms is expected to be less efficient than rotational cooling, especially at low temperatures. For instance, the rotational quenching cross-section computed with the close coupling scattering equations70 is about two orders of magnitude larger than the vibrational quenching cross-section for the CH+ molecule.To check this hypothesis we have performed QCT with surface hopping and AS calculations for v > 0 described above and the results are shown in Fig. 9. Clearly, the reaction rate constants decrease with initial vibrational excitation. In the QCT calculations this decrease with v seems to gradually reduce with increasing v and saturates for v = 5. For v = 5 the total reaction state-dependent rate is nearly a factor of 10 lower than for v = 0, and very close to the experimental results, considering the error bars.
 | ||
| Fig. 9 Total CH+ (v = 0, 1, 2, 3, 4, and 5, j = 0) + H → C+ + H2 reaction rate constants obtained with QCT calculations including surface hopping (left panel) and the AS 3 × 1 (right panel) methods. The thermal rate constant is also presented as a dashed black line in the right panel. The experimental results are taken from the studies by Plasil et al.34 and Federer et al.32 | ||
In the right panel of Fig. 9, the same rate constants obtained with the AS method show a similar trend. The AS approach is closer to the full quantum WP results, as described above. The statistical character of the reaction is not only more accurate than the QCT results, but also produces a more drastic reduction of the rate constant with increasing v.
What is the reason why vibrational excitation produces a diminution of the reaction rate constant? AS results give a very simple explanation in terms of the density of states of reactants and products, as illustrated in Fig. 1 of the ESI,† Section S3. As the total energy increases, the density of states of CH+ reactants increases more rapidly than that of H2 simply because it has much lower rotational constant and lower vibrational frequency.
Hence, one can see that the magnitude of the CH+ + H rate constants measured by Plasil et al.34 strongly depends on the vibrational temperature of CH+ in the cell. Plasil et al.34 considered that the internal degrees of freedom of CH+ are coupled to the cold environment efficiently by inelastic collisions with helium buffer gas so that both the rotational and vibrational temperatures of CH+ are equal to the kinetic temperature after a few ms. Hence, CH+ was expected to be only in the ground vibrational manifold and in the first few rotational levels when it reacted with H. One could consider that local thermodynamic equilibrium (LTE) conditions are reached if kα × [He] × Δt > 1 (α = vib or rot), where kvib and krot are the quenching rate constants, [He] is the density of He in the cell and Δt is the time before the reaction.
Lets consider a typical density of He of 1013 cm−3 and a time of 10 ms for relaxing hot CH+ formed by electronic impact on CH4 (those values are the typical values provided by Plasil et al.34). One would hence see that kvib and krot have to be of the order of ≈10−11 cm−3 s−1 to reach LTE conditions after 10 ms. Stoecklin & Voronin70 computed rotational and vibrational quenching cross-sections for the He–CH+ collisional system. The corresponding rotational quenching rate coefficients derived from their cross-sections were found to be of the order of magnitude of ≈10−10 cm−3 s−1 so that one can safely assume that the rotational temperature of the gas is equal to the kinetic temperature. In contrast, the corresponding vibrational quenching rate coefficients derived from the cross-sections of Stoecklin & Voronin70 were found to be of the order of ≈10−12 cm−3 s−1 at 10 K indicating that a time of 10 ms is certainly not enough to reach LTE conditions for the vibrational distribution. Hence, for the measurement at low temperature (T < 50 K), one could expect that part of the CH+ in the cell was in vibrationally excited states when it reacted with H. Because of the lower reactivity of CH+ in vibrationally excited states, one could see that the determination of the thermal CH+ + H rate constants derived by Plasil et al.34 should have considered the vibrational distribution of CH+ in the cell that is unlikely to be the one of a Boltzmann distribution. Rate coefficients for the vibrational quenching of ions are expected to rapidly increase with increasing temperature and vibrational states. This increase of the rate coefficients would help in reaching LTE conditions faster when the temperature is above 50 K explaining the better agreement between the experiments and the theoretical calculations (assuming that only CH+(v = 0) is populated) above 60 K.
Therefore, we conclude that the most plausible reason for the disagreement between theory and the experimental measurements at low temperatures below 50 K is that the vibrational energy transfer at this low temperature with the He atoms is not efficient enough, and CH+ in the trap is still excited in v > 1 vibrational levels. Under this assumption, appropriately weighting the rate constants for several vibrational states over a non-Boltzmann vibrational distribution, the theoretical description can reasonably describe the measured results. New experimental measurements are therefore needed to check this assumption.
In order to validate this assumption, the vibrational relaxation of CH+ with He as a function of temperature should be studied in detail for highly excited vibrational states. Also, new experimental studies under different conditions, ideally with controlled vibrational distribution of CH+ reactants, are needed.
4. Conclusions
In this work we have developed new coupled diabatic potential energy surfaces, including three electronic states and accurate long-range interactions, to study the non-adiabatic dynamics of the CH+ + H → C+ + H2 reaction as a possible explanation for the one order of magnitude decrease of the reactive rate constant measured below 50 K.34 To do so, a new diabatization technique has been developed based on neural networks and guided by information of highly symmetric configurations.A variety of dynamical methods have been used to study the non-adiabatic dynamics, revealing that the inclusion of electronic couplings produces some changes in the reactive cross-sections and rate constants, but were unable to reproduce the drastic reduction of the reactive rate constant below 50 K. Initial rotational excitation of CH+ has been analyzed and produces a slight decrease, in agreement with previous results.38
Finally, the initial vibrational excitation of CH+ has been studied, showing a remarkable decrease of the reactive rate constant as a function of v, so that for v = 5 the rate is about ten times lower than that for v = 0, and in near agreement with the experiment. Above 100 K, the calculated rate constants for v = 0 are in agreement with the experiment. We therefore conclude here that the thermalization of CH+ reactants, originated by electron bombardment, with He atoms below 50 K is not efficient enough to relax the vibrational excitation of CH+, and this is the reason why the experimental results show a dramatic one order reduction below 50 K.
New experiments are needed to check this finding, and the determination of the vibrational excitation of CH+ obtained after electron bombardment of methane. Also, the efficiency of the vibrational excitation in a gas of He atoms should be studied as a function of temperature, both experimentally and theoretically.
The decrease of the destruction rate constant of CH+ with atomic hydrogen when increasing the vibrational excitation has a potential impact on the relative abundances of vibrationally excited CH+, recently observed in PDRs and PPDs,15 since in these highly UV illuminated objects, there is a relatively high abundance of atomic hydrogen.
Data availability
The fortran codes with the new 3 × 3 coupled diabatic potential energy surfaces and rate constants (with the adiabatic statistical approach) for the CH+ (v, j) + H → C+ + H2 reactions are available at ZENODO https://zenodo.org/records/15356500. The codes used for the calculations have been properly cited, and the details of the calculations are provided in the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has received funding from Ministerio de Ciencia, Innovación y Universidades, MICIU (Spain), under Grant No. PID2021-122549NB-C21, PID2021-122549NB-C22. Computational assistance was provided by the Supercomputer facilities of Lusitania founded by the CénitS and Computaex Foundation.Notes and references
- D. Smith, The Ion Chemistry of Interstellar Clouds, Chem. Rev., 1992, 92, 1473 CrossRef CAS.
- E. Herbst, Unusual Chemical Processes in Interstellar Chemistry: Past and Present, Front. Astron. Space Sci., 2021, 8, 776942 CrossRef.
- A. Stenberg and A. Dalgarno, Chemistry in Dense Photon-dominated Regions, Astrophys. J., 1995, 99, 565 Search PubMed.
- D. S. N. G. Adams and E. Alge, Some H/D exchange reactions involved in the deuteration of interstellar molecules, Astrophys. J., 1982, 263, 123 CrossRef.
- O. Asvany, S. Schlemmer and D. Gerlich, Deuteration of CHn+ (n = 3–5) in collisions the HD measured in low-temperature ion trap, Astrophys. J., 2004, 617, 685 CrossRef CAS.
- O. Asvany, S. Thorwirth, B. Redlich and S. Schlemmer, Spectroscopy of the low-frequency vibrational modes of CH3+, J. Mol. Spectrosc., 2018, 347, 1–6 CrossRef CAS.
- G. K. S. Prakash and P. V. R. Schleyer, Stable carbocation chemistry, John Wiley and Sons, New York, 1997 Search PubMed.
- G. A. Olah and G. K. S. Orakash, Carbocation chemistry, John Wiley and Sons, Hoboken, 2004 Search PubMed.
- M. W. Crofton, M.-F. Jagod, B. D. Rehfuss, W. A. Kreiner and T. Oka, Infrared spectroscopy of carbo-ions. III v3 band of methyl cation CH3+, J. Chem. Phys., 1988, 88, 666 CrossRef CAS.
- M. Jagod, M. Rösslein, M.-F. Gabrys, D. D. Rehfuss, F. Scappini, M. W. Crofton and T. Oka, Infrared spectroscopy of carbo-ions. VI. C–H stretching vibration of the acetylene ion C2H2+ and isotopic species, J. Chem. Phys., 1992, 97, 7111 CrossRef CAS.
- E. T. White, J. Tang and T. Oka, CH5+: the infrared spectrum observed, Science, 1999, 284, 135 CrossRef CAS PubMed.
- H. Wang, C. Neese, C. Morong, M. Kleshcheva and T. Oka, High-Resolution Near-Infrared Spectroscopy of CH2+ and Its Deuterated Isotopologues, J. Phys. Chem. A, 2013, 117, 9908 CrossRef CAS.
- A. E. Douglas and G. Herzberg, AstroPhys. J., 1941, 94, 981 Search PubMed.
- O. Berné, M.-A. Martin-Drumel and I. Schroetter, et al., Formation of the methyl cation by photochemistry in a protoplanetary disk, Nature, 2023, 621, 56 CrossRef PubMed.
- M. Zannese, B. Tabone, E. Habart, E. Dartois, J. R. Goicoechea, L. Coudert, B. Gans, M.-A. Martin-Drumel, U. Jacovella, A. Faure, B. Godard, A. G. G. M. Tielens, R. Le Gal, J. H. Black, S. Vicente, O. Berné, E. Peeters, D. Van De Putte, R. Chown, A. Sidhu, I. Schroetter, A. Canin and O. Kannavou, PDRs4All XI. Detection of infrared CH+ and CH3+ rovibrational emission in the Orion Bar and disk d203-506: evidence of chemical pumping, Astron. Astrophys., 2025, 696, A99 CrossRef.
- D. Gerlich, R. Disch and S. Scherbarth, C+ +H2 (j) → CH+ +H: effect of reagent rotation on the integral cross section in the threshold region, J. Chem. Phys, 1987, 87, 350 CrossRef CAS.
- W. B. MaierII, Atom Transfer in Endothermic Ion Molecule Reactions, J. Chem. Phys, 1967, 46, 4991 CrossRef.
- B. Mahan and T. M. Sloane, Dynamics of the C+–H2 reaction, J. Chem. Phys., 1973, 59, 5661 CrossRef CAS.
- E. Herbst, R. L. Champion and L. Doverspike, Low energy dynamics for reactive collisions of C+ with D2, J. Chem. Phys., 1975, 63, 3677 CrossRef CAS.
- H. H. Harris, M. G. Crowley and J. J. Leventhal, Luminescence from C+ (H2, H) CH+ below 20 eV, Phys. Rev. Lett., 1975, 34, 67 CrossRef CAS.
- C. A. Jones, K. L. Wendell, J. J. Kaufman and W. S. Koski, Internal energy of CH+ produced by the C+ (H2,H)CH+ reaction, J. Chem. Phys., 1977, 66, 5325 CrossRef CAS.
- E. Zamir, R. Levine and R. B. Bernstein, The practice of surprisal inference: products' state distribution in the chemiluminescent-molecule reaction of C+ + H2, Chem. Phys., 1981, 55, 57 CrossRef CAS.
- K. M. Ervin and P. B. Armentrout, C+ (2P) + H2 (D2,HD)→CH+ (CD+) + H(D). I. Reaction cross sections and kinetic isotope effects from threshold to 15 eV cm, J. Chem. Phys., 1986, 84, 6738 CrossRef CAS.
- T. Glenewinkel-Meyer, U. Hope, A. Kowalski, C. Ottinger and D. Rabenda, Mass-dependent dynamics of the luminescent exchange reactions C+ (2P), P+ (3P)+ H2, D2, HD, Int. J. Mass Spectrom. Ion Processes, 1995, 144, 167 CrossRef CAS.
- J. P. Sullivan and E. Herbst, A classical trajectory study of the ion-molecule reaction between C+ and H2, Chem. Phys. Lett., 1978, 55, 226 CrossRef CAS.
- M. González, A. Aguilar and Y. Fernández, Analysis of the importance of the 3A2 NH2+ minimum in the ion-molecule reaction N+(3P) +H2 → NH+ +H by quasi-classical trajectory method using a plausible single surface model, Chem. Phys., 1986, 104, 57 CrossRef.
- P. Halvick, T. Stoecklin, P. Larrégaray and L. Bonnet, Cross sections and low temperature rate coefficients for the H + CH+ reaction: a quasiclassical trajectory study, Phys. Chem. Chem. Phys., 2009, 9, 582 RSC.
- R. Warmbier and R. Schneider, Ab initio potential energy surface and reaction dynamics of H + CH+, Phys. Chem. Chem. Phys., 2011, 13, 10285 RSC.
- W. J. Chesnavich, V. E. Akin and D. Webb, Reevaluation of the rate constants for the reactions C+ + H2 yields CH+ + H and CH+ + H yields C+ + H2 at temperatures characteristic of ambient and shocked diffuse interstellar clouds, Astrophys. J., 1984, 287, 676 CrossRef CAS.
- A. Zanchet, B. Godard, N. Bulut, O. Roncero, P. Halvick and J. Cernicharo, H2 (v = 0,1) + C(2P) → H + CH+ state-to-state rate constants for chemical pumping models in astrophysical media, Astrophys. J., 2013, 766, 80 CrossRef.
- A. Faure, P. Halvick, T. Stoecklin, P. Honvault, E. Epe, J. Z. Mezei, O. Motapon, I. F. Schneider, J. Tennyson, O. Roncero, N. Bulut and A. Zanchet, State-to-state chemistry and rotational excitation of CH+ in photon-dominated regions, Mon. Not. Royal Astronm. Soc., 2017, 469, 612 CrossRef CAS PubMed.
- W. Federer, H. Villinger, F. Lindinger, P. Tosi, D. Bassi and D. Ferguson, Reaction of O+, CO+, and CH+ Ions with Atomic Hydrogen, Phys. Rev. Lett., 1984, 52, 2084 CrossRef CAS.
- W. Federer, H. Villinger, P. Tosi, D. Bassi, D. Ferguson and W. Lindinger, Laboratory Studies of Ion Reactions with Atomic Hydrogen, Molecular astrophysics, Reidel, Dordrecht, 1985, p. 649 Search PubMed.
- R. Plasil, T. Mehner, P. Dohnal, T. Kotrik, J. Glosik and D. Gerlich, Reactions of cold trapped CH+ ions with slow H atoms, Astrophys. J., 2011, 737, 1 CrossRef.
- R. Warmbier and R. Schneider, Ab initio potential energy surface of CH+2 and reaction dynamics of H + CH+, Phys. Chem. Chem. Phys., 2011, 12, 10285 RSC.
- S. Bovino, T. Grassi and F. A. Gianturco, CH+ Destruction by Reaction with H: Computing Quantum Rates To Model Different Molecular Regions in the Interstellar Medium, J. Phys. Chem, 2015, 119, 11973–11982 CrossRef CAS.
- T. Stoecklin and P. Halvick, Low temperature quantum rate coefficients of the H + CH+ reaction, Phys. Chem. Chem. Phys., 2005, 7, 2446 RSC.
- G. Werfelli, P. Halvick, P. Honvault, B. Kerkeni and T. Stoecklin, Low temperature rate coefficients of the H + CH+→ C+ + H2 reaction: New potential energy surface and time-independent quantum scattering, J. Chem. Phys., 2015, 143, 114304 CrossRef PubMed.
- R. A. Jara-Toro, O. Roncero and F. Lique, The temperature variation of the CH+ + H reaction rate coefficients: a puzzle finally understood?, Phys. Chem. Chem. Phys., 2024, 26, 21370 RSC.
- D. H. Liskow, C. F. Bender and H. F. Schaefer, Potential energy surfaces related to the ion-molecule reaction C+ + H2, J. Chem. Phys., 1974, 61, 2507 CrossRef CAS.
- S. Gómez-Carrasco, A. Aguado, M. Paniagua and O. Roncero, Coupled diabatic potential energy surfaces for studying the non-adiabatic dynamics at conical intersections in angular resolved photodetachment simulations of OHF−→OHF + e−, J. Chem. Phys., 2006, 125, 164321 CrossRef PubMed.
- W. Li, B. Dong, X. Niu, M. Wang and Y. Zhang, Non-adiabatic dynamics studies of the C+ (2P1/2,3/2) + H2 reaction: Based on global diabatic potential energy surfaces of CH2+, J. Chem. Phys., 2024, 161, 074302 CrossRef CAS PubMed.
- F. T. Smith, Diabatic and adiabatic representations for atomic collisition problems, Phys. Rev., 1969, 179, 111 CrossRef.
- M. Baer, Adiabatic and diabatic representations for atom-molecule collisions: treatment of the collinear arrangement, Chem. Phys. Let., 1975, 35, 112 CrossRef CAS.
- C. A. Mead and D. G. Truhlar, Conditions for the definition of a strictly diabatic electronic basis for molecular systems, J. Chem. Phys., 1982, 77, 6090 CrossRef CAS.
- A. Thiel and H. Köppel, Proposal and numerical test of a simple diabatization scheme, J. Chem. Phys., 1999, 110, 9371 CrossRef CAS.
- H. Köppel, in Diabatic representation: methods for the construction of diabatic electronic states, ed. D. Y. W. Domcke, H. Köppel, Conical Intersections: electronic structure, dynamics and spectroscopy, Advanced series in Physical Chemistry, World Scientific Publishing Co., 2004, p. 175 Search PubMed.
- H. Köppel, W. Domcke and L. Cederbaum, Multimode molecular dynamics beyond the born-oppenheimer approximation, Adv. Chem. Phys., 1984, 57, 59 CrossRef.
- J. C. Tully, Molecular dynamics with electronic transitions, J. Chem. Phys., 1990, 93, 1061 CrossRef CAS.
- H. Guo and D. R. Yarkony, Accurate nonadiabatic dynamics, Phys. Chem. Chem. Phys., 2016, 18, 26335–26352 RSC.
- W. Li, Y. Liang, X. Niu, D. He, W. Xing and Y. Zhang, Construction of diabatic potential energy surfaces for the SiH2+ system and dynamics studies of the Si+ (2P1/2,3/2) + H2 reaction, J. Chem. Phys., 2024, 161(4), 044310 CrossRef CAS PubMed.
- Y. Shu and D. G. Truhlar, Diabatization by Machine Intelligence, J. Chem. Theory Comput., 2020, 16(10), 6456–6464 CrossRef CAS PubMed.
- Y. Shu, F. A. Badichi, H. Guo and D. G. Truhlar, Parametrically Managed Activation Functions for Improved Global Potential Energy Surfaces for Six Coupled 5A’ States and Fourteen Coupled 3A’ States of O + O2, J. Phys. Chem. A, 2024, 128(7), 1207–1217 CrossRef CAS PubMed.
- K. Shao, J. Chen, Z. Zhao and D. H. Zhang, Communication: Fitting potential energy surfaces with fundamental invariant neural network, J. Chem. Phys., 2016, 145, 071101 CrossRef PubMed.
- C. Sanz-Sanz, A. Aguado, O. Roncero and F. Naumkin, Non-adiabatic couplings and dynamics in proton transfer reactions of Hn+ systems: Application to H2 + H2+ → H + H3+ collision, J. Chem. Phys., 2015, 143, 234303 CrossRef PubMed.
- O. Roncero and P. del Mazo-Sevillano, Madwave3: a quantum time dependent wave packet code for nonadiabatic state-to-state reaction dynamics of triatomic systems, Comp. Phys. Commun., 2025, 109471 CrossRef CAS.
- V. A. Mandelshtam and H. S. Taylor, A simple recursion polynomial expansion of the green's function with absorbing boundary conditions. application to the reactive scattering, J. Chem. Phys., 1995, 103, 2903 CrossRef CAS.
- Y. Huang, D. J. Kouri and D. K. Hoffman, General, energy-separable Faber polynomial representation of operator functions: theory and application in quantum scattering, J. Chem. Phys., 1994, 101, 10493 CrossRef CAS.
- G. J. Kroes and D. Neuhauser, Performance of a time-independent scattering wave packet technique using real operators and wave functions, J. Chem. Phys., 1996, 105, 8690 CrossRef CAS.
- R. Chen and H. Guo, Evolution of quantum system in order domain of chebyshev operator, J. Chem. Phys., 1996, 105, 3569 CrossRef CAS.
- S. K. Gray and G. G. Balint-Kurti, Quantum dynamics with real wavepackets, including application to three-dimensional (J = 0) D + H2 → HD + H reactive scattering, J. Chem. Phys., 1998, 108, 950 CrossRef CAS.
- T. González-Lezana, A. Aguado, M. Paniagua and O. Roncero, Quantum approaches for the insertion dynamics of the H+ + D2 and D+ + H2 reactive collisions, J. Chem. Phys., 2005, 123, 194309 CrossRef PubMed.
- S. Gómez-Carrasco and O. Roncero, Coordinate transformation methods to calculate state-to-state reaction probabilities with wave packet treatments, J. Chem. Phys., 2006, 125, 054102 CrossRef PubMed.
- E. Aslan, N. Bulut, J. F. Castillo, L. Bañares, O. Roncero and F. J. Aoiz, Accurate Time-Dependent Wave Packet Study of the Li + H2+ Reaction and Its Isotopic Variants, J. Phys. Chem. A, 2012, 116, 132 CrossRef CAS PubMed.
- M. Quack and J. Troe, Ber. Bunsenges, Specific rate constants of unimolecular processes II. Adiabatic channel model, Phys. Chem., 1974, 78, 240 CAS.
- S. Gómez-Carrasco, D. Félix-González, A. Aguado and O. Roncero, Spin–orbit transitions in the N+ (3PJA) + H2 → NH+ (X2Π, 4Σ−)+ H(2S) reaction, using adiabatic and mixed quantum-adiabatic statistical approaches, J. Chem. Phys., 2022, 157, 084301 CrossRef PubMed.
- T. P. Grozdanov and E. A. Solov'ev, Semiclassical quantisation of the hydrogen atom in crossed electric and magnetic fields, J. Phys. B, 1982, 15, 1195 CrossRef CAS.
- C. Qu and J. M. Bowman, Revisiting adiabatic switching for initial conditions in quasi-classical trajectory calculations: application to ch4, J. Phys. Chem. A, 2016, 120, 4988 CrossRef CAS PubMed.
- P. Defazio, B. Bussery-Honvault, P. Honvault and C. Petrongolo, Nonadiabatic quantum dynamics of C(1D) + H2 → CH + H: coupled-channel calculations including Renner-Teller and Coriolis terms, J. Chem. Phys., 2011, 135, 114308 CrossRef PubMed.
- T. Stoecklin and A. Voronin, Vibrational and rotational energy transfer of CH+ in collisions with 4He and 3He, Eur. Phys. J. D, 2008, 46(2), 259–265 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp01718a |
| This journal is © the Owner Societies 2025 |