Revealing SO₂ and CO₂ adsorption features on forsterite via IR spectroscopy and automated computational approaches

Abstract

The interaction between interstellar molecules and silicate dust plays a critical role in the chemical evolution of interstellar and circumstellar environments. In this work, we combine in situ infrared (IR) spectroscopy with automated density functional theory (DFT) calculations to investigate the adsorption and vibrational signatures of CO₂ and SO₂ on forsterite surfaces. Experimental IR spectra collected under cryogenic conditions reveal coverage- and temperature-dependent features that evolve from physisorbed to chemisorbed regimes. To interpret these observations, we construct theoretical spectra from a large ensemble of adsorption configurations across multiple surface terminations, weighted by their Boltzmann distributions at 100 K and by a per-surface abundance factor. The resulting spectra reproduce key experimental features, enabling the identification of binding trends. For CO₂, we predict the transition from weakly bound species to carbonate-like modes at lower frequencies. For SO₂, our simulations identify the dominant bands due to bidentate and tridentate chemisorption. This integrative approach highlights the importance of surface morphology and thermodynamic weighting in reconciling theory and experiments providing a framework for the spectroscopic analysis of molecular adsorption on interstellar dust analogs.

---

Introduction

Silicates are ubiquitous in cosmic and early-Earth environments. This family of minerals, particularly forsterite (Mg₂SiO₄) and enstatite (MgSiO₃), have been observed in protoplanetary disks, around young stellar objects (YSOs) and conforming dust shells around evolved stars, both in their crystalline and amorphous forms.^1–3 While dust grains grown in the interstellar medium (ISM) are expected to contain purely amorphous silicates,⁴ the upper limit for the fraction of crystalline silicate grains injected into the ISM is up to 20%,¹ yielding a total fraction of crystalline to amorphous mineral of 10% in active starburst regions.⁵ Silicates are also abundant in chondritic meteorite samples recovered on Earth,^6,7 in interplanetary dust particles (IDPs) collected in the stratosphere^8,9 and in the nuclei of the 81P/Wild (trapped within the aerogel of the Stardust mission)¹⁰ and 67P/CG comets.¹¹ Thus, assessing the interactions between common interstellar molecules and forsterite is key to understand the primary steps of the ice growth on interstellar dust particles, to rationalize molecular abundance in diffuse and molecular clouds, and to decipher the formation of interstellar compounds, including those categorized as complex organic molecules (iCOMs). For instance, quantum chemical computations based on a cluster approach to model forsterite grain particles have shown that simple S-bearing species strongly bind on the silicate surfaces, potentially accounting for the missing sulfur in the gas phase in observational spectra.¹² Calculations on crystalline forsterite surfaces have also elucidated how H₂ and H₂O may form from the adsorption, diffusion and reaction of two H atoms and H addition to O, respectively.^13,14 Combined theoretical and synthetic laboratory experiments showcasing the reactivity of HCN and H₂CO on forsterite surfaces have also shown promising results to rationalize the catalytic potential of this mineral for the formation of nucleobases and sugars, respectively.^15–18

To realistically model the interactions between silicates and key interstellar molecules in a way that can be extrapolated to astronomical observations, quantum chemical calculations and spectroscopic laboratory measurements must work in tandem. In this regard, recent work by some of us has been devoted to understanding the true nature of the interactions between forsterite and HCN by fitting calculated infrared (IR) spectra to that obtained in low-temperature laboratory experiments, revealing a mainly dissociative mechanism undergoing on the forsterite interface, catalyzed by the Lewis acid–base behavior of surface O²⁻ and Mg²⁺ sites.¹⁹ Similarly, calculations have shown that the spectroscopic features of the molecular species upon interaction with forsterite are heavily influenced by its complex surface morphology.²⁰ Thus, modeling atomistically a sufficiently large pool of adsorption structures in different coordination environments on the silicate surfaces is key to obtain an accurate representation of the potential vibrational modes in the laboratory and, ultimately, to unravel the true nature of the interaction between molecules and these mineral surfaces in the interstellar and circumstellar environments.

Among the most spectroscopically relevant astrochemical molecules, CO₂ stands out due to its observed abundance in interstellar ices, ranging from 10 to 23% relative to H₂O in dense molecular clouds and forming segregated CO₂-rich ice phases upon thermal processing of the grain.²¹ Given the affinity of CO₂ towards forsterite surfaces,²² the adsorption of CO₂ and incorporation into the mineral parent body of interstellar dust particles as carbonates has been postulated to account for the anomalous oxygen depletion in the denser ISM.^23,24 Furthermore, the interaction of CO₂ and silicate-bearing meteoritic and volcanic particles has shown to be essential for the formation of key precursors in the abiotic synthesis of relevant biomolecules on early-Earth environments.²⁵

In a similar context, SO₂ is a key sulfur-bearing molecule in the ISM. Jointly with OCS, they are both major carriers of gaseous sulfur and are the only sulfurated molecules detected in interstellar ices to date.^26,27 SO₂ adsorption and subsequent incorporation into silicate samples is of most interest given the long-standing problem of sulfur depletion in the gas phase.^12,28 Previous analyses on the adsorption of SO₂ on MgO surfaces have shown an efficient activation of SO₂ onto terminal lattice O²⁻ sites,^29,30 hinting at the potential role of acid and basic sites of forsterite in similar mechanisms.

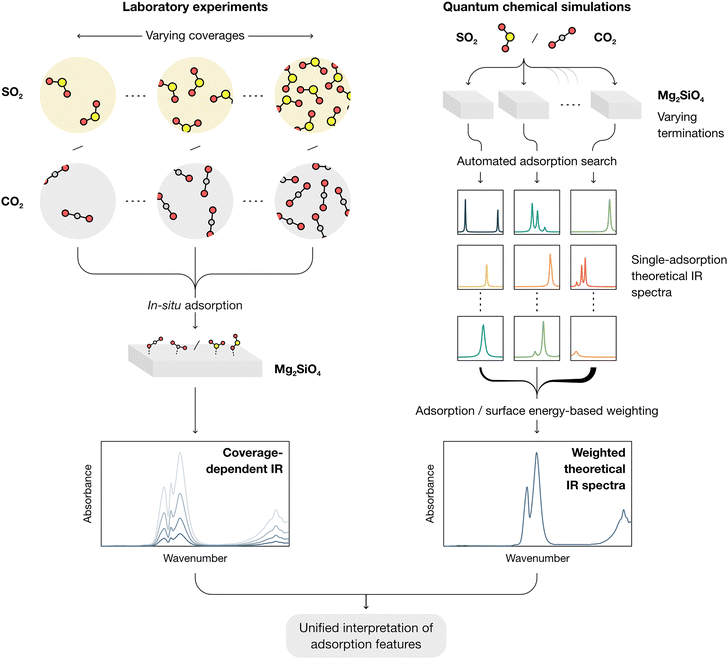
In this work, a combined framework for a comprehensive study of the interactions of CO₂ and SO₂ with forsterite surfaces (here used as a test case for cosmic silicates) is showcased, as schematized in Fig. 1. From the experimental side, molecular adsorption is studied by in situ IR spectroscopy at progressively declining coverages both on amorphous (AMS) and crystalline (CMS) forsterite at 100 K, akin to the conditions found in collapsing dense molecular clouds and cometary grains. From the modelling side, an automated computational approach is followed to obtain all potential adsorption structures of both molecules onto all theorized forsterite terminations, aimed at representing the local chemical environments found both in crystalline and amorphous surfaces. This approach simplifies the treatment of the amorphous forsterite, whose atomistic structure is unknown and would require modelling large and amorphized unit cell as recently studied by some of us.³¹ A termination-factored adsorption energy-based Boltzmann distribution is then utilized to obtain total weighed spectra of the interaction of SO₂ and CO₂ and forsterite (ensuring that the final theoretical IR spectra reflect the complexity of dust grain interfaces under astrophysical conditions), which are compared with the experimental measurements.

Fig. 1 Scheme of the combined framework presented in this work, by which the adsorption features of the studied molecules, SO₂ and CO₂, on forsterite, are studied by: in situ adsorption IR spectra at different surface coverages both on amorphous and crystalline forsterite; and an automated computational approach that models all potential adsorptions on the theoretical terminations of crystalline forsterite, and aggregates the individual spectra of adsorption configurations weighed on an adsorption energy-based Boltzmann distribution and a surface energy factor. Ultimately, this workflow provides a complete understanding of the adsorption features on the studied interface.

Methods

Experimental details

Materials. Amorphous magnesium silicate (Mg₂SiO₄, AMS) was prepared by Yamamoto et al. through the evaporation of Mg(OH)₂ and SiO₂ precursors in a high temperature plasma (∼10 000 K) and following quenching.³² Its specific surface area was 37 m² g⁻¹.

Crystalline magnesium silicate (Mg₂SiO₄, CMS) was prepared from AMS by heating it at 1073 K for 24 h in air. Its specific surface area was 26 m² g⁻¹.

IR spectroscopy. The samples were pressed in the form of self-supporting pellets, suitable for transmission IR measurements, and placed in a quartz low-temperature infrared cell equipped with KBr windows, directly connected to a conventional vacuum line, which allows performing all thermal treatments and adsorption–desorption experiments in situ.³³ Prior to the measurements, the pellets were activated at 400 °C for 1 hour under vacuum for cleaning the materials surfaces from undesired adsorbed molecules, mainly atmospheric H₂O molecules. The CO₂ and SO₂ adsorption were monitored using a Bruker Equinox 55 spectrometer equipped with a DTGS detector at 4 cm⁻¹ resolution and averaging 128 scans to obtain a good signal/noise ratio. The activated samples were cooled down for 10 minutes by the admission of liquid-N₂ into the IR cell reservoir reaching a T ∼ 100 K. Subsequently, 5 mbar of CO₂ or SO₂ were admitted inside the IR cell, then the temperature was freely increased by the natural liquid-N₂ evaporation until room temperature producing a progressive desorption of the selected molecules from the materials surfaces.

The spectrum of the sample before the adsorbate admission was subtracted to the whole batch of subsequent spectra. The spectra were also normalized by the optical density (weight of the of pellet in mg/area of the pellet in cm²) to normalize for the differences in the thickness of the pellets.

Computational details

Generation and optimization of Mg₂SiO₄ slabs. Periodic density functional theory (DFT) calculations were performed using the Vienna Ab Initio Simulation Package (VASP) code, version 6.3.2.³⁴ The bulk structure of orthorhombic forsterite (Mg₂SiO₄), belonging to the Pbnm space group, was obtained through the Materials Project³⁵ (id mp-2895), and was optimized using the Perdew–Burke–Ernzerhof (PBE) functional,³⁶ with a plane wave energy cut-off of 500 eV and a force-based convergence criterion of 0.015 eV Å⁻¹. Equilibrium lattice constants were obtained by extracting the minima of the Birch–Murnaghan equation of state of the energy of the unit cell against its volume, which was adjusted by a factor ranging from 0.98 to 1.02, incrementing in steps of 0.01. This yielded a cell with a, b and c lattice constants of 4.779 Å, 6.017 Å and 10.271 Å, respectively. During lattice optimization, sampling of the first Brillouin zone was performed using Γ-centered k-point grids of 2 × 2 × 1, 4 × 4 × 2, 8 × 6 × 4 and 12 × 10 × 6. The 4 × 4 × 2 k-point grid was selected following an energy convergence criterion of 1 meV atom⁻¹, corresponding to a mean k-point density of 21.24 k-points/Å⁻¹ along all axes. This setting was used in all subsequent DFT calculations, unless stated otherwise.

Surface models of forsterite were built using PolyCleaver,³⁷ an in-house algorithm that generates charge-neutral and non-polar slabs from crystalline bulks of ionic compounds with polyatomic anions. Hence, our base systems were modelled as slabs with thicknesses of ca. 15 Å (value above which surface energy became invariable) and containing the most energetically favorable Miller indices predicted for forsterite,^17,37,38i.e., (001), (010), (021), (101), (110), (111) and (120) (note that indices in the frequently used Pbnm space group can be converted to the standard Pnma space group by exchanging the last two indices). A vacuum of at least 15 Å was included in the c axis to avoid spurious interactions within the direction perpendicular to the plane. Atomic positions were optimized by considering a free-standing slab model, where all atoms were allowed to relax while keeping the unit cell parameters fixed at the bulk values. Surface energies, as well as the fraction of each termination in the equilibrium shape of forsterite using a Wulff construction method, were taken from previous work;³⁷ these values are reported in Table S1 (ESI†).

Active surface site identification and molecular adsorption sampling. Surface sites on the modelled slabs of forsterite were identified through a Delaunay triangulation of surface atomic centers, as described elsewhere.³⁹ In this framework, points at the vertices, edge midpoints and centers of the generated triangles were deemed to represent surface atop, bridge and fcc/hcp sites akin to those found on conventional metallic surfaces. In contrast with literature, where determination of surface atoms is performed via height-based criteria (e.g., all atoms below 0.5 Å from the highest atom are deemed as surface species), the roughness of the studied surfaces (especially those of high Miller indexes) yields surface atoms with very diverse z coordinates, and thus requires a different approach. Hence, identification of those atoms which belong to the surface is done through a systematic procedure: a given atom will be classified as superficial if it is above all atoms around it, i.e., if the coordinates of its atomic center are not eclipsed in the positive c direction by any circle defined by all other atomic center coordinates plus the ionic radii of the atoms they define. A K-dimensional tree was constructed from the coordinates of all calculated potential surface adsorption sites and was used iteratively to calculate all pairs of points within 0.7 Å along the ab plane and replace them by their centroid, until all points were separated by a distance above the threshold value. This was to both reduce dimensionality of the adsorption space and to avoid any group of closely neighboring points describing the same potential adsorption site.

The adsorption of CO₂ and SO₂ was investigated on the unit cell of the modelled slabs of forsterite on supercells with p(1 × 2) or p(2 × 1) multiplicity to ensure all slabs were close in size for consistency and avoid spurious interactions of the adsorbates with neighboring images. Then, molecule–surface interaction was assessed using a procedural approach: first, for each predicted adsorption site point, the molecule was positioned on the xy coordinates of the point and 3 Å away from the surface along the z coordinate. Then, the molecule was rotated and approached to the surface through a given anchor point until contact (defined as overlapping of the covalent radii of the atomic species of the molecule and of the surface, at which point was then separated by 0.5 Å to remove any steric hindrance and allow any diffusion to a neighboring stable position). This was carried out for one anchor point per molecule (O in both CO₂ and SO₂). The initial guess geometry of the approached molecule on the slab was then optimized using the semiempirical GFN1-xTB tight binding method implemented for periodic systems in the tblite package,⁴⁰ keeping the atoms of the slab fixed to limit the drawbacks of the GFN1-xTB method with highly ionic surfaces. The Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm implemented in the atomic simulation environment package (ASE)⁴¹ was used for structural optimization with a convergence criterion of 0.001 eV Å⁻¹. This method allows us to rapidly screen how the molecules interact with the surface at each adsorption site and potentially migrate to a neighboring site, yielding geometries akin to those obtainable using DFT. Nonetheless, an initial assessment of the method revealed that GFN1-xTB often encountered structural global minima corresponding to bidentately chemisorbed molecules which are then found to be higher in energy than their respective monodentate counterparts using DFT. To ensure that our initial screening did not fall in spurious energy pitfalls induced by this method, an additional per-atom constraint was introduced where an external Hookean-type repulsive force of 15 eV Å⁻² was applied between surface and adsorbate atoms within a distance cut-off of 2.4 Å. To account for structures converging to the same highly stable adsorption site, final geometries were then passed through a filter to remove similar structures within a root-mean-square deviation (RMSD) threshold of 2 Å. After careful inspection of the final optimized structures, this automated pipeline allows us to obtain geometrically accurate initial candidates with minimal user intervention, upon which high-precision optimizations at the DFT level of theory will be subsequently applied, as detailed below.

Finally, the positions of all atoms in the filtered geometries were optimized at the PBE level using the residual minimization method with direct inversion in the iterative subspace (RMM-DIIS) algorithm⁴² to ensure geometrical accuracy and replicability. Long-range interactions were considered by using Grimme's D2 dispersion model⁴³ for all atoms, including the modified parameters for Mg²⁺ outlined in the revised D*(N) model to take into account its highly ionic character.⁴⁴ At variance with surface relaxation, optimizations of the molecule adsorptions were performed at Γ-point only; this method yielded sufficiently accurate geometries while limiting the computational cost, given the large amount of molecular adsorptions modelled. To prevent spurious molecular dissociation of some SO₂ molecules observed in preliminary DFT calculations (where the GFN1-xTB method yielded adsorbates too close to the surface), the z distance of the adsorbate atoms in the filtered geometries that showed that behavior with respect to the surface was increased by 1.5 to 2.5 Å prior to relaxation with DFT. In these latter cases, a blocked-Davidson iteration scheme was used for optimization.

Adsorption energies (ΔE_B) of the optimized molecule–surface systems were calculated as:

ΔE_B = E_i − E^m_slab − E_mol

where E_i is the total energy of the molecule–surface adsorption complex i, E^m_slab is total energy of the isolated slab, and E_mol is the total energy of the isolated molecule in the gas phase. With the above definition, negative ΔE_B values result in favorable adsorption. 3D representations of representative adsorbates were rendered with the OVITO software.⁴⁵

Simulation of multiconfigurational infrared spectra. To model the infrared (IR) spectra of the molecules adsorbed on the forsterite surfaces, Γ-point vibrational frequencies and Born effective charges were calculated using density functional perturbation theory (DFPT), in a routine implemented in the VASP code. It is important to note that while the Hessian matrix is computed using a molecular fragment, the associated energy variations and gradients due to nuclear displacements account for the entire electronic response of the system. This ensures that all electronic charge redistributions are included in the fragment calculation. Mechanical coupling with the rest of the structure, into which the fragment is embedded, is indeed neglected, but the computed vibrational frequencies and IR intensities are minimally affected, since the interaction of the ad-atoms with the phonon modes of the mineral surface are very weak. Vibrational intensities were calculated by the approach described by Gianozzi and Baroni,⁴⁶ as implemented in the VASP-infrared-intensities script.⁴⁷ To account for any systematic errors in the adopted functional and anharmonicity, adsorbate vibrational harmonic frequencies involving the adsorption of CO₂ were scaled by a factor of 0.997, corresponding to the difference of the largest IR-active stretching vibrational mode of ¹²C¹⁶O₂ calculated with PBE (2356 cm⁻¹) with respect to tabulated data⁴⁸ (2349 cm⁻¹); similarly, frequencies of the adsorbed SO₂ molecule were scaled by a factor of 1.067, corresponding to the difference between the largest calculated ³²S¹⁶O₂ molecule stretching mode (1277 cm⁻¹) compared to tabulated data (1362 cm⁻¹). The theoretical infrared spectra for CO₂ and SO₂ are obtained by summing Lorentzian-broadened vibrational peaks at full width at half maximum of each individual adsorption. The absolute intensity of each peak is weighted by a Boltzmann factor, accounting for the relative stability of each adsorption with respect to the least energetic configuration on a given termination, plus a surface factor, representing the fractional proportion of each surface termination in the equilibrium shape obtained by the Wulff construction method. The final IR spectrum, S, is given by:
where f_m is the surface factor for the surface with Miller index m, I_i and [small nu, Greek, tilde]_i are the unweighted intensity and the wavenumber (in cm⁻¹) of the theoretical IR peak of adsorption mode i, respectively, Γ is the Lorentzian broadening parameter (which was conservatively set to 15 cm⁻¹), and w_i is the weighted Boltzmann factor, defined as:
where E_min,m is the energy of the most stable adsorption on each surface termination with Miller index m and k_B is the Boltzmann constant. The temperature T is set to the experimental value of 100 K. Final spectra are normalized.

Results and discussion

IR spectroscopy

Fig. 2 reports the experimental IR spectra of CO₂ adsorption on the dehydrated Mg-silicates. In both samples, in the initial stages of the adsorption at low temperature (blue spectra), the most intense peak is centered at 2345 cm⁻¹ and can be assigned to weakly adsorbed CO₂.^49,50 During the temperature increase (see experimental section), we observe the progressive desorption of the physisorbed CO₂ and the parallel growth of new bands in the 1700–1200 cm⁻¹ spectral region, which are due to the formation of surface carbonates.^49,50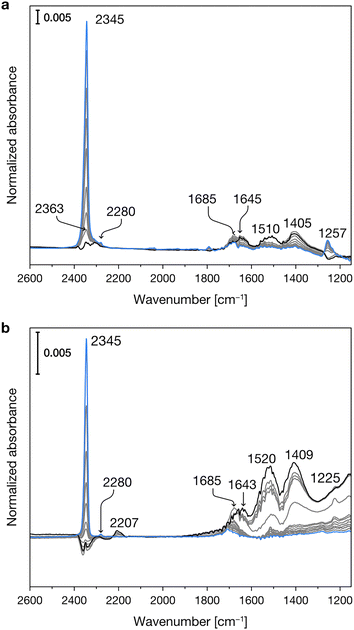

Fig. 2 Experimental IR spectra of CO₂ adsorbed at progressively increasing temperatures (from blue to black spectra) on crystalline (a) and amorphous (b) Mg-silicates previously outgassed at 673 K.

Fig. 3 shows the experimental IR spectra of SO₂ adsorption on the dehydrated Mg-silicates. For both amorphous and crystalline materials, the main band is centered at ca. 1340 cm⁻¹ and can be ascribed to the asymmetric stretching mode of adsorbed SO₂. The slightly higher wavenumber observed for the amorphous sample (1341 vs. 1338 cm⁻¹) can be related to its higher surface basicity.⁵¹ Around 1150 cm⁻¹, we can note the presence of the corresponding symmetric stretching mode. Finally, we can observe signals between 1375 and 1360 cm⁻¹, which have been attributed to the coexistence of SO₂ in both the liquid-like and gas phases.⁵² The different intensities of these signals in the crystalline and amorphous Mg-silicates are likely due to their differing porosity.

Fig. 3 Experimental IR spectra of SO₂ adsorbed at progressively increasing temperatures (from blue to black spectra) on crystalline (a) and amorphous (b) Mg-silicates previously outgassed at 673 K.

Computational results

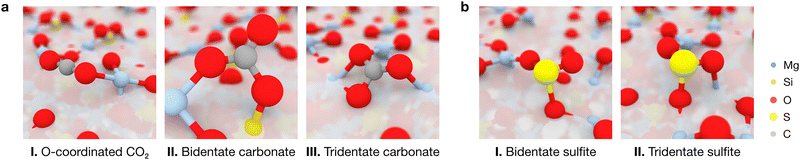
To obtain a complete picture of the binding modes of CO₂ and SO₂ on the forsterite terminations, we assessed the interactions of both molecules with the seven characteristic forsterite terminations present in the crystalline shape of the crystal at the PBE-D*(N) level (see Methods section). Fig. 4 shows all studied adsorption configurations based on their computed adsorption energy, arranged from left to right by increasing surface energy of their corresponding forsterite termination; the position of the corresponding optimized adsorbates on the surfaces is displayed in Fig. S1 (ESI†). Generally, this analysis revealed that the surface energy of the bare surface is inversely correlated with their binding potential: more stable terminations—those with lower surface energies, such as the (010) or the (120) surfaces—have a lower adsorption energy towards both CO₂ (middle panel) and SO₂ (lower panel) than high surface energy terminations such as (110) or (021), whose adsorbates possess more favorable adsorption energy values. This is, in part, due to the nature of both CO₂ and SO₂, and the surface atoms of every surface; CO₂ has been shown to spontaneously activate on the surface basic O²⁻ sites of forsterite,²² effectively forming carbonate units with surface O ions. In our analysis, this predominantly occurs on higher surface energy terminations, accounting for the low adsorption energy structures presented in the middle panel of Fig. 4. This results in two main energy differentiated regimes for CO₂ adsorption: it either adsorbs through a terminal O atom on acidic Mg²⁺ sites with adsorption energies of up to −100 kcal mol⁻¹, or it activates on the surface upon interaction of its C and O atoms with an exposed O²⁻ ion and either one or two Mg²⁺ sites (depending on the steric availability), forming bidentate or tridentate bound carbonates with adsorption energies of −100 to −200 kcal mol⁻¹ (Fig. 5a). The former configuration conforms the largest population of adsorbates on all surfaces, as shown in the kernel density distribution (see Fig. 4).

Fig. 4 Surface energy of the calculated baseline terminations (top panel), along with adsorption energy distribution of CO₂ and SO₂ on each surface. Each point denotes a unique adsorption on each termination, as indicated by their color code. A kernel density estimate distribution is included denoting the range of energies where adsorptions are scattered on each surface.

Fig. 5 Atomic models of representative adsorption modes of (a) CO₂ and (b) SO₂ on the forsterite surfaces. Panel (a) depicts the most stable adsorptions on the (120), (101) and (021) surfaces, corresponding to monodentate CO₂ interacting with a Mg²⁺ site through a terminal O atom, or forming bidentate and tridentate surface carbonates, respectively. Panel (b) depicts the most and eight-most stable SO₂ adsorptions on the (120) surface, yielding to the formation of bidentate or tridentate surface sulfites. Sub-surface atoms have been whitened out for clarity.

In contrast to the non-polar CO₂, the polar nature of SO₂ as a bent geometry facilitates its interaction with surface O²⁻ sites which, sterically, are unavailable for CO₂ activation. Hence, SO₂ adsorbates on the studied forsterite terminations display strikingly more favorable adsorption energies, up to −340 kcal mol⁻¹; more importantly, we see that the energetic distribution of the adsorbates is spread out across all adsorption energy values, yielding a broader kernel density distribution. This is partly due to SO₂ interacting similarly in all simulations, i.e., S interacts with a surface O²⁻ site and one or both of the O atoms of SO₂ bind to surface Mg²⁺ sites, forming bidentate or tridentate bound sulfites, analogous to its behavior on stepped MgO surfaces²⁹ (Fig. 5b).

To elucidate the vibrational modes governing the spectroscopic features observed experimentally, we then generated per-surface IR spectra including all adsorptions of SO₂ and CO₂, as displayed in Fig. 6a. In these spectra, a weight was applied to the calculated IR intensities of each configuration following a Boltzmann distribution based on their relative adsorption energies, as detailed in the Methods section. This procedure is aimed at representing a low-coverage situation in which the contribution of each adsorbate structure to the simulated total IR spectra is determined by the probability of an adsorbate to bind to that respective site in each orientation.

Fig. 6 (a) IR spectra of the adsorbed CO₂ and SO₂ molecules on the modelled terminations of forsterite. Spectra are arranged from top to bottom with respect to the surface energy of their respective surface termination. All spectra contain the peaks arising from a Boltzmann distribution of the adsorptions on the surface, where the reference value is selected as the most stable adsorption, as described in the Methods section. (b) Total IR spectrum of CO₂ considering all adsorption sites, adsorption configurations and surface terminations (see Methods). Representations of the atomic displacements within the vibrational modes corresponding to the theoretical peaks in the IR spectrum are included as insets. In these, atomic displacements within the vibrational mode are represented as black arrows with scaled magnitudes, and atoms belonging to the adsorbate are outlined. Atomic bonds are depicted as dotted lines. (c) Total IR spectrum of SO₂, in a similar fashion to (b). Schematic representations for calculated vibrational modes corresponding to non-adsorbed and physisorbed SO₂ on the forsterite are included and labelled with a reddish background; these features are present in the high-coverage experimental regime but contain a negligible weight in the Boltzmann energy distribution in the calculations, and thus display no associated peaks in the global theoretical IR spectrum. Relevant distances between the SO₂ molecule and the surface, in Å, are depicted in italics.

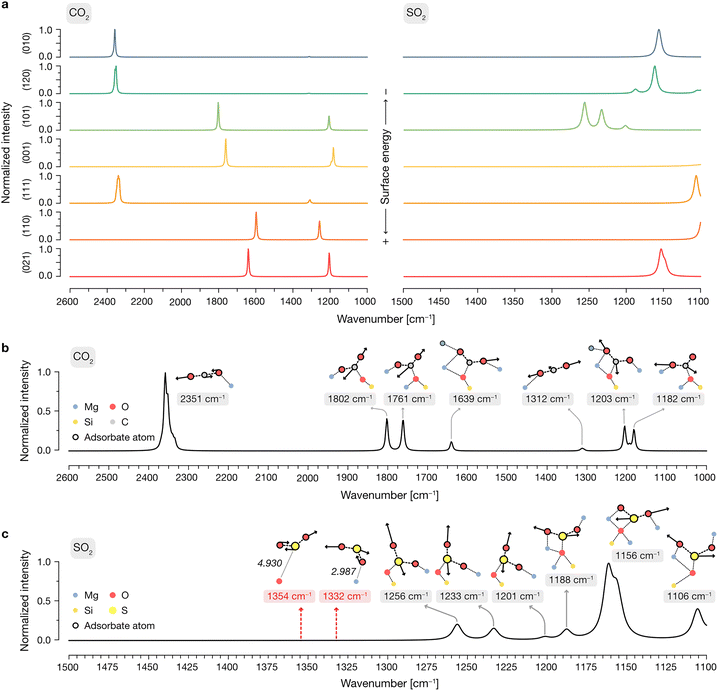
In the case of CO₂, this approach yields very different features depending on the surface: given that the low surface energy terminations cannot activate CO₂ due to their peculiar exposed O²⁻/Mg²⁺ site distribution (see above), the predominant features present in the adsorbate spectra of the (010), (120) and (111) are those of the gas-phase CO₂, arising from physisorbed molecules on the surface with relatively low favorable adsorption energies. In contrast, given the ability of the (101), (001), (110) and (021) surfaces to activate CO₂ with lower adsorption energies than its physisorbed counterpart, any contributions of the latter to the global IR are wiped away by the Boltzmann factor by those of newly conformed carbonate structures on the surface.

After determining the predominant IR features on each forsterite termination, we then proceeded to build a global spectrum where the contribution of each surface to the crystalline equilibrium shape (Table S1, ESI†) is computed. These global spectra are depicted in Fig. 6b and c for CO₂ and SO₂, respectively, displaying representative vibrational modes contributing to each theoretical peak.

Our simulations show that the IR features arising from low surface energy terminations such as (010) and (120) dominate the spectrum: we predict the characteristic peak corresponding to the asymmetric stretching of CO₂ to appear prominently at 2351 cm⁻¹, indicative of weakly physisorbed CO₂. The slight redshift of this mode relative to gas-phase CO₂ (2349 cm⁻¹) is due to the interaction of a terminal O with a surface Mg²⁺ site; this interaction breaks the symmetry of the adsorbed molecule, rendering the normally IR-inactive symmetric stretching mode weakly activated at a frequency of 1312 cm⁻¹. We assign all other calculated features to vibrational modes associated with the formation of surface-bound carbonates, with frequencies of 1802, 1761, 1639, 1203 and 1182 cm⁻¹. In these configurations, CO₂ binds either in a bidentate fashion, with its C and one O atom interacting with surface O²⁻ and Mg²⁺ sites, respectively, or in a tridentate mode, where the second terminal oxygen of CO₂ also coordinates to a nearby Mg²⁺ site.

For SO₂, our simulations do not predict the existence of gas-phase features in the most stable adsorption configurations on each termination, as any peaks arising from weakly physisorbed molecules have a negligible impact in the computed Boltzmann distribution due to their high adsorption energies compared to those coming from the chemisorbed SO₂. Upon building the global IR spectrum, our calculations predict the modes of these weakly adsorbed molecules to be redshifted relative to gas-phase SO₂ due to their interaction with the surfaces, as exemplified in the representative red-labeled modes in Fig. 6c. Thus, all modes present in the global IR spectrum are assigned to chemisorbed SO₂ which, akin to CO₂, binds to surface O²⁻ and Mg²⁺ sites in a bidentate fashion through its S and a terminal O atom, respectively, or in a tridentate fashion where the remaining O binds to a neighboring Mg²⁺ site. The resulting features in the IR spectrum span a range of frequencies, with increasing coordination strength leading to more pronounced redshifts: while bidentate bound molecules yield peaks at 1256, 1233 and 1201 cm⁻¹, the strongest redshifts are associated with tridentate binding, producing peaks at 1188, 1156, and 1106 cm⁻¹. Notably, the peak at 1156 cm⁻¹, corresponding to the “symmetric” stretching of the tridentate SO₂, dominates the spectrum due to its association with the most thermodynamically favored adsorption configurations on the low surface energy (010) and (120) terminations.

Integrating experiments and theory

A comparison between experimental results and the simulated global IR spectrum for CO₂ and SO₂ reveals good agreement in both the position and evolution of key spectral features (as shown in Fig. S2 (ESI†) for the case of CMS as an illustrative case). In the case of CO₂, low temperature experimental IR spectra are dominated by a peak at 2345 cm⁻¹, progressively diminishing with increasing temperature and giving rise to new absorptions between 1700 and 1200 cm⁻¹, consistent with a predominance of carbonates at low coverages. In the experimental spectra, the carbonate signals become more evident at higher temperatures because their formation requires overcoming a relatively high activation barrier to bend the CO₂ molecule. This aspect is not considered in the theoretical part, in which the adsorbed species are already prepared to be ready for carbonate formation. These trends are present in the theoretical spectrum: while the contributions from low-energy terminations—particularly (010) and (120)—account for the physisorbed CO₂ signal, higher surface energy terminations contain peaks ranging from approximately 1800 to 1200 cm⁻¹. While our calculations do not account for the formation of additional carbonate layers at higher CO₂ coverages, nor for the interaction of CO₂ with traces of co-adsorbed water—which may contribute to the observed discrepancies in carbonate peak positions—the theoretical results suggest that as the most favorable adsorption sites become occupied, configurations with higher adsorption energies begin to dominate. This leads to an increased contribution from carbonate-like modes, which progressively overshadow the spectral features associated with physisorbed CO₂ in the high temperature regimes.

In the case of SO₂, our simulations accurately predict the presence of chemisorbed structures, characterized by the peak located around 1150 cm⁻¹ both in theory and experiments. Our calculations predict this peak to be prominent under both high and low coverage conditions: at high coverages (low temperature), we expect it to arise from the symmetric stretching mode of weakly physisorbed SO₂ and from the modes of surface-bound species, whereas at low coverages (high temperature), it originates exclusively from chemisorbed SO₂ molecules predicted by the simulations. Additionally, both the experimental broad bands and the peak observed at 1255 cm⁻¹ in the CMS samples are consistent with the simulated results, which suggest a diverse landscape of interaction modes that drastically affect the spectroscopic features. Illustrative representations of the atomic configurations conforming the most stable adsorptions of CO₂ and SO₂ on each surface termination are shown in Fig. S3–S16 (ESI†).

Conclusions

In this work, we have combined in situ IR spectroscopy and an automated computational framework to systematically investigate the adsorption behavior of CO₂ and SO₂ on amorphous and crystalline forsterite surfaces under astrophysical relevant conditions. Our results reveal that both molecules exhibit distinct spectroscopic signatures depending on their interaction strength with the surface, the surface termination, and the coverage regime.

By explicitly accounting for the relative stability of adsorption modes via Boltzmann statistics and the morphological distribution of surface terminations in the equilibrium shape of the crystal, our theoretical approach achieves good agreement with experimental IR spectra. This methodology not only enables the assignment of vibrational features to specific surface configurations, but also provides a framework to study the spectroscopic behavior of other interstellar molecules on mineral surfaces of cosmic relevance.

Data availability

The data supporting this article, including supporting figures and tables, have been included as part of the ESI.† All computational data presented herein, including the Jupyter notebooks for the generation of weighed theoretical IR spectra and scripts for the automatic optimization of adsorbates on the silicate surfaces, are shared with a GNU General Public License v4.0 license through a Zenodo dataset with the following DOI: https://doi.org/10.5281/zenodo.15341156.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

E. M-.T. acknowledges the support from the Spanish Ministry of Universities and the European Union's Next Generation EU fund. This project received funding from the European Research Council (ERC) under the European Union's Horizon 2020 Research and Innovation Program (Grant Agreement 865657) for Project “Quantum Chemistry on Interstellar Grains” (QUANTUMGRAIN). MICIN is also acknowledged for financing the projects PID2021-126427NBI00 and CNS2023-144902. The Italian MUR (PRIN 2020, “Astrochemistry beyond the second period elements”, Prot. 2020AFB3FX) and the Italian Space Agency (Bando ASI Prot. n. DC-DSR-UVS-2022-231, Grant no. 2023-10-U.0 “Modeling Chemical Complexity: all'Origine di questa e di altre Vite per una visione aggiornata delle missioni spaziali (MIGLIORA)” Codice Unico di Progetto (CUP) F83C23000800005) are gratefully acknowledged. This research has received funding from the Project CH4.0 under the MUR program “Dipartimenti di Eccellenza 2023–2027” (CUP: D13C22003520001). We also thank the the EuroHPC Joint Undertaking for the provision of computational resources through the Regular Access call program, project no. 2023R01-112, hosted by the Ministry of Education, Youth and Sports of the Czech Republic through the e-INFRA CZ (ID: 9025). A. R. gratefully acknowledges support through a 2023 ICREA Award.

Notes and references

1. T. Do-Duy, C. M. Wright, T. Fujiyoshi, A. Glasse, R. Siebenmorgen, R. Smith, B. Stecklum and M. Sterzik, Mon. Not. R. Astron. Soc., 2020, 493, 4463–4517.
2. A. Takigawa, S. Tachibana, H. Nagahara, K. Ozawa and M. Yokoyama, Adv. Pharm. J., 2009, 707, L97–L101.
3. B. L. De Vries, M. Min, L. B. F. M. Waters, J. A. D. L. Blommaert and F. Kemper, Astron. Astrophys., 2010, 516, A86.
4. B. T. Draine, in Cosmic Dust - Near and Far, ed. Th. Henning, E. Grün and J. Steinacker, ASP Conference Series, 2009, vol. 414, pp. 453–472.
5. H. W. W. Spoon, A. G. G. M. Tielens, L. Armus, G. C. Sloan, B. Sargent, J. Cami, V. Charmandaris, J. R. Houck and B. T. Soifer, Adv. Pharm. J., 2006, 638, 759–765.
6. A. L. Graham, A. J. Easton and R. Hutchison, Mineral. Mag., 1977, 41, 201–210.
7. M. Kołodziej, D. Michalska, K. Załęski, I. Iatsunskyi, A. Muszyński and E. Coy, Sci. Rep., 2025, 15, 6866.
8. S. Messenger, L. P. Keller, F. J. Stadermann, R. M. Walker and E. Zinner, Science, 2003, 300, 105–108.
9. J. Bradley, in Astromineralogy, ed T. Henning, Springer Berlin Heidelberg, Berlin, Heidelberg, 2010, vol. 815, pp. 259–276.
10. K. Nakamura-Messenger, L. P. Keller, S. J. Clemett, S. Messenger and M. Ito, Meteorit. Planet. Sci., 2011, 46, 1033–1051.
11. H. Sierks, C. Barbieri, P. L. Lamy, R. Rodrigo, D. Koschny, H. Rickman, H. U. Keller, J. Agarwal, M. F. A’Hearn, F. Angrilli, A.-T. Auger, M. A. Barucci, J.-L. Bertaux, I. Bertini, S. Besse, D. Bodewits, C. Capanna, G. Cremonese, V. Da Deppo, B. Davidsson, S. Debei, M. De Cecco, F. Ferri, S. Fornasier, M. Fulle, R. Gaskell, L. Giacomini, O. Groussin, P. Gutierrez-Marques, P. J. Gutiérrez, C. Güttler, N. Hoekzema, S. F. Hviid, W.-H. Ip, L. Jorda, J. Knollenberg, G. Kovacs, J. R. Kramm, E. Kührt, M. Küppers, F. La Forgia, L. M. Lara, M. Lazzarin, C. Leyrat, J. J. Lopez Moreno, S. Magrin, S. Marchi, F. Marzari, M. Massironi, H. Michalik, R. Moissl, S. Mottola, G. Naletto, N. Oklay, M. Pajola, M. Pertile, F. Preusker, L. Sabau, F. Scholten, C. Snodgrass, N. Thomas, C. Tubiana, J.-B. Vincent, K.-P. Wenzel, M. Zaccariotto and M. Pätzold, Science, 2015, 347, aaa1044.
12. J. Perrero, L. Beitia-Antero, A. Fuente, P. Ugliengo and A. Rimola, Mon. Not. R. Astron. Soc., 2023, 527, 10697–10704.
13. G. Molpeceres, A. Rimola, C. Ceccarelli, J. Kästner, P. Ugliengo and B. Maté, Mon. Not. R. Astron. Soc., 2019, 482, 5389–5400.
14. J. Navarro-Ruiz, M. Sodupe, P. Ugliengo and A. Rimola, Phys. Chem. Chem. Phys., 2014, 16, 17447–17457.
15. R. Santalucia, M. Pazzi, F. Bonino, M. Signorile, D. Scarano, P. Ugliengo, G. Spoto and L. Mino, Phys. Chem. Chem. Phys., 2022, 24, 7224–7230.
16. V. Vinogradoff, V. Leyva, E. Mates-Torres, R. Pepino, G. Danger, A. Rimola, L. Cazals, C. Serra, R. Pascal and C. Meinert, Earth Planet. Sci. Lett., 2024, 626, 118558.
17. N. Bancone, S. Pantaleone, P. Ugliengo, A. Rimola and M. Corno, Phys. Chem. Chem. Phys., 2023, 25, 26797–26812.
18. N. Bancone, S. Pantaleone, P. Ugliengo, A. Rimola and M. Corno, ACS Earth Space Chem., 2025, 9, 303–313.
19. N. Bancone, R. Santalucia, S. Pantaleone, P. Ugliengo, L. Mino, A. Rimola and M. Corno, J. Phys. Chem. C, 2024, 128, 15171–15178.
20. L. Zamirri, S. Pantaleone and P. Ugliengo, J. Chem. Phys., 2019, 150, 064702.
21. P. A. Gerakines, D. C. B. Whittet, P. Ehrenfreund, A. C. A. Boogert, A. G. G. M. Tielens, W. A. Schutte, J. E. Chiar, E. F. Van Dishoeck, T. Prusti, F. P. Helmich and T. De Graauw, Adv. Pharm. J., 1999, 522, 357–377.
22. Y. Ermolov, A. Vasilchenko and G. Lazorenko, Int. J. Mater. Sci., 2024, 25, 12639.
23. A. P. Jones and N. Ysard, Astron. Astrophys., 2019, 627, A38.
24. F. Kemper, C. Jäger, L. B. F. M. Waters, Th Henning, F. J. Molster, M. J. Barlow, T. Lim and A. De Koter, Nature, 2002, 415, 295–297.
25. S. Peters, D. A. Semenov, R. Hochleitner and O. Trapp, Sci. Rep., 2023, 13, 6843.
26. M. K. McClure, W. R. M. Rocha, K. M. Pontoppidan, N. Crouzet, L. E. U. Chu, E. Dartois, T. Lamberts, J. A. Noble, Y. J. Pendleton, G. Perotti, D. Qasim, M. G. Rachid, Z. L. Smith, F. Sun, T. L. Beck, A. C. A. Boogert, W. A. Brown, P. Caselli, S. B. Charnley, H. M. Cuppen, H. Dickinson, M. N. Drozdovskaya, E. Egami, J. Erkal, H. Fraser, R. T. Garrod, D. Harsono, S. Ioppolo, I. Jiménez-Serra, M. Jin, J. K. Jørgensen, L. E. Kristensen, D. C. Lis, M. R. S. McCoustra, B. A. McGuire, G. J. Melnick, K. I. Öberg, M. E. Palumbo, T. Shimonishi, J. A. Sturm, E. F. van Dishoeck and H. Linnartz, Nat. Astron., 2023, 7, 431–443.
27. W. R. M. Rocha, E. F. Van Dishoeck, M. E. Ressler, M. L. Van Gelder, K. Slavicinska, N. G. C. Brunken, H. Linnartz, T. P. Ray, H. Beuther, A. Caratti, O. Garatti, V. Geers, P. J. Kavanagh, P. D. Klaassen, K. Justtanont, Y. Chen, L. Francis, C. Gieser, G. Perotti, Ł. Tychoniec, M. Barsony, L. Majumdar, V. J. M. Le Gouellec, L. E. U. Chu, B. W. P. Lew, Th Henning and G. Wright, Astron. Astrophys., 2024, 683, A124.
28. J. C. Laas and P. Caselli, Astron. Astrophys., 2019, 624, A108.
29. G. Pacchioni, A. Clotet and J. M. Ricart, Surf. Sci., 1994, 315, 337–350.
30. J. A. Rodriguez, T. Jirsak, A. Freitag, J. Z. Larese and A. Maiti, J. Phys. Chem. B, 2000, 104, 7439–7448.
31. J. Martínez-González, J. Navarro-Ruiz and A. Rimola, Minerals, 2018, 8, 353.
32. D. Yamamoto and S. Tachibana, ACS Earth Space Chem., 2018, 2, 778–786.
33. C. Pavan, R. Santalucia, G. Escolano-Casado, P. Ugliengo, L. Mino and F. Turci, Int. J. Mater. Sci., 2023, 24, 11482.
34. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
35. A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002.
36. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
37. E. Mates-Torres and A. Rimola, J. Appl. Crystallogr., 2024, 57, 503–508.
38. M. Bruno, F. R. Massaro, M. Prencipe, R. Demichelis, M. De La Pierre and F. Nestola, J. Phys. Chem. C, 2014, 118, 2498–2506.
39. J. H. Montoya and K. A. Persson, npj Comput. Mater., 2017, 3, 14.
40. S. Grimme, C. Bannwarth and P. Shushkov, J. Chem. Theory Comput., 2017, 13, 1989–2009.
41. A. Hjorth Larsen, J. Jørgen Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. Bjerre Jensen, J. Kermode, J. R. Kitchin, E. Leonhard Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. Bergmann Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys.: Condens. Matter, 2017, 29, 273002.
42. P. Pulay, Chem. Phys. Lett., 1980, 73, 393–398.
43. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
44. M. Cutini, L. Maschio and P. Ugliengo, J. Chem. Theory Comput., 2020, 16, 5244–5252.
45. A. Stukowski, Modelling Simul. Mater. Sci. Eng., 2010, 18, 015012.
46. S. Baroni, S. De Gironcoli, A. Dal Corso and P. Giannozzi, Rev. Mod. Phys., 2001, 73, 515–562.
47. D. Karhánek, Dakarhanek/VASP-infrared-intensities (version v1.0) Zenodo, 2020.
48. T. Shimanouchi, Tables of molecular vibrational frequencies, consolidated volume i, National Bureau of Standards, Gaithersburg, MD, 1972.
49. F. X. L. I. Xamena and A. Zecchina, Phys. Chem. Chem. Phys., 2002, 4, 1978–1982.
50. L. Mino, F. Cesano, D. Scarano, G. Spoto and G. Martra, Res. Chem. Intermed., 2019, 45, 5801–5829.
51. M. Waqif, A. M. Saad, M. Bensitel, J. Bachelier, O. Saur and J.-C. Lavalley, Faraday Trans., 1992, 88, 2931.
52. D. B. Nash and B. H. Betts, Icarus, 1995, 117, 402–419.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp01699a

‡ These authors contributed equally to this work.

§ Present address: Department of Chemistry and Biochemistry, Mendel University in Brno, Zemedelska 1, CZ-613 00, Brno, Czech Republic.

---