 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Component-wise AO basis reduction: norm loss, negative contribution normalization, and functional implications†
Mindaugas
Macernis
 *
*
Institute of Chemical Physics, Vilnius University, Saulėtekio av. 3, Vilnius, LT-10257, Lithuania. E-mail: mindaugas.macernis@ff.vu.lt
First published on 17th June 2025
Abstract
Atomic orbital (AO) normalization is a foundational assumption in electronic structure theory, yet in practice, the norm of contracted basis functions can deviate from unity due to internal reduction and transformation mechanisms applied by quantum chemistry packages. This work presents a systematic framework for analyzing the physical and numerical consequences of primitive basis function elimination and AO-level norm inconsistency. The implemented methodology quantifies norm loss, separates constructive and destructive contributions, and enables precise renormalization by retaining both positive and negative terms within AO representations. Using two representative systems—a Raman-active carotenoid (lycopene) and a phosphorus dimer with through-space J(P–P) coupling—sensitivity to AO normalization was evaluated. While vibrational frequencies remained stable across normalization schemes, Raman intensities and J-coupling constants showed non-negligible shifts: up to 6 Hz for phosphorus and over 50 units in Raman activity. The results demonstrate that AO normalization is not merely a numerical refinement, but a physically impactful step with implications for precision spectroscopy and quantum computing applications.
Introduction
The accuracy of quantum chemical methods depends mainly on three general features such as the choice of the Hamiltonian, approximate treatment of electron correlation by truncating the many-particle Hilbert space, and the definition of the basis set determining the one-particle orbital representation.1,2 Regardless of the level of theory, an insufficient basis set yields erroneous results, whereas an appropriate basis set can be expected to produce at least qualitatively correct results.Gaussian-type orbitals (GTOs), centered on atomic nuclei, are commonly used as basis functions in the linear combination of atomic orbitals (LCAO) method.1,3,4 Generally contracted basis sets include the correlation-consistent (cc) families proposed by Dunning & coworkers,5–12 widely used in the form of cc-pVXZ (X = D, T, Q, 5, 6), where X denotes the number of contracted Gaussian-type orbitals (CGTOs) used to represent each occupied atomic orbital. These sets can be systematically extended with diffuse functions, denoted by aug-, d-aug-, and t-aug-prefixes for singly, doubly, and triply augmented variants.
Another general contraction approach is the atomic natural orbital (ANO) basis set, in which the contraction coefficients are obtained by optimizing atomic energies.13 Optimized atomic Slater-type orbitals (STOs) were often approximated by fixed linear combinations of Gaussian functions,14 forming the basis of widely used Pople-type basis sets such as 3-21G and 6-311G.15–17 Basically, molecular orbitals have a functional2,18 form given by equation:
 | (1) |
The effects of basis set reduction have been extensively studied across multiple quantum chemical methods—including density functional theory (DFT), Hartree–Fock (HF), and coupled-cluster (CC)-to improve accuracy or reduce computational cost.18–34 However, studies targeting high-precision results26,30,31,35–46 or analysing basis set superposition errors (BSSE)35–37,40,43,46 often face reproducibility challenges due to undocumented and automatically applied normalization procedures, as demonstrated in this work. Notably, the widely used cc-pVDZ basis set provides a clear example of predefined reductions embedded in default system libraries, despite its frequent use in high-accuracy applications.30,39–42,44–46 For this reason, cc-pVDZ was selected as a test case to evaluate how AO reduction and normalization affect computed results.
This paper introduces a framework for evaluating the physical and numerical effects of primitive Gaussian basis function elimination. Norm loss and component-level analysis reveal that atomic orbital (AO) pruning—often applied automatically and without user control—can impact computed molecular properties. AO normalization is revisited through the separation of positive and negative contraction contributions, representing constructive and destructive superposition components.
A case study using the cc-pVDZ5,47 basis set is presented for hydrogen, carbon, and phosphorus, elements selected for their typical angular momentum behaviour and susceptibility to internal reduction in system libraries. Calculations were performed using Gaussian,48 which enables explicit basis input and reflects normalization behaviour during SCF processing. The study assesses the impact of normalization strategies on total energies, dipole moments, Raman intensities, and J(P–P) couplings.
Two representative systems were selected to assess the physical implications of AO normalization: lycopene (LYC), a conjugated carotenoid (Car) with well-defined Raman-active modes,49–53 and bis(diphenylphosphino)methane (dppm), which enables through-space P–P spin–spin coupling relevant to quantum computing54–58 and other studies.59 These molecules provide sensitivity benchmarks for vibrational intensities and sub-Hz nuclear coupling constants.
All results are based on a reproducible methodology implemented in the open-source tool BasisSculpt, which supports precise and controlled AO normalization.
Results and discussion
Normalization theory and reduction of basis sets
The basis set representing contracted atomic orbitals must be normalized and can written as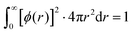 | (2) |
The reduction procedure involves eliminating a single atomic orbital component, which ideally should only affect the total norm at the level of numerical noise or computational precision. For illustration, it can be considered reducing a three-term expansion to two terms:
| ϕfull = c1N1e−α1r2 + c2N2e−α2r2 + c3N3e−α3r2 | (3) |
| ϕreduced = c1N1e−α1r2 + c2N2e−α2r2 | (4) |
Renormalization should result in the integrals being almost equal:
 | (5) |
However, the effect of the reduction is lost in this case, as both integrals are normalized to one. Therefore, the most informative approach is to compare the original and reduced integrals before renormalization. This allows for quantifying the relative contribution of the removed term as a percentage.
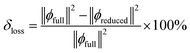 | (6) |
This raises the question of whether eliminating negative contraction coefficients is justified, given their suppressive contributions. In the normalization procedure, their impact is expected to be negligible if the coefficients are very small, and the total energy should remain unaffected. In such cases, renormalization may not be physically meaningful. However, when multiple negative contraction coefficients are involved, the function can be separated into constructive and destructive components.
| ϕ(r) = ϕ+(r) + ϕ−(r) | (7) |
If renormalization is applied to only one component, the imbalance causes the remaining component to dominate, degrading the function's physical accuracy. Thus, normalization must be applied proportionally to all components to preserve the functional balance.
| s+2·‖ϕ+‖2 + s−2·‖ϕ−‖2 + 2s+s−·〈ϕ+,ϕ−〉 = 1 | (8) |
A computational simplification involves splitting the normalization into two steps and verifying consistency between pre- and post-normalization values.
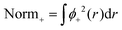 | (9) |
 | (10) |
However, it must be noted that
| ‖ϕ‖2 ≠ ‖ϕ+‖2 + ‖ϕ−‖2 | (11) |
| 〈ϕ+,ϕ−〉 | (12) |
From this point, a proportional analysis was performed to assess whether the atomic orbitals (AOs) in the basis set are appropriately normalized. This involves evaluating the total contribution of all Gaussian primitives constructing a given AO, regardless of whether the AO is defined across multiple blocks (e.g., multiple entries for S orbitals).
Impact of primitive elimination and normalization on DFT results
In order to understand the effects of basis set reduction, the loss of norm resulting from both primitive-level and block-level eliminations should be qualified. The contribution of individual Gaussian primitives was evaluated for each atomic orbital (AO) block, and their removal simulated.However, when there are repeated α values across blocks the entire block can be reduced. In order to take this into account, the intra-block reduction effects on all selected AO blocks were treated as one joined block (Join-block). This technique allows calculation of the contribution of individual primitive Gaussian functions to the AO, based on their grouping into a Join-block.
Norm reduction was expressed as a percentage relative to the originally selected full block. The current analysis focuses on hydrogen (H), carbon (C), and phosphorus (P) atoms, which were chosen to investigate the effects of basis set normalization on molecular properties in the selected systems. The analysis was performed with cc-pVDZ taken from the basis set exchange.60
We used different cc-pVDZ basis set normalization approaches A1, A2, A3Exc and A4BS:
A1 – the typical basis set normalization as implemented in Gaussian software;48
A2 – the basis set normalization as implemented in Gaussian software by using the keyword which prevents basis set reduction;48
A3Exc – the typical basis set normalization as implemented in software48 but with the basis set provided from the basis set exchange (BSE);60
A4BS – renormalized basis set by saving AO positive and negative contributions with BasisSculpt implementation by taking the basis set provided from the basis set exchange.60
The analysed normalization approaches – A1, A2, A3Exc, and A4BS – apply different reduction strategies. A3Exc uses the original cc-pVDZ basis set without any reduction. A4BS retains both constructive and destructive components after explicit normalization. In contrast, A2 provided by default within the internal system library, includes only initial reductions without renormalization. A1 applies48 a more aggressive reduction strategy by using an A2-type basis set.
It should be noted that the initial basis set for A1 and A2 is the basis set from the internal Gaussian software database which has reduction applied already, for example: hydrogen has 3 α in the first block (AO labelled as S) while in A3Exc from BSE it has 4; carbon has 8 α in the first two blocks (AO labelled as S) while in BSE it is reported as 9, the forth block (AO labelled as P) has 3 α while in BSE there are 4; phosphorus has 11 α in the first three blocks (AO labelled as S) while in BSE it is reported as 12, the fifth and sixth blocks (AO labelled as P) have 7 α while in BSE there are 8.
The next AO-labelled S block for carbon, although having the same α values, exhibits different reductions in the A1-type basis set normalization due to differing contraction coefficients. Carbon exhibits a reduction at α = 1000, α = 228 and α = 0.1596 in the block, whose contributions to the block are 6.324%, 10.352% and 4.517%, respectively, and causes a 0.007%, 0.079% and 75.216% loss in normalization. When considering the Join-block, the contributions change to 1.274%, 2.086% and 0.91%, and the corresponding normalization loss changes to −0.001%, −0.016% and 19.677%. Initially, the block consists of 2 primitives forming the constructive part ϕ+(r), and 7 forming the destructive part ϕ−(r). After reduction, the block consists of 3 constructive components and 4 destructive components. In the internal system library (A2), all 8 components are present, with 1 constructive component reduced (Table 1).
| A | ϕ (l) | α | δ loss, % | δ contribution, % | ||
|---|---|---|---|---|---|---|
| Block | Join-block | Block | Join-block | |||
| H | S | 13.01 | 0.9082 | 0.3129 | 18.5385 | 7.8348 |
| 1.962 | 15.6778 | 6.1664 | 31.4458 | 13.2897 | ||
| 0.4446 | 68.0162 | 29.8528 | 35.7908 | 15.1260 | ||
| 0.122 | 65.4686 | 29.0632 | 14.2248 | 6.0117 | ||
| S | 0.122 | — | 51.5294 | — | 11.9937 | |
| P | 0.727 | — | 50.7382 | — | 45.7441 | |
| C | S | 6665 | 0.0053 | 0.0002 | 4.7585 | 3.1704 |
| 1000 | 0.1478 | 0.0057 | 8.8341 | 5.8857 | ||
| 228 | 1.7935 | 0.0730 | 14.8105 | 9.8675 | ||
| 64.71 | 11.7803 | 0.5400 | 21.6343 | 14.4138 | ||
| 21.06 | 41.2350 | 2.4047 | 25.1787 | 16.7753 | ||
| 7.495 | 67.2472 | 6.0494 | 18.9417 | 12.6199 | ||
| 2.797 | 39.7860 | 6.0679 | 5.7477 | 3.8294 | ||
| 0.5215 | 1.1944 | 0.5472 | 0.0870 | 0.0579 | ||
| 0.1596 | −0.1204 | −0.1151 | 0.0075 | 0.0050 | ||
| S | 6665 | 0.0002 | −0.0000 | 3.3191 | 0.6689 | |
| 1000 | 0.0068 | −0.0013 | 6.3244 | 1.2746 | ||
| 228 | 0.0790 | −0.0161 | 10.3523 | 2.0863 | ||
| 64.71 | 0.5217 | −0.1346 | 16.3915 | 3.3034 | ||
| 21.06 | 1.3848 | −0.6407 | 19.3767 | 3.9050 | ||
| 7.495 | −0.9100 | −2.3578 | 20.9376 | 4.2196 | ||
| 2.797 | −7.2674 | −2.9047 | 8.4826 | 1.7095 | ||
| 0.5215 | 63.2844 | 18.5204 | 10.2985 | 2.0755 | ||
| 0.1596 | 75.2160 | 19.6771 | 4.5174 | 0.9104 | ||
| S | 0.1596 | — | 32.3308 | — | 1.5683 | |
| P | 9.439 | 2.4915 | 0.5202 | 20.6336 | 1.2746 | |
| 2.002 | 25.0107 | 5.1258 | 35.4482 | 2.1897 | ||
| 0.5456 | 69.0712 | 17.2413 | 32.4600 | 2.0052 | ||
| 0.1517 | 57.4163 | 15.9485 | 11.4583 | 0.7078 | ||
| P | 0.1517 | — | 32.0338 | — | 1.5097 | |
| D | 0.55 | — | 32.0229 | — | 3.9667 | |
| P | S | 94![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 840 840 |
0.0011 | 0.0000 | 3.1353 | 1.8169 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 220 220 |
0.0330 | 0.0009 | 5.8598 | 3.3958 | ||
| 3236 | 0.4426 | 0.0127 | 10.0105 | 5.8011 | ||
| 917.1 | 3.5326 | 0.1063 | 15.6963 | 9.0962 | ||
| 299.5 | 17.2745 | 0.5714 | 21.5746 | 12.5026 | ||
| 108.1 | 47.9026 | 1.9171 | 23.4950 | 13.6156 | ||
| 42.18 | 63.5880 | 3.5418 | 15.8078 | 9.1607 | ||
| 17.28 | 31.6595 | 2.6245 | 4.2889 | 2.4855 | ||
| 4.858 | 1.5508 | 0.2862 | 0.1219 | 0.0706 | ||
| 1.818 | −0.1362 | −0.0578 | 0.0090 | 0.0052 | ||
| 0.3372 | 0.0122 | 0.0239 | 0.0008 | 0.0004 | ||
| 0.1232 | −0.0026 | −0.0102 | 0.0002 | 0.0001 | ||
| S | 94![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 840 840 |
3.1353 | −0.0000 | 2.1813 | 0.4956 | |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 220 220 |
5.8598 | −0.0003 | 4.0366 | 0.9171 | ||
| 3236 | 10.0105 | −0.0036 | 7.0493 | 1.6016 | ||
| 917.1 | 15.6963 | −0.0310 | 11.0007 | 2.4994 | ||
| 299.5 | 21.5746 | −0.1898 | 16.3825 | 3.7222 | ||
| 108.1 | 23.4950 | −0.7379 | 19.3444 | 4.3951 | ||
| 42.18 | 15.8078 | −2.0254 | 18.9770 | 4.3116 | ||
| 17.28 | 4.2889 | −1.4660 | 5.6376 | 1.2809 | ||
| 4.858 | 0.1219 | 8.2875 | 9.8274 | 2.2328 | ||
| 1.818 | 76.9352 | 12.6235 | 5.4570 | 1.2398 | ||
| 0.3372 | 3.8829 | 1.1728 | 0.0945 | 0.0215 | ||
| 0.1232 | −0.5893 | −0.2986 | 0.0117 | 0.0027 | ||
| S | 94![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 840 840 |
0.0000 | 0.0000 | 1.8084 | 0.1360 | |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 220 220 |
0.0002 | 0.0001 | 3.3552 | 0.2523 | ||
| 3236 | 0.0025 | 0.0010 | 5.8412 | 0.4392 | ||
| 917.1 | 0.0190 | 0.0084 | 9.1741 | 0.6897 | ||
| 299.5 | 0.0886 | 0.0507 | 13.6330 | 1.0250 | ||
| 108.1 | 0.1576 | 0.1969 | 16.4258 | 1.2349 | ||
| 42.18 | −0.3314 | 0.5350 | 16.3365 | 1.2282 | ||
| 17.28 | −0.7092 | 0.4414 | 5.3130 | 0.3994 | ||
| 4.858 | 1.3662 | −3.4933 | 11.0748 | 0.8326 | ||
| 1.818 | −19.393 | −8.8649 | 10.1957 | 0.7665 | ||
| 0.3372 | 60.5582 | 18.7893 | 4.8343 | 0.3635 | ||
| 0.1232 | 70.7104 | 16.0662 | 2.0079 | 0.1510 | ||
| S | 0.1232 | — | 27.8086 | — | 0.2736 | |
| P | 370.5 | 0.1269 | 0.0168 | 5.3800 | 0.4389 | |
| 87.33 | 2.2678 | 0.2291 | 13.9373 | 1.1370 | ||
| 27.59 | 15.5405 | 1.3645 | 25.1540 | 2.0521 | ||
| 10 | 47.1860 | 4.4096 | 29.7118 | 2.4239 | ||
| 3.825 | 64.8942 | 7.9124 | 20.1593 | 1.6446 | ||
| 1.494 | 33.4986 | 5.8694 | 5.5160 | 0.4500 | ||
| 0.3921 | 1.4516 | 0.5302 | 0.1349 | 0.0110 | ||
| 0.1186 | −0.0870 | −0.0632 | 0.0068 | 0.0006 | ||
| P | 370.5 | 0.0060 | −0.0041 | 4.2919 | 0.1067 | |
| 87.33 | 0.0929 | −0.0547 | 10.7575 | 0.2673 | ||
| 27.59 | 0.4846 | −0.3601 | 20.8513 | 0.5182 | ||
| 10 | 0.1021 | −1.1660 | 23.6949 | 0.5888 | ||
| 3.825 | −5.1057 | −2.5715 | 19.5532 | 0.4859 | ||
| 1.494 | −0.7868 | −0.2182 | 0.6515 | 0.0162 | ||
| 0.3921 | 66.5573 | 16.0722 | 14.1101 | 0.3506 | ||
| 0.1186 | 75.0254 | 16.4273 | 6.0896 | 0.1513 | ||
| P | 0.1186 | — | 27.6062 | — | 0.2659 | |
| D | 0.3730 | — | 28.7026 | — | 0.6280 | |
In the case of larger basis sets, greater and less intuitive reductions can be expected. For example, the carbon cc-pVTZ5,6 case also shows a significant imbalance between constructive and destructive components, as presented in the ESI.†
The second AO-labelled S block for phosphorus should have the same α values as for the first S block, but exhibits different reductions in the A1-type basis set normalization due to differing contraction coefficients. Phosphorus exhibits a reduction at α = 94![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 840, α = 14
840, α = 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 220, α = 0.3372 and α = 0.1232 in the block, which results in contributions to the block of 2.181%, 4.037%, 0.095% and 0.012%, respectively, and causes a 3.135%, 5.86%, 3.883% and −0.589% loss in normalization. When considering the Join-block, the contributions change to 0.496%, 0.917%, 0.022% and 0.003%, and the corresponding normalizations loss change to >−0.001%, >−0.001%, 1.173% and −0.299%. Initially, the block consists of 4 primitives forming the constructive part ϕ+(r), and 8 forming the destructive part ϕ−(r). After reduction, the block consists of 2 constructive components and 6 destructive components and this number is smaller by 1 α value compared with the first AO-labelled S block. In the internal system library (A2), all 11 components are present, with 1 destructive component reduced.
220, α = 0.3372 and α = 0.1232 in the block, which results in contributions to the block of 2.181%, 4.037%, 0.095% and 0.012%, respectively, and causes a 3.135%, 5.86%, 3.883% and −0.589% loss in normalization. When considering the Join-block, the contributions change to 0.496%, 0.917%, 0.022% and 0.003%, and the corresponding normalizations loss change to >−0.001%, >−0.001%, 1.173% and −0.299%. Initially, the block consists of 4 primitives forming the constructive part ϕ+(r), and 8 forming the destructive part ϕ−(r). After reduction, the block consists of 2 constructive components and 6 destructive components and this number is smaller by 1 α value compared with the first AO-labelled S block. In the internal system library (A2), all 11 components are present, with 1 destructive component reduced.
The third AO-labelled S block for phosphorus should also have the same α values as for the first S block, but exhibits different reductions in the A1-type basis set normalization due to differing contraction coefficients also. Phosphorus exhibits a reduction at α = 94![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 840, α = 14
840, α = 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 220, α = 299.5 and α = 0.1232 in the block, with contributions to the block of 2.808%, 3.355%, 13.633% and 2.008%, respectively, and causes a >0.001%, >0.001%, 0.089% and 70.71% loss in normalization. When considering the Join-block, the contributions change to 0.136%, 0.252%, 1.025% and 0.151%, and the corresponding normalizations loss changes to >0.001%, >0.001%, 0.051% and 16.067%. Initially, the block consists of 10 primitives forming the constructive part ϕ+(r), and 2 forming the destructive part ϕ−(r). After reduction, the block consists of 5 constructive components and 3 destructive components. In the internal system library (A2), all 11 components are present, with 1 constructive component reduced.
220, α = 299.5 and α = 0.1232 in the block, with contributions to the block of 2.808%, 3.355%, 13.633% and 2.008%, respectively, and causes a >0.001%, >0.001%, 0.089% and 70.71% loss in normalization. When considering the Join-block, the contributions change to 0.136%, 0.252%, 1.025% and 0.151%, and the corresponding normalizations loss changes to >0.001%, >0.001%, 0.051% and 16.067%. Initially, the block consists of 10 primitives forming the constructive part ϕ+(r), and 2 forming the destructive part ϕ−(r). After reduction, the block consists of 5 constructive components and 3 destructive components. In the internal system library (A2), all 11 components are present, with 1 constructive component reduced.
The first AO-labelled P block for phosphorus exhibits a reduction at α = 0.3921 and α = 0.1186, in the block, with contributions to the block of 0.135% and 0.007%, respectively, and causes a 1.452% and −0.087% loss in normalization. When considering the Join-block, the contributions change to 0.011% and 0.006%, and the corresponding normalizations loss changes to 0.53% and −0.063%. Initially, the block consists of 7 primitives forming the constructive part ϕ+(r), and 1 forming the destructive part ϕ−(r). After reduction, the block consists of 6 constructive components without destructive components. In the internal system library (A2), all 7 components are present, with 1 destructive component reduced.
The second AO-labelled P block for phosphorus should have the same α values as for the first P block also, but exhibits different reductions in the A1-type basis set normalization due to differing contraction coefficients. Phosphorus exhibits a reduction at α = 370.5 and α = 0.1186 in the block, and its contributions to the block are 4.292% and 6.09%, respectively, and it causes a 0.006% and 75.025% loss in normalization. When considering the Join-block, the contributions change to 0.107% and 0.151%, and the corresponding normalizations loss changes to −0.004% and 16.427%. Initially, the block consists of 2 primitives forming the constructive part ϕ+(r), and 6 forming the destructive part ϕ−(r). After reduction, the block consists of 4 constructive components and 2 destructive components. In the internal system library (A2), all 7 components are present, with 1 constructive component reduced. This component results in a 75.025% loss in normalization, despite contributing only 6.09%. In contrast, destructive components with lower percentage contributions are not eliminated.
Using BasisSculpt, the actual norms of AO blocks used in the A1-type calculations were evaluated. Despite Gaussian applying internal normalization (A1), the resulting norms were not consistently equal to one. For example, the carbon atom P block reached 1.08, while phosphorus atom P blocks ranged from 1.01 to 1.13. These findings confirm that internal normalization in Gaussian software includes amplitude scaling, particularly for angular momentum components, which may affect sensitive properties.
Raman mode sensitivity to AO normalization for lycopene ν1
CARs, such as lycopene (LYC), contain an extended polyene chain that supports delocalized π-conjugation, giving rise to strong Raman activity (Fig. 1). The vibrational modes are commonly labelled from ν1 to ν4 corresponding to characteristic C–C (carbon–carbon single bonds) and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C (carbon–carbon double bonds) bond vibrations. LYC was chosen due to its relevance and recent theoretical and experimental characterization.49–51,53
C (carbon–carbon double bonds) bond vibrations. LYC was chosen due to its relevance and recent theoretical and experimental characterization.49–51,53
 | ||
| Fig. 1 Raman spectrum of lycopene showing three main peaks, with the chemical structure displayed below. | ||
Ground state, dipole moment, UV spectra, frequency and Raman activity calculations for LYC were performed using DFT (B3LYP/cc-pVDZ) with four different basis set normalization strategies: A1 (default Gaussian), A2 (system library), A3Exc (original cc-pVDZ from basis set exchange), and A4BS (BasisSculpt-renormalized). The LYC structures were optimized with the same DFT methodology as results analysed.
In all cases, the dipole moment (field-independent) remained constant at 0.5882 Debye. The total energy was identical for A1, A2, and A3Exc (−1557.93462692 Hartree), while for A4BS it differed slightly by −0.0001533472 eV, which is within the numerical noise range (0.0001 Hartree). Zero-point energy corrections were effectively the same, with A4BS differing only by 0.000001 Hartree per particle.
UV spectra were calculated using time-dependent density functional theory (TDDFT). In all cases, the lowest excited states were identical; for example, S1 was calculated at 2.0866 eV, with an oscillator strength of 4.3861 and a major contribution (0.7104) from HOMO to LUMO.
Taking A1 as the reference, the ν1 frequency (1553.6621 cm−1) decreased by 0.0001 cm−1 for A2, increased by 0.0001 cm−1 for A3Exc, and increased by 0.0017 cm−1 for A4BS. The corresponding Raman activity changes were −1.1379, −12.1227, and +5.088, respectively.
For ν2 (1191.1613 cm−1), the frequency decreased by 0.0002 cm−1 for A2, decreased by 0.0001 cm−1 for A3Exc, and increased by 0.0008 cm−1 for A4BS. The Raman activity differences were +1.5469, +6.9930, and +1.5918.
For ν3 (1012.7001 cm−1), all basis sets yielded the same frequency, with a minor decrease of 0.0001 cm−1 for A4BS. Raman activity shifts were +3.2633, +35.0093, and +51.2232.
These results show that even minor deviations in AO normalization – particularly when destructive components are either retained or removed – can lead to measurable differences in Raman intensities, despite the fact that all calculations involved additional renormalization and yielded virtually identical total energies, UV spectra and vibrational frequencies.
Basis set normalization effect on J-coupling of P–P
Bis(diphenylphosphino)methane (dppm) (see Fig. 2) provides access to through-space phosphorus–phosphorus couplings, which are important in the context of quantum computing.54–58 While in conventional quantum chemistry applications a sensitivity of 3–4 Hz is typically sufficient, quantum computing implementations often operate within sub-Hz precision, in the range of 0.1 Hz. Therefore, even small changes in orbital amplitude and spatial shape can significantly impact computed coupling constants, especially for heavier elements such as phosphorus.Ground-state properties, dipole moments, and J-coupling values for dppm were calculated using DFT (B3LYP/cc-pVDZ) under four different basis set normalization strategies: A1 (default Gaussian), A2 (system library), A3Exc (original cc-pVDZ from basis set exchange), and A4BS (BasisSculpt-renormalized). Geometry optimization was performed with A1 to ensure consistent phosphorus–phosphorus distances across the first comparison group. To fully evaluate the effect of AO normalization on structure itself, an additional geometry optimization was performed using the A4BS basis set (labelled A4BSopt).
As expected, the field-independent dipole moment remained constant (1.6010 Debye) for A1, A2, A3Exc, and A4BS. However, in the A4BSopt case, the dipole moment increased to 1.6153 Debye. This change corresponds to a slight increase in the P–P distance by ∼0.01 Å (from 3.13586 Å to 3.14435 Å) indicating subtle structural rearrangements in the dppm geometry associated with renormalized AO amplitudes.
The total energies were identical (−1648.69310726 Hartree) for A2 and A3Exc, A1 differed marginally (−1648.69310645 Hartree), remaining within numerical noise. In contrast, A4BS and A4BSopt exhibited a decrease in total energy by 0.031 eV and 0.095 eV, respectively.
Total nuclear spin–spin coupling constants J(P–P) for A1, A2, A3Exc, and A4BS were found to be 100.89 Hz, 101.033 Hz, 101.034 Hz, and 101.247 Hz, respectively. This means that even at a fixed geometry (3.13586 Å), the J value varied by up to 0.4 Hz depending solely on the AO normalization strategy. In the A4BSopt case, where structural relaxation was allowed under renormalized AO functions, the J-coupling decreased more substantially to 95.322 Hz – highlighting a 6 Hz shift solely due to basis set normalization effects.
The results demonstrate that AO normalization is not merely a numerical refinement, but a physically impactful operation that directly influences computed spin–spin couplings. For systems involving heavy atoms such as phosphorus and properties requiring sub-Hz resolution, such as J(P–P), strict control over AO norms becomes essential. The observed variations confirm that even when total energies remain nearly identical, the shape and amplitude of AO functions – especially in normalized or destructively altered blocks – can significantly affect sensitive observables. Future work should explore scenarios in which package-level renormalization is fully disabled, as this may substantially alter the resulting physical predictions and reveal normalization-dependent effects more explicitly.
Computational methods
Basis set structure
The basis set database is presented in such a way that, for each atom, basis functions are grouped into several blocks corresponding to selected types of atomic orbitals (e.g., S, P, D, etc.). This is described by the following equation: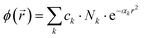 | (13) |
This is a contracted atomic orbital (AO), composed of primitive GTOs with primitive exponents αk, normalization coefficients Nk, and contraction coefficients ck, typically provided in the S and P (SP, D etc.) blocks of the basis set file. Each contracted block is expected to be normalized to unity.2
Implementation
The implementation (BasisSculpt) was written in Java and is available under a BSD license. It allows reading and analysing Gaussian-type basis sets, computing the norm of contracted atomic orbitals, and applying multiple normalization schemes. Projection-based normalization is included, along with a robust numerical fallback using a golden-section search for stability. The code supports BigDecimal arithmetic for high precision and is accessible via command-line or as a library module. BasisSculpt implementation retains both constructive and destructive contributions to the atomic orbital. When the discriminant in the analytical normalization equation is negative, the algorithm automatically resorts to numerical optimization.DFT calculations
For computational analyses, the cc-pVDZ basis set5,47 from the Gaussian 16 database48 was used, as it allows automatic basis set reduction to be computed and analysed. The default approach (A1) has primitive eliminations while the non-eliminating approach (A2) has internal renormalization only. The unmodified reference (A3Exc) basis was also taken from the basis set exchange.60 The renormalized basis set (A4BS) was generated using the BasisSculpt implementation with 64-digit mathematical precision. The normalization threshold was set to 1 × 10−10, ensuring that each AO function was normalized to within ten decimal digits—matching the internal precision used by the Gaussian software and exposed to the user. It should be noted that in all cases, renormalization was performed prior to the computations, as it cannot be suppressed.48For the chosen basis set sensitivity was calculated with energies, Raman spectra, and UV spectra of lycopene. The J-coupling was calculated for bis(diphenylphosphino)methane (dppm) as it has P–P interactions. All structures were optimised with the B3LYP61 functional. All computations were performed by using Gaussian 16 Rev C.01.48
Conclusions
This study demonstrates that atomic orbital (AO) normalization – often treated as a technical detail – can have a physically significant impact on computed molecular properties, particularly in cases involving heavy atoms and precision-sensitive observables. Through a comparison of four normalization strategies (A1, A2, A3Exc, and A4BS), it is shown that AO components, when removed or retained without phase-aware normalization, can measurably influence Raman intensities and spin–spin coupling constants, even when total energies remain numerically indistinguishable.Projection-based normalization, incorporating both constructive and destructive contributions, was shown to be essential for preserving the physical form of AO blocks. The results reveal that default package-level normalization – such as in Gaussian – can lead to amplitude scaling, with AO norms varying up to ±13% across S and P blocks.
The vibrational frequency shifts remain negligible under different normalization schemes, but Raman intensities and spin–spin couplings (e.g., J(P–P)) exhibit differences of up to 6 Hz. The AO normalization directly affects second- and fourth-order properties, which are critical for spectroscopic interpretation and quantum technology applications.
While basis set reduction does not significantly affect total energies or UV-vis spectra for larger molecules (e.g., >20 atoms), the results of this study suggest otherwise for Raman intensities and spin–spin coupling constants. AO normalization influences the radial amplitude and curvature of contracted atomic orbitals, particularly near the nucleus. When constructive or destructive interference patterns are altered through primitive elimination or renormalization, the local electron density at the nucleus can change – even if the total molecular energy remains stable. These localized changes directly impact properties such as Fermi contact terms in NMR and Raman activity, which depend sensitively on electronic response near nuclei. This suggests that higher-order response properties, such as hyperpolarizabilities, may be even more susceptible to AO norm deviations and should be treated with particular care when using reduced or automatically normalized basis sets.
On the other hand, the use of larger basis sets – especially in contexts requiring high precision – is expected to increase. However, predefined basis set reduction may unintentionally degrade accuracy in such cases. For example, hydrogen bond interaction analysis presented in ref. 62 demonstrated accuracy limitations when reduction affects delicate intermolecular features.
Future work should focus on enabling control over, or fully disabling, internal normalization mechanisms in electronic structure packages to ensure full transparency and reproducibility in basis set behaviour. As the results indicate, it is sometimes insufficient to report only the DFT method and package version, as even different deployments of the same software version may apply distinct internal basis set reduction procedures. This highlights the need to explicitly report the applied basis set normalization strategy alongside computational results.
While the proposed framework in this study is based on contracted Gaussian primitives and is therefore formally compatible with ANO-type basis sets, its practical application requires further adjustments. ANO constructions often involve irregular contraction patterns, unbalanced block structures, and uncontracted diffuse functions optimized for correlated methods. Accordingly, block-wise normalization, primitive elimination, and contribution analysis must be adapted to handle flexible contraction schemes and extended numerical integration domains. These adjustments are technical in nature and do not limit the conceptual generality of the approach.
The approach proposed in this study is not intended as an alternative to normalization, but rather a method to preserve the constructive and destructive character of the AO block components during renormalization. Whether these contributions are critical depends not only on atomic type (e.g., heavy elements) or molecular polarity, but also on the specific structure of the basis set – particularly in cases where destructive components compensate for large positive amplitudes. In such cases, improper reduction or reshaping may distort the intended shape of the contracted orbital.
Finally, it is important to emphasize that nearly all major quantum chemistry packages—including TURBOMOLE,63 NWChem,64 ORCA,65–67 Q-Chem,68 Molpro,69,70 Dalton71 and GAMESS72—perform internal normalization of user-supplied basis functions. Moreover, most quantum chemistry software packages include predefined reductions in their internal basis set databases. This is not specific to Gaussian 16 Rev. C.01; similar reductions are also present in the internal basis set database of NWChem. While NWChem documentation states that the basis set content is the responsibility of the system administrator, in practice, this means that the basis set database may vary depending on the specific installation or user's environment. Consequently, different installations of the same software version may include different internal basis sets. A similar situation applies to Gaussian, where internal corrections – such as modifications to the internal basis set database by the system administrator (e.g., based on the basis set exchange) – can also vary. This leads to ambiguity regarding the origin and extent of predefined basis set reductions. This behaviour, while intended to ensure stability and consistency, may obscure the origin of differences in computed properties and complicate reproducibility unless explicitly documented. Therefore, reporting the applied normalization strategy, or disabling internal renormalization where possible, should be considered standard practice in high-precision computations.
Author contributions
CRediT: Mindaugas Macernis: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting this article have been included in the GitHub repository at https://github.com/BasisSculpt/BasisSculpt, which contains input files, normalized basis sets, result summaries, and the source code of the BasisSculpt tool.Acknowledgements
Supported by the Research Council of Lithuania (Grant No. S-MIP-23-48). Computations were performed on resources at the supercomputer “VU HPC” Saulėtekis of Vilnius University in Faculty of Physics.References
- T. Helgaker and P. R. Taylor, Modern Electronic Structure Theory, World Scientific, River Edge, 1995 Search PubMed.
- D. Young, Computational Chemistry: A Practical Guide for Applying Techniques to Real-World Problems, Wiley, 2001, p. 408 Search PubMed.
- S. F. Boys and A. C. Egerton, Proc. R. Soc. London, Ser. A, 1950, 200, 542–554, DOI:10.1098/rspa.1950.0036.
- E. R. Davidson and D. Feller, Chem. Rev., 1986, 86, 681–696, DOI:10.1021/cr00074a002.
- T. H. Dunning, Jr., J. Chem. Phys., 1989, 90, 1007–1023, DOI:10.1063/1.456153.
- R. A. Kendall, T. H. Dunning, Jr. and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806, DOI:10.1063/1.462569.
- D. E. Woon and T. H. Dunning, Jr., J. Chem. Phys., 1993, 98, 1358–1371, DOI:10.1063/1.464303.
- K. A. Peterson, R. A. Kendall and T. H. Dunning, Jr., J. Chem. Phys., 1993, 99, 9790–9805, DOI:10.1063/1.465461.
- D. E. Woon and T. H. Dunning, Jr., J. Chem. Phys., 1994, 100, 2975–2988, DOI:10.1063/1.466439.
- K. A. Peterson, D. E. Woon and T. H. Dunning, Jr., J. Chem. Phys., 1994, 100, 7410–7415, DOI:10.1063/1.466884.
- D. E. Woon and T. H. Dunning, Jr., J. Chem. Phys., 1995, 103, 4572–4585, DOI:10.1063/1.470645.
- A. K. Wilson, T. van Mourik and T. H. Dunning, THEOCHEM, 1996, 388, 339–349, DOI:10.1016/S0166-1280(96)80048-0.
- J. Almlöf and P. R. Taylor, J. Chem. Phys., 1987, 86, 4070–4077, DOI:10.1063/1.451917.
- S. Huzinaga, J. Chem. Phys., 1965, 42, 1293–1302, DOI:10.1063/1.1696113.
- R. F. Stewart, J. Chem. Phys., 1969, 50, 2485–2495, DOI:10.1063/1.1671406.
- W. J. Hehre, R. F. Stewart and J. A. Pople, J. Chem. Phys., 1969, 51, 2657–2664, DOI:10.1063/1.1672392.
- W. J. Hehre, R. Ditchfield, R. F. Stewart and J. A. Pople, J. Chem. Phys., 1970, 52, 2769–2773, DOI:10.1063/1.1673374.
- F. Jensen, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 3, 273–295, DOI:10.1002/wcms.1123.
- P. O. Widmark, P. Å. Malmqvist and B. O. Roos, Theor. Chim. Acta, 1990, 77, 291–306, DOI:10.1007/BF01120130.
- C. W. Bauschlicher and P. R. Taylor, Theor. Chim. Acta, 1993, 86, 13–24, DOI:10.1007/Bf01113513.
- S. Saebø and P. Pulay, Annu. Rev. Phys. Chem., 1993, 44, 213–236, DOI:10.1146/annurev.pc.44.100193.001241.
- R. Pouamerigo, M. Merchan, I. Nebotgil, P. O. Widmark and B. O. Roos, Theor. Chim. Acta, 1995, 92, 149–181, DOI:10.1007/Bf01114922.
- M. Filatov and D. Cremer, J. Chem. Phys., 2005, 122, 064104, DOI:10.1063/1.1844298.
- A. G. Taube and R. J. Bartlett, Collect. Czech. Chem. Commun., 2005, 70, 837–850, DOI:10.1135/cccc20050837.
- T. A. Barnes, J. D. Goodpaster, F. R. Manby and T. F. Miller, J. Chem. Phys., 2013, 139, 024103, DOI:10.1063/1.4811112.
- C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, J. Chem. Phys., 2013, 139, 134101, DOI:10.1063/1.4821834.
- R. Sure and S. Grimme, J. Comput. Chem., 2013, 34, 1672–1685, DOI:10.1002/jcc.23317.
- D. I. Lyakh, Int. J. Quantum Chem., 2014, 114, 1607–1618, DOI:10.1002/qua.24732.
- S. Grimme, J. G. Brandenburg, C. Bannwarth and A. Hansen, J. Chem. Phys., 2015, 143, 054107, DOI:10.1063/1.4927476.
- R. Sure, J. G. Brandenburg and S. Grimme, ChemOpen, 2016, 5, 94–109, DOI:10.1002/open.201500192.
- M. Welborn, F. R. Manby and T. F. Miller, J. Chem. Phys., 2018, 149, 144101, DOI:10.1063/1.5050533.
- M. Bensberg and J. Neugebauer, J. Chem. Phys., 2019, 150, 184104, DOI:10.1063/1.5084550.
- P. F. Loos, B. Pradines, A. Scemama, J. Toulouse and E. Giner, J. Phys. Chem. Lett., 2019, 10, 2931–2937, DOI:10.1021/acs.jpclett.9b01176.
- V. K. Prasad, A. Otero-de-la-Roza and G. A. DiLabio, J. Chem. Theory Comput., 2022, 18, 2913–2930, DOI:10.1021/acs.jctc.2c00036.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566, DOI:10.1080/00268977000101561.
- A. Ichihara and R. Itoh, Bull. Chem. Soc. Jpn., 1990, 63, 958–960, DOI:10.1246/bcsj.63.958.
- F. B. van Duijneveldt, J. G. C. M. van Duijneveldt-van de Rijdt and J. H. van Lenthe, Chem. Rev., 1994, 94, 1873–1885, DOI:10.1021/cr00031a007.
- H. Kruse, L. Goerigk and S. Grimme, J. Org. Chem., 2012, 77, 10824–10834, DOI:10.1021/jo302156p.
- F. R. Manby, M. Stella, J. D. Goodpaster and T. F. Miller, J. Chem. Theory Comput., 2012, 8, 2564–2568, DOI:10.1021/ct300544e.
- R. M. Richard, K. U. Lao and J. M. Herbert, J. Chem. Phys., 2013, 139, 224102, DOI:10.1063/1.4836637.
- C. Riplinger and F. Neese, J. Chem. Phys., 2013, 138, 034106, DOI:10.1063/1.4773581.
- M. A. Collins and R. P. A. Bettens, Chem. Rev., 2015, 115, 5607–5642, DOI:10.1021/cr500455b.
- J. Witte, J. B. Neaton and M. Head-Gordon, J. Chem. Phys., 2017, 146, 234105, DOI:10.1063/1.4986962.
- B. Hégely, P. R. Nagy and M. Kállay, J. Chem. Theory Comput., 2018, 14, 4600–4615, DOI:10.1021/acs.jctc.8b00350.
- M. Sharma and M. Sierka, J. Chem. Theory Comput., 2022, 18(11), 6892–6904, DOI:10.1021/acs.jctc.2c00380.
- F. Jensen, J. Chem. Theory Comput., 2024, 20, 767–774, DOI:10.1021/acs.jctc.3c01156.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358–1371, DOI:10.1063/1.464303.
- G. W. T. M. J. Frisch, H. B. Schlegel, et al., Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2019 Search PubMed.
- L. Diska, A. Bockuviene, R. Gruskiene, T. Kavleiskaja, J. Sereikaite, G. Bankovskaite and M. Macernis, Phys. Chem. Chem. Phys., 2025, 27, 7874–7881, 10.1039/d5cp00034c.
- M. Macernis, S. Streckaite, R. Litvin, A. A. Pascal, M. J. Llansola-Portoles, B. Robert and L. Valkunas, J. Phys. Chem. A, 2022, 126, 813–824, DOI:10.1021/acs.jpca.1c09393.
- S. Streckaite, M. Macernis, F. Li, E. K. Trsková, R. Litvin, C. H. Yang, A. A. Pascal, L. Valkunas, B. Robert and M. J. Llansola-Portoles, J. Phys. Chem. A, 2020, 124, 2792–2801, DOI:10.1021/acs.jpca.9b11536.
- M. J. Llansola-Portoles, A. A. Pascal and B. Robert, Carotenoids, 2022, 674, 113–135, DOI:10.1016/bs.mie.2022.03.068.
- D. Gill, R. G. Kilponen and L. Rimai, Nature, 1970, 227, 743–744, DOI:10.1038/227743a0.
- P. O. Boykin, T. Mor, V. Roychowdhury, F. Vatan and R. Vrijen, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 3388–3393, DOI:10.1073/pnas.241641898.
- N. A. Gershenfeld and I. L. Chuang, Science, 1997, 275, 350–356, DOI:10.1126/science.275.5298.350.
- D. G. Cory, A. F. Fahmy and T. F. Havel, Proc. Natl. Acad. Sci. U. S. A., 1997, 94, 1634–1639, DOI:10.1073/pnas.94.5.1634.
- P. Pyykkö, Theor. Chem. Acc., 2000, 103, 214–216, DOI:10.1007/s002149900011.
- J.-C. Hierso, D. Evrard, D. Lucas, P. Richard, H. Cattey, B. Hanquet and P. Meunier, J. Organomet. Chem., 2008, 693, 574–578, DOI:10.1016/j.jorganchem.2007.11.035.
- F. B. Mallory, C. W. Mallory, K. E. Butler, M. B. Lewis, A. Q. Xia, E. D. Luzik, L. E. Fredenburgh, M. M. Ramanjulu, Q. N. Van, M. M. Francl, D. A. Freed, C. C. Wray, C. Hann, M. Nerz-Stormes, P. J. Carroll and L. E. Chirlian, J. Am. Chem. Soc., 2000, 122, 4108–4116, DOI:10.1021/ja993032z.
- B. P. Pritchard, D. Altarawy, B. Didier, T. D. Gibson and T. L. Windus, J. Chem. Inf. Model., 2019, 59, 4814–4820, DOI:10.1021/acs.jcim.9b00725.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652, DOI:10.1063/1.464913.
- M. Macernis, B. P. Kietis, J. Sulskus, S. H. Lin, M. Hayashi and L. Valkunas, Chem. Phys. Lett., 2008, 466, 223–226, DOI:10.1016/j.cplett.2008.10.069.
- Y. J. Franzke, C. Holzer, J. H. Andersen, T. Begušić, F. Bruder, S. Coriani, F. Della Sala, E. Fabiano, D. A. Fedotov, S. Fürst, S. Gillhuber, R. Grotjahn, M. Kaupp, M. Kehry, M. Krstić, F. Mack, S. Majumdar, B. D. Nguyen, S. M. Parker, F. Pauly, A. Pausch, E. Perlt, G. S. Phun, A. Rajabi, D. Rappoport, B. Samal, T. Schrader, M. Sharma, E. Tapavicza, R. S. Treß, V. Voora, A. Wodyński, J. M. Yu, B. Zerulla, F. Furche, C. Hättig, M. Sierka, D. P. Tew and F. Weigend, J. Chem. Theory Comput., 2023, 19, 6859–6890, DOI:10.1021/acs.jctc.3c00347.
- E. Aprà, E. J. Bylaska, W. A. de Jong, N. Govind, K. Kowalski, T. P. Straatsma, M. Valiev, H. J. J. van Dam, Y. Alexeev, J. Anchell, V. Anisimov, F. W. Aquino, R. Atta-Fynn, J. Autschbach, N. P. Bauman, J. C. Becca, D. E. Bernholdt, K. Bhaskaran-Nair, S. Bogatko, P. Borowski, J. Boschen, J. Brabec, A. Bruner, E. Cauët, Y. Chen, G. N. Chuev, C. J. Cramer, J. Daily, M. J. O. Deegan, T. H. Dunning Jr, M. Dupuis, K. G. Dyall, G. I. Fann, S. A. Fischer, A. Fonari, H. Früchtl, L. Gagliardi, J. Garza, N. Gawande, S. Ghosh, K. Glaesemann, A. W. Götz, J. Hammond, V. Helms, E. D. Hermes, K. Hirao, S. Hirata, M. Jacquelin, L. Jensen, B. G. Johnson, H. Jónsson, R. A. Kendall, M. Klemm, R. Kobayashi, V. Konkov, S. Krishnamoorthy, M. Krishnan, Z. Lin, R. D. Lins, R. J. Littlefield, A. J. Logsdail, K. Lopata, W. Ma, A. V. Marenich, J. Martin del Campo, D. Mejia-Rodriguez, J. E. Moore, J. M. Mullin, T. Nakajima, D. R. Nascimento, J. A. Nichols, P. J. Nichols, J. Nieplocha, A. Otero-de-la-Roza, B. Palmer, A. Panyala, T. Pirojsirikul, B. Peng, R. Peverati, J. Pittner, L. Pollack, R. M. Richard, P. Sadayappan, G. C. Schatz, W. A. Shelton, D. W. Silverstein, D. M. A. Smith, T. A. Soares, D. Song, M. Swart, H. L. Taylor, G. S. Thomas, V. Tipparaju, D. G. Truhlar, K. Tsemekhman, T. Van Voorhis, Á. Vázquez-Mayagoitia, P. Verma, O. Villa, A. Vishnu, K. D. Vogiatzis, D. Wang, J. H. Weare, M. J. Williamson, T. L. Windus, K. Woliński, A. T. Wong, Q. Wu, C. Yang, Q. Yu, M. Zacharias, Z. Zhang, Y. Zhao and R. J. Harrison, J. Chem. Phys., 2020, 152, 184102, DOI:10.1063/5.0004997.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78, DOI:10.1002/wcms.81.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327, DOI:10.1002/wcms.1327.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108, DOI:10.1063/5.0004608.
- E. Epifanovsky, A. T. B. Gilbert, X. Feng, J. Lee, Y. Mao, N. Mardirossian, P. Pokhilko, A. F. White, M. P. Coons, A. L. Dempwolff, Z. Gan, D. Hait, P. R. Horn, L. D. Jacobson, I. Kaliman, J. Kussmann, A. W. Lange, K. U. Lao, D. S. Levine, J. Liu, S. C. McKenzie, A. F. Morrison, K. D. Nanda, F. Plasser, D. R. Rehn, M. L. Vidal, Z.-Q. You, Y. Zhu, B. Alam, B. J. Albrecht, A. Aldossary, E. Alguire, J. H. Andersen, V. Athavale, D. Barton, K. Begam, A. Behn, N. Bellonzi, Y. A. Bernard, E. J. Berquist, H. G. A. Burton, A. Carreras, K. Carter-Fenk, R. Chakraborty, A. D. Chien, K. D. Closser, V. Cofer-Shabica, S. Dasgupta, M. de Wergifosse, J. Deng, M. Diedenhofen, H. Do, S. Ehlert, P.-T. Fang, S. Fatehi, Q. Feng, T. Friedhoff, J. Gayvert, Q. Ge, G. Gidofalvi, M. Goldey, J. Gomes, C. E. González-Espinoza, S. Gulania, A. O. Gunina, M. W. D. Hanson-Heine, P. H. P. Harbach, A. Hauser, M. F. Herbst, M. Hernández Vera, M. Hodecker, Z. C. Holden, S. Houck, X. Huang, K. Hui, B. C. Huynh, M. Ivanov, Á. Jász, H. Ji, H. Jiang, B. Kaduk, S. Kähler, K. Khistyaev, J. Kim, G. Kis, P. Klunzinger, Z. Koczor-Benda, J. H. Koh, D. Kosenkov, L. Koulias, T. Kowalczyk, C. M. Krauter, K. Kue, A. Kunitsa, T. Kus, I. Ladjánszki, A. Landau, K. V. Lawler, D. Lefrancois, S. Lehtola, R. R. Li, Y.-P. Li, J. Liang, M. Liebenthal, H.-H. Lin, Y.-S. Lin, F. Liu, K.-Y. Liu, M. Loipersberger, A. Luenser, A. Manjanath, P. Manohar, E. Mansoor, S. F. Manzer, S.-P. Mao, A. V. Marenich, T. Markovich, S. Mason, S. A. Maurer, P. F. McLaughlin, M. F. S. J. Menger, J.-M. Mewes, S. A. Mewes, P. Morgante, J. W. Mullinax, K. J. Oosterbaan, G. Paran, A. C. Paul, S. K. Paul, F. Pavošević, Z. Pei, S. Prager, E. I. Proynov, Á. Rák, E. Ramos-Cordoba, B. Rana, A. E. Rask, A. Rettig, R. M. Richard, F. Rob, E. Rossomme, T. Scheele, M. Scheurer, M. Schneider, N. Sergueev, S. M. Sharada, W. Skomorowski, D. W. Small, C. J. Stein, Y.-C. Su, E. J. Sundstrom, Z. Tao, J. Thirman, G. J. Tornai, T. Tsuchimochi, N. M. Tubman, S. P. Veccham, O. Vydrov, J. Wenzel, J. Witte, A. Yamada, K. Yao, S. Yeganeh, S. R. Yost, A. Zech, I. Y. Zhang, X. Zhang, Y. Zhang, D. Zuev, A. Aspuru-Guzik, A. T. Bell, N. A. Besley, K. B. Bravaya, B. R. Brooks, D. Casanova, J.-D. Chai, S. Coriani, C. J. Cramer, G. Cserey, A. E. DePrince, III, R. A. DiStasio, Jr., A. Dreuw, B. D. Dunietz, T. R. Furlani, W. A. Goddard, III, S. Hammes-Schiffer, T. Head-Gordon, W. J. Hehre, C.-P. Hsu, T.-C. Jagau, Y. Jung, A. Klamt, J. Kong, D. S. Lambrecht, W. Liang, N. J. Mayhall, C. W. McCurdy, J. B. Neaton, C. Ochsenfeld, J. A. Parkhill, R. Peverati, V. A. Rassolov, Y. Shao, L. V. Slipchenko, T. Stauch, R. P. Steele, J. E. Subotnik, A. J. W. Thom, A. Tkatchenko, D. G. Truhlar, T. Van Voorhis, T. A. Wesolowski, K. B. Whaley, H. L. Woodcock, III, P. M. Zimmerman, S. Faraji, P. M. W. Gill, M. Head-Gordon, J. M. Herbert and A. I. Krylov, J. Chem. Phys., 2021, 155, 084801, DOI:10.1063/5.0055522.
- H.-J. Werner, P. J. Knowles, F. R. Manby, J. A. Black, K. Doll, A. Heßelmann, D. Kats, A. Köhn, T. Korona, D. A. Kreplin, Q. Ma, T. F. Miller, III, A. Mitrushchenkov, K. A. Peterson, I. Polyak, G. Rauhut and M. Sibaev, J. Chem. Phys., 2020, 152, 144107, DOI:10.1063/5.0005081.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253, DOI:10.1002/wcms.82.
- K. Aidas, C. Angeli, K. L. Bak, V. Bakken, R. Bast, L. Boman, O. Christiansen, R. Cimiraglia, S. Coriani, P. Dahle, E. K. Dalskov, U. Ekström, T. Enevoldsen, J. J. Eriksen, P. Ettenhuber, B. Fernández, L. Ferrighi, H. Fliegl, L. Frediani, K. Hald, A. Halkier, C. Hättig, H. Heiberg, T. Helgaker, A. C. Hennum, H. Hettema, E. Hjertenæs, S. Høst, I.-M. Høyvik, M. F. Iozzi, B. Jansík, H. J. A. Jensen, D. Jonsson, P. Jørgensen, J. Kauczor, S. Kirpekar, T. Kjærgaard, W. Klopper, S. Knecht, R. Kobayashi, H. Koch, J. Kongsted, A. Krapp, K. Kristensen, A. Ligabue, O. B. Lutnæs, J. I. Melo, K. V. Mikkelsen, R. H. Myhre, C. Neiss, C. B. Nielsen, P. Norman, J. Olsen, J. M. H. Olsen, A. Osted, M. J. Packer, F. Pawlowski, T. B. Pedersen, P. F. Provasi, S. Reine, Z. Rinkevicius, T. A. Ruden, K. Ruud, V. V. Rybkin, P. Sałek, C. C. M. Samson, A. S. de Merás, T. Saue, S. P. A. Sauer, B. Schimmelpfennig, K. Sneskov, A. H. Steindal, K. O. Sylvester-Hvid, P. R. Taylor, A. M. Teale, E. I. Tellgren, D. P. Tew, A. J. Thorvaldsen, L. Thøgersen, O. Vahtras, M. A. Watson, D. J. D. Wilson, M. Ziolkowski and H. Ågren, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 269–284, DOI:10.1002/wcms.1172.
- G. M. J. Barca, C. Bertoni, L. Carrington, D. Datta, N. De Silva, J. E. Deustua, D. G. Fedorov, J. R. Gour, A. O. Gunina, E. Guidez, T. Harville, S. Irle, J. Ivanic, K. Kowalski, S. S. Leang, H. Li, W. Li, J. J. Lutz, I. Magoulas, J. Mato, V. Mironov, H. Nakata, B. Q. Pham, P. Piecuch, D. Poole, S. R. Pruitt, A. P. Rendell, L. B. Roskop, K. Ruedenberg, T. Sattasathuchana, M. W. Schmidt, J. Shen, L. Slipchenko, M. Sosonkina, V. Sundriyal, A. Tiwari, J. L. Galvez Vallejo, B. Westheimer, M. Wloch, P. Xu, F. Zahariev and M. S. Gordon, J. Chem. Phys., 2020, 152, 154102, DOI:10.1063/5.0005188.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp01681a |
| This journal is © the Owner Societies 2025 |

