Energy partitioning in H₂ formation on interstellar carbonaceous grains. Insights from ab initio molecular dynamics simulations

Abstract

Molecular hydrogen (H₂) stands as the most abundant molecule within the interstellar medium (ISM), primarily originating from the coupling of two H atoms on the surfaces of dust grains. The role of dust grains during the H₂ formation is of third bodies, dissipating the nascent reaction energy and thereby stabilizing the newly formed molecule and preventing it from dissociating back. Whether the formed H₂ remains adsorbed or not on the surface (in this latter case undergoing chemical desorption, CD) largely depends on the type of grain and its capability to absorb the reaction energy excess. In diffuse interstellar clouds, dust grains are typically bare and are composed primarily of silicates or carbonaceous materials, while in denser regions they are covered in ices mostly of water. While water-ice-covered grains have been elucidated to be efficient third bodies, the behavior of carbonaceous grains is still unknown. In this study, ab initio molecular dynamics (AIMD) simulations are employed to analyze how the reaction energy is distributed between the newly formed H₂ and a large graphene slab, as a model of carbonaceous grains in diffuse clouds, and assess the feasibility of CD. The results indicate that only a fraction of the reaction energy is absorbed by the surface, leaving the newly formed H₂ with sufficient internal energy for CD to occur.

---

1 Introduction

Molecular hydrogen (H₂) is the most abundant molecule in the Universe and plays a fundamental role in the evolution of the interstellar medium (ISM). It is a major contributor to the cooling of interstellar clouds, a fundamental process that triggers star formation and drives galaxy evolution.^1,2 Additionally, H₂ serves as a key intermediate in the formation of larger molecules due to its ability to generate the transient H₃⁺ species, an exceptional protonation source that initiates complex ion–molecule reactions, ultimately leading to the synthesis of numerous interstellar molecules.^3,4

The efficiency of H₂ formation depends on the physical and chemical conditions of the ISM, which vary across different regions, including diffuse and dense molecular clouds, each with distinct characteristics. Diffuse clouds are characterized to present low atomic densities (10–500 atom cm⁻³) and gas temperatures between 50–100 K.⁵ Due to the low density, ultraviolet (UV) photons and cosmic rays can penetrate the cloud, destroying any chemical compound of more than three atoms. Thus, in diffuse clouds, the gas–grain interaction can be envisioned as bare grains, primarily composed of silicates⁶ and carbonaceous materials,⁷ with atoms and diatomic species adsorbed on them. In contrast, molecular clouds are denser (10⁴–10⁵ atom cm⁻³) and with lower temperatures (5–10 K).⁵ Here, the higher density largely prevents UV and cosmic rays from penetrating the cloud, and hence, relatively more complex chemical species can survive. Thus, the refractory material of the grains is covered in ices of volatile species due to their accretion and in situ formation on their surfaces, forming a core-mantle grain structure. The dominant species of the ices is H₂ O (the most abundant solid-state species in the ISM), along with CO, CO₂, NH₃, CH₃ OH, CH₄, among others.

Interstellar grains are essential in astrochemistry as they serve as solid-state supports for chemical reactions.^8–13 Their role can be divided into four main functions: (i) as reactant concentrators,^14,15 trapping molecules on their surfaces to facilitate reactions; (ii) as reactant suppliers,^16–18 directly participating themselves in reactions; (iii) as chemical catalysts,^19–22 providing alternative reaction pathways with lower activation energy; and (iv) as third bodies,^23–26 absorbing the excess of energy released by largely exoergic chemical reactions, this way stabilizing the newly formed products.

H₂ formation can result from the coupling of two hydrogen atoms. This H + H association reaction is thermodynamically largely favorable, with a reaction energy of ≈−440 kJ mol⁻¹ (≈−4.50 eV). However, to ensure the stability of the newly formed molecule, this energy excess must be dissipated; otherwise, H₂ would dissociate back to reactants. In the gas phase, direct association of two H atoms is extremely inefficient due to the need for radiative stabilization via quadrupole transitions with lifetimes on the order of 100 years. This renders such processes practically irrelevant under interstellar conditions. Radiative association processes (e.g., H + H⁺ or H + H⁻) are also insufficient, as their rate constants are 6 orders of magnitude lower than required to explain the observed abundance of H₂ in the ISM. Therefore, it is widely accepted that H₂ primarily forms on the surfaces of interstellar dust grains.^27,28

Acting as third bodies, grains do not participate directly in the reaction, but they facilitate the formation of H₂ by absorbing the energy released during the reaction. The third-body effect is essential not only for stabilizing the newly formed molecule but also for promoting its chemical desorption (CD). CD is a chemically driven process in which the newly formed molecule is ejected from the surface into the gas phase due to the energy released by the reaction. This excess energy can lead to localized heating of the surface,²⁹ or it may be retained as internal energy in the product (e.g., translation or rotation).³⁰ Experimental and theoretical studies^31–38 have highlighted the importance of CD in astrochemistry, particularly in cold ISM environments where thermal desorption is ineffective, thus explaining the unexpected gas-phase abundance of certain molecules.

Previous studies^23,24,26 have investigated the third-body effect of water-ice-covered grains^39–41 in various chemical reactions, like the formation of HCO,²³ NH₃,²⁴ PH,²⁵ as well as H₂via H + H association.²⁶ These studies focused on dense molecular clouds, where water ice mantles were found to be particularly efficient in dissipating reaction energies. This efficiency was attributed to an effective vibrational coupling between the newly formed products and the water molecules of the ice. Nevertheless, within diffuse clouds, the capability of the grain refractory materials as third bodies has never been explored, which is here hypothesized to be different due to their different heat capacity compared to water ice and the different nature of the molecule/surface interactions. Investigating their role is, therefore, critical to understanding formation in such environments. To this aim, in the present work, we address the H₂ formation on graphene (as a paradigmatic case of interstellar carbonaceous material) to assess its function as third body and the likelihood of CD of the newly formed H₂ molecule.

H₂ formation on surfaces has been postulated to occur via three mechanisms: Langmuir–Hinshelwood (LH), Eley–Rideal (ER), and hot-atom (HA). In the LH mechanism, two adsorbed H atoms diffuse and react to form H₂, a process supported by both experimental^42–46 and theoretical studies.^47–49

Adsorption of hydrogen atoms on carbonaceous surfaces can occur via physisorption and chemisorption, as demonstrated in numerous experimental and theoretical studies.^46,50–56 In the physisorbed state, H atoms are weakly bound through van der Waals interactions and preferentially located above the centre of the carbon hexagons, with an equilibrium distance of approximately 3.0 Å from the surface.⁵⁷ In contrast, chemisorption involves the formation of stronger covalent bonds directly atop carbon atoms, occurring at shorter equilibrium distances, around 1.8 Å. This bonding requires lattice reconstruction, where the carbon atom involved rehybridizes from sp² to sp³ and puckers out of the graphene plane by ≈0.36 Å.⁵⁸ Theoretical studies support that H atoms, once adsorbed, can diffuse/recombine through quantum tunnelling or thermal hopping.^55,59–62 A comprehensive review⁶³ has examined H₂ formation on various surfaces, including carbonaceous materials, highlighting key processes such as adsorption, diffusion, energy dissipation, and CD. The associative desorption of H₂ and D₂ from chemisorbed hydrogen on highly oriented pyrolytic graphite (HOPG) surfaces at 2100 K has been studied experimentally.⁶⁴ These investigations reveal that a significant portion of the total reaction energy (≈328 kJ mol⁻¹ or 3.4 eV) is converted into translational energy with distributions peaking near 125 kJ mol⁻¹ (1.3 eV). Quantum mechanical simulations further indicate that 40–50% of the total energy from H₂ formation via the ER mechanism is carried away as translational energy of H₂, the remaining energy being distributed between the internal energy of the product and transferred to the surface.⁶⁵ Several studies have investigated the vibrational excitation of nascent H₂. Some report low excitation levels with most molecules desorbing in the vibrational ground state (ν = 0).^44,65,66 Others, however, have found significant excitation with a substantial fraction of H₂ emerging in higher vibrational states such as ν = 4 and ν = 5.^49,67,68

Despite significant progress in understanding H₂ formation on surfaces, the mechanisms of energy dissipation and the role of grains as third bodies remain partly unexplored. A particularly powerful approach for studying the third-body effect is by means ab initio molecular dynamics (AIMD) simulations. These simulations incorporate electronic structure while treating nuclei classically, accounting for bond formation, breaking, and product behavior. In particular, microcanonical (NVE) AIMD simulations, where total energy remains constant, help analyze energy distribution of a chemical reaction, namely, in the form of potential energy and kinetic energy, and for the latter term, whether retained by the newly formed molecule or transferred to the surface.

A recent study⁶⁹ employing a similar ab initio molecular dynamics approach investigated H₂ formation on C₆₀ fullerene, primarily focusing on the ER mechanism following hydrogen atom impact. While they also explored LH reactions across a broad temperature range (10–4000 K), representing thermal shock, their emphasis remained on structural aspects of bond formation and surface reactivity. In contrast, our work focuses on the energy partitioning during H₂ formation, specifically tracking how the reaction energy is distributed between the product and the surface. Additionally, we provide detailed insight into the vibrational excitation state of the nascent H₂ molecule and the energy dissipation dynamics within the carbonaceous grain.

In this work, we employ AIMD simulations grounded on the density functional theory (DFT) to investigate energy dissipation and the feasibility of CD during H₂ formation on graphene. The formation of H₂ through the coupling of H atoms is assumed to proceed via an LH mechanism, where adsorbed H atoms diffuse and react on the graphene surface. AIMD calculations, combined with graphene models, provide an ideal framework to capture temperature effects and surface conditions relevant to diffuse interstellar clouds, allowing us to examine their impact on energy partitioning and the feasibility of CD processes.

2 Methodology

2.1 Atomistic slab model for graphene

Carbonaceous materials cover diverse systems, including amorphous carbon with aliphatic H-rich and aromatic H-poor components, graphite, silicon carbide, and polycyclic aromatic hydrocarbons (PAHs). In this study, we use a graphene surface as an atomistic model to represent carbonaceous materials. Graphene effectively captures the properties of graphite, PAHs, and partially aromatic H-poor carbonaceous materials in the context of H₂ formation.

The graphene structure was modeled using a periodic approach, starting from its primitive unit cell,⁷⁰ which was expanded into a (15 × 15) supercell resulting in a single-layer graphene sheet composed of 512 carbon atoms (see Fig. 1). This extended structure provides a sufficiently large surface to minimize finite-size effects. Upon optimization, the lattice parameters of the unit cell are a = 39.47 Å, b = 39.47 Å, and (α = β = 90°) and (γ = 120°). A 40 Å vacuum gap was introduced along the out-of-plane (c = 40 Å) to prevent interactions between simulation boxes.

Fig. 1 Top view of the super cell unit of the graphene slab model used in this work.

2.2 Computational details

Both static calculations and AIMD simulations were performed with the CP2K package,⁷¹ specifically employing the Quickstep module.⁷¹

The exchange–correlation energy was described using the generalized gradient approximation (GGA) PBEsol functional,⁷² which offers a good balance between computational efficiency and accuracy, and is particularly well-suited for solid-state systems as supported by previous benchmarking studies.^73,74 Additionally, we also performed preliminary calculations for the H₂ formation in the gas phase (i.e., in absence of the graphene surface) and found that the reaction energies calculated at PBEsol and CCSD(T)-F12 are in excellent agreement (results available in the ESI†). To account for dispersion interactions, the D3 correction with Becke–Johnson damping (D3(BJ)) was applied.⁷⁵ Although H₂ lacks a net electric dipole moment, it possesses a significant electric quadrupole moment, which leads to only weak interactions. As a result, dispersive forces arising from quadrupole moment interactions (like those present in the H₂/graphene system) play a crucial role. Previous studies have shown that neglecting these interactions can significantly underestimate binding energies (e.g., ref. 76).

Core electrons were described using Goedecker–Teter–Hetter pseudopotentials,⁷⁷ while a hybrid approach combining Gaussian and plane waves was used to describe valence electrons.⁷⁸ A contracted Gaussian double-ζ MOLOPT basis set⁷⁹ with a single polarization function (DZVP) was employed, along with plane waves with an energy cutoff set at 500 Ry.

The bare surface was first optimized by relaxing atomic positions and cell parameters. The optimized lattice parameters were then fixed for both static calculations and AIMD simulations, allowing only atomic positions to relax. Static calculations were performed to characterize the potential energy surfaces (PESs) of the H₂ formation reaction by locating the stationary points corresponding to reactants, products, and transition states (TSs). The reactant geometries were first optimized in the triplet electronic state to prevent spontaneous H₂ formation due to the Pauli exclusion principle. This optimized triplet structure was then used for a second optimization in the open–shell singlet biradical system. To locate TSs, we used the climbing image nudged elastic band (CI-NEB) method in CP2K⁷¹ and vibrational analysis was performed to confirm their structures. All calculations were carried out adopting the broken symmetry approach,⁸⁰ which is essential when dealing with systems involving open–shell singlet biradical systems.

AIMD simulations were run within the (NVE) microcanonical ensemble, which maintains a fixed number of particles (N), constant volume (V), and constant total energy (E). These simulations were run for two picoseconds with a timestep of 0.2 femtoseconds. Simulations were performed at varying initial temperatures (10, 30, and 50 K) to model different conditions typical of interstellar clouds. The dynamics of the system were propagated in time to observe the formation of the new H₂ molecule and analyze its subsequent behavior. Throughout the simulations, the energy released by the reactions was tracked by calculating the kinetic energy from the particle velocities along the trajectories. This approach allowed us to decompose the kinetic energy into contributions from the newly formed H₂ molecule and the graphene surface. Moving averages were calculated over 50 steps of the molecular dynamics trajectory to estimate observables. In cases where due to the random initial atomic velocities assigned in CP2K, we were not able to obtain H₂ product to form, we applied the cascade method. This method provides an additional 2.5 kJ mol⁻¹ of energy to each H atom in the correct direction, helping to drive the reaction forward while minimally perturbing the overall system dynamics.

To determine the vibrational states of the H₂ molecule during AIMD simulations, we constructed the H–H PES by scanning the H₂ bond length from 0.3 to 3.0 Å in 0.01 Å steps. The resulting energy profile was fitted to a Morse potential, providing the equilibrium bond length, dissociation energy, and force constant. These parameters determined the vibrational energy levels, turning points, and equilibrium position, which were then compared with AIMD trajectories to assign the vibrational state at each oscillation.

To study how energy transfers from the excited H₂ molecule to phonon modes of graphene, we used the trajectory analyzer and visualizer (TRAVIS),^81,82 a program designed for analyzing and visualizing trajectories from molecular dynamics simulation, including AIMD simulations. In particular, TRAVIS was here employed to calculate the vibrational density of states (VDOS) using the Fourier transform of the velocity autocorrelation function from the simulation trajectories. The VDOS helped identify surface vibrational modes involved in energy dissipation, providing insight into the interaction between graphene phonons and excited H₂ and the overall energy relaxation process.

2.3 Binding energy calculations

The binding energy (BE) of H₂ on the graphene surface was calculated to assess their interaction strength. The adsorption energy, ΔE_ads, was first calculated as:

ΔE_ads = E_CPLX − (E_graphene + E_H2) (1)

where E_CPLX is the absolute potential energy of the H₂/graphene complex, E_graphene is the absolute potential energy of the isolated optimized graphene surface, and E_H2 is the absolute potential energy of the isolated optimized H₂ molecule.

To correct for Basis Set Superposition Error (BSSE),⁸³ which arises when interacting molecules artificially overstabilize their energy due to basis functions overlap, the counterpoise correction⁸⁴ was applied. This estimates BSSE by recalculating energies with ghost orbitals and subtracting the error:

ΔE^CP_ads = ΔE_ads − BSSE (2)

Finally, the BE was determined as ΔE^CP_ads in opposite sign:

BE = −ΔE^CP_ads (3)

3 Results and discussion

3.1 Potential energy surface of the H₂ formation on graphene

Previous to the AIMD simulations, we first calculated the PES of the H₂ formation on the graphene slab model to determine if the process presents an energy barrier. While the reaction is barrierless in the gas phase due to spin–spin coupling, an energy barrier could emerge due to H/graphene interactions, as seen in radical–radical couplings on water ice surfaces.⁸⁵ Thus, different PESs were explored adopting an Lh mechanism and assuming that diffusion of the H atoms has already occurred, placing them in proximity to directly simulate the reaction. Three different initial H positions were considered, representing different adsorption regimes (i.e., physisorption and chemisorption), allowing us to explore the impact of the initial H adsorption states on the energy dissipation. These configurations, illustrated in Fig. 2 (see the reactant structures), are described as follows:

• PP structure: both H atoms are physisorbed above the centre of two adjacent hexagons in the graphene lattice, sharing a common edge defined by two interconnected carbon atoms. The optimized structure (triplet electronic state) shows an H–H separation of 3.02 Å and H–C distances of approximately 2.86 Å, placing the H atoms about 3.0 Å above the basal plane. These values are consistent with prior studies on physisorption of H atoms on graphene.^49,57

• PC structure: one H atom is chemisorbed on a carbon atom in the graphene lattice, while the second is physisorbed above the centre of the same hexagon. In the optimized triplet state, the H–H distance is 2.19 Å. The chemisorbed H atom forms a covalent bond with an H–C distance of 1.13 Å and induces a noticeable out-of-plane puckering of the bonded carbon atom. The physisorbed H atom is positioned approximately 2.79 Å above the surface.

• CC structure: both H atoms are chemisorbed on carbon atoms belonging to two adjacent hexagons. The optimized singlet open–shell structure is characterized by an H–H distance of 2.91 Å and H–C bond lengths of 1.13 Å. As in the PC case, clear puckering of the carbon atoms bonded to hydrogen takes place. This structural distortion is consistent with earlier reports.^58,65

Fig. 2 also represents the stationary points of the reactions starting from each initial structure. For PP and PC, reactants are optimized in the triplet electronic state, as the singlet open–shell biradical collapses spontaneously into the H₂ product, indicating a barrierless reaction.

Fig. 2 PBEsol-D3(BJ)-optimized geometries of the stationary points for the H₂ formation on graphene according to the initial structures: (a) PP, (b) PC, (c) CC. For each configuration, the lateral view is displayed on the left and the top view on the right. Colour-coding: white, H atoms; grey, C atoms.

In contrast, for CC, the reaction encounters a substantial potential energy barrier of 119.6 kJ mol⁻¹ due to the H–C bonds, which must be broken before H₂ can form. These bonds stabilize the CC reactant system at an energy minimum, thus reducing the energy released to −158.9 kJ mol⁻¹ (see Table 1), significantly lower than in the gas phase.

Table 1 PBEsol-D3(BJ)-calculated reaction energies (ΔE_rx) and potential energy barriers (ΔE^‡), in kJ mol⁻¹, for H₂ formation on graphene according to different initial structures

Initial structure	ΔErx (kJ mol^−1)	ΔE^‡ (kJ mol^−1)
PP	−443.2	Barrierless
PC	−356.8	Barrierless
CC	− 158.9	119.6

---

For PP, both H atoms are physisorbed, resulting in a larger energy release of −443.2 kJ mol⁻¹, closer to the gas-phase value. PC represents an intermediate case, where one H atom is chemisorbed, and the other is physisorbed, leading to a smaller energy release than PP but larger than CC (−356.8 kJ mol⁻¹).

3.2 Ab initio molecular dynamics simulations of H₂ formation on graphene

The results concerning the energy evolution and partitioning during the H₂ formation on the graphene layer obtained from the AIMD simulations are described here. For the barrierless reactions (namely, from structures PP and PC), the optimized geometries of the reactants were used as the starting points of the AIMD simulations. For the reaction presenting a potential energy barrier (that from structure CC), preliminary AIMD simulations from the open–shell singlet reactant were performed to check if CC spontaneously evolves towards H₂ formation caused by dynamic effects. As expected, given the substantial barrier, no spontaneous reaction was observed. Consequently, to facilitate the reaction, the TS was chosen as the starting structure for the AIMD simulations applying the cascade method (explained in Section 2, Methodology). Choosing the TS as the initial structure is justified by the potential role of quantum tunneling, which is not accounted for in AIMD simulations, as quantum phenomena such as tunneling cannot be captured. Tunneling is particularly significant in reactions involving hydrogen atoms and at very low temperatures. However, this approach overestimates the reaction energy to be considered in the analysis and accordingly, results for this specific case can be taken as insights and the values semi-qualitative.

3.2.1 H₂ formation on graphene. Fig. 3 shows the time evolution of the different energy components associated with the H₂ formation on graphene at the initial temperatures of 10, 30, and 50 K. The plot displays the average values of the total energy (E_tot), the potential energy (V_tot), and the total kinetic energy (T_tot), this latter decomposed into the kinetic energy of H₂ (T_H2) and the kinetic energy of the graphene (T_Graphene), derived from velocity data along the trajectories. For the sake of clarity and comparison, V_tot, T_tot and T_Graphene values were normalized with respect to the first point. This is not the case for T_Graphene, which remain unchanged; otherwise, nonphysically sounded negative values arise. Although the AIMD simulations were run for 2 ps, the plots display only the first 400 fs, as this timeframe is enough to capture the formation of H₂ and the stabilization of energy. Beyond this point, no significant changes occur in the system's behavior. The complete simulation dataset is available in the ESI.†

Fig. 3 Evolution of the averaged energy components (in kJ mol⁻¹) over 400 fs displayed in plots (a)–(i) depending on the initial temperature (10, 30 and 50 K): in green, the potential energy (V_tot); in orange, the total kinetic energy (T_tot); in red, the H₂ kinetic energy (T_H2); in blue, the graphene kinetic energy (T_graphene); in grey, the total energy (E_tot). The first data point has been subtracted from each series, normalizing all values to start at 0 kJ mol⁻¹ except for graphene kinetic energy.

The evolution of T_tot and V_tot exhibit a symmetric behavior in accordance with the principle of energy conservation. During H₂ formation, the system releases energy as the H–H bond forms, leading to a sharp rise in T_tot and a corresponding drop in V_tot.

The formation of H₂ is characterized by the rapid rise in T_H2, followed by an increase in T_Graphene, indicating an energy transfer from the energy released during H₂ formation to the graphene surface.

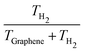
Analyses of the T_H2 and T_Graphene evolutions (shown in Table 2) reveal that the amount of the reaction energy that is transferred from H₂ to the surface depends on the initial temperature and the initial structure. In general, the larger the initial temperature, the larger the amount of energy transferred to the surface. While at an initial temperature of 10 K the fraction of kinetic energy retained by H₂ is 0.46–0.68 (meaning an absorption of 32–54% of the energy released during the H₂ formation by the graphene surface), at 50 K the fraction decreases to 0.28–0.40 (meaning an increment of the absorption of the released energy by graphene to 60–72%, see Table 2). Thus, it seems that higher temperatures improve the vibrational coupling between H₂ and graphene, this way favoring the energy transfer between the two partners. However, we observe an exception in PP at 10 K, where the energy transfer is higher than at 30 K. This coincides with the transient formation of a C–H bond along the trajectory of PP at 10 K, which favors a direct, enhanced energy transfer.

Table 2 Data derived from the (NVE) AIMD simulations for the investigated H₂ formation reactions on graphene: the initial structures of the reactions studied (first column); initial temperatures (in K) at which the simulations were run (second column); time at which the H₂ desorption occurs after the H₂ formation (t_des, third column) (in fs); fraction of the kinetic energy transferred to the surface (fourth column) and retained by H₂ at the end of the simulation (fifth column); translational kinetic energy (trans-T, sixth column) and the trans-T along the z-axis (trans-Tz, seventh column) of the newly formed species (in kJ mol⁻¹); calculated binding energies (BE, in kJ mol⁻¹) of H₂ on graphene (eighth column); vibrational state relaxations (ninth column) of H₂ over 200 steps immediately after its formation and vibrational state of H₂ over 200 steps following its desorption from the surface

Structure	Temperature	t des			trans-T	trans-Tz	BE	Vibrational state
PP	10	172.4	0.38	0.62	200.6	11.4	4.6–4.9	14 → 10
	30	117.6	0.32	0.68	203.3	21.1	4.6–4.9	14 → 14
	50	116.4	0.60	0.40	209.7	28.5	4.6–4.9	14 → 12
PC	10	129.4	0.32	0.68	106.7	48.4	4.6–4.9	10 → 9
	30	131.2	0.55	0.45	105.2	43.1	4.6–4.9	9 → 9
	50	132.2	0.67	0.33	105.2	39.9	4.6–4.9	9 → 9
CC	10	59.6	0.54	0.46	100.1	86.7	4.6–4.9	3 → 3
	30	58.8	0.71	0.29	100.4	87.7	4.6–4.9	3 → 2
	50	58.2	0.72	0.28	101.1	89.0	4.6–4.9	3 → 2

---

3.2.2 H₂ Chemical desorption. In every trajectory, the newly formed H₂ molecule undergoes CD. The desorption time of H₂ was determined as the moment when the molecule reaches a distance of 8 Å from the surface, chosen as an arbitrary threshold to indicate detachment. Once desorbed, the H₂ molecule does not return to the surface, indicating a definitive departure.

Clearly, once formed, the H₂ molecule retains a significant amount of the reaction energy in the form of internal kinetic energy, which is distributed among its degrees of freedom, that is, among the vibrational frequency (which becomes excited in the moment of the H₂ formation) and the rotational and translational components. Translational kinetic energy (trans-T) of H₂ along the x and y directions contributes to the diffusion of H₂ across the graphene surface. However, the z component of trans-T (perpendicular to graphene) is crucial for desorption, as it drives the possibility of CD. If the z component of the translational kinetic energy (trans-Tz) of H₂ exceeds the binding energy (BE) of H₂ on graphene, the molecule has enough internal energy to overcome the interaction with the surface as to be desorbed and ejected into the gas phase. This is what is observed in the simulations, which is explained as follows.

The BEs calculated for the distinct positions of H₂ on graphene span the 4.6–4.9 kJ mol⁻¹ range, which agree with BE values reported in previous studies.^86,87 CD of H₂ takes place within 58.2 to 172.4 fs after its formations (see Table 2). In these cases, graphene absorbs a small fraction of the energy released during H₂ formation, meaning that the rest is retained by the molecule. Accordingly, trans-Tz values for all the trajectories (between 11.4 and 89.0 kJ mol⁻¹, depending on the initial temperatures and the positions, see Table 2) are significantly larger than the H₂ BEs such that CD of the newly formed H₂ molecule thus takes place.

3.2.3 H₂ vibrational excitation and energy transfer to graphene. It is evident that part of the nascent reaction energy is transferred to the surface (as seen in Table 2), which is dissipated throughout the lattice phonon modes of graphene. However, prior to this energy transfer, the H₂ molecule forms, which due to the large reaction energy results in a vibrational excited state. Thus, the interaction with the surface through vibrational coupling enables the transfer of energy to graphene and the vibrational relaxation of the H₂ molecule. Here, we analyze this process in detail.

In the interstellar medium (ISM), the vibrational state of newly formed H₂ molecules is influenced by the likelihood of these molecules leaving the grain surface before being “thermalized” through interactions with the grain surfaces.⁸⁸ The level of vibrational excitation in these H₂ molecules has significant implications for two key astrophysical areas: (i) facilitating gas-phase reactions with high activation energy barriers, which are crucial for initiating the chemistry in molecular clouds;⁸⁹ and (ii) enabling the potential detection of newly formed H₂via emission resulting from its vibrational relaxation^49,65 through weak quadrupole transitions that can be detected with e.g., the NIRSpec and MIRI instruments of JWST, especially in warm molecular gas (T > 100 K) such as in shocked regions, photodissociation regions, star-forming regions and circumstellar disks, thereby allowing for the measurement of formation rates in molecular clouds and providing constraints for theoretical astrochemical models. Because of that, we analyse the level of vibrational excitations of H₂ once it is formed and its degree of relaxation on the surface and, to be the case, upon CD.

By adopting the procedure explained in Section 2 (Methodology), we identify that, in almost all the cases, H₂ is immediately excited once it is formed. Table 2 shows the vibrational states for each initial structure. For PP, H₂ initially forms in highly excited vibrational states, specifically at ν = 14, indicating that a significant amount of energy is stored in bond oscillations. At 30 K, there is no observed vibrational relaxation immediately after formation. However, at 10 K and 50 K, the final vibrational state decreases to ν = 10 and ν = 12 respectively, suggesting that some vibrational energy relaxation occurs over time. Remarkably, largest vibrational relaxation occurs at 10 K, which is consistent with the largest energy transfer due to forming the transient C–H chemical bond (see above). In contrast, for CC, H₂ forms in a much lower vibrational state (ν = 3), which is consistent with the lower reaction energy, with only a slight relaxation observed after desorption at 30 K and 50 K, lowering the vibrational state to ν = 2. For PC, H₂ is initially produced in a mid-to-high vibrational state at ν = 9–10. After desorption at 10 K, a small vibrational relaxation occurs, reducing the vibrational state from ν = 10 to ν = 9. However, at higher temperatures of 30 K and 50 K, no vibrational relaxation is observed.

Our simulations also highlight a correlation between the initial binding configuration of surface H atoms and the vibrational energy retained by the desorbing H₂ molecule. While this may appear intuitive, our analysis quantifies this effect and emphasizes how specific binding sites influence the internal energy budget of the product. For CC, where chemisorbed hydrogen atoms recombine, the lower reaction energy results in H₂ formed in a lower vibrational state. Conversely, for PP, a significant amount of energy is released upon recombination, leading to the formation of H₂ in highly excited vibrational states. PC represents an intermediate case, with moderate energy release and an initial vibrational state between the one of CC and PP. Additionally, our results show little to no vibrational relaxation after desorption, suggesting that energy dissipation through vibrational relaxation is minimal in these processes.

Previous experimental work⁶⁷ highlighted that recombination of (apparently physisorbed) H and D atoms on a highly oriented pyrolytic graphite (HOPG) surface at 15 K forms HD in ν = 5–7 vibrational states. Theoretically,⁶⁸ the H₂ formation on HOPG has been studied, in this case adopting an ER mechanism in which a chemisorbed H atom directly reacts with an incoming, gaseous H atom. To compare with the experimental data, authors performed a set of approximations to determine the vibrational states of a newly formed HD, showing a similar ν = 5–7 vibrational state distribution. This later study would be consistent with our PC initial structures, in which H₂ forms and keeps at ca. ν = 9. Although the results of these studies do not entirely agree, it is important to note that we are here considering H₂ formation, while the others focus on HD formation. Because HD has a larger reduced mass, its vibrational energy levels are more closely spaced than those of H₂. As a result, if the total energy transferred into the vibrational degree of freedom is similar for both molecules, vibrational state distribution of HD will center around a higher ν quantum number. However, assuming the energy transfer occurs on similar timescales, HD relaxation involves more vibrational states due to their smaller energy gaps, leading to a lower final vibrational state compared to H₂. This can help reconcile the differences between the studies.

To further investigate the energy transfer process, we computed the VDOS power spectrum (which highlights the surface vibrational modes during the simulations) considering only the graphene surface, both in its isolated state and during the reaction but neglecting the atoms of H₂. The difference between these two VDOS spectra (ΔVDOS) reveals the changes in the vibrational mode populations of graphene along the trajectories, thereby capturing the changes in the population of the surface vibrations due to the reaction. Thus, by examining the increase in the population of the graphene vibrational modes (reflected by an increase of the ΔVDOS) we can determine the magnitude of the vibrational coupling between the H₂ molecule and the graphene surface, gaining insight into the mechanism that governs the energy dissipation. Fig. 4 shows the calculated ΔVDOS for the H₂ formation on the different structures and temperatures.

Fig. 4 Difference of the simulated VDOS power spectrum (ΔVDOS) displayed in plots (a)–(i) depending on the initial temperature (10, 30 and 50 K), between the computed trajectories for the graphene surface when the reaction takes place and for the isolated layer.

Graphene presents a low-frequency region (ν = 0–1000 cm⁻¹) assigned to out-of-plane bending vibrations, and a higher frequency region (ν = 1000–1800 cm⁻¹) assigned to in-plane bending and stretching vibrations. According to ΔVDOS, in all the structures, these frequency regions become more populated, indicating that the main mechanism responsible for the dissipation of the large excess of the reaction energy is the intermolecular vibrational coupling between the vibrational mode of the newly born H₂ and the graphene phonon modes. As expected, in CC (that with the highest energy transfer), the graphene vibrations become more populated than in PP and PC, suggesting a stronger coupling effect in CC. Additionally, in PC at 10 K, we observe a population increase similar to CC, consistent with the transient C–H bond formation in this case, which likely contributes to the high energy transfer observed.

However, the vibrational coupling between H₂ and graphene is of limited efficiency. By comparing these results with those of Ferrero et al.²⁴ in the formation of NH₃ on amorphous water ice surface, the increase of the population of the vibrational modes of the water ice (particularly the low-frequency libration modes) is significantly greater than that occurring in the graphene surface. The difference is due to the fact that the interaction of NH₃ with water ice surface takes place mainly through hydrogen bonds, which establish a direct path towards favorable a vibrational coupling between the two components, while the interaction between H₂ and graphene is essentially through dispersion forces, giving rise a less efficient vibrational coupling.

Our results, thus, confirm the energy dissipation mechanism occurring during the H₂ formation on graphene. Upon H₂ formation, the molecule enters a highly excited vibrational state due to the significant energy released during the reaction, which is momentarily stored in its vibrational degree of freedom. Over time, this energy is transferred to the graphene surface, resulting in a progressive decrease in the vibrational state of the molecule. This energy transfer manifests as an increase in T_Graphene and in the population of its vibrational modes. The energy transfer is driven by the coupling between the H₂ highly excited vibrational mode and the graphene lattice phonon modes, these latter serving as key elements for absorbing and redistributing the energy released during the reaction.

Finally, to further investigate the spatial distribution of the energy dissipation throughout the graphene surface, we analyzed the transfer of energy from the reaction site to the surrounding environment. This analysis involved examining the distribution of kinetic energy per carbon atom across four concentric shells centered on the H₂ formation reaction site. The spheres were defined with radii of 5, 10, 15, and 20 Å, with each shell containing atoms not included in the smaller shells. Here, for the sake of brevity and in view that the trends are general, we only show the results for PP at the different temperatures (Fig. 5), while those for the other structures are available in the ESI.†

Fig. 5 Evolution of the averaged T_Graphene (normalized per carbon atom) over 400 fs (in kJ mol⁻¹) displayed in plots (a)–(c) depending on the initial temperature (10, 30 and 50 K), in concentric shells centered at the H₂ formation reaction site in the PP structure at the different temperatures.

Notable variations in the energy distribution across the shells of carbon atoms can be distinguished. Close to the reaction site, the first shell exhibits a sharp, highly localized peak. This energy then propagates outward like a wave, with the second shell experiencing a smaller, slightly delayed peak. This delay increases with each successive shell as the energy moves through the lattice. The highest peak occurs in the first shell, confirming that the reaction energy is initially concentrated at the reaction site. The energy dissipates rapidly as graphene efficiently distributes the energy across its structure until it becomes evenly spread over the surface. Ultimately, T_Graphene stabilizes, becoming uniformly distributed across the graphene sheet and preventing any localized energy concentration. However, as temperature increases, both the peak value in the second shell and the baseline level of the shell become higher. This indicates that at elevated temperatures, the ability of graphene to absorb and retain energy is enhanced.

3.2.4 Comparison with H₂ formation on water ice surface. The work of Pantaleone et al.²⁶ already addressed the H₂ formation but on interstellar water ice surfaces, adopting a similar computational approach, in that case using an initial temperature of 10 K simulating cold dense molecular clouds, where interstellar ices exist. Thus, here we compare the results between the two investigations to identify significant differences, which are primarily due to the different nature of the surfaces. For the sake of consistency, we focus the comparison on the simulations with an initial temperature of 10 K.

In Pantaleone's work, different initial structures were used, which differ on the surface morphology of the H adsorption sites. However, in all the cases, the reactive H atoms were physisorbed on the water ice surfaces and with an H to H distance of about 4 Å. Due to that, all the tested reactions were found to be barrierless, by means of both static calculations (aiming to characterize the PES) and AIMD simulations. This is similar to what happens on graphene when at least one H atom is physisorbed. But when both atoms are chemisorbed, an unfeasible situation on ices, the reaction has a potential energy barrier, which is associated with the H–C chemical bond cleavage to form H₂.

Another interesting aspect to compare is the capability of the surfaces to absorb and dissipate the energy released by the reaction. On both surfaces, the newly formed H₂ molecule relaxes, meaning that there is an energy transfer from the molecule to the surfaces. However, the fraction of energy transferred to the surface is different: on water ices, the surfaces absorbed about 45–65% of the released energy, while on graphene between 32–54%. From this data clearly emerges the fact that water ices are more efficient third bodies than graphene, as already mentioned above when comparing the vibrational population of a newly formed NH₃ molecule on water ice. The reason of this difference is the major capacity of water ice to vibrationally couple with the adsorbates, due to being a material presenting local dipole moments, at variance with graphene.

Interestingly, such a smaller capacity to absorb the reaction energy by graphene compared to water ice is important as regards CD. Indeed, on graphene, CD of the newly H₂ formed molecule is observed in almost all the cases, precisely because the H₂ retains a notable fraction of the released energy in the form of kinetic energy, which has not been transferred to the surface. In contrast, on water ice surfaces, CD is observed in only one case. In Pantaleone et al., the analysis of the trans-Tz was not done, and CD was predicted to occur on the basis that the total trans-T was greater than 10 times the H₂ BE. Furthermore, CD was observed to occur when the formed H₂ molecule diffuses across the surface and stumbles over a surface irregularity (in that case, a dangling H atom of an outermost H₂ O molecule of the ice), in which all the trans-T is channeled towards the desorption direction. This is different from the H₂ CD on the graphene layer, as it is an ideal surface without defects. Accordingly, on graphene, the CD is purely driven by the amount of trans-Tz contained by H₂ upon formation.

The different capability of the surfaces to dissipate the reaction energy excess and the chances to have CD is also reflected in the vibrational states of the emerging H₂ molecule. On water ices, the H₂ molecule also forms in a vibrationally excited state (between ν = 4–6), which lowers to ν = 1–2 along the simulation. On graphene, however, we observe a strong dependence of the initial excited vibrational state of H₂ with the initial H positions, which in turn is regulated by the reaction energy. When the two H atoms are physisorbed (PP structure, presenting the most favorable reaction energy), the H₂ molecule forms in highly excited vibrational states (ν = 14); when the two H atoms are chemisorbed (CC structure, presenting the less favorable reaction energies) the H₂ molecule forms in low vibrational states (ν = 3); when one H atom is physisorbed and the other chemisorbed (PC structure, presenting an intermediate reaction energy) the H₂ molecule forms in moderately high vibrational states (ν = 9–10).

4 Conclusions

This study investigates the role of graphene, as a test case of cosmic carbonaceous material, as a third body in energy dissipation during interstellar H₂ formation on its surface. Using (NVE) AIMD simulations, the partitioning of the reaction energy excess at three interstellar temperatures and considering different initial H adsorption states has been examined, revealing how energy is distributed between graphene and the newly formed H₂ molecule.

Our results show that between 32% and 72% of the reaction energy is transferred to the graphene surface, with higher temperatures enhancing energy transfer. Such values infer that in most of the cases, H₂ chemical desorption takes place due to the highly exothermic reaction providing enough energy to overcome the H₂ binding energy on graphene.

Energy dissipates through vibrational coupling, populating the vibrational modes of graphene. While graphene is less efficient at absorbing energy compared to water ice due to its stiffness and the weaker H₂/graphene intermolecular interactions (based on dispersion forces), the energy transfer occurs quickly, dissipating and reaching an uniform distribution across the surface. Notably, sites where H atoms were initially chemisorbed exhibit larger vibrational population, leading to greater energy transfer. As a result, the H₂ molecule formed from this initial adsorption state is in low vibrational states, as it is able to transfer their excess energy more effectively to the surface. In contrast, when H atoms are physisorbed, the vibrational population of the graphene modes is smaller, meaning a lower energy transfer to the surface. Consequently, for these cases, newly formed H₂ molecules are released into the gas in medium-high vibrational states.

Our analysis primarily focuses on the vibrational excitation of nascent H₂. Although rotational excitation is known to play a significant role in surface recombination reactions,^65,66 this aspect is not included in the present study. Clearly, incorporating rotational degrees of freedom would provide a more complete picture of energy partitioning during H₂ formation.

One key limitation of AIMD is neglecting the zero-point energy correction, which can lead to an underestimation of the actual energy available in the system. Additionally, AIMD treats energy transfer classically, while in reality, vibrational relaxation occurs in discrete quantum steps. Studying this process through ring polymer molecular dynamics simulations in the future would help to better understand the vibrational relaxation dynamics of H₂ on graphene.

In view of the present results, we consider that exploring other molecules and surfaces is essential to generalizing (or not) these findings in astrophysical environments. Extending this approach to different chemical species and grain surfaces of different nature, such as amorphous carbon, silicates, or mixed-composition grains, would provide a broader understanding of energy dissipation mechanisms and chemical desorption phenomenon.

Author contributions

Léana Jubert: data curation (equal); formal analysis (equal); investigation (equal); methodology (equal); software (equal); validation (equal); visualization (equal); writing – original draft (lead). Berta Martínez-Bachs: data curation (equal); formal analysis (equal); investigation (equal); methodology (equal); software (equal); supervising (equal); validation (equal); visualization (equal); writing – review & editing (supporting) Gerard Pareras: data curation (equal); formal analysis (equal); investigation (equal); methodology (equal); software (equal); supervising (equal); validation (equal); visualization (equal); writing – review & editing (supporting) Albert Rimola: conceptualization (lead); funding acquisition (lead); investigation (equal); project administration (lead); resources (lead); supervision (equal); validation (equal); writing – review & editing (lead).

Conflicts of interest

There are no conflicts to declare.

Data availability

The data underlying this article are freely available in Zenodo at https://doi.org/10.5281/zenodo.15005628.

Acknowledgements

This project has received funding within the European Unions Horizon 2020 research and innovation program from the European Research Council (ERC) for the projects “Quantum Chemistry on Interstellar Grains” (QUANTUMGRAIN), grant agreement no. 865657, and the European Unions Horizon Europe research and innovation program under the Marie Sklodowska-Curie grant agreement no. 101105235 for the funding of CHAOS project. The Spanish MICINN is also acknowledged for funding the projects PID2021-126427NB-I00 and CNS2023-144902. The authors thankfully acknowledge the supercomputational facilities provided by CSUC. A. R. acknowledges Accademia delle Scienze di Torino for supporting the project “In silico interstellar grain-surface chemistry”. A. R. gratefully acknowledges support through 2023 ICREA Award.

References

1. S. Schlemmer, Angew. Chem., Int. Ed., 2011, 50, 2214–2215.
2. J. Le Bourlot, G. Pineau des Forêts and D. R. Flower, Mon. Not. R. Astron. Soc., 1999, 305, 802–810.
3. T. R. Geballe, Philos. Trans. R. Soc., A, 2000, 358, 2503–2513.
4. T. Oka, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 12235–12242.
5. T. P. Snow and B. J. McCall, Annu. Rev. Astron. Astrophys., 2006, 44, 367–414.
6. T. Henning, Annu. Rev. Astron. Astrophys., 2010, 48, 21–46.
7. B. Draine, Annu. Rev. Astron. Astrophys., 2003, 41, 241–289.
8. W. D. Watson and E. E. Salpeter, Astrophys. J., 1972, 174, 321.
9. W. Duley and D. Williams, Interstellar Chemistry, Academic Press, 1984.
10. D. A. Williams, Astrochemistry, 1987, pp. 531–536.
11. E. Herbst, Chem. Soc. Rev., 2001, 30, 168–176.
12. E. Herbst, Q. Chang and H. M. Cuppen, J. Phys.: Conf. Ser., 2005, 6, 18.
13. T. Suhasaria and V. Mennella, Front. Astron. Space Sci., 2021, 8, 655883.
14. N. Watanabe and A. Kouchi, Astrophys. J., 2002, 571, L173.
15. A. Rimola, V. Taquet, P. Ugliengo, N. Balucani and C. Ceccarelli, Astron. Astrophys., 2014, 572, A70.
16. A. Rimola, D. Skouteris, N. Balucani, C. Ceccarelli, J. Enrique-Romero, V. Taquet and P. Ugliengo, ACS Earth Space Chem., 2018, 2, 720–734.
17. G. Molpeceres and J. Kästner, Astrophys. J., 2021, 910, 55.
18. J. Perrero, J. Enrique-Romero, B. Martínez-Bachs, C. Ceccarelli, N. Balucani, P. Ugliengo and A. Rimola, ACS Earth Space Chem., 2022, 6, 496–511.
19. B. Martinez-Bachs, A. Anguera-Gonzalez, G. Pareras and A. Rimola, ChemPhysChem, 2024, 25, e202400272.
20. G. Pareras, V. Cabedo, M. McCoustra and A. Rimola, Astron. Astrophys., 2024, 687, A230.
21. V. Cabedo, G. Pareras, J. Allitt, A. Rimola, J. Llorca, H. H. P. Yiu and M. R. S. McCoustra, Mon. Not. R. Astron. Soc., 2024, 535, 2714–2723.
22. G. Pareras, V. Cabedo, M. McCoustra and A. Rimola, Astron. Astrophys., 2023, 680, A57.
23. S. Pantaleone, J. Enrique-Romero, C. Ceccarelli, P. Ugliengo, N. Balucani and A. Rimola, Astrophys. J., 2020, 897, 56.
24. S. Ferrero, S. Pantaleone, C. Ceccarelli, P. Ugliengo, M. Sodupe and A. Rimola, Astrophys. J., 2023, 944, 142.
25. G. Molpeceres, V. Zaverkin, K. Furuya, Y. Aikawa and J. Kästner, Astron. Astrophys., 2023, 673, A51.
26. S. Pantaleone, J. Enrique-Romero, C. Ceccarelli, S. Ferrero, N. Balucani, A. Rimola and P. Ugliengo, Astrophys. J., 2021, 917, 49.
27. D. Hollenbach and E. E. Salpeter, Astrophys. J., 1971, 163, 155.
28. R. J. Gould and E. E. Salpeter, Astrophys. J., 1963, 138, 393.
29. J. Takahashi and D. A. Williams, Mon. Not. R. Astron. Soc., 2000, 314, 273–278.
30. A. Fredon, A. K. Radchenko and H. M. Cuppen, Acc. Chem. Res., 2021, 54, 745–753.
31. F. Dulieu, E. Congiu, J. Noble, S. Baouche, H. Chaabouni, A. Moudens, M. Minissale and S. Cazaux, Sci. Rep., 2013, 3, 1338.
32. M. Minissale, F. Dulieu, S. Cazaux and S. Hocuk, Astron. Astrophys., 2016, 585, A24.
33. M. Minissale and F. Dulieu, J. Chem. Phys., 2014, 141, 014304.
34. E. Congiu, E. Matar, L. E. Kristensen, F. Dulieu and J. L. Lemaire, Mon. Not. R. Astron. Soc.: Lett., 2009, 397, L96–L100.
35. R. T. Garrod, V. Wakelam and E. Herbst, Astron. Astrophys., 2007, 467, 1103–1115.
36. A. I. Vasyunin and E. Herbst, Astrophys. J., 2013, 769, 34.
37. S. Cazaux, V. Cobut, M. Marseille, M. Spaans and P. Caselli, Astron. Astrophys., 2010, 522, A74.
38. S. Cazaux, M. Minissale, F. Dulieu and S. Hocuk, Astron. Astrophys., 2016, 585, A55.
39. R. G. Smith, K. Sellgren and A. T. Tokunaga, Astrophys. J., 1988, 334, 209.
40. T. J. Millar and D. A. Williams, Dust and chemistry in astronomy, 1993.
41. A. A. Boogert, P. A. Gerakines and D. C. Whittet, Annu. Rev. Astron. Astrophys., 2015, 53, 541–581.
42. V. Pirronello, C. Liu, L. Shen and G. Vidali, Astrophys. J., 1997, 475, L69.
43. V. Pirronello, C. Liu, J. E. Roser and G. Vidali, Astron. Astrophys., 1999, 344, 681–686.
44. J. S. Perry, J. M. Gingell, K. A. Newson, J. To, N. Watanabe and S. D. Price, Meas. Sci. Technol., 2002, 13, 1414.
45. G. Vidali, J. Roser, G. Manicò and V. Pirronello, Adv. Space Res., 2004, 33, 6–13.
46. N. Katz, I. Furman, O. Biham, V. Pirronello and G. Vidali, Astrophys. J., 1999, 522, 305.
47. H. M. Cuppen and E. Herbst, Mon. Not. R. Astron. Soc., 2005, 361, 565–576.
48. S. Morisset, F. Aguillon, M. Sizun and V. Sidis, J. Chem. Phys., 2004, 121, 6493–6501.
49. B. Kerkeni and D. C. Clary, Chem. Phys., 2007, 338, 1–10.
50. Z. Medina and B. Jackson, J. Chem. Phys., 2008, 128, 114704.
51. S. Cazaux, S. Morisset, M. Spaans and A. Allouche, Astron. Astrophys., 2011, 535, A27.
52. M. Bonfanti, R. Martinazzo, G. F. Tantardini and A. Ponti, J. Phys. Chem. C, 2007, 111, 5825–5829.
53. S. Morisset and A. Allouche, J. Chem. Phys., 2008, 129, 024509.
54. L. Hornekær, i c v Šljivančanin, W. Xu, R. Otero, E. Rauls, I. Stensgaard, E. Lægsgaard, B. Hammer and F. Besenbacher, Phys. Rev. Lett., 2006, 96, 156104.
55. L. Hornekær, E. Rauls, W. Xu, i c v Šljivančanin, R. Otero, I. Stensgaard, E. Lægsgaard, B. Hammer and F. Besenbacher, Phys. Rev. Lett., 2006, 97, 186102.
56. D. Bossion, A. Sarangi, S. Aalto, C. Esmerian, S. R. Hashemi, K. K. Knudsen, W. Vlemmings and G. Nyman, Astron. Astrophys., 2024, 692, A249.
57. L. Jeloaica and V. Sidis, Chem. Phys. Lett., 1999, 300, 157–162.
58. X. Sha, B. Jackson, D. Lemoine and B. Lepetit, J. Chem. Phys., 2004, 122, 014709.
59. E. Han, W. Fang, M. Stamatakis, J. O. Richardson and J. Chen, J. Phys. Chem. Lett., 2022, 13, 3173–3181.
60. O. Biham, I. Furman, N. Katz, V. Pirronello and G. Vidali, Mon. Not. R. Astron. Soc., 1998, 296, 869–872.
61. S. Cazaux and A. G. G. M. Tielens, Astrophys. J., 2004, 604, 222.
62. T. P. M. Goumans and J. Kästner, Angew. Chem., Int. Ed., 2010, 49, 7350–7352.
63. V. Wakelam, E. Bron, S. Cazaux, F. Dulieu, C. Gry, P. Guillard, E. Habart, L. Hornekær, S. Morisset, G. Nyman, V. Pirronello, S. Price, V. Valdivia, G. Vidali and N. Watanabe, Mol. Astrophys., 2017, 9, 1–36.
64. S. Baouche, G. Gamborg, V. V. Petrunin, A. C. Luntz, A. Baurichter and L. Hornekær, J. Chem. Phys., 2006, 125, 084712.
65. A. J. H. M. Meijer, A. Farebrother, D. C. Clary and A. J. Fisher, J. Phys. Chem. A, 2001, 105, 2173–2182.
66. S. C. Creighan, J. S. A. Perry and S. D. Price, J. Chem. Phys., 2006, 124, 114701.
67. E. R. Latimer, F. Islam and S. D. Price, Chem. Phys. Lett., 2008, 455, 174–177.
68. S. Casolo, G. F. Tantardini and R. Martinazzo, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 6674.
69. Y. Guo and D. R. McKenzie, Commun. Chem., 2025, 8, 97.
70. A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002.
71. T. D. Kühne, M. Iannuzzi, M. Del Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schütt, F. Schiffmann, D. Golze, J. Wilhelm, S. Chulkov, M. H. Bani-Hashemian, V. Weber, U. Borštnik, M. Taillefumier, A. S. Jakobovits, A. Lazzaro, H. Pabst, T. Müller, R. Schade, M. Guidon, S. Andermatt, N. Holmberg, G. K. Schenter, A. Hehn, A. Bussy, F. Belleflamme, G. Tabacchi, A. Glöβ, M. Lass, I. Bethune, C. J. Mundy, C. Plessl, M. Watkins, J. VandeVondele, M. Krack and J. Hutter, J. Chem. Phys., 2020, 152, 194103.
72. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
73. M. De La Pierre, R. Orlando, L. Maschio, K. Doll, P. Ugliengo and R. Dovesi, J. Comput. Chem., 2011, 32, 1775–1784.
74. L. Maschio, M. Ferrabone, A. Meyer, J. Garza and R. Dovesi, Chem. Phys. Lett., 2011, 501, 612–618.
75. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
76. S. Ferrero, L. Zamirri, C. Ceccarelli, A. Witzel, A. Rimola and P. Ugliengo, Astrophys. J., 2020, 904, 11.
77. S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710.
78. G. Lippert, J. Hutter and M. Parrinello, Mol. Phys., 1997, 92, 477–487.
79. J. VandeVondele and J. Hutter, J. Chem. Phys., 2003, 118, 4365–4369.
80. F. Neese, J. Phys. Chem. Solids, 2004, 65, 781–785.
81. M. Brehm and B. Kirchner, J. Chem. Inf. Model., 2011, 51, 2007–2023.
82. M. Brehm, M. Thomas, S. Gehrke and B. Kirchner, J. Chem. Phys., 2020, 152, 164105.
83. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566.
84. E. R. Davidson and D. Feller, Chem. Rev., 1986, 86, 681–696.
85. J. Enrique-Romero, A. Rimola, C. Ceccarelli, P. Ugliengo, N. Balucani and D. Skouteris, Astrophys. J., Suppl. Ser., 2022, 259, 39.
86. W. Tian, Y. Zhang, Y. Wang, T. Liu and H. Cui, Int. J. Hydrogen Energy, 2020, 45, 12376–12383.
87. J. Petucci, C. LeBlond, M. Karimi and G. Vidali, J. Chem. Phys., 2013, 139, 044706.
88. N. Watanabe, Y. Kimura, A. Kouchi, T. Chigai, T. Hama and V. Pirronello, Astrophys. J., Lett., 2010, 714, L233.
89. M. Agúndez, J. R. Goicoechea, J. Cernicharo, A. Faure and E. Roueff, Astrophys. J., 2010, 713, 662.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp01585e

---