 Open Access Article
Open Access ArticleNuclear magnetic resonance study of the relationship between phase behaviour and reorientational and transrational dynamics in N,N-diethylpyrrolidinium bis(fluorosulfonyl)amide with a plastic crystal phase†
Keiko
Nishikawa
 *a,
Kozo
Fujii
b and
Masahiro
Yoshizawa-Fujita
*a,
Kozo
Fujii
b and
Masahiro
Yoshizawa-Fujita
 *c
*c
aGraduate School of Science, Chiba University, Chiba 263-8522, Japan. E-mail: k.nishikawa@faculty.chiba-u.jp
bCenter for Analytical Instrumentation, Chiba University, Chiba 263-8522, Japan
cDepartment of Materials & Life Sciences, Sophia University, Tokyo 102-8554, Japan. E-mail: masahi-f@sophia.ac.jp
First published on 3rd July 2025
Abstract
We investigated the phase transition dynamics between the ordered crystal, plastic crystal (PC), and liquid phases of N,N-diethylpyrrolidinium bis(fluorosulfonyl)amide by measuring the temperature dependences of spin–lattice relaxation time (T1) and spin–spin relaxation time (T2) for 1H and 19F using low-frequency pulsed nuclear magnetic resonance. T1 and T2 are sensitive to the reorientational and translational dynamics of ions, respectively. Because H and F atoms are exclusively present in the cation and anion, respectively, their dynamic behaviours can be investigated separately. The temperature-dependent T1 curves for 1H (or 19F) in the PC and liquid phases were smoothly connected at the melting point, indicating similar rotational motions for the cations (or anions) in both phases. In the PC phase, distinct T2 components were observed for both 1H and 19F, reflecting heterogeneous dynamics due to cooperative translational motion of the cations and anions. These dynamics are attributed to the presence of core and surface phases within each PC crystallite. At the melting point, the T2 values of the surface phase transitioned smoothly to those of the liquid phase.
1. Introduction
Ionic liquids (ILs) are defined as salts with melting points below 373 K.1,2 Many ILs and related materials exhibit plastic crystal (PC) phases,3–5 known as ionic PCs (IPCs)6 or organic IPCs (OIPCs).5 In the PC phase, the molecular or ionic centers of mass form an ordered lattice, whereas their orientations are disordered or freely rotating.7 In other words, a PC phase is an intermediate state between the ordered crystalline solid and the liquid state, where the translational motions of molecules or ions are restricted but rotational motions remain active. Early investigations of PC primarily focused on the structure and physical properties of this intermediate state.7–12 Recently, since the work by MacFarlane et al.,3 IPCs have attracted significant attention, both academically and in terms of application as soft, electrically conducting solids for use as solid electrolytes.3–5,13–15 To understand their properties and mechanisms of ionic conduction, it is essential to investigate the dynamic behaviours of cations and anions. Nuclear magnetic resonance (NMR) is suitable for this purpose, as the ion dynamics in ILs and related materials are slow and occur at time scales that align with NMR sensitivity.6,16–29In this study, we selected N,N-diethylpyrrolidinium bis(fluorosulfonyl)amide ([C2epyr][FSA]), a typical IPC with potential as a solid electrolyte owing to its high functionality.30,31 To investigate the relationship between the phase transitions—from the ordered crystal to the PC and liquid phases—and the dynamics of cations and anions, we measured two types of NMR relaxation times exhibited by [C2epyr][FSA]: spin–lattice relaxation time (T1) and spin–spin relaxation time (T2). Reorientation motion is primarily reflected in T1, and translational motion in T2.20,32,33 For T2 of the ([C2epyr][FSA]) sample, we observed a peculiar phenomenon wherein the T2 values split into two in the PC phase. In a preliminary study, we reported this phenomenon as the existence of heterogeneous translational dynamics.34 Based on enhanced data accuracy and new added insights, including T1 information, we present this paper as a comprehensive report on the dynamics of [C2epyr][FSA] obtained from NMR relaxation times.
In general, NMR measurements are divided into high-frequency NMR (HF-NMR) and low-frequency NMR (LF-NMR), depending on whether the resonance frequency is higher or lower. They correspond to the ability to separate nuclides in different environments by the chemical shift. Roughly speaking, the boundary seems to be around 200 MHz for 1H. Numerous NMR studies have been conducted to investigate the dynamics of ILs and related materials.6,16–29,33 Among these, the use of HF-NMR is common.16–20,25,26 However, we adopted a different experimental method and perspective. Our method is characterized by the following three features. (1) We employed pulsed LF-NMR spectroscopy, which offers several advantages over HF-NMR. The application of HF-NMR is limited to liquids and solutions, whereas LF-NMR can also be applied to viscous fluids, glasses, PCs, and ordinary crystals, which are essential components in the investigation of dynamic behaviours between phases. In HF-NMR, signals from nuclides in different environments can be extracted separately, and in some cases, the corresponding correlation time τc can also be estimated. In contrast, signals from nuclides in different environments overlap in LF-NMR and cannot be extracted separately. Despite this, relaxation time measurements by LF-NMR provide coarse-grained information about the molecular or ionic motion dynamics across all phases.21–24,27–29 Therefore, it provides a broader perspective of phenomena and complements various methods that provide detailed information. (2) Experiments were conducted for two nuclides, 1H and 19F, using an instrument capable of performing measurements of both nuclides under the same experimental conditions. In case of [C2epyr][FSA], H and F atoms are exclusively present in the cation and anion, respectively. As previously mentioned, LF-NMR does not detect individual atoms but rather provides coarse-grained data on aggregates of atoms. Consequently, the insights on dynamics obtained from the 1H and 19F atoms of [C2epyr][FSA] reflect the dynamics of cations and anions, respectively. (3) T1 exhibits sensitivity to reorientational motions, whereas T2 exhibits sensitivity to both translational and diffusive motions.20,32,33 The temperature dependences of T1 and T2 enable the detection of phase changes in the sample and differences in the modes of reorientational and translational motions at the phase transition points.21–24,27–29
2. Experimental
The preparation of [C2epyr][FSA] followed a previously reported procedure.31 The sample was placed in a 10-mm NMR tube, dried under vacuum (approximately 10−3 Pa) at 333 K for 6 h, and sealed. This preliminary step is necessary due to the hygroscopic nature of ILs and related compounds.A pulse NMR instrument capable of measuring both 1H and 19F at resonance frequencies of 25 and 23.52 MHz, respectively, was used to measure T1 and T2 and free induction decay (FID) signals (MV25, Japan REDOX). Owing to the low resonance frequencies, chemical shifts were minimal, allowing for the observation of the overall dynamics of 1H and 19F atoms in [C2epyr]+ and [FSA]−. T1 values were obtained using the inversion recovery method. T2 measurements were performed using the Carr–Purcell–Meiboom–Gill method for the liquid and PC phases with higher T2 values (>1 ms) and the solid echo method for the crystalline and PC phases with lower T2 values (<1 ms).32
The measurements were performed at temperatures ranging from 210 (Phase II) to 300 K (Phase I) and from 300 (Phase I) to 420 K (liquid phase), in 10-K increments. The changeover at 300 K was performed by switching the temperature controller. The temperature dependence of the physical properties associated with the phase change of the sample is characterized by a pronounced thermal history. Therefore, the experimental configuration was carefully set up. This included the standardization of the initial conditions and the implementation of adequate waiting times after reaching the measurement temperature.
At temperatures above the melting point (∼405 K), sample decomposition progressed gradually. In addition, the magnetic field of the permanent magnet of the used instrument became unstable at temperatures above 400 K. Therefore, data collection above 400 K lacked sufficient reproducibility and other considerations.
3. Background on NMR relaxation times, T1 and T2, for 1H (or 19F) in this study
To facilitate the discussion of the experimental results, we briefly summarize the theories on 1H spin–lattice relaxation time (T1) and spin–spin relaxation time (T2), which are important parameters for investigating the dynamic behaviour associated with phase changes in ILs. As the nuclear spin of 19F is 1/2, identical to that of 1H, the same theoretical framework applies.Spin–lattice relaxation corresponds to the enthalpy relaxation of nuclear spins from the nonequilibrium state induced by the excitation pulse to the state of the equilibrium distribution, accompanied by a change in spin orientation. In contrast, spin–spin relaxation refers to entropy relaxation, where nuclear spins revert back to the phase-disordered state of the equilibrium distribution from the phase-aligned precession induced by the excitation pulse.
Several mechanisms contribute to T1 and T2.32 Among these, the magnetic dipole–dipole relaxation mechanism is generally dominant in viscous liquids and glassy samples. In this mechanism, translational motions of molecules or ions primarily contribute to T2, whereas the reorientational motions and intramolecular motions are key contributors in T1.20,32,33
For a pair of protons, the T1 and T2 values for the magnetic dipole–dipole relaxation mechanism are expressed as follows:32,35,36
 | (1) |
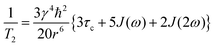 | (2) |
| J(ω) = τc/(1 + ω2τc2) | (3) |
 | (4) |
 | (5) |
| Jij(ω) = τc(ij)/(1 + ω2τc(ij)2) | (6) |
In eqn (4)–(6), subscripts i and j are specific nuclei under consideration, and τc(ij) denotes their correlation time. 1/T1 and 1/T2 are proportional to rij−6 (eqn (4) and (5)); thus, sum of only the atomic pair contributions within the ion provides a reasonable approximation.
The FID signal obtained from pulsed NMR is direct insights into the dynamics of particles containing the target nuclei. In the inversion recovery method to obtain the T1 value, the longitudinal component of magnetization at t after the application of excitation pulse is expressed as follows:32
M(t) = M0[1–2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/T1)] exp(−t/T1)] | (7) |
The FID signal for T2 is a transverse component of magnetization that appears immediately after the application of excitation pulse. The z-axis is defined as the direction of the static magnetic field. When an excitation pulse is applied along the x-axis, transverse magnetization is observed in the y-axis direction. After time t,
My(t) = M0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/T2) exp(−t/T2) | (8) |
If the sample comprises two components with different spin–spin relaxation times, Thard2 and Tsoft2, the FID signal is expressed as follows:
My(t) = (1 − x) M0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/Thard2) + x M0 exp(−t/Thard2) + x M0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) exp(−t/Tsoft2) exp(−t/Tsoft2) | (9) |
For NMR experiments using low magnetic fields, the dynamics behaviour of samples is occasionally evaluated in comparison with reference data from glycerol, which exhibits typical T1 and T2 behaviours as a viscous, noncrystalline material. The details of glycerol reference are provided in the ESI† in our previous study.34
Finally, it should be noted that the specific points of the sample, H and F atoms, are present only in [C2epyr]+ and [FSA]−, respectively. In addition to this exclusivity, we assume that atomic pairs with magnetic moments can be evaluated only within each ion. For 1H, it is reasonable to assume that the 1H relaxation times represent dynamics of the cation, because the homonuclear 1H–1H couplings will dominate. For 19F, 19F–1H coupling between ions may have to be considered. This is because the F–F distance in one anion is relatively long and the distance between the H atoms in the cation and the F atoms in the anion may be short. Unfortunately, the H–F distances are not known for this sample, since detailed structural analysis has not been carried out for either the regular crystal phase or the PC phase. Nevertheless, it does not seem to be an unreasonable assumption to ignore the 19F–1H interaction, since the H atoms and F atoms are always moving due to the high flexibility of both the cation and anion even in the PC phase and the absence of strong F–H hydrogen bonds. Thus, it is reasonable to assume that the 1H- and 19F-relaxation times represent separate dynamics for the cation and anion, respectively.
4. Results and discussion
4.1. Background information
The chemical structures of [C2epyr]+ and [FSA]− are shown in Fig. 1. Only the most stable configurations, calculated using density functional theory (DFT), are presented. | ||
| Fig. 1 Structure of [C2epyr][FSA]. For each ion, the most stable configuration calculated by DFT is drawn. | ||
Before discussing the NMR relaxation times, the phase behaviour of [C2epyr][FSA] is outlined based on the differential scanning calorimetry (DSC) results.30,31Fig. 2 shows the DSC traces measured in the range of 170–410 K at a scanning speed of 5 K min−1. Two endothermic and two exothermic peaks were observed during the heating and cooling processes, respectively, indicating that [C2epyr][FSA] exhibits two crystalline phases within the measured range. The phases are named phases I and II in the order of decreasing temperature. ILs and related materials are generally prone to undercooling phase changes, resulting in temperature differences in the phase changes. The transition temperature during the cooling process depends on the experimental conditions induced by the nonequilibrium process of structural relaxation. Therefore, the phase transition temperature from phases II to I and the melting point were determined to be 238 K and 405 K, respectively, which were obtained during the heating process. Considering that the [C2epyr][FSA] sample was prone to phase changes over a wide temperature range, each peak of the DSC trace was considered the phase transition point. The enthalpy and entropy changes at each phase transition are listed in Table S1 of the ESI.†
The powder X-ray diffraction patterns of [C2epyr][FSA], as shown in Fig. S1 of ESI,† indicate that phase I is the PC phase of a CsCl-type structure and that phase II exhibits a regular crystal phase.30 As shown in Fig. 1, the anion and cation exhibit low symmetries. However, the constituent ions must have a symmetry of m![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m to locate the lattice points in the CsCl-type structure. Considering the aforementioned symmetries, we conclude that both [C2epyr]+ and [FSA]− must freely rotate around the lattice points in phase I.37,38
m to locate the lattice points in the CsCl-type structure. Considering the aforementioned symmetries, we conclude that both [C2epyr]+ and [FSA]− must freely rotate around the lattice points in phase I.37,38
4.2. Temperature dependence of 1H-T1 and 19F-T1
As an example, an inversion recovery trace for 1H is shown in Fig. S2 of ESI.† As the result of all T1 measurements, Fig. 3 shows the temperature dependences of 1H-T1 and 19F-T1, plotted with closed circles and open squares, respectively. From a phase transition perspective, changes in the heating process are considered more important than those in the cooling process, as the former is less likely to induce nonequilibrium phase changes such as supercooling. Therefore, only the T1 values of the heating process are indicated. The two broken lines in Fig. 3 indicate the temperatures of the phase transition peaks determined by the DSC experiment.30,31We first discuss the overall temperature dependences of 1H-T1 and 19F-T1, with reference to the temperature-dependent behaviour of glycerol T1 (and T2) as a typical viscous sample described in the ESI† of our previous paper.34 Discontinuous changes are observed in both the 1H-T1 and 19F-T1 plots at approximately 240 K, corresponding to the transition from phases II to I observed in the DSC data at 238 K.30,31 These changes reflect the difference in the respective rotational and intramolecular dynamics of the cations and anions in each phase. As mentioned in Section 4.1, phase II is a regular crystal phase, and phase I shows a PC phase with cations and anions in free rotation.37,38 Therefore, we can conclude that the jumps in 1H-T1 and 19F-T1 values at approximately 240 K are associated with the onset of overall free rotation in both ionic species. Changes in other rotational modes may contribute to the phase transition; however, the presence or absence of free rotation in the ions is considered the most important contributor to the phase transition of [C2epyr][FSA] at approximately 240 K. In addition, the acquisition of the free rotation modes of cations and anions is also carried out jointly.
In contrast, the curves for both 1H-T1 and 19F-T1 are smoothly connected at 405 K, which is the transition point from phase I to the liquid phase, as shown in the DSC results.30,31 This smooth connection indicates that the rotational dynamics of the [C2epyr]+ and [FSA]− ions in phase I are almost identical to those in the liquid phase. This result proves—with respect to the T1 data—that the orientations of the ions are mobile but their centers of mass form a regular lattice in the PC phase.
As previously mentioned, the molecular reorientational and intramolecular motions for viscous liquids and solids are predominantly reflected in the T1 values when the dipole–dipole relaxation mechanism is predominant.20,32,33 When multiple reorientational modes contribute to T1, we denote them as A, B, C, … modes, with corresponding relaxation time constants TA1, TB1, TC1, …, respectively. The observed overall spin–lattice relaxation time, Tall1, is expressed as follows:
 | (10) |
For [C2epyr]+ ions, the following modes are considered to contribute to T1 values: overall rotation of the molecular ion, puckering of the pyrrolidinium ring, conformational change of the ethyl group, and rotation of the methyl group. For [FSA]− ions, the overall rotation of the ion and the change in conformation due to the rotation of the SO2F group around the N–S axis can influence T1 values. In general, for a sample with multiple rotational modes, the observed value, Tall1, is not a simple linear combination of individual component, as indicated in eqn (10). In addition, each rotational mode has a characteristic correlation time, which exhibits different temperature dependencies according to its activation energy. Therefore, the interpretation of Fig. 3 as a simple summation of each motion mode is inadequate.
For the [C2epyr]+ cations observed in 1H, all rotational and reorientational modes are assumed to be activated in the liquid state, and only methyl group rotations may remain in the normal crystalline phase (phase II). In the intermediate region of the liquid and regular crystalline states, namely the PC phase, the temperature-dependent curve of 1H-T1 for the [C2epyr][FSA] sample deviates from that for glycerol, which exhibits a relatively simple relaxation mechanism. This deviation can be attributed to the freezing process of various rotational modes and the contribution of the five-membered pyrrolidinium ring motion to T1.
For the anions observed through 19F-T1 measurements, all rotational or reorientational modes and conformational changes are assumed to be activated in the liquid state, and only the librational mode of the F atoms around the N–S axis may remain active in the ordered crystalline phase (phase II).
4.3. Experimental results of 1H-T2 and 19F-T2 and their accuracy
Although the temperature dependences of 1H-T2 and 19F-T2 values for [C2epyr][FSA] were previously reported,34 we reconducted the experiment to improve the measurement accuracy. 1H-T2 values did not differ significantly from the previous results; however, 19F-T2 values exhibited a significant improvement in data quality. This improvement can be attributed to the consideration of the notable thermal history characteristics of the samples during measurements. Given that the present re-experiments yielded more accurate data and revealed new insights, and considering that this study aims to provide a comprehensive summary of the NMR relaxation phenomena in [C2epyr][FSA], the results and discussion of T2 behaviours are described here.The most characteristic behaviour of [C2epyr][FSA] was the separation of both 1H-T2 and 19F-T2 into two components above 330 K in the PC phase. The FID curve exhibits a single exponential decay below 320 K and can be analyzed under the single-component assumption; however, the two-component assumption (eqn (9)) becomes the appropriate analysis method at temperatures above approximately 330 K. The separations of T2 values were specifically shown in the analysis using FID curves in Fig. 3 of ref. 34. The component with the smaller T2 value is contributed by the harder and less mobile domains, whereas the component with the larger T2 value is contributed by the softer and more mobile domains. Therefore, the T2 values for these components are represented as Thard2 and Tsoft2, respectively. The separation of T2 values into two components is discussed in Section 4.5.
Fig. 4 plots the measured 1H-T2 values as a function of temperature. The T2 values during the heating and cooling processes are indicated by closed circles and cross symbols, respectively. This is useful in determining the presence or absence of a phase transition.21–24,28,29 In Fig. 4, the black marks represent the 1H-T2 values analyzed under the single-component assumption, denoted as 1H-T21C. The two types of T2 values, 1H-Thard2 and 1H-Tsoft2, are represented by blue and red circles, respectively.
The accuracy of the experimental values for 19F-T2 was not satisfactory due to the extremely weak 19F NMR signal.34 Therefore, the experiment was carefully reconducted, particularly considering the presence of thermal history. In Fig. 5, 19F-T2 values obtained during the heating process are indicated using open squares. For 19F, T2 separation was also observed above 330 K, similar to 1H-T2. In addition to the notation of 19F-T21C obtained under the single-component assumption, the two separated values are denoted by 19F-Thard2 and 19F-Tsoft2. The color scheme follows that of the 1H data; however, open squares are used to distinguish 19F results from the 1H data.
The measurements were systematically repeated several times. Both the 1H-T2 and 19F-T2 values exhibited significant fluctuations in the temperature ranges of 320–340 K and near the melting point (400–420 K). As previously mentioned, the temperature range of 320–340 K is the region in which a higher-order phase transition may occur (see Section 4.5). In this temperature range, both 1H-T2 and 19F-T2 values occasionally exhibited large T2 values in the order of seconds, as typically observed in liquids. We encountered a “softening” event, a phenomenon known as structural loosening that occurs simultaneously with a phase transition, as explained in Section 4.5. In ILs and related materials, phase changes are generally very slow. In a previous study, we reported that the softening of [C4mim]Br could take as long as an hour.24 This higher-order phase change with slow softening is likely responsible for the variation in T2 values. In the present data, anomalous values that appear as softening events were not plotted in Fig. 4 and 5.
Next, we describe the challenges associated with T2 measurements near the melting point. As shown in Fig. 2, the melting temperature was determined to be 405 K based on the DSC endothermic peak.30,31 However, the melting process of the sample was very slow, and 1H-Thard2 and 19F-Thard2 remained at temperatures higher than 405 K when the waiting time was insufficient. Jelly-like solids (likely the hard component with a core structure described in Section 4.5) were observed in the melted material for several tens of minutes even at temperatures 10–20 K above the melting points. The amount of sample used in the NMR experiment was 1–2 g, and the heat transfer was uneven. However, the melting point of [C2epyr][FSA] was unclear. Thus, [C2epyr][FSA] can be regarded as a sample in which the superheating phenomenon is pronounced during the melting process. Therefore, the 1H-Thard2 and 19F-Thard2 values in the superheating region are not shown in Fig. 4 and 5. In addition, the sample gradually began to decompose near the melting point; thus, it was not possible to perform experiments with sufficient reproducibility.
With the exception of the two aforementioned temperature regions, a waiting period of 10 min allowed the determination of the T2 value with good reproducibility. Fig. 4 and 5 show the average of the measurement results. For 1H, the deviations of the T2 values from the single-component analysis (1H-T21C, black circles) and those of the 1H-Thard2 values from the two-component analysis (blue circles) were in the range of ±3%. The deviations of the 1H-Tsoft2 values (red circles) were as large as ±10%. For 19F, the deviations of the T21C values (black squares) from the single-component analysis and those of the Thard2 values from the two-component analysis (blue squares) were in the range of ±5%. The deviations of the Tsoft2 values (red squares) were in the range of ±20%.
4.4. Temperature dependence of T2 behaviour and phase transitions
In rough approximation, T2 values exhibit a positively correlation with 1/τc (τc = correlation time) across the entire region, primarily reflecting translational motion. Thus, the more active the translational motion, the larger the T2 values. In this section, we discuss the relationship between T2 and phase transitions based on the temperature dependence graphs of 1H-T2 and 19F-T2 plotted in Fig. 4 and 5, respectively. First, we focus on the 1H-T21C and 19F-T21C values obtained under the single-component assumption and the hard components 1H-Thard2 and 19F-Thard2 obtained under the two-component assumption because they were contributed by the core structure of the sample (see Section 4.5).Discontinuous changes were observed in the 1H-T21C and 19F-T21C plots for the heating process (closed circular and open square symbols) at approximately 238 K, as indicated by the broken lines in Fig. 4 and 5. As shown in Fig. 4, the 1H-T21C values in the cooling process (cross symbols) exceed those in the heating process (closed symbols). The difference in the T2 values between the heating and cooling processes supports the existence of a supercooling state and the resulting phase transition. This corresponds to the phase transition phase II → phase I observed in the DSC experiment (Fig. 2). As clarified in previous studies, phase II is a regular crystal phase,30 and phase I is a PC phase with a CsCl-type structure.30,38 In the PC phase, the centers of mass of ions are assumed to form an ordered lattice and are fixed, as in the regular crystal phase.7–12 However, the discontinuous increase in T2 indicates a slightly higher translational motion in the PC phase than in the regular crystal phase. This result indicates that the mobile diffusion motion of ions also exists in the PC phase. This motion becomes more active with increasing temperature. A T21C jump was observed in each 1H and 19F graph of [C2epyr][FSA] at the same temperature. This suggests a cooperative translational motion of the cation (1H) and anion (19F). The T2 values in phase II of [C2epyr]+ (1H) and [FSA]− (19F) were of approximately the same order of magnitude as those of the cations and anions in regular crystalline phases of ILs.21–24,27–29 Compared with other IL and OIPC compounds, no specific translational behaviour was observed for the cation and anion of [C2epyr][FSA] in terms of magnitude of the T2 values.
As discussed in Section 4.3, the thermal phenomena near the melting point of the [C2epyr][FSA] sample are characterized by the onset of pyrolysis, a slow phase transition, and superheating. Therefore, it is difficult to obtain accurate T2 values. However, by attempting to describe the phase transition between phase I and the liquid phase in terms of T2 behaviours, we can obtain the following results, which are described as common behaviours for both 1H and 19F, i.e., the cations and the anions. The hard component Thard2, one of the two types of T2 values in phase I discussed in Section 4.5, slowly increases with increasing temperature and breaks off at the melting point. The softer component Tsoft2 increases with increasing temperature and exhibits smooth connections with that of the liquid or slight jumps, if any, near the melting point to become the T2 value of the liquid phase, Tliq2. As shown in Fig. 6, the soft component increases near the melting point, wherein most of the components are soft. Based on these results, we conclude that the soft region with Tsoft2 transitions smoothly or with a slight jump to the liquid with Tliq2. In other words, the translational motion between the cations and anions in the hard region of the PC phase qualitatively differs from the motion in the liquid phase. However, their motions in the soft region appear to merge smoothly into those of the liquid, and the differences between the modes of movement in both phases are minimal.
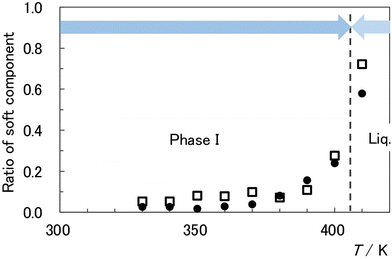 | ||
| Fig. 6 Temperature dependence of the soft component ratios for 1H-T2 (closed circles) and 19F-T2 (open squares). | ||
4.5. Heterogeneous dynamics in T2
As previously mentioned, the temperature dependence curves of T2 for 1H and 19F are divided into two respective components. The component with the smaller T2 value (Thard2) is contributed by the harder and less mobile part, and the component with the larger T2 value (Tsoft2) is contributed by the softer and more mobile part. 1H-Thard2 and 1H-Tsoft2 are represented by blue and red circles in Fig. 4, and 19F-Thard2 and 19F-Tsoft2 are represented by blue and red squares in Fig. 5. This separation implies the existence of heterogeneous transrational dynamics in the PC phase. In this section, we discuss the behaviour and attribution of these unique components.The ratios of soft components provide valuable insights into heterogeneous dynamics. The ratios are plotted in Fig. 6, with closed circles and open squares representing 1H and 19F, respectively. Similar to the Tsoft2 values, the variations in the ratios are large, approximately 30% and 50% for 1H and 19F, respectively. This is likely due to the thermal history effects. Despite the large deviation, the ratios of 1H-Tsoft2 and 19F-Tsoft2 exhibit similar temperature dependences. From 330 to 380 K, the observed ratios remain almost constant or slightly increase with increasing temperature, and the ratios are below 0.1. However, as the melting point is approached, the ratio rapidly increases in tandem with an increase in Tsoft2 values. Although there are differences in the behaviours of 1H and 19F, considering the large variation, their values are within the margin of error, and the cations (1H) and anions (19F) can be assumed to be in coordinated motion when the separation of T2 values occurs.
We review the unique temperature dependence of T2 for 1H observed in the PC phase at temperatures above 330 K (Fig. 4). 1H-Thard2 (blue circles) exhibits a discontinuous change from 1H-T21C (black circles) that appears below 330 K and gradually increases with increasing temperature. 1H-Thard2 continues to increase and appears to reach 1H-Tliq2 with a significant jump near the melting point; in other words, 1H-Thard2 disappears and is dominated by the softer component because of the drastic increase in the ratio of the soft components. In contrast, 1H-Tsoft2 suddenly appears at approximately 330 K and changes significantly with increasing temperature, transitioning to Tliq2. The accuracy of the Tliq2 values is not satisfactory at temperatures above 400 K because of the onset of pyrolysis of the [C2epyr][FSA] sample and the destabilization of the permanent magnet of the instrument. Therefore, we cannot determine whether 1H-Tsoft2 transitions smoothly to 1H-Tliq2 or exhibits a slight jump. As shown in Fig. 5, the temperature-dependent behaviours of T2 for 19F and 1H are similar. These experimental facts indicate that [C2epyr][FSA] exhibits two distinct dynamic behaviours in the PC phase at temperatures above 320–330 K, i.e., the existence of heterogeneous translational dynamics. In addition to the subsequent discussion in Section 4.6, we conclude that cations (1H) and anions (19F) move cooperatively rather than independently in the hard and soft regions.
The jumps in the temperature-dependent behaviours of T2 for both 1H and 19F at approximately 320–330 K suggest phase changes in this region. To investigate this change, the behaviours of T2 are first compared with those of T1. As shown in Fig. 3, both 1H-T1 and 19F-T1 exhibit respective smooth temperature dependences, and no anomaly is detected in the temperature region. T1 primarily reflects the reorientation and conformational changes of molecular ions, whereas T2 primarily reflects the translational and diffusive motions of molecular ions.20,32,33 This indicates that the anomalous T2 behaviours in the region are caused by changes in the translational and diffusive motions rather than in the rotational motions of ions. Next, the temperature-dependent behaviours of T2 are compared with the DSC trace shown in Fig. 2. We focus on the behaviours of Thard2 for 1H and 19F, postponing the discussion on Tsoft2, because hard components dominate except in the melting point region (Fig. 6). No signal indicating a first-order phase transition was observed in the DSC trace at approximately 320–330 K, whereas there were discontinuous jumps in the 1H-Thard2 values for 1H and 19F (Fig. 4 and 5). In addition to the jumps, differences in 1H-Thard2 values between the heating and cooling processes (black circles and blue crosses, respectively) were observed at temperatures below 320 K. Such differences are typically observed during supercooling, supporting the existence of phase transitions. Such phenomena were observed at the phase transition points.21–24,27–29 In addition to these two facts, the Tsoft2 values for 1H and 19F could not be obtained in a stable form at 320–330 K. As described in Section 4.3, the Tsoft2 value in the temperature region varied significantly in each experiment, occasionally exhibiting large values in the order of seconds, as often seen in liquids. As previously mentioned, we believe that softening occurs, which is typically observed when a phase change occurs.
These results show that heterogeneous dynamics exist in the PC phase. The presence of this heterogeneous dynamics has been reported not only for this sample but also for several samples with PC phases although the methodologies differ. The existence of heterogeneous dynamics was first reported in the PC phase of ammonium salts by Ikeda et al.,6,39–43 and more recently by MacFarlane, Forsyth, and colleagues (Australian group) in their systematic studies on OIPCs.16,44–49 In the studies by Ikeda et al.,6,39–43 the methods involved relaxation time measurements of T1 using low-frequency pulsed NMR and second-moment analysis. The Australian group employed NMR linewidth analysis in high-field NMR measurements,16,44–47 solid-state magnetic resonance imaging,47–49 and computer simulations.50 In general, the possible forms of ion dynamics in IPC phases include free rotation of ions, localized large vibrational rotation of ions that may be accompanied by conformational changes, and translational or diffusive movements, including ion jumps between lattice points. In linewidth studies, heterogeneous dynamics are thought to manifest as an increase in mobility, such as rotation and conformational changes in constituent ions.45,46 Magnetic resonance imaging studies have reported the concept of domains, which is expressed as image contrast anisotropy sensitive to the orientation of grain boundaries in polycrystalline samples.47–49 In contrast, the present detailed T2 measurements demonstrate heterogeneous dynamics as two translational motion types of ions. The rotational motion and large vibrational rotation of ions are precisely the dynamics that characterize PC phases, and the conformational changes correspond to the softness of ILs. Although these phenomena are commonly observed in IPCs, they do not characterize the observed heterogeneous dynamics. The rotational dynamics is independent of the heterogeneous dynamics in our sample. The unique contributions of the present study is its identification of translational motion as the responsible factor for the observed heterogeneity in various ion dynamics.
The anomalous behaviour of T2 values in the PC phase indicates a phase transition. No signal is observed in the DSC data; thus, the phase change is not accompanied by an enthalpy change. However, obvious jumps are observed in T2 values, which are difficult to stabilize over a relatively wide temperature range. We conclude that these phenomena indicate the occurrence of a higher-order phase transition in the PC phase. Recently, we performed precise density measurements on this sample and found that there was a clear anomaly in the temperature dependence curve of density at approximately 320–330 K. This finding also supports the existence of a unique phase transition that has not been previously reported. These results will be reported in future studies.
4.6. Cause of heterogeneous dynamics
The cause of the two types of dynamics is discussed here. Based on the analysis results of heterogeneous dynamics observed in several IPCs, the Australian research group proposed a model in which the presence of a domain structure comprising of fine grains of PC and their surrounding regions contributes to the observed dynamics.48,49 In a review,15 Hwang et al. described the existence of static and dynamic regions in IPCs. These regions correspond to the hard and soft domains provided by Thard2 and Tsoft2, respectively. Our heterogeneous dynamics model is identical to their model.15,48,49 In other words, it complements previous studies by using T2 values to quantify the properties of hard (static) and soft (dynamic) regions. In addition, the temperature dependence of the soft-region abundance ratio is clarified.In general, in IPCs, the orientation of ions involves free rotation, large local rotation, or high levels of disorder; however, the mass centers of ions form a regular lattice. In this study, the region with the PC lattice is referred to as the “core phase” that affords Thard2. The region surrounding the core phase is referred to as the “surface phase” affording Tsoft2. The surface phase structurally differs from the core phase and is prone to surface or interface melting at high temperatures. Our model is identical to that proposed by the Australian group.48,49 However, our model further speculates that the origin of the soft component is a surface or interface structure different from the core. This soft component leads to surface and interface melting with increasing temperature. The nearly seamless transition from Tsoft2 to Tliq2 (see Section 4.5) is explained by our model.
Using [N1112][FSA] as a sample, we demonstrated that IL salts are prone to surface and interface melting.51 In addition, different melting points of the core and surface phases were observed.51 Surface/interface melting or the appearance of a structure different from the bulk structure at the surface is a well-known phenomenon in water,52–54 metals, and semiconductors.55,56 This occurs because of the abrupt interruption of the ionic and molecular arrangements at the surface, where they adopt a structure different from the bulk and adapt to the surface environment.55–57 The rotational motions of ions and molecules in the PC phase are smoothly coupled with those in the liquid phase, which is expected to result in smooth structural perturbations at the surfaces and interfaces.
The above model explains without contradiction that thermal history phenomena occur easily. The domain structure, comprising the core and surface phases, appeared to form during sample preparation. Once the domain structure was established, the proportions of the components did not significantly change with temperature. This is supported by the fact that the change in the ratio of the surface phase region with increasing temperature was almost constant or increased only slightly within the range of 330–380 K (Fig. 6). In this temperature range, Tsoft2 increased with increasing temperature, and the translational motions of the cations and anions became cooperatively active. As the melting point was approached, premelting and surface melting were observed. As shown in Fig. 6, the surface phase region expanded abruptly, and the Tsoft2 value increased rapidly as the Tliq2 value was asymptotically approached.
For the [C2epyr][FSA] sample, the heterogeneous translational dynamics suddenly appeared as two different T2 values at approximately 320–330 K. However, it is speculated that the surface phase region did not suddenly appear at this temperature range but was formed during sample preparation. The T2 values for the core and surface regions are also assumed to be identical up to this temperature range. This result is attributed to the fact that no significant difference was observed in the translational motion of the ions in the core and surface regions. We then conclude that the component ions begin translational motion with different T2 values at 320–330 K, which is the temperature region where abrupt jumps in T2 values are observed. At 320–330 K, small jumps in the hard component values for 1H and 19F were observed, whereas the soft component values were approximately two orders of magnitude larger. The cause of this abrupt change in the translational dynamics is unclear. In T1, which is sensitive to the rotational motion of ions, no special change was observed in this temperature region. The mechanism of heterogeneous dynamics remains an area for future research, including the investigation of their effects on relevant properties such as ionic conductivity.
4.7. Temperature dependences of T2 for 1H and 19F
By comparing the temperature dependences of 1H-T2 and 19F-T2 shown in Fig. 4 and 5, respectively, we observed similar behaviour for both. The physical significance of this similarity is discussed below. The ratios of 19F-T2 to 1H-T2 values are presented in Fig. 7. The color of each symbol corresponds to the same scheme used in Fig. 4 and 5: the black symbols indicate the quotients obtained under the single-component assumption, and the blue and red symbols indicate the quotients for the hard and soft components obtained under the two-component assumption. In phase I (PC phase), all values converged to 1.3 ± 0.2. Considering the experimental errors, we conclude that the 19F-T2/1H-T2 values are constant in the PC phase regardless of the respective states indicated by the three different color symbols.The T2 value resulting from the dipole–dipole interaction is expressed in eqn (5). As previously mentioned, the behaviours of T2 for 1H and 19F correspond to the translational motion of cations and anions, respectively. In addition, the sums expressed in eqn (5) should be considered only for each ion. The fact that the 19F-T2/1H-T2 values are nearly constant indicates that the quantities affecting T2, namely the distance rij between the nuclides and the correlation time τij, are kept constant. This indicates that the anions and cations move together in a translational motion, and there are no reorientation modes in the time domain that contribute to T2.
In general, the reorientational motions of ions and rotational motions that alter their conformations are primarily reflected in T1, whereas translational and diffusive motions are reflected in T2.20,32,33 To the best of our knowledge, this finding in which the parameters indicating the motions of cations and anions remain constant in a phase is the first experimental evidence that T2 is determined by translational or diffusive motion.
For the PC phase (phase I) of [C2epyr][FSA], we conclude that the anions and cations exhibit cooperative motion in both the core (blue symbols) and surface (red symbols) phases. The translational or diffusive motion of ions in phase II (regular crystal phase) is difficult to visualize. In this phase, the cations and anions appear to behave differently, although they are in slight translational motion.
5. Conclusions
Using [C2epyr][FSA] as a representative sample with a PC phase, the temperature dependences of T1 and T2 for 1H and 19F nuclides were determined. In particular, we focused on the dynamics of the phase transitions between the ordered crystal, PC, and liquid phases. The experiments were conducted using a low-frequency pulsed NMR apparatus, resulting in the collective observation of all signals rather than for individual 1H or 19F nuclides. In addition, in [C2epyr][FSA], the H and F atoms are exclusively present in the cation and anion, respectively. Therefore, the T1 and T2 measurements of 1H and 19F provided information about the reorientation and translation dynamics of the cations and anions, respectively.At the phase transition point between the ordered crystalline phase (phase II) and the PC phase (phase I), the T1 values for both 1H and 19F exhibit jumps, indicating that the reorientation modes for both cations and anions are different in the two phases. In contrast, at the phase transition point between the PC and liquid phases, the temperature dependence curves of 1H-T1 (19F-T1) for the two phases are smoothly connected, confirming the same rotational motion of the cations (anions) in both phases.
The unique phase behaviour observed in the [C2epyr][FSA] sample is characterized by the splitting of T2 values for both 1H and 19F into two components at approximately 320–330 K: hard and soft components. The two components are attributed to the core phase forming the PC and the surrounding surface phase. The formation of this heterogeneous phase is assumed to be responsible for the heterogeneous dynamics. Near the phase transition between the PC and liquid phases, the hard component of the PC phase transitions to a soft component, and the T2 value transitions almost seamlessly into the liquid T2. The sudden appearance of this phenomenon at approximately 320–330 K is considered a higher-order phase transition. The appearance of this strange phenomenon in T2 but not in T1 suggests that translational rather than reorientational motion is responsible for the phenomenon.
In summary, we conclude that both the cations and anions exhibit cooperative motion in the PC and liquid phases.
Author contributions
All authors were involved in the conception of the project and the discussion on the methodology and experimental results. K. N.: NMR experiments and their analysis, interpretation of NMR results, and manuscript writing. K. F.: NMR experiments and their analysis and interpretation of NMR results. M. Y. F.: synthesis of the sample and DSC measurements.Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting this article have been included in the ESI.†Acknowledgements
We would like to thank Mr Yoshifumi Hirotsu (Sophia University) for his assistance with sample synthesis, and Professor Kazuhiko Matsumoto (Kyoto University) and Professor Hiroshi Abe (National Defense Academy of Japan) for helpful discussion. This study was partly supported by JSPS KAKENHI Grant Number 19H02671 for K. N., JSPS KAKENHI Grant Number 23K26765 for M. Y. F., and a Sophia University Special Grant for Academic Research for M. Y. F.References
- J. S. Wilkes and M. J. Zaworotko, Chem. Commun., 1992, 965–967 RSC.
- Ed. B. Kirchner, Topics in Current Chemistry, 1st edn, Springer-Verlag Berlin, Berlin, 2009 Search PubMed.
- D. R. MacFarlane, J. Huang and M. Forsyth, Nature, 1999, 402, 792–794 CrossRef.
- D. R. MacFarlane and M. Forsyth, Adv. Mater., 2001, 13, 957–965 CrossRef.
- J. M. Pringle, P. C. Howlett, D. R. MacFarlane and M. Forsyth, J. Mater. Chem., 2010, 20, 2056–2062 RSC.
- U. Ishida, T. Iwachido and R. Ikeda, Ber. Bunsen-Ges., 1992, 96, 1468–1470 CrossRef.
- I. Nitta, Z. Krist., 1959, 112, 234–254 CrossRef CAS.
- J. Timmermans, J. Phys. Chem. Solids, 1961, 18, 1–8 CrossRef CAS.
- W. J. Dunning, Phys. Chem. Solids, 1961, 18, 21–27 CrossRef.
- S. Seki, Chem. Chem. Ind. J., 1962, 15, 1226–1236 Search PubMed (in Japanese).
- L. A. K. Sravery, Ann. Rev. Phys. Chem., 1962, 13, 351–368 CrossRef.
- Ed. J. N. Sherwood, The plastically crystalline state: orientationally disordered crystals, John Wiley & Sons, Chichester, 1979 Search PubMed.
- J. M. Pringle, Phys. Chem. Chem. Phys., 2013, 15, 1339–1351 RSC.
- H. Zhu, D. R. MacFarlane, J. M. Pringle and M. Forsyth, Trends Chem., 2019, 1, 126–140 CrossRef.
- J. Hwang, K. Matsumoto, C.-Y. Chen and R. Hagiwara, Energy Environ. Sci., 2021, 14, 5834–5863 RSC.
- H. Zhu and L. A. O’Dell, Chem. Commun., 2021, 5609–5625 RSC.
- J. H. Antony, D. T. Mertens, A. Dölle, P. Wasserscheid and W. R. Carper, ChemPhysChem, 2003, 4, 588–594 CrossRef.
- W. R. Carper, P. G. Wahlbech and A. Dölle, J. Phys. Chem. A, 2004, 108, 6096–6099 CrossRef.
- S. H. Chung, R. Lopato, S. G. Greenbaum, H. Shirota, E. W. Castner Jr. and J. W. Wishart, J. Phys. Chem. B, 2007, 111, 4885–4893 CrossRef.
- K. Hayamizu, S. Tsuzuki and S. Seki, J. Phys. Chem. A, 2008, 112, 12027–12036 CrossRef PubMed.
- M. Imanari, K. Uchida, K. Miyano, H. Seki and K. Nishikawa, Phys. Chem. Chem. Phys., 2010, 12, 2959–2967 RSC.
- T. Endo, T. Imanari, H. Seki and K. Nishikawa, J. Phys. Chem. A, 2011, 115, 2999–3005 CrossRef.
- T. Endo, H. Murata, M. Imanari, N. Mizushima, H. Seki and K. Nishikawa, J. Phys. Chem. B, 2012, 116, 3780–3788 CrossRef.
- M. Imanari, K. Fujii, T. Endo, H. Seki, K. Tozaki and K. Nishikawa, J. Phys. Chem. B, 2012, 116, 3991–3997 CrossRef PubMed.
- T. Endo, S. Widgeon, P. Yu, S. Sen and K. Nishikawa, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 054307-1–9 CrossRef.
- T. Endo, H. Murata, M. Imanari, N. Mizushima, H. Seki, S. Sen and K. Nishikawa, J. Phys. Chem. B, 2013, 117, 326–332 CrossRef PubMed.
- M. Imanari, K. Fujii, T. Mukai, N. Mizushima, H. Seki and K. Nishikawa, Phys. Chem. Chem. Phys., 2015, 17, 8750–8757 RSC.
- Y. Shimizu, Y. Wachi, K. Fujii, M. Imanari and K. Nishikawa, J. Phys. Chem. B, 2016, 120, 5710–5719 CrossRef PubMed.
- K. Nishikawa and K. Fujii, Bull. Chem. Soc. Jpn., 2023, 96, 931–937 CrossRef.
- H. Yamada, Y. Miyachi, Y. Takeoka, M. Rikukawa and M. Yoshizawa-Fujita, Electrochim. Acta, 2019, 303, 293–298 CrossRef.
- M. Yoshizawa-Fujita, H. Yamada, S. Yamaguchi, H. Zhu, M. Forsyth, Y. Takeoka and M. Rikukawa, Batteries Supercaps, 2020, 3, 884–891 CrossRef.
- T. C. Farrar and E. D. Becker, Pulse and Fourie Transform NMR, Introduction to Theory and Method, Academic Press, New York, 1971 Search PubMed.
- K. Hayamizu, S. Tsuzuki, S. Seki and Y. Umebayashi, J. Phys. Chem. B, 2012, 116, 11284–11291 CrossRef CAS.
- K. Nishikawa, K. Fujii, K. Matsumoto, H. Abe and M. Yoshizawa-Fujita, Bull. Chem. Soc. Jpn., 2024, 97, uoae088 CrossRef CAS.
- N. Bloembergen, E. M. Purcell and R. V. Pound, Phys. Rev., 1948, 73, 679–712 CrossRef CAS.
- I. Solomon, Phys. Rev., 1955, 99, 559–565 CrossRef CAS.
- K. Nishikawa, T. Yamada, K. Fujii, H. Masu, K. Tozaki and T. Endo, Bull. Chem. Soc. Jpn., 2021, 94, 2011–2018 CrossRef CAS.
- K. Nishikawa, K. Fujii, T. Yamada, M. Yoshizawa-Fujita and K. Matsumoto, Chem. Phys. Lett., 2022, 803, 139771 CrossRef CAS.
- H. Ishida, T. Takagi and R. Ikeda, Chem. Lett., 1992, 605–608 CrossRef CAS.
- H. Ishida, N. Hayama and R. Ikeda, Chem. Lett., 1992, 1333–1336 CrossRef CAS.
- H. Ono, R. Seki, R. Ikeda and H. Ishida, J. Mol. Struct., 1995, 345, 235–243 CrossRef CAS.
- H. Ishida, Y. Furukawa, S. Kashino, S. Sato and R. Ikeda, Ber. Bunsen-Ges., 1996, 100, 433–439 CrossRef CAS.
- T. Shimizu, S. Tanaka, S. O. Yamamuro, S. Ishimura and R. Ikeda, J. Chem. Soc., Faraday Trans., 1997, 95, 321–326 RSC.
- J. Adebahr, A. J. Seeber, D. R. MacFarlane and M. Forsyth, J. Phys. Chem. B, 2005, 109, 20087–20092 CrossRef CAS.
- L. Jin, K. M. Mairn, C. M. Forsyth, A. J. Seeber, D. R. MacFarlane, P. C. Howlett, M. Forsyth and J. M. Pringle, J. Am. Chem. Soc., 2012, 134, 9688–9697 CrossRef CAS PubMed.
- L. Jin, K. M. Nairn, C. D. Ling, H. Zhu, L. A. O’Dell, J. Li, F. Chen, A. F. Pavan, L. A. Madsen, P. C. Howlett, D. R. MacFarlane, M. Forsyth and J. M. Pringle, J. Phys. Chem. B, 2017, 121, 5439–5446 CrossRef CAS PubMed.
- M. Forsyth, F. Chen, L. A. O’Dell and K. Romanenko, Solid State Ionics, 2016, 288, 160–166 CrossRef CAS.
- K. Romanenko, L. Jin, L. A. Madsen, J. M. Pringle, L. A. O’Dell and M. Forsyth, J. Am. Chem. Soc., 2014, 136, 15638–15645 CrossRef CAS PubMed.
- K. Romanenko, J. M. Pringle, L. A. O’Dell and M. Forsyth, Phys. Chem. Chem. Phys., 2015, 17, 18991–19000 RSC.
- I. Jin, S. Leeuw, M. V. Koudriachova, J. M. Pringle, P. C. Howlett, F. Chen and M. Forsyth, Phys. Chem. Chem. Phys., 2013, 15, 19570–19674 RSC.
- K. Nishikawa, K. Fujii, Y. Hashimoto and K. Tozaki, Phys. Chem. Chem. Phys., 2020, 22, 20634–20642 RSC.
- M. Faraday, 7 June 1850, reported in Athenaeum, Lecture given at Royal Institution, London, 1850, p. 650 Search PubMed.
- Y. Furukawa, M. Yamamoto and T. Kuroda, J. Cryst. Grouth, 1987, 82, 665–677 CrossRef CAS.
- K. Murata, H. Asakawa, K. Nagashima, Y. Furukawa and G. Sazaki, Proc. Natl. Acad. Sci. U. S. A., 2016, 17, E6741 Search PubMed.
- V. G. Lifshits, A. A. Saranin and A. V. Zotov, Surface phases on Silicon: Preparation, Structures, and properties, Wiley, New York, 1995 Search PubMed.
- K. Oura, V. G. Lifshits, A. A. Saranin, A. V. Zotov and M. Katayama, Surface Science: An Introduction, Springer, 2003 Search PubMed.
- J. Trenkler, P. C. Chow, P. Wochner, H. Abe, K. E. Bassler, R. Paniago, H. Reichert, D. Scarfe, T. H. Metzger, J. Peisl, J. Bai and S. C. Moss, Phys. Rev. Lett., 1998, 14, 2276–2279 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp01503k |
| This journal is © the Owner Societies 2025 |





