Influence of substitution pattern on the dynamics of internal conversion and intersystem crossing in thiopyridone isomers

Abstract

We report a combined experimental and theoretical investigation of the ultrafast internal conversion (IC) and intersystem crossing (ISC) dynamics of two thiopyridone (TP) isomers in solution. Our study used ultrafast transient X-ray absorption spectroscopy (XAS) at the sulfur K-edge, in conjunction with electronic excited state surface hopping molecular dynamics and simulations of the excited state XAS, to investigate the impact of the functional group substitution pattern and solvent on the dynamics of IC and ISC. The combination of the localized X-ray probe and the simulation results enables, in part, the differentiation between ππ* and nπ* character excited states, as well as singlet and triplet states. Access to nπ* character excitations has particular value since they often prove challenging to assess with optical spectroscopy. For 2-TP, the photoexcited S₂ (ππ*) state rapidly undergoes IC to the S₁ (nπ*) state below the instrument response time, followed by ISC to the T₁ (ππ*) state on a timescale of 600 fs in acetonitrile. For 4-TP, the timescale of S₂ to S₁ IC increases to 330 fs and the timescale of ISC increases to more than 10 ps. The differences between isomers are rationalized by considering the key role of the, nπ* intermediates in mediating the intersystem crossing of these systems. Varying the substitution pattern of the molecule can stabilize or destabilize these intermediates leading to the increase in ISC rate in the ortho isomer as compared to the para isomer, while changing the solvent from acetonitrile to water had minimal effect on the electronic excited state relaxation mechanism.

---

1 Introduction

The interplay of internal conversion and intersystem crossing is crucial in determining the excited state properties and reactivity of organic molecules. Many organic chromophores undergo rapid internal conversion to the ground state following photoexcitation making them photo-stable and non-reactive, important properties for the photoprotection of DNA from ultraviolet (UV) light.^1,2 Intersystem crossing generates population in triplet and higher lying spin states which have long radiative lifetimes.³ For triplet states with slow non-radiative decay, these long-lived electronic excited states often prove photochemically active, making them useful in organic photosensitizers and in organic photocatalysis.^4–6 Understanding the chemical and environmental factors which determine the relative rates and efficiency of ISC and IC therefore offers a route towards optimizing the excited state properties of a molecular system for a particular application. The rate and efficiency of these processes ultimately depend on the character of the electronic excited states,^7–9 the shape of the corresponding excited state potential energy surfaces^9,10 and the dynamics at points where these surfaces are close in energy or intersect. In organic heteroaromatic compounds internal conversion and intersystem crossing are often mediated by excited states with nπ* character. These states have low absorption cross section from the ground state meaning that they are populated indirectly via internal conversion from bright ππ* character states following photoexcitation. In a single-electron picture, nπ* states correspond to excitation of a lone pair electron which is localized at the heteroatom and in the plane of the π-conjugated molecule to an out-of-plane, delocalized π* orbital. The strong localization of the n hole and the fact that the orbital is perpendicular to the π molecular orbital enables efficient intersystem crossing between states of nπ* and ππ* character in accordance with El-Sayed's rules.^11,12 Therefore the relative energetics and coupling between the nπ* and ππ* character states are important in determining the rate of intersystem crossing in these systems. In turn the energetics of these states can be strongly influenced by both solvent environment and chemical modifications.

The class of thiocarbonyl compounds form a striking example of how substitution of an oxygen atom with a sulfur can dramatically impact the optical properties and excited state dynamics of a system. Thiocarbonyls typically undergo efficient intersystem crossing to form long-lived triplet excited states with rich photochemistry.¹³ Of particular recent interest are sulfur substituted nucleobases (thiobases) which absorb in the UV A–B region and have close to unity triplet yield, leading to potential applications in photodynamic therapy.^14–16 This behavior is unlike that of the canonical nucleobases which absorb below 250 nm and undergo rapid and efficient IC to the ground state.^17,18 Previous time resolved studies on these systems^19–21 have suggested that the efficient triplet state population in thiobases is primarily due to the stabilizing effect of the sulfur atom on the heteroatom-centered nπ* and ππ* excited states. This lowers the energy of these states relative to the conical intersections responsible for the fast non-radiative decay of canonical nucleobases to the ground state and therefore blocks these relaxation channels in thiobases. The efficient ISC is then due to a combination of the strong localization of the n and π orbitals on the sulfur atom and the energetic proximity of the sulfur centered nπ* and ππ* states.

Directly probing these processes with optical spectroscopy is challenging due to their ultrafast nature and the fact that nπ* states typically have low optical cross section,²² meaning that their role is often inferred indirectly. Time resolved X-ray spectroscopy offers a new tool in this regard due to the distinct X-ray transitions which, in an orbital picture, depend on the dipole overlap between core orbitals localized at the heteroatom and the unoccupied valence orbitals of the molecule.^23–25 This has been utilized in pioneering X-ray absorption studies to directly probe the role of dark nπ* excitations in the internal conversion and electronic relaxation of organic chromophores^26–29 using either high-harmonic generation or X-ray free electron laser (XFEL) based sources in the soft X-ray range. Extending time resolved heteroatom K-edge absorption spectroscopy to biologically and chemically relevant sulfur containing compounds requires probing in the tender X-ray range (2–5 keV). Time resolved studies at synchrotron facilities have demonstrated the chemical sensitivity of S K-edge X-ray spectroscopy to photochemical reaction products,^30–33 and more recently developed XFEL sources and beamlines in the tender X-ray spectral range are opening up time-resolved S K-edge spectroscopy on femtosecond timescales.^34,35

The focus of this work is thiopyridone (TP), the sulfur substituted analogue of hydroxypyridine, which in turn is one of the simplest model systems for the photophysics and tautomerization of DNA base-pairs. Photo-excitation of thiopyridone leads to rapid and efficient intersystem crossing to a long-lived reactive triplet state.^36,37 Previous X-ray and optical studies on 2-thiopyridone^38,39 have focused on the photochemistry of the triplet state, in particular the possibility of it undergoing excited-state proton transfer to form the thiol form 2-mercaptopyridine (2-MP). However, the process of triplet state formation has not been resolved due to the ultrafast timescales involved. Theoretical calculations for 2-TP^40–42 have predicted rich intersystem crossing dynamics which proceed via a dark singlet nπ* character state and a triplet excited state of mixed nπ*, ππ* character to form the lowest triplet state within 1 ps.

Here, we directly probe the role of the intermediate dark nπ* states in the IC and ISC of thiopyridone with time resolved sulfur K-edge X-ray absorption spectroscopy, electronic excited state molecular dynamics with surface hopping to describe non-adiabatic changes in electronic state, and quantum chemical simulations of the sulfur K-edge X-ray absorption spectra. To understand the impact of chemical structure and solvent environment on the excited state dynamics, we compare 2-TP (ortho isomer) with 4-TP (para isomer) dissolved in acetonitrile and water. This combination of experimental and theoretical methods provides a firm foundation for interpreting the isomer dependence of the electronic excited state dynamics of solution phase thiopyridone.

1.1 Methods

1.1.1 Experimental methods. Time resolved sulfur K-edge X-ray absorption (XA) experiments were performed at the Alvra Prime instrument at swissFEL (proposal no. 20221944). XA spectra were measured in total fluorescence yield using an avalanche photodiode placed 1.5 cm from the sample and a Si(111) crystal monochromator to select the photon energy. The resolution of the monochromator was sufficient to resolve the 0.7 eV lifetime broadening of the XA features at the sulfur K-edge. Thiopyridone isomers 2-mercaptopyridine and 4-mercaptopyridine were purchased from TCI chemical and used without further purification. When dissolved in acetonitrile or water, both 2- and 4-mercaptopyridine convert to the 2- and 4-thiopyridone structures. The photon energy axis of the monochromator was calibrated to align the S_1s → π* resonance position of 2-TP in acetonitrile with the spectra reported in ref. 38, which are in turn calibrated to the sulfur K edge XA spectrum of sodium thiosulfate. 2-TP was dissolved in water or acetonitrile at 43 mM concentration and 4-TP was dissolved at 11 mM concentration also in water and acetonitrile. The samples dissolved in acetonitrile were stored over molecular sieves and argon was bubbled through the solvent prior to use to remove dissolved H₂O. Samples were delivered to the interaction point as a cylindrical jet with 50 micron diameter. The experiments were performed under a helium atmosphere at a pressure of 1 bar to maximize the X-ray flux at the sample.

We pumped 2-TP/4-TP in acetonitrile and 2-TP in water at a wavelength of 357 nm (3.47 eV) at a fluence of 5.9 mJ cm⁻² giving an excitation fraction of approximately 8% for 2-TP and 30% for 4-TP. The pulse intensity was chosen so that the pulse energy dependence of the transient bleach signal at 5 ps was in the linear regime (see Fig. S4, ESI†). We recorded the majority of the data with the pump polarization parallel to the X-ray polarization. For 2-TP in acetonitrile, we also recorded a full dataset of kinetic and spectral traces with perpendicular pump and probe polarization in order to resolve the polarization anisotropy of the XA signal. For all samples, we recorded energy scans for a series of quasi-logarithmically spaced time delays between 0.2 and 200 ps and time delay scans to ∼100 ps (sample dependent) were recorded at the main absorption features. The temporal instrument response function was estimated to be 90 fs from fits to the kinetic traces. To account for temporal drifts in the laser X-ray arrival time, reference kinetic traces at the bleach feature were recorded regularly and the time axis of subsequent or prior scans were aligned to the nearest reference scan. Note that this means that there is a systematic uncertainty in the exact position of time zero in the experimental kinetic traces. We also subtracted the below-edge absorption from the static spectra and normalized the difference spectra to the static absorption above the edge.

1.1.2 Theoretical methods. We used density functional theory (DFT) and multi-configurational quantum chemical calculations to accurately describe chemical bonding and electronic excitations in the 2-TP and 4-TP isomers. The calculations of electronic excitations, excited state molecular dynamics (ESMD) simulations, and computation of XA spectra were performed on different gas phase and solution models. Geometry optimizations for both ground states and various valence excited states were performed with the Gaussian 16 software package⁴³ using DFT and linear-response time-dependent DFT (TDDFT)⁴⁴ with the ωB97XD⁴⁵ exchange–correlation functional and the def2-TZVP^46,47 basis set. For additional details on the theoretical methods, please see Section S5 in the ESI.† In 4-TP, geometry optimizations resulted in ground and excited state structures with C_2v symmetries. However, in 2-TP, due to unsuccessful attempts to optimize all structures in C₁ symmetry, geometry optimizations were also performed in C_s symmetry, and used to derive sulfur K-edge XA spectra. Nevertheless, the 2-TP ground and excited state structures in C₁ and C_s symmetries, exhibit only negligible differences in geometries (please see Table S10, ESI†). Structural analysis also revealed an alternative geometry featuring an out-of-plane C–S bond in the S₂ excited state of 4-TP. This structure was found to be 0.2 eV more stable than the planar C_2v configuration and was thus included in subsequent spectral comparisons. However, this geometry was obtained only for the S₂ state of 4-TP on imposing no symmetry constraint; similar optimization for the ground and excited states of 2-TP and 4-TP (other than S₂) did not provide such non-planar structures. The primary conclusions are derived from the results within an implicit acetonitrile solvation model⁴⁸ for the two isomers, 2-TP^aceto_impl and 4-TP^aceto_impl. Information on additional gas phase and explicit solvation models considered in the analysis are collected in the ESI,† under Section S5.1, Fig. S12 and Tables S8–S11. Electronic valence excitations for the ground state geometries were calculated in the ORCA-5.0.3 program package⁴⁹ using the def2-TZVP basis set and exchange–correlation functional ωB97X⁵⁰ together with D4 dispersion correction.⁵¹ This provides reference to the valence excitation energies at the same level of theory prior to the dynamical simulations.

ESMD simulations of the two constitutional isomers were executed using the surface hopping⁵² approach, as implemented in the SHARC-3.0 code.^53–55 Simulations were performed on the 2-TP^aceto_impl and 4-TP^aceto_impl models, with forces, energies, and wavefunction overlaps from TDDFT calculations in ORCA using the same settings as in the static calculations. Initial conditions with geometries and associated velocities were generated from a discrete sampling of the Wigner distribution of vibrational normal modes. From analysis of the corresponding UV-visible spectra, we concluded that photoexcitations associated with 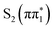excitations are deemed essential for the current study. Accordingly, out of the 300 initial conditions in the Wigner sampling, we simulated 150 trajectories from the ESMD-S₂ set for the 2-TP and 4-TP models. The default parameters in SHARC were used for determining the non-adiabatic coupling and spin–orbit coupling (SOC) in the ESMD simulations.^56–63

We simulated sulfur K-edge XA spectra for 2-TP and 4-TP with a multi reference approach to assign features in the transient spectra. Initially, we compared the valence excitation results from TDDFT with those obtained using multistate complete active space perturbation theory (MS-CASPT2)^64–68 with a CAS(12, 10) active space in OpenMolcas v.23.06.⁶⁹ To accommodate the core excitations, the active space was expanded using restricted active space perturbation theory (RASPT2).^65,70 The sulfur 1s core orbital (with two electrons) was incorporated into the active space alongside at most one hole in the core orbital. The resulting RAS(14,1,0;1,10,0) active space, combined with the highly excited state scheme,^71,72 allowed us to determine the core excited states and derive XA spectra for ground and valence excited states. The transition dipole moments of the valence and core excitations were calculated in the integrated restricted active space state interaction (RASSI) framework^73,74 in OpenMolcas.

2 Results

2.1 Valence electronic excited states

To understand the character of the valence electronic excited state structure, we first examine the energy and orbital character of the excited states of 2-TP and 4-TP at the optimized geometry of the ground state (Franck–Condon point).

Fig. 1A and B presents the vertical excitation energies and energetic ordering of the low lying singlet and triplet states in 2-TP and 4-TP calculated via TDDFT in an implicit acetonitrile solvent medium. The full datasets at the TDDFT and CASPT2 levels of theory are tabulated in Tables S12, S15 (2-TP) and S13, S16 (4-TP) in the ESI.† The frontier molecular orbitals contributing to the low-lying singlet and triplet states are shown in Fig. 1D. The complete active space implemented in the multi reference approach is illustrated in Fig. S13 in the ESI.† As noted in previous studies, the n and π orbitals both have significant sulfur 3p character and are distinguished by the orientation of the orbital with respect to the plane of the molecule. The n orbitals are in the molecular plane and the π orbitals are out of plane. Transient S K-edge X-ray absorption spectroscopy (XAS) directly probes the S 3p character of the unoccupied molecular orbitals and provides a powerful means of characterizing the orbital character of electronic excited states.

Fig. 1 (A) Qualitative depiction of the singlet (S_n) and triplet (T_n) excited state energies of 2-TP at the Franck–Condon point calculated at the TDDFT level (energies summarized in Tables S12 and S13 in the ESI†). The dominant expected IC and ISC pathway is depicted on the diagram. (B) Equivalent diagram for 4-TP, ISC from S₁ to T₂ in this isomer is expected to be less efficient due to the same orbital character of these states at the Franck–Condon point as illustrated with the dashed orange line. (C) Experimental UV-vis spectra of 2-TP and 4-TP in water and acetonitrile. The inset in the top right shows a zoom-in on the 2.2 eV to 3.5 eV region of 2-TP and 4-TP in acetonitrile. (D) Frontier molecular orbitals which describe the low lying singlet and triplet states of 2-TP and 4-TP.

Experimentally measured UV-visible spectra for both isomers in acetonitrile and water are shown in Fig. 1C. The UV-visible spectrum of 2-TP shows two absorption bands at approximately 3.4 and 4.2 eV in acetonitrile. This finding is in qualitative agreement with the computed UV-vis spectra in Fig. S14 (ESI†). Based on the TDDFT and CASPT2 calculations, and consistent with previous studies,^75,76 we assign the lower lying absorption band to the state, while the higher lying band is assigned to and higher singlet state excitations. The UV-visible spectrum of 4-TP is dominated by a single absorption at around 3.55 eV which is assigned primarily to the 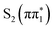state. Higher lying singlet states in this isomer absorb above 5 eV. For both isomers, photo-excitation at 3.5 eV populates the state.

The TDDFT calculations suggest that the S₁ state of 2-TP has character and is very close in energy to the 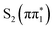state (separated by less than 200 meV). Indeed, the CASPT2 calculation in this study of 2-TP gives an inverted energetic ordering and character singlet states but also place them very close in energy. The lowest lying triplet state of 2-TP has 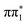character and is separated by more than 1 eV from , indicating that direct intersystem crossing from 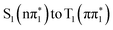is unlikely to be efficient. However, in between these states are two higher lying triplet states of 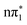and characters which are not only close in energy to each other but also to the state at the Franck–Condon point. The small energy separation between these states gives a potential ISC pathway from to 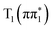through these states.

For 4-TP, TDDFT calculations at the electronic ground state geometry give the same energetic ordering of the singlet and triplet states as 2-TP but predict a stabilization of the , and states relative to the bright 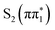state and the higher lying 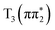state. We see evidence for the stabilization of the state of 4-TP in the UV-vis spectra, which has a very weak low energy shoulder on the 3.5 eV absorption band in acetonitrile due to the state (see Fig. S5, ESI†). The strength of this absorption feature is approximately 0.5% of the main ππ* band. The equivalent lowest energy band in 2-TP does not exhibit a low energy shoulder, consistent with the weak absorption of the S₁ state overlapping in energy with the bright state transitions at the Franck–Condon point. Therefore, the energy separation between the S₁ state and the bright S₂ state calculated to be larger in 4-TP than in 2-TP appears consistent with the experimental spectra.

2.2 ESMD calculations

Fig. 2 summarizes the results from the excited state molecular dynamics simulations performed for 2-TP and 4-TP in an implicit acetonitrile solvent. Panels A and B show the time-dependent adiabatic state populations over the 1 ps simulation time for 2-TP and 4-TP respectively. For additional details, see Section S5.2.2 of the ESI.† In general and consistent with the qualitative interpretation of the excited state ordering in the ground state geometry, we see a much faster build-up of the T₁ state population in 2-TP than in 4-TP. For 2-TP, T₁ exhibits a dominant state population among all the adiabatic states within 1 ps. In contrast, in 4-TP only a minimal triplet state population appears within the first picosecond, with a significant population accumulating in the S₁ state.

Fig. 2 Dynamical simulations of 2-TP and 4-TP molecules in acetonitrile solution (implicit solvation model). The population is presented in the adiabatic representation. Panels (A) and (B) show population dynamics of the ESMD-S₂ set of trajectories for 2-TP and 4-TP respectively.

For 2-TP, the simulations initially show a very rapid IC from the bright S₂ state into the dark S₁ state, followed by a subsequent rise of triplet states population. A transient T₂ population builds up over the first 200 fs, which eventually decays into T₁. To identify the ISC pathway, we follow the transition matrix shown in Table 1, which collects the number of hops between states in the dynamical simulation. This shows a large number of S₂ → S₁ transitions consistent with the fast initial IC to S₁. The dominant ISC transition occurs through S₁ → T₂, followed by the S₁ → T₃ channel, corresponding to triplet 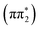and electronic state configurations in the Franck–Condon region, respectively. The S₁ → T₃ pathway does not lead to significant T₃ population within the state dynamics, largely due to a fast T₃ → T₂ internal conversion. Subsequently, an efficient IC from T₂ to T₁ results in a considerable T₁ population within 1 ps. The ESMD simulation thus suggests that the dominant photorelaxation pathway to T₁ in 2-TP is as follows: 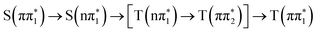. Excitations to higher lying singlet states are insignificant and do not affect the ISC dynamics due to rapid internal conversion to the S₁ state within the first 50 fs.

Table 1 The difference transition matrices determined from dynamical simulations of 2-TP and 4-TP. In each case, the positive values define the overall (net) number of transitions from state^column → state^row, while the negative values define the same, but from state^row → state^column

	S0	S1	S2	S3	S4	S5	T1	T2	T3
2-TP
S0	0	0	0	0	0	0	0	0	0
S1	0	0	140	0	−1	0	0	−83	−30
S2	0	−140	0	0	1	0	0	8	−17
S3	0	0	0	0	0	0	0	0	0
S4	0	1	−1	0	0	0	0	0	0
S5	0	0	0	0	0	0	0	0	0
T1	0	0	0	0	0	0	0	102	−11
T2	0	83	−8	0	0	0	−102	0	53
T3	0	30	17	0	0	0	11	−53	0
4-TP
S0	0	0	0	0	0	0	0	0	0
S1	0	0	134	−4	0	0	1	−20	−2
S2	0	−134	0	3	1	0	0	−1	−1
S3	0	4	−3	0	−1	0	0	0	0
S4	0	0	−1	1	0	0	0	0	0
S5	0	0	0	0	0	0	0	0	0
T1	0	−1	0	0	0	0	0	18	0
T2	0	20	1	0	0	0	−18	0	2
T3	0	2	1	0	0	0	0	−2	0

---

For 4-TP, the ESMD simulations show a much slower rate of internal conversion from S₂ to S₁ with population transfer between these states taking place over a time scale of ∼200 fs. This is consistent with an increased energy separation between the S₁ state and the higher lying singlet states in 4-TP as compared to 2-TP. ISC from S₁ is also much slower in this isomer and primarily proceeds via S₁ → T₂ ISC followed by T₂ → T₁ IC, as shown in Table 1. Therefore despite the S₁ → T₂ pathway being the predominant route for singlet-to-triplet transitions in both isomers, the rate of intersystem crossing is significantly faster in the ortho than in the para isomer. This can be explained by considering the underlying electronic characters of these states. While the S₁ state is in both 2-TP and 4-TP, the character of the T₂ state is 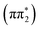in 2-TP and in 4-TP. Consequently, the dominant ISC pathway is El-Sayed^11,12,77 allowed in 2-TP, but El-Sayed forbidden in 4-TP. For 4-TP, the corresponding El-Sayed allowed pathway is an S₁ → T₃ transition, which is inefficient due to the large energy gap between the S₁ and T₃ states.

We also note oscillatory population dynamics along the S₁, S₂, T₂, and T₃ states of 2-TP in the ESMD. These oscillations are due to minimal energy separation between the two singlet states, which leads to frequent re-ordering of nπ* and ππ* states. The same is true for the two triplet states. This results in recurrent state transitions between the electronic states. However, the oscillatory behavior vanishes when the population dynamics is followed along the character of these states, instead of the adiabatic state representation. Such oscillatory behavior is absent in the T₁ population of 2-TP and all electronic states in 4-TP, suggesting that the states are energetically distinct. Additionally, photo-induced stretching vibrations have been observed in the dynamical simulation. These vibrations tend to induce motion in the aromatic ring, which is governed by the geometrical differences between the relaxed geometries of S₁ and S₂. Thus, the recurrent surface crossings along these modes can give rise to the oscillatory population transfer between S₁ and S₂. An analysis was performed on the evolution of the vibrational normal modes of the ground state in the simulation, which allowed for the identification of some of the associated vibrations. We present a detailed discussion of these vibrational dynamics in Section S5.2.3 of the ESI,† including Fig. S17–S19, and Table S18.

The theoretical predictions point towards the key importance of the energy and character of the triplet intermediates in the intersystem crossing dynamics of thiopyridone. The simulations show a slower ISC rate in 4-TP than in 2-TP, in agreement with picosecond optical transient absorption measurements by Alam et al.,³⁶ which reported a delayed rise time of 144 ps of the triplet–triplet absorption band in 4-TP and an instrument response limited, sub 100 ps ISC timescale in 2-TP. However, optical spectroscopy is not strongly sensitive to nπ* character states and the time resolution of these measurements was not sufficient to resolve the formation of the T₁ state in 2-TP.

2.3 Time-resolved X-ray absorption spectroscopy

To probe the IC and ISC dynamics of these isomers, we employ time resolved X-ray absorption spectroscopy at the sulfur K-edge. This method probes the sulfur 3p character of the unoccupied valence orbitals of the molecule and is therefore expected to be sensitive to both nπ* and ππ* excited states due to the significant sulfur 3p character of the n and π orbitals holes created by the valence excited states.

The static S K-edge XA spectra of 2-TP and 4-TP in water and acetonitrile (Fig. 3) show three main absorption features around the absorption edge. The lowest peak at around 2471 eV corresponds to a S_1s → π* transition associated with the C=S bond and the two higher lying peaks at 2473.3 eV and 2475 eV correspond to S_1s → σ* transitions. The energy of the S_1s → π* peak is 0.4 eV lower in energy in 4-TP compared to 2-TP and shows a solvatochromic shift in going from acetonitrile to water. Comparison with the calculated ground state XA spectra shown in Fig. 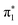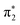5 indicates that this peak has contributions from transitions to the and orbitals in 2-TP, while in 4-TP it corresponds to a transition to the 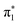orbital, reflecting the lack of amplitude on the sulfur atom in the 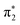orbital in this isomer (see Fig. 1D). The peak at 2475 eV, visible in the acetonitrile spectra of both isomers, also shows a strong sensitivity to hydrogen bonding and is significantly broadened and shifted to higher energy in water.

Fig. 3 (A) Static XA spectra of 2-TP and 4-TP in acetonitrile and water. (B) Illustration of the sulfur K-edge X-ray transient absorption spectroscopy methodology, where the UV pulse in orange opens a new channel for the subsequent X-ray pulse in blue. The plot shows static and pumped XA spectra recorded for 2-TP in acetonitrile at 2 ps. The orbital character of the XA features are labeled on the plot. The inset shows a qualitative illustration of the time resolved X-ray absorption methodology. An optical pump pulse photo-excites the system and the ensuing dynamics are probed with a time delayed X-ray pulse at the sulfur K-edge. The strong new feature below the edge in the pumped spectrum is due to a transition into the vacancy in the π or n orbital.

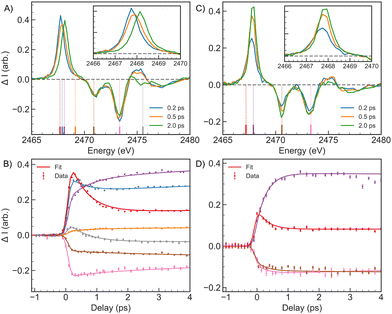
For the time resolved measurements, we first focus on a comparison between 2-TP and 4-TP in acetonitrile. The key spectral changes observed in 2-TP and 4-TP over the first 4 ps following photo-excitation are depicted in Fig. 4. The difference XA spectra of 2-TP (Fig. 4A) show a strong below-edge transient absorption at positive time delays corresponding to a transition into the vacant n or π orbital. At short time delays this absorption feature is accompanied by an increase in absorption at around 2475 eV. Within the first picosecond, the below-edge transient absorption peak blue-shifts in energy by (0.37 ± 0.01) eV from (2467.78 ± 0.01) eV to (2468.15 ± 0.01) eV with a time constant of (0.58 ± 0.04) ps. The fit of the spectral data indicates that this shift in energy is best described by a change in amplitude of two discrete peaks, corresponding to distinct electronic states, rather than a continuous energy shift of a single peak. A detailed discussion of this analysis can be found in Section S4 of the ESI.† The shift in the below-edge absorption is accompanied by the decay of the 2475 eV feature, also on a sub-picosecond timescale. After this point in time, the energy of the spectral features remains constant, but the relative amplitudes of the peaks continue to evolve on a timescale of 5 ps, with the magnitude of the below-edge transient absorption and S_1s → π* bleach increasing with time and the magnitude of the S_1s → σ* bleach decreasing with time.

Fig. 4 Summary of the experimental transient XA spectra of 2-TP and 4-TP in acetonitrile. (A) Full transient XA spectra of 2-TP recorded at 0.2, 0.5 and 2 ps time delay. The inset shows a zoom in to the below edge transient absorption feature. (B) Kinetic traces of 2-TP at select photon energies over the first 4 ps. The energetic positions of the traces correspond to the color coded lines in panel (A). The data points show the raw data and associated uncertainty while the solid lines show the result of a global fit to the traces detailed in the text. (C) and (D) Equivalent plots for 4-TP in acetonitrile.

This spectral evolution is reflected in the kinetic traces and corresponding fits, as shown in Fig. 4B. We fit the kinetics with a global sequential kinetic model described in detail in Section S2.2 of the ESI,† where the final species in the model is assumed to be long-lived on the timescale of the experimental data and corresponds to a triplet electronic excited state. The number of kinetic species required was determined by comparing the reduced χ² of the fit for 2, 3 and 4 species models as discussed in the ESI,† Section S3. For 2-TP, three kinetic species gave the best description of the data. The time constants obtained from the model using three kinetic species are collected in Table 2 and the result of the fit can be found in Fig. 4B. The first kinetic species, which decays with a (0.58 ± 0.04) ps time constant describes the spectral shift in the below-edge feature and the decay of the 2475 eV absorption, while the second spectral evolution associated with a (4.8 ± 0.5) ps time constant describes changes in peak amplitudes associated with a decay in the anisotropy of the transient XA signal as discussed in the ESI,† Section S3.1.3. Therefore, we assign the first time constant to ISC to the long-lived triplet state, while we assign the slower time constant to rotational diffusion effects. Our analysis indicates our measurement lacks the time resolution to resolve the S₂ → S₁ IC consistent with the sub-50 fs IC dynamics seen in the ESMD for 2-TP.

Table 2 Energies of the below-edge induced absorption feature and time constants describing the sequential kinetic model fit to the data recorded for 2-TP and 4-TP in acetonitrile. The energies are obtained by fitting two (2-TP) or three (4-TP) Lorentzian peaks with fixed energies and widths and variable amplitude to the spectra recorded between 0.2 ps and 20 ps. The fit optimizes the energy and width of the peaks as described in detail in Section S4 (ESI). The decay constants are obtained from a global fit of a three or four component kinetic model to the traces shown in Fig. 4 and described in detail in the ESI, Section S2.2

Parameter	2-TP acetonitrile	4-TP acetonitrile
E1 (eV)	(2467.78 ± 0.01) eV	(2467.2 ± 0.2) eV
E2 (eV)	(2468.15 ± 0.01) eV	(2467.7 ± 0.1) eV
E3 (eV)	N/A	(2467.93 ± 0.07) eV
τ1 (ps)	(0.58 ± 0.04) ps	(0.33 ± 0.03) ps
τ2 (ps)	(4.8 ± 0.5) ps	(15 ± 6) ps
τ3 (ps)	N/A	(46 ± 1) ps

---

To assign the spectral features, we compare the experimental spectra with RASPT2 calculations of the S K-edge XA spectra for 2-TP in its low lying singlet and triplet excited states shown in Fig. 5A. Note that the state associated with a particular character may vary with molecular geometry and computation method. Moreover, in the ESMD simulation, the dynamics primarily involves singlet or triplet states associated with character orbital. Therefore, we focus on states exhibiting the desired characteristics ( and 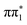) and spin multiplicity in the X-ray spectral calculations, rather than their precise excited state ordering. When referring specifically to the calculated XA spectra we therefore drop the subscript denoting the adiabatic ordering of the state and label them , , 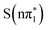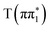and . We reintroduce the subscript when making assignments of spectra to adiabatic states in the ESMD calculations. Sulfur K-edge XA spectra were calculated for the ground state geometry and for the relaxed geometries of the excited states to investigate the effect of vibrational relaxation. The calculated spectra shown in Fig. 5 correspond to the excited state geometry. Additional discussion of the computed spectral features can be found in Section S5.3.1 of the ESI,† including Fig. S20 and Tables S19 and S20. Consistent with the experimental data, the calculated XA spectra for all the excited states considered show a strong absorption feature below the edge and an additional absorption feature above the S_1s → σ* transition. An analysis of the features based on the natural transition orbitals (NTO) and transition dipole moments is shown in Fig. 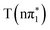S8 and discussed in Section S5.3.2 of the ESI.† In essence, the below-edge feature corresponds to a transition into the vacant n orbital in the case of and states or the vacant π orbital for the and states while the higher lying feature is due to a change in energy of the S_1s → σ* transition in the excited state.

Fig. 5 S K-edge XA spectra of (A) 2-TP^aceto_impl and (B) 4-TP^aceto_impl models for the S₁, S₂, T₁ and T₂ states. Spectra are calculated at the optimized geometry of the respective valence excited state. The experimental spectra at 0.2 ps, 2 ps are shown for comparison. The dashed lines on the experimental spectra show the peak position obtained from a multi-peak fit to the spectra summarized in Table 2. The energy axis of the theoretical spectra is shifted by 4.45 eV to align the ground state π* resonance with the experiment. Ground state experimental and RASPT2-computed spectra are compared in the top panel (black and gray curves respectively).

While the singlet and triplet states with 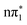character have essentially identical XA spectra at their relaxed geometries, there are clear differences between these and the calculated XA spectra of the ππ* character states and . The spectral position of the below-edge transient absorption feature is within 10 meV for the , 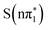and 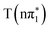states, but is significantly blue-shifted in the state, consistent with differences between the experimental spectra at 0.2 ps and 2 ps, as shown in Fig. 5. The calculated energies of the below-edge peak for each state are summarized in Table S21 of the ESI.† The absolute energetics and magnitude of the predicted shift of the 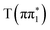state relative to is in excellent agreement with the experimentally measured value of (0.37 ± 0.01) eV. Furthermore, the experimentally measured timescale for the shift in the energy of the transient absorption of (0.58 ± 0.04) ps shows excellent agreement with the ESMD prediction of the timescale of the state formation in 2-TP.

We also considered the effect of vibrational relaxation on the excited state sulfur K-edge spectra by calculating the spectra for both the ground and excited state geometries. As discussed in the ESI,† Section S5.3.1, structural relaxation blue-shifts the energy of the below-edge feature in the singlet states by 400 meV to 500 meV but does not significantly affect the triplet spectra. However, the energy of the below-edge XA feature in the ground state geometry in either the or state is calculated to be much lower than what is observed experimentally at 200 fs and therefore ISC to 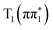from a higher lying state gives a better description of the measured data than vibrational relaxation of the state. In addition, vibrational relaxation would lead to a continuous shift in energy of the below-edge feature with time delay. Fitting to the available experimental spectra (Fig. S10 described in Section S4 of the ESI†) shows that a transition between two discrete peaks better represents the experimental observations than a single shifting peak.

Based on the below-edge absorption feature alone, the time-resolved experimental difference spectra of 2-TP are consistent with an electronic transition from eithe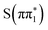r , , or to the long-lived state. We also considered the high-lying absorption feature at ∼2475 eV which shows differences in energy and amplitude between the calculate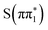d , , , and 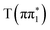XA spectra. The feature is predicted to be strongest and at highest energy in the nπ* character states, 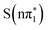, . It is somewhat red shifted and reduced in amplitude in and further red shifted and reduced in amplitude for . Therefore the experimental data, which shows a decay of the feature to a small residual shoulder of the S_1s → σ* transition with the same time constant as the blue-shift of the lower energy excited state absorption, is in better agreement with an nπ* to ππ* transition (either 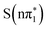, or to ) rather than a direct to 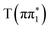transition, which would give an increase in the magnitude of this feature with time. The assignment of the photo-induced absorption at 2475 eV based on the calculated spectra is less robust than the analysis of the excited-state absorption at 2468 eV because of the limitations for higher energy transitions in the active space used for the RASPT2 calculations.

2.4 4-TP

Fig. 4C and D summarizes the measured S K-edge time-resolved XA spectra of 4-TP in acetonitrile. We see similar features in this isomer as in 2-TP, including a strong below-edge transient absorption feature and a weaker increase in absorption above the S_1s → σ* transition accompanied by bleaching of the static XA features. However, there are some notable differences with respect to the 2-TP spectra. Focusing on the kinetic traces shown in Fig. 4D, there is a faster decay (0.33 ± 0.03 ps time constant) in the lowest energy trace recorded at 2467.19 eV (red kinetic trace in Fig. 4D). Secondly, the amplitude of the difference signal at very early time delays is reduced relative to the signal strength at 2467.89 eV after 1 ps (purple kinetic trace). This is reflected in the full spectra shown in Fig. 4 panel C, which shows only a weak shoulder on the low energy side of the below-edge peak at 200 fs. Then, between 200 and 500 fs, there is an increase in the amplitude of the below-edge peak. The kinetic traces and the evolution associated spectra obtained from a global fit to these traces shown in Fig. S6 of the ESI† indicate that this shoulder is due to a reduced amplitude feature which has mostly decayed by 200 fs. Note that we did not record spectra at shorter time delays due to uncertainty in the position of time zero. As detailed in Section S4 of the ESI,† we fit the below-edge absorption feature recorded at select time delays with three Lorentzian peaks. In this fit, we constrain the energy of the peaks to be constant with time delay and the width of the peaks to be the same. The energy of the fitted peaks is summarized in Table 2. The lowest energy fitted peak at (2467.2 ± 0.2) eV only has amplitude in the earliest time delay spectrum, indicating that it corresponds to the fast decay component seen in the 2467.19 eV kinetic trace.

Fig. 5B shows the calculated sulfur K-edge spectra of 4-TP for the two lowest lying singlet and triplet excited states. The states with nπ* character, and , are again predicted to have identical below-edge absorption in 4-TP. The state is also predicted to give a very similar below-edge feature with slightly reduced amplitude and shifted energy. Therefore transitions between these states do not explain the reduced amplitude of the below-edge feature at early time delays observed in the experiment. This means that intersystem crossing from 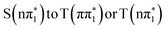would not explain the experimental observations in 4-TP on sub-picosecond timescale. In contrast, the calculated state spectrum shows reduced below-edge absorption cross section and is red shifted with respect to the other states. The calculated energy of this feature in the state of 2467.28 eV shows good agreement with the experimental value of (2467.2 ± 0.2) eV obtained from the fit. Therefore, we conclude the experimental spectra are most consistent with the (0.33 ± 0.03) ps time constant describing the relaxation of the 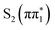state. In principle, this could be due to either internal conversion to or ISC to one of the triplet states. However, the measured time constant is also in excellent agreement with the predicted timescale of internal conversion from the ESMD calculations. Therefore, while we cannot rule out alternative ISC or IC channels in 4-TP on the basis of the experimental spectra alone, the good theoretical agreement between both the XA spectra and the observed timescales indicates S₂ (ππ*) → S₁ (nπ*) internal conversion with a time constant of (0.33 ± 0.03) ps provides the best description of the data recorded at short time delays.

Unlike 2-TP, which does not show significant spectral evolution beyond the first picosecond, we observe subtle changes in the spectral position of the below-edge absorption feature on longer timescales in 4-TP. Between 0.2 ps and 20 ps there is a small shift in the central energy of the below-edge absorption feature as well as a decay of the low energy shoulder assigned to the state. Within the three peak spectral model described above, this corresponds to a transition between a peak centered at (2467.7 ± 0.1) eV, which has dominant amplitude at 0.2 ps to a peak centered at (2467.93 ± 0.07) eV which grows in amplitude and dominates the spectrum at 20 ps (see Fig. S4 in Section S4 of the ESI†). Further, in the para isomer, the ESMD simulations and previous optical studies by Alam et al.³⁶ suggest that the triplet state will be formed on longer timescales. The calculated spectra show a small difference in the energy of the below-edge absorption feature between the singlet and triplet nπ* states at around 2467.66 eV and the state at 2467.83 eV. These energies are in good agreement with the experimentally fitted values indicating that intersystem crossing from 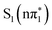to may play a role in the spectral changes observed on a ∼10 ps timescale. With this in mind, we fit the kinetic traces in 4-TP to a 4 component sequential kinetic model, which gives two time constants describing the longer timescale evolution summarized in Table 2. We tentatively assign the faster (15 ± 6) ps component to rotational diffusion, and the (46 ± 1) ps component to the formation of the triplet state (see Section S4 of the ESI† for detailed discussion). However, due to the limited number of kinetic traces recorded and the lack of distinct spectral changes, it is difficult to definitively distinguish rotational dynamics from potential electronic state changes in this isomer. We also note that Alam et al. concluded ISC occurred with a significantly longer time constant of 144 ps.

2.4.1 Solvent dependence. Experimental data recorded for 2-TP and 4-TP in water are presented in the ESI,† Section S1.1. We observe very similar dynamics and spectral features as in acetonitrile and therefore apply the same fitting procedures to these datasets. Time constants obtained from a global fit to the kinetic traces and the energetic positions of spectral features are summarized in Table S1 in the ESI.† The static XA spectra of 2-TP show a strong solvent dependence in the energy of the S_1s → π* transition and in the shape of the spectrum in the vicinity of the S_1s → σ* transitions. In contrast, the energy of the pre-edge absorption at early times and the magnitude of the energetic shift in the feature over the first picosecond do not show a solvent dependence and are the same as in acetonitrile. The main solvent induced difference in the excited state dynamics is the increase in the ISC time constant from (0.58 ± 0.04) ps in acetonitrile to (0.68 ± 0.04) ps in water. The timescale of rotational diffusion is also increased to (12 ± 2) ps in water, consistent with the increased solvent viscosity. The calculated XA spectra and the absorption energies for the gas phase and explicit water solvation model are collected in Fig. S21, S22, and Table S21 (ESI†), with additional discussion in Section S5.3.4 of the ESI.† It should be noted that while the various solvation models provide excellent agreement with each other, the gas model exhibits the largest discrepancy in computed spectral shifts. The experimental data-set recorded for 4-TP in water is limited with lower signal to noise than the other measurements. As shown in Fig. S1D (ESI†), we nonetheless obtain a (0.30 ± 0.08) ps IC timescale from a fit to the kinetic traces, which is the same within the uncertainty as in acetonitrile. We also see an evolution in the kinetic traces on a similar timescale to 4-TP in acetonitrile (see Fig. 3). However, the reduced data quality precludes quantitative characterization of these dynamics for 4-TP in water.

3 Discussion and closing remarks

We have used time resolved X-ray absorption spectroscopy at the sulfur K-edge to access the IC and ISC dynamics of 2-TP and 4-TP in acetonitrile and water. The experimental measurements are in excellent agreement with key predictions from ESMD simulations of the excited state dynamics and calculated excited-state S K-edge spectra. For 2-TP, the sulfur K-edge time-resolved XAS primarily probes the timescale of triplet state formation which is measured to be (0.58 ± 0.04) ps in acetonitrile and (0.68 ± 0.04) ps in water. This observed timescale is in good agreement with the overall triplet formation time from the ESMD calculations. The energetic shift in the below-edge absorption feature of (0.37 ± 0.01) eV is also in excellent agreement with the calculated energy difference between this feature for the state and the higher lying excited states. However, the definitive assignment of the short timescale experimental spectra based on the RASPT2 calculations of the XA spectra is precluded by the small predicted energy shift between the , , and states. The similarity of the XA spectra of these states in part reflects the theoretical prediction that they are very close in energy and mixed in character in 2-TP. Despite this limitation, a comparison of the calculated ESMD and the S K-edge XAS for the electronic excited state difference spectra with the experimental spectral dynamics leads us to conclude that the population dynamics are dominated by the decay of the excited state and the formation of the long-lived character excited state. The simulation of 2-TP dynamics indicates the experiment lacks the necessary time-resolution to observe the S₂ → S₁ IC.

In contrast both IC and ISC are much slower in 4-TP. We assign the sub-ps population dynamics in the experiment to the S₂ → S₁ internal conversion on a (0.33 ± 0.03) ps timescale in acetonitrile and (0.30 ± 0.08) ps in water. This adds evidence in support of the hypothesis that a stabilization of the S₁ (nπ*) state in 4-TP is responsible for the increased IC timescale in this isomer. We also observe subtle spectral changes on a timescale of (46 ± 1) ps in 4-TP which we tentatively assign to ISC to the T₁ triplet state. This is again consistent with the theoretical prediction that ISC is less efficient in this isomer due to the energetically favored pathway being nominally El-Sayed forbidden and the El-Sayed allowed pathway through 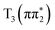being inefficient due to the higher energy of the state relative to S₁. We note that the determination of the ISC pathway proves less experimentally conclusive for 4-TP than 2-TP, due to challenges in separating ISC on >10 ps timescale from rotational effects. Therefore, the conclusions drawn for 4-TP regarding the timescale ISC relies on the good agreement between the fast time constant extracted from the experimental data and timescale of IC predicted in the ESMD calculations, as well as the good agreement between the calculated XA spectra and the peak positions extracted from the available experimental spectra.

Due to the large contribution of sulfur 3p character in the π and n frontier orbitals occupied in the electronic ground state and depopulated in the lowest energy valence electronic excited states of 2-TP and 4-TP, time-resolved sulfur K-edge absorption proves to be sensitive to both nπ* and ππ* character excited states with either singlet and triplet spin multiplicities. While time resolved S K-edge XAS provides a universal probe of the low lying electronic excited states in these systems, distinguishing nπ* and ππ* states, which are close in energy, is challenging due to the ∼0.7 eV lifetime broadening of the absorption features and the similar S_1s → π and S_1s → n cross-sections. We have augmented our measurements with electronic excited state molecular dynamics simulations and RASPT2 simulations of the S K-edge difference spectra for distinct electronic excited state configurations. These theoretical findings prove essential to extract robust mechanistic information from the experimental results. Future studies targeting time resolved S K-edge RIXS could improve the spectral resolution beyond the 1s core hole lifetime broadening and potentially distinguish singlet from triplet excitations based on the anti-Stokes scattering signal.⁷⁸ In general, polarization-dependent ultrafast XAS will assist in identifying the character of the electronic excited states. Unfortunately for 2-TP and 4-TP, excitation of the S-1s electron into the n or the π vacancy created in nπ* and ππ* character valence excited states have polarizations nearly orthogonal to the S₂ (ππ*) valence excited state and, consequently, exhibit the same polarization dependence. Also combining S K-edge spectroscopy with either X-ray measurements at a complimentary absorption edge or optical spectroscopy could further disentangle nπ* and ππ* states which are close in energy. For example in thiopyridone, the nπ* states are predicted to have reduced electron density on the nitrogen atom meaning that nitrogen or carbon K-edge spectroscopy could selectively probe the role of ππ* states in the photophysics of these molecules.

In the theoretical investigations, we assessed the accuracy of the implicit solution models in comparison with other gas phase and micro-solvated models, referred to as 2-TP^gas, 2-TP^water_expl, 4-TP^gas, and 4-TP^water_expl. To summarize briefly, the results indicate consistency between the overall non-adiabatic dynamics of the explicit aqueous (micro-solvated) solvation models and those observed in the implicit acetonitrile solvation models. These similarities are primarily noticed in the evolution of electronic states, while structural variations exist between the two solvent models. In contrast, simulations of gas phase models at the TDDFT and CASSCF levels, including the previously published investigation,⁴¹ suggest large variations in the electronic structure of the gas phase and the solvated thiopyridone systems. Such alterations are attributed to the difference in the valence excited states and their underlying characteristics, which may modify the nature of the dynamics. Similar observations are also made in the computed sulfur K-edge absorption spectra of 2-TP. For instance, as presented in Table S21 (ESI†), while the computed spectral shifts of the transient absorption features of 2-TP are consistent among the solvated models, the largest deviations are noted for the gas phase calculations. Nevertheless, these intricate details of the theoretical aspects are outside the scope of the present paper and will be the subject of an independent study.⁷⁹

Finally, previous studies have suggested that 2-TP may undergo excited-state proton transfer on ultrafast timescales⁷⁶ prior to triplet state formation. We did not see evidence for this process in the isomers and solvents addressed here. Our results are consistent with previous studies which found that the photochemistry of thiopyridones originates from the long-lived triplet state rather than the singlets which are rapidly depopulated in <1 ps in the case of 2-TP. We also performed comparative measurements on the triplet state photochemistry between the isomers and solvents discussed in this work. These measurements indicate that the formation of excimers is the dominant deactivation mechanism of the triplet state. The dynamics of excimer formation will be discussed in a future publication.⁸⁰

Author contributions

DG: formal analysis, investigation, project administration. SKD: formal analysis, software. KJN: investigation, formal analysis. JH: investigation. AF: investigation. CB: investigation. CC: investigation, software. PJMJ: investigation. RGC: investigation. MRZ: investigation. RPW: investigation. HL: investigation. AAC: supervision, resources. NH: supervision, resources. MO: conceptualization, supervision, funding acquisition. KG: conceptualization, supervision, funding acquisition. DG, SKD, MO and KG wrote the manuscript with comments from all of the authors.

Conflicts of interest

There are no conflicts to declare.

Data availability

Data for this article, including underlying datasets for each figure are available at supporting data: influence of substitution pattern on the dynamics of internal conversion and intersystem crossing in thiopyridone isomers at https://doi.org/10.17605/OSF.IO/CTJ7A. Additional supporting data has been included as part of the ESI.†

Acknowledgements

We acknowledge the Paul Scherrer Institute, Villigen, Switzerland for provision of free-electron laser beamtime at the Alvra instrument of the SwissFEL ARAMIS branch. We thank Emma V. Beale and Dardan Gashi for sample delivery support in the experiments. K. G., D. G., M. Z., H. L., K. J. N. and A. A. C. were supported by the Department of Energy, Laboratory Directed Research and Development program at SLAC National Accelerator Laboratory, under contract DE-AC02-76SF00515. M. O. acknowledges funding from Swedish Research Council grant agreement no. 2021-04521. S. K. D. and M. O. acknowledge support from the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement no. 860553 (ITN Network SMART-X) and valuable discussions with Michael R. Coates, who also prepared a series of structures for the explicit aqueous solvation model. The computations were enabled by resources provided by the National Academic Infrastructure for Supercomputing in Sweden (NAISS) and the Swedish National Infrastructure for Computing (SNIC) at NSC and PDC partially funded by the Swedish Research Council through grant agreement no. 2022-06725 and no. 2018-05973. J. H., A. F. and N. H. acknowledge financial support from the Cluster of Excellence ‘CUI: Advanced Imaging of Matter’ of the Deutsche Forschungs-gemeinschaft (DFG) – EXC 2056 – project ID 390715994.

Notes and references

1. W. J. Schreier, P. Gilch and W. Zinth, Annu. Rev. Phys. Chem., 2015, 66, 497–519.
2. A. Pinnola and R. Bassi, Biochem. Soc. Trans., 2018, 46, 467–482.
3. D. Sasikumar, A. T. John, J. Sunny and M. Hariharan, Chem. Soc. Rev., 2020, 49, 6122–6140.
4. X. Zhang, Z. Wang, Y. Hou, Y. Yan, J. Zhao and B. Dick, J. Mater. Chem. C, 2021, 9, 11944–11973.
5. M. A. Bryden and E. Zysman-Colman, Chem. Soc. Rev., 2021, 50, 7587–7680.
6. T. Bortolato, S. Cuadros, G. Simionato and L. Dell’Amico, Chem. Commun., 2022, 58, 1263–1283.
7. M. C. Daza, M. Doerr, S. Salzmann, C. M. Marian and W. Thiel, Phys. Chem. Chem. Phys., 2009, 11, 1688–1696.
8. M. Baba, J. Phys. Chem. A, 2011, 115, 9514–9519.
9. T. J. Penfold, E. Gindensperger, C. Daniel and C. M. Marian, Chem. Rev., 2018, 118, 6975–7025.
10. C. M. Marian, Annu. Rev. Phys. Chem., 2021, 72, 617–640.
11. M. A. El-Sayed, Acc. Chem. Res., 1968, 1, 8–16.
12. S. Lower and M. El-Sayed, Chem. Rev., 1966, 66, 199–241.
13. J. D. Coyle, Tetrahedron, 1985, 41, 5393–5425.
14. T. C. Pham, V.-N. Nguyen, Y. Choi, S. Lee and J. Yoon, Chem. Rev., 2021, 121, 13454–13619.
15. V.-N. Nguyen, Y. Yan, J. Zhao and J. Yoon, Acc. Chem. Res., 2020, 54, 207–220.
16. J. Tang, L. Wang, A. Loredo, C. Cole and H. Xiao, Chem. Sci., 2020, 11, 6701–6708.
17. R. Borrego-Varillas, A. Nenov, P. Kabaciński, I. Conti, L. Ganzer, A. Oriana, V. K. Jaiswal, I. Delfino, O. Weingart and C. Manzoni, et al., Nat. Commun., 2021, 12, 7285.
18. V. I. Prokhorenko, A. Picchiotti, M. Pola, A. G. Dijkstra and R. D. Miller, J. Phys. Chem. Lett., 2016, 7, 4445–4450.
19. S. Mai, M. Pollum, L. Martínez-Fernández, N. Dunn, P. Marquetand, I. Corral, C. E. Crespo-Hernández and L. González, Nat. Commun., 2016, 7, 13077.
20. R. Borrego-Varillas, D. C. Teles-Ferreira, A. Nenov, I. Conti, L. Ganzer, C. Manzoni, M. Garavelli, A. Maria de Paula and G. Cerullo, J. Am. Chem. Soc., 2018, 140, 16087–16093.
21. D. Mayer, F. Lever, D. Picconi, J. Metje, S. Alisauskas, F. Calegari, S. Düsterer, C. Ehlert, R. Feifel and M. Niebuhr, et al., Nat. Commun., 2022, 13, 198.
22. D. C. Teles-Ferreira, I. Conti, R. Borrego-Varillas, A. Nenov, I. H. Van Stokkum, L. Ganzer, C. Manzoni, A. M. de Paula, G. Cerullo and M. Garavelli, Chem. – Eur. J., 2020, 26, 336–343.
23. R. M. Jay, K. Kunnus, P. Wernet and K. J. Gaffney, Annu. Rev. Phys. Chem., 2022, 73, 187–208.
24. D. Garratt, M. Matthews and J. Marangos, Struct. Dyn., 2024, 11, 010901.
25. U. Bergmann, J. Kern, R. W. Schoenlein, P. Wernet, V. K. Yachandra and J. Yano, Nat. Rev. Phys., 2021, 3, 264–282.
26. T. Wolf, R. H. Myhre, J. Cryan, S. Coriani, R. Squibb, A. Battistoni, N. Berrah, C. Bostedt, P. Bucksbaum and G. Coslovich, et al., Nat. Commun., 2017, 8, 29.
27. V. Scutelnic, S. Tsuru, M. Pápai, Z. Yang, M. Epshtein, T. Xue, E. Haugen, Y. Kobayashi, A. I. Krylov and K. B. Møller, et al., Nat. Commun., 2021, 12, 5003.
28. Y.-P. Chang, T. Balciunas, Z. Yin, M. Sapunar, B. N. Tenorio, A. C. Paul, S. Tsuru, H. Koch, J.-P. Wolf and S. Coriani, et al., Nat. Phys., 2024, 1–9.
29. A. Freibert, D. Mendive-Tapia, N. Huse and O. Vendrell, J. Phys. B: At., Mol. Opt. Phys., 2022, 54, 244003.
30. M. Ochmann, I. Von Ahnen, A. A. Cordones, A. Hussain, J. H. Lee, K. Hong, K. Adamczyk, O. Vendrell, T. K. Kim and R. W. Schoenlein, et al., J. Am. Chem. Soc., 2017, 139, 4797–4804.
31. M. Ochmann, A. Hussain, I. Von Ahnen, A. A. Cordones, K. Hong, J. H. Lee, R. Ma, K. Adamczyk, T. K. Kim and R. W. Schoenlein, et al., J. Am. Chem. Soc., 2018, 140, 6554–6561.
32. K. Ledbetter, C. B. Larsen, H. Lim, M. R. Zoric, S. Koroidov, C. D. Pemmaraju, K. J. Gaffney and A. A. Cordones, Inorg. Chem., 2022, 61, 9868–9876.
33. A. A. Cordones, J. H. Lee, K. Hong, H. Cho, K. Garg, M. Boggio-Pasqua, J. J. Rack, N. Huse, R. W. Schoenlein and T. K. Kim, Nat. Commun., 2018, 9, 1989.
34. M. Ochmann, J. Harich, R. Ma, A. Freibert, Y. Kim, M. Gopannagari, D. H. Hong, D. Nam, S. Kim and M. Kim, et al., Nat. Commun., 2024, 15, 8838.
35. Y. Kim, D. Nam, R. Ma, S. Kim, M.-J. Kim, J. Kim, I. Eom, J. H. Lee and T. K. Kim, J. Synchrotron Radiat., 2022, 29, 194–201.
36. M. Alam, et al., J. Chem. Soc., Perkin Trans. 2, 1998, 817–824.
37. R. Du, C. Liu, Y. Zhao, K.-M. Pei, H.-G. Wang, X. Zheng, M. Li, J.-D. Xue and D. L. Phillips, J. Phys. Chem. B, 2011, 115, 8266–8277.
38. B. E. Van Kuiken, M. R. Ross, M. L. Strader, A. A. Cordones, H. Cho, J. H. Lee, R. W. Schoenlein and M. Khalil, Struct. Dyn., 2017, 4, 044021.
39. S. Eckert, J. Norell, R. M. Jay, M. Fondell, R. Mitzner, M. Odelius and A. Föhlisch, Chem. – Eur. J., 2019, 25, 1733–1739.
40. J. Norell, S. Eckert, B. E. Van Kuiken, A. Föhlisch and M. Odelius, J. Chem. Phys., 2019, 151, 114117.
41. J. Norell, M. Odelius and M. Vacher, Struct. Dyn., 2020, 7, 024101.
42. J. Norell, A. Ljungdahl and M. Odelius, J. Phys. Chem. B, 2019, 123, 5555–5567.
43. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian∼16 Revision C.01, Gaussian Inc., Wallingford CT, 2016.
44. E. Runge and E. K. U. Gross, Phys. Rev. Lett., 1984, 52, 997–1000.
45. J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
46. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
47. A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835.
48. R. Cammi, B. Mennucci and J. Tomasi, J. Phys. Chem. A, 2000, 104, 5631–5637.
49. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606.
50. J.-D. Chai and M. Head-Gordon, J. Chem. Phys., 2008, 128, 084106.
51. E. Caldeweyher, S. Ehlert, A. Hansen, H. Neugebauer, S. Spicher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2019, 150, 154122.
52. J. C. Tully, J. Chem. Phys., 1990, 93, 1061–1071.
53. M. Richter, P. Marquetand, J. González-Vázquez, I. Sola and L. González, J. Chem. Theory Comput., 2011, 7, 1253–1258.
54. S. Mai, P. Marquetand and L. González, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1370.
55. S. Mai, P. Marquetand and L. González, Int. J. Quantum Chem., 2015, 115, 1215–1231.
56. G. Granucci, M. Persico and A. Toniolo, J. Chem. Phys., 2001, 114, 10608–10615.
57. F. Plasser, G. Granucci, J. Pittner, M. Barbatti, M. Persico and H. Lischka, J. Chem. Phys., 2012, 137, 22A514.
58. F. Plasser, M. Ruckenbauer, S. Mai, M. Oppel, P. Marquetand and L. González, J. Chem. Theory Comput., 2016, 12, 1207–1219.
59. D. R. Yarkony, Nonadiabatic Derivative Couplings, John Wiley & Sons, Ltd, 2002.
60. B. H. Lengsfield III and D. R. Yarkony, J. Chem. Phys., 1986, 84, 348–353.
61. B. De Souza, G. Farias, F. Neese and R. Izsak, J. Chem. Theory Comput., 2019, 15, 1896–1904.
62. G. Granucci and M. Persico, J. Chem. Phys., 2007, 126, 134114.
63. G. Granucci, M. Persico and A. Zoccante, J. Chem. Phys., 2010, 133, 134111.
64. B. O. Roos, P. R. Taylor and P. E. Siegbahn, Chem. Phys., 1980, 48, 157–173.
65. P. Å. Malmqvist, A. Rendell and B. O. Roos, J. Chem. Phys., 1990, 94, 5477–5482.
66. B. O. Roos, et al., Adv. Chem. Phys., 2007, 69, 399–445.
67. K. Andersson, P.-Å. Malmqvist and B. O. Roos, J. Chem. Phys., 1992, 96, 1218–1226.
68. J. Finley, P.-Å. Malmqvist, B. O. Roos and L. Serrano-Andrés, Chem. Phys. Lett., 1998, 288, 299–306.
69. G. Li Manni, I. F. Galván, A. Alavi, F. Aleotti, F. Aquilante, J. Autschbach, D. Avagliano, A. Baiardi, J. J. Bao and S. Battaglia, et al., J. Chem. Theory Comput., 2023, 19, 6933–6991.
70. V. Sauri, L. Serrano-Andrés, A. R. M. Shahi, L. Gagliardi, S. Vancoillie and K. Pierloot, J. Chem. Theory Comput., 2011, 7, 153–168.
71. M. Guo, L. K. Sørensen, M. G. Delcey, R. V. Pinjari and M. Lundberg, Phys. Chem. Chem. Phys., 2016, 18, 3250–3259.
72. M. G. Delcey, L. K. Sørensen, M. Vacher, R. C. Couto and M. Lundberg, J. Comput. Chem., 2019, 40, 1789–1799.
73. P. Å. Malmqvist and B. O. Roos, Chem. Phys. Lett., 1989, 155, 189–194.
74. P. Å. Malmqvist, B. O. Roos and B. Schimmelpfennig, Chem. Phys. Lett., 2002, 357, 230–240.
75. S. Eckert, P. Miedema, W. Quevedo, B. O’Cinneide, M. Fondell, M. Beye, A. Pietzsch, M. Ross, M. Khalil and A. Föhlisch, Chem. Phys. Lett., 2016, 647, 103–106.
76. S. Eckert, J. Norell, P. S. Miedema, M. Beye, M. Fondell, W. Quevedo, B. Kennedy, M. Hantschmann, A. Pietzsch and B. E. Van Kuiken, et al., Angew. Chem., Int. Ed., 2017, 56, 6088–6092.
77. M. El-Sayed, J. Chem. Phys., 1963, 38, 2834–2838.
78. K. Kunnus, I. Josefsson, I. Rajkovic, S. Schreck, W. Quevedo, M. Beye, S. Grübel, M. Scholz, D. Nordlund and W. Zhang, et al., New J. Phys., 2016, 18, 103011.
79. S. K. Das, D. Garratt, K. Gaffney and M. Odelius, Frontier Orbital Changes Induce Slow-down of Excited State Population Dynamics in Thiopyridone Isomers, https://chemrxiv.org/engage/chemrxiv/article-details/67c180a6fa469535b94b0725.
80. S. K. Das, D. Garratt, K. J. Nelson, J. Harich, A. Freibert, C. Bacellar, C. Cirelli, P. J. M. Johnson, M. Zoric, R.-P. Wang, H. Lim, A. A. Cordones, N. Huse, K. Gaffney and M. Odelius, Probing Excimer Dynamics in Aromatic Thiones with Sulfur K-edge Absorption Spectroscopy (Unpublished).

---

Footnotes

† Electronic supplementary information (ESI) available: Supplemental experimental datasets for 2-TP, 4-TP in water. Full experimental data-sets to 100 ps time delay. Power titration scans performed for each sample. Anisotropy of the XAS signal in 2-TP and a discussion of rotational effects. Detailed description of the data analysis and fitting procedures. Computational details, optimized molecular structures, Wigner sampling, UV-vis spectra, excited state dynamics dynamics trajectories, polarization dependence of calculated XA spectra, comparison of theoretical solvation models. See DOI: https://doi.org/10.1039/d5cp01456e

‡ These authors contributed equally.

---