Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Structural and environmental effects on the mechanism of biological proton-coupled electron transfer using DFTB/MM metadynamics†
Katharina Spies ab,
Leonie Pfeffera,
Tomáš Kubař
ab,
Leonie Pfeffera,
Tomáš Kubař *a and
Natacha Gillet
*a and
Natacha Gillet *b
*b
aInstitute of Physical Chemistry, Karlsruhe Institute of Technology (KIT), 76131 Karlsruhe, Germany. E-mail: tomas.kubar@kit.edu; Fax: +49 721 608-45710; Tel: +49 721 608-43574
bCNRS, ENS de Lyon, LCH, UMR 5182, 69342, Lyon Cedex 07, France. E-mail: natacha.gillet@ens-lyon.fr; Fax: +334 72 72 88 60; Tel: +334 72 72 81 44
First published on 23rd June 2025
Abstract
Proton-coupled electron transfer (PCET) between non-metallic molecules plays an important role in several biological processes involving the oxidation and reduction of aromatic cofactors and amino acids such as tyrosine and tryptophan. Computational chemistry approaches based on quantum-classical multi-scale description can provide atomic insights to understand how a complex biomolecular structure can tune PCET mechanisms. However, the dynamical description of the environment is limited by the cost of the quantum method. In this work, we propose a protocol based on the efficient DFTB3 method and one-dimensional metadynamics at a nanosecond timescale to generate ground-state free energy surfaces of PCET. The proton transfer coordinate is biased in the simulation, while the electron transfer coordinate is evaluated a posteriori through calculations of the difference in molecular charges with an improved DFTB Hamiltonian. This procedure was tested for several biomimetic peptides in QM/MM simulations, involving tyrosine, tryptophan and histidine residues. We found that the adiabatic mechanism of PCET in the studied biomimetic peptides depends not only on the orientation of the donor and acceptor residues but also on environmental factors. Specifically, we demonstrate how interactions between the reaction center and nearby protein components, as well as solvent exposure, influence both the mechanism and kinetics of PCET. Additionally, we identify two distinct concerted PCET mechanisms between tyrosine side chains: fully synchronous and potentially asynchronous. Our results constitute a first validation of this efficient QM/MM protocol for detailed investigation of the structural and dynamical aspects of biological PCET.
1 Introduction
Proton coupled electron transfer (PCET) is a crucial redox reaction that occurs in a variety of processes including energy conversion (solar cells), radical catalysis, and enzymatic reactions. Prominent PCET examples from biological systems include photosystem II (PSII), prostaglandin H synthase, ribonucleotide reductase (RNR), cytochrome P450, and galactose oxidase.1 They can involve metal-center but also organic cofactors only, including residues such as, predominantly, tyrosine (Y), tryptophan (W), histidine (H) or glycine (G) and cysteine (C).In its broadest definition, the term PCET describes the intertwined motion of a proton (Proton transfer, PT) and an electron (Electron transfer, ET), regardless of the mechanism. It can occur simultaneously, i.e. in a concerted manner, or stepwise, i.e. sequentially, involving or not a reaction intermediate. Also, the donor and acceptor molecules can be different for the proton and the electron, so that three partners can be involved in the reaction.2 The PCET mechanism strongly depends on the nature of the cofactors but can also be tuned by the close environment. For instance, long-range PCET in RNR is activated by the protein conformational change and its directionality over more than 30 Å is ensured by the close environment of the different tyrosines along the path.3,4 Consequently, insights into the environment of the tyrosines and its dynamical behavior along the transfer process are important to understand PCET.
Both experimental and computational studies of complex proteins such as PSII and RNR are costly, time-consuming and difficult to set up. An alternative way to control the environment of the active centers and explore the underlying PCET mechanisms turns out to be investigations on biomimetic peptides and model proteins. These facilitate, for example, an understanding of how non-covalent interactions affect the redox potentials of metal clusters or, as in our case, how the protein environment shifts the reduction potential and thus the electron transfer rate according to Marcus theory.5,6
From this perspective, Sibert et al. designed an 18-residue β-hairpin structure in which an oxidized tyrosine can interact with a histidine residue via an interstrand PCET mechanism along a water chain (Fig. 1a).5 NMR data confirm the stability of the β-hairpin structure for the peptide and dipolar contacts between the histidine and tyrosine side chains.5 Electrochemical and electron paramagnetic resonance experiments show that the protein environment and the proton donors and acceptors control the midpoint potential and the reaction rate of the PCET. The oxidation of tyrosine leads to a PCET to histidine as the pKa of histidine increases.5,7,8 Experimental and computational analyses support a water-bridged PCET mechanism in this peptide. A series of mutant peptides were analyzed to investigate environmental factors that alter the mechanism.7–9
Besides, Tommos et al. synthesized a radical maquette α3Y that folds into a stable α-helical structure (Fig. 1b).10 Tyrosine radicals that are generated in this maquette are incorporated into the protein structure and appear to be stable. The midpoint potential is increased at neutral pH compared to tyrosine in aqueous solution, indicating that the protein environment modulates the redox properties. The estimated lifetime for the tyrosine radical is ≤30 ms, indicating that the protein environment strongly stabilizes the radical species. More recently, using a similar protein model, Nilsen-Moe et al. have described how the modulation of ET and PT driving forces, i.e., donor and acceptor redox properties and pKa, modifies the PCET mechanism involving one tyrosine.11 Indeed, tyrosine, thanks to its aromatic ring, has a relatively low ionization potential,5,12 but its radical cation state presents a negative pKa of −2.13 However, the oxidized, deprotonated state of the tyrosine can be stabilized by the protein environment to lifetimes of up to 2.6 s.14 Moreover, reactions following tyrosine oxidation by means of fluorotyrosinated molecules have been studied computationally15–17 and experimentally.18,19 These studies demonstrate that the protein environment and its motions influence the reactivity and PCET mechanism.
Theoretical studies bring a deeper understanding of PCET mechanisms, by determining kinetic and thermodynamic properties with a system description at an atomistic level. Quantum mechanics/molecular mechanics (QM/MM) multiscale simulations are crucial to model PCET in biomolecules: the protein environment, which is described by molecular force field methods, can influence the donor and acceptor molecules that are involved in the transfer mechanism, which is described by quantum mechanics to represent the particle motions. Free energy surfaces for PCET in soybean lipoxygenase were obtained by means of finite-temperature string approach combined with umbrella sampling simulations at a DFT/MM level of theory (B3LYP/6-31G**/MM).20 The same technique using a higher DFT level (ωB97X-D/6-31G**) was used to investigate the direct and water-mediated PCET between tyrosine residues in RNR.21,22 Subsequent work investigated further PCET reactions in RNR, taking into account hydrogen tunneling and non-adiabatic effects.4 Photoinduced PCET during the photocycle of multiple blue light using flavin (BLUF) photoreceptors was studied using multireference wavefunction calculations23,24 and DFT-based approaches.25,26 A review, in which surface hopping is applied to describe photoinduced PCET, can be found in ref. 27. Long-range PCET dynamics are studied in the respiratory chain enzyme complex I28 and the III2IV2 mycobacterial supercomplex29 using QM/MM MD simulations with free energy sampling based on umbrella sampling or its string variant performed on the DFT level of theory (B3LYP-D/def2-SVP). MD simulations and DFT/MM calculations were performed to study the PCET mechanisms in cytochrome P450 reductase and reductive dehalogenase PceA.30,31 However, these methods are computationally expensive so not always suitable for sampling the complex dynamical behavior of large biomolecules.
In this study, we propose a protocol based on QM/MM and metadynamics simulations in which we track collective variables (CV) describing proton and electron transfer and recalculate the free energy surface to compare PCET in different biomimetic peptides using a methodology suitable for extended time scales and large biomolecules. Indeed, DFTB3 and/or LC-DFTB calculations are 100 to 1000 times faster than those performed with full DFT, allowing longer simulations.32,33 They can be combined with a larger number of replicas in a multiple-walker metadynamics simulation setup for a qualitatively more thorough sampling of the conformational space of donors, acceptors and their environment. Here, 1D metadynamics simulation is used, applying the extended sampling algorithm to the PT CV. The ET CV remains unbiased at the runtime of the simulation, and is actually only introduced in the post-processing of trajectories by way of reweighting. In fact, we have previously developed a methodology to apply bias to an ET CV in 2D metadynamics simulations.34,35 Although it would generate a FES in the CVs for PT and ET directly, that approach remains too computationally demanding so far.
To assess our computational protocol, we focus on the simulation of the two model systems shown in Fig. 1. We explore different donor–acceptor pairs and different configurations of the partners and the environment. Apart from investigating the effects of the mentioned factors on the PCET process, this application has two rather technical aims: (i) it will be shown how a CV constructed as the difference of molecular charges can describe the charge state during the complex PCET process. (ii) It will provide reliable benchmark data that can be used later to validate the simulation protocol involving biasing potentials on the ET CV, as soon as the optimized algorithms are finished.
2 Methodology
2.1 Retrieving the FES of the PCET reaction from unbiased and biased MD simulations
One or more CVs (s) must be introduced in order to describe the reaction of interest and to introduce the corresponding biasing potentials in metadynamics. In our case, the proton transfer (PT) is described by the difference in the distances of the hydrogen to the donor and acceptor (sPT, eqn (1)), where X is the heavy atom bound to the transferred proton – an oxygen or a nitrogen atom, and the electron transfer (ET) by the difference in the total charges (sET, eqn (2)).34,35
sPT(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) = Δd = dXDonorH − dXAcceptorH ) = Δd = dXDonorH − dXAcceptorH
| (1) |
 | (2) |
The Mulliken charges Δqi are directly available in the QM method that is used, density functional tight-binding (DFTB), and the atomic charges are summed for each residue involved in the PCET. Each respective charge QDonor or QAcceptor includes the charges of side chain atoms up to and including Cβ and the hydrogens bonded to it (including the linking hydrogen atom introduced in the QM/MM setup, see below), and it excludes any backbone atoms. The charge of the transferred proton is excluded from the difference. The CV for the proton transfer between two tyrosine residues consists in the difference between the proton-donor atom and the proton-acceptor atom, as shown in Fig. 2.
 | ||
| Fig. 2 The proton transfer collective variable sPT = Δd = dODonorH − dOAcceptorH for the PCET reaction between two tyrosine residues. | ||
We have performed two sets of simulations to represent the PCET free energy surfaces along these reaction coordinates: first, unbiased simulations where the proton is free to move; second, metadynamics simulations along the proton transfer coordinate. In the post-processing of the unbiased QM/MM MD simulations, these CVs are used to obtain a 2D histogram from the probability distribution P0(s) ≡ P0(sPT, sET), which is also recalculated to the free energy G(s) as
 | (3) |
 (T, thermodynamic temperature, kB, Boltzmann constant).
(T, thermodynamic temperature, kB, Boltzmann constant).
The second set of simulations consisted of metadynamics that applied biasing potentials on the PT CV (sPT). Standard metadynamics and well-tempered metadynamics were described in detail elsewhere.36–38 An unbiased probability distribution has been retrieved from the biased one by means of reweighting.39–41 A more complex reweighting procedure was required because (i) metadynamics uses a time-dependent biasing potential V(s, t), and (ii) the desired histogram involved a CV that was not subject to the biasing potentials: those were applied to sPT, and the goal was to estimate P0(sPT, sET).
Here, the reweighting factor40,42
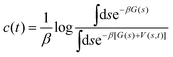 | (4) |
 | (5) |
![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) (s), obtained directly from the metadynamics simulation, with a factor of eβ[V(s,
(s), obtained directly from the metadynamics simulation, with a factor of eβ[V(s,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t)−c(t)]. Importantly, it is possible to introduce an additional variable s′(R) as a CV that however was not biased in the metadynamics simulation. This was used in our work to create 2D histograms P0(sPT, sET), by introducing an additional CV to describe the ET process, s′(R) ≡ sET(ΔQ(R)). The unbiased histogram (probability) was generated from the biased histogram (obtained directly from the metadynamics) using the quantity c(t):
t)−c(t)]. Importantly, it is possible to introduce an additional variable s′(R) as a CV that however was not biased in the metadynamics simulation. This was used in our work to create 2D histograms P0(sPT, sET), by introducing an additional CV to describe the ET process, s′(R) ≡ sET(ΔQ(R)). The unbiased histogram (probability) was generated from the biased histogram (obtained directly from the metadynamics) using the quantity c(t):
P0(s, s′) ∝ ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) (s, s′)eβ[V(s, (s, s′)eβ[V(s,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t)−c(t)] t)−c(t)]
| (6) |
Practically, the numpy.histogram2d function was used to generate the distribution of both CVs, applying the weights eβ[V(s,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t)−c(t)], previously obtained from rbias by activating the CALC_RCT keyword in PLUMED. The resulting histogram was then converted to a free energy surface using eqn (3) and normalized such that the minimum of ΔG was set to zero.
t)−c(t)], previously obtained from rbias by activating the CALC_RCT keyword in PLUMED. The resulting histogram was then converted to a free energy surface using eqn (3) and normalized such that the minimum of ΔG was set to zero.
2.2 β-Hairpin peptide and α-helical protein
The α-helical protein structure inspired by the work of Tommos et al.10 is based on PDB ID 2MI7.19 The secondary structure schemes of the β-hairpin peptide and of the α-helical protein are shown in Fig. 3, indicating the different mutations considered in this work. An overview of the biomimetic peptides investigated in this work is provided in Table 1 together with comments pointing out important differences between them.
 | ||
| Fig. 3 Secondary structure scheme of the β-hairpin peptide (left) and α-helical protein (right) with emphasis on the residues involved in the PCET mechanism. | ||
| Tyr˙ | PCET partner | Comments | |
|---|---|---|---|
| β-H14 | Y5 | H14 (WT) | qH = 1 |
| β-W14 | Y5 | H14W | |
| β-Y14s | Y5 | H14Y | π-Stacked conformation |
| β-Y14f | Y5 | H14Y | Flipped conformation |
| β-Y7 | Y5 | V7Y | |
| α-Y56 | Y34 | V56Y | Embedded inside protein |
| α-Y31 | Y34 | K31Y | Solvent exposed |
| α-Y30 | Y34 | L30Y | Embedded inside protein |
The WT and mutant structures of both systems are simulated using the Amber ff19SB force field and the SPC water model.46,47 An additional set of simulations was set up, in which each of the two systems β-Y7 and α-Y30 was solvated using the OPC water model.48 The atomic charges of the deprotonated radical tyrosine have been obtained using the restrained electrostatic potential fitting method (RESP) as implemented in Antechamber49,50 from the AmberTools software suite.46 This new parametrization has been used to model the side chain Y5 (in the β-hairpin peptides) and that of Y34 (in the α-helical proteins) in a deprotonated radical state. An underlying electron density was calculated on the HF/6-31G* level with Gaussian09.51 The simulation box is cubic with a minimum solute to box distance of 12 Å and a salt concentration of 0.1 mM using an appropriate number of Na+ and Cl− atoms. Periodic boundary conditions were applied. The Verlet neighbor-searching scheme was used, the cutoff distance for neighbor-searching and for the Lennard-Jones interactions was set to 12 Å, and the long range electrostatic interactions were treated with PME.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 kJ mol−1 nm−1 followed by a 60 ps NVT equilibration at 300 K using the SHAKE algorithm to constrain hydrogen–heavy atom bonding. The time step is 2 fs and Langevin dynamics is used to maintain the temperature of 300 K with a collision frequency of 5 ps−1. NPT equilibration was performed for 2 ns at 300 K using constant pressure and the SHAKE algorithm to constrain hydrogen bonding as before. The collision frequency is set to 1 ps−1. The production run is performed with the same parameters as the NPT equilibration for 200 ns with a time step of 2 fs.
000 kJ mol−1 nm−1 followed by a 60 ps NVT equilibration at 300 K using the SHAKE algorithm to constrain hydrogen–heavy atom bonding. The time step is 2 fs and Langevin dynamics is used to maintain the temperature of 300 K with a collision frequency of 5 ps−1. NPT equilibration was performed for 2 ns at 300 K using constant pressure and the SHAKE algorithm to constrain hydrogen bonding as before. The collision frequency is set to 1 ps−1. The production run is performed with the same parameters as the NPT equilibration for 200 ns with a time step of 2 fs.The simulation protocol of the β-hairpins β-H14 (WT) and β-W14 (H14W) was slightly different. Steepest descent minimization was performed until the maximum force dropped below 1000 kJ mol−1 nm−1. NVT equilibrations were performed at 300 K for 100 ps, with a time step of 2 fs, using the leap-frog Verlet integrator. Bonds to hydrogen atoms were constrained using the LINCS algorithm. The NPT equilibration time was set to 10 ns with time steps of 2 fs. The reference pressure was 1.0 bar and the Parrinello–Rahman barostat was introduced. All other simulation parameters were set as for the β-hairpin systems.
All of the classical simulations were performed using the Gromacs package (version 2021.5).52,53
All QM/MM optimizations and simulations were performed with the QM method DFTB332 as implemented in DFTB+,54 using the standard 3OB parameter set.33 The spin-polarized formalism of DFTB is used to describe the electronic structures with a radical character.55 The QM region consisted of the side chains of the two residues involved in PCET. To saturate the valence spheres of the relevant Cα atoms, hydrogen link atoms were introduced in the QM regions on the Cα–Cβ covalent bonds being cut by the QM–MM boundary. The MM region was described using the Amber ff19SB force field.47 The distance between the proton donor and acceptor atoms was restrained with an upper wall restraint of 3 Å, and the sum of the distances between the hydrogen to each donor/acceptor atom was also restrained with an upper wall restraint of 3 Å using the PLUMED plugin (version 2.5.1).43,44 The QM/MM simulations were performed for 1 ns with a time step of 0.5 s. The QM/MM interface is the implementation in our local versions of DFTB+ and Gromacs.56,57 The values of both CVs were extracted directly from the QM/MM simulation and used to compute the probability distributions and subsequently the FES according to eqn (3). The ET CV was derived from Mulliken charges obtained using spin polarized DFTB3/3OB.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 were tested, each with an iteration number of 200 for the bootstrapping. More details can be found in the ESI,† Section E.1.
000 were tested, each with an iteration number of 200 for the bootstrapping. More details can be found in the ESI,† Section E.1.Based on this comparison, the Mulliken charges from single-point spin-polarized LC-DFTB/OB2 calculations, treating the protein environment as point charges, were selected as the representation of atomic charges to be used in eqn (2). Thus, a total of 4000 snapshots per walker from the QM/MM metadynamics simulations were used for subsequent calculation of the ET CV ΔQ with this method. This is in fact the first step in the post-processing of the metadynamics trajectories before the procedure according to Section 2.1 was carried out: build 2D histograms (using additionally the values of the PT CV Δd), and reweight to yield a 2D FES.
3 Results
We studied several biomimetic peptides (see Fig. 4), which differ in their secondary structure (β-hairpin peptides or α-helical proteins), the residues involved in the PCET mechanism – deprotonated radical tyrosine (Tyr˙) paired with histidine (His), tryptophan (Trp), or tyrosine (Tyr) – as well as their relative spatial arrangement and solvation environment (either solvent exposed or buried within the protein). For a detailed description of the peptide structure and the generation of initial configurations for the QM/MM simulations, refer to the ESI,† Section A1.3.1 Unbiased QM/MM simulations
Unbiased DFTB3/MM simulations, i.e., simulations without enhanced sampling methods based on biasing potentials, were performed including a radical tyrosine Tyr˙ and a second protonated residue in the QM zone. The free energy surfaces are shown in Fig. 5.No proton transfer was observed during the simulation time of 1 ns in the β-hairpin peptides H14 (WT) (Fig. 5a) and W14 (Fig. 5b), in which the radical tyrosine is expected to react with a histidine or with a tryptophan.7,68,69 A narrow free energy minimum is observed at 0.7 e for the β-hairpin peptide H14 (WT). Indeed, the histidine is doubly protonated at the starting point of the simulation (positively charged QM system), the radical stabilizes on the tyrosine residue, and so a formal hydrogen atom transfer appears highly unlikely. The partial charge of the hydrogen being transferred is qH = 0.3 e, and the summed charge of the radical tyrosine is QY˙ = 0 along the simulation, which results in ΔQ = QH − 0 = 0.7 e; see Fig. C.1a in the ESI,† for details.
In the β-hairpin peptide W14, the proton remains on the tryptophan. On average, a charge of 0.15 e is localized on the tyrosine (Fig. C.1b in the ESI†), as also reflected by the average value of ΔQ about 0.1 e. This delocalization may be due to the π-stacking between the phenol and indole rings.
Several proton transfer events occurred within the time scale of the simulations in both β-hairpin peptide Y14 configurations (stacked as in Fig. 5d and flipped as in Fig. 5e) and in the β-hairpin peptide Y7 (as in Fig. 5c). All three of these systems exhibit a similar rate-limiting barrier ΔG‡ lower than 5 kcal mol−1. We observe a strong fluctuation of ΔQ, which is also reflected by the free energy minima that are broad along the vertical axis. During simulations, we observe a delocalization of the electron, which is more pronounced in the stacked geometry (Y14s) than in the flipped conformations Y14f and β-hairpin Y7, which are almost identical.
Only one or two proton transfer events happen during the unbiased simulations of the α-helical proteins Y56 (Fig. 5f) or Y30 (Fig. 5h) respectively. This led to a poor sampling of the transition region, and thus a high statistical uncertainty in the rate-limiting barrier ΔG‡ ≈ 5 kcal mol−1, slightly higher than for the above-mentioned β-hairpin peptides. No proton transfer reaction was observed in the α-helical protein Y31 (Fig. 5g). Overall, less electron delocalization occurred in Y56 and Y30 than in the β-hairpins. This observation can be related to the relative orientations of the tyrosine rings, as these were not in a π-stacked geometry during much of the simulation time (see Table D.1 in the ESI†). Y31 exhibits a similar propensity to π-stacking as the β-hairpin peptides Y7 and Y14f, and the reactant basin in the FES also appears similar to those in Y7 and Y14f.
The QM method of our choice, DFTB3, tends to over-delocalize the electron density due to the SIE of the underlying exchange–correlation functional of the generalized gradient approximation type.62,70–73 However, over-delocalization of electron density is problematic when describing ET phenomena, and an example of a fine effect in which the over-delocalization manifests itself, is the large width of the minimum-energy basins along the ET coordinate in the β-hairpin peptides (see Fig. 5b–e). Note that while such an over-delocalization can occur in on-the-fly simulations, a large class of calculations used in previous work by others consider the electron to be constrained to one of the moieties,74 effectively mitigating the over-delocalization problem. In this work, a comparison to several other DFT approaches was conducted to assess the accuracy of the description of ET with DFTB3; the findings are briefly summarized in the following, while the ESI,† Section B may be referred to for details.
It turned out that the electron over-delocalization in DFTB3 calculations is largely resolved by employing LC-DFTB2, which was in reasonable agreement with the two DFT reference methods (M06-2X and B97X-D). With both of the DFT functionals considered, ΔQ obtained from MK charges are markedly larger in magnitude than those from CM5-corrected Hirshfeld charges (which only slightly differ from the ΔQ yielded by Mulliken charges). While it appears difficult to decide which of these approaches is more accurate, we observe that ΔQ obtained using the Mulliken charges from LC-DFTB2 with spin-polarization are always within the interval spanned by those two extremes. Therefore, in this work, ΔQ from Mulliken charges obtained from LC-DFTB2 with spin-polarization is considered as a reasonable compromise, suffering little from electron over-delocalization due to SIE and thus suitable to describe ET phenomena.
3.2 Metadynamics simulations
One-dimensional (1D) metadynamics simulations were performed with a bias applied to the PT reaction coordinate (sPT) to better sample the transition region and the entire FES. In order to improve upon the over-delocalization of the electron density with DFTB3 – which leads to an inappropriate description of the atomic charges during the PT mechanism – the Mulliken charges were recalculated with LC-DFTB2 along the metadynamics trajectories, prior to generating the FES. The 2D FES for PCET in all of the biomimetic peptides and proteins under investigation are shown in Fig. 6 and a concise overview in tabular form is provided in Table 2.| Name | QM region | π-stack/% | ΔG‡/kcal mol−1 | ΔGR→P/kcal mol−1 | H-bonds | Environment |
|---|---|---|---|---|---|---|
| β-H14 | Tyr˙ + His | 6 | 17.3 | 12.4 | 2.03 | Solvent |
| β-W14 | Tyr˙ + Trp | 52 | 17.5 | 7.8 | 0.54 | Solvent |
| β-Y7 | Tyr˙ + Tyr | 13 | 4.1 | — | 2.14 | Solvent |
| β-Y14s | Tyr˙ + Tyr | 72 | 3.7 | — | 2.39 | Solvent |
| β-Y14f | Tyr˙ + Tyr | 24 | 4.2 | −0.6 | 2.34 | Solvent |
| α-Y56 | Tyr˙ + Tyr | 0 | 6.4 | 1.2 | 1.28 | Protein |
| α-Y31 | Tyr˙ + Tyr | 7 | 7.2 | 2.3 | 1.94 | Solvent/protein |
| α-Y30 | Tyr˙ + Tyr | 1 | 4.4 | 1.0 | 1.27 | Protein |
Although PCET is observed in all considered peptides and proteins, the free energy barrier is significantly higher whenever PCET occurs between a tyrosine and a different amino acid (histidine or tryptophan) than in the cases involving a pair of tyrosines. Indeed, the activation free energy ΔG‡ exceeds 15 kcal mol−1 for the β-hairpin peptides H14 (WT) and W14 (Fig. 6a and b), while they are around 4 kcal mol−1 for the β-hairpin peptides containing a pair of tyrosines (Fig. 6c–e) and between 4–8 kcal mol−1 in the α-helical proteins (Fig. 6f–h). The reaction free energy ΔGR→P of the reaction is close to zero for the Tyr˙–Tyr systems, but it is quite high for the Tyr˙–His/Trp systems. This first result indicates that the radical tyrosine state is favored, which is the reactant state in our simulations.
Additionally, PCET in two selected systems, β-Y7 and α-Y30, was investigated using the ff19SB force field for the biomolecule together with the OPC water model, which is the recommended combination.47 The central regions in the resulting FES are largely similar to those obtained with SPC water. A detailed description of these results is provided in the ESI,† Section F, which includes a complete 2D FES in Fig. F.2 (ESI†).
Furthermore, the minimum energy pathway between the reactant and the product states can be read from the FES. It appears that a partial ET can occur during the proton transfer while the free energy increases up to the saddle point which stands around 0.4 Å. A proton transfer pathway seems as probable as a pathway combining a partial charge transfer at Δd = 0 Å. The product basin suggests a delocalization of the electron charge, but histidine seems to be unable to form a stable radical in this state. The formal reaction mechanism can be described as a proton transfer with the formation of an unstable radical cation tyrosine. The proximity of Asp3 helps to stabilize the positive charge of the reactive center. This residue can form hydrogen bonds with His14, see Table D.2 in the ESI,† which also contributes to the stabilization of positively charged histidine. It may strengthen the asymmetry of this system.
In contrast, for β-hairpin W14, the reaction mechanism can be described as a formal hydrogen transfer with the ET CV changing from −0.2 e at the reactants to 0.4 e at the products (Fig. 6b) with a barrier of 17 kcal mol−1. The reactant state with the tyrosyl radical lies 8 kcal mol−1 below the product state. Consequently, the deprotonated Trp seems less favorable than the radical Tyr, but still stable at 300 K with a backward free energy barrier of 9 kcal mol−1. An electron delocalization between the two residues is observed when tryptophan is protonated, with a broader basin along the ΔQ coordinate (over 0.5 e), but also at the transition state to some extent. However, the electron localizes more on the tryptophan after PT to tyrosine. The saddle point in the W14 system is located at Δd = 0.18 Å, also underlining the asymmetric character of this system. Compared to the other β-hairpin peptides, the hydrogen bond network around the Tyr–Trp pair is relatively limited (see Table D.2 in the ESI†). However, the Tyr–Trp pair maintains a π-stacked orientation for more than half of the simulation time (Table 2), which can favor partial electron transfer between the aromatic rings. Stable cationic and neutral tryptophan radicals have been characterized in proteins,75–77 including Trp–Tyr pairs involved in the electron transfer chains in cytochrome c peroxidase,78 DNA photolyase79 and animal-like cryptochrome.80
For all three of the β-hairpin peptides with Tyr–Tyr pairs (Y7, Y14s and Y14f), the central parts of the FES are similar, exhibiting a center of symmetry in agreement with the identical nature and solvent exposure of the respective PCET donors and acceptors. Moreover, the free energy barrier is 4 times lower than the previous asymmetric transfers while the transition region is centered at Δd = 0 Å and ΔQ = 0 e for all three peptides. The product and reactant basins are relatively broad, suggesting energy-free partial electronic transfers during the proton motion. The larger occurrence of π-stacking conformations in β-hairpin Y14s (Table 2) is associated with a slightly flatter surface. A small preference for the neutral state of the tyrosines emerges as the minima are located at ΔQ = ±0.38 e (Y7 and Y14f) or ΔQ = ± 0.32 e which compensates the charge of the transferred proton. The surface's shape allows fully concerted or asynchronous transfer with a partial electron transfer up to 0.5 e before or after proton motion, which is indicated in Fig. 6d with three yellow arrows.
Additional basins at ΔQ = ±1.3 e are observed on the FES for Y14s and Y14f. These correspond to intermediate states resulting from elementary ET events not accompanied by a PT, as they would appear in a step-wise PCET mechanism. Here, these are Tyr+/Tyr− states, as opposed to the states that have both Tyr uncharged, which are located around ΔQ = 0.4 e (see above). Importantly, this means that the ET CV ΔQ, in combination with Δd as the PT CV, is in fact capable of distinguishing the four possible relevant states of the system.
The accessible region on the FES of the α-helical protein Y31 (Fig. 6g) is spread along the ΔQ-axis much like in the β-hairpins Tyr–Tyr FES. Similarly, the two minima in the FES are at ΔQ = −0.31 e and ΔQ = 0.36 e, close to the positions of the minima on those surfaces described above. However, the reactant state is 3 kcal mol−1 more favorable than the product state, reflecting a slight asymmetry of the PCET, and the free energy barrier ΔG‡ is of 7 kcal mol−1 height, so 3 kcal mol−1 higher than in Y7 or Y14. Y31 is the only peptide with two tyrosines which features an asymmetric FES. A possible cause of this is the rather different character of the molecular environment: there is a strong salt bridge Lys19–Glu15 right next to Tyr34, and the strong induced electric field may be the factor that leads to the preference of protonated Tyr34. The saddle point is shifted to Δd = 0.09 Å, in agreement with the asymmetry character of the system. Apparently, the FES for Y31 supports both synchronous PCET and asynchronous with a partial electron transfer. Also, an additional basin on the FES is observed around Δd = −1 Å and ΔQ = +1.4 e. Similarly to the FES of β-hairpin peptides Y14s and Y14f, this corresponds to an intermediate state resulting from an ET step that has not been accompanied by a PT. The basin itself is not well resolved, because of the lack of sampling of this electronic state.
The α-helical protein with Y56 and Y30 exhibits a nearly symmetrical FES with a driving force of 1 kcal mol−1 (Fig. 6f and h). Their shape is similar, as well as the location of the minima at ΔQ = −0.37 e and 0.36 e, in relatively narrow basins. Both surfaces also differ from other FES on their more restricted accessible range of ΔQ values: for instance, in Y30, ΔQ can fluctuate over ca. 0.5 e for a given position of the proton, while it can reach 0.8–1 e for Y31. Then, we observe a narrow corridor connecting the reactant and the product. Consequently, only a concerted transfer can be drawn on the FES in these two systems (see the yellow arrow in Fig. 6f). However, their free energy barriers differ by 2 kcal mol−1, from 4.6 kcal mol−1 for Y30 to 6.6 kcal mol−1 for Y56. This difference may arise from variations in conformation and/or the local environment. Visual inspection reveals that in Y30, the aromatic rings are closer together and a partial overlap of their π-system can occur during the simulation. In contrast, in Y56, the rings adopt a flipped geometry and maintain a larger distance (see Fig. D.1 in the ESI†). The close proximity of the aromatic rings in combination with the conformational arrangement that facilitates the electron transfer motion in Y30 through the π-system could explain the increase in the reaction rate. Besides, a water molecule approaches the reaction center of Y30 but it only does so rarely in Y56 (see Fig. D.2 in the ESI†).
4. Discussion and conclusions
PCET between aromatic amino-acid side chains was investigated computationally in several laboratories previously. Earlier studies were based on single-point calculations of the donor–acceptor systems. So, DFT calculations (UB3LYP/6-31+G(d,p)) of a direct PCET reaction between the aromatic rings of Trp radical and Tyr with varying number of additional amino-acid residues separating the donor and acceptor in a peptide chain yielded activation energies of Ea = 7–19 kcal mol−1.81 Later studies obtained free energies by additionally including thermal corrections based on statistical mechanics; these were still single point calculations rather than averaging based on a sampling of configurational space however. A study of this kind estimated the activation free energy of the phenoxyl/phenol self-exchange reaction in a flipped conformation in the gas phase to be 5.6 kcal mol−1.82 Another DFT study (D-B3LYP/def2-TZVPP) of a PCET between a pair of stacked tyrosine side chains in the gas phase yielded reaction free energy barriers of ΔG‡ = 6.5 and 11.0 kcal mol−1 for direct and water-mediated PCET processes, respectively.83 It was also found that the effect of the electric field induced by the protein environment as point charges shifts the energies by only ca. 0.5 kcal mol−1. Most recently, PCET in biologically relevant complexes has been investigated by including sampling of configurational space with MD simulation. This kind of study of PCET between two Tyr residues in RNR found ΔG‡ = 4.2 kcal mol−1 for the side-chains in a stacked orientation and 9 kcal mol−1 for those in a flipped orientation, using QM/MM finite-temperature string simulations with umbrella sampling at a DFT level of theory (B97X-D/6-31+G**).4The application of the efficient density-functional method DFTB3 in a QM/MM framework allowed the generation of long MD trajectories for several biomimetic peptides in which PCET reactions take place. By combining our setup with an enhanced sampling scheme, extended regions of the conformational space are covered, and even high energy barriers are overcome within the available simulation time. Our current protocol only makes it possible to sample the most stable electronic state along the PT coordinate, so to say, an adiabatic (ground) electronic surface. Any higher-lying electronic states are not explored, and the coupling between them cannot be evaluated. Consequently, on the basis of our current data, no decision can be made on the adiabatic or non-adiabatic nature of the ET, nor on the ET rate. Another protocol dealing with the specificity of ET, such as the coupling and the energy gap between the different involved charge state must be developed to answer these issues.
Furthermore, there are two important considerations that any computational study of ET needs to account for. One is the degree of spatial extension of the electron being transferred. It is especially DFT-based approaches that tend to overly delocalize the electron density, and DFTB is no exception. In this work, the use of LC-DFTB2 largely avoids over-delocalization of excess electron, which would otherwise be observed with DFTB, and improves the description of ET. The other is the reaction coordinate (or CV) that describes the electronic behavior. In this study, the difference of summed atomic charges ΔQ turned out to be an effective CV that makes it possible to distinguish all of the states of the system that are relevant for PCET. The current simulation protocol evaluates ΔQ only after the simulation has been performed, instead of placing a biasing potential on ΔQ in what would be a 2D metadynamics procedure. The latter approach would clearly be desirable, and the aim of our ongoing work is the optimization of the coupled-perturbed DFTB framework that would make it practicable for realistic biomolecular complexes. Still, the fact that the ET-associated CV is not biased results in limited sampling: while two charge states resulting from elementary ET events are observed for some of the systems under investigation in the PT product or reactant state, they are not sampled along the PT reaction path. It appears that fully converged 2D FES will only become available with the full 2D metadynamics scheme that considers biasing potentials as a function of both PT and ET CV; this will also make it possible to deduce whether a concerted or step-wise mechanism is in action in adiabatic PCET.
Our free energy barriers to direct PCET taking place between two Tyr side-chains range between 4 and 7 kcal mol−1, in good agreement with these previous reports. Furthermore, our value of 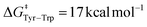 for the peptide β-W14 lies within the above-mentioned range of Ea = 7–19 kcal mol−1. Our results are thus in quantitative agreement with previous studies. Inspecting the six peptides and proteins featuring PCET between two Tyr side chains, we observe two different kinds of transition region topology. For instance, the α-helical proteins Y56 and Y30 FES describe a relatively narrow transition state area which suggests synchronous ET and PT. In contrast, the transition region is relatively broad in the FES of the other peptides and proteins under investigation, as exemplified by the case of β-Y14s. In this kind of situation, different pathways can connect the reactant and product basins with an identical free energy cost. Although all of these pathways still correspond to a concerted, one-step PCET, they may involve a partial transfer of the electron taking place before or after PT. We call this process asynchronous concerted PCET and emphasize that it consists of a single step mechanism and features no intermediates.
for the peptide β-W14 lies within the above-mentioned range of Ea = 7–19 kcal mol−1. Our results are thus in quantitative agreement with previous studies. Inspecting the six peptides and proteins featuring PCET between two Tyr side chains, we observe two different kinds of transition region topology. For instance, the α-helical proteins Y56 and Y30 FES describe a relatively narrow transition state area which suggests synchronous ET and PT. In contrast, the transition region is relatively broad in the FES of the other peptides and proteins under investigation, as exemplified by the case of β-Y14s. In this kind of situation, different pathways can connect the reactant and product basins with an identical free energy cost. Although all of these pathways still correspond to a concerted, one-step PCET, they may involve a partial transfer of the electron taking place before or after PT. We call this process asynchronous concerted PCET and emphasize that it consists of a single step mechanism and features no intermediates.
Our study outlines some of the factors that affect the mechanism of PCET, and the height of free energy barrier ΔG to the reaction, in peptide and protein complexes. The small difference between the peptides β-Y14s and β-Y14f does not point at any sizable influence of the orientation of the participating residues. The presence or absence of π-stacking between the aromatic residues does not appear to affect the free energy surfaces largely. Moreover, our methodology allows extended sampling of the environment of the reaction center. Solvent exposure seems to facilitate asynchronous mechanisms. However, we observe that, despite similar solvent exposure, π-stacking and hydrogen bonding occurrences in β-hairpins Y7-Y14f on the one hand and α-Y31 on the other, the barrier height is 3 kcal mol−1 higher in the latter system.
A possible explanation for this difference lies in the local electrostatic interactions: in the β-hairpin peptides (see Fig. D.2 in the ESI† for details), several positively charged side-chains stay close to the reactive center, such as Arg12 and Arg16. In contrast, in α-Y31, the positively charged Lys19 stands nearby the tyrosines, but it forms a salt bridge with Glu15. A different effect may be in action in the α-helical proteins Y56 and Y30, where only synchronous transfers are allowed in our simulations: their reaction centers are buried in the protein and predominantly surrounded by the side-chains of mostly apolar amino acid residues, such as Leu, Val and Ile. However, the barrier height is 2 kcal mol−1 higher in Y56 than in Y30. Two factors could explain this difference: the presence of a water molecule in Y30 and the conformational arrangements of the aromatic rings. Indeed, in Y56, the tyrosines adopt a flipped conformation only, while in Y30, their rings can partially overlap and are closer. In contrast, β-Y14f, despite also adopting a flipped conformation as the starting point, displays greater conformational flexibility which leads to a conformational landscape allowing π-stacking.
In summary, we find that the PCET mechanism is affected both by the orientation of the residues involved in the reaction and by environmental factors. Specifically, it was revealed how the interactions between the reaction center and the nearby protein components as well as solvent exposure affect the mechanism and kinetics of the PCET. We take advantage of the low computational cost of our approach for a better sampling of this environment and different conformations of the reactive center.
Our development so far has focused on increased efficiency, and thus precision of the simulations by maximizing the sampling of configurational space. In an ongoing work, our aim is to implement an enhanced sampling workflow that includes biasing potentials on both the proton and electron transfer CVs.34,35 Furthermore, we are aiming to improve the accuracy of the approach by passing to more refined DFTB models, based on LC-DFTB for a better description of the electronic behaviour, but keeping a good description of PT and hydrogen bonding. A pertaining limitation is that the method as it stands is currently restricted to the ground electronic state, so that any non-adiabaticity and quantum effects, potentially affecting PCET in enzymes,4,28 cannot be considered.
The presented simulation framework can be readily adopted to investigate PCET occurring in more complex reaction centers, such as PCET processes involving three amino-acid side-chains. For example, in animal-like cryptochrome and Methanosarcina mazei class II DNA photolyase, a tryptophan, a tyrosine and a nearby positioned histidine could possibly participate in a PCET reaction to stabilize a radical state.79,80 Another case of considerable research interest is water-mediated PCET, in which a larger number of water molecules may be involved. This kind of application might utilize one of the previously developed CVs for the description of long-range proton transfers, which were demonstrated to be practicable for long-range water-mediated PT processes in biomolecular complexes.84
Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting this article have been included as part of the ESI.†Acknowledgements
We thank Marcus Elstner for fruitful discussions. We gratefully acknowledge the support by the German Research Foundation (DFG) through the Research Training Group 2450 “Tailored Scale-Bridging Approaches to Computational Nanoscience”. Additional support by the state of Baden-Württemberg through bwHPC and the German Research Foundation (DFG) through grant no. INST 40/575-1 FUGG (JUSTUS 2 cluster) is appreciated. We also gratefully acknowledge support from the CBPsmn (PSMN, Pôle Scientifique de Modélisation Numérique) of the ENS de Lyon and GENCI-IDRIS (project A0130800609) for the computing resources. The platform operates the SIDUS solution (https://dl.acm.org/doi/abs/10.5555/2555789.2555792) developed by Emmanuel Quemener.References
- J. Stubbe and W. A. Van Der Donk, Chem. Rev., 1998, 98, 705–762 CrossRef CAS PubMed.
- S. Hammes-Schiffer, Energy Environ. Sci., 2012, 5, 7696 RSC.
- U. Uhlin and H. Eklund, Nature, 1994, 370, 533–539 CrossRef CAS PubMed.
- J. Zhong, A. V. Soudackov and S. Hammes-Schiffer, J. Phys. Chem. Lett., 2024, 15, 1686–1693 Search PubMed.
- R. Sibert, M. Josowicz, F. Porcelli, G. Veglia, K. Range and B. A. Barry, J. Am. Chem. Soc., 2007, 129, 4393–4400 Search PubMed.
- B. A. Barry, Biochim. Biophys. Acta, Bioenerg., 2015, 1847, 46–54 CrossRef CAS.
- R. S. Sibert, M. Josowicz and B. A. Barry, ACS Chem. Biol., 2010, 5, 1157–1168 Search PubMed.
- C. V. Pagba, T. G. McCaslin, S.-H. Chi, J. W. Perry and B. A. Barry, J. Phys. Chem. B, 2016, 120, 1259–1272 Search PubMed.
- T. G. McCaslin, C. V. Pagba, S.-H. Chi, H. J. Hwang, J. C. Gumbart, J. W. Perry, C. Olivieri, F. Porcelli, G. Veglia, Z. Guo, M. McDaniel and B. A. Barry, J. Phys. Chem. B, 2019, 123, 2780–2791 CrossRef CAS PubMed.
- C. Tommos, J. J. Skalicky, D. L. Pilloud, A. J. Wand and P. L. Dutton, Biochemistry, 1999, 38, 9495–9507 CrossRef CAS.
- A. Nilsen-Moe, C. R. Reinhardt, P. Huang, H. Agarwala, R. Lopes, M. Lasagna, S. Glover, S. Hammes-Schiffer, C. Tommos and L. Hammarström, Chem. Sci., 2024, 15, 3957–3970 RSC.
- A. Harriman, J. Phys. Chem., 1987, 91, 6102–6104 CrossRef CAS.
- W. T. Dixon and D. Murphy, J. Chem. Soc., Faraday Trans. 2, 1976, 72, 1221 RSC.
- S. Oldemeyer, S. Franz, S. Wenzel, L.-O. Essen, M. Mittag and T. Kottke, J. Biol. Chem., 2016, 291, 14062–14071 CrossRef CAS PubMed.
- C. R. Reinhardt, R. Sequeira, C. Tommos and S. Hammes-Schiffer, J. Phys. Chem. B, 2021, 125, 128–136 CrossRef CAS PubMed.
- K. R. Ravichandran, A. B. Zong, A. T. Taguchi, D. G. Nocera, J. Stubbe and C. Tommos, J. Am. Chem. Soc., 2017, 139, 2994–3004 CrossRef CAS.
- A. Nilsen-Moe, C. R. Reinhardt, S. D. Glover, L. Liang, S. Hammes-Schiffer, L. Hammarström and C. Tommos, J. Am. Chem. Soc., 2020, 142, 11550–11559 CrossRef CAS PubMed.
- B. W. Berry, M. C. Martínez-Rivera and C. Tommos, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 9739–9743 CrossRef CAS.
- S. D. Glover, C. Jorge, L. Liang, K. G. Valentine, L. Hammarström and C. Tommos, J. Am. Chem. Soc., 2014, 136, 14039–14051 CrossRef CAS PubMed.
- P. Li, A. V. Soudackov and S. Hammes-Schiffer, J. Am. Chem. Soc., 2018, 140, 3068–3076 CrossRef CAS PubMed.
- C. R. Reinhardt, E. R. Sayfutyarova, J. Zhong and S. Hammes-Schiffer, J. Am. Chem. Soc., 2021, 143, 6054–6059 CrossRef CAS PubMed.
- J. Zhong, C. R. Reinhardt and S. Hammes-Schiffer, J. Am. Chem. Soc., 2023, 145, 4784–4790 CrossRef CAS PubMed.
- E. R. Sayfutyarova, J. J. Goings and S. Hammes-Schiffer, J. Phys. Chem. B, 2019, 123, 439–447 CrossRef CAS PubMed.
- J. J. Goings and S. Hammes-Schiffer, J. Am. Chem. Soc., 2019, 141, 20470–20479 CrossRef CAS.
- P. Mazzeo, S. Hashem, F. Lipparini, L. Cupellini and B. Mennucci, J. Phys. Chem. Lett., 2023, 14, 1222–1229 CrossRef CAS.
- S. Hashem, G. B. Alteri, L. Cupellini and B. Mennucci, J. Phys. Chem. A, 2023, 127, 5065–5074 CrossRef CAS PubMed.
- J. M. Toldo, M. T. Do Casal, E. Ventura, S. A. Do Monte and M. Barbatti, Phys. Chem. Chem. Phys., 2023, 25, 8293–8316 RSC.
- V. R. I. Kaila, Acc. Chem. Res., 2021, 54, 4462–4473 CrossRef CAS PubMed.
- M. C. Pöverlein, A. Hulm, J. C. B. Dietschreit, J. Kussmann, C. Ochsenfeld and V. R. I. Kaila, J. Chem. Theory Comput., 2024, 20, 5751–5762 CrossRef PubMed.
- N. Li, S. Yan, P. Wu, J. Li and B. Wang, ACS Catal., 2024, 14, 7893–7900 CrossRef CAS.
- X. Zhang, Z. Wang, Z. Li, S. Shaik and B. Wang, ACS Catal., 2023, 13, 1173–1185 CrossRef CAS.
- M. Gaus, Q. Cui and M. Elstner, J. Chem. Theory Comput., 2011, 7, 931–948 CrossRef CAS.
- M. Gaus, A. Goez and M. Elstner, J. Chem. Theory Comput., 2013, 9, 338–354 CrossRef CAS.
- N. Gillet, M. Elstner and T. Kubar, J. Chem. Phys., 2018, 149, 072328 CrossRef.
- D. Maag, J. Böser, H. A. Witek, B. Hourahine, M. Elstner and T. Kubar, J. Chem. Phys., 2023, 158, 124107 CrossRef CAS.
- A. Barducci, M. Bonomi and M. Parrinello, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 826–843 CAS.
- O. Valsson, P. Tiwary and M. Parrinello, Annu. Rev. Phys. Chem., 2016, 67, 159–184 CrossRef CAS PubMed.
- G. Bussi and A. Laio, Nat. Rev. Phys., 2020, 2, 200–212 CrossRef.
- M. Bonomi, A. Barducci and M. Parrinello, J. Comput. Chem., 2009, 30, 1615–1621 CrossRef CAS PubMed.
- P. Tiwary and M. Parrinello, J. Phys. Chem. B, 2015, 119, 736–742 CrossRef CAS PubMed.
- T. M. Schäfer and G. Settanni, J. Chem. Theory Comput., 2020, 16, 2042–2052 CrossRef.
- F. Giberti, B. Cheng, G. A. Tribello and M. Ceriotti, J. Chem. Theory Comput., 2020, 16, 100–107 CrossRef CAS.
- G. Bussi and G. A. Tribello, Biomolecular Simulations, Springer New York, New York, NY, 2019, vol. 2022, pp. 529–578 Search PubMed.
- G. A. Tribello, M. Bonomi, D. Branduardi, C. Camilloni and G. Bussi, Comput. Phys. Commun., 2014, 185, 604–613 CrossRef CAS.
- N. Mandard, P. Bulet, A. Caille, S. Daffre and F. Vovelle, Eur. J. Biochem., 2002, 269, 1190–1198 CrossRef CAS.
- D. Case, H. Aktulga and P. Kollman, Amber 2023, 2023 Search PubMed.
- C. Tian, K. Kasavajhala, K. A. A. Belfon, L. Raguette, H. Huang, A. N. Migues, J. Bickel, Y. Wang, J. Pincay, Q. Wu and C. Simmerling, J. Chem. Theory Comput., 2020, 16, 528–552 CrossRef PubMed.
- S. Izadi, R. Anandakrishnan and A. V. Onufriev, J. Phys. Chem. Lett., 2014, 5, 3863–3871 CrossRef CAS.
- J. Wang, W. Wang, P. A. Kollman and D. A. Case, J. Mol. Graphics Modell., 2006, 25, 247–260 CrossRef CAS PubMed.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, J. R. Cheeseman, G. Scalmani, M. Caricato, H. P. Hratchian, X. Li, V. Barone, J. Bloino, G. Zheng, T. Vreven, J. A. Montgomery, G. A. Petersson, G. E. Scuseria, H. B. Schlegel, H. Nakatsuji, A. F. Izmaylov, R. L. Martin, J. L. Sonnenberg, J. E. Peralta, J. J. Heyd, E. Brothers, F. Ogliaro, M. Bearpark, M. A. Robb, B. Mennucci, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, A. Rendell, R. Gomperts, V. G. Zakrzewski, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao and H. Nakai, Gaussian 09, Gaussian Inc, Wallingford CT, 2009 Search PubMed.
- S. Pronk, S. Páll, R. Schulz, P. Larsson, P. Bjelkmar, R. Apostolov, M. R. Shirts, J. C. Smith, P. M. Kasson, D. van der Spoel, B. Hess and E. Lindahl, Bioinformatics, 2013, 29, 845–854 CrossRef CAS.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- B. Hourahine, B. Aradi, V. Blum, F. Bonafé, A. Buccheri, C. Camacho, C. Cevallos, M. Y. Deshaye, T. Dumitrica, A. Dominguez, S. Ehlert, M. Elstner, T. van der Heide, J. Hermann, S. Irle, J. J. Kranz, C. Köhler, T. Kowalczyk, T. Kubar, I. S. Lee, V. Lutsker, R. J. Maurer, S. K. Min, I. Mitchell, C. Negre, T. A. Niehaus, A. M. N. Niklasson, A. J. Page, A. Pecchia, G. Penazzi, M. P. Persson, J. Rezác, C. G. Sánchez, M. Sternberg, M. Stöhr, F. Stuckenberg, A. Tkatchenko, V. W.-Z. Yu and T. Frauenheim, J. Chem. Phys., 2020, 152, 124101 CrossRef CAS PubMed.
- C. Köhler, T. Frauenheim, B. Hourahine, G. Seifert and M. Sternberg, J. Phys. Chem. A, 2007, 111, 5622–5629 CrossRef.
- T. Kubař, tomaskubar/dftbplus, 2022, https://github.com/tomaskubar/dftbplus, original-date: 2020-02-20T09:43:17Z.
- T. Kubař, tomaskubar/gromacs-dftbplus, 2025, https://github.com/tomaskubar/gromacs-dftbplus, original-date: 2019-04-24T16:05:16Z.
- D. B. Rubin, Ann. Stat., 1981, 9, 130–134 Search PubMed.
- S. S. D. Marco, salvatoredimarco/rna-membrane, 2024, https://github.com/salvatoredimarco/rna-membrane, original-date: 2024-11-07T09:31:05Z.
- G. A. Tribello and M. Bonomi, plumed/masterclass-21-4: Repository of the data for PLUMED Masterclass 21.4, https://github.com/plumed/masterclass-21-4.
- PLUMED: Lugano tutorial: Metadynamics simulations with PLUMED, https://www.plumed.org/doc-v2.8/user-doc/html/lugano-3.html.
- J. J. Kranz, M. Elstner, B. Aradi, T. Frauenheim, V. Lutsker, A. D. Garcia and T. A. Niehaus, J. Chem. Theory Comput., 2017, 13, 1737–1747 CrossRef CAS PubMed.
- V. Q. Vuong, J. Akkarapattiakal Kuriappan, M. Kubillus, J. J. Kranz, T. Mast, T. A. Niehaus, S. Irle and M. Elstner, J. Chem. Theory Comput., 2018, 14, 115–125 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639–5648 CrossRef CAS.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS.
- J.-D. Chai and M. Head-Gordon, J. Chem. Phys., 2008, 128, 084106 CrossRef PubMed.
- C. V. Pagba, S.-H. Chi, J. Perry and B. A. Barry, J. Phys. Chem. B, 2015, 119, 2726–2736 CrossRef CAS PubMed.
- C. V. Pagba, T. G. McCaslin, G. Veglia, F. Porcelli, J. Yohannan, Z. Guo, M. McDaniel and B. A. Barry, Nat. Commun., 2015, 6, 10010 CrossRef CAS.
- B. Hourahine, S. Sanna, B. Aradi, C. Köhler, T. Niehaus and T. Frauenheim, J. Phys. Chem. A, 2007, 111, 5671–5677 CrossRef CAS PubMed.
- A. J. Cohen, P. Mori-Sánchez and W. Yang, Science, 2008, 321, 792–794 CrossRef CAS.
- M. Rapacioli, F. Spiegelman, A. Scemama and A. Mirtschink, J. Chem. Theory Comput., 2011, 7, 44–55 CrossRef CAS PubMed.
- T. A. Niehaus and F. Della Sala, Phys. Status Solidi B, 2012, 249, 237–244 CrossRef CAS.
- A. V. Soudackov and S. Hammes-Schiffer, J. Phys. Chem. Lett., 2014, 5, 3274–3278 CrossRef CAS.
- M. Sivaraja, D. B. Goodin, M. Smith and B. M. Hoffman, Science, 1989, 245, 738–740 CrossRef CAS PubMed.
- F. Himo and L. A. Eriksson, J. Phys. Chem. B, 1997, 101, 9811–9819 CrossRef CAS.
- A. Piatkivskyi, S. Osburn, K. Jaderberg, J. Grzetic, J. D. Steill, J. Oomens, J. Zhao, J. K.-C. Lau, U. H. Verkerk, A. C. Hopkinson, K. W. M. Siu and V. Ryzhov, J. Am. Soc. Mass Spectrom., 2013, 24, 513–523 CrossRef CAS PubMed.
- M. A. Miller, L. Vitello and J. E. Erman, Biochemistry, 1995, 34, 12048–12058 CrossRef CAS PubMed.
- P. Müller, E. Ignatz, S. Kiontke, K. Brettel and L.-O. Essen, Chem. Sci., 2018, 9, 1200–1212 RSC.
- F. Lacombat, A. Espagne, N. Dozova, P. Plaza, P. Müller, K. Brettel, S. Franz-Badur and L.-O. Essen, J. Am. Chem. Soc., 2019, 141, 13394–13409 CrossRef CAS PubMed.
- X. Chen, L. Zhang, L. Zhang, J. Wang, H. Liu and Y. Bu, J. Phys. Chem. B, 2009, 113, 16681–16688 CrossRef CAS.
- J. M. Mayer, D. A. Hrovat, J. L. Thomas and W. T. Borden, J. Am. Chem. Soc., 2002, 124, 11142–11147 CrossRef CAS PubMed.
- V. R. I. Kaila and G. Hummer, J. Am. Chem. Soc., 2011, 133, 19040–19043 CrossRef CAS PubMed.
- P. H. König, N. Ghosh, M. Hoffmann, M. Elstner, E. Tajkhorshid, T. Frauenheim and Q. Cui, J. Phys. Chem. A, 2006, 110, 548–563 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: (A) classical MD, structural analysis; (B) benchmark DFTB charges; (C) partial atomic charges; (D) environmental & structural analysis; (E) 1D metadynamics, FES; (F) OPC water model. See DOI: https://doi.org/10.1039/d5cp01359c |
| This journal is © the Owner Societies 2025 |