Mechanistic diversity in the reactive adsorption of chlorine trifluoride on monohydrogenated silicon

Abstract

We present first-principles molecular dynamic simulations of chlorine trifluoride impinging upon the monohydrogenated Si{001} surface. Our computed trajectories reveal a rich variety of reactive adsorption events, most of which differ considerably from the behaviour predicted in previous quasistatic transition state calculations for the dihydrogenated surface. In addition to reactions involving the abstraction of adsorbed hydrogen, we find that direct interaction of the molecule's equatorial fluorine atom with silicon atoms as deep as the third layer may also lead to reactive adsorption. Amongst the surface defects induced by these processes, we find cationic bridges of Si–H–Si or Si–F–Si type; anionic motifs of Si–Si–F type; and silicon dangling bonds, which may be of cationic, anionic, or radical character. Chlorine monofluoride is evolved in the majority of reactive trajectories, with hydrogen fluoride, hydrogen chloride, and difluorochlorate species generated on occasion.

---

I. Introduction

In recent years, first-principles molecular dynamic calculations have revealed a rich complexity of radical reactions involving strong oxidants at the monohydrogenated Si{001} surface.^1–3 In the presence of ozone (O₃) it was found, for example, that hydrogen could be abstracted from the surface to form a hydrotrioxy (HO₃) radical that rapidly dissociated into adsorbed hydroxyl (OH) and desorbing dioxygen (O₂) species.¹ Similarly, molecular fluorine (F₂) was capable of abstracting hydrogen to form a short-lived hydrodifluoro (HF₂) radical that dissociated to yield adsorbed adatomic fluorine (F) and either desorbing hydrogen fluoride (HF) or molecular dihydrogen (H₂).² In contrast, with oxygen difluoride (OF₂) there was no evidence for hydrogen abstraction; instead, a single fluorine atom was preferentially deposited on the surface, leaving an oxygen monofluoride (OF) radical that either desorbed or dissociated to yield a second fluorine adatom and adatomic oxygen.³ Interestingly, while the oxygen adatom adopted a Si–O–Si bridge geometry, the fluorine adatoms either adopted an unusual Si–Si–F motif or induced the formation of an equally unusual Si–H–Si bridge. The latter two structures are surmised to be stabilised by three-centre bonding, involving four or two electrons respectively.

To further explore the role of radicals in the reactions of highly oxidising species on monohydrogenated silicon, we turn now to chlorine trifluoride (ClF₃) – an exceptionally strong fluorinating agent that reacts violently with a range of otherwise inert materials including glass, sand, and water.^4,5 Despite significant safety concerns, ClF₃ finds commercial use in the semiconductor industry as an alternative to various greenhouse gases in the cleaning of chambers used for chemical vapour deposition (CVD).⁶ Moreover, we suggest that it may be suitable for the deliberate fluorination of semiconductors in efforts toward surface transfer doping of thin films. It is therefore of some interest to determine the nature of whatever surface products may arise from exposure to this species, and to understand the mechanisms by which such products are generated. We are aware of just one prior first-principles study of ClF₃ adsorption on a silicon surface, but this treats dihydrogenated Si{001} and we focus on the monohydrogenated version.^7,8 Moreover, the earlier study is based upon a quasistatic transition state search, which reveals the isothermal pathway between reactants and products but likely misses several alternative pathways that may be accessed under adiabatic conditions. In this connection, first-principles molecular dynamic simulation is becoming established as a viable option for the study of surface scattering, adsorption, diffusion, reaction and desorption.^{1–3,10–32} For the record, the transition state obtained on the dihydrogenated surface involves replacement of an adsorbed hydrogen atom by a single fluorine atom, leading to desorption of a hydrogen difluorochlorate (HClF₂) molecule. This unusual species may be thought of as comprising a proton bound to the central atom of a linear difluorochlorate anion.⁹ As will be seen below, such an outcome is seen in just two of our first-principles molecular dynamic simulations, suggesting that it is only a minority process.

Before introducing our computational methodology in detail, it will be wise first to expend a little effort toward understanding the substrate and adsorbate chosen for the current study. On the ideal Si{001} surface, each top-layer atom would possess two dangling bonds, giving rise to electronic states within the fundamental band gap of the bulk material. At the fully passivated surface, each of these dangling bonds is saturated by an adsorbed hydrogen atom, identifying it as the dihydrogenated case. On the clean surface, one dangling bond per atom would be saturated by the formation of silicon dimers instead, and these would tilt to force the bands associated with remaining dangling bonds out of the band gap region. Our monohydrogenated surface, being in some sense intermediate between these extremes, shares features with both situations. The formation of silicon dimers again saturates half of the otherwise dangling bonds, but the remainder are passivated by adsorbed hydrogen atoms, thus obviating the driving force toward tilting of the dimers.^33,34

Turning to the adsorbate, ClF₃ is a classic example of a hypervalent molecule, traditionally described in terms of three-centre four-electron bonding. Its “T-shaped” geometric structure is based upon a trigonal bipyramid – the central chlorine atom can be thought of as possessing an equatorial plane (comprising three sp² hybrid orbitals) and an axial direction (defined by a single p orbital). An sp³ hybrid orbital from one fluorine atom is then assumed to form a regular two-centre two-electron bond with one of the equatorial orbitals, and the other two equatorial orbitals may be thought of as lone pairs. This leaves two fluorine atoms to combine one sp³ hybrid orbital each with the axial p orbital of the central chlorine atom, making one bonding orbital, one non-bonding orbital, and one antibonding orbital. The first two of these would be fully occupied and the last unoccupied, together comprising the three-centre four-electron bond.

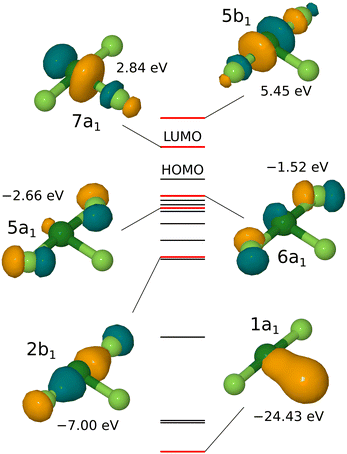
In fact, the foregoing rationalisation bears only passing resemblance to the molecular eigenstates that emerge from a first-principles calculation, the results of one such are shown in Fig. 1. Here, we see little to support the usefulness of sp² or sp³ hybridisation in understanding the electronic structure; individual orbitals are readily interpreted in terms of admixtures involving only s or p orbitals from any one atom. For instance, the lowest-energy valence orbital (1a₁) appears to be a σ-bonding combination of the Cl p_x orbital with the s orbital of the equatorial fluorine atom rather than with a hybrid orbital. A three-centre bonding orbital is, nevertheless, represented fairly clearly by the 2b₁ state, comprising a σ-bonding combination of p_y orbitals located on the chlorine and both axial fluorine atoms, while the anti-bonding counterpart of the same is the second-lowest unoccupied state, labelled 5b₁. The expected non-bonding orbital is split (due to interference from the p_x orbital of the central chlorine atom) into two components (5a₁ and 6a₁) that each primarily involve mixtures of p_x and p_y orbitals on the axial fluorine atoms. We stress that the language of three-centre bonding remains useful as an abstraction, however, even when difficult to identify amongst the molecular orbitals. On the other hand, the lowest unoccupied state (7a₁) corresponds very clearly to a σ-antibonding combination of the p_x orbitals belonging to the chlorine atom and to the equatorial fluorine atom. We expect, in consequence, that the molecule will be most reactive when approaching an electron donor along the line of this bond, and that the equatorial fluorine atom will be the most susceptible to dissociation from the remainder of the molecule.

Fig. 1 Selected orbitals of ClF₃ and their energies relative to the highest-occupied molecular orbital. Dark- and light-green spheres represent chlorine and fluorine atoms, respectively, while orange and teal isosurfaces represent opposite phases of the wavefunction.

II. Computational method

In the present work, we conduct molecular dynamic simulations at the level of first-principles Density Functional Theory (DFT) as implemented in the CASTEP computer code (Version 18.1).³⁵ Fundamental parameters pertaining to the calculations were the same as those adopted in our recent work on F₂ and OF₂ adsorption,^2,3 but may be summarised thus: electronic wavefunctions were expanded in a plane-wave basis up to a kinetic energy cutoff at 350 eV; electron–ion interactions were incorporated via ultrasoft pseudopotentials,³⁶ and the exchange–correlation interaction was included through the Perdew–Burke–Ernzerhof functional.³⁷ Calculations were performed within a supercell of lateral dimensions consistent with a c(4 × 4) surface unit cell to minimise interaction with periodic images; the vertical dimension was equivalent to 16 layers of silicon in the [001] crystallographic direction, within which space the surface itself was modelled by means of an eight-layer silicon slab. The back three layers of this slab were held fixed at bulk positions, while five layers on the side of interest were permitted to relax according to calculated forces. The back layer was terminated with hydrogen atoms in a dihydride geometry, which were also allowed to relax during initial geometry optimisation but frozen during dynamic runs. The top-layer atoms were initialised as symmetric silicon dimers in a (2 × 2) pattern, and their remaining dangling bonds saturated with mobile hydrogen atoms. Brillouin zone sampling was achieved using a 2 × 2 × 1 Monkhorst–Pack mesh.³⁸

Following optimisation of the monohydride surface geometry in the absence of ClF₃ individual dynamic trajectories were initialised in the NVE ensemble (fixed particle numbers, volume, and energy) with the molecule's centre of mass just over 6 Å above the plane containing the top-layer silicon atoms. The initial molecular motion in each case was directed along the inward surface normal at a speed of 225 m s⁻¹ (kinetic energy 0.0245 eV) toward one of five sites (A–E) chosen to uniformly sample the surface unit cell. All atoms were vibrationally and rotationally cold at the start of each simulation. Initial orientations were chosen with reference to the molecule's principal axes of inertia, following a similar approach to that used by us recently for our study of OF₂ adsorption on the same surface. In descending order of their moments of inertia, the principal axes of the ClF₃ molecule may be taken to lie along

where r₁ is the Cl–F vector involving the single equatorial fluorine atom, and where r₂ and r₃ represent (in either order) the Cl–F vectors involving the two axial fluorine atoms. We then specify how the first two of these axes align with high-symmetry directions of the surface, for which purpose we define the α direction to lie along the dimer rows, the β direction to lie across the dimer rows, and the γ direction to be the outward surface normal (Fig. 2). That is, for example, the βα orientation aligns the I₁ axis of the molecule across the dimer-row direction of the surface and the I₂ axis of the molecule along it. In similar fashion, the [small gamma, Greek, macron]β orientation aligns the I₁ axis along the inward surface normal (the overline signifying negation) and the I₂ axis across the dimer-row direction.

Fig. 2 Schematic top-down view of the monohydrogenated Si{001} surface, highlighting two adjacent dimer rows with double-headed arrows. The surface exhibits a (2 × 1) reconstruction, whose primitive cell is marked with the inner rectangle, but calculations were performed within a c(4 × 4) unit cell, marked with the large square. Incoming molecules were aimed at sites A–E, shown here in multiple instances to emphasise the uniformity of their distribution; for complete specification, the left-most of the indicated E sites was used for the calculations. Reference axis orientations are indicated by vectors labelled α (along the dimer rows) and β (across the dimer rows). A third orientation, γ, corresponds to the outward surface normal.

Since OF₂ and ClF₃ both conform to the C_2v point group, our analysis of symmetry matches that described in our earlier work.³ We once again find that there are eight symmetrically distinct orientations when aiming the molecule at one of the high-symmetry sites (A–D) but twelve when aiming at the low-symmetry site (E). Taking sites and orientations together, we are faced with investigating a total of 44 distinct trajectories, listed in Table 1 alongside their symmetry equivalents. If one were to count symmetry-equivalent replicas separately, this ensemble would map onto a total of 60 trajectories (including eight mirror-image pairs). For each of the 14 trajectories described in detail below, we have also performed a geometry optimisation starting from the final step of its molecular dynamics run, having first deleted any species that are in the act of desorption. Energies for such species are calculated separately in the gas phase and added to that of the optimised surface structure, whereupon subtraction of the energies of gas-phase chlorine trifluoride and of the original monohydride surface yields an effective adsorption heat for each individual trajectory.

Table 1 Initial molecular orientations, labelled according to the directions of principal rotational axes (I₁ and I₂ from eqn (1)) with respect to surface-related axes (α, β and γ defined as in Fig. 2). Each distinct orientation may be labelled in two ways, listed here under headings of primary and redundant, of which the former involves the fewest negative projections (indicated with overlines) onto the surface-related axes. In addition, under the reflection heading, we note orientations that are mirror-equivalent to those listed in the first two columns and need not be separately studied. Entries listed under the primary column comprise 44 symmetrically distinct site/orientation combinations; including the reflection column raises this to 60 in total

Site	Primary	Redundant	Reflection
A–D	αβ	[small alpha, Greek, macron]β	α[small beta, Greek, macron], [small alpha, Greek, macron][small beta, Greek, macron]
	βα	[small beta, Greek, macron]α	β[small alpha, Greek, macron], [small beta, Greek, macron][small alpha, Greek, macron]
	αγ	[small alpha, Greek, macron]γ	—
	α[small gamma, Greek, macron]	[small alpha, Greek, macron][small gamma, Greek, macron]	—
	βγ	[small beta, Greek, macron]γ	—
	β[small gamma, Greek, macron]	[small beta, Greek, macron][small gamma, Greek, macron]	—
	γα	[small gamma, Greek, macron]α	γ[small alpha, Greek, macron], [small gamma, Greek, macron][small alpha, Greek, macron]
	γβ	[small gamma, Greek, macron]β	γ[small beta, Greek, macron], [small alpha, Greek, macron][small beta, Greek, macron]
E	αβ	[small alpha, Greek, macron]β	—
	βα	[small beta, Greek, macron]α	—
	αγ	[small alpha, Greek, macron]γ	—
	α[small gamma, Greek, macron]	[small alpha, Greek, macron][small gamma, Greek, macron]	—
	βγ	[small beta, Greek, macron]γ	—
	β[small gamma, Greek, macron]	[small beta, Greek, macron][small gamma, Greek, macron]	—
	γα	[small gamma, Greek, macron]α	—
	γβ	[small gamma, Greek, macron]β	—
	α[small beta, Greek, macron]	[small alpha, Greek, macron][small beta, Greek, macron]	—
	β[small alpha, Greek, macron]	[small beta, Greek, macron][small alpha, Greek, macron]	—
	γ[small alpha, Greek, macron]	[small gamma, Greek, macron][small alpha, Greek, macron]	—
	γ[small beta, Greek, macron]	[small gamma, Greek, macron][small beta, Greek, macron]	—

---

For the purpose of visual analysis, we not only provide snapshots of intermediate structures but also plot selected interatomic separations as a function of time. Where appropriate to the discussion of results, we report vibrational stretch frequencies estimated from such plots (quoted to the nearest multiple of 5 cm⁻¹) by noting the periodic spacing of successive minima (averaging over at least five) in the relevant traces.

Following our practice from previous work,^2,3 we are aided in identifying instances of bond making or breaking by consulting plots of two different spin measures. The first of these is the integrated net spin, defined as

where ρ_α(r) and ρ_β(r) are the spin densities of the two spin species accounted for in our calculations; the second is the integrated spin modulus, defined asin which the modulus of the integrand is taken, rather than that of the integral. In a hypothetical system featuring a single unpaired electron (per supercell) one would ideally expect both of these measures to take a value of 1 μ_B (per supercell). If two unpaired electrons were present, however, one could imagine the integrated net spin (σ₁) taking per-supercell values of either 0 μ_B or 2 μ_B, corresponding to singlet or triplet configurations respectively, but the integrated spin modulus (σ₂) should be 2 μ_B regardless. In practice, both spin measures pass through non-integer values as the system evolves, but they nevertheless provide a helpful indication of the degree to which parts of the system may or may not exhibit radical character. In addition, we also report Mulliken analysis at selected junctures,³⁹ but stress that the spin and charge values thus obtained should be taken with a pinch of salt, especially in extended systems where their correspondence with formal charges, in particular, is often quite tenuous. Nonetheless, the sign of these values is typically reliable, and the directions of any changes may be good indicators of trends.

III. Results

In line with previous studies of ozone,^1,11 molecular fluorine,² and oxygen difluoride,³ a significant fraction of our computed trajectories (10 out of 44) failed to result in adsorption on the monohydrogenated Si{001} surface; the molecule simply rebounded from the surface without undergoing any significant reorientation or lateral motion. Moreover, amongst those trajectories in which some form of adsorption did occur, several (13 out of 34) are best categorised under the heading of physisorption, with the molecule rotating and/or translating across the surface but showing no sign of an imminent chemical reaction.

Nevertheless, almost half of all trajectories (21 out of 44) resulted in at least partially dissociative chemisorption. Most of these (18 out of 21) were prompt events, in which reaction occurred during the molecule's initial approach to the surface, while a few (3 out of 21) were delayed, in the sense that the molecule reacted only after considerable deformation, rotation and/or translation subsequent to its initial approach. Importantly, all of our reactive trajectories must have activation barriers no greater than the 0.0245 eV kinetic energy supplied to the incoming molecule from the start, implying that corresponding transition states either do not exist or are poorly defined and of little consequence. We do not rule out the possibility that alternative adsorption pathways may be followed by more energetic incoming molecules, involving activation barriers inaccessible to our present calculations, but such events will be exponentially less likely to occur than the trajectories described below.

In analysing our results, we shall introduce a high-level categorisation of mechanism based upon the nature and/or locality of the molecule's first interaction with the surface. That is, we shall identify six basic types (see Table 2) in which the initial stage may best be described as: (i) hydrogen abstraction; (ii) attack on a dimer bond; (iii) attack on a dimer atom; (iv) attack on a second-layer atom; (v) attack on a third-layer atom; and (vi) post-dissociation axial attack. Within each separate type, we shall see below that there is a degree of uniformity, but it will nevertheless be seen that several sub-types may be identified according to the intermediate and final states of the surface. Our aim, however, will be to highlight similarities rather than differences, and trends rather than peculiarities. For this reason, we shall omit detailed descriptions of some trajectories where these might otherwise be repetitive.

Table 2 Classification of the trajectories calculated in the present work. Column headings refer to the adsorption sites at which the molecule is initially aimed (cf. Fig. 2) while row headings define its orientation (cf. Table 1). Roman numerals then indicate the type of reaction observed (see the typology described in the main text) with parentheses indicating those cases that were not prompt. Instances marked “P” were those in which the molecule became physisorbed, while those marked “N” were trajectories in which no sticking was observed at all

	A	B	C	D	E
αβ	N	IV	N	VI	P
βα	(II)	P	V	V	N
αγ	N	(II)	N	P	P
α[small gamma, Greek, macron]	N	II	P	IV	I
βγ	N	N	N	P	P
β[small gamma, Greek, macron]	N	III	V	IV	I
γα	II	II	V	IV	P
γβ	P	III	I	IV	P
α[small beta, Greek, macron]	—	—	—	—	P
β[small alpha, Greek, macron]	—	—	—	—	P
γ[small alpha, Greek, macron]	—	—	—	—	(IV)
γ[small beta, Greek, macron]	—	—	—	—	P

---

A. Type I: hydrogen abstraction

Snapshots of the three Type I trajectories (those involving hydrogen abstraction) are shown together in Fig. 3 for ease of comparison. We shall begin our detailed examination with arguably the simplest of these scenarios, in which the molecule starts with its equatorial fluorine atom pointing down toward a location just to one side of an adsorbed hydrogen atom.

Fig. 3 Snapshots of the three Type I trajectories (E/β[small gamma, Greek, macron], E/α[small gamma, Greek, macron], and C/γβ). Beige and white spheres represent silicon and hydrogen atoms, while dark- and light-green spheres represent chlorine and fluorine atoms.

1. E/β[small gamma, Greek, macron] Trajectory. For almost the first 700 fs of this simulation, the molecule does little other than drift toward the surface at fairly constant velocity, as exemplified by the gradually declining Si–F distance involving the equatorial fluorine atom and the silicon atom to which it will eventually bond (Fig. 4, first panel, red trace). The soon-to-be abstracted hydrogen atom shows a similarly uniform decline in its distances from the equatorial fluorine atom and from the chlorine atom (second panel, green and blue traces).

Fig. 4 Evolution of the E/β[small gamma, Greek, macron] trajectory. The three upper panels show interatomic separations, coded as follows: bond-making is depicted with red or blue traces; bond-breaking is depicted with cyan or orange traces; and separations having equivocal character with respect to these criteria are depicted with green or grey traces. The lower panel shows the integrated net spin in magenta and the integrated spin modulus in black.

Nevertheless, just before the 700 fs mark this hydrogen atom moves decisively toward the equatorial fluorine atom (second panel, green trace) and away from the silicon atom to which it had hitherto been attached (third panel, orange trace). At the same time, the distance between the equatorial fluorine atom and the chlorine atom abruptly increases (first panel, cyan trace) indicating incipient formation of a transient HF molecule. The integrated spin modulus (fourth panel, black trace) increases to around 1 μ_B although the integrated net spin (fourth panel, magenta trace) remains close to zero. This is most consistent with partial radical character on the vacated silicon site and on the nascent ClF₂ moiety (implied by detachment of the equatorial fluorine atom). According to a Mulliken analysis, these bear magnetic moments of −0.22 μ_B and +0.37 μ_B respectively, at the 725 fs mark, with minor spin components on some neighbouring atoms; the ClF₂ moiety also has partial anionic character at this point in time, with a net charge of −0.44|e| being balanced by a charge of +0.40|e| acquired by the abstracted hydrogen atom.

This state of affairs is exceedingly short-lived, however, as the abstracted hydrogen atom rapidly rotates around the previously equatorial fluorine atom, bonding to the chlorine atom by the 760 fs mark (second panel, blue trace) and leaving its erstwhile partner to form a Si–F bond (first panel, red trace) no later than the 800 fs mark. Both spin measures drop back to zero at this time, indicating that all moieties are now of the closed shell variety. On the surface itself, this simply means that an original Si–H bond has been replaced by a Si–F bond, oscillating at a frequency of 755 cm⁻¹ around a mean length of 1.63 Å. These parameters are not drastically different from those observed previously for Si–F bonds formed upon dissociative adsorption of F₂ or OF₂ on this surface,^2,3 and in any case some natural variation is expected as a result of differing local environments.

In the space above the surface, on the other hand, we have replaced ClF₃ with HClF₂. This latter species is highly rotationally excited from the moment of its creation, with the hydrogen atom rapidly circulating (in an inconsistent sense) around the equator of its F–Cl–F axis. For a few hundred femtoseconds, the HClF₂ molecule remains in the vicinity of the surface, its hydrogen atom occasionally approaching quite close to the fluorine adatom (second panel, green trace) but from the 1500 fs mark onward it irrevocably desorbs. After desorption, the H–Cl bond (second panel, blue trace) oscillates at a frequency of 2710 cm⁻¹ around a mean length of 1.30 Å, while the two remaining Cl–F bonds (first panel, two overlapping green traces) each oscillate at 450 cm⁻¹ around a mean length of 1.80 Å.

Quasistatic optimisation of the geometry achieved in the final step of the dynamic trajectory yields an effective adsorption heat of 3.53 eV after compensating for the gas-phase energy of desorbed HClF₂. Considering that the original surface was passivated, this represents a rather substantial liberation of potential energy and underlines the highly oxidising nature of chlorine trifluoride.

2. E/α[small gamma, Greek, macron] Trajectory. This simulation begins similarly to the last, with the equatorial fluorine atom pointing down toward precisely the same location on the surface – a little to one side of an adsorbed hydrogen atom. Indeed, the starting geometries differ only in that the molecule is rotated by 90° about a surface-normal axis. It is not unexpected, therefore, that the initial phase of the trajectory proceeds much as before, with the Si–F distance between the equatorial fluorine atom and its eventual bonding partner (Fig. 5, first panel, red trace) declining with little evidence of acceleration for roughly the first 700 fs of the simulation. The distances from the crucial hydrogen atom to the equatorial fluorine atom and to the chlorine atom (second panel, green and blue traces) do likewise.

Fig. 5 Evolution of the E/α[small gamma, Greek, macron] trajectory. The three upper panels show interatomic separations (colours as per Fig. 4) while the lower panel shows integrated net spin in magenta and integrated spin modulus in black.

Once again, the first sign of a reaction occurs just before the 700 fs mark when this hydrogen atom lurches toward the equatorial fluorine atom (second panel, green trace) and away from its silicon bonding partner (third panel, orange trace). The bond between the chlorine atom and the equatorial fluorine atom is also broken at this time (first panel, cyan trace) and for the very brief period when a transient HF moiety exists, the two spin measures (fourth panel, black and magenta traces) suggest partial radical character on the temporarily vacant silicon site and on a very short-lived ClF₂ species. Within 60 fs, however, the abstracted hydrogen atom flips around and bonds to the chlorine atom (second panel, blue trace) while the previously equatorial fluorine atom bonds to the silicon atom that has just been vacated (first panel, red trace). The latter bond eventually settles down to oscillate at a frequency of 730 cm⁻¹ about a mean length of 1.65 Å, consistent with a slightly higher degree of vibrational excitation than in the previously discussed trajectory.

In the space above the surface, the newly created HClF₂ molecule exists for about 150 fs from roughly the 750 fs mark, during which time the H–Cl bond oscillates at a frequency of 2585 cm⁻¹ around a mean length of about 1.34 Å, suggesting that it may be a little more vibrationally excited than in the previous trajectory. It is probably not a coincidence, therefore, that the lifetime of this species is too short to extract a reliable estimate for the stretch frequencies and mean lengths of the remaining Cl–F bonds. At the 925 fs mark the abstracted hydrogen atom transfers back to the fluorine adatom (second panel, green trace) before leaping onto the nearest axial fluorine atom (second panel, blue trace) just 10 fs later. At this point, the bond between this axial fluorine atom and the chlorine atom essentially breaks (first panel, grey trace) and the newly formed HF moiety persists for the remainder of the simulation, apart from another period between the 1060 fs and 1080 fs marks when the hydrogen atom dallies briefly with the fluorine adatom once again (second panel, blue and green traces). Although it subsequently acquires considerable lateral velocity across the surface, the HF moiety does not show much sign of decisively desorbing, however, so we cannot rule out the possibility of a secondary chemisorption event were the simulation to be continued indefinitely. As for the rump of the original molecule, chlorine monofluoride (ClF) ends the simulation travelling more directly away from the surface but comparatively sluggishly.

Compensating for the gas-phase energies of both apparently desorbing species, geometry optimisation of the surface starting from its final dynamic state yields an effective adsorption heat of 4.38 eV – a little higher than for the E/β[small gamma, Greek, macron] trajectory described above. Since the relaxed surface structures are actually very similar in both instances, the difference is primarily attributable to the greater stability of the desorbing species involved in the present case.

3. C/γβ Trajectory. In contrast to the two previous trajectories, this simulation begins with the molecular plane lying parallel to the surface. Nevertheless, the initial phase is superficially familiar, with the distance between the equatorial fluorine atom and the silicon atom to which it will eventually bond (Fig. 6, first panel, red trace) showing no great evidence of acceleration over at least the first 700 fs. That this is a little misleading becomes evident, however, when one concentrates upon the hydrogen atom that is to be abstracted from the surface; its distance from the equatorial fluorine atom (second panel, green trace) drops considerably faster than does its distance from the chlorine atom (second panel, blue trace) in stark contrast to the previous two cases we have examined. In actual fact, the molecule as a whole is gradually tilting during its initial approach, bringing its equatorial fluorine atom into close proximity to its nearest hydrogen atom and facilitating the creation of a transient HF moiety at the 800 fs mark. As before, formation of the H–F bond (second panel, green trace) is accompanied by a marked increase in the distances between the equatorial fluorine atom and the chlorine atom (first panel, cyan trace) and between the abstracted hydrogen atom and its silicon bonding partner (third panel, orange trace). Once again, the two spin measures suggest that the vacant silicon site and the newly created ClF₂ moiety each very briefly possess partial radical character at this moment (fourth panel, black and magenta traces).

Fig. 6 Evolution of the C/γβ trajectory. The three upper panels show interatomic separations (colours as per Fig. 4) while the lower panel shows integrated net spin in magenta and integrated spin modulus in black.

In similar fashion to the previous trajectories, however, the scenario we have just articulated is not at all stable, with the abstracted hydrogen atom being rapidly transferred to the chlorine atom (second panel, green and blue traces) leading to complete spin compensation and the formation of an HClF₂ molecule along with a Si–F bond (first panel, red trace). The latter oscillates at a frequency of 680 cm⁻¹ about a mean length of around 1.70 Å, indicating a yet more vibrationally excited bond than in either of the previous two cases. Nevertheless, the nature of the chemisorbed product is broadly consistent across all three of the Type I trajectories.

The fate of the HClF₂ molecule, on the other hand, is rather different, neither desorbing (as in the E/β[small gamma, Greek, macron] trajectory) nor dissociating (as in the E/α[small gamma, Greek, macron] trajectory). Instead, we find that this molecule remains tethered to the surface by way of a directional interaction between its hydrogen atom and one of the other hydrogen adatoms. Specifically, these two atoms point directly at one another, while maintaining a separation in the range 1.38–1.78 Å (third panel, blue trace). This is clearly far too distant to interpret as any kind of covalent bond, but an attractive interaction clearly exists. The rotational motion of the molecule's hydrogen atom about the F–Cl–F axis is strongly suppressed, as too is the vibrational energy associated with the H–Cl bond (second panel, blue trace) which oscillates at a considerably lower frequency (2285 cm⁻¹) than in either previous case, about a mean length of 1.34 Å. For all the world, it appears as if the ClF₂ moiety of the HClF₂ molecule acts as a hydrogen-bond donor, while the corresponding acceptor is not a traditional electronegative atom but another hydrogen atom. This surprising observation may nevertheless be rationalised, however, on the basis (i) that hydrogen adatoms on a silicon surface carry a partial negative charge, and (ii) that the combination of an electronegative chlorine atom with two even more electronegative fluorine atoms ought naturally to engender in the molecule's hydrogen atom a particularly strong partial positive charge. For instance, Mulliken analysis at the 2000 fs mark indicates charges of +0.31|e| on the chlorine-bound hydrogen atom and −0.15|e| on the nearest adsorbed hydrogen atom (to be compared with a mean charge of −0.05|e| found on the other adsorbed hydrogen atoms). Precedent may be found for similar “dihydrogen bonding” within the inorganic literature,^40,41 but it is undoubtedly a relatively unusual phenomenon. At any rate, geometry optimisation following the dynamic simulation yields an effective adsorption heat of 3.71 eV on the assumption that HClF₂ remains bound to the surface, exceeding by 0.18 eV the value we obtain by deleting the molecule at the surface and accounting for it in the gas phase. The equilibrium H–H separation in the dihydrogen bond is 1.51 Å – around twice the covalent bond length found in molecular dihydrogen but only around two thirds of the expected contact distance between a pair of non-bonded hydrogen atoms.⁴²

B. Type II: attack on a dimer bond

In total, we find five Type II trajectories (those involving an initial attack on a dimer bond) of which three are prompt while two (A/βα and B/αγ) are delayed and react only upon their second attempt. Amongst the three prompt examples, two of them (A/γα and B/γα) begin with the molecular plane parallel to the surface, while the third (B/α[small gamma, Greek, macron]) starts with the equatorial fluorine atom pointing down toward the midpoint between two nearest-neighbour dimers. In all three prompt cases, however, the molecule is steered into a geometry in which the equatorial fluorine atom approaches the centre of a dimer bond, and after this they all proceed in very similar fashion to one another. We shall therefore describe in detail only the third of these trajectories, shown as a series of snapshots in the upper panel of Fig. 7.

Fig. 7 Snapshots of the Type II (B/α[small gamma, Greek, macron]) and Type III (B/β[small gamma, Greek, macron], and B/γβ) trajectories. Colour scheme as in Fig. 3.

1. B/α[small gamma, Greek, macron] Trajectory. During the first 700 fs of this simulation, the molecule drifts toward the surface with only slight acceleration. In Fig. 8, we plot the distances between the equatorial fluorine atom and each of the two silicon atoms forming the dimer to which it is first attracted (second panel, red and green traces, initially overlapping). Throughout this opening phase, the three Cl–F bonds retain the same length as for the isolated molecule, but by the 800 fs mark the distance between the chlorine atom and the equatorial fluorine atom abruptly increases (first panel, cyan trace) while the above-mentioned Si–F distances start more rapidly to decline. The distance between the two dimer atoms (second panel, orange curve) then starts to increase, and by the 1000 fs mark one might reasonably conclude that the original Si–Si bond has been replaced by a Si–F–Si bridge. The two spin measures (third panel, black and magenta traces) are both zero at this point, having initially risen to around 1 μ_B during the 700–800 fs period. This implies that the residual ClF₂ moiety must not have radical character (in contrast to the three trajectories discussed in the previous section) and instead exists in anionic form; our Mulliken analysis indicates a net charge of −0.83|e| on the molecular species at this time. This then permits the Si–F–Si bridge to be cationic (we compute a net charge of +0.69|e| for its three constituent atoms) consistent with three-centre two-electron bonding.

Fig. 8 Evolution of the B/α[small gamma, Greek, macron] trajectory. The three upper panels show interatomic separations (colours as per Fig. 4) while the lower panel shows integrated net spin in magenta and integrated spin modulus in black.

In view of this ionic interpretation, it is perhaps unsurprising that ClF₂ fails to escape the surface, instead remaining nearby for around 500 fs after its creation. During this time, the two remaining Cl–F bonds (first panel, green and orange traces) increase in length to around 1.86 Å (cf. 1.73 Å in gas-phase ClF₃). Just before the 1400 fs mark, however, the molecule re-orients to bring one of the axial fluorine atoms close to one of the dimer atoms of the Si–F–Si bridge. Shortly thereafter, the bridge itself breaks apart, with the initially equatorial fluorine atom binding now to just one of the dimer atoms (second panel, red and green traces) while the initially axial fluorine atom binds to the other (second panel, blue trace). The dimer remains broken (second panel, orange trace) and at each end the dangling bonds on the silicon atoms are saturated by a hydrogen atom and a fluorine atom. The two Si–F bonds (second panel, red and blue traces) each vibrate at a frequency of around 785 cm⁻¹ about mean bond lengths of 1.63 Å. All of this leaves a closed-shell ClF molecule, which rapidly desorbs from the surface whilst undergoing oscillations in its Cl–F bond (first panel, green trace) at a frequency of 710 cm⁻¹ about a mean length of 1.65 Å. Compensating for the gas-phase energy of this species, optimisation of the remaining surface structure yields a particularly high adsorption heat of 5.49 eV, reflecting the rather stable bonding arrangement established upon arrival of the second fluorine adatom.

C. Type III: attack on a dimer atom

In the preceding section, we discussed five trajectories (describing one in detail) in which the equatorial fluorine atom of the incoming molecule attacked the centre of a silicon dimer bond. In each case, a symmetric Si–F–Si bridge was formed and it was only later, when the transient ClF₂ attacked one end of the bridge, that this even-handed situation was disrupted. In contrast, we present in this section two trajectories (B/β[small gamma, Greek, macron] and B/γβ) where the initial attack involves just a single dimer atom; both are prompt, with reaction occurring during the initial approach of the molecule to the surface. Snapshots of these are shown in the second and third panels of Fig. 7.

1. B/β[small gamma, Greek, macron] Trajectory. The first of our Type III trajectories starts with the incoming molecule rotated by 90° about the surface normal, relative to its orientation in the Type II trajectory discussed in detail above. This seemingly minor variation nevertheless has significant consequences, first evident in the approach of the equatorial fluorine atom to the silicon atoms of the dimer with which it first interacts. Although one of the two relevant Si–F distances (Fig. 9, second panel, blue trace) shortens to 1.75 Å during the first 800 fs, the other (second panel, red trace) does not fall below 2.10 Å in the same period. That is to say, the initial approach of the equatorial fluorine atom to the dimer is inherently asymmetric, leading to the formation of a clear bond with one silicon atom and not the other. The distance between the equatorial fluorine atom and the chlorine atom rises at around the same time (first panel, cyan trace) while the Si–Si bond of the dimer breaks slightly more slowly but just as surely (second panel, orange trace). The two spin measures vary in quite complicated fashion (third panel, black and magenta traces) but are consistent with some degree of radical character during this phase. There are, it should be noted, two possible radical centres at this stage – a dangling bond (left on one of the top-layer silicon atoms after cleavage of the dimer bond) and the newly created ClF₂ moiety that remains in much the same vicinity.

Fig. 9 Evolution of the B/β[small gamma, Greek, macron] trajectory. The three upper panels show interatomic separations (colours as per Fig. 4) while the lower panel shows integrated net spin in magenta and integrated spin modulus in black.

Just after the 1000 fs mark, however, something unexpected occurs – the originally equatorial fluorine atom moves toward the silicon dangling bond and forms a Si–F–Si bridge, essentially the same as was formed transiently in the five Type II trajectories (counting prompt and delayed alike). Here, in contrast, it will persist for the remaining duration of the simulation. The two Si–F bonds comprising the bridge (second panel, red and blue traces) share broadly similar mean bond lengths of around 1.85 Å, but both vibrate quite inconsistently so it is difficult to determine their frequencies. Nevertheless, this demonstrates that the bridged arrangement can be quite stable given the right circumstances. Since the two spin measures (fourth panel, black and magenta traces) fall to zero at around this time, it seems likely that these circumstances include transfer of an electron from the bridge to the nearby ClF₂ moiety, so that the bridge can adopt a stable three-centre two-electron bonding arrangement.

In contrast, at some point shortly after the 1100 fs mark, the ClF₂ moiety partially dissociates into a closed-shell ClF molecule and a temporarily isolated fluorine atom, the latter seemingly anionic in character since the system spin remains zero. Having departed from the chlorine atom (first panel, orange trace) this fluorine atom rapidly attaches itself to one of the silicon atoms from a second top-layer dimer (third panel, red trace). This activates the hydrogen atom attached to this silicon atom, which then forms a bond with the chlorine atom. For a brief period from about 1380 fs to about 1500 fs, this hydrogen atom appears to be involved with both a Si–H bond (third panel, cyan trace) and a H–Cl bond (third panel, blue trace). This unstable situation is then resolved, by the 1600 fs mark, through cleavage of the remaining Cl–F bond (first panel, green trace) and of the uncomfortable Si–H bond (third panel, cyan trace). In the end, a Si–H bond on the second dimer has simply been replaced by a Si–F bond, with little influence on the Si–Si dimer bond (third panel, grey trace) alongside the creation of a closed-shell hydrogen chloride (HCl) molecule and a free-floating fluorine atom. Both spin measures (fourth panel, black and magenta traces) return to values around 1 μ_B at this time, presumably associated with the latter species. We find the speed of the departing fluorine radical to be 340 m s⁻¹ (kinetic energy 0.0115 eV) at the end of the simulation, with its motion directed at an angle of 71° from the outward surface normal. It is uncertain whether this species would escape from the surface if the simulation were continued, especially in light of neglected dispersion forces, but it is notable that such an eventuality may even be considered plausible.

If we assume that fluorine does, indeed, depart in radical form, geometry optimisation of the remaining neutral surface results in cleavage of the Si–F–Si bridge to leave one of the top-layer silicon atoms possessed of a dangling bond. The magnetic moment localised at this site amounts to 0.88 μ_B out of a total of 1.00 μ_B for the entire slab. Despite expectations that such a state of affairs ought to be relatively unstable, however, the effective adsorption heat associated with ejection of radical fluorine and creation of this dangling bond is 3.44 eV – not out of line with values found for the other trajectories discussed in the present work. We anticipate that the Si–F–Si bridge could be stabilised if the surface were to carry a net positive charge (with fluorine departing in anionic form) but defer analysis of this possibility to a forthcoming publication in which we shall reconcile relative stability for a variety of different charge and spin states.

2. B/γβ Trajectory. The second Type III trajectory commences with the molecular plane parallel to the surface, but as in similar situations described above the molecule soon tilts to bring the equatorial fluorine atom closer to the surface than the chlorine and axial fluorine atoms. For the first 700 fs, however, very little else of note occurs. The first inkling of impending action may be gleaned only when the bond between the chlorine atom and the equatorial fluorine atom starts significantly to stretch (Fig. 10, first panel, orange trace) at around the 800 fs mark. For a short while thereafter, this fluorine atom exists in isolation and the rise of both spin measures (fourth panel, black and magenta traces) to around 1 μ_B suggests that some radical character has emerged (for indicative purposes, our Mulliken analysis gives magnetic moments on the chlorine and equatorial fluorine atoms of +0.39 μ_B and +0.28 μ_B respectively at the 800 fs mark).

Fig. 10 Evolution of the B/γβ trajectory. The three upper panels show interatomic separations (colours as per Fig. 4) while the lower panel shows integrated net spin in magenta and integrated spin modulus in black.

Initially equidistant from two silicon atoms on neighbouring dimers, asymmetry quickly arises and the isolated fluorine atom attaches decisively to a single silicon atom by around the 900 fs mark (first panel, blue trace). Over the following 150 fs, the hydrogen atom with which it competes is displaced to create a Si–H–Si bridge between the first-layer silicon atom and one of its second-layer neighbours. The corresponding Si–Si bond is broken (second panel, orange trace) while the existing Si–H bond stretches very slightly (second panel, green trace) and a second Si–H bond forms (second panel, blue trace). This structural motif has been observed previously in our study of OF₂ adsorption on the same surface,³ where it was argued that three-centre two-electron bonding must be invoked. This would require the surface defect to become cationic and the nearby ClF₂ moiety anionic, consistent with the marked drop in both spin measures observed at this moment (fourth panel, black and magenta traces). Mulliken analysis at the 1200 fs mark indicates that the three atoms of the Si–H–Si bridge possess a net charge of +0.93|e| while the net charge of the ClF₂ moiety is −0.75|e| at the same time. Over the period from 950 fs to 1350 fs, the two remaining Cl–F bonds (first panel, overlapping green and cyan traces) vibrate in phase with one another at a common frequency of 405 cm⁻¹ about mean lengths of around 1.84 Å. After an initial 400 fs of somewhat erratic vibration, the two Si–H bonds of the Si–H–Si bridge (second panel, green and blue traces) settle down, for the remainder of the simulation, to vibrate in anti-phase with one another at a common frequency of 1650 cm⁻¹ about mean lengths of around 1.60 Å. Meanwhile, the Si–F bond (first panel, blue trace) oscillates at 820 cm⁻¹ about a mean length of 1.59 Å.

Since the surface now carries a net positive charge and the ClF₂ moiety a net negative one, it is unsurprising that the latter does not readily desorb from the former. Instead, it hovers a short distance from the surface until, at around the 1400 fs mark, it starts to rotate such that one of the axial fluorine atoms is brought into proximity with a hydrogen adatom. Over the course of next 100 fs, a new H–F bond is formed (third panel, red trace) and existing Si–H (third panel, cyan trace) and Cl–F (first panel, cyan trace) bonds are broken. Any residual spin in the system is fully quenched at this point (fourth panel, black and magenta traces). Since the HF and ClF molecules thus formed are both closed-shell neutrals, we surmise that the negative charge balancing the cationic nature of the Si–H–Si bridge (net charge of +0.91|e| at the 1500 fs mark) must now largely reside upon the newly created silicon dangling bond. The net charge on the undercoordinated silicon atom is found to be −0.21|e| at this time, which may be compared with the charge of +0.11|e| that it will have borne on the unperturbed monohydrogenated surface.

Indeed, whilst the ClF molecule slowly desorbs from the surface, the HF molecule remains in close proximity to the dangling bond and with its hydrogen atom consistently pointing in that direction until at least the 4000 fs mark. In effect, the F moiety of the HF molecule acts as a hydrogen-bond donor, while the silicon atom with the dangling bond acts as the corresponding acceptor, so that the Si–H distance (third panel, cyan trace) varies only within the 1.75–2.45 Å range – too far for a covalent interaction, but consistent with a fluctuating hydrogen bond. Post-dynamics geometry optimisation indicates an adsorption heat of 2.63 eV with HF bound to the surface (having a Si–H distance of 2.18 Å) compared with just 2.25 eV if both species are assumed to desorb.

D. Type IV: attack on a second-layer atom

In all, we found six trajectories in which the molecule attacked a second-layer silicon atom (five being prompt, the other delayed) but we shall describe only three of these in detail. The trajectory labelled D/α[small gamma, Greek, macron] is essentially rather similar to that labelled D/γα (except that there is interference between neighbouring cells in the later stages of the simulation) and so can be omitted. Similarly, the trajectory labelled D/β[small gamma, Greek, macron] will be omitted in favour of the rather similar D/γβ trajectory. In contrast, the E/γ[small alpha, Greek, macron] and B/αβ trajectories are each unique. All four described trajectories may be viewed in snapshot form in Fig. 11.

Fig. 11 Snapshots of the Type IV (D/γα, D/γβ, E/γ[small alpha, Greek, macron], and B/αβ) trajectories. Colour scheme as in Fig. 3. Note the uneven distribution of timestamps.

1. D/γα Trajectory. This trajectory begins with the molecule positioned between dimer rows and oriented with its plane parallel to the surface. As it approaches, however, the molecule tilts so that its equatorial fluorine atom points downwards into the trench. By around the 850 fs mark, the corresponding Cl–F bond breaks (Fig. 12, first panel, cyan trace) and the now-isolated fluorine atom continues to descend. At first, it is not clear to which of three nearby silicon atoms this fluorine atom will eventually bond, but after roughly 200 fs it is decisively captured by one from the second layer. The bond thus formed (first panel, red trace) oscillates at 730 cm⁻¹ about a mean length of 1.64 Å, while the bond between the involved silicon atom and one of its third-layer partners is broken (first panel, orange trace) leaving a dangling bond on the latter atom.

Fig. 12 Evolution of the D/γα trajectory. The three upper panels show interatomic separations (colours as per Fig. 4) while the lower panel shows integrated net spin in magenta and integrated spin modulus in black.

As for the rump of the original molecule, the remaining Cl–F bonds each oscillate at around 440 cm⁻¹ about mean bond lengths of 1.82 Å. By the 1750 fs mark, the integrated net spin of the system (second panel, magenta trace) lies close to 1 μ_B, while the integrated spin modulus (second panel, black trace) is a little higher. According to our Mulliken analysis, the under-coordinated third-layer silicon atom is associated with a magnetic moment of 0.41 μ_B at this time, while the ClF₂ moiety carries a moment of 0.53 μ_B. We expect that these must both ultimately resolve to integer values, as occurred in the latter stages of the B/β[small gamma, Greek, macron] trajectory discussed above, but we terminated the simulation before this happened as the desorbing species was approaching the back surface of the slab image from the next supercell.

Notably, optimisation of the surface geometry after deletion of desorbed ClF₂ led to an effective adsorption heat of just 1.11 eV, which is less than half of the next-smallest value calculated in the present work. This presumably reflects the inherent instability of the third-layer dangling bond, associated with a magnetic moment of 0.61 μ_B out of a total of 0.99 μ_B in the relaxed geometry.

2. D/γβ Trajectory. This trajectory starts in similar fashion to the previously described case, with the molecule simply rotated by 90° about the surface normal. Once again, it tilts as it descends, so that the equatorial fluorine atom points downwards. The corresponding Cl–F bond (Fig. 13, first panel, cyan trace) breaks at around the 850 fs mark, with the magnetic moments of the separating atoms being +0.39 μ_B and +0.29 μ_B respectively at this instant. A bond between the equatorial fluorine atom and one of the second-layer silicon atoms (second panel, green trace) is formed almost immediately thereafter, and one of the bonds between that silicon atom and a third-layer neighbour (second panel, orange trace) is broken at about the same time. This results in a third-layer dangling bond, with radical character evidenced by both spin measures approaching 1 μ_B. By the 1100 fs mark, however, the adsorbed fluorine atom moves into a position that bridges between the second- and third-layer silicon atoms (second panel, green and blue traces). Such a Si–F–Si bridge was noted above in relation to the B/β[small gamma, Greek, macron] trajectory, where it was inferred to involve three-centre two-electron bonding. This implies donation of an electron to the nascent ClF₂ moiety, which must therefore be regarded as anionic rather than radical. Accordingly, both spin measures drop to zero at this time and for the remainder of the simulation (fourth panel, magenta and black traces). Mulliken analysis confirms that the three atoms of the Si–F–Si bridge possess a net charge of +0.40|e| at the 1250 fs mark, while the ClF₂ moiety carries a charge of −0.82|e| at the same time.

Fig. 13 Evolution of the D/γβ trajectory. The three upper panels show interatomic separations (colours as per Fig. 4) while the lower panel shows integrated net spin in magenta and integrated spin modulus in black.

Since the Si–F–Si bridge and the ClF₂ anion bear opposing charges, it is unsurprising that they remain in close proximity for some time. At the 1750 fs mark, however, one of the axial fluorine atoms closely approaches one of the two top-layer silicon atoms that are nearest to the Si–F–Si bridge, resulting in formation of a Si–F bond (third panel, blue trace) and cleavage of a Cl–F bond (first panel, orange trace). This instigates a cascade of changes to the surface bonding arrangement, completed within the following 100 fs. First, the dimer bond associated with the affected top-layer silicon atom breaks (third panel, cyan trace). Then, the second-layer silicon atom from the Si–F–Si bridge forms a bond to the far atom of the now-broken dimer (third panel, red trace). And finally, the Si–F–Si bridge disintegrates, with its fluorine atom now decisively attaching to the third-layer silicon atom and breaking from the second-layer silicon atom; the remaining Si–F bond (second panel, blue trace) then oscillates at a frequency of 715 cm⁻¹ about a mean length of 1.63 Å, while the Si–F distance corresponding to the broken bond (second panel, green trace) never again falls below 2.20 Å. The Si–F bond whose formation gave rise to all these changes (third panel, blue trace) oscillates at a frequency of 740 cm⁻¹ about a mean length of 1.62 Å.

The upshot of this remarkably complex rearrangement is that the surface attains a structure with no dangling bonds, and hence no radical character. The desorbing ClF molecule is likewise a closed-shell species. Relaxation of the final dynamic geometry confirms the stability of the complex surface structure, yielding an effective adsorption heat of 3.98 eV after compensation for the desorbed molecule.

3. E/γ[small alpha, Greek, macron] Trajectory. This trajectory represents the only delayed reaction that we shall describe in detail. In common with several of the cases discussed above, the molecule starts with its plane parallel to the surface and progressively tilts as it descends. At around the 800 fs mark, however, the molecule rebounds so that its centre-of-mass moves slightly away from the surface even as its tilt continues to increase. Only after the 1400 fs mark does the molecule start to descend once more, heading decisively into the trough between two rows of dimers in a substantially tilted orientation. Cleavage of the bond involving the equatorial fluorine atom occurs at around the 2250 fs mark (Fig. 14, first panel, cyan trace) and the same atom forms a bond with a second-layer silicon atom roughly 100 fs later (second panel, red trace). After a further 200 fs, a Si–F–Si bridge is created when this fluorine atom bonds to a neighbouring third-layer atom (second panel, blue trace) and the corresponding Si–Si bond is broken (second panel, orange trace). Both spin measures, which had risen to around 1 μ_B during the above rearrangement, fall back to zero at this time and remain so for the duration of the simulation (fourth panel, magenta and black traces).

Fig. 14 Evolution of the E/γ[small alpha, Greek, macron] trajectory. The three upper panels show interatomic separations (colours as per Fig. 4) while the lower panel shows integrated net spin in magenta and integrated spin modulus in black.

As per the immediately preceding trajectory (D/γβ) we infer that the Si–F–Si bridge is stabilised in cationic form by three-centre two-electron bonding, and that the rump of the molecule must therefore be anionic. Mulliken analysis indeed indicates a net charge of +0.44|e| shared amongst the three bridge atoms at the 2550 fs mark, while the ClF₂ moiety bears a charge of −0.92|e| at the same time. In line with the previous case, however, the latter species is unstable and rapidly transfers one of its fluorine atoms to a top-layer silicon atom by around the 2700 fs mark (third panel, red trace). This not only involves loss of a Cl–F bond (first panel, orange trace) but also instigates cleavage of a bond between the top-layer silicon atom and one of its second-layer neighbours (third panel, cyan trace). Anionic character is then associated with the consequent dangling bond at that second-layer silicon atom, and the Si–F–Si bridge remains intact and cationic. The surface thus achieves an electronic structure without radical character, as does the departing neutral ClF molecule. After compensation for the latter, geometry optimisation of the former yields an effective adsorption heat of 3.21 eV, relative to the original monohydrogenated surface and gas-phase chlorine trifluoride.

4. B/αβ Trajectory. In contrast to all of the cases described in detail above, this trajectory starts with the molecule's F–Cl–F axis oriented parallel to the surface normal. Remarkably little deformation or reorientation of the molecule takes places during the initial 1000 fs of the simulation, but there is subsequently a significant rotation that causes the equatorial fluorine atom to point downwards into the trench between two dimer rows. At the same time, the corresponding Cl–F bond (Fig. 15, first panel, orange trace) becomes substantially stretched, if not decisively broken. At the 1250 fs mark, for example, with the bond stretched by 34% from its gas-phase value, the chlorine atom exhibits a magnetic moment of +0.46 μ_B and the equatorial fluorine atom one of +0.47 μ_B, suggesting that separation into a pair of radicals is not yet complete.

Fig. 15 Evolution of the B/αβ trajectory. The three upper panels show interatomic separations (colours as per Fig. 4) while the lower panel shows integrated net spin in magenta and integrated spin modulus in black.

Nevertheless, by the 1650 fs mark, the equatorial fluorine atom attaches to a second-layer silicon atom (first panel, grey trace) and very shortly thereafter the bond connecting that silicon atom to one of its neighbouring third-layer atoms is broken (first panel, cyan trace) Within a further 150 fs, however, one of the axial fluorine atoms also breaks from the chlorine atom (second panel, cyan trace) and bonds with the same second-layer silicon atom (second panel, red trace) forcing the first fluorine atom to bond instead with the third-layer silicon atom (first panel, blue trace). In this new location, it oscillates at a frequency of 700 cm⁻¹ with a mean Si–F bond length of 1.63 Å. Having risen as high as 1 μ_B during this process, both spin measures drop to zero at this point (fourth panel, magenta and black traces) reflecting the fact that the surface now features no dangling bonds and the rump ClF molecule has a closed-shell electronic structure.

Shortly after the 2000 fs mark, however, the picture changes drastically. First, the ClF molecule dissociates (third panel, cyan trace) depositing its chlorine atom onto the same second-layer silicon atom that already hosts a previously axial fluorine atom (second panel, blue trace). This then causes the only remaining Si–Si bond between that second-layer atom and a third-layer atom to break (second panel, orange trace) and implies that a dangling bond must be localised upon the latter. Tethered only by its bonds with two top-layer atoms, the second-layer atom then rises upward to become the highest-lying silicon atom by the 2200 fs mark – a distinction it maintains for the remainder of the simulation – and it is tempting to believe that it may potentially be susceptible to desorption if subsequently attacked by a second incoming molecule. This atom is party to a Si–F bond (second panel, red trace) that oscillates at a frequency of 800 cm⁻¹ about a mean length of 1.62 Å, and to a Si–Cl bond (second panel, blue trace) for which the equivalent parameters are 485 cm⁻¹ and 2.07 Å.

The final non-adsorbed species at this point is a single fluorine atom but at around the 2400 fs mark this too is captured, forming a Si–F bond (third panel, red trace) with a top-layer atom from a dimer somewhat distant from the first three adatoms. After a further 400 fs, the bond between this top-layer atom and one of its second-layer neighbours breaks (third panel, orange trace) and the integrated spin modulus (fourth panel, black trace) rises to around 2 μ_B. This reflects the fact that the surface now features two semi-occupied dangling bonds – one in the third layer, induced by adsorption of the first three adatoms, and one in the second layer, induced by adsorption of the last. This is an inherently unstable situation, however, as charge transfer can remove the radical character of both sites.

In fact, the final significant surface modification occurs just after the 3000 fs mark, when a Si–H–Si bridge is formed between a second-layer silicon atom and the top-layer silicon atom that binds the final fluorine atom; this may be seen in the two constituent Si–H distances, the one involving the top-layer atom remaining constant (third panel, grey trace) and that involving the second-layer atom showing bond formation (third panel, blue trace). Such a motif has been noted above in relation to the B/γβ trajectory, as well as in previous work on OF₂ adsorption,³ and can be rationalised only in terms of three-centre two-electron binding. This implies donation of an electron to the third-layer dangling bond, which becomes fully occupied, and the integrated spin modulus returns to zero at this point (fourth panel, black trace). Mulliken analysis at the 3500 fs mark reveals the three atoms of the Si–H–Si bridge to possess a net charge of +0.93|e| while the silicon atom that hosts the dangling bond carries a charge of −0.17|e| (to be compared with −0.02|e| on the unperturbed monohydrogenated surface). The two constituent bonds of the Si–H–Si bridge (third panel, grey and blue traces) vibrate slightly erratically, making it difficult to extract reliable frequencies. The nearby Si–F bond (third panel, red trace) oscillates at 740 cm⁻¹ about a mean bond length of 1.61 Å.

Consistent with the complete dissociation of ClF₃ observed in this trajectory, post-dynamics geometry optimisation indicates a rather high adsorption heat of 7.63 eV, exceeding by almost 40% the next-highest value (5.49 eV, obtained in the B/α[small gamma, Greek, macron] case) and by more than 100% the value corresponding to the only other trajectory where no species desorb (3.71 eV, obtained in the C/γβ case).

E. Type V: attack on a third-layer atom

Four of our computed trajectories resulted in reactions that started with an attack on a third-layer silicon atom. Of these, the C/βα and D/βα trajectories were rather similar to one another, so we shall describe in detail only the former. The C/γα and C/β[small gamma, Greek, macron] trajectories differ significantly, on the other hand, and so warrant separate consideration. Snapshots of all three described trajectories may be seen in Fig. 16.

Fig. 16 Snapshots of the Type V (C/βα, C/γα, and C/β[small gamma, Greek, macron]) trajectories. Colour scheme as in Fig. 3. Note the uneven distribution of timestamps.

1. C/βα Trajectory. In common with the previously described B/αβ trajectory, this simulation commences with the molecule's F–Cl–F axis perpendicular to the surface. That orientation is maintained throughout the first 500 fs of its approach, but over the following 500 fs the molecule tilts so that its equatorial fluorine atom points down into the trench between dimer rows. At around the 1100 fs mark, the Cl–F bond involving this atom breaks (Fig. 17, first panel, cyan trace) and both spin measures rise to around 1 μ_B (third panel, magenta and black traces). The free fluorine atom then rapidly descends into the trench, forming a bond with a third-layer silicon atom (second panel, red trace) at around the 1250 fs mark. About 100 fs later, the bond between this silicon atom and one of its fourth-layer neighbours is broken (second panel, green trace) leaving a dangling bond on the latter. We infer that this orbital must be empty, since both spin measures (third panel, magenta and black traces) fall to zero at this moment, and the fourth-layer atom relaxes towards a trigonal planar local bonding geometry.

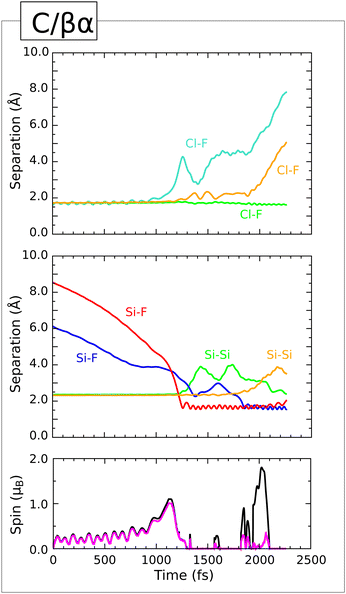Fig. 17 Evolution of the C/βα trajectory. The three upper panels show interatomic separations (colours as per Fig. 4) while the lower panel shows integrated net spin in magenta and integrated spin modulus in black.

Indeed, these changes in surface bonding coincide with significant distortion of the ClF₂ moiety, consistent with it acquiring anionic character. The Cl–F bond lying closest to the surface stretches but does not quite break (first panel, orange trace) and the situation persists for at least 500 fs; only at around the 1850 fs mark does this bond break, coincident with formation of a Si–F bond (second panel, blue trace) involving a second-layer silicon atom. This, in turn, induces cleavage of that atom's bond with one of the third-layer silicon atoms (second panel, orange trace).

At around the 2000 fs mark, therefore, the system comprises a closed-shell ClF molecule above a surface featuring two dangling bonds – one on a fourth-layer silicon atom, induced by adsorption of the first fluorine atom, and one on a third-layer silicon atom, induced by adsorption of the second fluorine atom. Evidently, both of these now possess radical character, since the integrated spin modulus (third panel, black trace) rises to around 2 μ_B at this stage. Rather than resolving the inherent instability of this scenario by charge transfer alone, however, the system undergoes one final restructuring at the 2100 fs mark, when the Si–Si bond that was severed on adsorption of the first fluorine atom is reinstated (second panel, green trace). This implies five-fold coordination for the involved third-layer silicon atom, comprising a trigonal planar arrangement of silicon neighbours around a central Si–Si–F axis. Such a conformation was noted previously in our study of OF₂ adsorption on this surface³ and makes sense only if the central axis exhibits three-centre four-electron bonding and hence anionic character. The stretch vibration of the constituent Si–F bond (second panel, red trace) drops by at least 150 cm⁻¹ upon formation of the Si–Si–F motif, and its mean length increases from 1.67 Å to at least 1.92 Å. The necessary additional electron is naturally supplied by the third-layer dangling bond, which consequently loses its radical character. The integrated spin modulus of the system (third panel, black trace) falls back to zero at this point. The ClF molecule desorbs slowly from the surface, its Cl–F bond vibrating at a frequency of 720 cm⁻¹ about a mean length of 1.64 Å. Relaxation of the remaining surface structure allows us to infer an effective adsorption heat of 2.27 eV – rather on the low side compared with other trajectories, and perhaps reflective of the fact that neither of the two adsorbed fluorine atoms attaches to one of the relatively accessible top-layer silicon atoms.

2. C/γα Trajectory. With this simulation, we return to a trajectory that begins with the molecular plane parallel to the surface. This attitude is more-or-less maintained through the first 500 fs of the molecule's descent, but a progressive tilt over the subsequent 400 fs orients the equatorial fluorine atom firmly toward the trench between dimer rows. At around the 900 fs mark, the corresponding Cl–F bond (Fig. 18, first panel, cyan trace) is broken, and the free fluorine atom accelerates rapidly downward, forming a bond with one of the third-layer silicon atoms after a further 200 fs (second panel, red trace). The bond between this silicon atom and one of its fourth layer neighbours (second panel, green trace) is subsequently broken by the 1200 fs mark, and the integrated spin modulus (third panel, black trace) settles at around 1 μ_B. Since the integrated net spin (third panel, magenta trace) falls to zero at this point, however, it is clear that the system must exhibit two regions with partial radical character, rather than one region of fully radical character. Mulliken analysis indicates a magnetic moment of 0.42 μ_B associated with the under-coordinated fourth-layer silicon atom at the 2000 fs mark, balanced by an equal and opposite magnetic moment localised on the ClF₂ moiety. This situation is remarkably stable, with the latter species floating in place for around 3000 fs in total. Things only begin to change as we approach the 4000 fs mark, when the integrated spin modulus (third panel, black trace) starts to fall toward zero.

Fig. 18 Evolution of the C/γα trajectory. The three upper panels show interatomic separations (colours as per Fig. 4) while the lower panel shows integrated net spin in magenta and integrated spin modulus in black.

At the 4100 fs mark, one of the two remaining Cl–F bonds breaks (first panel, orange trace) and a new Si–F bond is formed (second panel, blue trace) that oscillates at 815 cm⁻¹ about a mean length of 1.59 Å. This latter bond involves a top-layer silicon atom, which for a brief time is five-fold coordinated with three silicon atoms and one hydrogen atom as bonding partners beside the newly arrived fluorine atom. Within about 250 fs, however, the hydrogen atom swings around and forms a Si–H–Si bridge between the top-layer silicon atom and one of its second-layer neighbours. The corresponding Si–Si bond is broken (third panel, orange trace) and a new Si–H bond is formed (third panel, red trace) to complement the existing one (third panel, green trace). The oscillations of these bonds are a little too chaotic to extract reliable estimates of frequency and length, but they are evidently quite comparable to those noted in our descriptions of the B/γβ and B/αβ trajectories above, as well as to an equivalent structure found in our previous study of OF₂ adsorption on the same surface.³ In all of those cases, formation of the Si–H–Si bridge could only be stabilised by donation of an electron and consequent adoption of a three-centre two-electron orbital configuration.

It is doubtless not a coincidence, therefore, that within 50 fs of the Si–H–Si bridge taking shape, the Si–Si bond that was broken upon adsorption of the first fluorine atom is reconstituted (second panel, green trace). This results in a five-fold coordinated silicon atom in the third layer, in which three neighbouring silicon atoms adopt a trigonal planar arrangement intersected by a central Si–Si–F axis. This exact situation was seen in the C/βα trajectory described above, not to mention our previous work on OF₂ adsorption,³ and can only sensibly be stabilised by accepting an electron to achieve a three-centre four-electron configuration. The resulting situation, with cationic Si–H–Si bridge (net charge +1.04|e| at the 5000 fs mark) and anionic Si–Si–F motif (net charge −0.27|e| at the same time) constitutes the final state of the surface, and barring blips both spin measures are essentially zero beyond this point in the simulation (third panel, magenta and black traces). The departing ClF molecule is of closed-shell character, as expected, and the effective adsorption heat after relaxation of the post-dynamics surface structure is 3.22 eV.

3. C/β[small gamma, Greek, macron] Trajectory. This trajectory starts with the molecule situated between dimer rows and oriented with its equatorial fluorine atom pointing toward the surface. Such an orientation is maintained for the first 1100 fs of the simulation, at which point the equatorial Cl–F bond is broken (Fig. 19, first panel, cyan trace). In common with the other Type V trajectories described above, the liberated fluorine atom then descends rapidly into the trench, before bonding with one of the third-layer silicon atoms after a further 200 fs (second panel, red trace). The bond between this silicon atom and one of the fourth-layer silicon atoms breaks at about the same time (third panel, cyan trace) leaving a dangling bond on the latter. The integrated net spin, which had risen as high as 1 μ_B falls to zero at this point (third panel, magenta trace) but the integrated spin modulus remains distinctly non-zero (third panel, black trace). As before, this implies the existence of two regions having partial radical character, namely the dangling bond and the rump of the molecule.

Fig. 19 Evolution of the C/β[small gamma, Greek, macron] trajectory. The three upper panels show interatomic separations (colours as per Fig. 4) while the lower panel shows integrated net spin in magenta and integrated spin modulus in black.

Over the following 700 fs, the ClF₂ moiety gradually rotates into a nearly vertical orientation, until at around the 2000 fs mark the downward-directed Cl–F bond breaks (first panel, orange trace) and the corresponding fluorine atom binds instead to the same silicon atom that already hosts the first fluorine atom (second panel, blue trace). Shortly thereafter, the second Si–Si bond linking this silicon atom to the third layer is broken (second panel, orange trace) and it starts to rise upward, reaching a position almost level with the top-layer silicon atoms by around the 2300 fs mark. Conceivably, this silicon atom might be susceptible to desorption if attacked by a subsequently arriving molecule, since it maintains only two bonds with other silicon atoms. Remarkably, the two undercoordinated fourth-layer silicon atoms display neither significant charge nor any magnetic moment, suggesting that they may share a covalent bond with one another, notwithstanding their separation of 3.17 Å (roughly 33% longer than a typical bond in bulk silicon). As for the ClF molecule, this desorbs with its Cl–F bond (first panel, green trace) oscillating at 765 cm⁻¹ about a mean length of 1.63 Å. Despite the somewhat extreme restructuring of the surface, including cleavage of two Si–Si bonds, the adsorption heat deduced from relaxation of the trajectory's final geometry is a sizeable 2.90 eV – only a little lower than values obtained for several of the less disrupted surface structures discussed above.

F. Type VI: post-dissociation axial attack

In all of the preceding trajectories, the equatorial fluorine atom has been the first to make a bond with either the silicon surface or one of its hydrogen adatoms. Typically, this has coincided with, or at least very closely followed, cleavage of the corresponding Cl–F bond. In just one trajectory, however, we found that loss of the equatorial fluorine did not immediately result in adsorption of the liberated atom. Instead, it travelled some distance across the surface while one of the axial fluorine atoms adsorbed first, finally coming to rest only after some non-trivial time. This trajectory (see Fig. 20 for snapshots) we shall describe in detail below.

Fig. 20 Snapshots of the Type VI (D/αβ) trajectory. Colour scheme as in Fig. 3.

1. D/αβ Trajectory. Our final simulation begins with the F–Cl–F axis of the ClF₃ molecule oriented parallel to the surface normal, and for the first 800 fs of the trajectory the molecule drifts toward the surface with little evident acceleration and almost no rotation. Over the following 400 fs, however, the molecule rocks back and forth while the Cl–F bond involving the lower axial fluorine atom (Fig. 21, first panel, orange trace) and that involving the equatorial fluorine atom (first panel, cyan trace) start to stretch. Both spin measures rise to around 1 μ_B at the same time (fourth panel, black and magenta traces) and by the 1200 fs mark the equatorial fluorine atom has effectively started to detach itself from a nascent ClF₂ moiety; the latter carries a magnetic moment of +0.47 μ_B and the former one of +0.51 μ_B. The semi-isolated equatorial fluorine atom is, at this stage, more than 2.30 Å distant from any other atom and no discernible attack on the surface has yet taken place.

Fig. 21 Evolution of the D/αβ trajectory. The three upper panels show interatomic separations (colours as per Fig. 4) while the lower panel shows integrated net spin in magenta and integrated spin modulus in black.

Very shortly after the departure of the equatorial fluorine atom, the lower-lying axial fluorine atom also detaches from the chlorine atom (leaving a ClF molecule) and forms a Si–F bond (second panel, red trace) with a nearby second-layer silicon atom. At the same time, the Si–Si bond (second panel, green trace) between this silicon atom and one in the third layer stretches dramatically, to as much as 3.83 Å. A dangling bond is thus created on the third-layer silicon atom and one might expect this to inherit any radical character previously associated with the originally axial fluorine atom. At this time, the Si–F bond (second panel, red trace) vibrates at a frequency of 690 cm⁻¹ about a mean length of 1.63 Å.

Apart from a brief encounter with one particular top-layer silicon atom at around the 1400 fs mark (second panel, grey trace) the previously equatorial fluorine atom moves freely across the surface until it is captured by a different top-layer silicon atom (second panel, blue trace) at around the 1600 fs mark (around 300 fs after the axial fluorine atom was captured). The integrated spin modulus (fourth panel, black trace) rises to around 2 μ_B at this point, having briefly dropped to zero just after the earlier close encounter; the integrated net spin (fourth panel, magenta trace) remains negligible at this time.

Following binding of the originally equatorial fluorine atom, the hydrogen atom attached to the capturing silicon atom is displaced into a Si–H–Si bridge, similar to that noted in the B/γβ, B/αβ, and C/β[small gamma, Greek, macron] trajectories, and indeed to an equivalent structure observed in our previous work on OF₂ adsorption.³ As before, we find that the Si–Si bond between the capturing atom and one of its second-layer neighbours breaks (third panel, orange trace) while the existing Si–H bond stretches a little (third panel, green trace) and a new Si–H bond is formed (third panel, red trace). These two bonds then vibrate in anti-phase with one another at a common frequency of 1785 cm⁻¹ about mean lengths of around 1.66 Å. The newly formed Si–F bond (second panel, blue trace) vibrates at a frequency of 815 cm⁻¹ about a mean length of 1.58 Å, indicating a less vibrationally excited bond than that linking the originally axial fluorine atom to its second-layer silicon neighbour.

Returning to that first-formed Si–F bond, however, we note that it almost ceases to vibrate at this time (second panel, red trace) while the Si–Si bond that was broken on its formation (second panel, green trace) now oscillates between a length of 2.34 Å and 3.03 Å at a frequency of 200 cm⁻¹. These lengths are consistent with an intact Si–Si bond (albeit quite stretched at times) and imply that the second-layer silicon atom is five-fold coordinated, with three neighbouring silicon atoms arranged in trigonal planar fashion around a central Si–Si–F axis. Both spin measures have dropped to zero by this stage, which can best be explained if the Si–H–Si bridge formed in response to adsorption of the originally equatorial fluorine atom adopts three-centre two-electron binding by donating an electron to the Si–Si–F motif associated with the originally axial fluorine atom. We have previously inferred three-centre four-electron binding for the exact same motif in our previous study of OF₂ adsorption, and indeed in the C/βα and C/γα trajectories described above. Here, our Mulliken analysis indicates a net charge for the three atoms of the Si–H–Si bridge that amounts to +0.87|e| at the 2000 fs mark, while the Si–Si–F motif caries a net charge of −0.23|e| at the same time. The ClF molecule desorbs, meanwhile, with its axis very nearly parallel to the surface normal and in a closed-shell configuration.

In some respects, the final surface structure of this trajectory bears a degree of resemblance to that achieved in the C/γα case, with both situations characterised by the presence of cationic Si–H–Si and anionic Si–Si–F motifs. Where they differ is that here the latter motif involves silicon atoms from the second and third layers, whereas in the previous trajectory the involved silicon atoms were from the third and fourth layers. Accordingly, relaxation of the post-dynamics geometry leads to a slightly different (higher) adsorption heat in the present case (3.59 eV) from that found after relaxing the end-state of the C/γα trajectory (3.22 eV). We surmise that similar defects may more readily be accommodated into the surrounding structure if they occur closer to the surface of the material.

IV. Discussion

The calculations presented here reveal a potentially bewildering variety of adsorption mechanisms for chlorine trifluoride on the monohydrogenated silicon surface, but some general principles may nevertheless be outlined. In doing so, we emphasise that behaviours seen repeatedly within a relatively small number of trajectories may reasonably be deduced to be commonplace, while those that are absent may simply be missing through chance and not necessarily as rare as they might appear. With this caveat in mind, we cautiously proceed.

To start at the most basic level, we first note that 10 of our 44 symmetrically distinct trajectories resulted in the molecule rebounding from the surface and returning whence it came. Allowing for symmetry-equivalent replica trajectories, this corresponds to 12 from a total of 60, implying an effective scattering rate of 20%. Of the 34 symmetrically distinct trajectories in which the molecule did not simply scatter, 13 resulted in physisorption. Once again allowing for symmetry-equivalent replicas, this translates to 15 from 60 trajectories, implying a sticking probability for physisorption of 25%. This leaves 21 symmetrically distinct trajectories that lead to reaction, corresponding to 33 from 60 trajectories once symmetry-equivalent replicas are included and implying a sticking probability for chemisorption of 55%. The numerical proportions cited here ought not to be regarded as statistically reliable, of course, but they are qualitatively indicative that reactive chemisorption likely dominates.

Among the 21 symmetrically distinct reactive trajectories that we have calculated, 18 were prompt and 3 were delayed, in the sense that the molecule reacted either immediately upon arrival at the surface (prompt) or only after substantial reorientation and/or lateral repositioning (delayed). Allowing for symmetry-equivalent replicas, this translates to 30 prompt and 3 delayed trajectories, suggesting that the majority of reactive chemisorption events will likely take place on the first attempt. Since some fraction of physisorbed molecules may react and chemisorb on timescales much longer than those probed in our calculations, however, the true proportion may in reality be rather more balanced. We nevertheless expect that such extremely delayed reactions are likely to involve mechanisms similar to those of the chemisorption events identified in the present work.

Turning to the details of these reactions, therefore, we find that in every case the first mechanistic step involves cleavage of the bond between the chlorine atom and the equatorial fluorine atom. In 4 out of 33 cases (3 out of 21 symmetrically distinct) this coincides with abstraction of a single hydrogen atom from the surface, followed swiftly by deposition of the equatorial fluorine atom into the site that is thus vacated. In 8 cases (5 symmetrically distinct) the equatorial fluorine atom eschews hydrogen abstraction and attacks a dimer bond between top-layer silicon atoms, while in a further 4 cases (2 symmetrically distinct) it attacks just a single top-layer atom instead. The equatorial fluorine atom attacks a second-layer silicon atom in 10 cases (6 symmetrically distinct) and a third-layer silicon atom in 6 cases (4 symmetrically distinct) but we see no events where atoms in the fourth or lower layers are initially attacked. In only a single case (even allowing for symmetry-equivalent replicas) do we find that the equatorial fluorine atom is not the first to form a bond with the surface. In this solitary scenario, although it detaches from the molecule first the equatorial fluorine atom adsorbs only after one of the axial fluorine atoms has also detached from the molecule and formed a surface bond of its own.

Regarding the surface products of these reactions, a number of structural motifs are found to recur, although the details differ considerably between trajectories. These include Si–H–Si and Si–F–Si bridges, which we infer are stabilised by three-centre two-electron bonding, and Si–Si–F motifs, which make sense only in terms of three-centre four-electron bonding. Such electronic structures further imply that the former two defect types must be cationic in nature and the latter anionic, if they are to exist as anything other than transient radical species. More traditional defects, where a dangling bond is created, can be either cationic, anionic, or radical in nature, depending upon whether the corresponding localised orbital is empty, full, or partially occupied. In most cases, we find that the surface contrives eventually to avoid radical character by adopting multiple structures of complementary charge and zero spin, but this need not necessarily be the case throughout the whole course of each reaction.

Next, so far as gas-phase products are concerned, the most commonly occurring is chlorine monofluoride, which is produced in 23 out of 33 trajectories (15 out of 21 symmetrically distinct). Hydrogen fluoride is generated as a co-product in 3 of these cases (2 symmetrically distinct) but never on its own. Hydrogen chloride, on the other hand, is produced in 2 trajectories (1 symmetrically distinct) but only alongside an isolated fluorine atom. A difluorochlorate anion is produced in 4 trajectories (2 symmetrically distinct) and hydrogen difluorochlorate in 3 trajectories (2 symmetrically distinct). The latter molecule desorbs in one symmetrically distinct instance, but remains tethered to the surface through a dihydrogen bond in the other. Finally, in only a single trajectory (even allowing for symmetry-equivalent replicas) do we observe complete chemisorption of all products.

V. Conclusions

To sum up, molecular dynamic simulations reveal the reactive adsorption of chlorine trifluoride on this surface to proceed via a much more diverse range of mechanisms than could have been predicted on the basis of quasistatic transition state calculations. While hydrogen abstraction is possible, direct interaction with silicon atoms as deep as the third layer cannot be ruled out and may, in fact, dominate. Dangling-bond defects may be induced in the surface, but so too may be a variety of three-centre motifs (involving either two-electron or four-electron bonding). And while chlorine monofluoride is the most commonly evolved gas-phase product, halogen hydrides and more exotic species must also be anticipated. In seeking to understand systems of this nature, the additional complexity and expense of molecular dynamic simulation is more than justified.

Conflicts of interest

There are no conflicts to declare.

Data availability

The trajectories analysed in this study are openly available in the University of Cambridge Data Repository at DOI: 10.17863/CAM.119383

Acknowledgements

Computational resources were provided by the Cambridge Service for Data-Driven Discovery (CSD3). For the purpose of open access, the authors have applied a Creative Commons Attribution (CC BY) licence to any Author Accepted Manuscript version arising.

References

1. C. K. Fink and S. J. Jenkins, Radical-Mediated Adsorption: Ozone Oxidation of Passivated Silicon, Surf. Sci., 2008, 602, L100.
2. I. Y. H. Wu and S. J. Jenkins, First Principles Dynamics of Fluorine Adsorption on Clean and Monohydrogenated Si{001}, Langmuir, 2022, 38, 7256–7271.
3. H. Thake and S. J. Jenkins, Role of Radicals in the Reaction of Oxygen Difluoride with Monohydrogenated Silicon, Phys. Chem. Chem. Phys., 2025, 27, 660–671.
4. N. V. Sidgwick, The Chemical Elements and Their Compounds, Oxford University Press, 1950, vol. II.
5. J. E. House and K. A. House, Descriptive Inorganic Chemistry, Academic Press, 2016, 3rd edn.
6. W.-T. Tsai, Environmental and Health Risks of Chlorine Trifluoride (ClF₃), an Alternative to Potent Greenhouse Gases in the Semiconductor Industry, J. Hazard. Mater., 2011, 190, 1–7.
7. T. Chowdhury, R. Hidayat, T. R. Mayangsari, J. Gu, H.-L. Kim, J. Jung and W.-J. Lee, Density Functional Theory Study of the Fluorination Reactions of Silicon and Silicon Dioxide Surfaces Using Different Fluorine-Containing Molecules, J. Vac. Sci., Technol. A, 2019, 37, 021001.
8. T. Chowdhury, R. Hidayat, T. R. Mayangsari, J. Gu, H.-L. Kim, J. Jung and W.-J. Lee, Erratum: Density Functional Theory Study of the Fluorination Reactions of Silicon and Silicon Dioxide Surfaces Using Different Fluorine-Containing Molecules [J. Vac. Sci. Technol. A 37, 021001 (2019)], J. Vac. Sci. Technol., A, 2019, 40, 047001.
9. K. O. Christe and J. P. Guertin, The Difluorochlorate(I) Anion, ClF₂⁻, Inorg. Chem., 1965, 4, 905–908.
10. C. K. Fink and S. J. Jenkins, First-Principles Molecular Dynamics of the Initial Oxidation of Si{001} by Ozone, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 195407.
11. C. K. Fink, K. Nakamura, S. Ichimura and S. J. Jenkins, Silicon Oxidation by Ozone, J. Phys.: Condens. Matter, 2009, 21, 183001.
12. M. Sacchi, D. J. Wales and S. J. Jenkins, Mode-Specific Chemisorption of CH₄ on Pt{110} − (1 × 2) Explored by First-Principles Molecular Dynamics, J. Phys. Chem. C, 2011, 115, 21832.
13. M. Sacchi, D. J. Wales and S. J. Jenkins, Bond-Selective Energy Redistribution in the Chemisorption of CH₃D and CD₃H on Pt{110} − (1 × 2): A First-Principles Molecular Dynamics Study, Comput. Theor. Chem., 2012, 990, 144.
14. M. Sacchi, D. J. Wales and S. J. Jenkins, Mode-Specificity and Transition State-Specific Energy Redistribution in the Chemisorption of CH₄ on Ni{100}, Phys. Chem. Chem. Phys., 2012, 14, 15879.
15. G.-J. Kroes, M. Pavanello, M. Blanco-Rey, M. Alducin and D. J. Auerbach, Ab Initio Molecular Dynamics Calculations on Scattering of Hyperthermal H Atoms from Cu(111) and Au(111), J. Chem. Phys., 2014, 141, 054705.
16. A. Chatterjee, F. Cheng, L. Leung, M. Luo, Z. Ning and J. C. Polanyi, Molecular Dynamics of the Electron-Induced Reaction of Diiodomethane on Cu(110), J. Phys. Chem. C, 2014, 118, 25525–25533.
17. D. G. Sangiovanni, D. Edström, L. Hultman, I. Petrov, J. E. Greene and V. Chirita, Ab Initio and Classical Molecular Dynamics Simulations of N₂ Desorption from TiN(001) Surfaces, Surf. Sci., 2014, 624, 25–31.
18. D. G. Sangiovanni, B. Alling, P. Steneteg, L. Hultman and A. Abrikosov, Nitrogen Vacancy, Self-Interstitial Diffusion, and Frenkel-Pair Formation/Dissociation in B1 TiN Studied by Ab Initio and Classical Molecular Dynamics with Optimised Potentials, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 054301.
19. W. Y. Guo, S. J. Jenkins, W. Ji, J. C. Polanyi, M. Sacchi and G.-C. Wang, Repulsion-Induced Surface Migration by Ballistics and Bounce, Chem. Lett., 2015, 6, 4093–4098.
20. A. Groß, Ab Initio Molecular Dynamics Simulations of the O₂/Pt(111) Interaction, Catal. Today, 2016, 260, 60–65.
21. G. Füchsel, M. del Cueto, C. Díaz and G.-J. Kroes, Enigmatic HCl + Au(111) Reaction: A Puzzle for Theory and Experiment, J. Phys. Chem. C, 2016, 120, 25760–25779.
22. K. Huang, O. MacLean, S. Y. Guo, I. R. McNab, Z. Ning, G.-C. Wang, W. Ji and J. C. Polanyi, Dynamics of Surface Migration: Electron-Induced Reaction of 1,2-Dihaloethanes on Si(100), Surf. Sci., 2016, 652, 312–321.
23. F. Nattino, O. Galparsoro, F. Costanzo, R. Díez Muiñno, M. Alducin and G.-J. Kroes, Modelling Surface Motion Effects in N₂ Dissociation on W(110): Ab Initio Molecular Dynamics Calculations and Generalized Langevin Oscillator Model, J. Chem. Phys., 2016, 144, 244708.
24. D. G. Sangiovanni, A. B. Mei, L. Hultman, V. Chirita, I. Petrov and J. E. Greene, Ab Initio Molecular Dynamics Simulations of Nitrogen/VN(001) Surface Reactions: Vacancy-Catalyzed N₂ Dissociative Chemisorption, N Adatom Migration, and N₂ Desorption, J. Phys. Chem. C, 2016, 120, 12503–12516.
25. D. Novko, I. Loncarić, M. Blanco-Rey, J. I. Juaristi and M. Alducin, Energy Loss and Surface Temperature Effects in Ab Initio Molecular Dynamics Simulations: N Adsorption on Ag(111) as a Case Study, Phys. Rev. B, 2017, 96, 085427.
26. D. G. Sangiovanni, G. K. Gueorguiev and A. Kakanakova-Georgieva, Ab Initio Molecular Dynamics of Atomic-Scale Surface Reactions: Insights into Metal Organic Chemical Vapor Deposition of AlN on Graphene, Phys. Chem. Chem. Phys., 2018, 20, 17751–17761.
27. G. Füchsel, X. Zhou, B. Jiang, J. I. Juaristi, M. Alducin and G.-K. Kroes, Reactive and Nonreactive Scattering of HCl from Au(111): An Ab Initio Molecular Dynamics Study, J. Phys. Chem. C, 2019, 123, 2287–2299.
28. S. C. Matysik, D. J. Wales and S. J. Jenkins, Surface Chirality Influences Molecular Rotation upon Desorption, Phys. Rev. Lett., 2021, 126, 126101.
29. S. C. Matysik, D. J. Wales and S. J. Jenkins, Rotational Dynamics of Desorption: Methane and Ethane at Stepped and Kinked Platinum Surfaces, J. Phys. Chem. C, 2021, 125, 27938.
30. S. C. Matysik, D. J. Wales and S. J. Jenkins, Dynamic Diastereomerism on Chiral Surfaces, J. Phys. Chem. C, 2023, 127, 229–233.
31. D. G. Sangiovanni, R. Faccio, G. K. Gueorguiev and A. Kakanakova-Georgieva, Discovering Atomistic Pathways for Supply of Metal Atoms from Methyl-Based Precursors to Graphene Surface, Phys. Chem. Chem. Phys., 2023, 25, 829–837.
32. H. Thake and S. J. Jenkins, First-Principles Dynamics of the Surface Fluorination of Diamond, Langmuir DOI:10.1021/acs.langmuir.5c01587.
33. G. P. Srivastava, Theory of Semiconductor Surface Reconstruction, Rep. Prog. Phys., 1997, 60, 561–613.
34. S. J. Jenkins, Foundations of Surface Science, Oxford University Press, 2023.
35. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, First Principles Methods using CASTEP, Z. Kristallogr., 2005, 220, 567–570.
36. D. Vanderbilt, Soft Self-Consistent Pseudopotentials in a Generalized Eigenvalue Formalism, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895.
37. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
38. H. J. Monkhorst and J. D. Pack, Special Points for Brillouin Zone Integrations, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192.
39. R. S. Mulliken, Electronic Population Analysis on LCAO-MO Molecular Wave Functions. I, J. Chem. Phys., 1955, 23, 1833–1840.
40. R. H. Crabtree, A New Type of Hydrogen Bond, Science, 1998, 282, 2000–2001.
41. R. Custelcean and J. E. Jackson, Dihydrogen Bonding: Structures, Energetics, and Dynamics, Chem. Rev., 2001, 101, 1963–1980.
42. R. S. Rowland and R. Taylor, Intermolecular Nonbonded Contact distances in Organic Crystal Structures: Comparison with distances Expected from van der Waals Radii, J. Phys. Chem., 1996, 100, 7384–7391.

---