Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Combining simulations and experiments – a perspective on maximum entropy methods
Johannes
Stöckelmaier
 a and
Chris
Oostenbrink
a and
Chris
Oostenbrink
 *ab
*ab
aInstitute of Molecular Modeling and Simulation (MMS), BOKU University, Vienna, Austria. E-mail: chris.oostenbrink@boku.ac.at
bChristian Doppler Laboratory Molecular Informatics in the Biosciences, BOKU University, Vienna, Austria
First published on 2nd July 2025
Abstract
To elucidate the connection between the structure and function of intrinsically disordered proteins (IDPs) a description of their conformational ensembles is crucial. These are typically characterized by an extremely large number of similarly low energy conformations, which can hardly be captured by either experimental or computational means only. Rather, the combination of data from both simulation studies and experimental research offers a way towards a more complete understanding of these proteins. Over the last decade, a number of methods have been developed to integrate experimental data and simulations into one model to describe the conformational diversity. While many of these methods have been successfully applied, they often remain black-boxes for the scientist applying them. In this work, we review maximum entropy methods to optimize conformational ensembles of proteins. From a didactical perspective, we aim to present the mathematical concepts and the optimization processes in a common framework, to increase the understanding of these methods.
1 Introduction
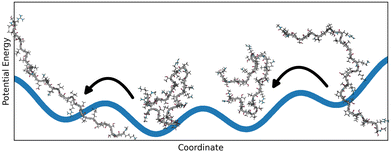
The reproducible folding of biopolymers into functional enzymes, receptors or structural entities is described as the foundation of structural biology and one of the key enablers of life. The observed correlation between amino acid sequence and geometric structure led to the theory of structure–function relationship and has been a solid pillar in the understanding of biochemistry1,2 since the mid-20th century. New scientific insights started to weaken this dogma in the early 2000s, revealing that proteins can be classified into different levels of overall structural stability.3 Structured proteins feature a well-defined 3D geometry that is thermodynamically stable, while increased flexibility is observed with disordered proteins. Proteins lacking a stable geometry entirely are named intrinsically disordered proteins (IDPs4), those that are partly disordered are said to contain intrinsically disordered regions (IDRs).5The elucidation and characterization of structures and the associated dynamics of flexible proteins turned out to be a substantial scientific challenge that requires a close cooperation between experimental studies, data science and molecular simulations.6–8 Flexible proteins are often characterized by complex, multifunneled potential energy landscapes with multiple, often shallow, minima.9,10 Flatter parts of the landscapes may span multiple conformations, allowing rapid switches between them at ambient temperatures11 as visualized in Fig. 1. The observable molecular properties cannot be fully explained by a single structure and therefore it is necessary to create an appropriate representation of the structural diversity. A frequently used model consists of a superposition of different geometric structures, each showing a single relevant structure. The observable molecular properties then emerge as an average over the different structures. All of those structures together represent the conformational ensemble12–14 which is a set of molecule geometries with an affiliated probability coefficient or weight.15 The true amount of conformations in an ensemble is unknown and depends on the definition of discrete conformations, but can grow very large even with mid-sized molecules.16,17
Many established computational methods like comparative modeling18 and AI-based structure predictors like Rosettafold19 or Alphafold20 are designed to calculate static structures of stable proteins. The extension of these methods to also describe conformational ensembles, which are typically described by the sampling of the relevant conformations, is currently a major topic of research.21–24 Alternatively, molecular dynamics (MD) simulation uses the ergodic theory, which predicts that a conformational ensemble is captured by following the molecular motions of a molecule over a sufficiently long time. The computational challenge of appropriately sampling all conformations is closely related to the MD simulation of protein folding25–27 which has, while still being very challenging especially for larger proteins, seen substantial improvements of parameters and methodology. MD simulation can be applied to investigate the dynamic nature of an IDP and to generate an ensemble. The ensemble obtained with such method contains both conformations and associated probability coefficients. For a straightforward MD simulation, which follows the appropriate equations of motion based on an accurate energy function, and from which conformations are sampled at regular time intervals, the probability coefficients would be identical for all samples. The ensemble can subsequently be reduced in size to group very similar structures into single conformations and to assign their weights according to the occurrence of these conformations in the larger ensemble.
The complex potential energy surfaces of most IDPs and flexible proteins make these probability coefficients prone to errors due to force-field inaccuracies. To obtain not just valid geometrical structures but also the correct associated weights, it is necessary to model not just the well populated conformational minima but also to describe the (reversible) transitions from one conformation to the next and the associated energy barrier correctly.28 If the transitions between conformations are not observed sufficiently often, the weights assigned to specific conformations belonging to different minima may not be statistically robust. To address this challenge and to refine the weights of the geometrical ground states it thus seems reasonable to optimize weights a posteriori after completing the simulation. A fundamental prerequisite for the successful reweighting of ensembles lies in the complete sampling of the conformational space, often necessitating enhanced sampling methods. Reweighting methods depend on a reasonable sampled conformational space as they cannot create new conformations by them self, but are designed to create an appropriate ensemble from an existing set of conformations to better reproduce experimental data. Thus, initial ensembles obtained from such enhanced sampling methods featuring a wide set of relevant conformations with lower confidence statistical weights represent an ideal use case for a posteriority reweighting.
In the last decade, numerous methods have been developed to correct and improve computationally obtained ensembles by optimizing the associated weights using experimental data. Since then, these reweighting methods became an established tool in computational structure elucidation of flexible proteins.29–32 The aim of this study is to review some of the most prominent reweighting techniques and to give insights into what are often considered black box methods.
2 Refinement of ensembles
As described in the introduction, MD simulations are used to study the behavior of large chemical and biophysical systems, enabling the calculation of in silico estimates of the system's biophysical properties. Applying the physical laws of motion, computers can approximate the movement and dynamics of the biophysical system. The forces on atoms, used in the equations of motion, are typically derived from a force field, as an approximation of the interactions between atoms and molecules, more precisely described by quantum mechanical principles. The physical ensemble of the system of interest is obtained from the trajectory in time, sampled at N regular intervals, with each conformer having a weight of 1/N. In silico estimates of observables are initially calculated individually from single conformers of the trajectory and may later be averaged with estimates from other conformers. Therefore, the choice of conformers to calculate an observable is of high importance as different geometrical structures may yield slightly different values for an observable as many are sensitive to conformation.Experimental observables may also give insight into the relevant conformations of a biomolecule. Particularly insightful for IDPs is nuclear magnetic resonance (NMR) spectroscopy, offering e.g. chemical shifts, 3J-coupling constants, residual dipolar couplings (RDCs) and paramagnetic relaxation enhancement (PRE). During an experimental measurement, a very large number of molecules is measured simultaneously and the averaging timescales are typically long with respect to the molecular motion. Consequently, the measured observables represent directly both a time and ensemble average of the measured molecules.33–36 It is therefore invalid to compare observables calculated from a single conformation to the ensemble-averaged experimental results. Accordingly, it is necessary to compute the expectation value for each observable from a representative set of conformations (i.e. the computationally derived ensemble) to accurately compare results of experiment and simulation. In many cases, a weighted average over the simulation trajectory is calculated. Eqn (1) shows such an averaging where the ensemble average 〈Ocalc〉, indicted by angular brackets, is calculated. The ensemble consists of in total N conformations and each conformer t has an individual calculated observable Ocalct and a statistical weight wt:
 | (1) |
This approach is valid for most experimental data, but not for residual dipolar couplings (RDCs) and nuclear Overhauser effects (NOEs), where different averaging schemes are required. Before the calculation of ensemble averages, the physical nature of each type of observable needs to be considered and the correct averaging scheme must be chosen. For example, NOEs arise from dipolar coupling between the nuclear spin of two protons. The intensity of such signals is highly dependent on the distance in space between a given proton pair and weakens proportional to the third or sixth power of the distance, depending on the timescale of the experiment and the tumbling time of the molecule.37 Pairs closer than 3 Å result in strong NOE signals while the limit of detection is reached with pairs 6 Å apart. In ensemble averaging, this means that a small number of conformations with short distances between a proton pair have a dominating influence on the intensity of the NOE signal. To reproduce this behavior, NOE-derived distances require r−3 or r−6 averaging,38,39e.g.:
 | (2) |
Interpreting the weights, wt, in eqn (1) and (2) as probabilities that the conformation t occurs in the ensemble, leads to the condition that the sum of all individual probabilities needs to be one:
 | (3) |
Due to the approximate nature of force fields it is unavoidable to introduce some level of inaccuracy into the simulation. In some simulation settings, such as those involving intrinsically disordered proteins (IDPs), these small inaccuracies are of increased relevance, as most force fields are originally optimized for stable proteins, and can potentially affect the prediction of the observables of the system. The simulated and ensemble-averaged observables, as obtained from the conformational ensemble, may be compared with those measured in experimental studies to confirm the validity of the simulations, identify differences and possibly to correct the simulation to allow further investigation into the properties of the system.
To validate and optimize molecular ensembles, a set of techniques known as reweighting methods can be applied. The basic principle of all of these methods is similar: an initial probability density representing the weights of each conformation of the unbiased ensemble is transformed into a probability density which represents the refined ensemble, aiming to improve the agreement between computationally and experimentally derived ensemble averages of the biophysical observables.
In biophysical experiments the behavior of a measured molecule is determined by its potential-energy landscape (natural potential). This potential-energy surface, governed by nature's physics, is a computationally inaccessible potential which can only be approximated by the force field (or the quantum mechanical method). To illustrate this concept, imagine a hypothetical force field that accurately represents the natural potential except for one region. In this example, the force field potential includes an additional energy valley that does not exist in the natural potential (compare Fig. 2A).
Fig. 2B, illustrates the distribution of simulated values of a hypothetical observable for an unbiased ensemble. An experimental ensemble average could be measured (green line). The computational estimate of the same observable can be predicted by averaging over the samples of the simulation, shown as red line. In this example, the experimental value corresponds to the left population of the simulated observable. Due to force field errors (Fig. 2A), some samples of the simulation are likely overrepresented, shifting the computational ensemble average away from the experimental result. In this hypothetical example, the right population is an artifact of the force field, causing the simulated expectation value (red line) to be overestimated.
In general, there are two main approaches to address such miscalculated observables due to force field errors. Experimentally derived boundary conditions can be imposed during the simulation, to correct the force field for a specific system. Because these conditions are set a priori, they are baked into the trajectory, making later adjustments complicated and expensive. An a priori approach, to impose experimental restraints during the simulation, may guide the ensemble towards otherwise unsampled conformations, but bears the risk of getting stuck in a small amount of local minima due to too strong restraints, potentially leading to unintentional overfitting to the experimental observable.
Alternatively, ensemble reweighting can be used a posteriori to increase the impact of conformations that agree with the experiment, while reducing the impact of conformations that are in disagreement with the experiment. Reweighting methods yield new weights for the ensemble such that inappropriate conformations become insignificant. In our example, the refined simulated value of the observable can be seen in Fig. 2C (blue line) after the reweighting. Now the simulated average is in much better agreement with the experimental observable. This example already demonstrates key requirements necessary for the successful reweighting of conformational ensembles. The initial ensembles needs to be well-sampled, covering the entire relevant conformational space. In a second step, after the initial ensembles has been generated, the reweighting algorithm picks a sub-ensemble to better represent the experimental data by adjusting the statistical weights of the ensemble. As ensemble reweighting cannot generate new conformations that were not in the initial ensemble all relevant conformations must be sampled beforehand. An in-depth discussion on imposing boundary conditions a priori as compared to a posteriori reweighting can be found in Rangan et al.40
3 Reweighting algorithm
Over the course of years, several methods have been developed to integrate simulations with experimental data to further the understanding of biophysical processes. These methods can be divided into two main groups, depending on the optimization objective set. Maximum parsimony methods try to find a minimal41–43 or deliberately small44–46 ensemble in agreement in the data, for which multiple algorithms have been proposed. On the other hand entropy maximizing29,47–53 and Bayesian methods54–62 try to use as much of the initial information collected from MD simulations while balancing those with the experimental data. Maximum entropy methods may also be used to optimize force fields.63 Further reading beyond the scope of this work on the comparison of methods, including the maximum occurrence method,64,65 can be found with Medeiros Selegato et al.66 Additionally, a comprehensive overview about available methods has been collected by Bonomi et al.67Regarding the nomenclature of methods, we understand the term maximum entropy methods as an umbrella term for a group of specific methods and implementations in which the initial ensembles are modified as little as possible given the conditions. This clearly separates maximum entropy methods from maximum parsimony methods, which maximally reduce the ensemble. The scope of this work focuses on the explanation and investigation of Bayesian ensemble refinement and the minimum relative entropy method, both commonly used methods within the maximum entropy umbrella term due to their closeness to the maximum entropy principle. A special case of the minimum relative entropy method, in which the initial weights are uniform, may also be referred to as entropy maximizing, as described in the appendix.
3.1 Bayesian ensemble refinement
Bayesian ensemble refinement has its foundations in Bayes' theorem which allows one to update the probability of an established hypothesis as new data becomes available. Accordingly, a method to update an existing model with new data allows for extensive opportunities to optimize conformational ensembles.54,60Bayes’ theorem allows to calculate the conditional probabilities of events:
 | (4) |
The prior probability P0(model) is the estimated probability of being correct before any data is observed. In the context of ensemble reweighting, the associated model parameters could be obtained from MD simulations. The conditional probability P(data|model) is a measure for the likelihood that the assumed model parameters can reproduce the observed data. The marginal probability can be interpreted as normalization constant such that the posterior probability qualifies as probability. It can be ignored in the case of an optimization problem where we search for the model that maximizes the posterior probability.
The basic formulation of Bayesian ensemble refinement sees the weight vector w as the model to describe the ensemble. As such, the method can be summarized as:
| P(w|data) ∝ P(data|w) × P0(w) | (5) |
To design an appropriate function that measures how well the model parameters explain the observed data, P(data|w) should have a maximum when simulated and observed data match each other. It may be interpreted as the likelihood that the data can be reproduced given the model weights w. In the context of ensemble reweighting such a function can be designed as shown in eqn (6) if a Gaussian error can be postulated:
 | (6) |
For the prior probability of a model, we postulate that the model obtained from the unbiased simulation (w0) is the best representation of the true system. Thus, the probability to yield correct values for observables should be highest if w = w0.68 A qualifying (but not normalized) function comparing w with w0 can be found in the theta-scaled Kullback–Leibler divergence,69 which is equal to the relative entropy (eqn (7)) if the targeted distribution is normalized [ref. 70, p. 90] and theta is one:
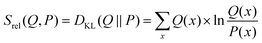 | (7) |
| P0(w,w0) ∝ exp(−θSrel(w,w0)) | (8) |
To find the ideal model wopt, the global maximum of the posterior probability (eqn (5)) needs to be found:
 | (9) |
From eqn (9) the natural logarithm can be applied on both sides of the equation as the logarithm is a positive monotone transformation which does not alter the position of the extreme. After reordering the equation, the negative log posterior can be renamed to a cost function which leads to eqn (10):
 | (10) |
The minimum of the newly created cost function has to be found. The first term refers to the divergence to the initial distribution which should be small and the second term to the error to the experiment which also should be minimized:
| optimize cost(w0, w1, …, wN) → min | (11) |
The choice of θ is system specific and an expression of the quality of the initial distribution of weights. A large value of θ results in an optimization that stays very faithful to w0 and accepts more significant violations in the data. A value of θ close to zero leads to a better agreement with the experimental data but w0 is only of little relevance, which exposes the risk of overfitting.54
The second term of the cost function evaluates the error of the simulated observables Ocalc compared to the measured observables Oexp and resembles closely the  distribution, except for a constant. The constant is utilized in some implementations while not in others. This leads to a change of scale of theta depending on the specific implementation. In both cases, the value of
distribution, except for a constant. The constant is utilized in some implementations while not in others. This leads to a change of scale of theta depending on the specific implementation. In both cases, the value of 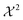 quantifies the error between the experiment and the simulation (weighted by wt).60
quantifies the error between the experiment and the simulation (weighted by wt).60
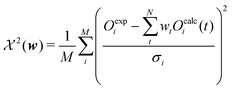 | (12) |
Eqn (12) may be adjusted if the measured observable is not a scalar with a specific value but a range of valid results. In the case of NOE analysis the measured distance of a proton pair is described by a range of values enclosed by a lower and upper bound.71 For reweighting lower and upper bounds are set independently as one-sided limits; therefore implementations must make sure that only violated bounds contribute to eqn (12).
3.2 The minimum relative entropy (MRE) method
The minimum relative entropy method allows to find a set of weights that minimizes the relative entropy compared to the ensemble obtained from a MD simulation while fulfilling predefined conditions.In addition to the relative entropy (Srel, eqn (7), ref. 69) it is common to define two additional types of entropy that depend on one or two probability distributions (Q and P):72,73
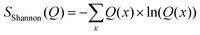 | (13) |
 | (14) |
The maximum entropy method introduced by Jaynes74,75 allows to find a probability distribution that is in agreement with external conditions while preserving maximal entropy given the conditions.76 The relative entropy can be interpreted as the information lost when using distribution Q(x) as an approximation of distribution P(x). If minimized, the distribution Q(x) can be assumed to be the distribution that meets all necessary conditions while requiring minimal additional information.77
The Shannon entropy (eqn (13)) reaches its maximum when the probability distribution is uniform.78 This property of the Shannon entropy explains why most methods in conformational ensemble reweighting that try to preserve the initial ensemble generated with MD are called maximum entropy methods. It can be shown (Appendix A.1) that the maximum entropy method can be a special case of the minimum relative entropy method if the weights w0 are uniform [ref. 79, pp. 291–292].
The relative entropy (also called Kullback–Leibler divergence, eqn (7)) is the difference between Shannon- and cross-entropy (eqn (14)) and a metric to evaluate the similarity of two probability distributions. If both discrete probability distributions Q and P are equal, the relative entropy is zero. The relative entropy is positive and increases with diverging distributions Q and P [ref. 70, p. 90]. An important property of the KL-divergence is it being not symmetric and failing to satisfy the triangle inequality, thus making it a divergence between the distributions and not a distance.80,81
From eqn (14) follows an alternative notation of the relative entropy:
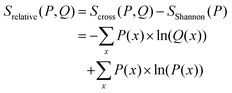 | (15) |
Due to the non-symmetry of the relative entropy a distinction between a forward case and a reversed case can be made (see ref. 80, pp. 71–74 and ref. 81–85). In the context of optimization methods, one of the two distributions is kept constant (P(x), reference distribution) while the other (Qv(x), approximated distribution) is being learned and therefore dependent on the optimization parameter.86
Forward KL-divergence (eqn (16))
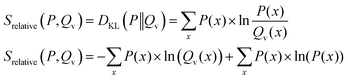 | (16) |
From eqn (16) it becomes apparent that the contribution of the Shannon entropy is independent from the variable distribution Qv(x) and doesn't influence the minimization of the relative entropy. Therefore, the minimization of the relative entropy in the forward formulation is equal to the minimization of the cross-entropy and often referred to as the minimum cross entropy method in literature.
It can be shown that the forward formulation of the KL-divergence is closely related to the maximum likelihood P(x) is chosen (Appendix A.2).
Reversed KL-divergence (eqn (17))
 | (17) |
In contrast to the forward formulation, the contribution of the Shannon entropy to the relative entropy is variable and cannot be ignored when using the reversed KL-divergence as loss function.
In practice, differences become relevant when systems with a low number of independent parameters are optimized. Fig. 3 shows an example illustrating the influence of the chosen loss function on the fitted distribution. The bimodal reference distribution P(x) in blue is to be approximated by a single Gaussian optimised distribution, Qv(x). An optimization using the forward KL-divergence is referred to as mode-covering (inclusive) and leads to a single broad distribution. The reversed KL-divergence optimization is called a mode seeking (exclusive) approach and leads to the selection of a single signal in the reference distribution.83,84,86 The relation of the reverse formulation of the minimum relative entropy method to the maximum entropy method given a uniform target distribution is shown in Appendix A.1.
The directionality of KL-divergence based loss functions is an important theoretical consideration when designing algorithms in data science. While Fig. 3 shows an example specifically designed to present the directionality of the loss function, its effect during reweighting of ensembles is more subtle. Nevertheless, we see minor differences when optimizing the same data using the same strength of optimization θ. In our work Stöckelmaier et al.87 we created a validation system for ensemble refinement using the small dialanine peptide. While a quantitative assessment of the algorithm presented here is beyond the scope of this work, we would like to refer to the Appendix A.3 showing the impact of the loss function directionality of Bayesian ensemble refinement. This and other comparisons in our previous work87 indicate, that the effect of the directionality is not dramatic but noticeable when refining conformational ensembles.
An initial distribution of weights (w0) is typically available from MD. It may be uniform if the data comes straight from MD or non-uniform if the data is reduced by clustering the conformational ensemble or obtained from biased ensemble methods like replica exchange MD. Both cases can be treated with the minimum relative entropy method. If the initial ensemble has been reduced by clustering, each calculated observable representing the cluster should, by itself, be an ensemble-average of the cluster.88 To optimize the conformational ensemble, the set of weights wopt has to be found that minimizes the relative entropy S (eqn (18)) in reference to w0:
 | (18) |
However, the minimization should be performed obeying two boundary conditions. The first represents the condition that the calculated and experimental ensemble averages of the observables should match:
 | (19) |
The second condition is a reformulation of eqn (3) and enforces that the updated probability distribution remains normalized:
 | (20) |
An optimization under the constraints given by eqn (19) and (20) can be solved using Lagrange-multipliers, λi and μ. The sign in front of each condition term does not influence the solution.
 | (21) |
The partial derivative of eqn (21) with respect to each vector element wt is taken:
 | (22) |
This equation can be rearranged and we can define λ0 as:
| λ0 := 1 + μ | (23) |
such that
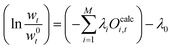 | (24) |
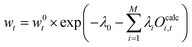 | (25) |
 | (26) |
The term e−λ0 should be interpreted as normalization term. The value of e−λ0 can be obtained using the condition (20) which leads to eqn (27):
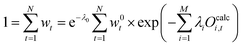 | (27) |
We define a partition function, Z:
 | (28) |
 | (29) |
Combining eqn (26) and (29) the reweighted probabilities can be calculated:
 | (30) |
Eqn (30) connects the optimal weights for the N conformations in the ensemble to the Lagrange multipliers, λi for each of the M observables. This significantly reduces the dimensionality of the optimization problem, but solving a M-dimensional optimization problem still remains a difficult task. To calculate the vector λ it is possible to turn the problem into an easier optimization problem using the Lagrangian duality formalism. A solution is described in ref. 48, 89 and 90 and used in ref. 29, 91 and 92.
The concave Lagrangian dual Γ(λ,μ) is introduced as a function of the primal optimization problem  :
:
 | (31) |
Remember that the vector wopt should fulfill conditions (19) and (20). Accordingly, for the optimal solution, the condition terms of eqn (21) become zero. To calculate the infimum of the Lagrangian dual  , eqn (24) gets substituted into the entropy term of eqn (21) which leads to eqn (32):
, eqn (24) gets substituted into the entropy term of eqn (21) which leads to eqn (32):
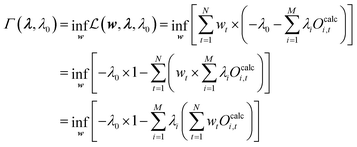 | (32) |
Replacing −λ0 with eqn (29) then leads to:
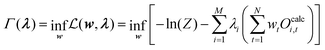 | (33) |
From the initial condition (19) it is defined that  .
.
 | (34) |
To determine the optimal Lagrangian multipliers, the maximum of the concave Lagrangian dual is determined (supλΓ(λ)). The function Γ (eqn (34)) should be maximized without constraints.
Treatment of experimental error in the MRE method. Until now, the resulting weights are constrained to exactly recover the experimental average (eqn (19)). In many cases, solving the fully constrained formulation of the problem would lead to unwarranted overfitting as both the simulated observables and the experimental data contain some level of error which needs to be taken into account. Error treatment as shown below was described by Cesari et al.,29,91 introducing:
| Oexpi + 〈εi〉 = 〈Ocalci〉 | (35) |
Instead of the original condition (19) an error corrected condition  can be used. Therefore, the modified Γ-function for optimization problems including error is obtained:
can be used. Therefore, the modified Γ-function for optimization problems including error is obtained:
 | (36) |
Cesari et al.29 further describe the methodology of treating a Gaussian shaped error with preassigned variance. The third term in eqn (36), describing the error, becomes:
 | (37) |
Finally, a proportionality constant θ is introduced which defines the influence of the error εi on the optimization. A choice of a large θ indicates that larger error are tolerated. If Gaussian shaped errors are assumed, eqn (38) should be maximized:
 | (38) |
According to the definition of the forward KL-divergence, we define the relative entropy as
 | (39) |
The Lagrangian function is set up similar to (21) but with the alternative entropy term. The partial derivative of the modified Lagrangian is taken and set to zero.
 | (40) |
Here, a significant difference to eqn (22) can be seen as the fraction w0t/wt in the equation is outside of a logarithm. The solution for the forward direction can still be formulated in terms of an optimization of the Langrange multipliers (viaeqn (41)) but solving the problem as described previously is difficult, as the 'normalization constant’ μ cannot be calculated easily.
 | (41) |
In practice, the reverse formulation of the KL-divergence remains more accessible when using a Lagrangian solution strategy. It is the regular choice as loss function even though the mode-covering behavior of the forward case remains interesting for the optimization of molecular ensembles. Non-Lagrangian solution strategies to optimize ensembles using the forward case remain attractive and can be seen as a further area of research. As a basic solution, Bayesian ensemble refinement described in Section 3.1 can easily be modified to apply both the forward and the reversed KL-divergence.
3.3 Estimation of the hyper-parameter θ
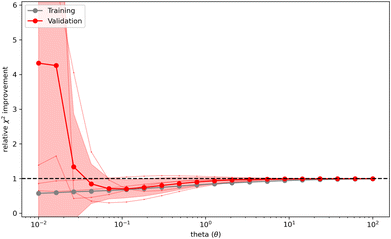
Both the direct optimization of the weights using Bayesian ensemble refinement in Section 3.1 as well as the (error-aware) indirect optimization using the maximum entropy formalism in Section 3.2 uses a hyper parameter theta (θ), to set the strength of the optimization. It can be freely tuned taking any positive value and sets the balance between faithfulness to w0 and reduction in error compared to the experimental data. The optimal choice of θ avoids overfitting of the data while allowing sufficient reweighting. As θ is difficult to set in advance, a strategy to find a suitable value for theta has to be introduced.Bottaro et al.92 describes a five-fold cross-validation to estimate the optimal value of θ for their implementation of the reversed maximum entropy approach. The observables and the conformational ensemble are split into a training and validation data-set. The training set is used to calculate the optimized weights w while the validation set uses these weights to calculate the relative 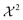 improvement (
improvement ( , where
, where  is calculated using the initial weights w0) as a validation score. This process is repeated for a set of different θ values. If a set of weights improves not only the agreement between simulation and experiment in regard to the fitted observables, but also in regard to previously unknown ones from the validation set, a validation score below one is calculated. It may be interpreted as the ability to find a set of weights compatible with the prior information, simulated and experimental data that is likely an improvement over the initial set of weights. On the other hand, a validation score over one may be interpreted as the inability to find a set of weights in agreement with prior information, simulated and experimental data that is an improvement over the initial set of weights in regard to previously unknown observables. Thus, it may indicate overfitting of the data. A plot (Fig. 4) showing the relative
is calculated using the initial weights w0) as a validation score. This process is repeated for a set of different θ values. If a set of weights improves not only the agreement between simulation and experiment in regard to the fitted observables, but also in regard to previously unknown ones from the validation set, a validation score below one is calculated. It may be interpreted as the ability to find a set of weights compatible with the prior information, simulated and experimental data that is likely an improvement over the initial set of weights. On the other hand, a validation score over one may be interpreted as the inability to find a set of weights in agreement with prior information, simulated and experimental data that is an improvement over the initial set of weights in regard to previously unknown observables. Thus, it may indicate overfitting of the data. A plot (Fig. 4) showing the relative  improvement as function of θ is used to tune the strength of the optimization. In the best case, a well behaving curve with little uncertainty is shown, indicating an ideal choice of θ at the minimum of the curve. In practice, the curve often shows substantial levels of noise and lacks an obvious minimum but shows a steep increase of the relative
improvement as function of θ is used to tune the strength of the optimization. In the best case, a well behaving curve with little uncertainty is shown, indicating an ideal choice of θ at the minimum of the curve. In practice, the curve often shows substantial levels of noise and lacks an obvious minimum but shows a steep increase of the relative  improvement at low theta values. In this case, it may be reasonable to choose a value of θ just before the steep increase in slope manifests. To confirm the plausibility of the chosen θ, the resulting ensemble after reweighting should be checked manually to confirm that the new ensemble remains plausible, both in size and conformations.
improvement at low theta values. In this case, it may be reasonable to choose a value of θ just before the steep increase in slope manifests. To confirm the plausibility of the chosen θ, the resulting ensemble after reweighting should be checked manually to confirm that the new ensemble remains plausible, both in size and conformations.
Alternatively, it is also possible to tune the strength of optimization such that the optimized ensemble evaluates to an error estimate of  .60,93,94 A
.60,93,94 A 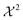 -value of one quantifies that the average error of the ensemble is equal to the sum of uncertainty from experiment and simulation. While this approach is straightforward at first glance, it assumes that the uncertainty from simulation and experimental measurement is additive and well characterized. In many practical application, as in our recent work,87 both the uncertainty from simulation and experiment is guessed, making the absolute value of
-value of one quantifies that the average error of the ensemble is equal to the sum of uncertainty from experiment and simulation. While this approach is straightforward at first glance, it assumes that the uncertainty from simulation and experimental measurement is additive and well characterized. In many practical application, as in our recent work,87 both the uncertainty from simulation and experiment is guessed, making the absolute value of  a reasonable indicator but difficult to use as a conclusive criterion.
a reasonable indicator but difficult to use as a conclusive criterion.
3.4 Mutual similarities and differences
Bayesian ensemble refinement and the minimum relative entropy method show similarities and differences in regard to each other. Their relationship with the maximum entropy principle is mutual but their specific properties show interesting differences. Additional information about the connection between Bayesian probability theory and maximum entropy methods can be found in the literature, where the work of Jaynes95 and Skilling96 should be noted.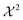 -like error, allowing for a compensation of errors. In the minimum relative entropy method θ scales the error constraint between simulation and experiment while in the classical Bayesian approach the influence of error and entropy regularization gets balanced.
-like error, allowing for a compensation of errors. In the minimum relative entropy method θ scales the error constraint between simulation and experiment while in the classical Bayesian approach the influence of error and entropy regularization gets balanced.
4 Conclusions
Maximum entropy based ensemble optimization shows promising properties to allow the integration of experimental and simulated data. To gain a better understanding of flexible and intrinsically disordered proteins, the combination of experimental techniques like liquid state NMR and molecular dynamics (MD) simulations seems essential. Contrary to globular proteins, flexible proteins cannot be described using just a single (crystal) structure but require the creation of a conformational ensemble. Each conformer within the ensemble is associated with a statistical weight quantifying their importance to the ensemble. The calculation of these weights is non-trivial and requires computational studies. MD allows to sample appropriate weights but is prone to inaccuracies, especially with disordered proteins where the sampling may be expected to be incomplete. Maximum entropy based ensemble optimization allows us to adapt these initial weights, such that the resulting ensemble remains close to the MD-simulation and agrees with the experimental data.In the last decade, numerous implementations of maximum entropy methods have been developed and applied. The theoretical foundation behind the methods is based on the established information theory by Claude Shannon. While the theory behind ensemble refinement is solid and well established, most methods work as black-box optimizer for many users. In this work, we focused on the foundation of the technique to promote a broader understanding of the methods as we believe this is important to allow for proper interpretation of the refined conformational ensembles. We want to emphasize that reweighting methods require well curated data, both simulated, experimental and in regard to prior weights. Ill curated data used during the process of reweighting may lead to misleading findings that are difficult to spot and may promote incorrect findings. In summary, however, it can be stated that reweighting works well if used carefully with well curated data. Maximum entropy methods show a solid theoretical foundation and promising properties to integrate simulated and experimental data, allowing new and exciting insights into molecular behavior.
Author contributions
JS reviewed and summarized the theoretical foundation of maximum entropy methods and wrote the manuscript. CO acted as supervisor, organized the funding of the project, edited and reviewed the writing of the manuscript. All authors have read and agreed to the published version of the manuscript.Conflicts of interest
The authors declare that there are no conflicts of interest.Data availability
No primary research results, software or code have been included and no new data were generated or analysed as part of this review.Appendix: A
A.1 Maximum entropy – minimum relative entropy79
Consider the reversed formulation of the Kullback–Leibler divergence: | (42) |
In the case of a uniform distribution P(x) this leads to:
 | (43) |
 | (44) |
 | (45) |
| DKL(Qv‖P) = −(SShannon) + const | (46) |
As ln(N) is a constant, optimizing Qv with respect to minimizing the relative entropy is equivalent to maximizing the Shannon entropy if the target distribution is uniform. Thus, maximum entropy optimizations are closely related to the minimum relative entropy optimizations in its reversed formulation.
A.2 Log probabilities – minimum relative entropy81
Consider the forward formulation of the Kullback–Leibler divergence: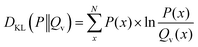 | (47) |
In the case of a uniform distribution P(x) this leads to:
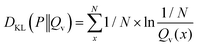 | (48) |
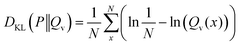 | (49) |
 | (50) |
 | (51) |
The first term of eqn (50) is constant. In consequence, the close relation between the relative entropy minimization in its forward formulation and the negative log-likelihood minimization is shown if a uniform distribution P(x) is chosen.
A.3 The directional dependence of Bayesian ensemble refinement
Fig. 5 shows the weights of the reweighted dialanine system which is described in ref. 87. To interpret the results, the ensemble preservation (e.p.) metric as introduced in ref. 87 is used. In a simplified way, the e.p. can be understood such, that a preservation of 100 indicates that all conformations remain in the ensemble; a preservation of 33 indicates that only one third of initial conformations still contribute to the optimized ensemble. | ||
| Fig. 5 The loss-function of Bayesian ensemble refinement allows for an easy implementation of both the forward and reversed direction of the KL-divergence. Using the dialanine system with equipotential (uniform) initial weights as presented in ref. 87 to test ensemble refinement, the directional dependence of Bayesian ensemble refinement was tested. The top row shows the result of the reweighting using the forward (mode-covering) direction with four different values of theta tested. The second row shows the same system with the same θ-values tested using the reversed (mode-seeking) direction. | ||
Column two (θ = 0.25) demonstrates the subtle differences between the directions. While in general the same regions get populated, the ensemble preservation of the forward (mode-covering) direction remains higher with (on average) lower weights in the preferred β-sheet region.
Acknowledgements
Financial support by the Austrian Science Fund (FWF; grant number I-4588) and by the Austrian Federal Ministry for Digital and Economic Affairs, the National Foundation for Research, Technology and Development and the Christian Doppler Research Association is gratefully acknowledged. We thank Kresten Lindorff-Larsen and Fernando Cordero for the good discussions on the topic.References
- E. Fischer, Einfluss der Configuration auf die Wirkung der Enzyme, Ber. Dtsch. Chem. Ges., 1894, 27, 2985–2993 CrossRef CAS.
- C. B. Anfinsen, Principles that Govern the Folding of Protein Chains, Science, 1973, 181, 223–230 CrossRef CAS PubMed.
- V. N. Uversky and P. Kulkarni, Intrinsically disordered proteins: Chronology of a discovery, Biophys. Chem., 2021, 279, 106694 CrossRef CAS PubMed.
- J. Ward, J. Sodhi, L. McGuffin, B. Buxton and D. Jones, Prediction and Functional Analysis of Native Disorder in Proteins from the Three Kingdoms of Life, J. Mol. Biol., 2004, 337, 635–645 CrossRef CAS PubMed.
- P. Kulkarni, V. B. P. Leite, S. Roy, S. Bhattacharyya, A. Mohanty, S. Achuthan, D. Singh, R. Appadurai, G. Rangarajan, K. Weninger, J. Orban, A. Srivastava, M. K. Jolly, J. N. Onuchic, V. N. Uversky and R. Salgia, Intrinsically disordered proteins: Ensembles at the limits of Anfinsen's dogma, Biophys. Rev., 2022, 3, 011306 CrossRef CAS PubMed.
- F. Trovato, J. Trylska, P. J. Bond and P. G. Wolynes, Front. Mol. Biosci., 2021, 8, 797754 CrossRef PubMed.
- H. Wang, R. Xiong and L. Lai, Rational drug design targeting intrinsically disordered proteins, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2023, 13, e1685 CAS.
- D. Piovesan, A. Del Conte, M. Mehdiabadi, M. C. Aspromonte, M. Blum, G. Tesei, S. von Bülow, K. Lindorff-Larsen and S. C. E. Tosatto, MOBIDB in 2025: integrating ensemble properties and function annotations for intrinsically disordered proteins, Nucleic Acids Res., 2025, 53, D495–D503 CrossRef PubMed.
- Y. Chebaro, A. J. Ballard, D. Chakraborty and D. J. Wales, Intrinsically Disordered Energy Landscapes, Sci. Rep., 2015, 5, 10386 CrossRef PubMed.
- R. G. Viegas, I. B. S. Martins and V. B. P. Leite, Understanding the Energy Landscape of Intrinsically Disordered Protein Ensembles, J. Chem. Inf. Model., 2024, 64, 4149–4157 CrossRef CAS PubMed.
- M. R. Jensen, M. Zweckstetter, J.-R. Huang and M. Blackledge, Exploring Free-Energy Landscapes of Intrinsically Disordered Proteins at Atomic Resolution Using NMR Spectroscopy, Chem. Rev., 2014, 114, 6632–6660 CrossRef CAS PubMed.
- R. M. Scheek, A. E. Torda, J. Kemmink and W. F. van Gunsteren, in Computational Aspects of the Study of Biological Macromolecules by Nuclear Magnetic Resonance Spectroscopy, ed. J. C. Hoch, F. M. Poulsen and C. Redfield, Springer US, Boston, MA, 1991, pp. 209–217 Search PubMed.
- H. Frauenfelder, S. G. Sligar and P. G. Wolynes, The Energy Landscapes and Motions of Proteins, Science, 1991, 254, 1598–1603 CrossRef CAS PubMed.
- K. Lindorff-Larsen, R. B. Best, M. A. DePristo, C. M. Dobson and M. Vendruscolo, Simultaneous determination of protein structure and dynamics, Nature, 2005, 433, 128–132 CrossRef CAS PubMed.
- C. K. Fisher and C. M. Stultz, Constructing ensembles for intrinsically disordered proteins, Curr. Opin. Struct. Biol., 2011, 21, 426–431 CrossRef CAS PubMed.
- Y. V. Borodina, E. Bolton, F. Fontaine and S. H. Bryant, Assessment of Conformational Ensemble Sizes Necessary for Specific Resolutions of Coverage of Conformational Space, J. Chem. Inf. Model., 2007, 47, 1428–1437 CrossRef CAS PubMed.
- W. Liu, X. Liu, G. Zhu, L. Lu and D. Yang, A Method for Determining Structure Ensemble of Large Disordered Protein: Application to a Mechanosensing Protein, J. Am. Chem. Soc., 2018, 140, 11276–11285 CrossRef CAS PubMed.
- T. Schwede, J. Kopp, N. Guex and M. C. Peitsch, SWISS-MODEL: An automated protein homology-modeling server, Nucleic Acids Res., 2003, 31, 3381–3385 CrossRef CAS PubMed.
- M. Baek, F. DiMaio, I. Anishchenko, J. Dauparas, S. Ovchinnikov, G. R. Lee, J. Wang, Q. Cong, L. N. Kinch, R. D. Schaeffer, C. Millán, H. Park, C. Adams, C. R. Glassman, A. DeGiovanni, J. H. Pereira, A. V. Rodrigues, A. A. van Dijk, A. C. Ebrecht, D. J. Opperman, T. Sagmeister, C. Buhlheller, T. Pavkov-Keller, M. K. Rathinaswamy, U. Dalwadi, C. K. Yip, J. E. Burke, K. C. Garcia, N. V. Grishin, P. D. Adams, R. J. Read and D. Baker, Accurate prediction of protein structures and interactions using a three-track neural network, Science, 2021, 373, 871–876 CrossRef CAS PubMed.
- J. Jumper, R. Evans, A. Pritzel, T. Green, M. Figurnov, O. Ronneberger, K. Tunyasuvunakool, R. Bates, A. Žídek, A. Potapenko, A. Bridgland, C. Meyer, S. A. A. Kohl, A. J. Ballard, A. Cowie, B. Romera-Paredes, S. Nikolov, R. Jain, J. Adler, T. Back, S. Petersen, D. Reiman, E. Clancy, M. Zielinski, M. Steinegger, M. Pacholska, T. Berghammer, S. Bodenstein, D. Silver, O. Vinyals, A. W. Senior, K. Kavukcuoglu, P. Kohli and D. Hassabis, Highly accurate protein structure prediction with AlphaFold, Nature, 2021, 596, 583–589 CrossRef CAS PubMed.
- S. Lewis, T. Hempel, J. Jiménez-Luna, M. Gastegger, Y. Xie, A. Y. K. Foong, V. G. Satorras, O. Abdin, B. S. Veeling, I. Zaporozhets, Y. Chen, S. Yang, A. Schneuing, J. Nigam, F. Barbero, V. Stimper, A. Campbell, J. Yim, M. Lienen, Y. Shi, S. Zheng, H. Schulz, U. Munir, R. Tomioka, C. Clementi and F. Noé, Scalable emulation of protein equilibrium ensembles with generative deep learning, bioRxiv, 2025, preprint DOI:10.1101/2024.12.05.626885.
- M. Cagiada, F. E. Thomasen, S. Ovchinnikov, C. M. Deane and K. Lindorff-Larsen, AF2: Predicting protein side-chain rotamer distributions with AlphaFold2, bioRxiv, 2025, preprint DOI:10.1101/2025.04.16.649219.
- G. Monteiro da Silva, J. Y. Cui, D. C. Dalgarno, G. P. Lisi and B. M. Rubenstein, Highthroughput prediction of protein conformational distributions with subsampled AlphaFold2, Nat. Commun., 2024, 15, 2464 CrossRef CAS PubMed.
- D. Sala, F. Engelberger, H. S. Mchaourab and J. Meiler, Modeling conformational states of proteins with AlphaFold, Curr. Opin. Struct. Biol., 2023, 81, 102645 CrossRef CAS PubMed.
- S. Piana, K. Lindorff-Larsen and D. E. Shaw, How Robust Are Protein Folding Simulations with Respect to Force Field Parameterization?, Biophys. J., 2011, 100, L47–L49 CrossRef CAS PubMed.
- K. Lindorff-Larsen, S. Piana, R. O. Dror and D. E. Shaw, How Fast-Folding Proteins Fold, Science, 2011, 334, 517–520 CrossRef CAS PubMed.
- S. Piana, K. Lindorff-Larsen and D. E. Shaw, Protein folding kinetics and thermodynamics from atomistic simulation, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 17845–17850 CrossRef CAS PubMed.
- W. Kang, F. Jiang and Y.-D. Wu, How to strike a conformational balance in protein force fields for molecular dynamics simulations?, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1578 CAS.
- A. Cesari, S. Reißer and G. Bussi, Using the Maximum Entropy Principle to Combine Simulations and Solution Experiments, Computation, 2018, 6(1), 15, DOI:10.3390/computation6010015.
- F. E. Thomasen and K. Lindorff-Larsen, Conformational ensemble of intrinsically disordered proteins and flexible multidomain proteins, Biochem. Soc. Trans., 2021, 50(1), 541–554 CrossRef PubMed.
- C. Czaplewski, Z. Gong, E. A. Lubecka, K. Xue, C. Tang and A. Liwo, Recent Developments in Data-Assisted Modeling of Flexible Proteins, Front. Mol. Biosci., 2021, 8 DOI:10.3389/fmolb.2021.765562.
- R. Gama Lima Costa and D. Fushman, Reweighting methods for elucidation of conformation ensembles of proteins, Curr. Opin. Struct. Biol., 2022, 77, 102470 CrossRef CAS PubMed.
- V. Ozenne, R. Schneider, M. Yao, J.-R. Huang, L. Salmon, M. Zweckstetter, M. R. Jensen and M. Blackledge, Mapping the Potential Energy Landscape of Intrinsically Disordered Proteins at Amino Acid Resolution, J. Am. Chem. Soc., 2012, 134, 15138–15148 CrossRef CAS PubMed.
- W. F. van Gunsteren, J. R. Allison, X. Daura, J. Dolenc, N. Hansen, A. E. Mark, C. Oostenbrink, V. H. Rusu and L. J. Smith, Deriving Structural Information from Experimentally Measured Data on Biomolecules, Angew. Chem., Int. Ed., 2016, 55, 15990–16010 CrossRef CAS PubMed.
- S. Grutsch, S. Brüschweiler and M. Tollinger, NMR Methods to Study Dynamic Allostery, PLoS Comput. Biol., 2016, 12, 1–20 CrossRef PubMed.
- A. R. Camacho-Zarco, V. Schnapka, S. Guseva, A. Abyzov, W. Adamski, S. Milles, M. R. Jensen, L. Zidek, N. Salvi and M. Blackledge, NMR Provides Unique Insight into the Functional Dynamics and Interactions of Intrinsically Disordered Proteins, Chem. Rev., 2022, 122, 9331–9356 CrossRef CAS PubMed.
- J. Tropp, Dipolar relaxation and nuclear Overhauser effects in nonrigid molecules: The effect of fluctuating internuclear distances, J. Chem. Phys., 1980, 72, 6035–6043 CrossRef CAS.
- X. Daura, I. Antes, W. F. van Gunsteren, W. Thiel and A. E. Mark, The effect of motional averaging on the calculation of NMR-derived structural properties, Proteins: Struct., Funct., Bioinf., 1999, 36, 542–555 CrossRef CAS.
- B. Zagrovic and W. F. van Gunsteren, Comparing atomistic simulation data with the NMR experiment: How much can NOEs actually tell us?, Proteins, 2006, 63, 210–218 CrossRef CAS PubMed.
- R. Rangan, M. Bonomi, G. T. Heller, A. Cesari, G. Bussi and M. Vendruscolo, Determination of Structural Ensembles of Proteins: Restraining vs. Reweighting, J. Chem. Theory Comput., 2018, 14, 6632–6641 CrossRef CAS PubMed.
- M. Pelikan, G. L. Hura and M. Hammel, Structure and flexibility within proteins as identified through small angle X-ray scattering, Gen. Physiol. Biophys., 2009, 28, 174–189 CrossRef CAS PubMed.
- K. Berlin, C. A. Castañeda, D. Schneidman-Duhovny, A. Sali, A. Nava-Tudela and D. Fushman, Recovering a Representative Conformational Ensemble from Underdetermined Macromolecular Structural Data, J. Am. Chem. Soc., 2013, 135, 16595–16609 CrossRef CAS PubMed.
- E. C. Ihms and M. P. Foster, MESMER: minimal ensemble solutions to multiple experimental restraints, Bioinformatics, 2015, 31, 1951–1958 CrossRef CAS PubMed.
- Y. Chen, S. L. Campbell and N. V. Dokholyan, Deciphering Protein Dynamics from NMR Data Using Explicit Structure Sampling and Selection, Biophys. J., 2007, 93, 2300–2306 CrossRef CAS PubMed.
- G. Nodet, L. Salmon, V. Ozenne, S. Meier, M. R. Jensen and M. Blackledge, Quantitative Description of Backbone Conformational Sampling of Unfolded Proteins at Amino Acid Resolution from NMR Residual Dipolar Couplings, J. Am. Chem. Soc., 2009, 131, 17908–17918 CrossRef CAS PubMed.
- P. Bernadó, E. Mylonas, M. V. Petoukhov, M. Blackledge and D. I. Svergun, Structural Characterization of Flexible Proteins Using Small-Angle X-ray Scattering, J. Am. Chem. Soc., 2007, 129, 5656–5664 CrossRef PubMed.
- B. Różycki, Y. C. Kim and G. Hummer, SAXS Ensemble Refinement of ESCRT-III CHMP3 Conformational Transitions, Structure, 2011, 19, 109–116 CrossRef PubMed.
- J. W. Pitera and J. D. Chodera, On the Use of Experimental Observations to Bias Simulated Ensembles, J. Chem. Theory Comput., 2012, 8, 3445–3451 CrossRef CAS PubMed , PMID: 26592995.
- W. Boomsma, J. Ferkinghoff-Borg and K. Lindorff-Larsen, Combining Experiments and Simulations Using the Maximum Entropy Principle, PLoS Comput. Biol., 2014, 10, 1–9 CrossRef PubMed.
- H. T. A. Leung, O. Bignucolo, R. Aregger, S. A. Dames, A. Mazur, S. Bernèche and S. Grzesiek, A Rigorous and Efficient Method To Reweight Very Large Conformational Ensembles Using Average Experimental Data and To Determine Their Relative Information Content, J. Chem. Theory Comput., 2016, 12, 383–394 CrossRef CAS PubMed.
- M. Hermann and J. S. Hub, SAXS-Restrained Ensemble Simulations of Intrinsically Disordered Proteins with Commitment to the Principle of Maximum Entropy, J. Chem. Theory Comput., 2019, 15, 5103–5115 CrossRef CAS PubMed.
- S. Bottaro, T. Bengtsen and K. Lindorff-Larsen, in Structural Bioinformatics: Methods and Protocols, ed. Z. Gáspári, Springer US, New York, NY, 2020, pp. 219–240 Search PubMed.
- Y. Yamamori and K. Tomii, An ensemble reweighting method for combining the information of experiments and simulations, Chem. Phys. Lett., 2021, 779, 138821 CrossRef CAS.
- G. Hummer and J. Köfinger, Bayesian ensemble refinement by replica simulations and reweighting, J. Chem. Phys., 2015, 143, 243150 CrossRef PubMed.
- C. K. Fisher, A. Huang and C. M. Stultz, Modeling Intrinsically Disordered Proteins with Bayesian Statistics, J. Am. Chem. Soc., 2010, 132, 14919–14927 CrossRef CAS PubMed.
- A. Sethi, D. Anunciado, J. Tian, D. M. Vu and S. Gnanakaran, Deducing conformational variability of intrinsically disordered proteins from infrared spectroscopy with Bayesian statistics, Chem. Phys., 2013, 422, 143–155 CrossRef CAS PubMed.
- X. Xiao, N. Kallenbach and Y. Zhang, Peptide Conformation Analysis Using an Integrated Bayesian Approach, J. Chem. Theory Comput., 2014, 10, 4152–4159 CrossRef CAS PubMed.
- D. H. Brookes and T. Head-Gordon, Experimental Inferential Structure Determination of Ensembles for Intrinsically Disordered Proteins, J. Am. Chem. Soc., 2016, 138, 4530–4538 CrossRef CAS PubMed.
- L. D. Antonov, S. Olsson, W. Boomsma and T. Hamelryck, Bayesian inference of protein ensembles from SAXS data, Phys. Chem. Chem. Phys., 2016, 18, 5832–5838 RSC.
- J. Köfinger, L. S. Stelzl, K. Reuter, C. Allande, K. Reichel and G. Hummer, Efficient Ensemble Refinement by Reweighting, J. Chem. Theory Comput., 2019, 15, 3390–3401 CrossRef PubMed , PMID: 30939006.
- C. Paissoni, A. Jussupow and C. Camilloni, Determination of Protein Structural Ensembles by Hybrid-Resolution SAXS Restrained Molecular Dynamics, J. Chem. Theory Comput., 2020, 16, 2825–2834 CrossRef CAS PubMed.
- R. M. Raddi, Y. Ge and V. A. Voelz, BICePs v2.0: Software for Ensemble Reweighting Using Bayesian Inference of Conformational Populations, J. Chem. Inf. Model., 2023, 63, 2370–2381 CrossRef CAS PubMed.
- A. P. Latham and B. Zhang, Maximum Entropy Optimized Force Field for Intrinsically Disordered Proteins, J. Chem. Theory Comput., 2020, 16, 773–781 CrossRef PubMed.
- I. Bertini, A. Giachetti, C. Luchinat, G. Parigi, M. V. Petoukhov, R. Pierattelli, E. Ravera and D. I. Svergun, Conformational Space of Flexible Biological Macromolecules from Average Data, J. Am. Chem. Soc., 2010, 132, 13553–13558 CrossRef CAS PubMed.
- I. Bertini, L. Ferella, C. Luchinat, G. Parigi, M. V. Petoukhov, E. Ravera, A. Rosato and D. I. Svergun, MaxOcc: a web portal for maximum occurrence analysis, J. Biomol. NMR, 2012, 53, 271–280 CrossRef CAS PubMed.
- D. Medeiros Selegato, C. Bracco, C. Giannelli, G. Parigi, C. Luchinat, L. Sgheri and E. Ravera, Comparison of Different Reweighting Approaches for the Calculation of Conformational Variability of Macromolecules from Molecular Simulations, ChemPhysChem, 2021, 22, 127–138 CrossRef CAS PubMed.
- M. Bonomi, G. T. Heller, C. Camilloni and M. Vendruscolo, Principles of protein structural ensemble determination, Curr. Opin. Struct. Biol., 2017, 42, 106–116 CrossRef CAS PubMed , Folding and binding • Proteins: Bridging theory and experiment.
- S. Orioli, A. H. Larsen, S. Bottaro and K. Lindorff-Larsen, Progress in Molecular Biology and Translational Science, in Computational Approaches for Understanding Dynamical Systems: Protein Folding and Assembly, ed. B. Strodel and B. Barz, Academic Press, 2020, pp. 123–176 Search PubMed.
- S. Kullback and R. A. Leibler, On Information and Sufficiency, Ann. Math. Stat., 1951, 22, 79–86 CrossRef.
- S. Boyd and L. Vandenberghe, Convex Optimization, Cambridge University Press, Cambridge, 2004 Search PubMed.
- L. J. Smith, M. J. Sutcliffe, C. Redfield and C. M. Dobson, Structure of Hen Lysozyme in Solution, J. Mol. Biol., 1993, 229, 930–944 CrossRef CAS PubMed.
- C. E. Shannon, A mathematical theory of communication, Bell Syst. Tech. J., 1948, 27, 379–423 CrossRef.
- A. Thomas, An introduction to entropy, cross entropy and KL divergence in machine learning, 2019 Search PubMed.
- E. T. Jaynes, Information Theory and Statistical Mechanics, Phys. Rev., 1957, 106, 620–630 CrossRef.
- E. T. Jaynes, Information Theory and Statistical Mechanics. II, Phys. Rev., 1957, 108, 171–190 CrossRef.
- T. M. Cover and J. A. Thomas, Chapter Introduction and Preview, John Wiley and Sons, Ltd, 1991, pp. 1–11 Search PubMed.
- M. Wittenberg, An Introduction to Maximum Entropy and Minimum Cross-entropy Estimation Using Stata, Stata J., 2010, 10, 315–330 CrossRef.
- A. Golan, G. Judge and D. J. Miller, Maximum Entropy Econometrics: Robust Estimation with Limited Data, Wiley, 1996, ch. 2 Search PubMed.
- J. C. Park and S. T. Abusalah, Maximum Entropy: A Special Case of Minimum Cross-entropy Applied to Nonlinear Estimation by an Artificial Neural Network, Complex Syst., 1997, 11, 289–307 Search PubMed.
- I. Goodfellow, Y. Bengio and A. Courville, Deep Learning, 2016, https://www.deeplearningbook.org Search PubMed.
- A. E. Abbas, A. H. Cadenbach and E. Salimi, A Kullback–Leibler View of Maximum Entropy and Maximum Log-Probability Methods, Entropy, 2017, 19(5), 232, DOI:10.3390/e19050232.
- C. M. Bishop, Pattern Recognition and Machine Learning (Information Science and Statistics), Springer-Verlag, Berlin, Heidelberg, 2006, ch. 10.1.2 Search PubMed.
- A. Chan, H. Silva, S. Lim, T. Kozuno, A. R. Mahmood and M. White, Greedification operators for policy optimization: investigating forward and reverse KL divergences, J. Mach. Learn. Res., 2022, 23, 253 Search PubMed.
- L. Vaitl, K. A. Nicoli, S. Nakajima and P. Kessel, Gradients should stay on path: better estimators of the reverse- and forward KL divergence for normalizing flows, Mach. Learn.: Sci. Technol., 2022, 3, 045006 Search PubMed.
- Y. Gu, L. Dong, F. Wei and M. Huang, MiniLLM: Knowledge Distillation of Large Language Models, arXiv, 2024, preprint, arXiv:2306.08543 DOI:10.48550/arXiv.2306.08543.
- M. Shen and N. Diamant, On KL Divergence in Discrete Spaces, https://argmax.blog/posts/kl-discrete/, accessed on 2024-08-14, 2022.
- J. Stöckelmaier, T. Capraz and C. Oostenbrink, Umbrella Refinement of Ensembles–An Alternative View of Ensemble Optimization, Molecules, 2025, 30(11), 2449, DOI:10.3390/molecules30112449.
- M. Kozak, A. Lewandowska, S. Ołdziej, S. Rodziewicz-Motowidło and A. Liwo, Combination of SAXS and NMR Techniques as a Tool for the Determination of Peptide Structure in Solution, J. Phys. Chem. Lett., 2010, 1, 3128–3131 CrossRef CAS.
- L. R. Mead and N. Papanicolaou, Maximum entropy in the problem of moments, J. Math. Phys., 1984, 25, 2404–2417 CrossRef.
- G. Alexander, Statistical Mechanics of Complex Systems, Lecture Notes 3-4, The University of Warwick, 2010 Search PubMed.
- A. Cesari, A. Gil-Ley and G. Bussi, Combining Simulations and Solution Experiments as a Paradigm for RNA Force Field Refinement, J. Chem. Theory Comput., 2016, 12, 6192–6200 CrossRef CAS PubMed , PMID: 27951677.
- S. Bottaro, T. Bengtsen and K. Lindorff-Larsen, Integrating Molecular Simulation and Experimental Data: A Bayesian/Maximum Entropy reweighting approach, bioRxiv, 2018, preprint DOI:10.1101/457952.
- S. F. Gull and G. J. Daniell, Image reconstruction from incomplete and noisy data, Nature, 1978, 272, 686–690 CrossRef.
- M. Groth, J. Malicka, C. Czaplewski, S. Ołdziej, L. Łankiewicz, W. Wiczk and A. Liwo, Maximum entropy approach to the determination of solution conformation of flexible polypeptides by global conformational analysis and NMR spectroscopy – Application to DNS1-c-[d-A2bu2, Trp4,Leu5]- enkephalin and DNS1-c-[d-A2bu2, Trp4, d-Leu5]enkephalin, J. Biomol. NMR, 1999, 15, 315–330 CrossRef CAS PubMed.
- E. T. Jaynes, in Maximum-Entropy and Bayesian Methods in Science and Engineering: Foundations, ed. G. J. Erickson and C. R. Smith, Springer, Netherlands, Dordrecht, 1988, pp. 25–29 Search PubMed.
- J. Skilling, in Maximum Entropy and Bayesian Methods: Cambridge, England, 1988, ed. J. Skilling, Springer, Netherlands, Dordrecht, 1989, pp. 45–52 Search PubMed.
| This journal is © the Owner Societies 2025 |