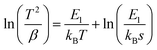Visualization of trap distribution in SrAl2O4:Eu2+,Dy3+ revealed by simulations of luminescence changes in charging and emission of persistent luminescence and thermoluminescence based on a random walk model†
Received
31st March 2025
, Accepted 14th June 2025
First published on 24th June 2025
Abstract
A stochastic analysis of the change in persistent luminescence (PersL) of Sr0.9Al2O4:Eu0.01x2+,Dy(0.1−0.01x)3+ (SAOEDx, x = 2, 4, 5, 6, 8, and 10) based on a one-dimensional random walk model (1D RWM) is presented. In the RWM, the excited electron is treated as a particle and can hop stochastically between reservoirs aligned in a straight line. Simulations of changes in PersL and the charging process are performed to determine the hopping probabilities and the electron distributions in reservoirs. We predict potential energies of the electron reservoirs through simulations of the thermoluminescence (TL) spectra of SAOEDx and present potential energy diagrams of the luminescence center and traps involved in PersL.
1. Introduction
Afterglow or persistent luminescence (PersL) has fascinated researchers involved in science and technology of light since the discovery of SrAl2O4:Eu2+,Dy3+ (SAOED) exhibiting outstanding long PersL over one night.1 Initially, PersL of SAOED has been employed for clock face as an alternative to radio-active materials or road signs without electrical power in the dark. Recently, it has been applied to photosensitizers and in vivo luminescent materials for photodynamic therapy,2 optical imaging,3 thermo-luminescence dosimetry,4 and solar cells.5 In addition to the application studies, many fundamental studies on PersL materials have been conducted to develop brighter phosphors with much longer lasting luminescence.6–13 The photoluminescence (PL) of SAOED originates from the 5d–4f electronic transition of Eu2+ as a dopant, where the excited electron in the 5d orbital is usually relaxed to the 4f orbital with a lifetime of around 1 μs along with green luminescence.14 For PersL, in contrast, the excited electron can be transferred to the host material by thermal or photoactivation and then be captured at trapping sites such as oxygen vacancies or defects, and thereafter the electron escaped from the trap by thermal activation returns to the 5d orbital of Eu3+ to reproduce the excited *Eu2+, resulting in emission of luminescence. The co-dopant Dy3+ plays the role of a better electron trap, which contributes to the longer PersL compared to oxygen vacancies or defects. The excited electron may be tightly captured by Dy3+ due to the electrostatic attraction, that is, Dy3+ might be reduced to Dy2+ by analogy to the result that Sm2+ and Ce4+ were detected during the investigation of the electron de-trapping process for an PersL material YPO4:Ce3+,Sm3+.15
Unlike PL, most PersL-decay features do not show a single-exponential curve. Therefore, the PersL decays have been frequently analysed using the double exponential equation,14
| | I(t) = I0 + A1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τ1) + A2 exp(−t/τ1) + A2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τ2). exp(−t/τ2). | (1) |
This equation consists of two exponential terms with the fast and slow decay times of
τ1 and
τ2, respectively, where
τ1 may be related to the de-trapping from the oxygen vacancy with a shallow trap depth and
τ2 may originate from the deep trap of Dy
3+. Occasionally, the PersL decay is analysed using the triple exponential function,
| | I(t) = I0 + A1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τ1) + A2 exp(−t/τ1) + A2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τ2) + A3 exp(−t/τ2) + A3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τ3). exp(−t/τ3). | (2) |
In this case, the additional component would be attributed to another trap involved in the PersL decay. Thus, it seems hard to find the electron-transfer mechanism satisfying the triple-exponential decay feature.
Some mechanisms for PersL proposed in previous studies are based on a local model composed of a single luminescent centre and a single trap, where an excited electron is assumed to move back-and-forth between the luminescent centre and the trap in the PersL process.16 In this model, the trap never captures two or more electrons, and the system of luminescence centres and traps is fully isolated and never interacts with others, that is, the electron cannot transfer to another trap in the adjacent system. In this situation, the observed PersL should always show a single-exponential decay curve, unless the electron transfer rates are slow compared with the time scale of PersL observation. On the other hand, a global model consisting of a luminescent centre, a trap, and the conduction band of host crystals has been applied to analyse the PersL decay.17 The conduction band may be the pathway of electrons between the luminescent centre and the trap, and therefore the electrons involved in PersL would be distributed over the entire crystal in the PersL process. The electron transfer between the excited *Eu2+ and the trap through the conduction band, based on the energy diagram with respect to the vacuum referred binding energy (VRBE) level,18,19 has been taken into account for the PersL process. When electron de-trapping is caused by thermal activation, as per the Boltzmann distribution law, the ratio of the number of electrons in the luminescent centre and those in traps (oxygen vacancies and Dy3+) is constant. Even when the excited electrons at the luminescence centre are consumed during the PersL emission, the immediate compensation of electrons from traps within the time scale of PersL observation guarantees that the ratio remains as the constant value. From this consideration, the PersL decay curve should follow a single exponential, even if multi-traps are incorporated in the global model. Therefore, it is better to consider that the electron transfer between the luminescence centre and the trap is slow or comparable to the time scale of PersL observation, when the PersL decay curve can be analysed with a double- or multi-exponential function. Previously, we showed that plural traps contribute to the complicated PersL-decay feature of β-Zn3(PO4)2:Mn2+ through the stochastic analysis using a one-dimensional random walk model (1D RWM).20 In the 1D RWM, the excited electron can randomly hop back-and-forth between adjacent traps and occasionally hop into the luminescent centre at the edge of the trap array to emit PersL.20 The simulation for electron migration based on the RWM was found to be simple yet significantly effective to reproduce the multi-exponential PersL decays.
For SAOED, we can observe the luminescence enhancement during continuous excitation corresponding to the charge of PresL.14 In this charging process, the luminescence intensity keeps increasing and eventually reaches the maximum value when the increase rate of excited electrons by photoexcitation is balanced with the depletion rate of electrons due to PL and PersL.16 The excited electrons seem to be continuously transferred to/from the host material and accumulated in traps until filling up. When the photoirradiation ceased, we can observe PersL alone from SAOED. Both PersL and charging processes should be accounted for by the electron transfer between the excited state of *Eu2+ and the trap state of (Eu3+–Trap−),11 where the electrons can move between the potential surfaces of these states by overwhelming the activation state by thermal energy. Even when PersL disappeared due to the depletion of trapped electrons, luminescence can be recovered by other excited electrons squeezed out from deep traps by heating. The thermoluminescence (TL) spectrum, which is the luminescence observed at a variety of temperatures, provides information of trap depths in SAOED. A peak temperature in the TL spectrum is related to the trap depth, and the peak intensity is proportional to the number of escaped electrons from the trap.21,22 Detailed analyses of the charging and PersL decay processes and the TL spectrum reveal the characteristics of dopants in SAOED and the mechanism of electron transfer between the luminescence centre and the trap involved in PersL.23
In this study, we show the effectiveness of the 1D RWM in simulating not only the non-exponential PersL decay curve of SAOED but also the charging process of PersL and TL. For the 1D RWM, we consider a train of multiple traps aligned in a straight line, where electrons can move back-and-forth between adjacent traps, and a luminescence centre is attached to the end of the trap line, where excitation of electrons and emission of luminescence take place. The simulation of the charging and PersL processes provides hopping probabilities among the luminescence centre and traps, corresponding to the electron transfer rates. Also, it provides evidence of electron population in traps, which helps to unveil the distribution of trap states in the SAOED crystal. In addition, the simulation of the TL spectrum provides the activation energy for each back-and-forth electron transfer process, which contributes to creating the energy diagram for traps involved in PersL for the SAOED crystal.
2. Simulation
2.1. A proposed mechanism of PersL emission
We propose a scheme for the PersL emission process based on the potential curves of Eu, *Eu, and trapping sites (Ts) in SAOED as shown in Fig. 1. The horizontal axis corresponds to a reaction coordinate along the electron transfer.11 We denote that the excitation rate of Eu is k0 and the relaxation rate of *Eu is ke. The electron transfer rates between potential curves are km (m = ±1, ±2, …, ±M), and the capturing rate at deep trap or quenching rate is kq. Although the tunnelling between potential curves might be necessary to consider the PersL emission mechanism, we do not treat the tunnelling explicitly in the RWM because all electrons are postulated to be particles. When focused on a single electron, a ground state configuration can be represented as G,
| G: (Eu)e − (*Eu) − (T1) − (T2) ⋯ − (TM) |
When *Eu is produced by photoexcitation, the electronic configuration can be represented as E0,
| E0: (Eu) − (*Eu)e − (T1) − (T2) ⋯ − (TM) |
The excited electron in the 5d orbital of *Eu can either relax to the 4f orbital to emit luminescence resulting in the G configuration or get trapped at closest trap T1 which is represented as the E1 configuration. The electron at T1 (E1) can move to the next trap T2 (E2) or return to the luminescence centre *Eu (E1). The electron at T2 can move to T3 and so on,
| E1: (Eu) − (*Eu) − (T1)e − (T2) ⋯ − (TM) |
| E2: (Eu) − (*Eu) − (T1) − (T2)e ⋯ − (TM) |
| EM: (Eu) − (*Eu) − (T1) − (T2) ⋯ − (TM)e |
Since there must be considerably many Eu ions in the bulk SAOED crystal, we should consider many sets of configurations {n0E0, n1E1, n2E2, …, nMEM} for the PersL process, where n0, n1, n2, …, nM are the numbers of respective excited configurations. We assume that this situation can be statistically equivalent to the following configuration with large numbers (n0, n1, n2, …, nM) of electrons in each trap:
| (*Eu)n0e − (T1)n1e − (T2)n2e ⋯ − (TM)nMe |
When n0 is decreased by luminescence emission, it will be compensated by the electron transfer from T1 to *Eu, which contributes to the elongation of the luminescence lifetime resulting in PersL. Since the emission intensity is proportional to the product of n0 and ke, the simulation of PersL decay is equivalent to the determination of n0ke as a function of t. The simulation will provide not only n0 and ke but also the other rate constants k±m and the number of electrons (n1, n2, …, nM) in each trap. For the charging process, since nm = 0 (m = 0, 1, 2, …, M) at the beginning, the photoexcitation contributes to an increase in n0 alone. After that, while n0 gradually decreases by the electron transfer to T1 and the relaxation to Eu, the continuous photoexcitation from Eu and the backward electron transfer from T1 contribute to an increase in n0. Thus, n0 initially increases and eventually will reach the maximum value when the increase and decrease rates of n0 are balanced. This charging process should also be simulated from n0ke as a function of t using the rate constants determined by the PersL simulation. Since the electron transfer rate km corresponds to the de-trapping rate of electrons from the potential well, it would strongly depend on temperature. Therefore, for simulations of the TL spectrum, the temperature dependence in the rate constant k±m can be incorporated as| | k±m = k0,±m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−ΔE±m/kBT), exp(−ΔE±m/kBT), | (3) |
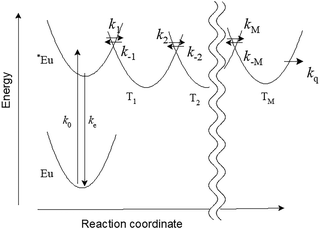 |
| | Fig. 1 A schematic energy diagram for Eu, *Eu, and Tm (m = 1, 2, …, M) for PersL of SAOED. km (m = ±1, ±2, …, ±M) are rate constants for electron transfer between potential wells. | |
where k0,±m (m = 1, 2, …, M) are pre-exponential factors, ΔE±m is trap depth or activation energy for each electron transfer process, kB is Boltzmann's constant, and T is the absolute temperature. The simulation of the TL spectrum is equivalent to the prediction of n0 as a function of T and contributes to the determination of the activation energies for electron transfer (ΔE±m).
2.2. A 1D random walk model (1D RWM) for the PersL
Based on the mechanism described above, we stochastically simulate the change in luminescence of the charging process, the non-exponential decay of PersL, and the TL spectrum using the 1D RWM as displayed in Fig. 2. The rectangle reservoirs being able to store electrons are aligned in a straight line, where each reservoir represents Eu, *Eu, or Ts. Eu is fixed at the left end, and *Eu is next to it. An array of Ts is set next to *Eu. We treat Dy3+ and other traps (oxygen vacancies or defects) as the same Tm. We assume that the electrons can move forward and backward between the very next reservoirs with certain probabilities, respectively, or can remain at the same reservoir. We introduce an electron-extinction path from TM to represent the dropping in deep traps or the quenching. In this model, we introduce a probability pm for each hopping between reservoirs instead of the electron-transfer rate constant km. Since the electron-transfer rate (km) to overwhelm the activation barrier (ΔEm) is represented as km = km,0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−ΔEm/kBT), we can describe the hopping probability as
exp(−ΔEm/kBT), we can describe the hopping probability as| | | pm = km/km,0 = exp(−ΔEm/kBT). | (4) |
 |
| | Fig. 2 Hopping probabilities (p0, pe, p±m, and pq) and numbers of electrons (N, N0, and Nm) at reservoirs (Eu, *Eu, and Tm) aligned in a straight line (m = 1 − M). Boxes are electron reservoirs, and small circles are excited electrons involved in the PersL. | |
For example, the electron at Eu can move to *Eu with a probability p0 (0 ≤ p0 ≤ 1) upon excitation. For the electron at *Eu, the probabilities of moving to Eu and T1 are pe (0 ≤ pe ≤ 1) and p1 (0 ≤ p1 ≤ 1), respectively, and probability of remaining at *Eu is 1 − pe − p1.
We define the number of electrons at reservoirs as N0 at *Eu and Nm at Tm (m = 1, 2, …, M). For the random walk of electrons in the charging process, we initially prepare Eu with N electrons and the empty *Eu and Ts, that is, N0m = 0 (m = 0, 1, 2, …, M). After the first step, Np0 electrons move to *Eu from Eu, but N(1 − p0) electrons remain in Eu, that is, N01 = Np0 and Nm1 = 0 (m = 1, 2, …, M). After the second step, we can find N02 = N(1 − p0)p0 + Np0(1 − pe) + Np0(1 − p1), N12 = Np0p1, and Nm2 = 0 (m = 2, …, M). The number of electrons Nnm (m = 0, 1, 2, …, M) at every reservoir after many steps (n) can be obtained in similar ways, which are represented as functions of step number. By converting the step number (n) into time (t), we can predict the luminescence change by time from peNn0. For PersL, since the photoirradiation is ceased, p0 alone is needed to be p0 = 0. After the first step, the numbers of electrons at *Eu and T1 are N01 = N0(1 − pe − p1) + N1p−1 and N11 = N0p1 + N1(1 − p−1 − p2) + N2p−2, respectively. After the second step, the number of electrons at *Eu is determined as N02 = N01(1 − pe − p1) + N11p−1. After n steps, we can analogously obtain the number of electrons at *Eu as Nn0 = Nn−10(1 − pe − p1) + Nn−11p−1. For both charging and PersL processes, we perform a curve-fitting of luminescence intensity of SAOED as a function of step number n to determine pe, p±m (m = 1, 2, …, M), pq and Nm (m = 0, 1, 2, …, M). Since the observation of charging and PersL processes was conducted at room temperature T300 = 300 K, the hopping probability can be described as p300±. Therefore, the probability at T can be represented as eqn (5) as a function of T,
| | pT±m = p300±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−ΔE±m/kB)(1/T − 1/T300)). exp(−ΔE±m/kB)(1/T − 1/T300)). | (5) |
Using
pT±m, we performed a simulation of the TL spectrum for SAOED, which contributes to the determination of Δ
E±m.
3. Results
3.1. Charging and PersL
We observed luminescence changes in the charging process for SAOEDx (x = 2, 4, 5, 6, 8, and 10) which had been heated at 500 K for 1 h to de-trap electrons prior to the luminescence measurement. The luminescence intensities (I) at 520 nm were recorded at time intervals of 0.5 s during the continuous photoirradiation with 370 nm light, and log(I) was plotted with grey circles against log(t) as shown in Fig. 3. As can be seen from the plots, the log(I) values in the charging process exhibit complicated curves. For SAOED2, SAOED4, and SAOED5, each log(I) increases, reaches the maximum value log(Imax), and then decreases. The increase in log(I) at the early stage becomes reduced with increasing x and disappeared for SAOED6, SAOED8, and SAOED10. Still, the simulation, red lines, based on 1D RWM successfully reproduces the complex decay features of the charging processes for the entire samples. The SAOEDx that underwent the charging process was employed for the PersL measurement. As shown in Fig. 3, the plot of each log(I) against log(t) for PersL shows an upward convex curve, suggesting that the PersL decays non-exponentially or multi-exponentially. The times when each PersL intensity becomes Imax/100 are t = 470 s (x = 2), 195 s (x = 4), 505 s (x = 5), 116 s (x = 6), 82 s (x = 8), and 70 s (x = 10). Among them, the SAOED5 likely shows the best performance for PersL. The red lines are simulated decay curves for the PersL and consistent with the experimental results.
 |
| | Fig. 3 (left) Changes in luminescence of SAOEDx (x = 2, 4, 5, 6, 8, and 10) monitored at 520 nm in the charging process with the continuous irradiation of 370 nm at 300 K. (right) PersL of SAOEDx (x = 2, 4, 5, 6, 8, and 10) monitored at 520 nm after the photoexcitation with 370 nm light for 1 min at 300 K. The relative integrated intensities of PersL for entire samples were 5.10 × 103 (x = 2), 2.06 × 103 (x = 4), 1.54 × 103 (x = 5), 4.30 × 102 (x = 6), 1.15 × 102 (x = 8), and 1.00 (x = 10). | |
Each hopping probability pm (m = e, 1, −1, 2, −2, …, or q) between reservoirs was restricted to be the same for the charging and PersL processes in the simulation and determined through curve fitting. Listed in Table 1 are pm values converted to the hopping probabilities per second. It is noticed that the probabilities (p5, p−5, p6, p−6, p7, and p−7) for the entire samples are almost zero, which suggests the very small contribution of reservoirs T5 T6, and T7 to the PersL of SAOEDx. In other words, we can focus on *Eu, T1, T2, T3, and T4 to analyse the charging and PersL processes. The averaged hopping-probability from *Eu to T1 (p1) is as half as the average probability pe, corresponding to the intrinsic relaxation probability from excited *Eu2+ in SAOEDx. This result means that the 5d electron in the luminescence center easily transfers to the adjacent trap, leading to PersL for the SAOEDx system. The simulation can provide the number of electrons Nm at reservoirs. Fig. S3 (ESI†) shows Nm (m = 0–6) for SAOEDx (x = 2, 4, 5, 6, 8, and 10), where N0 is normalized to unity. It is obvious that N5 and N6 are almost zero for the entire samples; there is no population of excited electrons. N2, N3, and N4 for SAOED5 are larger than those for the other samples, respectively. This result seems to relate to the best performance in PersL for SAOED5.
Table 1 Hopping probabilities between reservoirs predicted through the simulation of charging and PersL processes for SAOEDx (x = 2, 4, 5, 6, 8, and 10)
|
x
|
p
e
|
p
1
|
p
2
|
p
3
|
p
4
|
p
5
|
p
6
|
p
7
|
p
q
|
|
p
−1
|
p
−2
|
p
−3
|
p
−4
|
p
−5
|
p
−6
|
p
−7
|
| 2 |
0.312 |
0.218 |
0.166 |
0.009 |
0.002 |
0.000 |
0.074 |
0.083 |
0.068 |
| 0.410 |
0.061 |
0.012 |
0.002 |
0.039 |
0.026 |
0.019 |
| 4 |
0.338 |
0.157 |
0.042 |
0.007 |
0.003 |
0.001 |
0.083 |
0.032 |
0.186 |
| 0.154 |
0.034 |
0.007 |
0.001 |
0.000 |
0.000 |
0.000 |
| 5 |
0.233 |
0.115 |
0.369 |
0.012 |
0.002 |
0.000 |
0.099 |
0.032 |
0.067 |
| 0.200 |
0.135 |
0.010 |
0.002 |
0.000 |
0.000 |
0.000 |
| 6 |
0.280 |
0.064 |
0.109 |
0.006 |
0.001 |
0.000 |
0.099 |
0.032 |
0.059 |
| 0.152 |
0.076 |
0.012 |
0.002 |
0.000 |
0.000 |
0.000 |
| 8 |
0.328 |
0.082 |
0.294 |
0.007 |
0.001 |
0.000 |
0.100 |
0.032 |
0.188 |
| 0.236 |
0.165 |
0.015 |
0.002 |
0.000 |
0.000 |
0.000 |
| 10 |
0.469 |
0.164 |
0.077 |
0.019 |
0.001 |
0.000 |
0.099 |
0.032 |
0.000 |
| 0.380 |
0.067 |
0.014 |
0.003 |
0.000 |
0.000 |
0.000 |
| Ave |
0.330 |
0.116 |
0.178 |
0.010 |
0.001 |
0.001 |
0.096 |
0.032 |
0.111 |
| 0.224 |
0.096 |
0.016 |
0.002 |
0.000 |
0.000 |
0.000 |
3.2. Thermoluminescence
In Fig. 4, the thermoluminescence (TL) spectrum of each sample is plotted with grey circles from 200 to 400 K. We notice that the TL intensities of the entire samples increase from 0 at 200 K to the maximum value in the range of 250–300 K and decrease to 0 at 400 K. The peak of each spectrum would correspond to the trap depth in the corresponding sample. With increasing x, the peak temperature likely shifts to the low temperature region. It is suggested that the less the Eu2+ content (x) in SAOEDx, the deeper the trap depth. In addition, each spectral profile strongly depends on x. For example, we can see two peaks in the TL spectra of SAOED2 and SAOED4 but one for the others. We performed simulations of the TL spectra based on the RWM. In this simulation, the temperature dependence in hopping probability was incorporated using the following relationship:| | pm,T = pm,300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−(ΔEm/kB)(1/T − 1/300)), exp(−(ΔEm/kB)(1/T − 1/300)), | (6) |
where pm,300 (m = 1, −1, 2, −2, …, q) is the hopping probability at 300 K determined through the simulation of charging and PersL processes, kB is Boltzmann's constant, and ΔEm is the activation energy for hopping between reservoirs. As shown in Fig. 4, the simulated TL spectra plotted with red lines are consistent with the experimental spectra of the entire samples. Specifically, the twin peaks for SAOED2 are also well reproduced through the simulation. For each sample, we can prepare a potential energy diagram for the activation states and reservoirs from the resultant ΔEm as shown in Fig. 5, where the potential energies of them are relatively depicted with respect to that of *Eu. For the entire samples, the energies of T1 are lower than those of *Eu, and the activation energies ΔE1 from *Eu to T1 are 12 kJ mol−1 or less. These results strongly suggest that the 5d electron in the excited state of Eu2+ spontaneously transfers to the next trap T1. The ΔE−1 values for the backward hopping from T1 to *Eu are 35 kJ mol−1 (x = 2), 34 kJ mol−1 (x = 4), 27 kJ mol−1 (x = 5), 29 kJ mol−1 (x = 6), 24 kJ mol−1 (x = 8), and 20 kJ mol−1 (x = 10). With an increase in the Eu2+ content x, the electrons at T1 seem to become easier to move back to *Eu. This can reasonably account for the low temperature shift of peak temperature in TL when x is increased. For SAOED2 and SAOED4, both ΔE2 and ΔE−2 are large, that is, the activation states between T1 and T2 are energetically high compared with the others. Most electrons are suggested to be accommodated in the relatively deep traps T1 and/or T2, which might be related to the twin peaks in each TL spectrum of SAOED2 and SAOED4. For SAOED5, T1, T2, and T3 sink together, and the activation energy ΔE4 for hopping from T3 to T4 is remarkably large. These results suggest that the most excited electrons are populated in traps of T1 through T3. Although a high activation barrier of ΔE4 is found for SAOED6, the excited electrons would be mostly accommodated in T1 because T2 and T3 are higher in energy than T1. For SAOED8, it is considered that the electron populations at T1 and T3 are larger than the others. For SAOED10, it is characteristic that the reservoirs T1 through T4 act as sinks compared with *Eu. This result may suggest that the excited electrons are widely distributed over T1 through T6.
 |
| | Fig. 4 TL spectra (grey circles) and their simulations (red lines) for SAOEDx (x = 2, 4, 5, 6, 8, and 10). The samples were treated with the de-trapping at 500 K and the charging with 370 nm light for 10 min at 200 K. The luminescence of each sample was measured at 520 nm from 200 to 500 K with the increasing rate of 1.03 K s−1 after 10 min in the dark at 200 K. | |
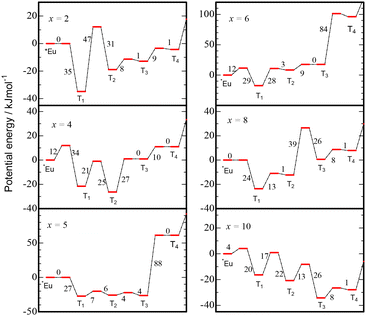 |
| | Fig. 5 Potential energy diagrams of *Eu and Tm (m = 1–4) for SAOEDx (x = 2, 4, 5, 6, 8, and 10) predicted by the simulation based on the RWM. The numbers are ΔE values in kJ mol−1 between the electron reservoir (*Eu or Tm) and the activation state, respectively. | |
4. Discussion
4.1. Multiple traps
X-ray crystallography revealed that there are two Sr2+ sites (Sr1 and Sr2) in host crystal SrAl2O4, where both Sr2+ sites are crystallographically nonequivalent to each other yet very similar in coordination structure.24 These Sr2+ sites in the SrAl2O4:Eu2+ crystal can be exchanged with dopant Eu2+ due to their similar ionic radii of 1.21 Å (Sr2+) and 1.20 Å (Eu2+)25 and the same electric charges. Since the electronic configuration of excited Eu2+ is represented as 4f65d1 involving the 5d orbital, the excited energy is sensitive to the difference in coordination geometry. Therefore, the modulation of coordination number of Eu2+ by O atoms by varying the SrO/Al2O3 ratio of host material results in the drastic change in the emission peak from 275 nm for SrAl12O19:Eu2+ to 467 nm for Sr3Al2O6:Eu2+.26 SrAl2O4:Eu2+ emits blue and green luminescence peaking at 455 and 520 nm, respectively, which are assigned to the emission from *Eu2+ at Sr1 and Sr2.26,27 The DFT calculation predicted that co-dopant Dy3+, as well as Eu2+, occupies the most energetically stable Sr2+ site.27 This is consistent with the result of field-emission scanning electron microscopy (FE-SEM) that Eu2+ and Dy3+ are evenly distributed in the SrAl2O4 host.28 On the other hand, another SEM measurement suggests the agglomeration of Dy3+ at grain boundaries in SrAl2O4.11 Given these reports for the SAOED structure, we should consider that there are a variety of coordination structures around Eu2+ and Dy3+ for SAOED depending on its crystal structure and the contents of Eu2+ and Dy3+. Especially, the variation in the coordination structure around Dy3+ will result in a variety of trap depths contributing to the multi-exponential PersL decay. Despite the complex trap system in SAOED, the simple 1D RWM is effective for the simulation of the charging and PersL processes and the TL spectra and contributes to the prediction of the traps and activation states in the SAOED crystals. The validity of the 1D trap array assumption would be rationally accounted for by the electron hopping path which can be uniquely determined when the hopping preferentially occurs between the closest traps in the crystal.
4.2. Analysis using the triple-exponential function
For SAOED2, we observed the rise-and-decay curve for the change in luminescence intensity during the charging process as mentioned above. In accordance with the global system consisting of a single *Eu–trap system with a conduction band, the luminescence rise at the early stage is accounted for by the increase in the number of excited electrons in the *Eu–trap system due to the continuous photoirradiation. When a curve fitting using an equation incorporating the rise component was carried out (Fig. S4, ESI†), we needed two additional decay components to match the simulation with the experimental result. This strongly suggests that the number of excited electrons at the luminescence centre *Eu does not remain constant even after filling them up. In this simulation, we employed eqn (7),| | Ic = Ic1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τc1) + Ic2 exp(−t/τc1) + Ic2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τc2) + Ic3 exp(−t/τc2) + Ic3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τc3) + Ic0 exp(−t/τc3) + Ic0 | (7) |
where τc1, τc2, and τc3 are lifetimes, Ic2, Ic2, and Ic3 are pre-exponential factors, and Ic0 is a constant. From the best fit, we determined τc1 = 44 s, τc2 = 5.1 × 104 s, and τc3 = 1.3 s, Ic1 = 0.025, Ic2 = 0.26, and Ic3 = −1.1, and Ic0 = 0.72, as listed in Table S2 (ESI†). The electron filling process represented by the rise component is likely completed within τc3 = 1.3 s in the present case. The decay components would correspond to electron transfer from the luminescence centre to traps and/or leaking electrons from the *Eu–trap system along with no luminescence such as quenching or dropping into deep traps. It might be essential that the electron transfer rate from *Eu to traps involved in PersL of SAOED2 is slow. At the later stage showing the constant intensity Ic0 = 0.72, the electron filling rate is likely balanced with the electron consuming rates due to the leaking and the luminescence emission. For PersL of SAOED2, Fig. S4 (ESI†) shows that a curve fitting using eqn (8) provides the best result and affords τp1 = 5.0 s (89%), τp2 = 65 s (10%), and τp3 = 430 s (1%),| | Ip = Ip1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τp1) + Ip2 exp(−t/τp1) + Ip2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τp2) + Ip3 exp(−t/τp2) + Ip3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τp3). exp(−t/τp3). | (8) |
This triple exponential function strongly suggests that there are at least three electron-trapping sites or reservoirs involving the PersL decay of SAOED2. For the other samples, the simulation using eqn (7) and (8) successfully reproduced the luminescence changes in the charging and PersL as shown in Fig. S4 (ESI†). The parameters determined by the simulation are listed in Table S2 (ESI†). The resultant τp1, τp2, and τp3 for PersL of each sample are roughly the same: τp1 = 3–7 s (ca. 90%), τp2 = 27–71 s (ca. 10%), and τp3 = 170–450 s (ca. 1%). No remarkable change in lifetimes is observed. On the other hand, for the charging process, although the result for SAOED4 is similar to that for SAOED2, the others are different. For SAOED5, two rise components, Ic2 = −0.025 (τc2 = 3.0 s) and Ic3 = −0.0083 (τc3 = 70 s), are needed to fit the experimental luminescence change. For SAOED6 and SAOED8, the luminescence change in the charging process can be reproduced with two decay components, since the third component is negligibly small. For SAOED10, three decay components are needed to reproduce the luminescence change. Although we can estimate lifetimes for the charging and PersL processes based on eqn (7) and (8), it seems hard to clarify the role of traps in the luminescence behaviours in the entire SAOEDx, even when we take multi-traps in a SAOED crystal into account for the PersL decay and the charging process. In contrast, it is significant that the stochastic analysis using the RWM can predict the energy diagram of *Eu and traps, the electron hopping probabilities between traps, and the electron distribution in traps for the entire samples.
4.3. Trap depth from TL spectra
According to the literature,29–31 we can determine the trap depth (E) for each SAOEDx from the corresponding TL spectrum, assuming the single luminescence centre-single trap system. To do so, we created a plot of ln(T2/β) vs. 1/kBT in accordance with Hoogenstraaten's equation:29| | 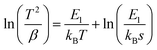 | (9) |
where T is the peak temperature resulting from a TL spectrum, kB is Boltzmann's constant, β is the heating rate, and s is the oscillating factor. The slope of the plot provides a trap depth E1 for each sample, which is listed in Table 2. Alternatively, we can also determine the trap depth from eqn (10) derived from the fact that the change in β brings the shift of the peak temperature of the TL spectrum:30,31| |  | (10) |
Table 2 Trap depths (E1 and E2 in kJ mol−1) for SAOEDx (x = 2, 4, 5, 6, 8, and 10) evaluated from the TL spectra, obtained from eqn (3) and (4), respectively. ΔEd values in kJ mol−1 are determined from the potential energies of deepest reservoirs for SAOEDx, respectively, with respect to that for *Eu
|
x
|
2 |
4 |
5 |
6 |
8 |
10 |
|
E
1 (kJ mol−1) |
53.3 |
41.3 |
32.6 |
38.6 |
73.5 |
84.4 |
|
E
2 (kJ mol−1) |
63.5 |
40.5 |
68.5 |
64.4 |
93.6 |
99.8 |
| ΔEd (kJ mol−1) |
35 |
26 |
27 |
17 |
24 |
34 |
The trap depths (E2) determined from this equation are listed in Table 2. The resultant E1 and E2 are in the range of 30–100 kJ mol−1, which are consistent with the values reported by other researchers.22 However, it seems that there is no relationship between the trap depth and the Eu2+ content x in SAOEDx. Especially, the deepest E1 and E2 are obtained from both methods for SAOED10, which is inconsistent with the physical intuition that the lower the peak temperature in the TL spectrum, the shallower the trap depth. Table 2 lists energy gaps ΔEd between *Eu and the deepest trap in SAOEDx obtained through the analyses for TL spectra using the RWM. ΔEd, the largest being 35 kJ mol−1 for SAOED2 among them, decreases and increases with increasing x. For SAOED10, ΔEd is comparable to that for SAOED2. It is interesting that this trend in ΔEd against x is similar to that in E1.
5. Conclusions
We employed SAOEDx (x = 2, 4, 5, 6, 8, and 10) containing 10% dopants (Eu2+ and Dy3+) in host crystal SrAl2O4 to produce a large amount of electron traps owing to Eu2+, Dy3+, oxygen vacancies, and defects. It should be noted that although the 1D trap array must be far apart from the actual arrangement of electron traps of Eu2+, Dy3+, oxygen vacancies, and defects in SAOEDx crystals, the simulation based on the 1D RWM successfully reproduced the complicated luminescence changes in charging and PersL and the TL spectrum for each SAOEDx. The resultant energy diagram of the luminescence centre and traps for each sample is simple and helpful for understanding the PersL of SAOEDx with a complicated trap system. The RWM is simple yet effective to visualize the picture that electrons migrate in the SAOED crystal with a variety of traps.
Author contributions
R. Koizumi and R. Takahashi conducted the preparation and identifications of materials, the luminescence measurements, and the simulation. S. Hattori and S. Yamada contributed to the experimental work and participated in discussions. K. Shinozaki supervised this project and wrote the manuscript.
Conflicts of interest
There are no conflicts to declare.
Data availability
The data supporting this article have been included as part of the ESI.†
References
- T. Matsuzawa, Y. Aoki, N. Takeuchi and Y. Murayama, J. Electrochem. Soc., 1993, 143, 2670 CrossRef.
- A. Bessière, J.-O. Durand and C. Noûs, Nanophotonics, 2021, 10, 2999 CrossRef.
- S. K. Sharma, D. Gourier, E. Teston, D. Scherman, C. Richard and B. Viana, Opt. Mater., 2017, 63, 51 CrossRef CAS.
- X. Tang, E. D. Ehler, E. Brost and D. C. Mathew, J. Appl. Clin. Med. Phys., 2021, 22, 191 CrossRef PubMed.
- S. Singh, V. Tanwar, A. P. Simantilleke and D. Singh, Nano-Struct. Nano-Objects, 2020, 21, 100427 CrossRef CAS.
- J. Xu and S. Tanabe, J. Lumin., 2019, 205, 581 CrossRef CAS.
- H. F. Brito, J. Hölsä, T. Laamanen, M. Lastusaari, M. Malkamäki and L. C. V. Rodrigues, Opt. Mater. Express, 2012, 2, 371 CrossRef CAS.
- C. Chiatti, C. Fabiani and A. L. Pisello, Annu. Rev. Mater. Res., 2021, 51, 409 CrossRef CAS.
- K. Van den Eeckhout, P. F. Smet and D. Poelman, Materials, 2010, 3, 2536 CrossRef CAS.
- R. E. Rojas-Hernandez, F. Rubio-Marcos, M. Á. Rodriguez and J. F. Fernandez, Renewable Sustainable Energy Rev., 2018, 81, 2759 CrossRef CAS.
- D. Van der Heggen, J. J. Joos, A. Feng, V. Fritz, T. Delgado, N. Gartmann, B. Walfort, D. Rytz, H. Hagemann, D. Poelman, B. Viana and P. F. Smet, Adv. Funct. Mater., 2022, 32, 2208809 CrossRef CAS.
- C. Jia, D. Gao, Z. Wang, X. Zhang, S. Yun, J. Z. Zhang and X. Wang, Mater. Today Chem., 2024, 39, 102182 CrossRef CAS.
- H. Li, R. Li and C. Chang, Ceram. Int., 2021, 47, 30156 CrossRef CAS.
- T. Delgado, N. Gartmann, B. Walfort, F. LaMattina, M. Pollnau, A. Rosspeintner, J. Afshani, J. Olchowka and H. Hagemann, Adv. Photonics Res., 2022, 3, 2100199 CrossRef.
- A. J. J. Bos, N. R. J. Poolton, J. Wallinga, A. Bessière and P. Dorenbos, Radiat. Meas., 2010, 45, 343 CrossRef CAS.
- J. Botterman, J. J. Joos and P. F. Smet, Phys. Rev. B:Condens. Matter Mater. Phys., 2014, 90, 085147 CrossRef CAS.
- C. Tydtgat, K. W. Meert, D. Poelman and P. F. Smet, Opt. Mater. Express, 2018, 6, 844 CrossRef.
- P. Dorenbos, J. Lumin., 2000, 91, 155 CrossRef CAS.
- P. Dorenbos, J. Lumin., 2003, 104, 239 CrossRef CAS.
- K. Ikegaya, S. Yamada and K. Shinozaki, Dalton Trans., 2019, 48, 6746 RSC.
- M. L. Chithambo, A. H. Wako and A. A. Finch, Radiat. Meas., 2019, 97, 1 CrossRef.
- P. Zeng, X. Wei, M. Yin and Y. Chen, J. Lumin., 2018, 199, 400 CrossRef CAS.
- K. Van den Eeckhout, A. J. J. Bos, D. Poelman and P. F. Smet, Phys. Rev. B:Condens. Matter Mater. Phys., 2013, 87, 045126 CrossRef.
- V. Vitola, D. Millers, I. Bite, K. Smits and A. Spustaka, Mater. Sci. Tech. Ser., 2019, 35, 1 Search PubMed.
- F. Clabau, X. Rocquefelte, S. Jobic, P. Deniard, M.-H. Whangbo, A. Garcia and T. Le Mercier, Chem. Mater., 2005, 19, 3904 CrossRef.
- D. Dutczak, T. Jüstel, C. Ronda and A. Meijerink, Phys. Chem. Chem. Phys., 2015, 19, 15236 RSC.
- K. Hoang, Phys. Rev. Appl., 2023, 19, 024060 CrossRef CAS.
- M. Zheng, X. Li, Y. Bai, S. Tang, P. Li and Q. Zhu, Coatings, 2023, 13, 1050 CrossRef CAS.
- W. Hoogenstraaten, Philips Res. Rep., 1958, 13, 515 CAS.
- R. Chen, J. L. Lawless and V. Pagonis, Radiat. Meas., 2022, 150, 106692 CrossRef CAS.
- M. Maghrabi, J. Lumin., 2018, 198, 54 CrossRef CAS.
|
| This journal is © the Owner Societies 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article and
Kazuteru
Shinozaki
and
Kazuteru
Shinozaki
 *
*
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τ1) + A2
exp(−t/τ1) + A2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τ2).
exp(−t/τ2).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τ1) + A2
exp(−t/τ1) + A2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τ2) + A3
exp(−t/τ2) + A3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τ3).
exp(−t/τ3).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−ΔE±m/kBT),
exp(−ΔE±m/kBT),
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−ΔEm/kBT), we can describe the hopping probability as
exp(−ΔEm/kBT), we can describe the hopping probability as![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−ΔE±m/kB)(1/T − 1/T300)).
exp(−ΔE±m/kB)(1/T − 1/T300)).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−(ΔEm/kB)(1/T − 1/300)),
exp(−(ΔEm/kB)(1/T − 1/300)),![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τc1) + Ic2
exp(−t/τc1) + Ic2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τc2) + Ic3
exp(−t/τc2) + Ic3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τc3) + Ic0
exp(−t/τc3) + Ic0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τp1) + Ip2
exp(−t/τp1) + Ip2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τp2) + Ip3
exp(−t/τp2) + Ip3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τp3).
exp(−t/τp3).