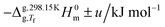Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
An all-atom force field for MD simulations on organosulfur and organohalogen active pharmaceutical ingredients developed from experimental sublimation enthalpies and single crystal X-ray diffraction data†
Cátia S. D. Lopes,
Manuel E. Minas da Piedade and
Carlos E. S. Bernardes
and
Carlos E. S. Bernardes *
*
Centro de Química Estrutural, Institute of Molecular Sciences, Departamento de Química e Bioquímica, Faculdade de Ciências, Universidade de Lisboa, Campo Grande, 1749-016 Lisboa, Portugal. E-mail: cebernardes@ciencias.ulisboa.pt
First published on 30th June 2025
Abstract
An all-atom force field for MD simulations on crystalline Active Pharmaceutical Ingredients (API) containing sulfur and halogens was developed and tested. Validation was performed by comparing the MD results with enthalpies of sublimation experimentally determined by Calvet microcalorimetry and reported single crystal X-ray diffraction data. The test set consisted of sulfanilamide, sulfapyridine, chlorzoxazone, clioquinol, and triclosan. The development was incremental. The OPLS-AA model was taken as the starting point. Then dihedral parameters missing in the OPLS-AA database were obtained from PES data computed at the MP2/aug-cc-pVDZ level of theory. Finally, several methods to determine atomic point charges were tested and a procedure based on the ChelpG methodology, with the inclusion of X-sites mimicking the σ-hole in the case of iodine, was found to provide the best overall accuracy in terms of unit cell dimensions and enthalpy of sublimation predictions.
1 Introduction
Molecular dynamics (MD) simulations have become a powerful tool to obtain microscopic insights into many chemical and physical properties of liquids, solutions, and solid materials.1 In the case of crystalline organic compounds, such as most active pharmaceutical ingredients (API), this theoretical approach has proven valuable to investigate aspects as diverse as solubility,2–4 crystallization,5–7 or polymorphism,8,9 just to name a few.At the heart of MD simulations is the force field, which describes the intermolecular and intramolecular interactions present in the crystal lattice. Force field models typically rely on atom–atom pair potentials, including terms that model van der Waals (VDW) interactions (e.g., 12-6 Lennard-Jones or Buckingham functions) and atomic point charges (APCs) that account for Coulomb interactions.10 Over the years, numerous force field parameterizations have been proposed and refined to describe the atom–atom interactions.10 For simulations involving solid materials a common practice consists in extracting VDW and intramolecular parameterizations from well-established sources (e.g. OPLS-AA,11 AMBER,12 and W9913) and calculating APCs for each molecule using quantum chemistry methods.14,15 The rationale behind this approach lies in the reasonably good transferability of VDW parameters for a given atom type.15 APCs are, however, significantly more sensitive to atomic connectivity/molecular environment. Various approaches have been proposed to obtain atomic point charges and describe electrostatic interactions in molecular organic solids, including the ChelpG,16 RESP,17 and PIXEL18 procedures, as well as the use of distributed multipole models.19
In previous studies, we have emphasized the importance of validating the development of force fields for MD simulations against both structural and energetic experimental data, namely, unit cell dimensions and standard molar enthalpies of sublimation (ΔsubH0m), the latter reflecting the lattice energy of the crystal.14,20–22 Information on the crystal structures of a vast number of organic compounds is available in the Cambridge Structural Database.23 Enthalpies of sublimation that can be linked to a specific crystal structure are, however, rather scarce.20,24–27 It is also fairly common that the crystal structures and ΔsubH0m values reported for a specific compound do not refer to the same temperature, an aspect that adds another level of complexity to the benchmarking. The need to overcome these problems has fostered a very recent European initiative, the COST Action CA22107 (https://bestcsp.eu/about/), which brings together leading experimental groups focused on the determination of structural and thermodynamic data, and simulation groups engaged in the development of methodologies for the prediction of crystal structures, thermodynamic properties, and spectroscopic properties of molecular organic solids.
In this work, we developed a force field model for MD simulations of organosulfur and organohalogen compounds. The selected test set consisted of five APIs containing S, Cl, and I (Fig. 1), namely sulfanilamide (SN), sulfapyridine (SP), chlorzoxazone (CZ), clioquinol (CL), and triclosan (TR). The force field development was incremental, and the validation was based on reported unit cell dimensions for specific crystal forms of the test set and on corresponding ΔsubH0m values here determined using Calvet-drop sublimation microcalorimetry.
2 Materials and methods
2.1 General
Elemental analyses (EA; C, H, N, S) were performed on a Fisons Instruments EA1108 apparatus. The results correspond to the molar percentage of the mean of two determinations and the uncertainties quoted are twice the average absolute deviation of the determinations.Reversed-phase high-performance liquid chromatography–electrospray mass spectrometry (HPLC–ESI/MS) was carried out on a Dionex Ultimate 3000 HPLC apparatus, equipped with a HPG3200 binary pump, a WPS300 autosampler, a TCC3000 column oven, and a DAD 3000 detector. This system was coupled in-line to an LCQ Fleet ion trap mass spectrometer including an ESI ion source from Thermo Scientific. The Xcalibur software was used to obtain and process the data. Methanolic solutions were prepared and injected into a Phenomenex Luna C18 column (150 mm × 2 mm, 5 μm) kept at 303 K. The separation was performed with a flow rate of 4.17 × 10−3 cm3 s−1, using a mobile phase consisting of 0.1% (v/v) formic acid in water (eluent A) and acetonitrile (eluent B), with the following gradient elution program: (i) 120 s isocratic 5% B; (ii) 1080 s linear gradient to 70% B; (iii) 120 s linear gradient to 100% B; (iv) 480 s isocratic 100% B; and (v) 300 s linear gradient to 5% B. Afterwards a re-equilibration time of 600 s for the column was used. The mass spectra were obtained in the ESI (+/−) ion modes from 100 to 700 Da, with an average of 20 to 35 scans. The following optimized parameters were used: ion spray voltage, ±4.5 kV; capillary voltage, +16 V or −18 V; tube lens offset, −70 V or +58 V; sheath gas (N2) pressure, 80 arbitrary units; auxiliary gas (N2) pressure, 5 arbitrary units; capillary temperature, 543 K.
Nuclear magnetic resonance (NMR) analyses were performed on a Bruker Ultrashield 400 MHz spectrometer, at 295 ± 2 K. The 1H-NMR were obtained using solutions of the compounds in hexadeuterodimethyl sulfoxide (DMSO-d6, Sigma-Aldrich, 99.9 atom% D).
Powder X-ray diffraction (PXRD) experiments were carried out at 293 ± 1 K, on a Philips X’Pert PRO apparatus equipped with a PW 3050/60 vertical goniometer and a X’Celerator detector. The X’Pert Data Collector v2.0b software was used for automatic data acquisition. The radiation source was a Cu-Kα tube (λ = 1.5406 Å), operated at 40 kV and 30 mA. The data collection was performed in continuous mode, with a scan step of 20 s and a step size of 0.017° (2θ). The 2θ range covered was 7° to 35°. The samples were placed on a silicon sample holder. The indexation of the powder patterns was done with the CELREF software.28 The uncertainties of the lattice parameters correspond to standard deviations (u) calculated as previously described.29
Differential scanning calorimetry (DSC) experiments were performed on a PerkinElmer DSC 7. The apparatus was controlled by a TAC 7/DX thermal analysis unit and the Pyris V. 7.0 software. The temperatures of fusion (Tfus, taken at the onset of the fusion peak) and corresponding specific enthalpies of fusion (Δfush/J g−1) were determined at a heating rate of 5 K min−1 under a nitrogen (Praxair 5.0) flow of 30 cm3 min−1. The calibration of the temperature and enthalpy scales of the apparatus was carried out at the same heating rate, and was based on a previously described procedure that relies on the temperatures and enthalpies of fusion of several reference materials.30 The samples with 1–11 mg mass, were weighed with a precision of ±0.1 μg on a Mettler XP2U ultra-micro balance, and sealed in air inside aluminum crucibles. The temperatures (Tfus,) and standard molar enthalpies of fusion (ΔfusH0m) obtained from the DSC experiments are means of five replicates and the associated errors correspond to expanded uncertainties for 95% confidence level (2uc).
2.2 Materials
Sulfanilamide (SN; TCI, 99.7%) was used as received. EA for C6H8N2O2S: expected C 41.85%, H 4.68%, N 16.27%, S 18.62%; found C 41.98 ± 0.20%, H 4.76 ± 0.02%, N 16.39 ± 0.06%, S 19.08 ± 0.08%. 1H-NMR analysis (400 MHz, DMSO-d6; see ESI†): δ/ppm = 7.45 (d, CH, 2H, H4), 6.90 (s, NH, 2H, H6), 6.59 (d, CH, 2H, H3), 5.81 (s, NH, 2H, H1). The powder pattern was indexed as β-SN, monoclinic, space group P21/c, Z = 4, a = 899.4 ± 0.9 pm, b = 902.3 ± 0.4 pm, c = 1005.2 ± 1.1 pm, β = 111.52 ± 0.10°, and density ρ = 1507.4 ± 5.1 kg m−3 (see ESI†). These results are in agreement with the single crystal X-ray diffraction data previously reported for β-SN at 295 K (CSD refcode SULAMD03):23,31 monoclinic, space group P21/c, Z = 4, a = 897.5 ± 0.3 pm, b = 900.5 ± 0.3 pm, c = 1003.9 ± 0.4 pm, β = 111.43 ± 0.05°, and density ρ = 1514.5 ± 2.1 kg m−3. The DSC traces (see ESI†) revealed a β to γ phase transition at with a peak maximum at Tmax = 370.7 ± 1.0 K and ΔtrsH0m = 1.3 ± 0.2 kJ mol−1. This thermal event was followed by the fusion of phase γ with Tfus = 438.1 ± 0.0 K, Tmax = 439.7 ± 0.1 K, and ΔtrsH0m = 23.5 ± 0.2 kJ mol−1. These results are compatible with previously reported values, obtained at higher heating rates (10 and 20 K min−1) than that employed in this work (5 K min−1): Ttrs = 407.0 K and ΔtrsH0m = 1.63 kJ mol−1;32 Ttrs = 381.9–401.8 K and ΔtrsH0m = 1.6–1.9 kJ mol−1;33 Tfus = 435.4 K and ΔfusH0m = 23.28 ± 0.79 kJ mol−1;34 Tfus = 434.8–437.8 K and ΔfusH0m = 22.2–23.1 kJ mol−1;33 Tfus = 438.8 ± 1.2 K and ΔfusH0m = 22.7 ± 1.9 kJ mol−1;35 Tfus = 439.3 K, and ΔfusH0m = 24.02 kJ mol−1;32 Tfus = 347.6 K, and ΔfusH0m = 23.4 kJ mol−1.36Sulfapyridine (SP; Acrös Organics, 99.9%), was used as received. EA for C11H11N3O2S: expected C 53.00%, H 4.45%, N 16.86%, S 12.86%; found C 53.26 ± 0.26%, H 4.58 ± 0.12%, N 16.61 ± 0.12%, S 12.35 ± 0.12%. 1H-NMR analysis (400 MHz, DMSO-d6; see ESI†): δ/ppm = 10.92 (s, NH, 1H, H6), 8.09 (d, CH, 1H, H11), 7.64 (t, CH, 1H, H10), 7.51 (d, CH, 2H, H4), 7.06 (d, CH, 1H, H8), 6.89 (t, CH, 1H, H9), 6.54 (d, CH, 2H, H3), 5.93 (s, NH2, 2H, H1). The powder pattern was indexed as SP form III, monoclinic, space group C2/c, Z = 8, a = 1271.5 ± 3.8 pm, b = 1166.9 ± 2.7 pm, c = 1537.3 ± 5.7 pm, β = 93.70 ± 1.00°, density ρ = 1454.9 ± 15.7 kg m−3 (see ESI†). These results are consistent with the single crystal X-ray diffraction data previously reported for SP form III at 298 K (CSD refcode BEWKUJ04):23,37 monoclinic, space group C2/c, Z = 8, a = 1280.7 ± 0.3 pm, b = 1171.1 ± 0.3 pm, c = 1537.9 ± 0.2 pm, β = 94.07 ± 0.02°, density ρ = 1439.4 ± 1.1 kg m−3. The onset and maximum temperatures of the fusion peak were Tfus = 463.4 ± 0.2 K and Tmax = 466.0 ± 0.1 K, respectively, and the molar enthalpy of fusion was ΔfusH0m = 38.4 ± 0.1 kJ mol−1. These results are in good agreement with the recently published Tfus = 464.2 ± 0.1 K and ΔfusH0m = 38.7 ± 0. 4 kJ mol−1,38 and Tfus = 462.0 ± 2.0 K and ΔfusH0m = 38.7 ± 1.2 kJ mol−1,38 obtained by conventional DSC and fast scanning calorimetry, respectively. They are also, in most cases, compatible with other literature values determined at a higher heating rate (10 K min−1) than that employed in this work (5 K min−1): Tfus = 462.7 K and ΔfusH0m = 40.47 ± 0.14 kJ mol−1;34 Tfus = 464.77 K and ΔfusH0m = 33.31 kJ mol−1;39 Tfus = 463.95 K and ΔfusH0m = 44.06 kJ mol−1;40 and Tfus = 464.7 K and ΔfusH0m = 38.8 kJ mol−1.36 It should also be noted that, in contrast with the present work, all previously reported Tfus and ΔfusH0m values for sulfapyridine refer to samples that were not characterized in terms of polymorphism.
Chlorzoxazone (CZ; Alfa Aesar, 98.0%) was purified by sublimation at 1.33 Pa and 343 K. EA C7H4ClNO2: expected C 49.58%, H 2.38%, N 8.26%; found C 49.16 ± 0.06%, H 2.16 ± 0.04%, N 8.10 ± 0.02%. The level of impurities in the sublimed sample was below the detection limit of the HPLC-ESI/MS method, suggesting a purity >99.9%. 1H-NMR analysis (400 MHz, DMSO-d6; see ESI†): δ/ppm = 11.86 (s, NH, 1H, H4), 7.31 (ds, CH, 1H, H2), 7.16 (d, CH, 1H, H7), 7.12 (dd, CH, 1H, H8). The powder pattern was indexed as triclinic, space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , Z = 2, a = 381.7 ± 0.4 pm, b = 902.1 ± 0.8 pm, c = 1004.8 ± 0.8 pm, α = 93.38 ± 0.08°, β = 95.50 ± 0.08°, γ = 98.32 ± 0.09°, density ρ = 1657.2 ± 5.4 kg m−3 (see ESI†). These results agree with previously reported single crystal X-ray diffraction data at 295 K (CSD refcode NEWKOP):23,41 triclinic, space group P
, Z = 2, a = 381.7 ± 0.4 pm, b = 902.1 ± 0.8 pm, c = 1004.8 ± 0.8 pm, α = 93.38 ± 0.08°, β = 95.50 ± 0.08°, γ = 98.32 ± 0.09°, density ρ = 1657.2 ± 5.4 kg m−3 (see ESI†). These results agree with previously reported single crystal X-ray diffraction data at 295 K (CSD refcode NEWKOP):23,41 triclinic, space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , Z = 2, a = 381.5 ± 0.1 pm, b = 903.8 ± 0.1 pm, c = 1006.3 ± 0.1 pm, α = 93.35 ± 0.01°, β = 95.52 ± 0.01°, γ = 98.41 ± 0.01°, density ρ = 1652.8 ± 1.0 kg m−3. The onset and maximum temperatures of the fusion peak were Tfus = 463.6 ± 0.2 K and Tmax = 465.3 ± 0.2 K, respectively, and the molar enthalpy of fusion was ΔfusH0m = 25.8 ± 0.2 kJ mol−1 (see ESI†). These results are consistent with Tfus = 464.2 K and ΔfusH0m = 25.62 kJ mol−1, previously determined at a heating rate of 10 K min−1.42
, Z = 2, a = 381.5 ± 0.1 pm, b = 903.8 ± 0.1 pm, c = 1006.3 ± 0.1 pm, α = 93.35 ± 0.01°, β = 95.52 ± 0.01°, γ = 98.41 ± 0.01°, density ρ = 1652.8 ± 1.0 kg m−3. The onset and maximum temperatures of the fusion peak were Tfus = 463.6 ± 0.2 K and Tmax = 465.3 ± 0.2 K, respectively, and the molar enthalpy of fusion was ΔfusH0m = 25.8 ± 0.2 kJ mol−1 (see ESI†). These results are consistent with Tfus = 464.2 K and ΔfusH0m = 25.62 kJ mol−1, previously determined at a heating rate of 10 K min−1.42
Clioquinol (CL; Maybridge, 95.0%) was purified by sublimation at 1.33 Pa and 368 K. EA for C9H5ClNO: expected C 35.38%, H 1.65%, N 4.58%; found C 35.84 ± 0.22%, H < 2%, N 4.56 ± 0.02%. The level of impurities in the sublimed sample was below the detection limit of the HPLC-ESI/MS method, suggesting a purity >99.9%. 1H-NMR analysis (400 MHz, DMSO-d6; see ESI†): δ/ppm = 8.96 (d, CH, 1H, H5), 8.48 (d, CH, 1H, H7), 7.98 (s, CH, 1H, H10), 7.76 (m, CH, 1H, H6). The powder pattern recorded at 293 ± 2 K, was indexed as monoclinic, space group P2/c, Z = 4, a = 1455.4 ± 2.2 pm, b = 412.7 ± 0.8 pm, c = 1660.5 ± 2.4 pm, β = 111.63 ± 0.14°, density ρ = 2188.5 ± 13.5 kg m−3 (see ESI†). These results agree with the published single crystal X-ray diffraction data at 296 K (CSD refcode CIQUOL02):23,43 monoclinic, space group P2/c, Z = 4, a = 1446.28 ± 0.10 pm, b = 409.86 ± 0.03 pm, c = 1653.36 ± 0.11 pm, β = 111.379 ± 0.002°, density ρ = 2223.1 ± 0.4 kg m−3. The DSC curves obtained for CL revealed a reversible phase transition characterized on heating mode by onset temperature Ttrs = 381.2 ± 0.6 K and enthalpy ΔtrsH0m = 0.5 ± 0.2 kJ mol−1, and on cooling mode by onset temperature Ttrs = 367.9 ± 1.6 K and enthalpy ΔtrsH0m = −0.3 ± 0.7 kJ mol−1 (Fig. S13 and Tables S9, S10 in the ESI†). To the best of our knowledge this phase transition had not been previously reported. Nevertheless, because the sublimation experiments on clioquinol were performed below this temperature the obtained enthalpy of sublimation can be safely assigned to the monoclinic form mentioned above (CSD refcode CIQUOL02). After the solid–solid phase transition, the fusion of the compound was recorded with the onset and maximum temperatures at Tfus = 453.0 ± 1.0 K, Tmax = 454.9 ± 0.6 K, and molar enthalpy of fusion ΔfusH0m = 23.6 ± 2.2 kJ mol−1. The later values should, however, be considered with caution due to the decomposition of the material on melting. The Tfus here obtained is lower than that previously reported by Padmanabhan et al., Tfus = 458.15 K,44 which corresponds to a heating rate of 10 K min−1. Because in the later study, the crystal form used was not identified and no phase transition was reported, the difference in the fusion temperatures may suggest that different polymorphs were investigated here and by Padmanabhan et al.44
Triclosan (TR; Alfa Aesar, 99.7%) was sublimed at 1.33 Pa and 328 K prior to use. EA for C12H7Cl3O2: expected C 49.78%, H 2.44%; found C 49.40 ± 0.08%, H 2.23 ± 0.04%. The level of impurities in the sublimed sample was below the detection limit of the HPLC-ESI/MS method, suggesting a purity >99.9%. 1H-NMR analysis (400 MHz, DMSO-d6; see ESI†): δ/ppm = 10.33 (s, OH, 1H, H11), 7.69 (s, CH, 1H, H13), 7.31 (d, CH, 1H, H2), 7.02 (d, CH, 1H, H6), 7.01 (s, CH, 1H, H9), 6.88 (d, CH, 1H, H7), 6.73 (d, CH, 1H, H3). The powder pattern recorded at 293 ± 2 K, was indexed as trigonal, space group P31, Z = 3, a = 1264.4 ± 0.9 pm, b = 1264.4 ± 0.4 pm, c = 672.1 ± 1.1 pm, density ρ = 1550.1 ± 6.4 kg m−3 (see ESI†). These results are consistent with published data from single crystal X-ray diffraction experiments carried out at 293 K (CSD refcode QUBQIO01):45 trigonal, space group P31, Z = 3, a = 1264.1 ± 0.0 pm, b = 1264.1 ± 0.0 pm, c = 671.6 ± 0.0 pm, crystal density ρ = 1551.9 ± 0.1 kg m−3. The onset and maximum temperatures of the fusion peak were Tfus = 328.7 ± 0.5 K and Tmax = 332.0 ± 0.3 K, respectively, and the molar enthalpy of fusion was ΔfusH0m = 26.0 ± 0.4 kJ mol−1. The origin of the discrepancy between the DSC results obtained here and the previously reported,46 Tfus = 331.05 K and ΔfusH0m = 17.75 kJ mol−1, was impossible to assess since in the latter case, the crystal form used was not identified and no details regarding the experiments from which Tfus and ΔfusH0m were obtained, or uncertainties of the results, were given by the authors.
2.3 Calvet-drop microcalorimetry
Enthalpies of sublimation or vaporization were determined using the Calvet-drop microcalorimetry apparatus and experimental procedure previously described.47,48 In a typical experiment, samples with a mass of 1–6 mg were placed inside glass capillaries and weighted with a precision of ±0.1 μg on a Mettler UMT2 ultra-micro balance. The capillary was placed inside the drop furnace and left to equilibrate at Ti ∼ 298.15 K for ∼1800 s. After a suitable baseline was acquired, the capillary was dropped into the calorimetric cell whose temperature was set to Tf = 419.1 K for SN, Tf = 423.9 K for SP, Tf = 419.3 K for CZ, Tf = 369.7 K for CL, and Tf = 351.4 K for TR. The curve corresponding to the heating of the sample and capillary from Ti to Tf (which in the case of triclosan also included melting at 328.7 ± 0.5 K) was recorded, and once the signal returned to the baseline, the sample and reference cells were simultaneously evacuated to 0.13 Pa. This started the sublimation/vaporization process, which was monitored until the signal returned to the baseline. The area, A, of the corresponding curve is related to the specific sublimation/vaporization enthalpy, Δsub/vaph, by:
 | (1) |
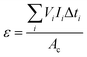 | (2) |
The calculation of standard molar enthalpies of sublimation, ΔsubH0m, at 298.15 K from the obtained Δsub/vaph values relied on the equation:
 | (3) |
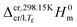 and
and  represent the enthalpy corrections needed to bring the crystal/liquid and gas phases at Tf to solid and gas phases at 298.15 K, respectively. The first term was obtained from the area, Ah, of the curve associated with heating the sample from Ti to Tf (which, as mentioned above also reflects melting in the case of triclosan) using the equation:
represent the enthalpy corrections needed to bring the crystal/liquid and gas phases at Tf to solid and gas phases at 298.15 K, respectively. The first term was obtained from the area, Ah, of the curve associated with heating the sample from Ti to Tf (which, as mentioned above also reflects melting in the case of triclosan) using the equation:
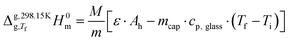 | (4) |
 | (5) |
The enthalpy correction for the gas phase was evaluated from:
 | (6) |
| C0p,m(g)/(J K−1 mol−1) = a(T/K)2 + b(T/K) + c | (7) |
For all compounds, visual inspection of the calorimetric cell and the capillary after the sublimation experiments showed no evidence of residues indicating sample decomposition. Furthermore, 1H-NMR analysis of materials sublimed at the same temperatures used in the Calvet-drop microcalorimetry runs demonstrated that no decomposition occurred during the solid → gas transition (see ESI†).
2.4 Quantum chemistry modelling
For sulfanilamide, sulfapyridine, chlorzoxazone, and triclosan, the C0p,m(g) data needed to correct the calorimetrically measured ΔsubH0m values from the temperature of the experiments to 298.15 K (eqn (6)), were calculated by statistical thermodynamics,49 using harmonic vibration frequencies computed at the B3LYP/aug-cc-pVDZ level of theory50–53 and scaled by 0.970.54 In the case of CL, iodine was modeled with the 6-311G(d,p) basis set (the corresponding aug-cc-pVDZ basis set is not available)55,56 and the aug-cc-pVDZ basis set was used for all other elements. The CL vibration frequencies were also scaled by 0.970. The calculations were performed using Gaussian-09.57The atomic point charges needed for the MD simulations were computed by the ChelpG16 and RESP58 methodologies using Multiwfn 3.8.59 The wavefunctions were obtained with ORCA 5.0.4,60 using the B3LYP-D352,61,62 model with the def2-TZVP63 basis set, the def2/J64 auxiliary basis set, and the RIJCOSX approximation.65 These calculations were preceded by a molecular structure optimization with the composite model B97-3c.66 The above models and basis sets were selected to allow the same type of approach for all compounds, independently of the elements and number of atoms (e.g., some of the calculations included clusters of molecules with more than 100 atoms). Files with the atomic coordinates obtained after structure optimization are provided as ESI.†
The potential energy barriers associated with dihedral angle rotations were obtained from potential energy scans (PES) carried out at the MP2/aug-cc-pVDZ51,53,67,68 level of theory using Orca 5.0.4.60
2.5 Molecular dynamics simulations
Unless otherwise stated, MD simulations were performed with LAMMPS (version 2, Aug 2023)69 and the input files were prepared with DLPGEN 3.0.70 The simulation boxes for the crystal phases were set up using single crystal X-ray diffraction data retrieved from the Cambridge Structural Database (CSD refcodes: SULAMD03 for sulfanilamide, BEWKUJ04 for sulfapyridine, NEWKOP for chlorzoxazone, CIQUOL02 for clioquinol, and QUBQIO01 for Triclosan).23 A cutoff of 1.5 nm was considered in all simulations and several unit cells were stacked along the three-coordinate axes to obtain large enough boxes to accommodate this limit (4–5 nm side). The particle–particle particle–mesh Ewald method was used to compute the electrostatic interactions beyond the cutoff distance.71 The simulations were run at 298.15 K and 1 bar, employing a Nosé–Hoover thermostat (2 ps time constant) and anisotropic barostat (20 ps time constant), respectively (NσT ensemble). The simulation involved an initial equilibration stage, where the crystals were heated from 10 K to 298.15 K during 1 ns, followed by a 2 ns production stage, at 298.15 K, to obtain the average standard molar configurational internal energy, U0conf,m(cr), and unit cell parameters. A 2 fs timestep was used for all simulations.Standard molar enthalpies of sublimation, ΔsubH0m, were calculated from:
| ΔsubH0m = U0conf,m(g) − U0conf,m(cr) + RT | (8) |
The configurational internal energies in the solid and gaseous phases were obtained from:
 | (9) |
The force field implementation started from the OPLS-AA scheme,11 which already includes widely tested parametrizations for a variety of functional groups (particularly, van der Waals terms). This strategy73 facilitates the extension of force fields to study new types of molecules and complex phenomena (e.g. solubility and crystallization) in a straightforward and consistent way.
At the beginning of this work, it was found that several dihedral parameters in the molecules studied were missing in the OPLS-AA database. These were, therefore, obtained by fitting the dihedral term in eqn (9) to PES data computed at the MP2/aug-cc-pVDZ level of theory. The procedure used was previously described74 and further details are given as ESI.†
To improve the agreement between the computed and experimental enthalpies of sublimation and unit cell parameters, an assessment of MD results based on the original OPLS-AA APC data and on APC values obtained here from DFT calculations was made. The following approaches were used:
• MODEL A. Original OPLS-AA force field charges, qopls.
• MODELS BC and BR. APCs computed for an isolated molecule in the gas phase using the ChelpG, qChelpGgas, and RESP, qRESPgas, methodologies, respectively. In this case, a full geometry optimization of the molecule was run before the APC calculations.
• MODELS CC and CR. APCs computed by the ChelpG, qChelpGcryst, and RESP, qRESPcryst, methodologies, for small clusters of molecules retrieved from the single crystal X-ray diffraction structures. The aggregates were defined by considering a central molecule and all neighbor molecules connected to it by hydrogen or halogen bonds.14,20 To maintain the relative orientation of the molecules as in the crystal structure, only the position of hydrogens was optimized before APC calculations. The APCs used in the simulations were those obtained for the central molecule.
• MODEL DC and DR. APCs, qxpart, computed by using:
| qxpart = 0.5qxgas + 0.5qxcryst | (10) |
Model C is rooted in the previous observation from our group, that using APCs calculated for small clusters of molecules reflecting molecular packing, seems to lead to a better description of the electrostatic interactions in the crystal lattice.11,16 Model D was inspired by the recently proposed restrained electrostatic potential approach (RESP2).75 In this case APCs were computed by considering weighed contributions from molecules isolated in the gas phase and solvated. This idea was extended here to crystals based on eqn (10) where qgas refers to an APC obtained for an isolated molecule in the gas phase and qcryst to a central molecule in a cluster mimicking the molecular organization of the crystal lattice. Calculations using ChelpG (MODEL DC) and RESP (MODEL DR) procedures were used in conjunction with eqn (10).
In the case of CL, CZ, and TR, halogen bonds are present in the crystal structure. To account for this type of interaction Jorgensen and Schyman76 proposed the inclusion in the model of “X-sites” located at the σ-hole of the halogen atom (a massless particle located at 180° relative to the C–Cl or C–I bond, with no LJ parameters and charges of 0.075e and 0.110e in the case of chlorine and iodine, respectively), to explicitly describe the formation of halogen bonds. In the present work, two variations of the force field with and without X-sites were considered for CL, CZ, and TR. The implementation closely followed the procedures described by Jorgensen and Schyman.76 For models B, C, and D, where APCs differed from the OPLS-AA values, charge neutrality was achieved by subtracting the charge of the X-site from that of the corresponding halogen element.
Due to the impossibility of using massless particles in LAMMPS, the simulations of halogenated compounds were made with DL_POLY 4.10.77 The clioquinol and triclosan molecules were considered flexible, except for the fragments C–Cl–X and C–I–X which were modeled as rigid units. In the case of CZ this approach led to unstable simulations. Since CZ is relatively small and exhibits little flexibility, a fully rigid model was considered in this case.
Full details of the force field parametrization are given as ESI.†
3 Results and discussion
3.1 Standard molar enthalpies of sublimation
The standard molar enthalpies of sublimation at 298.15 K, ΔsubH0m (298.15 K), obtained in this work from Calvet-drop microcalorimetry experiments, are given in Table 1. Also included in the Table 1 are the enthalpies of sublimation or vaporization, Δsub/vapH0m(Tf), directly measured at the temperature, Tf, of the calorimetric experiments and the correction terms,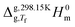 and
and  necessary to convert Δsub/vapH0m(Tf) to ΔsubH0m (298.15 K).
necessary to convert Δsub/vapH0m(Tf) to ΔsubH0m (298.15 K).
| Compound | Tf ± u/K | Δsub/vapH0m(Tf) ± U/kJ mol−1 | ΔsubH0m (298.15 K) ± U/kJ mol−1 | |||
|---|---|---|---|---|---|---|
| This work | Lit. | |||||
| a Details of the uncertainty calculations are provided as ESI.b Uncertainty assuming an arbitrary error of 2% in the computed value.c Ref. 38 and Table S23 (ESI).d Ref. 78 and Table S23 (ESI).e Enthalpy of vaporization of TR at 351.44 K. | ||||||
| β-SN | 29.15 ± 0.54c | 25.68 ± 0.51 | 130.8 ± 1.2 | |||
| γ-SN | 419.10 ± 0.01 | 127.30 ± 1.00b | 129.5 ± 1.3 | |||
| SP | 423.94 ± 0.02 | 147.47 ± 1.28 | 39.65 ± 0.76 | 38.39 ± 0.77 | 148.7 ± 1.7 | 167.2 ± 4.8c |
| CZ | 419.28 ± 0.00 | 107.07 ± 0.39 | 21.43 ± 0.49 | 20.48 ± 0.41 | 108.0 ± 0.7 | |
| CL | 369.72 ± 0.01 | 110.47 ± 0.99 | 18.29 ± 0.40 | 14.04 ± 0.28 | 114.7 ± 1.1 | 115.6 ± 1.0d |
| TR | 351.44 ± 0.00 | 89.36 ± 1.02e | 43.96 ± 0.63 | 14.20 ± 0.28 | 119.1 ± 1.2 | |
It is worth noting that attempts to determine ΔsubH0m of sulfonamide compounds other than sulfanilamide and sulfapyridine failed, due to either low vapor pressure (sulfadiazine and sulfamethizole) or decomposition during sublimation (sulfalene and sulfacetamide).
As mentioned in the Materials and methods section, in the case of SN, the experimental sublimation temperature (Tf = 419.10 K) was higher than the temperature at which the β → γ solid–solid phase transition occurs (Ttrs = 370.7 K). Therefore, the obtained enthalpy value corresponds to the sublimation of form γ at 419.10 K, 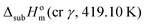 . The enthalpies of sublimation of forms β and γ at 298.15 K, could be determined as ΔsubH0m(cr β, 298.15 K) = 130.8 ± 1.2 kJ mol−1 and ΔsubH0m(cr γ, 298.15 K) = 129.5 ± 1.3 kJ mol−1 from:
. The enthalpies of sublimation of forms β and γ at 298.15 K, could be determined as ΔsubH0m(cr β, 298.15 K) = 130.8 ± 1.2 kJ mol−1 and ΔsubH0m(cr γ, 298.15 K) = 129.5 ± 1.3 kJ mol−1 from:
ΔsubH0m(cr β, 298.15 K) = ΔsubH0m(cr γ, 419.10 K) + Δg,298.15Kg,419.10KH0m − Δcr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β,298.15Kcr β,298.15Kcr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ,419.10KH0m γ,419.10KH0m
| (11) |
| ΔsubH0m(cr γ, 298.15 K) = ΔsubH0m(cr β, 298.15 K) + ΔtrsH0m(β → γ) | (12) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β,298.15Kcr
β,298.15Kcr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ,419.10KH0m values in Table 1 and ΔtrsH0m(β → γ) = 1.3 ± 0.2 kJ mol−1 obtained by DSC at 370.7 ± 1.0 K. The procedure used in the calculation of ΔsubH0m (298.15 K) for all other molecules is described in the Materials and Methods section (Section 2.3).
γ,419.10KH0m values in Table 1 and ΔtrsH0m(β → γ) = 1.3 ± 0.2 kJ mol−1 obtained by DSC at 370.7 ± 1.0 K. The procedure used in the calculation of ΔsubH0m (298.15 K) for all other molecules is described in the Materials and Methods section (Section 2.3).
To the best of our knowledge, enthalpies of sublimation have only been reported for SP38 and CL.78 For consistency in the comparison, all literature results were corrected to 298.15 K using the auxiliary data selected in this work and eqn (3) (see ESI†). The obtained values are listed in Table 1. In the case of CL, there is an excellent agreement between the calorimetric result here obtained, ΔsubH0m = 114.7 ± 1.1 kJ mol−1, and that reported by Monte and Ribeiro da Silva (ΔsubH0m = 115.6 ± 1.0 kJ mol−1),78 from Knudsen effusion measurements on a sample with unspecified phase purity. This is not, however, the case for SP, where a discrepancy of 18.5 kJ mol−1 is noted between the results from the present work and those obtained by Nagrimanov et al.38 from vapor pressure measurements by fast scanning calorimetry. The origin of this large discrepancy was impossible to assess, given the nature of the experiments performed by Nagrimanov et al.38 which require melting the compound prior to the sublimation experiments.
3.2 MD simulations
The performance of the different force-field approaches considered here was benchmarked against experimental enthalpies of sublimation and unit cell dimensions of the test set. The results are summarized in Fig. 2 and further details are given as ESI† (Tables S29–S32). Fig. 2 refers to all molecules and models, except that based on the Jorgensen and Schyman76 approach (“X-sites” located at the σ-hole of the halogen atom). The latter is specific for halogenated compounds and the corresponding results were, therefore, separately analyzed (Fig. 3).In terms of structural predictions, Fig. 2a shows that the largest deviations of unit cell parameters (e.g. deviations larger than 10% in the case of the b and β cell parameters of the SN polymorphs, Table S29, ESI†) are found for the original OPLS-AA parametrization (model A). This is, however, in line with previous observations.14,20 The best performance was achieved when ChelpG charges were employed (the range of values within the percentile 25–75% is the smallest), particularly when the calculations relied on gas phase (model BC) or averaged APCs (model DC). This is particularly evident in the case of the two polymorphs of SN, for which all tested models (except the original OPLS-AA) reproduced the experimental data with deviations lower than 3.3% (Table S29, ESI†).
The analysis of the difference between the computed enthalpies of sublimation and the corresponding experimental values (ΔΔsubH, Fig. 2b), revealed a poorer performance of all models for capturing the lattice energetics compared to volumetric properties. Indeed, while most of the deviations in unit cell dimensions are smaller than ca. 4% (Fig. 2a), ΔΔsubH deviations larger than ca. 8 kJ mol−1 (>7%) were observed, a value significantly larger than the aimed chemical accuracy of 1 kcal ≡ 4.184 kJ mol−1.79 Nevertheless, the best performance (smaller box amplitude and ΔΔsubH median closer to zero) corresponds to models CC, CR, and DC. This showcases the importance of validating force-field models using both structural and energetic data.
It is interesting to note that of all molecules included in this work, SP is the only one that packs in zwitterionic form. It is also the molecule with the larger deviations between predicted and experimental enthalpy of sublimation values (outliers in Fig. 2b). It can, therefore, be speculated that the VDW parametrization in OPLS-AA needs to be reassessed to account for this type of molecular structure. Such task is, however, outside the scope of this work, since it will require a reparameterization of the model using a large set of experimental data for zwitterionic molecules.
The results obtained for the halogenated compounds (clioquinol, chlorzoxazone, and triclosan) with and without considering X-sites are compared in Fig. 3. Fig. 3 shows that, when only chlorine is present in the molecule (CZ and TR) no significant accuracy gain in the prediction of volumetric and energetic properties is obtained by considering the Cl σ-hole (Fig. 3c–f). In contrast, modelling the I σ-hole of CL, led to better agreement between the calculated and benchmark values of unit cell dimensions and enthalpy of sublimation (Fig. 3a and b). This probably reflects the ability of iodine to form stronger halogen bonds than chlorine.80
4 Conclusions
In summary, model DC is the one that gave the best overall performance and is, therefore, recommended here to study organosulfur and organohalogen molecules of the types included in our test set. It is also advised that for halogenated molecules X-sites mimicking the σ-hole in these atoms are considered in the calculations, particularly if they contain iodine.Also worth noting is the fact that all modified force fields considered here performed better than the original OPLS-AA model, both in terms of unit cell dimensions and enthalpy of sublimation predictions.
Last but not the least, the observation that all models tested performed poorer in terms of lattice energy than volumetric properties prediction, stresses again the importance of using both these types of data in the validation of new force fields.
Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting this article have been included as part of the ESI.†Acknowledgements
This work was supported by FCT, Portugal, through projects UIDB/00100/2020 (https://doi.org/10.54499/UIDP/00100/2020), UIDP/00100/2020 (https://doi.org/10.54499/UIDB/00100/2020), LA/P/0056/2020 (https://doi.org/10.54499/LA/P/0056/2020), 2021.03239.CEECIND (https://doi.org/10.54499/2021.03239.CEECIND/CP1650/CT0003), 2023.12474.PEX (https://doi.org/10.54499/2023.12474.PEX), and the grant awarded to C. S. D. Lopes (SFRH/BD/128794/2017, COVID/BD/152581/2022). We also thank Prof. M. C. Oliveira (CQE-IST, Portugal) for the HPLC-ESI/MS analysis and Dr Ana Mourato for the PXRD analysis. Finally, we thank COST Action CA22107 – Bringing Experiment and Simulation Together in Crystal Structure Prediction (BEST-CSP), for providing a forum where helpful discussions related to the present work were promoted.References
- C. Chipot, J. Phys. Chem. B, 2024, 128, 12023–12026 CrossRef CAS PubMed.
- T. Yagasaki, M. Matsumoto and H. Tanaka, J. Chem. Theory Comput., 2020, 16, 2460–2473 CrossRef CAS PubMed.
- D. Gobbo, P. Ballone, S. Decherchi and A. Cavalli, J. Chem. Theory Comput., 2020, 16, 4126–4140 CrossRef CAS PubMed.
- R. G. Simões, P. L. T. Melo, C. E. S. Bernardes, M. T. Heilmann, F. Emmerling and M. E. Minas da Piedade, Cryst. Growth Des., 2021, 21, 544–551 CrossRef.
- A. Gavezzotti, Chem. – Eur. J., 1999, 5, 567–576 CrossRef CAS.
- H. Y. Tian, H. J. Zhang, J. L. Zhang and Y. Han, J. Phys. Chem. C, 2023, 127, 1507–1518 CrossRef CAS.
- D. Golodnizky, C. E. S. Bernardes and M. Davidovich-Pinhas, Food Chem., 2023, 439, 138066 CrossRef PubMed.
- R. G. Simões, C. E. S. Bernardes, A. Joseph, M. F. M. Piedade, W. Kraus, F. Emmerling, H. P. Diogo and M. E. Minas da Piedade, Mol. Pharmaceutics, 2018, 15, 5349–5360 CrossRef PubMed.
- R. G. Simões, C. S. D. Lopes, M. F. M. Piedade, C. E. S. Bernardes, H. P. Diogo and M. E. Minas da Piedade, Cryst. Growth Des., 2020, 20, 2321–2336 CrossRef.
- F. Jensen, Introduction to Computational Chemistry, John Wiley & Sons, Chichester, UK, Hoboken, NJ, 3rd edn, 2017 Search PubMed.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- W. D. Cornell, P. Cieplak, C. I. Bayly, I. R. Gould, K. M. Merz, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell and P. A. Kollman, J. Am. Chem. Soc., 1996, 118, 2309 CrossRef CAS.
- D. E. Williams, J. Mol. Struct., 1999, 485, 321–347 CrossRef.
- C. E. S. Bernardes, M. E. Minas da Piedade and J. N. Canongia Lopes, J. Phys. Chem. B, 2012, 116, 5179–5184 CrossRef CAS PubMed.
- J. Nyman, O. S. Pundyke and G. M. Day, Phys. Chem. Chem. Phys., 2016, 18, 15828–15837 RSC.
- C. M. Breneman and K. B. Wiberg, J. Comput. Chem., 1990, 11, 361–373 CrossRef CAS.
- W. D. Cornell, P. Cieplak, C. I. Bayly and P. A. Kollman, J. Am. Chem. Soc., 1993, 115, 9620–9631 CrossRef CAS.
- A. Gavezzotti, Z. Kristallogr., 2005, 220, 499–510 Search PubMed.
- M. Leslie, Mol. Phys., 2008, 106, 1567–1578 CrossRef CAS.
- C. E. S. Bernardes and A. Joseph, J. Phys. Chem. A, 2015, 119, 3023–3034 CrossRef CAS PubMed.
- C. E. S. Bernardes, M. T. Donato, M. F. M. Piedade, H. P. Diogo, J. N. Canongia Lopes and M. E. Minas da Piedade, J. Chem. Thermodyn., 2019, 133, 60–69 CrossRef CAS.
- A. O. L. Évora, D. F. Valente-Matias, C. E. S. Bernardes, C. M. Lousada, M. F. M. Piedade, M. Lusi, H. P. Diogo and M. E. Minas da Piedade, Cryst. Growth Des., 2024, 24, 9465–9481 CrossRef.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., 2016, B72, 171–179 Search PubMed.
- W. Acree and J. S. Chickos, J. Phys. Chem. Ref. Data, 2016, 45, 033101 CrossRef.
- W. Acree and J. S. Chickos, J. Phys. Chem. Ref. Data, 2017, 46, 013104 CrossRef.
- W. Acree and J. S. Chickos, J. Phys. Chem. Ref. Data, 2022, 51, 043101 CrossRef CAS.
- J. S. Chickos and A. Gavezzotti, Cryst. Growth Des., 2019, 19, 6566–6576 CrossRef CAS.
- J. Laugier and B. Bochu, CELREF V3: LMGP-Suite Suite of Programs for the interpretation of X-ray Experiments, ENSP/Laboratoire des Matériaux et du Génie Physique, 1997, https://www.ccp14.ac.uk/tutorial/lmgp/ Search PubMed.
- G. M. Sheldrick, SHELXL-97: Program for the Refinement of Crystal Structure, University of Göttingen, Germany, 1997 Search PubMed.
- C. E. S. Bernardes, I. O. Feliciano, C. Naese, F. Emmerling and M. E. Minas da Piedade, J. Chem. Thermodyn., 2023, 186, 107137 CrossRef CAS.
- A. M. O'Connell and E. N. Maslen, Acta Crystallogr., 1967, 22, 134–145 CrossRef PubMed.
- I. Ciocazanu and V. Meltzer, J. Therm. Anal., 1996, 47, 1755–1758 CrossRef CAS.
- S. Toscani, S. Thorén, V. Agafonov, R. Céolin and J. Dugué, Pharm. Res., 1995, 12, 1453–1456 CrossRef CAS PubMed.
- F. Martínez and A. Gómez, J. Solution Chem., 2001, 30, 909–923 CrossRef.
- M. Przybyłek, P. Walczak, D. Ziółkowska, I. Grela and P. Cysewski, J. Chem. Thermodyn., 2021, 153, 106308 CrossRef.
- Z. J. Cárdenas, D. M. Jiménez, O. A. Almanza, A. Jouyban, F. Martínez and W. E. Acree, J. Solution Chem., 2016, 45, 1479–1503 CrossRef.
- A. K. Basak, S. Chaudhuri and S. K. Mazumdar, Acta Crystallogr., 1984, C40, 1848–1851 Search PubMed.
- R. N. Nagrimanov, A. R. Italmasov, A. V. Buzyurov, S. E. Lapuk, R. A. Larionov, A. V. Gerasimov and M. A. Ziganshin, J. Therm. Anal. Calorim., 2024, 149, 1433–1442 CrossRef CAS.
- D. R. Mantheni, M. P. K. Maheswaram, R. Munigeti, I. Perera, A. Riga and K. S. Alexander, J. Therm. Anal. Calorim., 2014, 115, 2253–2260 CrossRef CAS.
- Y. Miyako, N. Khalef, K. Matsuzaki and R. Pinal, Int. J. Pharm., 2010, 393, 48–54 CrossRef CAS PubMed.
- S. Íde and A. Topaçh, J. Chem. Crystallogr., 1997, 27, 303–306 CrossRef.
- J. A. Baird, B. V. Eerdenbrugh and L. S. Taylor, J. Pharm. Sci., 2010, 99, 3787–3806 CrossRef CAS PubMed.
- X. He, Y. J. Jiang, H. P. Zhou and Q. H. Zhu, ChemistrySelect, 2021, 6, 5191–5194 CrossRef CAS.
- G. Padmanabhan, I. Becue and J. B. Smith, Anal. Profiles Drug Subst., 1990, 18, 57–90 Search PubMed.
- J. N. Latosińska, M. Latosińska, M. A. Tomczak, J. Seliger, V. Žagar and J. K. Maurin, Magn. Reson. Chem., 2012, 50, 89–105 CrossRef.
- J. Lim, S. Jang, M. S. Shin and H. Kim, Fluid Phase Equilib., 2012, 332, 144–150 CrossRef CAS.
- T. Kiyobayashi and M. E. Minas da Piedade, J. Chem. Thermodyn., 2001, 33, 11–21 CrossRef CAS.
- C. E. S. Bernardes, L. M. N. B. F. Santos and M. E. Minas da Piedade, Meas. Sci. Technol., 2006, 17, 1405–1408 CrossRef CAS.
- Computational Thermochemistry. Prediction and Estimation of Molecular Thermodynamics, ed. K. K. Irikura and D. J. Frurip, ACS Symposium Series No. 677, Washington, 1998 Search PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358–1371 CrossRef CAS.
- NIST Computational Chemistry Comparison and Benchmark Database, NIST Standard Reference Database Number 101, Release 22, May 2022 DOI:10.18434/T47C7Z, https://cccbdb.nist.gov/.
- M. N. Glukhovtsev, A. Pross, M. P. Mcgrath and L. Radom, J. Chem. Phys., 1995, 103, 1878–1885 CrossRef CAS.
- B. P. Pritchard, D. Altarawy, B. Didier, T. D. Gibson and T. L. Windus, J. Chem. Inf. Model., 2019, 59, 4814–4820 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., New York, 2009 Search PubMed.
- C. I. Bayly, P. Cieplak, W. D. Cornell and P. A. Kollman, J. Phys. Chem., 1993, 97, 10269–10280 CrossRef CAS.
- T. Lu and F. W. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606 Search PubMed.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109 CrossRef CAS.
- J. G. Brandenburg, C. Bannwarth, A. Hansen and S. Grimme, J. Chem. Phys., 2018, 148, 064104 CrossRef PubMed.
- M. J. Frisch, M. Head-Gordon and J. A. Pople, Chem. Phys. Lett., 1990, 166, 275–280 CrossRef CAS.
- M. J. Frisch, M. Head-Gordon and J. A. Pople, Chem. Phys. Lett., 1990, 166, 281–289 CrossRef CAS.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. I. Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 10817 CrossRef.
- C. E. S. Bernardes, J. Chem. Inf. Model., 2022, 62, 1471–1478 CrossRef CAS PubMed.
- R. W. Hockney and J. W. Eastwood, Computer Simulation Using Particles, A. Hilger, Bristol England, Philadelphia, 1988 Search PubMed.
- E. Tiesinga, P. J. Mohr, D. B. Newell and B. N. Taylor, Rev. Mod. Phys., 2021, 93, 033105 CrossRef PubMed.
- J. N. Canongia Lopes, P. Cabral do Couto and M. E. Minas da Piedade, J. Phys. Chem. A, 2006, 110, 13850–13856 CrossRef PubMed.
- C. E. S. Bernardes and J. N. Canongia Lopes, J. Chem. Theory Comput., 2017, 13, 6167–6176 CrossRef CAS PubMed.
- M. Schauperl, P. S. Nerenberg, H. Jang, L. P. Wang, C. I. Bayly, D. L. Mobley and M. K. Gilson, Commun. Chem., 2020, 3, 44 CrossRef CAS PubMed.
- W. L. Jorgensen and P. Schyman, J. Chem. Theory Comput., 2012, 8, 3895–3901 CrossRef CAS PubMed.
- I. T. Todorov, W. Smith, K. Trachenko and M. T. Dove, J. Mater. Chem., 2006, 16, 1911–1918 RSC.
- M. A. V. Ribeiro da Silva and M. J. S. Monte, J. Chem. Thermodyn., 1992, 24, 715–724 CrossRef CAS.
- J. A. Pople, Rev. Mod. Phys., 1999, 71, 1267–1274 CrossRef CAS.
- G. Cavallo, P. Metrangolo, R. Milani, T. Pilati, A. Priimagi, G. Resnati and G. Terraneo, Chem. Rev., 2016, 116, 2478–2601 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Fig. S1–S10 with the 1H-NMR spectra. Tables S1–S5 with the results of powder X-ray diffraction indexation. Fig. S11–S13 and Tables S6–S11 with the differential scanning calorimetry results. Tables S12–S21 with the Calvet-drop microcalorimetry results. Table S22 with the coefficients of eqn (7). Table S23 with details of the revision of enthalpy of sublimation data from literature. Fig. S14 showing the atoms labeling scheme used in the MD simulations. Tables S24–S28 with the APCs used in the MD simulations. Tables S29–S32 with the comparison between the experimental and MD simulation results. Files with the atomic coordinates of the optimized molecular structures used in the APCs calculations, and files used to prepare the MD simulations using the program DLPGEN (including a file with the force field parametrization). See DOI: https://doi.org/10.1039/d5cp01216c |
| This journal is © the Owner Societies 2025 |