Theoretical comparison of ethylene-, disilane- and ethynylene-bonded aromatic compounds from the viewpoint of conjugation formation

Abstract

Oligosilanes, which contain Si–Si σ bonds in the molecules, exhibit properties of σ conjugation analogous to the π conjugation observed in C=C π bonds. Similarly, Si–Si σ-bonded aromatic compounds display interactions between Si–Si σ and aromatic π bonds, resulting in the unique optical properties of conjugated systems such as intense absorption in the UV-vis region. This phenomenon is known as σ–π conjugation. While σ-conjugation and π-conjugation are well understood and various reviews have been published, σ–π conjugation in Si–Si σ-bonded aromatic compounds has not received much attention. In this paper, quantum chemical calculations were performed on representative compounds to examine the interaction of C–C σ, Si–Si σ, and C=C π orbitals with aromatic π orbitals. Their Frontier orbitals and electronic transitions were analyzed to elucidate their similarities and differences. The conformation of the phenyl group in the Si–Ph moiety plays a crucial role in aromatic disilanes, and conjugation is the most effective when the overlap between Si–Si σ and phenyl π orbitals is maximized. The relationship between the silicon chain length in oligosilanes and their optical properties was also examined. The results indicated that σ–π conjugations increase the HOMO energy level and σ*–π* conjugation decreases the LUMO energy level in Si–Si σ-bonded aromatic molecules, leading to a reduction in the HOMO−LUMO gap. NBO analysis further supports the presence of modest π*–σ and σ*–π conjugations in aromatic disilanes. The results presented in this work provide fundamental insights into the design and application of functional Si–Si σ-bonded aromatic molecules.

---

1. Introduction

Carbon and silicon, both nonmetallic elements in group 14 of the periodic table, have the ability to catenate, enabling the formation of oligosilane molecules in the case of silicon. Oligosilanes exhibit unique physical properties, which arise from σ conjugation among Si–Si σ bonds. Therefore, Si–Si σ bonds exhibit reactivity and physical properties that are notably similar to those of C=C π bonds. The σ conjugation in oligosilanes has been thoroughly reviewed in several studies.¹ When a Si–Si σ bond is linked to an aromatic substituent, they show electron delocalization, resulting in a decrease of the HOMO−LUMO energy gap. The interaction between the Si–Si σ and aromatic π orbitals is referred to as σ–π conjugation.²

During the past decade, researchers have focused on studying the structures and physical properties of Si–Si σ-bonded aromatic molecules.³ These molecules display diverse optical properties in the crystalline state due to the σ–π conjugation between Si–Si σ bonds and aromatic π bonds. This unique behavior in the crystalline state is attributed to the larger size of the silicon atom compared to the carbon atom and the relatively weak covalent bonds formed by the outermost electrons in the 3sp³ hybrid orbitals of silicon atom. Therefore, there is no quenching factor such as π-stacking in σ–π conjugated molecules because the intermolecular interactions in the crystalline state are weaker.

While the σ conjugation in oligosilanes and the π conjugation in aromatic molecules are well-established fields of study, comprehensive research on the interplay between Si–Si σ and aromatic π orbitals in the σ–π conjugation of Si–Si σ-bonded aromatic molecules, especially from a molecular orbital perspective, remains limited.⁴ The shape of molecular orbitals is directly related to the photophysical properties of the corresponding organic molecules. In this study, quantum chemical calculations were conducted on a series of molecules 1–9 based on C–C/C–C–C–C σ, Si–Si/Si–Si–Si–Si σ, and C=C/C=C–C=C π bonds with phenyl groups as the model aromatic substrates (Fig. 1 and 6),⁵ using the commonly employed density functional theory (DFT) method, B3LYP, for organic dyes.⁶ Computational chemistry was also used to compare the relationship between the length of the silicon chain in Ph–(SiMe₂)_n–Ph (n = 1–4: 2, 8, 10 and 11) and the molecular orbitals (Fig. 9). TD-DFT calculations were conducted to assign the electronic transitions in the absorption spectra.

Fig. 1 Chemical structures of 1–6. The dashed square represents a plane.

2. Results and discussion

2.1. Molecular orbitals and energy levels of 1–3

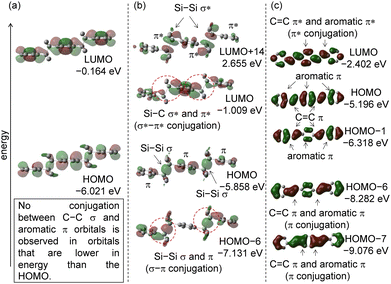
Initially, (2,3-dimethylbutane-2,3-diyl)dibenzene (1), 1,1,2,2-tetramethyl-1,2-diphenyldisilane (2), and trans-stilbene (3)⁷ were selected as model compounds, and calculations were performed at the B3LYP/6-31G(d,p) level of theory after examining several basis sets (Table S1, ESI†). The molecular orbital results for compound 1 are shown in Fig. 2(a).⁸ In the optimized molecular structure, the calculated dihedral angle of the C(sp²)–C–C–C(sp²) unit is 180°, indicating an antiperiplanar conformation. The optimized dihedral angle between the central C–C σ bond and the phenyl ring was 90.3°. This is consistent with the single-crystal X-ray structure analysis results.⁹ The HOMOs were examined, but no obvious interaction was observed between the C–C σ bond and the phenyl group π orbital. No increased effect on the HOMO energy level was observed due to no σ(C–C)–π conjugation. The LUMO displays an antibonding characteristic with regard to the C–C σ* bond, suggesting a decreased single bond characteristic. Although there is a little interaction between σ* and π* in the LUMO, the HOMO−LUMO energy gap is large (6.123 eV).

Fig. 2 Molecular orbitals and energy levels of 1–3. (a) LUMO and HOMO of 1. (b) LUMO+8, LUMO, HOMO, and HOMO−4 of 2. (c) LUMO, HOMO, HOMO−3, and HOMO−4 of 3. Hydrogen atoms are omitted for clarity. The isovalues are set to 0.03.

The molecular orbital results for compound 2 are presented in Fig. 2(b). In the optimized molecular structure, the calculated dihedral angle of the C(sp²)–Si–Si–C(sp²) unit is approximately 179.9°, showing an antiperiplanar conformation. The dihedral angle between the C–C σ bond and the phenyl ring was 89.2°. This conformation favors σ–π interactions between the Si–Si σ orbitals and the aromatic ring π orbitals. This is in close agreement with the results of single crystal X-ray structure analysis.¹⁰ In HOMO−4, there is an interaction between Si–Si σ and aromatic π orbitals, which stabilizes the molecular orbital through σ–π conjugation. The reason why the Si–Si σ bond readily engages in σ–π conjugation is that, compared to the C–C σ bond, the 3sp³ orbitals of silicon atoms are more spatially extended, resulting in larger σ orbital lobes and better overlap with adjacent π orbitals.

The HOMO has a relatively high energy level due to the lack of interaction between Si–Si σ and aromatic π orbitals. The LUMO exhibited interaction between the Si–Si σ* and π* orbitals, indicating σ*–π* conjugation. The corresponding molecular orbital consisting of σ* and π* is LUMO+8. The LUMO displays antibonding characteristics with regard to the Si–Si bond, indicating the decreased single bond characteristic. These phenomena led to a reduction in the HOMO−LUMO energy gap (5.595 eV) compared to 1, where there is no interaction between π and σ orbitals. The structure and physical properties of 2 are dominated by σ–π interactions (HOMO−3 and HOMO) and σ*–π* interactions (LUMO).

Interactions such as σ*–π and π*–σ are also possible in 2. The interaction σ*–π is a common phenomenon in silicon chemistry, but π*–σ is less common.¹¹ One explanation is that the energy gap between σ*–π is smaller than the energy gap between π*–σ (see Fig. S1. σ*–π: 7.624 eV, π*–σ: 8.545 eV, ESI†). Because the molecular orbitals were calculated as the integration of many orbitals, bond–anti-bond interactions can be estimated by natural bond orbital (NBO) analysis.¹² In addition to the molecular orbital considerations, NBO analysis was performed on 2 to confirm the presence of σ*–π conjugations. The second-order perturbation energy for the interaction between the π orbital and the Si–Si σ* orbital was 2.00 kcal mol⁻¹. Although the value is not large, the electron-donating interactions influence the molecular conformation and physical properties.

As a comparative π conjugated compound, quantum chemical calculations were performed on trans-stilbene (3), where the –CMe₂–CMe₂– moiety in 1 and –SiMe₂–SiMe₂– moiety in 2 were replaced with a –CH=CH– moiety.¹³ The calculated dihedral angle of C(sp²)–C=C–C(sp²) is 180°, which exhibits a planar structure. The molecular orbitals are presented in Fig. 2(c). The Frontier orbitals of 3 are similar in shape to those of 2. The HOMO of 3 is destabilized due to the absence of interaction between the C=C π orbital and the aromatic π orbital. In contrast, HOMO−4 involved molecular orbitals in which the C=C π orbital and aromatic π orbital are conjugated. The π–π* interaction is observed in HOMO−3 of 3. The LUMO also displays antibonding characteristics with regard to the central alkene, illustrating the decreased double bond character, and an interaction between the C=C π* and aromatic π* orbitals is observed which is stabilized by the π*–π* interaction, lowering the LUMO energy level. As with compound 2, the extended conjugation in compound 3 leads to an increase in the HOMO energy level and a decrease in the LUMO energy level. Therefore, the HOMO−LUMO energy gap narrows (4.144 eV).

2.2. Comparison of HOMO−LUMO energy levels and calculated absorption spectra of 1–3

The HOMO−LUMO energy levels and electronic transitions (predict UV-vis absorption) of 1–3 are shown in Fig. 3 and Tables S1–S3 (ESI†). The HOMO and LUMO levels of 1 were −6.222 eV and −0.099 eV, respectively. The large HOMO−LUMO gap can be attributed to a lack of conjugation. In contrast, compound 2 has HOMO and LUMO levels of −6.035 eV and −0.440 eV, respectively. Compound 3 has HOMO and LUMO levels of −5.519 eV and −1.375 eV, respectively.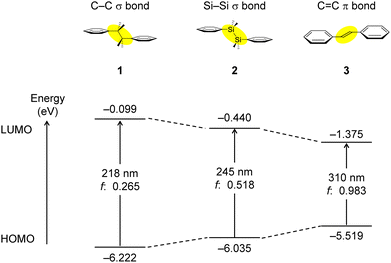

Fig. 3 HOMO and LUMO energy levels, HOMO−LUMO energy gaps, calculated absorption wavelengths, and oscillator strengths of 1–3.

Comparing 1 (no conjugation), 2 (σ–π conjugation) and 3 (π conjugation), the HOMO level was higher and the LUMO level was lower in this order. The reason why the rise in the HOMO level of 1 is not large is due to stabilization by the interaction between Si–C(sp³) σ and π orbitals in the HOMO. Regarding the LUMO, the degree of stabilization in 1 is lower than that in 2 or 3. Therefore, the conjugated chain is expanded in both cases, and the HOMO−LUMO energy difference becomes narrower, but the HOMO−LUMO energy difference is larger in the σ–π conjugation.

The absorption maximum of compound 1 is predicted to occur at 218 nm, corresponding to the HOMO → LUMO transition, with an oscillator strength of f = 0.265, which is relatively low. In 1, the absorption due to the phenyl ring π–π* was also predicted by calculation. In contrast, the absorption maximum of compound 2 is predicted at 245 nm, also corresponding to the HOMO → LUMO transition, with a larger oscillator strength of f = 0.518. Compound 3 has an absorption maximum and oscillator strength of 310 nm and f = 0.983, respectively, with greater conjugation. The trend reflects the conjugative ability of the bonds with C–C < Si–Si ≪ C=C, where the Si–Si σ bond exhibits intermediate characteristics between the C–C σ and the C=C π bonds. The photophysical properties predicted by calculations are consistent with the experimental data.¹⁴

2.3. Considerations on the conformational isomers of 1 and 2

When considering σ–π interactions, the orientation of the phenyl group in Si–Ph must also be taken into account. Compounds 1 and 2 in Fig. 1 adopt structures with the dihedral angle between C–C or Si–Si σ bonds and the phenyl rings of ca. 90°. As representative conformational isomers, structures with the dihedral angles of 180° for C=C–C–C and C=C–Si–Si are considered and designated as 1′ and 2′, respectively (Fig. 4). In this section, these conformers are compared from the viewpoint of molecular orbitals.

Fig. 4 Conformational isomers of 1, 1′, 2 and 2′. The dashed square represents a plane.

First, the molecular orbitals of 1 and 1′ are compared in Fig. S4 (ESI†). The HOMO−LUMO energy gap of 1 (6.123 eV) is smaller than that of 1′ (6.147 eV). In both compounds, the orbitals from HOMO−3 to HOMO−1 are mainly composed of π orbitals of aromatic rings. However, orbital distribution of HOMO is observed on the central C–C σ bond in 1, whereas no such distribution is found in 1′. Furthermore, σ*–π* interactions were observed in LUMO of 1, whereas such interactions were not observed in 1′. Due to these differences, conformation 1 is energetically stable and the HOMO−LUMO energy gap is smaller.

Next, the molecular orbitals of 2 and 2′ are compared in Fig. S5 (ESI†). The energy difference between HOMO−LUMO is as follows, 2: 5.569 eV and 2′: 6.344 eV. The HOMO of 2 extends to the Si–Si bond, and antibonding interactions are observed between the π orbital of the aromatic ring and the Si–Si σ bond. A bonding interaction corresponding to the HOMO is observed in HOMO−3, suggesting the existence of hyperconjugative interactions in 2. In contrast, such orbital interaction was not observed in 2′. In the LUMO orbital, σ*−π* interactions were observed in 2, whereas no such interactions were confirmed in 2′.

The NBO analysis of 2′ showed no contribution from σ*–π interactions (second-order perturbation energy: <0.5 kcal mol⁻¹). In order to explain these interactions, a change in dihedral angle would lead to a loss in orbital overlap, which is energetically unfavorable. Consequently, it is considered that intramolecular rotation is suppressed in conformation 2. These effects result in a smaller HOMO−LUMO gap in 2 than in 2′.

The above orbital differences contribute to the stability of conformer 2 and the expression of the optical properties derived from σ−π conjugation. In particular, it is suggested that the overlap of σ–π orbitals is maximized in conformation 2, where the dihedral angles of C=C–Si–Si and C(sp²)–Si–Si–C(sp²) are perpendicular.

2.4. Molecular orbitals and energy levels of 4–6

Next, the molecular orbitals of extended conjugation structures were investigated. Quantum chemical calculations were performed on 1,4-bis(2,3-dimethyl-3-phenylbutan-2-yl)benzene (4), 1,4-bis(1,1,2,2-tetramethyl-2-phenyldisilaneyl)benzene (5) and 1,4-bis((E)-3-phenylbut-2-en-2-yl)benzene (6), which have extended conjugation molecules in this section.

Fig. 5(a) shows the frontier orbitals of 4. Both C(sp²)–C–C–C(sp²) dihedral angles were calculated to be 180°. The dihedral angle of C=C–C–C was 90.3°. The C–C σ bond does not participate in conjugation (interaction) with phenyl rings. The large energy gap between the HOMO and LUMO prevents conjugation.

Fig. 5 Molecular orbitals and energy levels of 4–6. (a) The LUMO and HOMO of 4. (b) The LUMO+14, LUMO, HOMO, and HOMO−6 of 5. (c) The LUMO, HOMO, HOMO−1, HOMO−5, HOMO−6, and HOMO−7 of 6. Hydrogen atoms are omitted for clarity. The isovalues are set to 0.03.

Fig. 5(b) shows the molecular orbitals of 5. Ar–Si–Si–Ar–Si–Si–Ar compounds are a group of molecules that we have been actively studying recently and are characterized by intense luminescence in the crystalline state.¹⁵ In the optimized molecular structure, the dihedral angles of two C(sp²)–Si–Si–C(sp²) moieties are 179.9°. The dihedral angle between the Si–Si σ bond and the phenyl ring was 89.2°. The fact that the Si–Si σ bond has an anti–anti conformation is consistent with the results of single crystal X-ray structure analysis.¹⁶ In this case, the Si–Si σ bond and π bond are also in a position that provides σ–π interaction. The energy levels of the HOMO increase because there is no interaction between Si–Si σ and the aromatic π orbitals. There were interactions which are Si–Si σ and π orbitals stabilized in the HOMO−6 orbital. There were interactions between Si–Si σ* and aromatic π* orbitals (σ*–π* interaction) in the LUMO, which resulted in lowering the energy level. The orbital displays antibonding characteristics with regard to the Si–Si bond illustrating the decreased single bond characteristic. The corresponding molecular orbital consisting of σ* and π* is LUMO+14. The HOMO and LUMO orbitals of 5 are similar to those of 2, but the HOMO−LUMO energy difference of 5 is smaller due to longer conjugation (HOMO−LUMO energy difference. 2: 5.442 eV. 5: 4.109 eV).

In addition to the other molecular orbital considerations, NBO analysis was performed on 5 to confirm the presence of σ*–π conjugations. The second-order perturbation energy for the interactions between the π orbital and σ orbital was 1.90–2.01 kcal mol⁻¹. Although the value is not large, the electron-donating interactions also influence the molecular structure and physical properties.

The molecular orbitals of 6, in which the –SiMe₂–SiMe₂– moiety of 5 was converted to –CH=CH–, were calculated by DFT calculation. The results are shown in Fig. 5(c). The optimized molecular structure was a completely planar structure. The calculated dihedral angle of C(sp²)–C=C–C(sp²) is 180°. There was no interaction between the C=C π and the aromatic π orbitals in the HOMO and HOMO−1, which increased their energy levels. Therefore, the HOMO energy level is high. HOMO−6 and HOMO−7 are orbitals in which the C=C π orbital and the aromatic ring π orbital interact with lower energy levels. Next, we consider the LUMO orbitals of 6. There are interactions between C=C π* and aromatic π* in the LUMO.

2.5. Comparison of HOMO−LUMO energy levels and electronic transitions of 4–6

A comparison of the HOMO−LUMO energy levels of 4–6 is shown in Fig. 6. The HOMO and LUMO levels of 4 are −6.421 eV and −0.062 eV, respectively. The compound shows a large HOMO−LUMO energy gap because it does not form a conjugated chain between the C–C σ bond and phenyl group.

Fig. 6 HOMO and LUMO energy levels, HOMO−LUMO energy gaps, calculated absorption wavelengths, and oscillator strengths of 4–6.

On the other hand, the HOMO and LUMO levels of 5 are −5.858 eV and −0.662 eV, respectively. The HOMO−LUMO gaps of 4 and 5 were smaller than those of 1 and 2 due to the extended conjugation. Comparing the molecular orbitals of 4 and 5, the shapes of the HOMO and LUMO molecular orbitals are similar. This is the same phenomenon as in 1, which shows σ–π conjugation. The HOMO−LUMO gap of 4 is larger than that of 3. The HOMO and LUMO levels of 6 are –5.179 eV and –1.793 eV, respectively. The HOMO−LUMO energy gap becomes smaller.

To consider the absorption transition, TD-DFT calculations of 4–6 were performed. The results are shown in Tables S4–S6 (ESI†). The calculated wavelength of the S₀ → S₁ transition corresponds to the HOMO → LUMO. The calculated absorption wavelengths were 229 nm (4), 266 nm (5) and 386 nm (6) with high oscillator strengths, respectively. In particular, the absorption wavelengths of 5 and 6 are shifted to longer wavelengths in comparison with 2 and 3. This is because the longer conjugated systems are provided with narrower HOMO−LUMO energy gaps. These results are in good agreement with the reported data.¹⁷

2.6. Expanded linkage chains: molecular orbitals and energy levels of 7–9

The correlation was considered between the expanded spacer chains due to catenation and the physical properties. Specifically, the compounds in Fig. 7(b) were considered, in which the linking chain was extended as in Fig. 7(a). (2,3,3,4,4,5-Hexamethylhexane-2,5-diyl)dibenzene (7), 1,1,2,2,3,3,4,4-octamethyl-1,4-diphenyltetrasilane (8), and (1E,3E)-1,4-diphenylbuta-1,3-diene (9) were selected as model compounds in this section, and calculations were performed at the B3LYP/6-31G(d,p) level of theory.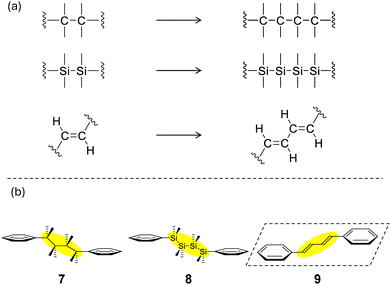

Fig. 7 (a) Expansion of the linkage chain. (b) Chemical structures of 7–9. The dashed square represents a plane.

The molecular orbital results for compound 7 are shown in Fig. 8(a). The alkyl groups are in a trans zig-zag conformation, and there is no interaction between the terminal phenyl groups (π orbitals) and the spacer alkyl groups (σ orbitals). Longer alkyl chains increase molecular flexibility, causing the dihedral angle to deviate slightly from 180°. The optimized dihedral angles of C(sp²)–C–C–C and C–C–C–C in 7 were 169.1° and 161.3°. The dihedral angle between the C–C σ bond and the phenyl ring was 91.6°. No increased effect on the HOMO energy level was observed due to no σ(C–C)–π conjugation. For the LUMO, the alkyl chain shows antibonding characteristics in the σ* orbital, weakening the single-bond character. There is no interaction between the σ* orbital and the π* orbital of the aromatic ring.

Fig. 8 Molecular orbitals and energy levels of 7–9. (a) The LUMO and HOMO of 7. (b) The LUMO+12, LUMO, HOMO, and HOMO−5 of 8. (c) The LUMO, HOMO, HOMO−4, and HOMO−5 of 9. Hydrogen atoms are omitted for clarity. The isovalues are set to 0.03.

The molecular orbital of 8 is shown in Fig. 8(b). The optimized structure showed trans zig-zag and the dihedral of C(sp²)–Si–Si–Si and Si–Si–Si–Si were 173.0° and 167.7°, respectively. Similarly, the presence of a long connecting chain results in a deviation of the dihedral angle from 180°. The smaller deviation of the dihedral angle in the former case is due to the formation of σ–π conjugation. The optimized dihedral angle between the Si–Si σ bond and the phenyl ring was 89.1°. The orbital of HOMO−5 has interactions (σ–π conjugation) between the π orbital of the aromatic ring and the Si–Si σ orbital, as well as interactions (σ conjugation) between the Si–Si σ orbitals. This raises the HOMO energy level. In the HOMO, there was an interaction between the Si–C(sp³) and the π orbital of the aromatic ring. In the LUMO orbital, there is an interaction between the Si–Si σ* and the π* orbitals of the aromatic rings, lowering the energy level. Orbitals consisting of π* and σ* conjugation were observed in LUMO+12.

In addition to the molecular orbital considerations, NBO analysis was performed on 8 to confirm the presence of σ*–π conjugations. The second-order perturbation energy for the interaction between the π orbital and the Si–Si σ* orbital was 2.01–2.03 kcal mol⁻¹. Although these values are not large, the electron-donating interactions also influence the molecular conformation and physical properties.

The molecular orbital of 9 is shown in Fig. 8(c). The molecular structure is completely planar. The calculated dihedral angles of C(sp²)–C=C–C and C=C–C=C in 9 were 180°. In HOMO−4 and HOMO−5, there is an interaction between the π orbital of the spacer and the aromatic ring, which raises the HOMO energy level, and there is an interaction between the π* orbital of the aromatic ring and the π* orbital of the spacer, which lowers the LUMO level.

2.7. Comparison of HOMO−LUMO energy levels and electronic transitions of 7–9

A comparison of the HOMO−LUMO energy levels of 7–9 is shown in Fig. 9. The HOMO and LUMO levels of 7 are −6.369 eV and −0.034 eV, respectively. The compound shows a large HOMO−LUMO energy gap because it does not form a conjugated interaction in Frontier orbitals.

Fig. 9 HOMO and LUMO energy levels, HOMO−LUMO energy gaps, calculated absorption wavelengths, and oscillator strengths of 7–9.

On the other hand, the HOMO and LUMO levels of 8 are −5.779 eV and −0.506 eV, respectively. The HOMO−LUMO gap is smaller than that of 7 due to σ–π conjugation and σ*–π* conjugation. Comparing the molecular orbitals of 7 and 8, the shapes of the HOMO and LUMO molecular orbitals are similar. This is the same phenomenon as 2 and 5, which shows σ–π conjugation. The HOMO and LUMO levels of 9 are −5.246 eV and −1.643 eV, respectively. The HOMO−LUMO gap of 9 is smaller than that of 7 and 8. This means that the increase of the HOMO level and decrease of the LUMO level due to conjugation become more pronounced.

To consider the optical absorption transition, TD-DFT calculations of 7–9 were performed. The results are shown in Tables S5 and S6 (ESI†). The calculated wavelength of the S₀ → S₁ transition corresponds to the HOMO → LUMO and HOMO → LUMO+1 for 7 and HOMO → LUMO for 8 and 9, respectively. The absorption wavelength shifts to longer wavelengths in the order of 7 (239 nm), 8 (269 nm), and 9 (394 nm). The oscillator strength also increases in this order (7: 0.697, 8: 0.847, and 9: 1.573). This is because the longer conjugated systems provide narrower HOMO−LUMO energy gaps. These results are in good agreement with the reported data of similar compounds.¹⁸

2.8. Effect of silicon chain length: molecular orbitals and energy levels of 2, 8, 10, and 11

Quantum chemical calculations were conducted to investigate the relationship between the length of silicon chains and their optical properties. The studied systems include diphenyldimethylsilane (Si: 10), 1,1,2,2-tetramethyl-1,2-diphenyldisilane (Si–Si: 2), 1,1,2,2,3,3-hexamethyl-1,3-diphenyltrisilane (Si–Si–Si: 11), and 1,1,2,2,3,3,4,4-octamethyl-1,4-diphenyltetrasilane (Si–Si–Si–Si: 8).¹⁹ The molecular structures of these compounds are shown in Fig. 10.

Fig. 10 Structures of α,ω-diphenyloligosilanes to study the effect of silicon length.

First, the molecular orbitals of monosilane 10 were calculated and presented in Fig. 11(a). The structure is a regular tetrahedron, and the two benzene rings take a conformation that avoids steric repulsion. The HOMO is predominantly derived from the π orbital of the aromatic ring. The LUMO, on the other hand, exhibits the interaction between the π* orbital on one phenyl ring and Si–C(sp²) σ* orbital. There is no significant conjugation or interaction between Si and the aromatic ring in orbitals at the lower HOMO energy level. Compound 10 shows a large HOMO−LUMO energy gap (6.026 eV).

Fig. 11 Molecular orbitals of 10 and 11. (a) LUMO and HOMO of 10. (b) LUMO+8, LUMO, HOMO, HOMO−1, and HOMO−4 of 11. Hydrogen atoms are omitted for clarity. The isovalues are set to 0.03.

In contrast, for disilane 2, interaction between the Si–Si bond and the aromatic π orbitals is observed in HOMO–4, leading to improving the HOMO level. The LUMO exhibited interaction between the Si–Si σ* and π* orbitals, indicating σ*–π* conjugation as described in section 2.1. These phenomena narrow the HOMO−LUMO energy gap. Similar behavior is observed in trisilane 11, as shown in Fig. 11(b). The optimized structure showed both dihedral angles of C(sp²)–Si–Si–Si were ca. 179.0°. Here, HOMO−4 displays significant interaction between the Si–Si bonds and aromatic π orbitals. In HOMO−1, σ conjugation between σ orbitals is observed. The results increase the HOMO energy level. The LUMO also shows σ*–π* interactions, resulting in a reduction in its energy level and further narrowing of the HOMO−LUMO gap compared to that of compound 2.

The trend continues with tetrasilane 8, where σ–π and σ conjugation effects are evident in orbitals below the HOMO level. The optimized structure showed both dihedral angles were C(sp²)–Si–Si–Si: 170.7°, Si–Si–Si–Si: 165.0°, Si–Si–Si–Si: 164.9°, and Si–Si–Si–C(sp²): 170.6°. The dihedral angle between the C–C σ bond and the phenyl ring was 89.3°. As the molecular degree of freedom increases, the dihedral angle deviates from the ideal (180°). The HOMO energy level is further elevated due to enhanced σ and σ–π conjugation effects at HOMO−1, HOMO−5, and HOMO−6. Although the LUMO exhibits a σ*–π* interaction in these cases, the lowering of the energy levels is slower due to the similarity of the orbital structure. These interactions collectively demonstrate that the silicon chain length directly influences the electronic structure and optical properties of these molecules. Considering the efficiency of synthesis, Si–Si σ-bonded aromatic molecules are suitable for the development of optically functional materials.

2.9. Comparison of the HOMO−LUMO energy levels and electronic transitions of 2, 8, 10, and 11

Fig. 12 illustrates the HOMO−LUMO energy levels and electronic transitions for compounds 2, 8, 10 and 11, highlighting the effect of silicon chain length between two benzene rings. TD-DFT calculations reveal that the primary electronic transition responsible for the absorption peak arises from the HOMO to LUMO transition in each compound.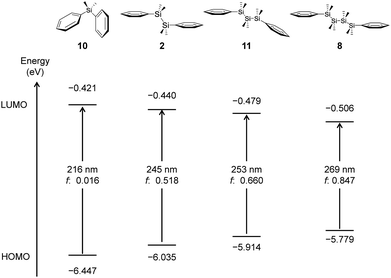

Fig. 12 The HOMO and LUMO energy levels, HOMO−LUMO energy gaps, calculated absorption wavelengths, and oscillator strengths of 2, 8, 10 and 11.

As the silicon chain length increases, the HOMO−LUMO gap progressively narrows, resulting in a redshift of the absorption wavelength. The molar extinction coefficient (ε) also increases with the number of Si atoms. Notably, the change in absorption wavelength is the most pronounced when extending the chain length from monosilane (10) to disilane (2). These phenomena are consistent with experimental results.²⁰ However, the wavelength shift becomes less significant with further elongation of the silicon chain beyond disilane.

Comparatively, the extent of the redshift induced by increasing the silicon chain length is smaller than that observed with extended conjugation through C=C π bonds. This suggests that while silicon chain extension modifies the electronic structure and optical properties, its impact is limited in comparison to organic π-conjugated systems. This is because the oligosilane group has a flexible structure, and the dihedral angle deviates from the ideal one as the chain becomes longer.

2.10. Consideration on anti and gauche conformational isomers

Oligosilane-bonded compounds show two stable conformational isomers against the Si–Si bond, gauche and anti ones.²¹ Therefore, as representative examples, the gauche structures of 2, 11, and 8 were optimized and energy calculations were performed. The results are shown in Fig. S2 (ESI†).

Initially, the stability of gauche-2 was considered. The calculated dihedral angle of C(sp²)–Si–Si–C(sp²) and C=C–Si–Si of gauche-2 was optimized as 66.3° and 89.4°, respectively. In the case of molecule 2, the anti conformation was more stable than the gauche conformation (Fig. S2(a), ESI†). The instability of the gauche form can be attributed to greater steric repulsion between the phenyl groups compared to the anti form, which is consistent with the anti conformation being observed in the crystalline state. The HOMO and HOMO−4 energy levels of the gauche form are identical, but its LUMO energy level is higher (Fig. S3, ESI†). As a result, the absorption of the gauche form is shifted to a shorter wavelength.

In the case of molecule 11, there are three possible conformational isomers: anti–anti, anti–gauche, and gauche–gauche conformations (Fig. S7(b), ESI†). In this case, the energy difference is small, and the order of stability is gauche–gauche < anti–gauche < anti–anti. The calculated dihedral angles of C(sp²)–Si–Si–Si in gauche–gauche conformation were 90.1° and 53.1°. The dihedral angle between the Si–Si σ bond and the phenyl ring was 89.9°. The conformation is unstable due to high steric hindrance between two sterically hindered groups. The C(sp²)–Si–Si–Si dihedral angles of the anti–gauche are 49.7° and 172.5°, respectively. The dihedral angle between the Si–Si σ bond and the phenyl ring was 89.4°. The C(sp²)–Si–Si–Si dihedral angles of the anti–anti are 179.1° and 179.0°, respectively. The dihedral angle between the Si–Si σ bond and the phenyl ring was 87.6°.

In the case of 8, there are five isomers: anti–anti–anti, gauche–anti–gauche, gauche–gauche–gauche, anti–gauche–gauche, and anti–gauche–anti conformations (Fig. 2(c)). The stability order is as follows: gauche–gauche–gauche < anti–gauche–gauche < anti–gauche–anti < gauche–anti–gauche < anti–anti–anti conformations. The calculated dihedral angles are as follows; anti–anti–anti: C(sp²)–Si–Si–Si 171.0°/170.9°, Si–Si–Si–Si 165.6°; gauche–anti–gauche: C(sp²)–Si–Si–Si 52.6°/51.8°, Si–Si–Si–Si 179.4°; anti–gauche–anti: C(sp²)–Si–Si–Si 164.3°/164.3°, Si–Si–Si–Si 55.2°; anti–gauche–gauche: C(sp²)–Si–Si–Si 161.8°/47.0°, Si–Si–Si–Si 60.2°; gauche–gauche–gauche: C(sp²)–Si–Si–Si 111.2°/52.0°, Si–Si–Si–Si 52.4°. In this case, the energy difference between anti–anti–anti and gauche–anti–gauche is small. The difference in stability is due to steric repulsion caused by differences in conformation.

The steric repulsion between phenyl groups in conformational isomers decreases with increasing chain length. Therefore, the energy difference between the conformational isomers is small. Although there are many reports of anti conformation in crystals, intermolecular CH–π interactions are dominant in the aggregated state. These results suggest the possibility of creating molecules that can switch anti–gauche in response to external stimuli in the crystalline state.

3. Conclusions

In this paper, the differences among C–C σ, Si–Si σ, and C=C π bonds were investigated by performing molecular orbital calculations on 1–9. Maximum absorption wavelengths of all compounds are attributed to HOMO → LUMO transitions. The trend of the peak shift and intensity in the absorption spectra of experimental results is consistent with the results of TD-DFT calculations.

Aromatic compounds linked via C–C or C–C–C–C σ bonds do not exhibit conjugation between C–C σ and aromatic π orbitals, resulting in a large HOMO−LUMO energy gap. In contrast, aromatic compounds linked via Si–Si or Si–Si–Si–Si σ bonds exhibit conjugation (σ–π and σ*–π* conjugations), which reduces the HOMO−LUMO gap. NBO calculations showed that σ*–π interaction is not so large, but they contribute to the molecular conformations and physical properties. Aromatic compounds linked by C=C or C=C–C=C π bonds also exhibit conjugation (π conjugation), leading to a smaller HOMO−LUMO gap.

Aromatic disilanes exhibited the greatest conjugation when the dihedral angle between the Si–Si σ bond and the phenyl ring was 90°. This result differs from a π-conjugated structure in which the C=C π bond and the phenyl group lie in the same plane. The presence and strength of the conjugated chain depends on the energy levels of the HOMO of the π orbital of the aromatic ring and the HOMO orbital of the linker. The energy gap follows the trend σ–π > π, as in the case of aromatic disilanes, there is an interaction between the Si–Si σ and π orbitals in the HOMO−3, which lowers the HOMO energy level. This is the reason why the optical absorption of σ–π conjugation is less likely to shift to longer wavelengths than that of π conjugation.

By comparing α,ω-diphenyloligosilanes 2, 8, 10, and 11, the correlation between silicon chains and optical properties was examined using DFT and TD-DFT calculations. As the Si–Si bond becomes longer, the absorption wavelength shifts to the longer wavelength. These molecules have interactions that are Si–Si σ conjugations in HOMO−1 and HOMO−3. This causes the HOMO energy level to increase. Even if the Si–Si bond is lengthened, the ability to shift the absorption to longer wavelengths is smaller than that of C=C π bonds. This indicates that the conjugation ability with an aromatic ring is C–C σ bond< Si–Si σ bond< C=C π bond. The Si–Si σ bond is fundamentally different from the C–C σ bond and C=C π bond that constitute the framework of organic chemistry. These findings are significant for a comprehensive investigation of the unique characteristics of the Si–Si bond.

The Si–Si σ bond has restricted rotation, and anti and gauche isomers are possible as stable conformers maintaining σ–π or σ*–π* conjugation. The energy difference between these conformers is very small, suggesting that they could be used as crystal molecules whose structures change in conjugation with photophysical properties under external stimuli.

4. Experimental

DFT calculation. Geometries of the molecules were optimized at the BLYP/6-31G(d,p) level of theory using the Gaussian 16 rev C program package.²² Absorption wavelengths were characterized by using the time-dependent density functional theory (TD-DFT) approach with BLYP/6-31G(d,p). No imaginary frequencies were found.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was financially supported by Grant-in-Aids for Scientific Research (C) (no. JP25K08585) from the Ministry of Education, Culture, Sports, Science, and Technology, Japan.

References

1. For reviews on σ-conjugation, see: (a) T. Schepers and J. Michl, J. Phys. Org. Chem., 2002, 15, 490–498; (b) H. Tsuji, J. Michl and K. Tamao, J. Organomet. Chem., 2003, 685, 9–14; (c) Y. Hatanaka, J. Organomet. Chem., 2003, 685, 207–217; (d) T. Karatsu, J. Photochem. Photobiol., C, 2008, 9, 111–137; (e) H. A. Fogarty, D. L. Casher, R. Imhof, T. Schepers, D. W. Rooklin and J. Michl, Pure Appl. Chem., 2003, 75, 999–1020; (f) H. Tsuji, J. Michl, A. Toshimitsu and K. Tamao, Yuki Gosei Kagaku Kyokaishi, 2002, 60, 762–773; (g) D. R. Silva, E. Blokker, J. M. van der Schuur, T. A. Hamlin and F. M. Bickelhaupt, Chem. Sci., 2024, 15, 1648–1656; (h) R. D. Miller and J. Michl, Chem. Rev., 1989, 89, 1359–1410.
2. (a) M. Kira, T. Miyazawa, H. Sugiyama, M. Yamaguchi and H. Sakurai, J. Am. Chem. Soc., 1993, 115, 3116–3124; (b) J. Ohshita, Yuki Gosei Kagaku Kyokaishi, 2001, 59, 11–22; (c) C. G. Pitt, J. Organomet. Chem., 1973, 61, 49–70.
3. (a) Y. Yamanoi, Acc. Chem. Res., 2023, 56, 3325–3341; (b) Y. Yamanoi and M. Hattori, Bull. Chem. Soc. Jpn., 2024, 97, uoad019; (c) M. Shimada, Y. Yamanoi and H. Nishihara, Yuki Gosei Kagaku Kyokaishi, 2016, 74, 1098–1107; (d) Y. Yamanoi and H. Nishihara, Yuki Gosei Kagaku Kyokaishi, 2009, 67, 778–786; (e) T. Nakae, M. Nishio and Y. Yamanoi, Sakutai Kagaku, 2020, 76, 31–39.
4. (a) C. G. Pitt and H. Bock, J. Chem. Soc., Chem. Commun., 1972, 28–29; (b) H. Tsuji, Y. Shibano, T. Takahashi, M. Kumada and K. Tamao, Bull. Chem. Soc. Jpn., 2005, 78, 1334–1344; (c) J. Ohshita, Y. Hatanaka, S. Matsui, T. Mizumo, Y. Kunugi, Y. Honsho, A. Saeki, S. Seki, J. Tibbelin, H. Ottosson and T. Takeuchi, Dalton Trans., 2010, 39, 9314–9320; (d) Y. Ding, X. Wang and F. Ma, Chem. Phys., 2008, 348, 31–38; (e) S. Feng, Z. Zhao, X. Xiang, H. Feng, Z. Qu and H. Lu, ACS Omega, 2020, 5, 19181; (f) C. G. Pitt, E. C. Toren and R. N. Carey, J. Am. Chem. Soc., 1972, 94, 3806–3811.
5. (a) Compounds 1, 2, and 4 were commercially available; (b) 3: M. Ishikawa, K. Watanabe, H. Sakamoto and A. Kunai, J. Organomet. Chem., 1992, 435, 249–256; (c) 5: H. Hiratsuka, H. Horiuchi, Y. Takanoha, H. Matsumoto, T. Yoshihara, T. Okutsu, K. Negishi, S. Kyushin and H. Matsumoto, Chem. Lett., 2007, 1168–1169; (d) 6: Z. Wang, Q. Ding, X. He and J. Wu, Org. Biomol. Chem., 2009, 7, 863–865.
6. D. Jacquemin, E. A. Perpète, I. Ciofini and A. Adamo, Acc. Chem. Res., 2009, 42, 326–334.
7. (E)-But-2-ene-2,3-diyldibenzene, methylated analogue of trans-stilbene, cannot maintain planarity throughout the molecule due to steric repulsion between methyl group and phenyl group, and the conjugated chain does not expand.
8. X.-Q. Yao, X.-J. Hou, G.-S. Wu, Y.-Y. Xu, H.-W. Xiang, H. Jiao and Y.-W. Li, J. Phys. Chem. A, 2002, 106, 7184–7189.
9. E. K. Kim and J. K. Kochi, J. Org. Chem., 1993, 58, 786–792.
10. M. Linnemannstöns, J. Schwabedissen, B. Neumann, H.-G. Stammler, R. J. F. Berger and N. W. Mitzel, Chem. – Eur. J., 2020, 26, 2169–2173.
11. S. A. Ponomarenko and S. Kirchmeyer, Conjugated Organosilicon Materials for Organic Electronics and Photonics, in Silicon Polymers. Advances in Polymer Science, ed. A. Muzafarov, Springer, Berlin, Heidelberg, 2010, vol. 235.
12. F. Weinhold and C. R. Landis, Discovering Chemistry with Natural Bond Orbitals, Wiley-VCH, Hoboken, NJ, 2012.
13. T. Tsutsumi, Y. Ono and T. Taketsugu, J. Chem. Theory Comput., 2022, 18, 7483–7495.
14. For representative examples, see: (a) H. Sakurai, H. Sugiyama and M. Kira, J. Phys. Chem., 1990, 94, 1837–1843; (b) V. Molina, M. Merchán and B. O. Roos, J. Phys. Chem. A, 1997, 101, 3478–3487; (c) H. Sakurai, H. Yamamori and M. Kumada, Bull. Chem. Soc. Jpn., 1965, 38, 2024.
15. (a) H. Miyabe, M. Ujita, M. Nishio, T. Nakae, T. Usuki, M. Ikeya, C. Nishimoto, S. Ito, M. Hattori, S. Hayashi, D. Saito, M. Kato, H. Nishihara, T. Yamada and Y. Yamanoi, J. Org. Chem., 2022, 87, 8928–8938; (b) T. Nakae, M. Nishio, T. Usuki, M. Ikeya, C. Nishimoto, S. Ito, H. Nishihara, M. Hattori, S. Hayashi, T. Yamada and Y. Yamanoi, Angew. Chem., Int. Ed., 2021, 60, 22871–22878; (c) T. Usuki, K. Omoto, M. Shimada, Y. Yamanoi, H. Kasai, E. Nishibori and H. Nishihara, Molecules, 2019, 24, 521; (d) T. Usuki, M. Shimada, Y. Yamanoi, T. Ohto, H. Tada, H. Kasai, E. Nishibori and H. Nishihara, ACS Appl. Mater. Interfaces, 2018, 10, 12164–12172; (e) M. Shimada, M. Tsuchiya, R. Sakamoto, Y. Yamanoi, E. Nishibori, K. Sugimoto and H. Nishihara, Angew. Chem., Int. Ed., 2016, 55, 3022–3026.
16. T. Nakae, K. Omoto, M. Yoshida, M. Kato and Y. Yamanoi, J. Organomet. Chem., 2024, 1010, 123093.
17. S. E. Estrada-Flórez, F. S. Moncada, A. E. Lanterna, C. A. Sierra and J. C. Scaiano, J. Phys. Chem. A, 2019, 123, 6496–6505.
18. (a) C. Zhou, Z. Zhou, F. Yu, W. Xie, W. Zhang, Q. Yang, X. Xu, L. Gai and H. Lu, J. Mater. Chem. C, 2022, 10, 18182–18188; (b) R. S. Klause, J. R. Widawsky, M. L. Steigerwald, L. Venkataraman and C. Nuckolls, J. Am. Chem. Soc., 2012, 134, 4541–4544.
19. J. Michl and R. West, Acc. Chem. Res., 2000, 33, 821–823.
20. (a) H. Gilman, W. H. Atwell and G. L. Schwebke, J. Organomet. Chem., 1964, 2, 369–371; (b) H. Gilman and P. J. Morris, J. Organomet. Chem., 1966, 6, 102–104.
21. For relationship between the conformation and properties of oligosilanes, see: (a) F. Fang, Q. Jiang and R. S. Klausen, J. Am. Chem. Soc., 2022, 144, 7834–7843; (b) H. Li, M. H. Garner, Z. Shangguan, Q. Zheng, T. A. Su, M. Neupane, P. Li, A. Velian, M. L. Steigerwald, S. Xiao, C. Nuckolls, G. C. Solomon and L. Venkataraman, Chem. Sci., 2016, 7, 5657–5662.
22. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2019.

---

Footnote

† Electronic supplementary information (ESI) available: HOMO and LUMO energy levels of benzene π, ethane C–C σ, disilane Si–Si σ, and ethylene C=C π bonds, conformational isomers, comparison of calculation methods, TD-DFT calculation of 1–11, and considerations on conformational isomers of 1 and 2. See DOI: https://doi.org/10.1039/d5cp01166c

---