Quantum-embedded equation-of-motion coupled-cluster approach to single-atom magnets on surfaces

Abstract

We investigate electronic states and magnetic properties of transition-metal atoms on surfaces using projection-based density embedding that combines equation-of-motion coupled-cluster singles and doubles (EOM-CCSD) theory with density functional theory (DFT). As a case study, we explore Co adsorbed on MgO(001), an ideal model for single-atom magnet design, known for its record magnetic anisotropy among transition-metal adatoms. Periodic DFT-based calculations of the magnetic anisotropy energy, i.e., the energy required to rotate the magnetization from parallel to perpendicular relative to the surface normal, predict in-plane magnetic anisotropy, contradicting the experimentally observed easy-axis anisotropy. This failure stems from the inability of the approximate density functionals to describe the multiconfigurational, non-aufbau spin states of Co/MgO(001). In contrast, embedded EOM-CCSD calculations on Co/Mg₉O₉ finite models of the adsorption complex capture the system's unquenched orbital angular momentum (L ≈ 3) and strong spin–orbit coupling, leading to easy-axis anisotropy and a spin-inversion energy barrier that agrees with experiment within spectroscopic accuracy. When treating both the oxygen adsorption site and the Co magnetic center at the EOM-CCSD level of theory, embedded calculations accurately reproduce the state ordering, spin–orbit coupling, and susceptibility curve of all-atom EOM-CCSD calculations. These results demonstrate that embedded EOM-CCSD provides a reliable description of the electronic states and magnetic properties of magnetic adsorbates on surfaces, offering a robust framework for future investigations of surface-bound magnetic systems.

---

I. Introduction

Magnetic atoms serve as the ultimate building blocks at the atomic scale for next-generation quantum devices, with applications in high-density data storage, quantum computing, and sensing.^1–3 The design of atomic quantum devices begins with surface adsorption, which enables single-atom addressability—the ability to initialize, control, and detect individual spins—while also allowing scalability to surface spin arrays.^4,5 Recent advancements in scanning tunneling microscopy (STM) combined with electron paramagnetic resonance (EPR) spectroscopy have made it possible to control and detect individual atomic spins on surfaces.^6–9 In the pursuit of scalability, STM techniques now enable the bottom-up, atom-by-atom construction and characterization of atomic spin lattices on surfaces.^10–13

Currently available theoretical approaches for magnetic adsorbates lag behind these experimental breakthroughs. Density functional theory (DFT) with periodic boundary conditions (pbc) remains the workhorse for ab initio simulations of magnetic materials.¹⁴ However, DFT often fails to provide even a qualitatively correct description of key ground-state properties,^15,16 such as adsorption energies¹⁷ and charge-transfer processes,¹⁵ which are crucial at adsorbate–surface interfaces. To compute magnetic properties, the Hubbard (U) correction to DFT is widely used.¹⁸ However, choosing the appropriate U parameter can be challenging,^19,20 often resulting in only qualitative agreement with experiment,²¹ or failing to predict correct state energy splitting and fundamental properties.⁸ While more accurate post-Hartree–Fock methods for periodic systems are available, they are mostly used for ground-state properties of dynamically-correlated materials and become computationally prohibitive as the number of atoms increases in the simulation cell.²²

For local phenomena, such as molecular and atomic adsorbates on surfaces, quantum embedding theories^23–34 provide a way to reduce computational effort without compromising accuracy. Among these methods, a groundbreaking development was the introduction of a density-based embedding scheme that combines multireference methods with periodic DFT for molecular adsorbates on surfaces.²⁸ In this work, we adopt a more recent, projection-based version of density embedding,^33–36 which enforces orthogonality between fragment orbitals, eliminating the need for non-additive kinetic potentials or optimized embedding potentials that were required in previous formulations. Projection-based density embedding that combines equation-of-motion coupled-cluster singles and doubles (EOM-CCSD) theory with DFT has gained popularity for exploring both ground and excited states of molecular systems.^37–39 Additionally, EOM-CCSD-in-DFT has been extended to open-shell species⁴⁰ and was recently applied to investigate the spin states and magnetic properties of large transition-metal molecular magnets beyond the reach of standalone EOM-CCSD.⁴¹ Furthermore, some of us have applied embedded EOM-CCSD to elucidate dissociative electron attachment on metal surfaces, highlighting its effectiveness in addressing challenges in surface science.⁴²

EOM-CCSD methods^43–46 provide a robust and efficient framework for treating molecular magnets, describing their multiconfigurational wave functions within a single-reference approach. These methods have been extensively benchmarked across various transition-metal complexes, accurately predicting spin-state energy gaps, exchange couplings, g-tensors, spin-inversion energy barriers, and macroscopic magnetic properties such as magnetization and susceptibility.^47–51 Additionally, the second-order approximate coupled-cluster singles and doubles (CC2)⁵² method has recently been applied to molecular magnets,^41,53 accurately describing their spin states. However, the steep polynomial scaling of EOM-CCSD (N⁶) and CC2 (N⁵), where N is the system size, limits their applicability to small-to-medium-sized molecular systems. In this work, we employ the more cost-efficient embedded EOM-CCSD method to investigate the spin states and magnetic behavior of individual magnetic atoms on surfaces, going beyond traditional DFT approaches. As a case study, we focus on single Co atoms adsorbed on the MgO(001) surface. This system serves as an ideal platform for designing atomic-scale quantum devices. A combined experimental and DFT+U study has predicted that Co atoms on MgO(001) exhibit the highest magnetic anisotropy energy (or spin-inversion barrier) among 3d transition-metal adatoms, which is an essential feature for realizing efficient single-atom magnets.⁵⁴ This behavior is attributed to the axial ligand field of Co at the oxygen adsorption site, which preserves the orbital angular momentum of gas-phase Co atoms (L = 3), enhancing spin–orbit coupling (SOC) and resulting in a record magnetic anisotropy energy of 58 meV (468 cm⁻¹). In addition, the Co/MgO(001) system provides a simple yet insightful model for assessing the performance of EOM-CCSD-in-DFT compared to EOM-CCSD and CC2.

We first determine the most stable adsorption site (top or hollow) for single Co atoms on MgO(001) performing plane-wave DFT calculations on periodic models. To assess different DFT-based methods, we compare binding energies and magnetic anisotropy energy predictions across multiple levels of theory, including the generalized gradient approximation (GGA), hybrid-GGA, DFT+U, and beyond-DFT random-phase approximation (RPA). For the preferred binding site, we compute state energies and spin-related properties, including spin and orbital angular momentum, and SOC using EOM-CCSD-in-DFT on finite models of Co/MgO(001). The embedded EOM-CCSD method seamlessly integrates into the EOM-CCSD framework, granting access to all its variants, including excitation energy (EE), ionization potential (IP), electron attachment (EA), and spin flip (SF). This integration also enables the analysis of spin states and spin properties using reduced quantities, such as natural orbitals (NOs) and natural transition orbitals (NTOs).^55–62 Beyond state energies and SOCs, we derive spin-inversion energy barriers and susceptibilities using a protocol that follows a state-interaction approach^63–65 to treat relativistic effects and applies Boltzmann statistics for computing macroscopic properties.⁴⁹ The accuracy of EOM-CCSD-in-DFT is assessed against EOM-CCSD, CC2, and experimental data.⁵⁴

We show that for the preferred adsorption conformation of Co on MgO(001), DFT-based methods fail to predict the easy-axis magnetic anisotropy, providing a qualitatively incorrect description compared to experiments.⁵⁴ In contrast, embedded EOM-CCSD accurately captures the multiconfigurational, non-aufbau nature of the spin states, yielding results that closely match experimentally derived magnetic anisotropy energy values, and thus highlighting the effectiveness of this embedding approach for describing magnetic adsorbates. Furthermore, by comparing Co adsorbed on MgO(001) with a linear, twofold-coordinated Co(C(SiMe₂ONaph)₃)₂ single-molecule magnet (i.e., Co(II)-SMM),^41,66 we establish a parallelism in their electronic structure and magnetic behavior. Both systems exhibit a non-aufbau ground state and strong magnetic anisotropy, demonstrating how electronic structures and magnetic properties can be replicated in different environments through carefully tuning the local coordination of the magnetic center.

II. Theoretical and computational details

A. Periodic DFT calculations

We performed periodic spin-polarized DFT structure optimizations for Co atoms on MgO(001). The Mg(001) surface model was constructed by cleaving a DFT-optimized bulk cell along the (001) plane, using a lattice parameter of a = 2.119 Å, as determined in ref. 67. For the surface models, we employed a 2 × 2 supercell of dimensions 8.48 × 8.48 × 25 Å, consisting of four layers of Mg²⁺ and O²⁻ ions, with an 18 Å vacuum in the z direction. During structure optimizations, the two bottom layers and the supercell dimensions were kept frozen. We examined four different adsorption sites: atop an O²⁻ ion, Mg(O), atop a Mg²⁺ ion, (Mg)O, a hollow site, and a bridging site between Mg²⁺ and O²⁻ ions. Each adsorption model contains one Co atom per supercell. Fig. 1 shows the most stable adsorption system (see Table 2), where Co occupies one out of eight surface O²⁻ ions, namely Co/Mg(O)(001). To model the Co atom in the gas phase, we used a cubic cell of 25 Å edge length.

Fig. 1 Side (left) and top (right) view of the 2 × 2 supercell used, including four surface layers and one Co adatom per cell. The Co adatom occupies the oxygen atop site on the MgO(001) surface, named Co/Mg(O)(001) adsorption system. Color code: Mg – green, O – red, and Co – purple.

Structure optimizations were carried out using the PBE⁶⁸ functional, augmented by the D3 dispersion correction scheme.⁶⁹ We employed a plane-wave basis set with a 520 eV energy cutoff, along with projector-augmented wave (PAW) pseudopotentials^70,71 for the core electrons. For the surface models, the first Brillouin zone was sampled using a 2 × 2 × 1 k-point grid centered at the Γ point, while a 1 × 1 × 1 k-point grid was used for gas-phase Co atom calculations. At the PBE+D3 equilibrium structure of Co/Mg(O)(001), we performed single-point calculations using PBE+U,^68,72 HSE06,⁷³ and RPA.^74,75 For PBE+U, we adopted U = 6.9 eV, following ref. 54. RPA calculations employed a frequency integration grid density of 8 points for the surface models and 16 points for the isolated Co atoms. Due to computational constraints, RPA calculations were performed using a 1 × 1 × 1 Γ-centered k-point grid and a vacuum space in the z-direction reduced by 7 Å. Using a smaller k-point mesh affects the binding energy by 8 kJ mol⁻¹, whereas reducing the vacuum height affects it by 2 kJ mol⁻¹ only (see Table S1, ESI†). Electronic energy thresholds were set to 1 × 10⁻⁶ eV for DFT and 1 × 10⁻⁸ eV for RPA calculations. The magnetic anisotropy energy (MAE) for Co/Mg(O)(001) was computed by carrying out self-consistent, non-collinear PBE and PBE+U calculations, including spin–orbit coupling and considering magnetization directions [0,0,1] and [1,0,0].^76,77 A 2 × 2 × 1 Γ-centered k-point grid was used for periodic models and a 1 × 1 × 1 k-point for finite clusters, with denser k-point meshes having a negligible effect on the MAE (see Table S2, ESI†). To improve convergence, the linear mixing parameter for the magnetization density was set to 0.2. MAE calculations with the HSE06 functional failed to converge, highlighting the challenges DFT-based methods face in adequately describing the multiconfigurational spin states of Co adatoms. See Section IIC for further details on MAE calculations. PBE+D3 structure optimizations were carried out until all forces on relaxed atoms were converged below 0.005 eV Å⁻¹. DFT and RPA calculations were conducted using the Vienna ab initio simulation package (VASP version 6.3.0).^71,78–80 All relevant Cartesian coordinates are provided in the ESI.†

B. Embedded EOM-CCSD calculations

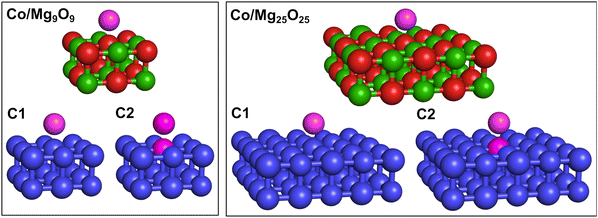
To compute the electronic states and spin-related and magnetic properties (i.e., spin–orbit coupling, spin-inversion energy barriers, and susceptibilities) of Co adatoms on MgO(001), we applied embedded EOM-CCSD to a cluster model representing the Co/Mg(O)(001) adsorption system. The adsorption cluster model consists of a single Co adatom positioned at the center of a finite MgO(001) cluster, extracted from the periodic PBE+D3 equilibrium structure. We considered two cluster sizes: a two-layer Mg₉O₉ cluster and a larger two-layer Mg₂₅O₂₅ cluster, as illustrated in Fig. 2. These cluster models have been widely employed in studies of molecular adsorption on MgO(001) using mechanical embedding schemes.^24,25 Both Co/Mg₉O₉ and Co/Mg₂₅O₂₅ clusters have C₁ point group symmetry. However, the Co atom, positioned atop the oxygen site, experiences a local axial coordination and an axial ligand field, which corresponds to C_∞v symmetry.

Fig. 2 Top: Co/Mg₉O₉ (left) and Co/Mg₂₅O₂₅ (right) cluster models of the Co/Mg(O)(001) periodic adsorption system. Color code: Mg – green, O – red, and Co – purple. Bottom: Two partitioning schemes, C1 and C2, for Co/Mg₉O₉ (left) and Co/Mg₂₅O₂₅ (right), illustrating the division into high-level (purple) and low-level (blue) fragments used in the embedded EOM-CCSD calculations.

To describe the 3d⁷ electronic states of Co/Mg₉O₉ and Co/Mg₂₅O₂₅, we employed the excitation energy (EE) variant of EOM-CCSD, in which a β electron is excited from the fully occupied and degenerate d_xz, d_yz orbital shell of the reference state |Ref〉. We computed two pairs of doubly-degenerate quartet states that we refer to as |1〉 and |2〉, and |3〉 and |4〉. Fig. 3 illustrates the electronic structure of the Co adatom, with state classifications based on the C_∞v symmetry point group. Additionally, Table 1 provides the electron configurations and corresponding angular momenta of the target states.

Fig. 3 Electron configurations of the quartet reference state |Ref〉, doubly-degenerate ground state (i.e., states |1〉 and |2〉), and quartet doubly-degenerate excited state (i.e., states |3〉 and |4〉) of Co/Mg₉O₉ and Co/Mg₂₅O₂₅ computed using EOM-EE-CCSD and EOM-EE-CCSD-in-DFT. Target states (quartet 3d⁷ non-aufbau electron configurations) are obtained by excitation of a β-electron from the reference state.

Table 1 Electron configurations of the reference and target states, and computed transition angular momenta for Co/Mg₉O₉, C1 (EOM-EE-CCSD-in-LRC-ωPBEh/6-31G*). States |1〉, |2〉, |3〉, and |4〉 are obtained by excitation of a β-electron from the reference state. Term symbols refer to the idealized point group C_∞v for Co⋯(O)Mg

State	Term (C∞v)	Configuration	〈Lz〉
|Ref〉	^4Σ^−	(dxy, dx^2−y^2)^2 (dxz, dyz)^4 (dz^2)^1
|1〉, |2〉	^4Φ	(dxy, dx^2−y^2)^3 (dxz, dyz)^3 (dz^2)^1	〈1|Lz|2〉 = 2.78i
|3〉, |4〉	^4Π	(dxy, dx^2−y^2)^3 (dxz, dyz)^3 (dz^2)^1	〈3|Lz|4〉 = 0.70i

---

For embedded EOM-EE-CCSD calculations, we employed two partitioning schemes. The first one (C1) partitions both Co/Mg₉O₉ and Co/Mg₂₅O₂₅ clusters into a high-level EOM-EE-CCSD fragment containing only the Co atom (highlighted in purple in Fig. 2), and a low-level DFT fragment representing the remaining surface atoms (shown in blue in Fig. 2). Since the computed spin density is distributed along the z-axis and localized on both the Co adatom and atop the O²⁻ site (see Fig. S1, ESI†), the second partitioning scheme (C2) extends the high-level fragment to include the oxygen adsorption site.

For the smaller Co/Mg₉O₉ cluster, we compared embedded EOM-EE-CCSD-in-DFT calculations with all-atom EOM-EE-CCSD and EE-CC2 results. In contrast, for the larger Co/Mg₂₅O₂₅ cluster, calculations were feasible only with embedded EOM-EE-CCSD. In the embedded EOM-EE-CCSD calculations, we truncated the virtual orbital space using concentric localization.⁸¹ For Co/Mg₉O₉, embedded EOM-EE-CCSD calculations were also possible without virtual space truncation. As low-level method, we employed the long-range corrected LRC-ωPBEh⁸² functional, which is expected to provide an adequate description for transition-metal molecular magnets.^41,83 Previous benchmarks have shown that replacing LRC-ωPBEh with other long-range corrected functionals such as CAM-B3LYP⁸⁴ does not affect the spin-state ordering nor significantly alter spin-related and magnetic properties (e.g., spin–orbit couplings, spin-inversion energy barriers, and susceptibilities).⁴¹ To Co/Mg₉O₉, we also applied the EE-CC2 variant with Cholesky decomposition⁸⁵ of the electron repulsion integrals. In all calculations the 6-31G* basis set was employed. Hartree–Fock calculations for the high-spin triplet reference state, |Ref〉 in Fig. 3, did not converge when using larger basis sets such as cc-pVTZ or def2-TZVP. However, previous benchmarks on Co, Fe, and Ni-based molecular magnets have shown that SOCs are largely independent of the adopted basis.^41,49,50 Such couplings differ by only a few tenths of wavenumbers with the increase of the basis set cardinal number from double- to triple-ζ, with a negligible impact on spin-reversal energy barriers and magnetic susceptibilities.

Core electrons were frozen in all calculations. Open-shell reference states were computed using unrestricted Hartree–Fock (UHF) theory. Spin contamination in both reference and target states was minimal, with 〈S²〉 values ranging from 3.75 to 3.78 for the quartet states of Co adatoms (Table S3, ESI†). All electronic–structure and property calculations for the clusters were carried out using the Q-Chem program package, version 6.0.⁸⁶

In the Q-Chem software, the code for spin-related properties, such as orbital angular momenta and SOCs, is general and can be interfaced with any method providing reduced density matrices. Electronic states and transition properties were characterized in terms of natural orbitals (NOs) and natural transition orbitals (NTOs). This approach has been widely applied to molecular magnets using various electronic structure methods, including EOM-CCSD, SF-TD-DFT, and EOM-CCSD-in-DFT.^41,49,50,83 In addition to computing state energies and spin properties, macroscopic magnetic properties—specifically, the magnetization and susceptibility—were computed, as implemented in the ezMagnet software.⁴⁹ This framework accounts for spin–orbit and Zeeman interactions via a two-step state-interaction scheme:^63–65 first, non-relativistic EOM-CCSD or EOM-CCSD-in-DFT states are computed; second, matrix elements of the spin–orbit (Ĥ^SO) and Zeeman (Ĥ^Z) Hamiltonians are evaluated in the basis of these non-relativistic states. As spin–orbit operator Ĥ^SO, we use the one-electron operator derived from the Breit–Pauli spin–orbit Hamiltonian,^87,88 within the spin–orbit mean-field approximation^65,89 of the two-electron part, as implemented by Pokhilko, Krylov, and co-workers.^48,90,91 Magnetic sublevels are then obtained by diagonalizing the perturbed Hamiltonian, i.e., Ĥ = Ĥ⁰ + Ĥ^SO + Ĥ^Z, where Ĥ⁰ is the Born–Oppenheimer Hamiltonian. This procedure also enables quantification of the spin-reversal barrier in single-molecule and single-atom magnets using the computed magnetic sublevels (see Fig. 4 in Section IIC). Magnetization and susceptibility are then derived from the resulting partition function using Boltzmann statistics.

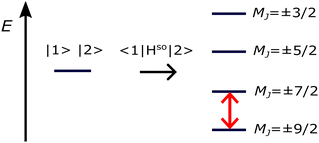Fig. 4 Spin–orbit splitting of the ground state (states |1〉 and |2〉) of Co/Mg(O) with S = 3/2, L = 3, and total angular momentum J = S + L = 9/2. The energy barrier for spin inversion is shown in red. Reprinted from ref. 41. Copyright Royal Society of Chemistry.

C. Magnetic anisotropy energy and spin-inversion energy barrier

Magnetic anisotropy refers to the directional dependence of the magnetic properties of a system. It originates from the interaction between spin and orbital angular momenta, giving rise to spin–orbit coupling and zero-field splitting. Magnetic anisotropy can be classified as either easy-axis or easy-plane, depending on whether the magnetization preferentially aligns parallel to a certain axis (conventionally the z-axis) or lies within a plane perpendicular to it. The energy that orients the magnetization along this direction of easy magnetization is known as the magnetic anisotropy energy (MAE).^76,77

For Co/Mg(O)(001), we determined the MAE by performing self-consistent, non-collinear PBE and PBE+U calculations with spin–orbit coupling for different magnetization orientations. The MAE was computed as the energy difference

E_MAE = E_[001] − E_[100], (1)

where E_[001] and E_[100] are the energies with the magnetization direction parallel and perpendicular to the MgO(001) surface, respectively. A positive E_MAE indicates easy-plane anisotropy, favoring in-plane magnetization, while a negative E_MAE corresponds to easy-axis anisotropy, where magnetization aligns along the z-axis. We achieved MAE convergence using a 2 × 2 × 1 k-point mesh for periodic models and a 1 × 1 × 1 k-point mesh for cluster models (see Table S2, ESI†).

The MAE is often expressed as an energy barrier for spin inversion, denoted as . For the Co/Mg₉O₉ and Co/Mg₂₅O₂₅ clusters representing Co/Mg(O)(001), the doubly degenerate ground state, computed using embedded EOM-CCSD, splits into four Kramers doublets due to spin–orbit interactions, as shown in Fig. 4. The spin-inversion energy barrier is then given as the energy difference between the ground M_J = ±9/2 state and the first excited M_J = ±7/2 state:

States with the highest M_J = ±9/2 angular momentum projection lie lowest in energy. This indicates easy-axis magnetic anisotropy with magnetization preferentially oriented perpendicular to the surface, which is consistent with experimental observations.⁵⁴ The first excited doubly-degenerate state, M_J = ±7/2, corresponds to a 70° rotation of the magnetic moment from the surface plane. Non-collinear DFT calculations for this deflection angle did not converge. Note that the values of E_MAE (eqn (1)) and (eqn (2)) differ due to a sign convention.

III. Results and discussion

A. Periodic and cluster DFT results

Table 2 summarizes the adsorption energies, and geometric and magnetic data for isolated Co atoms adsorbed on Mg²⁺, O²⁻, and hollow sites of the MgO(001) surface, as calculated with spin-polarized PBE+D3. The adsorption energy, ΔE_ads, is defined as

ΔE_ads = E_Co/MgO − (E_MgO + E_Co), (3)

where E_Co/MgO is the energy of the adsorbate–surface system, E_MgO is the energy of the relaxed MgO slab, and E_Co corresponds to the energy of the Co atom in the gas phase. On the MgO(001) surface, Co adatoms preferentially adsorb on the oxygen sites, with an equilibrium distance of 184 pm from the surface. This result agrees with a previous DFT study.⁵⁴ For Co/Mg(O)(001), dispersion computed using the D3 correction⁶⁹ to PBE contributes only 15% to the total adsorption energy. The total magnetic moment μ is 3 Bohr magneton, consistent with a spin S = 3/2 ground state. This magnetic moment is localized mainly on the Co atom (93%), with a minor contribution (7%) on the adjacent oxygen. Compared to the PBE binding energy of Co/Mg(O)(001), PBE+U, HSE06, and RPA yield progressively weaker adsorption energies by 98.8, 53.6, and 18.4 kJ mol⁻¹, respectively. PBE+U significantly overcorrects PBE binding energies, while HSE06 provides an intermediate result between PBE+U and RPA.

Table 2 Co⋯(O)Mg distances R in pm, magnetic moments μ in Bohr magneton, and adsorption energies ΔE_ads in kJ mol⁻¹ computed using PBE+D3. Three adsorption sites are considered: oxygen atop – Mg(O), magnesium atop – (Mg)O, and hollow site.^a For Co/Mg(O), ΔE_ads values were also evaluated using PBE+U, HSE06, and RPA at the PBE+D3 equilibrium structure

Adsorption site	R	μ^b	ΔEads
			PBE	D3	PBE+D3
a Calculations with Co at bridge positions on MgO(001) converged to the Co/Mg(O) adsorption configuration.b μ is localized on the Co adatom.c U = 6.9 eV is taken from ref. 54.
Mg(O)	184	3	−125.5	−22.5	−148.0
(Mg)O	281	3	−20.9	−38.0	−58.9
Hollow	233	3	−84.1	−26.1	−110.1

---

Adsorption site	ΔEads
	PBE+U^c	HSE06	RPA
Mg(O)	−26.7	−71.9	−107.1

---

The PBE+D3 density of states for the Co d-levels (Fig. 5) reveals weak interaction with Mg²⁺ ions, with the d_xy, d_x²−y² and d_xz, d_yz orbitals being twofold degenerate. The primary hybridization occurs between the out-of-plane d-orbitals of Co (d_xz, d_yz, and d_z²) and the p-orbitals of the O²⁻ adsorption site, where the d_xz, d_yz and d_z² orbitals also remain degenerate. This hybridization confirms the presence of an axial ligand field along the z-axis. Comparing spin-up and spin-down bands relative to the Fermi level, the d_xy, d_x²−y² orbitals are fully occupied by both alpha and beta spin electrons, while the d_xz, d_yz and d_z² orbitals are predominantly occupied by alpha electrons. This orbital occupation aligns more closely with that of a single-reference excited state of the Co adatom, i.e., (d_xy, d_x²−y²)⁴ (d_xz, d_yz)² (d_z²)¹, with fully quenched orbital angular momentum rather than with the non-aufbau configurations expected for its ground state (see Fig. 3). This suggests that DFT-based methods fail to adequately capture the true ground state of Co adatoms. The HSE06 density of states is similar; however, the hybrid-GGA functional predicts that the d_z² orbital is no longer degenerate with the d_xz, d_yz orbitals, better reflecting the expected d-orbital splitting in a linear coordination environment (Fig. 3). These results also align closely with the density of states reported in ref. 54, obtained using PBE+U.

Fig. 5 Atomic orbital-projected and spin-resolved density of states of Co/Mg(O) computed using PBE+D3 (left) and HSE06 (right).

To examine the convergence of the PBE+D3 adsorption energy with the cluster size, we compared adsorption energies calculated for two progressively larger clusters with the result from periodic DFT calculations. This step is crucial for assessing the validity of the cluster models used to approximate the periodic system.^24,25 Results are reported in Table 3. At the PBE+D3 equilibrium structure of Co/Mg(O), as the cluster size increases from Co/Mg₉O₉ to Co/Mg₂₅O₂₅, the long-range correction,^24,25

Δ_LR = ΔE_ads(pbc) − ΔE_ads(cluster), (4)

defined as the difference in adsorption energy between the periodic (pbc) and cluster models, decreases by 4.7 kJ mol⁻¹. The smaller Co/Mg₉O₉ cluster exhibits a higher PBE contribution to the binding, with the D3 correction accounting for only 6% of the total adsorption energy, compared to 15% in the periodic calculations. In contrast, the larger Co/Mg₂₅O₂₅ cluster yields a ratio between the PBE and D3 contributions that is closer to that of the periodic system. However, both cluster models provide an accurate description of the chemisorption of Co onto MgO(001), with errors of less than 5% on the total binding energy.

Table 3 PBE+D3 adsorption energies ΔE_ads and long-range corrections Δ_LR in kJ mol⁻¹ for Co/Mg(O) periodic and cluster models. All calculations were performed at the periodic PBE+D3 equilibrium structure of Co/Mg(O)(001) using a plane-wave basis set

System	ΔEads			ΔLR
	PBE	D3	PBE+D3
Co/Mg9O9	−146.2	−9.7	−155.9	7.9
Co/Mg25O25	−134.1	−17.1	−151.2	3.2
Co/Mg(O) (pbc)	−125.5	−22.5	−148.0

---

Furthermore, at both the PBE and PBE+U level, and regardless of whether the periodic or cluster model was used, the MAE calculated using eqn (1) remains positive, ranging between 30 and 54 cm⁻¹ (Table 4). Positive MAEs are indicative of in-plane magnetic anisotropy, which is qualitatively incorrect for Co adatoms on MgO(001).⁵⁴ This discrepancy in the computed MAE, the bad convergence behavior of the non-collinear DFT calculations, and the DOS, indicating fully occupied d_xy, d_x²−y² orbitals and thus quenching of the orbital angular momentum, showcase the difficulties that approximate exchange and correlation density functionals face in capturing the multiconfigurational, non-aufbau character of the spin states in Co/MgO(001). These issues suggest that beyond-DFT approaches are necessary to accurately describe the system.

Table 4 Magnetic anisotropy energies E_MAE in cm⁻¹ for Co/Mg(O) periodic and cluster models computed using PBE and PBE+U. All calculations were performed at the periodic PBE+D3 equilibrium structure of Co/Mg(O)(001) using a plane-wave basis set

System	EMAE^a
	PBE	PBE+U
a Positive EMAE indicates easy-plane magnetic anisotropy, while a negative value indicates easy-axis anisotropy.
Co/Mg9O9	46	54
Co/Mg25O25	41	44
Co/Mg(O) (pbc)	30	47

---

B. Embedded EOM-CCSD results and comparison with experiment

Table 5 presents the spin state energies for Co/Mg₉O₉ and Co/Mg₂₅O₂₅ clusters computed using embedded EOM-EE-CCSD. For the smaller Co/Mg₉O₉ cluster, we benchmarked embedded EOM-EE-CCSD against all-atom EOM-EE-CCSD and EE-CC2. Given that Co adatoms on MgO(001) experience a strong axial ligand field, similar to that of a linear, twofold-coordinated Co(C(SiMe₂ONaph)₃)₂ single-molecule magnet (Co(II)-SMM), the resulting spin state character and ordering are similar to those observed for the Co(II)-SMM described in ref. 41 and 66. All methods consistently predict a doubly-degenerate ground state (|1〉 and |2〉) dominated by four non-aufbau electronic configurations, as illustrated in Fig. 3. NO analysis shows that the two β electrons in the Co d orbitals are confined to the d_xy, d_x²−y², d_xz, and d_yz orbitals. Moreover, four NTO pairs drive the orbital angular momentum and spin–orbit coupling between states |1〉 and |2〉. Transitions between these states involve orbital reorientations from d_xy to d_x²−y², and from d_xz to d_yz, as depicted in Fig. 6.

Table 5 Relative energies of electronic states in cm⁻¹, orbital angular momenta, spin–orbit coupling constants SOCC in cm⁻¹, and spin-inversion energy barriers in cm⁻¹ of Co/Mg₉O₉ and Co/Mg₂₅O₂₅ computed using EOM-EE-CCSD, EE-CC2, and EOM-EE-CCSD-in-LRC-ωPBEh/6-31G*. All EOM-EE-CCSD-in-LRC-ωPBEh results are obtained with truncation of the virtual orbital space. Computations are performed at the periodic PBE+D3 equilibrium structure of Co/Mg(O)(001). The C1 and C2 partitioning schemes define whether the oxygen adsorption site is excluded (C1) or included (C2) in the high-level fragment

State	Co(II)-SMM^a	Co/Mg9O9				Co/Mg25O25
	EOM-CC-in-DFT	EOM-CC	CC2	EOM-CC-in-DFT		EOM-CC-in-DFT
				C1	C2	C1	C2
a Results for Co(C(SiMe2ONaph)3)2 single-molecule magnet (i.e., Co(II)-SMM) are taken from ref. 41.b The SOCC is computed between states |1〉 and |2〉.
|Ref〉	2492	4902	6211	3462	4444	3717	4522
|1〉	0	0	0	0	0	0	0
|2〉	45	0	0	0	0	0	0
|3〉	2721	3313	3234	3978	3412	4089	3472
|4〉	2722	3313	3234	3979	3412	4089	3472
〈1|Lz|2〉	2.99i	2.78i		2.85i	2.79i	2.89i	2.85i
SOCC^b	1059	956		978	958	986	973
	469	427		437	428	441	427

---

Fig. 6 Hole and particle NTOs for SOC between states |1〉 and |2〉 of Co/Mg₉O₉, C2 computed using EOM-EE-CCSD-in-LRC-ωPBEh/6-31G*. An isovalue of 0.05 was used.

For Co/Mg₉O₉, both EOM-EE-CCSD and EE-CC2 yield the same state ordering, with EE-CC2 deviating from EOM-EE-CCSD by less than 100 cm⁻¹ for the low-lying electronic states |3〉 and |4〉, and up to 1300 cm⁻¹ for the fourth excited state, which is the reference state |Ref〉. Using embedded EOM-EE-CCSD along with the C1 partitioning scheme, the |Ref〉 state lies lower than the doubly-degenerate excited state (|3〉 and |4〉), with energy differences of up to 1400 cm⁻¹ relative to all-atom EOM-EE-CCSD, a trend previously noted for simplified models of the Co(II)-SMM.⁴¹ However, incorporating the oxygen adsorption site in the high-level treatment through the C2 partitioning scheme corrects the EOM-EE-CCSD-in-DFT state ordering, reducing deviations from EOM-EE-CCSD to less than 500 cm⁻¹. This improvement suggests that the C2 partitioning scheme provides a more accurate representation of the all-atom cluster model. A similar trend holds for the larger Co/Mg₂₅O₂₅ cluster, with energy differences between Co/Mg₉O₉ and Co/Mg₂₅O₂₅ of less than 300 cm⁻¹.

The energies reported in Table 5 can be strongly affected by the choice of basis set; consequently, the values obtained using 6-31G* may be far from fully converged. However, it is the SOCs—rather than the absolute excited-state energies—that serves as the key quantities for benchmarking magnetic anisotropy and magnetic susceptibility. SOCs are computed between spin–orbit-coupled states that remain degenerate regardless of the basis set, and their values are insensitive to both the level of electron correlation and the basis.^41,49,50 As energies and SOCs exhibit different convergence behaviors with respect to the basis set, conclusions drawn below upon investigation of spin–orbit-related properties are not basis-set dependent.

For Co/Mg₉O₉, using EOM-EE-CCSD, we compute an orbital angular momentum of 〈L_z〉 = 2.8i and a large spin–orbit coupling constant (SOCC) of 956 cm⁻¹ between states |1〉 and |2〉. Large SOCCs are expected between states with different orbital orientations, i.e., involving transitions from d_xz to d_yz and from d_xy to d_x²−y² (Fig. 6), in accordance with El-Sayed's rule.⁹² The agreement between EOM-EE-CCSD and EOM-EE-CCSD-in-DFT is excellent, with SOCC differences between the two levels of theory of less than 20 cm⁻¹. Moving from the C1 to the C2 partitioning scheme reduces both the orbital angular momentum and SOCC values, improving the agreement with EOM-EE-CCSD even further. We observe that the SOCC remains largely unaffected by the cluster size, with deviations between Co/Mg₉O₉ and Co/Mg₂₅O₂₅ of less than 15 cm⁻¹.

This strong SOC leads to a large zero-field splitting of the ground state into eight pairwise degenerate magnetic levels (Fig. 4), whose energies are listed in Table S6 (ESI†). This spin–orbit splitting closely resembles that observed in the Co(II)-SMM.^41,66 From the magnetic sublevels of Co/Mg₉O₉ and following eqn (2), we obtain a spin-inversion energy barrier of 427 cm⁻¹ using EOM-EE-CCSD, which agrees well with embedded EOM-EE-CCSD results, with differences of only 10 cm⁻¹. These values are in close agreement also with that extracted from an inelastic electron tunneling spectroscopy (IETS) measurement (468 cm⁻¹)⁵⁴ and with the spin-inversion barrier computed for the Co(II)-SMM using embedded EOM-CCSD (469 cm⁻¹).⁴¹ By moving from the C1 to the C2 partitioning scheme and expanding the cluster size from Co/Mg₉O₉ to Co/Mg₂₅O₂₅, we reaffirm that the C2 partitioning provides a more accurate representation of the all-atom model, yielding spin-inversion barriers in closer agreement with EOM-EE-CCSD, whereas the impact of the cluster size remains minor.

For the smaller Co/Mg₉O₉ cluster, truncating the virtual orbital space has a negligible impact on the embedded EOM-EE-CCSD results (see Table S5, ESI†). The state energy differences remain within 100 cm⁻¹, while the effect on both the SOCC and spin-reversal energy barrier is minimal, staying below 5 cm⁻¹. These findings are consistent with previous observations for the Co(II)-SMM.⁴¹

The calculated temperature-dependent susceptibilities (χT vs. T) are shown in Fig. 7. For Co/Mg₉O₉, the EOM-EE-CCSD-in-DFT susceptibility curve obtained using the C2 partitioning scheme shows better agreement with the all-atom EOM-EE-CCSD susceptibilities than the curve computed with the C1 partitioning scheme. For the C2 model, increasing the cluster size to Co/Mg₂₅O₂₅ has a negligible effect. For Co adatoms on MgO(001), experimental susceptibility plots are not available. However, at 300 K, the calculated χT product for Co/Mg₉O₉ (C2, embedded EOM-EE-CCSD) is 4.51 cm³ K mol⁻¹, closely matching both the theoretical⁴¹ (4.89 cm³ K mol⁻¹) and the experimental⁶⁶ (4.80 cm³ K mol⁻¹) value reported for the Co(II)-SMM. These values significantly exceed the spin-only prediction of 1.876 cm³ K mol⁻¹ for an isotropic spin-3/2 ion that follows the Curie law, consistent with the magnetic behavior of a system with a substantial orbital angular momentum contribution (L = 3). The good agreement in the computed macroscopic magnetic properties between Co adatoms on MgO(001) and the Co(II)-SMM further emphasizes the similarity of their electronic structures and magnetic behaviors.

Fig. 7 Top: Calculated susceptibility curves of Co/Mg₉O₉ and Co/Mg₂₅O₂₅ between 50 and 300 K under an applied field of 7 T. Bottom: Calculated susceptibility curves of Co(C(SiMe₂ONaph)₃)₂ single-molecule magnet (Co(II)-SMM) and Co/Mg₉O₉ between 5 and 300 K under an applied field of 7 T. Susceptibilities are obtained using EOM-EE-CCSD and EOM-EE-CCSD-in-LRC-ωPBEh/6-31G*. “av” stands for isotropic powder averaging. Experimental and theoretical data for the Co(II)-SMM were taken from ref. 66 and 41, respectively.

IV. Conclusions

In this work, we combined a periodic DFT description of Co atom adsorption on the MgO(001) surface with an embedded EOM-CCSD approach to investigate the electronic structure and magnetic behavior, pioneering the application of many-body correlated methods to the study of magnetic adsorbates.

For Co atoms adsorbed at the preferred oxygen sites of MgO(001), we found that the binding energy is highly sensitive to the DFT method, ranging from −126 kJ mol⁻¹ (PBE) to −27 kJ mol⁻¹ (PBE+U). While PBE+U overcorrects the PBE binding energy relative to RPA, the hybrid HSE06 method yields intermediate results between PBE+U and RPA. Dispersion contributions account for less than 15% of the total adsorption energy. The DFT density of states indicates an overlap between the out-of-plane Co d orbitals and the oxygen p orbitals, leading to an axial ligand field along the z-axis. However, based on this DOS picture, the Co d_xy, d_x²−y² orbitals are fully occupied, resulting in quenched orbital angular momentum (L ≈ 0). Consequently, the approximate density functionals fail to capture the non-aufbau ground state with maximal L expected for the system. DFT-based methods were also unable to accurately predict both the magnitude and sign of the magnetic anisotropy energy, erroneously favoring in-plane magnetic anisotropy for Co/MgO(001). This discrepancy between experimental observations and most commonly used periodic DFT—including GGA, GGA+U, and hybrid GGA—highlights the need for more advanced post-Hartree–Fock methods.

In contrast, embedded EOM-CCSD calculations on two cluster models of different size predict a non-aufbau, doubly degenerate quartet ground state with nearly unquenched orbital angular momentum (L ≈ 3) and strong spin–orbit coupling (SOC). The resulting spin–orbit splitting favors states with the highest angular momentum projections (M_J = ±9/2), which are the lowest in energy, in agreement with experimental observations of easy-axis magnetic anisotropy.⁵⁴ The agreement between embedded EOM-CCSD and all-atom EOM-CCSD and CC2 predictions for state ordering and magnetic properties (SOC, spin-inversion energy barrier, and susceptibility) improves when the oxygen adsorption site is included in the high-level treatment. For this partitioning scheme—but independently of cluster size—the predicted spin-inversion energy barrier of 427 cm⁻¹ closely matches the experimentally reported magnetic anisotropy energy of 469 cm⁻¹.⁵⁴ Our ab initio estimate of the spin-inversion energy barrier also corroborates the results obtained through parametrized multiplet ligand field theory.⁵⁴ These findings establish the reliability of embedded EOM-CCSD for magnetic properties of adsorbates.

The embedding approach is versatile as the size and shape of the high-level fragment can be adjusted to capture the locality of the phenomena under study.⁴² The high-level method can be tailored to investigate systems of varying complexity and dimensionality.⁴² The combination of CC2 with DFT offers an appealing and more cost-effective alternative to EOM-CCSD-in-DFT, which we envision can be employed to investigate systems for which the high-level fragment size shall be extended, potentially including multiple metallic atoms.

Furthermore, mechanical embedding schemes combining perturbation theory or coupled-cluster theory with periodic DFT can accurately describe the reactivity of closed-shell, well-behaved adsorbates on various substrates.^24,25,93 Extending these approaches to embedded EOM-CCSD offers a promising route for accurately evaluating not only magnetic properties, but also adsorption and reaction energies of open-shell and complex adsorbates, thereby overcoming the limitations of approximate DFT.

On a broader level, this work also reveals a striking parallel between Co/MgO(001) and a linear, twofold-coordinate Co(II) molecular magnet, both of which exhibit an axial ligand field. In both systems, the ground state is a non-aufbau quartet state with maximal orbital angular momentum and strong spin–orbit coupling, resulting in a record-high spin-inversion barrier. Also, both systems have a comparable temperature dependence of the susceptibility. These findings further emphasize the crucial role of low and axial coordination in defining the desired electronic structures and magnetic properties of magnetic molecules and atoms. Moreover, they demonstrate how this fundamental design principle for achieving efficient nanomagnets can be replicated across vastly different environments.

Beyond this specific case, our work provides a robust framework for investigating magnetic adsorbates, improving on current DFT-based approaches. The insights gained also lay the foundation for further methodological advancements, such as embedding EOM-CCSD with periodic boundary conditions. This work, along with our recent efforts to estimate dissociation energies of diatomic molecules on metal surfaces,⁴² represents a valuable contributions to the description of a broad class of complex chemical systems with well-localized active sites, with implications for both magnetism and catalysis.

Conflicts of interest

There are no conflicts to declare.

Data availability

All data supporting this study are included in the article, with additional details available in the supplementary material. The ezMagnet software for computing macroscopic magnetic properties is available at https://iopenshell.usc.edu/downloads/ezmagnet/.

Acknowledgements

This work has been supported by a Marie Skłodowska-Curie Actions fellowship to M. A. (Grant Agreement No. 101062717). T.-C. J. gratefully acknowledges funding from the European Research Council (ERC) under the European Unions Horizon 2020 research and innovation program (Grant Agreement No. 851766) and the KU Leuven internal funds (Grant No. C14/22/083). T. S. acknowledges support from the Austrian Science Fund (FWF) [DOI: https://doi.org/10.55776/ESP335].

References

1. T. Choi, W. Paul, S. Rolf-Pissarczyk, A. J. Macdonald, F. D. Natterer, K. Yang, P. Willke, C. P. Lutz and A. J. Heinrich, Nat. Nanotechnol., 2017, 12, 420–424.
2. F. D. Natterer, K. Yang, W. Paul, P. Willke, T. Choi, T. Greber, A. J. Heinrich and C. P. Lutz, Nature, 2017, 543, 226–228.
3. F. Donati and A. J. Heinrich, Appl. Phys. Lett., 2021, 119, 160503.
4. M. J. Graham, J. M. Zadrozny, M. S. Fataftah and D. E. Freedman, Chem. Mater., 2017, 29, 1885–1897.
5. M. Atzori and R. Sessoli, J. Am. Chem. Soc., 2019, 141, 11339–11352.
6. S. Baumann, W. Paul, T. Choi, C. P. Lutz, A. Ardavan and A. J. Heinrich, Science, 2015, 350, 417–420.
7. K. Yang, W. Paul, S.-H. Phark, P. Willke, Y. Bae, T. Choi, T. Esat, A. Ardavan, A. J. Heinrich and C. P. Lutz, Science, 2019, 366, 509–512.
8. M. Steinbrecher, W. M. J. van Weerdenburg, E. F. Walraven, N. P. E. van Mullekom, J. W. Gerritsen, F. D. Natterer, D. I. Badrtdinov, A. N. Rudenko, V. V. Mazurenko, M. I. Katsnelson, A. van der Avoird, G. C. Groenenboom and A. A. Khajetoorians, Phys. Rev. B, 2021, 103, 155405.
9. S. Reale, J. Hwang, H. Brune, A. J. Heinrich, F. Donati and Y. Bae, Nat. Commun., 2024, 15, 5289.
10. C. F. Hirjibehedin, C. P. Lutz and A. J. Heinrich, Science, 2006, 312, 1021–1024.
11. S. Loth, S. Baumann, C. P. Lutz, D. M. Eigler and A. J. Heinrich, Science, 2012, 335, 196–199.
12. A. A. Khajetoorians, D. Wegner, A. F. Otte and I. Swart, Nat. Rev. Phys., 2019, 1, 703–715.
13. K. Yang, S.-H. Phark, Y. Bae, T. Esat, P. Willke, A. Ardavan, A. J. Heinrich and C. P. Lutz, Nat. Commun., 2024, 12, 1–7.
14. M. Briganti and F. Totti, Molecular Magnets on Surfaces: In Silico Recipes for a Successful Marriage, Springer, 2023, pp. 395–444.
15. A. Dreuw and M. Head-Gordon, Chem. Rev., 2005, 105, 4009–4037.
16. A. J. Cohen, P. Mori-Sánchez and W. Yang, Chem. Rev., 2012, 112, 289–320.
17. P. J. Feibelman, B. Hammer, J. K. Nørskov, F. Wagner, M. Scheffler, R. Stumpf, R. Watwe and J. Dumesic, J. Phys. Chem. B, 2001, 105, 4018–4025.
18. J. P. Malrieu, R. Caballol, C. J. Calzado, C. de Graaf and N. Guihéry, Chem. Rev., 2014, 114, 429–492.
19. P. Rivero, C. Loschen, I. de P. R. Moreira and F. Illas, J. Comput. Chem., 2009, 30, 2316–2326.
20. P. Rivero, I. de P. R. Moreira and F. Illas, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 205123.
21. P. Gambardella, S. Rusponi, M. Veronese, S. S. Dhesi, C. Grazioli, A. Dallmeyer, I. Cabria, R. Zeller, P. H. Dederichs, K. Kern, C. Carbone and H. Brune, Science, 2003, 300, 1130–1133.
22. I. Y. Zhang and A. Grüneis, Front. Mater., 2019, 6, 123.
23. L. W. Chung, W. M. C. Sameera, R. Ramozzi, A. J. Page, M. Hatanaka, G. P. Petrova, T. V. Harris, X. Li, Z. Ke, F. Liu, H.-B. Li, L. Ding and K. Morokuma, Chem. Rev., 2015, 115, 5678–5796.
24. M. Alessio, F. A. Bischoff and J. Sauer, Phys. Chem. Chem. Phys., 2018, 20, 9760–9769.
25. M. Alessio, D. Usvyat and J. Sauer, J. Chem. Theory Comput., 2019, 15, 1329–1344.
26. C. R. Jacob and J. Neugebauer, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 325–362.
27. T. A. Wesolowski, S. Shedge and X. Zhou, Chem. Rev., 2015, 115, 5891–5928.
28. F. Libisch, C. Huang and E. A. Carter, Acc. Chem. Res., 2014, 47, 2768–2775.
29. T. Schäfer, F. Libisch, G. Kresse and A. Grüneis, J. Chem. Phys., 2021, 154, 011101.
30. T. Schäfer, A. Gallo, A. Irmler, F. Hummel and A. Grüneis, J. Chem. Phys., 2021, 155, 244103.
31. D. Zgid and G. K.-L. Chan, J. Chem. Phys., 2011, 134, 094115.
32. G. Knizia and G. Chan, Phys. Rev. Lett., 2012, 109, 186404.
33. F. R. Manby, M. Stella, J. D. Goodpaster and T. F. Miller, J. Chem. Theory Comput., 2012, 8, 2564–2568.
34. S. J. R. Lee, F. Ding, F. R. Manby and T. F. Miller, J. Chem. Phys., 2019, 151, 064112.
35. S. Huzinaga and A. A. Cantu, J. Chem. Phys., 1971, 55, 5543–5549.
36. B. Hégely, P. R. Nagy, G. G. Ferenczy and M. Kállay, J. Chem. Phys., 2016, 145, 064107.
37. A. Severo Pereira Gomes and C. R. Jacob, Annu. Rep. Prog. Chem., Sect. C: Phys. Chem., 2012, 108, 222–277.
38. S. J. Bennie, B. F. E. Curchod, F. R. Manby and D. R. Glowacki, J. Phys. Chem. Lett., 2017, 8, 5559–5565.
39. V. Parravicini and T.-C. Jagau, Mol. Phys., 2021, 119, e1943029.
40. J. D. Goodpaster, T. A. Barnes, F. R. Manby and T. F. Miller, J. Chem. Phys., 2012, 137, 224113.
41. M. Alessio, G. P. Paran, C. Utku, A. Grüneis and T.-C. Jagau, Phys. Chem. Chem. Phys., 2024, 26, 17028–17041.
42. R. E. Moorby, V. Parravicini, T.-C. Jagau and M. Alessio, J. Phys. Chem. C, 2024, 128, 15421–15430.
43. J. F. Stanton and R. J. Bartlett, J. Chem. Phys., 1993, 98, 7029–7039.
44. A. I. Krylov, Annu. Rev. Phys. Chem., 2008, 59, 433–462.
45. K. Sneskov and O. Christiansen, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 566–584.
46. R. J. Bartlett, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 126–138.
47. N. Orms and A. I. Krylov, Phys. Chem. Chem. Phys., 2018, 20, 13127–13144.
48. P. Pokhilko, E. Epifanovsky and A. I. Krylov, J. Chem. Phys., 2019, 151, 034106.
49. M. Alessio and A. I. Krylov, J. Chem. Theory Comput., 2021, 17, 4225–4241.
50. M. Alessio, S. Kotaru, G. Giudetti and A. I. Krylov, J. Phys. Chem. C, 2023, 127, 3647–3659.
51. S. Kähler, A. Cebreiro-Gallardo, P. Pokhilko, D. Casanova and A. I. Krylov, J. Phys. Chem. A, 2023, 127, 8459–8472.
52. O. Christiansen, H. Koch and P. Jørgensen, Chem. Phys. Lett., 1995, 243, 409–418.
53. G. P. Paran, C. Utku and T.-C. Jagau, Phys. Chem. Chem. Phys., 2022, 24, 27146–27156.
54. I. G. Rau, S. Baumann, S. Rusponi, F. Donati, S. Stepanow, L. Gragnaniello, J. Dreiser, C. Piamonteze, F. Nolting, S. Gangopadhyay, O. R. Albertini, R. M. Macfarlane, C. P. Lutz, B. A. Jones, P. Gambardella, A. J. Heinrich and H. Brune, Science, 2014, 344, 988–992.
55. A. V. Luzanov, A. A. Sukhorukov and V. E. Umanskii, Theor. Exp. Chem., 1976, 10, 354–361.
56. A. V. Luzanov and V. F. Pedash, Theor. Exp. Chem., 1979, 15, 338–341.
57. F. Plasser, M. Wormit and A. Dreuw, J. Chem. Phys., 2014, 141, 024106.
58. F. Plasser, S. A. Bäppler, M. Wormit and A. Dreuw, J. Chem. Phys., 2014, 141, 024107.
59. A. I. Krylov, J. Chem. Phys., 2020, 153, 080901.
60. F. Plasser, A. I. Krylov and A. Dreuw, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1595.
61. S. A. Mewes, F. Plasser, A. Krylov and A. Dreuw, J. Chem. Theory Comput., 2018, 14, 710–725.
62. P. Pokhilko and A. I. Krylov, J. Phys. Chem. Lett., 2019, 10, 4857–4862.
63. A. Berning, M. Schweizer, H.-J. Werner, P. Knowles and P. Palmieri, Mol. Phys., 2000, 98, 1823–1833.
64. D. G. Fedorov, S. Koseki, M. W. Schmidt and M. S. Gordon, Int. Rev. Phys. Chem., 2003, 22, 551–592.
65. C. M. Marian, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 187–203.
66. P. C. Bunting, M. Atanasov, E. Damgaard-Møller, M. Perfetti, I. Crassee, M. Orlita, J. Overgaard, J. van Slageren, F. Neese and J. R. Long, Science, 2018, 362, 2146–2149.
67. A. D. Boese and J. Sauer, Phys. Chem. Chem. Phys., 2013, 15, 16481–16493.
68. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
69. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
70. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
71. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11185.
72. V. I. Anisimov, J. Zaanen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 943–954.
73. A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106.
74. D. Bohm and D. Pines, Phys. Rev., 1951, 82, 625–634.
75. D. Bohm and D. Pines, Phys. Rev., 1953, 92, 609–625.
76. D. Hobbs, G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 11556–11570.
77. S. Steiner, S. Khmelevskyi, M. Marsmann and G. Kresse, Phys. Rev. B, 2016, 93, 224425.
78. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 47, 558–561.
79. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
80. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1774.
81. D. Claudino and N. J. Mayhall, J. Chem. Theory Comput., 2019, 15, 6085–6096.
82. M. Rohrdanz, K. Martins and J. Herbert, J. Chem. Phys., 2009, 130, 054112.
83. S. Kotaru, S. Kähler, M. Alessio and A. I. Krylov, J. Comput. Chem., 2023, 44, 367–380.
84. T. Yanai, D. Tew and N. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
85. T. B. Pedersen, A. M. J. Sánchez de Merás and H. Koch, J. Chem. Phys., 2004, 120, 8887–8897.
86. E. Epifanovsky, A. T. B. Gilbert, X. Feng, J. Lee, Y. Mao, N. Mardirossian, P. Pokhilko, A. F. White, M. P. Coons, A. L. Dempwolff, Z. Gan, D. Hait, P. R. Horn, L. D. Jacobson, I. Kaliman, J. Kussmann, A. W. Lange, K. U. Lao, D. S. Levine, J. Liu, S. C. McKenzie, A. F. Morrison, K. D. Nanda, F. Plasser, D. R. Rehn, M. L. Vidal, Z.-Q. You, Y. Zhu, B. Alam, B. J. Albrecht, A. Aldossary, E. Alguire, J. H. Andersen, V. Athavale, D. Barton, K. Begam, A. Behn, N. Bellonzi, Y. A. Bernard, E. J. Berquist, H. G. A. Burton, A. Carreras, K. Carter-Fenk, R. Chakraborty, A. D. Chien, K. D. Closser, V. Cofer-Shabica, S. Dasgupta, M. de Wergifosse, J. Deng, M. Diedenhofen, H. Do, S. Ehlert, P.-T. Fang, S. Fatehi, Q. Feng, T. Friedhoff, J. Gayvert, Q. Ge, G. Gidofalvi, M. Goldey, J. Gomes, C. E. González-Espinoza, S. Gulania, A. O. Gunina, M. W. D. Hanson-Heine, P. H. P. Harbach, A. Hauser, M. F. Herbst, M. Hernández Vera, M. Hodecker, Z. C. Holden, S. Houck, X. Huang, K. Hui, B. C. Huynh, M. Ivanov, Á. Jász, H. Ji, H. Jiang, B. Kaduk, S. Kähler, K. Khistyaev, J. Kim, G. Kis, P. Klunzinger, Z. Koczor-Benda, J. H. Koh, D. Kosenkov, L. Koulias, T. Kowalczyk, C. M. Krauter, K. Kue, A. Kunitsa, T. Kus, I. Ladjánszki, A. Landau, K. V. Lawler, D. Lefrancois, S. Lehtola, R. R. Li, Y.-P. Li, J. Liang, M. Liebenthal, H.-H. Lin, Y.-S. Lin, F. Liu, K.-Y. Liu, M. Loipersberger, A. Luenser, A. Manjanath, P. Manohar, E. Mansoor, S. F. Manzer, S.-P. Mao, A. V. Marenich, T. Markovich, S. Mason, S. A. Maurer, P. F. McLaughlin, M. F. S. J. Menger, J.-M. Mewes, S. A. Mewes, P. Morgante, J. W. Mullinax, K. J. Oosterbaan, G. Paran, A. C. Paul, S. K. Paul, F. Pavošević, Z. Pei, S. Prager, E. I. Proynov, Á. Rák, E. Ramos-Cordoba, B. Rana, A. E. Rask, A. Rettig, R. M. Richard, F. Rob, E. Rossomme, T. Scheele, M. Scheurer, M. Schneider, N. Sergueev, S. M. Sharada, W. Skomorowski, D. W. Small, C. J. Stein, Y.-C. Su, E. J. Sundstrom, Z. Tao, J. Thirman, G. J. Tornai, T. Tsuchimochi, N. M. Tubman, S. P. Veccham, O. Vydrov, J. Wenzel, J. Witte, A. Yamada, K. Yao, S. Yeganeh, S. R. Yost, A. Zech, I. Y. Zhang, X. Zhang, Y. Zhang, D. Zuev, A. Aspuru-Guzik, A. T. Bell, N. A. Besley, K. B. Bravaya, B. R. Brooks, D. Casanova, J.-D. Chai, S. Coriani, C. J. Cramer, G. Cserey, A. E. DePrince, R. A. DiStasio, A. Dreuw, B. D. Dunietz, T. R. Furlani, W. A. Goddard, S. Hammes-Schiffer, T. Head-Gordon, W. J. Hehre, C.-P. Hsu, T.-C. Jagau, Y. Jung, A. Klamt, J. Kong, D. S. Lambrecht, W. Liang, N. J. Mayhall, C. W. McCurdy, J. B. Neaton, C. Ochsenfeld, J. A. Parkhill, R. Peverati, V. A. Rassolov, Y. Shao, L. V. Slipchenko, T. Stauch, R. P. Steele, J. E. Subotnik, A. J. W. Thom, A. Tkatchenko, D. G. Truhlar, T. Van Voorhis, T. A. Wesolowski, K. B. Whaley, H. L. Woodcock, P. M. Zimmerman, S. Faraji, P. M. W. Gill, M. Head-Gordon, J. M. Herbert and A. I. Krylov, J. Chem. Phys., 2021, 155, 084801.
87. H. A. Bethe and E. E. Salpeter, Quantum mechanics of one and two electron atoms, Plenum, New York, 1977.
88. Relativistic Electronic Structure Theory, ed. P. Schwerdtfeger, Elsevier, Amsterdam, 2002.
89. B. A. Heß, C. M. Marian, U. Wahlgren and O. Gropen, Chem. Phys. Lett., 1996, 251, 365–371.
90. A. Carreras, H. Jiang, P. Pokhilko, A. Krylov, P. M. Zimmerman and D. Casanova, J. Chem. Phys., 2020, 153, 214107.
91. S. Kotaru, P. Pokhilko and A. I. Krylov, J. Chem. Phys., 2022, 157, 224110.
92. M. A. El-Sayed, Acc. Chem. Res., 1968, 1, 8–16.
93. G. Piccini, M. Alessio and J. Sauer, Phys. Chem. Chem. Phys., 2018, 20, 19964–19970.

---

Footnote

† Electronic supplementary information (ESI) available: Spin density, convergence tests for the periodic DFT calculations, wave function analysis of Co-based systems, additional EOM-CCSD-in-DFT results. See DOI: https://doi.org/10.1039/d5cp01059d

---