CO oxidation on bimetallic Re–Pt clusters: unraveling the role of oxygen coverage

Abstract

ReO_x and PtO_x clusters are able to catalyze CO oxidation under mild pressure and temperature conditions. One possible way of designing novel catalysts with enhanced activity is to form bimetallic alloys. Here, we present a systematic theoretical study of the oxidation of Re_xPt_y clusters (x + y = 5) and their performance as catalysts for CO oxidation. Re-rich clusters reach high oxygen saturation levels, with up to 16 adsorbed oxygen atoms under standard reaction conditions, with a tendency to form interconnected ReO₃ and ReO₄ units. In contrast, Pt-rich clusters maintain some Pt–Pt bonds, with the amount of oxygen adsorbed decreasing steadily with increasing Pt concentration. Comparing reaction mechanisms for oxidized and unoxidized clusters, a superior catalytic performance for CO oxidation is found for the oxidized clusters, due to both a weaker interaction with CO and to a less stable nature of the adsorbed CO₂ reaction intermediate. Finally, strong changes in reactivity are found with varying Re:Pt stoichiometry. The most active cluster is Re₄Pt₁O₁₂, which can catalyze the reaction even at low temperatures, while the Re₃Pt₂O₁₂ and Re₂Pt₃O₁₂ clusters require higher temperatures for similar performance. These results provide insight into the oxidation of metal clusters on a subnanometer scale and their potential use as catalysts for the CO oxidation reaction.

---

1 Introduction

Metal oxidation is a process that is often accomplished under ambient conditions. The first step of oxidation involves oxygen dissociation by coordinatively unsaturated metal atoms on the surface.¹ In the process, several phenomena occur, such as the chemisorption of atomic oxygen, the oxygen coverage on the surface, the formation of buried oxides and oxygen atoms within the subsurface, and even surface reconstruction.^2,3 The final result can be a protective oxide layer or bulk oxide, depending on the properties of the metal and existing reaction conditions.⁴

The oxidation process at the subnanometer and nanometer scale has received increasing attention.^5–8 The stepwise adsorption of atomic oxygen is the initial step in this process, which results in the redistribution of charge, the formation of metal–oxygen bonds, and the loss of electrons from the metal atoms.^9,10 Trinchero et al. explored the oxidation of subnanometer clusters for several transition metals. The results showed that the energetic behavior of these clusters is in concordance with the periodic trends of oxidation of bulk metals. This indicates that the stability of the clusters may be determined by the nature of local bonding.¹¹ Subsequent studies have concentrated on the oxidation of Cu₅ clusters through the successive adsorption of O₂ molecules. They found that the Cu₅ clusters are resistant to irreversible oxidation, providing evidence of their thermal stability.^12,13 Apart from this, some computational research has also explored the oxidation of sub-nanometer Pt clusters, though not with oxygen saturation.^14–16 Investigating the lowest energy isomers and oxygen coverage for larger metal clusters, such as Cu₅₅ or Ni₁₃Ag₄₂, can be quite challenging.^17,18 Therefore, studying the thermal stability and oxygen saturation of sub-nanometer clusters is crucial.¹⁹

The degree of oxidation in these small metal clusters has a strong influence on their reactivity for a wide range of chemical reactions.^19–23 Among them, one prototypical case is the oxidation of CO. Several studies have analyzed the structure, stability and reactivity for CO₂ production in PtO_x clusters under realistic pressure and temperature conditions;^14–16,24 these clusters and Pt²⁺ ions are active for CO oxidation even at low temperatures.²⁵ The importance of the Pt–O–Pt motif in activating oxidation reactions has also been analysed.²⁶ An interesting way of enhancing the catalytic activity of platinum is to alloy it with rhenium.^27,28 It has been shown that the synergy between a Pt metal surface and neighboring ReO_x clusters enhances the catalytic performance for the preferential oxidation of CO.²⁹ In bimetallic Re–Pt clusters, the ratio of Re:Pt influences the catalytic activity of the system, where the lower affinity of Re atoms for CO compared to Pt atoms helps avoid catalyst poisoning.^30,31 However, to our knowledge, the effect of Re:Pt composition on the oxidation of bimetallic clusters and its role in the CO oxidation reaction have not been explored in a systematic way.

This has motivated us to investigate the structure, stability, and reactivity of oxidized Re_xPt_y (x + y = 5) clusters using density functional theory (DFT) calculations, first-principles thermodynamics, and the nudged elastic band (NEB) method for the search of transition states. First, we investigate the structures and oxygen binding energies of oxidized Re–Pt clusters up to saturation. Then, an ab initio thermodynamics approach³² is employed to study these oxidized clusters under different pressure and temperature conditions. Following this, CO is adsorbed onto the clusters, considering the effect of oxygen coverage. We finally study the reaction mechanisms for CO oxidation, comparing two scenarios with the clusters initially either oxidized or unoxidized, and taking into account thermal effects for each energy barrier. The results show that varying the Re:Pt relative stoichiometry has drastic effects in the reaction energetics leading to CO₂ production. Also, they highlight the importance of studying the reaction under realistic conditions with the clusters previously oxidized, since only in these cases meaningful conclusions can be derived about their intrinsic reactivity. Overall, the results indicate that for some compositions, binary Re–Pt clusters have the potential to act as very reactive catalysts for CO oxidation.

2 Computational setup

Density functional theory (DFT) calculations were performed using the VASP³³ code with the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional.³⁴ A plane-wave basis with a 400 eV cutoff energy was utilized. The projector augmented wave (PAW) method was adopted to describe the core–valence electron interactions.^35,36 Geometry optimizations were conducted with a convergence criterion of 0.01 eV Å⁻¹ for forces and an electronic convergence tolerance of 10⁻⁸ eV. The K-point sampling of the Brillouin zone was performed at the gamma point, and the electronic occupation was handled with the Methfessel–Paxton scheme, with a smearing width of 0.01 eV.³⁷

Gas-phase Re–Pt clusters were modeled within a cubic cell measuring 15 × 15 × 15 Å. The oxidation of Re–Pt clusters was studied through the sequential adsorption of oxygen atoms. The potential energy surface (PES) was thoroughly investigated to ascertain the most stable isomers of oxidized clusters. Subsequently, the projected density of states (DOS) for each atom was calculated to understand the electronic structure and bonding of the systems. Moreover, phonon calculations were performed using a finite differences approach, wherein the dynamical matrix was constructed and diagonalized to obtain the frequencies.³⁸

The reaction mechanisms for CO oxidation on unoxidized and oxidized Re–Pt clusters were calculated. Unoxidized clusters refer to metal clusters with a single O₂ molecule dissociated, while oxidized clusters correspond to metal clusters with the most stable oxygen coverage at 300 K and 1 bar. The transition states (TS) were identified using the climb image nudged-elastic-band (CI-NEB) method.³⁹ Each TS corresponds to a maximum in the PES characterized by a single imaginary frequency. Furthermore, the thermal correction for the CO oxidation mechanism was evaluated using first-principles atomistic thermodynamics.^32,40 This approach facilitates a better understanding of the reaction under realistic temperature and pressure conditions.

3 Results and discussion

3.1 Oxidation of Re_xPt_y clusters

Prior to the reactivity studies, an exhaustive isomer search for the most stable conformations of the bare Re_xPt_y clusters must be performed. For each of the six compositions under study (that is, Re₅, Re₄Pt₁, Re₃Pt₂, Re₂Pt₃, Re₁Pt₄ and Pt₅), this has been already done in previous works,^41,42 using the same DFT setup. Then, starting from such geometries (shown in Fig. 1), we have sequentially dissociated several oxygen molecules on each Re_xPt_y cluster. Fig. 1 shows the relaxed structures for the most stable conformations found during this oxidation process. For each additional oxygen molecule, we have calculated its dissociative binding energy as

E_b = E[(n − 2)O/Re_xPt_y)] + E[O₂] − E[nO/Re_xPt_y]

where E[(n − 2)O/Re_xPt_y] and E[nO/Re_xPt_y] are, respectively, the total energies of the Re_xPt_y cluster with (n − 2) and n adsorbed oxygen atoms, and E[O₂] is the energy of the free oxygen molecule in the gas phase.

Fig. 1 Most stable structures and dissociative binding energies (in eV) for the oxidized Re_xPt_y clusters. Teal spheres: Re atoms. Silver spheres: Pt atoms. Red spheres: oxygen atoms.

The isomer search for stable structures of nO–Re_xPt_y was performed sequentially, testing a large number of alternatives with the oxygen atoms adsorbed at various sites around the cluster. Once the most stable conformation was determined for a given oxygen coverage, it was used as the starting point for the adsorption of two more oxygen atoms, testing again various alternate structures. During this process, the clusters were found to be fluxional, undergoing important distortions as the oxygen coverage increased; therefore, for each case, other alternate Re_xPt_y conformations were tried. In the ESI† (Fig. S1–S6), the most relevant conformations for each nO–Re_xPt_y cluster are shown, together with the relative energies with respect to the global minimum.

In each case, we have added oxygen atoms to the cluster until its saturation coverage is found, according to the thermodynamic model which will be discussed below. In general, the high dissociation energies suggest that molecular O₂ will easily dissociate on these clusters, with small or moderate activation barriers. Previous work by the authors on bare Re_xPt_y clusters shows that, indeed, the activation barriers for O₂ dissociation at these clusters are small (usually below 0.5 eV) or even non-existent.⁴³ This indicates that thermal effects will only play a minor role, with the clusters reaching oxygen saturation coverages under standard reaction conditions, according to the results of the thermodynamic modeling discussed below.

In the case of pure Re₅, the high intrinsic reactivity of the Re atoms towards oxidation results in very high dissociation energies for each additional oxygen molecule. Since molecular adsorption of O₂ results in binding energies of the order of 3–4 eV (see Fig. 4 in ref. 43), by dissociating O₂ into adsorbed O atoms, there is an energy gain of more than 3 eV. Therefore, with relatively small barriers, even at small temperatures, kinetic effects will not prevent the expected complete oxidation of the Re₅ cluster. The dissociation energies for Re₅ remain very high up to 8 oxygen atoms, decreasing a little bit between 10 and 16 oxygen atoms. It is interesting to note that, as the oxygen coverage increases, strong changes take place in the structure of the Re₅ cluster. Up to 10 oxygen atoms (corresponding to a ReO₂ oxide stoichiometry), the Re–Re bond distances are similar to the ones for the clean Re₅ cluster. However, the addition of more oxygen results in a sharp increase of the Re–Re bond distances; the cluster, instead of being a Re₅ central unit surrounded by O adatoms, transforms into a collection of interconnected tetrahedral ReO₄ units. W. Chen and co-workers calculated the oxidation of a single rhenium atom and determined that the most stable structures for ReO₃ and ReO₄ are trigonal and distorted tetrahedral, respectively.⁴⁴ Another study found that the most stable structure of Re₃O₁₁ consists of tetrahedral and trigonal bipyramidal coordination for the Re atoms.⁴⁵ In contrast, Re₅O_x clusters with a high oxygen coverage (up to 10) only exhibit tetrahedral units.

For Re₄Pt₁, similar results are found, with incremental dissociation energies above 6 eV for up to 8 oxygen atoms (corresponding to the ReO₂ stoichiometry) and slightly smaller (4–5 eV) or larger oxygen coverages. An analogous behavior is found for clusters with increasing Pt content; addition of oxygen atoms beyond the ReO₂ ratio results in a decrease of dissociation energies below 6 eV per O₂ molecule. In the case of clusters with several Pt atoms, the higher reactivity of the Re sites causes the oxygen atoms to preferentially bind at those sites, until ReO₃ or ReO₄ tetrahedral units are formed. Depending on the relative amount of platinum in the cluster, these units can be linked together, or completely isolated from each other, as observed in Re₃Pt₂–12O and in all high oxygen content cases of Re₂Pt₃ and Re₁Pt₄.

For Pt-rich clusters (Re₂Pt₃ and Re₁Pt₄), after Re sites have been completely saturated with oxygen, additional oxygen atoms bind exclusively to the Pt sites. However, the intrinsic lower reactivity of Pt causes the dissociative binding energies to fall to around 2–3 eV per O₂ molecule. In the case of pure Pt₅, saturation coverage is found for only 6 oxygen atoms, with a sharp decrease above that number. Similar results are found for Re₂Pt₃ and Re₁Pt₄ where, after each Re atom adsorbs 3–4 oxygen atoms, it is only possible to bind a maximum of 1 oxygen atom per Pt site. Interestingly, for Re₂Pt₃ at its saturation coverage (12 oxygen atoms), the last O₂ molecule adsorbs molecularly, highlighting the much weaker bonding of oxygen at Pt sites. The structures found for the Pt₅O_x clusters are similar to those reported for other oxidized Pt clusters.^14,15,24,46 Pt atoms in the Pt₅O₁₀ cluster have a planar square coordination as the PtO bulk.⁴⁷ In oxygen saturation, Pt–Pt bonds preserve more than Re–Re bonds since Re atoms are more prone to oxidation. Some Pt₅O_x clusters exhibit a symmetrical structure. For instance, the Pt₅O₈ and Pt₅O₁₀ clusters have C_2v and D_5h symmetry groups, respectively.

In the process of gradual oxidation of the Re_xPt_y clusters, we have also performed a detailed analysis of the electronic structure of these nO–Re_xPt_y clusters. The complete results are shown in the ESI† (Fig. S15–S22). Fig. 2 shows a summary of the density of electronic states (DOS) for situations where the clusters are partially or completely covered by adsorbed oxygen atoms. In each case, the figures show the projected DOS into platinum, rhenium and oxygen states (black, green and red curves, respectively). The results show several interesting effects. First, it must be noted that for the Pt–Re mixed clusters, the DOS is formed by a superposition of Re d-states, which lie above and below the Fermi level, and Pt d-states, which are located just below the Fermi level. As oxygen atoms start to bind to the cluster, the oxygen sp states preferentially hybridize with Re states at the bottom of the valence d-band, with the Pt states being left unhybridized until oxygen accumulates on the cluster. Second, the accumulation of oxygen results in a broadening of the valence band and also in a shift of the Fermi level to lower binding energies (where we take the vacuum level as the energy reference). Finally, we note that as the amount of oxygen adatoms reaches concentrations corresponding to saturation coverages, the electronic structure resembles the one corresponding to a metallic oxide, with a sizable gap separating the valence and conduction bands of the oxide. However, as the relative concentration of Pt and Re changes, sizable variations take place, involving both the size of the HOMO–LUMO gap and the location of the Fermi level relative to this energy gap. For pure Re, some isolated states appear in the middle of the gap, with the Fermi level being located approximately at the bottom of the conduction band. For Pt, the situation is reversed, and the Fermi level lies at the top of the conduction band. Re₄Pt₁ is an interesting case, with a marked tendency, for almost every oxygen concentration, towards the opening of HOMO–LUMO gaps with the Fermi level at their center.

Fig. 2 Densities of electronic states (DOS) for some selected nO–Re_xPt_y oxidized clusters, with various degrees of oxidation. The black curves show the contribution from Pt states, the green curves show the contribution from Re states, while the red curves show the projection of the DOS on oxygen s and p orbitals. Dashed blue lines highlight the location of the Fermi level in each case. When the cluster has a non-zero magnetic moment, both spin-up and spin-down contributions are shown separately.

3.2 (p,T)-phase diagrams of oxidized nO–Re_xPt_y clusters

Next, the relative stability of oxidized Re–Pt clusters was determined by calculating the Gibbs free energy of formation.

ΔG(p,T) = G_RexPtyOn(p,T) − G_RexPty(p,T) − n·μ_O(p,T)

where G_RexPttOn, G_RexPt_y, and μ_O represent the Gibbs free energy of the oxidized Re–Pt cluster, the Gibbs free energy of the Re–Pt cluster, and the chemical potential of oxygen, respectively. Gibbs free energies were calculated using the atomic simulation environment (ASE)⁴⁸ package alongside the results obtained in the VASP (frequencies, optimized structures, and electronic state). Re–Pt clusters with different oxygen coverage were modeled using the ideal gas approximation, incorporating electronic, translational, vibrational, and rotational contributions to the thermal correction.^40,49 The pressure and temperature dependency of the chemical potential of oxygen is expressed as
where k_B is the Boltzmann constant and p₀ is the standard pressure (1 bar). The first term represents the temperature dependency of chemical potential at p₀, while the second term is the pressure dependency through the ratio p/p₀. The oxygen atoms in the Re–Pt clusters are in equilibrium with the gas-phase O₂. Consequently, the molecular oxygen potential can be related to the atomic oxygen potential through the following equation:

To ensure high accuracy, μ_O2(p₀,T) was sourced from the NIST-JANAF thermochemical tables.⁵⁰ The most stable phase is defined as the one that minimizes the Gibbs free energy of formation.⁵¹ Based on this principle, (p,T)-phase diagrams were used to determine the most stable oxygen coverage of the Re–Pt cluster for a given temperature and oxygen pressure. A range of pressures, from ultra-high vacuum (UHV) to standard pressure, was examined, while temperatures were varied from 200 K to 1000 K. This methodology for calculating the (p,T)-phase diagrams is analogous to other theoretical reports on oxidized metal clusters.^12,15,16,52

For the most stable nO–Re_xPt_y structures (Fig. 1), we have calculated the (p,T) phase diagram using the first principles atomistic thermodynamics. The results are shown in Fig. 3. The selected temperature and the oxygen partial pressure range have been chosen to circumvent crossing the phase boundaries of O₂. These parameters also comprise conditions relevant to industrial catalytic oxidation processes and ensure that the ideal gas assumption is valid. (p,T)-Phase diagrams indicate that Re–Pt clusters are susceptible to oxidation over a wide range of temperatures and pressures. The Pt₅ cluster constitutes the sole exception, manifesting as a metallic phase exclusively under low pressures (near UHV) and elevated temperatures (above 900 K). Conversely, the Re₅ cluster exhibits remarkable stability at oxygen saturation, even under very low O₂ pressure. All Re–Pt clusters reach their maximum oxygen coverage under standard pressure and temperature conditions. As it should be expected, increasing the Pt content results in a steady decrease of the amount of oxygen atoms adsorbed under standard conditions, from 16 oxygen atoms in the case of Re₅ to only six in the case of Pt₅. These results reflect the fact, discussed above, that a sharp drop in oxygen binding energy takes place when rhenium atoms are saturated with 3–4 oxygen adatoms each.

Fig. 3 Pressure–temperature (p,T) phase diagrams for oxidized Re_xPt_y clusters: (a) Re₅O_n, (b) Re₄Pt₁O_n, (c) Re₃Pt₂O_n, (d) Re₂Pt₃O_n, (e) Re₁Pt₄O_n, (f) Pt₅O_n. Each colored area represents a stable phase in thermodynamic equilibrium. The oxygen pressure ratio (p/p₀) is plotted on a logarithmic scale.

For Re-rich clusters (Re₄Pt₃ and Re₃Pt₂), the same phases are obtained (containing 10, 12, and 14 oxygen atoms) but in different proportions. At low O₂ pressure, the Re₄Pt₁O₁₄ cluster requires a higher temperature to lose oxygen atoms compared to the Re₃Pt₂O₁₄ cluster. Additionally, the 2 : 1 oxygen/metal ratio is more representative in the cluster with the lower Re content (Re₃Pt₂). In the case of Re₂Pt₃ and Re₁Pt₄ (Pt-rich clusters), the most stable phases under standard pressure and temperature conditions are represented by Re₂Pt₃O₁₂ and Re₁Pt₄O₈, respectively. The oxidation of subnanometer Re–Pt clusters is affected by the presence of a single Re atom. For example, the Re₁Pt₄ cluster does not present a metallic phase due to the strong affinity of rhenium for oxygen.

3.3 CO adsorption at oxidized nO–Re_xPt_y clusters

After obtaining the most stable conformations for oxidized Re_xPt_y clusters with a varying amount of dissociated oxygen atoms, the next step in the CO oxidation reaction involves the study of the interaction of CO with these oxygen-covered clusters. For each Re_xPt_y cluster with a varying amount of oxygen adatoms (up to saturation coverage), we have systematically studied the adsorption of CO at each possible binding site. Fig. 4 shows the most stable adsorption conformation of CO for each cluster under study, with varying amounts of dissociated O₂ molecules, representing situations where the cluster is partially or fully oxidized. In the ESI† (Fig. S7–S12) we report, for each case, the results of the extensive search for the most stable conformers, together with the relative energies.

Fig. 4 Structures and binding energies (in eV) for the adsorption of a CO molecule at oxidized Re_xPt_y clusters, with varying amounts of adsorbed oxygen. Teal spheres: Re atoms. Silver spheres: Pt atoms. Red spheres: oxygen atoms. Black spheres: carbon atoms.

For all the Re_xPt_y compositions, CO interacts strongly with the bare unoxidized clusters, with binding energies of the order of 2.3–2.7 eV. In the case of Re-rich clusters, saturating the cluster with oxygen adatoms has a strong influence on the strength of the CO–metal bonds. When the amount of oxygen on the cluster is below the stoichiometry corresponding to the ReO₂ composition, relatively high (1.5–2.0 eV) CO binding energies are found, only slightly smaller than the values found for the clean clusters without oxygen. However, a further increase in oxygen coverage generally results in a sharp drop in CO binding to values of the order of 1 eV or even smaller. It is interesting to note that when the cluster contains platinum, CO will always preferentially bind at Pt sites. Contrary to the case of Re-rich clusters, for Pt-rich clusters, the oxidation of the cluster does not cause a systematic decrease in CO binding energies. In many instances, the CO adsorption at a partially oxidized Pt site leads to a significant increase in the CO binding energy, which may sometimes exceed 3 eV.

Finally, we also considered the effect of multiple binding of CO molecules at the bare Re_xPt_y clusters. Results for adsorption of up to three CO molecules are shown in the ESI† (Fig. S13 and S14). In general, these clusters can adsorb several CO molecules without a noticeable drop in the binding energies (Re₁Pt₄ is the sole exception, which can nevertheless be attributed to isomerization effects). Since the difference in binding energies for CO and atomic oxygen is very high for Re-rich clusters, it can be concluded that CO accumulation at these types of cluster is very unlikely, as dissociating oxygen molecules will easily displace CO. This situation is reversed for pure Pt₅, where CO binding energies compete with dissociative oxygen binding energies. Then, it is possible that for this cluster, CO will accumulate under standard reaction conditions, preventing oxygen dissociation, and thus resulting in a reduced activity for CO oxidation.

3.4 CO₂ formation at unoxidized and oxidized Re_xPt_y clusters

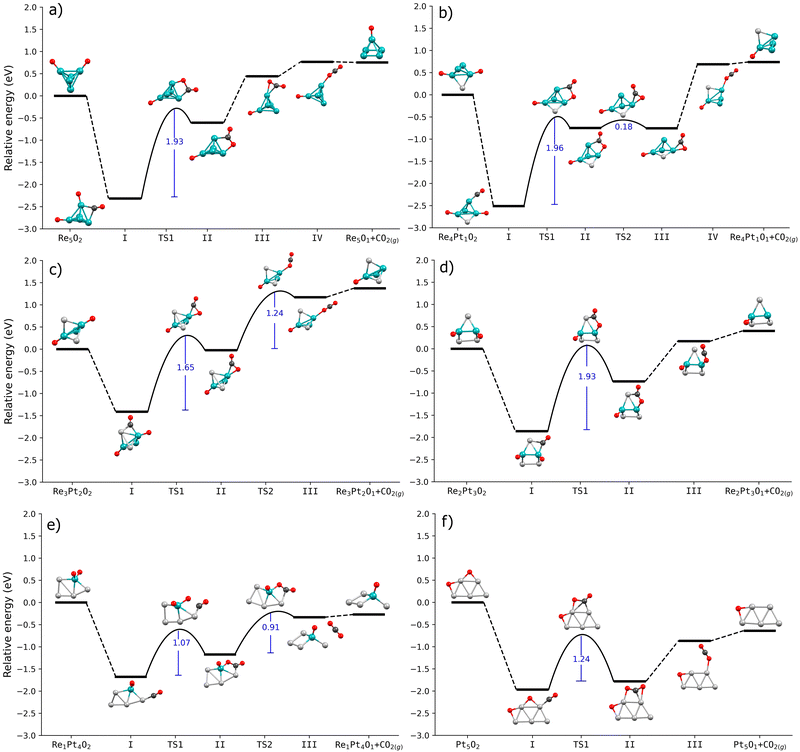
After identifying the most stable initial conformations for CO adsorbed at oxidized nO–Re_xPt_y clusters, we have studied the reaction between CO and a coadsorbed oxygen atom. This part of the reaction involves two steps. First, the carbon atom of CO reacts with a neighboring oxygen atom, forming a CO₂ molecule bonded to the Pt–Re cluster. Second, this bonded CO₂ entity needs to be desorbed to the gas phase, by breaking all C–metal and O–metal bonds. To gain a better understanding on the effect caused by the partial or total oxidation of the cluster, we have compared the reaction pathways leading to CO₂ formation in two situations. First, we have calculated the reaction barriers for clusters with a single O₂ molecule dissociated at the cluster. Second, we have studied the same process for CO₂ formation at nO–Re_xPt_y clusters with oxygen coverages corresponding to standard reaction conditions, obtained from the results in Fig. 3.

Fig. 5 shows the energy profiles for the case of clusters with only a single O₂ molecule dissociated on them. The highest barrier is always the first step, which involves forming a new C–O bond. This barrier is quite high, nearly 2 eV for Re-rich clusters, while for Pt-rich clusters, it decreases a little to values of the order of 1 eV. The formation of CO₂ involves the displacement of both the adsorbed CO and a nearby oxygen atom from their positions. In the intermediate I, the O–C⋯O distance varies from 3.13 Å (on Pt₅O₂) to 4.23 Å (on Re₁Pt₄O₂). Interestingly, the largest displacement along the reaction coordinate corresponds to the lowest energy barrier. For the transition states (TS1), the new C–O bond distance ranges from 1.6 Å to 1.9 Å, with the longest distance observed in the Re₁Pt₄O₂ cluster. It suggests that the energetic cost of CO₂ formation is not directly related to the adsorbate displacement along the reaction coordinate.

Fig. 5 Energy profiles of CO oxidation on Re_xPt_yO₂ clusters via the Langmuir–Hinshelwood (LH) mechanism: (a) Re₅O₂, (b) Re₄Pt₁O₂, (c) Re₃Pt₂O₂, (d) Re₂Pt₃O₂, (e) Re₁Pt₄O₂, (f) Pt₅O₂. The energy barrier values are shown in blue, with the first barrier corresponding to the formation of CO₂. Teal spheres: Re atoms. Silver spheres: Pt atoms. Red spheres: oxygen atoms. Black spheres: carbon atoms.

Comparing the results for all the Re_xPt_y compositions, we observe that the stability of the initial state (with CO and O coadsorbed, labeled as I in the figures) is quite high with respect to the relative energy of the final state, with CO₂ detached from the cluster. This means that we can expect a high energetic cost to both form CO₂ and to detach it from the cluster, something that will result in a very low activity for CO oxidation. For Re-rich clusters, this effect is more pronounced, with the total cost for the formation of C–O bonds (step II) and the final CO₂ desorption is of the order of 3 eV. For Pt-rich clusters, the intermediate states in the reaction are comparatively less stable, although the energetic cost for CO₂ formation is still relatively high (around 1.5 eV). These results can easily be interpreted in terms of the differences in binding energies of CO and O between Re-rich and Pt-rich clusters. Oxygen atoms bind very strongly to Re, and if we add the binding energy of CO (more than 2 eV), the sum of both values is much larger than the enthalpy for the CO + ^1/2O₂ reaction, meaning that it will be very costly to detach the CO₂ molecule adsorbed at the cluster. In the case of platinum, the binding energy of oxygen decreases, reducing slightly the stability of the intermediate states.

Then, we have extended the study of reaction mechanisms to the case of Re_xPt_y covered with oxygen atoms, at coverages consistent with standard reaction conditions, according to the calculated phase diagrams. For each cluster with a given oxygen coverage, we have studied the reaction mechanisms using the following procedure: first, starting with the most stable configuration for CO adsorption, we have calculated the stability of the adsorbed CO₂ intermediate species, for several cases where CO reacts with neighboring oxygen adatoms. Then, after identifying which oxygen atom is more reactive towards the production of CO₂, we have calculated for such situation the activation barriers for CO₂ formation and subsequent CO₂ detachment from the cluster. These results are displayed in Fig. 6.

Fig. 6 Energy profiles of CO oxidation on oxidized Re_xPt_yO_n clusters via the Langmuir–Hinshelwood (LH) mechanism: (a) Re₅O₁₆, (b) Re₄Pt₁O₁₂, (c) Re₃Pt₂O₁₂, (d) Re₂Pt₃O₁₂, (e) Re₁Pt₄O₈, and (f) Pt₅O₆. The energy barrier values are shown in blue, with the first barrier corresponding to the formation of CO₂. Teal spheres: Re atoms. Silver spheres: Pt atoms. Red spheres: oxygen atoms. Black spheres: carbon atoms.

We observe significant differences in the reaction pathways of a single dissociated O₂ molecule on Re_xPt_y clusters compared to clusters that have been oxidized at their saturation coverage. First of all, for both Re-rich and Pt-rich compositions, now the relative energies of states I and II (adsorbed CO, and CO₂ intermediate) are comparable with the relative energy of CO₂ desorbed into the gas phase. This means that once CO₂ is formed, it is not necessary to overcome large barriers to detach the reaction product from the cluster. In one case (Re₂Pt₃O₁₂), this reaction intermediate is actually less stable than CO₂ in the gas phase. We can attribute this behavior to the weaker O–metal bonding that occurs for clusters with increasing amount of adsorbed oxygen, as compared to the clusters with only a dissociated O₂ molecule on them. Also, for many compositions (specially for Re-rich clusters), CO binding energies are also smaller at increasing oxygen coverages. This indicates that since the reactants are less strongly bound, the CO₂ intermediate will also be less stable compared to the gas-phase molecule, making its desorption easier. The reduced CO binding energy has also some important consequences for the overall reactivity of the clusters. For example, in the case of Re₅O₁₆, the CO binding energy (0.97 eV) is smaller than the activation energy for the formation of absorbed CO₂ (1.22 eV). Consequently, it is energetically more favorable for CO to desorb back into the gas phase rather than forming CO₂. Therefore, the oxidized Re₅ is expected to exhibit low catalytic activity.

In the oxidized clusters, the energy barriers for the reaction between CO and oxygen adatoms show drastic changes with the Pt–Re stoichiometry. They change in a non regular fashion, with very high values (around 1.90 eV) for Re₃Pt₂ and Re₁Pt₄, moderately high values (1.2–1.3 eV) for Re₂Pt₃, Re₅ and Pt₅, and a very small 0.46 eV barrier for Re₄Pt₁. The case of the Re₄Pt₁ with 12 preadsorbed oxygen atoms is particularly interesting. Our findings indicate that the reaction pathway for this cluster combines all the favorable factors necessary for high reactivity toward CO₂ production. First, CO binding at the oxidized Re₄Pt₁ cluster is reasonably strong, with 1.35 eV. Second, there is only a very small barrier of 0.46 eV for the formation of adsorbed CO₂. Finally, the desorption of CO₂ is energetically unexpensive and involves only a moderate barrier of 0.69 eV. Contrary to the rest of cases, the rate-limiting step is the breaking of the CO₂–cluster bonds, and not the CO + O bond formation.

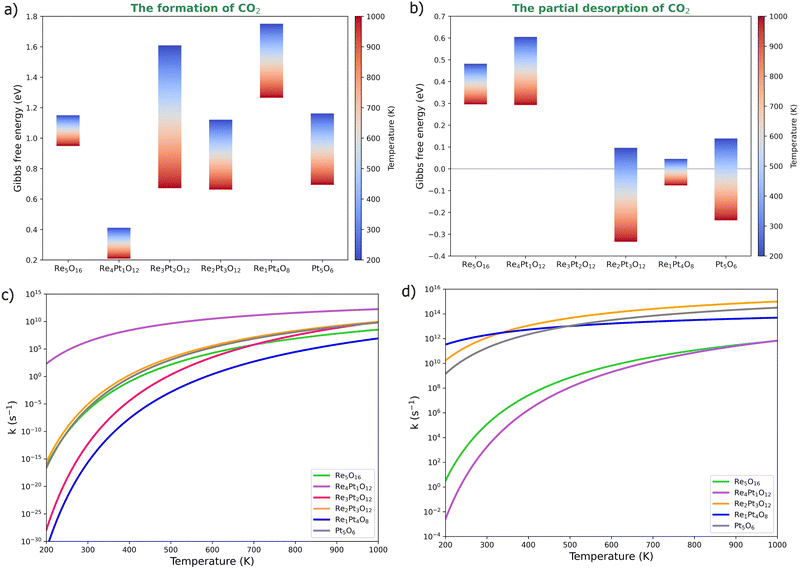
We have also evaluated the effect of temperature on the barriers of CO oxidation on the oxidized Re_xPt_y clusters (Fig. 7). The Gibbs free energy at 1 bar pressure was calculated using first-principles thermodynamics. The energy barrier of CO₂ formation decreases with temperature, particularly in Re₄Pt₁O₁₂, Re₃Pt₂O₁₂, Re₂Pt₃O₁₂ and Pt₅O₆ clusters. At high temperatures, these systems exhibit a energy barrier of less than 1 eV (Fig. 7a). The effect of temperature for the range studied (from 200 to 1000 K) is not the same in all clusters. For instance, the energy barrier of the Re₅O₁₆ cluster decreases by about 0.2 eV, while the Re₃Pt₂O₁₂ cluster exhibits a more significant reduction of around 0.9 eV. This variation is attributed to entropic effects resulting from conformational changes in CO₂ formation.

Fig. 7 Effect of temperature on the CO oxidation barriers at the oxidized Re_xPt_y clusters. (a) and (c) Gibbs free energies and rate constants for the formation of CO₂. (b) and (d) Gibbs free energies and rate constants for the partial desorption of CO₂.

As mentioned, CO₂ detachment on oxidized clusters occurs with low energy requirements, except for the Pt₅O₆ cluster, which requires approximately 1.5 eV to detach the product. CO₂ desorption was performed in steps, where partial desorption involves breaking a bond between CO₂ and the cluster, usually the metal–carbon bond. This elementary reaction involves an isomeric change in CO₂ formed on the cluster. The energy barriers for this step decrease with temperature, even disappearing in the Re₂Pt₃O₁₂, Re₁Pt₄O₈, and Pt₅O₆ clusters (Fig. 7b). Re-rich clusters (Re₅O₁₆ and Re₄Pt₁O₁₂) exhibit partial desorption energy barriers with a moderate height (less than 0.7 eV), which decrease to 0.3 eV with increasing temperature. Finally, total detachment involves the breaking of the last metal–oxygen bond holding CO₂ to the cluster, where no energy barrier was found for this final step.

Subsequently, the rate constants for the elementary reaction steps were calculated using the Arrhenius equation⁵³

where h is the Planck constant, ΔG_a is the Gibbs free energy of activation, and R is the universal gas constant. ΔG_a is equivalent to the difference in free energy between the transition state and the reactants. After analyzing the reaction constants for the formation and partial desorption of CO₂ (see Fig. 7c and d), it is evident that CO₂ formation is the rate-limiting step of the reaction. However, the Re₄Pt₁O₁₂ cluster shows a more favorable rate constant than the others, maintaining a significant value even at low temperatures. The partial desorption rate is divided into two groups: Re-rich (lower rate) and Pt-rich (higher rate) clusters. As mentioned above, this is not a rate-determining step of the reaction since, at room temperature, all constants are higher than 10⁴ s⁻¹. From these results, we can conclude that the Re₄Pt₁O₁₂ cluster can catalyze the CO oxidation reaction at low temperatures. In contrast, the Re₂Pt₃O₁₂ and Re₃Pt₂O₁₂ clusters can only catalyze this reaction at high temperatures.

4 Conclusions

In summary, a systematic study of the oxidation of subnanometer Re_xPt_y (x + y = 5) clusters has been carried out, determining the most stable structures for the dissociative adsorption of several oxygen molecules. Oxygen saturation is associated with a sharp decrease in the dissociate binding energy; this takes place between six (for pure Pt₅) and sixteen (for pure Re₅) oxygen adatoms, depending on the cluster stoichiometry. The higher intrinsic reactivity of Re atoms towards oxygen results in a steady increase of the oxygen saturation coverage as the clusters become richer in rhenium. Also, it results in a preferential binding of oxygen at Re sites, until ReO₃ or ReO₄ units are formed. Then, some oxygen atoms can also bind at Pt sites. When such ReO₄ units are formed, Re-rich clusters tend to elongate and eventually rupture their Re–Re bonds, while Pt-rich clusters preserve some of their Pt–Pt bonds. For Re₅, at the saturation coverage, the structure resembles that of the Re₂O₇ rhenium oxide, with interconnected tetrahedral ReO₄ units. In the case of Re₄ Pt, the cluster effectively becomes a platinum single-atom catalyst (SAC) adsorbed on a small rhenium oxide support. As the oxygen molecules adsorb and dissociate, the electronic structure is characterized by the hybridization of oxygen sp states with rhenium d-states, a broadening of the valence band, and shifts in the Fermi level. When the clusters become completely oxidized, the densities of states resemble the ones for metallic oxides, although they show very complex variations with the Re/Pt composition. In some cases (14O–Re₄ Pt, for example), large HOMO–LUMO gaps are found; in others (14O–Re₅), some isolated electronic states appear in the middle of the HOMO–LUMO gap.

The conclusions obtained after analyzing the sequential oxygen binding energies have been further confirmed by the results of the ab initio thermodynamics approach and the calculated (p,T) phase diagrams. Only the pure Pt₅ cluster has a stable metallic phase at high temperatures and low pressures. All the clusters containing Re are stable only in their oxidized phase at any given temperature and pressure, a fact which is a consequence of the strong oxophilic nature of this metal. As mentioned above, the degree of oxidation of the Re–Pt clusters is determined by their composition, ranging from 6 oxygen atoms in the Pt₅ cluster to 16 oxygen atoms in the Re₅ cluster under standard pressure and temperature conditions. Thus, the oxygen coverage for Re-rich clusters can exceed the 1 : 2 metal/oxygen ratio, indicating that rhenium can easily attain high oxidation states even at low temperatures.

The reactivity of the oxidized clusters as catalysts of the CO oxidation reaction has been also studied in detail. Reaction pathways and energy barriers were calculated for Re_xPt_y clusters with either a single dissociated O₂ molecule or a fully saturated molecule with oxygen under standard pressure and temperature conditions. Unoxidized clusters exhibit high CO adsorption energy, which is a factor that can lead to catalyst poisoning and loss of active sites. This situation changes when the clusters become fully oxidized; while Pt-rich clusters still have a relatively high affinity for CO (even when oxygen is coadsorbed at Pt sites), the oxidation of Re-rich clusters causes a sharp decrease in CO binding energies, as carbon monoxide cannot bind at Re sites where three or more oxygen atoms have already been adsorbed.

The comparison between unoxidized clusters and fully oxidized ones also shows that the overall reaction energetics undergo drastic changes with varying oxygen coverage. For clusters with a single dissociated O₂ molecule, a very strong adsorbed CO₂ reaction intermediate is formed. This is partially due to a high CO binding energy, but also to the high dissociative binding energy for the first two oxygen atoms. This results in a very difficult desorption of the CO₂ molecule to gas phase, rendering the clusters inactive at such low oxygen coverages. In contrast, fully oxidized clusters require much less energy for CO₂ desorption. Comparing various stoichiometries, we found large variations in the activation barriers, which will result in huge variations of reactivity with composition. The stoichiometry with the best performance was found to be Re₄Pt₁; when oxidized to 12O–Re₄Pt₁, CO can still easily adsorb at the Pt site, reacting with neighboring oxygen adatoms with very small activation barriers, forming a loosely bound CO₂ intermediate which can easily desorb from the cluster. Effectively, this case can be interpreted in terms of a favorable synergy caused by the presence of a reactive Pt species, which binds CO, and neighboring ReO_x species which provide reactive oxygen species. Such a cooperative effect between Re and Pt has been also reported in the experimental work of Ishida et al.,²⁹ where the interplay between Pt and ReO_x results in high activity for the preferential oxidation of CO.

Finally, we calculated the effect of temperature on CO oxidation using ab initio thermodynamics. The Re₄Pt₁O₁₂ cluster serves as a CO catalyst at low temperatures, while the Re₂Pt₃O₁₂ and Re₃Pt₂O₁₂ clusters may only catalyze the reaction at high temperatures (near 1000 K). The structure of oxidized Re₄Pt₁ can be considered as a prototype of a platinum single-atom-catalyst (SAC) supported on a small rhenium oxide support (Pt₁/Re₄O₁₂). The Pt atom has been used as the SAC, as it can be easily dispersed as stable supported entities on reducible metal oxides, such as CeO_x or FeO_x.^54–56 These highly localized active sites reduce CO poisoning and promote CO₂ desorption more effectively than conventional catalysts.⁵⁷ In the case of Pt₁/Re₄O₁₂, the Pt atom serves as an active site for CO oxidation at low temperatures in an oxidizing atmosphere.

Overall, our results contribute to a better understanding of the oxidation of metal clusters at the subnanometer scale. Also, we find that these small binary Pt–Re clusters can be active for the CO oxidation reaction even at low temperatures, with strong variations of activity with composition and oxidation state. Thus, these DFT calculations highlight the importance of studying the reaction mechanisms under realistic reaction conditions, which in the present case involve highly oxidized clusters.

Author contributions

Conceptualisation: AAG, ILG, and LMM; formal analysis: AAG, ILG, and LMM; funding acquisition: ILG and LMM; supervision: ILG and LMM; visualisation: AAG; writing – original draft: AAG; writing – review & editing: ILG and LMM.

Data availability

The data supporting this article have been included as part of the ESI.† Further information and details are available from the corresponding author upon reasonable request.

Conflicts of interest

The authors have no conflicts to disclose.

Acknowledgements

Andrés Álvarez-García gratefully thanks CONAHCyT-Mexico for the PhD scholarship No. 957574. Luis M. Molina acknowledges the support from Ministerio de Ciencia e Innovación of Spain (Grant PID2022-138340OB-I00 funded by MCIN/AEI/10.13039/501100011033 and FSE+) and from the University of Valladolid (GIR Nanostructure Physics). Ignacio L. Garzón was supported by PASPA-DGAPA-UNAM through a sabbatical fellowship at the Universidad de Valladolid, Spain. ILG also acknowledges the hospitality of the Departamento de Física Teórica, Atómica y Óptica de la Facultad de Ciencias de la Universidad de Valladolid, Spain, during a sabbatical year. Calculations were performed at the DGTIC-UNAM Supercomputing Center under Project LANCAD-UNAM-DGTIC-049. We also acknowledge networking within the COST Action CA21101 “Confined molecular systems: from a new generation of materials to the stars” (COSY) supported by COST (European Cooperation in Science and Technology).

References

1. H. Over and A. Seitsonen, Science, 2002, 297, 2003–2005.
2. J. C. Goloboy and W. G. Klemperer, Angew. Chem., Int. Ed., 2009, 48, 3562–3564.
3. W. X. Li, L. Österlund, E. K. Vestergaard, R. T. Vang, J. Matthiesen, T. M. Pedersen, E. Lægsgaard, B. Hammer and F. Besenbacher, Phys. Rev. Lett., 2004, 93, 146104.
4. H. Kan and J. Weaver, Surf. Sci., 2009, 603, 2671–2682.
5. M. B. Torres, E. M. Fernández and L. C. Balbás, J. Phys. Chem. A, 2008, 112, 6678–6689.
6. E. M. Fernández and L. C. Balbás, J. Chem. Phys., 2016, 144, 224308.
7. L. X. Chen, Z. Wen, Z. W. Chen, C. V. Singh and Q. Jiang, J. Mater. Chem. A, 2021, 9, 11726–11733.
8. E. Fernández, M. Boronat and A. Corma, Phys. Chem. Chem. Phys., 2022, 24, 4504–4514.
9. A. Sumer, J. Phys. Chem. A, 2021, 125, 5201–5211.
10. Z. Luo, A. W. Castleman and S. N. Khanna, Chem. Rev., 2016, 116, 14456–14492.
11. A. Trinchero, S. Klacar, L. O. Paz-Borbón, A. Hellman and H. Grönbeck, J. Phys. Chem. C, 2015, 119, 10797–10803.
12. D. Buceta, S. Huseyinova, M. Cuerva, H. Lozano, L. J. Giovanetti, J. M. Ramallo-López, P. López-Caballero, A. Zanchet, A. O. Mitrushchenkov, A. W. Hauser, G. Barone, C. Huck-Iriart, C. Escudero, J. C. Hernández-Garrido, J. J. Calvino, M. López-Haro, M. P. de Lara-Castells, F. G. Requejo and M. A. López-Quintela, Chem. – Eur. J., 2023, 29, e202301517.
13. J. Garrido-Aldea and M. P. de Lara-Castells, Phys. Chem. Chem. Phys., 2022, 24, 24810–24822.
14. C. Kerpal, D. Harding, A. Hermes, G. Meijer, S. Mackenzie and A. Fielicke, J. Phys. Chem. A, 2013, 117, 1233–1239.
15. M. Taleblou, M. Camellone, S. Fabris and S. Piccinin, J. Phys. Chem. C, 2022, 126, 10880–10888.
16. L. Xu, G. Henkelman, C. T. Campbell and H. Jónsson, Surf. Sci., 2006, 600, 1351–1362.
17. L. Ma and J. Akola, Phys. Chem. Chem. Phys., 2019, 21, 11351–11358.
18. R. H. Aguilera-Del-Toro, F. Aguilera-Granja and A. Vega, Phys. Chem. Chem. Phys., 2023, 26, 3117–3125.
19. M. Schmidt, P. Cahuzac, C. Bréchignac and H.-P. Cheng, J. Chem. Phys., 2003, 118, 10956–10962.
20. C. C. Chang, Y. C. Chen, K. C. Wu, H. N. Priyadarshini, L. Y. Lee, J. L. Chen, C. R. Lee, C. W. Pao and D. Y. Wang, ChemCatChem, 2024, e202400596.
21. S. Yamazoe, K. Koyasu and T. Tsukuda, Acc. Chem. Res., 2014, 47, 816–824.
22. M. D’Andria, F. Krumeich, Z. Yao, F. R. Wang and A. T. Güntner, Adv. Sci., 2024, 11, 2308224.
23. X. N. Li, L. N. Wang, L. H. Mou and S. G. He, J. Phys. Chem. A, 2019, 123, 9257–9267.
24. J. E. Q. Domínguez, K. M. Neyman and A. Bruix, J. Chem. Phys., 2022, 157, 094709.
25. E. A. Lashina, E. M. Slavinskaya, O. A. Stonkus, A. I. Stadnichenko, A. V. Romanenko and A. I. Boronin, Chem. Eng. Sci., 2023, 267, 118328.
26. D. Vasilchenko, T. Asanova, B. Kolesov, A. Tsygankova, A. Stadnichenko, E. Slavinskaya, E. Gerasimov, K. Lomachenko, A. Boronin and S. Korenev, ChemCatChem, 2020, 12, 1413–1428.
27. R. P. Galhenage, K. Xie, H. Yan, G. S. Seuser and D. A. Chen, J. Phys. Chem. C, 2016, 120, 10866–10878.
28. A. S. Duke, R. P. Galhenage, S. A. Tenney, P. Sutter and D. A. Chen, J. Phys. Chem. C, 2015, 119, 381–391.
29. Y. Ishida, T. Ebashi, S. I. Ito, T. Kubota, K. Kunimori and K. Tomishige, Chem. Commun., 2009, 5308–5310.
30. K. Azzam, I. Babich, K. Seshan and L. Lefferts, Appl. Catal., B, 2008, 80, 129–140.
31. K. G. Azzam, I. V. Babich, K. Seshan, B. L. Mojet and L. Lefferts, ChemCatChem, 2013, 5, 557–564.
32. K. Reuter, C. Stampf and M. Scheffler, in AB Initio Atomistic Thermodynamics and Statistical Mechanics of Surface Properties and Functions, ed. S. Yip, Springer, Netherlands, Dordrecht, 2005, pp. 149–194.
33. G. Kresse and J. Furthmüller, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
34. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
35. G. Kresse and D. Joubert, Phys. Rev. B:Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
36. P. E. Blöchl, Phys. Rev. B:Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
37. M. Methfessel and A. T. Paxton, Phys. Rev. B:Condens. Matter Mater. Phys., 1989, 40, 3616–3621.
38. X. Wu, D. Vanderbilt and D. R. Hamann, Phys. Rev. B:Condens. Matter Mater. Phys., 2005, 72, 035105.
39. G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904.
40. K. Reuter and M. Scheffler, Phys. Rev. B:Condens. Matter Mater. Phys., 2002, 65, 1–11.
41. L. E. Gálvez-González, L. O. Paz-Borbón and A. Posada-Amarillas, Surf. Sci., 2022, 725, 122157.
42. A. Álvarez-García, J. C. Luque-Ceballos, L. O. Paz-Borbón and I. L. Garzón, Comput. Mater. Sci., 2022, 214, 111697.
43. A. Álvarez García, L. M. Molina and I. L. Garzón, Phys. Chem. Chem. Phys., 2024, 26, 15902–15915.
44. W.-J. Chen, H.-J. Zhai, X. Huang and L.-S. Wang, Chem. Phys. Lett., 2011, 512, 49–53.
45. Y. X. Zhao, X. L. Ding, Y. P. Ma, Z. C. Wang and S. G. He, Theor. Chem. Acc., 2010, 127, 449–465.
46. Y. Nakajima, M. A. Latif, T. Nagata, K. Ohshimo and F. Misaizu, J. Phys. Chem. A, 2023, 127, 3570–3576.
47. J. R. McBride, G. W. Graham, C. R. Peters and W. H. Weber, J. Appl. Phys., 1991, 69, 1596–1604.
48. A. Hjorth Larsen, J. Jørgen Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dulak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. Bjerre Jensen, J. Kermode, J. R. Kitchin, E. Leonhard Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. Bergmann Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys. Condens. Matter., 2017, 29, 273002.
49. K. Reuter, Catal. Lett., 2016, 146, 541–563.
50. M. Chase, NIST-JANAF Thermochemical Tables, 4th edition, American Institute of Physics, vol. 1, 1998.
51. W. Zhang, J. R. Smith and X. G. Wang, Phys. Rev. B:Condens. Matter Mater. Phys., 2004, 70, 024103.
52. S. Bhattacharya, S. V. Levchenko, L. M. Ghiringhelli and M. Scheffler, Phys. Rev. Lett., 2013, 111, 084704.
53. J. T. Hirvi, T. J. J. Kinnunen, M. Suvanto, T. A. Pakkanen and J. K. Nørskov, J. Chem. Phys., 2010, 133, 084704.
54. D. Jiang, Y. Yao, T. Li, G. Wan, X. I. Pereira-Hernández, Y. Lu, J. Tian, K. Khivantsev, M. H. Engelhard, C. Sun, C. E. García-Vargas, A. S. Hoffman, S. R. Bare, A. K. Datye, L. Hu and Y. Wang, Angew. Chem., Int. Ed., 2021, 60, 26054–26062.
55. Y. Tang, Y. G. Wang and J. Li, J. Phys. Chem. C, 2017, 121, 11281–11289.
56. Z. Zhang, J. Tian, Y. Lu, S. Yang, D. Jiang, W. Huang, Y. Li, J. Hong, A. S. Hoffman, S. R. Bare, M. H. Engelhard, A. K. Datye and Y. Wang, Nat. Commun., 2023, 14, 2664.
57. B. Qiao, A. Wang, X. Yang, L. F. Allard, Z. Jiang, Y. Cui, J. Liu, J. Li and T. Zhang, Nat. Chem., 2011, 3, 634–641.

---

Footnote

† Electronic supplementary information (ESI) available: Fig. S1–S6 present the most stable isomers for multiple oxygen adsorption on Re_xPt_y clusters. Fig. S7–S12 show the most stable isomers for CO adsorption on oxidized Re_xPt_y clusters. Fig. S13 and S14 show the most stable isomers for multiple CO adsorption on Re_xPt_y clusters. Fig. S15–S22 present the projected densities of states for oxidized Re_xPt_y clusters. See DOI: https://doi.org/10.1039/d5cp00995b

---