Ground and excited state properties of ThB⁻ and ThB: a theoretical study

Abstract

In the present work, we studied a series of electronic and spin–orbit states of ThB⁻ and ThB using high-level multireference and coupled-cluster theories. We report the potential energy curves (PECs), equilibrium electron configurations, spectroscopic constants, energetics, and spin–orbit coupling effects of 17 and 19 electronic states of ThB⁻ and ThB, respectively. The ground state of ThB⁻ is a single-reference 1³Π with a 1σ²2σ²3σ¹1π³ electron configuration. Detachment of an electron from the doubly occupied 1π orbital of ThB⁻(1³Π) produces the single-reference ground electronic state of ThB (1⁴Σ⁻). The ground spin–orbit states of ThB⁻ and of ThB are 1³Π⁺₀ and 1⁴Σ⁻_3/2, respectively. The vertical electron detachment energy (VDE) of ThB⁻ and the adiabatic electron attachment energy (AEA) of ThB at our largest CBS-C-CCSD(T)+δT(Q)+δSO (complete basis set effect, spin–orbit effect, and triple and perturbative quadruple electron correlation effect added coupled-cluster theory with single, double, and perturbative triple excitations) level are 1.473 eV and 1.459, respectively. The reaction of Th(³F) + B(²P^o) produces the ground state of ThB with a bond energy of 2.843 eV. Finally, we estimated a heat of formation, ΔH⁰_f (298 K), of 891.01 kJ mol⁻¹ for the ThB molecule. The high-level findings of this work are expected to aid and motivate future experimental spectroscopic investigations of ThB and ThB⁻ species.

---

I. Introduction

The fascination of actinide-based species in science and technology is ever-growing by virtue of their remarkably unique physicochemical properties and enormous potential in nuclear power. In this field, thorium (Th) based systems are prominent and have recently received special attention as promising candidates in generation-IV reactors.^1–5 Th-based species are distinctively appealing for large-scale industrial nuclear energy production due to the relatively abundant natural occurrence of Th-minerals and their lesser transuranic nuclear waste production compared to the other primordial actinide, uranium.⁴

Over the years, many laboratory scale attempts have been made to synthesize and characterize a verity of Th-based species aiming to highlight their remarkable chemistries (for example see ref. 6 and 7, references therein, and the literature citing these). Nevertheless, experimental studies of such species are challenging due to the need for sophisticated instruments and experimental conditions for their analysis,^6–11 and the safety measures necessary for avoiding possible radiation toxicities.¹² Thus, theoretical investigations on Th-based species are more appealing in research settings. However, the execution of theoretical studies on Th-based complexes and many other actinide systems is non-facile since they often possess a plethora of closely-lying electronic states causing a myriad of convergence issues. Indeed, theoretical analyses of their smaller complexes, diatomic molecular species in particular, are more challenging since many of their wave functions are often dominated by two or more electron configurations hindering the exploitation of the widely popular “black box-type” single-reference density functional theory (DFT) for their analysis. Even the single-reference states of such highly-correlated species are often problematic for DFT due to the dependence of DFT on the use of the exchange–correlation functional^13–17 and associated delocalization errors^18–20 and static correlation errors.^21,22 Therefore, multireference theoretical methods are highly recommended for their exploration. However, such multireference calculations for correlated actinide species are computationally expensive and challenging.^11,14,23,24 Furthermore, the relativistic effects and spin–orbit effects must be measured for acquiring better predictions of them.^11,25,26 Consequently, many actinide-based diatomic systems are yet to be studied using high-level wave function theories. Nonetheless, it is rather encouraging to see the recent high-level theoretical efforts made by the Peterson and Dixon research groups exploring the chemical bonding, spectroscopy, and energy related properties of a series of actinide-based diatomic species (i.e., AcH^0,−,²⁷ AcO,²⁸ AcF,²⁸ ThH^+,0,−,²⁹ ThN⁺,⁹ PaH^0,−,²⁷ UH^0,−,³⁰ UB^+,0,−,³¹ UC^+,0,−,³² UN^0,−,³³ UO^+,0,−,³⁴ UF^+,0,−,^34,35 NpH^+,0,−,³⁶ PuH^+,0,− 36). Furthermore, their collaborations with the Bowen group provided evidence on the importance of utilizing multireference tools for reaching theoretical harmony with experiments, which would accelerate the field of gas-phase chemistry.^29,30,32

To date, the ThB diatomic system remains poorly understood. Precisely, we were able to locate only one study on ThB that was reported in 1968 by Gingerich who utilized effusion measurements at 2804 K and mass spectrometry to estimate its bond energy (3.03 ± 0.35 eV) and ΔH⁰_f (298 K) (835.54 ± 52.30 kJ mol⁻¹).³⁷ Gingerich further estimated the r_e (2.38 Å) and ω_e (430 cm⁻¹) of ThB using a theoretical approach and also predicted a quartet-spin for the molecule.³⁷ The investigation of the interaction between Th and B is truly an exciting problem to pursue due to the electron deficient boron's ability to produce a diverse set of stable chemical bonding motifs with correlated metals.^{15,16,38–41} Furthermore, exploration of ThB diatomic molecule in itself is beneficial for the spectroscopy community and its chemistries could aid bottom-up synthesis of Th–B reactive moiety based catalysts and materials.

In the present work, we have analyzed the ThB⁻ and ThB species using state-of-the-art multireference and coupled-cluster theoretical methods. The implemented Davidson corrected multireference configuration interaction level of theory (MRCI+Q) has been proven to provide accurate predictions for both single-reference and multireference electronic states of highly correlated diatomic systems accurately^{13,24,42–45} and hence is ideal for investigating the electronic states of ThB⁻ and ThB. On the other hand, CCSD(T) is excellent for studying the single-reference electronic states of reasonably small molecules with high efficacy and hence also adopted in this work. It has been reported that the higher-order electron correlation effects can also improve theoretical predictions of actinide-based species.^29,30,33 For this reason, in the present work, we have tested the triple and perturbative quadruple electron correlation effects at the coupled-cluster level [i.e., CCSDT(Q)] on several spectroscopic and energy related properties of ThB⁻ and ThB. Under these theoretical levels, we examined 17 and 19 electronic states of ThB⁻ and ThB, respectively. We introduced their equilibrium electron configurations, chemical bonding patterns, spectroscopic constants, and energetics. At the MRCI+Q level, the spin–orbit coupling effects were evaluated for both ThB⁻ and ThB. Specifically, 26 and 40 spin–orbit states of ThB⁻ and ThB were explored, respectively. We expect this work to further promote and motivate the ongoing experimental and theoretical attempts on highly correlated actinide-based species aiding the advancement of the field of actinide chemistry.

II. Computational details

The internally contracted multireference configuration interaction (MRCI or MRCISD),^46–48 MRCI+Q,⁴⁹ and CCSD(T)⁵⁰ calculations were performed using the MOLPRO 2023.2^51–53 code implementing its default convergence criteria. The C_2v Abelian subgroup of the original C_∞v non-Abelian symmetry of ThB/ThB⁻ was used for all calculations. Initially, the PECs of the 17 lowest energy electronic states of ThB⁻ were produced at the MRCI+Q level using the triple-ζ quality correlation consistent aug-cc-pVTZ basis set of B⁵⁴ and the cc-pVTZ-PP⁵⁵ basis set of Th. For simplicity, from now on, the findings obtained with this basis set combination is denoted by the prefix ATZ. The energy-consistent pseudopotential (ECP60) was used to replace the inner 60 electrons (1s²2s²2p⁶3s²3p⁶3d¹⁰4s²4p⁶4d¹⁰4f¹⁴) of the Th atom.⁵⁶ Complete active space self-consistent field^57–60 (CASSCF) reference wave functions were provided for MRCI(+Q) calculations. The CASSCF wave function of ThB⁻ was constructed by allocating 8 electrons in 10 active orbitals [CAS(8,10)]. At the dissociation limit, the selected active orbitals are purely the five 6d and 7s atomic orbitals of Th and 2s and three 2p atomic orbitals of B. Specifically, at the C_2v symmetry, these orbitals are 5a₁ (6d_z², 6d_x²−y², and 7s of Th and 2s and 2p_z of B), 2b₁ (6d_xz of Th and 2p_x of B), 2b₂ (6d_yz of Th and 2p_y of B), and 1a₂ (6d_xy of Th). The same set of active orbitals were provided to produce the wave function of multireference calculations of ThB [CAS(7,10)]. To investigate ThB, first, the reactions of Th(³F) + B(²P^o), Th(³P) + B(²P^o), Th(¹D) + B(²P^o), and Th(⁵F) + B(²P^o) were examined at the MRCI+Q level to produce the PECs of the 19 lowest energy electronic states of ThB at the cc-pVQZ⁶¹ basis set of B and the cc-pVQZ-PP⁵⁵ basis set of Th (hereafter QZ). At the MRCI(+Q) level, single and double electron promotions to the virtual space were permitted (for all the valence electrons of ThB⁻ and ThB including the 6s and 6p electrons of Th). The produced PECs of ThB⁻ and ThB were used to solve the rovibrational Schrödinger equation to determine their equilibrium bond length (r_e), adiabatic excitation energy (T_e), harmonic vibrational frequency (ω_e), and anharmonicity (ω_ex_e) values. Utilizing the same active spaces and the basis sets, the spin–orbit coupling effects of ThB⁻ and ThB were explored at the MRCI+Q level by employing the spin–orbit pseudopotential as implemented in MOLPRO. The spin–orbit coupling effects of ThB were also investigated at the AQZ-MRCI+Q level. For MRCI+Q spin–orbit calculations, the MRCI spin–orbit matrix elements were used, but the MRCI electronic energies were replaced with the MRCI+Q energies. More information on the spin–orbit analysis is provided in the Results and discussion section of the paper.

The CCSD(T) calculations built on top of the Hartree–Fock (HF) wavefunctions were also used to produce PECs around the equilibrium bond distance region for several low-lying single-reference electronic states of ThB⁻ and ThB. At the CCSD(T) level, all valence electrons and the 6s, 6p, and 5d electrons of Th were correlated. For these calculations, the AXZ (aug-cc-pVXZ⁵⁴ of B and cc-pwCVXZ-PP⁵⁵ of Th, where X = T and Q) basis sets were used and hereafter these basis sets are denoted by the prefix AXZ-C. The ATZ-C-CCSD(T) PECs, AQZ-C-CCSD(T) PECs, and their corresponding reference HF PECs were used to extrapolate the PECs to the complete basis set (CBS) limit [CBS-C-CCSD(T)]. The CBS extrapolation of the HF energies was carried out according to the scheme introduced by Pansini et al. (ref. 62, eqn (9)), and the dynamic correlation energies were extrapolated using the unified-single-parameter-extrapolation approach provided in ref. 63, eqn (2). The ground state of ThB was also studied at the CCSD(T) level using the aug-cc-pVQZ-DK^54,64 basis set of B and the cc-pwCVQZ-DK3⁶⁵ basis set of Th by correlating all valence electrons and the 6s, 6p, and 5d electrons of Th [hereafter, AQZ-DK-C-CCSD(T)]. For these calculations the third-order Douglas–Kroll–Hess Hamiltonian was used. To further investigate the bonding properties of ThB, natural bond orbital (NBO) population analysis was performed using the NBO7^66,67 code linked to MOLPRO.

The MRCC^68,69 code connected to MOLPRO was used to construct ADZ-CCSD(T) and ADZ-CCSDT(Q) PECs of the ground electronic state of ThB⁻ and the first three electronic states of ThB to obtain their higher-order electron correlation effects [i.e., δT(Q) = E_ADZ-CCSDT(Q) − E_ADZ-CCSD(T)]. Note that ADZ represents the aug-cc-pVDZ⁵⁴ of B and cc-pVDZ-PP⁵⁵ of the Th basis set. In these calculations, the electron correlations of all valence electrons and the 6s and 6p of Th were considered. The calculated δT(Q) effects were added to the CBS-C-CCSD(T) PECs to obtain highly accurate CBS-C-CCSD(T)+δT(Q) PECs. The ATZ-C-CCSD(T), AQZ-C-CCSD(T), CBS-C-CCSD(T), and CBS-C-CCSD(T)+δT(Q) PECs were used to calculate the corresponding r_e, T_e, ω_e, and ω_ex_e values of the ThB⁻ and ThB species.

III. Results and discussion

III.A. ThB⁻

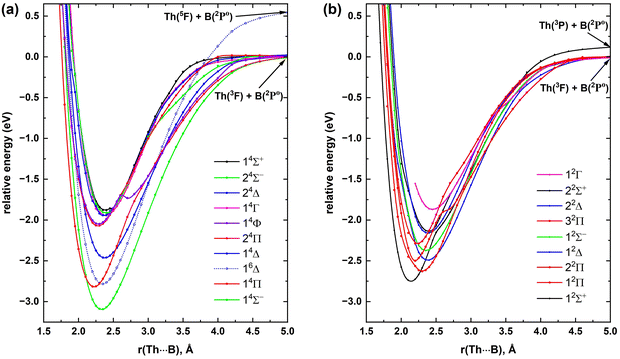
To investigate the low-lying electronic states of ThB⁻, first we produced its potential energy profile around 2–2.8 Å. Specifically, we studied 17 electronic states of this system and their PECs are illustrated in Fig. 1. The low lying electronic states of ThB⁻ are somewhat energetically resolved but the electronic spectrum becomes dense with closely lying states when shifting to higher energy (Fig. 1). The dominant electron configurations and configuration interaction coefficients of all studied electronic states of ThB⁻ are listed in Table 1. The CASSCF state-average molecular orbitals populated by these 17 electronic states of ThB⁻ are illustrated in Fig. 2.

Fig. 1 ATZ-MRCI+Q PECs of ThB⁻ as a function of Th⋯B distance [r(Th⋯B), Å]. The relative energies are referenced to the equilibrium energy of 1³Π, which is set to 0 eV. The Σ⁺, Σ⁻, Π, Δ, Φ, and Γ states are shown in black, green, red, blue, purple, and pink, respectively. The dotted, solid, and dashed PECs correspond to the singlet, triplet, and quintet spin states, respectively.

Table 1 Dominant electronic configurations at equilibrium distances of the 17 studied electronic states of ThB^− a

State^b	Coefficient^c	Configuration^d
a The coefficients and electron configurations were collected at state-average CASSCF performed with all 17 studied electronic states of ThB^−. b The B1 components of Π and Φ states and A1 of the Δ and Γ states under C2v symmetry are listed. c Only the configuration interaction coefficients that are equal to or larger than 0.29 of the corresponding natural orbital representations are reported. d β- and α-spin electrons are specified with and without bars over the spatial orbital, respectively.
1^3Π	0.86	1σ^22σ^23σ1πx1π^2y
1^1Σ^+	0.91	1σ^22σ^21π^2x1π^2y
1^3Σ^−	0.84	1σ^22σ^23σ^21πx1πy
1^5Δ	0.88	1σ^22σ^23σ1πx1πy1δxy
1^1Π	0.59
	−0.59
1^3Δ	0.68
	−0.29
	−0.29
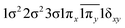
1^1Δ	−0.55	1σ^22σ^23σ^21π^2y
	0.55	1σ^22σ^23σ^21π^2x
1^3Σ^+	0.85	1σ^22σ3σ1π^2x1π^2y
2^3Π	0.59	1σ^22σ^21πx1π^2y(1δx^2−y^2)
	0.59	1σ^22σ^21π^2x1πy1δxy
1^3Φ	−0.60	1σ^22σ^21πx1π^2y(1δx^2−y^2)
	0.60	1σ^22σ^21π^2x1πy1δxy
1^5Π	0.65	1σ^22σ3σ1π^2x1πy1δxy
	0.65	1σ^22σ3σ1πx1π^2y(1δx^2−y^2)
1^1Φ	0.42
	−0.42
	0.42
	−0.42
2^1Σ^+	0.56	1σ^22σ^23σ^21π^2x
	0.56	1σ^22σ^23σ^21π^2y
3^3Π	0.75	1σ^22σ3σ^21πx1π^2y
2^3Δ	0.62
	−0.34
1^3Γ	−0.43	1σ^22σ^23σ1π^2y(1δx^2−y^2)
	0.43	1σ^22σ^23σ1π^2x(1δx^2−y^2)
	−0.43
	0.43
2^1Π	0.39
	−0.39
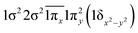
	−0.39
	0.39

---

Fig. 2 Selected CASSCF state-average orbitals of ThB⁻ at r_e = 2.264 Å. The Th and B atoms of each orbital contour are depicted in wine and green spheres, respectively. Orbitals were calculated by including all 17 electronic states given in Table 1. The two phases of orbitals are shown in red and blue. The rotations of 1π_y and 1δ_x²−y² orbitals by 90° and 45° along the z-axis (Th–B bond) produce the contours of 1π_x and 1δ_xy, respectively. IboView⁷⁰ software was used to produce molecular orbitals.

The 1σ molecular orbital is predominantly composed of the 2s of B, with a small contribution from the 7s and 6d_z² of Th (Fig. 2). While 2σ renders the 7s of Th, 3σ represents the hybridization of 6d_z² of Th and 2p_z of B. The 1π orbitals of ThB⁻ are made of 6d_xz (or 6d_yz) of Th and 2p_x (or 2p_y) of B. The 6d_x²−y² and 6d_xy directly translate to the 1δ_x²−y² and 1δ_xy molecular orbitals of ThB⁻, respectively. The % compositions of these CASSCF orbitals are listed in Table S1 (ESI†). In the equilibrium bond region, three active orbitals are antibonding in nature [i.e., resulting from 6d_z²(Th) − 2p_z(B), 6d_xz(Th) − 2p_x(B), and 5d_yz(Th) − 2p_y(B) combinations]. These σ* and two π* orbitals are not occupied by the 17 reported electronic states of ThB⁻ and hence not illustrated in Fig. 2. We present the contours of all active orbitals calculated at 2.264, 3.5, and 7.0 Å in Fig. S1–S3 (ESI†), respectively. These orbital plots illustrate the transformation of the atomic orbitals of the fragments to the molecular orbitals of ThB⁻.

Based on the configuration interaction coefficient, the 1³Π ground electronic state of ThB⁻ is single-reference in nature. Even though ideally we would like to see an approximately 0.95 or greater coefficient for a single-reference electronic state, these coefficients are sensitive to the starting wavefunction as well as the number of electronic states that are being used in the CASSCF calculation. Furthermore, more recently we have found that the configuration interaction coefficients are also sensitive to the active space utilized.¹³ Specifically, we noticed that the dominant configuration interaction coefficient of the X⁴Δ of FeH increased from 0.75 to 0.87 moving from CAS(9,10) to CAS(9,15).¹³ Note that the CASSCF electron configurations listed in Table 1 are collected using a state-average wave function that was produced by including all 17 studied electronic states of ThB⁻. To further understand the configuration interaction coefficients of the ground state, a CASSCF calculation was performed by including only its ³B₁ + ³B₂ states (at C_2v), which increased its coefficient to 0.93, suggesting its single-reference nature. We can predict a bond order of 1.48 for the ground state of ThB⁻ considering its state-average configuration interaction coefficient (74%) (Table 1 and Fig. 2). ThB⁻(1³Π) has Th^+0.07B^−1.07 charge localization and Th(6d^1.887s^1.825f^0.147p^0.06)B(2s^1.752p^2.26) electron distribution according to our NBO analysis. The promotion of the 3σ¹ electron of ThB⁻(1³Π) to its singly occupied 1π orbital gives rise to its first excited state (1¹Σ⁺). This electron transfer increases the bond order of the system by ∼0.2 (i.e., the bond orders of 1³Π and 1¹Σ⁺ are 1.48 and 1.66, respectively), which could be a reason for its shorter r_e compared to the ground state. On the other hand, transferring an electron from the doubly occupied 1π of ThB⁻(1³Π) to the singly occupied 3σ creates its second excited state (1³Σ⁻). Among the first three electronic states of ThB⁻, 1³Σ⁻ bears the longest r_e, which indeed carries the lowest bond order among them (i.e., 1.41). The high-spin third excited state of ThB⁻ is its first state to host electrons in a non-bonding 1δ orbital (1⁵Δ: 1σ²2σ²3σ¹1π²1δ¹). Its relatively longer r_e (compared to the first 3 states) is obviously due to this bonding to non-bonding electron transfer, which decreases its bond order to 1.16. The subsequent electronic states of ThB⁻ carry some multireference characters, except for the 1³Σ⁺ state that bears the shortest r_e and the largest bond order among all the studied states (Fig. 1 and Table 1). To represent the electron arrangements and bonding of this system pictorially, we have introduced valence-bond Lewis (vbL) diagrams for its first 7 electronic states and these diagrams are given in Fig. 3.

Fig. 3 Proposed vbL diagrams for the first 7 electronic states of ThB⁻. In each case, the 2s orbital of boron is doubly occupied and not shown for clarity. Open circles are used to illustrate the two components of each of the 1³Π, 1¹Π, 1⁵Δ, and 1³Δ states, where either of the two open circles is populated by an electron. The two of the four open circles are doubly occupied in the 1¹Δ state. See Table 1 for their exact electronic configurations.

The coupled-cluster methods are ideal for investigating the single-reference electronic states of small molecular systems. Hence, we have performed ATZ-C-CCSD(T) and AQZ-C-CCSD(T) calculations for the dominantly single-reference 1³Π, 1¹Σ⁺, and 1³Σ⁻ electronic states of ThB⁻. Note that due to the associated low computational cost [compared to the MRCI(+Q)], we were able to correlate the 5d¹⁰ outer-core electrons of Th at the CCSD(T) level. Furthermore, we performed ADZ-CCSDT(Q) calculations for the 1³Π of ThB⁻ aiming to capture the higher-order electron correlation effects. Our high-level coupled-cluster and MRCI+Q spectroscopic parameters of ThB⁻ are reported in Table 2.

Table 2 Adiabatic excitation energy T_e (eV), bond length r_e (Å), harmonic vibrational frequency ω_e (cm⁻¹), and anharmonicity ω_ex_e (cm⁻¹) of 17 low-lying electronic states of ThB⁻

State	Method	T e	r e	ω e	ω e x e
1^3Π	CBS-C-CCSD(T)+δT(Q)	0	2.264	571	2.5
	CBS-C-CCSD(T)	0	2.250	583	2.3
	AQZ-C-CCSD(T)	0	2.254	581	2.3
	ATZ-C-CCSD(T)	0	2.261	577	2.4
	ATZ-MRCI+Q	0	2.274	573	2.2
1^1Σ^+	CBS-C-CCSD(T)	0.0968	2.188	597	2.7
	AQZ-C-CCSD(T)	0.1073	2.192	594	2.7
	ATZ-C-CCSD(T)	0.1242	2.200	588	2.7
	ATZ-MRCI+Q	0.1177	2.197	587	2.5
1^3Σ^−	CBS-C-CCSD(T)	0.3050	2.324	548	2.4
	AQZ-C-CCSD(T)	0.2956	2.326	546	2.2
	ATZ-C-CCSD(T)	0.2789	2.331	544	2.2
	ATZ-MRCI+Q	0.2030	2.355	534	2.3
1^5Δ	ATZ-MRCI+Q	0.2633	2.421	496	2.9
1^1Π	ATZ-MRCI+Q	0.3995	2.280	538	2.8
1^3Δ	ATZ-MRCI+Q	0.6018	2.412	497	2.5
1^1Δ	ATZ-MRCI+Q	0.6391	2.386	484	2.0
1^3Σ^+	ATZ-MRCI+Q	0.6552	2.168	662	2.1
2^3Π	ATZ-MRCI+Q	0.8323	2.347	420	6.5
1^3Φ	ATZ-MRCI+Q	0.8608	2.360	482	2.5
1^5Π	ATZ-MRCI+Q	0.8641	2.277	556	4.1
1^1Φ	ATZ-MRCI+Q	0.9227	2.369	476	−1.6
2^1Σ^+	ATZ-MRCI+Q	0.9460	2.408	469	8.3
3^3Π	ATZ-MRCI+Q	0.9816	2.259	726	9.9
2^3Δ	ATZ-MRCI+Q	1.0271	2.452	442	5.2
1^3Γ	ATZ-MRCI+Q	1.0294	2.480	402	−2.2
2^1Π	ATZ-MRCI+Q	1.0454	2.349	462	15.4

---

At all coupled-cluster and MRCI+Q levels, the first excited state of ThB⁻ lies ∼0.1 eV above the ground state and the differences between each level for the T_e of 1¹Σ⁺ are less than 0.03 eV (Table 2). Upon comparison of the ATZ-MRCI+Q and ATZ-C-CCSD(T) PECs of the first three states, the 1³Π and 1¹Σ⁺ PECs at both levels are approximately similar in shape around the equilibrium region (ESI,† Fig. S4), which addresses their similar T_e, r_e, ω_e, and ω_ex_e values (Table 2). The largest mismatch between ATZ-MRCI+Q and ATZ-C-CCSD(T) PECs was observed for the 1³Σ⁻ (ESI,† Fig. S4). The difference between the ATZ-MRCI+Q versus ATZ-C-CCSD(T) T_e of 1³Σ⁻ is ∼0.08 eV. This energy difference is still within the margins of error of the method and basis set; hence, overall, ATZ-MRCI+Q findings are reliable. The difference between the largest implemented coupled-cluster approach for T_e [i.e., CBS-C-CCSD(T)] versus ATZ-MRCI+Q is ∼0.02 eV. The difference in T_e between these two levels of theory for the 1³Σ⁻ state is ∼0.1 eV. All applied levels of theories for the first three electronic states of ThB⁻ predicted approximately similar r_e, ω_e, and ω_ex_e values (Table 2). Importantly, we observed only a slight change in the spectroscopic constants for the 1³Π states even with higher-order δT(Q) correction (Table 2).

The spin–orbit coupling effects are dominant for heavy actinide based species and are essential for providing accurate predictions. Hence, we have calculated the spin–orbit states of ThB⁻ at the ATZ-MRCI+Q level of theory at an r_e of 2.264 Å, which is the CBS-C-CCSD(T)+δT(Q) r_e of ThB⁻(1³Π). Note that the CBS-C-CCSD(T)+δT(Q) r_e was selected to perform spin–orbit calculations since this level accounts for the core electron correlation, complete basis set effects, and single, double, triple, and perturbative quadruple electron correlation effects, and is hence expected to be more accurate compared to the r_e values predicted by other theoretical approaches utilized here. We have considered all 17 electronic states of ThB⁻ listed in Table 1 to construct the spin–orbit matrix and the corresponding spin–orbit products are listed in Table S2 (ESI†). The spin–orbit calculations converged smoothly under the default convergence criteria available in MOLPRO. Our calculated vertical excitation energy (ΔE) values of the spin–orbit states of ThB⁻ and their dominant ΛS compositions are given in Table 3. The spin–orbit effects give rise to an Ω = 0⁺ ground state for ThB⁻, which is dominantly 1³Π (65%) with a substantial composition of 1¹Σ⁺ (24%) (Table 3). Similarly, many excited spin–orbit states of ThB⁻ carry heavy mixings of several electronic states. As expected, the spin–orbit effect accounted spectrum of ThB⁻ is much more complicated with a series of closely lying Ω states (Table 3). Specifically, we observed 26 Ω states for ThB⁻ that span within 0.94 eV (Table 3). It is important to note that all these states of ThB⁻ are stable with respect to the substantially large VDE of ThB⁻ and the AEA of ThB (i.e., 1.4732 eV and 1.4594 eV, respectively, at the CBS-C-CCSD(T)+δT(Q)+δSO level) (ESI,† Table S3).

Table 3 Vertical excitation energy ΔE (eV) and % ΛS composition of 26 spin–orbit states of ThB⁻ at the ATZ-MRCI+Q level of theory^a

Ω	ΔE	% ΛS composition
a ΔE values and the corresponding % ΛS compositions were computed at re = 2.264 Å, which is the CBS-C-CCSD(T)+δT(Q) re of ThB^−(1^3Π).
0^+	0.0000	65% 1^3Π + 24% 1^1Σ^+ + 6% 1^5Δ + 4% 1^3Σ^− + 1% 2^3Π
2	0.0429	98% 1^3Π + 1% 1^5Δ + 1% 1^1Δ
1	0.0608	90% 1^3Π + 4% 1^3Σ^− + 4% 1^5Δ + 1% 1^1Π
0^−	0.0969	87% 1^3Π + 12% 1^5Δ
0^+	0.2913	67% 1^1Σ^+ + 12% 1^3Π + 10% 1^3Σ^− + 9% 1^5Δ + 1% 2^3Π
1	0.3418	82% 1^3Σ^− + 10% 1^1Π + 4% 1^3Π + 3% 1^5Δ
0^+	0.3497	74% 1^3Σ^− + 22% 1^5Δ + 2% 1^3Π + 1% 1^1Σ^+ + 1% 2^1Σ^+
0^−	0.4029	84% 1^5Δ + 12% 1^3Π + 3% 2^3Π
0^+	0.4162	61% 1^5Δ + 20% 1^3Π + 10% 1^3Σ^− + 4% 2^3Π + 4% 1^1Σ^+ + 1% 2^1Σ^+
1	0.4357	87% 1^5Δ + 6%1^3Π + 4% 1^3Δ + 2% 1^3Σ^− + 1% 2^3Π
2	0.4711	88% 1^5Δ + 10% 1^3Δ + 1% 1^3Π
1	0.5131	87% 1^1Π + 11% 1^3Σ^− + 2% 1^3Σ^+
3	0.5160	78% 1^5Δ + 16% 1^3Δ + 4% 1^3Φ + 1% 1^1Φ
4	0.6244	97% 1^5Δ + 2% 1^3Φ
1	0.7408	63% 1^5Π + 33% 1^3Σ^+ + 1% 1^1Π + 1% 2^3Π
0^−	0.7581	43% 1^3Σ^+ + 32% 1^5Π + 23% 2^3Π + 1% 1^5Δ
3	0.7737	52% 1^3Δ + 21% 1^5Δ + 15% 1^1Φ + 11% 1^3Φ
2	0.7995	74% 1^1Δ + 11% 1^3Δ + 7% 2^3Π + 4% 3^3Π + 1% 1^5Δ
2	0.8344	64% 1^3Δ + 14% 1^1Δ + 11% 2^3Π + 8% 1^5Δ + 2% 3^3Π
1	0.8365	67% 1^3Δ + 21% 2^3Π + 5% 1^5Δ + 2% 2^1Π + 1% 1^3Σ^+ + 1% 3^3Π
0^+	0.8382	48% 2^3Π + 43% 1^5Π + 5% 3^3Π + 2% 1^1Σ^+ + 1% 1^5Δ
0^−	0.8734	59% 2^3Π + 19% 1^3Σ^+ + 16% 3^3Π + 3% 1^5Π + 2% 1^5Δ
1	0.8927	44% 1^5Π + 37% 1^3Σ^+ + 12% 1^3Δ + 4% 2^3Π + 2% 3^3Π + 1% 1^5Δ
0^+	0.9123	57% 1^5Π + 37% 2^3Π + 2% 3^3Π + 2% 1^5Δ + 1% 1^1Σ^+ + 1% 2^1Σ^+
3	0.9341	46% 1^3Φ + 29% 1^3Δ + 20% 1^1Φ + 3% 1^3Γ
0^−	0.9368	63% 1^5Π + 26% 1^3Σ^+ + 5% 2^3Π + 5% 3^3Π + 1% 1^5Δ

---

III.B. ThB

We examined four reactions of Th and B to identify the low-lying electronic states of ThB. Specifically, the interactions of the first four electronic states of Th (i.e., ³F, ³P, ¹D, and ⁵F) with the ground state of B (i.e., ²P⁰) were considered.⁷¹ Note that since the first excited state of B is relatively high in energy (∼28 650 cm⁻¹), we did not study its reactions with the low-lying electronic states of Th.⁷¹ Similarly, we did not pursue the ionic interactions between Th⁺ + B⁻ due to their higher energy. Specifically, the lowest energy Th⁺ + B⁻ fragments exist 6.03 eV above the Th(³F) + B(²P^o) asymptote.⁷² The Th(³F) + B(²P^o), Th(³P) + B(²P^o), Th(¹D) + B(²P^o), and Th(⁵F) + B(²P^o) reactions produce ^4,2[Σ⁺, Σ⁻(2), Π(3), Δ(3), Φ(2), Γ], ^4,2[Σ⁺, Σ⁻(2), Π(2), Δ], ²[Σ⁺(2), Σ⁻, Π(3), Δ(2), Φ], and ^6,4[Σ⁺, Σ⁻(2), Π(3), Δ(3), Φ(2), Γ] molecular states of ThB, respectively.^73,74 At the MRCI+Q level, we have identified the 19 lowest energy electronic states of ThB and their PECs are illustrated in Fig. 4. The doublet spin PECs originating from Th(¹D) + B(²P^o) are not within the 19 lowest energy electronic states of ThB and hence are not included in Fig. 4.

Fig. 4 QZ-MRCI+Q PECs of ThB as a function of Th⋯B distance [r(Th⋯B), Å]. The relative energies are referenced to the dissociation limit of Th(³F) + B(²P^o), which is set to 0 eV. The Σ⁺, Σ⁻, Π, Δ, Φ, and Γ states are shown in black, green, red, blue, purple, and pink, respectively. The quartet and sextet spin PECs of ThB are illustrated in plot (a), whereas its doublet spin PECs are given in plot (b).

The interaction of ground state fragments [i.e., Th(³F) + B(²P^o)] gives rise to the 1⁴Σ⁻ ground state of ThB, which confirms that Gingerich's spin prediction of ThB is indeed correct.³⁷ The same fragments produce the first excited state of ThB (1⁴Π). The second excited state of ThB is a 1⁶Δ resulting from Th(⁵F) + B(²P^o), which lies very close in energy to its third excited state 1²Σ⁺. Within the studied r(Th⋯B), all electronic states, except for 1²Γ, converged accurately. The convergence issues of 1²Γ were observed at shorter distances (<2.2 Å), and hence its PEC is plotted within 2.2–5 Å. Overall, the excited state spectrum of ThB is rather complex due the proximity of the electronic states (Fig. 4) and hence several PECs undergo avoided crossings (i.e., 1²Σ⁺versus 2²Σ⁺ at ∼2.5 Å, 1²Π versus 2²Π at ∼2.2 and 2.9 Å, 2²Π versus 3²Π at ∼2.5 Å, 1⁴Π versus 2⁴Π at ∼2.8 Å).

The equilibrium electron configurations of the 19 investigated electronic states of ThB are reported in Table 4. The contours of the occupied molecular orbitals of ThB are qualitatively similar to those of ThB⁻ (Fig. 2). The 1⁴Σ⁻ ground state of ThB possesses the single-reference 1σ²2σ²3σ¹1π² electron arrangement, which translates to the ground state electron configurations of Th (³F; 6d²7s²) and B (²P⁰; 2s²2p¹). Indeed, this is in accordance with our findings from the potential energy profile, in which the ground state PEC stems from the ground state fragments of Th and B. Based on the dominant electron configuration, a bond order of 1.22 can be assigned for 1⁴Σ⁻ (Table 4 and Fig. 2). The ground state of ThB(1⁴Σ⁻) can be created by detaching an electron from the doubly occupied 1π²_y (or 1π²_x) of ThB⁻(1³Π) (Tables 1 and 4). According to our NBO analysis, at the equilibrium distance 1⁴Σ⁻ bears a Th^+0.69B^−0.69 charge distribution with the valence electron population of Th(6d^1.307s^1.845f^0.13)B(2s^1.662p^2.00). The first excited electronic state of ThB (1⁴Π; 1σ²2σ¹3σ¹1π³) can be produced by promoting an electron from 2σ² to the 1π orbital (of 1⁴Σ⁻). This transition gives rise to a bond order of 1.62 for the 1⁴Π state, which rationalizes its shorter r_e compared to the ground state (1⁴Σ⁻). The 2σ² to 1δ electron transition (from 1⁴Σ⁻) gives rise to the electron configuration of the second excited state of ThB (1⁶Δ). Similar to the first three states, the next two electronic states of ThB are predominantly single-reference in nature (Table 4). Based on the electron arrangements and the contours of the molecular orbitals, we have proposed vbL diagrams for the first 5 electronic states of ThB and these diagrams are given in Fig. 5. Their NBO population analysis findings are given in Table S4 (ESI†). In all these states, the population of the 5f orbitals of Th is minor (0.13–0.16 electrons), and hence we expect them to exhibit transition metal-like properties. The next 14 excited electronic states of ThB display significant multireference character, which clearly reflects the complexity of this system (Table 4).

Table 4 Dominant electronic configurations at equilibrium distances of the 19 studied electronic states of ThB^a

State^b	Coefficient^c	Configuration^d
a The coefficients and electron configurations were collected at state-average CASSCF performed with all 19 studied electronic states of ThB. b Only one component under C2v symmetry is listed for Π, Δ, Φ, and Γ states. The corresponding irreducible representations are given in parentheses. c Only the configuration interaction coefficients that are larger than 0.30 of the corresponding natural orbital representations are reported. d β- and α-spin electrons are specified with and without bars over the spatial orbital, respectively.
1^4Σ^−	0.90	1σ^22σ^23σ1πx1πy
1^4Π (B1)	0.90	1σ^22σ3σ1πx1π^2y
1^6Δ (A1)	0.97	1σ^22σ3σ1πx1πy1δxy
1^2Σ^+	0.89	1σ^22σ1π^2x1π^2y
1^2Π (B1)	0.88	1σ^22σ^21πx1π^2y
2^2Π (B1)	0.73
	−0.46
1^2Δ (A2)	−0.44
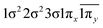
	0.44
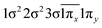
	0.42
1^4Δ (A1)	−0.41
	0.49
1^2Σ^−	0.66
	−0.33
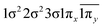
	−0.33
3^2Π (B1)	0.66
	−0.53
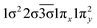
2^2Δ (A1)	−0.40	1σ^22σ^23σ1π^2y
	0.40	1σ^22σ^23σ1π^2x
	−0.40
2^2Σ^+	0.53	1σ^22σ^23σ1π^2y
	0.53	1σ^22σ^23σ1π^2x
2^4Π (B1)	−0.64	1σ^22σ1πx1π^2y(1δx^2−y^2)
	0.64	1σ^22σ1π^2x1πy1δxy
1^4Φ (B1)	0.65	1σ^22σ1πx1π^2y(1δx^2−y^2)
	0.65	1σ^22σ1π^2x1πy1δxy
1^4Γ (A1)	−0.47
	0.47
	0.47	1σ^22σ3σ1π^2x(1δx^2−y^2)
	−0.47	1σ^22σ3σ1π^2y(1δx^2−y^2)
2^4Δ (A1)	0.68
	−0.43
	−0.43
2^4Σ^−	−0.45
	0.45
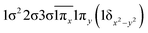
	0.45	1σ^22σ3σ1π^2x1δxy
	−0.45	1σ^22σ3σ1π^2y1δxy
1^4Σ^+	0.47
	−0.47
	0.47	1σ^22σ3σ1π^2y(1δx^2−y^2)
	−0.47	1σ^22σ3σ1π^2y(1δx^2−y^2)
1^2Γ (A2)	−0.33
	0.33
	−0.33
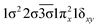
	0.33

---

Fig. 5 Proposed vbL diagrams for the first 5 electronic states of ThB. In each case, the 2s orbital of boron is doubly occupied and not shown for clarity. Open circles are used to illustrate the two components of each 1⁴Π, 1⁶Δ, and 1²Π, where open circles are populated by an electron. See Table 4 for their exact electronic configurations.

All our coupled-cluster levels and the QZ-MRCI+Q predicted an identical order of states for the first 5 electronic states of ThB (i.e., 1⁴Σ⁻, 1⁴Π, 1⁶Δ, 1²Σ⁺, and 1²Π) (Table 5). The δT(Q) correction slightly increased the T_e of the 1⁴Π state [compare the T_e values of 1⁴Π at CBS-C-CCSD(T)+δT(Q) and CBS-C-CCSD(T) levels]. It is important to note the good agreement of the first T_e of ThB at CBS-C-CCSD(T)+δT(Q) versus QZ-MRCI+Q levels (Table 5). In all cases, we observed slightly lower T_e values at the QZ-MRCI+Q level compared to the AQZ-C-CCSD(T) (by ∼0.01–0.06 eV; Table 5). Compared to ATZ-C-CCSD(T), AQZ-C-CCSD(T) predicted slightly lower T_e values. The excitation energies of all multireference electronic states are provided only under QZ-MRCI+Q and several of these states lie within the margins of error of the basis set and method.

Table 5 Adiabatic excitation energy T_e (eV), bond length r_e (Å), harmonic vibrational frequency ω_e (cm⁻¹), and anharmonicity ω_ex_e (cm⁻¹) of 19 low-lying electronic states of ThB

State	Method	T e	r e	ω e	ω e x e
1^4Σ^−	CBS-C-CCSD(T)+δT(Q)	0	2.324	551	2.7
	CBS-C-CCSD(T)	0	2.316	570	2.5
	AQZ-DK-C-CCSD(T)	0	2.323	564	2.5
	AQZ-C-CCSD(T)	0	2.320	567	2.6
	ATZ-C-CCSD(T)	0	2.326	563	2.6
	QZ-MRCI+Q	0	2.327	551	2.3
1^4Π	CBS-C-CCSD(T)+δT(Q)	0.2584	2.209	626	2.4
	CBS-C-CCSD(T)	0.2574	2.205	629	2.2
	AQZ-C-CCSD(T)	0.2831	2.209	625	2.6
	ATZ-C-CCSD(T)	0.3219	2.215	620	2.6
	QZ-MRCI+Q	0.2770	2.222	616	2.7
1^6Δ	AQZ-C-CCSD(T)	0.3317	2.334	570	2.3
	ATZ-C-CCSD(T)	0.3415	2.339	566	2.4
	QZ-MRCI+Q	0.3115	2.343	559	2.5
1^2Σ^+	AQZ-C-CCSD(T)	0.3616	2.135	652	2.5
	ATZ-C-CCSD(T)	0.4209	2.143	645	2.5
	QZ-MRCI+Q	0.3454	2.140	640	9.4
1^2Π	AQZ-C-CCSD(T)	0.5228	2.279	475	−0.2
	ATZ-C-CCSD(T)	0.5413	2.286	485	−0.1
	QZ-MRCI+Q	0.4662	2.296	467	0.1
2^2Π	QZ-MRCI+Q	0.5952	2.199	658	10.1
1^2Δ	QZ-MRCI+Q	0.6010	2.380	524	3.1
1^4Δ	QZ-MRCI+Q	0.6308	2.375	509	2.6
1^2Σ^−	QZ-MRCI+Q	0.7200	2.355	496	1.7
3^2Π	QZ-MRCI+Q	0.8023	2.228	611	6.0
2^2Δ	QZ-MRCI+Q	0.9342	2.382	498	1.9
2^2Σ^+	QZ-MRCI+Q	0.9542	2.396	457	1.7
2^4Π	QZ-MRCI+Q	1.0244	2.280	507	2.8
1^4Φ	QZ-MRCI+Q	1.0462	2.286	552	8.9
1^4Γ	QZ-MRCI+Q	1.1505	2.382	515	1.8
2^4Δ	QZ-MRCI+Q	1.1513	2.372	525	2.1
2^4Σ^−	QZ-MRCI+Q	1.1811	2.426	523	3.9
1^4Σ^+	QZ-MRCI+Q	1.2128	2.382	486	−2.4
1^2Γ	QZ-MRCI+Q	1.2238	2.446	429	0.9

---

All our theoretical approaches predicted that the r_e, ω_e, and ω_ex_e values of the first 5 electronic states of ThB are in good agreement with each other (Table 5). Similarly, the zero-point energy corrected dissociation energies (D₀) of 1⁴Σ⁻ predicted by our methods are in great harmony with each other. Specifically, the D₀ of ThB with respect to the Th(³F) + B(²P^o) ground state fragments at QZ-MRCI+Q, ATZ-C-CCSD(T), AQZ-C-CCSD(T), AQZ-DK-C-CCSD(T), CBS-C-CCSD(T), and CBS-C-CCSD(T)+δT(Q) levels are 3.09, 3.05, 3.10, 3.04, 3.13, and 3.15 eV, respectively (ESI,† Table S3). Note that the QZ-MRCI+Q D₀ (both with and without spin–orbit effects) of ThB was computed with respect to the aforementioned fragments placed 200 Å apart. The spin–orbit effects on the D₀ of ThB are discussed later in the paper.

We have calculated the spin–orbit coupling effects of ThB at the QZ-MRCI+Q level and its spin–orbit matrix was produced by including all 19 electronic states given in Table 4. These 19 electronic states give rise to 51 Ω states and are listed in Table S5 (ESI†). Similar to the ThB⁻ case, all spin–orbit calculations of ThB converged without giving rise to any issues. The QZ-MRCI+Q curves of the 6 most stable spin–orbit states of ThB are illustrated in Fig. S5 (ESI†). The spectroscopic constants and the ΛS compositions collected at their equilibrium bond distances are listed in Table 6. At the QZ-MRCI+Q level, the ground spin–orbit state of ThB is Ω = 3/2, which is slightly more stable than Ω = 1/2 (Table 6). At their r_e values, these states are predominantly 1⁴Σ⁻, which rationalizes their almost identical r_e values to the parent 1⁴Σ⁻ (Tables 5 and 6). Upon moving away from r_e, we observed large spin–orbit mixings, which justify the slightly different ω_e and ω_ex_e of 1⁴Σ⁻_3/2 and 1⁴Σ⁻_1/2 compared to those of 1⁴Σ⁻ (Tables 5 and 6). Our 1⁴Σ⁻_3/2r_e is in good agreement with Gingerich's estimated r_e of the ThB molecule (i.e., 2.324 versus 2.38 Å). On the other hand, our ω_e of 1⁴Σ⁻_3/2 is 52 cm⁻¹ larger than Gingerich's estimated ω_e of ThB (i.e., 482 versus 430 cm⁻¹).³⁷ The next three spin–orbit states carry a larger component of the 1⁶Δ state (Ω = 1/2, 1/2, 3/2), followed by the Ω = 5/2 of 1⁴Π (Table 6).

Table 6 Adiabatic excitation energy T_e (eV), bond length r_e (Å), harmonic vibrational frequency ω_e (cm⁻¹), anharmonicity ω_ex_e (cm⁻¹), and % ΛS composition of the first 6 spin–orbit states of ThB at the QZ-MRCI+Q level of theory

Ω	T e	r e	ω e	ω e x e	% ΛS composition
3/2	0.0000	2.324	482	3.6	93% 1^4Σ^− + 4% 1^2Π + 2% 1^4Π
1/2	0.0001	2.323	539	3.5	89% 1^4Σ^− + 6% 1^4Π + 2% 1^6Δ + 1% 1^2Π
1/2	0.1248	2.318	499	3.4	72% 1^6Δ + 20% 1^4Π + 4% 1^4Σ^− + 2% 1^2Σ^+ + 1% 2^4Π
1/2	0.1875	2.319	485	1.5	72% 1^6Δ + 21% 1^4Π + 3% 1^4Σ^− + 3% 1^4Δ
3/2	0.2437	2.287	526	2.5	49% 1^6Δ + 45% 1^4Π + 3% 1^4Δ + 2% 1^4Σ^−
5/2	0.2580	2.224	515	4.4	84% 1^4Π + 12% 1^6Δ + 3% 1^2Δ + 1% 1^4Δ

---

Using the same spin–orbit matrix, another spin–orbit calculation was performed at the AQZ-MRCI+Q level at r_e = 2.324 Å, which is the r_e of ThB(1⁴Σ⁻) at CBS-C-CCSD(T)+δT(Q). The ΔE values and the ΛS compositions of the 40 lowest energy spin–orbit states of ThB are reported in Table 7. It should be observed that these 40 spin–orbit states are lying within 1.2 eV, which again demonstrates the intricacy of this system. Aiming to aid future experimental photoelectron spectroscopy studies of ThB⁻/ThB, we have performed another spin–orbit calculation at the AQZ-MRCI+Q level at r_e = 2.264 Å, which is the r_e of ThB⁻(1³Π) at the CBS-C-CCSD(T)+δT(Q) level. The calculated ΔE values, corresponding VDE values, and the states are given in Table S6 (ESI†).

Table 7 Vertical excitation energy ΔE (eV) and % ΛS composition of 40 spin–orbit states of ThB at the AQZ-MRCI+Q level of theory^a

Ω	ΔE	% ΛS composition
a ΔE values and the corresponding % ΛS compositions were computed at re = 2.324 Å, which is the CBS-C-CCSD(T)+δT(Q) re of ThB(1^4Σ^−).
3/2	0.0000	93% 1^4Σ^− + 4% 1^2Π + 2% 1^4Π
1/2	0.0003	89% 1^4Σ^− + 6% 1^4Π+ 2% 1^6Δ + 1% 1^2Π
1/2	0.1252	73% 1^6Δ + 20% 1^4Π + 4% 1^4Σ^− + 2% 1^2Σ^+ + 1% 2^4Π
1/2	0.1877	72% 1^6Δ + 20% 1^4Π + 3% 1^4Σ^− + 3% 1^4Δ
3/2	0.2456	66% 1^6Δ + 27% 1^4Π + 4% 1^4Δ + 1% 1^4Σ^−
5/2	0.2869	66% 1^4Π + 28% 1^6Δ + 3% 1^2Δ + 1% 1^4Δ
5/2	0.3659	63% 1^6Δ + 26% 1^4Π + 5% 1^2Δ + 5% 1^4Δ
1/2	0.3767	41% 1^4Π + 29% 1^2Σ^+ + 24% 1^6Δ + 2% 2^2Π + 2% 1^4Δ + 2% 1^4Σ^−
3/2	0.3827	54% 1^4Π + 20% 1^6Δ + 12% 1^2Π + 9% 1^2Δ + 2% 1^4Δ
7/2	0.4046	94% 1^6Δ + 4% 1^4Δ + 1% 1^4Φ
1/2	0.4295	75% 1^4Π + 20% 1^6Δ + 1% 1^2Σ^+ + 1% 1^2Σ^−
3/2	0.4420	62% 1^2Π + 13% 1^4Π + 9% 1^2Δ + 8% 1^6Δ + 5% 1^4Σ^− +2% 1^4Δ
9/2	0.4717	98% 1^6Δ + 2% 1^4Φ
1/2	0.4917	74% 1^2Π + 20% 1^4Δ + 1% 1^6Δ + 1% 2^2Σ^+ + 1% 1^2Σ^− + 1% 1^4Σ^−
1/2	0.5679	30% 1^2Σ^+ + 27% 1^4Π + 16% 2^2Π + 12% 1^4Δ + 5% 1^2Π + 4% 2^4Π + 3% 1^6Δ + 2% 3^2Π
5/2	0.6056	60% 1^2Δ + 27% 1^4Δ +5% 1^4Π + 5% 1^6Δ + 3% 2^2Δ
3/2	0.6249	58% 1^4Δ + 13% 1^2Π + 12% 2^2Π + 8% 1^2Δ + 5% 1^6Δ + 4% 2^2Δ
1/2	0.6396	54% 1^4Δ + 17% 1^2Σ^+ + 12% 1^2Π +6% 1^2Σ^− + 5% 1^4Π + 3% 2^4Π + 1% 1^6Δ + 1% 2^2Σ^+ + 1% 3^2Π
3/2	0.7027	64% 1^2Δ + 13% 2^2Π + 8% 1^2Π + 5% 1^4Δ + 4% 3^2Π + 3% 2^2Δ + 2% 1^4Π
3/2	0.7342	46% 2^2Π + 32% 1^4Δ + 14% 1^2Δ + 2% 2^2Δ +2% 3^2Π + 1% 1^6Δ + 1% 1^4Π
1/2	0.7359	71% 1^2Σ^− + 16% 3^2Π + 4% 1^2Π + 3% 1^4Δ + 3% 2^4Δ + 2% 2^2Σ^+ + 1% 1^4Π
5/2	0.7360	56% 1^4Δ + 35% 1^2Δ + 5% 2^2Δ + 2% 1^6Δ + 1% 1^4Π
7/2	0.7602	95% 1^4Δ + 4% 1^6Δ
1/2	0.8313	71% 2^2Π + 16% 2^4Π + 6% 1^4Δ + 4% 1^2Σ^+ + 1% 2^2Σ^+
1/2	0.8441	58% 3^2Π + 17% 2^4Δ + 16% 1^2Σ^− + 4% 2^2Σ^+ + 1% 1^2Σ^+ + 1% 1^4Σ^+ + 1% 2^4Π
3/2	0.8769	73% 3^2Π + 8% 2^4Σ^− + 6% 1^2Δ + 5% 2^4Δ + 4% 1^4Σ^+ + 2% 1^4Δ
1/2	0.9188	80% 2^4Π + 9% 1^2Σ^+ + 6% 2^2Π + 2% 1^4Σ^+ + 1% 1^6Δ
3/2	0.9759	94% 1^4Φ + 4% 2^2Δ + 1% 1^4Δ
5/2	0.9920	89% 2^2Δ + 8% 1^4Δ + 1% 2^4Π + 1% 1^4Φ
5/2	1.0015	53% 1^4Φ + 44% 1^4Γ + 2% 2^2Δ
1/2	1.0135	82% 2^4Π + 4% 1^2Σ^+ + 3% 2^2Σ^+ + 3% 2^2Π + 2% 1^4Δ + 2% 2^4Σ^− + 1% 1^6Δ + 1% 1^4Σ^+ + 1% 2^4Δ
3/2	1.0186	84% 2^2Δ + 5% 1^4Φ + 4% 1^4Δ + 4% 2^4Π + 1% 3^2Π + 1% 2^4Σ^−
1/2	1.0326	76% 2^2Σ^+ + 12% 2^4Δ + 5% 2^4Π + 2% 2^4Σ^− + 2% 1^2Π + 2% 1^2Σ^−
7/2	1.0721	57% 1^4Φ + 41% 1^4Γ + 1% 1^6Δ + 1% 1^2Γ
1/2	1.0882	66% 2^4Δ + 18% 3^2Π + 10% 2^2Σ^+ + 2% 2^4Σ^− + 1% 1^2Σ^− + 1% 1^4Σ^+
5/2	1.1079	55% 1^4Γ + 43% 1^4Φ + 1% 2^4Δ
3/2	1.1190	88% 2^4Π + 4% 1^4Σ^+ + 3% 2^2Δ + 2% 1^4Δ + 1% 2^4Δ
3/2	1.1305	50% 2^4Δ + 27% 2^4Σ^− + 19% 1^4Σ^+ + 1% 3^2Π + 1% 2^4Π
9/2	1.1614	67% 1^4Φ + 31% 1^4Γ + 1% 1^6Δ
7/2	1.1762	45% 1^4Γ + 37% 1^4Φ + 17% 1^2Γ

---

The spin–orbit effects decreased the D₀ of ThB (1⁴Σ⁻) by 0.251 eV. On the other hand, we can account a 0.054 eV ECP correction considering the D₀ predictions at AQZ-DK-C-CCSD(T) and AQZ-C-CCSD(T) levels. By introducing the spin–orbit correction and ECP correction to CBS-C-CCSD(T)+δT(Q) D₀, we arrived at our best theoretical estimation of D₀ of 2.843 eV for ThB (1⁴Σ⁻). This D₀ value is well within the margin of error of the D₀ value reported by Gingerich (i.e., 3.03 ± 0.35 eV).³⁷ The D₀ of 2.843 eV (or 274.31 kJ mol⁻¹) in this work, ΔH⁰_f (0 K, Th) reported by Wagman et al.⁷⁵ (i.e., 598.65 kJ mol⁻¹), and ΔH⁰_f (0 K, B) reported by Karton and Martin⁷⁶ (i.e., 565.26 ± 0.84 kJ mol⁻¹) were used to calculate ΔH⁰_f (0 K, ThB) using the equation: ΔH⁰_f (0 K, ThB) = ΔH⁰_f (0 K, Th) + ΔH⁰_f (0 K, B) − D₀ (ThB). This approach provided us with a ΔH⁰_f (0 K, ThB) of 889.60 kJ mol⁻¹. At the AQZ-CCSD(T) level, we have calculated [H⁰ (298 K, ThB) − H⁰ (0 K, ThB)] to be 9.13 kJ mol⁻¹. This value and the thermal corrections of 6.51 and 1.21 kJ mol⁻¹ of Th [i.e., H⁰ (298 K, Th) − H⁰ (0 K, Th)]⁷⁵ and B [i.e., H⁰ (298 K, B) − H⁰ (0 K, B)]⁷⁵ were used to calculate the ΔH⁰_f (298 K, ThB) of 891.01 kJ mol⁻¹ using the equation: ΔH⁰_f (298 K, ThB) = ΔH⁰_f (0 K, ThB) + [H⁰ (298 K, ThB) − H⁰ (0 K, ThB)] − [H⁰ (298 K, Th) − H⁰ (0 K, B)] − [H⁰ (298 K, B) − H⁰ (0 K, B)].⁷⁷

IV. Conclusions

Calculations utilizing the MRCI+Q, CCSD(T), and CCSDT(Q) wave function theory conjoined with correlation consistent basis sets were performed to investigate the ground and excited electronic states of ThB⁻ and ThB. Specifically, we reported the PECs, equilibrium electron arrangements, T_e, r_e, ω_e, and ω_ex_e values of 17 and 19 electronic states of ThB⁻ and ThB, respectively. Based on the contours of the occupied molecular orbitals and the electron configurations, vbL diagrams of several low-lying states of ThB⁻ and ThB were also presented. The ground states of ThB⁻ and ThB are 1³Π and 1⁴Σ⁻ with 1σ²2σ²3σ¹1π³ and 1σ²2σ²3σ¹1π² single-reference electron configurations, respectively. The excited state spectra of these systems are highly complex in nature and the reported 17 and 19 electronic states of ThB⁻ and ThB are densely arranged within 1.04 and 1.23 eV, respectively. The spin–orbit coupling effects are dominant for both systems. Specifically, we observed 26 and 40 spin–orbit states of ThB⁻ and ThB that span within 0.94 and 1.18 eV, respectively, which highlights the intricacy of these systems. The spin–orbit ground state of ThB⁻ (Ω = 0⁺) is mostly 1³Π (65%) but exhibits significant 1¹Σ⁺ character (24%). On the other hand, the spin–orbit ground state of ThB (Ω = 3/2) is predominantly 1⁴Σ⁻ (93%). Many excited spin–orbit states of ThB⁻ and ThB are hybrids of several electronic states that are energetically closely arranged. The spin–orbit effect accounted CBS-C-CCSD(T)+δT(Q)+δSO VDE of ThB⁻ and AEA of ThB are 1.4732 eV and 1.4594. The estimated D₀ of ThB(1⁴Σ⁻_3/2) is 2.843 eV. Our theoretical values of D₀, r_e, ω_e, and ω_ex_e of ThB(1⁴Σ⁻_3/2) are in reasonable agreement with the only experimental study of ThB available in the literature reported 56 years ago.³⁷ We combined our D₀ of ThB(1⁴Σ⁻_3/2) with several thermochemical properties of Th and B atoms from the literature to estimate the ΔH⁰_f (298 K) of ThB, which is 891.01 kJ mol⁻¹. We believe that this theoretical investigation of ThB⁻ and ThB provides the much needed insight into their electronic properties and spectroscopic parameters aiding the future experimental spectroscopic studies of ThB⁻ and ThB.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The support of the Los Alamos National Laboratory (LANL) Laboratory Directed Research and Development program (Project No. 20240737PRD1) is acknowledged. This research used resources provided by the Los Alamos National Laboratory Institutional Computing Program, which is supported by the U.S. Department of Energy National Nuclear Security Administration under Contract No. 89233218CNA000001. Professor Kirk A. Peterson is thanked for useful discussions on the higher-order coupled-cluster calculations performed under the MRCC code. Reviewers are thanked for their useful comments on improving this work.

References

1. D. Shi, J. Song, Y. Qin, X. Chen, Y. Guo, S. Du and X. Gong, J. Phys. Chem. C, 2022, 126, 17759–17768.
2. U. E. Humphrey and M. U. Khandaker, Renewable Sustainable Energy Rev., 2018, 97, 259–275.
3. K. Insulander Björk, V. Fhager and C. Demazière, Prog. Nucl. Energy, 2011, 53, 618–625.
4. Current and future generation Thorium, World nuclear association, https://world-nuclear.org, (accessed February 2, 2025).
5. H. György and S. Czifrus, Prog. Nucl. Energy, 2016, 93, 306–317.
6. C. D. Tutson and A. E. V. Gorden, Coord. Chem. Rev., 2017, 333, 27–43.
7. M. S. Wickleder, B. Fourest and P. K. Dorhout, Thorium, in The Chemistry of the Actinide and Transactinide Elements, Springer, Netherlands, 3 edn, 2006, ch. 3.
8. J. Li, B. E. Bursten, M. Zhou and L. Andrews, Inorg. Chem., 2001, 40, 5448–5460.
9. R. M. Cox, A. Kafle, P. B. Armentrout and K. A. Peterson, J. Chem. Phys., 2019, 151, 034304.
10. Thorium fuel cycle—Potential benefits and challenges, International Atomic Energy Agency IAEA in Austria, 2005.
11. M. C. Heaven and K. A. Peterson, Probing Actinide Bonds in the Gas Phase, Chapter 1 in Experimental and Theoretical Approaches to Actinide Chemistry, John Wiley & Sons Ltd, 2018.
12. ToxGuide for Thorium, CAS # 7440-29-1, U.S. Department of Health and Human Services Public Health Service Agency for Toxic Substances and Disease Registry .
13. I. R. Ariyarathna, J. A. Leiding, A. J. Neukirch and M. C. Zammit, J. Phys. Chem. A, 2024, 128, 9412–9425.
14. I. R. Ariyarathna, Phys. Chem. Chem. Phys., 2024, 26, 28337–28348.
15. I. R. Ariyarathna, C. Duan and H. J. Kulik, J. Chem. Phys., 2022, 156, 184113.
16. I. R. Ariyarathna, Phys. Chem. Chem. Phys., 2024, 26, 22858–22869.
17. I. R. Ariyarathna, Y. Cho, C. Duan and H. J. Kulik, Phys. Chem. Chem. Phys., 2023, 25, 26632–26639.
18. M. C. Kim, E. Sim and K. Burke, Phys. Rev. Lett., 2013, 111, 073003.
19. X. Zheng, M. Liu, E. R. Johnson, J. Contreras-Garcia and W. Yang, J. Chem. Phys., 2012, 137, 214106.
20. E. R. Johnson, A. Otero-de-la-Roza and S. G. Dale, J. Chem. Phys., 2013, 139, 184116.
21. A. J. Cohen, P. Mori-Sanchez and W. Yang, Science, 2008, 321, 792–794.
22. T. J. Duignan and J. Autschbach, J. Chem. Theory Comput., 2016, 12, 3109–3121.
23. I. R. Ariyarathna and E. Miliordos, Phys. Chem. Chem. Phys., 2019, 21, 24469–24477.
24. S. C. North, N. M. S. Almeida, T. R. L. Melin and A. K. Wilson, J. Phys. Chem. A, 2023, 127, 107–121.
25. M. Pepper and B. E. Bursten, Chem. Rev., 1991, 91, 719–741.
26. P. Pyykko, Annu. Rev. Phys. Chem., 2012, 63, 45–64.
27. G. F. de Melo and D. A. Dixon, J. Phys. Chem. A, 2022, 126, 6171–6184.
28. J. G. F. Romeu and D. A. Dixon, J. Phys. Chem. A, 2025, 129, 1396–1410.
29. M. Vasiliu, K. A. Peterson, M. Marshall, Z. Zhu, B. A. Tufekci, K. H. Bowen and D. A. Dixon, J. Phys. Chem. A, 2022, 126, 198–210.
30. G. F. de Melo, M. Vasiliu, M. Marshall, Z. Zhu, B. A. Tufekci, S. M. Ciborowski, M. Blankenhorn, R. M. Harris, K. H. Bowen and D. A. Dixon, J. Phys. Chem. A, 2022, 126, 4432–4443.
31. G. F. de Melo and D. A. Dixon, J. Phys. Chem. A, 2023, 127, 1588–1597.
32. G. F. de Melo, M. Vasiliu, G. Liu, S. Ciborowski, Z. Zhu, M. Blankenhorn, R. Harris, C. Martinez-Martinez, M. Dipalo, K. A. Peterson, K. H. Bowen and D. A. Dixon, J. Phys. Chem. A, 2022, 126, 9392–9407.
33. G. F. de Melo, M. Vasiliu, G. Liu, S. Ciborowski, Z. Zhu, M. Blankenhorn, R. Harris, C. Martinez-Martinez, M. Dipalo, K. A. Peterson, K. H. Bowen and D. A. Dixon, J. Phys. Chem. A, 2022, 126, 7944–7953.
34. J. G. F. Romeu, A. R. E. Hunt, G. F. de Melo, K. A. Peterson and D. A. Dixon, J. Phys. Chem. A, 2024, 128, 5586–5604.
35. B. A. Tufekci, K. Foreman, J. G. F. Romeu, D. A. Dixon, K. A. Peterson, L. Cheng and K. H. Bowen, J. Phys. Chem. Lett., 2024, 15, 11932–11938.
36. G. F. de Melo and D. A. Dixon, J. Phys. Chem. A, 2023, 127, 3179–3189.
37. K. Gingerich, High Temp. Sci., 1969, 1, 258–267.
38. C. Demetriou, C. E. Tzeliou, A. Androutsopoulos and D. Tzeli, Molecules, 2023, 28, 8016.
39. D. M. Merriles, C. Nielson, E. Tieu and M. D. Morse, J. Phys. Chem. A, 2021, 125, 4420–4434.
40. D. Tzeli and A. Mavridis, J. Chem. Phys., 2008, 128, 034309.
41. D. M. Merriles and M. D. Morse, J. Chem. Phys., 2022, 157, 074303.
42. N. M. S. Almeida, T. R. L. Melin and A. K. Wilson, J. Chem. Phys., 2021, 154, 244304.
43. N. M. S. Almeida, B. K. Welch, S. C. North and A. K. Wilson, Phys. Chem. Chem. Phys., 2024, 26, 10427–10438.
44. I. R. Ariyarathna and E. Miliordos, Phys. Chem. Chem. Phys., 2018, 20, 12278–12287.
45. N. M. S. Almeida, I. R. Ariyarathna and E. Miliordos, J. Phys. Chem. A, 2019, 123, 9336–9344.
46. H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1988, 89, 5803–5814.
47. P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1988, 145, 514–522.
48. K. R. Shamasundar, G. Knizia and H. J. Werner, J. Chem. Phys., 2011, 135, 054101.
49. S. R. Langhoff and E. R. Davidson, Int. J. Quantum Chem., 1974, 8, 61–72.
50. K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483.
51. H. J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 2, 242–253.
52. H. J. Werner, P. J. Knowles, F. R. Manby, J. A. Black, K. Doll, A. Hesselmann, D. Kats, A. Kohn, T. Korona, D. A. Kreplin, Q. Ma, T. F. Miller, 3rd, A. Mitrushchenkov, K. A. Peterson, I. Polyak, G. Rauhut and M. Sibaev, J. Chem. Phys., 2020, 152, 144107.
53. H.-J. Werner and P. J. Knowles, et al., MOLPRO, version 2023.2, a package of ab initio programs, see https://www.molpro.net.
54. R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806.
55. K. A. Peterson, J. Chem. Phys., 2015, 142, 074105.
56. A. Weigand, X. Cao, T. Hangele and M. Dolg, J. Phys. Chem. A, 2014, 118, 2519–2530.
57. H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1985, 82, 5053–5063.
58. P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1985, 115, 259–267.
59. D. A. Kreplin, P. J. Knowles and H. J. Werner, J. Chem. Phys., 2019, 150, 194106.
60. D. A. Kreplin, P. J. Knowles and H. J. Werner, J. Chem. Phys., 2020, 152, 074102.
61. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023.
62. F. N. N. Pansini, A. C. Neto and A. J. C. Varandas, Theor. Chem. Acc., 2016, 135, 261.
63. F. N. N. Pansini, A. C. Neto and A. J. C. Varandas, Chem. Phys. Lett., 2015, 641, 90–96.
64. W. A. de Jong, R. J. Harrison and D. A. Dixon, J. Chem. Phys., 2001, 114, 48–53.
65. R. Feng and K. A. Peterson, J. Chem. Phys., 2017, 147, 084108.
66. E. D. Glendening, C. R. Landis and F. Weinhold, J. Comput. Chem., 2019, 40, 2234–2241.
67. E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, P. Karafiloglou, C. R. Landis and F. Weinhold, Natural Bond Order 7.0, Theoretical Chemistry Institute, University of Wisconsin, Madison, WI, 2021.
68. M. Kallay, P. R. Nagy, D. Mester, Z. Rolik, G. Samu, J. Csontos, J. Csoka, P. B. Szabo, L. Gyevi-Nagy, B. Hegely, I. Ladjanszki, L. Szegedy, B. Ladoczki, K. Petrov, M. Farkas, P. D. Mezei and A. Ganyecz, J. Chem. Phys., 2020, 152, 074107.
69. M. Kállay, P. R. Nagy, D. Mester, L. Gyevi-Nagy, J. Csóka, P. B. Szabó, Z. Rolik, G. Samu, J. Csontos, B. Hégely, Á. Ganyecz, I. Ladjánszki, L. Szegedy, B. Ladóczki, K. Petrov, M. Farkas, P. D. Mezei and R. A. Horváth, MRCC, A Quantum Chemical Program Suite, Budapest University of Technology and Economics, Budapest, https://www.mrcc.hu, (Accessed December 26, 2024).
70. G. Knizia, J. Chem. Theory Comput., 2013, 9, 4834–4843.
71. A. Kramida, Y. Ralchenko and J. Reader, NIST Atomic Spectra Database (Version 5.3), National Institute of Standards and Technology, Gaithersburg, MD, 2015, https://physics.nist.gov/asd.
72. D. R. Lide, CRC Handbook of Chemistry and Physics, CRC Press, New York, 93rd edn, 2012.
73. R. S. Mulliken, Rev. Mod. Phys., 1932, 4, 1–86.
74. E. Wigner and E. E. Witmer, Z. Phys., 1928, 51, 859–886.
75. D. D. Wagman, W. H. Evans, V. B. Parker, R. H. Schumm, I. Halow, S. M. Bailey, K. L. Churney and R. L. Nuttall, J. Phys. Chem. Ref. Data, 1982, 11(Suppl. 2) DOI:10.18434/m32124.
76. A. Karton and J. M. Martin, J. Phys. Chem. A, 2007, 111, 5936–5944.
77. L. A. Curtiss, K. Raghavachari, P. C. Redfern and J. A. Pople, J. Chem. Phys., 1997, 106, 1063–1079.

---

Footnote

† Electronic supplementary information (ESI) available: Table S1 lists the molecular orbital compositions of ThB⁻; Fig. S1–S3 illustrate the contours of the CASSCF active orbitals of ThB⁻; Fig. S4 illustrates the ATZ-MRCI+Q and ATZ-C-CCSD(T) PECs of ThB⁻; Table S2 lists the Ω states of ThB⁻; Table S3 lists the VDE of ThB⁻ and the AEA and D₀ of ThB; Table S4 lists the NBO charges and electron populations of ThB; Table S5 lists the Ω states of ThB; Fig. S5 shows the spin–orbit curves of ThB; Table S6 lists the vertical excitation energies of ThB and the VDEs of ThB⁻ at MRCI+Q. See DOI: https://doi.org/10.1039/d5cp00925a

---