Alterations in vibrational spectra of adsorbed water in MIL-101(Cr) and functionalized MIL-101(Cr) using molecular simulations

Abstract

The vibrational dynamics of adsorbed water, as reflected in its vibrational density of states (VDOS) spectra, differ significantly from those of bulk water. This study employs molecular simulations to explore these modifications in water confined within MIL-101(Cr) and its sulfonic acid-functionalized derivative, MIL-101-SO₃H(Cr). Various water models are tested, with systematic adjustments made to identify the one that best replicates the experimental infrared (IR) spectrum. The optimized model is then used to analyze the vibrational properties of adsorbed water. Normal mode analysis (NMA) decomposes the vibrational signal into the underlying normal modes of water molecules, allowing for a detailed examination of water adsorbed at specific framework sites. At low pressures, water molecules preferentially bind to high-affinity sites, such as the unsaturated Cr centers in MIL-101(Cr) and the sulfonic acid hydroxyl (–OH) groups in MIL-101-SO₃H(Cr), exhibiting distinct asymmetric stretching modes compared to bulk water. However, as water uptake increases at higher pressures, the VDOS spectra of adsorbed and bulk water begin to converge, signaling the onset of capillary condensation.

---

1. Introduction

Water adsorption and transport within mesoporous cavities is a complex phenomenon with applications across multiple disciplines. In adsorption heat pumps, it plays a crucial role in enhancing energy efficiency and sustainability.^1–3 In dehumidification, water adsorption helps maintain optimal humidity levels in various environments. This process is also fundamental to seawater desalination and atmospheric water harvesting, offering potential solutions to global water scarcity.^4–6 Moreover, water adsorption is critical for proton conduction in fuel cells, underscoring the importance of understanding its underlying dynamics.

Among the materials investigated for water adsorption, metal–organic frameworks (MOFs) have shown exceptional performance and hold great promise for various applications. Effective MOFs for water adsorption must exhibit high water uptake capacity, strong stability under humid conditions, and rapid adsorption kinetics. The hydrophilic nature of the metal centers, combined with the hydrophobicity of the organic linkers, facilitates faster water diffusion within the MOF pores. Additionally, MOFs possess highly porous structures with large surface areas, and their adsorption properties can be tuned by functionalizing the organic ligands. MIL-101(Cr) (MIL = Materials Institute Lavoisier) is a notable MOF due to its high stability in water vapor and even in liquid water, maintaining structural integrity under diverse environmental conditions. As a result, MIL-101(Cr) has emerged as a promising material for water adsorption applications, driving extensive multidisciplinary research on its adsorption behavior (see Fig. 1a).

Fig. 1 Water adsorbed in MIL-101(Cr) and MIL-101-SO₃H(Cr). (a) Molecular dynamic (MD) simulation images (obtained from VMD) for water adsorption in MIL-101(Cr). Water chains are formed from the chromium metal center to the highly electronegative fluorine atom. (b) The 1,4-benzenedicarboxylate (BDC) ligand in MIL-101(Cr) (top) and a sulfonic acid functionalized 1,4-BDC ligand in MIL-101-SO₃H(Cr) (bottom). (c) Enhanced water adsorption in MIL-101-SO₃H(Cr) forms water network in the pores by forming H-bonds with the hydrophilic sulfonic acid. (d) Comparison of the absorption spectra among bulk liquid water (black), water adsorbed in MIL-101-SO₃H(Cr) (green), and water adsorbed in MIL-101(Cr) (blue), and bulk water vapor (red). All the simulations are run at 300 K and N is the number of water molecules per unit cell of the respective MOF.

The adsorption characteristics of MIL-101(Cr) can be tailored by modifying the surface chemistry of its porous framework, for example, by incorporating hydrophilic functional groups such as sulfonic acid (–SO₃H) or amine (–NH₂) onto the 1,4-benzenedicarboxylate (BDC) ligands. Fig. 1b illustrates the structures of 1,4-BDC and its sulfonic acid-functionalized counterpart within MIL-101(Cr) and MIL-101-SO₃H(Cr), respectively. The impact of these modifications on adsorption isotherms has been previously reported by Akiyama et al.⁷ However, for practical applications, understanding the dynamic properties of adsorbed water—such as its vibrational density of states (VDOS) spectra—is crucial for elucidating the underlying adsorption mechanisms.

While previous studies have primarily focused on equilibrium adsorption properties, such as isotherms and adsorption enthalpy,^8,9 these parameters alone provide an incomplete picture of the adsorption process. In this study, we shift our focus to the vibrational characteristics of water adsorbed within the MIL-101(Cr) and MIL-101-SO₃H(Cr) frameworks. As depicted in Fig. 1a, water molecules adsorbed in MIL-101(Cr) form linear chains facilitated by hydrogen bonding between electropositive unsaturated Cr centers and electronegative F atoms. In contrast, the introduction of the hydrophilic -SO₃H group in MIL-101(Cr) enhances water adsorption by promoting the formation of an interconnected network of water molecules at lower pressures, as shown in Fig. 1c. The differences in the VDOS spectra, particularly in the OH stretching region 3200–3700 cm⁻¹ (as illustrated in Fig. 1d), arise from distinct water adsorption mechanisms at low concentrations, governed by the nature of water-framework interactions. In MIL-101, water molecules interact mainly with Cr^{3 +} sites and exhibit two primary vibrational features corresponding to metal-coordinated and weakly hydrogen-bonded water. In contrast, MIL-101–SO₃H exhibits four distinct OH stretching peaks, reflecting the presence of multiple strong hydrogen-bonding motifs enabled by the –SO₃H group, including water acting as both a donor and acceptor with sulfonic acid moieties, as well as water–water bridges and small clusters. These varying environments alter O–H bond strengths and produce well-resolved vibrational signatures.

The structure of this paper is as follows: Section 2 details the molecular simulation methodology, including modifications made to the water model and the benchmarking of these adjustments (Section 2.1). The molecular simulations of water adsorbed in MIL-101(Cr) and MIL-101-SO₃H(Cr) are described in Section 2.2. In Section 3, we present the analysis and decomposition of the resulting VDOS spectra. Finally, Section 4 summarizes our findings.

2. Molecular simulations

Ab initio molecular dynamics (AIMD) is widely used to accurately determine the dynamic properties of water. However, simulating adsorbed water within AIMD frameworks—where additional external interactions with adsorbent molecules must be considered—is computationally prohibitive. Consequently, this study adopts a classical molecular dynamics (MD) approach as a more practical alternative.

Classical MD simulations require a molecular model for water, but fixed-charge models struggle to accurately predict dynamic properties such as the IR spectra of water. To address this limitation, we evaluated several well-known flexible water models for simulating adsorbed water, each exhibiting notable shortcomings. For instance, the FTIR spectra of the SPC/fw model deviates from experimental data, with distinct peaks for symmetric and asymmetric stretches revealing the limitations of the harmonic bond potential. To overcome these issues, we investigated the flexible TIP4P/2005f water model,¹⁰ which employs a Morse potential to describe bonded interactions within the water molecule. The Morse potential offers a more realistic representation of bond behavior, inherently accounting for the fact that bonds tend to stretch more readily than they contract relative to their equilibrium bond length, as shown in Fig. S2a [in the ESI† ¹¹]. However, using the Morse potential alone led to an underestimation of bond strength, causing premature bond breaking during interactions with hydrophilic surfaces. To mitigate this issue, we incorporated angular interactions between hydrogen atoms, following the approach of Praprotnik et al.,¹² ensuring molecular stability in hydrophilic environments. Despite this improvement, the absorption spectra generated by the modified model still deviated from experimental results. To further refine the model, we integrated parameters from the Kuchitsu-Morino correction¹³ alongside the Morse bond potential. However, using zero Lennard–Jones (L–J) parameters for hydrogen, as suggested in prior studies, resulted in numerical instabilities, particularly due to overlaps between hydrogen atoms and adsorbent molecules. To resolve this, we developed a hybrid water model that combines characteristics of the TIP3P-CHARMM and SPC/E models with Morse bond interactions and Kuchitsu–Morino corrections. This approach yields a robust and accurate water model for simulating adsorbed water, effectively balancing physical fidelity and numerical stability.

2.1. Water model

Our flexible water model employs a Lennard–Jones interatomic potential with arithmetic mixing rules. Electrostatic interactions are incorporated using partial charges assigned to each water molecule, where oxygen carries a charge of (− 0.82|e|) and each hydrogen atom carries (+0.41|e|). Long-range Coulombic interactions are computed using periodic boundary conditions, with the standard Ewald summation method applied at a precision of 10⁻⁶ to ensure accurate electrostatic calculations. The intramolecular [bonded (O–H) and non-bonded (H–O–H)] potential follows the formulation by Toukan and Rehman,¹⁴ as described in eqn (1).where, Δr_1k and Δr_2k represent the extensions in O–H bond lengths, while Δr_3k denotes the stretch in the H–H distance of the kth water molecule. The parameter D_e corresponds to the depth of the Morse potential, and α represents the stiffness parameter. The intramolecular potential is further defined by the force constants k_θ, k_rθ, and k_rr, which govern angular and bond interactions within the molecule. To simulate this water model using the large-scale atomic/molecular massively parallel simulator (LAMMPS),¹⁵ we have described the anharmonic angle potential in the ESI,† ¹¹ submitted along with this paper. The parameters used in this model are listed in Table 1.

Table 1 Parameters used in the water model of this work

Parameter	Value
r 0	1.0	Å
θ 0	109.47°	—
D e	95.94	kcal mol^−1
α	2.57	Å^−1
k θ	244.09	kcal mol^−1 Å^−2
k rθ	−184.11	kcal mol^−1 Å^−2
k rr	126.58	kcal mol^−1 Å^−2
ε 0	0.1554	kcal mol^−1
σ 0	3.1660	Å
ε H	0.0046	kcal mol^−1
σ H	0.4000	Å
q O	−0.8200	e
q H	0.4100	e

---

The proposed model is benchmarked against experimental data and existing water models by comparing classical MD results for density variations (Fig. S2b, ESI†) and IR spectra (Fig. S2d, ESI†), demonstrating its improved accuracy and reliability. The details of the molecular simulations used for this benchmarking are presented in the following sections.

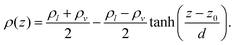2.1.1. Density variation. The proposed water model was evaluated by simulating the liquid–vapor coexistence equilibrium densities using the simulation methods detailed by Quoika and Zacharias et al.¹⁶ A system comprising 512 water molecules was initialized in a cuboid simulation box with dimensions 25 × 25 × 20 Å, after which the z-dimension was rapidly expanded to 100 Å to create a liquid–vapor interface (as shown in Fig. S1a, ESI†). The system was equilibrated for 1.25 ns in the canonical ensemble (NVT), with temperature control achieved using a Nosé–Hoover thermostat.^17,18 The velocity Verlet integration algorithm was employed with a timestep of 0.25 fs. A subsequent production run was performed for an additional 15 ps. The equilibrium densities were determined as follows: the vapor phase density was computed by averaging the density in the vapor region, ensuring measurements were taken at least 10 Å away from the boundaries of the central liquid region. The liquid phase density was obtained by fitting the density distribution across the liquid–vapor interface using eqn (2). The averaged production run density distributions for temperatures ranging from 400 K to 650 K are plotted in Fig. S1b (ESI†).

We then estimated the critical parameters by fitting the coexistence densities using the eqn (3) and (4)

where, A and Δρ₀ are system-specific fitting parameters, and the three-dimensional Ising model critical exponent β is 0.326.¹⁹ For the 512-molecule system, state points were examined from T = 400 K to T = 650 K to ensure reliable coexistence density calculations. At lower temperatures, the number of molecules in the vapor phase is too low for an accurate density estimation.

The water model presented in this work shows good agreement with experimental data from the steam tables provided by the National Institute of Standards and Technology (NIST),²⁰ as illustrated in Fig. S2b (ESI†). The critical point obtained for this model is ρ_crit ≈ 293 kg m⁻³ and T_crit ≈ 631 K, compared to the experimental values of ρ_crit ≈ 322 kg m⁻³ and T_crit ≈ 647 K, respectively.

2.1.2. Vibrational density of states (VDOS) spectra. Liquid water at 300 K was simulated using 525 water molecules in a 25 × 25 × 25 Å box (equivalent to ρ_l = 998 kg m⁻³), while water vapor at 300 K was simulated using 100 water molecules in a 470 × 470 × 470 Å box (equivalent to ρ_v = 0.0028 kg m⁻³).

All other simulation parameters remained consistent with those described in the previous section. The equilibration run lasted 2 ns, followed by a 15 ps production run with a 0.25 fs timestep. Trajectory data were recorded every 4 timesteps, effectively yielding a timestep of 1 fs and generating 15 000 data points.

The intensity of the VDOS spectrum for these water molecules is proportional to the fast Fourier transform (FFT) of the velocity autocorrelation function, as described in eqn (5).²¹

where, the VACF [C_vv(t)] for N number of total atoms is described in eqn (6)

Therefore, in Cartesian co-ordinates,

where, T(→∞) is the total time of the production run and dt is the each recorded timestep. The code for this analysis is written in MATLAB and is available upon request.

The vibrational density of states (VDOS) spectra obtained from the simulations of various water models were compared to experimental infrared spectra^22,23 in Fig. S2d (ESI†). The SPC/Fw model,²⁴ referred to as harmonic in Fig. S2d (ESI†), employs harmonic O–H bonded interactions, resulting in three distinct peaks corresponding to bend-stretch, symmetric stretch, and asymmetric stretch modes. However, these distinct peaks are inconsistent with experimental data. The model proposed by Praprotnik et al.,¹² labeled morse-km in Fig. S2d (ESI†), extends the SPC/E water model by incorporating Morse potentials and Kuchitsu-Morino corrections for O–H bond interactions. While this model improves upon the harmonic approximation, it overestimates the bending frequency of the water molecule. The TIP4P/2005f model,¹⁰ labeled morse in Fig. S2d (ESI†), is a four-point charge model that employs Morse potentials for O–H bonds and a harmonic potential for H–O–H angular interactions. This model predicts vibrational modes with reasonable accuracy. However, its assumption of the hydrogen atom as a point charge introduces numerical instabilities when simulating interactions with other electronegative species. This simplification causes the hydrogen atom to overlap with electronegative atoms, leading to unphysically large interaction energies. Finally, the VDOS spectra of the water model proposed in this work were compared with experimental IR spectra for both liquid and vapor phases at 300 K. The vibrational frequencies predicted by the simulation show good agreement with the experimental data, demonstrating the model's accuracy in capturing the fundamental vibrational modes of water. A detailed comparison of frequency values is presented in Table 2.

Table 2 Comparison of the VDOS frequencies obtained from simulations in this work and the experimental IR frequencies

Stretching Mode	Liquid	Vapor
	Current (cm^−1)	Experimental (cm^−1)	Current (cm^−1)	Experimental (cm^−1)
ν 1 (symmetric stretch)	3262	3242	3615	3610
ν 2 (bend stretch)	1674	1641	1380	1490
ν 3 (asymmetric stretch)	3416	3398	3775	3730

---

2.2. Adsorbed water

2.2.1. Structures of MIL-101(Cr) and MIL-101-SO₃H(Cr). The crystallographic information file (.cif) for the MIL-101(Cr) structure was obtained from the Cambridge Crystallographic Data Centre (CCDC) repository, as reported by Férey et al.²⁵ Charge equilibration was performed using the Wilmer and Snurr method,²⁶ implemented within the RASPA simulation framework.²⁷

To generate the crystallographic information for MIL-101-SO₃H(Cr), one hydrogen atom in each 1,4-benzene-dicarboxylate (1,4-BDC) ligand was substituted with a –SO₃H functional group. Using the Forcite module in Material Studio and the oxidation states of the base groups, we optimized the geometry employing the generalized gradient approximation by Perdew–Burke–Ernzerhof (GGA-PBE) functional. The optimized structure was subsequently imported into RASPA for charge equilibration.

The X-ray diffraction data obtained from both simulations and experiments are provided in the ESI,† for comparison (see Fig. S3).

2.2.2. Simulation dynamics. The resulting P1 symmetry.cif files from the charge equilibration were converted into LAMMPS data (.lmpdata) format using the lammps_interface tool developed by Boyd et al.,²⁸ employing the Universal Force Field (UFF). The generated.cif files are available as ESI.† Adsorbed water simulations were performed using the LAMMPS data file for the frameworks and the water model presented in this study. Simulations were conducted in the canonical ensemble (NVT), with temperature regulation achieved via a Nosé–Hoover thermostat.^17,18 All simulations were performed at T = 300 K using a single unit cell of MIL-101(Cr). Intermolecular interactions were modeled using Lennard-Jones potentials with arithmetic mixing rules. To reduce computational costs, the framework structure was treated as rigid throughout the simulations. Water molecules were introduced into the simulation region in batches of 50, with energy minimization performed after each insertion. Following the insertions, the system was equilibrated for 1.5 ns with a timestep of 0.25 fs. A subsequent production run of 15 ps was carried out with the same timestep, during which water molecule trajectories were recorded every 1 fs. Additional simulation results that elucidate the adsorption behavior and structural characteristics of confined water are provided in the ESI.† ¹¹ Specifically, Fig. S4 (ESI†) presents the radial distribution functions of water molecules relative to dominant adsorption sites within the framework, while Fig. S5 (ESI†) reports the interaction energies between water molecules and these adsorption sites. The data indicate that at low pressures, the SO₃H functional group does not constitute a favorable adsorption site on its own. However, due to its electron-withdrawing nature, it induces a higher partial positive charge on the adjacent unsaturated Cr centers, thereby enhancing their affinity for water molecules. Finally, Fig. S6 (ESI†) illustrates the average number of hydrogen bonds per water molecule as a function of loading, revealing a monotonic increase that asymptotically approaches the value characteristic of bulk liquid water.

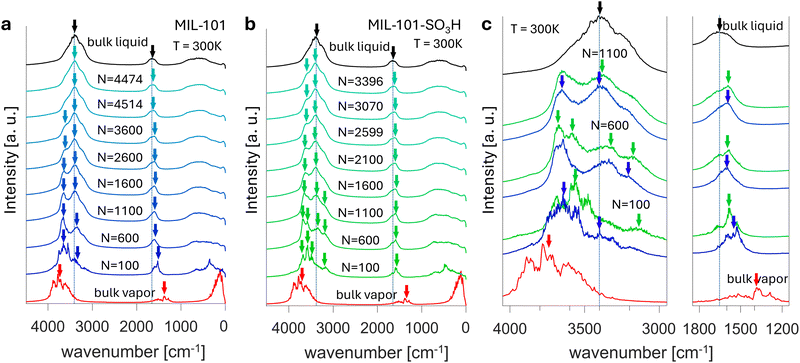
The VDOS spectra were then computed using the methodology described in the preceding section, providing insights into the vibrational characteristics of water adsorbed within the MIL-101(Cr) and MIL-101-SO₃H(Cr) frameworks, as depicted in Fig. 2a and b, respectively. A comparative analysis of the VDOS spectra for water adsorbed in both frameworks is presented in Fig. 2c. At low water concentrations (N = 100 and N = 600), the spectra exhibit notable differences, reflecting the distinct adsorption mechanisms during the initial stages of water uptake.

Fig. 2 VDOS spectra of adsorbed water with increasing amount of water. At low water concentrations, where water molecules predominantly adsorb onto the specific adsorption sites of (a) MIL-101(Cr) and (b) MIL-101-SO₃H(Cr), the absorption spectra deviate significantly from those of bulk liquid and vapor phases. However, as saturation is approached, a majority of the water molecules exhibit liquid-like behavior, therefore the absorption spectra converge to resemble those characteristic of liquid water. (c) At low concentrations of adsorbed water, the VDOS spectra for water in MIL-101(Cr) and MIL-101-SO₃H(Cr) deviate significantly from one another and from bulk water. These differences highlight distinct adsorption mechanisms at low water concentrations, influenced by the specific interactions within each framework.

Fig. 2c highlights two key wavenumber regions: 1200–1800 cm⁻¹ (bending mode) and 3000–4000 cm⁻¹ (symmetric and asymmetric stretching modes). At a loading of 600 water molecules per unit cell, the VDOS spectrum for water adsorbed in MIL-101(Cr) features three distinct peaks at 3229 cm⁻¹, 3342 cm⁻¹, and 3669 cm⁻¹. In contrast, water adsorbed in MIL-101-SO₃H(Cr) exhibits a four-peak response, with peaks at 3202 cm⁻¹, 3342 cm⁻¹, 3582 cm⁻¹, and 3675 cm⁻¹. For comparison, bulk water is characterized by a single broad peak encompassing two components corresponding to the symmetric (3262 cm⁻¹) and asymmetric (3416 cm⁻¹) stretches.

To further elucidate the differences between adsorbed and bulk water, the subsequent section provides a detailed spectral decomposition, identifying the specific vibrational modes contributing to the observed behavior.

3. Analysis and discussion

To investigate the shifts in vibrational frequencies of adsorbed water and understand the origins of the three peaks observed for MIL-101(Cr) and the four peaks for MIL-101-SO₃H(Cr) in the 3000–4000 cm⁻¹ region, the spectra were decomposed into their constituent normal modes (Fig. 3) and analyzed based on specific adsorption sites (Fig. 4). This decomposition provides deeper insights into the contributions of different vibrational modes and adsorption environments to the observed spectral features.

Fig. 3 Decomposition of VDOS spectra in normal modes. The vibrational density of states (VDOS) spectra (navy blue dashed line) is decomposed into the normal modes: liberation due to rotational motion (green), bend stretch (pink) and symmetric (dark blue) and asymmetric (light blue) stretches responsible for the different peaks in the spectra. (a) Liquid water at 300 K and ρ = 998 kg m⁻³, (b) water adsorbed in MIL-101(Cr) at 300 K and N = 600 molecules per unit cell, and (c) water adsorbed in MIL-101-SO₃H(Cr) at 300 K and N = 600 molecules per unit cell.

Fig. 4 Decomposition of VDOS spectra based on the adsorption site of the molecules. Water adsorbed in (a) MIL-101(Cr) pores, have two major adsorption sites: the unsaturated chromium (Cr) metal center (shades of Green) and the highly electronegative fluorine (F) atom (shades of purple). Whereas, in (b) MIL-101-SO₃H(Cr), the major adsorption sites include the Hydrogen (H) of –SO₃H group (shades of Grey) and the oxygen atoms (O7 and O8) in the –SO₃H group (shades of red). The square bracket in the legend indicates the molecule focused during the investigation.

3.1. Decomposition of spectra in the normal modes of vibration

In a normal mode analysis, we assume that all vibrational motions are harmonic, meaning each normal mode behaves as an independent harmonic oscillator. The motion of this oscillator is governed by the differential equation given in eqn (8)

The solution to this differential equation is

−kx = 4π²ν²x. (9)

Therefore for a system of N atoms, corresponding generalized equation for Cartesian coordinates can be written as eqn (10)

HX = 4π²ν²X (10)

where, H is a 3N × 3N Hessian matrix, and X is a 3N × 1 matrix representing atomic positions. From molecular dynamics simulations, we obtain the trajectory data of water molecules, which provides the positional matrix in eqn (10). To approximate the Hessian matrix, we use the relation described in eqn (11), following the approach of²⁹

〈ΔR_i·ΔR_j〉 = 3k_BTH⁻¹ (11)

For pure liquid water at 300 K, the decomposed vibrational modes are presented in Fig. 3a. The dotted line represents the total vibrational spectrum, while individual contributions are as follows: the green line corresponds to libration, which arises from rotational motions and hydrogen bonding interactions; the pink line represents the bending vibrational mode of water; the dark blue line indicates the symmetric stretching mode; and the light blue line reflects the asymmetric stretching mode.

For water adsorbed in MIL-101(Cr) (Fig. 3b), both the symmetric and asymmetric stretching modes exhibit two distinct peaks, suggesting the presence of at least two distinct categories of adsorbed water molecules. These arise from interactions with different adsorption sites within the framework. The additional interactions with framework atoms contribute to the observed vibrational band shifts.

Similarly, for water adsorbed in MIL-101-SO₃H(Cr) (Fig. 3c), hydrogen bonding with the –SO₃H group and interactions with unsaturated chromium sites result in four distinct peaks in the spectra. This indicates that water molecules adsorbed at different sites experience variations in bond stretching.

3.2. Decomposition of spectra according to the adsorption site

To analyze the impact of specific adsorption sites on the vibrational spectra, the spectra of water molecules adsorbed at distinct locations were separated. In Fig. 4, “Water adsorbed near Cr (1st layer)” refers to molecules identified over a 15 ps trajectory, where the oxygen atoms of water molecules remain consistently within 3 Å of electropositive unsaturated Cr sites. Similarly, for water adsorbed near electronegative sites, such as fluorine, molecules are classified as adsorbed when the hydrogen atoms of water remain within 2.5 Å of fluorine atoms. Furthermore, the second and third adsorption layers are defined based on hydrogen-bonding interactions with the preceding layer. Specifically, water molecules are assigned to these layers if their hydrogen bonds with molecules in the previous layer remain consistently below 2.5 Å. This hierarchical classification provides deeper insights into the structural organization and vibrational dynamics of water molecules across different adsorption layers.

All water molecules that do not fall into any of these defined categories—such as those near specific adsorption sites or within the second and third hydrogen-bonded layers—are classified as loosely bound. This category includes molecules with weaker or less consistent interactions with the framework or other water molecules, representing a distinct adsorption environment.

Fig. 4a presents the decomposed water adsorption spectra in MIL-101(Cr) within the 3000–4000 cm⁻¹ range. At low water concentrations (N = 100), the spectra are primarily influenced by water molecules adsorbed at unsaturated chromium sites. However, at higher water concentrations (N = 1100), the spectra are dominated by contributions from loosely bound water molecules. At an intermediate concentration (N = 600), the peaks at 3204 cm⁻¹ and 3647 cm⁻¹ are attributed to interactions with unsaturated Cr sites, whereas the peaks at 3364 cm⁻¹ and 3691 cm⁻¹ arise from loosely bound water molecules. These findings highlight the evolution of adsorption mechanisms as water loading increases.

Similarly, the decomposed spectra for water adsorbed in MIL-101-SO₃H(Cr) are presented in Fig. 4b. The trends in water adsorption spectra with increasing concentration are similar to those observed for MIL-101(Cr). However, at an intermediate concentration (N = 600), the spectra for water adsorbed near unsaturated Cr sites exhibit notable differences, with two distinct peaks at 3178 cm⁻¹ and 3585 cm⁻¹ for the first adsorption layer. Additionally, adsorption in the second and third layers further enhances the peak at 3669 cm⁻¹. We hypothesize that this additional peak originates from stronger hydrogen bonding interactions facilitated by the SO₃H functional group, as well as increased steric hindrance introduced by functionalization.

4. Conclusions

This study employs molecular simulations to investigate the vibrational density of states (VDOS) spectra of water adsorbed in metal–organic frameworks (MOFs), specifically MIL-101(Cr) and its sulfonic acid-functionalized counterpart, MIL-101-SO₃H(Cr). The research highlights the critical role of water adsorption and transport in mesoporous materials such as MOFs, which are essential for enhancing performance and energy efficiency in applications including dehumidification, desalination, water harvesting, and proton conduction in fuel cells.

To explore the vibrational properties of adsorbed water, this study utilizes normal mode analysis (NMA) and examines water molecules localized at specific adsorption sites within the MOF framework. At low pressures, water preferentially adsorbs at high-affinity sites, such as the unsaturated Cr centers in MIL-101(Cr) and the hydroxyl (–OH) group of the sulfonic acid moiety in MIL-101-SO₃H(Cr). This selective adsorption results in distinct asymmetric stretching modes that differ from those of bulk water. At higher pressures, as water uptake increases, the VDOS spectra of adsorbed water gradually converge with those of bulk water, aligning with the process of capillary condensation.

The molecular simulations employ a modified water model that integrates the TIP3P-CHARMM and SPC/E models, augmented with Morse bond interactions and Kuchitsu-Morino corrections, to better replicate experimental infrared (IR) spectra. The VDOS spectra are further decomposed to distinguish the contributions of different vibrational modes within various adsorption environments. This decomposition reveals distinct peaks associated with symmetric and asymmetric stretching modes, influenced by the specific adsorption sites.

Key findings indicate that functionalizing MOFs with sulfonic acid groups significantly enhances water adsorption by promoting the formation of interconnected hydrogen-bonded water networks. Furthermore, the vibrational spectra of adsorbed water vary depending on their adsorption environment: water molecules near unsaturated Cr centers and electronegative fluorine sites in MIL-101(Cr) exhibit different vibrational signatures compared to those interacting with the hydrogen or oxygen atoms of the SO₃H group in MIL-101-SO₃H(Cr).

Author contributions

GA – concept, simulations, writing, reviewing and editing. HJ – simulations, writing. JJD – concept, review and editing. HD – concept, funding, review and editing.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by JST, CREST Grant Number JPMJCR17I3, Japan.

References

1. A. Entezari, O. C. Esan, X. Yan, R. Wang and L. An, Adv. Mater., 2023, 35, 2210957.
2. B. Han and A. Chakraborty, Energy Convers. Manage., 2020, 213, 112825.
3. J. Togawa, A. Kurokawa and K. Nagano, Appl. Therm. Eng., 2020, 173, 115241.
4. R. Ou, H. Zhang, V. X. Truong, L. Zhang, H. M. Hegab, L. Han, J. Hou, X. Zhang, A. Deletic and L. Jiang, et al. , Nat. Sustainability, 2020, 3, 1052–1058.
5. N. Hanikel, M. S. Prévot and O. M. Yaghi, Nat. Nanotechnol., 2020, 15, 348–355.
6. Z. Zheng, H. L. Nguyen, N. Hanikel, K. K.-Y. Li, Z. Zhou, T. Ma and O. M. Yaghi, Nat. Protoc., 2023, 18, 136–156.
7. G. Akiyama, R. Matsuda, H. Sato, A. Hori, M. Takata and S. Kitagawa, Microporous Mesoporous Mater., 2012, 157, 89–93.
8. G. Auti, Y. Kametani, H. Kimura, S. Paul, W.-L. Hsu, S. Kusaka, R. Matsuda, T. Uemura, S. Chiashi and H. Daiguji, J. Mater. Chem. A, 2023, 11, 20043–20054.
9. G. Auti, S. Paul, W.-L. Hsu, S. Chiashi, S. Maruyama and H. Daiguji, Phys. Rev. Res., 2024, 6, 023333.
10. M. A. González and J. L. Abascal, J. Chem. Phys., 2011, 135, 224516.
11. See ESI† at [URL will be inserted by publisher] for further information.
12. M. Praprotnik, D. Janežič and J. Mavri, J. Phys. Chem. A, 2004, 108, 11056–11062.
13. K. Kuchitsu and Y. Morino, Spectrochim. Acta, 1966, 22, 33–46.
14. K. Toukan and A. Rahman, Phys. Rev. B: Solid State, 1985, 31, 2643.
15. A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in’tVeld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171.
16. P. K. Quoika and M. Zacharias, J. Phys. Chem. B, 2024, 128, 2457–2468.
17. S. Nosé, J. Chem. Phys., 1984, 81, 511–519.
18. W. G. Hoover, Phys. Rev. A, 1985, 31, 1695.
19. R. Guida and J. Zinn-Justin, J. Phys. A: Math. Gen., 1998, 31, 8103.
20. A. Harvey, Steam Tables, Encyclopedia of Physical Science and Technology, 2001.
21. A. R. Leach, Molecular Modelling: Principles and Applications, Longman, Singapore, 1996.
22. NIST Chemistry WebBook, SRD 69, https://webbook.nist.gov/cgi/cbook.cgi?ID=C7732185Type=IR-SPECIndex=1, Accessed on 1st December, 2024.
23. NIST Chemistry WebBook, SRD 69, https://webbook.nist.gov/cgi/inchi?ID=C7732185Type=IR-SPECIndex=0, Accessed on 1st December, 2024.
24. Y. Wu, H. L. Tepper and G. A. Voth, J. Chem. Phys., 2006, 124, 024503.
25. G. Férey, C. Mellot-Draznieks, C. Serre, F. Millange, J. Dutour, S. Surblé and I. Margiolaki, Science, 2005, 309, 2040–2042.
26. C. E. Wilmer, K. C. Kim and R. Q. Snurr, J. Phys. Chem. Lett., 2012, 3, 2506–2511.
27. D. Dubbeldam, S. Calero, D. E. Ellis and R. Q. Snurr, Mol. Simul., 2016, 42, 81–101.
28. P. G. Boyd, S. M. Moosavi, M. Witman and B. Smit, J. Phys. Chem. Lett., 2017, 8, 357–363.
29. C. Atilgan, O. B. Okan and A. R. Atilgan, Annu. Rev. Biophys., 2012, 41, 205–225.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp00878f

---