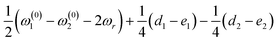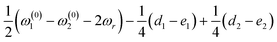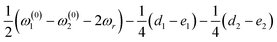Open Access Article
Open Access ArticleModeling dissipative magnetization exchange dynamics in magnetic resonance†
Neelam
Sehrawat
 a,
Manoj Kumar
Pandey
a,
Manoj Kumar
Pandey
 *b and
Ramesh
Ramachandran
*b and
Ramesh
Ramachandran
 *c
*c
aIndian Institute of Technology (IIT) Ropar, Rupnagar, Punjab 140001, India
bIndian Institute of Technology (IIT) Ropar, Rupnagar, Punjab 140001, India. E-mail: mkpandey@iitrpr.ac.in
cDepartment of Chemical Sciences, Indian Institute of Science Education and Research (IISER) Mohali, Sector 81, Manauli, P.O. Box-140306, Mohali, Punjab, India. E-mail: rramesh@iisermohali.ac.in
First published on 20th May 2025
Abstract
Quantifying the role of the environment in a quantum system of interest has remained an active pursuit for studying the effects of dissipation in a wide-range of problems in chemical physics and spectroscopy. From an operational perspective, the complexities encountered in the description of open systems have ushered in the development of models without explicit consideration of the complete system. To this end, phenomenological descriptions that involve the inclusion of exponential damping terms have remained the method of choice. While such methods have gained prominence in providing a qualitative explanation for observations in spectroscopy, they are of limited utility in quantitative studies that involve the estimation of molecular constraints. As an alternative, the present report explores the possibility of understanding the nuances of dissipation found in open systems through analytic methods. Specifically, the magnetization exchange between a pair of spins (say I1 and I2) is examined under periodic modulation in the presence of a surrounding bath of other spins. Employing the concept of effective Hamiltonians and utilizing the block-diagonal structure of the derived effective Hamiltonians, analytic expressions are derived for describing the effects of dissipation (due to neighboring spins) on the system of interest without increasing the dimension of the problem.
I. Introduction
The versatility of solid-state nuclear magnetic resonance (ssNMR) spectroscopy as a reliable tool for structure determination (at the atomic level) relies on its ability to measure and quantify the anisotropic spin interactions present in the solid state. While rapid molecular motion in the liquid state provides (only) an average estimate of the molecular constraints (such as intra/inter-atomic distances, chemical shifts, etc.), the restricted mobility in the solid state should, at least in principle, facilitate the determination of conformations through measurement of orientation-dependent anisotropic spin interactions (such as dipolar-coupling interactions, chemical shift anisotropy (CSA), etc.). A detailed account on the progress made in the field of structure determination using solid-state NMR is well-summarized in recent reports in the literature.1–8 From a practical viewpoint, the restricted mobility in the solid state only broadens the spectrum, often suppressing the information content present in the anisotropic interactions. Although experiments that involve physical rotation of a sample (e.g., magic angle spinning (MAS)9,10) have drastically improved the resolution of the NMR spectrum in solids,1,2,5,11,12 the improvements in resolution have always been achieved at the expense of structural information present in the anisotropic interactions. To this end, sophisticated experiments that compensate for the averaging effects of MAS (both in the presence and absence of oscillating magnetic fields) have emerged in the past.1,2 It is important to realize that in MAS experiments that involve structure determination, the anisotropic spin interactions (such as dipolar interactions and CSA interactions) are only partially introduced without compromising the spectral resolution. Here in this report, we focus on experiments that involve reintroduction of dipolar interactions in MAS experiments (commonly referred to as dipolar recoupling experiments). From an experimental perspective, the introduction of the dipolar interactions in MAS experiments is highly dependent on the information desired from such studies. For example, to establish the local connectivity in spectral assignment studies, the dipolar interactions are introduced in a non-selective manner, while in the measurement of intra/inter-atomic distance constraints, the dipolar interactions are introduced in a selective fashion to minimize multi-spin effects. To this end, suites of dipolar recoupling experiments have emerged in the field and are well-documented in the literature.1,13–18 Here in this report, we focus on the Rotational Resonance (R2) experiment, a selective dipolar recoupling experiment employed for measuring homonuclear intra-atomic distances (such as 13C–13C).From a historical perspective, the phenomenon of rotational resonance (R2) was first observed in 1963 by Andrew and coworkers.19,20 In the R2 experiment, the dipolar interactions between a pair of spins is reintroduced when the sample rotation frequency (say, ωr) is adjusted to the chemical shift separations between the two spins (say, |ω(0)1 − ω(0)2| = Nωr, N = 1 or 2, where ω(0)1 and ω(0)2 denote the chemical shift of the spins 1 and 2, respectively). Consequently, the spectral resolution afforded by sample rotation is compromised (under such special conditions), leading to a broadened spectrum. Due to the presence of intermolecular dipolar interactions, the line-broadening observed under R2 conditions remained qualitative and less informative. To this end, Griffin and coworkers21–23 employed selectively labeled samples to monitor the magnetization exchange (minimize intermolecular effects) between a pair of spins. From a theoretical viewpoint, the initial description of the spin dynamics between the two spins under R2 conditions was explained through a pseudo-two-spin model comprising virtual spin states.24 In an alternate approach, employing a phenomenological damping/dissipation term25–28 (to account for multi-spin effects) and the internuclear distance as free-fit parameters, the magnetization exchange between a pair of spins was employed to estimate the distance between them in R2 experiments for selectively labeled samples.
While such models have been successful in providing a decent estimate of 13C–13C distances in the strong-coupling limit (short-range distances, 2.5–3.5 Å), the spin dynamics in the intermediate and weak-coupling limit (3.5–7.0 Å) were fraught with difficulty. To address this issue, models that employ multiple dissipative terms29 were also proposed for fitting the magnetization exchange trajectories observed in R2 experiments. As an alternative, to minimize the effects of other spin interactions, modifications in the form of constant-time R2 (commonly referred to as rotational resonance width (RRW)30) experiments have also been proposed to separate the dipolar contributions from the dissipation (or depolarization) observed in the weak-coupling limit. Subsequently, employing this modified approach, in combination with two-dimensional NMR spectroscopy31 and two-spin models (in the presence of phenomenological damping), the RRW experiment was employed to measure multiple distances in uniformly labeled solids.32–35 Nevertheless, estimation of the distances in the intermediate- and weak-coupling limits has always been fraught with difficulty.
To address this issue, alternate models based on the spherical tensor operator formalism employing three different damping terms36 were also explored to fit the exchange trajectories observed in RRW experiments. Nevertheless, significant deviations still persisted in the weak-coupling limit. From an operational perspective, the dissipative terms employed to fit trajectories differ depending on the model37,38 and could yield ambiguous results when the magnitude of the estimated dipolar coupling is on par with the magnitude of other spin interactions (such as chemical shift anisotropy and residual heteronuclear dipolar-coupling interactions) present in the system. In such cases, the dissipative effects introduced by the phenomenological damping terms often result in ambiguous distance measurements. This theoretical prediction was well-substantiated by an in-depth analysis of R2 experiments based on numerical methods.39 The dissipative effects observed were attributed to the residual dipolar-coupling interactions (between 13C–1H) and described numerically using model systems comprising four to five protons. Since extraction of molecular constraints involves iterative fitting of experimental data, such methods are of limited utility.
To this end, an analytic framework based on the concept of effective Hamiltonians is proposed to describe the multi-spin effects observed in R2 experiments. To present a tangible description of the spin dynamics, the depolarization effects emerging from the CSA interactions of the observed spin (say spins I1 and I2) as well as the surrounding S-spins (say, ‘N’ S-spins) is described employing effective Floquet Hamiltonians.40–44 In contrast to methods based on effective Hamiltonians defined in the rotating frame, the proposed theoretical approach presents a framework for separating the CSA contributions emerging from the observed (say, I spins) as well as the unobserved spins (say, S-spins). Accordingly, employing the block-diagonal form of the derived effective Hamiltonians, the polarization transfer from spin I1 to spin I2 in the presence of the surrounding ‘N’ S-spins is described using simple trigonometric expressions analogous to the one obtained in the description of an isolated two-spin system (I1–I2). In contrast to phenomenological models (that employ a single damping term), the damping effects due to the observed (I-spins) and the unobserved spins (say, the S-spins that are decoupled) are well-separated and rigorously verified through simulations emerging from exact numerical methods.
To improve the readability, the article is structured as follows. In Section-II, the basic theory underlying the derivation of effective Hamiltonians in the rotating frame and CSA interaction frame is discussed. Through comparison with simulations emerging from analytic expressions and numerical methods, the exactness of the effective Hamiltonians is verified. This is then followed by the extension of the theoretical method for estimating distances in real systems. Employing simple analytic expressions, the dissipative effects in multi-spin systems emerging from residual dipolar-coupling interactions (say, 13C–1H dipolar-coupling interactions) are identified and discussed through rigorous comparisons with simulations emerging from exact numerical methods. In contrast to other existing phenomenological models, the proposed analytic model presents an attractive framework for estimating both the 13C–13C and 13C–1H distances besides the signs/magnitude of the CSA tensors of the spins. This is then followed by a brief summary in the final section.
II. Theory and simulations
One of the primary motivations for quantifying the spin dynamics in R2 experiments lies in its ability to provide internuclear distance information, a typical practical scenario being the measurement of 13C–13C distances in biological solids. Being less sensitive and less abundant, the distance measurements are often carried out in uniformly 13C-labeled samples (with an appropriate dilution in natural abundance to minimize intermolecular effects). While isotopic enrichment helps in improving the sensitivity of the 13C spins, the interaction with the surrounding (abundant) 1H-spins often complicates the interpretation of the experimental data. Hence, decoupling of the 13C–1H dipolar interactions is routinely employed in experiments that involve measurement of 13C–13C distances. Nevertheless, the dissipation due to residual dipolar-coupling contributions (from 13C–1H) persists and still plays an important role. Additionally, the magnitude and sign of the CSA interactions of the 13C spins also have a prominent role in the magnetization exchange observed among spins in R2 experiments. To outline the relative contributions of the various spin interactions in the R2 experiments, we divide the discussion into two parts. In the first part of the discussion, the role of the spin interactions associated with the system of interest (active ‘I’ spins such as 13C) is discussed within an isolated two-spin model (i.e., I1–I2). In the second part of the discussion, the role of the surroundings (i.e., abundant ‘S’ spins, say protons, 1H) is discussed employing a multi-spin model comprising ‘N’ S-spins (say, I1–I2–SN).A. Effective Hamiltonian for the isolated two-spin system
To quantify and exemplify the relevance of the chemical shift anisotropy (CSA) interactions (of the observed spins) in R2 experiments, we begin with a model system comprising two spins (say, I1 = I2 = 1/2). Accordingly, the Hamiltonian for such a system under MAS45,46 conditions is expressed as a sum in terms of the single-spin and two-spin interactions. | (1) |
In the present case, the single-spin interaction comprises the chemical shift interaction and has both an isotropic (represented by Hiso) and anisotropic (represented by HCSA) component. Due to physical rotation of the sample, only the anisotropic part of the chemical shift interaction becomes time-dependent and is summarised by the following equations:
 | (2) |
In the above equation, ω(0)i denotes the isotropic component of the chemical shift interaction (commonly referred to as chemical shift), while, ω(m)i45,47 denotes the orientation-dependent (or anisotropic) component of the chemical shift interaction (commonly referred to as chemical shift anisotropy (CSA)). The index ‘m’ denotes the component of the CSA interaction associated with a particular spin, i = 1 or 2. The notation Iiz is representative of the z-component of the spin angular momentum operator associated with the spins I1 and I2. The coupling between spins in the solid state is predominantly established through the dipolar-coupling interactions and is represented by the two-spin Hamiltonian given below:45
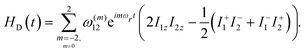 | (3) |
Analogous to the CSA interactions, the anisotropic components of the dipolar-coupling interactions are time-dependent and are represented by ω(m)12 coefficients. The detailed description of the anisotropic coefficients (refer to the ESI†) is well-documented45–47 and is omitted here to minimize repetition.
As illustrated above, physical rotation of the sample renders the anisotropic interactions (CSA and dipolar-coupling interactions) time-dependent and averages them out in MAS experiments. Since structural constraints (such as intra-atomic distances, torsion angles and chemical shift tensors (both magnitude and sign along with asymmetry parameter)) are concealed in the anisotropic interactions, experiments that involve their presence (or reintroduction) without compromising spectral resolution become inevitable in the solid state. To realize this (dual) objective, the anisotropic spin interactions of interest are reintroduced in a controlled fashion in MAS experiments without compromising the spectral resolution. From an experimental perspective, this implies the compensation of the averaging effects of MAS and is often realized through the application of oscillating radio-frequency (RF) fields.13–18 Interestingly enough, in the case of R2 experiments, the dipolar interactions are reintroduced without RF pulses through careful choice of the spinning frequency. In a typical R2 MAS experiment, the dipolar-coupling interaction between a pair of spins (i and j) is reintroduced when the sample spinning frequency is adjusted to the isotropic chemical shift difference between the spins (i.e., |ω(0)1 − ω(0)2| = Nωr, N = 1 or 2). Under such conditions, a part of the dipolar-coupling Hamiltonian (refer to eqn (3)) becomes time-independent and provides the source for estimating distances from R2 experiments. Although several theoretical formulations24–30,32–36 exist for describing the underlying spin dynamics, a compact analytic expression explicating the contributions emerging from the CSA and dipolar-coupling interactions in R2 experiments has remained elusive. This forms the main motivation behind the present study.
To explicate the interference effects resulting from the sample spinning frequency, the quantum-Liouville equation (refer to eqn (4a)) is transformed by the unitary transformation operator, U1 (U1 = einωrtI1ze−inωrtI2z).
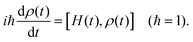 | (4a) |
Accordingly, in the interaction frame defined by U1, the above equation reduces to the following form.
 | (4b) |
The above choice of the transformation operator32,36,37 is based on the sign of the offsets employed for the spins (in the present context, the spins I1 and I2 have +ve and −ve offsets, respectively). Depending on the desired resonance conditions (i.e., |ω(0)1 − ω(0)2| = Nωr, N = 1 or 2), the choice of ‘n’ employed in U1 varies (for e.g., when N = 1, n = 0.5; N = 2, n = 1.0). Such a transformation facilitates the description of the off-resonant behaviour observed in the resonance width experiment.
Accordingly, the Hamiltonians (eqn (2) and (3)) get transformed (in the new interaction frame) and are summarized by the equations given below:
![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) iso = U1HisoU1−1 = (ω(0)1 − nωr)I1z + (ω(0)2 + nωr)I2z, iso = U1HisoU1−1 = (ω(0)1 − nωr)I1z + (ω(0)2 + nωr)I2z, | (5) |
![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) CSA(t) = U1HCSA(t)U1−1 = HCSA(t), CSA(t) = U1HCSA(t)U1−1 = HCSA(t), | (6) |
 | (7) |
Depending on the matching conditions (i.e., |ω(0)1 − ω(0)2| = 2nωr, where n = 0.5 or 1), a part of the dipolar interaction (refer to eqn (7)) becomes time-independent and plays an important role in the magnetization exchange observed between spins in R2 experiments. To highlight the significant role of the CSA interactions in R2 experiments, here in this report, we focus on the matching condition, |ω(0)1 − ω(0)2| = 2ωr. The discussion that follows is equally valid for the N = 1 resonance condition.
Consequently, the dipolar-coupling Hamiltonian (refer to eqn (7)) reduces to a form that comprises both time-dependent (![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) D,T(t)) and time-independent terms (
D,T(t)) and time-independent terms (![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) D,S), as shown below:
D,S), as shown below:
![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) D(t) = D(t) = ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) D,S + D,S + ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) D,T(t), D,T(t), | (8) |
 | (9) |
 | (10) |
From an experimental perspective, the above matching condition facilitates the implementation of the R2 experiments at lower spinning frequencies and also minimizes the interference effects emerging from other residual heteronuclear dipolar-coupling interactions (between the spins of interest (say, I1, I2) and the surrounding abundant spins, S). Since the number of structural constraints (such as intramolecular distances) available in the solid state is limited due to resolution, the accuracy of the estimated constraints plays an important role in the quality of structures derived from ssNMR measurements. To realize this objective, analytic models that provide a general description of the spin dynamics independent of the internal (magnitudes of the spin interactions (such as magnitudes of the CSAs of spins)) and external parameters (such as spinning frequency and RF fields employed) remain essential. When the chemical shift difference is smaller than the magnitude of the CSA interactions, both the N = 1 and 2 resonance conditions (|ω(0)1 − ω(0)2| = Nωr) are influenced by the CSA interactions. In such cases, an additional transformation into the CSA interaction frame is required for faster convergence of the corrections to the effective Hamiltonian. Depending on the magnitude of the CSA interactions (indicated by δCSA) relative to both the spinning frequency and the measured dipolar-coupling constant, the approximations employed (in the analytic models) to quantify the magnetization transfer among spins may be divided into three categories discussed below. A pedagogical discussion is presented below by examining the exactness of analytic models through comparisons with simulations emerging from exact numerical methods.
 | (11) |
Subsequently, the magnetization transfer from spin I1 to spin I2 is evaluated using the standard expression given below.
〈Ĩ2z(t)〉 = Tr[![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) (t)·Ĩ2z]. (t)·Ĩ2z]. | (12) |
![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) (t) = U(t)
(t) = U(t)![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) (0)U−1(t), is the density operator at time ‘t’ and ρ(0) is the initial density operator. The term U(t) represents the time propagator, i.e., U(t) = exp(−iHefft).
(0)U−1(t), is the density operator at time ‘t’ and ρ(0) is the initial density operator. The term U(t) represents the time propagator, i.e., U(t) = exp(−iHefft).
In the present context, magnetization transfer from spin ‘I1’ to spin ‘I2’ is calculated (i.e., the initial state, ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) (0) = I1z). Accordingly, the magnetization loss on spin I1 (due to transfer to spin ‘I2’) is calculated based on the equation given below:
(0) = I1z). Accordingly, the magnetization loss on spin I1 (due to transfer to spin ‘I2’) is calculated based on the equation given below:
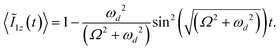 | (13) |
In a similar vein, the magnetization build up on spin I2 (that had an initial magnetization of zero) is calculated employing the equation given below:
 | (14) |
In the above equations, the term  denotes the effective offset experienced by the spins, while ωd denotes the effective dipolar-coupling constant between the spins
denotes the effective offset experienced by the spins, while ωd denotes the effective dipolar-coupling constant between the spins  .
.
While the form of the above expression (eqn (14)) resembles the one obtained by Rabi48 for describing the detuning effect in a two-level system (TLS), it is important to note that the spin dynamics of a two-spin-1/2 system (described by a vector space of dimension ((2I1 + 1) × (2I2 + 1))) is effectively reduced to a single two-level system. The term ‘ωd’ represents the frequency (containing the dipolar coupling constant) of oscillation, while the term ‘Ω’ models the detuning effect (or depolarization) observed in experiments.
 | (15) |
In contrast to the description in the previous subsection, the effective dipolar-coupling constant (ω12,e) in the present case has contributions from the time-dependent terms and is summarized by the following equation:
 | (16a) |
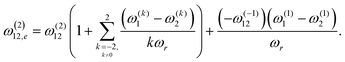 | (16b) |
As the form of the effective Hamiltonian (refer to eqn (15)) is similar to eqn (11), the exchange trajectories are calculated using identical equations given above (refer to eqn (13) and (14)). To verify the exactness of the derived effective Hamiltonians (eqn (11) and (15)), simulations emerging from the above analytic expressions were compared to those obtained from exact numerical methods based on SPINEVOLUTION software.50
As depicted in Fig. 1, when the spinning frequency exceeds the magnitude of the CSA interactions, the analytic expressions (indicated by blue dotted lines based on the first-order effective Hamiltonians given in eqn (11)) give results in good agreement (refer to panel (A1)) with those obtained from exact numerical methods. However, when the magnitudes of the CSA interactions become significant and are on par with the spinning frequency, ωr, the role of the time-dependent contributions (evaluated from the Magnus formula49 (refer to the ESI†)) becomes significant, as evident in the simulations. Nevertheless, significant deviations are still observed in the analytic simulations (refer to panels (A3) and (A4) of Fig. 1) despite the inclusion of second-order corrections (indicated by red dashed lines). Since higher-order corrections in the Magnus formula involve the evaluation of multiple time integrals, possible extensions beyond second-order are cumbersome, thereby limiting their utility in analytic methods for describing the spin dynamics. To this end, an alternate approach is proposed in the following section.
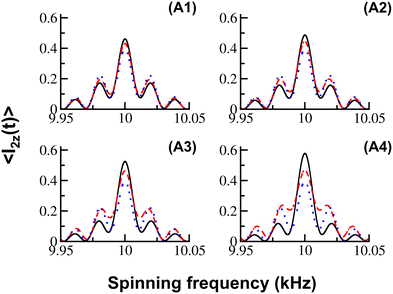 | ||
| Fig. 1 In the simulations illustrated, magnetization build-up on spin ‘I2’ (say, magnetization transfer from spin ‘I1’ to spin ‘I2’, eqn (14)) in the R2 (corresponding to the N = 2 matching condition) experiment is depicted as a function of the spinning frequency. The simulations resulting from SPINEVOLUTION (indicated in black) are compared with the analytic simulations based on effective Hamiltonians comprising (i) first-order corrections only (eqn (11), indicated by blue dotted lines), and (ii) both first- and second-order corrections (eqn (15), indicated by red broken lines). The following specific parameters were employed in the panels: (A1) (δ1 = 2 kHz, δ2 = 4 kHz), (A2) (δ1 = 2 kHz, δ2 = 6 kHz), (A3) (δ1 = 2 kHz, δ2 = 10 kHz) and (A4) (δ1 = 2 kHz, δ2 = 14 kHz). The spin interaction parameters given below were held constant in the simulations: isotropic chemical shifts (ω(0)1 = −ω(0)2 = 10 kHz), CSA parameters (η1 = 0.0, Ω(1) = (0°, 0°, 0°); η2 = 1.0, Ω(2) = (0°, 90°, 0°)); dipolar-coupling parameter (rI1I2 = 3.879 Å), and mixing time (tmix = 30 ms). The simulations correspond to a powder sample and were implemented using 6044 orientations (zcwt6044). | ||
A.3.1. Method-I: description in the standard Hilbert space. In the standard Hilbert space, the transformation into the CSA interaction frame is effected using the unitary transformation, U2 (U2 = exp(iHCSA(t))). As the isotropic interaction commutes with the transformation function, U2, the isotropic part of the chemical shift interaction remains invariant.
 | (17) |
From an experimental perspective, the form of the dipolar-coupling Hamiltonian in the CSA interaction frame remains interesting and is discussed below. In contrast to the description in the interaction frame, the static part of the dipolar-coupling Hamiltonian (say, ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) D,S; refer to eqn (9)) in the CSA interaction frame has both a (scaled) static and time-dependent terms. In a similar vein, the time-dependent parts of the dipolar-coupling interaction in the interaction frame have additional time-dependent factors due to the CSA interactions. A detailed description of the transformed dipolar-coupling Hamiltonians is summarized by the equations given below:
D,S; refer to eqn (9)) in the CSA interaction frame has both a (scaled) static and time-dependent terms. In a similar vein, the time-dependent parts of the dipolar-coupling interaction in the interaction frame have additional time-dependent factors due to the CSA interactions. A detailed description of the transformed dipolar-coupling Hamiltonians is summarized by the equations given below:
 | (18) |
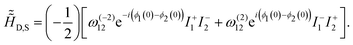 | (19) |
As illustrated above, the static part of the dipolar-coupling Hamiltonian in the CSA interaction frame has an additional (time-independent) phase factor (i.e., 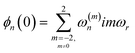 ) when compared to the one given in the interaction frame (refer to eqn (9)). In a similar vein, the time-dependent dipolar-coupling terms (in the interaction frame, refer to eqn (10)), get transformed as represented below:
) when compared to the one given in the interaction frame (refer to eqn (9)). In a similar vein, the time-dependent dipolar-coupling terms (in the interaction frame, refer to eqn (10)), get transformed as represented below:
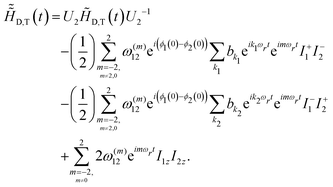 | (20) |
The coefficients ‘bk1’, ‘bk2’ are derived from Bessel functions53 and are bit complicated to evaluate. A detailed description of the procedure is described in the ESI.† As the ‘bk’ coefficients constitute a product of (eight) Bessel functions, their magnitudes are significantly lower than 1.52 Consequently, the time-dependent terms (in eqn (20)) are ignored in further discussion. Accordingly, as a first level of approximation, the effective Hamiltonian in the CSA interaction frame is represented by the equation given below:
 | (21) |
To verify the exactness of the proposed effective Hamiltonians, a comparison between simulations and numerical methods is indicated in Fig. 2. As illustrated, the analytic simulations emerging from the effective Hamiltonian (refer to eqn (21)) are in good agreement, even in cases where the magnitudes of the CSA interactions are larger in comparison to the spinning frequency employed. Nevertheless, significant deviations are still observed (refer to panels (A3) and (A4) of Fig. 2) in the simulations. To resolve this issue, an alternate approach is proposed for deriving effective Hamiltonians in the CSA interaction frame.
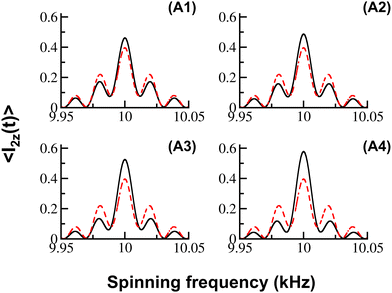 | ||
| Fig. 2 In the simulations illustrated, magnetization build-up on spin ‘I2’ (say, magnetization transfer from spin ‘I1’ to spin ‘I2’, eqn (14)) in the R2 (corresponding to the N = 2 matching condition) experiment is depicted as a function of the spinning frequency. The simulations resulting from SPINEVOLUTION (indicated in black) are compared with the analytic simulations based on effective Hamiltonians in the CSA interaction frame based on eqn (21) (indicated by red broken lines). All other parameters are identical to those provided in the caption of Fig. 1. | ||
A.3.2. Method-II: description in the extended Hilbert space. To describe the transformations in the extended Hilbert space, the time-dependent Hamiltonians in the interaction frame (eqn (5)–(7)) are transformed into a time-independent Floquet Hamiltonian.
| HF = ωrIF + Hiso,F + HCSA,F + HSD,F + HTD,F. | (22) |
In the Floquet representation,54 the time-independent terms (eqn (5) and (9)) are represented through Floquet spin operators, diagonal in the extended space, while the time-dependent terms (eqn (6) and (10)) are represented through Floquet operators, off-diagonal in the extended space. The detailed description of this procedure is well-documented40–44 and is omitted to avoid repetition.
| Hiso,F = (ω(0)1 − ωr)[I1z]0 + (ω(0)2 + ωr)[I2z]0. | (23) |
 | (24) |
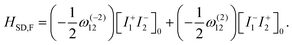 | (25) |
 | (26) |
The ‘G’ coefficients described in the Floquet Hamiltonian are derived from the coefficients of the Hamiltonian in the interaction frame and are summarized in Table 1.
To describe the transformation into the CSA interaction frame, the Hamiltonian is initially expressed as a sum of zero-order (H0) and perturbing terms (H1). The perturbing Hamiltonian, H1, is further expressed as a sum of diagonal, H1,d, and off-diagonal, H1,od, terms, as illustrated below:
| H0 = ωrIF. | (27) |
| H1,d = Hiso,F + HSD,F + HTD,F. | (28) |
| H1,od = HCSA,F. | (29) |
In contrast to the description in the standard Hilbert space, the transformation into the CSA interaction frame in the extended space is effected through the transformation function, S1 .
.
Accordingly, the Floquet Hamiltonian (eqn (22)) is transformed into an effective Floquet Hamiltonian, Heff, as represented below.
| Heff = eiλS1HFe−iλS1. | (30) |
The C-coefficients in the transformation function, S1 are chosen to compensate for the CSA interactions defined in H1,od (i.e., H1,od = HCSA,F).
| HCSA,F + i[S1, H0] = 0. |
Subsequently, employing the transformation function, S1, the various terms in H1,d are transformed, as given below:
![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) iso,F = eiλS1Hiso,Fe−iλS1 = Hiso,F. iso,F = eiλS1Hiso,Fe−iλS1 = Hiso,F. | (31) |
As illustrated above, the isotropic part of the chemical shift interaction remains invariant in the CSA interaction frame. This result is consistent with the description in the standard Hilbert space (refer to eqn (17)). In a similar vein, the static part of the dipolar-coupling interaction in the CSA interaction frame does get transformed into diagonal and off-diagonal terms. For illustrative purposes, we confine our discussion only to the diagonal part of the Hamiltonian in the extended space. Accordingly, the static part of the dipolar-coupling interaction in the CSA interaction frame is represented by the following equation:
 | (32) |
The effective dipolar-coupling coefficients in the above equation have the following definitions: ω(−2)12,e = ω(−2)12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(q) and ω(2)12,e = ω(2)12
cos(q) and ω(2)12,e = ω(2)12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(q), where
cos(q), where 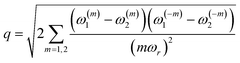 . While the form of the Hamiltonian in the CSA interaction frame is similar to the one derived in eqn (19), the coefficients associated with them are significantly different. As a first level of approximation, all other off-diagonal contributions emerging from the HSD,F and HTD,F are completely ignored in further calculations. Under the above approximation, the effective Floquet Hamiltonian in the CSA interaction frame reduces to the form given below:
. While the form of the Hamiltonian in the CSA interaction frame is similar to the one derived in eqn (19), the coefficients associated with them are significantly different. As a first level of approximation, all other off-diagonal contributions emerging from the HSD,F and HTD,F are completely ignored in further calculations. Under the above approximation, the effective Floquet Hamiltonian in the CSA interaction frame reduces to the form given below:
 | (33) |
To verify the exactness of the description in the extended Hilbert space, analytic simulations emerging from the effective Floquet Hamiltonian [eqn (33)] were compared with those obtained from SPINEVOLUTION.50 As illustrated in Fig. 3, the simulations emerging from the effective Hamiltonian based on eqn (33) are in excellent agreement with those obtained from numerical methods across all regimes. From an operational perspective, the exact role of the CSA interactions (due to ‘I’ spins) could be deduced from the form of the two-spin effective Hamiltonian given in eqn (33). As represented, the CSA interaction scales down the dipolar-coupling coefficient (ωd) and is directly responsible for the depolarization observed in systems with a large CSA interaction. In axially symmetric systems (η1 = η2 = 0) both the sign of the anisotropy parameter (δ) and the relative orientation of the CSA tensors (of the two spins I1 and I2) play an important role in the magnitude of the scaling factor (the ‘cos(q)’ term present in eqn (33)). In systems with positive anisotropic coefficients (δ1, δ2 > 0), the CSA contributions become positive when CSA tensors are orthogonal to each other, contributing to the depolarization observed (the cos(q) factor decreasing) in R2 experiments. In a similar vein, when the anisotropic coefficients are of opposite signs, the CSA contributions become additive when the CSA tensors are collinear.
 | ||
| Fig. 3 In the simulations illustrated, magnetization build-up on spin ‘I2’ (say, magnetization transfer from spin ‘I1’ to spin ‘I2’, eqn (14)) in the R2 (corresponding to the N = 2 matching condition) experiment is depicted as a function of the spinning frequency. The simulations resulting from SPINEVOLUTION (indicated in black) are compared with the analytic simulations based on effective Hamiltonians in the CSA interaction frame defined in the extended Hilbert space based on eqn (33) (indicated by red broken lines). All other parameters are identical to those provided in the caption of Fig. 1. | ||
Interestingly, the above predictions emerging from analytic theory are well-replicated in the simulations illustrated in Fig. 4. As illustrated, when the CSA interactions are additive (refer to panels (A2) and (A3)), the analytic simulations emerging from the effective Hamiltonians derived from the Bessel function approach (eqn (21)) are less accurate when compared to those obtained from numerical methods. By contrast, the analytic simulations emerging from the effective Hamiltonians (eqn (33)) defined in the extended space are in excellent agreement with those obtained from the numerical methods. In the section that follows, the dissipative effects emerging from the surrounding abundant spins is discussed in the extended Hilbert space through effective Floquet Hamiltonians.
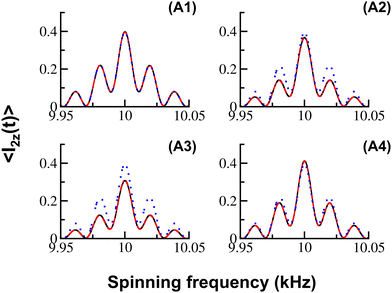 | ||
| Fig. 4 In the simulations illustrated, magnetization build-up on spin ‘I2’ (say, magnetization transfer from spin ‘I1’ to spin ‘I2’, eqn (14)) in the R2 (corresponding to the N = 2 matching condition) experiment is depicted as a function of the spinning frequency. The simulations resulting from SPINEVOLUTION (indicated in black) are compared with the analytic simulations, based on Bessel formula (indicated by blue dotted lines) and effective Hamiltonians in the CSA interaction frame defined in the extended Hilbert space based on eqn (33) (red broken lines). The following specific parameters were employed in the panels: (A1) (δ1 = 5 kHz, δ2 = 5 kHz), (A2) (δ1 = 5 kHz, δ2 = 5 kHz), (A3) (δ1 = 5 kHz, δ2 = −5 kHz) and (A4) (δ1 = 5 kHz, δ2 = −5 kHz). The isotropic chemical shifts (ω(0)1 = −ω(0)2 = 10 kHz), internuclear distance (rI1I2 = 3.879 Å), and mixing time (tmix = 30 ms) were held constant in the simulations. For panels (A1) and (A3), the CSA parameters are η1 = 0.0, Ω(1) = (0°, 0°, 0°); η2 = 0.0, Ω(2) = (0°, 0°, 0°) and for panels (A2) and (A4), the CSA parameters are η1 = 0.0, Ω(1) = (0°, 0°, 0°); η2 = 0.0, Ω(2) = (0°, 90°, 0°). The simulations correspond to a powder sample and were implemented using 6044 orientations (zcwt6044). | ||
B. Effective Hamiltonians for the system and the surroundings
As discussed in the previous section, in a real system (say, a biological sample), the 13C spins are surrounded by 1H spins, which are highly abundant as well as sensitive. As the 13C–1H dipolar-coupling interactions are stronger in magnitude when compared to the 13C–13C dipolar-coupling interactions, decoupling of the 13C–1H dipolar-coupling interactions becomes mandatory in experiments that involve measurement of 13C–13C distances. To minimize the contributions emerging from the 13C–1H dipolar-coupling interactions, strong decoupling fields are employed on the 1H (proton) spins during the magnetization exchange between the 13C spins. Nevertheless, residual contributions from the 13C–1H dipolar-coupling interactions remain and contribute to the dissipation observed in R2 experiments. To account for this dissipation, a phenomenological damping rate constant (1/TZQ) is often incorporated in existing descriptions in the literature.25–30,32–36 In the present context, this is established by including a phenomenological damping term in eqn (14), as given below. | (34) |
While the above description (or model) of the spin dynamics is conceptually flawed,37 a lack of alternate theoretical models has encouraged the use of other experiments55–60 for providing a qualitative estimate of homonuclear distances in solids abandoning the need for accurate measurements. The implications of this conceptual digression are beyond the scope of this article.
From a theoretical perspective, the dissipation (or depolarization) observed on the system of interest (say, spins I1 and I2) resulting from its coupling to the surrounding environment or bath (say, abundant ‘S’ spins) is studied using the following general equation.
| H(t) = HSystem(t) + HBath(t) + HSystem–Bath(t). | (35) |
The interactions of the observed spins (say, I1 and I2) are contained in the system Hamiltonian, HSystem(t) (similar to eqn (1)). In the present context, the bath Hamiltonian comprises the chemical shift and the homonuclear dipolar interactions in addition to the decoupling field employed.
| HBath(t) = HS(t) + HRF | (36) |
 | (37) |
 | (38) |
A detailed description of the coefficients employed in the above equations is given in the ESI.†
The interaction between the system and the bath is depicted through the heteronuclear dipolar interactions and is represented by HSystem–Bath(t).
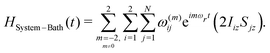 | (39) |
From an operational perspective, the solution to the quantum-Liouville equation (eqn (4a)) becomes quite complicated due to the time-dependent coefficients as well as the increased dimensionality of the problem (dimension is given by 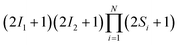 ). Hence, phenomenological models (employing exponential damping terms) have been integrated within a two-spin framework.
). Hence, phenomenological models (employing exponential damping terms) have been integrated within a two-spin framework.
As an alternative, below we present an analytic formulation for describing the dissipative effects observed in R2 experiments. In the proposed approach, effective Floquet Hamiltonians (defined in the CSA interaction frame of the 13C-spins) are derived for describing the spin dynamics in the presence of protons under heteronuclear decoupling. A detailed description of the calculations within the Floquet framework is summarized in the ESI.† In contrast to the description based on the effective Hamiltonians in the interaction frame,41 the present framework affords a spin dynamical description in the CSA interaction frame and facilitates studies even in systems with larger chemical shift anisotropies. For illustrative purposes, the multi-spin effects observed in R2 experiments are described through models (comprising a finite number of spins) based on effective Floquet Hamiltonians.
 | (40) |
The coefficients ‘d1’ and ‘e1’ represent the residual heteronuclear dipolar-coupling interactions (due to cross terms between the 1H-CSA interaction and 13C–1H heteronuclear dipolar interactions) associated with the spins, I1 and I2, respectively. Accordingly, in the presence of a single ‘S’-spin (say, 1H-spin), the effective Hamiltonian (of dimension 8 × 8) is decomposed into two two-level systems (TLSs) (refer to Fig. 5) and the magnetization transfer between the spins I1 and I2 is described by two oscillatory functions given below:
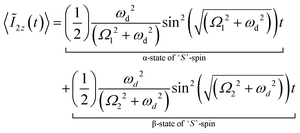 | (41) |
 | ||
| Fig. 5 Representation of the effective Hamiltonian in the model two-, three-, and four-spin systems in the block-diagonal form (of 2 × 2 matrices). | ||
The factor 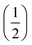 in the trigonometric expression represents the normalization factor and could be related to the number of spin states of the ‘S’-spin (say, 1H). This factoring of the result could also be deduced from the matrix representation of the effective Hamiltonians depicted in Fig. 5.
in the trigonometric expression represents the normalization factor and could be related to the number of spin states of the ‘S’-spin (say, 1H). This factoring of the result could also be deduced from the matrix representation of the effective Hamiltonians depicted in Fig. 5.
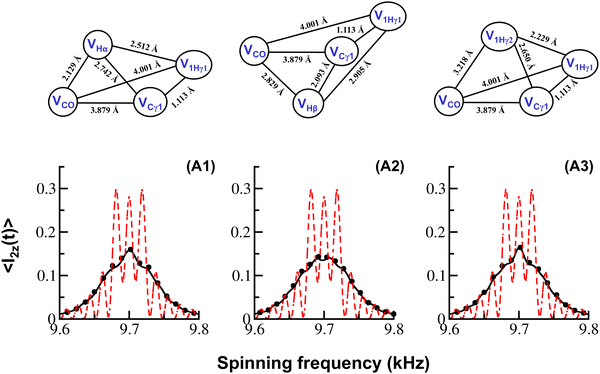
In contrast to the isolated two-spin model (refer to eqn (14)), the effective offset term (denoted by Ω) experienced by spins I1 and I2 comprises additional contributions from the residual heteronuclear dipolar-coupling interactions and is primarily responsible for the increased dissipation observed in the presence of a single proton. A detailed description of the effective offset, Ω, is summarized in Table 2. In contrast to the constant dissipative term, TZQ, introduced in eqn (34), the dissipation due to Ω is orientation-dependent. To verify the exactness of the above analytic expression, simulations in the model dipeptide N-acetyl-L-valine-L-leucine (VL)61 were employed as a model system in the present study. The above choice of the model system is only for demonstrative purposes and has nothing to do with the suitability of the theoretical framework presented in this report.
To demonstrate the dissipative effects emerging from protons, the magnetization exchange between the 13C spins (say, VCO and VCγ1, corresponding to a distance of 3.879 Å) was examined in the presence of different protons (say, Hα, Hβ and Hγ1 in the valine residue). As depicted in the simulations (refer to Fig. 6), the simulations emerging from eqn (41) (indicated in black dots) are in excellent agreement with those obtained from SPINEVOLUTION (indicated by solid black lines). For comparative purposes, the simulations emerging from the isolated two-spin model are also indicated (by red broken lines) in the backdrop. As depicted, the dissipative effect is significant (see panel (A3)) in systems with stronger heteronuclear dipolar-coupling interactions (say, between 13C–1H in the present case). A detailed description of the parameters employed is summarized in the ESI.† Hence, as the number of proton spins increases in the system, the dissipative effects should in principle increase and are verified below employing four- and five-spin model systems.
 | ||
| Fig. 6 In the three-spin simulations illustrated, magnetization build-up on spin ‘I2’ (say, magnetization transfer from spin ‘I1’ to spin ‘I2’, eqn (41)) in the R2 (corresponding to the N = 2 matching condition) experiment is depicted as a function of the spinning frequency. The simulations resulting from SPINEVOLUTION (indicated in black) are compared with the analytic three-spin simulations based on eqn (41) (indicated by black dots). The simulations depicted in the panels correspond to the following model systems: (A1) – VCOVCγ1VHα, (A2) – VCOVCγ1VHβ, and (A3) – VCOVCγ1V1Hγ1. Analytic simulations emerging from the isolated two-spin model (VCO–VCγ1) are indicated by red broken lines in the backdrop. Information about all the simulation parameters employed in the simulations is given in Table S2 in the ESI.† | ||
 | (42) |
Analogous to the three-spin problem, the effective Hamiltonian for the above four-spin system (described by a 16 × 16 matrix) is block-diagonal and could be expressed in terms of four TLSs (refer to Fig. 5). Consequently, the magnetization transfer between spins I1 and I2 in the presence of two S-spins (say, S1 and S2) is described in terms of the four oscillatory functions given below.
 | (43) |
In line with the discussion presented in the three-spin model, four oscillatory functions could be associated with the four spin states of the two protons considered. In the simulations depicted in Fig. 7, the magnetization transfer between spins I1 and I2 is described in the presence of two ‘S’ spins. As illustrated, the analytic simulations based on eqn (43) are in good agreement and validate the theoretical model presented above. In contrast to the three-spin simulations, the dissipative effects are significant in the four-spin system and are well-validated in the analytic simulations.
 | ||
| Fig. 7 In the four-spin simulations illustrated, magnetization build-up on spin ‘I2’ (say, magnetization transfer from spin ‘I1’ to spin ‘I2’, eqn (43)) in the R2 (corresponding to the N = 2 matching condition) experiment is depicted as a function of the spinning frequency. The simulations resulting from SPINEVOLUTION (indicated in black) are compared with the analytic simulations based on eqn (43) (indicated by black dots). The simulations depicted in the panels correspond to the following model systems: (A1) – VCOVCγ1VHαV1Hγ1, (A2) – VCOVCγ1VHβV1Hγ1, and (A3) – VCOVCγ1V1Hγ1V1Hγ2. Analytic simulations emerging from the isolated two-spin model (VCO–VCγ1) are indicated by red broken lines in the backdrop. The parameters employed in the simulations are given in Table S2 in the ESI.† | ||
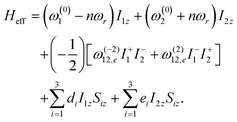 | (44) |
 | (45) |
As illustrated above, magnetization transfer in the model five-spin system is described by eight oscillatory functions (corresponding to eight different terms, represented by Ωi). A brief summary of the dissipative terms is summarized in Table 2. In accord with eqn (41) and (43), the normalization factor, (1/2N), depends on the number of spins (say, S-spins) coupled to the spin system of interest (say, I1 and I2).
To elucidate the role of protons, magnetization transfer in the weak-coupling regime was also examined in the simulations depicted in Fig. 8.
 | ||
| Fig. 8 In the simulations illustrated, magnetization build-up on spin ‘I2’ (say, magnetization transfer from spin ‘I1’ to spin ‘I2’, eqn (45)) in the R2 (corresponding to the N = 2 matching condition) experiment is depicted as a function of the spinning frequency. The simulations resulting from SPINEVOLUTION (indicated in black) are compared with the analytic simulations based on eqn (45) (indicated by black dots). The simulations depicted in the panels correspond to the following model systems: panel (A1) – VCOVCγ1VHαVHβV1Hγ1, panel (A2) – VCOLCδ2LHαLHγL1Hδ1, and panel (A3) – LCOVCβVHαV1Hγ1LHβ1LHγ. Analytic simulations emerging from the isolated two-spin model are indicated (panel (A1) – VCOVCγ1, r = 3.879 Å, panel (A2) – VCOLCδ2, r = 5.902 Å, and panel (A3) – LCOVCβ, r = 4.981 Å) by red broken lines in the backdrop. The parameters employed in the simulations are given in Table S2 in the ESI.† | ||
As depicted through the simulations illustrated in Fig. 6–8, the depolarization effects observed in magnetization exchange experiments (between spins I1 and I2) is largely influenced by the spin topology of the system under consideration. In contrast to other existing descriptions, the spin dynamics in a multi-spin system are described in a reduced subspace (spanned by 2 × 2 matrices) resulting in simple trigonometric expressions analogous to the one obtained in the description of an isolated two-spin system. As illustrated in the above examples, depending on the number of ‘S’ spins coupled to the system of interest, the polarization transfer from spin I1 to I2 in a model I1–I2–SN system is described in terms of simple trigonometric expressions emerging from 2N two-level systems (TLSs). Such an approach is computationally robust and presents an attractive framework for estimating multiple anisotropic constraints (such as 13C–13C, 13C–1H dipolar information besides the orientation and magnitude of the chemical shift and dipolar tensors). When the spinning frequency (based on the chemical shift difference between spins I1 and I2) is lower than the magnitude of the CSA interactions (of the observed spins),62 the CSA interaction coefficients play a prominent role in scaling down the recoupled dipolar-coupling constant and are directly responsible for decreasing the efficiency of polarization transfer, even in an isolated coupled system.
By contrast, the CSA interactions of the unobserved/decoupled spins (say, ‘S’ spins) play an active role in the dissipative effects emanating from the coupling to the neighboring ‘S’ spins. In the present context, the depolarization effects are manifested through the offset terms, Ωi, and have contributions from (i) the isotropic chemical shifts of the observed spins (I1 and I2), and (ii) the cross terms between the (transverse components) CSA interactions of the unobserved spins (say, ‘S’ spins) and the (transverse components) residual heteronuclear dipolar interactions (i.e.,  ).
).
When the CSA interactions associated with the ‘S’ spins are absent (or compensated for through multiple pulse-based methods), the depolarization effects emerging from the residual couplings to the ‘S’ spins should vanish (in principle), thereby reducing the spin dynamics to that of an isolated two-spin system. This prediction emerging from the analytic theory is well-substantiated through the simulations given in Fig. 9. As illustrated in Fig. 9, in the absence of the CSA interactions (of the S-spins), the simulations from the multi-spin model system, I1–I2–SN (depicted in Fig. 8), reduce to that of an isolated two-spin system (I1–I2). Hence, compensating for the effects of the CSA interactions of the decoupled spins plays an important role in improving the efficiency of magnetization transfer among spins in R2 experiments.
 | ||
| Fig. 9 In the simulations illustrated, magnetization build-up on spin ‘I2’ (say, magnetization transfer from spin ‘I1’ to spin ‘I2’, eqn (45)) in the R2 (corresponding to the N = 2 matching condition) experiment is depicted as a function of the spinning frequency in both the presence (refer to panels (A1)–(A3)) and absence (refer to panels (B1)–(B3)) of the CSA interactions of proton spins. The simulations resulting from SPINEVOLUTION (indicated in black) are compared with the analytic simulations based on eqn (45) (indicated by black dots). The simulations depicted in the panels correspond to the following model systems: panels (A1) and (B1) – VCOVCγ1VHαVHβV1Hγ1, panels (A2) and (B2) – VCOLCδ2LHαLHγL1Hδ1, and panels (A3) and (B3) – LCOVCβVHαV1Hγ1LHβ1LHγ. Analytic simulations emerging from the isolated two-spin model are indicated (panel (B1) – VCOVCγ1, r = 3.879 Å, panel (B2) – VCOLCδ2, r = 5.902 Å, and panel (B3) – LCOVCβ, r = 4.981 Å) by red broken lines in the backdrop. The parameters employed in the simulations are given in Table S2 in the ESI.† | ||
Besides its implications in quantifying the R2 experiments, the proposed analytic model (trigonometric expressions) also offers a framework for describing magnetization transfer among spins (I1 and I2) induced by multiple-pulse-based dipolar recoupling experiments. From an operational perspective, the only difference arises from the scaling factors associated with the coefficients ‘ωd’ and ‘Ωi’ employed in eqn (13) and (14). Depending on the desired applications, multiple-pulse experiments are designed to scale down both the anisotropic interactions (such as dipolar and CSA interactions) as well as the isotropic chemical shift interactions of interest. Hence, the proposed framework is well-suited to describe polarization transfer in I1–I2–SN systems both in the presence and absence of multiple pulses. We believe that the theoretical framework presented in this article would benefit in the analysis of longitudinal relaxation times measured under R2 conditions and its potential in other related areas.62
As evident from the present framework, the CSA interactions of the observed spins (say, ‘I’ spins) directly scale the estimated dipolar coupling, while the CSA interactions of the unobserved/decoupled spins (say, ‘S’ spins) directly contribute to the residual dipolar-coupling interactions leading to different offset terms Ωi. This directly results in different trigonometric terms and is directly responsible for the dissipation observed in the R2 experiments.
III. Conclusions and perspectives
In summary, the present study explicates the exact role of chemical shift anisotropic spin interactions in magnetization exchange between spins observed in R2 experiments. From the proposed theoretical framework, the dissipation (or dissipative effects) observed in R2 experiments could be explained in terms of both the (i) scaling factors associated with the measured dipolar-coupling constant (between the ‘I’ spins) and (ii) effective offset term (Ωi) experienced by spins I1 and I2. The scaling factor associated with the dipolar-coupling constant is derived in terms of effective Hamiltonians defined in the CSA interaction frame (defined by the ‘I-spins’). By contrast, the CSA interactions of the unobserved (abundant) spins play an important role in the effective offset (Ωi) experienced by the spins, I1 and I2. In the effective Hamiltonian framework, the cross terms between the CSA interactions (of the abundant 1H’s) and the heteronuclear dipolar-coupling interactions (say, 13C–1H) result in two-spin longitudinal operators, IzSz. This, in turn, contributes to the offset experienced by the spins, I1 and I2. Depending on the number of S-spins, the number of trigonometric functions increases and is directly responsible for the dissipation observed in magnetization exchange experiments between spins I1 and I2 in R2 experiments. Hence, the CSA interactions of the S-spins play an important role in the dissipation observed in the R2 experiments. In contrast to (existing) phenomenological models, the dissipation observed in R2 experiments is orientation-dependent and has a profound dependence on the dipolar coupling and CSA parameters of the unobserved S-spins. Additionally, the trigonometric expressions derived from the proposed analytic method present an attractive framework for estimating the dipolar-coupling constant and CSA parameters of the observed spins (I1, I2) in addition to estimating the coupling constant associated with the heteronuclear dipolar-coupling interactions (say, 13C–1H).Data availability
Data sharing is not applicable to paper as no data were created or analyzed in this study.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
N. S. would like to thank IIT Ropar for the graduate assistantship. M. K. P. would like to acknowledge IIT Ropar for the research infrastructure.References
- Y. Nishiyama, G. Hou, V. Agarwal, Y. Su and A. Ramamoorthy, Ultrafast magic angle spinning solid-state NMR spectroscopy: advances in methodology and applications, Chem. Rev., 2023, 123, 918–988 CrossRef CAS PubMed.
- B. Reif, S. E. Ashbrook, L. Emsley and M. Hong, Solid-state NMR spectroscopy, Nat. Rev. Methods Primers, 2021, 1, 2 CrossRef CAS PubMed.
- Z. J. Berkson, S. Bjorgvinsdottir, A. Yakimov, D. Gioffre, M. D. Korzynski, A. B. Barnes and C. Coperet, Solid-state NMR spectra of protons and quadrupolar nuclei at 28.2 T: resolving signatures of surface sites with fast magic angle spinning, JACS Au, 2022, 2, 2460–2465 CrossRef CAS PubMed.
- A. A. Smith, M. Ernst, S. Riniker and B. H. Meier, Localized and collective motions in HETs (218–289) fibrils from combined NMR relaxation and MD simulation, Angew. Chem., 2019, 131, 9483–9488 CrossRef.
- R. Zhang, K. H. Mroue and A. Ramamoorthy, Proton-based ultrafast magic angle spinning solid-state NMR spectroscopy, Acc. Chem. Res., 2017, 50, 1105–1113 CrossRef CAS PubMed.
- D. Good, C. Pham, J. Jagas, J. R. Lewandowski and V. Ladizhansky, Solid-state NMR provides evidence for small-amplitude slow domain motions in a multispanning transmembrane α-helical protein, J. Am. Chem. Soc., 2017, 139, 9246–9258 CrossRef CAS PubMed.
- S. J. Opella, Solid-state NMR and membrane proteins, J. Magn. Reson., 2015, 253, 129–137 CrossRef CAS PubMed.
- S. Wang and V. Ladizhansky, Recent advances in magic angle spinning solid state NMR of membrane proteins, Prog. Nucl. Magn. Reson. Spectrosc., 2014, 82, 1–26 CrossRef CAS PubMed.
- E. R. Andrew, A. Bradbury and R. G. Eades, Nuclear magnetic resonance spectra from a crystal rotated at high speed, Nature, 1958, 182, 1659 CrossRef CAS.
- I. J. Lowe, Free induction decays of rotating solids, Phys. Rev. Lett., 1959, 2, 285–287 CrossRef CAS.
- Y. Nishiyama, Fast magic-angle sample spinning solid-state NMR at 60–100 kHz for natural abundance samples, Solid State Nucl. Magn. Reson., 2016, 78, 24–36 CrossRef CAS PubMed.
- K. Takeda, Microcoils and microsamples in solid-state NMR, Solid State Nucl. Magn. Reson., 2012, 47–48, 1–9 CrossRef CAS PubMed.
- Y. K. Lee, N. D. Kurur, M. Helmle, O. G. Johannessen, N. C. Nielsen and M. H. Levitt, Efficient dipolar recoupling in the NMR of rotating solids. a sevenfold symmetric radiofrequency pulse sequence, Chem. Phys. Lett., 1995, 242, 304–309 CrossRef CAS.
- M. Hohwy, H. J. Jakobsen, M. Edén, M. H. Levitt and N. C. Nielsen, Broadband dipolar recoupling in the nuclear magnetic resonance of rotating solids: a compensated c7 pulse sequence, J. Chem. Phys., 1998, 108, 2686–2694 CrossRef CAS.
- A. Brinkmann and M. H. Levitt, Symmetry principles in the nuclear magnetic resonance of spinning solids: heteronuclear recoupling by generalized Hartmann-Hahn sequences, J. Chem. Phys., 2001, 115, 357–384 CrossRef CAS.
- M. Edén, Advances in Symmetry-Based Pulse Sequences in Magic-Angle Spinning Solid-State NMR, EMagRes, 2007, 351–364 Search PubMed.
- M. H. Levitt, Symmetry in the design of NMR multiple-pulse sequences, J. Chem. Phys., 2008, 128, 052205 CrossRef PubMed.
- N. C. Nielsen, L. A. Strassø and A. B. Nielsen, Dipolar recoupling, in Solid State NMR, 2012, pp. 1–45 Search PubMed.
- E. R. Andrew, A. Bradbury, R. G. Eades and V. T. Wynn, Nuclear cross-relaxation induced by specimen rotation, Phys. Lett., 1963, 4, 99–100 CrossRef CAS.
- E. R. Andrew, S. Clough, L. F. Farnell, T. D. Gledhill and I. Roberts, Resonant rotational broadening of nuclear magnetic resonance spectra, Phys. Lett., 1966, 21, 505–506 CrossRef CAS.
- D. P. Raleigh, G. S. Harbison, T. G. Neiss, J. E. Roberts and R. G. Griffin, Homonuclear Jcouplings and rotationally inducedsideband enhancements in NMR spectra of rotating solids, Chem. Phys. Lett., 1987, 138, 285–290 CrossRef CAS.
- D. P. Raleigh, M. H. Levitt and R. G. Griffin, Rotational resonance in solid state NMR, Chem. Phys. Lett., 1988, 146, 71–76 CrossRef CAS.
- D. P. Raleigh, F. Creuzet, S. K. Das Gupta, M. H. Levitt and R. G. Griffin, Measurement of internuclear distances in polycrystalline solids: rotationally enhanced transfer of nuclear spin magnetization, J. Am. Chem. Soc., 1989, 111, 4502–4503 CrossRef CAS.
- Z. Gan and D. M. Grant, Pseudo-spin rotational resonance and homonuclear dipolar NMR of rotating solids, Mol. Phys., 1989, 67, 1419–1430 CrossRef CAS.
- A. Kubo and C. A. McDowell, Spectral spin diffusion in polycrystalline solids under magicangle spinning, J. Chem. Soc., Faraday Trans. 1, 1988, 84, 3713–3730 RSC.
- M. H. Levitt, D. P. Raleigh, F. Creuzet and R. G. Griffin, Theory and simulations of homonuclear spin pair systems in rotating solids, J. Chem. Phys., 1990, 92, 6347–6364 CrossRef CAS.
- M. G. Colombo, B. H. Meier and R. R. Ernst, Rotor-driven spin diffusion in natural-abundance 13C spin systems, Chem. Phys. Lett., 1988, 146, 189–196 CrossRef CAS.
- P. T. F. Williamson, A. Verhoeven, M. Ernst and B. H. Meier, Determination of internuclear distances in uniformly labeled molecules by rotational-resonance solid-state NMR, J. Am. Chem. Soc., 2003, 125, 2718–2722 CrossRef CAS PubMed.
- M. Helmle, Y. Lee, P. Verdegem, X. Feng, T. Karlsson, J. Lugtenburg, H. De Groot and M. Levitt, Anomalous rotational resonance spectra in magic-angle spinning NMR, J. Magn. Reson., 1999, 140, 379–403 CrossRef CAS PubMed.
- P. R. Costa, B. Sun and R. G. Griffin, Rotational resonance NMR: separation of dipolar coupling and zero quantum relaxation, J. Magn. Reson., 2003, 164, 92–103 CrossRef CAS PubMed.
- R. R. Ernst, G. Bodenhausen and A. Wokaun, Principles of Nuclear Magnetic Resonance in One and Two Dimensions, Oxford University Press, 1990 Search PubMed.
- R. Ramachandran, V. Ladizhansky, V. S. Bajaj and R. G. Griffin, 13C–13C Rotational ResonanceWidth Distance Measurements in Uniformly 13C-Labeled Peptides, J. Am. Chem. Soc., 2003, 125, 15623–15629 CrossRef CAS PubMed.
- P. C. van der Wel, M. T. Eddy, R. Ramachandran and R. G. Griffin, Targeted 13C–13C Distance Measurements in a Microcrystalline Protein via J-Decoupled Rotational ResonanceWidth Measurements, ChemPhysChem, 2009, 10, 1656–1663 CrossRef CAS PubMed.
- R. Janik, X. Peng and V. Ladizhansky, 13C–13C distance measurements in U-13C, 15N-labeled peptides using Rotational Resonance Width Experiment with a homogeneously broadened matching condition, J. Magn. Reson., 2007, 188, 129–140 CrossRef CAS PubMed.
- X. Peng, D. Libich, R. Janik, G. Harauz and V. Ladizhansky, Dipolar chemical shift correlation spectroscopy for homonuclear carbon distance measurements in proteins in the solid state: application to structure determination and refinement, J. Am. Chem. Soc., 2008, 130, 359–369 CrossRef CAS PubMed.
- R. Ramachandran, J. R. Lewandowski, P. C. van der Wel and R. G. Griffin, Multipolemultimode Floquet theory of rotational resonance width experiments: 13C–13C distance measurements in uniformly labeled solids, J. Chem. Phys., 2006, 124, 214107 CrossRef PubMed.
- M. K. Pandey and R. Ramachandran, A theoretical perspective on the accuracy of rotational resonance (R2)-based distance measurements in solid-state NMR, Mol. Phys., 2010, 108, 619–635 CrossRef CAS.
- M. K. Pandey and R. Ramachandran, Operator-based analytic theory of decoherence in NMR, Mol. Phys., 2011, 109, 1545–1565 CrossRef CAS.
- L. Sonnenberg, S. Luca and M. Baldus, Multiple-spin analysis of chemical-shift-selective (13C, 13C) transfer in uniformly labeled biomolecules, J. Magn. Reson., 2004, 166, 100–110 CrossRef CAS PubMed.
- R. Ramesh and M. S. Krishnan, Effective Hamiltonians in Floquet theory of magicangle spinning using van Vleck transformation, J. Chem. Phys., 2001, 114, 5967–5973 CrossRef CAS.
- U. SivaRanjan and R. Ramachandran, Unraveling multi-spin effects in rotational resonance nuclear magnetic resonance using effective reduced density matrix theory, J. Chem. Phys., 2014, 140, 054101 CrossRef PubMed.
- R. Garg and R. Ramachandran, On the exactness of effective Floquet Hamiltonians employed in solid-state NMR spectroscopy, J. Chem. Phys., 2017, 146, 184201 CrossRef.
- R. Garg and R. Ramachandran, Theory of coherent averaging in magnetic resonance using effective Hamiltonians, J. Chem. Phys., 2020, 153, 034106 CrossRef CAS PubMed.
- S. Ganguly, R. Garg and R. Ramachandran, On the equivalence between different averaging schemes in magnetic resonance, J. Chem. Phys., 2020, 153, 094103 CrossRef CAS PubMed.
- M. Mehring, Principles of High-Resolution NMR in Solids, Springer, Berlin, 1983 Search PubMed.
- M. Maricq and J. S. Waugh, NMR in rotating solids, J. Chem. Phys., 1979, 70, 3300–3316 CrossRef CAS.
- S. A. Smith, W. E. Palke and J. T. Gerig, The Hamiltonians of NMR. part I, Concepts Magn. Reson., 1992, 4, 107–144 CrossRef CAS.
- I. I. Rabi, Space quantization in a gyrating magnetic field, Phys. Rev., 1937, 51, 652–654 CrossRef CAS.
- W. Magnus, On the exponential solution of differential equations for a linear operator, Commun. Pure Appl. Math., 1954, 7, 649–673 CrossRef.
- M. Veshtort and R. G. Griffin, SPINEVOLUTION: a powerful tool for the simulation of solid and liquid state NMR experiments, J. Magn. Reson., 2006, 178, 248–282 CrossRef CAS PubMed.
- P. Caravatti, G. Bodenhausen and R. R. Ernst, Selective pulse experiments in high-resolution solid state NMR, J. Magn. Reson., 1983, 55, 88–103 CAS.
- M. Bansal and R. Ramachandran, Theory of finite pulse effects beyond perturbation limit: Challenges and Perspectives, J. Magn. Res. Open, 2022, 10–11, 100042 Search PubMed.
- G. B. Arfken, H. J. Weber and F. E. Harris, Mathematical Methods for Physicists, Academic Press, Elsevier, 7th edn, 2013 Search PubMed.
- J. H. Shirley, Solution of the Schrödinger equation with a Hamiltonian periodic in time, Phys. Rev., 1965, 138, B979 CrossRef.
- D. Suter and R. R. Ernst, Spin diffusion in resolved solid-state NMR spectra, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 32, 5608–5627 CrossRef CAS PubMed.
- K. Takegoshi, S. Nakamura and T. Terao, 13C–1H dipolar-assisted rotational resonance in magic-angle spinning NMR, Chem. Phys. Lett., 2001, 344, 631–637 CrossRef CAS.
- K. Takegoshi, S. Nakamura and T. Terao, 13C–1H dipolar-driven 13C–13C recoupling without 13C RF irradiation in nuclear magnetic resonance of rotating solids, J. Chem. Phys., 2003, 118, 2325–2341 CrossRef CAS.
- C. R. Morcombe, V. Gaponenko, R. A. Byrd and K. W. Zilm, Diluting abundant spins by isotope edited radio frequency field assisted diffusion, J. Am. Chem. Soc., 2004, 126, 7196–7197 CrossRef CAS PubMed.
- M. Wilhelm, H. Feng, U. Tracht and H. W. Spiess, 2d CP/MAS 13C isotropic chemical shift correlation established by 1H spin diffusion, J. Magn. Reson., 1998, 134, 255–260 CrossRef CAS PubMed.
- A. Lange, S. Luca and M. Baldus, Structural constraints from proton-mediated rare-spin correlation spectroscopy in rotating solids, J. Am. Chem. Soc., 2002, 124, 9704–9705 CrossRef CAS PubMed.
- P. J. Carroll, P. L. Stewart and S. J. Opella, Structures of two model peptides: N-acetyl-D,L-valine and N-acetyl-L-valyl-L-leucine, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1990, 46, 243–246 CrossRef.
- A. Afrough, N. V. Christensen, R. W. M. Jensen, D. W. Juhl and T. Vosegaard, Magic angle spinning effects on longitudinal NMR relaxation: 15N in L-histidine, AIP Adv., 2023, 13, 115123 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: (i) Definition of anisotropic coefficients in MAS experiments, (ii) derivation of corrections based on Magnus formula, (iii) description of the CSA interaction frame using Bessel functions, (iv) description of the CSA interaction frame in the extended Hilbert space, and (v) description of R2 in the I1–I2–SN system. A detailed description of the G-coefficients along with the operators involved in the Floquet Hamiltonian HF derived for the multi-spin (I1–I2–SN) model system and NMR parameters employed in the multi-spin simulations are listed in Tables S1 and S2, respectively, of the ESI. See DOI: https://doi.org/10.1039/d5cp00806a |
| This journal is © the Owner Societies 2025 |