Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Static, dynamic and electronic properties of some trivalent liquid rare earth metals near melting: ab initio and neural network simulations
Beatriz G.
del Rio
 * and
Luis E.
González
* and
Luis E.
González

Departamento de Física Teórica, Universidad de Valladolid, 47011 Valladolid, Spain. E-mail: beatriz.gonzalez.rio@uva.es
First published on 13th May 2025
Abstract
We report a study on several static and dynamic properties of the early trivalent liquid rare-earth metals at thermodynamic conditions near their respective melting points. It has been performed by resorting to machine learning (ML) techniques, in which the associated neural network-based interatomic potentials were derived from ab initio molecular dynamics simulations within Hubbard-corrected density functional theory. We report the results obtained for the static structural properties, including an analysis of the local short-range order. Single-particle and collective dynamic properties have also been obtained, from which transport coefficients and wavevector-dependent dispersion relations are evaluated. The results show a quite homogeneous behavior of the structural, dynamic, and transport properties throughout the series. The electronic properties have been obtained from the ab initio simulations, and show important discrepancies with respect to the low temperature solids, portraying a more band-like picture of the 4f states in the liquid.
1 Introduction
The rare-earth (RE) elements form the largest chemically coherent group in the periodic table; it consists of the fifteen lanthanide elements, with scandium and yttrium sometimes also included in the family. Their metallurgical, chemical, catalytic, electrical, magnetic, and optical properties make them suitable for a range of industrial applications, such as electronics, clean energy, aerospace, automotive (mainly in electric cars) and defense (for instance, to obtain hard materials for armoring vehicles). These metals are characterized by a 4fn shell (where n increases from 0 for Lanthanum to 14 for Lutetium). The other outer shells are 6s (2 electrons) and 5d (generally 1 electron) and they also contribute to the conduction band.In the specific case of their molten state and despite their technological relevance, there is a scarcity of experimental data concerning their static, dynamic and electronic properties.
The static structure factor, S(q) and the pair distribution function, g(r), are standard magnitudes used to describe the structural arrangement of atoms in a disordered system such as a liquid. In the case of the liquid RE metals considered in this work, the available experimental structural data were obtained nearly fifty years ago. In 1975, Bellisent and Tourand1 performed neutron scattering (NS) measurements of the S(q) of liquid Ce (l-Ce) and l-Pr at a temperature slightly higher than their respective melting points. However, as indicated by the authors, their obtained S(q) showed an anomalous behavior because they exhibited just the main maximum with no additional oscillations. Shortly after, the NS measurements of Enderby and Nguyen2 for l-Ce and the X-ray diffraction (XD) data of Waseda and Tamaki3 for liquid Ce, Pr, Eu, Gd, and Yb at thermodynamic conditions near their respective melting points, as well as those of Waseda and Miller4 for Nd, Dy, Ho, Er, and Lu, yielded structure factors with a main peak followed by additional oscillations of decreasing amplitude. Ever since, no additional measurements of the S(q) have been performed for any of these liquid metals; moreover, their dynamical structure, as characterized by the dynamic structure factor, has not been measured yet.
Additional available experimental data for these liquid RE metals pertain to some transport coefficients only. Specifically, the isothermal compressibility, sound velocity5 and shear viscosities6 have been measured for l-Ce and l-Pr only; however, their diffusion coefficients have not been determined yet.
This dearth of experimental data emphasizes the importance of resorting to other strategies such as theoretical and computer simulation methods to extract information about their structural, dynamical, transport and electronic properties.
Even though the RE elements constitute a large family of atoms in the periodic table and have quite a few high-technology and environmental applications, ab initio studies of their electronic properties are scarce. This may be explained by the fact that the RE elements involve 4f electrons whose strong correlation effects pose specific problems for ab initio methods.
In the context of density functional theory (DFT), it is known that the Kohn–Sham (KS) formalism of DFT,7,8 with local density approximation (LDA) or generalized gradient approximation (GGA), does not account properly for the electronic exchange and correlation interactions. Therefore, a usual way of going beyond the LDA and GGA is by resorting to the DFT+U method,9 which offers the possibility of a more accurate description of the properties of highly correlated systems at a reasonable computational cost.
Most studies have focused on the low-temperature solid phase and among those we mention the work by Eriksson et al.10,11 who used the linearized muffin-tin orbital (LMTO) method within the LDA approximation to study the cohesive energies for some RE and actinide elements. Also, Delin et al.12 used the DFT theory combined with both the LDA and GGA approximations to study the equilibrium volumes, bulk moduli, and cohesive energies of the RE elements by assuming both the fcc and hcp crystal structures. Their results showed that GGA approximation improves the results obtained through LDA for these elements, correcting the overbinding tendencies of the latter approximation. A similar study was performed by Soderlind et al.13 who, within the context of the DFT theory evaluated equilibrium volumes, bulk moduli, and magnetic moments of the RE elements; moreover, they analyzed the influence on those properties of the exchange–correlation functional, spin–orbit interaction, and orbital polarization.
Going beyond standard DFT, Strange et al. used self-interaction corrections to analyze the reasons underlying the change in the valence number along the lanthanide series at their low-temperature equilibrium structures, that were ascribed to the evolution in the position of high-energy f-type bands relative to the Fermi energy.14 More recently, Locht et al.15 have used a combination of the DFT with the dynamical mean-field theory to study the electronic structure of the RE elements and analyze the equilibrium volume, bulk modulus, magnetic and spectral properties.
However, when it comes to the molten state of the RE metals, we are only aware of the DFT+U simulation study performed by Siberchicot and Clerouin16 for l-Ce at a somewhat higher temperature, T = 1320 K. They considered 12 valence electrons (as in the present calculation) along with a Hubbard U term of 5.4 eV which was taken from a DFT+U study on the γ and β phases of solid Ce.17 They reported results for static properties (g(r) and S(q)), electrical conductivity, and optical indices.
In this paper we have carried out a comprehensive characterization of some liquid RE metals near their melting temperatures, studying several electronic and ionic properties, where the latter include the static structure and also dynamic and transport magnitudes. The calculations have been performed by resorting to machine learning (ML) interatomic potentials obtained from a database generated by DFT-based simulations. More specifically, for each metal, we have first performed a DFT+U simulation calculation in which the liquid metal has been modeled as an interacting system of ions and electrons whose associated electronic ground state is evaluated for any ionic configuration, following the Born–Oppenheimer approximation, using the DFT+U formalism. The Hellmann–Feynman theorem delivers the forces on the ions, and these are used within the Newtonian equations of motions in order to evolve the atomic positions. This DFT+U simulation method requires large computational capabilities and imposes severe limitations concerning the simulation times and size of the systems under study; nonetheless, these disadvantages are somewhat balanced by the accuracy of the obtained results.
These restrictions are very important when wavevector-dependent properties are studied, since the minimum value attainable in the simulations is inversely proportional to the cubic root of the number of particles, leading in the case of ab initio simulations to relatively high values for the minimum wavevector that hinder the possible extrapolation towards the hydrodynamic region, which is necessary in order to obtain several transport properties. Alleviating such problems would require a large number of atoms/ions (tens of thousands), and improving the statistics would imply longer simulation times (∼100–1000's of ns). At present, this is not directly feasible for ab initio methods, whereas it can be routinely achieved by resorting to classical MD (CMD) simulations based on interatomic potentials. Such an approach, however, usually has a negative impact on the accuracy of the results as compared to first principles data. ML techniques have recently appeared as a way of addressing the above mentioned problems by enabling the construction of interatomic potentials which predict the system energy and forces by numerical interpolation using a database generated by quantum mechanical (commonly DFT-based) calculations. These ML-based interatomic potentials allow to use system sizes and simulation times typical of CMD simulations but with a quantum mechanical accuracy.
The paper has been structured as follows: the next section summarizes the basic ideas underlying the DFT+U and ML simulation methods along with some technical details. Section 3 contains the results obtained in the study and a discussion on them in comparison with the experimental data available. Section 4 finally summarizes the results drawing some conclusions.
2 Computational method
Table 1 lists the specific RE metals and the corresponding thermodynamic states for which this simulation study has been performed. The first step was the generation of a reference database and this was achieved by means of DFT+U simulations performed using the DFT-based Quantum-ESPRESSO (QE) package.18,19 In this part of the calculation, the electronic exchange and correlation energies were described by the generalized gradient approximation (GGA) of Perdew–Burke–Ernzerhof.20 The ion-electron interaction was characterized by means of projected augmented wave (PAW) pseudopotentials specifically derived, along with Hubbard U values, by Topsakal and Wentzcovitch21 to be used in DFT+U calculations for the RE metals. These were constructed from a scalar-relativistic calculation which included non-linear core corrections and by imposing the condition that QE calculations for solid rare-earth nitrides using these PAW pseudopotentials yielded total densities of states matching those obtained by an all-electron calculation.21 In these pseudopotentials the 6s, 5s, 5p, 5d and 4f orbitals are considered as valence states; therefore the number of electrons explicitly considered in the valence shell ranged from 12 (Ce) to 18 (Gd) electrons. The present QE-based simulations were carried out by using a cubic cell containing 100 atoms which implied that the number of electrons explicitly considered varied from 1200 to 1800 electrons. The energy cut-off for the plane-wave expansion of the wavefunction was in the range 340–530 eV, and the single Γ point was used for sampling the Brillouin zone. We notice that the QE simulation method has already shown its power to describe accurately the properties of several other liquid metals.22–31| Code | ρ (Å−3) | T (K) | Np | Δt (fs) | Z val | U (eV) | N c | |
|---|---|---|---|---|---|---|---|---|
| Ce | QE | 0.0287 | 1143 | 100 | 6.0 | 12 | 2.5 | 9500 |
| ML | 6400 | 1.0 | — | — | 180![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
|||
| Pr | QE | 0.0283 | 1223 | 100 | 6.0 | 13 | 4.0 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| ML | 6400 | 1.0 | — | — | 180![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
|||
| Nd | QE | 0.0289 | 1325 | 100 | 6.0 | 14 | 2.4 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| ML | 6400 | 1.0 | — | — | 180![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
|||
| Pm | QE | 0.0287 | 1350 | 100 | 6.0 | 15 | 3.4 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800 |
| ML | 6400 | 1.0 | — | — | 180![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
|||
| Sm | QE | 0.0280 | 1400 | 100 | 6.0 | 16 | 3.3 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| ML | 6400 | 1.0 | — | — | 180![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
|||
| Gd | QE | 0.0265 | 1610 | 100 | 4.5 | 18 | 4.0 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
| ML | 6400 | 1.0 | — | — | 120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
Afterwards, we used the results of the previous DFT+U simulations as a reference database from which deep neural network potentials (DNNP) were constructed using the SIMPLE-NN package.32 To transform the atomic coordinates into descriptors of the atomic environment, we employed Behler-Parrinello Gaussian functions,33,34 using the Gastegger method35 to select the parameters. Between 21 and 35 Gaussians were employed for each element. The architecture of the neural networks employed for the DNNPs ranged from two layers for Sm, to three for Ce, Pm, and Gd, and four for Pr and Nd. All of them used 50 neurons per layer except Sm, which employed 100. In all cases, the DNNPs were trained using a training and validation split of 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20. The subsequent CMD simulations were performed using the LAMMPS package.36Table 1 gives information concerning both the DFT+U and ML-based simulations along with other technical details. The configurations obtained from the ML simulations were used for the evaluation of the static, dynamic, and transport properties of the corresponding liquid metal.
20. The subsequent CMD simulations were performed using the LAMMPS package.36Table 1 gives information concerning both the DFT+U and ML-based simulations along with other technical details. The configurations obtained from the ML simulations were used for the evaluation of the static, dynamic, and transport properties of the corresponding liquid metal.
3 Results and discussion
3.1 Static properties
The static structure factors, S(q), obtained for all the systems studied are plotted in Fig. 1, where they are compared with the corresponding experimental data for the cases where the latter is available. The results for l-Ce, l-Nd, and l-Gd exhibit a fair agreement with the XD data with respect to the position and shape of the first peak; however, we obtain some mismatch concerning the position of the second peak. Fig. 1 also provides a closer look at the shape of the second peak of the S(q) for which the ML simulations predict a discernible asymmetric shape for l-Ce to l-Pm, whereas it becomes more symmetric for the two other systems. For comparison, we note that the present S(q) for l-Ce is qualitatively similar to that obtained by the ab initio simulations of Siberchicot and Clerouin16 which also showed some asymmetry of the second peak after a smoothing procedure, that was needed because of a very noisy result due to the relatively short simulation time. Additionally, we can stress that the height of the second peak obtained in our study is more in line with the experimental data than the one obtained in the previous ab initio study, which was quite higher. | ||
| Fig. 1 Static structure factor, S(q), of l-Ce, l-Pr, l-Nd, l-Pm, l-Sm and l-Gd. Continuous line: present ML simulation results. Open circles: XD data from ref. 3,4,37. The inset shows a closer view of the second maximum. | ||
In the ML study the smallest wavevector attainable for all the RE metals was q ≈ 0.10 Å−1, whereas in the case of the DFT+U simulations the smallest q-value was always greater than 0.40 Å−1. The smaller value of the ML results allows a more accurate estimatation of the isothermal compressibility, κT, related to S(q) by the formula S(0) = ρkBTκT where kB is Boltzmann's constant. The values of S(q) for q ≤ 0.40 Å−1 were fitted to the form S(q) = S(0) + bq2, and the obtained results are also given in Table 2 along with the corresponding isothermal compressibilities. In the case of l-Ce and l-Pr, McAlister et al.5 used their experimental data for the sound velocity along with the mass density and an assumption for the ratio of the specific heats, γ ≈1.03, to obtain an “experimental” estimate for the κT. For the other RE metals, and because of the lack of experimental data, we have reported the estimates obtained by resorting to semiempirical expressions which involve measured and/or estimated values of other thermophysical magnitudes.38 Excepting l-Pr and l-Gd, the present ML calculations show fair agreement with the experimental/semiempirical data. In the case of l-Pr, we think that its calculated S(0) is somewhat small even when compared with the other RE metals considered in the work.
| r min | CN | S(0) | κ T | |
|---|---|---|---|---|
| Ce | 4.72 | 13.4 | 0.021 ± 0.001 | 4.80 ± 0.20 (5.30) |
| Pr | 4.77 | 13.0 | 0.014 ± 0.002 | 2.83 ± 0.20 (4.17) |
| Nd | 4.73 | 12.8 | 0.026 ± 0.002 | 5.00 ± 0.20 (4.55) |
| Pm | 4.71 | 12.5 | 0.021 ± 0.002 | 4.00 ± 0.20 |
| Sm | 4.72 | 12.6 | 0.027 ± 0.002 | 5.04 ± 0.20 (5.27) |
| Gd | 4.80 | 12.5 | 0.037 ± 0.002 | 6.28 ± 0.20 (4.27) |
The pair distribution function, g(r), provides some insight into the short-range order in the liquid metal and Fig. 2 depicts the obtained ML simulation results along with the available experimental data. As it happened with the S(q), we observe a fair agreement with the available experimental data. In the case of l-Ce, we note again that our ML results for g(r) compare better with the experimental data of Waseda et al.3,37 than the previous ab initio simulations of Siberchicot and Clerouin.16
 | ||
| Fig. 2 Pair distribution function, g(r), of l-Ce, l-Pr, l-Nd, l-Pm, l-Sm and l-Gd. Continuous line: present ML simulation results. Open circles: XD data from ref. 3,4,37. | ||
The average number of nearest neighbors around a given ion, also known as the coordination number (CN), is given by the integral of the radial distribution function, 4πρr2g(r), up to its first minimum, rmin. Table 2 lists the results obtained for all the systems studied, and it is observed that these values are in line with those corresponding to other simple liquid metals near melting.39
A more detailed characterization of short-range order in liquid metals is achieved through the common neighbor analysis (CNA) method.40–42 This method provides three-dimensional insights into the local environment of ions surrounding each neighboring pair. Each pair is described by four indices that differentiate between various local structures, such as body-centered cubic (bcc), different close-packed arrangements, and icosahedral configurations.
For instance, different close-packed structures are associated with distinct proportions of 1421 and 1422-type pairs, while bcc order is characterized by six 1441-type pairs and eight 1661-type pairs. In contrast, a 13-atom icosahedron is composed of twelve 1551-type pairs. When a bond in the regular 1551-type structure is broken, it results in 1541 and 1431-type pairs, which indicate a somewhat distorted icosahedral order. For more details about the CNA method we refer to ref. 29–31,40–44.
Fig. 3 summarizes the results obtained in this work, also including the results for l-La obtained previously within the same scheme followed in the present study.45 The five-fold symmetry dominates in all these metals because the sum of perfect and distorted icosahedral structures ranges between ≈52% (l-La) and ≈65% (l-Gd) of the pairs. The amount of local bcc-type pairs is also significant, varying between ≈19% (l-Gd) and ≈29% (l-Pr) of the pairs. On the other hand, there is an almost negligible amount of close-packed pairs. These results for the local environments found in the liquid are in line with the fact that, even though the low-temperature phases are close-packed in all the systems considered, all of them melt from a bcc phase. It may be concluded that the information given by this CNA method points to a very uniform behavior for all these RE metals. Similar studies performed for the 3d, 4d and 5d transition metals29–31,46 have revealed much greater variations when moving along the corresponding row of the periodic table.
3.2 Dynamic properties
Several time correlation functions have been evaluated in order to obtain information about some dynamical properties. In those cases where there is a wave-vector q dependence, we have taken into account the macroscopically isotropic behavior of the fluid to reduce it to a dependence on q ≡ |q| only.| Z(t) = 〈vi(t)·vi(0)〉/〈vi2〉, | (1) |
The obtained ML results for Z(t) are plotted in Fig. 4, where we observe the usual decaying behavior with a noticeable first minimum followed by decreasing weak oscillations around zero. This first minimum is due to the collision of any given ion with its nearest neighbors, which results in a short-lived vibrational motion. All the systems have very similar number densities and masses, and this is reflected in the fact that the position of this backscattering minimum is located at approximately the same time. The Fourier Transform (FT) of the Z(t) into the frequency domain gives the associated power spectra, Z(ω), and these are plotted as insets in Fig. 4.
 | ||
| Fig. 4 Normalized ML calculated velocity autocorrelation function of l-Ce, l-Pr, l-Nd, l-Pm, l-Sm and l-Gd. The inset represents the corresponding power spectrum Z(ω). | ||
From the value of Z(ω) at ω = 0, which coincides with the time integral of the VACF, one obtains the self-diffusion coefficient, D. This can also be calculated from the slope of the atomic mean square displacement. We have checked that both routes give practically the same results and the values are given in Table 3.
| D (Å2 ps−1) | c s (m s−1) | η (GPa ps) | |
|---|---|---|---|
| Ce | 0.340 ± 0.020 (0.262)6 | 1750 ± 150 (1693)6 | 1.85 ± 0.20 (3.25)6 |
| Pr | 0.200 ± 0.020 (0.334)6 | 2350 ± 150 (1925)6 | 3.70 ± 0.25 (2.85)6 |
| Nd | 0.272 ± 0.020 (0.349)6 | 1710 ± 150 (1873, 2212)6,47,48 | 2.40 ± 0.25 (2.96, 2.88)6 |
| Pm | 0.327 ± 0.020 (0.378)6 | 1950 ± 150 | 2.74 ± 0.25 (3.22, 2.83)6 |
| Sm | 0.295 ± 0.020 (0.377)6 | 1640 ± 150 (1422, 1672)6,47,48 | 2.55 ± 0.25 (3.23, 2.51)6 |
| Gd | 0.362 ± 0.020 (0.365)6 | 1250 ± 150 (1725, 1972, 2041)6,47,48 | 2.70 ± 0.25 (3.49)6 |
We are not aware of any experimental self-diffusion data for the RE metals considered in this work. Nevertheless, for the sake of comparison, we have included in Table 3 some estimates obtained from semiempirical expressions based on modified Stokes–Einstein type formulas which relate the self-diffusion coefficient to viscosity,6 which is more amenable to measurement.
 | (2) |
Its time FT gives the frequency spectrum, known as the dynamic structure factor, S(q,ω), which can be directly measured by either inelastic neutron scattering or inelastic X-ray experiments.
Fig. 5 depicts for l-Sm, the calculated ML results for F(q,t). The general structure is similar for the other elements considered in this work, and parallels the behavior of other liquid metals29–31,43,44 near melting, namely, the strong oscillatory shape observed at small q gets more and more damped at higher wavevectors until it eventually disappears near qp, showing a monotonic decreasing behavior therefrom.
A deeper understanding of the microscopic mechanisms driving the collective dynamics can be gained through a more detailed analysis of F(q,t). To achieve this, we employed the generalized Langevin formalism. Specifically, we began by examining the time evolution of F(q,t) in relation to its second-order memory function, N(q,t), i.e.
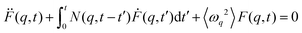 | (3) |
| N(q,t) = As(q)e−t/τs(q) + Af(q)e−t/τf(q) | (4) |
From a physical point of view, one relaxation channel is considered to have a thermal origin and the other one is associated to the viscoelastic behavior of the liquid.
We utilized the ML simulation results for F(q,t) to compute its corresponding second-order memory functions N(q,t). These were then fitted to eqn (4). The fitting results were analyzed to determine whether the obtained N(q,t) align with either a generalized hydrodynamic model (featuring a fast viscoelastic channel and a slow thermal one) or a generalized viscoelastic model, where the fast channel is thermal.
To explore this further, we evaluated the generalized heat capacity ratio, γ(q), which approaches the thermophysical value γ0 in the q → 0 limit, representing the ratio of specific heats at constant pressure to constant volume. This quantity was chosen due to its strong sensitivity to the underlying model.
If thermal relaxation occurs through the slow channel, then its amplitude takes the form As(q) = (γth(q) − 1) 〈ωq2〉 and τs(q) = (γth(q)DT(q))−1. On the other hand, if viscoelastic relaxation happens along the slow channel, then As(q) = N(q,t = 0) + (1 − γvis(q)) 〈ωq2〉. Here, γth(q) and γvis(q) represent the values taken by γ(q) when thermal and viscoelastic relaxations, respectively, occur along the slow channel.
Fig. 6 shows, for the liquid RE metals studied in this paper, the obtained results for γth(q) and γvis(q). Their respective shapes are quite different and the values of γth(q) are always smaller than those of γvis(q). The observed general trends of the γth(q) are as follows: starting from the smallest possible value (q ≈ 0.10 Å−1), it smoothly increases, goes through a maximum, and then decreases attaining values close to unity. This shape of the ML calculated γth(q) is more physically appealing than the one corresponding to γvis(q), as it is qualitatively similar to the “experimental” γ(q) data for l-Fe near melting, which was derived by of Hosokawa et al.49 by fitting the experimental S(q,ω) to a model and then applying the Landau–Placzek relation. Their result showed that the γexp,Fe(q) starts with a value of ≈1.40 at q ≈ 0.21 Å−1, it smoothly increases reaching a value of ≈1.55 at q ≈ 0.63 Å−1, and then decreases towards a value of ≈1.1 at q ≈ 2.00 Å−1 (qp,Fe ≈ 2.98 Å−1). Additionally, we have also observed this behavior in liquid La.45
 | ||
| Fig. 6 Generalized specific heat ratio, γ(q), as obtained from the generalized hydrodynamic model (grey circles) and the generalized viscoelastic model (red triangles). | ||
There are no experimental data for the γ0 of any liquid RE metals, but extrapolation of the results presented in Fig. 6 yields the following estimates: 1.05 ± 0.03 (Ce), 1.04 ± 0.03 (Pr), 1.04 ± 0.03 (Nd), 1.10 ± 0.03 (Pm) and 1.04 ± 0.03 (Sm). The results for l-Ce and l-Pr support the assumption made by McAlister et al.5 of taking γ ≈ 1.03 to obtain an “experimental” estimate for the κT.
Summing up, the above calculation shows that in these rare-earth metals, the thermal relaxation proceeds along the slow channel and, more importantly, it provides an estimation for their respective γ(q) along with its thermophysical value γ0 ≡ γ(q → 0). On the other hand, the obtained γvis(q) shows an unphysical behaviour as a result of assuming that the viscoelastic relaxation is associated to the slow channel.
The associated S(q,ω) is plotted in Fig. 7 for the case of l-Sm, and the most noticeable feature is the existence, up to q ≈ (3/5)qp, of side-peaks characteristic of collective density excitations. Then, for greater q-values the S(q,ω) display a monotonic decreasing behavior. This same qualitative trend is exhibited by all the other RE metals considered in this paper.
We also computed the frequency of the side-peaks as a function of the wavevector q, denoted as ωm(q), which corresponds to the dispersion relation of density excitations. In the hydrodynamic limit (q → 0), the dispersion curve exhibits a linear slope, characterized by the adiabatic sound velocity, cs. By defining the phase velocity cs(q) such that ωm(q) = q·cs(q), we find that cs is equivalent to cs(q → 0).
Fig. 8 depicts the calculated cs(q) values where we observe some degree of positive dispersion. Additionally, we have estimated cs by a linear fitting of the ML simulation data using the smaller q-values (q ≤ 0.3 Å−1) and the results are given in Table 3, which also includes, for comparison, the available experimental (l-Ce and l-Pr) and semiempirical (l-Nd, l-Pm, l-Sm and l-Gd) data. These latter data are estimates obtained from measured values of other properties such as surface tension, melting temperature and density, using semiempirical formulas.6,47,48 Overall, we observe a fair agreement between the ML simulation results and the experimental and/or semiempirical data.
 | ||
| Fig. 8 q-Dependent adiabatic sound velocity. The red and grey symbols are the DFT+U and ML simulation results respectively. | ||
In the study of collective dynamics, another important quantity is the current associated with the overall motion of particles, j(q,t), given by
 | (5) |
 | (6) |
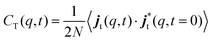 | (7) |
The time Fourier transforms of these correlation functions yield the corresponding spectra, CL(q,ω) and CT(q,ω).
The ML calculated longitudinal spectrum, CL(q,ω), exhibits a peak for any fixed value of q, with the associated frequency, ωL(q), representing the dispersion relation of the longitudinal modes. These functions are depicted in Fig. 9.
The CT(q,t) decays monotonically with time both in the free particle limit (q → ∞) and in the hydrodynamic limit (q → 0). For intermediate q-values it can show a more complex structure with oscillations around zero,39,50–52 characteristic of propagating shear waves, that translate into side peaks in the corresponding spectra, CT(q,ω). In the present ML simulations, it is found that for the lowest attainable q value, namely qmin = 0.10 Å−1, no peaks are visible yet, but when q ≈ 0.15 Å−1 the CT(q,ω) starts displaying a peak which points to the propagation of shear waves. With increasing q-values, we obtain that the peak's frequency, ωT(q), increases, goes through a maximum at q ≈ (2/3)qp, and then slowly decreases and fades away at q ≈ 3.0qp when the peaks disappear.
Moroever, the CT(q,ω) shows within a much smaller q-range, located around the position of the main peak of the S(q), a second, higher frequency, peak that gives rise to another transverse dispersion branch. This can be observed in Fig. 9 where we have plotted the high and low-frequency dispersion relations for the transverse modes. In accordance with previous findings53–57 we observe some correlation between the existence of a high-frequency peak or shoulder in Z(ω) and the development of a high-frequency branch in the transverse dispersion relation. Although there is still no self-consistent theory to explain this possible correlation, we mention that, by using mode coupling ideas, Gaskell and Miller58–60 developed a theory of the VACF based on contributions arising from the coupling of the single particle motion to the collective longitudinal and transverse currents.
From the ML simulation results for the CT(q,t), we have also evaluated the associated shear viscosity coefficient, η. This has been achieved by using the memory function representation of the CT(q,t), which allows to determine a q-dependent shear viscosity, η(q).50,51,61,62 In the q → 0 limit, this yields the shear viscosity coefficient η ≡ η(q → 0), which has been obtained by fitting the ML simulation results to the expression η(q) = η/(1 + a2q2). Table 3 shows the results along with other experimental (l-Ce and l-Pr) and semiempirical (l-Nd, l-Pm, l-Sm and l-Gd) data. The latter are semiempirical estimates6 obtained from values of other measured magnitudes (melting temperature, sound velocity, surface tension and density). Excepting l-Ce, we observe a fair agreement between the ML simulation results and the experimental and/or semiempirical data.
In the context of Brownian motion of a macroscopic particle with diameter d in a liquid of viscosity η, the Stokes–Einstein (SE) relation, ηD = kBT/2πd, establishes a link between the viscosity η and the self-diffusion coefficient D. Although originally not intended for atoms, this relation is often used to estimate η (or D) by approximating d with the position of the main peak in the radial distribution function g(r).
In MD simulations, computing the self-diffusion coefficient D requires significantly less computational effort than calculating shear viscosity. As a result, the SE relation is frequently employed to estimate viscosity. Additionally, this relation is commonly used in semiempirical formulas that connect shear viscosity and self-diffusion coefficient in terms of other thermophysical properties.
We have used the present ML results to analyze the accuracy of this relation when applied to several RE liquid metals studied in this work. The results are plotted in Fig. 10, including the data corresponding to l-La.45 It shows that the SE relation holds fairly well excepting l-Nd for which the error is ≈25%.
3.3 Electronic properties: density of states
The ML study allows the determination of structural and dynamic properties of the metals studied, but is not capable, in the form used here, of delivering electronic properties. These are however available from the original QE simulations used for the training. From these, we have calculated the partial and total electronic density of states, n(E). These have been obtained from the self-consistently determined eigenvalues, and were averaged over four ionic configurations well separated in time (≈15.0 ps), sampling the Brillouin zone with eight points.Fig. 11 shows the obtained results for the electronic partial and total n(E) associated to the outer valence electrons (the 5s and 5p electrons lie well below the Fermi energy, EF), and Table 4 reports the corresponding occupations of the partial bands.
| Ce | Pr | Nd | Pm | Sm | Gd | |
|---|---|---|---|---|---|---|
| s | 0.45 | 0.56 | 0.55 | 0.60 | 0.65 | 0.74 |
| p | 0.10 | 0.09 | 0.09 | 0.08 | 0.08 | 0.06 |
| d | 2.40 | 2.25 | 1.92 | 1.94 | 1.55 | 1.30 |
| spd | 2.95 | 2.90 | 2.56 | 2.62 | 2.28 | 2.10 |
| f | 0.85 | 2.10 | 3.55 | 4.17 | 5.75 | 7.80 |
The f bands behave quite different in the liquid as compared to the low temperature solids.14 In the latter, they are magnetically split into spin up and down f states. Moreover, there are low lying quasi-localized occupied states well below EF and a partly occupied f band overlapping and hybridizing with the sd band, whose position with respect to EF varies as the atomic number changes within the lanthanide series. From Ce to Sm the occupation of the low lying states increases from 1 to 5, whereas the occupation of the upper f band increases from basically 0 to 0.65 as its energy decreases towards EF,14 leading to a number of sd electrons that decreases gradually from 3 in Ce to 2.35 in Sm. In Gd 7 electrons fill the low lying spin up states, the 4f upper band gets back to higher energy and its occupation returns to 0, restarting the whole process again with the spin-down states.
In the liquid, we observe that the f bands overlap completely with the spd bands in Ce, Nd, Sm, and Gd, that have an even number of valence electrons. In Pr and Pm, there are some subbands just below the spd ones and another subband overlapping with the high-energy part of the spd band that lies just above EF. Despite this even-odd behavior, it is observed that the total number of spd electrons show a decreasing trend, extending also to Gd.
We consider that the factor mostly responsible for this different behavior is the decrease of the most probable distance to the first neighbor of a given atom in the liquid. From the simulation we find that it ranges from the smallest value of 2.90 Å in l-Ce to a maximum value of 3.12 Å in l-Pr and these values are in all cases much shorter than in the corresponding low-temperature solids (where the closest distance ranges from the smallest value of 3.57 Å in hcp-Gd to a maximum value of 3.65 Å in fcc-Ce). This amounts to a reduction around 15 to 20%, and favors the interatomic orbital overlap. Note that the most probable first neighbor distance is different from the maxima of the radial distribution function (shown in Fig. 2), since the latter corresponds to the average of the ≈13 neighbors of the first coordination shell.
4 Conclusions
We have applied ML techniques in order to develop accurate interatomic potentials for some liquid RE metals; these potentials were derived from a reference database generated by previously performed DFT+U based simulations. The combination of both techniques allowed us to study, with ab initio accuracy, various properties, achieving a very low uncertainty due to the large size of the systems simulated with ML.Results have been reported for a range of static, dynamic, and electronic properties of several liquid RE metals. We stress that, excepting l-Ce, this is the first ab initio study performed for these RE metals in the molten state.
Concerning the static structure, the ML results show fair agreement with the experiment in the case of those metals (l-Ce, l-Pr, l-Nd, and l-Gd) for which XD data are available. However, given that the XD data were collected more than fifty years ago, it would be interesting to perform the comparison with new experimental data. A more detailed study of the short-range order, as afforded by the CNA method, has shown a very similar abundance of different types of local environments in all these liquid RE metals, dominated by icosahedral structures with a noticeable contribution of bcc ones as corresponds to the hot solid from which the systems melt.
The ML dynamic structure factors, S(q,ω), show side-peaks which are indicative of collective density excitations. From the associated dispersion relation we have evaluated a q-dependent sound velocity from which the adiabatic sound velocity in the liquid metal has been evaluated.
The ML transverse current correlation functions, CT(q,t), display oscillations around zero, and their spectra, CT(q,ω), show peaks characteristic of shear waves. Furthermore, the possible correspondence between the frequency structure of the spectrum of the VACF and the transverse dispersion relations is attested for yet another set of liquid systems.
From the previous time correlation functions, we have evaluated the heat capacity ratio as well as some transport coefficients, namely the self-diffusion, adiabatic sound velocity and shear viscosity coefficients. This calculation has been aided by the capability of the ML simulations to deliver time correlation functions up to very small wavevectors, namely q-values up to 0.1 Å−1. Taking into account the scarcity of data concerning most of these coefficients we expect that the present results will be of some interest. Additionally, by using the previous results for the shear viscosity and self-diffusion, we have tested the validity of the Stokes–Einstein relation.
Finally, the DFT+U simulations have provided results for the electronic structure that in general deviate from the data corresponding to the low temperature solids, and the possible reason for this discrepancy has been discussed.
Author contributions
Beatriz G. del Rio: conceptualization, investigation, software, writing – original draft, funding acquisition. Luis E. Gonzalez: conceptualization, investigation, writing – review and editing, supervision, funding acquisition.Data availability
Data for this article are available from the UVAdoc public repository of the University of Valladolid, at https://uvadoc.uva.es/handle/10324/75117.Conflicts of interest
There are no conflicts to declare.Acknowledgements
D. J. González is acknowledged for many useful discussions. We acknowledge the support of the Spanish Ministry of Economy and Competitiveness (Project PGC2018-093745-B-I00) which is also partially supported by ERDF funds. BGR additionally acknowledges the funding received from the Spanish Ministry of Universities through the Maria Zambrano program partly funded by NextGenerationEU funds and the University of Valladolid.References
- R. Bellissent and G. Tourand, J. Phys., 1975, 36, 97 CrossRef CAS.
- J. E. Enderby and V. T. Nguyen, J. Phys. C, 1975, 8, L112 CrossRef CAS.
- Y. Waseda and S. Tamaki, Philos. Mag., 1977, 36, 1 CrossRef CAS.
- Y. Waseda and W. A. Miller, Philos. Mag. B, 1978, 38, 21 CAS.
- S. P. McAlister and E. D. Crozier, Solid State Commun., 1981, 40, 375 CrossRef CAS.
- T. Iida and R. I. L. Guthrie, The Thermophysical Properties of Metallic Liquids, Oxford University Press, Oxford, 2015 Search PubMed.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133 CrossRef.
- I. V. I. Anisinov, J. Zaanen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 943 CrossRef PubMed.
- O. Eriksson, M. S. S. Brooks and B. Johansson, J. Less-Common Met., 1989, 158, 207 CrossRef.
- J. Melsen, J. M. Wills, B. Johansson and O. Eriksson, J. Alloys Compd., 1994, 209, 15 CrossRef CAS.
- A. Delin, L. Fast, B. Johansson, O. Eriksson and J. M. Wills, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 4345 CrossRef CAS.
- P. Soderlind, P. E. A. Turchi, A. Landa and V. Lordi, J. Phys.: Condens. Matter, 2014, 26, 416001 CrossRef PubMed.
- P. Strange, A. Svane, W. M. Temmerman, Z. Szotek and H. Winter, Nature, 1999, 399, 756 CrossRef CAS.
- I. L. M. Locht, Y. O. Kvashnin, D. C. M. Rodrigues, M. Pereiro, A. Bergman, L. Bergqvist, A. I. Lichtenstein, M. I. Katsnelson, A. Delin, A. B. Klautau, B. Johansson, I. Di Marco and O. Eriksson, Phys. Rev. B, 2016, 94, 085137 CrossRef.
- B. Siberchicot and J. Clerouin, J. Phys.: Condens. Matter, 2012, 24, 455603 CrossRef PubMed.
- B. Amadon, F. Jollet and M. Torrent, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 155104 CrossRef.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. D. Corso, S. de Gironcoli, P. Delugas, R. A. D. Jr, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H.-Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. O. De-la Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- M. Topsakal and R. M. Wentzcovitch, Comput. Mater. Sci., 2014, 95, 263 CrossRef CAS.
- L. Calderin, D. J. González, L. E. González and J. M. López, J. Chem. Phys., 2008, 129, 194506 CrossRef CAS PubMed.
- L. Calderín, L. E. González and D. J. González, J. Chem. Phys., 2009, 130, 194505 CrossRef PubMed.
- L. Calderín, L. E. González and D. J. González, J. Phys.: Condens. Matter, 2011, 23, 375105 CrossRef PubMed.
- L. Calderín, L. González and D. J. González, J. Phys.: Condens. Matter, 2013, 25, 065102 CrossRef PubMed.
- B. G. del Rio, O. Rodriguez, L. E. González and D. J. González, Comput. Mater. Sci., 2017, 139, 243 CrossRef CAS.
- B. G. del Rio, D. J. González and L. E. González, Phys. Fluids, 2016, 28, 107105 CrossRef.
- B. G. del Rio, D. J. González and L. E. González, J. Chem. Phys., 2017, 146, 034501 CrossRef CAS PubMed.
- B. G. Del Rio, C. Pascual, O. Rodriguez, L. E. González and D. J. González, Condens. Matter Phys., 2020, 23, 23606 CrossRef CAS.
- B. G. Del Rio, L. E. González and D. J. González, J. Phys.: Condens. Matter, 2020, 32, 214005 CrossRef CAS PubMed.
- L. E. González and D. J. González, Int. J. Refract. Met. Hard Mater., 2022, 107, 105898 CrossRef.
- K. Lee, D. Yoo, W. Jeong and S. Han, Comput. Phys. Commun., 2019, 242, 95 CrossRef CAS.
- J. Behler, J. Chem. Phys., 2011, 134, 074106 CrossRef PubMed.
- J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 14 CrossRef PubMed.
- M. Gastegger, L. Schwiedrzik, M. Bittermann, F. Berzsenyi and P. Marquetand, J. Chem. Phys., 2018, 148, 241709 CrossRef CAS PubMed.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in’t Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 10817 CrossRef.
- Y. Waseda, The Structure of Non-Crystalline Materials, McGraw-Hill, New York, 1980 Search PubMed.
- Y. Marcus, Chem. Thermodyn., 2017, 109, 11 CrossRef CAS.
- U. Balucani and M. Zoppi, Dynamics of the Liquid State, Clarendon, Oxford, 1994 Search PubMed.
- J. D. Honeycutt and H. C. Andersen, J. Phys. Chem., 1987, 91, 4950 CrossRef CAS.
- A. S. Clarke and H. Jonsson, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 3975 CrossRef CAS PubMed.
- W. K. Luo, H. W. Sheng, F. M. Alamgir, J. M. Bai, J. H. He and E. Ma, Phys. Rev. Lett., 2004, 92, 145502 CrossRef CAS PubMed.
- M. Marques, L. González and D. González, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 134203 CrossRef.
- M. Marques, L. González and D. González, J. Phys.: Condens. Matter, 2016, 28, 075101 CrossRef PubMed.
- B. G. del Rio and L. E. González, J. Chem. Theory Comput., 2024, 20, 3285 CrossRef CAS PubMed.
- D. J. González and L. E. González, Condens. Matter Phys., 2023, 26, 33601 Search PubMed.
- S. Blairs, Intern. Mater. Rev., 2007, 52, 321 CrossRef CAS.
- S. Blairs, Phys. Chem. Liq., 2007, 45, 399 CrossRef CAS.
- S. Hosokawa, M. Inui, K. Matsuda, D. Ishikawa and A. Q. R. Baron, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 174203 CrossRef.
- D. J. González, L. E. González, J. M. López and M. J. Stott, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 184201 CrossRef.
- D. J. González, L. E. González, J. M. López and M. J. Stott, J. Chem. Phys., 2001, 115, 2373 CrossRef.
- J. P. Hansen and I. R. McDonald, Theory of Simple Liquids, Academic Press, London, 1986 Search PubMed.
- B. del Rio and L. Gonzalez, Phys. Rev. B, 2018, 95, 224201 CrossRef.
- B. del Rio, M. Chen, L. E. Gonzalez and E. A. Carter, J. Chem. Phys., 2018, 149, 094504 CrossRef PubMed.
- T. Bryk, T. Demchuk and N. Jakse, Front. Phys., 2018, 6, 00006 CrossRef.
- T. Bryk, T. Demchuk and N. Jakse, Phys. Rev. B, 2019, 99, 014201 CrossRef CAS.
- T. Bryk and N. Jakse, J. Chem. Phys., 2019, 151, 034506 CrossRef PubMed.
- T. Gaskell and S. Miller, J. Phys. C: Solid State Phys., 1978, 11, 3749 CrossRef CAS.
- T. Gaskell and S. Miller, J. Phys. C: Solid State Phys., 1978, 11, 4839 CrossRef CAS.
- T. Gaskell and S. Miller, Phys. Lett. A, 1978, 66, 307 Search PubMed.
- B. J. Palmer, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 49, 359 CrossRef CAS PubMed.
- U. Balucani, J. P. Brodholt, P. Jedlovszky and R. Vallauri, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 2971 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2025 |