Gurney and cylinder wall velocities of explosives: analytical estimates and thermochemical simulations

Abstract

Gurney velocity (u_G) and cylinder wall velocity (v_s) of energetic materials are calculated using the semi-empirical Cγ method, an analytical model previously developed for CHNO high explosives and presently extended to additional elements and to explosives at low loading density. The results are compared to recent procedures based on thermochemical simulations. Regarding u_G, both approaches perform similarly well for organic high explosives, with an average relative error close to 2.6%. However, Cγ underestimates u_G for tritonal, an explosive with 20–40 wt% aluminium powder. Regarding v_s, a newly introduced empirical equation is shown to perform better than the Gurney model, although not as well as a recent correlation involving the detonation energy derived from thermochemical simulations, which are still required to predict cylinder wall velocities with optimal accuracy. With regard to the application of present models to the design of new materials, Cγ is not recommended for metal-containing compounds. However, for the high-thoughput design of organic high explosives, it is an invaluable tool allowing fast and reproducible calculations of Gurney energies with state-of-the-art accuracy. A very simple, hackable Python script is provided for this purpose as supplementary information.

---

1. Introduction

In contrast to thermal stability and sensitivities, the performances of explosives are primarily determined by the difference in properties between their initial unreacted state and the final state of their detonation products.^1,2 As a result, detonation parameters and specific impulses may be accurately estimated from thermochemical simulations.^3–5 However, such performance indicators do not provide any information regarding how fast the material can accelerate the surrounding metal liner. For this purpose, the most used performance indicator is the Gurney velocity u_G, which is experimentally derived from cylinder wall velocities measured in cylinder expansion tests. This quantity is specially relevant for applications involving the design of shaped charges or other explosive devices that rely on the generation of high-velocity jets or fragments.⁶ Prompt values correspond to systems in which confining cases rupture at small expansion, while terminal values correspond to systems in which more ductile case materials expand further before rupturing.⁷ In any case, u_G critically depends on energy losses, like those occurring as the detonation products fracture the cylinder wall and leak out between the fragments. As a result, it is clear that Gurney velocities cannot be predicted rigorously on the basis of first-principles thermochemical simulations, in sharp contrast to detonation parameters. To get around this difficulty, empirical relationships linking u_G directly to molecular structure have been reported.^8–10 However, they may exhibit significant errors, as discussed in previous papers.^10–13

In this context, a more reliable approach was recently put forward by Sućeska and coworkers.^11,12 It relies on the fact that experimental Gurney velocities obtained for a given expansion ratio V/V₀ approximately match 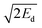, where E_d is the detonation energy released for a lower value of V/V₀.¹⁴ This procedure will be hereafter referred to as the EXPLO5 method, since the authors compute E_d with the help of the eponymous software.¹⁵ In view of its enhanced accuracy compared to empirical methods, it is well suited to case-by-case calculations on a small number of materials. However, as pointed out by Jeremić and Bogdanov,¹⁶ it also has a number of drawbacks. First, the output of thermochemical codes depends on many parameters describing the properties and equation of state of the detonation products, which hampers cross-comparisons between simulations made with different codes, or even with different versions of the same code. Secondly, as a proprietary software, the EXPLO5 code is only available to engineers who have a sufficiently recurring need for it to justify its purchase. More generally, current thermochemical software is limited in availability for reasons of cost and/or confidentiality. Finally, such codes typically describe the gaseous detonation products using the Becker–Kistiakowsky–Wilson (BKW) equation of state (EoS), whose mathematical formulation is computationally expensive and requires the gas composition to be iteratively determined via an appropriate chemical equilibrium solver.¹⁷ While this is no significant issue for a chemist in need of performance data for a few molecules he has in mind, this becomes more of a problem in the context of modern approaches to the design of energetic materials based on large scale screening of the chemical space.¹⁸ Indeed, with the availability of extremely efficient models to estimate crystal density,^19,20 heat of formation,^21,22 and to a lesser extent sensitivity^23,24 and thermal stability,^25,26 the search for the equilibrium composition and properties of the detonation products stands out as a major bottleneck in the high-throughput assessment of explosives.

Fortunately, this costly step can be avoided using simple rules of thumb regarding the composition of the detonation products.^16,27 For instance, it was recently shown²⁸ that detonation parameters can be predicted with very good reliability and for a wide range of explosive compositions using the H₂O−CO₂ arbitrary introduced by Kamlet and Jacobs, i.e. the following hierarchy in product formation: H₂O, CO₂, N₂, O₂, C and H₂. Regarding prediction of Gurney velocities, the same rule is used by an earlier analytical model referred to as Cγ,¹³ where the name refers to the fact that this model starts from an equation obtained assuming a polytropic expansion of the detonation products in the case where the polytropic index γ is constant. As detailed in ref. 13, Cγ predicts Gurney velocities with much better reliability than earlier empirical methods, with a reduction in the average error by a factor of between 2 and 3, depending on the expansion rate considered. Therefore, it would be interesting to compare the EXPLO5 procedure to Cγ, as the former has previously been compared solely to crude empirical methods, whereas the latter is more convenient for engineering applications and more widely available as it requires only paper and pencil. This comparison is the goal of the present paper.

2. Detailed procedures

Full details of the EXPLO5 and Cγ procedures compared in this work may be found respectively in ref. 12 and 13 For completeness, a brief outline is provided below.

2.1. EXPLO5 procedure

The EXPLO5 procedure described in ref. 11 and 12 is based on the empirical observation that the detonation energies calculated at about threefold expansion of the products matches very well with experimental Gurney energies. More specifically, E_G is assumed to be proportional to the detonation energy calculated for an expansion ratio V/V₀ = 3:

E_G ∝ E_d(V/V₀ = 3) (1)

In principle, the proportionality coefficient depends on the expansion ratio considered. It proves very close to unity for small expansion ratios, for which the approach proves especially successful, with a determination coefficient R² as large as 0.95 between estimated and observed u_G values.¹²

2.2. Cγ model

In contrast to most empirical methods,^8–10 the Cγ model derives u_G from the Gurney energy E_G = u_G²/2, defined as follows:

E_G = E₀ − E_s(V/V₀) (2)

where E₀ is the value of the detonation energy E_d at infinite volume, and E_s is the part of this chemical energy that does not contribute to accelerate the driven metal, i.e. the internal energy remaining in the detonation products as their expansion ratio equals V/V₀.

The Cγ model was initially introduced in ref. 13 on the basis of an isentropic expansion of the decomposition products involving a polytropic exponent γ. As its names implies, this model starts with the assumption of a constant γ. This leads to the following equation for the Gurney energy:¹³

The dependence of γ on the expansion ratio is re-introduced in a second step, by using distinct values of γ for data sets corresponding to different V/V₀ values. The effective value to be used in eqn (3) is estimated on the basis of the loading density ρ₀ and number of moles N of gaseous species produced per gram of explosive:

V/V₀ = v × ρ₀N (4)

where the proportionality constant v is homogeneous to a volume. Any potential dependence of γ and v on the nature of the expanding gases and solid particles is neglected. This allows these two quantities to be fitted against experimental u_G data for any value of the observed expansion ratio. They can then be used to predict Gurney velocities for new materials.

This simple procedure may be alternatively obtained without reference to a polytropic expansion, simply assuming that the energy that does not contribute to the metal acceleration is a fraction of E₀ that depends on the expansion ratio as (V₀/V)^η with an adjustable proportionality constant and an empirical exponent η that do not depend on the chemical composition of the explosive.

In principle, having estimated the Gurney velocity u_G using the method described above, the cyclinder wall velocity v_s to be expected from cylinder test experiments can be calculated using the Gurney model in reverse. This is especially straightforward in the configuration of such experiments, due to the simple cylindrical geometry involved:

where M_C/M_E, which stands for the ratio of the weight of the copper cylinder to the weight of the explosive sample, is obtained as (4.033 g cm⁻³)/ρ₀, as detailed in ref. 12.

In the present work, unless mentioned otherwise, we use previously introduced parameters γ = 2.3 and v = 37 cc mol⁻¹ that proved suitable to estimate terminal Gurney velocities,¹³ which are more important in practice than prompt values.¹⁰ On the other hand, to make the model applicable to additional elements beyond CHNO, an extended hierarchy is used regarding product formation. Namely, Al₂O₃, BaO, NaCl, HF, CF₄, HCl, CCl₄ are assumed to be produced before the H₂O−CO₂ arbitrary is applied. The formation enthalpies required as input to the calculations were preferably taken from the original ref. 4, 10 and 29–33 otherwise from the Dobratz explosive handbook.⁷

2.3. Cγ versus EXPLO5 comparison

This work compares the outcome of Cγ and EXPLO5 regarding Gurney velocities at terminal expansion compiled by EXPLO5 developers.^11,12 The predictive value of both methods is primarily assessed on the basis of root mean square error (RMSE) data in km s⁻¹, and corresponding value δ in percent, following ref. 13.

Previously introduced data sets are used, namely the Stimac et al. data set from ref. 11 and the Sućeska et al. data set from ref. 12. The names and corresponding structures of the explosives presently considered may be found in these two papers. For completeness, they are also reported in ESI,† along with presently used values of the formation enthalpies. It should be noted that since the latter were obtained from third-party literature, they could possibly differ from the values assumed in the reference EXPLO5 calculations.^11,12 We focus on organic explosives for two reasons.

First, in view of its reliance on the H₂O−CO₂ arbitrary, the current Cγ model is in principle specially well-suited to CHNO compounds. In contrast, its application to aluminium-containing explosives is more questionable as we systematically assume Al to be completely converted in Al₂O₃. Similar ambiguities arise for any metal-containing explosive.

Secondly, the data reported in ref. 12 does not make it possible to account for the wide variability of ANFO data, that might arise as a result of experimental uncertainties and possible differences in the precise composition of the materials. Indeed, several inconsistencies may be noted regarding this data. For instance, regarding Gurney velocities of ANFO, ref. 12 reports a value of 2.14 km s⁻¹ at 0.82 g cc⁻¹ taken from Fedoroff²⁹ and a much lower value of 1.63 km s⁻¹ at 0.83 g cc⁻¹ that could not be found in the reference cited.³⁴ As a result, it is not possible for us to draw any reliable conclusion from the data reported for ammonium nitrate (AN) based explosives.

3. Results

3.1. Validation of the Cγ equation

Keeping in mind the fact that v and γ are fitted against experiment, the Cγ equations may be alternatively derived without reference to the polytropic exponent γ, simply assuming that the internal energy E_s = E₀ − E_G of the detonation products decreases with the molar density ρ₀N according to a power law with exponent η, in other words:

E_s/E₀ = k/(ρ₀N)^η (6)

where the two parameters η and k may be fitted against experiment, or equivalently obtained from previously fitted values of v and γ as η = γ − 1 and:

Therefore, the above mentioned Cγ assumption (eqn (6)) is equivalent to assuming a linear decrease of log[1 − E_G/E_D(∞)] with log(ρ₀N). The validity of this assumption is checked in Fig. 1 using all data reported by Stimac et al.¹¹ for a set of 39 measurements carried out for various organic explosives and loading densities. Cγ may be readily applied to this data set as most compounds included in it contain only CHNO elements, except for three formulations (LX-04, LX-09 and LX-10) with negligible amounts of fluorine in the binder.

Fig. 1 Values of ln[1 − E_G/E_D(∞)] plotted as a function of ln(ρ₀N) for the 39 entries considered in ref. 11, including Locking (full symbols) as well as Fedoroff (empty symbols) data. Labels indicate the name of the explosive along with the corresponding density (g cc⁻¹).

Even in the case of such organic high explosives for which an ideal detonation behavior is expected, it is clear that experimental data found in this compilation exhibit significant uncertainties, especially when considering values taken from different sources. For instance, three experimental values are reported for the Gurney velocity of Comp B at a density ρ₀ = 1.72 g cc⁻¹, namely values u_G = 2.71 km s⁻¹ and u_G = 2.79 km s⁻¹ taken from Locking¹⁰ and a value u_G = 2.80 km s⁻¹ taken from Fedoroff.²⁹ The deviation of about 3.6% between extremal values is larger than the root mean square deviation of 3.28% reported between measured and estimated values,¹¹ which clearly shows that experimental uncertainties may significantly contribute to such statistical indicators. Similarly, considering the value u_G = 2.79 km s⁻¹ taken from Locking for cyclotol 77/23, a slightly lower value might be expected for cyclotol 75/25 in view of its slightly reduced fraction of RDX. For the latter material, a larger value u_G = 2.86 km s⁻¹ is actually found in Fedoroff encyclopedia.²⁹ Therefore, we presently consider Locking and Fedoroff entries separately, keeping in mind that experimental uncertainties of about 0.1 km s⁻¹ are to be expected. A distinctive feature of the Fedoroff subset is that it includes data measured for very low loading densities, namely for HMX at a density of 1.2 g cc⁻¹ and for PETN at densities of 1.27 and 1.5 g cc⁻¹.

Despite uncertainties inherent to present data, Fig. 1 does confirm the validity of the correlation at the basis of Cγ. However, Fedoroff entries corresponding to high explosives at reduced loading densities tend to fall away from the main trend. For such samples, the low density stems from the occurrences of voids in the sample. Since these voids get closed as a shock is applied to the system, the significance of the initial loading density when it comes to describing the detonation products is questionable.

3.2. Generalizing Cγ to reduced loading densities

Fig. 2 shows the drop in u_G on going from a loading density close to the theoretical maximal density (TMD) of the crystal to reduced loading densities. In contrast to both Cγ and EXPLO5 procedures that predict an approximately linear decrease of u_G on going to smaller ρ₀ values, experiments suggest a qualitative change from a convex to a concave dependence on going from HMX to PETN, possibly due to the uncertainties inherent to such measurements. In any case, Fig. 2 strongly suggests that the drop in u_G on going to much reduced loading densities is overestimated by both models. We might attribute this to the neglect of the collapse of the porosity as the sample is primed.

Fig. 2 Drop in Gurney velocity u_G on going to reduced loading densities.

For the 30 entries taken from Locking, this systematic error does not show up as this data set does not include any experiment at low explosive density. Therefore, EXPLO5 is about as good as Cγ on average, as reflected by δ-values of respectively 2.9% and 2.5%. Gurney velocities fall systematically within 6% from experiment using both models, except for TACOT for which u_G is overestimated by almost 8% using Cγ and over 10% using EXPLO5, as already noted by Stimac et al.¹¹ As pointed out by a reviewer and detailed in ESI,† the experimental value of 2.12 km s⁻¹ reported for TACOT appears to be the prompt instead of terminal value, which should be in the range 2.30–2.40 km s⁻¹ according to careful estimates, in fair agreement with the values of 2.28 and 2.34 km s⁻¹ calculated using Cγ and EXPLO5, respectively.

In contrast, Fedoroff data includes measurements carried out for reduced loading densities, as mentioned above, and for which u_G is severely underestimated. For instance, both models predict a velocity of 2.71 km s⁻¹ for PETN at 1.5 g cc⁻¹, much lower than the measured value of 2.9 km s⁻¹. This flaw is especially serious for Cγ, leading to even more serious errors for extremely low densities: −10.6% for HMX at 1.2 g cc⁻¹ and −8.4% for PETN at 1.27 g cc⁻¹. The much too small velocities predicted in such cases is reflected by δ values as large are 4.4% for EXPLO5 and 5.3% for Cγ. Considering the whole Stimac data set including Locking as well as Fedoroff entries, both Cγ and EXPLO5 yield similar performance with δ = 3.3%, proving satisfactory on average except for reduced loading densities.

Using the Cγ model, a simple empirical way to mitigate the too fast decrease in u_G on considering reduced loading density is to replace ρ₀ by the geometric mean in the equations, where ρ_max is the TMD, when available, otherwise the largest density obtained in cylinder wall experiments for the material considered. In so doing, δ increases from 2.5% to 2.9% for the Locking subset which does not contain any measurement at very low density. However, for the nine Fedoroff measurements, δ drops from 5.3% down to 1.9%.

3.3. Further assessment of Gurney velocities

After it was originally introduced by Stimac et al.¹¹ the EXPLO5 approach was subsequently compared to additional data sets from the same group of Suceska et al.¹² These data sets, compiled in Table 1 of ref. 12, include high explosives, ammonium nitrate-based non-ideal explosives, and aluminized explosives.

Table 1 Parameters used to derive cylinder wall velocities as a function of the V/V₀ ratio, including γ (dimensionless) and v (cm³ mol⁻¹) values required to apply the Gurney model, as well as ρ_c (g cm⁻³) and u_c (km s⁻¹) parameters involved in eqn (8)

V/V0	γ	v	ρc	uc
2.2	1.73 ± 0.07	43.4 ± 3.1	4.496 ± 0.032	0.40 ± 0.03
3.9	1.99 ± 0.09	43.7 ± 3.0	4.305 ± 0.041	0.49 ± 0.04
6.2	2.14 ± 0.10	43.9 ± 2.8	4.202 ± 0.044	0.53 ± 0.04

---

In this section, Cγ is assessed against this comprehensive data set. The TMD scaling described in Section 3.2 is systematically applied to experiments made at reduced loading densities. All results are compiled in Table S4 (ESI†), using data from Table S5 (ESI†), and summarized in Fig. 3. Although the model was originally designed for ideal high explosives, a good agreement with experiment is obtained for all data taken from the Fedoroff compilation, including materials made of ammonium nitrate mixed with RDX or TNT and two ANFO slurries. Larger deviations may be observed for data taken from alternative sources, which comes as no surprise due to a lack in information regarding the details of the compositions studied and the apparent inconsistencies in the experimental data, as discussed above in Section 2.3 for ammonium-based explosives (ANFO) and in Section 3.1 for high explosives.

Fig. 3 Comparison of predicted versus measured Gurney velocities for explosives without (circles) and with (squares) Al. Calculations are made using Cγ (turquoise symbols) and EXPLO5 (empty symbols). Cγ predicts a value u_G = 1.1 km s⁻¹ for Tritonal (not shown) much smaller than the experimental value of 2.32 km s⁻¹.

In view of applying Cγ to the nine Al-containing explosives introduced in ref. 12, Al is assumed to be fully converted to Al₂O₃. This yields good predictions, except for tritonal, a mixture of 80% TNT and 20% Al for which u_G is dramatically underestimated, as shown in Fig. 3. Upon closer examination, it may be noted that the specially low Gurney velocity predicted for this material arises because the present Al₂O₃–H₂O–CO₂ arbitrary yields a specially small amount of gases evolved from combustion, namely 0.025 cc g⁻¹, versus over 0.3 cc g⁻¹ for HTA-3 and HBX-3, two materials with an even larger Al weight fraction. Consequently, E_G represents only about 7% of the total detonation energy for tritonal, versus about 30% for HTA-3 and HBX-3. Given the complexities induced by Al particles in non-ideal explosives,³⁵ there is presently no simple and reliable model to predict the performances of such materials without resorting to numerical simulations.

The remaining 43 high explosives represent in principle a more challenging data test set for Cγ compared to the Stimac et al. data set considered above. This is due to the occurrence of fluorine compounds, as well as explosives with Al/Ba in significant amounts. In order to handle those elements with Cγ, all fluorine and aluminium atoms are assumed to be converted to HF and Al₂O₃, respectively. For these compounds, both Cγ and EXPLO5 performs about equally well on average. The small increase in δ observed by comparison wih the Stimac et al. data set (from 3.3% to 3.6%) stems from the addition of more challenging data, namely baratol, an explosive including barium nitrate, for which u_G is predicted too small by about 8%, and measurements at reduced loading densities of about 1.5 g cc⁻¹ (EDD, HNS) for which u_G is predicted too low, especially for HNS, an explosive with a very negative oxygen balance (−68%) and for which the loading densities of 1.2 and 1.6 g cc⁻¹ are much lower than the theoretical maximal density (TMD) of 1.75 g cc⁻¹.³⁶

The experimental velocity for baratol should be considered with caution as it was derived using a 1D (flyer plate) configuration, in contrast to all other data which were obtained using a 2D (cylinder) configuration.³⁷ Anyway, the measured value of 1.62 km s⁻¹ being specially small, the relative deviation of 8% corresponds in fact to a difference of only 0.12 km s⁻¹ between measured and calculated velocities.

Finally, Gurney velocities were calculated using Cγ for a set of nine additional explosives for which experimental u_G data were reported in miscellaneous sources brought to our attention by a reviewer.^38–44 In some cases, a number of distinct plausible values could be found for their formation enthalpies and were used in the calculations. See ESI† for further details and references.† The overall results are summarized in Fig. 4.

Fig. 4 Comparison of predicted versus measured u_G data reported in earlier studies.^38–44 Calculations are made using formation enthalpies either suggested by the reviewer (close symbols) or presently retrieved from standard compilations^45,46 (open symbols) as detailed in ESI.†

In this Figure, the vertical lines link symbols corresponding to distinct calculations for the same material, differing only in the input value assumed for the formation enthalpy. This demonstrates the relatively moderate role of the uncertainties on formation enthalpies.

Considering only the seven explosives with formation enthalpies suggested by the reviewer (close symbols), an average relative error of 2.8% is obtained. As clear from Fig. 4, the most significant deviation is observed for DINGU/HNE/wax, a formulation based on dinitroglycoluril (DINGU) and hexanitroethane (HNE) with wax as binder. Hypothesizing that the value of −47 kJ mol⁻¹ used for this formulation was overestimated, we calculated an alternative value from the enthalpies of its individuals constituting species (see ESI†). However, no significant reduction of the discrepancy between calculation and experiment could be obtained for this formulation.

This prompted us to estimate u_G for a somewhat similar formulation reported by the same author,⁴⁴ namely NTO/HNE/wax. Two values were obtained, corresponding to the two experimental formation enthalpies of −101 and −129.4 kJ mol⁻¹ reported for NTO,⁴⁵ leading to an overestimated u_G in both cases. Interestingly, u_G is specially overestimated for the two HNE-containing formulations, with an apparent correlation between deviation from experiment and weight fraction of HNE, suggesting issues associated with the latter compound, whose structure (NO₂)₃C–C(NO₂)₃ is unique.

3.4. Cylinder wall velocities

The ability of Cγ to predict Gurney velocities with an accuracy comparable to that of numerical simulations warrants its application, along with the Gurney model (eqn (5)), to the problem of calculating cylinder wall velocities v_s. This involves an adjustment of the model parameters γ and v so as to reflect the V/V₀ values of 2.2, 3.9 and 6.2 considered in this study. The newly optimized parameters are compiled in Table 1. The corresponding results thus obtained are compiled in Table S6 (ESI†) and shown in Fig. 5a.

Fig. 5 Estimated cylinder wall velocities plotted against experimental values. Circles, squares and diamonds represent data for V/V₀ values of respectively 2.2, 3.9 and 6.2. Estimated values obtained: (a) using the Gurney and Cγ models; (b) using the correlation involving density and Gurney velocity (eqn (8)). Table 1 compiles all parameters involved. See text for further details.

As clear from this figure, two liquids stand out as outliers, namely 1,2-bis(difluoroamino)propane or 1,2-DP (blue symbols) and tetranitromethane or TNM (red symbols). The large deviations from experiment observed for these compounds are all the more puzzling as v_s is reasonably well predicted for the two other liquid compounds in the database, namely nitromethane and FEFO. In fact, notwithstanding 1,2-DP and TNM, cylinder wall velocities are reasonable well described overall, with an average relative error of about 2%. Nevertheless, a deviation from experiment close to 10% is observed for PETN.

Therefore, following ref. 12, we consider empirical alternatives to the Gurney model (eqn (5)) to estimate cylinder wall velocities. However, present analytic estimates of E_d do not allow us to reproduce the striking correlation between v_s and reported by these authors using simulated E_d data. In contrast, our best model for v_s(V/V₀) consists in a linear relationship with ρ₀·u_G, namely:

v_s(V/V₀) = (ρ₀/ρ_c)u_G + u_c (8)

where the characteristic density ρ_c and velocity u_c are model parameters that depend on the expansion ratio V/V₀ under consideration. Their values are reported in Table 1.

The v_s estimates thus obtained are compiled in Table S6 (ESI†) and plotted against experimental values in Fig. 5b. Interestingly, the measured data for 1,2-DP and TNM are satisfactorily predicted by eqn (8). The only significant outlier observed using this equation is triaminotrinitrobenzene (TATB) for which v_s is consistently overestimated (green symbols in Fig. 5b). Just like 1,2-DP, trinitrotoluene (TNT) and hexanitrostilbene (HNS), this compound is largely sub-oxygenated, with an oxygen balance (OB) below −50%. Accurately assessing the performance of such compounds has always been a challenge because they often deviate from the ideal behavior upon which the classical Chapman–Jouguet (CJ) detonation theory and most current thermochemical codes for explosive performances are based. Furthermore, TATB exhibits higher nitrogen content compared to most explosives with OB< −50%, including those in the present data set. In fact, it was recently reported that TATB soot substantially differs from other high explosives.⁴⁷ More specifically, the authors showed that recovered soot of a polymer-bonded TATB sample exhibits a nitrogen–carbon molar ratio N/C as high as 0.25, compared to 0.03 for other explosives of practical interest. They showed evidence that N-trapping in TATB soot is likely to be responsible for detonation parameters to be lower than predicted from thermochemical simulations.

In view of these complications, and given that TATB also stands out among well-studied explosives for its large porosity,⁴⁸ the fact that the EXPLO5 correlation predicts the corresponding cylinder wall velocity with good precision is quite remarkable.

4. Conclusions

Two approaches to the evaluation of explosive performances were compared regarding their abilities to predict Gurney velocity and cyclinder wall velocity (v_s) using stoichiometry, formation enthalpy and loading density as only inputs.

The first one, called EXPLO5 in this article, is based on numerical simulations of cylinder test experiments performed using the eponymous thermochemical code. The latter provides an accurate description of the expanding products and the corresponding values of the detonation energy E_d as a fonction of the expansion ratio V/V₀. The Gurney and cylinder wall velocities are then obtained from linear correlations with computed values of E_d(V/V₀ = 3) and 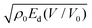, respectively.

The second one, named Cγ, relies of the detonation products as obtained on the basis of the H₂O−CO₂ arbitrary. Therefore, in contrast to EXPLO5, it cannot describe the detonation products as they expand. The prompt and terminal Gurney energies are instead calculated using simple analytic expressions derived from the assumption of a polytropic expansion of the detonation products and fitted against experiment.

Regarding the comparison of the two methods, inconsistencies in experimental data at hand do not allow us to draw definite conclusions for ammonium nitrate-based explosives. However, for metal-rich explosives, the current Cγ parameterization is clearly inappropriate and should not be used, as demonstrated by the dramatic error observed for tritonal.

This analytic model is actually focused on CHNO high explosives. However, due to the use of the H₂O−CO₂ arbitrary instead of rigorous thermochemical simulations, it can only estimate the final equilibrium composition of the products and the corresponding enthalpy, in contrast to EXPLO5 that provides such data as a function of V/V₀. This prevents the accurate determination of cylinder wall velocities through the 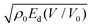correlation. In fact, an alternative linear correlation with ρ₀u_G as descriptor proves more successful when using Cγ data as input. In any case, both correlations prove more successful than application of the Gurney model (eqn (5)).

Finally, the detonation parameters calculated by thermochemical codes as a function of the expansion ratio of the products prove invaluable inputs in view of predicting Gurney and cylinder wall velocities with optimal accuracy. However, despite a more restricted scope, the Cγ model provides an equally accurate and more efficient alternative. An interactive Python script is provided as ESI† for easy application of the model. Using a similar script, Gurney velocities can be estimated at a rate of about 50 k materials per second, which is of major interest in the context of high throughput virtual screening of organic high explosives. However, the main bottleneck in the accurate prediction of detonation performances lie in the efficient evaluation of gas-phase formation enthalpies for the molecules. Indeed, although fast methods are available for this purpose, based either on additivity considerations⁴⁹ or machine learning,⁵⁰ they are still lacking in accuracy compared to high level ab initio methods for some families of compounds.^51,52

Nevertheless, even when more costly quantum chemical calculations are used to obtain the enthalpy of formation with optimum accuracy, cancelling out the Cγ advantage in terms of efficiency, there are a number of reasons why this model may be preferred over EXPLO5. First, in contrast to the many parameters required to describe the expanding products in thermochemical codes, Cγ requires just two empirical parameters to predict terminal Gurney velocity, thus avoids annoying variations in results due to different parameterizations. Secondly, being trivial to implement, Cγ may be straightforwardly integrated into any existing workflow, for instance downstream of molecule generation algorithms in the context of high-throughput virtual screening of the chemical space.

Data availability

The data supporting this article have been included as part of the ESI,† including all input data and results of present calculations and a Python script for easy application of the Cγ model to Gurney velocity prediction.

Conflicts of interest

The authors declare no potential conflict of interests.

References

1. J. Akhavan, The Chemistry of Explosives, Royal Society of Chemistry, Cambridge, UK, 2004, pp. 77–80.
2. D. Mathieu and S. Beaucamp, in Matériaux EnergétiquesTraité “Sciences Fondamentales”, Fascicule AF 6710, Paris, 2004.
3. M. Sućeska, Propellants, Explos., Pyrotech., 1999, 24, 280–285.
4. P. C. Souers, J. W. Forbes, L. E. Fried, W. M. Howard, S. Anderson, S. Dawson, P. Vitello and R. Garza, Propellants, Explos., Pyrotech., 2001, 26, 180–190.
5. M. Genetier and G. Baudin, Choc. Focus, 2017, 5, 14–15.
6. P. W. Cooper, Explosives Engineering, Wiley-VCH, New York, 1996.
7. B. M. Dobratz and P. C. Crawford, LLNL Explosives Handbook: Properties of Chemical Explosives and Explosives Simulants, UCRL-52997 Change 2, Lawrence Livermore National Laboratory, Livermore, CA, USA, 1985.
8. D. R. Hardesty and J. E. Kennedy, Combust. Flame, 1977, 28, 45.
9. M. J. Kamlet and M. Finger, Combust. Flame, 1979, 34, 213.
10. P. Locking, Proc. of the 30 th International Symposium on Ballistics, Long Beach, CA, 2017, pp. 1415–1426.
11. B. Stimac, V. Bohanek, M. Dobrilović and M. Sućeska, New Trends in Research of Energetic Materials, Pardubice, Czech Republic, 2020, pp. 693–704.
12. M. Suceska, M. Dobrilovic, V. Bohanek and B. Stimac, Z. Anorg. Allg. Chem., 2021, 647, 231–238.
13. D. Mathieu, J. Energ. Mater., 2015, 33, 102–115.
14. J.-F. Danel and L. Kazandjian, Propellants, Explos., Pyrotech., 2004, 29, 314–316.
15. M. Sućeska, Proceedings of the 32nd International Annual Conference of ICT, Karlsruhe, Germany, 2001, pp. 110/1–110/13.
16. R. Jeremić and J. Bogdanov, J. Serb. Chem. Soc., 2012, 77, 371–380.
17. L. Neron and R. Saurel, J. Comput. Phys., 2024, 513, 113165.
18. L. Wen, B. Wang, T. Yu, W. Lai, J. Shi, M. Liu and Y. Liu, Fuel, 2022, 310, 122241.
19. S. Beaucamp, D. Mathieu and V. Agafonov, Acta Crystallogr., Sect. B: Struct. Sci., 2007, 63, 277–284.
20. C. Wespiser and D. Mathieu, Propellants, Explos., Pyrotech., 2023, 48, e202200264.
21. D. Mathieu, J. Chem. Inf. Model., 2018, 58, 12–26.
22. D. Mathieu, Ind. Eng. Chem. Res., 2018, 57, 13856–13865.
23. D. Mathieu and T. Alaime, J. Phys. Chem. A, 2014, 118, 9720–9726.
24. D. Mathieu, Propellants, Explos., Pyrotech., 2020, 45, 966–973.
25. E. Theerlynck, D. Mathieu and P. Simonetti, Thermochim. Acta, 2005, 426, 123–129.
26. D. Mathieu, T. Alaime and J. Beaufrez, J. Therm. Anal. Calorim., 2017, 129, 323–337.
27. M. J. Kamlet and S. J. Jacob, J. Chem. Phys., 1968, 48, 23.
28. F. G. Bastante, M. Araújo and E. Giráldez, Phys. Chem. Chem. Phys., 2022, 24, 8189–8195.
29. B. T. Fedoroff and O. E. Sheffield, Encyclopedia of Explosives and Related Items, US Department of Army, USA, 1969.
30. E.-C. Koch, Def. Technol., 2019, 15, 467–487.
31. L. L. Davis and L. G. Hill, AIP Conf. Proc., 2002, 620, 165–168.
32. S. E. Ans, U. Nyberg, H. Arai and F. Ouchterlony, Determination of energetic characteristic of commercial explosives using the cylinder expansion test technique, Swedish Blasting Research Centre Technical Report Swebrec Report, 2005, vol. 1, p. 2005.
33. D. Frem, Def. Technol., 2020, 16, 225–231.
34. J. Sanchidrián and L. López, Propellants, Explos., Pyrotech., 2006, 31, 25–32.
35. J. P. Lu, Evaluation of the Thermochemical Code - CHEETAH 2.0 for Modelling Explosives Performance, DSTO-TR-1199, DSTO Aeronautical and Maritime Research Laboratory, 506 Lorimer St, Fishermans Bend, Victoria 3207, Australia, 2001.
36. F. Gérard and A. Hardy, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1988, 44, 1283–1287.
37. S. M. Kay, Encyclopedia of Explosives and Related Items, Vol. 10, US Army Research and Development Command (TACOM, ARDEC) Warheads, Energetics and Combat Support Center, Picatinny Arsenal, NJ, 1983.
38. P. C. Souers, B. Wu and J. L. C. Haselman, Detonation Equation of State at LLNL, Lawrence Livermore National Laboratory Technical Report UCRL-TD-119262, 1996.
39. W. A. Trzcinski, S. Cudzilo, S. Dyjak and M. Nita, Cent. Eur. J. Energ. Mater., 2014, 11, 443–455.
40. R. Lewczuk, J. Rećko and B. Florczak, Proc. of the 21st International Seminar New Trends in Research of Energetic Materials, Pardubice, Czech Republic, 2014, pp. 847–863.
41. S. Cudzilo and W. A. Trzciński, J. Energ. Mater., 2001, 19, 1–21.
42. R. Simpson, P. Pagoria, A. Mitchell and C. Coon, Propellants, Explos., Pyrotech., 1994, 19, 174–179.
43. B. C. Tappan, J. M. Budzinski, E. M. Mas, L. M. Hull, L. G. Hill, P. R. Bowden, J. P. Lichthardt, A. M. Schmalzer, M. Shorty, P. I. Miller, D. L. McDonald and M. W. Burkett, AIP Conf. Proc., 2020, 2272, 050031–050030-4.
44. H.-H. Licht, Propellants, Explos., Pyrotech., 2000, 25, 126–132.
45. NIST Chemistry WebBook, NIST Standard Reference Database Number 69, ed. P. J. Linstrom and W. G. Mallard, National Institute of Standard and Technology, Gaithersburg, MD, 2011, https://webbook.nist.gov.
46. M. A. Suntsova and O. V. Dorofeeva, J. Chem. Eng. Data, 1963, 59, 2813–2826.
47. J. G. Christenson, L. E. Fried, S. Bastea, M. H. Nielsen, T. M. Willey and M. Bagge-Hansen, J. Appl. Phys., 2022, 132, 095901.
48. B. Dai, W.-b Zhang, L.-g Lan and Y. Tian, Propellants, Explos., Pyrotech., 2015, 40, 688–698.
49. D. Mathieu, J. Chem. Inf. Model., 2018, 58, 12–26.
50. G. Yang, W. Y. Chiu, J. Wu, Y. Zhou, S. Chen, W. Zhou, J. Fan and G. Chen, J. Phys. Chem. A, 2022, 126, 6295–6300.
51. M. J. Cawkwell, A. C. Burch, S. R. Ferreira, N. Lease and V. W. Manner, J. Chem. Inf. Model., 2021, 61, 3337–3347.
52. D. Mathieu, Mol. Inf., 2022, 41, 2100064.

---

Footnote

† Electronic supplementary information (ESI) available: PDF file with discussion of dubious experimental data and in-depth validation of the Cγ model, including Tables S1–S3; Excel file compiling Gurney energies (Table S4), relevant material properties (Table S5) and cylinder wall velocities (Table S6); Python script for quick and easy application of the Cγ model. This supporting information may be found in the online version of the article at the publisher's website. See DOI: https://doi.org/10.1039/d5cp00761e

---