Open Access Article
Open Access ArticleSelf-propulsion of liquid droplet assemblies controlled by the functionalities of their components†
Rony
Mallick
a,
Chiho
Watanabe
 b and
Shinpei
Tanaka
b and
Shinpei
Tanaka
 *a
*a
aGraduate School of Advanced Science and Engineering, Hiroshima University, 1-7-1 Kagamiyama, Higashi-Hiroshima 739-8521, Japan. E-mail: shinpei@hiroshima-u.ac.jp
bGraduate School of Integrated Sciences for life, Hiroshima University, 1-7-1 Kagamiyama, Higashi-Hiroshima 739-8521, Japan
First published on 3rd April 2025
Abstract
The self-propulsion of droplet assemblies consisting of droplets of 1-decanol and either an ethyl salicylate (ES) or a composite droplet of ES and liquid polydimethylsiloxane (PDMS) is reported. The ES-PDMS composite droplets have an ES core covered by a PDMS layer that stabilizes the assembly significantly. Their self-propulsion exhibits characteristic predator–prey behavior, with a decanol droplet closely chasing the ES or ES-PDMS composite droplet, forming a bound droplet pair. Furthermore, the stability that PDMS gives the system enables us to construct more complex assemblies, such as two, three, and four decanol droplets closely chasing an ES-PDMS droplet, whose motion patterns depend strongly on the symmetry in the structure of the assemblies. Our findings demonstrate that long-lived assemblies composed of droplets with distinct functionalities can serve as a versatile platform for developing self-organizing and adaptive droplet systems, functioning as “droplet robots”.
1 Introduction
Active matter is a type of matter that can convert thermal or environmental energy into motion by autonomously breaking symmetry while consuming free energy.1 The free energy can be derived from processes such as the dissolution of substances into the environment2 or the catalytic chemical reactions.3 There are many types of active matter, such as colloidal Janus particles, which can swim in water due to their built-in polarization or head–tail asymmetry.3–5 Another example is so-called active emulsions,6,7 that can spontaneously create the head–tail asymmetry through their motion. Thus, the head–tail asymmetry is crucial for self-propulsion.Among active matter systems, those composed of liquid droplets exhibit unique and characteristic properties that distinguish them from their solid counterparts. They can not only self-propel,8–13 but also deform in response to external forces and environmental changes.14 They can produce surfactant15 or split and merge15–18 driven by factors like energy input or interactions with their surroundings. They also exhibit dynamic structures formed by the collective behavior of multiple droplets.12,19 They tend to exhibit stronger or longer-lasting self-propulsion.19 Furthermore, liquid droplets are easy to manipulate, observe, and modify. A drawback of active droplets is that they typically lack an internal structure to define their direction of motion, unlike solid systems with head–tail asymmetry such as Janus colloids.
Due to their versatility, active droplets have been used as models for living systems1,20 and are sometimes referred to as wet artificial life.21,22 They are also considered soft robots,23,24 known as “droplet robots”. These robots can sense their environment through chemotaxis25 and respond to external stimuli.26,27
In studies of droplet robots, the focus is often limited to droplets composed of a single component, lacking any internal structures.26 As a result, there have been relatively few attempts to investigate the potential for developing new functionalities through the combination or interaction of multiple droplets. However, this approach to droplet robot design, which emphasizes assemblies of different droplets having different internal structures and functionalities, aligns with a fundamental design principle observed in both living organisms and artificial engineering systems, where complexity and functionality arise from the integration and coordination of simpler components. Exploring such combinations could open new pathways for innovative applications and enhanced capabilities in droplet-based systems.
The simplest combination design involves pairing two types of droplets, which have been shown to exhibit enhanced propulsion.28–31 Such paired motion is described as the “predator–prey” mode of motion,20 where one droplet actively chases the other, while the other moves away. This mode of motion is particularly significant for droplet robots, as it naturally gives the system a head–tail asymmetry, and effectively rectifies energy dissipation, leading to more efficient propulsion and potentially enhancing the functionality and energy economy of droplet-based robotic systems.
Recently, we discovered31 that a combination of a droplet of 1-decanol and a droplet of liquid paraffin can exhibit the predator–prey mode of motion. We attributed this behavior to a source–sink relationship between the two droplets: the decanol droplet acts as a source of surfactant (1-decanol), while the paraffin droplet serves as a sink. This interaction generates a surface tension gradient on the water surface, directed from the source to the sink, which drives the propulsion of the droplets. This mechanism highlights the intricate interplay of chemical and physical processes underlying the predator–prey dynamics in droplet systems.
In this study, based on the previous study, we first explore alternative chemicals as sinks to construct more dynamic and active pairs of predator–prey droplets. Then we propose that ethyl salicylate (ES) is an optimal candidate for a sink droplet. We conduct numerical simulations to study how the source–sink relation creates and drives the paired droplets. Next, we introduce a third component, liquid polydimethylsiloxane (PDMS), which forms a protective layer around the sink droplet, significantly enhancing the system's stability. Furthermore, we will demonstrate that the long-term stability PDMS gives the system allows us to develop complex active assemblies of multiple droplets. They serve as proof-of-concept examples of droplet robots. The functionality of these multi-droplet robots is highly dependent on the number of droplets and their spatial configurations. We propose that the droplet assemblies consisting of different types of droplets and composite droplets as new design and control principles of droplet-based robots.
2 Methods
2.1 Material
1-Decanol, ethyl salicylate (ES), and Oil Orange SS were purchased from Tokyo Chemical Industry Co., Ltd (Tokyo, Japan). Liquid polydimethylsiloxane (PDMS, viscosity 20 cSt) was purchased from Sigma-Aldrich Japan (Tokyo, Japan). Oil Red O and Sudan Black B were purchased from Nacalai Tesque (Kyoto, Japan). Materials were used without further purification. Deionized water (18.2 MΩ cm) was produced with a Milli-Q water purification system (Merck Millipore Corp, Tokyo, Japan). For visualization, droplets were dyed: decanol droplets with Sudan Black B, ES droplets with Oil Red O, and PDMS with Oil Orange SS. The concentration of the dyes was 0.05 wt%.2.2 Experiments
The setup for the visual observation was published elsewhere.31 Briefly, droplet motion was captured using a high-speed CMOS camera (Baumer VCXU-04C, Frauenfeld, Switzerland), recording time-stamped images at a resolution of 720 × 540 pixels with a frame rate of 10 Hz. Both the camera and the Petri dish were placed in an insulation box whose inner temperature was controlled with a heater at 25 ± 0.5 °C in a room at about 24 °C controlled by air conditioners. The droplets were detected using their color, and their positions were extracted as a function of time. The velocity was calculated from the difference in the position averaged over 1 s.A typical experimental procedure is as follows. A Petri dish of 90 mm in inner diameter was filled with 30 ml Milli-Q water. The depth of water was about 5 mm. First, a 10 μl decanol droplet was placed on the water surface. Decanol droplets need to be placed first to stabilize the water surface because ES does not form droplets on the surface of pure water. Then the required amount of PDMS for each experiment was added as several small droplets. Finally, a 10 μl ES droplet was placed. The Petri dish was then covered by a glass lid without tight sealing. The lid was about 5 mm above the water surface. The elapsed time, t, was measured from the moment when the lid was placed on the dish.
2.3 Model
To understand the mechanism of propulsion, we use a simple model to reproduce the experimental results by considering one-dimensional surface to which source and sink particles are stuck. Their position is modeled by a particle phase field, p1 for the source particle at x1 and p2 for the sink particle at x2, as | (1) |
 | (2) |
Let c1(x, t) be the concentration field of surface active molecules supplied by the source particle and c2(x, t) be the concentration field of the sink particle. Both c1 and c2 are assumed to cover the surface above the particles too. We assume that c2(x, t) does not diffuse and is proportional to p2(x, t), whereas c1(x, t) obeys the diffusion–reaction equation,
 | (3) |
The particles' motion is coupled with the concentration field through the equation of motion,
 | (4) |
 | (5) |
After non-dimensionalization, the above equations are simplified as
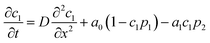 | (6) |
| c = c1 + c2 = c1 + p2 | (7) |
 | (8) |
 | (9) |
We use the system size, L ∼ 0.1 m and the mass of a particle, m ∼ 10−5 kg as the unit of length and mass in the simulation. The unit of time, t ∼ 1 s, was chosen so that ζt/m ≃ 1, where ζ ∼Aη/d with A being the area of a particle, η the viscosity of water, and d the depth of the system. The concentration is normalized by cs. The diffusion coefficient of surface molecules has been measured as D ≃ 10−9 m2 s−1.33 We used, however, the value 103 times larger than this value as the effective diffusion coefficient to include the effect of surface flow.34–37 The non-dimensionalized diffusion coefficient thus we used was D = 10−4. a2 was fixed at 0.1, which corresponds about 10−7 N when there is a concentration drop as large as cs. We used the forward-time centered-space method for the reaction–diffusion equation, and the fourth-order Runge–Kutta method for the equation of motion. The mesh size was x = 10−3, and the time step was determined by dt = (dx)2/(8D) ≃ 0.00124.
3 Results and discussion
3.1 Predetor–prey mode of motion
First, we confirmed that a droplet of 1-decanol exhibited random motion when it was placed on the surface alone31 (see Fig. S1 in ESI†). It is propelled by the surface tension field created by the spread of 1-decanol molecules around it. The average speed of the droplet was 0.5 mm s−1 for the first 10 min and less than 0.1 mm s−1 for the entire duration of propulsion for 5 hours. The droplet went to the glass wall and stuck to it when the droplet lost the propulsion.Then, we tested several organic solvents listed in Table 1 as potential sink droplets for absorbing 1-decanol spreading from a decanol droplet. We found that a decanol droplet chased a droplet of all organic solvents tested. Moreover, all of them except diethyl phthalate form a predator–prey pair where a decanol droplet chases closely a droplet of the organic solvent listed in Table 1. A diethyl phthalate droplet merged with a decanol droplet before forming the pair.
| Classification | Organic solvent | T (h) | v (mm s−1) |
|---|---|---|---|
| Hydrocarbon mixture | Liquid paraffin | 10 | 0.1 |
| n-Alkane | Tridecane | 7 | 0.2 |
| Tetradecane | 9 | 0.2 | |
| Diester | Diethyl phthalate | <1 | 0.6 |
| Monocarboxylic acid | Benzyl acetate | 4 | 0.2 |
| Alkyl salicylate | Methyl salicylate | <1 | 1 |
| Ethyl salicylate | <1 | 4 | |
| Butyl salicylate | <1 | 2 |
Table 1 lists their characteristic quantities, the duration of propulsion, T and the average speed of the droplets, v. All the droplets exhibited a propulsion speed roughly similar to that of a solitary decanol droplet on the surface, except for alkyl salicylates, which showed significantly higher speeds, particularly ethyl salicylate (ES). On the other hand, the propulsion duration was shorter for alkyl salicylates compared to other organic solvents, whose droplets formed a predator–prey pair.
Considering the purpose of designing droplet robots, we chose ES in this study for its high activity to further test its ability of structuring and self-propulsion with decanol droplets.
3.2 Propulsion of decanol and ES droplets as a bound droplet pair
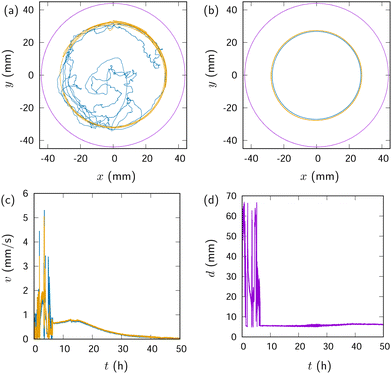
We confirmed that no propulsion was observed when a droplet of ES alone was placed on the surface of water slightly contaminated by 1-decanol. Without first contaminating the surface of water, ES could not form a droplet.When an ES droplet was placed on the surface after a decanol droplet, the decanol droplet started chasing the ES droplet. Then after an induction period of about 15 min (900 s) as shown in Fig. 1, they formed a predator–prey pair in which their surface-to-surface distance was less than 0.5 mm (see mov1 in ESI†). We refer to a predator–prey pair with a separation much smaller than their radius as a bound droplet pair hereafter.
Fig. 2(a) shows the trajectories of the two droplets before they form a bound droplet pair. The ES droplet tended to be pushed towards the dish wall while the decanol droplet was moving randomly [Fig. 2(a)]. Then as shown in Fig. 2(b), they formed a bound droplet pair and started moving along the glass wall.
Once the bound droplet pair formed, their propulsion became more directed and enhanced, as shown in Fig. 2(c). The speed increased and then stabilized at an almost constant value after the bound droplet pair was established. The pair formation was also seen in the sudden drop in their center-to-center distance shown in Fig. 2(d).
This bound droplet pair is an essential starting structure for designing our droplet robot. Because of the pair formation, the radial symmetry of the propulsion direction is broken to be unidirectional and thus the propulsion is enhanced as seen in Fig. 1. In the sense that it possesses a polarized, head–tail structure, the pair can be considered a bilaterian – a design adopted by most animals as their body plan, likely due to its efficiency in movement.38 In this structure, the decanol droplet functions as the engine, while the ES droplet serves as the steering component, as the pair is propelled by a surface tension gradient generated by the decanol droplet and rectified by the ES droplet.
3.3 Numerical modeling for the predator–prey mode of motion
We found that the predator–prey mode of motion appears in a variety of organic solvents as a sink (Table 1), at least in a certain stage during its decaying process. This is likely because the surface active 1-decanol molecules spreading from a source, a decanol droplet, are miscible with organic solvents examined. This source–sink relation creates a steady flow of surface active molecules, which stabilizes the surface tension gradient. This gradient can first induce the bound droplet pair formation and then propel the pair. To test the above scenario, we model the system using the diffusion–reaction equation [eqn (6)] coupled with the equation of motion of the two droplets [eqn (8) and (9)].Fig. 3 shows the concentration profile c(x, t) created by the presence of both the source particle, p1(x, t), and the sink particle, p2(x, t), when the two particles are placed on the initially clean surface. At first [Fig. 3(a)], the surfactants spread from the source particle symmetrically. Then the symmetry is broken by the presence of the sink particle [Fig. 3(b)]. Due to the asymmetric concentration distribution, the source particle starts moving towards the sink particle. Thus there is an effective attraction between the source and sink particles. The source particle is attracted by the sink particle until the concentration field of the sink particle itself repels the source particle. As a result, they form a closely bound and aligned pair [Fig. 3(c)] spontaneously. Furthermore, they move together as a pair because the concentration in front of the pair is lower than that in the back position (see mov2 in ESI†).
Even after the surface is mostly saturated, the concentration difference between the front and back is maintained [Fig. 3(d)] by the action of the source and sink. As a result, the source–sink pair moves in the direction of the sink particle steadily. Thus the experimental findings, the spontaneous pair formation and its stable propulsion, are well reproduced by this simple reaction–diffusion model.
3.4 Propulsion of decanol and ES-PDMS droplets as a bound droplet pair
A bound droplet pair of decanol and ES droplets exhibits high activity with a strong connection between them. This is a promising capability as a candidate for droplet robots. However, the stability of the pair is not satisfactory. As shown in Fig. 1(c) and (d), the two droplets merged at about 20 min after they formed a pair. The merged droplet quickly lost activity and stopped. Such short-lived activity limits the potential applications of droplet robots.To stabilize the pair, we need to prevent the direct contact between its components. Once the two droplets make a direct contact, it is known that the two droplets start merging through the formation of a “neck” structure.13 To prevent this, we introduced a third component: a protective membrane around an ES droplet.
The membrane material must be immiscible with water, ES, and 1-decanol. We found that liquid polydimethylsiloxane (PDMS) possesses this property, likely due to its silicon backbone. PDMS also meets the requirement for the spontaneous membrane formation around the ES droplets as shown in Fig. 4.
Fig. 4(a) shows droplets of 1-decanol, ES, and PDMS immediately after being placed on the water surface, while Fig. 4(b) illustrates how the ES droplet spontaneously and preferentially engulfed by the PDMS droplet, forming an ES-PDMS composite droplet. In the ES-PDMS droplet, the ES and PDMS phases were separated by a clear boundary due to their immiscibility as shown in Fig. 5(a). Furthermore, the ES phase settled down at the bottom of the droplet because the density of ES (1.13 g ml−1) is higher than that of PDMS (0.97 g ml−1), causing PDMS to form a top layer [Fig. 5(b)]. We observed that the PDMS layer, acting as a protective cap, significantly enhanced the system's stability as shown in Fig. 6 and 7.
After the ES-PDMS droplet was formed, the decanol droplet moved erratically and the ES-PDMS droplet always moved away from it, preventing the pair formation [Fig. 4(c) and 6(a)]. It took several hours before they formed a bound droplet pair. Fig. 4(c)–(f) shows how a decanol droplet started chasing the ES-PDMS droplet.
After the formation of the bound droplet pair as shown in Fig. 4(f), they moved along the dish wall stably for more than two days (see mov3 in ESI†). During this circular motion, the decanol droplet always chased the ES-PDMS droplet [Fig. 4(f)], similar to the behavior observed between the decanol and ES droplets shown in Fig. 1(d)–(f). Notably, unlike the pair shown in Fig. 1, the decanol droplet was not deformed [Fig. 4(f)].
Fig. 6 shows the trajectories of the decanol and the ES-PDMS droplets shown in Fig. 4. For the first approximately 6.5 hours, no stable bound droplet pair was observed [Fig. 6(a)]. In this process, the ES-PDMS droplet remained primarily on a circular path. At t ≃ 6.5 h, they formed a bound droplet pair that began moving on a circular trajectory along the wall [Fig. 6(b)].
Fig. 6(c) shows the speed of both droplets shown in Fig. 4. After significant fluctuations, the speed stabilized at t ≃ 6.5 h, coinciding with the formation of a bound droplet pair and the initiation of stable circular motion. The speed continued to increase slightly for several hours, reaching a maximum of approximately v ∼ 1 mm s−1 around t ∼ 15 h. Then it started decreasing. This behavior is qualitatively the same as observed in the system without PDMS [Fig. 2]. Though the maximum speed of the pair is lower than that of the decanol-ES pair, about 7 mm s−1, it is still higher than the speed found in organic solvents other than alkyl salicylates listed in Table 1.
The bound droplet pair between decanol and ES-PDMS droplet shown in Fig. 4(f) could propel themselves for more than two days [Fig. 6(c)]. This is more than two orders of magnitude longer than the duration of the decanol-ES pair, about 20 min, shown in Fig. 2. This enhanced duration stands out from any of the durations listed in Table 1.
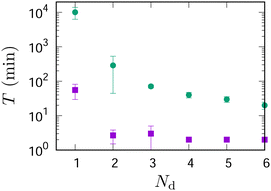
3.5 Stability endowed by PDMS
Fig. 7 shows the duration, T, of self-propulsion as a function of the PDMS volume, VPDMS, added to the system. It was measured as an indicator of the system's stability, defined as the duration for which two droplets could self-propel before being disrupted by merging or adhesion to a glass wall.Without PDMS (VPDMS = 0 μl), the decanol and ES droplets merged typically within an hour. However, as shown in Fig. 2, adding only 10 μl PDMS increased T by more than 200 times compared to the case without PDMS. The duration T did not depend significantly on VPDMS when VPDMS ≳ 10 μl as shown in the inset of Fig. 7.
Fig. 8(a) shows how the speed, v, of the bound droplet pair was affected by the volume of the PDMS layer in experiments. On the other hand, Fig. 8(b) shows the dependence of v on the reciprocal of the dissolution rate 1/a1 in the numerical simulation. There is a qualitative agreement between the results from the experiments and those from the numerical simulations: the speed decreased as VPDMS or 1/a1 increased. This agreement suggests again that our numerical model is qualitatively reproducing the experimental results.
The decrease in v observed in both experiments and numerical simulations was not large, within roughly an order of magnitude. This stands in stark contrast to the case of the duration T (Fig. 7), where even a slight increase in VPDMS led to a change of more than two orders of magnitude. These results suggest that the stability provided by PDMS is not correlated with the speed of the bound droplet pair. In other words, the decrease in speed, thus the decrease in surface tension gradient, does not directly explain the mechanism behind the increase in stability.
The precise mechanism by which the PDMS layer prevents droplet merging, thereby increasing the stability of the bound droplet pair, remains unclear. However, based on the observation that a decanol droplet was neither attracted to nor merged with a pure PDMS droplet, it is likely that the PDMS layer surrounding an ES-PDMS droplet acts as a protective barrier, preventing direct contact between the decanol droplet and the ES core. Without first forming a narrow “neck” between the two droplets, the merge does not take place.13
3.6 Droplet robots: multiple decanol droplets
It is known that droplets can exhibit complex dynamic ordering collectively when multiple droplets coexist on the surface of water.12,19 A multiple droplet system is also of interest in terms of multicellularity, that is, a functional entity composed of multiple units.The bound droplet pair of decanol and ES-PDMS droplets, discussed in previous sections, can be viewed as a “droplet robot” – a system composed of and powered by droplets – that is capable of unidirectional motion [Fig. 6(b)]. This property is realized only when these two droplets form a bound droplet pair; when they are alone, they move only randomly.
The directionality of motion comes from the broken symmetry in the pair: it has a front-back asymmetry that gives the axis of motion. In biology, most animals exhibit this symmetry, called bilateral symmetry, and are called bilaterians.38,39 In contrast, animals without this symmetry, such as starfish, are categorized as radially symmetrical and are referred to as radiates or non-bilaterians. The bilaterian body design is ubiquitous not only among animals but also in engineering vehicles, highlighting its efficiency for motion. In bilaterians, separating the driving component from the steering component minimizes functional conflicts, enabling smoother and more coordinated movement.
In the bound droplet pairs shown in this study, the bilateral symmetry in their structure rectifies the flow of surfactants thus creates effectively the surface tension gradient around the pair. Moreover, the steering takes place by tilting its axis against its propulsion direction, which is achieved easily because the joint between the two droplets is flexible. In short, the pair has an engine (the decanol droplet) connected to a steering body (the ES or ES-PDMS droplet).
The stability provided by the ES-PDMS droplet plays a crucial role in studying the behavior of droplet robots composed of multiple droplets. On top of the bound droplet pairs shown above, we here show proof-of-concept examples of the droplet robots, consisting Nd decanol droplets and an ES-PDMS droplet.
Fig. 9 shows the duration of propulsion for a system of droplets with and without PDMS. Without PDMS, decanol droplets were absorbed by an ES droplet quickly; the duration that a system could maintain multiple droplets was less than 5 minutes at most when there were more than a decanol droplet. By adding 10 μl of PDMS to the ES droplet, on the other hand, the duration was increased by roughly 10–50 times. This increased stability allows us to observe motion patterns of the droplet robots. We found that the motion patterns depended strongly on the number of decanol droplets, Nd, in a robot.
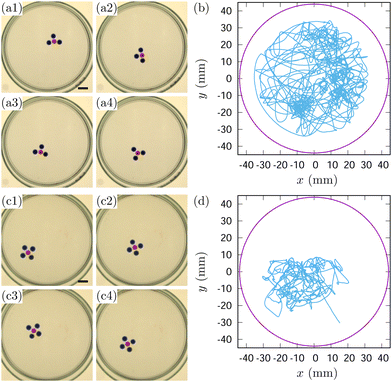
The unidirectional motion of a robot of Nd = 1 was already shown in Fig. 4 and 6. Fig. 10 shows a robot with two decanol droplets (Nd = 2, see also mov4 in ESI†). This robot has two decanol droplets acting as engines connected through an ES-PDMS droplet. Interestingly, it still maintains a propulsion axis and moves unidirectionally along it [Fig. 10(a) and (c)]. The head–tail asymmetry arises from its motion; as long as it remains in motion, the ES-PDMS droplet always leads the decanol droplets. Thus, the robot with Nd = 2 can be considered as a bilaterian.
We found two modes of motion for a Nd = 2 robot: back-and-forth motion [Fig. 10(a) and (b)] and circular motion [Fig. 10(c) and (d)]. Both motions were essentially unidirectional. The back-and-forth motion was observed when the robot was active and maintained its symmetric axis parallel to the direction of motion [Fig. 10(a) and (b)]. The reflection on the wall caused the back-and-forth motion pattern; though the reflection turned the robot's back to the new front, it maintained the front-back asymmetry after the reflection.
On the other hand, circular motion emerged when the robot's propulsion weakened approximately 5 hours after the experiment began. The robot's axis of symmetry tilted against the direction of motion so that it could move along the glass wall [Fig. 10(c) and (d)].
Self-propelled particles, including solids, liquids, and even bacteria, have been reported to exhibit a tendency to move along walls.40 The behavior can be explained, for example, a coupling between the direction of propulsion and the velocity.41–44 When a self-propelled particle is confined within a harmonic potential or a circular boundary, its motion is governed by the relaxation time required for alignment between its velocity and propulsion force.42 The reflection from walls causes a slight shift in the particle's motion along the boundary, ultimately resulting in the particle moving persistently along the wall. A notable exception occurs when the propulsion force weakens near the wall, preventing the motion along the wall.11 There the repulsion from the wall can induce a rectilinear back-and-forth motion when the relaxation time is small enough [Fig. 10(b)].
Fig. 11 show the case when Nd = 3 and Nd = 4 (see mov5 and mov6 in ESI†). Compared to the Nd = 1 and Nd = 2 robots shown above, their motion pattern was random. We argue that the robots shown in Fig. 11(a) and (c) are radiates rather than bilaterians, as they have difficulty establishing front-back asymmetry even while in motion. The lack of a structural uniaxis prevents them from exhibiting unidirectional motion. Therefore, like a starfish, it can move in any direction. (Interestingly, despite their radial body plan, certain starfishes become bilaterians when they move by deforming their bodies.45) The propulsion in multiple directions, however, creates conflicting forces, resulting in random motion.
An ES-PDMS droplet could accommodate four decanol droplets at most under the conditions used. When Nd > 4, the rest of Nd − 4 droplets were inactive, and could not participate in the robot (see mov7 and mov8 in ESI†).
4 Conclusions
We reported here the impact of liquid polydimethylsiloxane (PDMS) on the self-propulsion of a droplet system capable of exhibiting predator–prey behavior: a system where a droplet of 1-decanol chases a droplet of ethyl salicylate (ES). PDMS, when added to the system, always engulfs the ES droplet to form an ES-PDMS composite droplet where an ES core is covered by a layer of PDMS. Although PDMS itself is inert, it acts as a protective layer and significantly stabilizes the self-propulsion, increasing its duration by nearly a factor of 200. We also demonstrated that the increased stability given by PDMS enables the observation of complex dynamic structures formed by multiple droplets.Our numerical modeling suggested that the origin of the self-propulsion observed in the systems is 1-decanol molecules spreading on the surface of the water from a decanol droplet and absorbed by an ES droplet. The two droplets form a source–sink pair. The distribution of 1-decanol molecules on the surface creates a surface tension gradient such that it creates the effective attraction between the decanol and ES droplets as well as propulsion of the pair.
We found that a bound droplet pair of decanol and ES or decanol and ES-PDMS droplets moves unidirectionally, whereas independent droplets move randomly. Thus, it can be considered as a droplet “robot” with the front-back asymmetry where the decanol droplet acts as an engine and the ES or ES-PDMS droplet acts as a steering part.
Furthermore, we showed the behavior of droplet robots with more than one decanol droplets around an ES-PDMS composite droplet. We found that one and two decanol droplets make the robots “bilaterian” that move unidirectionally along their structural axis. The axis is fixed in their structure for the case of one decanol droplet, while it is created by the motion for the case of two decanol droplets. Three and four decanol droplets, on the other hand, make the robots “radiates” that move randomly due to their multiple structural axes of symmetry.
The difference between bilaterians and radiates plays a significant role in applications. For applications requiring directional motion, such as targeted delivery, bilaterians may be preferred. Conversely, when a diffusive motion pattern is essential, such as for inspection or dispersion, radiates may be more effective. Our study demonstrates that both motion modes can be tailored by adjusting the symmetry of the droplet robots.
Our results revealed the valuable protective properties of PDMS in a droplet system. Building on this finding, we demonstrated a proof-of-concept for droplet robots composed of multiple and composite droplets. This concept is reminiscent of the basic strategy to design and construct a robot or seen in the evolution of living organisms, where functions are carried out as combinations of multiple constituents. Many aspects of the composite droplets remain to be elucidated, such as what other functions can be incorporated, or what dynamic structures might emerge collectively from multiple coexisting composite droplets.
Author contributions
RM designed and conceived this study. RM also collected data. RM, CW and ST analyzed and interpreted the results and drafted the manuscript. All authors read and approved the final manuscript.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by JSPS KAKENHI Grant Number 20K03881.References
- M. J. Bowick, N. Fakhri, M. C. Marchetti and S. Ramaswamy, Phys. Rev. X, 2022, 12, 010501 CAS.
- M. Chaigne, M. Berhanu and A. Kudrolli, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2301947120 CrossRef CAS PubMed.
- S. J. Ebbens and D. A. Gregory, Acc. Chem. Res., 2018, 51, 1931–1939 CrossRef CAS PubMed.
- S. Samin and R. van Roji, Phys. Rev. Lett., 2015, 115, 188305 CrossRef PubMed.
- S. Auschra, A. Bregulla, K. Kroy and F. Cichos, Eur. Phys. J. E: Soft Matter Biol. Phys., 2021, 44, 90 CrossRef CAS PubMed.
- S. Herminghaus, C. C. Maass, C. Krüger, S. Thutupalli, L. Goehring and C. Bahr, Soft Matter, 2014, 10, 7008–7022 RSC.
- C. C. Maass, C. Krüger, S. Herminghaus and C. Bahr, Annu. Rev. Condens. Matter Phys., 2016, 7, 171–193 CrossRef CAS.
- K. Nagai, Y. Sumino, H. Kitahata and K. Yoshikawa, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 065301(R) CrossRef PubMed.
- Y.-J. Chen, Y. Nagamine and K. Yoshikawa, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 016303 CrossRef PubMed.
- V. Pimienta and C. Antoine, Curr. Opin. Colloid Interface Sci., 2014, 19, 290–299 CrossRef CAS.
- S. Tanaka, Y. Sogabe and S. Nakata, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 032406 CrossRef PubMed.
- J. Čejková, K. Schwarzenberger, K. Eckert and S. Tanaka, Colloids Surf., A, 2019, 566, 141–147 CrossRef.
- P. N. Panday, A. Bandopadhyay and P. K. Das, Eur. Phys. J.-Spec. Top., 2022, 232, 735–768 CrossRef.
- J. Čejková, F. Štěpánek and M. M. Hanczyc, Langmuir, 2016, 32, 4800–4805 CrossRef PubMed.
- Y. Nagasaka, S. Tanaka, T. Nehira and T. Amimoto, Soft Matter, 2017, 13, 6450–6457 RSC.
- F. Caschera, S. Rasmussen and M. M. Hanczyc, ChemPlusChem, 2013, 78, 52–54 CrossRef CAS.
- M. Matsuo, H. Hashishita, S. Tanaka and S. Nakata, Langmuir, 2023, 39, 2073–2079 CrossRef CAS PubMed.
- Y. Sumino, R. Yamashita, K. Miyaji, H. Ishikawa, M. Otani, D. Yamamoto, E. Okita, Y. Okamoto, M. P. Krafft, K. Yoshikawa and A. Shioi, Sci. Rep., 2023, 13, 123777 Search PubMed.
- S. Tanaka, S. Nakata and T. Kano, J. Phys. Soc. Jpn., 2017, 86, 101004 CrossRef.
- C. L. A. Berli and M. G. Bellino, Biomicrofluidics, 2023, 17, 021302 CrossRef CAS PubMed.
- M. M. Hanczyc, Life, 2014, 4, 1038–1049 CrossRef PubMed.
- C. Gershenson, Artif. Life, 2023, 29, 153–167 CrossRef PubMed.
- J. Čejková, T. Banno, M. M. Hanczyc and F. Štěpánek, Artif. Life, 2017, 23, 528–549 CrossRef PubMed.
- L. Zheng, S. Handschuh-Wang, Z. Ye and B. Wang, Appl. Mater. Today, 2022, 27, 101423 CrossRef.
- I. Lagzi, S. Soh, P. J. Wesson, K. P. Browne and B. A. Grzybowski, J. Am. Chem. Soc., 2010, 132, 1198–1199 CrossRef CAS PubMed.
- X. Fan, X. Dong, A. C. Karacakol, H. Xie and M. Sitti, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 27916–27926 CrossRef CAS PubMed.
- R. Zhang, C. Zhang, X. Fan, C. C. K. A. Yeung, H. Li, H. Lin and H. C. Shum, Nat. Commun., 2024, 15, 6220 CrossRef CAS PubMed.
- N. J. Cira, A. Benusiglio and M. Prakash, Nature, 2015, 519, 446–450 CrossRef CAS PubMed.
- C. H. Meredith, P. G. Moerman, J. Groenewold, Y.-J. Chiu, W. K. Kegel, A. van Blaaderen and L. D. Zarzar, Nat. Chem., 2020, 12, 1136–1142 CrossRef CAS PubMed.
- C. H. Meredith, A. C. Castonguay, Y.-J. Chiu, A. M. Brooks, P. G. Moerman, P. Torab, P. K. Wong, A. Sen, D. Velegol and L. D. Zarzar, Matter, 2022, 5, 616–633 CrossRef CAS.
- C. Watanabe, S. Tanaka, R. J. Löffler, M. M. Hanczyc and J. Górecki, Soft Matter, 2022, 18, 6465–6474 RSC.
- H. Tanaka and T. Araki, Phys. Rev. Lett., 2000, 85, 1338 CrossRef CAS PubMed.
- Z. Cao, D. Wang, K. Koynov and H.-J. Butt, Colloid Polym. Sci., 2014, 292, 1817–1823 CrossRef CAS.
- T. Bickel, A. Majee and A. Würger, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 012301 CrossRef PubMed.
- N. J. Suematsu, T. Sasaki, S. Nakata and H. Kitahata, Langmuir, 2014, 30, 8101–8108 CrossRef CAS PubMed.
- H. Kitahata and N. Yoshinaga, J. Chem. Phys., 2018, 148, 134906 CrossRef PubMed.
- S. Tanaka, S. Nakata and M. Nagayama, Soft Matter, 2021, 388–396 RSC.
- G. Holló and M. Novák, Biol. Direct, 2012, 7, 22 CrossRef PubMed.
- M. Q. Martindale, J. R. Finnerty and J. Q. Henry, Mol. Phylogenet. Evol., 2002, 24, 358–365 CrossRef PubMed.
- P. Galajda, J. Keymer, P. Chaikin and R. Austin, J. Bacteriol., 2007, 189, 8704–8707 CrossRef CAS PubMed.
- N. Shimoyama, K. Sugawara, T. Mizuguchi, Y. Hayakawa and M. Sano, Phys. Rev. Lett., 1996, 76, 3870–3873 CrossRef CAS PubMed.
- O. Dauchot and V. Démery, Phys. Rev. Lett., 2019, 122, 068002 CrossRef CAS PubMed.
- G. Du, F. Ye and R. Podgornik, EPL, 2021, 136, 58003 CrossRef CAS.
- G. Du, F. Ye and R. Podgornik, Phys. Rev. Res., 2022, 4, L042010 CrossRef CAS.
- H. C. Astley, J. Exp. Biol., 2012, 215, 1923–1929 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp00597c |
| This journal is © the Owner Societies 2025 |